Research on Vibration Measurement and Analysis Technology of Circuit Breaker Based on VMD and LSTM

Abstract

In this paper, we propose a mechanical fault diagnosis technology for circuit breakers based on the NGO-VMD, aiming to improve the accuracy and efficiency of fault diagnosis. The circuit breaker is a key protection device in power systems, and its operational status is crucial to grid security. This paper introduces the NGO-VMD method to decompose its vibration signals, aiming to improve the accuracy and efficiency of fault diagnosis. Failure to detect and address mechanical faults in circuit breakers can lead to equipment damage, power outages, and even personal injury. Therefore, it is of great significance to develop efficient and accurate mechanical fault diagnosis technology for after converting the mechanical fault signal of the vacuum circuit breaker in the distribution network into the IMF form, the modal information of the vibration signal under different faults of the circuit breaker is effectively extracted, and the singular value decomposition of the IMF signal component is carried out to make the information characteristics contained more obvious, Finally, LSTM is used to achieve precise identification of circuit breaker faults. In this paper, the experimental test is carried out on the basis of the actual vacuum circuit breaker in the distribution network, and the feasibility of the design scheme is verified by comprehensive analysis. The comparison and analysis with other methods can be obtained, and the scheme has the advantages of higher efficiency, stronger stability and more accuracy.

1. Introduction

In the distribution network, high-voltage circuit breakers shoulder the crucial task of interrupting the system. Once a mechanical failure occurs in a circuit breaker, it is highly likely to trigger a series of safety hazards. For instance, the current may not be cut off in a timely manner, the contacts may melt due to overheating, and the internal components may be damaged. The interior of a circuit breaker has an extremely complex structure, with its core components including the release, contact system, operating mechanism, and arc-extinguishing system. The stable operation of these mechanical structures serves as the cornerstone for ensuring the overall safety and reliability of the circuit breaker [1]. The occurrence and development of mechanical failures in circuit breakers can be manifested through changes in physical parameters. Therefore, diagnosing mechanical failures of circuit breakers by means of variations in physical quantities proves to be an effective approach.

Research on circuit breaker fault diagnosis mainly falls into two categories: fault diagnosis methods based on simulation calculations and those based on the collection of operating parameters. Some scholars, according to operational experience, proposed using the simulated data of the dynamic characteristics of the mechanism as the dataset for neural network model training to identify the mechanical fault states of vacuum circuit breakers [2]. Others designed an intelligent fault diagnosis algorithm based on DRM features through COMSOL5.6’s three-dimensional physical simulation of the circuit breaker contacts (including moving and fixed contacts) [3]. However, there is always a certain error between simulated data and the actual situation, and the established models cannot be directly applied to actual working conditions. Therefore, fault diagnosis methods based on actual operating data have developed rapidly. Among them, the fluctuation of the tripping coil current is directly related to the subtle changes in mechanical characteristics. Grant, JA, took advantage of this and established a diagnostic model based on the tripping coil current [4]. Changes in mechanical characteristics also cause changes in the control coil current. Fault diagnosis can be carried out based on the waveform characteristics of the coil current [5]. However, due to the complex internal electromagnetic interference, a large number of complex algorithms are still required for signal pre-processing in the reflected coil current changes, and when changing to another circuit breaker, the pre-processing method often needs further adjustment. Some scholars also proposed an early-stage fault detection method for abnormal circuit breaker states based on the sequence of breakdown current ratios at different times [6], which can detect potential hazards at an earlier stage. But like the coil current diagnosis method, it is vulnerable to interference and has certain limitations. For mechanical faults in structures, fault diagnosis can often be achieved through vibration signal analysis [7]. Especially for complex structures, even minor changes in the structure itself can be reflected in the vibration signals, such as in the gearboxes of aircraft engines, scraper chain faults, and rolling bearing fault diagnosis. In particular, this method can avoid the influence of electromagnetic interference and provide a more reliable means for the fault diagnosis of electrical equipment, such as using vibration signals for the fault diagnosis of internal winding deformation in power transformers, motor broken bar fault diagnosis, wind turbine fault diagnosis, and fault diagnosis of internal defects in GIS.

During the opening and closing processes of high-voltage circuit breakers, the vibration signals are much stronger than those of power equipment such as transformers and GIS, and are easy to collect [8]. However, their complex mechanical structures make it difficult to extract the key components in the signals. Therefore, signal decomposition is an important task for identification. Yang, QY [9] and Dou, LJ [10] both used VMD for the decomposition of circuit breaker vibrations. However, the selection of k and α remains a difficult problem. In addition, the extraction of modal parameters and fault diagnosis after decomposition are also difficulties of this method [11,12].

Based on this, this paper proposes a mechanical fault diagnosis method for circuit breakers based on VMD optimized by NGO, SVD, and an LSTM neural network. Firstly, the key parameters of VMD are adaptively optimized using NGO. By constructing a fitness function centered on envelope entropy or correlation degree, a global search for the optimal decomposition mode number K and penalty factor α is conducted, thereby enhancing the modal decomposition performance of VMD and the accuracy of signal feature extraction. Secondly, SVD is introduced. The obtained IMFs from VMD are reconstructed into matrices and decomposed, from which singular value sequences are extracted. These singular values can stably and compactly characterize the core energy distribution and structural information within the IMF components, thus forming a high-dimensional and robust feature vector. Finally, the extracted singular value feature sequences are fed into an LSTM network for training and testing. Leveraging its gated mechanism, the LSTM network effectively learns the temporal dependencies and dynamic variations within the features, ultimately achieving accurate identification and classification of various mechanical fault types in high-voltage circuit breakers.

2. The Mechanical Fault Diagnosis Process of Circuit Breakers

In terms of structure, a vacuum circuit breaker mainly consists of three major parts: the electromagnetic or spring operating mechanism, the vacuum interrupter, the support and other components.

The basic actions of a high voltage circuit breaker include opening, closing, overlapping and reclosing. The opening operation is the most basic function of the circuit breaker, which performs functions such as breaking the high-voltage circuit, cutting off the load power supply, cutting off the high-voltage power supply, and cutting off the faulty power supply. The closing operation performs functions such as normal power transmission of the line, load switching, and voltage introduction. After closing, the circuit breaker is in an alert state. If a fault occurs, it can be ordered to trip at any time. The closing operation refers to the situation where the circuit breaker is required to trip immediately when it encounters a short circuit during the closing process. The circuit breaker needs to have the ability to respond in time, that is, the circuit breaker can be closed to the bottom immediately for normal opening without delay [13]. The reclosing and reclosing operation refers to the ability of the circuit breaker in the power system to quickly reclose after an accident tripping, with the aim of obtaining high system stability.

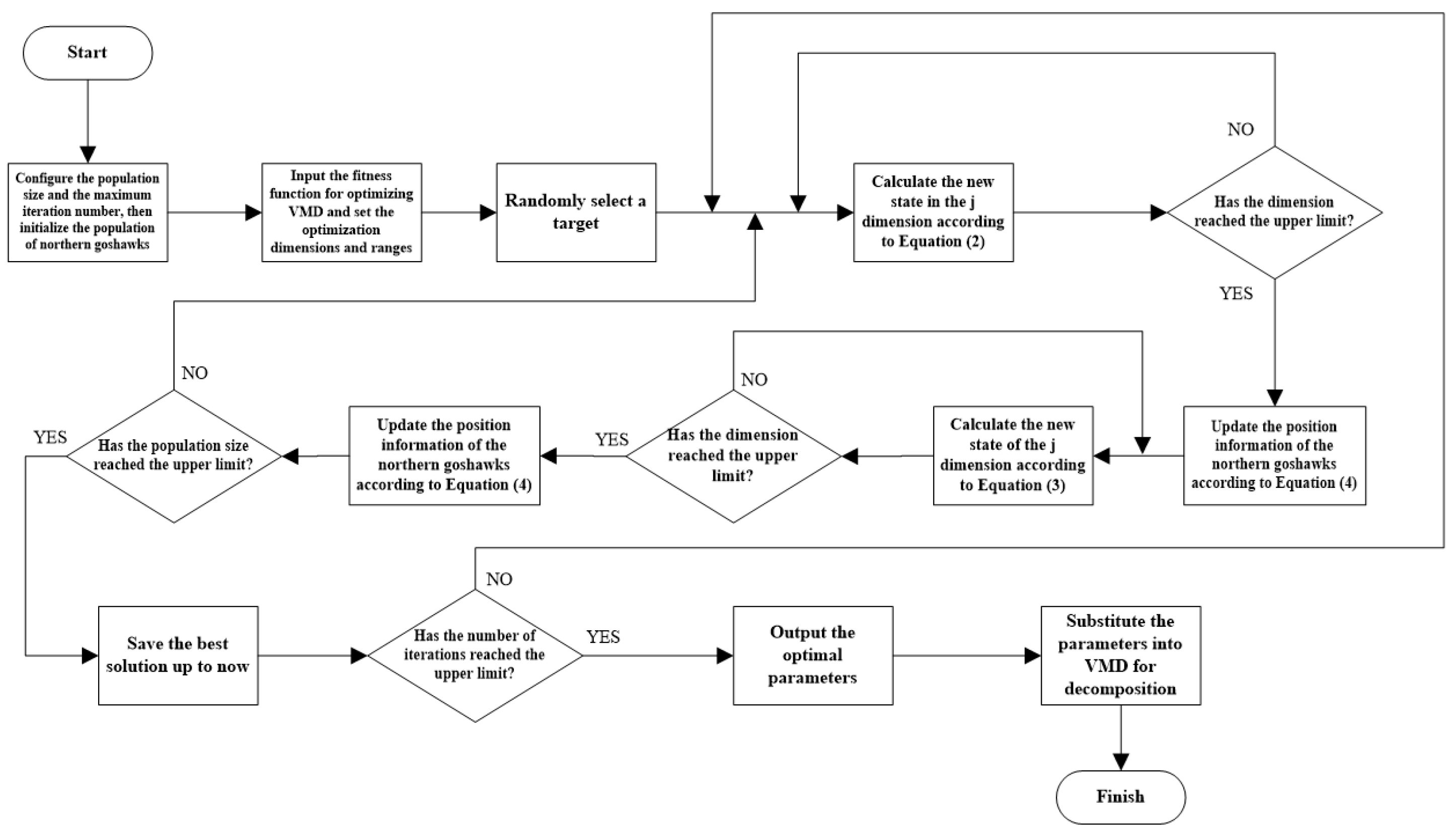
Under different mechanical states, the opening and closing actions of high-voltage circuit breakers exhibit different vibration signals. Therefore, a circuit breaker mechanical fault state recognition model based on parameter-optimized variational mode decomposition and long short-term memory neural network is proposed. The specific modeling steps are shown in Figure 1.

• The NGO-VMD is adopted to decompose the vibration signal into a series of IMFs;
• Perform singular value decomposition on each order of IMF components to obtain singular values;
• Using the singular values as feature vectors, divide them into a training set and a test set, and then implement the classification of circuit breaker mechanical faults under different states in the LSTM network.

Figure 1. Flowchart of the algorithm based on NGO-VMD.

Figure 1. Flowchart of the algorithm based on NGO-VMD.

2.1. Variational Mode Decomposition (VMD)

VMD is an effective tool for processing and analyzing nonlinear and non-stationary signals. Its core idea is to iteratively optimize the variational problem, decompose the complex signal into a series of modal components with limited bandwidth IMF [14]. At the same time, VMD can handle problems such as spectral overlap and resonant frequency, and improve the accuracy and reliability of signal decomposition. By controlling the bandwidth and center frequency of the modal components, VMD can effectively separate different frequency components in the signal and avoid the occurrence of spectral aliasing. Applying it to the vibration signal processing of circuit breaker opening and closing, it can decompose the information of each order frequency (natural frequency) under different vibration states.

When processing non-stationary mechanical vibration signals, VMD can adaptively decompose the signal into a series of band-limited IMFs by iteratively solving a variational problem, based on preset parameters such as the number of modes and the penalty factor. This effectively isolates and extracts feature components that characterize different fault sources. In comparison, classical methods like EMD, which rely on the local extrema and envelope fitting of the signal, are more susceptible to mode mixing in the presence of noise or complex signal components, resulting in reduced physical interpretability. In this study, VMD is employed and integrated with an NGO for adaptive optimization of its key parameters. This strategy aims to enhance the robustness and adaptability of the approach in handling non-stationary and nonlinear signals. By optimizing the decomposition performance, the most physically interpretable modal components can be obtained, thereby improving the accuracy of subsequent fault diagnosis.

Variational mode decomposition decomposes the original signal f into intrinsic mode components IMF of a specified order k with different center frequencies. The calculation process is as follows:

$$\begin{array}{r}\underset{\left\{u_k\right\},\left\{{\omega }_k\right\}}{\min }\left\{{\displaystyle \sum _k{‖{\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\times u_k\left(t\right)\right]e^{-j{\omega }_{k}t}‖}_2^2}\right\}\\ s.t.{\displaystyle \sum _k{u}_k=f}\end{array}$$

(1)

Among them, $u_k$ and ${\omega }_k$ are the sets of all modes and the corresponding center frequencies, respectively. δ(t) is the Dirac function, K is the number of modes, and f is the original signal.

In VMD, for each IMF component, the analytical signal is first calculated through the Hilbert transform. The Hilbert transform is a linear transformation that can convert a real-valued signal into a complex-valued signal to obtain the single-sided spectrum of the signal $\left[\delta (t)+j/\pi t)\times um(t)\right]$ The spectrum of each order mode is shifted towards the optimal center frequency through the mixed exponent. The bandwidth of each order IMF is estimated by the Gaussian smoothness of the demodulated signal, and then constrained to obtain Equation (1). However, there are still constraint problems in Equation (1). The Lagrange multiplier algorithm and the ADMM are used for alternating iterative optimization to solve this optimization problem. In VMD, we continuously update the bandwidth, center frequency, and reconstructed signal of the IMF components through the ADMM algorithm until the convergence condition is met or the maximum number of iterations is reached, thus completing the variational mode decomposition [15].

In VMD, the quadratic penalty term and Lagrange multipliers are used to address the reconstruction constraint problem. The advantage of combining these two is that the quadratic penalty function exhibits good convergence at finite weights, and the Lagrange multipliers ensure strict enforcement of the constraints. The augmented Lagrangian is represented by Equation (2).

$$\begin{array}{r}L\left(\left\{u_k\right\},\left\{{\omega }_k\right\},\lambda \right)=\alpha {{\displaystyle \sum _k‖{\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\times u_k\left(t\right)\right]e^{-j{\omega }_{k}t}‖}}_2^2{\displaystyle \frac{-b\pm \sqrt{b^2-4ac}}{2a}}\\ +{‖f\left(t\right)-{\displaystyle \sum _k{u}_k\left(t\right)}‖}_2^2+〈\lambda \left(t\right),f\left(t\right)-{\displaystyle \sum _k{u}_k\left(t\right)}〉\end{array},$$

(2)

In the equation, α is the penalty factor, and λ is the Lagrange operator.

Through this process, VMD can decompose a complex signal into a series of IMF components with finite bandwidths and center frequencies. These IMF components are mutually independent in the frequency domain, which can better describe different components and characteristics in the original signal.

2.2. Northern Goshawk Algorithm (NGO)

The NGO is a multi-objective optimization algorithm proposed by Mohammad Dehghani and others in 2022. It is based on the predation strategy of the northern goshawk. The NGO mimics the behavior of the northern goshawk during the hunting process [16]. This imitation endows the algorithm with a powerful global search ability. It is not limited to local optimal solutions but can search the entire solution space to find the global optimal solution. Meanwhile, the NGO is relatively simple in terms of parameter adjustment. In the NGO, the main parameters include the population size and the number of iterations. The iterative process of the NGO mainly consists of two stages: prey identification and attack (global search), and pursuit and escape (local search). The iterative rules of these two stages are relatively simple and easy to understand and implement.

In VMD, the parameters K and α need to be determined manually, which is rather difficult. However, the use of optimization algorithms can solve this problem. The predation process mainly goes through two steps, namely identifying the prey and chasing the prey:

First of all, when hunting, the northern goshawk will randomly select a prey and attack it quickly. This process is aimed at exploring and selecting the best predation area, enabling the algorithm to more accurately and quickly identify the optimal area under global search. The predation exploration behavior of the northern goshawk can be described by Equation (3):

$$x_{i,j}^{new,P1}=\left\{\begin{array}{c}{x}_{i,j}+r(p_{i,j}-I_{xi,j}),F_{pi}<F_i\\ x_{i,j}+r(x_{i,j}-p_{ij}),F_{pi}\ge F_i\end{array}\right.,$$

(3)

In the equation, P represents the position information of the northern goshawk’s prey, x represents the position information of the northern goshawk, Fi is the fitness function representing its position, and i and j represent the information about the number and dimension, respectively.

After determining the prey target, the northern goshawk will pursue the escaping prey within the assumed pursuit range radius R. The northern goshawk has a high predation speed and a high pursuit success rate, which makes the algorithm’s ability to optimize the local space more remarkable. The pursuit process of the northern goshawk can be described by Equations (4) and (5) describe the position change in the northern goshawk:

$$x_{i,j}^{new,P2}=x_{i,j}+R(2r-1)x_{i,j},$$

(4)

$$xi=\left\{\begin{array}{c}{x}_i^{new,P},F_i^{new,P}<F_i\\ xi,F_i^{new,P}\ge F_i\end{array}\right.,$$

(5)

In the equation, set R as the radius of its hunting range. t and t represent the current and maximum number of pursuit attempts, respectively, and the remaining parameters are the same as those described above.

In order to make the decomposition result reasonable under the corresponding VMD parameters, it is necessary to set the threshold range [2, p] of K and the threshold range [a, b] of α. The NGO is used to search for the optimal parameters of the VMD, so as to minimize the objective function within the VMD threshold range.

Meanwhile, the position [k, α] represents the candidate solution for the VMD parameter optimization. The formula is as follows:

$$\left\{\begin{array}{c}\arg \underset{\left(K,\alpha \right)}{\min }\left\{1/\left({\displaystyle {\sum }_{n\to N}E{K}_n}/N\right)\right\}\\ s.t.K=2,3,\cdots p\\ \alpha \in \left[a,b\right]\end{array}\right.,$$

(6)

After inputting the optimization ranges of K and α, the fitness function Fi is established according to the criteria for determining the parameters K and in VMD theory:

$$F(K,\alpha )={\displaystyle \sum _{i=1}^K{E}_e^{(i)}}$$

(7)

Here, k is the decomposition level and $\alpha$ is the penalty factor, which are variables to be optimized; $E_E^{(i)}$ represents the envelope entropy of the i-th IMF component.

Thus, VMD based on Northern Goshawk Optimization can be realized. The specific process is as follows:

• Obtain the mechanical vibration data of the circuit breaker;
• Set the parameter ranges of and in VMD, and initialize the population of northern goshawks;
• Calculate the fitness function and select parameter sets for iterative loops;
• Output the optimal parameters and substitute them into VMD for operation to obtain the decomposition result of NGO-VMD.

2.3. Singular Value Decomposition (SVD)

Through the NGO-VMD algorithm, we can obtain a set of IMFs that accurately represent the specific characteristics of the vibration process. To precisely extract the core information from each IMF, we adopt the method of SVD. By performing singular value decomposition on each order of IMF, the extracted singular values can efficiently characterize and approximately describe the important modal features of the corresponding IMF, thus achieving the accurate capture and representation of the deep-level information of the signal [17].

SVD is a matrix decomposition method. In the separated state of a matrix, some hidden information and weak information can be obtained [18]. Suppose the matrix is $X$, and its decomposition formula is as follows:

$$X=US{V}^T$$

(8)

In the formula, U and V are orthogonal matrices, and S is a diagonal matrix of singular values.

According to the singular value decomposition formula and the singular value theory, U, V are not unique, while the matrix V has uniqueness. The singular values represent the important information features of this matrix. When the signal is disturbed, its singular values will not change significantly, thus avoiding the random false features existing in the time series, and making it have strong stability and adaptability in the field of feature extraction. That is to say, using [σ1, σ2, σ3, …, σk − 1] as the feature vector of the original signal can effectively reflect the status information of the structure of the vacuum circuit breaker.

2.4. Long Short-Term Memory Neural Networks

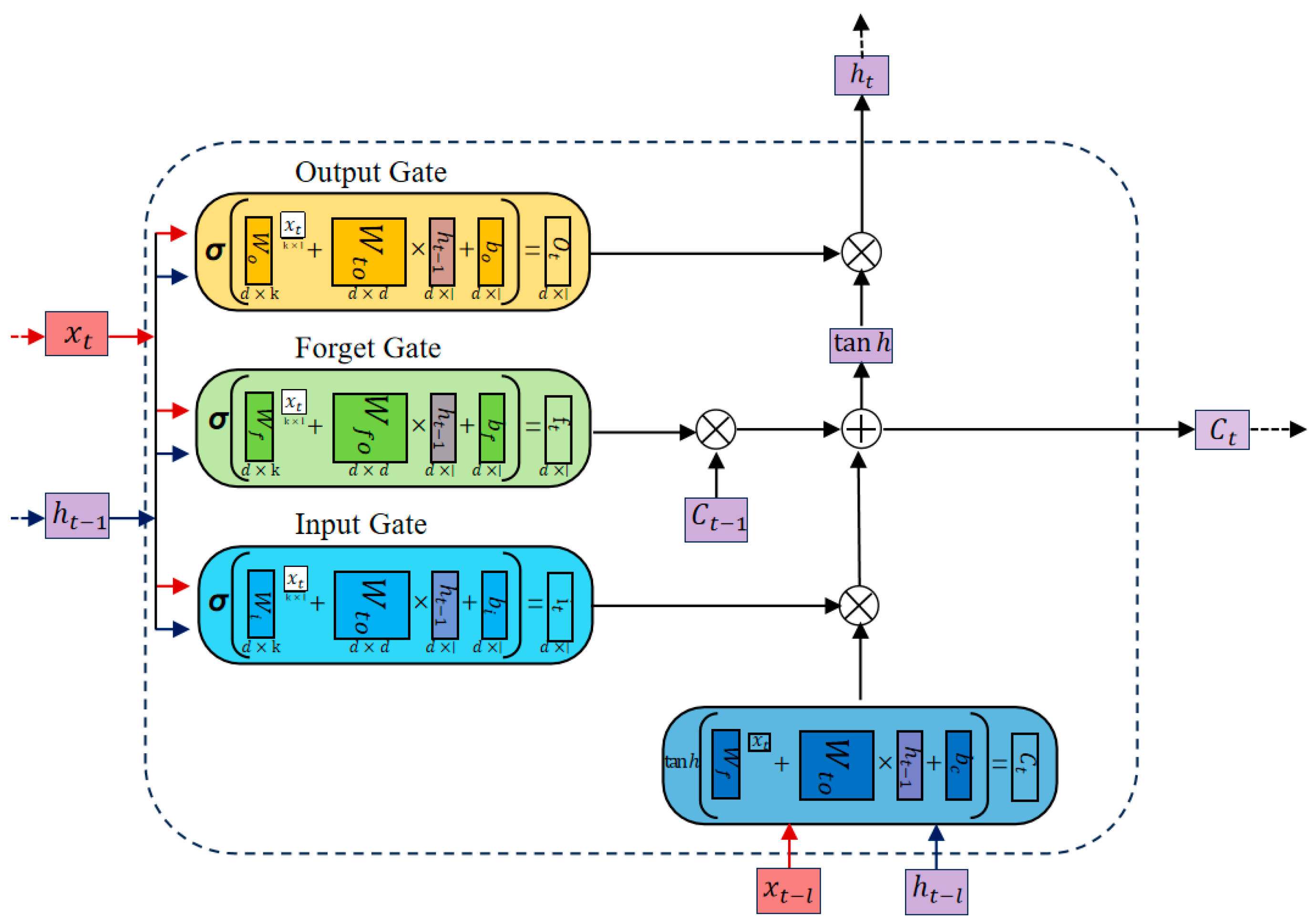
The mechanical vibration signal of the circuit breaker is processed by NGO-VMD to obtain a set of IMFs and singular value vectors. How to reflect the overall structural state of the vacuum circuit breaker through the feature vectors is a multi-input, single-output and nonlinear problem [19]. LSTM is a type of RNN architecture used to manage long-term information values. It introduces gate units to control the propagation of inputs and outputs. The LSTM unit shown in Figure 2 consists of three gates. The forget gate determines how long the given information value can be retained in the unit and how much of the previous information the memory unit should discard; the input gate decides whether new information should be sent into the unit; the output gate determines when to discard the information stored in the unit [20].

The state of the unit is determined by the output of each gate at the discrete instant t. The calculation order is the forget gate f_t, the input gate i_t, and the output gate O_t in sequence. In each formula, σ is the activation function, w is the weight related to the input in each gate, wh is the recurrent weight, and b is the bias component in each gate. C_t represents he candidate state information within the unit, $\tanh$ is the hyperbolic tangent function. C_t, together with the output value of each gate and the state information C_t−1 of the previous unit, jointly determine the state information C_t in the next-level unit [21]; the output gate and the state information C_t in the next-level unit determine the hidden layer information h_t in the next-level unit:

$$c_t=f_t{c}_{t-1}+i_t{\stackrel{⌢}{c}}_t$$

(9)

$$h_t=o_t\tanh c_t$$

(10)

The establishment of the gate unit gives LSTM more advantages in processing input information. When the feature vector is input into the LSTM, it is possible to appropriately filter out the valid and invalid information through the cooperation among the various gates [22].

3. Experimental

3.1. Test Platform and Data Collection

The theoretical basis for selecting the mechanical vibration signals of the circuit breaker as the characteristics for fault diagnosis lies in that, through appropriate detection means and signal processing methods, the excitation source of the vibration can be identified, and then the source of the fault can be found out. The operation of the mechanical part of the high-voltage circuit breaker may lead to situations such as fatigue aging, rusting, contact wear, improper assembly of parts, etc. By analyzing the travel signal of the switch action and extracting relevant mechanical characteristic parameters, many potential mechanical fault hazards can be discovered, and the possible faulty components can be predicted.

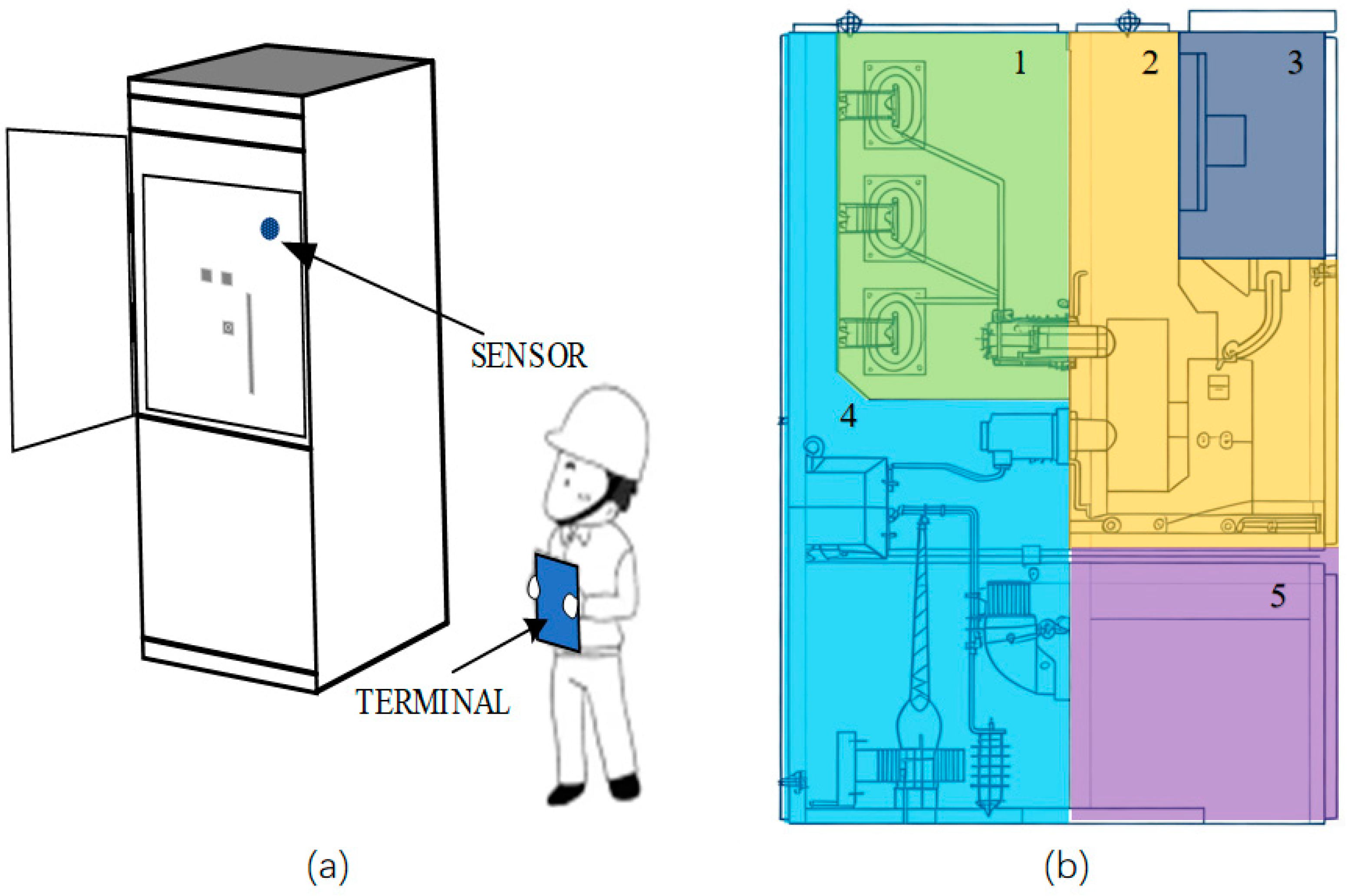
The object of study in the experimental system is the KYN28A-12 type indoor AC high-voltage vacuum circuit breaker (Shenzhen Zhongji Electric Technology Co., Ltd., Shenzhen, China). The mechanical vibration signals of the high-voltage circuit breaker are high-frequency signals, which have a short effective time and a large vibration impact. An acceleration vibration sensor is used for measurement. The acceleration sensor selected for this experiment is the TST100A type produced by Jiangsu Test Instrument Co., Ltd. (Jingjiang, China). The acquisition platform collects vibration data at a sampling frequency of 6000 Hz, as shown in Figure 3.

Prior to the commencement of the experiment, the circuit breaker switchgear used was thoroughly inspected to ensure normal operation and the absence of any initial internal faults. All experiments were performed under controlled laboratory conditions, with ambient temperature and humidity kept at stable levels. The following operations were sequentially performed on the switchgear to induce faults at specified locations, followed by vibration signal acquisition:

• Adjust the tightness of the bolt at the end of the insulating rod to induce a fault in the electromagnetic and spring operating mechanism. The circuit breaker was then operated to open and close, during which vibration signals were collected. After acquisition, the setup was restored to its original state.
• Loosen the screws connecting the relay and the circuit to induce a fault in the relay compartment. The circuit breaker was operated to open and close, and vibration signals were collected. After acquisition, the setup was restored.
• Loosen the connection between the grounding busbar and the grounding switch to allow movement, thereby simulating a fault. The circuit breaker was operated to open and close, and vibration signals were collected. After acquisition, the connection was restored.
• Loosen the internal wiring connections of the circuit breaker while ensuring it can still open and close normally. The circuit breaker was operated, vibration signals were collected, and the connections were subsequently restored.
• Loosen the screws at the support connections of the switchgear to induce a fault. The circuit breaker was operated to open and close, vibration signals were collected, and the setup was then restored.

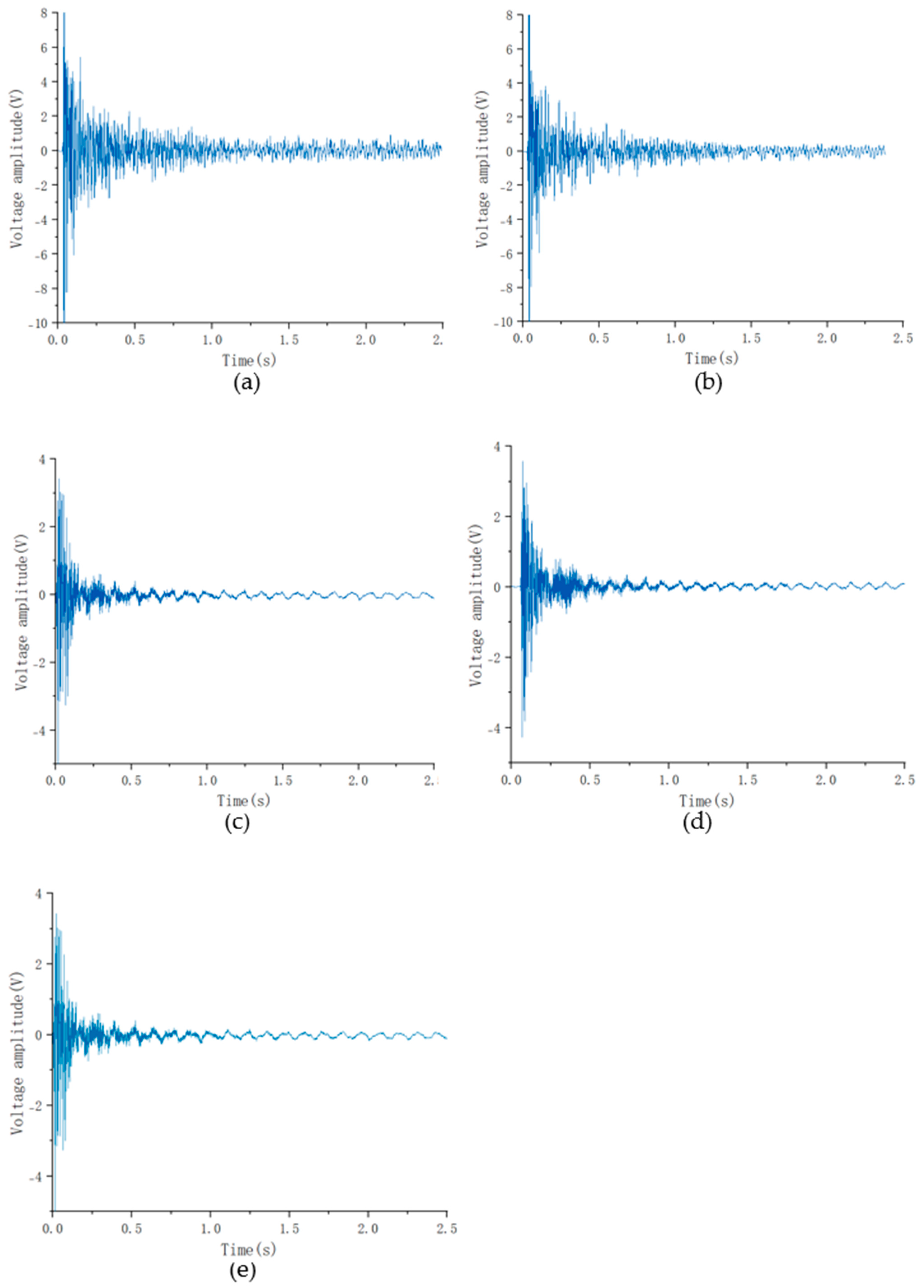
Through the experimental procedures described above, five types of vibration signal data were collected. Each type was repeated for 36 trials, resulting in a total of 180 experimental datasets. As the signals tend to stabilize after 2.5 s, only the signal segments before 2.5 s were retained for subsequent signal processing. The five signals presented in Figure 4 correspond to the five fault types described above.

3.2. Parameter Optimization and Feature Extraction

The parameters of the NGO are configured as follows: the population size is set to 50 to balance search diversity and computational efficiency, and the maximum number of iterations is set to 30, determined based on the convergence behavior observed in preliminary experiments. The search space is defined by two key parameters of VMD: the number of modes K ∈ [2, 10] and the penalty factor α ∈ [500, 2500], forming a two-dimensional optimization problem. This configuration ensures the algorithm efficiently identifies the optimal parameter set, consistent with established practices in related research [23].

Taking the normal condition as an example, the vibration signals are processed using the VMD improved by the NGO and three other algorithms, respectively, and the improvement effects are compared. The population sizes of the NGO, the I-GWO, the GWO, and the GAV are all set to 20. The range of the decomposition level is [2, 10], and the range of the penalty factor is [500, 2500]. Figure 5 shows the fitness curves of the four optimization algorithms during operation. The four algorithms converge at 2, 6, 9, and 4, respectively. Except that the accuracy of the GAV is slightly lower, the convergence accuracies of the other algorithms are similar, and the NGO-VMD has the fastest convergence speed. The results show that the NGO-VMD has stronger global optimization ability compared with other improved VMD methods.

As shown in

Table 1. Comparison of classification results with different parameter settings.

	K	$\mathit{\alpha }$	Classification Accuracy Rate
Fixed value	2	1800	71.25%
	3	1800	78.93%
	4	1800	83.49%
	5	1800	87.12%
	6	1800	91.71%
	7	1800	96.15%
	8	1800	97.23%
	9	1800	95.02%
	10	1800	93.71%
NGO	8	1815	97.68%
I-GWO	8	1793	96.80%
GWO	7	1549	93.21%
GAV	7	1762	94.34%

, with the penalty factor $\alpha$ fixed at 1800, the decomposition level K was adjusted, and the resulting classification accuracy is illustrated in the figure. It can be observed that the fault diagnosis accuracy reaches its highest when the decomposition level is 8, which aligns with the results obtained from the NGO optimization algorithm. A comparison of the four optimization algorithms reveals that the NGO exhibits superior performance, as the K and $\alpha$ values obtained through its optimization are closer to the optimal parameter values, resulting in higher classification accuracy compared to the other algorithms.

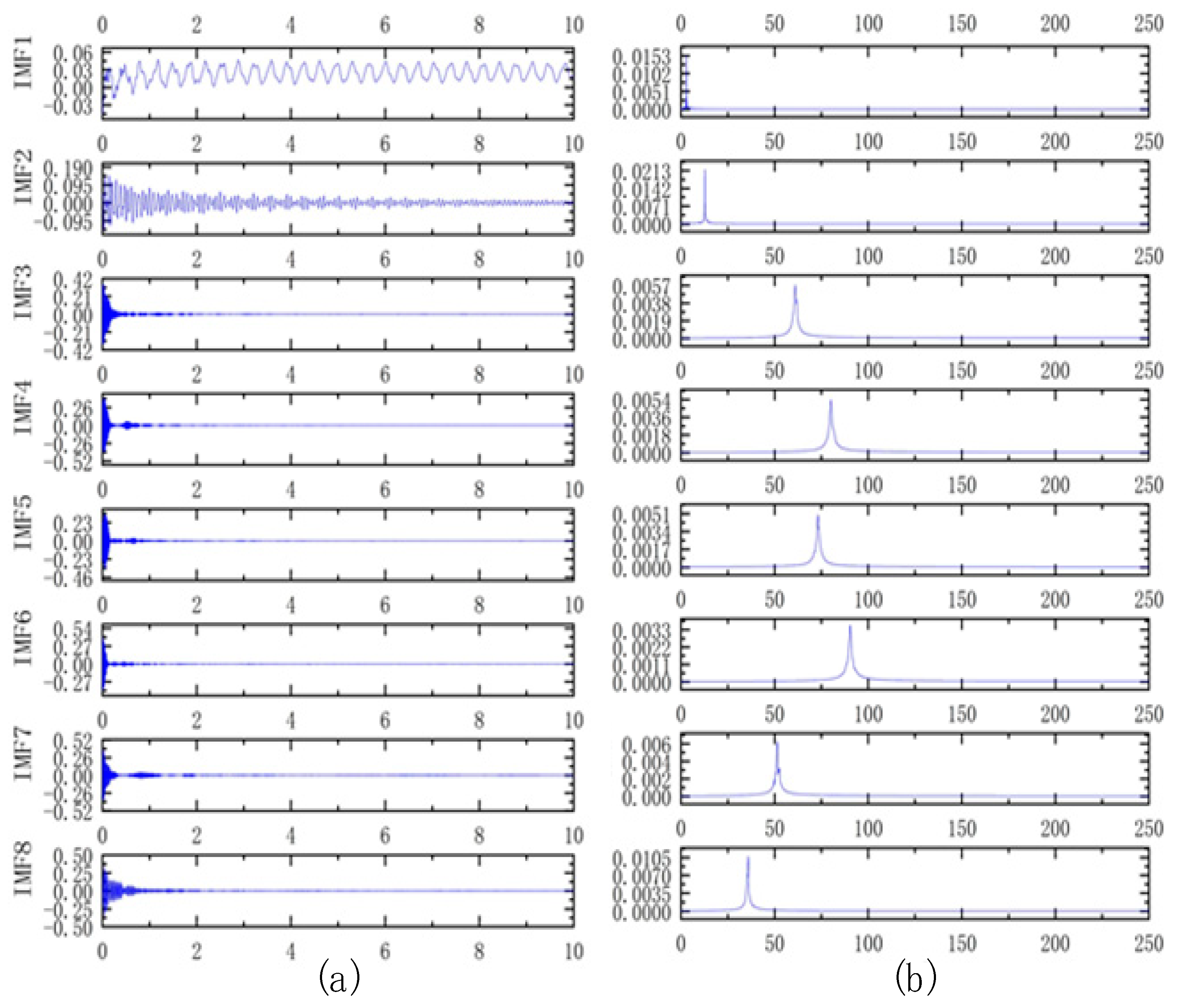
After being optimized by the NGO, the optimal parameter combination of the VMD is obtained as the decomposition level and the penalty factor. Substitute the relevant parameters into the VMD for decomposition. Figure 6 shows the time–domain and frequency–domain results of the decomposition by NGO-VMD. It can be found that the original signal is decomposed into 8-order IMF components, and there is no obvious mode mixing phenomenon in the frequency–domain diagrams of each order of IMF components, indicating a good decomposition situation.

3.3. LSTM Network Classification

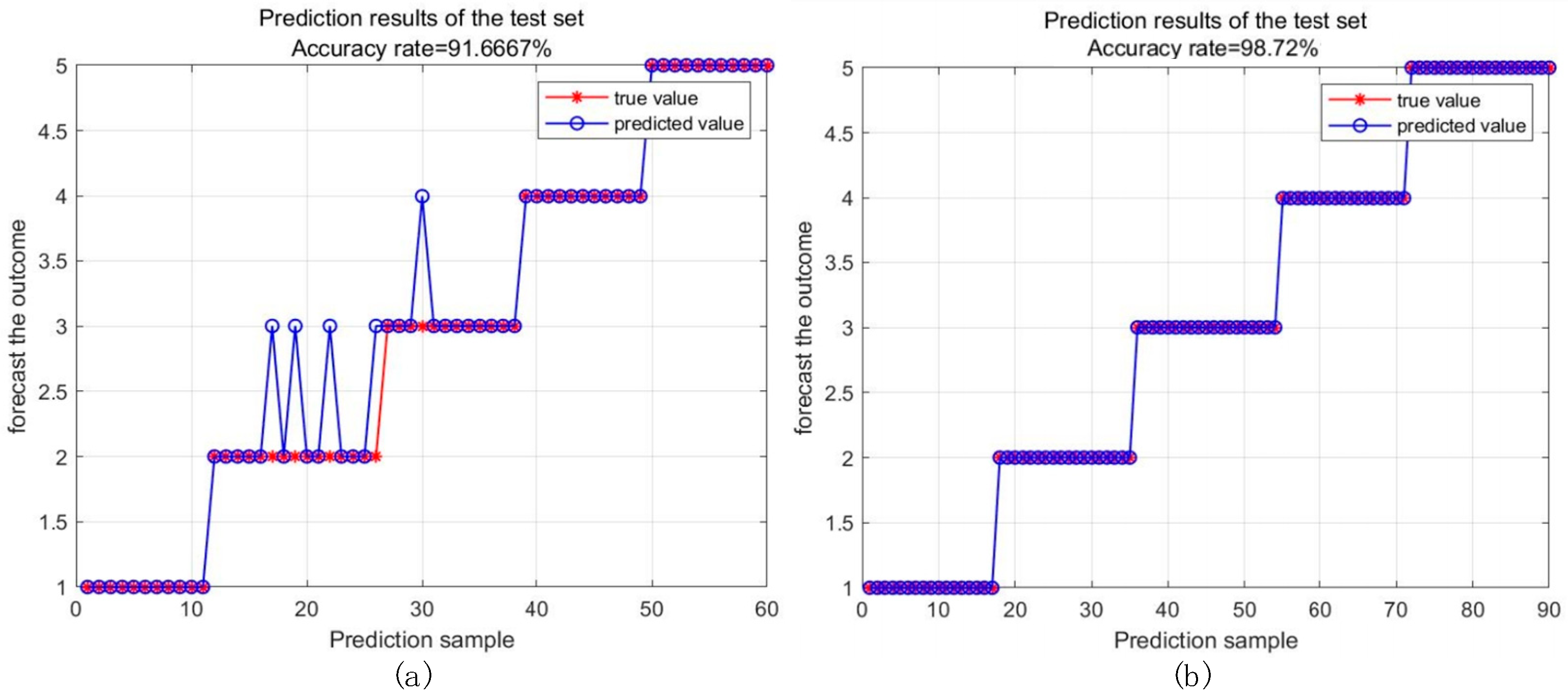
In this paper, 180 sets of measurement data were divided into a test set and a training set. Among them, 90 sets of data were used for training, and 90 sets of data were used for testing. The labels for different fault types were defined as 1, 2, 3, 4, and 5. The solver was specified as adam, the gradient threshold was 13, and the maximum number of iterations was 480. After 3000 iterations, the classification results of the LSTM neural network are shown in Figure 7. Compared with the BP neural network algorithm, the classification effect of the LSTM neural network is better; as the training progresses, the accuracy continues to increase, and the loss function also tends to stabilize and converge. Finally, the accuracy reached 98.72%.

As shown in the figure, based on the classification results of the LSTM network, the fault characteristics of the circuit breaker are divided into five categories. If the classification result is 1, it indicates that a fault has occurred in the electromagnetic or spring operating mechanism; if the classification result is 2, it indicates a fault in the relay chamber; if the classification result is 3, it indicates a fault in the grounding switch or grounding bus; if the classification result is 4, it indicates a fault in the circuit breaker chamber; if the classification result is 5, it indicates a fault at the support and other components.

3.4. Comparison of Algorithm Performance

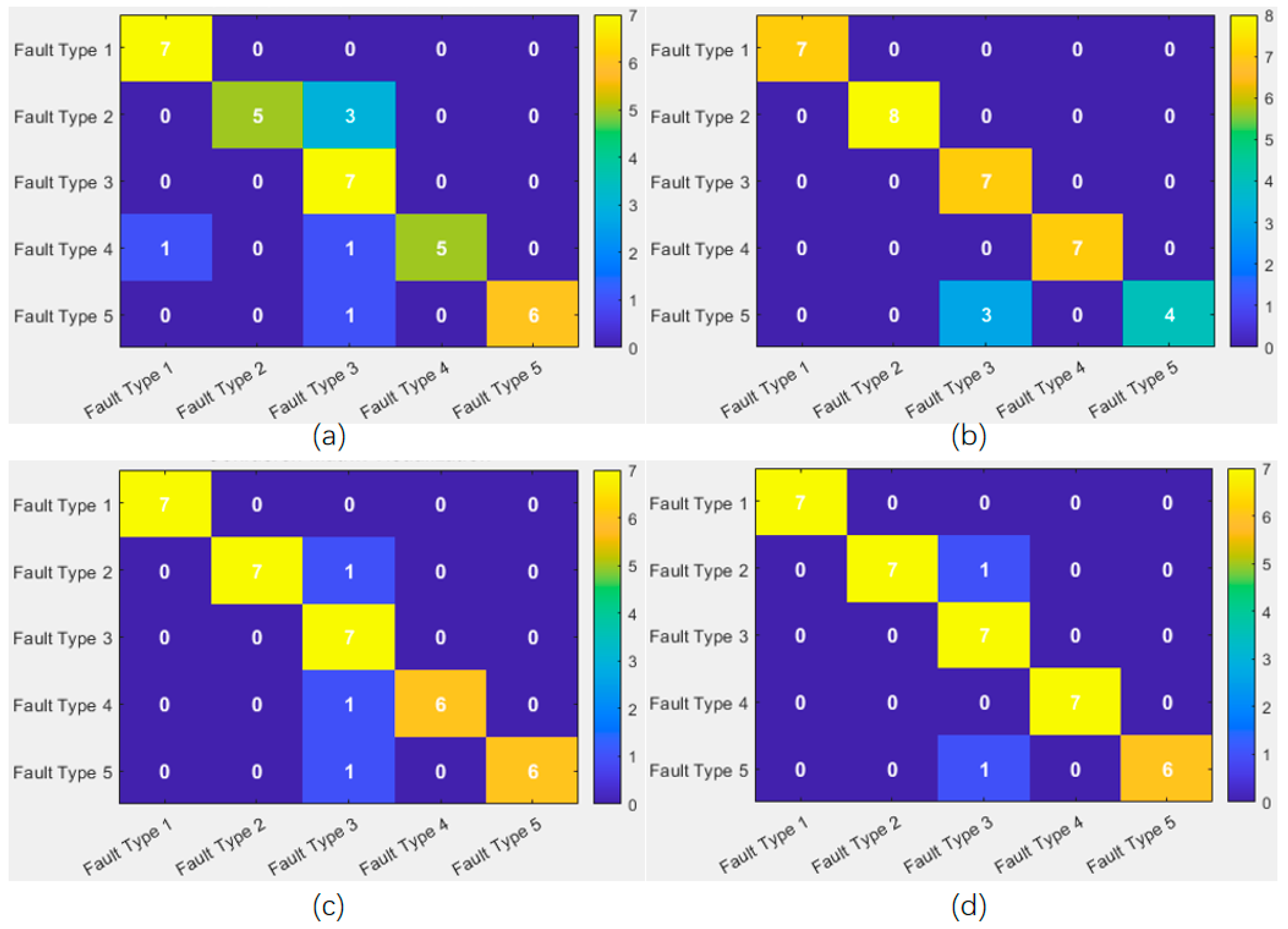
A comparative evaluation was performed against three benchmark algorithms: a 1D Convolutional Neural Network (1D-CNN), a Backpropagation (BP) neural network, and a Support Vector Machine (SVM). As illustrated by the confusion matrices in Figure 8, the proposed LSTM-based optimizer achieves a superior classification accuracy compared to the 1D-CNN and SVM models. While the performance gap between the LSTM and the BP network is less pronounced, the LSTM consistently demonstrates the highest predictive precision among all methods tested. This initial result establishes the competitive edge of the LSTM framework over alternative architectures for the given task.

Following the initial accuracy comparison, a detailed performance analysis was conducted using precision, recall, F1-score, and support for each class across all models. The comprehensive results are summarized in

Table 2. Performance comparison of different algorithms.

		Precision	Recall	F1-Score	Support
1D-CNN	Fault type 1	1	1	1	7
	Fault type 2	0.72	0.67	0.71	8
	Fault type 3	1	1	1	7
	Fault type 4	0.72	0.67	0.635	7
	Fault type 5	0.85	0.857	0.923	7
SVM	Fault type 1	1	1	1	7
	Fault type 2	1	0.935	1	8
	Fault type 3	1	0.87	1	7
	Fault type 4	1	1	1	7
	Fault type 5	0.57	0.87	0.625	7
BP neural network	Fault type 1	1	1	1	7
	Fault type 2	0.875	0.87	0.935	8
	Fault type 3	1	1	1	7
	Fault type 4	0.85	0.857	0.923	7
	Fault type 5	0.85	0.857	0.923	7
LSTM neural network	Fault type 1	1	1	1	7
	Fault type 2	0.875	0.95	0.935	8
	Fault type 3	1	1	1	7
	Fault type 4	1	1	1	7
	Fault type 5	0.85	1	0.923	7

. This granular evaluation reveals that both the LSTM and BP neural network algorithms achieve higher precision rates compared to the 1D-CNN and SVM, indicating their superior capability in minimizing false positives for the target classes. However, a more nuanced distinction emerges when examining recall and the harmonic mean F1-score. The proposed LSTM optimizer consistently attains higher recall and F1-scores than the BP network, demonstrating a better balance between identifying all relevant instances (recall) and maintaining classification purity (precision). This indicates that the LSTM model offers more robust and comprehensive performance, effectively reducing false negatives without compromising precision. Therefore, considering the combined metrics that reflect both the correctness and completeness of the classification, the LSTM-based optimization algorithm demonstrates superior overall performance compared to all other benchmarked methods, as substantiated by the data in Table 2.

4. Online Health Monitoring System of the Circuit Breaker

4.1. Composition of System

In order to realize the fault detection and identification of the circuit breaker, this paper designs a fault diagnosis system based on a vibration sensor. The system consists of two parts, namely the wireless sensor and the diagnostics terminal, as shown in Figure 9a. The wireless sensor is attached to the circuit breaker of the switchgear cabinet to measure the vibration acceleration value. Then, the vibration acceleration signal is sent to the diagnostics terminal, which conducts data analysis and displays it. The data communication is carried out via WIFI. The diagnostics terminal embeds the calculation method described in the first part, enabling it to automatically identify the final result. Figure 9b shows the internal structure diagram of the circuit breaker. The detection device collects vibration signals from the circuit breaker switchgear, and through a series of algorithmic processes, the fault location of the circuit breaker switchgear can be accurately identified, facilitating timely maintenance by personnel.

4.2. Design of Sensors

In this paper, a wireless sensor is designed, which consists of an accelerometer, a CPU, a WIFI module, and a power module. Figure 10 shows the structure diagram of the sensor. To function longer, all parts of the sensor select low power consumption to achieve low power consumption. Due to the large amount of data, the STM32L475 microprocessor (STMicroelectronics, Geneva, Switzerland) is selected for simple calculation. The STM32L475 microprocessor features a 32-bit Cortex^® -M4 CPU with a maximum operating speed of 48 MHz and a minimum current of 1.1 μA in the low-power mode, and with 128k of SRAM to meet the needs of use. The LIS2DH12 is used for measuring the vibration of a circuit breaker. Its maximum measurement range can reach ±16 g, and its sensitivity can also reach 16 mg, which is sufficient for use. It is linked to the CPU through the SPI interface. The power supply adopts lithium batteries for easy charging.

4.3. Design of Terminal

The terminal uses a Surface tablet, and its built-in WIFI module is used to receive data. The receiving software is developed using the app development function in MATLAB 2023. We have designed an automatic prompt function for sensor connection, which can display basic information such as battery level, signal strength, and online status on the interface. The calculation and analysis adopt a one-key operation. After clicking the “Collect” button, data collection, calculation, and diagnosis will be carried out.

Figure 11a shows the time–domain graph, frequency–domain graph and three-dimensional energy spectrum graph of the circuit breaker’s vibration signal. The signal in the time–domain graph is judged for any offset, and the frequency–domain graph is checked for any abnormal frequency parts to determine if the circuit breaker is working normally. Figure 11b is the analysis interface of the upper computer, where the left side shows the modal frequencies of each order of the circuit breaker’s vibration signal, and the right side shows the modal shapes of each order of the circuit breaker. Finally, the upper computer identifies the fault type based on the classification results of LSTM and sends the fault category to the user through a pop-up window.

4.4. Field Test

The developed system was tested on the 12-kV switchgear cabinet within the central distribution room of a manufacturing enterprise in Shaanxi Province, located in western China, as shown in Figure 12. The system is capable of achieving data collection and analysis.

5. Conclusions

To accurately identify mechanical faults in high-voltage circuit breakers, this paper presents a fault diagnosis method based on parameter-optimized VMD and LSTM neural networks, and further develops a structural health monitoring system. The main conclusions are summarized as follows:

• To address the constraints of the decomposition level and penalty factor on VMD, an NGO-optimized VMD method is proposed. Analysis of experimental data confirms its effectiveness in extracting structural modal information.
• By collecting the vibration data of the circuit breaker under different fault conditions and processing the signals using the combined method of NGO-VMD and SVD, the results show that this method can effectively represent different fault states of the circuit breaker.
• This paper presents a comparative analysis of LSTM neural networks and other deep learning network algorithms. The LSTM algorithm demonstrates significantly superior overall performance in comparison to other classification algorithms.
• The processed signals are presented to users in tabular form, and users assess the fault conditions of the circuit breaker via the diagnostic terminal software.