Research on STA/LTA Microseismic Arrival Time-Picking Method Based on Variational Mode Decomposition

Abstract

The complex environment of metal mines causes significant noise interference in microseismic signals. This leads to low accuracy and high false alarm rates when using the conventional Short-Term Average/Long-Term Average (STA/LTA) method for first-arrival picking. To address these issues, this paper proposes an improved approach that combines Variational Mode Decomposition (VMD) with STA/LTA(V-STA/LTA). The proposed method selects effective mode components through multimodal decomposition. Subsequently, an energy-weighted fusion is achieved based on energy distribution characteristics to improve the accuracy of arrival time-picking. First, the microseismic signal is decomposed by VMD. The center frequencies of the Intrinsic Mode Functions (IMFs) are then calculated through Fast Fourier Transform (FFT). This helps identify and retain the effective mode components, reducing noise interference. Next, the STA/LTA method is applied to each selected mode component for first-arrival picking. Finally, the results from the different components are fused based on their energy weights for improving picking precision. In low signal-to-noise ratio (SNR) conditions, the effectiveness of the V-STA/LTA method was verified through simulation experiments and field data tests. In theoretical simulations, according to test results from multiple sets of different signal-to-noise ratios, the root mean square error (RMSE) (0.0005) and mean absolute error (MAE) (0.00055) of V-STA/LTA are significantly lower than those of STA/LTA and AIC. In actual data, the average accuracy (99.77%) is nearly 1 percentage point higher than that of the traditional STA/LTA (98.93%), improving the accuracy of microseismic signal arrival time-picking.

1. Introduction

As shallow mineral resources are exhausted, mining operations are extending to greater depths [1], where increasingly complex stress conditions significantly raise the risk of sudden disasters such as rock bursts and roof collapses [2]. Conventional monitoring techniques like drilling cuttings analysis and stress detection have limitations such as high cost, low efficiency, and poor real-time performance, making it difficult to achieve large-scale real-time monitoring [3]. The microseismic monitoring technique is one of the most effective methods for early warning of disasters in deep mines [4], and its key aspect is the accurate detection of the arrival time of P-waves.

Microseismic signals are characterized by weak energy and a low signal-to-noise ratio (SNR), which pose significant challenges for accurate first-arrival picking [5]. The precision of arrival picking directly impacts source location accuracy. Traditional manual picking methods are inefficient and cannot meet the needs of real-time monitoring [6]. To address these challenges, researchers have developed various automatic picking algorithms, such as the Short-Term Average/Long-Term Average (STA/LTA) [7,8] method and the Akaike Information Criterion (AIC) [9].

The STA/LTA algorithm, introduced by Allen [10], is a classical method for first-arrival picking in seismology due to its computational efficiency and straightforward implementation. However, in practical applications, problems such as arrival time delays and reduced accuracy under low signal-to-noise ratio (SNR) conditions frequently occur [11]. Li et al. [12] proposed a new feature function that can reflect the signal energy and dispersion; their results revealed that the improved method could accurately pick up the first arrival of microseismic events. To mitigate threshold dependency, Stewart and Chen [13] employed envelope functions with dynamic thresholds, eliminating the need for manual threshold selection, although this method remains vulnerable to abnormal vibration interference. Akram et al. [14] incorporated weighting coefficients to enhance signal detection. Liu Xiaoming et al. [15] proposed a novel characteristic function and adopted a global maximum approach for first-arrival picking, which reduced the need for frequent threshold adjustments but suffered from limited real-time performance.

Due to the generally low signal-to-noise ratio (SNR) of noise-contaminated microseismic data, single algorithms often struggle to accurately pick first arrivals. As a result, multi-method fusion has emerged as a key research direction. Zhang et al. [16] developed the W-AIC picking method, which integrates AIC detectors with wavelet multi-scale analysis. This approach exploits the persistence of signals across scales and enhances noise attenuation at higher decomposition levels, thereby mitigating noise interference. Wang and Liu [17] proposed a novel microseismic event identification technique using support vector machines. To address the tendency of the AIC method to generate false picks, Liu et al. [18] combined correction trigger functions and fourth-order statistics with the AIC algorithm, improving arrival detection accuracy while reducing both false alarms and missed detections. Shang [19] introduced a method combining empirical mode decomposition with AIC that better preserved the amplitude and phase spectrum of P-wave arrivals. In addition, various other methods can be integrated with AIC or alternative techniques to further enhance picking precision.

To overcome the limitations of the Fourier transform method in processing non-stationary signals, Huang et al. proposed the Empirical Mode Decomposition (EMD) method [20]. This method decomposes a signal into several intrinsic mode functions (IMFs) and a residual component based on the local time-scale characteristics of the signal, thereby effectively highlighting the physical properties of the signal. Liu et al. [21] applied EMD to decompose signals and successfully addressed the challenge of identifying arrival times caused by dispersive signals and strong background noise. However, their study did not consider that, under special noise conditions, IMF1 may still contain a significant amount of noise, and it lacked a mechanism for adaptively selecting the effective components. Li [22] et al. proposed the EMD–AIC hybrid method, which achieves signal purification through adaptive decomposition via EMD and precisely locates the signal using AIC, achieving high-precision detection under complex noise conditions. Nevertheless, this method only selects a single IMF component and does not fully utilize complementary information among multiple effective components. However, EMD itself has the problem of end effects—where there are insufficient local extrema at the signal boundaries—leading to inaccurate decomposition results [23]. In addition, when the frequency characteristics of signal components are similar, mode mixing can occur. To address these issues, Dragomiretskiy and Zoss proposed Variational Mode Decomposition (VMD) [24]. VMD decomposes the signal into frequency components with different bandwidths by estimating the central frequency and bandwidth, effectively suppressing mode mixing and avoiding end effects.

This paper presents a VMD-based STA/LTA method for microseismic arrival picking, which combines the advantages of VMD and STA/LTA. First, VMD decomposes microseismic signals into different frequency modes. Next, Fast Fourier Transform (FFT) [25] is used to calculate the central frequency of each mode component in order to select the effective mode components according to the average value. The STA/LTA method is then applied to pick the arrival time of the selected mode component. The final arrival time is determined by calculating the energy-weighted fusion of the selected components. Finally, the proposed method is compared to manual and STA/LTA results using the field data.

2. Materials and Methods

2.1. STA/LTA Method

The Short-Time Average/Long-Time Average (STA/LTA) method captures the variations in microseismic signal characteristics by comparing the amplitude mean ratios within short and long time windows. When a microseismic signal arrives, the amplitude mean of the Short-Time Average (STA) changes more significantly than that of the Long-Time Average (LTA), resulting in a sudden change in the STA/LTA ratio. If this ratio exceeds a preset threshold, the arrival point of the microseismic signal is identified [26].

The characteristic function is used to describe the variation characteristics of a signal by calculating the ratio of the short-time and long-time energy averages. It is primarily used to reflect changes in the amplitude or frequency of the signal. The most commonly used characteristic functions are as follows:

$$\left\{\begin{array}{l}CF(i)=y(i)\\ CF(i)=y{(i)}^2\\ CF(i)=y{(i)}^2-y(i-1)y(i+1)\\ CF(i)=y{(i)}^2+{\left[y(i)-y(i-1)\right]}^2\end{array}\right.,$$

(1)

In the equation, $y(i)$ is the seismic signal and $i$ is the sampling point.

Equation (1) presents the feature functions for four types of microseismic signals. Among them, $CF(i)=y(i)$ and $CF(i)=y{(i)}^2$ represent the instantaneous value or energy of the signal; $CF(i)=y{(i)}^2-y(i-1)y(i+1)$ detects signal mutations through differences in local stationarity; and $CF(i)=y{(i)}^2+{\left[y(i)-y(i-1)\right]}^2$ simultaneously captures both the signal amplitude and local fluctuations [27]. In this experiment, the background noise fluctuations of the microseismic signals were gentle and had low amplitude. The instantaneous amplitude at the onset of the signal shows a significant difference from the noise. Directly using the original sampled values of the signal as features can preserve the original amplitude information of the signal to the greatest extent.

The Short-Time Average/Long-Time Average (STA/LTA) method is influenced by several parameters, such as the LTA, STA, characteristic function, and threshold. Variations in these parameters can affect the picking results of the microseismic signal. Among them, the short time window is used to capture the microseismic signal. The length of the short time window is inversely proportional to the STA/LTA value. When the short time window is shorter, the STA/LTA value is larger, making it more likely to exceed the threshold and leading to a higher chance of misjudgment. Conversely, when the short time window length increases, the STA/LTA ratio decreases, reducing the sensitivity to the microseismic signal and making it less likely to trigger the threshold [7].

2.2. VMD Method

VMD is a signal processing technique used to decompose non-linear and non-stationary signals into a set of IMFs. As an improved method of EMD, VMD demonstrates superior performance in addressing the issue of modal mixing [28].

The VMD algorithm redefines the IMFs with finite bandwidth by introducing more stringent constraints. These mode functions are referred to as amplitude–frequency-modulated signals. The core concept of this method is to optimize signal decomposition. This is achieved by formulating and solving a constrained variational problem. The process decomposes the original signal into a preset number of IMF components [29]. Its mathematical model can be expressed as the following constrained variational problem [30]:

$$\underset{u_k,{\omega }_k}{\min }\left\{\sum _{k=1}^K{‖{\partial }_t\left[\left(\delta (t)+{\displaystyle \frac{j}{\pi t}}\right)\cdot u_k(t)\right]e^{-j{\omega }_{k}t}‖}_2^2\right\},$$

(2)

$$s.t.\sum _{k=1}^K{u}_k=f(t)$$

(3)

In the equation, $t\ne 0$, $f(t)$ is the original signal; $u_k$ represents the components of each mode; ${\omega }_k$ denotes the center frequency of each mode component; $\delta (t)$ is the impulse function; $K$ is the number of modes obtained from the decomposition; and $s.t.$ stands for subject to.

Equations (2) and (3) define a variational problem. To solve it optimally, Lagrange multipliers $\lambda$ and a quadratic penalty factor $\alpha$ are introduced. This transformation converts the original constrained problem into an unconstrained one. Thus, when solving for the constrained solution, it can be computed using Equation (4);

$$\begin{array}{l}L(u_k,{\omega }_k,\lambda )=\alpha {\displaystyle \sum _{k=1}^K}{‖{\partial }_t\left[\left(\delta (t)+{\displaystyle \frac{j}{\pi t}}\right)*u_k(t)\right]e^{-j{\omega }_{k}t}‖}_2^2\\ +\parallel f(t)-{\displaystyle \sum _{k=1}^K}{u}_k(t){\parallel }_2^2+〈\lambda (t),f(t)-{\displaystyle \sum _{k=1}^K}{u}_k(t)〉\end{array},$$

(4)

In the formulation, $L$ is the Lagrangian function, $K$ denotes the preset number of modes, $u_k(t)$, is the k-th IMF, $\lambda (t)$ represents the Lagrange multiplier, $\alpha$ is the bandwidth penalty parameter, $\delta (t)$ is the Dirac delta function, $*$ is the convolution operator, ${\partial }_t$ is the partial derivative with respect to time, ${\Vert \Vert }_2^2$ denotes the squared L²-norm, and $〈,〉$ represents the L² inner product operator.

The decomposition process of VMD primarily depends on two factors: the number of IMFs, denoted as $K$, and the penalty factor, denoted as $\alpha$. If parameter $K$ is set too small, decomposition may be insufficient. In this case, noise is amplified, and the decomposition quality degrades. If $K$ is too large, over-decomposition and mode mixing may occur. In this case, noise is amplified, and decomposition quality degrades. If penalty factor $\alpha$ is too small, frequency constraints become weak. This leads to excessively broad modal bandwidths, unstable frequencies, or frequency overlap. If $\alpha$ is too large, some detailed information may be lost in later decomposition stages. Therefore, the key to the VMD algorithm is accurately determining the optimal values for $K$ and $\alpha$ to achieve the best decomposition results. The optimization of these parameters ensures the effectiveness and reliability of VMD in signal processing [31].

To address the difficulty of presetting the parameter $K$ in VMD, an effective strategy is to use permutation entropy as a criterion. Wang et al. [32] adaptively determined the value of $K$ through the Permutation Entropy Optimization (PEO) algorithm. This algorithm effectively distinguishes normal physical modes from abnormal noise or spurious components by calculating and comparing the permutation entropy values of each IMF component with a preset threshold, thereby automatically determining the optimal decomposition level. To solve the difficult problem of determining the decomposition level $K$ and penalty factor $\alpha$ in VMD, this paper proposes a parameter-adaptive selection method based on permutation entropy minimization. The core idea of this method is that an optimal parameter combination minimizes the average permutation entropy of the obtained IMFs, thereby ensuring that each modal component exhibits optimal regularity and clear physical significance.

To determine the optimal parameter combination for VMD, this study uses permutation entropy as a quantitative indicator to evaluate the decomposition performance. The lower the permutation entropy value, the stronger the regularity of the decomposed IMFs and the lower the random noise content, indicating higher decomposition quality. This study conducted a comprehensive analysis of the parameter combinations: the number of modes, $K$, was set within the integer range of 3 to 8, the penalty factor was chosen within the range of 1000 to 7000, the time delay was fixed at 1, and the embedding dimension at 5. By calculating the permutation entropy under different parameter combinations, all results were finally integrated into Figure 1 for visual presentation and comprehensive analysis.

By analyzing the average permutation entropy of IMFs obtained from VMD decomposition under different K and alpha values, it was found that when $K$ = 4–6 and $\alpha$ = 2000–4000, the permutation entropy remained at a relatively stable level with gradual variation. This indicates that the modal complexity of the decomposition at this stage is moderate and the information content is abundant, making it suitable for the time-frequency feature extraction and subsequent analysis of microseismic signals.

To select the optimal combination of $K$ and $\alpha$, we introduced the instantaneous frequency [33], as illustrated in Figure 2.

Based on the trends observed in all the subplots of Figure 2, when $K$ = 5—regardless of whether $\alpha$ was 2000, 3000, or 4000—the instantaneous frequency curve exhibited a clear and gentle upward trend. It neither showed the abrupt jumps observed with $K$ = 3 nor the excessive dispersion seen with $K$ = 6. The overall variation pattern aligned more closely with the expected features of the modal frequencies after VMD decomposition. Moreover, changes in α had a minimal impact on the curve trend for $K$ = 5, indicating that $K$ = 5 demonstrated greater stability. The variation of α had little effect on the curve trend for $K$ = 5, indicating that $K$ = 5 demonstrated greater stability.

2.3. The Proposed Method

This study combines the advantages of VMD and STA/LTA to propose a VMD-based STA/LTA method for microseismic arrival time-picking. The corresponding picking procedure is illustrated in Figure 3. The specific steps are as follows:

(1)

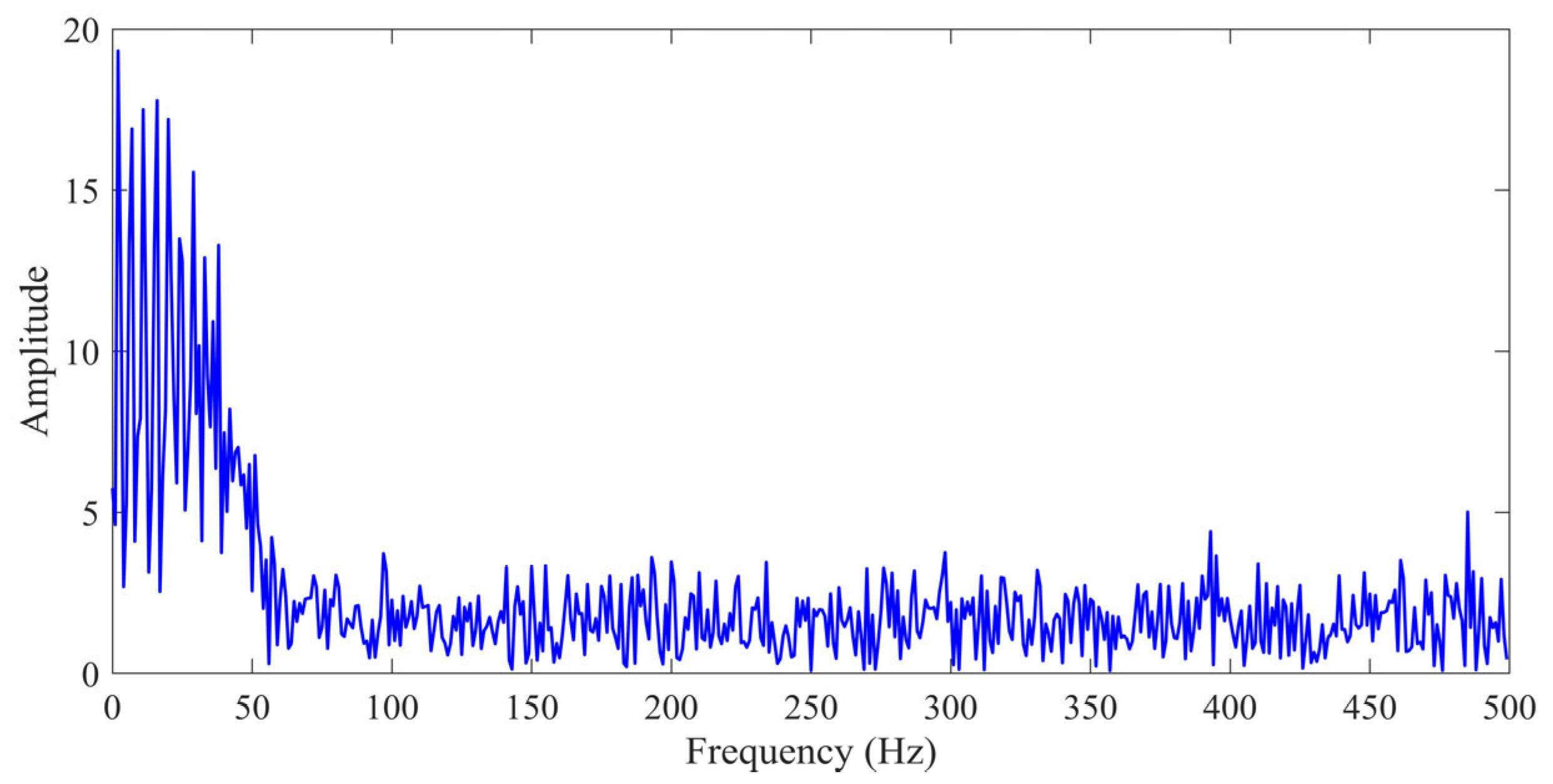
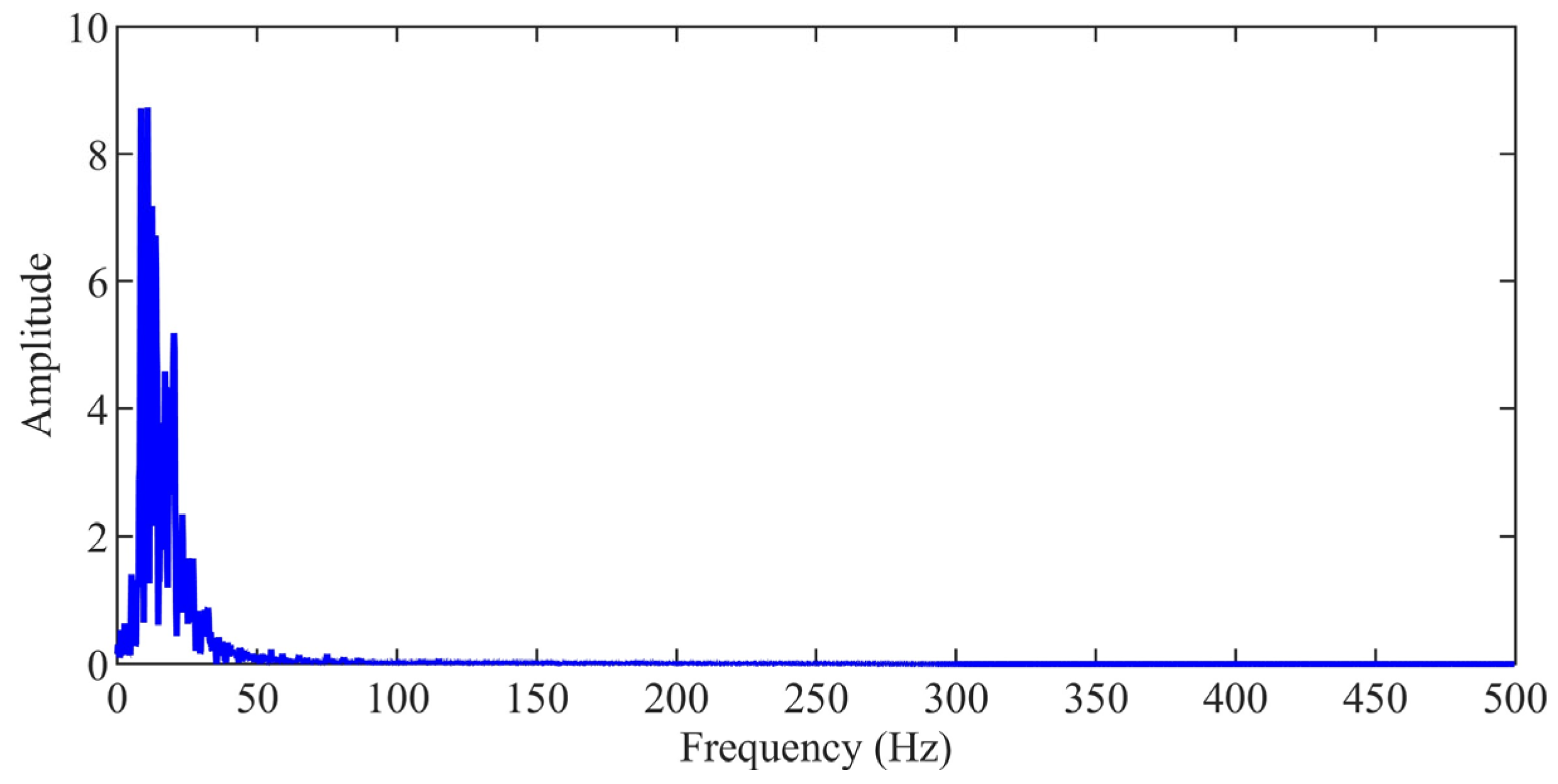
In order to investigate the dominant frequency distribution characteristics, the frequency spectrum of the microseismic signal is obtained through FFT. The equation can be expressed as

$$X(f)={\displaystyle {\int }_{-\infty }^{\infty }x(t)\cdot e^{-j2\pi ft}dt}$$

(5)

where $X(f)$ is the FFT result of the microseismic signal $x(t)$.

(2)

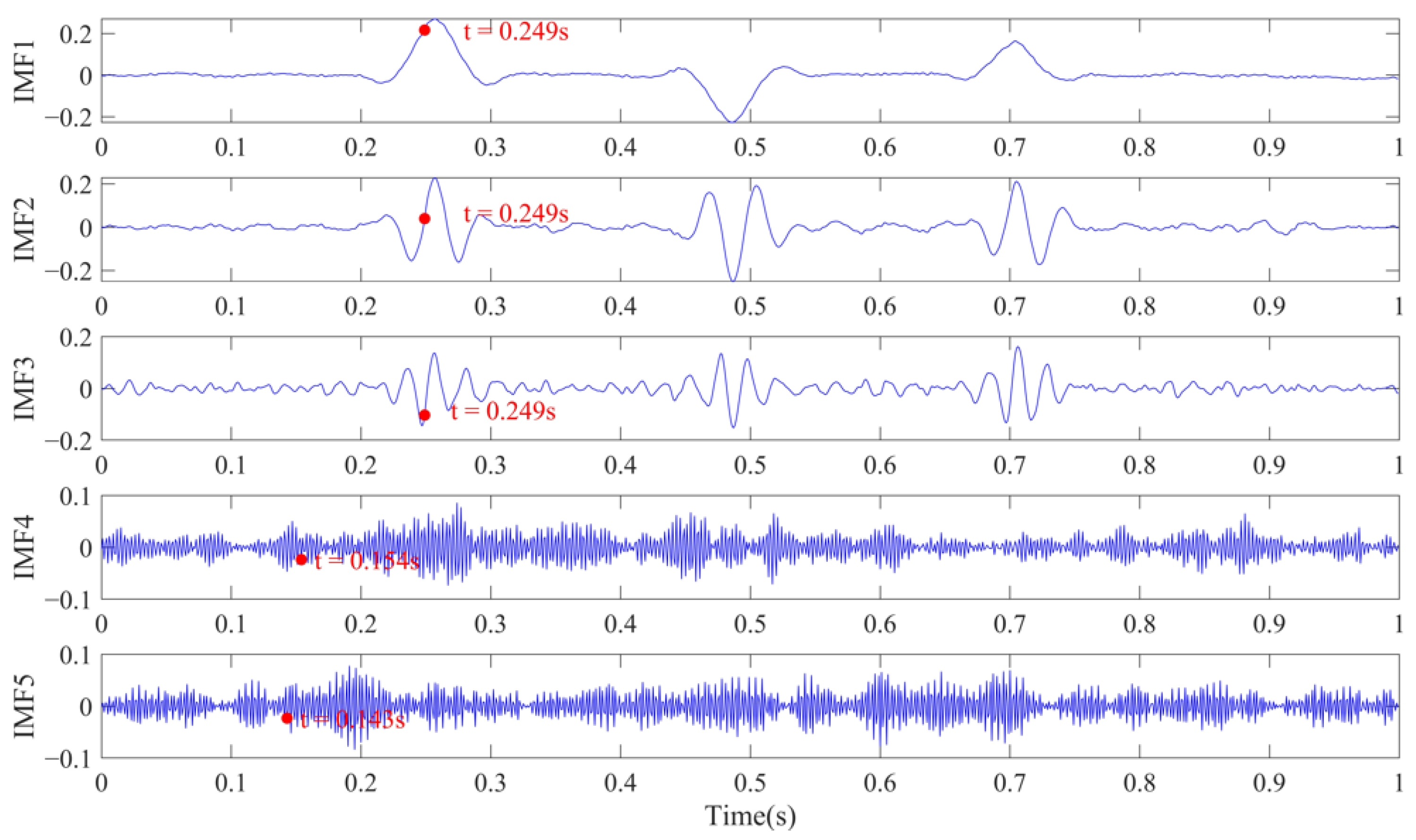
$x(t)$ is decomposed into several mode signals, $u_k(t)$ and a residual term $r(t)$ through VMD. Each mode signal represents different frequency components.

$$x(t)={\displaystyle \sum _{k=1}^k{u}_k(t)}+r(t)$$

(6)

(3)

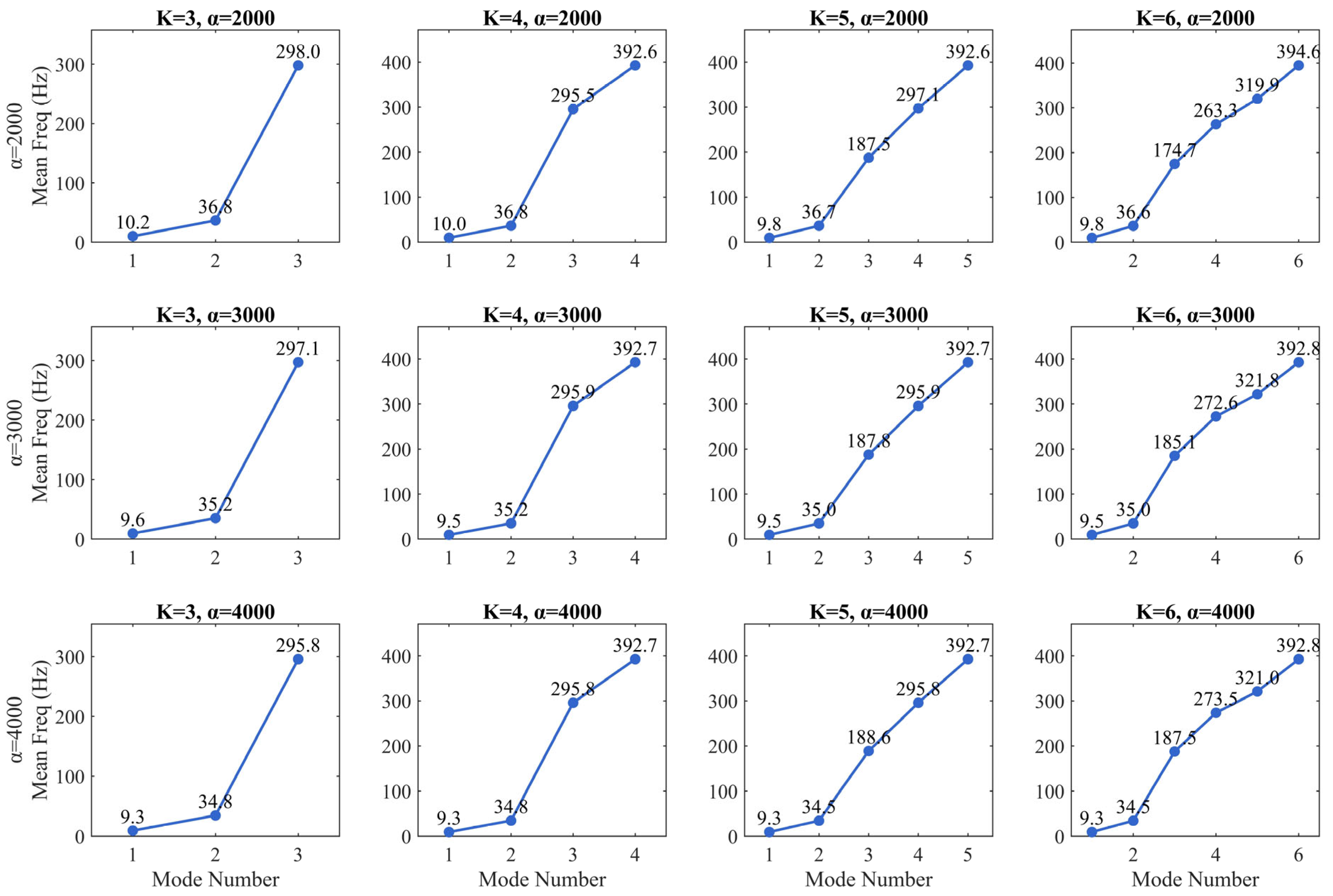
For selecting the effective modal components according to the frequency distribution of a microseismic signal, we need to calculate the center frequencies of each IMF. This helps differentiate effective signals from noise. Assuming $Uk(f)$ is the frequency spectrum of $uk(t)$, the center frequency $f(c,k)$ can be calculated using the following equation:

$$fc,k={\displaystyle \frac{{\displaystyle {\int }_{-\infty }^{\infty }f{\left|Uk(f)\right|}^{2}df}}{{\displaystyle {\int }_{-\infty }^{\infty }{\left|Uk(f)\right|}^{2}df}}}$$

(7)

where ${\left|Uk(f)\right|}^2$ is the Power Spectral Density of mode $K$, representing the energy at frequency $f$, and $fc,k$ denotes the central frequency of the mode component, which represents the frequency point with the most concentrated energy distribution in the spectrum.

(4)

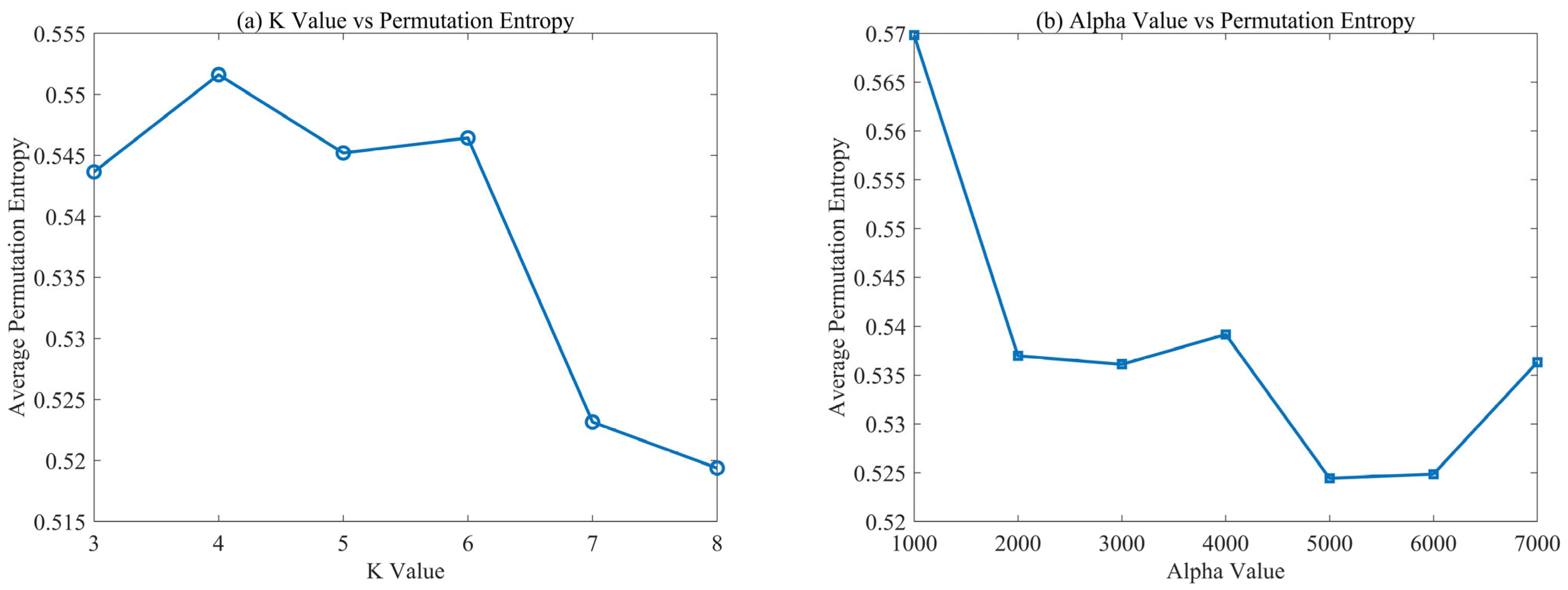
The proposed method establishes the mean value of IMFs’ center frequencies as the selection criterion, classifying modal components with sub-average center frequencies as the effective signal-bearing elements. STA/LTA is implemented on the selected IMFs to pick arrival time. The STA and LTA are then computed as follows:

$$STA(t)={\displaystyle \frac{1}{Nsta}}{\displaystyle \sum _{i=t-Nsta+1}^{t}ui(t)}$$

(8)

$$LTA(t)={\displaystyle \frac{1}{Nlta}}{\displaystyle \sum _{i=t-Nlta}^{t}ui(t)}$$

(9)

$STA(t)$ donates the short-time average at time $t$, $LTA(t)$ represents the long-time average at time $t$, and $Nsta$ and $Nlta$ represent their respective window lengths.

(5)

We calculate the ratio of STA to LTA and manually set a threshold, $\theta$, to determine whether a microseismic event has occurred.

$$Ratio(t)={\displaystyle \frac{STA(t)}{LTA(t)}}$$

(10)

If $Ratio(t)>\theta$, a microseismic event is considered to have occurred.

(6)

To fuse the arrival time-picking results from the selected IMFs, an adaptive energy-weighted approach is employed that requires computing the energy value of each selected IMF component as follows:

$$Ei={{\displaystyle \int \left|ui(t)\right|}}^{2}dt$$

(11)

In the equation, $Ei$ represents the energy of mode component $i$, and $\left|ui(t)\right|$ denotes the amplitude value.

According to the calculated energy values, the energy of an IMF component is positively correlated with the ‘effective information’ it contains. Components with higher energy often carry the core characteristics and main power of the signal, meaning they contain a larger proportion of the effective components in the overall composition. Therefore, higher weight coefficients should be assigned to these high-energy components. The corresponding weighting coefficients are computed by using the following equation:

$$\omega i={\displaystyle \frac{Ei}{{\displaystyle {\sum }_{i=1}^{K}Ei}}}$$

(12)

where $\omega i$ represents the weighting coefficients.

(7)

The final arrival time $T$ is obtained by computing the weighted fusion of the arrival picks from the selected components using their corresponding weighting coefficients.

$$T={\displaystyle \sum ti\cdot \omega i}.$$

(13)

In the equation, $ti$ represents the picking time for each component, and $T$ is the final picking result.

3. Simulation Experiment

As shown in the top panel of Figure 4, to validate the proposed method, three groups of Ricker wavelets were simulated with centre frequencies of 20, 25, and 30 Hz, corresponding to the dominant frequency band of microseismic P-waves recorded in deep mines. The simulation contained 1000 sampling points, with a sampling interval of 1 ms. Then, Gaussian noise was added to the simulated signal, resulting in an SNR of 5 dB, as shown in Figure 4 (middle). The bottom panel of Figure 4 shows the STA/LTA picking result.

Figure 5 presents the frequency spectrum obtained from the microseismic signal using FFT. As can be observed from Figure 5, the frequency distribution of this microseismic signal was predominantly distributed within the 10–50 Hz range, indicating the presence of effective signal content in this band. The sharp roll-off of amplitude beyond the primary peak indicates limited bandwidth and the absence of significant higher-order harmonics or noise in the frequency domain above 150 Hz.

The microseismic signal was decomposed into five modal components by VMD [31], as shown in Figure 6. It can be observed from the figure that IMF1, IMF2, and IMF3 primarily consisted of effective signals with minimal noise, exhibiting high SNR. In contrast, IMF4 and IMF5 were predominantly composed of noise with negligible effective signals, resulting in low SNR. Figure 5 clearly demonstrates that the picking results were highly consistent for IMF1–3, while IMF4 and IMF5 exhibited noticeable picking errors due to noise interference.

Based on the differences in the center frequencies of each IMF, IMF1–3 were selected as the effective components, and the energy values were then calculated by Equation (11). Then, the corresponding weight coefficients were obtained by Equation (12). The results are shown in Figure 7.

The arrival time-picking results are shown in Figure 8. The green dots represent the manually picked result (0.248 s). Here, we used the manual result as an accurate arrival time. The blue dots denote the STA/LTA-picked result (0.251 s). The red dots indicate the proposed method’s picking results (0.248 s). The method proposed in this paper achieved a picking accuracy of first-arrival times that was closer to the manually picked benchmark results and outperformed the conventional STA/LTA method.

This experiment applied the same process to data with different signal-to-noise ratios, yielding the results shown in

Table 1. Comparison of VMD picking results with manual, AIC, and STA/LTA.

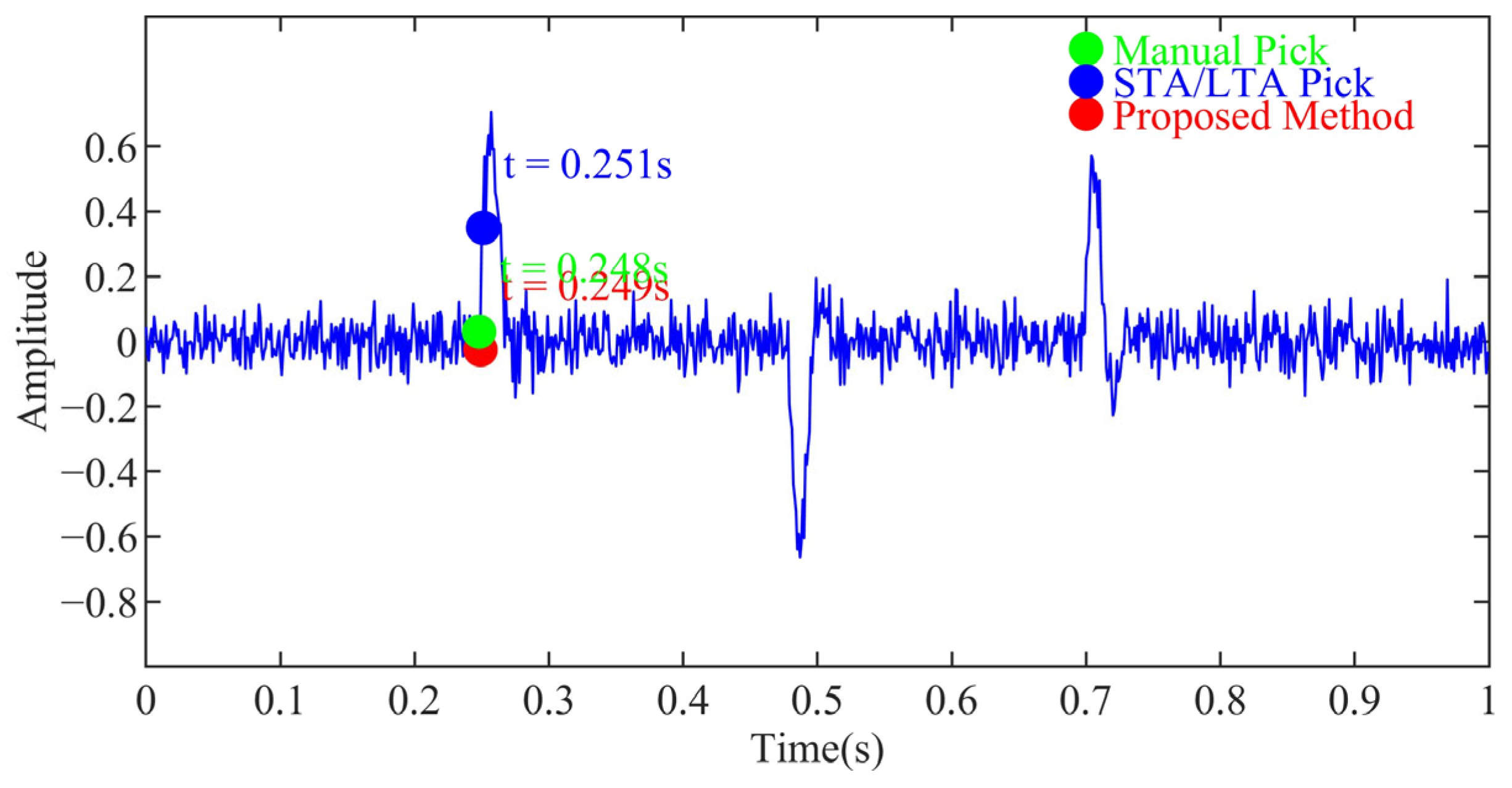
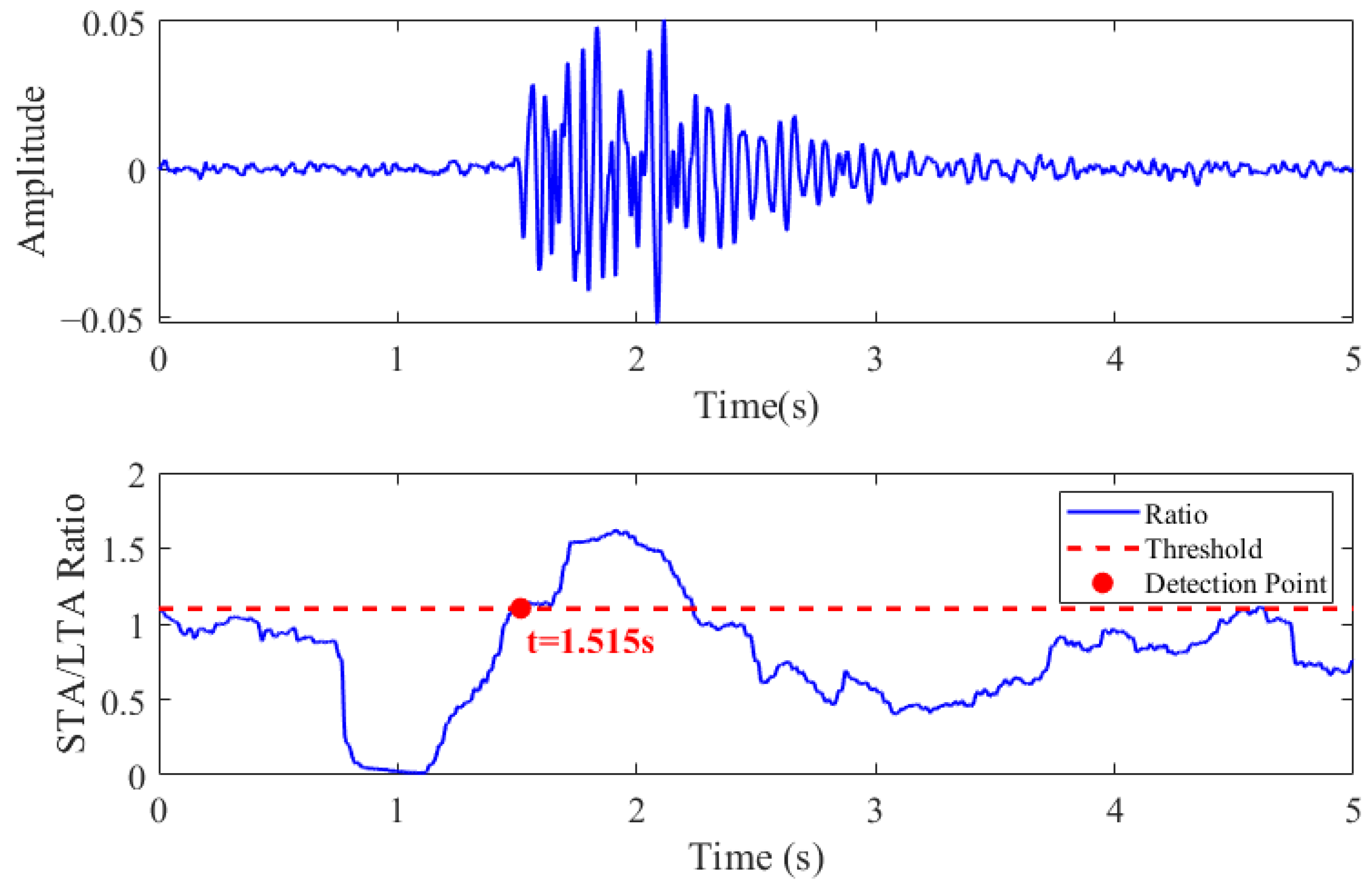
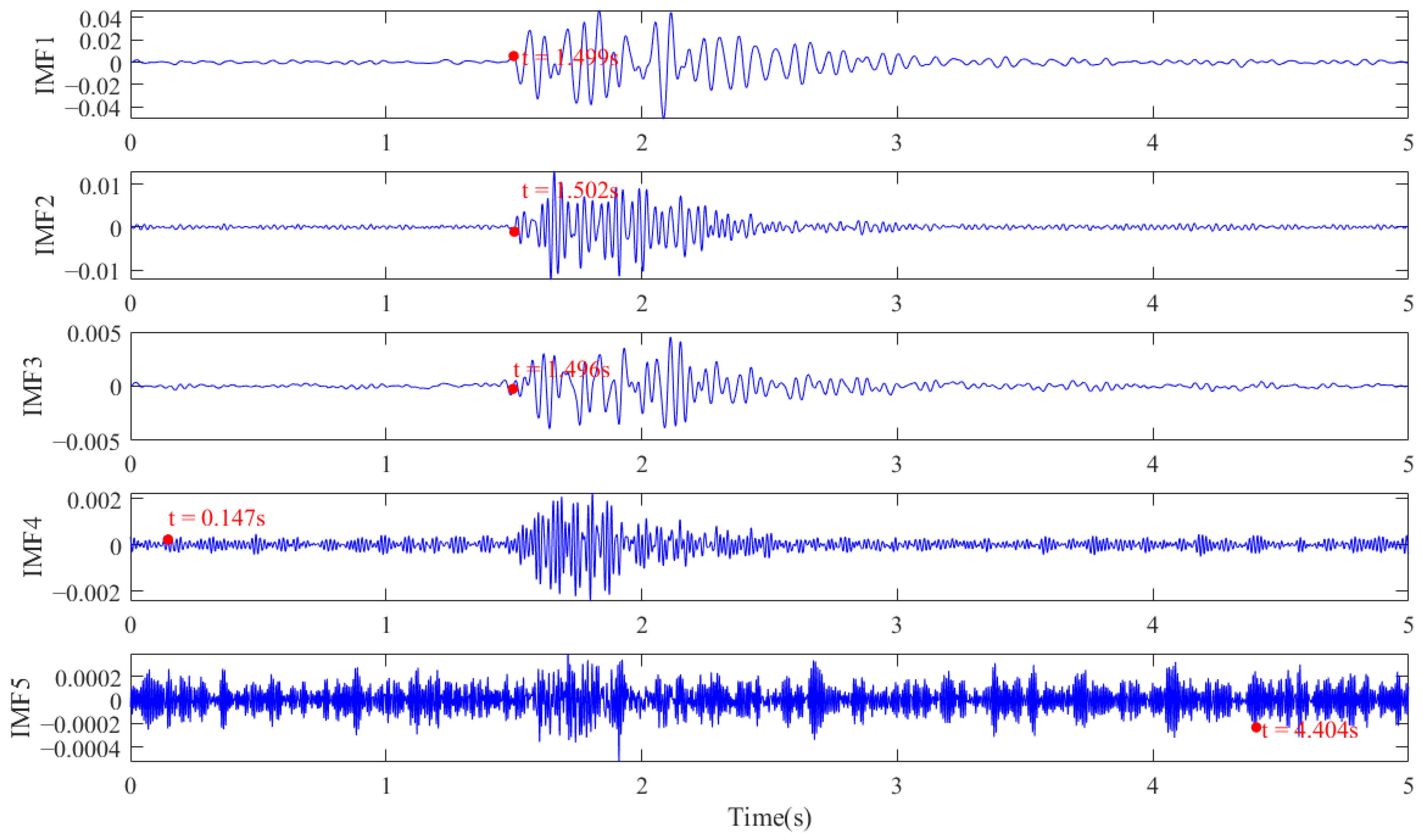
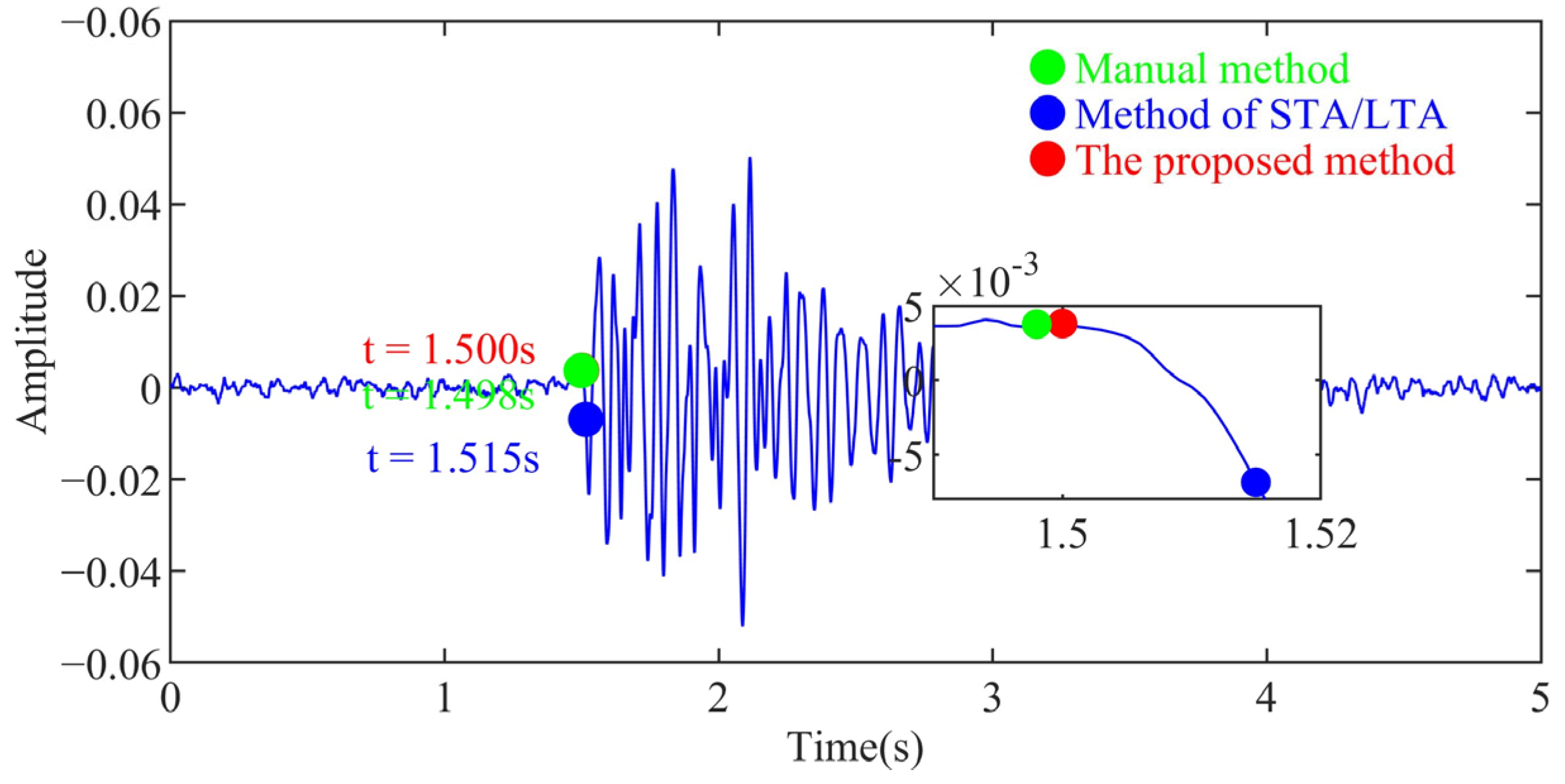
SNR (dB)	Manual Picking Result (s)	STA/LTA Picking Results (s)	Absolute Error of STA/LTA (s)	AIC Picking Result (s)	Absolute Error of AIC (s)	V-STA/LTA Picking Result (s)	Absolute Error of V-STA/LTA (s)
0	0.248	0.253	0.005	0.251	0.003	0.2484	0.0004
5		0.251	0.003	0.250	0.002	0.249	0.001
10		0.252	0.004	0.247	0.001	0.2488	0.0008
15		0.250	0.002	0.248	0	0.248	0
Root Mean Squared Error (RMSE)			0.0015		0.0011		0.0005
Mean Absolute Error (MAE)			0.0035		0.0015		0.00055
Standard Deviation (SD)			0.0013		0.0012		0.0004

; the quantitative comparison results of root mean square error (RMSE = 0.0005 s), mean absolute error (MAE = 0.00055 s), and standard deviation (SD = 0.0004 s) indicate that the V-STA/LTA method proposed in this paper significantly outperformed the traditional STA/LTA (RMSE = 0.0015 s, MAE = 0.0035 s) and AIC methods (RMSE = 0.0011 s, MAE = 0.0015 s) in first arrival picking accuracy. Moreover, it exhibited smaller error fluctuations under different SNR conditions, demonstrating superior stability and robustness, thereby comprehensively validating the method’s overall advantages in both accuracy and stability.

4. Field Data Examples

4.1. Instances 1

To verify the practical accuracy of the proposed method, we conducted validation tests using field data. This study used ESG Solutions’ microseismic monitoring system for data collection. The core of the system is the Paladin series digital recorder, which supports a maximum sampling rate of 20 kHz. Data are collected through various sensors such as geophones (frequency band 2–1000 Hz) and accelerometers (frequency band DC-8 kHz), then transmitted to the acquisition computer via optical fiber or wireless network. This study introduced the mine microseismic monitoring data shown in Figure 9 (top). The data had a sampling rate of 1000 Hz and contains 5000 sampling points. This study used the STA/LTA method to determine the arrival time of microseismic signals, as shown in Figure 9 (bottom).

Figure 10 presents the frequency spectrum obtained from the microseismic signal using FFT. As can be observed from the Figure 10, the frequency distribution of this microseismic signal was predominantly within the 10–40 Hz range, indicating the presence of effective signal content in this band. The high-frequency components (>40 Hz) showed negligible energy levels, which are likely attributable to background noise.

Figure 11 presents the five mode components obtained through the VMD of the microseismic signal. As can be observed from the Figure 11, IMF1, IMF2, and IMF3 exhibited higher SNR compared to IMF4 and IMF5, with a gradual decrease in energy. Then, the arrival times for each IMFs were picked using the STA/LTA method, as illustrated in the Figure 11. This figure clearly demonstrates that the picking results were highly consistent for IMF1–3, while IMF4 and IMF5 exhibited noticeable picking errors due to noise interference.

To fuse the arrival time-picking results from the selected IMFs, it was required to computed the energy value of each selected mode component for calculating the corresponding weighting coefficients. We calculated the energy values of IMF1–3 with Equation (11). Then, the corresponding weight coefficients were obtained by Equation (12). Finally, we calculated the precise arrival time results by Equation (13).

The arrival time-picking results are shown in Figure 12. The green dots represent the manually picked result (1.498 s). This study used the manual result as an accurate arrival time. The blue dots denote the STA/LTA picked result (1.515 s). The red dots indicate the proposed method’s picking results (1.500 s).

4.2. Instances 2

To validate the stability and reliability of the proposed method, another microseismic record was analyzed, as shown in Figure 13. This study used the STA/LTA method to determine the arrival time of microseismic signal, as shown in Figure 13 (bottom).

As can be observed from Figure 14, the microseismic signal exhibited a frequency spectrum primarily concentrated within the 10–30 Hz range, suggesting the existence of effective signal components within this frequency band. In contrast, the high-frequency components (>40 Hz) exhibited minimal energy contribution, which is most likely associated with ambient background noise.

Then, this study used VMD decomposed microseismic signal into five modes, as shown in Figure 15. IMF1, IMF2, and IMF3 exhibited higher SNR compared to IMF4 and IMF5. Then, arrival times for each IMFs were picked using the STA/LTA method, as illustrated in Figure 15.

This study integrated the arrival time picks from the selected IMFs by first computing the energy of each mode (IMF1–3) with Equation (11). Using these values, we then determined the weighting coefficients via Equation (12), which enabled the final calculation of a precise arrival time using Equation (13).

The arrival time-picking results are shown in Figure 16. The green dots represent the manually picked result (0.951 s). This study used the manual result as an accurate arrival time. The blue dots denote the STA/LTA picked result (0.989 s). The red dots indicate the proposed method’s picking results (0.951 s).

In order to systematically evaluate the performance of different automatic picking methods for microseismic P-wave arrivals, this study compared three automatic methods—STA/LTA, AIC, and V-STA/LTA—from the perspectives of picking accuracy and error analysis, using manually picked results as the benchmark.

In terms of picking accuracy, as shown in Figure 17, an analysis of 15 sets of test data indicated that the accuracy of all automatic methods remained at a high level (>98%) and were closely centered around the ideal accuracy (100%). Among them, the V-STA/LTA method demonstrated the most outstanding overall performance, with an average accuracy of 99.77%, surpassing the STA/LTA (98.93%) and AIC (99.44%) methods, showing excellent stability and reliability across different events.

In terms of error analysis, as shown in

Table 2. Comparison of VMD picking results with manual, AIC, and STA/LTA methods.

Method	Manual (s)		STA/LTA (s)		AIC (s)		V-STA/LTA (s)
No.
1	1.498		1.515		1.487		1.500
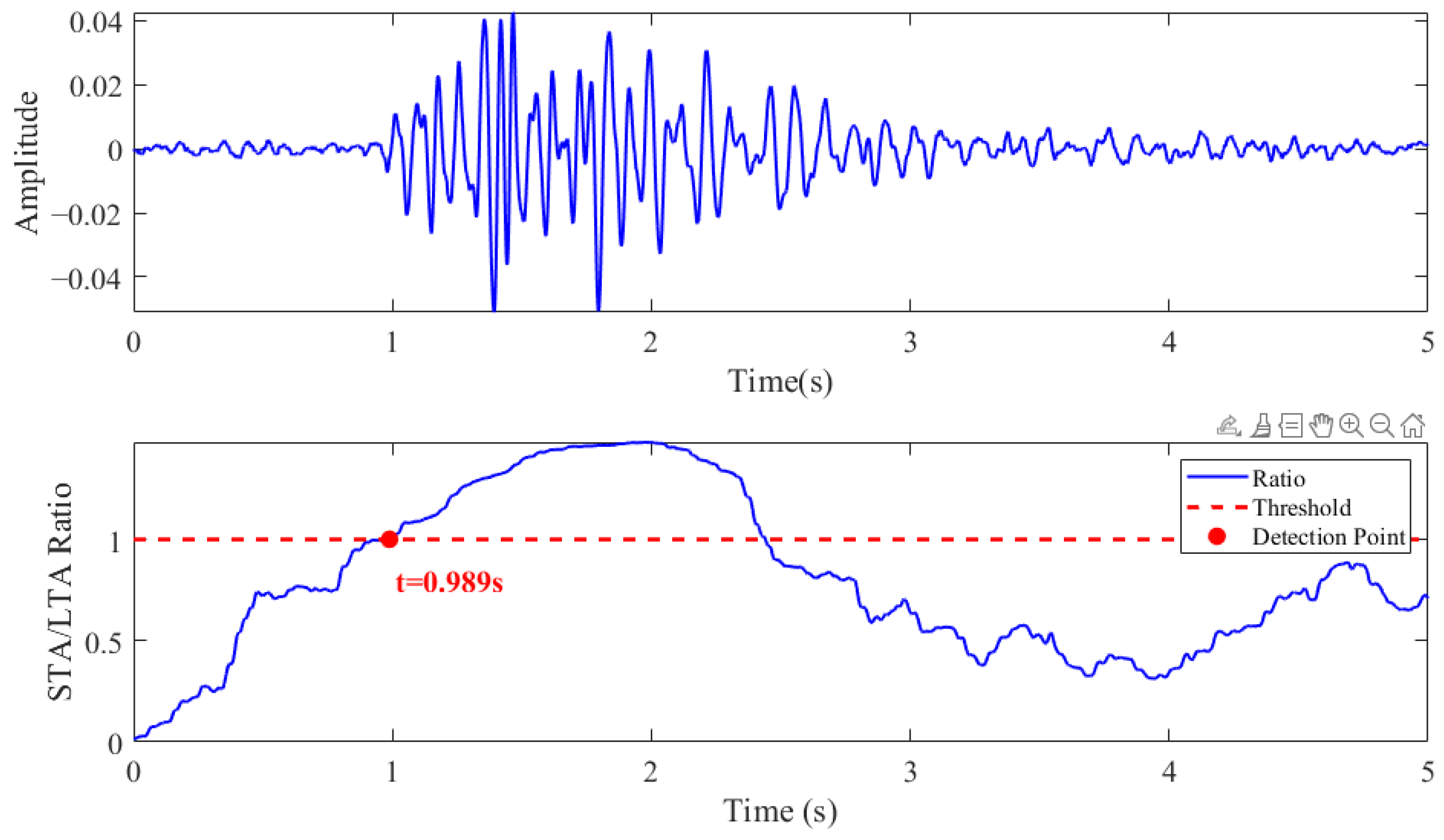
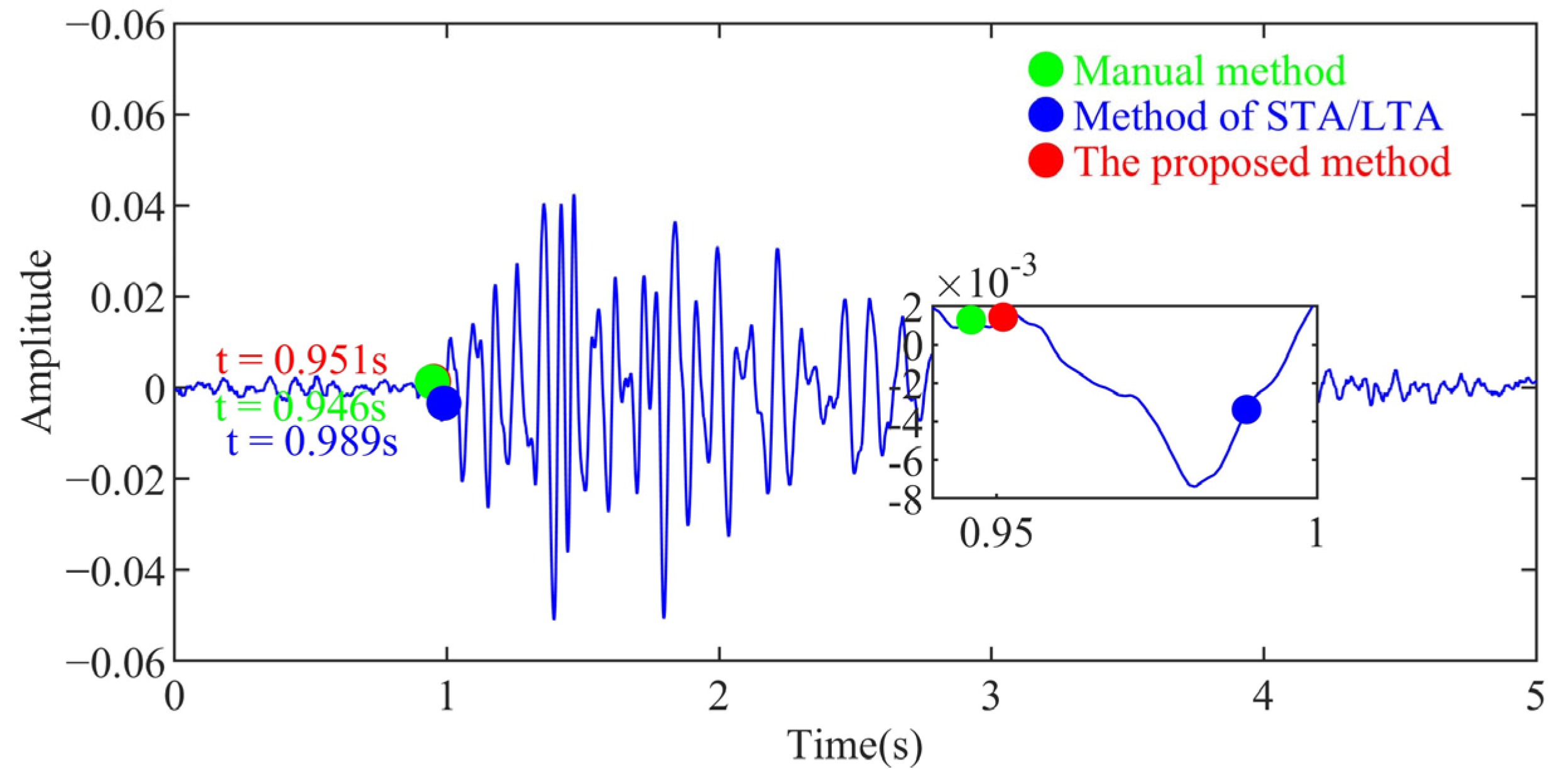
2	0.946		0.989		0.968		0.951
3	1.225		1.235		1.230		1.228
4	1.125		1.132		1.12		1.128
5	1.344		1.348		1.345		1.344
6	1.405		1.410		1.408		1.405
7	1.514		1.521		1.519		1.514
8	1.490		1.504		1.499		1.494
9	1.302		1.308		1.304		1.303
10	1.201		1.207		1.203		1.199
11	1.339		1.343		1.341		1.340
12	1.424		1.438		1.434		1.429
13	1.53		1.557		1.555		1.548
14	1.509		1.517		1.511		1.508
15	1.540		1.582		1.545		1.543
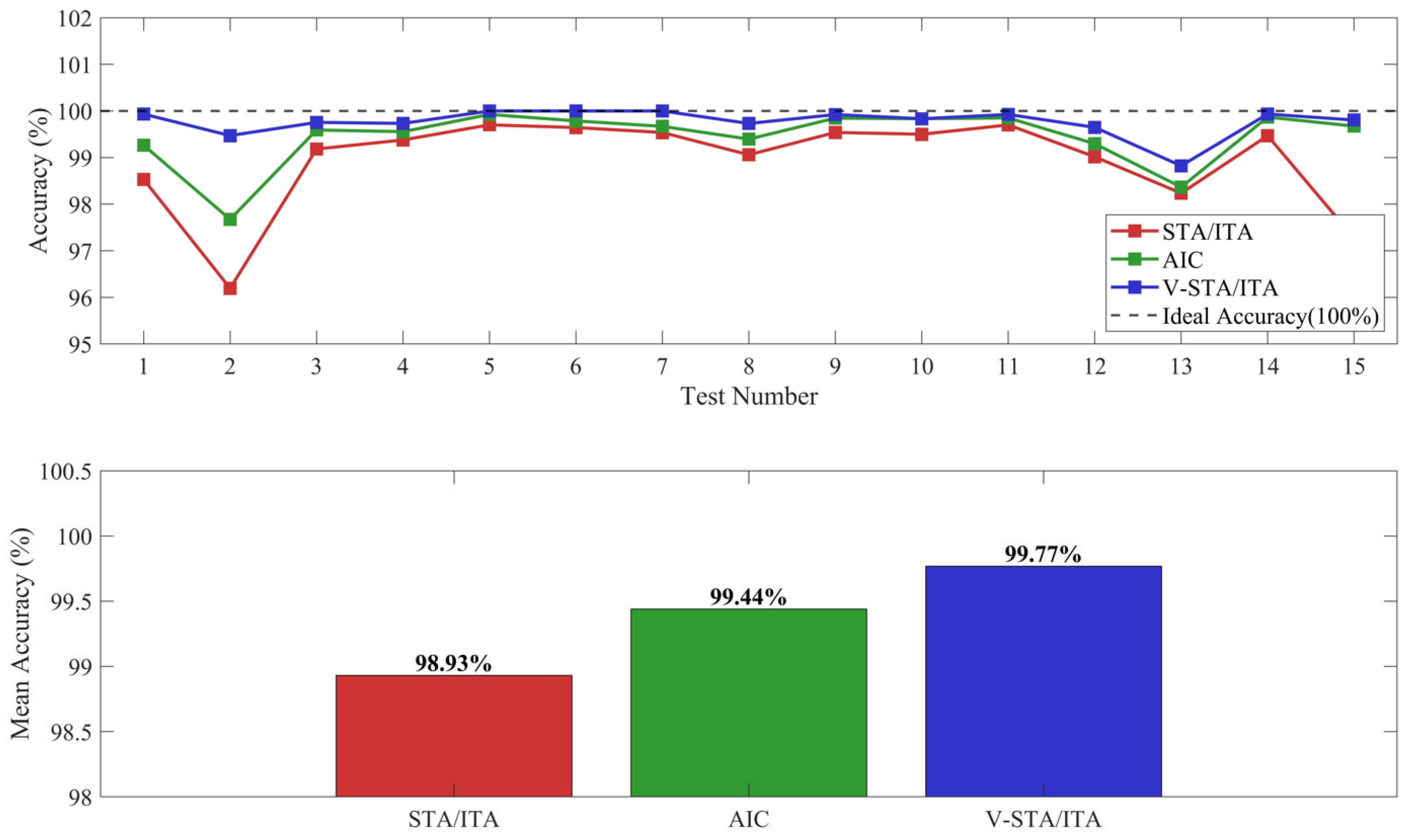
Mean error		0.0121		0.0087		0.0021
Mean absolute error (MAE)		0.0153		0.0115		0.0050
Root mean square error (RMSE)		0.0192		0.0143		0.0063
Standard deviation (SD)		0.0198		0.0147		0.0065

, this study calculated various error metrics between each automatic method and the manually picked results. The V-STA/LTA method achieved the lowest values for all key metrics, with a mean error (ME) of 0.0021 s, mean absolute error (MAE) of 0.0050 s, root mean square error (RMSE) of 0.0063 s, and standard deviation (SD) of 0.0065 s. These data consistently indicate that the picking results of the V-STA/LTA method were closest to the manually picked standard values, with the least dispersion and the best reproducibility. In contrast, the STA/LTA method had the highest values for all error metrics.

5. Discussion

In both theoretical simulations and experimental data tests, the proposed V-STA/LTA method enhanced performance over the traditional STA/LTA for the following reasons: Traditional STA/LTA operates directly on the raw signal, making it vulnerable to noise and signal interference, whereas V-STA/LTA first decomposes the raw signal into multiple modal components using VMD, then selects the components that match the effective signal before executing STA/LTA detection. This procedure leverages VMD’s adaptive denoising capability to separate signal from noise while preserving the simplicity of STA/LTA. Consequently, in theoretical simulations, it achieved a significant reduction in RMSE (0.0005) and MAE (0.00055), and, in real data, the average accuracy (99.77%) improved by nearly 1 percentage point compared to traditional STA/LTA (98.93%), demonstrating particularly stable performance in low signal-to-noise ratio scenarios (e.g., SNR = 0) or in cases of signal overlap.

The limitations of V-STA/LTA are also focused on process dependency: the modal decomposition effect of VMD is influenced by parameters such as the number of decomposition layers and penalty factors. If the parameters and component selection are not adapted to the data scenario (such as different types of seismic phases), it may lead to reduced picking accuracy and increase the debugging cost in practical applications. In comparison, the AIC method does not require threshold settings, but it lacks a signal preprocessing step and is easily affected by noise in weak signal scenarios. While machine learning methods can automatically learn signal features, they rely on a large number of labeled samples and have difficulty explaining the processing logic at the modal hierarchy level, making them less suitable than V-STA/LTA in scenarios with small samples or where interpretability is required.

Future research will focus on further enhancing the automation and intelligence of this method. Specifically, exploring the introduction of intelligent optimization algorithms to automatically match the optimal decomposition parameters of VMD could fundamentally reduce the intervention and uncertainty caused by manual parameter tuning. On the other hand, it is possible to try embedding a lightweight modal classification model to automatically identify and filter the decomposed intrinsic mode functions, thereby intelligently retaining effective signal components in complex noisy scenarios and significantly enhancing the robustness and generalization capability of the entire method.

6. Conclusions

This paper proposes a V-STA/LTA method that integrates VMD with the STA/LTA algorithm. The method first employs permutation entropy and instantaneous frequency to determine the optimal parameters for VMD decomposition and subsequently, through an effective intrinsic mode component selection mechanism and an adaptive weight allocation mechanism, enhances the accuracy of microseismic signal arrival time-picking. However, this paper still has many shortcomings.

The dataset relied on in the current experiment mainly came from on-site monitoring data of specific mining areas. In the future, by integrating microseismic monitoring data from different mines, it is possible to build a large-scale, multi-scenario standardized database, further verifying the method’s adaptability under complex geological engineering conditions and providing a data foundation for cross-scenario microseismic signal processing.

In this study, parameters such as the number of decomposition levels and penalty factors of VMD needed to be determined through experience or trial and error, and the time window length of STA/LTA also depended on manual settings, which to some extent affects the model’s level of automation and generalization capability. Future research could introduce machine learning algorithms to achieve adaptive parameter optimization and automatic feature extraction in a data-driven manner, constructing an end-to-end model from microseismic signals to arrival picking. Such a model would not require manual intervention for parameter selection, could better adapt to microseismic signals with different characteristics, further improve the accuracy and generalization of arrival picking, and provide a new pathway for the intelligent upgrading of microseismic monitoring in mines.