Experimental Study on Wavefront Distortion Correction in Atmospheric Turbulence Using Zernike-Wavelet Hybrid Basis

Abstract

In adaptive optics systems, most methods rely on reconstruction techniques centered on regional or global orthogonal bases, which struggle to accommodate the multi-scale characteristics of atmospheric turbulence wavefronts. This paper adopts a hybrid basis wavefront reconstruction method based on mutual information sorting, combining Zernike modes with Daubechies wavelet modes for mutual information calculation and sorting. The modes with the highest correlation are selected for reconstruction, effectively reducing the scale of the reconstruction matrix while considering both global and local features. The reconstruction results show that when the number of modes is 20, the root mean square (RMS) of the wavefront residual error of the hybrid basis reconstruction drops to 0.14 rad, outperforming 0.19 rad of the Zernike mutual information method and 0.33 rad of the Zernike expansion method. The peak-to-valley (PV) value after wavefront correction converges to 0.057 μm at the 39th iteration, demonstrating a faster convergence speed and smaller residual error; the RMS value converges to 0.027 μm at the 77th iteration after correction.

1. Introduction

Wavefront reconstruction algorithms typically use low-order Zernike polynomials of a fixed order for wavefront fitting [1]. However, this approach, which neglects the complex composition of real wavefront aberrations, is prone to mode confusion or coupling, thereby degrading reconstruction accuracy [2]. In adaptive optical systems, there are mainly two types: wavefront sensors and non-wavefront sensors [3]. Adaptive systems with wavefront sensors usually can reconstruct the wavefront quite well using Zernike polynomials [4]. In order to further enhance the reconstruction efficiency, people calculate the mutual information between atmospheric turbulence distortion and each Zernike mode, and rearrange the polynomial sequence according to the correlation, thereby reducing the complexity of the reconstruction matrix [5]. By introducing the tight-support Daubechies wavelet and solving the maximum a posteriori estimation within the wavelet haodedomain, an efficient and stable wavefront reconstruction was achieved, resulting in a higher Strehl ratio. In recent years, researchers have also compared the performance of various basis functions such as Zernike, DCT, Haar, and Daubechies wavelets, and found that each of them has its own advantages in extracting low-frequency and high-frequency features [6]. Wavelet transform, as an effective mathematical analysis tool, can simultaneously obtain the time-domain and frequency-domain information of signals and images. In 2011, Han Chengshan [7] combined multi-resolution analysis and thresholding techniques to optimize performance and compared it with the least squares method, Zernike mode method and iterative method. The results showed that the wavelet mode method was superior in terms of calculation speed and convergence accuracy. In 2022, Ma Shengjie [8] introduced wavelet transformation based on fractal interpolation to address the issue of high-frequency information loss caused by the smoothing effect. By using wavelet basis to reconstruct the distorted wavefront, it was found that the wavefront reconstructed using this method had higher resolution, richer texture information and details.

This paper combines Zernike polynomials with wavelet bases to analyze the coefficient variance (information content) and mutual information after pattern projection, and selects the most important and least redundant set of patterns, namely some low-order Zernike and some mid–high-frequency wavelets. The reconstruction method is based on the pattern design perspective, combines the global patterns of Zernike with the local patterns of Daubechies wavelets, and then selects the most important subset of patterns adaptively through the mutual information sorting mechanism. It can achieve the joint expression of the global structure and local details of atmospheric turbulence without clearly dividing the frequency bands, thereby achieving better reconstruction results. Although Zernike and wavelets are not directly used for low-frequency and high-frequency reconstructions separately, they are combined as a joint basis. Through mutual information analysis with atmospheric turbulence, the independence and contribution of each pattern are evaluated, and the most important subset is selected from it. The final result is a minimum basis set that best represents the turbulence structure for reconstruction.

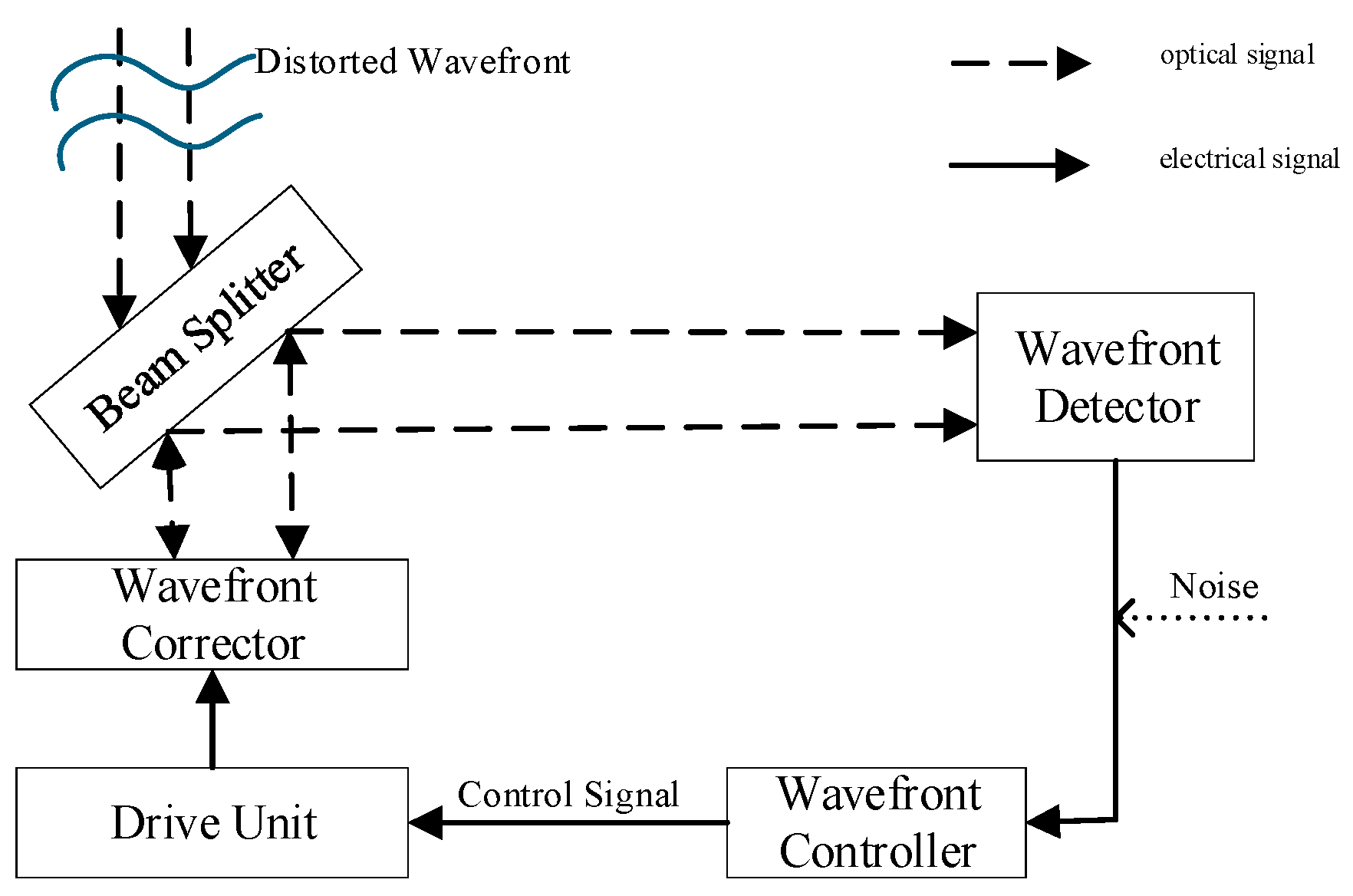
2. Theoretical Foundation of Adaptive Optics

The article focuses on the correction system with a wavefront sensor. This system consists of three major parts: a wavefront detector, a wavefront controller, and a wavefront corrector, forming a closed-loop control circuit to achieve dynamic wavefront distortion correction [9]. The wavefront-sensing adaptive optics system is shown in Figure 1.

In an adaptive optics (AO) system, the wavefront detector—typically a Shack-Hartmann sensor—measures the local slopes of the incident wavefront. The wavefront controller then reconstructs the phase distribution from these slope measurements using algorithms such as the mode method or the zonal method, and translates the reconstructed phase into control signals. These signals drive the wavefront corrector (e.g., a deformable mirror or liquid crystal spatial light modulator) to compensate for wavefront aberrations in real time, thereby improving system performance—such as image resolution in astronomical imaging or beam quality in laser transmission applications. The fidelity of wavefront reconstruction is critical to correction accuracy, making algorithm optimization a key factor in achieving high-performance AO operation [10]. The typical Shack-Hartmann wavefront sensor consists of a microlens array and a CCD, as shown in Figure 2. It shows the schematic diagram of the Shack–Hartmann wavefront sensor and the focal spot displacement from the aberrated wavefront.

It calculates the local wavefront slope by measuring the offset of the light spot within each sub-aperture relative to the reference position [11]. Centroid localization is employed to compute the center position of each light spot. Finally, the wavefront sensor measures the average wavefront slope data within each sub-aperture. Now, I will introduce the mode reconstruction method used in this paper.

3. Classic Mode Method

The mode method is a technique that describes and corrects wavefront distortion through mathematical models. The wavefront within the aperture is expanded into a weighted superposition of different modes, and then the coefficients of each mode are calculated based on the detected wavefront slope data, thereby reconstructing the phase information of the wavefront. The phase at each point of the wavefront can be expressed as a linear combination of a series of orthogonal basis functions. The coefficients of each mode can be calculated using the gradient information obtained from detecting the wavefront slope, thereby restoring the complete wavefront phase [12]. This section mainly introduces Zernike polynomials and the Daubechies wavelet mode method.

3.1. Zernike Polynomial

The mode method uses the wavefront defined by Zernike polynomials as [13]

$$\phi \left(x,y\right)={\displaystyle \sum _{i=1}^N{a}_i{Z}_i\left(x,y\right)}$$

(1)

In the formula: $a_i$ for the i-th Zernike coefficient; $N$ represents the number of Zernike terms; $Z_i\left(x,y\right)$ represents each Zernike polynomial. According to Noll’s definition, the Zernike polynomials can be expressed in polar coordinates on the unit circle as

$$Z_n^m\left(r,\theta \right)=R_n^m\left(r\right){\mathsf{\Theta }}_n^m\left(\theta \right)$$

(2)

In the formula: $m$ and $n$ are the angular order and radial order of the polynomial [14]; $Z_n^m\left(r,\theta \right)$ denotes the nth-order, mth-degree Zernike polynomial in polar coordinates; r is the radial distance and its range is [0, 1]; θ is the angular coordinate and its range is [0, 2π]; $R_n^m\left(r\right)$ is the radial function, and its expression is

$$R_n^m\left(r\right)={\displaystyle \sum _{s=0}^{\frac{n-m}{2}}\frac{{\left(-1\right)}^s\cdot \left(n-s\right)!}{s!\cdot \left[\frac{n+m}{2}-s\right]!\cdot \left[\frac{n-m}{2}-s\right]!}\cdot }{r}^{\left(n-2s\right)}$$

(3)

In the formula: $R_n^m\left(r\right)$ determine the shape that varies with the radius; $s$ is the summation variable. ${\mathsf{\Theta }}_n^m\left(\theta \right)$ as an angular function, the expression is

$${\mathsf{\Theta }}_n^m\left(\theta \right)=\left\{\begin{array}{l}\sqrt{2\left(n+1\right)}\cos \left(m\theta \right) \mathrm{m}\ne 0 \mathrm{and} \mathrm{even}\\ \sqrt{2\left(n+1\right)}\sin \left(m\theta \right) \mathrm{m}\ne 0 \mathrm{and} \mathrm{odd}\\ \sqrt{\left(n+1\right)} \mathrm{m}=0\end{array}\right.$$

(4)

In the formula: ${\mathsf{\Theta }}_n^m\left(\theta \right)$ determine the rotational symmetry around the center; m determines periodicity; $\sqrt{2\left(n+1\right)}$ is the normalization factor that makes the entire Zernike polynomial orthogonal on the unit circle; when m = 0, $\sqrt{\left(n+1\right)}$ it is a constant.

3.2. Daubechies Wavelet

The Daubechies wavelet family is denoted as dbN, where $N$ represents the number of vanishing moments. The larger the $N$, the smoother the basis function. Unlike the global characteristics of Zernike polynomials, the Daubechies wavelet basis has compact support and good spatial locality [15,16]. It can accurately depict the local variations and high-frequency components of the wavefront phase on multiple scales, with efficient computation and suitable for applications with high real-time requirements. In one dimension, the Daubechies wavelet basis consists of the scale function $\phi \left(t\right)$ and the mother wavelet $\psi \left(t\right)$, and any signal $f\left(t\right)$ can be expanded as

$$f\left(t\right)={\displaystyle \sum _k{c}_{J,k}{\varphi }_{J,k}\left(t\right)}+{\displaystyle \sum _{j=J}^{j_{\max }}{\displaystyle \sum d_{j,k}{\psi }_{j,k}\left(t\right)}}$$

(5)

In the formula: $c_{J,k}$ is the scale function coefficient; $d_{j,k}$ is the wavelet coefficient; ${\varphi }_{(J,k)}=2^{(J/2)}\varphi (2^{J}t-k)$ and ${\psi }_{j,k}\left(t\right)=2^{(j/2)}\psi (2^{j}t-k)$ are, respectively, the scaled and shifted scale function and wavelet function; $2^{(j/2)}$ is used for normalization, so that the energy of each scale’s basis function under the $L^2$ norm is 1, thereby ensuring orthogonality and reconstruction stability.

For the wavefront phase $\phi \left(x,y\right)$ defined on the aperture plane $(x,y)$, the one-dimensional wavelet is extended to two dimensions using the tensor product method, and multi-directional two-dimensional Daubechies wavelet basis functions are constructed. Usually, the high-frequency details are decomposed into three types of sub-band basis functions: horizontal, vertical, and diagonal. Among them, the horizontal detail (H) basis is expressed as

$${\psi }_{j,k_x,k_y}^H(x,y)=2^j\psi (2^{j}x-k_x)\varphi (2^{j}y-k_y)$$

(6)

In the formula: j represents the scale; $k_x,k_y$ is the translation index; $2^j$ is the product of the scaling coefficients $2^{(j/2)}$ in the x and y directions, ensuring that the energy of the two-dimensional basis functions is 1 under the norm. The two-dimensional basis functions are orthogonal at each scale and position, and can be stably used for wavefront reconstruction. To enhance the ability to capture multi-directional features, the x direction captures the high-frequency changes in the horizontal direction, and the y direction maintains the smoothness in the vertical direction.

The vertical detail (V) basis is expressed as

$${\psi }_{j,k_x,k_y}^V(x,y)=2^j\varphi (2^{j}x-k_x)\psi (2^{j}y-k_y)$$

(7)

In the formula: the x-axis maintains a smooth horizontal direction, while the y-axis captures the high-frequency changes in the vertical direction.

The diagonal detail (D) basis is expressed as

$${\psi }_{j,k_x,k_y}^D(x,y)=2^j\psi (2^{j}x-k_x)\psi (2^{j}y-k_y)$$

(8)

In the formula: the diagonal direction of high-frequency variations is captured in the x and y directions. Additionally, a two-dimensional scale function needs to be introduced as a low-frequency approximation term, which is expressed as

$${\varphi }_{j_0,k_x,k_y}(x,y)=2^{(j_0)}\varphi (2^{j_0}x-k_x)\varphi (2^{j_0}y-k_y)$$

(9)

The horizontal, vertical and diagonal types of basis functions, together with the scaling function, constitute the complete two-dimensional Daubechies wavelet basis. This basis can perform multi-scale and multi-directional local feature decomposition and reconstruction of the wavefront phase $\left(x,y\right)$ on the sub-aperture plane. The wavefront phase on the aperture plane can be expanded using the two-dimensional wavelet basis functions as

$$\phi (x,y)={\displaystyle {\sum }_{k_x}{\displaystyle {\sum }_{k_y}{a}_{j_0,k_x,k_y}}}{\varphi }_{j_0,k_x,k_y}(x,y)+{\displaystyle \sum _{j=j_{\min }}^{j_{\max }}{\displaystyle {\sum }_{k_x}{\displaystyle {\sum }_{k_y}{b}_{j,k_x,k_y}}}}{\psi }_{j,k_x,k_y}(x,y)$$

(10)

In the formula: $a_{j_0,k_x,k_y}$ as the scale coefficient; $b_{j,k_x,k_y}$ as the wavelet coefficient of the j-th layer and the $\left(k_x,k_y\right)$th position. The expansion form is a multi-scale and multi-directional local feature decomposition and stable reconstruction of the wavefront phase.

4. Hybrid Basis Reconstruction of Wavefront

4.1. Constructing a Hybrid Basis Function Set

To simultaneously account for both global and local features of wavefront distortion, this paper unifies Zernike polynomials and Daubechies patterns into a hybrid basis function set within the same coordinate domain. Assume that within a unit circular aperture, the Zernike modes are truncated to the first N_Z terms according to the wavefront aberration order, and the Daubechies wavelet modes are truncated to N_D terms according to multi-resolution scales and orientations, then the hybrid basis function set is represented as $\mathcal{M}$

$$\mathfrak{M}=\left\{M_1,M_2,M_3,\dots \dots ,M_{N_{total}}\right\},N_{total}=N_Z+N_D$$

(11)

In the formula: the first $N_Z$ set of basis functions $M_1,M_2,\dots \dots ,M_Z$ corresponds to Zernike modes; the latter $N_D$ set of basis functions $M_{N+1},\dots \dots ,M_{total}$ corresponds to Daubechies wavelet modes. The paper adds a category label to each basis function when constructing the hybrid basis function set as follows

$$Cat=\left\{ca{t}_1,ca{t}_2,ca{t}_3,\dots \dots ca{t}_{1N_{total}}\right\}, ca{t}_k=\left\{\begin{array}{l}Zernike, k\le N_z\\ Daubechies, k>N_z\end{array}\right.$$

(12)

For each function ${\mathrm{M}}_k\left(x,y\right)$, the gradient on the sub-aperture can be calculated according to formula (1) for subsequent construction of the reconstruction matrix F, which can be expressed as

$$\left\{\begin{array}{l}{M}_k^x(j)=\frac{\partial M_k(x,y)}{\partial x}{|}_{\mathrm{the} \text{j-th} \mathrm{subaperture}}\\ M_k^y(j)=\frac{\partial M_k(x,y)}{\partial y}{|}_{\mathrm{the} \text{j-th} \mathrm{subaperture}}\end{array}\right.$$

(13)

Through the construction method outlined above, this paper not only unifies the two types of patterns into the same base set $\mathfrak{M}$, but also retains the source category information in each pattern object.

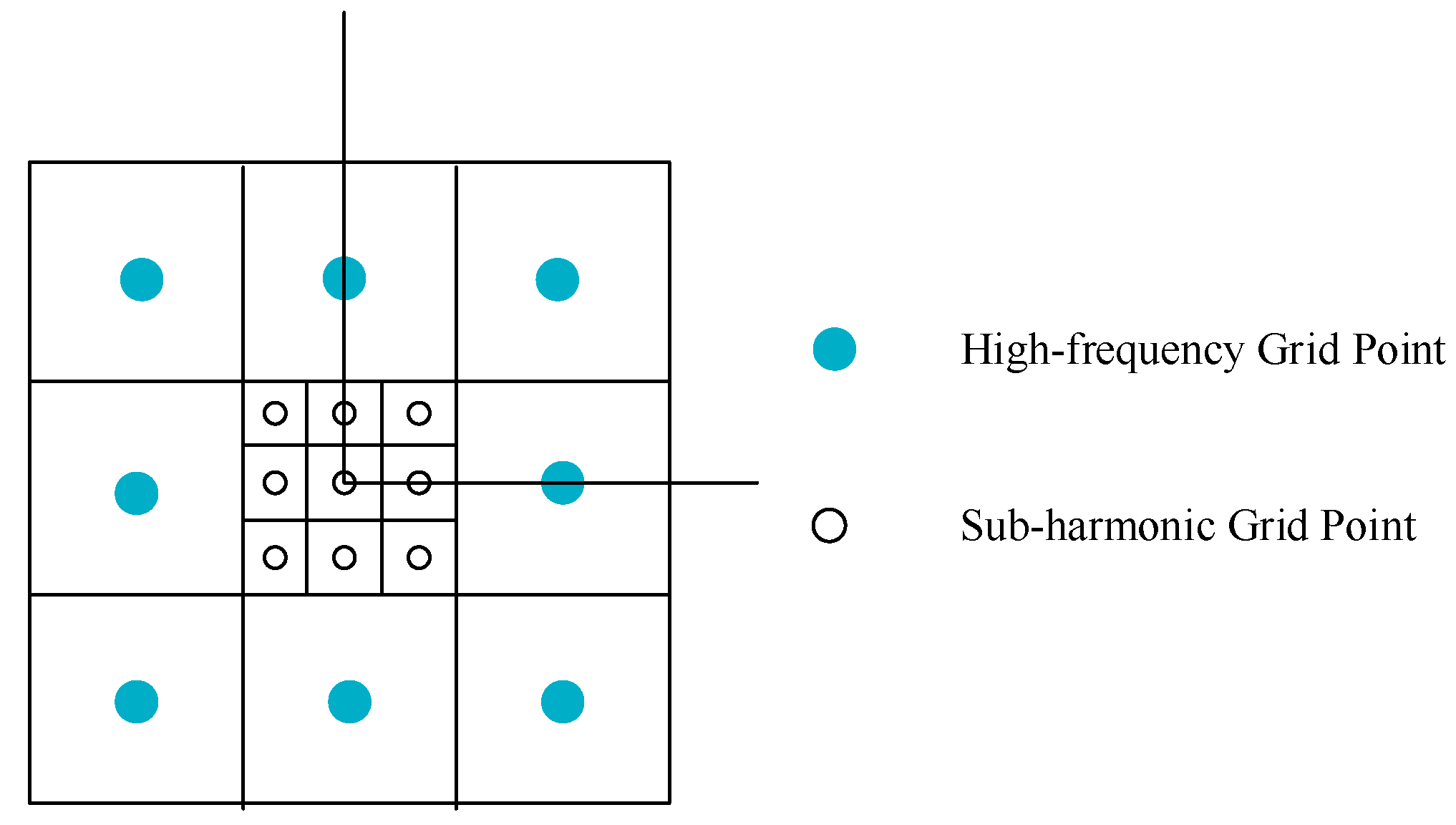
4.2. Numerical Simulation of Turbulence and Mutual Information Theory

Common methods for numerical simulation of atmospheric turbulence include power spectrum inversion method [17], Zernike polynomial simulation method [18], and fractal method. In this section, the power spectrum inversion method is used to simulate turbulence [19]. By performing an inverse Fourier transform on this random field, the distorted phase quantity is obtained and then converted to the spatial frequency domain, expressed as

$$\varphi \left(m,n\right)={\displaystyle \sum _{m^{\prime }=-\frac{N_x}{2}}^{\frac{N_x}{2}-1}{\displaystyle \sum _{n^{\prime }=-\frac{N_y}{2}}^{\frac{Ny}{2}-1}a\left(m^{\prime },n^{\prime }\right)}}\sqrt{{\mathsf{\Phi }}_{\varphi }\left(m^{\prime },n^{\prime }\right)}{e}^{i2\pi \left(\frac{m^{\prime }m}{N_x}+\frac{n^{\prime }n}{N_y}\right)}$$

(14)

In the formula: $N_x$ and $N_y$ are the number of sampling points in the x and y directions; $a\left(m^{\prime },n^{\prime }\right)$ is a complex Gaussian random matrix; ${\mathsf{\Phi }}_{\varphi }\left(m^{\prime },n^{\prime }\right)$ is the power spectral density of the atmospheric phase. In this paper, the hill spectrum and subharmonic compensation are used to generate the atmospheric turbulence phase screen. The power spectrum of the atmospheric phase under the hill spectrum model is [20].

$${\mathsf{\Phi }}_{\varphi }\left(k_r\right)=2\pi k^2\cdot 0.033\left[1+1.802\left(\frac{{\kappa }_r}{{\kappa }_l}\right)-0.254{\left(\frac{{\kappa }_r}{{\kappa }_l}\right)}^{\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}\right]\cdot {\displaystyle \frac{\exp \left(-\frac{{\kappa }_r^2}{{\kappa }_l^2}\right)}{{\left({\kappa }_0^2+{\kappa }_r^2\right)}^{\raisebox{1ex}{$11$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}}{\displaystyle \underset{z}{\overset{z+\delta z}{\int }}{C}_n^2\left(\xi \right)d\xi }$$

(15)

In the formula: ${\delta }_z$ refers to the thickness of the turbulent thin layer, ${\kappa }_r={\left({\kappa }_x^2+{\kappa }_y^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, $r_0=0.185{\left[{\lambda }^2/{\displaystyle {\int }_z^{z+{\delta }_z}{C}_n^2\left(\xi \right)}\right]}^{\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$5$}\right.}$. The atmospheric phase power spectrum is

$${\mathsf{\Phi }}_{\varphi }\left(k_r\right)=0.49{r_0}^{-\frac{3}{5}}\left[1+1.802\left(\frac{{\kappa }_r}{{\kappa }_l}\right)-0.254{\left(\frac{{\kappa }_r}{{\kappa }_l}\right)}^{\raisebox{1ex}{$7$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}\right]\cdot {\displaystyle \frac{\exp \left(-\frac{{\kappa }_r^2}{{\kappa }_l^2}\right)}{{\left({\kappa }_0^2+{\kappa }_r^2\right)}^{\raisebox{1ex}{$11$}\!\left/ \!\raisebox{-1ex}{$6$}\right.}}}$$

(16)

In the formula: ${\kappa }_l=3.3/l_0$; ${\kappa }_0=2\pi /L_0$. Next, low-frequency compensation needs to be performed on the phase screen. The schematic diagram of low-frequency harmonic compensation is shown in Figure 3.

The expression is as follows

$${\varphi }_{SH}(m,n)={\displaystyle \sum _{p=1}^{N_p}{\displaystyle \sum _{m^{\prime }=-1}^1{\displaystyle \sum _{n^{\prime }=-1}^{1}R(m^{\prime },n^{\prime })f(m^{\prime },n^{\prime })}}}exp(j2\pi 3^{-p}(\frac{m{m}^{\prime }}{N}+\frac{n{n}^{\prime }}{N}))$$

(17)

In the formula: p for the subharmonic series, $f(m^{\prime },n^{\prime })=C\cdot 3^{-2p}{r}_0^{-5/6}({f_{lx}}^2+{f_{ly}}^2)$, $f_{lx}=3^{-p}{m}^{\prime }\Delta f_x$, $f_{ly}=3^{-p}{m}^{\prime }\Delta f_y$. Substituting Expression (18) into Expression (15) yields

$$\begin{array}{l}\varphi \left(m,n\right)={\displaystyle \sum _{m^{\prime }=0}^{N_x}{\displaystyle \sum _{n^{\prime }=0}^{N_y}a\left(m^{\prime },n^{\prime }\right)}}\frac{2\pi }{L}\sqrt{0.00058}{r}_0^{-\frac{5}{6}}{\left(\exp \left(-{\displaystyle \frac{f_r^2}{f_l^2}}\right)\right)}^{\frac{1}{2}}{\left(f_0^2+f_r^2\right)}^{-{\displaystyle \frac{11}{12}}}\\ \hspace{1em}\hspace{1em}{\left(1+1.802\left(\frac{f_r}{f_l}\right)-0.254{\left(\frac{f_r}{f_l}\right)}^{\frac{7}{6}}\right)}^{\frac{1}{2}}\end{array}$$

(18)

In the formula: $f_r={({f_x}^2+{f_y}^2)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$, $f_l={\kappa }_l/2\pi$, $f_0={\kappa }_0/2\pi$. This solves the problems of insufficient low-frequency components and high-frequency modeling, ensuring accurate reflection of atmospheric turbulence phase perturbations across all frequency bands, thereby more realistically simulating the propagation effects of light waves in turbulence [21].

To evaluate the statistical correlation between the mixed basis function set and atmospheric turbulence, mutual information is required. Mutual information (MI for short) is an important concept describing the relationship between two random variables, which measures the degree of mutual dependence between the two variables [22]. It can be expressed as

$$\mathrm{I}\left(X;Y\right)=H\left(X\right)+H\left(Y\right)-H\left(X,Y\right)$$

(19)

In the formula: H(X) and H(Y) represent the entropy of two variables X and Y, respectively, while H(X,Y) denotes the joint entropy of variables X and Y, expressed as

$$\mathrm{H}\left(X\right)=-{\displaystyle {\sum }_{i}p\left(x_i\right)\log }p\left(x_i\right)$$

(20)

$$\mathrm{H}\left(Y\right)=-{\displaystyle {\sum }_{i}p\left(y_i\right)\log }p\left(y_i\right)$$

(21)

$$\mathrm{H}\left(X,Y\right)=-{\displaystyle {\sum }_i{\displaystyle {\sum }_{j}p\left(x_i,y_j\right)}\log }p\left(x_i,y_j\right)$$

(22)

In the formula: p(x) and p(y) represent the probability density functions of X and Y, respectively; p(x,y) denotes the joint probability density function.

To quantify the statistical dependence between the mixed basis and atmospheric turbulence, this paper employs a histogram binning-based method to estimate the marginal probability distributions px and py. The input variables x and y are divided into $B=\min \left(50,⌊\sqrt{n}⌋\right)$ equally spaced intervals, where n represents the number of samples. The frequency of samples in each bin is counted and normalized to obtain the marginal probability distribution

$$\left\{\begin{array}{l}{p}_x\left(i\right)=\frac{c_x\left(i\right)}{{\displaystyle {\sum }_j{c}_x\left(j\right)}}\\ p_y\left(j\right)=\frac{c_y\left(j\right)}{{\displaystyle {\sum }_i{c}_y\left(i\right)}}\end{array}\right.$$

(23)

In the formula: $c_x\left(i\right)$, $c_y\left(j\right)$ represent the number of corresponding samples in the ith and jth bins, respectively. The joint probability distribution $p_{xy}$ is estimated through a two-dimensional histogram. The value ranges of variables x and y are divided into B bins, and the number of samples that fall into each pair of bin combinations $\left(i,j\right)$ simultaneously $c_{xy}\left(i,j\right)$ is counted. After normalization, the joint probability distribution is represented as

$$p_{xy}\left(i,j\right)=\frac{c_{xy}\left(i,j\right)}{{\displaystyle {\sum }_{i,j}{c}_{xy}\left(i,j\right)}}$$

(24)

Using the above definition, the mutual information expression is calculated as

$$I\left(X;Y\right)={\displaystyle {\sum }_{i,j}{p}_{xy}\left(i,j\right){\log }_2\left(\frac{p_{xy}\left(i,j\right)}{p_x\left(i\right)p_y\left(j\right)}\right)} , p_{xy}\left(i,j\right)>0$$

(25)

This formula reflects the amount of shared information between variables X and Y. A higher value indicates a stronger statistical dependence between the two variables. In this work, MI is used to evaluate the correlation between each basis mode and the measured wavefront data under atmospheric turbulence. A higher MI value indicates that the mode contains more relevant information for reconstructing the true wavefront. Therefore, modes with higher MI are prioritized in the hybrid reconstruction process, enabling a more efficient and accurate representation of the wavefront with fewer modes. We simulated 300 phase screens and calculated their average mutual information with each mode, as shown in Figure 4a,b. These figures demonstrate the variation in mutual information between Zernike and Daubechies wavelets (abbreviated as Db) and atmospheric turbulence wavefronts under different mode numbers. The abscissa represents the mode number, and the ordinate represents the mutual information value.

As can be seen from Figure 4a, the first mode has almost no mutual information with the wavefront phase distortion caused by atmospheric turbulence. The mutual information value exhibits a certain fluctuation trend with the mode number; that is, the mutual information of the Zernike modes generally decreases as the order increases, verifying that low-order modes have a more significant impact on atmospheric turbulence. Figure 4b shows the mutual information between some modes and turbulence under the four-level decomposition of the Daubechies wavelet, indicating strong local sensitivity and non-uniform distribution of mutual information at different scales. This difference suggests that a single basis function is difficult to fully characterize the multi-scale characteristics of the turbulent wavefront. Therefore, a hybrid basis function is proposed, utilizing mutual information for selection, which can retain the global descriptive ability of Zernike while enhancing the wavelet’s response to local perturbations, thereby constructing a more efficient hybrid reconstruction model.

4.3. Mode Selection and Establishment of Reconstruction Matrix

By calculating the mutual information between each basis function and the actual wavefront perturbation, and sorting them according to the strength of correlation, the top M high mutual information patterns are selected to form the optimized basis set. The mutual information $\left\{I_k\right\}$ of all N patterns calculated in Section 4.2 is arranged in descending order as follows

$$I_{k_1}\ge I_{k_2}\ge I_{k_3}\ge \dots \dots \ge I_{k_N}$$

(26)

Assuming the Shack-Hartmann wavefront sensor has a total of m sub-apertures, the first M modes are extracted from the descending order of mutual information, and the wavefront reconstruction matrix F is constructed as follows

$$F=\left[\begin{array}{cccc}{M}_{k_1}^x\left(1\right)& M_{k_2}^x\left(1\right)& \dots & M_{k_M}^x\left(1\right)\\ \begin{array}{l}{M}_{k_1}^y\left(1\right)\\ M_{k_1}^x\left(2\right)\\ M_{k_1}^y\left(2\right)\\ ⋮\\ ⋮\end{array}& \begin{array}{l}{M}_{k_2}^y\left(1\right)\\ M_{k_2}^x\left(2\right)\\ M_{k_2}^y\left(2\right)\\ ⋮\\ ⋮\end{array}& \begin{array}{l}\dots \\ \dots \\ \dots \\ \ddots \\ \ddots \end{array}& \begin{array}{l}{M}_{k_M}^y\left(1\right)\\ M_{k_M}^x\left(2\right)\\ M_{k_M}^y\left(2\right)\\ ⋮\\ ⋮\end{array}\\ M_{k_1}^x\left(m\right)& M_{k_2}^x\left(m\right)& \dots & M_{k_M}^x\left(m\right)\\ M_{k_1}^y\left(m\right)& M_{k_2}^y\left(m\right)& \dots & M_{k_M}^y\left(m\right)\end{array}\right]$$

(27)

In the formula: F is the wavefront reconstruction matrix, which maps the sampled values of the basis function modes to the wavefront slopes observed by the sensor; $k_n$ is the index of the mode in M, in the order after mutual information sorting; n is the selected mode and $n=1,2,\dots ,M$; $M_{k_n}^x(j)$ represents the gradient in the x direction of the j-th subaperture for the n-th mode after sorting; represents the gradient in the y direction of the j-th subaperture for the n-th mode after sorting.

Based on mutual information, the mixed basis function set $\mathcal{M}$ is sorted, and the top M patterns are selected to construct the reconstruction matrix F. Introduce the Zernike mode and Daubechies wavelet mode correction factors ${\beta }_Z$ and ${\beta }_D$. Normalize the mutual information to obtain the initial weight for each mode

$$w_{k_n}^{\left(0\right)}=\frac{I_{k_n}}{{\displaystyle {\sum }_{n=1}^M{I}_{k_n}}}$$

(28)

In the formula: $I_{k_n}$ It represents the mutual information value between the nth pattern and the turbulent wavefront. The category correction factor and the final weight are expressed as

$${\beta }_{ca{t}_{k_n}}=\left\{\begin{array}{l}{\beta }_z, ca{t}_{k_n}=Zernike\\ {\beta }_D, ca{t}_{k_n}=Daubechies\end{array}\right.$$

(29)

$${\tilde{w}}_{k_n}={\beta }_{ca{t}_{k_n}}\cdot w_{k_n}^{\left(0\right)}$$

(30)

This paper adopts the statistical estimation method, using the average mutual information of the two modes as the benchmark for the correction factor, expressed as

$${\beta }_D=\frac{mean\left(I_D\right)}{mean\left(I_H\right)}, {\beta }_z=1.0$$

(31)

Introducing weights into the reconstruction matrix is equivalent to multiplying each column of the pattern gradient by the corresponding weight coefficient

$$F_w=\left[{\tilde{w}}_{k_1}{f}_{k_1} {\tilde{w}}_{k_2}{f}_{k_2} \dots \dots {\tilde{w}}_{k_M}{f}_{k_M}\right]$$

(32)

In the formula: $f_{k_n}$ represents the combined x and y direction gradient column vector of the nth pattern across all sub-apertures; $F_w$ is a weighted reconstruction matrix, which can be expanded as follows

$$F_w=\left[\begin{array}{cccc}{\tilde{w}}_{k_1}{M}_{k_1}^x\left(1\right)& {\tilde{w}}_{k_2}{M}_{k_2}^x\left(1\right)& \dots & {\tilde{w}}_{k_M}{M}_{k_M}^x\left(1\right)\\ \begin{array}{l}{\tilde{w}}_{k_1}{M}_{k_1}^y\left(1\right)\\ {\tilde{w}}_{k_1}{M}_{k_1}^x\left(2\right)\\ {\tilde{w}}_{k_1}{M}_{k_1}^y\left(2\right)\\ ⋮\\ ⋮\end{array}& \begin{array}{l}{\tilde{w}}_{k_2}{M}_{k_2}^y\left(1\right)\\ {\tilde{w}}_{k_2}{M}_{k_2}^x\left(2\right)\\ {\tilde{w}}_{k_2}{M}_{k_2}^y\left(2\right)\\ ⋮\\ ⋮\end{array}& \begin{array}{l}\dots \\ \dots \\ \dots \\ \ddots \\ \ddots \end{array}& \begin{array}{l}{\tilde{w}}_{k_M}{M}_{k_M}^y\left(1\right)\\ {\tilde{w}}_{k_M}{M}_{k_M}^x\left(2\right)\\ {\tilde{w}}_{k_M}{M}_{k_M}^y\left(2\right)\\ ⋮\\ ⋮\end{array}\\ {\tilde{w}}_{k_1}{M}_{k_1}^x\left(m\right)& {\tilde{w}}_{k_2}{M}_{k_2}^x\left(m\right)& \dots & {\tilde{w}}_{k_M}{M}_{k_M}^x\left(m\right)\\ {\tilde{w}}_{k_1}{M}_{k_1}^y\left(m\right)& {\tilde{w}}_{k_2}{M}_{k_2}^y\left(m\right)& \dots & {\tilde{w}}_{k_M}{M}_{k_M}^y\left(m\right)\end{array}\right]$$

(33)

In this way, patterns of different categories and importance levels contribute in a reasonable proportion during the reconstruction process, effectively enhancing the accuracy and robustness of mixed-basis reconstruction, and allowing for flexible adjustment of the correction factors based on experimental results.

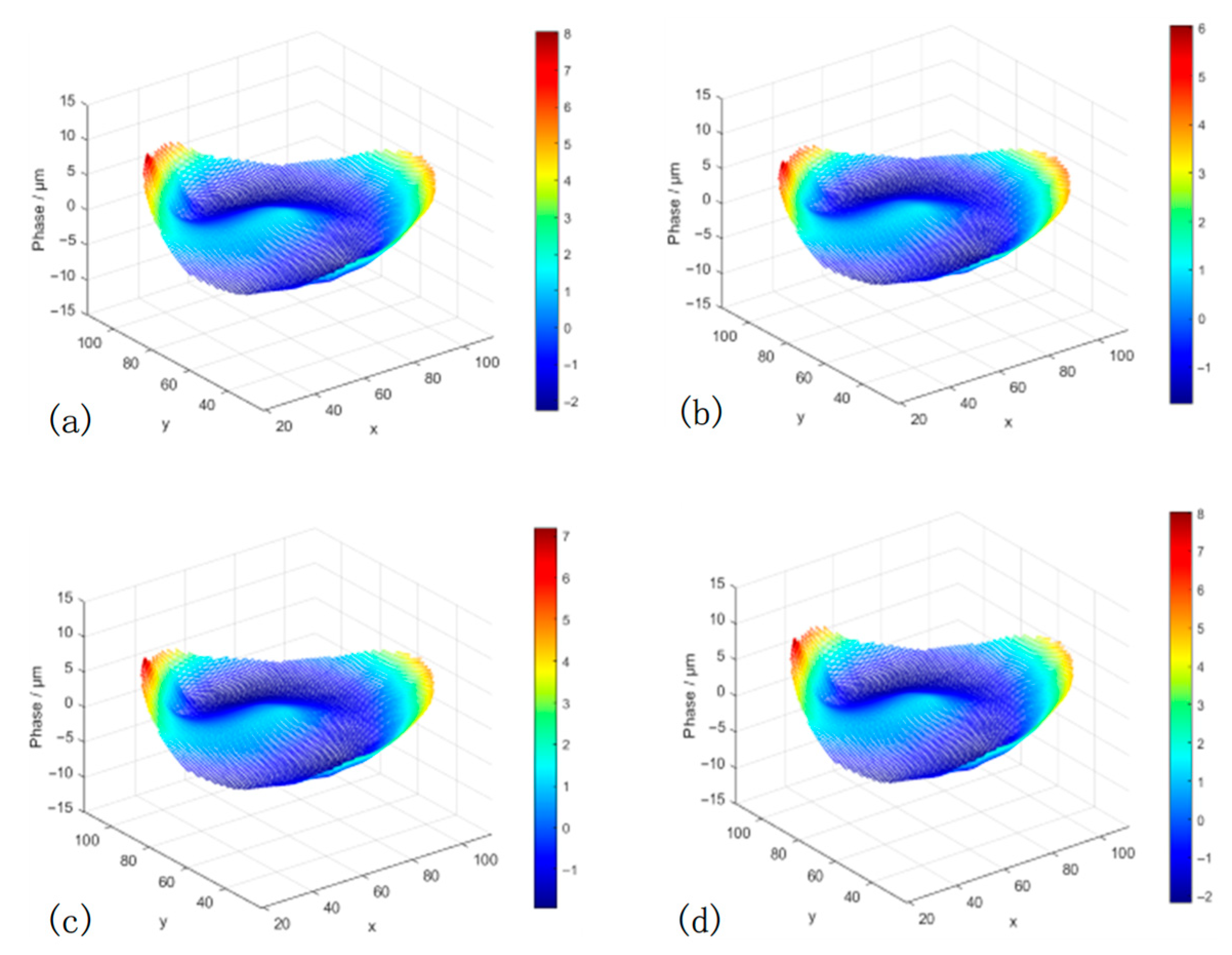
4.4. Wavefront Reconstruction

After deriving the wavefront reconstruction matrix in Section 4.3, the distorted wavefront is fitted using the first M terms of the polynomial as follows

$$\left[\begin{array}{l}{G}_{1x}\\ G_{1y}\\ G_{2x}\\ G_{2y}\\ \dots \\ \dots \\ G_{Mx}\\ G_{My}\end{array}\right]={\left[\begin{array}{cccc}{\tilde{w}}_{k_1}{M}_{k_1}^x\left(1\right)& {\tilde{w}}_{k_2}{M}_{k_2}^x\left(1\right)& \dots & {\tilde{w}}_{k_M}{M}_{k_M}^x\left(1\right)\\ \begin{array}{l}{\tilde{w}}_{k_1}{M}_{k_1}^y\left(1\right)\\ {\tilde{w}}_{k_1}{M}_{k_1}^x\left(2\right)\\ {\tilde{w}}_{k_1}{M}_{k_1}^y\left(2\right)\\ ⋮\\ ⋮\end{array}& \begin{array}{l}{\tilde{w}}_{k_2}{M}_{k_2}^y\left(1\right)\\ {\tilde{w}}_{k_2}{M}_{k_2}^x\left(2\right)\\ {\tilde{w}}_{k_2}{M}_{k_2}^y\left(2\right)\\ ⋮\\ ⋮\end{array}& \begin{array}{l}\dots \\ \dots \\ \dots \\ \ddots \\ \ddots \end{array}& \begin{array}{l}{\tilde{w}}_{k_M}{M}_{k_M}^y\left(1\right)\\ {\tilde{w}}_{k_M}{M}_{k_M}^x\left(2\right)\\ {\tilde{w}}_{k_M}{M}_{k_M}^y\left(2\right)\\ ⋮\\ ⋮\end{array}\\ {\tilde{w}}_{k_1}{M}_{k_1}^x\left(m\right)& {\tilde{w}}_{k_2}{M}_{k_2}^x\left(m\right)& \dots & {\tilde{w}}_{k_M}{M}_{k_M}^x\left(m\right)\\ {\tilde{w}}_{k_1}{M}_{k_1}^y\left(m\right)& {\tilde{w}}_{k_2}{M}_{k_2}^y\left(m\right)& \dots & {\tilde{w}}_{k_M}{M}_{k_M}^y\left(m\right)\end{array}\right]}_{2m\times M}\cdot {\left[\begin{array}{l}{c}_1\\ c_2\\ \dots \\ c_M\end{array}\right]}_{M\times 1}$$

(34)

$$G=F_{w}C$$

(35)

In the formula: G represents the wavefront slope vector, where $G_{ix}$ and $G_{iy}$ are the wavefront slopes measured in the x and y directions for the j-th sub-aperture, respectively; F denotes the matrix for wavefront reconstruction; C stands for the orthogonal polynomial coefficient vector. The reconstruction coefficients are obtained using an inversion algorithm

$$C={F_w}^{+}G$$

(36)

Convert these slope data into a complete wavefront to achieve precise wavefront reconstruction. The final wavefront phase is represented as

$$\varphi (x,y)={\displaystyle \sum _{n=1}^M{c}_n{M}_{k_n}(x,y)}$$

(37)

In the formula: $c_n$ is the coefficient for the nth mode; $M_{k_n}(x,y)$ is the value of the nth selected mode in $(x,y)$; M is the total number of truncated reconstructed modes. In this paper, the PID (Proportional–Integral–Derivative) control algorithm is adopted to adaptively adjust the driving voltage of the DM (Deformable Mirror), thereby achieving high-precision and rapid wavefront correction [23]. The wavefront error obtained from the current reconstruction is expanded under the selected basis functions to obtain the mode coefficients $c_{err}=-c$. Combining the calibrated influence matrix of the deformable mirror, the required correction voltage is calculated as

$$V_{dn}(k)=M\cdot \left\{K_p\cdot c_{err}(k)+K_i\cdot {\displaystyle \sum _{i=1}^k{c}_{err}}(i)+K_d\cdot \left[c_{err}(k)-c_{err}(k-1)\right]\right\}$$

(38)

In the formula: $K_p,K_i,K_d$ are the proportional, integral, and derivative gain parameters; M represents the influence matrix of the deformable mirror. The control strategy implements closed-loop feedback in the mode space. Through multiple iterations of control, the system can continuously reduce the wavefront residuals, gradually approximating the reconstructed wavefront to the ideal plane wave, thereby improving the correction performance of the entire adaptive optics system. To comprehensively evaluate the performance of the hybrid basis function reconstruction method, this paper adopts the root mean square (RMS) and peak-to-valley (PV) as the main evaluation indicators to quantify the degree of distortion before and after wavefront reconstruction and correction. The reliability of this method is observed through computation time and correction results.

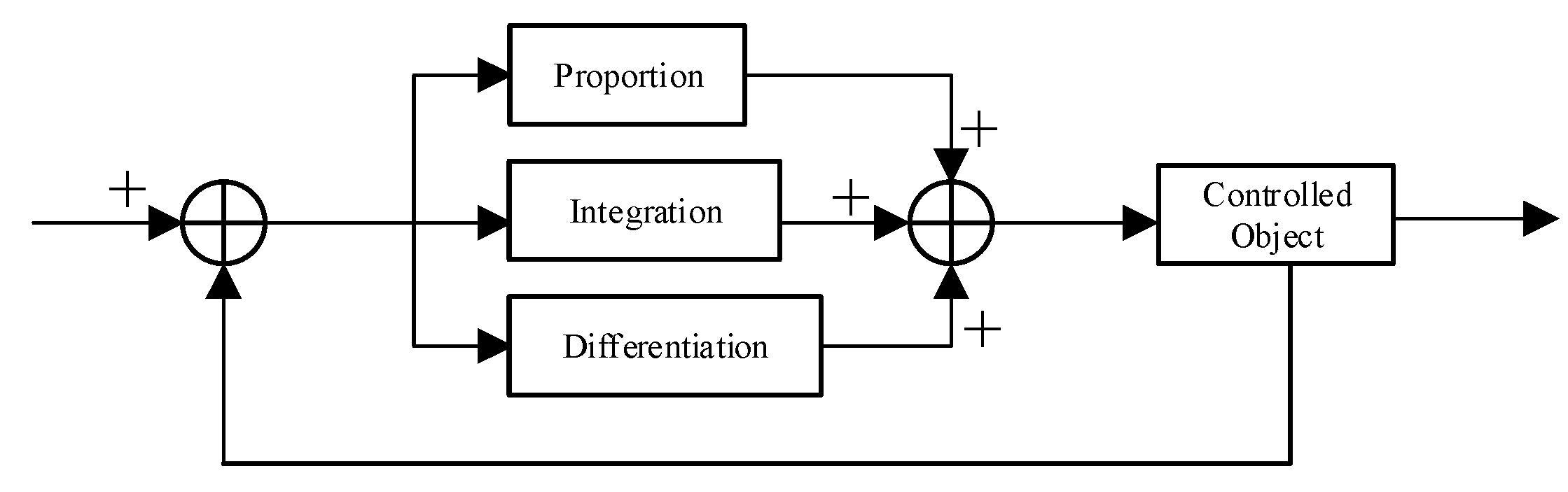
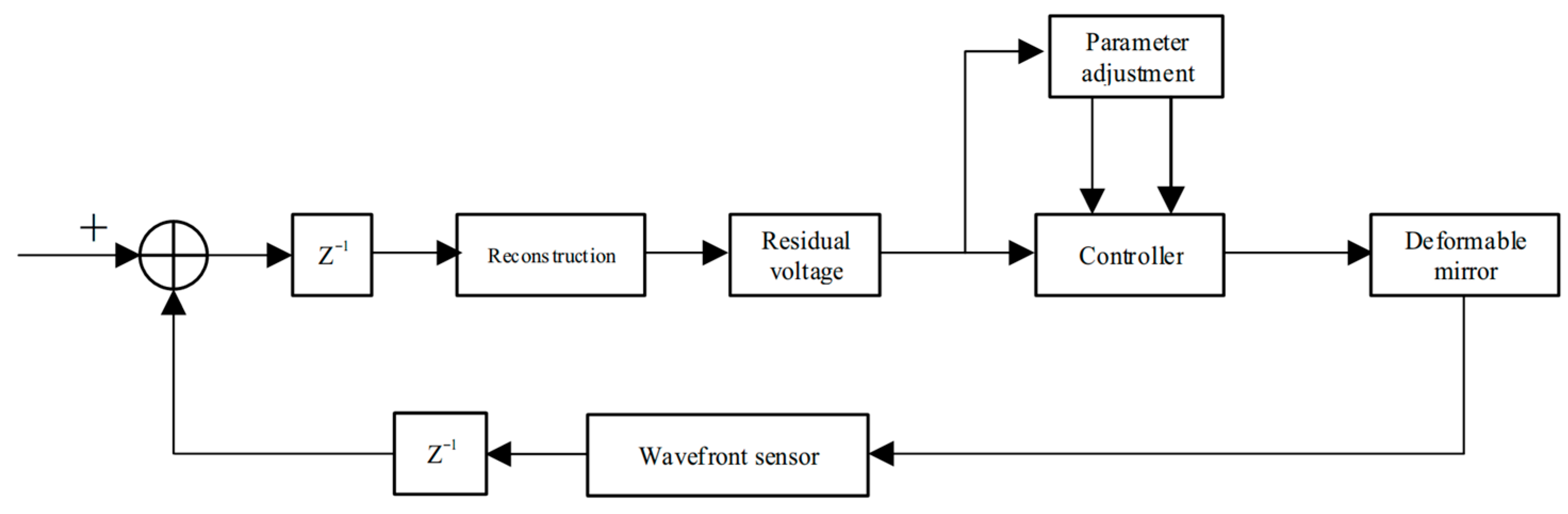
5. Wavefront Correction

5.1. Wavefront Reconstruction

In this section, the Zernike mode method and the hybrid mode method are compared through a numerical simulation system for the reconstruction of wavefront distortion caused by atmospheric turbulence. The simulation conditions are set as follows: grid size 128 × 128, receiving telescope diameter D = 0.4 m, coherence length r₀ = 0.2 m, spatial frequency grid d_f = 1/D, outer scale L₀ = 30 m, inner scale l₀ = 0.005 m, wavenumber parameters k₀ = 2π/L₀ and k₁ = 5.92/l₀.

As shown in Figure 5, Figure 5a represents the distorted wavefront caused by atmospheric turbulence, Figure 5b shows the wavefront reconstructed using Zernike polynomials, Figure 5c illustrates the wavefront reconstructed using the Zernike-MI (Zernike-Mutual Information) method, and Figure 5d displays the wavefront reconstructed using the Zernike-Db-MI hybrid basis (Zernike-Daubechies-Mutual Information) reordering method. The overall contour of the wavefront reconstructed using Zernike polynomials is largely restored, but the edge regions exhibit over-smoothing, indicating the limitations of Zernike basis functions in handling local high-frequency components. After introducing mutual information for modal reordering, the identification of key distortion modes becomes more targeted, significantly enhancing the reconstruction accuracy and improving local details. However, the transition in the edge regions still appears smooth and lacks sufficient sharpness, suggesting that although mutual information enhances the physical relevance of basis function selection, it does not fundamentally overcome the limitations of Zernike polynomials as global basis functions in representing local high-frequency features. In contrast, the Zernike-Db-MI hybrid basis reordering method combines the global representation capability of Zernike polynomials with the local high-frequency capture capability of Daubechies wavelets. The transition in the edge regions is natural, and local details (such as the steep slope in the upper left corner) are finely restored without significant oscillation or blurring, reflecting good frequency resolution and achieving highly accurate reconstruction of the original distorted wavefront. By integrating multi-scale analysis capabilities, it effectively compensates for the limitations of single basis functions, providing an efficient solution for high-precision wavefront reconstruction.

Figure 6 illustrates the relationship between the reconstruction error and the mode number for the Zernike expansion, the Zernike method based on mutual information reordering (Zernike-MI), and the Zernike-Db-MI hybrid basis reordering method (Zernike-Daubechies-Mutual Information). The Zernike expansion method truncates the expansion in order of mode number, failing to effectively distinguish the information contribution of each mode to turbulence distortion, resulting in slow convergence speed and large residual error. Zernike-MI calculates the mutual information between each mode and atmospheric turbulence and reorders them, preferentially retaining low-order modes with large amounts of information, significantly improving the low-order approximation capability and reducing the error more rapidly. Zernike-Db-MI further introduces the Daubechies wavelet basis to form a hybrid basis function set, and performs global reordering based on mutual information. While retaining the global description capability of Zernike’s low-frequency terms, it utilizes the wavelet basis’s advantage in capturing high-frequency local details, gradually introducing db bases from the 10th term to enhance high-frequency compensation capability, thereby achieving more efficient representation. When the mode number is 20, the root mean square of the wavefront residual drops to 0.14 rad, significantly better than the 0.19 rad of Zernike-MI and the 0.33 rad of traditional Zernike. When the mode number increases to 38, the residual of the hybrid basis method reaches a minimum value of about 0.03 rad, representing the optimal reconstruction accuracy in the entire process. Afterwards, the error fluctuates slightly but remains stable overall, tending to converge by the 52nd mode, indicating that the method has good stability and resistance to overfitting. The results show that the hybrid basis reconstruction strategy can more accurately match the statistical characteristics of atmospheric turbulence, significantly improving the accuracy and stability of wavefront reconstruction.

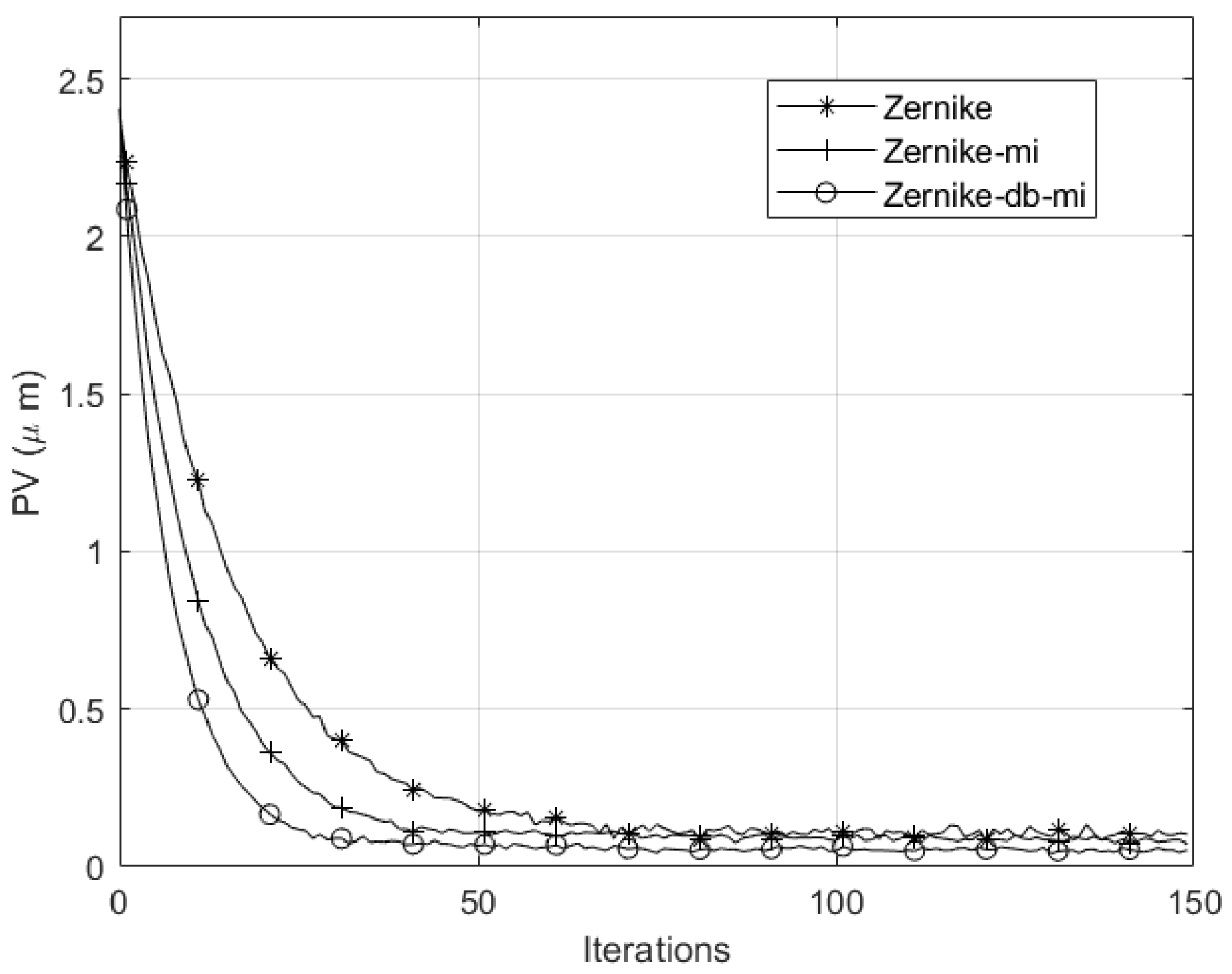
5.2. Wavefront Correction Experiment

To evaluate the performance of different wavefront reconstruction methods in a real turbulent environment, a laser transmission measurement experimental link was established in Xi’an, Shaanxi Province on 9 September 2025. The weather was overcast, with wind speeds ranging from 1.0 to 2.7 m/s and temperatures between 20 and 29 °C. The experimental setup was conducted in a clear environment with no obstructions, and the link length was 0.42 km. The terrain the link traversed was primarily composed of trees and buildings. The transmitting end, equipped with a solid-state laser emitting at a wavelength of 532 nm, with a power of 200 mW and a beam diameter of 5 mm, was located on the 11th floor of Building 6 on the Jinhua Campus of Xi’an University of Technology. The receiving end was situated on the 8th floor of Building 2 on the same campus. The signal beam emitted by the laser entered the atmospheric channel through a transmitting antenna (both the transmitting and receiving optical antennas were equipped with Markar optical telescopes with an aperture of 105 mm). At the receiving end, the signal beam was received by a receiving antenna, passed through a collimating lens into the collimation system, and detected by a wavefront sensor placed behind the lens. The detection information was transmitted to a controller, specifically an incremental proportional-integral controller, whose schematic diagram is shown in Figure 7.

The light beam is reflected by a beam splitter and then incident on the surface of a deformable mirror. The driver controls the deformable mirror to produce a certain surface shape, compensating and correcting the distorted wavefront. The corrected light beam passes through the beam splitter again for transmission and is incident on a lens for beam reduction. The controller derives the control voltage through a control algorithm and sends it to the deformable mirror for wavefront correction. The adaptive correction system formed is shown in Figure 8. By analyzing the peak-to-valley (PV) and root mean square (RMS) values of the corrected wavefront, the correction performance of the three methods is evaluated. This section will conduct comparative experiments, including the Zernike expansion method, the Zernike-MI method, and the Zernike-Db-MI hybrid basis reordering method.

Figure 9 depicts the phase maps after correction through adaptive optics systems using different mode methods. It can be clearly observed that the wavefront in most areas has been effectively corrected using the three methods. However, the phase maps after correction using the Zernike mode method and the Zernike-MI mode method still exhibit areas of incomplete correction at the edges. This is primarily due to the poor reconstruction of the high-frequency components of the distorted wavefront, which affects the correction accuracy of the adaptive system. It is evident that high-frequency components are crucial for accurately describing wavefront distortions, and their absence directly leads to incomplete correction at the edges during the correction process. In contrast, the hybrid basis reconstruction algorithm enhances the ability to capture high-frequency components, achieving more complete phase compensation in the edge regions and significantly optimizing the overall correction effect.

Figure 10 illustrates the convergence process of the PV value as a function of the number of iterations when correcting distorted wavefronts using three different wavefront reconstruction methods: Zernike expansion, Zernike-MI, and Zernike-Db-MI. The three curves in the figure represent the PV changes after correcting the wavefronts reconstructed by the Zernike, Zernike-MI, and Zernike-Db-MI modal methods, respectively. During the first 30 iterations, all three curves exhibit a rapid decline trend. Specifically, the PV curves for the Zernike expansion and Zernike-MI reconstructed wavefronts converge to values of 0.076 μm and 0.069 μm at the 76th and 48th iterations, respectively. The hybrid-basis reconstructed wavefront exhibits the best PV convergence effect, with a convergence value of 0.057 μm achieved at the 39th iteration. This method not only converges fastest but also has the smallest final residual error, indicating its strong noise resistance and stability while maintaining high accuracy.

Figure 11 illustrates the process of RMS variation with the number of iterations after correcting the distorted wavefront using three different wavefront reconstruction methods: Zernike expansion, Zernike-MI, and Zernike-Db-MI. These curves represent the RMS variation after correcting the wavefront reconstructed using the Zernike, Zernike-MI, and Zernike-Db-MI mode methods, respectively. For the method using only Zernike expansion, the RMS value decreases relatively slowly, with a slower rate of decrease in the initial iterations compared to the other two methods, reaching a convergence value of 0.038 μm only after approximately 112 iterations. The RMS decrease rate of the Zernike-MI method is superior to that of the method using only Zernike expansion, reaching a convergence value of 0.036 μm at the 94th iteration, indicating a certain improvement in convergence speed compared to the method using only Zernike expansion. The Zernike-Db-MI hybrid basis reconstruction method exhibits superior performance, with the RMS value decreasing most rapidly, reaching a convergence value of 0.027 μm at the 77th iteration. This method not only converges faster than the previous two methods but also achieves a smaller final RMS convergence value, indicating its superior correction effect on distorted wavefronts.

Figure 10 and Figure 11 demonstrate the effective utilization of mutual information as an indicator to identify and select the Zernike modes that best characterize the wavefront distortion properties under current atmospheric turbulence conditions. The adoption of hybrid basis functions not only inherits the advantages of mode selection based on mutual information but also further enhances the adaptability and reconstruction accuracy for wavefront distortion. It can achieve higher correction accuracy with fewer iterations, achieve better wavefront reconstruction effects, accelerate convergence speed, and improve correction accuracy, providing strong support for real-time wavefront control in adaptive optics systems.

6. Conclusions

(1) Experimental and simulation results demonstrate that the Zernike-Db hybrid basis reordering method based on mutual information can effectively enhance the accuracy of wavefront reconstruction. When the mode number is 20, the root mean square of the wavefront residuals for the Zernike-Db-MI method is as low as 0.14 rad, significantly outperforming the 0.19 rad of the Zernike-MI method and the 0.33 rad of the traditional Zernike method, verifying that this method achieves superior reconstruction performance under limited modes.

(2) As the number of modes increases to 38, the wavefront residual of the Zernike-Db-MI method further decreases to approximately 0.03 rad, reaching the minimum value throughout the entire reconstruction process and significantly outperforming other methods. Simulation results show that this method can more accurately restore the local details (edges and steep-slope areas in the upper-left corner) of the original distorted wavefront, indicating that by integrating the advantages of different basis functions, it effectively overcomes the limitations of a single basis function in expressing complex phase distortions.

(3) The Zernike-Db-MI hybrid reconstruction method achieves superior wavefront correction performance compared to both conventional Zernike expansion and Zernike-MI approaches. Specifically, its peak-to-valley (PV) error converges to 0.057 μm at the 39th iteration, outperforming Zernike-MI (0.069 μm at 48 iterations) and Zernike expansion (0.076 μm at 76 iterations) in both convergence speed and final accuracy. Similarly, the RMS error reaches 0.027 μm at the 77th iteration, significantly faster and lower than those of Zernike-MI (0.036 μm at 94 iterations) and Zernike expansion (0.038 μm at 112 iterations). The consistently faster convergence and smaller residual errors indicate that the hybrid method provides higher correction precision and improved numerical stability under experimental conditions.