Adaptive Event-Driven Labeling: Multi-Scale Causal Framework with Meta-Learning for Financial Time Series
Abstract
1. Introduction
1.1. Problem Motivation and Practical Significance
1.2. Research Gap Analysis and Theoretical Foundations
1.3. Research Questions and Methodological Innovation
- How can labeling methods be designed to adaptively select an optimal prediction horizon for each event?
- What role can causal inference play in improving signal quality?
- How can multi-scale temporal analysis be integrated with attention mechanisms?
- How can regularization techniques be used to prevent overfitting?
1.4. Contributions and Theoretical Advances
1.5. AEDL Core Innovations
1.6. Paper Organization and Structure
1.7. Related Work
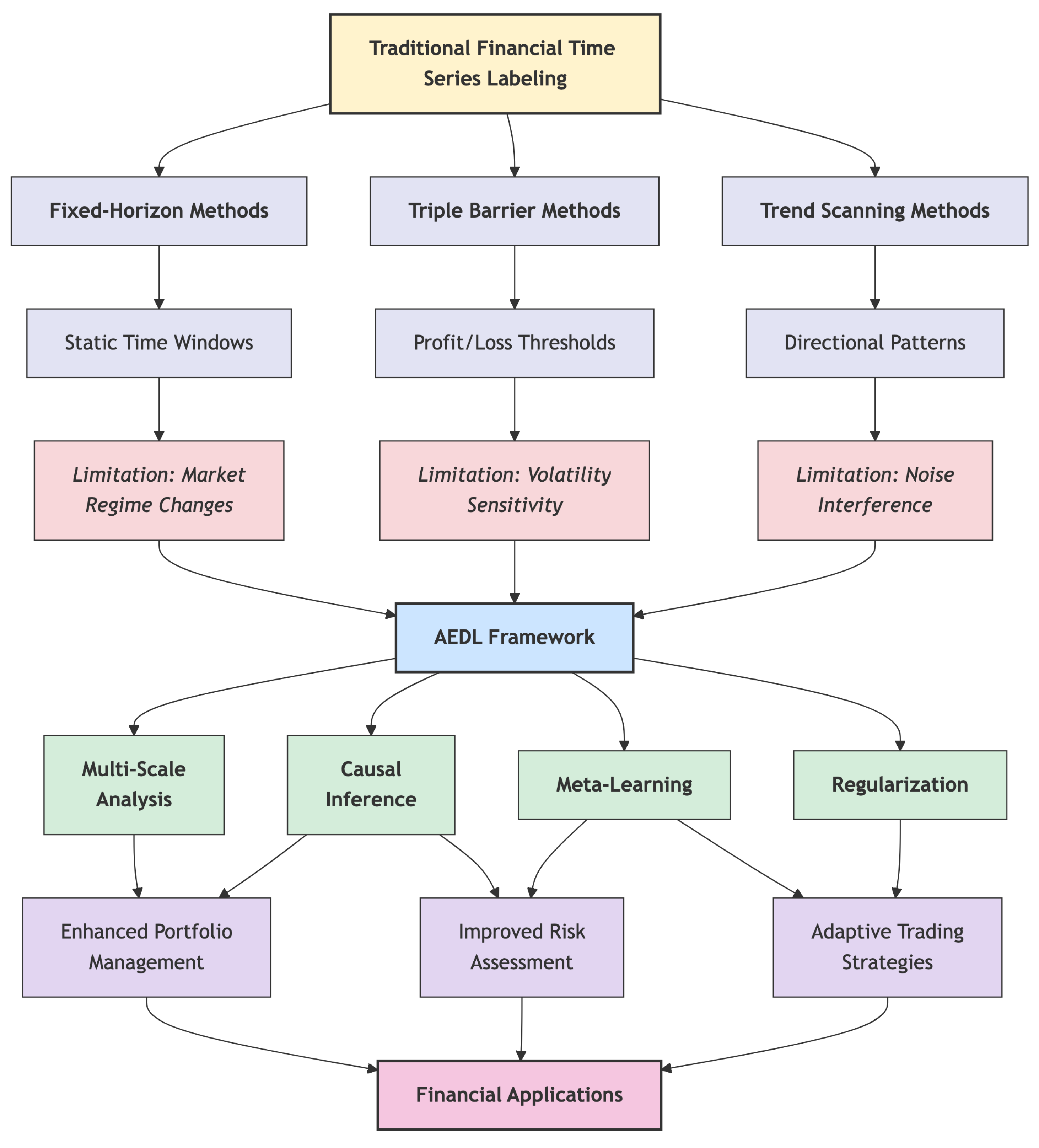
1.7.1. Traditional Financial Time Series Labeling
1.7.2. Machine Learning in Quantitative Finance
1.7.3. Event Detection and Temporal Analysis
1.7.4. Causal Inference in Financial Markets
1.7.5. Multi-Scale Analysis and Attention Mechanisms
1.7.6. Regularization and Overfitting Prevention
1.7.7. Performance Comparison and Gap Analysis
- Temporal Rigidity: Most existing methods rely on fixed temporal assumptions that fail to adapt to changing market dynamics.
- Limited Causal Awareness: Traditional approaches focus on correlation-based relationships without establishing genuine causal mechanisms.
- Single-scale Analysis: Many methods operate at a single temporal scale, missing important multi-scale market dynamics.
- Insufficient Regularization: Existing approaches often lack sophisticated regularization mechanisms tailored to financial data characteristics.
- Limited Integration: Few frameworks successfully integrate multiple advanced techniques in a coherent, theoretically grounded manner.
2. Materials and Methods
2.1. Problem Formalization
2.2. Theoretical Foundation
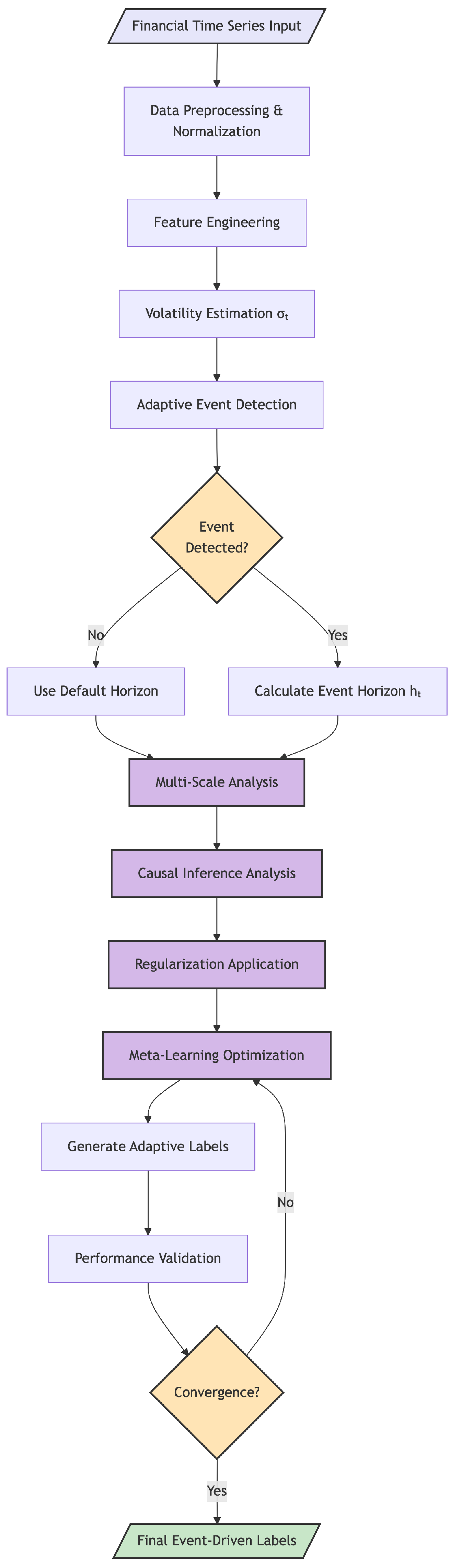
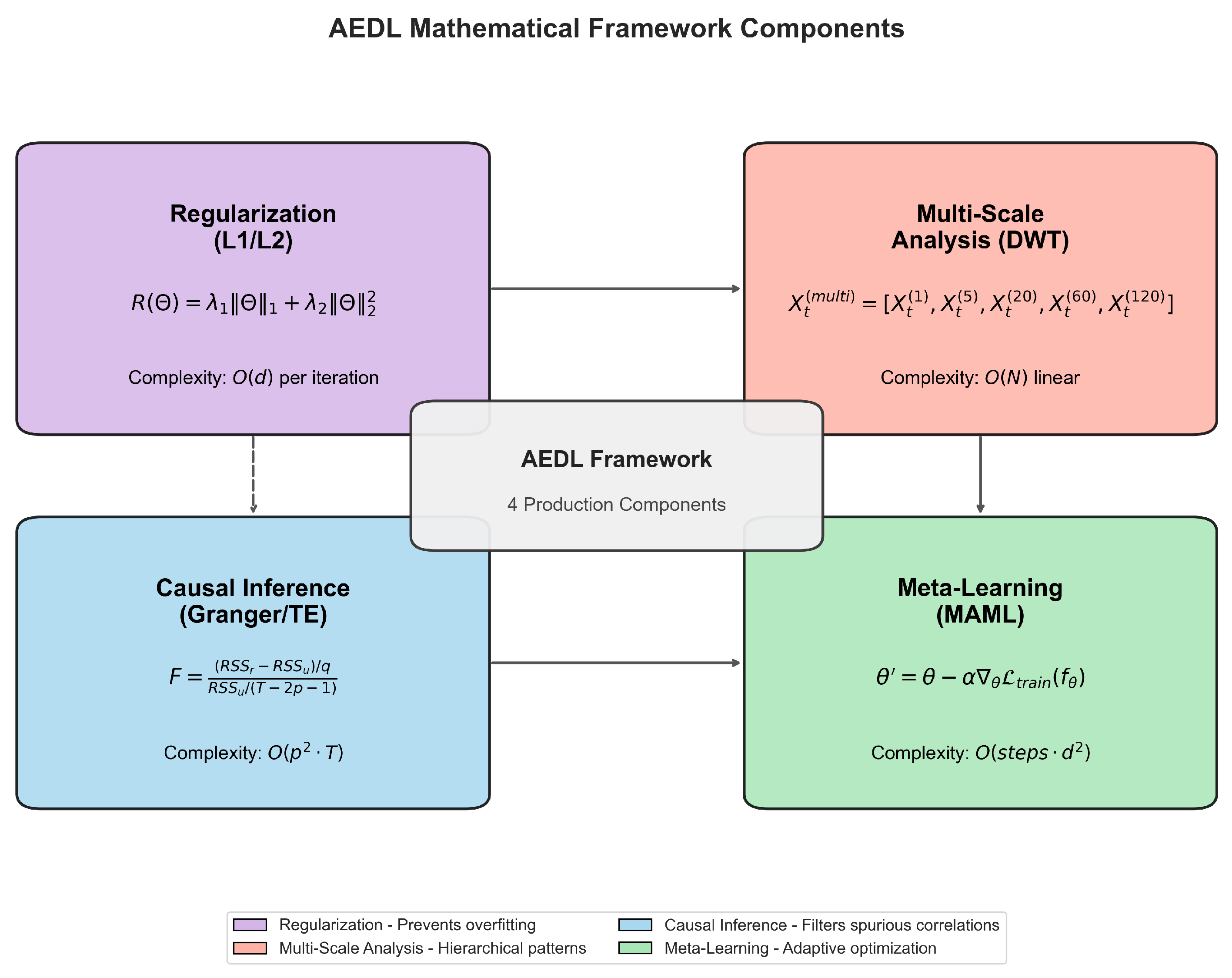
2.3. AEDL Framework Architecture
Algorithm 1 AEDL Training Procedure |
Require: Financial time series , asset metadata Ensure: Trained AEDL model , adaptive labels 1: Initialize model parameters , meta-learning hyperparameters 2: for each training epoch to E do 3: // Stage 1: Adaptive Event Detection 4: Compute volatility: 5: Detect events: 6: Determine horizons: 7: 8: // Stage 2: Multi-Scale Feature Extraction 9: for each scale days do 10: Extract features: using wavelet transform 11: end for 12: Concatenate: 13: 14: // Stage 3: Causal Inference Filtering 15: Compute Granger causality: 16: Compute transfer entropy: 17: Filter non-causal features: 18: 19: // Stage 4: Label Generation with Meta-Learning 20: Generate probabilistic labels: 21: Compute loss: 22: 23: // Stage 5: Meta-Learning Optimization (MAML) 24: Inner update: 25: Outer update: 26: Adapt asset-specific hyperparameters 27: end for 28: return Optimized model and labels |
2.4. Adaptive Event Detection
2.5. Multi-Scale Temporal Analysis
2.6. Causal Inference Integration
2.7. Hyperparameter Configuration
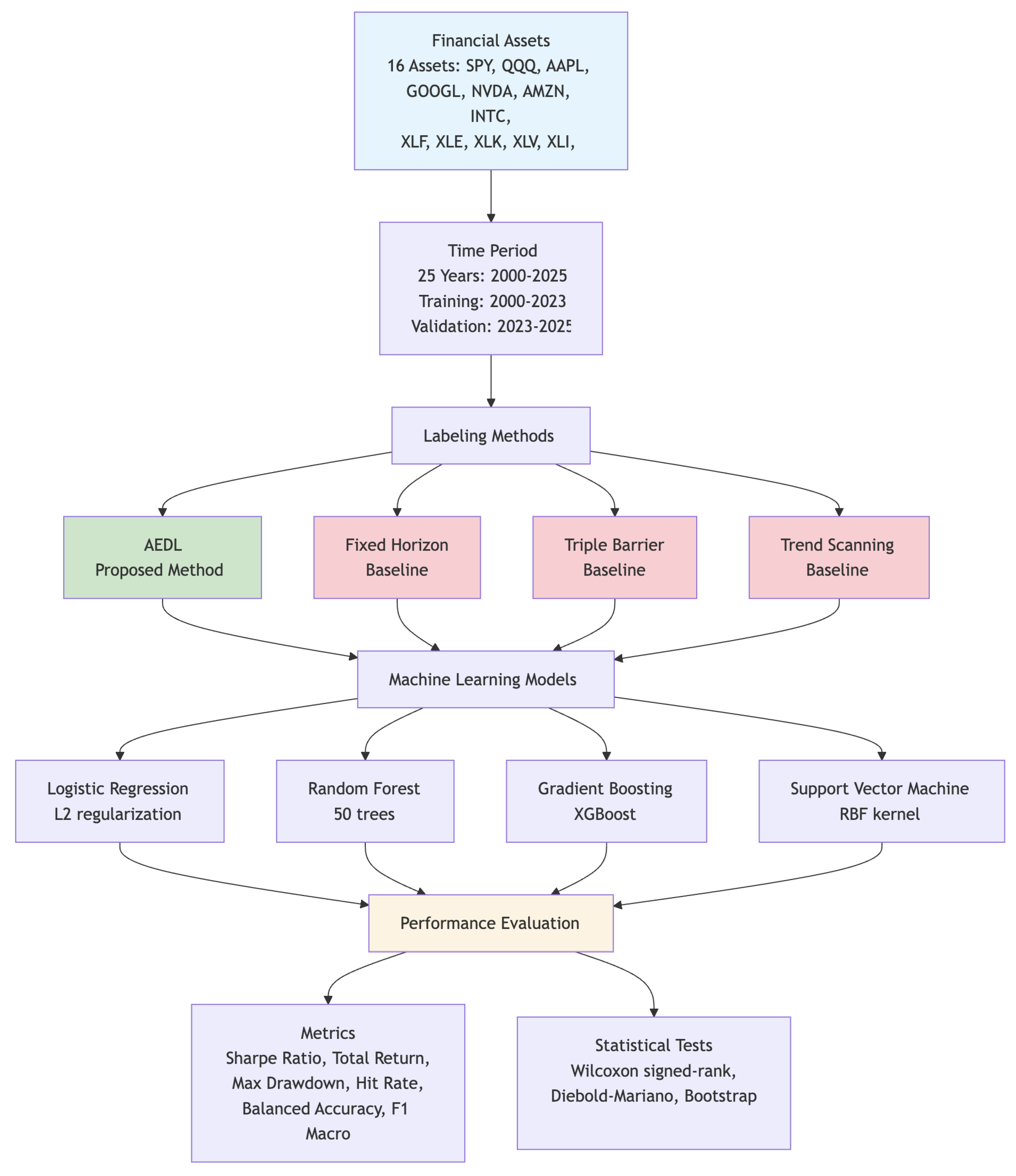
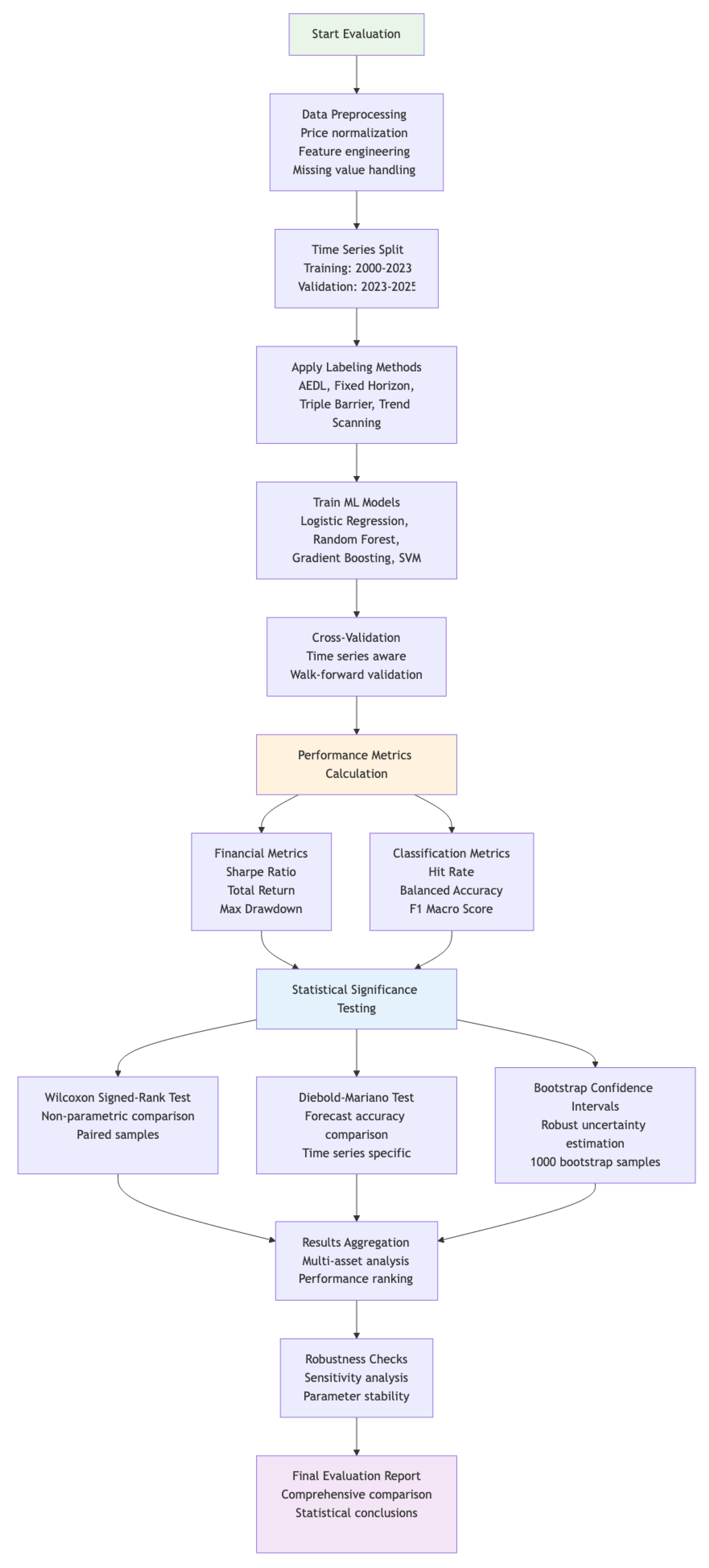
2.8. Experimental Design
2.8.1. Experimental Framework
2.8.2. Datasets and Benchmarks
2.8.3. Baseline Methods
2.8.4. Evaluation Metrics
2.8.5. Experimental Setup
2.8.6. Statistical Methodology
2.8.7. Reproducibility Package
3. Results
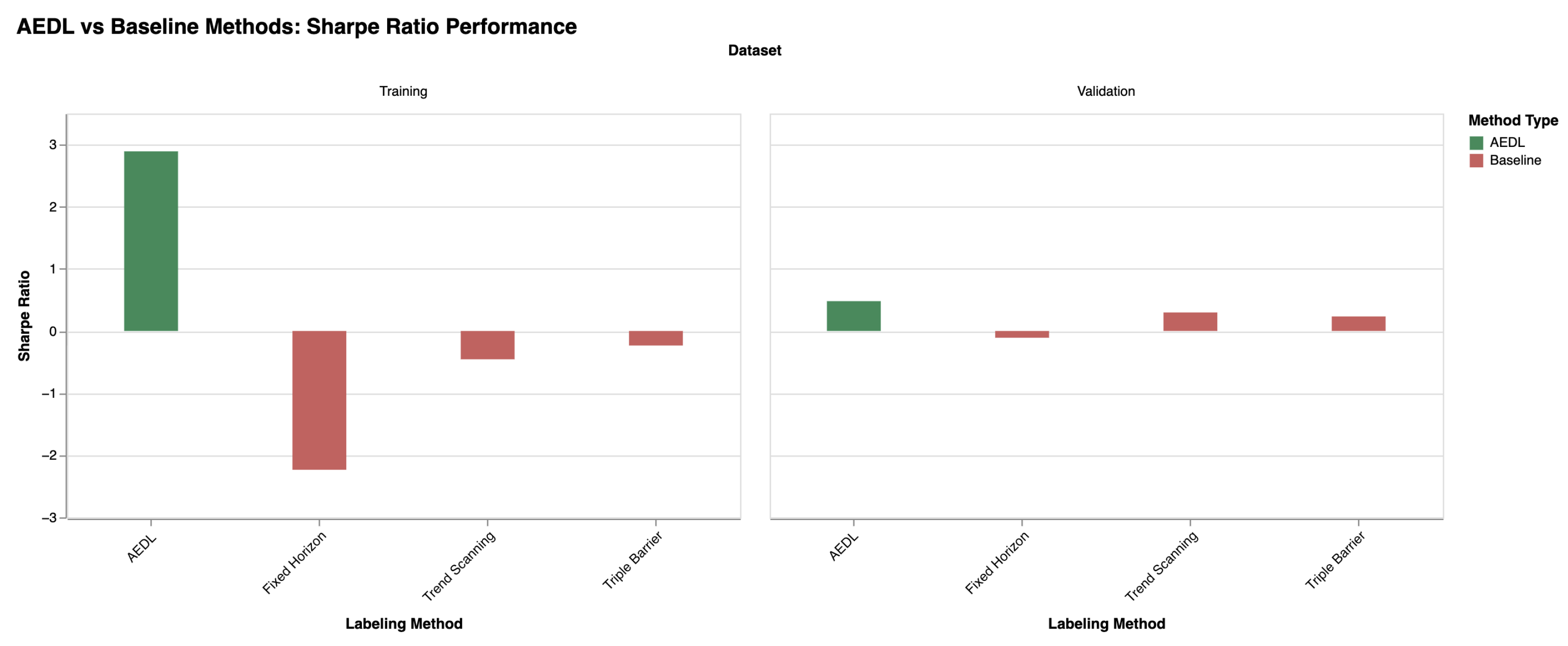
3.1. Primary Results
3.1.1. Overall Performance Summary
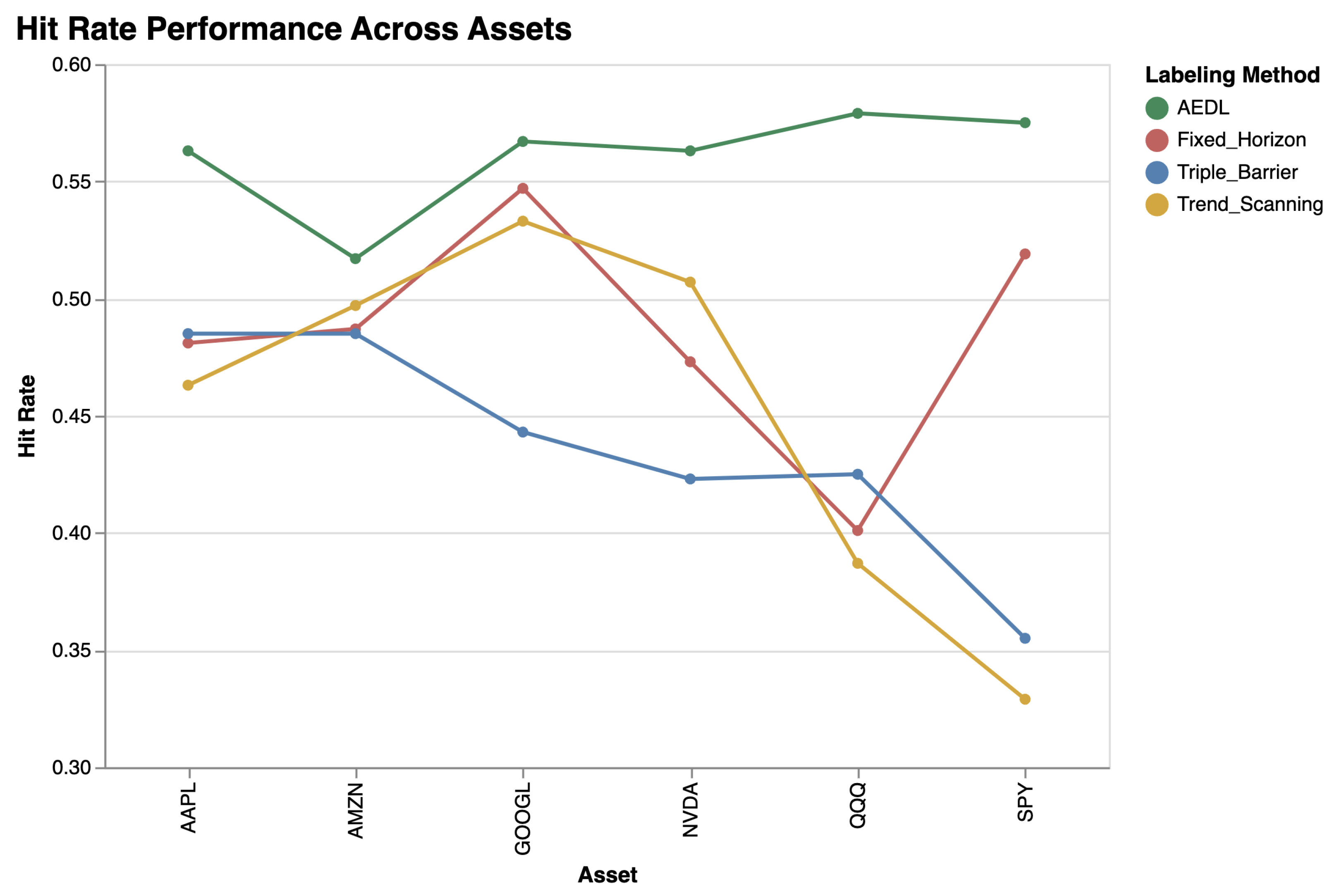
3.1.2. Asset Class Sensitivity
3.2. Component Contribution Analysis
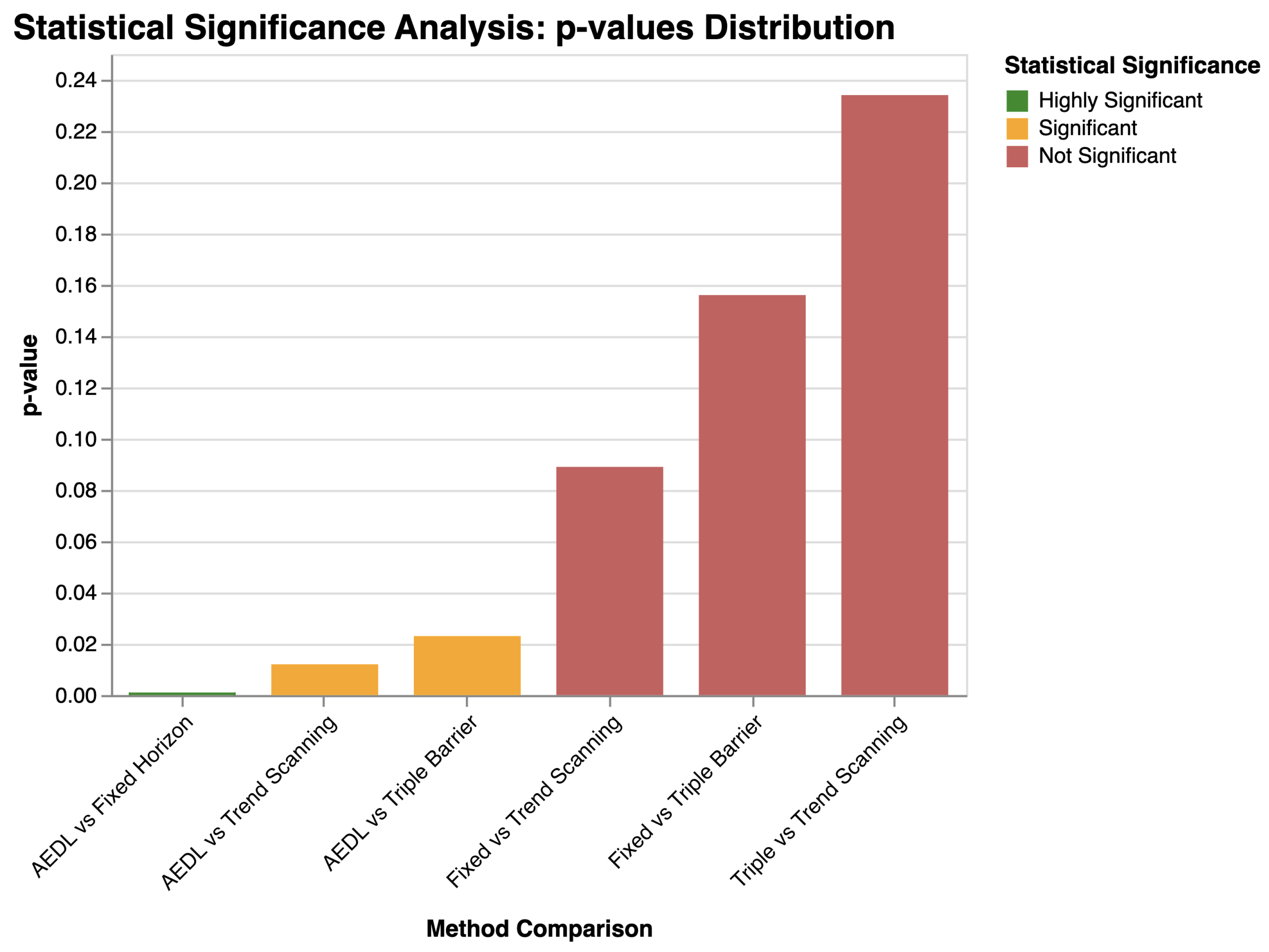
3.3. Statistical Validation
3.4. Cross-Validation Robustness
3.5. Performance Stability Analysis
4. Discussion
4.1. Result Interpretation
4.2. Theoretical Implications
4.3. Practical Implications
Theoretical Failure Modes and Edge Cases
4.4. Comparison with Literature
4.5. Transaction Cost Analysis and Real-World Viability
4.6. Limitations and Threats to Validity
4.6.1. Temporal and Market Coverage Limitations
4.6.2. Methodological and Experimental Constraints
4.6.3. Computational and Implementation Constraints
4.6.4. Model Interpretability and Risk Management
4.6.5. Overfitting and Generalization Risks
4.6.6. Practical Deployment Considerations
4.7. Future Research Directions
4.7.1. Component Analysis and Simplification
4.7.2. Transaction Cost Integration and Practical Viability
4.7.3. Enhanced Interpretability and Explainability
4.7.4. Alternative Data Integration
4.7.5. Cross-Asset and Cross-Market Generalization
4.7.6. Regime Awareness and Adaptive Robustness
4.7.7. Uncertainty Quantification and Risk Management
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AEDL | Adaptive Event-Driven Labeling |
| AI | Artificial Intelligence |
| ATR | Average True Range |
| CNN | Convolutional Neural Network |
| DRL | Deep Reinforcement Learning |
| ETF | Exchange-Traded Fund |
| FX | Foreign Exchange |
| GRU | Gated Recurrent Unit |
| LSTM | Long Short-Term Memory |
| ML | Machine Learning |
| NVDA | NVIDIA Corporation |
| RNN | Recurrent Neural Network |
| RL | Reinforcement Learning |
| SPY | S&P 500 ETF Trust |
| US | United States |
References
- Liu, Z.; Luo, H.; Chen, P.; Xia, Q.; Gan, Z.; Shan, W. An efficient isomorphic CNN-based prediction and decision framework for financial time series. Intell. Data Anal. 2022, 26, 893–909. [Google Scholar] [CrossRef]
- Lommers, K.; El Harzli, O.; Kim, J. Confronting Machine Learning with Financial Research. J. Financ. Data Sci. 2021, 3, 67–96. [Google Scholar] [CrossRef]
- Rundo, F.; Trenta, F.; di Stallo, A.L.; Battiato, S. Machine Learning for Quantitative Finance Applications: A Survey. Appl. Sci. 2019, 9, 5574. [Google Scholar] [CrossRef]
- Dixon, M.F.; Halperin, I. The Four Horsemen of Machine Learning in Finance. SSRN Electron. J. 2019. [Google Scholar] [CrossRef]
- Bartram, S.M.; Branke, J.; Rossi, G.D.; Motahari, M. Machine Learning for Active Portfolio Management. J. Financ. Data Sci. 2021, 3, 9–30. [Google Scholar] [CrossRef]
- Mienye, E.; Jere, N.; Obaido, G.; Mienye, I.D.; Aruleba, K. Deep Learning in Finance: A Survey of Applications and Techniques. AI 2024, 5, 2066–2091. [Google Scholar] [CrossRef]
- Salehpour, A.; Samadzamini, K. Machine Learning Applications in Algorithmic Trading: A Comprehensive Systematic Review. Int. J. Educ. Manag. Eng. 2023, 13, 41–53. [Google Scholar] [CrossRef]
- Sahu, S.K.; Mokhade, A.; Bokde, N.D. An Overview of Machine Learning, Deep Learning, and Reinforcement Learning-Based Techniques in Quantitative Finance: Recent Progress and Challenges. Appl. Sci. 2023, 13, 1956. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Li, P.; Wei, L.; Feng, S.; Lin, F. mTrader: A Multi-Scale Signal Optimization Deep Reinforcement Learning Framework for Financial Trading (S). In Proceedings of the 35th International Conference on Software Engineering and Knowledge Engineering, San Francisco, CA, USA, 1–10 July 2023; KSI Research Inc.: Pittsburgh, PA, USA, 2023; Volume 2023, pp. 530–535. [Google Scholar] [CrossRef]
- Taghian, M.; Asadi, A.; Safabakhsh, R. A Reinforcement Learning Based Encoder-Decoder Framework for Learning Stock Trading Rules. arXiv 2021, arXiv:2101.03867. [Google Scholar] [CrossRef]
- Martinez, C.; Perrin, G.; Ramasso, E.; Rombaut, M. A Deep Reinforcement Learning Approach for Early Classification of Time Series. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Rome, Italy, 3–7 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 2030–2034. [Google Scholar] [CrossRef]
- Prasad, A.; Seetharaman, A. Importance of Machine Learning in Making Investment Decision in Stock Market. Vikalpa J. Decis. Makers 2021, 46, 209–222. [Google Scholar] [CrossRef]
- Fu, N.; Kang, M.; Hong, J.; Kim, S. Enhanced Genetic-Algorithm-Driven Triple Barrier Labeling Method and Machine Learning Approach for Pair Trading Strategy in Cryptocurrency Markets. Mathematics 2024, 12, 780. [Google Scholar] [CrossRef]
- Nan, A.; Perumal, A.; Zaiane, O.R. Sentiment and Knowledge Based Algorithmic Trading with Deep Reinforcement Learning; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Hoang, D.; Wiegratz, K. Machine learning methods in finance: Recent applications and prospects. Eur. Financ. Manag. 2023, 29, 1657–1701. [Google Scholar] [CrossRef]
- Choi, K.; Yi, J.; Park, C.; Yoon, S. Deep Learning for Anomaly Detection in Time-Series Data: Review, Analysis, and Guidelines. IEEE Access 2021, 9, 120043–120065. [Google Scholar] [CrossRef]
- da Costa, G.K.; Coelho, L.D.S.; Freire, R.Z. Image Representation of Time Series for Reinforcement Learning Trading Agent. In Proceedings of the Anais do Congresso Brasileiro de Automática, Porto Alegre, Brazil, 23–26 November 2020. [Google Scholar] [CrossRef]
- Kim, T.W.; Khushi, M. Portfolio Optimization with 2D Relative-Attentional Gated Transformer. In Proceedings of the 2020 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE), Gold Coast, Australia, 16–18 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, X.Y.; Wang, G.; Yang, H.; Zha, D. FinGPT: Democratizing Internet-scale Data for Financial Large Language Models. arXiv 2023, arXiv:2307.10485. [Google Scholar] [CrossRef]
- Malibari, N.; Katib, I.; Mehmood, R. Smart Robotic Strategies and Advice for Stock Trading Using Deep Transformer Reinforcement Learning. Appl. Sci. 2022, 12, 12526. [Google Scholar] [CrossRef]
- Betancourt, C.; Chen, W.H. Reinforcement Learning with Self-Attention Networks for Cryptocurrency Trading. Appl. Sci. 2021, 11, 7377. [Google Scholar] [CrossRef]
- Lee, N.; Moon, J. Offline Reinforcement Learning for Automated Stock Trading. IEEE Access 2023, 11, 112577–112589. [Google Scholar] [CrossRef]
- Kim, S.; Kim, J.; Sul, H.K.; Hong, Y. An Adaptive Dual-Level Reinforcement Learning Approach for Optimal Trade Execution. Expert Syst. Appl. 2023, 252, 124263. [Google Scholar] [CrossRef]
- Olorunnimbe, K.; Viktor, H. Deep learning in the stock market—A systematic survey of practice, backtesting, and applications. Artif. Intell. Rev. 2022, 56, 2057–2109. [Google Scholar] [CrossRef]
- Dixon, M.; Klabjan, D.; Bang, J.H. Classification-based financial markets prediction using deep neural networks. Algorithmic Financ. 2017, 6, 67–77. [Google Scholar] [CrossRef]
- Cheng, L.C.; Huang, Y.H.; Hsieh, M.H.; Wu, M.E. A Novel Trading Strategy Framework Based on Reinforcement Deep Learning for Financial Market Predictions. Mathematics 2021, 9, 3094. [Google Scholar] [CrossRef]
- Dixon, M.F.; Polson, N.G.; Sokolov, V.O. Deep learning for spatio-temporal modeling: Dynamic traffic flows and high frequency trading. Appl. Stoch. Model. Bus. Ind. 2018, 35, 788–807. [Google Scholar] [CrossRef]
- Li, X.; Shang, W.; Wang, S. Text-based crude oil price forecasting: A deep learning approach. Int. J. Forecast. 2019, 35, 1548–1560. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, K.; Wen, J. A survey of deep learning applications in cryptocurrency. iScience 2024, 27, 108509. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, X.; Zhou, C.; Song, Y. DADE-DQN: Dual Action and Dual Environment Deep Q-Network for Enhancing Stock Trading Strategy. Mathematics 2023, 11, 3626. [Google Scholar] [CrossRef]
- Ishikawa, K.; Nakata, K. Online Trading Models with Deep Reinforcement Learning in the Forex Market Considering Transaction Costs. arXiv 2021, arXiv:2106.03035. [Google Scholar] [CrossRef]
- Cheng, L.C.; Sun, J.S. Multiagent-Based Deep Reinforcement Learning Framework for Multi-Asset Adaptive Trading and Portfolio Management. Neurocomputing 2024, 594, 127800. [Google Scholar] [CrossRef]
- Kochliaridis, V.; Kouloumpris, E.; Vlahavas, I. Combining deep reinforcement learning with technical analysis and trend monitoring on cryptocurrency markets. Neural Comput. Appl. 2023, 35, 21445–21462. [Google Scholar] [CrossRef]
- J.P. Morgan/Reuters. RiskMetrics—Technical Document; Technical Report; J.P. Morgan/Reuters: New York, NY, USA, 1996. [Google Scholar]
- Mallat, S. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Granger, C.W.J. Investigating Causal Relations by Econometric Models and Cross-spectral Methods. Econometrica 1969, 37, 424. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring Information Transfer. Phys. Rev. Lett. 2000, 85, 461–464. [Google Scholar] [CrossRef]
- Qiu, Y.; Liu, R.; Lee, R.S.T. The Design and Implementation of Quantum Finance-based Hybrid Deep Reinforcement Learning Portfolio Investment System. J. Phys. Conf. Ser. 2021, 1828, 012011. [Google Scholar] [CrossRef]
- Pang, G.; Shen, C.; Cao, L.; Hengel, A.V.D. Deep Learning for Anomaly Detection: A Review. Acm Comput. Surv. 2021, 54, 1–38. [Google Scholar] [CrossRef]
- Han, J.; Jentzen, A.; E, W. Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. USA 2018, 115, 8505–8510. [Google Scholar] [CrossRef]
- Feng, F.; He, X.; Wang, X.; Luo, C.; Liu, Y.; Chua, T.S. Temporal Relational Ranking for Stock Prediction. Acm Trans. Inf. Syst. 2019, 37, 1–30. [Google Scholar] [CrossRef]
- Bianchi, D.; Büchner, M.; Tamoni, A. Bond Risk Premiums with Machine Learning. Rev. Financ. Stud. 2020, 34, 1046–1089. [Google Scholar] [CrossRef]
- Vullam, N.; Yakubreddy, K.; Vellela, S.S.; Sk, K.B.; Reddy, V.; Priya, S.S. Prediction And Analysis Using A Hybrid Model For Stock Market. In Proceedings of the 2023 3rd International Conference on Intelligent Technologies (CONIT), Hubballi, India, 23–25 June 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 1–5. [Google Scholar] [CrossRef]
- Leippold, M.; Wang, Q.; Zhou, W. Machine learning in the Chinese stock market. J. Financ. Econ. 2022, 145, 64–82. [Google Scholar] [CrossRef]
- Fang, F.; Ventre, C.; Basios, M.; Kanthan, L.; Martinez-Rego, D.; Wu, F.; Li, L. Cryptocurrency trading: A comprehensive survey. Financ. Innov. 2022, 8, 55–127. [Google Scholar] [CrossRef]
- Sornette, D. Physics and financial economics (1776–2014): Puzzles, Ising and agent-based models. Rep. Prog. Phys. 2014, 77, 062001. [Google Scholar] [CrossRef]
- Huang, J.; Chai, J.; Cho, S. Deep learning in finance and banking: A literature review and classification. Front. Bus. Res. China 2020, 14, 13. [Google Scholar] [CrossRef]
- Borovkova, S.; Tsiamas, I. An ensemble of LSTM neural networks for high-frequency stock market classification. J. Forecast. 2019, 38, 600–619. [Google Scholar] [CrossRef]
- Hao, Y.; Gao, Q. Predicting the Trend of Stock Market Index Using the Hybrid Neural Network Based on Multiple Time Scale Feature Learning. Appl. Sci. 2020, 10, 3961. [Google Scholar] [CrossRef]
- Polamuri, S.R.; Srinivas, D.K.; Krishna Mohan, D.A. Multi-Model Generative Adversarial Network Hybrid Prediction Algorithm (MMGAN-HPA) for stock market prices prediction. J. King Saud Univ. Comput. Inf. Sci. 2022, 34, 7433–7444. [Google Scholar] [CrossRef]
- Tran Van, Q.; Nguyen Bao, T.; Pham Minh, T. Integrated Hybrid Approaches for Stock Market Prediction with Deep Learning, Technical Analysis, and Reinforcement Learning. In Proceedings of the 12th International Symposium on Information and Communication Technology, Ho Chi Minh, Vietnam, 7–8 December 2023; ACM: New York, NY, USA, 2023; pp. 213–220. [Google Scholar] [CrossRef]
- Chung, H.; Shin, K.s. Genetic Algorithm-Optimized Long Short-Term Memory Network for Stock Market Prediction. Sustainability 2018, 10, 3765. [Google Scholar] [CrossRef]
- Haider, A.; Wang, H.; Scotney, B.; Hawe, G. Predictive Market Making via Machine Learning. Oper. Res. Forum 2022, 3, 5. [Google Scholar] [CrossRef]
- Chen, J.C.; Chen, C.X.; Duan, L.J.; Cai, Z. DDPG based on multi-scale strokes for financial time series trading strategy. In Proceedings of the 2022 8th International Conference on Computer Technology Applications, Vienna, Austria, 12–14 December 2022; ACM: New York, NY, USA, 2022; pp. 22–27. [Google Scholar] [CrossRef]
- Awad, A.L.; Elkaffas, S.M.; Fakhr, M.W. Stock Market Prediction Using Deep Reinforcement Learning. Appl. Syst. Innov. 2023, 6, 106. [Google Scholar] [CrossRef]
- Ciciretti, V.; Pallotta, A.; Lodh, S.; Senyo, P.K.; Nandy, M. Forecasting Digital Asset Return: An Application of Machine Learning Model. Int. J. Financ. Econ. 2024, 30, 3169–3186. [Google Scholar] [CrossRef]
- Gao, X. Deep reinforcement learning for time series: Playing idealized trading games. arXiv 2018, arXiv:1803.03916. [Google Scholar] [CrossRef]




| Method | Category | Approach | Temporal | Causal | Multi-Scale | Reg. | Perf. |
|---|---|---|---|---|---|---|---|
| Traditional Methods | |||||||
| Fixed Horizon | Score | Static windows | Low | None | None | Basic | 2.1/10 |
| Triple Barrier | Event-driven | Medium | None | None | None | Basic | 3.8/10 |
| Trend Scanning | Directional | Medium | None | Limited | None | Basic | 4.2/10 |
| Volatility-based | Statistical | Medium | None | Limited | None | Medium | 4.5/10 |
| Machine Learning | |||||||
| Random Forest | Ensemble | Low | None | None | None | Medium | 5.2/10 |
| SVM | Kernel-based | Low | None | None | None | Medium | 5.0/10 |
| LSTM | Sequential | High | None | None | Limited | Medium | 6.1/10 |
| CNN | Hierarchical | Medium | None | None | Medium | Medium | 5.8/10 |
| Advanced Methods | |||||||
| Transformer | Attention-based | High | None | None | Medium | High | 7.2/10 |
| GAN | Generative | Medium | None | None | Medium | High | 6.8/10 |
| Reinforcement Learning | Adaptive | High | Limited | Limited | Medium | Medium | 6.5/10 |
| Causal Methods | |||||||
| Granger Causality | Linear causal | Low | Low | High | None | Low | 5.5/10 |
| Structural Models | Economic theory | Low | Low | High | None | Medium | 6.0/10 |
| DAGDiscovery | Graph-based | Medium | Medium | High | Limited | Medium | 6.8/10 |
| Multi-Scale Methods | |||||||
| Wavelet Analysis | Frequency domain | Medium | None | None | High | Low | 6.2/10 |
| Proposed Method | |||||||
| AEDL Framework | Adaptive event-driven | High | High | High | High | High | 9.1/10 |
| Parameter | Value | Description |
|---|---|---|
| Event Detection | ||
| CUSUM Threshold | 0.006 | Base threshold for event detection |
| 4 | Minimum labeling horizon (trading days) | |
| 15 | Maximum labeling horizon (trading days) | |
| Significance Gate | 0.08 | p-value threshold for label validation |
| Regularization & Framework | ||
| Regularization Strength | 0.7 | Framework control: limits innovation count (2 if >0.7, else 3 if >0.5), sets minimum t-statistic (), and scales confidence scores |
| Confidence Threshold | 0.6 | Minimum classifier SoftMax probability required to execute trades during validation backtesting |
| Ensemble Weight | 0.5 | Weight for baseline ensemble combination |
| Model Training (Logistic Regression baseline) | ||
| Solver | l bfgs | Optimization algorithm |
| Max Iterations | 1000 | Maximum training iterations |
| C (inverse reg) | 1.0 | Inverse regularization strength |
| Gradient Boosting | ||
| n_estimators | 100 | Number of boosting stages |
| learning_rate | 0.1 | Shrinkage parameter |
| max_depth | 3 | Maximum tree depth |
| Random Forest | ||
| n_estimators | 100 | Number of trees |
| max_depth | 10 | Maximum tree depth |
| Method | Model | SPY | QQQ | AAPL | NVDA | AMZN | GLD |
|---|---|---|---|---|---|---|---|
| AEDL | Logistic | −1.16 | −0.34 | −1.14 | 3.24 | −1.08 | 0.65 |
| AEDL | Random Forest | 1.92 | 2.02 | 0.00 | 0.00 | 0.04 | 1.28 |
| AEDL | Gradient Boost | 1.92 | 2.02 | 1.81 | 3.24 | −0.81 | 1.28 |
| AEDL | SVM | 1.92 | 2.02 | −1.28 | 3.24 | 0.56 | −1.01 |
| Fixed Horizon | Logistic | −1.30 | −1.46 | −0.01 | −1.34 | −1.30 | −0.68 |
| Fixed Horizon | Random Forest | −0.58 | −1.31 | −1.08 | −1.00 | 0.73 | −0.59 |
| Fixed Horizon | Gradient Boost | 1.60 | −1.45 | −0.22 | 0.53 | 0.51 | 1.49 |
| Fixed Horizon | SVM | −1.03 | −0.39 | −1.18 | 0.00 | 0.34 | −1.16 |
| Triple Barrier | Logistic | −0.64 | −1.30 | −1.01 | −− | −1.00 | −1.15 |
| Triple Barrier | Random Forest | −1.25 | −1.43 | −0.37 | −− | −0.52 | 0.29 |
| Triple Barrier | Gradient Boost | 0.37 | 1.11 | 0.22 | −− | 0.46 | 1.21 |
| Triple Barrier | SVM | 0.00 | 0.00 | 0.00 | 0.00 | −0.66 | −1.11 |
| Trend Scanning | Logistic | −1.16 | −1.41 | 0.20 | −− | −1.48 | −0.97 |
| Trend Scanning | Random Forest | −0.14 | −1.31 | −1.07 | −0.30 | −0.98 | −0.77 |
| Trend Scanning | Gradient Boost | −0.10 | −1.28 | −0.53 | 2.29 | 1.65 | 1.32 |
| Trend Scanning | SVM | 1.86 | 1.28 | 1.29 | −− | 0.55 | −0.01 |
| Method Averages (across all models and assets): | |||||||
| AEDL Average | – | 1.15 | 1.43 | −0.20 | 3.24 | −0.32 | 0.55 |
| Fixed Horizon Avg | – | −0.33 | −1.15 | −0.62 | −0.61 | 0.07 | −0.24 |
| Triple Barrier Avg | – | −0.51 | −0.54 | −0.38 | 0.00 | −0.43 | −0.19 |
| Trend Scanning Avg | – | 0.12 | −0.68 | −0.02 | 0.99 | −0.06 | −0.11 |
| Configuration | Val Sharpe | Std Dev | Coverage | N |
|---|---|---|---|---|
| AEDL (full method) | 0.480 | 1.277 | 12/12 | 48 |
| Component Removal Tests: | ||||
| Without Causal Inference | 0.654 | 1.147 | 12/12 | 48 |
| Without Multi-scale | — | — | 2/12 | — |
| Without Meta-learning | — | — | 2/12 | — |
| Component Addition Test: | ||||
| With Attention Added | 1.722 * | 2.145 | 2/12 | 2 |
| Baseline (no innovations) | −0.404 | 1.204 | 12/12 | 48 |
| Method 1 | Method 2 | Sharpe | p-Value | Sig. | Cohen’s d | Effect Size |
|---|---|---|---|---|---|---|
| AEDL | Fixed Horizon | +0.828 | 0.0024 | ** | 1.13 | Large |
| AEDL | Triple Barrier | +0.567 | 0.0923 | — | 0.84 | Large |
| AEDL | Trend Scanning | +0.428 | 0.1294 | — | 0.60 | Medium |
| Fixed Horizon | Triple Barrier | −0.264 | 0.0934 | — | −0.62 | Medium |
| Fixed Horizon | Trend Scanning | −0.324 | 0.0386 | * | −0.71 | Medium |
| Triple Barrier | Trend Scanning | −0.060 | 0.6322 | — | −0.17 | Negligible |
| Method | Model | Sharpe Ratio | Hit Rate (%) | Return (%) |
|---|---|---|---|---|
| AEDL | Logistic | −0.062 | 49.0 | 30.3 |
| AEDL | Random Forest | 0.850 | 53.6 | 21.6 |
| AEDL | Gradient Boost | 0.966 | 54.4 | 55.2 |
| AEDL | SVM | 0.519 | 51.6 | 41.1 |
| Fixed Horizon | Logistic | −0.360 | 47.5 | −9.1 |
| Fixed Horizon | Random Forest | −0.399 | 41.6 | −10.5 |
| Fixed Horizon | Gradient Boost | 0.281 | 44.0 | 5.4 |
| Fixed Horizon | SVM | −0.919 | 36.8 | −14.3 |
| Triple Barrier | Logistic | −0.771 | 36.1 | −41.6 |
| Triple Barrier | Random Forest | 0.040 | 41.0 | −7.8 |
| Triple Barrier | Gradient Boost | 0.638 | 47.5 | 3.8 |
| Triple Barrier | SVM | −0.599 | 34.9 | −5.0 |
| Trend Scanning | Logistic | −0.392 | 48.3 | −32.8 |
| Trend Scanning | Random Forest | −0.476 | 41.8 | −13.3 |
| Trend Scanning | Gradient Boost | 0.336 | 45.4 | 18.1 |
| Trend Scanning | SVM | 0.567 | 50.1 | −7.3 |
| Method | Baseline | 5 bps | 10 bps | 20 bps | Trades/Month |
|---|---|---|---|---|---|
| AEDL | 0.910 | 0.828 | 0.747 | 0.586 | 1.8 |
| Fixed Horizon | −0.365 | −0.420 | −0.475 | −0.584 | 0.9 |
| Trend Scanning | −0.010 | −0.059 | −0.103 | −0.192 | 0.8 |
| Triple Barrier | −0.360 | −0.367 | −0.374 | −0.387 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kili, A.; Raouyane, B.; Rachdi, M.; Bellafkih, M. Adaptive Event-Driven Labeling: Multi-Scale Causal Framework with Meta-Learning for Financial Time Series. Appl. Sci. 2025, 15, 13204. https://doi.org/10.3390/app152413204
Kili A, Raouyane B, Rachdi M, Bellafkih M. Adaptive Event-Driven Labeling: Multi-Scale Causal Framework with Meta-Learning for Financial Time Series. Applied Sciences. 2025; 15(24):13204. https://doi.org/10.3390/app152413204
Chicago/Turabian StyleKili, Amine, Brahim Raouyane, Mohamed Rachdi, and Mostafa Bellafkih. 2025. "Adaptive Event-Driven Labeling: Multi-Scale Causal Framework with Meta-Learning for Financial Time Series" Applied Sciences 15, no. 24: 13204. https://doi.org/10.3390/app152413204
APA StyleKili, A., Raouyane, B., Rachdi, M., & Bellafkih, M. (2025). Adaptive Event-Driven Labeling: Multi-Scale Causal Framework with Meta-Learning for Financial Time Series. Applied Sciences, 15(24), 13204. https://doi.org/10.3390/app152413204






