Opto-Mechatronic–Electrical Synergistic Capacitive Sensor for High-Resolution Micro-Displacement Measurement Targeting Cost-Sensitive Applications

Featured Application

This paper presents a prototype of a micro-displacement measurement system based on parallel-plate capacitance. Employing an opto-mechatronic–electrical design, it achieves low cost (~90% reduction vs. laser interferometry) and operates without strict vibration isolation or a darkroom. Experimental validation of micrometer-level displacement measurement confirms the hardware’s potential for nanometer-level resolution. This work offers a new approach for educational and proof-of-concept applications in cost-sensitive sectors like semiconductor manufacturing and MEMS testing.

Abstract

To address the limitations of optical interferometry (strict environmental requirements, high cost) and piezoelectric methods (hysteresis, creep) in micro-displacement measurement, this study proposes a collaborative measurement approach based on the parallel plate capacitance principle—with its core innovation lying in integrated optimization rather than original principles. Unlike existing studies that separately optimize mechanics, hardware, or algorithms, this work achieves the first synergy of three components: a mechanical coupling mechanism (integrating a high-resolution optical mount and a micrometer) for parallel plate regulation, a 21-bit capacitance detection module based on the STM32-PCAP01 (with a resolution of 0.0001 pF), and a linear response model relating capacitance to the reciprocal of displacement. Experimental validation confirms its engineering feasibility for sub-nanometer-level precision: with a 10 cm plate radius and 3–20 mm initial spacing, the system achieves 277.215 ± 0.244 pF·mm sensitivity and <0.05 μm displacement resolution. The relative error of micro-displacement measurement in the 10 μm range is less than 1.56%. Based on the hardware resolution, the system possesses the theoretical capability to detect displacements as low as 10⁻⁸ to 10⁻⁹ m. Compared to laser interferometry, it operates stably in common industrial environments without vibration isolation or darkrooms, reducing costs by ~90% while maintaining comparable accuracy. This cost-effective solution enables online precision measurement in semiconductor manufacturing and MEMS testing, with its multi-physics collaborative design offering a new paradigm for intelligent sensor development.

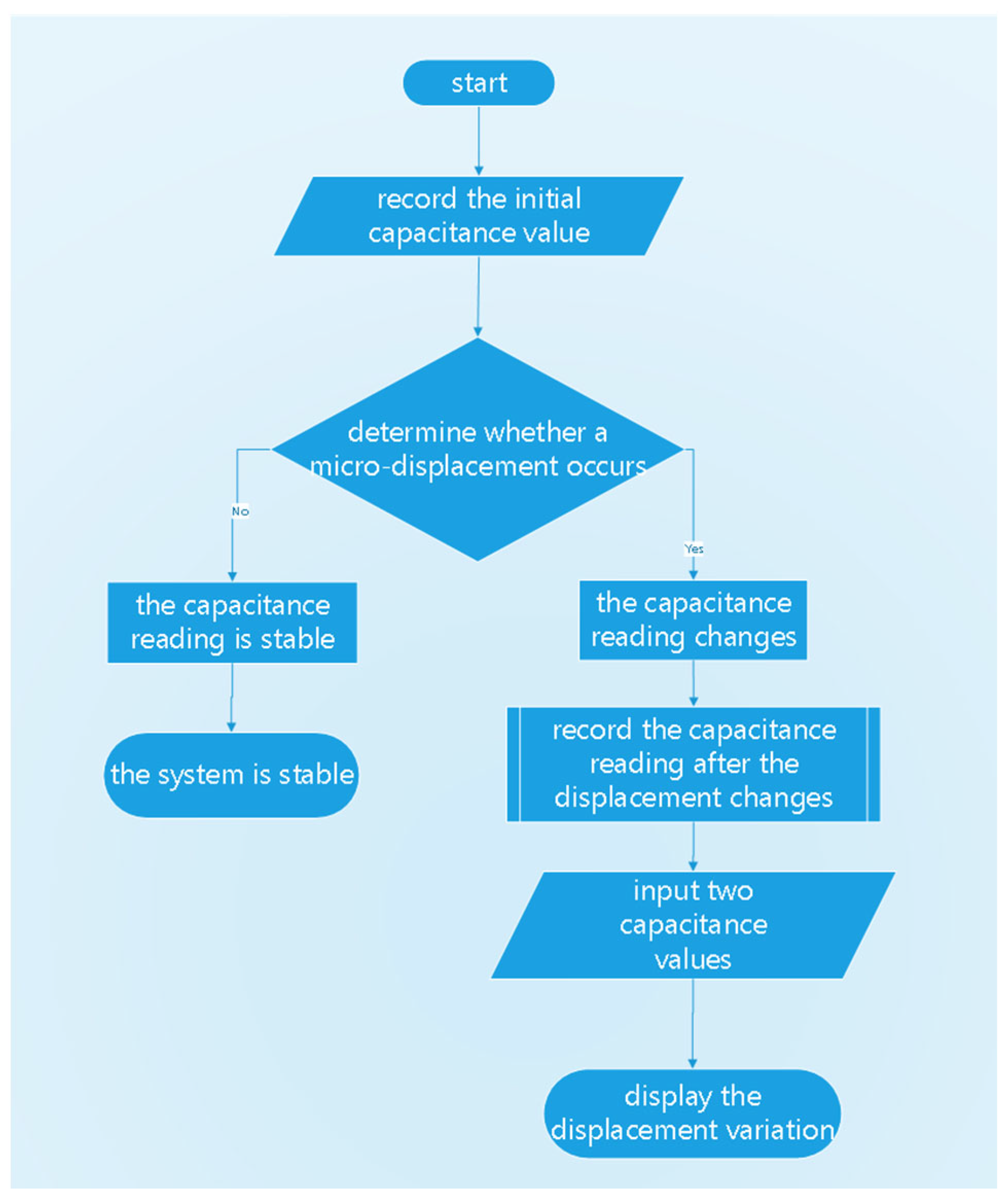
1. Introduction

Precision Measurement Technology [1] is a package that supports semiconductor chips (such as wafer bonding precision control [2]), MEMS [3] device performance testing (such as micro-actuator displacement calibration [4]), and ultra-precision machining equipment with the feature size of integrated circuits entering into 7 nm and below. The triple demand of “high precision (submicron and below), high robustness, and low cost” for displacement measurement in industry is increasingly urgent. However, the contradiction between accuracy, environmental adaptability, and cost of current mainstream measurement technology is difficult to reconcile, resulting in most high-end solutions being limited to laboratory scenarios, while low-cost solutions are difficult to meet the accuracy requirements, forming a “measurement technology bottleneck” in the field of advanced manufacturing.

At present, the micro-displacement measurement methods have formed a pattern of coexistence of multiple technical paths, but each method has significant differences in accuracy, environmental requirements, cost, and engineering applicability, such as laser interferometry [5] based on the Michelson interference principle, which can achieve nano-scale (0.1~10 nm) resolution, and is the standard of high-precision laboratory measurement. But it depends on a high-purity He-Ne laser [6], a precision optical lens group, and a strict vibration isolation system; the total cost of the whole set of equipment is generally more than CNY 100,000, and complex operation requires professionals to use. At the same time, this method is sensitive to environmental vibration and dark room, air refractive index, completely unable to adapt to workshop-level complex working conditions, can only be used in an ultra-clean laboratory at constant temperature and humidity, and cannot be applied on a large scale. The optical fiber sensor [7] based on the principle of interference and refraction of light is more resistant to vibration than laser interferometry, can suppress the influence of temperature, and is applicable to a wider range of environments than laser interferometry, with a resolution of 0.5~5 μm. However, its core shortcomings lie in the complexity of optical path calibration, high debugging cost, and easy loss of optical fiber probes. It is difficult to achieve large-scale deployment of multiple measurement points. There are also piezoelectric ceramic driving methods [8] that convert voltage signals into micro-displacements by using the “inverse piezoelectric effect [9]” of piezoelectric materials. The resolution can reach the sub-nanometer level, and the response speed is fast. However, piezoelectric ceramics have inherent “hysteresis nonlinearity [10]” and “creep characteristics [11]”, and, even if PID closed-loop feedback control is adopted, it is still necessary to additionally design complex error compensation algorithms. In addition, high-precision piezoelectric ceramic drivers have high unit prices, the cost of supporting control modules exceeds CNY 50,000, and the measurement range is limited.

In view of the above, the optical method environment requirements are strict and high cost, the pressure point material range is limited, and other bottlenecks. Consider that the traditional capacitive sensor has the advantages of non-contact measurement, strong anti-electromagnetic interference ability, and strong environmental adaptability, but the accuracy is limited to 0.1~30 μm [12], and the accuracy is easily affected by parasitic capacitance [13] and other errors. Based on the idea of “optical–mechanical–electrical collaborative optimization”, a new method of micro-displacement measurement based on the parallel plate capacitance principle is proposed in this paper. Through the deep fusion of mechanical structure optimization, high-resolution hardware design, and error separation algorithm, the measurement goal of “high resolution, low cost, and wide range” is realized. The dynamic parallel calibration of the polar plate is realized through the optical-bench [14] micrometer mechanical coupling mechanism, wherein the return clearance and inclination error of the traditional slide rail structure are eliminated, the sub-millimeter displacement of the polar plate is realized, and the cost and the limitation of small range of the polar plate displacement by using the stepper motor [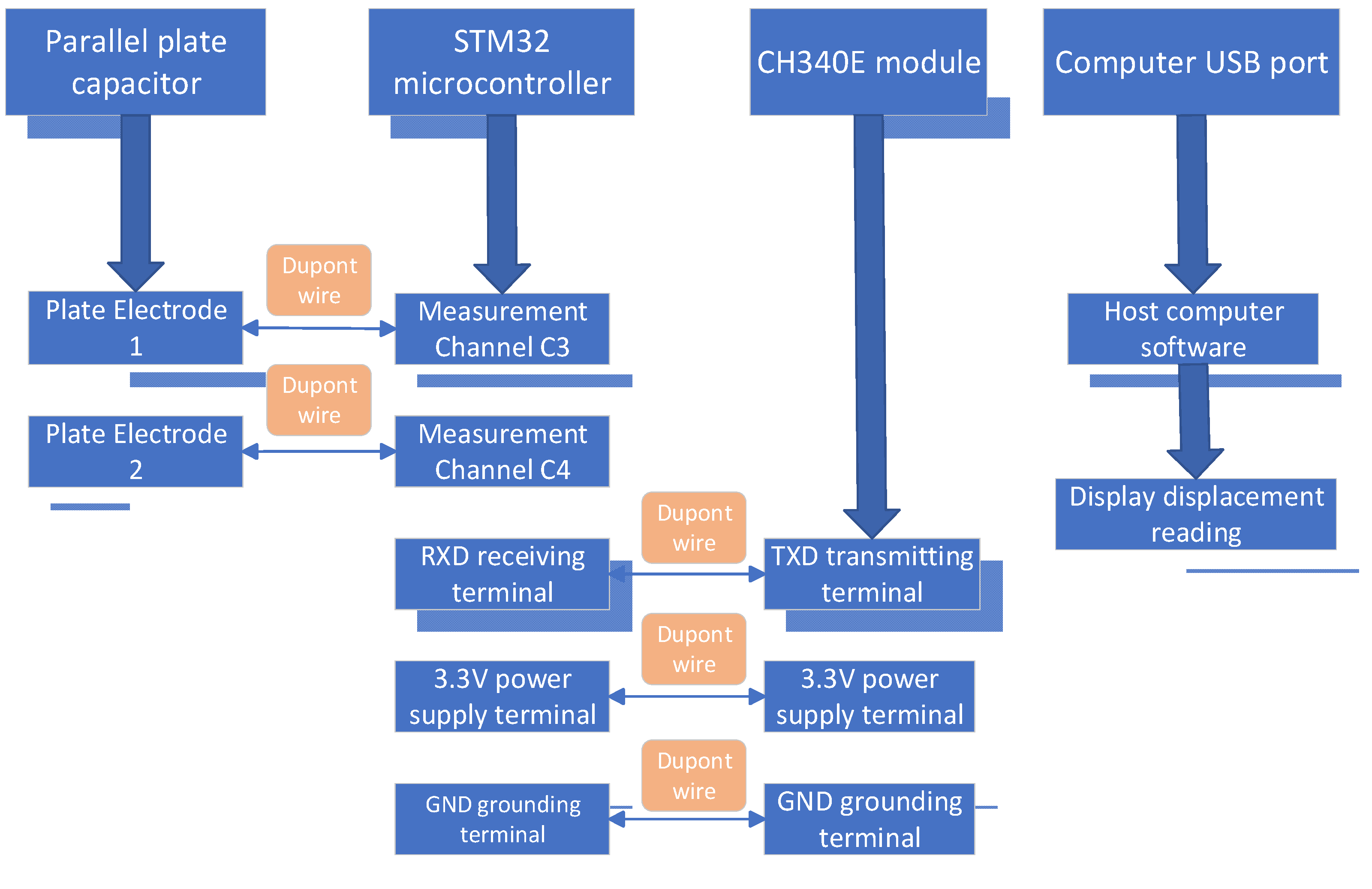15] and the like are greatly reduced. 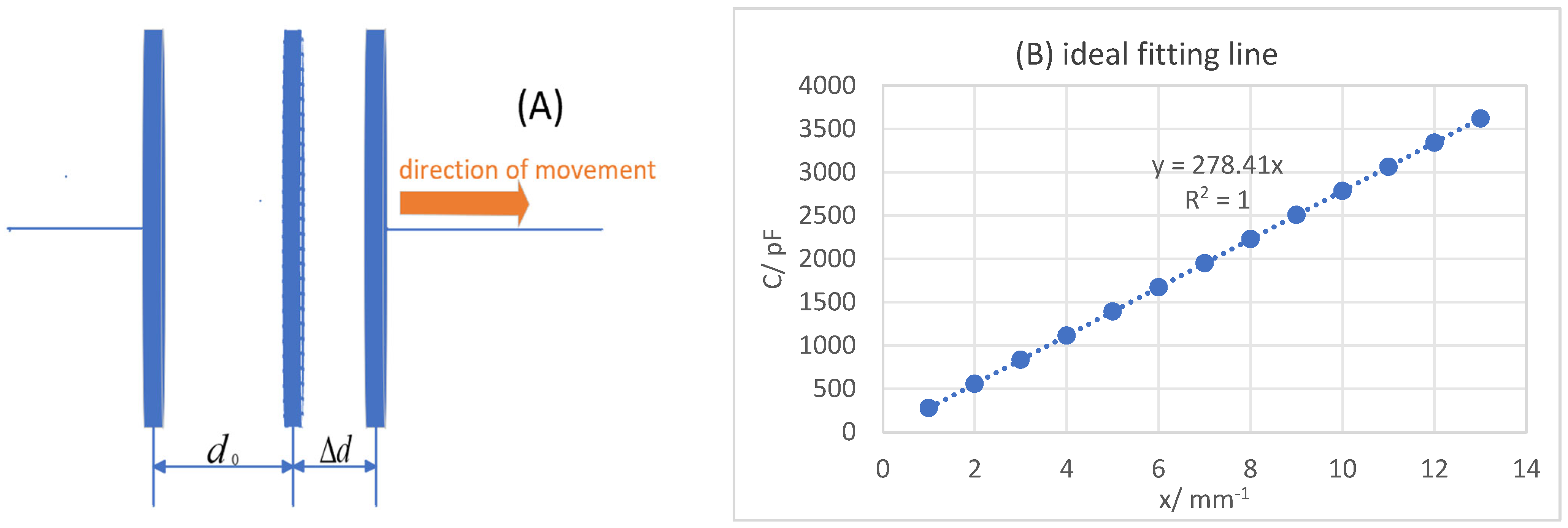The precision of the 21-bit high-resolution capacitance detection module constructed by the STM32-PCAP01 chip [16] is 0.001 pF. Based on the charge transfer principle, the module compares the charge–discharge time ratio of the measured capacitor with the reference capacitor to detect the small capacitance change, compensates for the temperature drift, and has strong electromagnetic interference ability and environmental adaptability. A complete micro-displacement measurement system is researched and constructed. 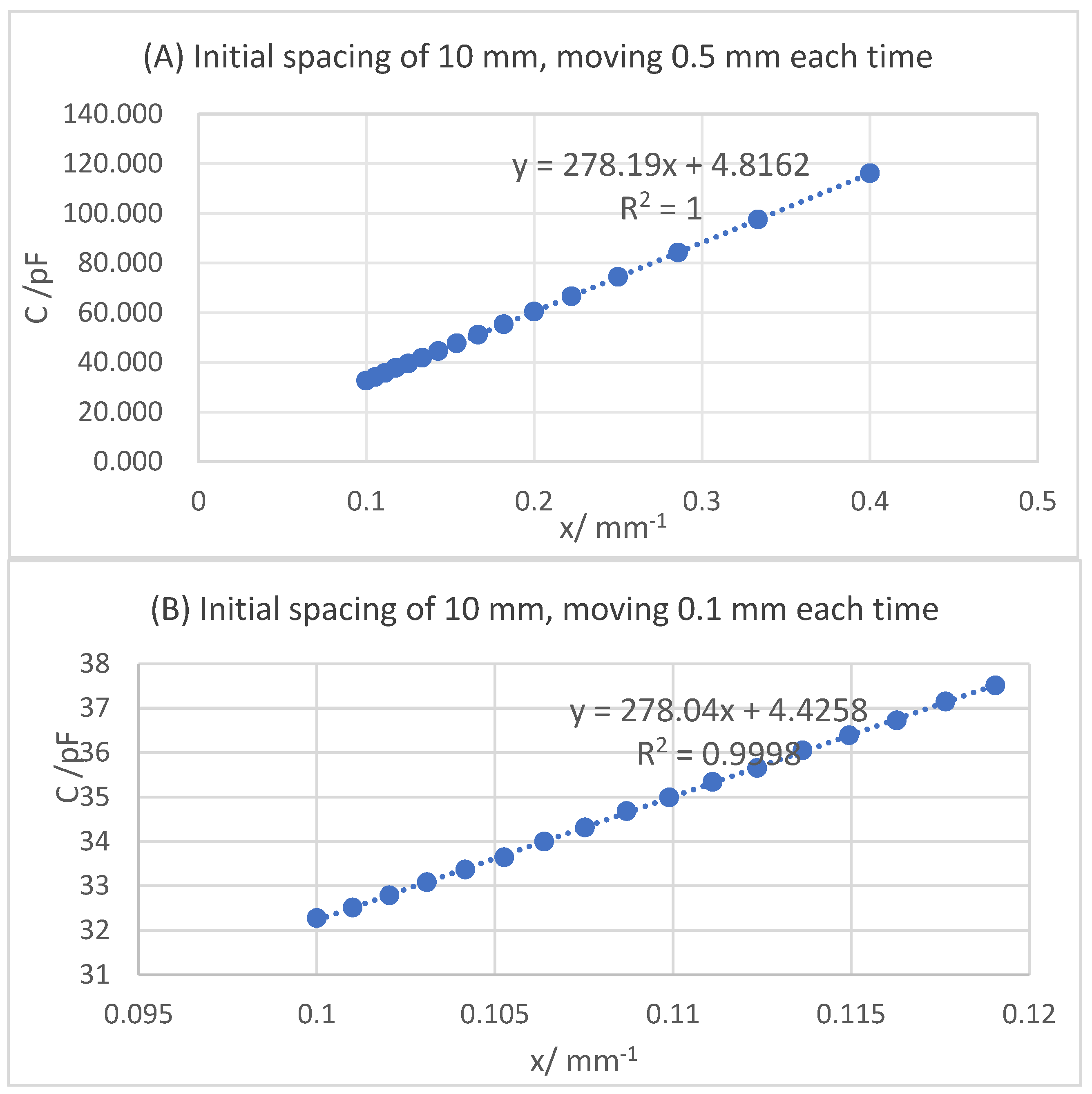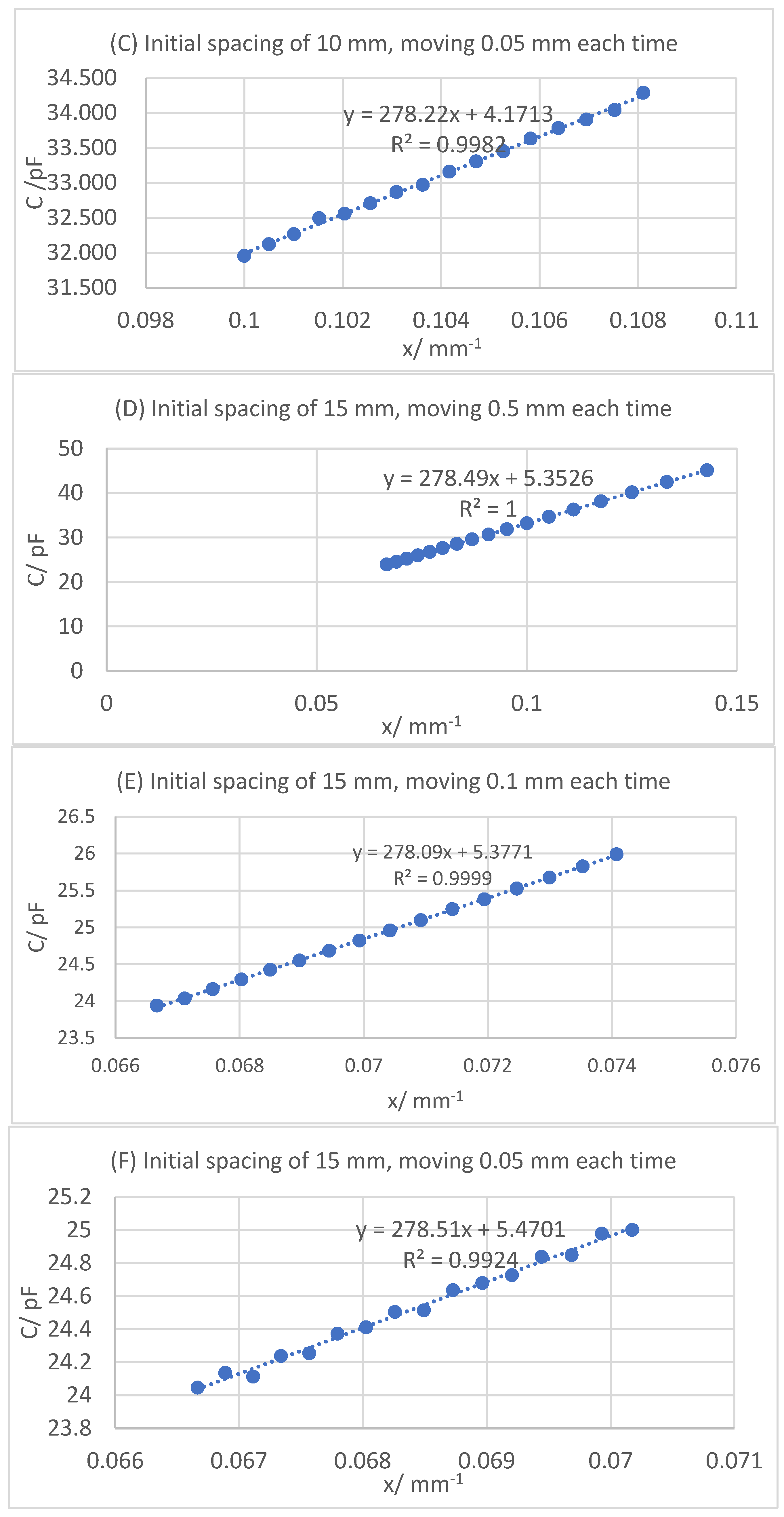The complex nonlinear fitting model [17] of data is not directly based on the inverse relationship between parallel plate capacitance and displacement, but the experimental data is processed by the linear fitting [18] method, and the physical quantity of the system is effectively calibrated again. 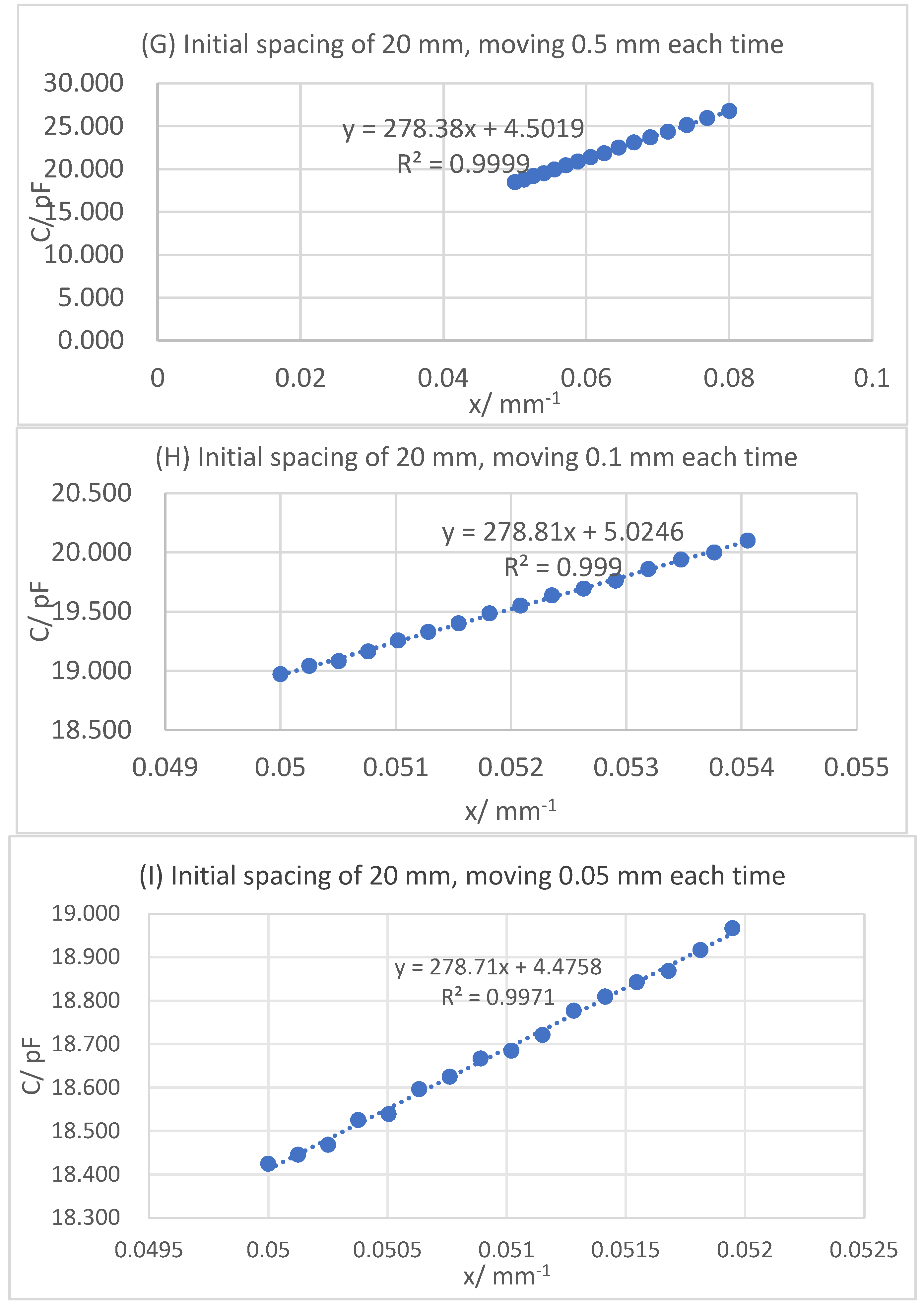The calibration under multiple working conditions [19] can cover different use scenarios, avoiding the problem of “high local accuracy and low global accuracy” caused by a single calibration. System calibration also effectively reduces random errors caused by different environments and initial states. The slope and intercept of a linear system have definite physical analysis meaning. The slope of linear fitting can be directly related to the sensitivity of the system. The intercept can effectively separate the errors of parasitic capacitance of the system. Through software design calibration, the pain point of “parasitic capacitance cannot be quantified” of the traditional capacitance sensor is solved, and the capacitance measurement error is remarkable.

2. Principle and Method

2.1. Micro-Displacement Measurement Principle

The known parallel plate capacitor [20] definition formula is as follows:

$$C={\displaystyle \frac{Q}{U}}$$

(1)

where C is the capacitance of the parallel plate capacitor, Q is its charge, and U is the potential difference between the two plates.

Gauss’s theorem of an infinite plane and an electric field derivation model is as follows:

$$E={\displaystyle \frac{\sigma }{2{\epsilon }_0{\epsilon }_r}}$$

(2)

where E is the uniform strong electric field formed by the parallel plate capacitor, $\sigma$ is the surface charge density, ${\epsilon }_0$ is the vacuum dielectric constant [21], selected in the experiment ${\epsilon }_0=8.854\times {10}^{-12}(\mathrm{F}/\mathrm{m})$, and ${\epsilon }_r$ is the air dielectric constant [22], selected in the experiment ${\epsilon }_r=1.0006$.

The definition of the surface charge density [23] of the plate is as follows:

$$\sigma ={\displaystyle \frac{Q}{S}}$$

(3)

where S is the opposite area of the parallel plates, selected in the experiment $S=314.16{\mathrm{c}\mathrm{m}}^2$.

Due to the different electrical properties of the two plates,

$$U=2Ed={\displaystyle \frac{Qd}{{\epsilon }_0{\epsilon }_{r}S}}$$

(4)

where d is the spacing between parallel capacitor plates.

Equations (1)–(4) are combined to obtain the following:

$$C={\displaystyle \frac{{\epsilon }_0{\epsilon }_{r}S}{d}}$$

(5)

The schematic illustration depicting the relationship between parallel plate capacitance and displacement is presented in Figure 1. A change in the plate spacing of a parallel-plate capacitor results in a change in its capacitance. Specifically, when one plate of the parallel-plate capacitor is fixed, and the other is moved (Figure 1A), the capacitance varies accordingly—with increasing plate spacing leading to a decrease in capacitance value, as dictated by Equation (5). For linear fitting analysis in the experiment, the reciprocal of the plate spacing was defined as the variable x; this yields a theoretical proportional relationship between the capacitor’s capacitance and the reciprocal of the plate spacing, which is illustrated as a straight line in Figure 1B. According to the formula, the capacitance of a parallel plate capacitor is proportional to the dielectric constant and the area of the opposite plates, and inversely proportional to the distance between the plates. Because the direct fitting of physical quantity needs to establish a complex nonlinear regression model [24], the calculation amount is large, and it is easy to be disturbed by noise; the inverse relationship between capacitance and plate spacing is treated as the proportional relationship between capacitance and the reciprocal of plate spacing. It is found that the linear fitting algorithm [25] has a fast calculation speed and high stability, which is suitable for embedded systems and real-time processing. The parameters obtained by the least square method [26] have clear physical meaning, and the slope of the fitting line is directly related to system sensitivity. Corresponding to the ideal capacitance value of a parallel aluminum plate with a radius of 10 cm in the study, the distance between plates is 1 mm. Intercept can characterize the zero-offset caused by errors such as parasitic capacitance [27], which can be directly extracted for systematic error analysis to improve the displacement measurement accuracy.

2.2. Micro-Displacement Measurement System

Based on an opto-mechatronic-electric cooperative design, the micrometer is coupled with the slide rail of the optical bench, while the polar plate is secured to the fixture of the optical bench-thereby forming a high-precision mechanical displacement structure. Communication between the STM32 microcontroller and the host computer is achieved via a CH340E converter. Meanwhile, PC-side software is developed using Python 3.13, enabling the real-time input of capacitance values and the display of displacement variations; this thus realizes displacement measurement over a range from sub-nanometers to nanometers. The connection diagram of the test system is presented in Figure 2.

In that study, two Dupont wires with alligator clips are used to connect the two electrodes of a parallel plate capacitor and the capacitance channel of a single-chip microcomputer, and three Dupont wires are used to connect the data transmission and receiving terminal, power supply terminal, and grounding terminal of the single-chip microcomputer and the CH340E module. The capacitance reading is changed due to the small displacement of the experimental device. The displacement change value is calculated in the upper computer software through two capacitance changes. The electrode plate spacing is close to the corresponding capacitance reading, and the displacement display decreases to a negative value. The electrode plate spacing is far away from the corresponding capacitance reading, and the displacement display increases to a positive value. The overall experimental device is shown in Figure 3.

2.3. System Calibration of Experimental Setup

The system calibration [28] of the experimental device is carried out by collecting 3 groups of data with initial intervals of 10 mm, 15 mm, and 20 mm, respectively. The same micro-displacement changes are produced each time by using the advancing micrometer with different initial intervals, and the capacitance readings and electrode plate intervals of each measurement data are recorded with step sizes of 0.5 mm, 0.1 mm, and 0.05 mm, respectively. For each fixed displacement point, independent repeated measurements were performed more than 10 times to ensure the statistical reliability of the data. The results of the 9 groups of fitted lines are shown in Figure 4.

Nine groups of experimental data tables are obtained. The displacement of 9 groups of experimental data is converted into the reciprocal of displacement, and the capacitance and the reciprocal of displacement are linearly fitted. It is found that the fitting coefficients of each group are above 0.99, and the fitting effect is good. This preliminarily indicates that the experimental setup is capable of maintaining good short-term stability even in an ordinary laboratory environment without strict temperature control, vibration isolation, or darkroom conditions. The fitting straight line of the measured data is close to the theoretical straight-line equation. C = 277.215x + 4.933 (where C is capacitance, x is reciprocal displacement, 277.215 is the slope of fit, 4.9333 is the intercept of fit, and the coefficient of fit is 0.9993). The fitted straight line for system calibration is shown in Figure 5.

The calibration experiment of the experimental system was conducted on a conventional laboratory optical platform. The ambient temperature was approximately 25 ± 2 °C, with no active temperature control or specialized vibration isolation implemented. Electrical connections ensured that the measurement system was grounded via the ground terminal to minimize interference, though no additional metal shielding enclosure was employed. The parallelism of the electrode plates was initially ensured and maintained through optical methods and the mechanical guidance of the micrometer. However, due to experimental constraints, quantitative parallelism error data, such as that measured by laser interferometry, could not be provided, which is acknowledged as one of the potential sources of error.

3. Results and Discussion

3.1. Calibration Results for Test Research

The flow diagram of the research and test system is shown in Figure 6.

In order to avoid artificial calculation and visual display of micro-displacement, a host computer software is designed using the formula of parallel plate capacitance calibration. After inputting the slope and intercept parameters corresponding to the calibration line of the system, according to the test flow diagram, if micro-displacement occurs, the capacitance value changes, and two capacitance readings before and after the change are input. The software will automatically calculate the magnitude of micro-displacement, and the positive and negative indicate the direction of displacement. We measured micro-displacements using the experimental apparatus and evaluated the results. The micro-displacements produced by randomly turning the micrometer and turning the optical bench knob are shown in

Table 1. Random rotation micrometer measurement.

Random Rotation Micrometer Measurement Data
data number	1	2	3	4	5
C1/pF	94.4260	94.8101	96.1664	96.4307	97.0416
C2/pF	94.7575	94.8127	96.3099	96.4379	97.0847
x/m	$-1.14\times {10}^{-5}$	$-6.86\times {10}^{-8}$	$-4.77\times {10}^{-6}$	$-2.98\times {10}^{-8}$	$-1.41\times {10}^{-6}$
data number	6	7	8	9	10
C1/pF	97.0610	97.4291	97.7991	98.3406	98.4788
C2/pF	97.0628	97.5810	97.8017	98.4513	98.4803
x/m	$-5.88\times {10}^{-8}$	$-4.91\times {10}^{-6}$	$-8.36\times {10}^{-8}$	$-3.51\times {10}^{-6}$	$-4.75\times {10}^{-8}$
data number	11	12	13	14	15
C1/pF	98.9854	100.6421	100.7194	100.7765	37.3121
C2/pF	98.9871	100.6493	100.7197	100.7802	37.3260
x/m	$-5.33\times {10}^{-8}$	$-2.18\times {10}^{-7}$	$-9.06\times {10}^{-9}$	$-1.12\times {10}^{-7}$	$-3.67\times {10}^{-6}$
data number	16	17	18	19	20
C1/pF	37.3749	37.3963	37.4105	37.4339	37.4485
C2/pF	37.3752	37.4012	37.4118	37.4350	37.4492
x/m	$-7.90\times {10}^{-8}$	$-1.29\times {10}^{-6}$	$-2.71\times {10}^{-6}$	$-2.89\times {10}^{-7}$	$-1.84\times {10}^{-7}$

and

Table 2. Random rotation of the optical instrument base knob.

Random Rotation of the Optical Mount Base Knob
data number	1	2	3	4	5
C1/pF	56.1861	55.6858	55.8387	55.9870	56.2669
C2/pF	56.1838	55.6773	55.8442	55.9887	56.2719
x/m	$-2.43\times {10}^{-7}$	$-9.15\times {10}^{-7}$	$-5.88\times {10}^{-7}$	$-1.81\times {10}^{-7}$	$-5.26\times {10}^{-7}$
data number	6	7	8	9	10
C1/pF	55.4824	52.0062	51.8002	50.0414	49.9883
C2/pF	55.5003	52.0054	51.8074	50.0427	49.9801
x/m	$-1.94\times {10}^{-6}$	$-1.00\times {10}^{-7}$	$-9.09\times {10}^{-7}$	$-1.77\times {10}^{-7}$	$-1.12\times {10}^{-6}$

below. According to the data, the displacement measurement resolution ranged from ${10}^{-5} \mathrm{t}\mathrm{o} {10}^{-9} \mathrm{m}$.

In order to investigate the displacement measurement values under different initial distances, the experiment used a micrometer to push the plate to produce a small displacement under different initial distances. The measurement tables are

Table 3. Data of measured displacement when the initial spacing is 50 mm.

Initial Spacing 50 mm
data number	1	2	3	4	5
C1/pF	10.4744	10.8754	11.1629	12.0612	12.2231
C2/pF	10.4751	10.8761	11.1646	12.0620	12.2247
x/m	$6.32\times {10}^{-6}$	$5.50\times {10}^{-6}$	$1.21\times {10}^{-5}$	$4.36\times {10}^{-6}$	$8.34\times {10}^{-6}$
data number	6	7	8	9	10
C1/pF	12.3577	12.4487	12.4554	12.4689	12.4763
C2/pF	12.3591	12.4502	12.4663	12.4701	12.4779
x/m	$7.04\times {10}^{-6}$	$7.36\times {10}^{-6}$	$5.33\times {10}^{-5}$	$5.86\times {10}^{-6}$	$7.79\times {10}^{-6}$

,

Table 4. Data of measured displacement when the initial spacing is 40 mm.

Initial Spacing 40 mm
data number	1	2	3	4	5
C1/pF	11.8631	11.8752	11.9321	11.9431	11.9567
C2/pF	11.8645	11.8767	11.9334	11.9448	11.9574
x/m	$8.08\times {10}^{-6}$	$8.63\times {10}^{-6}$	$7.36\times {10}^{-6}$	$9.59\times {10}^{-6}$	$3.93\times {10}^{-6}$
data number	6	7	8	9	10
C1/pF	11.9788	11.9943	12.1432	12.2354	12.3545
C2/pF	11.9794	11.9958	12.1449	12.2368	12.3556
x/m	$3.35\times {10}^{-6}$	$8.34\times {10}^{-6}$	$9.06\times {10}^{-6}$	$7.28\times {10}^{-6}$	$5.54\times {10}^{-6}$

,

Table 5. Data of measured displacement when the initial spacing is 30 mm.

Initial Spacing 30 mm
data number	1	2	3	4	5
C1/pF	14.1707	14.1456	14.1534	14.1621	14.1677
C2/pF	14.1719	14.1473	14.1546	14.1635	14.1698
x/m	$3.90\times {10}^{-6}$	$5.55\times {10}^{-6}$	$3.91\times {10}^{-6}$	$4.56\times {10}^{-6}$	$6.83\times {10}^{-6}$
data number	6	7	8	9	10
C1/pF	14.1731	14.1764	14.1794	14.1812	14.1834
C2/pF	14.1751	14.1782	14.1802	14.1824	14.1849
x/m	$6.49\times {10}^{-6}$	$5.84\times {10}^{-6}$	$2.59\times {10}^{-6}$	$3.89\times {10}^{-6}$	$4.86\times {10}^{-6}$

,

Table 6. Data of measured displacement when the initial spacing is 20 mm.

Initial Spacing 20 mm
data number	1	2	3	4	5
C1/pF	18.7912	18.8943	18.9433	19.1422	19.2143
C2/pF	18.7931	18.8954	18.9451	19.1434	19.2155
x/m	$2.74\times {10}^{-6}$	$1.56\times {10}^{-6}$	$2.54\times {10}^{-6}$	$1.65\times {10}^{-6}$	$1.63\times {10}^{-6}$
data number	6	7	8	9	10
C1/pF	19.3548	19.4654	19.5435	19.6548	19.8542
C2/pF	19.3567	19.4667	19.5461	19.6571	19.8561
x/m	$2.53\times {10}^{-6}$	$1.70\times {10}^{-6}$	$3.38\times {10}^{-6}$	$2.94\times {10}^{-6}$	$2.37\times {10}^{-6}$

,

Table 7. Data of measured displacement when the initial spacing is 10 mm.

Initial Spacing 10 mm
data number	1	2	3	4	5
C1/pF	32.6520	32.6724	32.6841	32.3932	32.3954
C2/pF	32.6527	32.6733	32.6852	32.3945	32.3968
x/m	$2.53\times {10}^{-7}$	$3.24\times {10}^{-7}$	$3.96\times {10}^{-7}$	$4.78\times {10}^{-7}$	$5.15\times {10}^{-7}$
data number	6	7	8	9	10
C1/pF	32.3975	32.4584	32.6845	32.7950	33.7464
C2/pF	32.3991	32.4597	32.6865	32.7964	33.7469
x/m	$5.88\times {10}^{-7}$	$4.76\times {10}^{-7}$	$7.20\times {10}^{-7}$	$5.00\times {10}^{-7}$	$1.67\times {10}^{-7}$

and

Table 8. Data of measured displacement when the initial spacing is 5 mm.

Initial Spacing 5 mm
data number	1	2	3	4	5
C1/pF	60.3740	60.4875	61.5645	64.3254	65.8566
C2/pF	60.3748	60.4879	61.5651	64.3259	65.8572
x/m	$7.21\times {10}^{-8}$	$4.00\times {10}^{-8}$	$5.18\times {10}^{-8}$	$3.93\times {10}^{-8}$	$4.48\times {10}^{-8}$
data number	6	7	8	9	10
C1/pF	66.5845	67.5661	69.5684	73.5456	79.5644
C2/pF	66.5853	67.5669	69.5694	73.5464	79.5648
x/m	$5.83\times {10}^{-8}$	$5.65\times {10}^{-8}$	$6.64\times {10}^{-8}$	$4.71\times {10}^{-8}$	$1.99\times {10}^{-8}$

. The experimental data analysis shows that the minimum measured displacement resolution is ${10}^{-6}\mathrm{m}$ at initial spacing of 50 mm, 40 mm, 30 mm, and 20 mm. The measured displacement resolution is ${10}^{-7}\mathrm{m}$ at an initial spacing of 10 mm and ${10}^{-8}\mathrm{m}$ at an initial spacing of 5 mm.

In this experiment, we selected d/R = 0.05 (with an initial spacing of 5 mm) as the measurement range and adopted a micrometer scale with a minimum graduation of 0.01 mm as the step input. This approach not only satisfies the theoretical condition that the edge field contribution [29] remains below 1% when d < 10 mm, but also enables high-resolution measurements at sub-nanometer scales. The data are shown in

Table 9. Data of measured displacement when the initial spacing is 5 mm, and the micrometer is advanced by 0.01 mm each time.

Initial Spacing 5 mm, Each Advance 0.01 mm
data number	1	2	3	4	5
C1/pF	60.3740	61.1932	62.2201	63.7933	65.1193
C2/pF	60.4855	61.3081	62.3402	63.9205	65.2510
x/mm	0.0100362	0.0100429	0.0101239	0.0101562	0.0100570
data number	6	7	8	9	10
C1/pF	66.2873	67.9871	69.2934	72.3849	75.6639
C2/pF	66.4233	68.1314	69.4447	72.5495	75.8456
x/mm	0.0099934	0.0100386	0.0101020	0.0100048	0.0100427

.

3.2. Analysis of Micrometer-Level Micro-Displacement Test

Based on the measurement data in Table 9, the absolute error and relative error corresponding to each measured displacement are calculated, and the results are presented in

Table 10. Record of absolute error and relative error of measured displacement when the initial spacing of plates is 5 mm and advanced by 0.01 mm each time.

Absolute Error and Fractional Error
data number	1	2	3	4	5
absolute error	0.0000362	0.0000429	0.0001239	0.0001563	0.0000570
fractional error/mm	0.36	0.43	1.24	1.56	0.57
data number	6	7	8	9	10
absolute error/mm	0.0000065	0.0000387	0.0001021	0.0000049	0.0000427
fractional error	0.07	0.39	1.02	0.05	0.43

. The average value of the measured displacement is calculated as follows:

$$∆\overline{d}={\displaystyle \frac{\sum _{i=1}^{10}{d}_i}{10}}=0.0100598 \mathrm{m}\mathrm{m}$$

(6)

The Type A uncertainty [30] is calculated as follows:

$$u_A\left(d\right)=\sqrt{{\displaystyle \frac{\sum _{j=1}^m{(d_i-∆\overline{d})}^2}{m-1}}}=0.000082 \mathrm{m}\mathrm{m}$$

(7)

The Type B uncertainty [31] is calculated as follows:

The standard uncertainty of capacitance measurement is as follows:

$$u_C={\displaystyle \frac{0.001 \mathrm{p}\mathrm{F}}{\sqrt{3}}}\approx 0.0005773 \mathrm{p}\mathrm{F}$$

(8)

The relationship between displacement and capacitance in system calibration is as follows:

$$d={\displaystyle \frac{277.215}{C-4.9333}}$$

(9)

The uncertainty of displacement variation is calculated by error propagation:

$${\displaystyle \frac{\partial d}{\partial C}}={\displaystyle \frac{277.215}{{\left(C-4.9333\right)}^2}}$$

(10)

The contribution of capacitance measurement uncertainty to displacement uncertainty is as follows:

$$u_B=\left|{\displaystyle \frac{\partial d}{\partial C}}\right|\times u_C$$

(11)

The final calculated result of the Type B uncertainty of displacement is as follows:

$$u_B=\left|{\displaystyle \frac{\partial d}{\partial C}}\right|\times u_C={\displaystyle \frac{277.215}{{\left(60.3740\right)}^2}}\times 0.0005773\approx 0.0000439 \mathrm{m}\mathrm{m}$$

(12)

The calculated total uncertainty of the measured displacement is as follows:

$$u_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\sqrt{(u_A^2+u_B^2)}\approx 0.00009 \mathrm{m}\mathrm{m}$$

(13)

The calculated expanded uncertainty is as follows:

$$U=2\times u_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=2\times 0.00009=0.00018 \mathrm{m}\mathrm{m} (K=2)$$

(14)

where U is the expanded uncertainty.

The measurement results of the micro-displacement generated by pushing the polar plate with a micrometer in the experiment are expressed as follows:

$$x=0.01006\pm 0.00018 \mathrm{m}\mathrm{m}$$

(15)

Meanwhile, for the slope calculated from the experimental final fitting line equation and the theoretical fitting line equation, the standard error is 0.122 pF/mm, and the relative deviation is 0.43%; the standard error of the intercept is 1.400 pF.

Based on the data analysis of Table 3, Table 4, Table 5, Table 6, Table 7 and Table 8, it is concluded that when the initial plate spacing is different, the capacitance value changes by 0.001 pF both before and after the micro-displacement is generated. The different displacement measurement accuracies obtained are shown in

Table 11. Theoretical resolution of measured displacement corresponding to different initial spacings.

Plate Spacing (d/mm)	Measurement Resolution (m)
$16.7 \mathrm{m}\mathrm{m}\le d\le 50 \mathrm{m}\mathrm{m}$	${10}^{-6}$
$5.3 \mathrm{m}\mathrm{m}\le d\le 16.6 \mathrm{m}\mathrm{m}$	${10}^{-7}$
$1.7 \mathrm{m}\mathrm{m}\le d\le 5.2 \mathrm{m}\mathrm{m}$	${10}^{-8}$
$d\le 1.6 \mathrm{m}\mathrm{m}$	${10}^{-9}$

.

3.3. Boundaries and Limitations of Measurement Resolution Verification

The measurement verification in this study has defined boundaries. The core issue is that the verification of the sensor system’s resolution and measurement accuracy is constrained by the available reference instruments. We have directly calibrated and evaluated the measurement uncertainty of the system at the micrometer scale (e.g., 10 μm) using a high-precision micrometer (with its own accuracy at the micrometer level). The results (such as an expanded uncertainty of ±0.18 μm) are solid and traceable. However, for the theoretical displacement resolution (e.g., 10⁻⁸–10⁻⁹ m) calculated based on hardware parameters (0.001 pF capacitance resolution), which surpasses the micrometer level, this study did not conduct direct comparative verification using higher-precision displacement references like laser interferometers. This is due to the high cost of such high-grade metrology equipment and the current lack of access in the laboratory. Therefore, the sub-micrometer and nanometer-scale displacement values reported in the paper should be strictly defined as the system’s theoretical detection capability or resolution potential under ideal conditions, rather than an absolute measurement accuracy fully validated by experiment. This limitation is crucial for assessing the final performance of the system and also points to the necessity of future comprehensive performance calibration through comparison with external high-precision standards.

4. Conclusions

In order to solve the bottleneck problems of traditional micro-displacement measurement technology, such as poor environmental adaptability, high cost, and low resolution, a set of capacitive sensing micro-displacement collaborative measurement system based on optical–mechanical–electrical collaborative optimization is successfully designed and built, featuring the advantage of low cost (less than CNY 600). The optical-seat micrometer coupling mechanism realizes the dynamic parallel calibration of the polar plate and effectively eliminates the mechanical return gap error; the high-resolution capacitance measurement module enhances the stability of the reading and improves the displacement measurement resolution; and the linear fitting algorithm effectively separates the parasitic capacitance, enhances the robustness of the measurement data, and can compensate the interference caused by the system error in real time. The system has been experimentally validated for micro-scale displacement and demonstrates theoretical potential for achieving nanometer-level displacement resolution based on its hardware parameters. The research system provides cost-effective solutions and application prospects for semiconductor chip packaging (avoiding mechanical probe scratching wafers), MEMS device resonance detection (relative error less than 2.5%), and ultra-precision machine tool compensation, especially in the field of industrial field and educational demonstration scenarios. Its optical–mechanical–electrical collaborative framework offers a new paradigm for the development of intelligent sensors. Future work will focus on comparative studies with high-precision benchmarks to comprehensively evaluate its measurement accuracy and systematically test its environmental adaptability.