GOG-RT-DETR: An Improved RT-DETR-Based Method for Graphite Ore Grade Detection

Abstract

To address the inefficiencies and inaccuracies of traditional ore grade identification methods in complex mining environments, and the challenge of balancing accuracy and speed on edge devices, this paper proposes a lightweight, high-precision, and high-speed detection model named GOG-RT-DETR. Built on the RT-DETR framework, the model incorporates a Faster-Rep-EMA module in the backbone network to reduce computational redundancy and enhance feature extraction. Additionally, a BiFPN-GLSA module replaces the CCFM module in the Neck network, improving feature fusion between the backbone and Neck networks, thus strengthening the model’s ability to capture both global and local spatial features. A Wise-Inner-Shape-IoU loss function is introduced to optimize the bounding box regression, accelerating convergence and improving localization accuracy. The model is evaluated on a custom-built graphite ore dataset with simulated data augmentation. Experimental results show that, compared to the baseline model, the mAP and FPS of GOG-RT-DETR are improved by 2.5% and 8.2%, with a 26.0% reduction in model parameters and a 23.37% reduction in FLOPs. This model enhances detection accuracy and reduces computational complexity, offering an efficient solution for ore grade detection in industrial applications.

1. Introduction

Graphite, as a critical material for modern industry and national security, is widely used in metallurgy, machinery, aerospace, electronics, and new energy vehicles due to its unique polymorphic structure and physicochemical properties. It has become a vital raw material in high-tech industries [1,2]. Particularly in the rapidly developing field of new energy vehicles, the increasing demand for high-quality graphite in batteries for both electric vehicles and stationary energy storage has made graphite a key raw material for ensuring supply chain stability and enhancing the core competitiveness of the new energy vehicle industry [3]. At the same time, as the global transition towards carbon neutrality and clean energy accelerates, the importance of graphite is also rising. As a critical mineral for battery anodes, the demand for graphite is expected to quadruple by 2030 compared to 2023, with overall demand doubling during the same period [4]. Against this backdrop, the growing global demand for graphite materials has made the rapid and accurate detection of graphite ore grade a crucial step in improving the efficiency of graphite resource development and promoting the sustainable growth of the industry. This process not only impacts production costs and product quality control but also plays a key role in ensuring the security and stability of strategic mineral resource supply chains, as well as driving the green and low-carbon transformation of the new energy sector.

Graphite ore grade refers to the mass content of valuable carbon components in graphite ore, expressed as a percentage. As a key indicator for measuring the fixed carbon content in graphite ore, it directly affects the evaluation of the economic value and feasibility of mining resources and serves as an essential basis for mine operation decisions [5]. Traditional graphite ore grade detection primarily relies on physicochemical testing methods, including manual grade measurement and instrumental analysis techniques, such as X-ray diffraction (XRD) for mineral grade analysis and LECO carbon-sulfur analyzers for detection [6,7]. For instance, Cui et al. [8] proposed using XRD and electron microscopy to characterize the physicochemical properties of flake graphite ore and assess its potential for beneficiation and process optimization. Sader et al. [9] introduced a classic chemical method using a LECO carbon-sulfur analyzer to measure total carbon content by burning ore samples. The graphite ore samples are fully combusted in a high-temperature induction furnace, converting carbon elements into carbon dioxide gas, which is then analyzed by measuring its absorption of infrared light at specific wavelengths to accurately determine the total carbon content in the original sample. While these methods can provide precise grade detection results, they also have significant drawbacks, such as long detection cycles, high labor and resource costs, and challenges in recording and collecting detection data, making quantitative analysis difficult.

With the rapid development of machine vision and machine learning, the integration of mineral imagery and machine learning algorithms into intelligent sorting technology is gradually becoming a mature and efficient processing method [10]. For instance, Cevik et al. [11] applied machine learning algorithms such as random forests and support vector classification for unsupervised clustering and supervised classification of model data, achieving consistent categorization of mineral resources. Pereira et al. [12] used machine learning algorithms like nearest neighbors and decision trees to analyze digital images of mineral thin sections under different polarized light conditions. They verified the effectiveness of optical features such as color and texture in mineral identification, thus enabling the classification of rock thin sections. However, the performance of these machine learning methods heavily relies on manually preset shallow optical features such as color and texture, which limits the model’s ability to deeply explore the intrinsic correlations within complex mineral images. This results in insufficient robustness and generalization when facing dynamic industrial environments.

In recent years, with the widespread research on deep learning algorithms, deep learning models have emerged as an innovation in the field of intelligent mineral identification. These models can autonomously learn and construct features from data, effectively overcoming the subjectivity and limitations associated with manually designed features. Through their powerful nonlinear fitting ability, deep learning models have significantly improved the accuracy of mineral grade classification. However, existing ore grade detection methods still have certain limitations. For example, Qiu et al. [13] proposed a graphite ore grade detection framework based on YOLOv3, which achieved a balance between efficiency and robustness through an innovative asymmetric architecture. However, its ability to capture both global and local information, as well as the model’s convergence speed, still require improvement. Xiang et al. [14] proposed a graphite ore grade recognition method based on Faster R-CNN, which optimizes key feature extraction by combining high-level semantic features with low-level detail features, and integrating a relational-aware attention mechanism (RGA) capable of capturing global context, along with data augmentation through image slicing. This method achieved an mAP of 80.21%, though there is still significant room for improvement in accuracy.

Although existing ore grade detection methods have made significant progress, addressing issues such as the reliance on manually designed feature extraction and the high costs in terms of labor and resources inherent in traditional methods [15,16], several challenges remain. These challenges include difficulty in balancing accuracy and speed, insufficient feature extraction capabilities, low detection accuracy for irregularly shaped ores, interference from complex environments (such as dust, lighting changes, and occlusions), limited availability of annotated datasets, and the computational trade-offs involved in real-time deployment on edge devices [17].

Therefore, there is an urgent need in the industrial inspection field for a detection model that combines high accuracy, high speed, and lightweight advantages, while also being robust enough to operate in real-world scenarios and meet the deployment requirements of edge devices.

To achieve the above goal, this paper proposes a graphite ore grade detection method based on an improved RT-DETR. The model optimizes the backbone network, feature fusion modules, and loss functions, aiming to achieve high-speed and accurate grade recognition. By reducing computational redundancy and accelerating convergence, it meets the real-time requirements of industrial applications, significantly enhancing its potential for practical use.

To systematically improve the performance of the detection model, this study focuses on targeted improvements and optimizations in the following key areas:

• To address the challenges of scarce annotated datasets and environmental interference in graphite ore grade detection, we have developed a systematic workflow that covers the entire process from mine sampling, precise preparation of ore grades through chemical methods, image data collection, to fine-grained annotation. This process has led to the creation of a proprietary graphite ore image dataset that includes both native and oxidized ore forms, covering high, medium, and low grade levels.
• To address the issue of inefficient feature extraction caused by computational redundancy and insufficient global context utilization in traditional residual networks, this paper introduces the lightweight Faster-Rep-EMA module to improve the ResNet18 backbone network. This modification dynamically allocates weights, effectively enhancing the model’s ability to capture key features for detecting graphite ore. As a result, the model reduces the number of parameters while significantly improving the richness of feature representation.
• To optimize the feature fusion mechanism of the Neck network, this method designs and introduces the BiFPN-GLSA module to replace the CCFM module in the Neck. This module combines a bidirectional multi-scale feature pyramid with a global–local spatial attention mechanism, aiming to significantly enhance the model’s ability to accurately locate and recognize targets under complex background interference.
• The GIoU loss function in the baseline model is replaced with the Wise-Inner-Shape-IoU loss function. By integrating the advantages of Wise-IoU [18], Shape-IoU [19], and Inner-IoU [20], this new loss function significantly enhances the model’s robustness to variations in target shape and scale. This not only refines defect localization but also accelerates convergence speed.

2. Methods

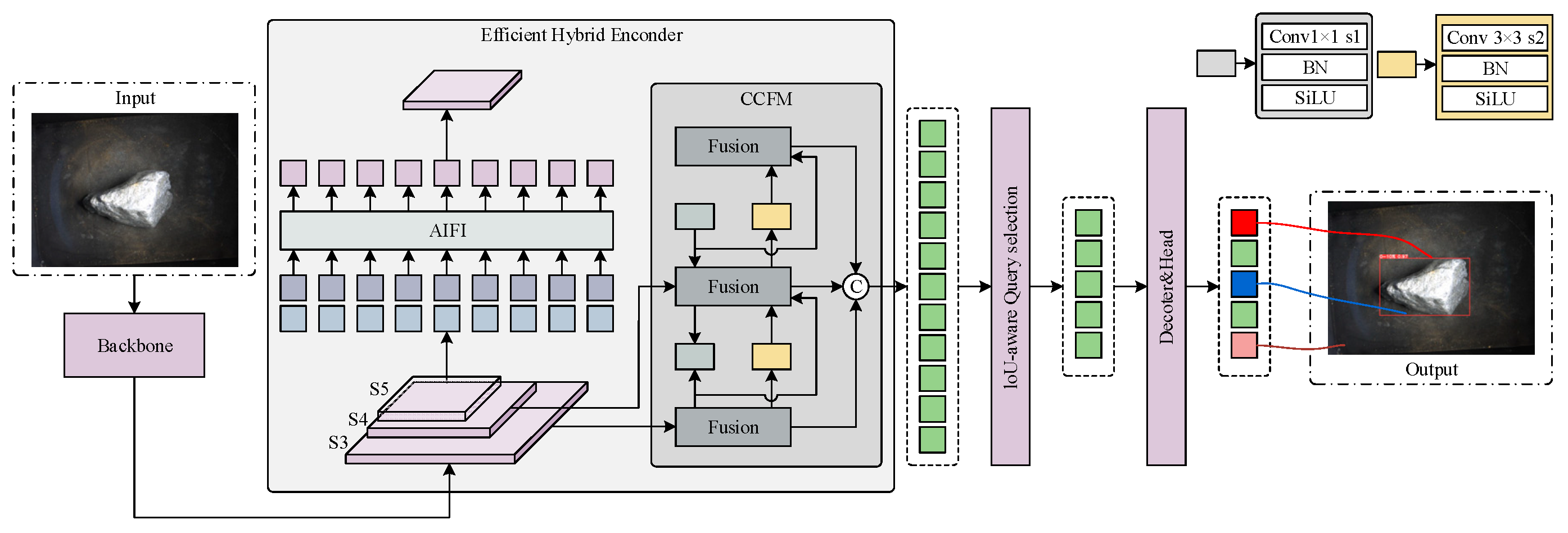
2.1. The Original RT-DETR Model

Building on the core concept of the end-to-end Transformer architecture in DETR, RT-DETR integrates a series of key technical innovations that combine high detection accuracy with outstanding real-time performance, making it a next-generation efficient object detection framework. The RT-DETR model structure is shown in Figure 1.

The overall architecture of RT-DETR consists primarily of the backbone network, an efficient hybrid encoder, a decoder [21], and IoU-aware query selection [22], among other core components.

Backbone Network: As the foundation of the model, the main role of the backbone network is to extract rich multi-scale features from the input image. RT-DETR typically uses lightweight Convolutional Neural Networks (CNNs), such as the ResNet series [23], as its backbone. These networks extract feature maps from different levels (S3, S4, S5) of the image, providing rich semantic and spatial information for subsequent processing.

Efficient Hybrid Encoder: This is one of the core innovations of RT-DETR, designed to efficiently process the multi-scale features generated by the backbone network. The encoder decouples within-scale interactions and cross-scale fusion, converting multi-scale feature maps into a sequential representation of image features [24,25]. Specifically, it achieves efficient feature interaction through two key mechanisms: (i) Attention-based Intra-scale Feature Interaction (AIFI), which enhances the feature representation within the same scale; and (ii) CNN-based Cross-scale Feature Fusion (CCFM), which merges features from different scales, allowing them to complement each other and thus improving the model’s ability to detect targets of varying sizes.

IoU-Aware Query Selection: To address the uncertainty in the query selection process, RT-DETR introduces an IoU-aware query selection mechanism [26]. This method utilizes the output features from the encoder and defines and minimizes feature uncertainty to select a set of high-quality, high-confidence features as the initial object queries for the decoder. This significantly improves the final accuracy of the detector.

Decoder: The decoder of RT-DETR adopts a multi-layer Transformer decoder structure, combined with auxiliary prediction heads for iterative optimization [27]. Based on object queries, the decoder refines the queries iteratively through multiple layers of attention and feed-forward network (FFN) modules, directly outputting the prediction results. This structure supports flexible adjustment of inference speed by dynamically adjusting the number of decoder layers, without the need for retraining.

In summary, RT-DETR, with its elegant modular design, establishes a powerful real-time end-to-end detection framework. The choice of RT-DETR-r18 as the base framework for this study is driven by its excellent balance between speed and accuracy, with targeted improvements made on top of it to meet the specific requirements of graphite ore grade detection tasks.

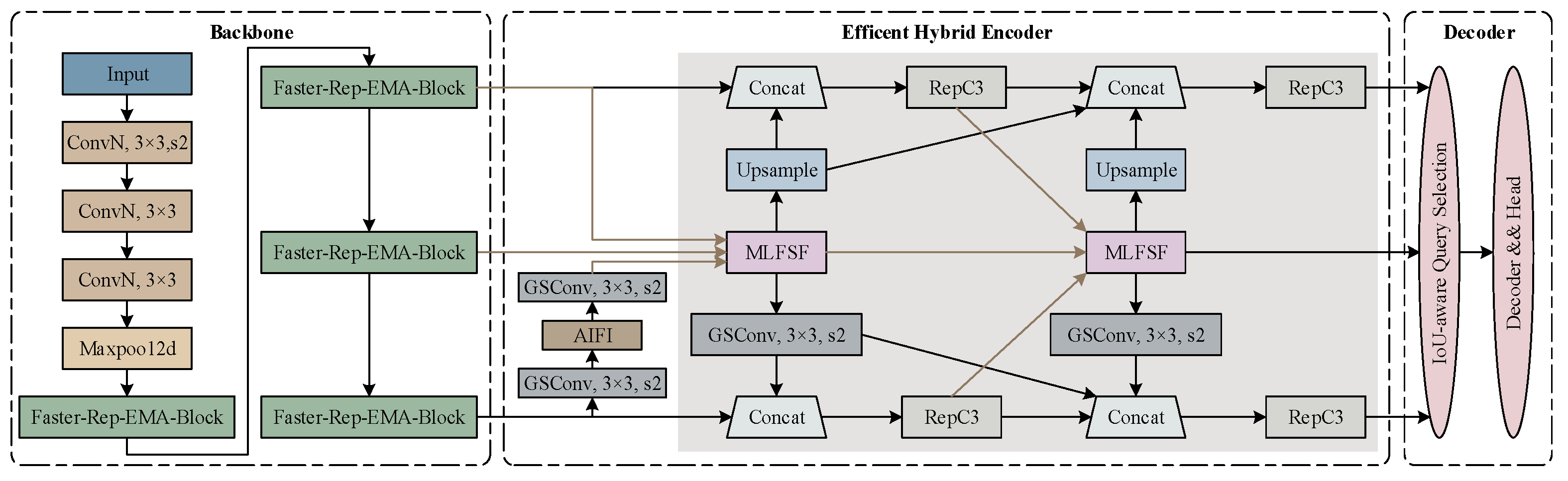
2.2. The Improved GOG-RT-DETR Model

The proposed GOG-RT-DETR model introduces three main improvements over the RT-DETR model. To optimize the backbone network, this method incorporates the Faster-Rep-EMA module, based on FasterNet, to replace the BasicBlock in ResNet18. With its attention mechanism, this module dynamically adjusts the weights of different feature regions, significantly enhancing feature extraction of graphite ore details while reducing computational redundancy.

For the Neck network, the method designs the BiFPN-GLSA module to replace the CCFM module in the Neck. By integrating bidirectional multi-scale feature flows with global–local spatial attention, the aim is to suppress interference from complex backgrounds and strengthen the model’s ability to precisely locate defective targets.

Finally, the improved Wise-Inner-Shape-IoU loss function is used, which enhances the model’s generalization ability to handle variations in target shapes and sizes. This results in faster training convergence and more accurate defect localization. The overall structure of the GOG-RT-DETR graphite ore grade detection model is shown in Figure 2.

2.3. Faster-Rep-EMA

When designing neural networks for real-time industrial applications, simply focusing on the reduction in floating-point operations (FLOPs) is not sufficient. It is also necessary to consider other practical factors that affect inference speed, such as memory access cost (MAC). To build a lightweight and efficient feature extraction network, this paper introduces the Faster-Rep-EMA module to improve the original RT-DETR backbone network. The design of this module integrates three advanced techniques: partial convolution (PConv), reparameterized convolution (RepConv), and efficient multi-scale attention (EMA). The goal is to fundamentally reduce computational redundancy, enhance feature extraction capabilities, and improve adaptability to multi-scale targets.

The core of this module is the partial convolution (PConv) proposed by FasterNet [28]. A comparison between the PConv structure and standard convolution is shown in Figure 3.

Unlike conventional convolutions that compute over all input channels, PConv exploits the intrinsic redundancy of feature maps by applying a standard convolution only to a subset of the input channels (for example, one quarter) while leaving the remaining channels unchanged. This strategy significantly reduces both computational load and memory access. The FLOPs for PConv can be calculated using the following formula:

$$FLOPs=H\times W\times K^2\times C_p^2,$$

(1)

The MAC for PConv can be calculated using the following formula:

$$MAC=H\times W\times 2C_p+K^2\times C_p^2\approx H\times W\times 2C_p,$$

(2)

where $H$ and $W$ represent the height and width of the input feature map, $K$ is the size of the convolution kernel, and $C_p$ is the number of channels involved in the convolution operation.

Theoretically, when PConv computes over 1/4 of the channels, the floating-point operations are reduced to 1/16 of those required by standard convolution, while the memory access cost is similarly reduced to 1/4. This reduction helps to maintain real-time performance and ease of deployment while effectively mitigating the issue of fine-grained feature loss caused by deep convolution operations.

Additionally, to further enhance the feature extraction capability of the backbone network and simplify the model structure, the standard convolution in the module is replaced with RepConv [29]. RepConv utilizes a multi-branch structure during training for efficient feature extraction. During inference, these multi-branch structures are reparameterized into a single convolutional layer. This “training-inference” heterogeneous strategy [30] allows the model to significantly reduce computational load and memory usage during inference, without sacrificing accuracy, thus making the backbone network more lightweight.

Considering that different regions of graphite ore images exhibit varying detection difficulties and the targets have significant scale variations, we introduce the Efficient Multi-scale Attention (EMA) mechanism [31], whose structure is shown in Figure 4.

The EMA module groups channels along the batch dimension and avoids channel reduction, thereby retaining information across all channels while integrating the advantages of both channel attention and spatial attention. It dynamically adjusts the weight distribution for each region in the image, allowing the model to focus more on extracting the key features of graphite ore during training [32]. This enhances the model’s ability to capture features at different scales, thereby improving detection accuracy in complex scenes. The overall structure of Faster-Rep-EMA is shown in Figure 5.

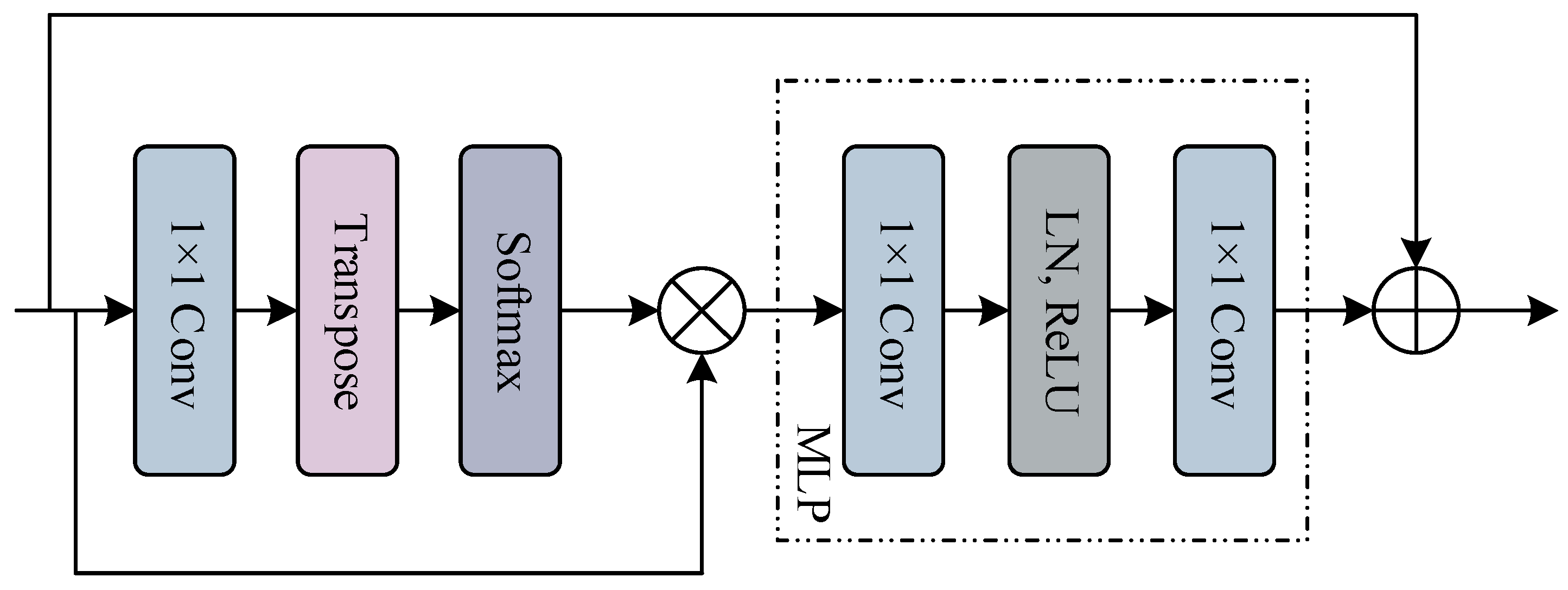
2.4. BiFPN-GLSA

Traditional feature pyramid networks (FPNs), while capable of integrating multi-scale information, still face limitations in effectively capturing both global context and local details. This issue becomes more pronounced when dealing with complex surface textures, such as those found in graphite ore, where fine-grained details may be lost, ultimately reducing detection accuracy. To overcome these limitations and better integrate the feature layers output from the backbone and Neck networks, we introduce the BiFPN-GLSA network to replace the original CCFM module in the Neck of RT-DETR.

The BiFPN (Bidirectional Feature Pyramid Network) [33] achieves efficient information flow by introducing bidirectional cross-scale connections and weighted feature fusion. It not only propagates high-level semantic information through top-down pathways but also preserves low-level local details via bottom-up pathways. Additionally, it simplifies the network by removing nodes with only a single input edge and introduces multiple skip connections at the same feature level, thereby facilitating more effective information exchange across feature scales.

Although BiFPN demonstrates excellent performance in feature fusion, its ability to precisely capture fine details of graphite ore remains limited. To address this, we integrate the Global–Local Spatial Attention (GLSA) mechanism [34] into the key layers of BiFPN (P3, P4, and P5). The input feature map $X\in {\mathrm{R}}^{B\times C\times H\times W}$ is decoupled into global and local components [35], enhancing the model’s capacity to jointly capture both global and local spatial features. The structure of the BiFPN-GLSA network is shown in Figure 6.

The GLSA module models features through a dual-path attention mechanism consisting of two independent submodules: Global Spatial Attention (GSA) and Local Spatial Attention (LSA).

The structure of the GSA module is shown in Figure 7. This module enhances feature representation through long-range interactions and models the overall structure of the target, defined as:

$$GSA\left(X\right)=MLP\left(Softmax\left(Q{K}^T\right)\otimes X\right)+X,$$

(3)

In the specific implementation, the query matrix $Q$ and key matrix $K$ are all generatedfrom the feature map through independent 1 × 1 convolution operations. The attention score map is computed via matrix multiplication (denoted by the symbol $\otimes$). Finally, the attention-weighted features are passed through a multi-layer perceptron (MLP) for nonlinear transformation, enabling further refinement of the extracted representations.

The LSA structure, as shown in Figure 8, is responsible for efficiently extracting locally relevant spatial features from the feature maps. This decoupled design preserves the individual modeling capabilities of each attention branch while achieving a balanced trade-off between accuracy and computational cost through channel separation, defined as:

$$LSA\left(X\right)=\left(\sigma \left(C_{1\times 1}\left(F_C\left(X\right)\right)+X\right)\right)\odot X+X,$$

(4)

In this computation, the symbol $F_C\left(X\right)$ represents the process of extracting local feature information from the input feature map $X$ through a convolution operation followed by an activation function $\sigma$. Subsequently, a 1 × 1 convolution layer (C_1×1) is applied to transform the features and adjust their channel dimensions. Finally, an element-wise multiplication operation ($\odot$) is used to apply the generated attention weights to the input feature map, thereby enhancing the representation of critical local features.

In BiFPN-GLSA, for input features with different resolutions, a fast normalized fusion method is employed to achieve weighted feature aggregation. The formula is expressed as follows:

$$O={\displaystyle \frac{\sum _i{w}_i{P}_i}{\epsilon +\sum _j{w}_j}},$$

(5)

To ensure the non-negativity of the weights $w_j$, the network applies a ReLU activation function as a constraint.

Meanwhile, to prevent numerical instability caused by a zero denominator, a small constant $\epsilon$ is introduced.

The BiFPN integrates bidirectional (top-down and bottom-up) cross-scale connection pathways with the aforementioned fast normalized fusion strategy.

Specifically, taking the feature fusion process at the 4th level of the network as an example, the computation can be formulated as follows:

$$P_4^{td}=Block\left({\displaystyle \frac{w_1\cdot P_4^{\mathrm{i}\mathrm{n}}+w_2\cdot Resize\left(P_5^{\mathrm{i}\mathrm{n}}\right)}{w_1+w_2+\epsilon }}\right),$$

(6)

$$P_4^{out}=Block\left({\displaystyle \frac{{w\prime }_1\cdot P_4^{in}+{w\prime }_2\cdot P_4^{td}+{w\prime }_3\cdot Resize\left(P_3^{out}\right)}{{w\prime }_1+{w\prime }_2+{w\prime }_3+\epsilon }}\right),$$

(7)

Among these components, $P_4^{in}$ denotes the input feature of the i-th layer, $P_4^{td}$ represents the intermediate feature generated in the top-down pathway at the 4th layer, and $P_4^{out}$ is the final output feature of the 4th layer in the bottom-up pathway.

The Resize operation is employed to perform upsampling or downsampling in order to align the resolutions of different feature maps, while Block refers to the convolutional processing unit—in this study, the C2f module is used for this operation.

Through this series of carefully designed mechanisms, BiFPN-GLSA provides an efficient and precise solution for graphite ore grade detection, significantly enhancing the model’s recognition accuracy across various scales and types of graphite ores.

2.5. Wise-Inner-Shape-IoU

The loss function plays a crucial role in object detection by quantifying the discrepancy between model predictions and ground-truth labels, thereby guiding the network’s training process [36]. In the task of graphite ore grade detection, the ore surfaces often exhibit complex textures and diverse morphologies, and in scenarios with dense targets or occlusions, the IoU (Intersection over Union) between predicted and ground-truth bounding boxes can be relatively low.

Under such conditions, the optimization signal provided by the traditional GIoU loss becomes weak, making it difficult for the model to achieve comprehensive optimization of target localization.

Therefore, designing a task-specific loss function that adapts to these challenges is essential for enhancing the detection accuracy and robustness of the model.

This paper proposes a novel loss function called Wise-Inner-Shape-IoU, which integrates the advantages of Wise-IoU, Inner-IoU, and Shape-IoU in a unified formulation.

The proposed loss is specifically designed to address the challenges of scale, shape, and feature diversity in graphite ore grade detection, enabling more precise localization and robust optimization across varying ore morphologies and structural complexities.

To prevent the model from excessively focusing on high-quality samples during training—which can reduce localization efficiency in complex scenarios—we introduce Wise-IoU. Wise-IoU employs a dynamic non-monotonic focusing mechanism (FM) that adaptively assigns gradient gains to anchor boxes of varying quality. By emphasizing medium-quality anchors, it effectively mitigates the negative impact of low-quality samples during bounding box regression. In this study, we adopt the Wise-IoU v3 variant, whose computation is formulated as follows:

$${\mathcal{L}}_{WIoUv3}=r{\mathcal{R}}_{WIoU}\times {\mathcal{L}}_{IoU},$$

(8)

$${\mathcal{R}}_{WIoU}=\exp \left({\displaystyle \frac{(x-x_{gt}{)}^2+(y-y_{gt}{)}^2}{(W_g^2+H_g^2{)}^{*}}}\right),$$

(9)

where $x$, $y$ and $x_{gt}$, $y_{gt}$ denote the center coordinates of the predicted box and the ground-truth box, respectively. $W_g$ and $H_g$ represent the width and height of the minimum enclosing rectangle that contains both boxes. The parameter $r$ is a non-monotonic focusing factor, which is used to regulate the gradient contribution of ${\mathcal{R}}_{WIoU}$, allowing the model to adaptively balance the optimization between high- and low-quality samples.

To improve regression convergence efficiency and enhance the model’s generalization capability on complex samples, Inner-IoU is introduced. Inner-IoU accelerates network convergence by adaptively assigning auxiliary bounding boxes of varying scales to samples with different IoU levels—smaller auxiliary boxes for high-IoU samples and larger ones for low-IoU samples [37]. The computation of Inner-IoU is defined as follows:

$$Inner-Iou={\displaystyle \frac{\left|B_p\cap B_t\right|}{\left|B_t\right|}},$$

(10)

Here, $B_p$ denotes the predicted bounding box, $B_t$ represents the ground-truth bounding box, $B_p\cap B_t$ is the intersection area between the two boxes, and $B_t$ is the area of the ground-truth box.

In graphite ore grade detection, the shapes and sizes of ores vary significantly. The traditional GIoU indirectly penalizes deviations only through the coarse bounding box enclosure, which limits its ability to directly optimize the geometric similarity between predicted boxes and irregular ore shapes. Therefore, we introduce Shape-IoU to further enhance localization accuracy. The Shape-IoU is calculated as follows:

$$Shape-Iou={\displaystyle \frac{\left|S_p\cap S_t\right|}{\left|S_p\cup S_t\right|}},$$

(11)

Here, $S_p$ and $S_t$ represent the shape information of the predicted and ground-truth boxes, respectively. $S_p\cap S_t$ denotes the intersection area of their shapes, while $S_p\cup S_t$ represents the union area.

By integrating the advantages of these three methods, we construct the Wise-Inner-Shape-IoU loss function, which effectively addresses the diversity challenges in graphite ore grade detection and achieves more precise localization. The proposed loss function is defined as follows:

$$\mathcal{L}=r\times {\mathcal{R}}_{WIoU}\times \left(1-{IoU}^{inner}+{distance}^{shape}+0.5\times {\mathsf{\Omega }}^{shape}\right).$$

(12)

3. Data and Experimental Preparation

3.1. Data Collection

The graphite ore image dataset used in this study was collected from the mining site of China Minmetals Group (Heilongjiang) Graphite Industry Co., Ltd., located in Hegang City, Heilongjiang Province, China. To ensure the diversity and representativeness of the samples, a variety of specimens—covering both primary graphite ore and oxidized graphite ore—were randomly selected from different mining zones and subsequently annotated under the supervision of experienced field professionals in July 2025.

Under visible-light illumination within the mineral processing plant environment, all verified graphite ore samples were imaged using a Hikrobot MV-CA050-12GC industrial camera (Hangzhou Hikrobot Co., Ltd., Hangzhou, Zhejiang, China). Based on the carbon content percentage thresholds accurately determined through chemical analysis under the assistance of laboratory professionals and further validated by expert evaluation, all samples were classified into three grades: low-grade (carbon content 0–10%), medium-grade (10–20%), and high-grade (above 20%).

Mineralogical analysis revealed distinct visual differences among ores of varying grades: high-grade ores appear darker and more uniform due to higher graphite content; low-grade ores exhibit lighter or mottled appearances owing to the presence of quartz, silicates, and other light-colored minerals; while oxidized ores often display reddish-yellow hues, attributed to secondary minerals such as hematite and pyrite [38].

To ensure comprehensive coverage of each sample’s characteristics, multiple images of different regions and angles of the same ore specimen were captured. All images were collected at a resolution of 640 × 640 pixels and saved in JPG format. Ultimately, a dataset comprising 1300 high-quality original images was established, providing a solid foundation for subsequent model training and evaluation. Representative examples of the graphite ore image dataset are shown in Figure 9.

3.2. Data Processing

To enhance the accuracy and robustness of graphite ore grade detection while simulating the complex conditions often encountered in industrial inspection environments and ensuring dataset diversity, this study employed a series of data augmentation techniques to enrich the limited graphite ore image dataset:

• Random Horizontal Flipping: By simulating random orientations of ore samples, this technique improves the model’s adaptability to directional variations, ensuring accurate recognition regardless of left–right orientation.
• Center Cropping: The central region of each image is cropped while maintaining its original aspect ratio. This effectively simulates variations in target scale caused by different shooting distances, thereby improving the model’s performance in detecting ores of varying sizes.
• Median Filtering Denoising: A median filter is applied to smooth images, effectively reducing random noise introduced by uneven illumination or sensor artifacts while preserving ore edge information. This enables the model to learn cleaner and more representative ore features.
• Contrast Adjustment: The image contrast is randomly adjusted within a limited range to simulate subtle variations in lighting intensity within mining environments. This enhances the model’s generalization capability under different illumination conditions and ensures stable grade recognition across light variations.
• Proportional Scaling and Padding: Each original image is rescaled proportionally to maintain its aspect ratio and then placed at the center of a standardized gray canvas. This process unifies input dimensions while avoiding geometric distortion from forced stretching, preserving the ore’s true morphological and textural characteristics—critical for accurate grade identification.

A comparison of the data augmentation results for the graphite ore dataset is shown in Figure 10.

After data augmentation, the entire dataset was manually annotated using the LabelImg tool [39]. The annotations were saved in .txt format, with three defined categories corresponding to the graphite ore grade levels: “0–10%”, “10–20%”, and “20%+”.

For model training and evaluation, the fully annotated dataset was systematically divided into training, validation, and testing subsets at a ratio of 7:1:2. The final processed dataset contains 3800 instances of graphite ore. Specifically, the numbers of low-, medium-, and high-grade samples are 1593, 1533, and 674, respectively.

This distribution was designed to reflect the realistic production ratios and operational demands of industrial graphite ore beneficiation, emphasizing the economic importance of accurately distinguishing between low- and medium-grade ores in practical applications.

The details of the dataset partitioning are presented in

Table 1. Details of the dataset partitioning.

	Training Set	Validation Set	Test Set	Total
Total	2660	760	380	3800
0–10%	1110	339	144	1593
10–20%	1094	280	159	1533
20%+	456	141	77	674

.

3.3. Experimental Environment

The training parameter settings for the proposed GOG-RT-DETR graphite ore grade recognition and detection model are as follows: the initial learning rate is set to 0.001, the batch size is 4, and the number of workers is 4. All models were trained with an input resolution of 640 × 640. The model is trained for a total of 200 epochs, using the Stochastic Gradient Descent (SGD) optimizer, with a momentum parameter of 0.09. The experiments were conducted on a workstation equipped with a 12th-generation Intel Core i5-12490F CPU (3.00 GHz; Intel Corporation, Ho Chi Minh City, Vietnam) and an NVIDIA GeForce RTX 3080 Ti GPU (NVIDIA Corporation, Santa Clara, CA, USA). The detailed experimental environment configuration is shown in

Table 2. Experimental Environment Configuration.

Name	Parameter
System	Windows10 (64bit)
CPU	12th-generation Intel Core i5-12490F
Memory	31 GB
GPU	NVIDIA GeForce RTX 3080 Ti
Video Memory	11 GB
Programming Software	Python 3.10.15
Deep Learning Framework	PyTorch 2.5.1
GPU Acceleration Library	CUDA 11.8

.

3.4. Evaluation Metrics

To systematically evaluate the performance of the proposed GOG-RT-DETR model, this study considers both detection accuracy and model lightweight efficiency, aligning with real-world industrial application requirements. The detection accuracy of the model is quantified using three core metrics: Precision (P), Recall (R), and Mean Average Precision (mAP). These indicators jointly assess the model’s localization accuracy and classification reliability in the graphite ore grade recognition task.

Meanwhile, the lightweight characteristics of the model are evaluated from the perspectives of computational efficiency and deployment feasibility, measured by Frames Per Second (FPS), Floating Point Operations (FLOPs), and the total number of network parameters (Params).

Precision (P) quantifies the confidence of the model in its positive predictions—that is, among all samples predicted as positive, the proportion that are truly positive. This directly measures the model’s accuracy and false detection rate in identifying graphite ore grades. Recall (R) measures the model’s ability to identify all actual positive samples, reflecting its effectiveness in detecting all true graphite ores and evaluating its missed detection rate [40]. The formula for precision is expressed as:

$$\mathrm{P}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{P}}}\times 100\%,$$

(13)

The formula for recall is as follows:

$$\mathrm{R}\mathrm{e}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{l}={\displaystyle \frac{\mathrm{T}\mathrm{P}}{\mathrm{T}\mathrm{P}+\mathrm{F}\mathrm{N}}}\times 100\%,$$

(14)

In the above two formulas, TP (True Positives) denotes the number of correctly predicted positive samples, FP (False Positives) represents the number of samples incorrectly predicted as positive, and FN (False Negatives) refers to the number of true positive samples that the model failed to identify.

The mean Average Precision (mAP) is a comprehensive evaluation metric used in multi-class detection tasks. It assesses the overall performance of a model by averaging the Average Precision (AP) values across all categories. In this study, the Intersection over Union (IoU) threshold between predicted and ground-truth bounding boxes was set to 0.5, thus we use mAP₅₀ to measure the detection accuracy. The calculation formula for mAP₅₀ is as follows:

$${\mathrm{m}\mathrm{A}\mathrm{P}}_{50}={\displaystyle \frac{1}{N}}{\sum }_{c=1}^N{\mathrm{A}\mathrm{P}}_c^{0.5},$$

(15)

Here, N represents the total number of categories in the dataset. In the graphite ore dataset used in this study, N = 3. AP denotes the average precision for each category, while AP₍c₎^0.5 represents the average precision of the c-th category when the IoU threshold is set to 0.5.

In addition, FPS, FLOPs, and Params serve as key indicators to quantify the lightweight characteristics of the model. FPS reflects the detection speed and inference efficiency, while FLOPs measure the computational complexity required for a single forward inference pass, which directly affects the model’s real-time processing capability on edge devices [41]. The formula for calculating FLOPs can be expressed as follows:

$$\mathrm{G}\mathrm{F}\mathrm{L}\mathrm{O}\mathrm{P}\mathrm{S}=W\times H\times K\times K\times \mathrm{C}\mathrm{i}\mathrm{n}\times \mathrm{C}\mathrm{o}\mathrm{u}\mathrm{t},$$

(16)

In this formula, $W$ and $H$ represent the spatial dimensions of the input feature map, namely its width and height. $K$ denotes the size of the convolution kernel, which is assumed here to be a square with a side length of $K$. Furthermore, $\mathrm{C}\mathrm{i}\mathrm{n}$ refers to the number of input channels (or the depth) of the feature map, while $\mathrm{C}\mathrm{o}\mathrm{u}\mathrm{t}$ corresponds to the number of output channels, which is also equal to the total number of convolution kernels used in that layer.

Params, on the other hand, affect the model’s memory usage and generalization ability—the fewer the parameters, the lower the hardware resource requirements. Optimizing these metrics is essential for the successful deployment of the graphite ore grade detection model in resource-constrained industrial environments, as it ensures a balanced trade-off among real-time analysis, detection accuracy, and device availability.

4. Results and Discussion

4.1. Confusion Matrix Visualization and Accuracy Comparison

The core function of the confusion matrix lies in cross-comparing the model’s predicted results with the ground-truth labels, thereby accurately quantifying the recognition performance of each category and effectively identifying the weak points in classification. As shown in Figure 11, the confusion matrix analysis on the test set demonstrates that the improved model not only significantly enhances the correlation between predictions and true labels but also effectively mitigates interference caused by the visual similarity among graphite ores. Moreover, it substantially reduces the misclassification rate across all categories—achieving a notable breakthrough particularly in distinguishing between low-grade and medium-grade ores, which had previously been the most challenging distinction. However, the confusion matrix also reveals remaining failure cases. For example, categories with fewer training samples exhibit relatively low recall, indicating that data imbalance still affects the stability of model learning. This suggests that future improvements could focus on targeted data augmentation and related strategies to further enhance performance.

As illustrated in Figure 12, the accuracy curve shows the performance trends of both the baseline RT-DETR model and the proposed GOG-RT-DETR model on the test set as training epochs increase. The curve clearly indicates that the improved model achieves a significant improvement in accuracy, validating its superior learning capability and robustness in complex ore classification tasks.

4.2. Ablation Experiments

To systematically verify the independent and synergistic effectiveness of the proposed innovative modules and to validate their feasibility, a series of ablation experiments were conducted in this study.

The experiments used RT-DETR-r18 as the baseline model and employed a progressive integration strategy, gradually incorporating the proposed enhancement modules. To ensure fairness and comparability, all experiments adhered to a controlled-variable principle, using identical training parameters and dataset configurations.

The proposed modification strategies are summarized as follows:

• A: Replace the original backbone network with the lightweight and efficient Faster-Rep-EMA module as the new feature extractor.
• B: In the neck network, replace the original CCFM feature fusion module with the improved BiFPN-GLSA module.
• C: In the loss function, adopt the Wise-Inner-Shape-IoU loss to optimize bounding box regression.

The results of the ablation experiments are shown in

Table 3. Results of the Ablation Experiments.

Methods	P (%)	R (%)	mAP50 (%)	FPS (Frame·s−1)	FLOPS (G)	Params (M)
RT-DETR-r18	81.6	84.4	81.2	80.6	56.9	19.88
A	84.3	86.8	82.5	83.9	51.4	16.90
B	84.5	85.6	82.8	85.2	49.9	17.76
C	83.1	84.4	82.2	81.3	55.3	19.69
A + B	84.4	86.1	83.1	88.5	44.6	14.71
A + C	83.5	84.6	82.9	82.1	53.0	17.15
B + C	84.6	86.0	83.2	85.0	49.9	17.76
GOG-RT-DETR (A + B + C)	85.4	87.3	83.7	87.2	43.6	14.71

. First, each strategy was evaluated independently. When applying Strategy A alone, the lightweight and efficient Faster-Rep-EMA backbone significantly reduced computational redundancy. Compared to the baseline model, FLOPs and parameter count were reduced by 9.7% and 15.0%, respectively, while mAP and FPS increased by 1.3% and 4.1%, demonstrating that Faster-Rep-EMA effectively achieves a balance between high efficiency and model compactness.

Next, when Strategies B and C were implemented independently, both yielded improvements in detection accuracy. This indicates that the introduction of the BiFPN-GLSA module and the Wise-Inner-Shape-IoU loss function not only reduced the model’s parameter count but also enhanced its ability to capture critical features of graphite ore.

Subsequently, these enhancements were combined into transitional models (A + B, A + C, and B + C). The results showed further optimization in model lightweighting while maintaining steady gains in accuracy and inference speed. Moreover, the significant reduction in FLOPs and parameter count highlights the potential of these modifications for efficient deployment on edge devices.

Finally, the fully integrated GOG-RT-DETR model (A + B + C) outperformed the original baseline in all key metrics, including detection accuracy, computational complexity, and inference speed. Under identical dataset and training conditions, the proposed model achieved improvements of +2.5% in mAP50, +8.2% in FPS, +3.8% in Precision (P), and +2.9% in Recall (R), while reducing parameter count and FLOPs by 26.0% and 23.4%, respectively.

These ablation results comprehensively validate the effectiveness and practicality of each proposed module. The synergistic integration of all components forms the core contribution to the model’s overall performance enhancement.

To comprehensively validate the contribution of each improved component to the graphite ore grade detection performance, a series of systematic ablation experiments were conducted by individually replacing the loss function, neck network, and backbone network while maintaining consistency with the original RT-DETR framework. The experimental results are shown in

Table 4. Ablation study results for individual modules.

Model	P (%)	R (%)	mAP50 (%)	FPS (Frame·s−1)	FLOPS (G)	Params (M)
Wise-IoU	82.0	84.2	81.6	80.7	57.9	21.3
Inner-IoU	82.3	83.9	82.0	81.1	58.3	20.09
Shape-IoU	82.5	84.0	81.5	80.8	57.4	20.02
Wise-Inner-Shape-IoU	83.1	84.4	82.2	81.3	55.3	19.69
HSFPN	84.4	86.2	82.9	82.4	54.4	18.22
CGRFPN	83.8	85.3	82.1	83.3	48.6	19.34
BiFPN-GLSA	84.5	85.6	82.8	85.2	49.9	17.76
DualConv	83.9	85.8	81.8	82.7	49.6	16.08
iRMB	84.0	86.3	82.1	83.2	50.8	16.73
Faster-Rep-EMA	84.3	86.8	82.5	83.9	51.4	16.90

.

In terms of bounding-box regression loss, Wise-IoU, Inner-IoU, and Shape-IoU each provide marginal improvements in accuracy over the baseline, but the overall gains remain limited. In contrast, the proposed Wise-Inner-Shape-IoU jointly incorporates scale proportion, bounding-box consistency, and shape constraints, enabling the model to better focus on maintaining the geometric integrity of ore particle contours. As a result, it improves mAP50 by 1.0% over the baseline while maintaining fast inference. This loss function proves particularly suitable for graphite ore detection scenarios, where complex particle geometries and blurred adhesion boundaries are common, significantly enhancing regression stability and localization precision.

For feature fusion, although traditional HSFPN and CGRFPN introduce moderate accuracy benefits, their computational overhead results in reduced inference speed. The proposed BiFPN-GLSA establishes an efficient bidirectional multi-scale fusion pathway, while the integration of local spatial attention enables the model to capture both the global texture characteristics and fine-grained mineral surface details of flaky graphite ore. Experimental results indicate that BiFPN-GLSA achieves the best balance between accuracy and inference speed, improving FPS to 85.2.

Regarding lightweight backbone design, DualConv and iRMB demonstrate commendable performances in reducing parameter size and increasing FPS, yet they show limited capability in accuracy enhancement. The Faster-Rep-EMA backbone, benefiting from enhanced structural re-parameterization and EMA-based representational refinement, improves the joint extraction of low-frequency structural cues and high-frequency texture information under low computational complexity. This results in simultaneous performance gains in precision and efficiency, successfully unifying lightweight architecture with high-accuracy detection.

These three modules provide complementary optimizations across accuracy, inference speed, and computational cost: Wise-Inner-Shape-IoU strengthens localization quality, BiFPN-GLSA enhances multi-scale feature representation, and Faster-Rep-EMA improves backbone feature extraction efficiency. With their integration, GOG-RT-DETR achieves an mAP50 of 83.7% and an inference speed of 87.2 FPS, while significantly reducing both parameter count and FLOPs. These results verify the effectiveness and practical value of the proposed improvements for industrial graphite ore grade detection.

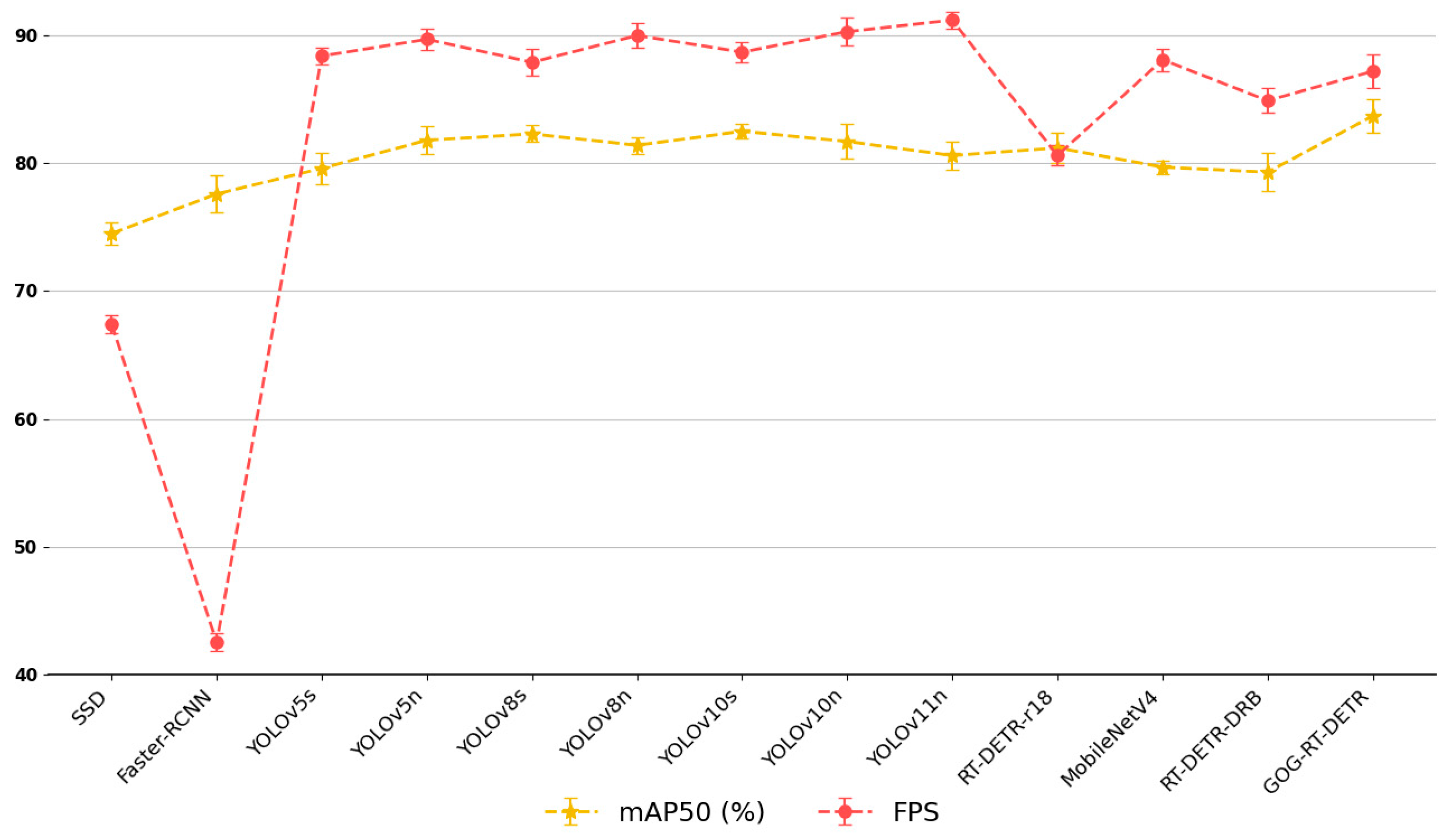
4.3. Comparative Experiments

To ensure the fairness of experimental comparisons, all models were trained from their standard initialization (without using any pre-trained weights), and the default hyperparameter settings were uniformly applied without any task-specific adjustments. The proposed GOG-RT-DETR model was comprehensively evaluated on the graphite ore grade detection task and compared against several mainstream lightweight object detection models, including the YOLO series [42] (YOLOv5s/n, YOLOv8s/n, YOLOv10s/n, YOLO11n) and RT-DETR lightweight variants (RT-DETR-MobileNetV4 and RT-DETR-DRB). Traditional models such as SSD [43] and Faster R-CNN [44] were also included as baselines for reference. All models were trained under identical configurations, without using pretrained weights, and with consistent default hyperparameters to ensure fairness in comparison. The comparative experiment results are summarized in

Table 5. Comparative experimental results.

Methods	P (%)	R (%)	mAP50 (%)	FPS (Frame·s−1)	FLOPS (G)	Params (M)
SSD	68.8	79.7	74.5	67.4	53.1	24.7
Faster-RCNN	76.1	81.8	77.6	42.5	370.2	136.5
YoLov5s	74.5	78.4	79.6	88.4	23.18	9.21
YoLov5n	76.8	79.1	81.8	89.7	7.16	2.51
YoLov8s	79.4	80.5	82.3	87.9	28.3	12.12
YoLov8n	75.9	78.3	81.4	90.0	8.16	3.01
YoLov10s	80.4	81.6	82.5	88.7	24.8	8.07
YoLov10n	76.3	78.6	81.7	90.3	8.40	2.71
YoLov11n	75.3	79.7	80.6	91.2	6.30	2.58
RT-DETR-r18	81.6	84.4	81.2	80.6	56.9	19.88
MobileNetV4	80.7	83.1	79.7	88.1	39.5	11.31
RT-DETR-DRB	82.1	82.9	79.3	84.9	42.4	13.70
GOG-RT-DETR	85.4	87.3	83.7	87.2	43.6	14.71

.

The results demonstrate that GOG-RT-DETR achieves superior detection accuracy, with a precision, recall, and mAP₅₀ of 85.4%, 87.3%, and 83.7%, respectively. Compared to the YOLO series, the mAP₅₀ improvement ranges from 1.2% to 4.1%, indicating a stronger ability to distinguish features and accurately identify ore grades.

Although the YOLO and RT-DETR lightweight variants exhibit the lowest parameter counts and computational complexity, their detection accuracy is notably lower than that of GOG-RT-DETR. Meanwhile, since FPS is significantly affected by computational complexity, models with lower computational cost—particularly lightweight YOLO variants—can achieve substantially higher FPS. In contrast, heavy two-stage detectors such as Faster R-CNN suffer from extremely low FPS due to excessive computational burden. The proposed GOG-RT-DETR achieves a favorable balance between inference speed and detection accuracy, achieving a real-time inference speed of 87.2 FPS while considerably improving the mAP compared with the baseline model. The model proposed in this paper achieves a better balance between accuracy and efficiency, making it more suitable for deployment on resource-constrained edge devices.

Overall, the GOG-RT-DETR model outperforms existing lightweight and traditional detection algorithms across multiple key performance metrics, highlighting its practical applicability and industrial deployment potential in real-world graphite ore grade detection.

As illustrated in Figure 13, the yellow dashed line represents the mAP50 performance of different models, while the red dashed line denotes FPS (frames per second), with error bars indicating the standard deviation over three independent runs. Under the same input settings, YOLO series models exhibit a clear trade-off between detection accuracy and inference speed. For example, although YOLOv8s and YOLOv11n achieve higher FPS than the proposed model—YOLOv11n reaching approximately 90 FPS—their detection accuracy remains 1.4–3.1% lower than that of GOG-RT-DETR. In contrast, GOG-RT-DETR attains a high inference speed of 87.2 FPS while achieving an mAP50 of 83.7%, outperforming the baseline RT-DETR by 2.5% in accuracy and approximately 8.2% in FPS. Even when compared with more lightweight models such as YOLOv5n and YOLOv10n, GOG-RT-DETR significantly improves detection accuracy without sacrificing real-time performance. These results demonstrate that GOG-RT-DETR achieves a superior balance across lightweight design, inference speed, and detection accuracy, and exhibits strong potential for rapid deployment in real-world mining scenarios.

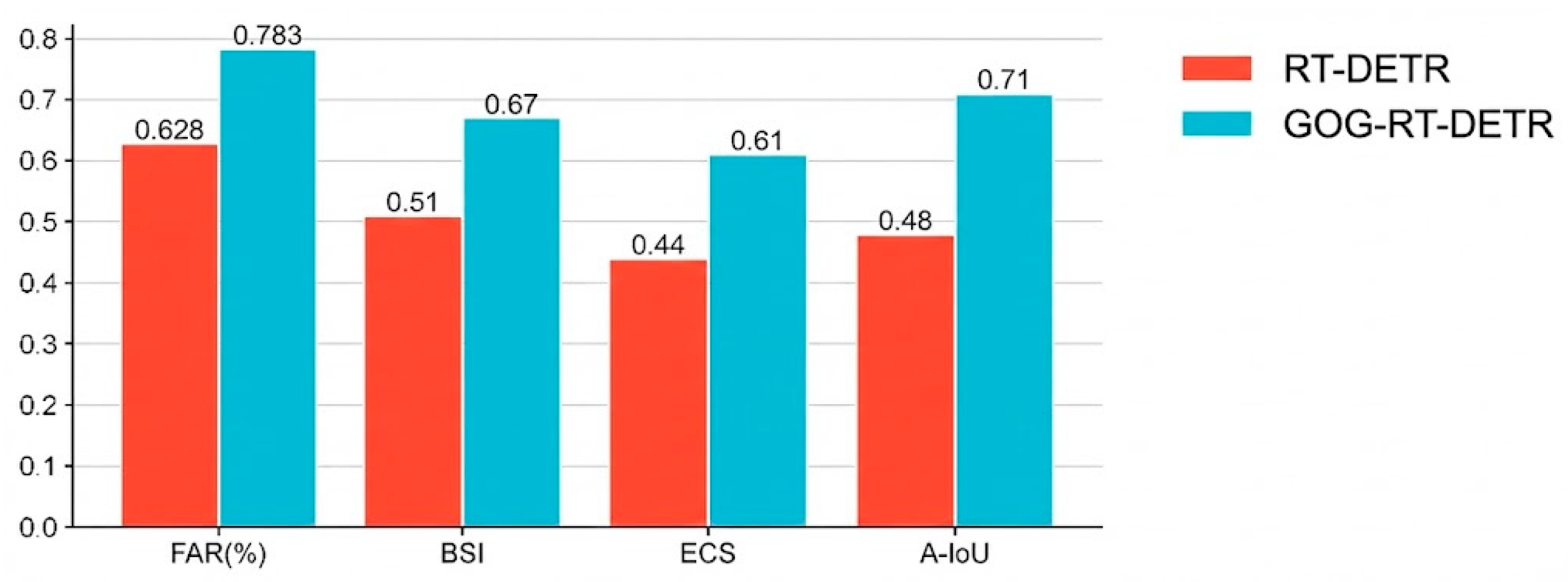
4.4. Visualization Experiments

To more intuitively demonstrate the practical advantages of the proposed GOG-RT-DETR model, a series of visualization experiments were conducted.

In these experiments, three models—YOLOv11n, the baseline RT-DETR, and the proposed GOG-RT-DETR—were employed to perform detection on randomly selected samples from the dataset.

These comparison samples encompass three grade levels of natural graphite ore and oxidized graphite ore, enabling a comprehensive assessment of model performance across different scenarios.

As shown in Figure 14, in the visualization results, different grade levels are marked with distinct colors for clarity: red represents low-grade, pink indicates medium-grade, and yellow denotes high-grade graphite ore. Each predicted bounding box is accompanied by a confidence score (ranging from 0 to 1), which quantifies the model’s certainty in accurately identifying the specific ore grade within the detected region.

The visual analysis across various scenarios demonstrates that, although all models successfully achieve accurate classification of graphite ore grades, they differ notably in both recognition precision and efficiency. Compared with the baseline RT-DETR and YOLOv11n models, the GOG-RT-DETR model exhibits significantly stronger robustness against environmental interference, as well as superior detection accuracy and efficiency in complex scenes.

Benefiting from its multi-module-enhanced feature extraction mechanism, GOG-RT-DETR not only improves detection precision and effectively reduces false detections but also suppresses interference caused by factors such as surface oxidation of graphite ore. Importantly, the confidence scores produced by GOG-RT-DETR are consistently higher than those of the baseline RT-DETR and YOLOv11n models, further confirming its outstanding reliability and stability under challenging conditions.

In conclusion, these experimental results fully demonstrate GOG-RT-DETR’s competitive advantage in graphite ore grade recognition and validate its practical application value in complex industrial environments requiring high-precision detection.

To further validate the rationality and effectiveness of the model design from the perspective of the internal decision-making mechanism, this study employs the Grad-CAM [45] visualization technique to conduct an in-depth analysis of the detection results produced by both the baseline RT-DETR model and the proposed GOG-RT-DETR model.

The core concept of Grad-CAM lies in utilizing the feature maps from the last convolutional layer of a deep convolutional neural network. By computing the gradient-weighted activations corresponding to a specific class, Grad-CAM generates a heatmap that highlights the image regions making the most significant contributions to the model’s final decision.

Figure 15 illustrates a comparative visualization analysis of the attention regions captured by the two models during training, before and after the proposed improvements. As shown in Figure 14, the heatmap visualization clearly demonstrates that the original RT-DETR model exhibits a relatively dispersed attention pattern during graphite ore grade detection, failing to effectively concentrate on the core feature regions of the target ore and being partially affected by background interference. In contrast, the optimized GOG-RT-DETR model shows a significant enhancement in attention concentration, accurately focusing on the relevant regions of the ore while effectively filtering out background noise, thereby reducing attention to irrelevant image areas.

This enhanced focus enables the model to more sharply identify visual features directly related to graphite ore grade—such as regions with distinct texture, color, and surface luster variations. Consequently, in the final test visualizations, our optimized model can precisely localize key regions in the heatmaps, successfully maintaining focus even under complex environmental conditions.

This demonstrates that the improved model possesses an exceptional ability to effectively comprehend both global and local features, allowing it to discern subtle differences between graphite ores of varying grades, ultimately leading to enhanced recognition performance.

To further evaluate whether the improved model exhibits enhanced attention focus on graphite ore regions, beyond the qualitative Grad-CAM visualization, we introduce four quantitative attention-concentration metrics: Attention-IoU, Foreground Attention Ratio (FAR), Background Suppression Index (BSI), and Energy Concentration Score (ECS). FAR measures the proportion of attention distributed over foreground ore regions, while BSI reflects the model’s capability to suppress irrelevant background responses. Additionally, A-IoU and ECS quantify the alignment between heatmap activation and the true geometric structure of the ore targets. As shown in Figure 16, compared with RT-DETR, GOG-RT-DETR achieves improvements of 24.7%, 31.4%, and 47.9% in FAR, BSI, and A-IoU, respectively, demonstrating that the proposed model can more accurately focus on the key structural regions of graphite ore while minimizing background distractions. These quantitative evaluations are consistent with the visual analyses, further validating the superior region-attention capability and discriminative feature extraction performance of our method in ore grade inspection tasks.

4.5. Limitations

Compared with other models, although GOG-RT-DETR demonstrates outstanding performance and lightweight advantages in graphite ore grade detection, it is essential to acknowledge its limitations to clearly define the research boundaries and guide future work:

• Although the dataset in this study was meticulously constructed and enhanced through simulated data augmentation, its scale and diversity remain relatively limited. The images were primarily collected from a specific industrial environment—the mining site of China Minmetals Corporation (Heilongjiang, China) Graphite Industry Co., Ltd. (Heilongjiang, China). This may restrict the model’s generalization ability to other mining areas, different geological backgrounds, or unseen oxidized graphite ore morphologies.
• While the core contribution of this research lies in the lightweight architectural innovation (e.g., Faster-Rep-EMA) and efficiency improvements, with significant reductions in FLOPs (−23.37%) and parameters (−26.0%) demonstrating theoretical efficiency, the model has not yet been fully validated on real edge computing hardware, such as NVIDIA Jetson devices or industrial PLCs, to evaluate its actual inference speed (FPS) and deployment performance in real-world conditions.
• The current GOG-RT-DETR framework relies entirely on visible-light (RGB) visual data for grade classification. However, graphite ores with similar grades may exhibit highly similar visual appearances. In future work, integrating multimodal sensing technologies—such as hyperspectral imaging, X-ray fluorescence (XRF), or near-infrared (NIR) imaging—could provide richer discriminative information reflecting mineralogical and chemical composition. This would be particularly valuable in ambiguous or visually indistinct boundary cases.

In summary, future research will focus on expanding the dataset, incorporating multimodal information (e.g., hyperspectral data), and conducting quantitative validation of deployment performance and robustness on real-world edge devices to address these challenges and enhance the model’s industrial applicability.

5. Conclusions

To address the challenges of low efficiency and limited accuracy in traditional graphite ore grade detection methods under complex industrial environments—as well as the difficulty of existing deep learning algorithms in balancing precision, speed, and computational complexity—this study proposes a lightweight, high-precision, and high-speed detection model, named GOG-RT-DETR. Building upon the RT-DETR framework, the model achieves systematic innovations across three key levels:

• The Faster-Rep-EMA module is introduced as the backbone network. By employing partial convolution and re-parameterization techniques, it effectively reduces computational redundancy and memory access costs, while the multi-scale attention mechanism strengthens the extraction of key graphite ore features.
• A new BiFPN-GLSA module replaces the original neck structure. This module fuses a bidirectional feature pyramid network with a global–local self-attention mechanism, substantially improving multi-scale feature fusion quality and enhancing the model’s ability to capture both global contextual information and fine-grained local details.
• The Wise-Inner-Shape-IoU loss function is applied for bounding box regression optimization. By integrating dynamic focus mechanisms, auxiliary bounding box alignment, and shape-awareness, it accelerates convergence and significantly improves localization accuracy.

Extensive experiments were conducted on a custom-built graphite ore dataset, enhanced through simulated data augmentation. The results demonstrate that, compared to the baseline RT-DETR model, GOG-RT-DETR achieved a 2.5% improvement in accuracy, while reducing model parameters and FLOPs by 26.0% and 23.37%, respectively.

Overall, these findings validate that the proposed approach substantially enhances detection accuracy while effectively reducing computational complexity. The GOG-RT-DETR model provides an efficient and advanced solution for the application of computer vision in automated mineral grade detection, showcasing strong potential for real-world industrial deployment.