Complex Predictions for Stress and Displacement of Deep Buried Tunnels with Concrete Lining in Parallel Inclined Multi-Layered Surrounding Rocks
Abstract
1. Introduction
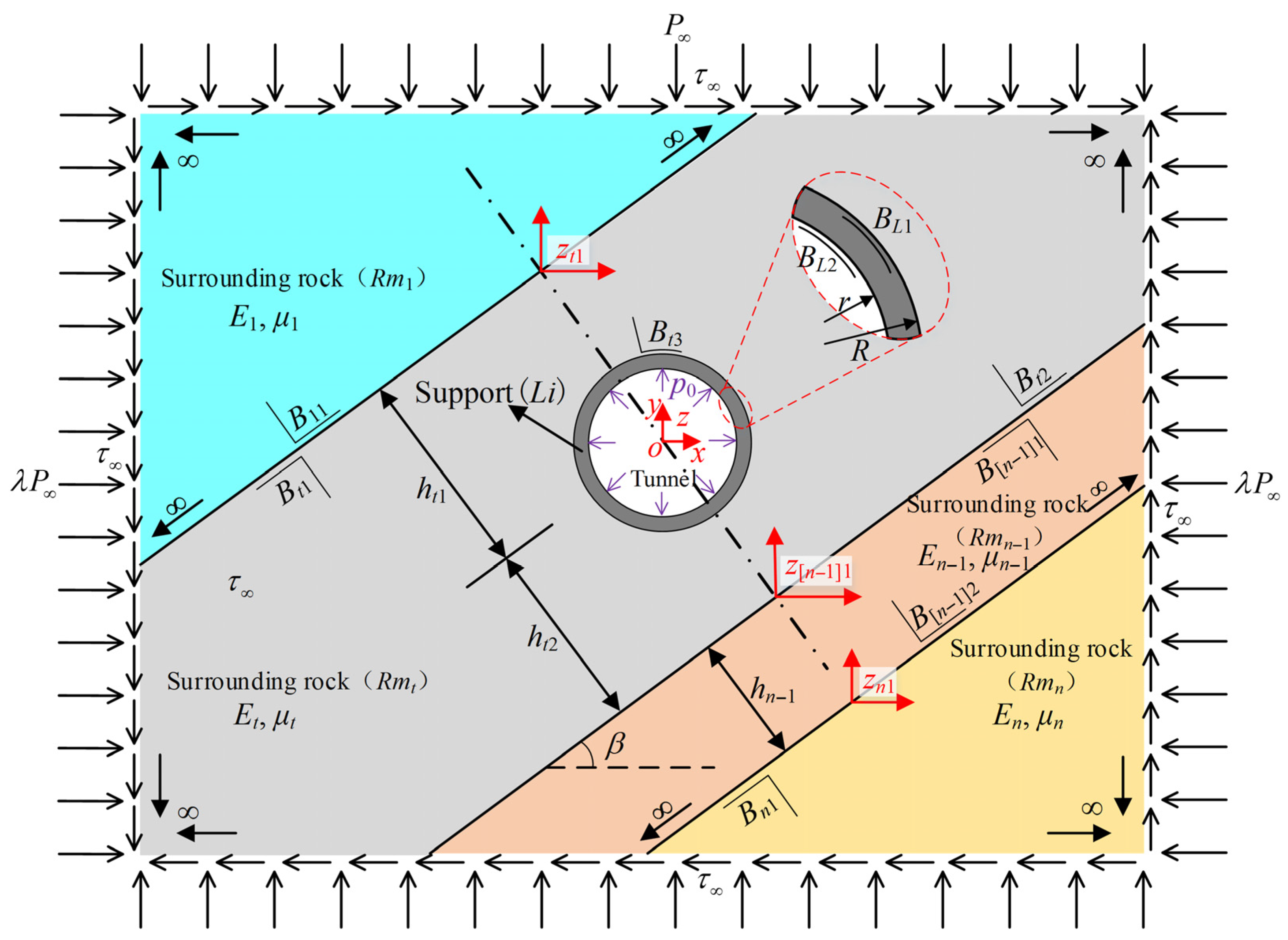
2. The Establishment of the Mechanical Model
- (1)
- The deeply buried composite surrounding rock is composed of several inclined strata interlayered with each other. The interfaces between the strata are parallel and non-intersecting. Each stratum is regarded as a homogeneous, isotropic, linear elastic body, which enables explicit analytical derivations while still reflecting the key interlayer stiffness mismatch that governs stress redistribution. The strata are assumed to remain perfectly bonded, without sliding or separation. This assumption is appropriate for deeply buried rock masses where strong interlayer confinement prevents noticeable slip or separation. In geological settings with weakly bonded or soft interlayers (e.g., weak fault zones), interlayer slip may occur and more realistic interaction models would be required. In this study, the analysis focuses on conditions where the interlayers are strongly constrained and can be reasonably treated as perfectly bonded.
- (2)
- Owing to the large burial depth of the tunnel, the effect of gravity is neglected, as the far-field in situ stresses significantly exceed the self-weight component.
- (3)
- The tunnel is sufficiently long in the longitudinal direction, so the problem is treated as a plane strain condition, a standard assumption for deep and long tunnels with negligible end effects.
3. Solution for Stresses and Displacements
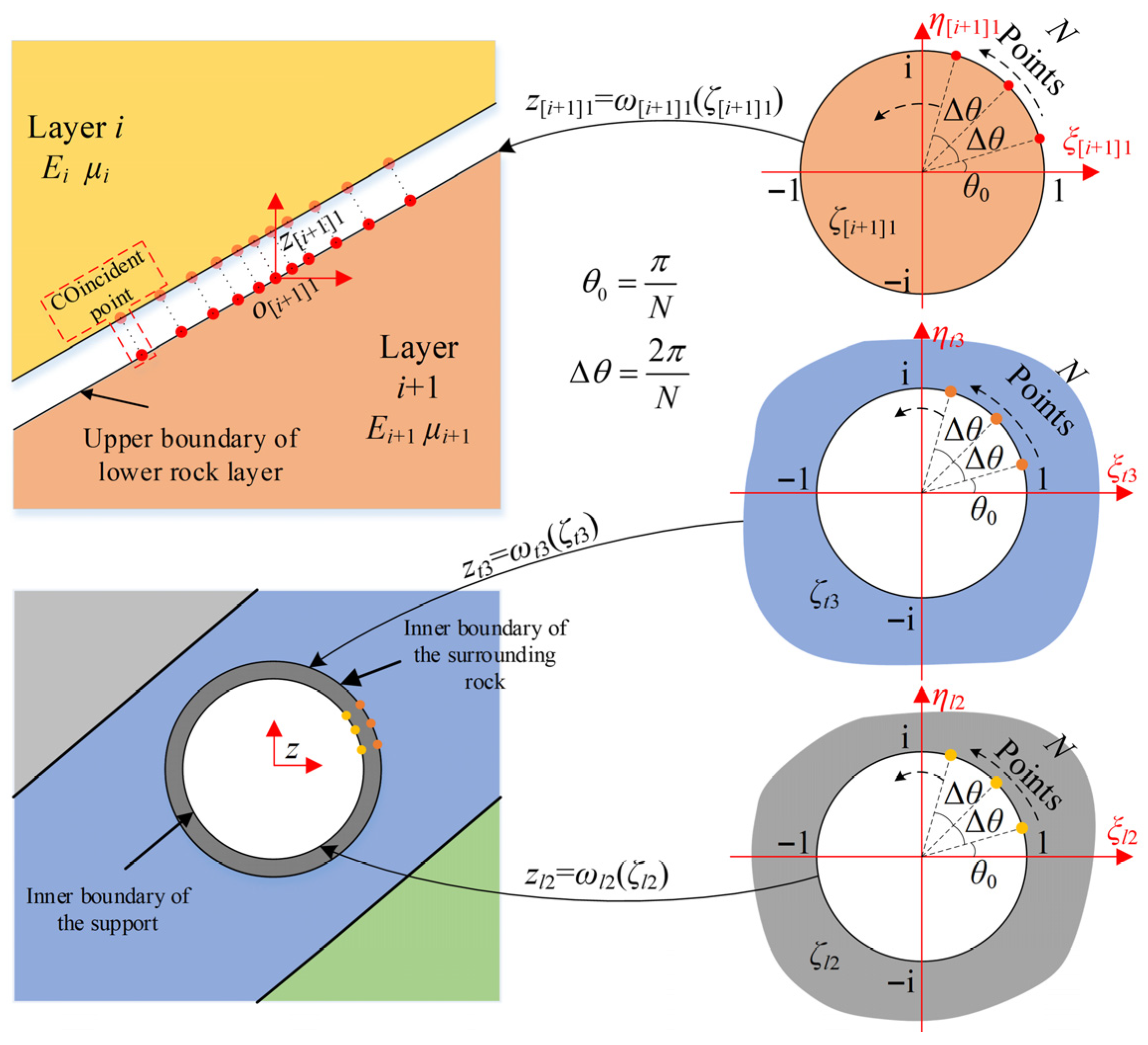
3.1. Complex Functions and Conformal Mapping
3.2. Solution of Stress and Displacement Components
3.3. Solution of Undetermined Complex Coefficients
3.4. Boundary Condition Constraint Equations
- (1)
- Continuity conditions at stratum interfaces
- (2)
- Stress conditions on the inner boundary of the concrete lining
- (3)
- Interaction equations between the concrete lining and the surrounding rock
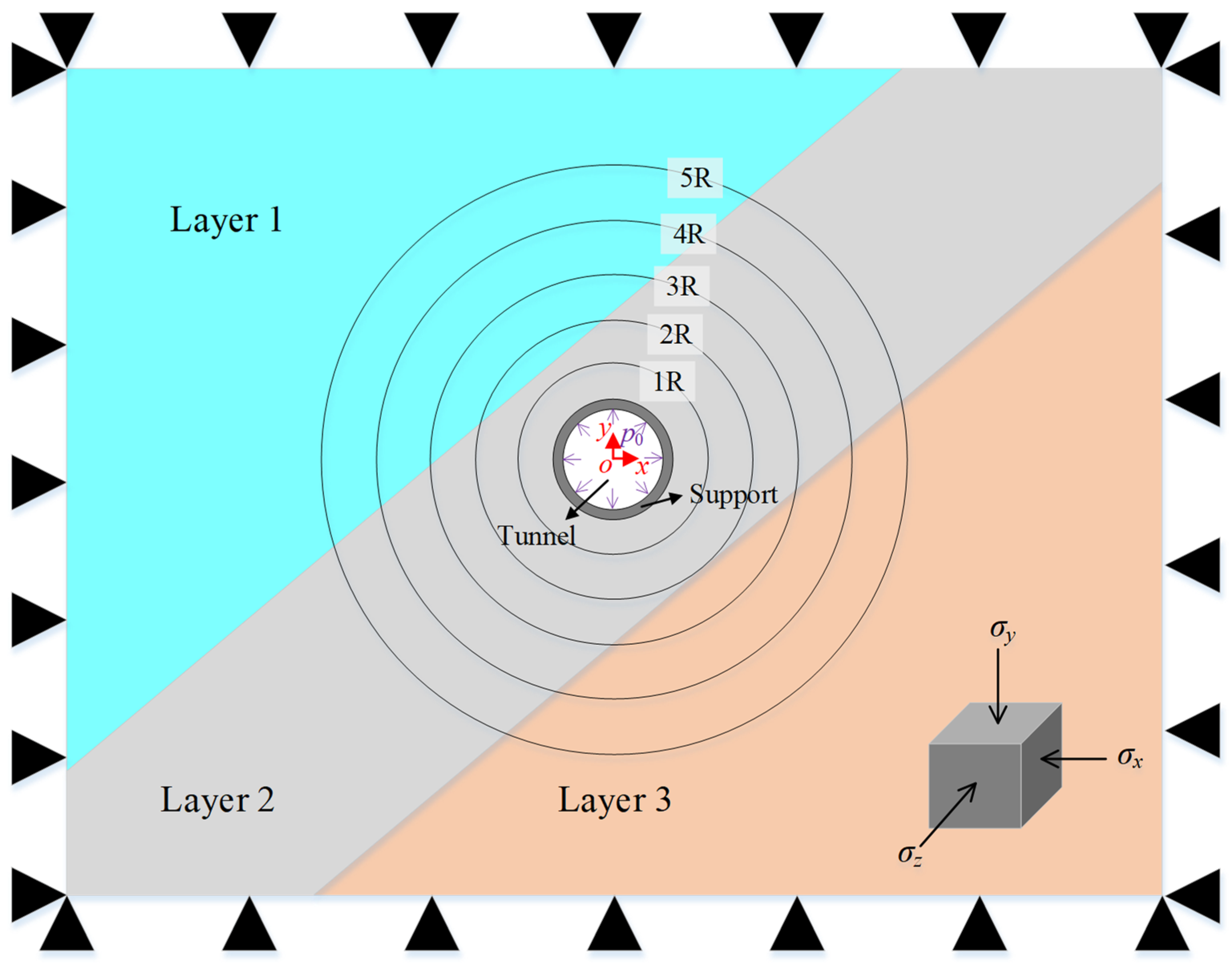
4. Verification of the Solution Method
4.1. Verification of Boundary Conditions
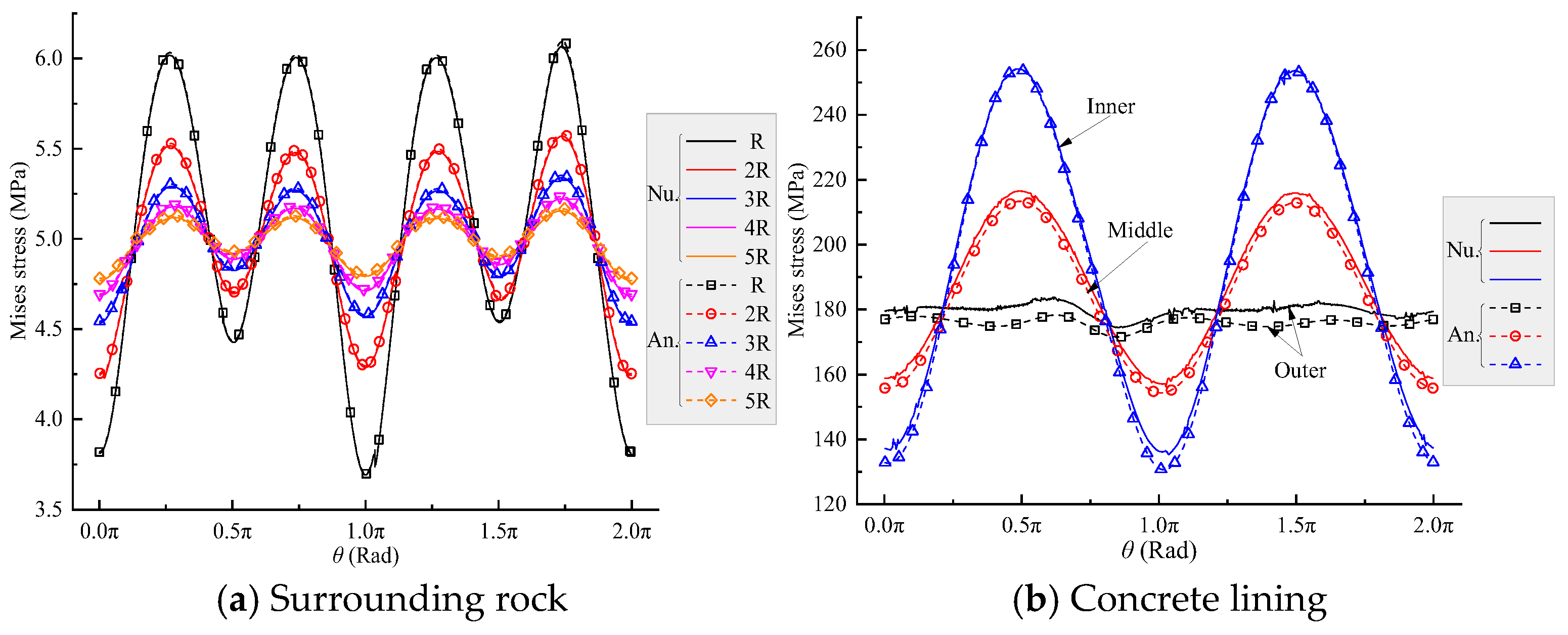
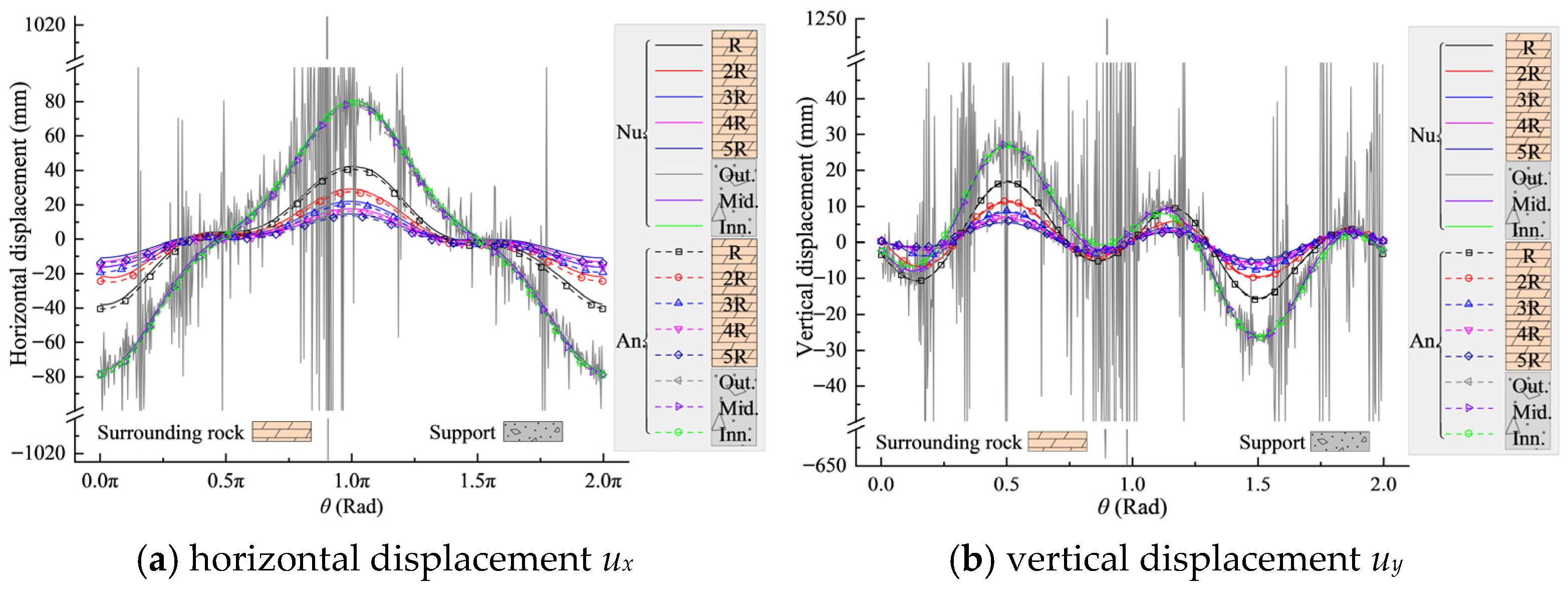
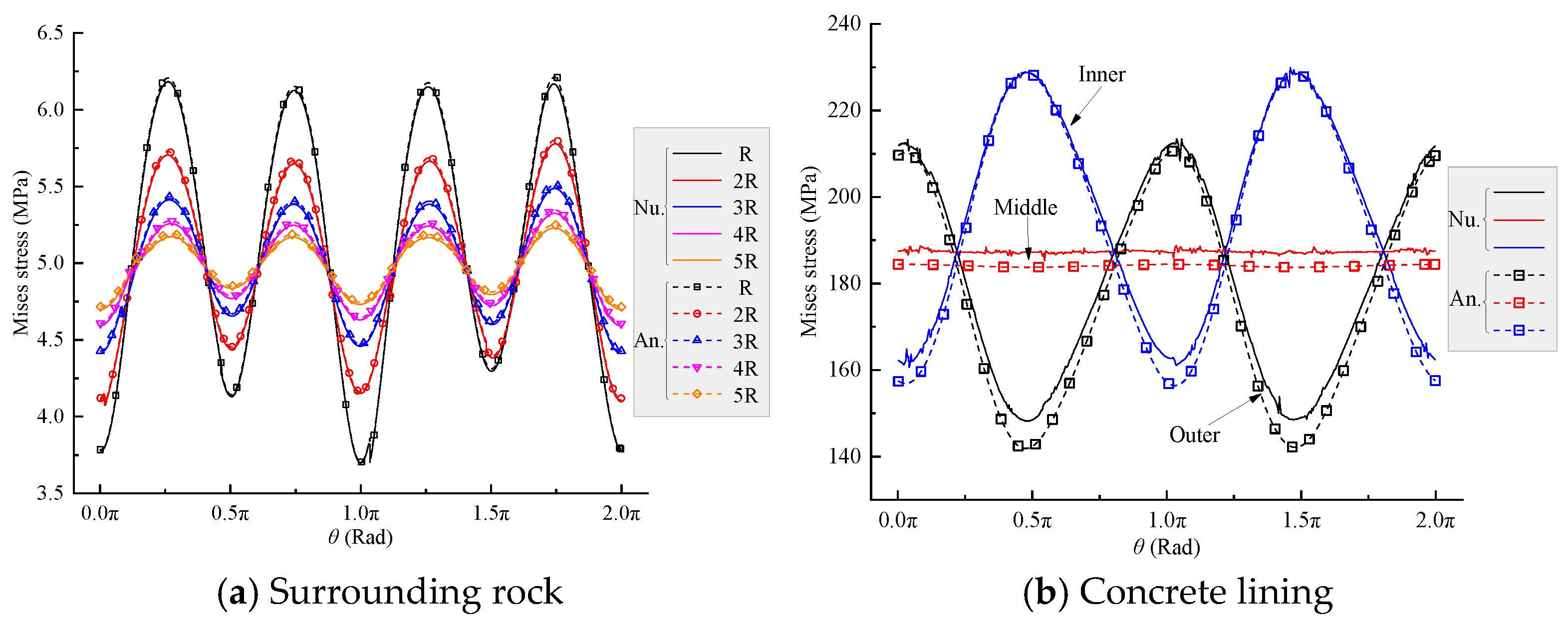
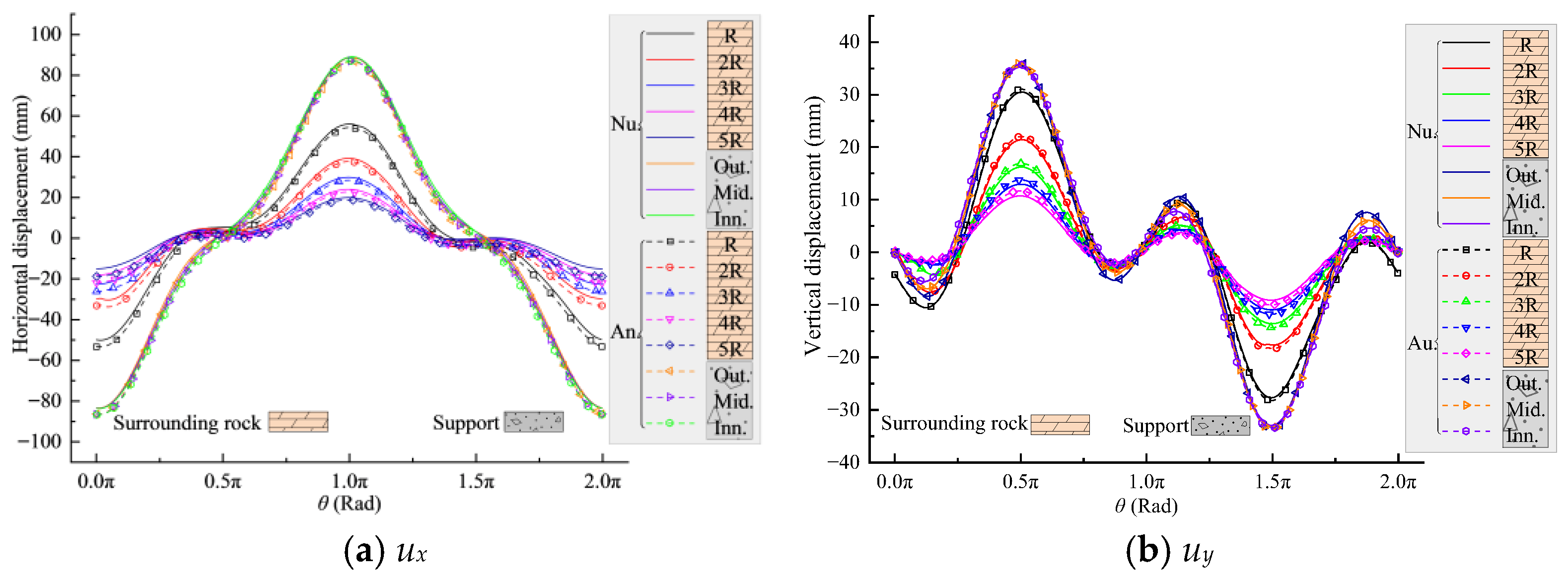
4.2. Numerical Validation
5. Conclusions
- (1)
- The analytical model effectively captures the complex mechanical characteristics arising from the differing properties of arbitrarily inclined multilayered rock strata. This departs significantly from conventional approaches that treat the surrounding rock as a single homogeneous medium. The model also incorporates the concrete lining and considers two typical extreme interface conditions between the lining and the rock—no-slip and fully-slip. By applying the non-iterative complex variable function theory, explicit stress and displacement solutions are obtained. These solutions enable efficient and accurate analysis of the coupled mechanical response of inclined multilayered rock and concrete lining structures in multiply connected domains with multiple planar boundaries.
- (2)
- Comprehensive boundary condition checks under varying contact modes, rock layer inclinations, and lateral pressure coefficients indicate that the stress calculation error on the inner surface of the concrete lining remains on the order of 10−2 Pa. The stress and displacement component curves on both sides of the rock–concrete lining and rock layer interfaces closely coincide, demonstrating that the proposed method effectively satisfies all boundary and continuity conditions.
- (3)
- Comparisons with numerical simulations under non-hydrostatic stress fields show that the analytical predictions of von Mises stress and displacement agree closely with FEM results. Stress errors are generally below 0.03 MPa, displacement errors remain under 0.2 mm, and the maximum relative error of von Mises stress does not exceed 4%. The analytical method also accurately captures stress jumps at rock–layer interfaces and avoids the numerical oscillations typically caused by large stiffness contrasts, demonstrating strong stability and reliability.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Z | Global physical coordinate system XOY; |
| z x + iy | Global physical coordinate in XOY; |
| Bij | The j-th independent boundary of the i-th inclined stratum; |
| Zij | Local physical coordinate system of Bij; |
| zij | Local physical coordinate in Zij; |
| ζij | Local mapping coordinate of zij using the conformal mapping function; |
| ωij | Conformal mapping function for Bij; |
| λij | Mapping scaling factor; |
| β | Inclination angle of parallel inclined multi-layered surrounding rocks; |
| Φij(zij), Ψij(zij) | The set of analytic complex potential functions for Bij; |
| φij(ζij), ψij(ζij) | Laurent series expansions of Φij(zij), Ψij(zij) in the mapped plane; |
| aij,0, aij,k, bij,0, bij,k | Undetermined complex coefficients in φij(ζij), ψij(ζij); |
| Ei, μi | Elastic modulus and Poisson’s ratio of the i-th stratum; |
| El, μl | Elastic modulus and Poisson’s ratio of the concrete lining; |
| Gi | Shear modulus of the i-th stratum, ; |
| κi | Material parameter of the i-th stratum, ; |
| R, r | Outer and inner diameters of the concrete lining; |
| P∞, τ∞ | Cartesian components of far-field stresses; |
| λ | Lateral pressure coefficient; |
| Polar components of far-field stresses; | |
| p0 | Normal inward pressure on the inner boundary of the concrete lining; |
| Cartesian components of stresses in the i-th stratum; | |
| Cartesian components of displacements in the i-th stratum; | |
| Polar components of stresses in the i-th stratum; | |
| Polar components of displacements in the i-th stratum; | |
| Cartesian components of stresses in the concrete lining; | |
| Cartesian components of displacements in the concrete lining; | |
| Polar components of stresses in the concrete lining; | |
| Polar components of displacements in the concrete lining. |
Appendix A
Appendix B
Appendix C
References
- Deng, Z.; Liu, X.; Zhou, X.; de la Fuente, A.; Han, Y.; Xiong, F.; Peng, H. Field monitoring of mechanical parameters of deep-buried jacketed-pipes in rock: Guanjingkou water control project. Tunn. Undergr. Space Technol. 2022, 125, 104531. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Han, Y.; Ding, P.; Xu, B.; Du, W. Study on the field monitoring, assessment and influence factors of pipe friction resistance in rock. Tunn. Undergr. Space Technol. 2024, 154, 106053. [Google Scholar] [CrossRef]
- Dong, W.; Huang, H.; Zhong, M.; Wang, H.; Hua, F. Monitoring and early warning mechanism of flood invasion into subway tunnels based on the experimental study of flooding patterns. J. Intell. Constr. 2024, 2, 9180011. [Google Scholar] [CrossRef]
- Ma, K.M.; Chen, S.J.; Cheng, L.; Liu, Y.; Hu, Z.N.; Zhang, J.R. Determination of the rock mass bearing mechanism following excavation of circular tunnels in layered surrounding rock. Tunn. Undergr. Space Technol. 2025, 164, 106863. [Google Scholar] [CrossRef]
- Man, J.H.; Huang, H.W.; Ai, Z.Y.; Chen, J.Y. Analytical model for tunnel face stability in longitudinally inclined layered rock masses with weak interlayer. Comput. Geotech. 2022, 143, 104608. [Google Scholar] [CrossRef]
- Shu, X.Y.; Zhu, Z.D.; Qu, S.; He, L.K.; Zeng, H.Y.; Zhang, C.X.; Tian, Y. Anisotropic characteristics and deformation behaviors of layered rocks surrounding tunnel: A review. J. Rock Mech. Geotech. Eng. 2025. in Press. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Zhou, X.; Yang, Q.; Chen, P.; de la Fuente, A.; Ren, L.; Du, L.; Han, Y.; Xiong, F.; et al. Main engineering problems and countermeasures in ultra-long-distance rock pipe jacking project: Water pipeline case study in Chongqing. Tunn. Undergr. Space Technol. 2022, 123, 104420. [Google Scholar] [CrossRef]
- Zhang, H.-Y.; He, B.-G.; Meng, X.-R.; Guan, J.-H.; Xu, H.-W. Wave-absorbing grouting for mitigating rockbursts triggered by multi dynamic disturbances in deep tunnels. Tunn. Undergr. Space Technol. 2026, 168, 107213. [Google Scholar] [CrossRef]
- Pan, P.Z.; Tan, F.Y.; Li, F.Q.; Chi, F.D.; Liu, X.F.; Wang, Z.F. A three-dimensional numerical study on the stability of layered rock spillway tunnels in alpine canyon areas. Deep Resour. Eng. 2024, 1, 100023. [Google Scholar] [CrossRef]
- Wang, H.; Ren, F.Q.; Chang, Y. Effect of bedding angle on tunnel slate failure behavior under indirect tension. Geomat. Nat. Hazards Risk 2020, 11, 428–445. [Google Scholar] [CrossRef]
- Assefa, E.; Tilahun, K.; Assefa, S.M.; Jilo, N.Z.; Pantelidis, L.; Sachpazis, C. Stability evaluation of tunnels in steeply dipping layered rock mass using numerical models: A case study. Sci. Rep. 2025, 15, 2046. [Google Scholar] [CrossRef]
- Wu, C.; Xia, H.; Qin, D.; Luo, J. Tunnel entrance crossing spoil heap deformations control by micropile combine with coupling beams. Geohazard Mech. 2024, 2, 21–28. [Google Scholar] [CrossRef]
- Denisova, E.V.; Khmelinin, A.P.; Sokolov, K.O.; Konurin, A.I.; Voitenko, A.A. Complex analysis of GPR signals to control contact zone of concrete lining and rock mass. Geohazard Mech. 2025, 3, 197–205. [Google Scholar] [CrossRef]
- Zhang, X.; Lin, X.; Zhang, W.; Feng, Y.; Lan, W.; Da, Y.; Hu, K. Intelligent recognition of voids behind tunnel linings using deep learning and percussion sound. J. Intell. Constr. 2023, 1, 9180029. [Google Scholar] [CrossRef]
- Luo, L.; He, M.; Li, G. Viscoelastic solution of optimal reserved deformation for deep soft rock tunnels with large deformation. Geohazard Mech. 2024, 2, 83–94. [Google Scholar] [CrossRef]
- Deng, Z.; Liang, N.; Liu, X.; de la Fuente, A.; Lin, P.; Peng, H. Analysis and application of friction calculation model for long-distance rock pipe jacking engineering. Tunn. Undergr. Space Technol. 2021, 115, 104063. [Google Scholar] [CrossRef]
- Liu, B.; Han, Q.; Fu, C.; Zhang, G.; He, Y.; Li, W. Development and engineering application of intelligent management and control platform for the shield tunneling construction close to risk sources. J. Intell. Constr. 2024, 2, 9180018. [Google Scholar] [CrossRef]
- Shi, C.; Tao, L.J.; Ding, P.; Wang, Z.G.; Jia, Z.B.; Shi, M. Analytical solution for deep non-circular tunnels considering slippage effects under far-field seismic SV waves. Tunn. Undergr. Space Technol. 2024, 144, 105552. [Google Scholar] [CrossRef]
- Wang, E.T.; Wang, H.N.; Jia, X.C. New analytical solutions for stress and displacement in deeply buried noncircular tunnels incorporating the influence of seepage flow. Appl. Math. Model. 2025, 142, 115990. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, S.; Chen, W.; Peng, Y. Analytical method for the vertical response of existing shield tunnel induced by above-crossing multiple parallel pipe jacking. Tunn. Undergr. Space Technol. 2025, 165, 106873. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problems of the Mathematical Theory of Elasticity; Noordhoff: Groningen, The Netherlands, 1963. [Google Scholar]
- Lu, A.Z.; Zhang, N.; Wang, S.J.; Zhang, X.L. Analytical Solution for a Lined Tunnel with Arbitrary Cross Sections Excavated in Orthogonal Anisotropic Rock Mass. Int. J. Geomech. 2017, 17, 04017044. [Google Scholar] [CrossRef]
- Mabe Fogang, P.; Liu, Y.; Zhao, J.L.; Ka, T.A.; Xu, S. Analytical Prediction of Tunnel Deformation Beneath an Inclined Plane: Complex Potential Analysis. Appl. Sci. 2023, 13, 3252. [Google Scholar] [CrossRef]
- Verruijt, A. A Complex Variable Solution for a Deforming Circular Tunnel in an Elastic Half-Plane. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 77–89. [Google Scholar] [CrossRef]
- Ai, Z.Y.; Pan, Y.X.; Ye, Z.K.; Wang, D.S. Stress and Displacement Fields of Elliptical Tunnels in Fractional Order Viscoelastic Transversely Isotropic Medium. Int. J. Numer. Anal. Methods Geomech. 2025, 1, 3917–3930. [Google Scholar] [CrossRef]
- Yan, Q.; Xu, B.S.; Yuan, Y. A Closed-Form Elastic Solution of Ground Response Curve for Noncircular Openings. Int. J. Geomech. 2021, 21, 04021235. [Google Scholar] [CrossRef]
- Yang, G.B.; Zhang, C.P.; Cai, Y.; Min, B. Complex Analysis of Ground Deformation and Stress for a Shallow Circular Tunnel with a Cavern in the Strata considering the Gravity Condition. KSCE J. Civ. Eng. 2019, 23, 4141–4153. [Google Scholar] [CrossRef]
- Zhang, D.L.; Xu, T.; Fang, H.C.; Fang, Q.; Cao, L.Q.; Wen, M. Analytical modeling of complex contact behavior between rock mass and lining structure. J. Rock Mech. Geotech. Eng. 2022, 14, 813–824. [Google Scholar] [CrossRef]
- Jia, X.C.; Wang, H.N.; Song, F.; Rodriguez-Dono, A. Theoretical analysis of stresses and displacements of twin tunnels excavated in saturated ground. Transp. Geotech. 2025, 50, 101449. [Google Scholar] [CrossRef]
- Zeng, G.S.; Wang, H.N.; Wu, L.; Jiang, M.J. A Generalized Analytical Model for Mechanical Responses of Rock during Multiple-Tunnel Excavation in Viscoelastic Semi-Infinite Ground. Int. J. Geomech. 2021, 147, 04021051. [Google Scholar] [CrossRef]
- Zeng, G.S.; Wang, H.N.; Jiang, M.J. Analytical stress and displacement of twin noncircular tunnels in elastic semi-infinite ground. Comput. Geotech. 2023, 160, 105520. [Google Scholar] [CrossRef]
- Wang, E.T.; Wang, H.N.; Song, F.; Jia, X.C. Analytical solutions for lined noncircular tunnels in deep ground considering hydromechanical coupling. Geomech. Geophys. Geo-Energy Geo-Resour. 2024, 10, 197. [Google Scholar] [CrossRef]
- Gao, X.; Wang, H.N.; Jiang, M.J.; Hu, T. A semi-analytical approach for the stress and displacement around lined circular tunnels at shallow depths. Eur. J. Environ. Civ. Eng. 2022, 27, 3449–3472. [Google Scholar] [CrossRef]
- Yu, H.T.; Chen, G. Pseudo-static simplified analytical solution for seismic response of deep tunnels with arbitrary cross-section shapes. Comput. Geotech. 2021, 137, 104306. [Google Scholar] [CrossRef]
- Chen, G.; Yu, H.T.; Bobet, A. Analytical Solution for Seismic Response of Deep Tunnels with Arbitrary Cross-Section Shape in Saturated Orthotropic Rock. Rock Mech. Rock Eng. 2022, 55, 5863–5878. [Google Scholar] [CrossRef]
- Fang, H.C.; Zhang, D.L.; Fang, Q.; Wen, M. A generalized complex variable method for multiple tunnels at great depth considering the interaction between linings and surrounding rock. Comput. Geotech. 2021, 129, 103891. [Google Scholar] [CrossRef]
- Fang, H.C.; Zhang, D.L.; Wen, M.; Hu, X.Y. A non-iterative analytical method for mechanical analysis of surrounding rock with arbitrary shape holes. Chin. J. Rock Mech. Eng. 2020, 39, 2204–2212. [Google Scholar] [CrossRef]
- Fang, H.C.; Zhang, D.L.; Huang, C.J.; Fang, Q.; Zhou, M.Z.; Cao, L.Q. Analytical method for mechanical analysis of multiple shallow tunnels with concrete linings. Appl. Math. Model. 2023, 116, 749–762. [Google Scholar] [CrossRef]
- Fang, H.C.; Zhang, D.L.; Fang, Q. A semi-analytical method for frictional contact analysis between rock mass and concrete linings. Appl. Math. Model. 2022, 105, 17–28. [Google Scholar] [CrossRef]
- Liu, X.; Fang, H.C.; Jiang, A.N.; Zhang, D.L.; Fang, Q.; Lu, T.; Bai, J.R. Mechanical behaviours of existing tunnels due to multiple-tunnel excavations considering construction sequence. Tunn. Undergr. Space Technol. 2024, 152, 105870. [Google Scholar] [CrossRef]
- Hong, X.F.; Zhang, D.L.; Sun, Z.Y. Mechanical responses of multi-layered ground due to shallow tunneling with arbitrary ground surface load. Front. Struct. Civ. Eng. 2023, 17, 745–762. [Google Scholar] [CrossRef]
- Sun, Z.Y.; Zhang, D.L.; Fang, H.C.; Hong, X.F. Generalized complex variable analysis of shallow tunneling through multi-layered ground. Appl. Math. Model. 2024, 125, 230–259. [Google Scholar] [CrossRef]
| Normal contact properties between the surrounding rock and the concrete lining | ||
| Tightly bonded normal contact | (33) | |
| (34) | ||
| Tangential contact properties between the surrounding rock and the concrete lining | ||
| Smooth tangential contact | (35) | |
| Fully bonded tangential contact | (36) | |
| (37) | ||
| Inner boundary of the concrete lining: B01 | Interface between surrounding rock and concrete lining: B23-B01 | Interface between rock strata: B21-B11 | |
| σρ | 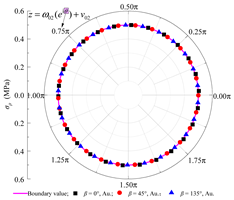 | 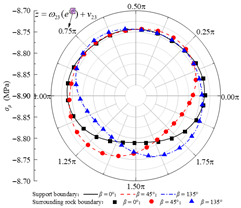 | 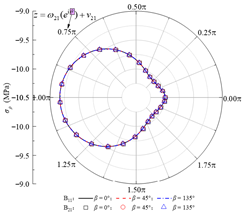 |
| τρθ | 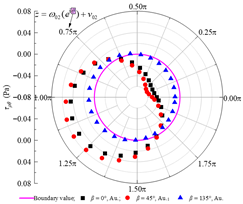 | 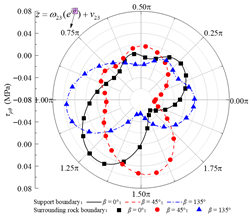 | 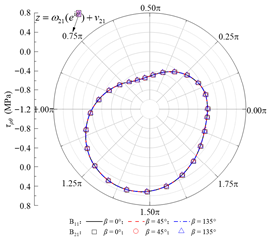 |
| uρ |  |  | |
| uθ | 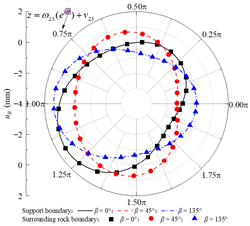 | 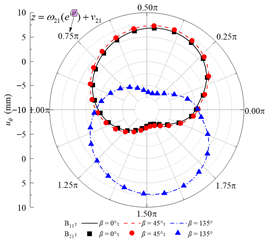 |
| Inner boundary of the concrete lining: B01 | Interface between surrounding rock and concrete lining: B23-B01 | Interface between rock strata: B21-B11 | |
| σρ | 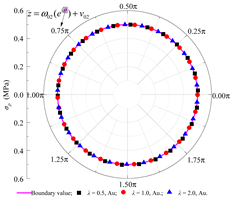 | 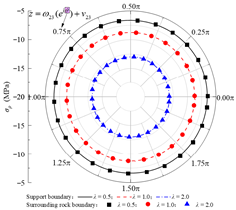 | 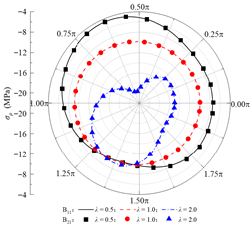 |
| τρθ | 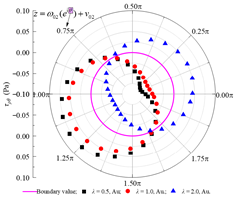 | 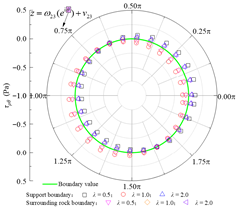 | 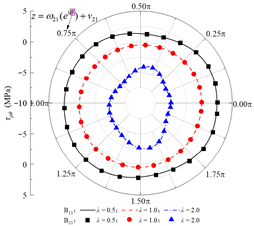 |
| uρ | 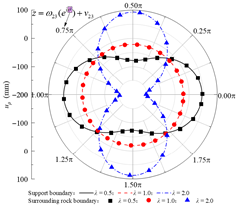 | 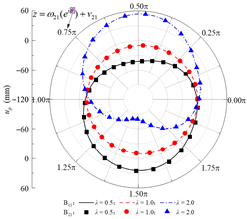 | |
| uθ | 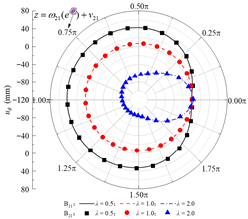 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, X.; Lin, P.; Liu, H.; Zhang, Z.; Xia, Y.; Deng, Z. Complex Predictions for Stress and Displacement of Deep Buried Tunnels with Concrete Lining in Parallel Inclined Multi-Layered Surrounding Rocks. Appl. Sci. 2025, 15, 13052. https://doi.org/10.3390/app152413052
Hong X, Lin P, Liu H, Zhang Z, Xia Y, Deng Z. Complex Predictions for Stress and Displacement of Deep Buried Tunnels with Concrete Lining in Parallel Inclined Multi-Layered Surrounding Rocks. Applied Sciences. 2025; 15(24):13052. https://doi.org/10.3390/app152413052
Chicago/Turabian StyleHong, Xuefei, Peng Lin, Haiyan Liu, Zongliang Zhang, Yong Xia, and Zhiyun Deng. 2025. "Complex Predictions for Stress and Displacement of Deep Buried Tunnels with Concrete Lining in Parallel Inclined Multi-Layered Surrounding Rocks" Applied Sciences 15, no. 24: 13052. https://doi.org/10.3390/app152413052
APA StyleHong, X., Lin, P., Liu, H., Zhang, Z., Xia, Y., & Deng, Z. (2025). Complex Predictions for Stress and Displacement of Deep Buried Tunnels with Concrete Lining in Parallel Inclined Multi-Layered Surrounding Rocks. Applied Sciences, 15(24), 13052. https://doi.org/10.3390/app152413052







