Parameter Calibration and Experimentation of the Discrete Element Model for Mixed Seeds of Vetch (Vicia villosa) and Oat (Avena sativa) in a Pneumatic Seed Drilling System

Abstract

This paper focuses on mixed seeds of Vicia villosa and Avena sativa, with their discrete element model and contact parameters being systematically calibrated and validated to provide reliable theoretical support for the structural design and parameter optimization of the air-assisted seed delivery system. The physical properties of both seed types, including triaxial dimensions, density, moisture content, Poisson’s ratio, and shear modulus, were first measured. The Hertz–Mindlin (no slip) contact model and the multi-sphere aggregation method were employed to construct the discrete element models of Vicia villosa and Avena sativa, with preliminary calibration of the intrinsic model parameters. Poisson’s ratio, elastic modulus, collision restitution coefficient, static friction coefficient, and rolling friction coefficient between the seeds and PLA plastic plate were determined through uniaxial compression, free fall, inclined sliding, and inclined rolling tests. Each test was repeated five times, and the calibration criterion for contact parameters was based on minimizing the relative error between simulation and experimental results. Based on this, experiments on the packing angle of mixed seeds, steepest slope, and a three-factor quadratic rotational orthogonal combination were conducted. The inter-seed collision restitution coefficient, static friction coefficient, and rolling friction coefficient were set as the experimental factors. A total of 23 treatments were designed with repetitions at the center point, and a regression model was established for the relative error of the packing angle with respect to each factor. Based on the measured packing angle of 28.01° for the mixed seeds, the optimal contact parameter combination for the mixed seed pile was determined to be: inter-seed collision restitution coefficient of 0.312, static friction coefficient of 0.328, and rolling friction coefficient of 0.032. The relative error between the simulated packing angle and the measured value was 1.32%. The calibrated inter-seed contact parameters were further coupled into the EDEM–Fluent gas–solid two-phase flow model. Simulations and bench verification tests were carried out under nine treatment combinations, corresponding to three fan speeds (20, 25, and 30 m·s⁻¹) and three total transport efficiencies (12.5, 17.5, and 22.5 g·s⁻¹), with the consistency coefficient of seed distribution in each row being the main evaluation variable. The results showed that the deviation in the consistency coefficient of seed distribution between the simulation and experimental measurements ranged from 1.24% to 3.94%. This indicates that the calibrated discrete element model for mixed seeds and the EDEM–Fluent coupled simulation can effectively reproduce the air-assisted seed delivery process under the conditions of Vicia villosa and Avena sativa mixed sowing, providing reliable parameters and methodological support for the structural design of seeders and DEM-CFD coupled simulations in legume–grass mixed sowing systems.

1. Introduction

Inter-seeding of legume and grass forages is recognized as an important cultivation strategy that leverages complementary traits; relative to monoculture, it significantly increases forage yield and quality [1,2] and enhances the economic value of the soil resource and overall production efficiency [3]. Among commonly used legume–grass mixtures, mixed sowing of vetch and oat exhibits a pronounced quality-complementarity effect. It has been shown that the mixing ratio is the primary determinant of forage yield [4,5,6]. When vetch and oat seeds are combined at a 4.5:5.5 ratio, higher dry-matter proportions and improved forage quality are achieved [7]. However, substantial differences in particle shape, size, and physical properties between legume and grass seeds complicate the calibration of physical parameters for seed mixtures; in particular, accurately reproducing motion and contact behaviors in discrete element method (DEM) simulations remains a pressing technical challenge.

With the development of computer technology, the Discrete Element Method (DEM) has been widely applied to analyze particle motion mechanisms and optimize seed metering devices [8,9,10]. It has been proven to be an effective tool for studying the working mechanism of seed metering devices and the movement characteristics of seed particles [11,12]. In the process of computer simulation for seed placement, physical parameters such as seed density, size, moisture content, Poisson’s ratio, and shear modulus, as well as contact parameters such as restitution coefficient, static friction coefficient, and rolling friction coefficient, are key variables in determining particle collision, sliding, and rolling behaviors [9,13]. Since the contact parameters between particles are difficult to obtain through actual experiments, the calibration and optimization of DEM contact parameters are particularly important. The calibration of discrete element method (DEM) contact parameters is an effective approach for obtaining the physical parameters of particulate materials. Hu et al. [9], Shi [13], and Yong [14] have, respectively, calibrated the elastic modulus and Poisson’s ratio for cotton and watermelon seeds. Chen et al. [15] and Wang et al. [16] conducted systematic experiments on the restitution coefficient and static friction coefficient for potato tubers and red pine seeds. Zhou et al. [17], Cao et al. [18], and Zhang et al. [19] calibrated the rolling friction coefficient through angle of repose or material flow tests. The results indicate that a reasonable combination of contact parameters can significantly improve the simulation accuracy of DEM for angle of repose and seed placement performance. Binnan Zhou et al. [20] utilized bonding bonds and the Hertz–Mindlin model to achieve high-precision simulations of walnut behavior during crushing and bending tests. Zhu et al. [21] constructed a discrete element method (DEM) model for edible sunflower seeds and validated its reliability through seeding and transport tests. Li et al. [22] and Adilet Sugirbay et al. [23], respectively, completed the calibration of contact parameters for maize and wheat seeds, providing important references for simulations of air seeding or mechanized operations for different crops. Although the aforementioned methods provide insights for this study, significant differences in physical characteristics such as size and shape exist between Malva sylvestris and oat seeds, and there is currently a lack of systematic research on their contact parameters, which limits the optimization of seeders under mixed planting conditions. In terms of constructing discrete element models, researchers generally begin with actual sizes and shapes to enhance the model’s realism. For example, Guopeng Mi et al. [24] extracted the outline of sorghum seeds using 3D scanning and developed a discrete element method (DEM) model for sorghum seeds using the spherical particle filling method in EDEM software, demonstrating that the model exhibits high accuracy in simulating sorghum packing and transport behaviors. Wang et al. [25] and Shi et al. [26] proposed a modeling strategy combining multiple spheres and polyhedra for sunflower seeds and maize kernels, respectively, and validated the model’s applicability through angle of repose and flow tests. Li et al. [27] and Chen et al. [28] compared assembly modeling methods under various combinations of particle shapes and sizes, using buckwheat and maize as research subjects, and demonstrated that reasonably simplified particle combinations can maintain shape characteristics while also ensuring computational efficiency. The aforementioned studies indicate that simulating real particle shapes through methods such as multi-sphere or polyhedron packing, combined with accurate contact parameter calibration, is an effective approach to improving the quality and computational efficiency of DEM simulations. Existing work has predominantly focused on the calibration of physical and contact parameters for individual crop seeds, while systematic studies on mixed seed systems with significant differences in particle shape and density, particularly legume–grass seed mixtures, remain limited.

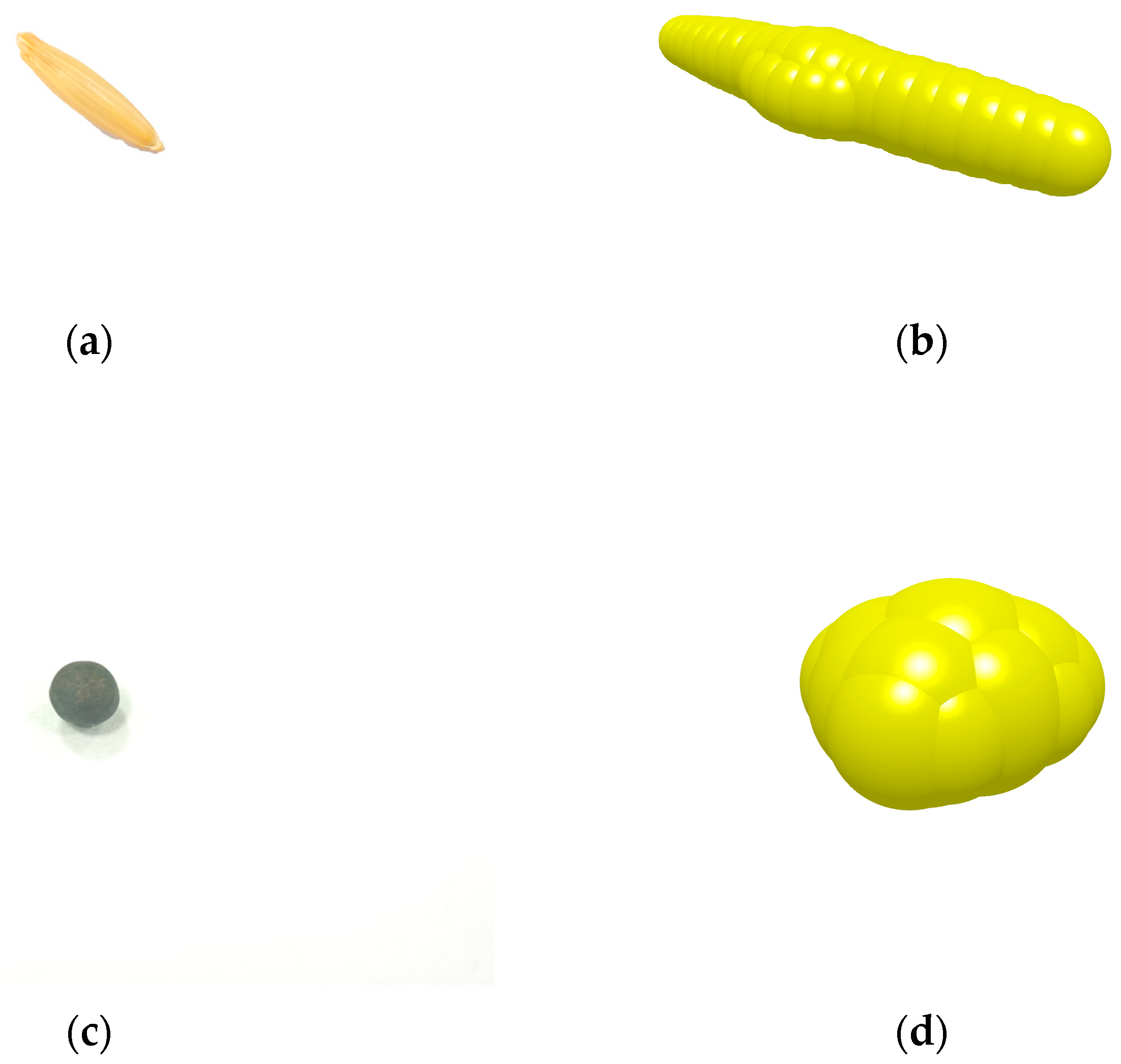
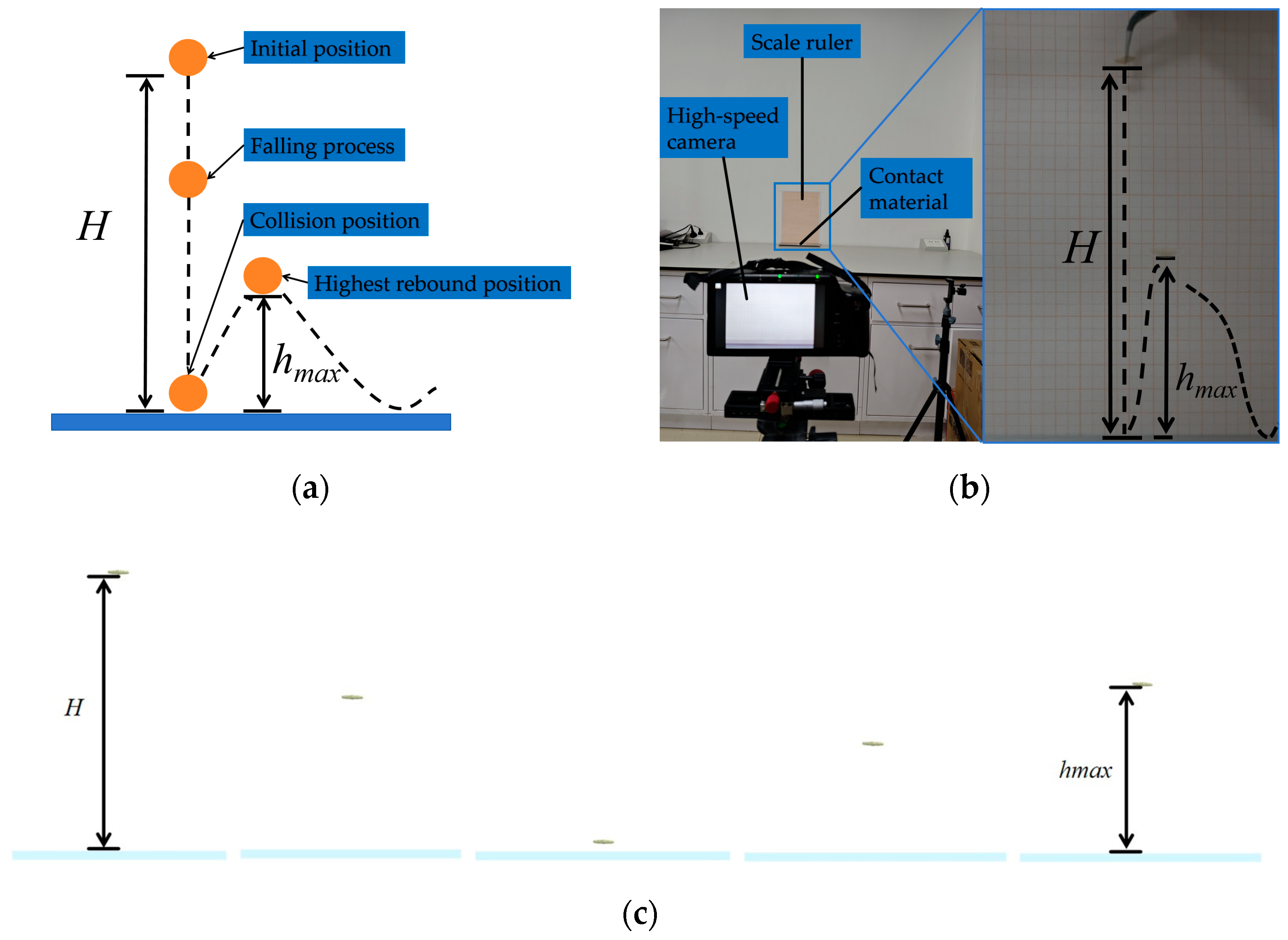
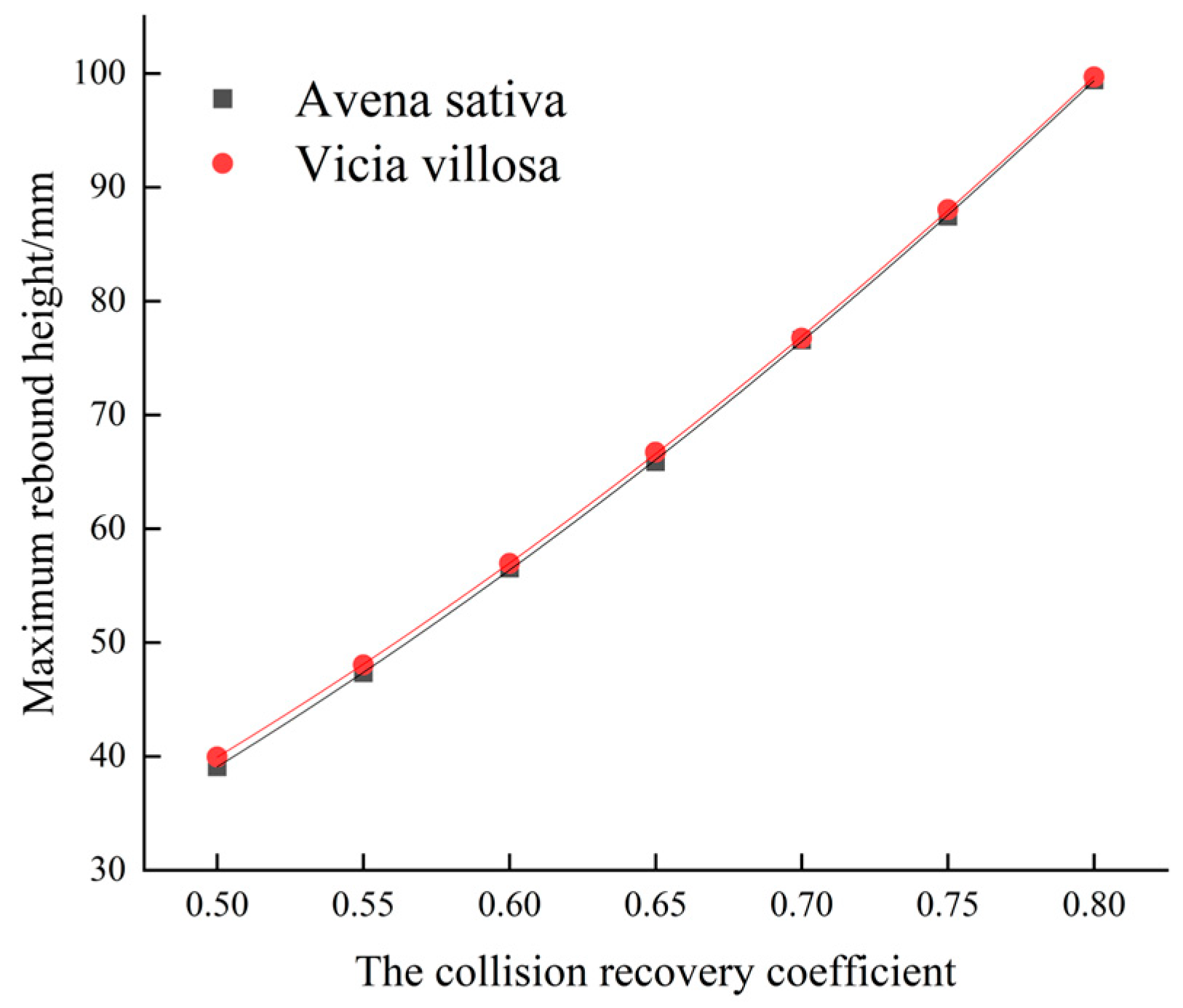
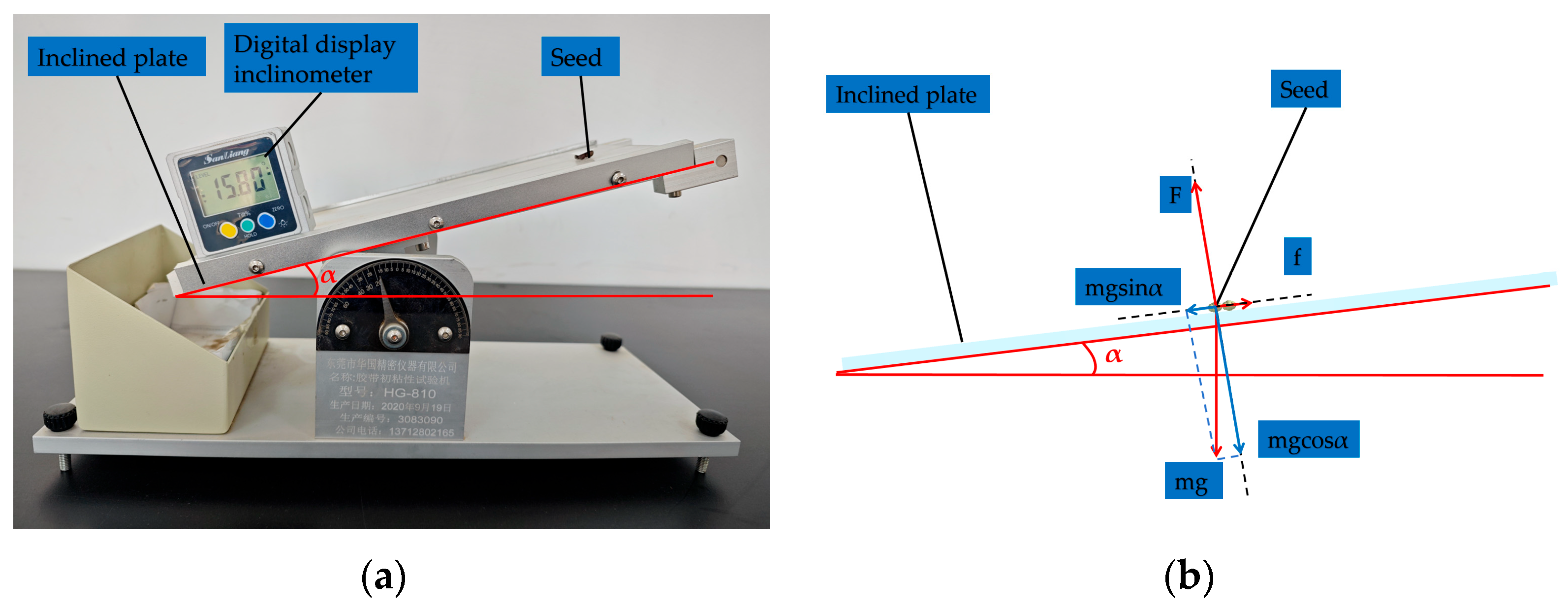
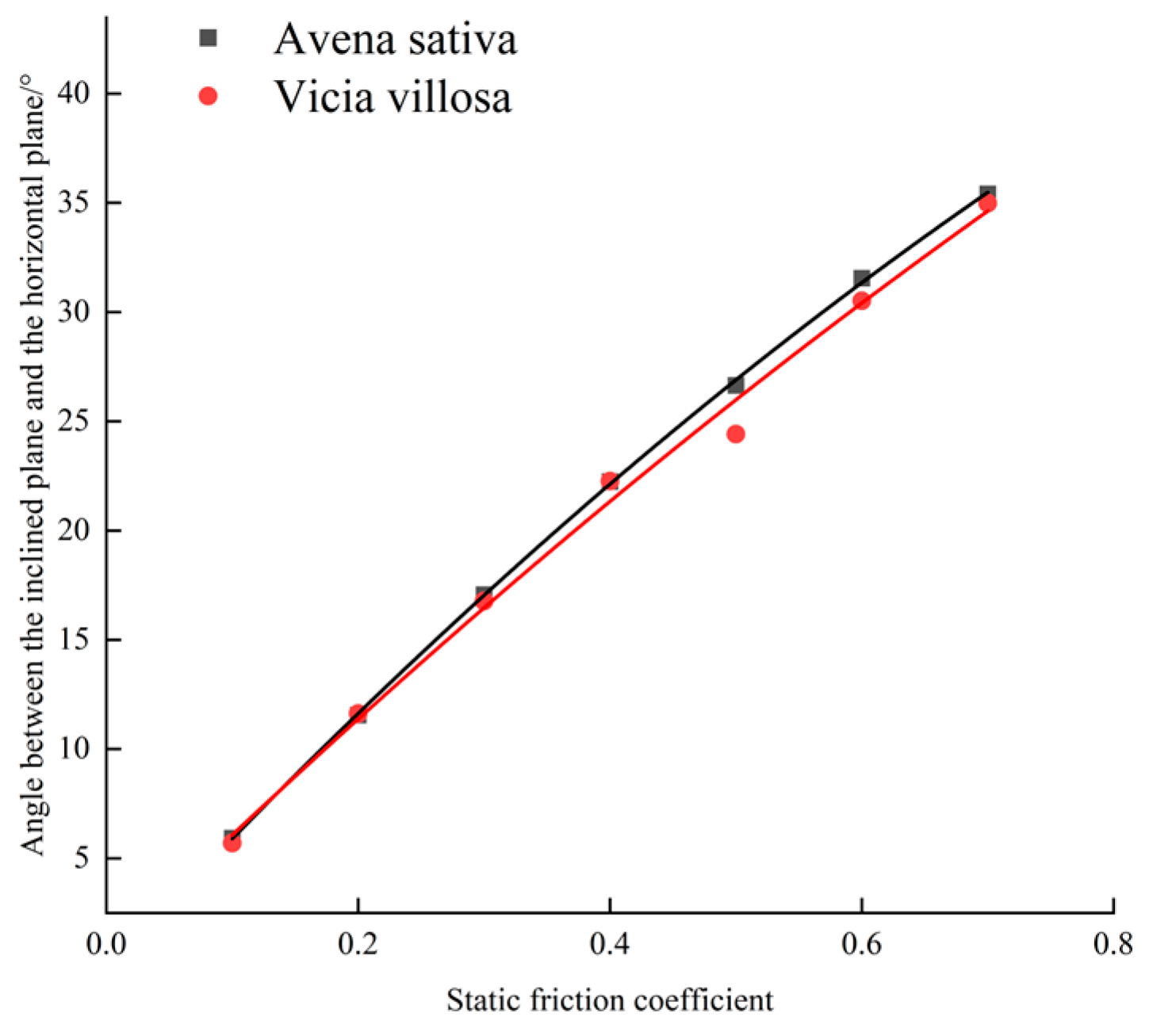
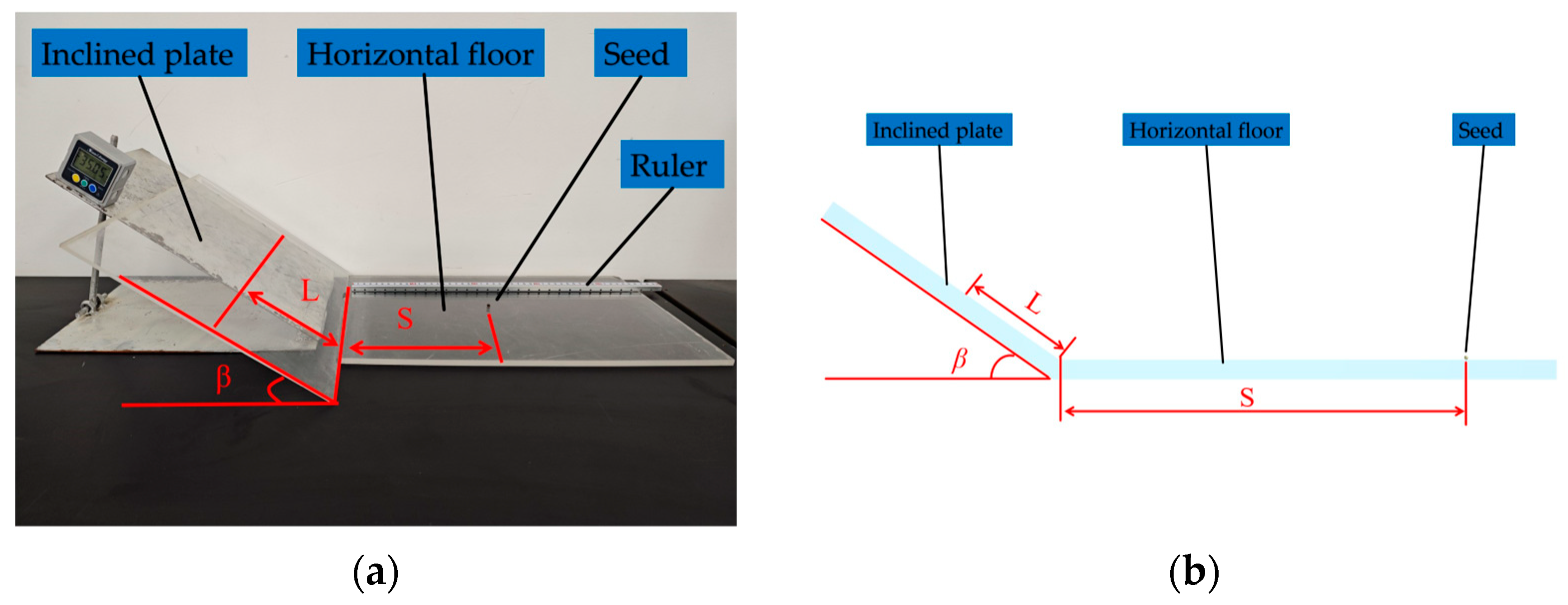
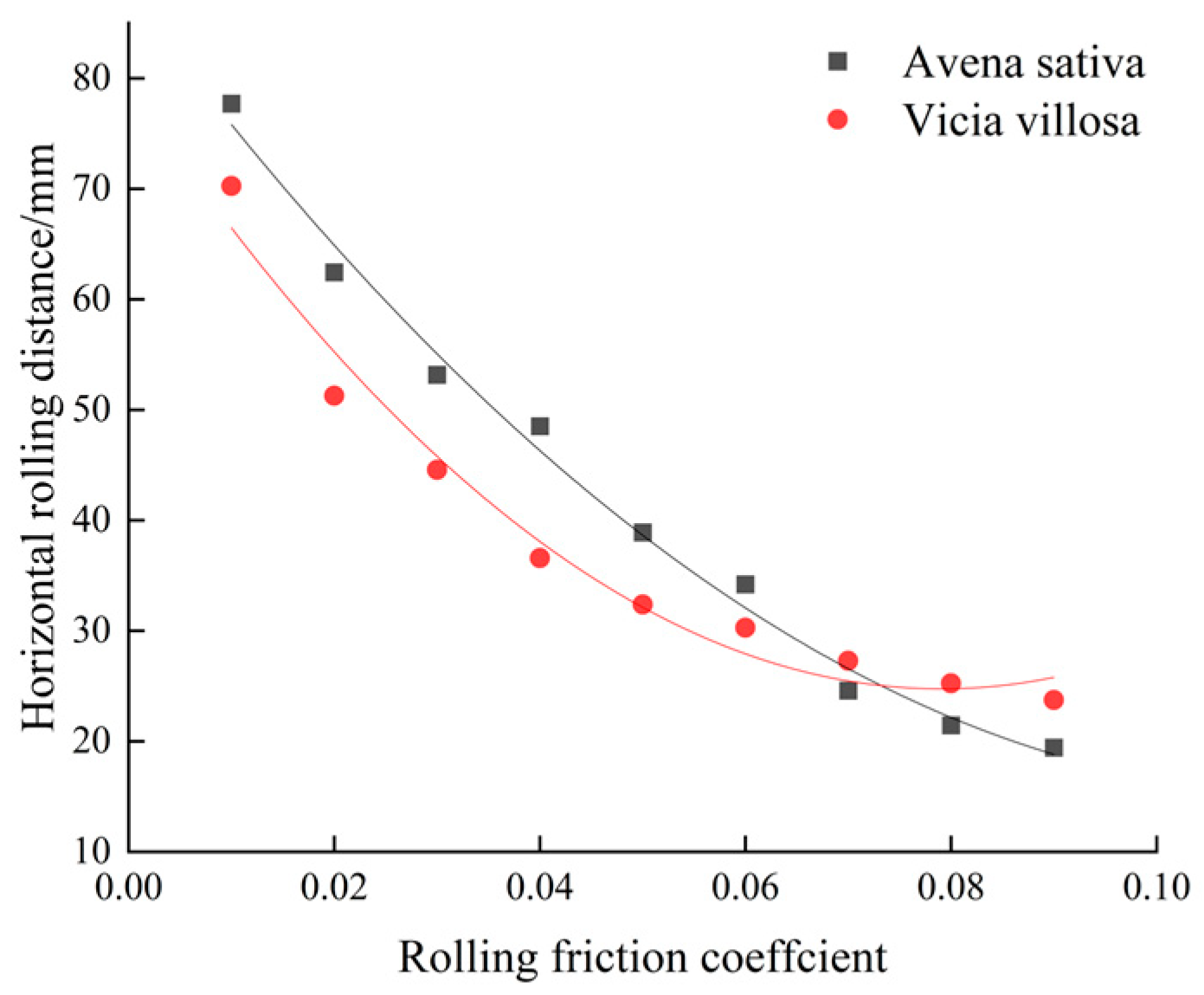
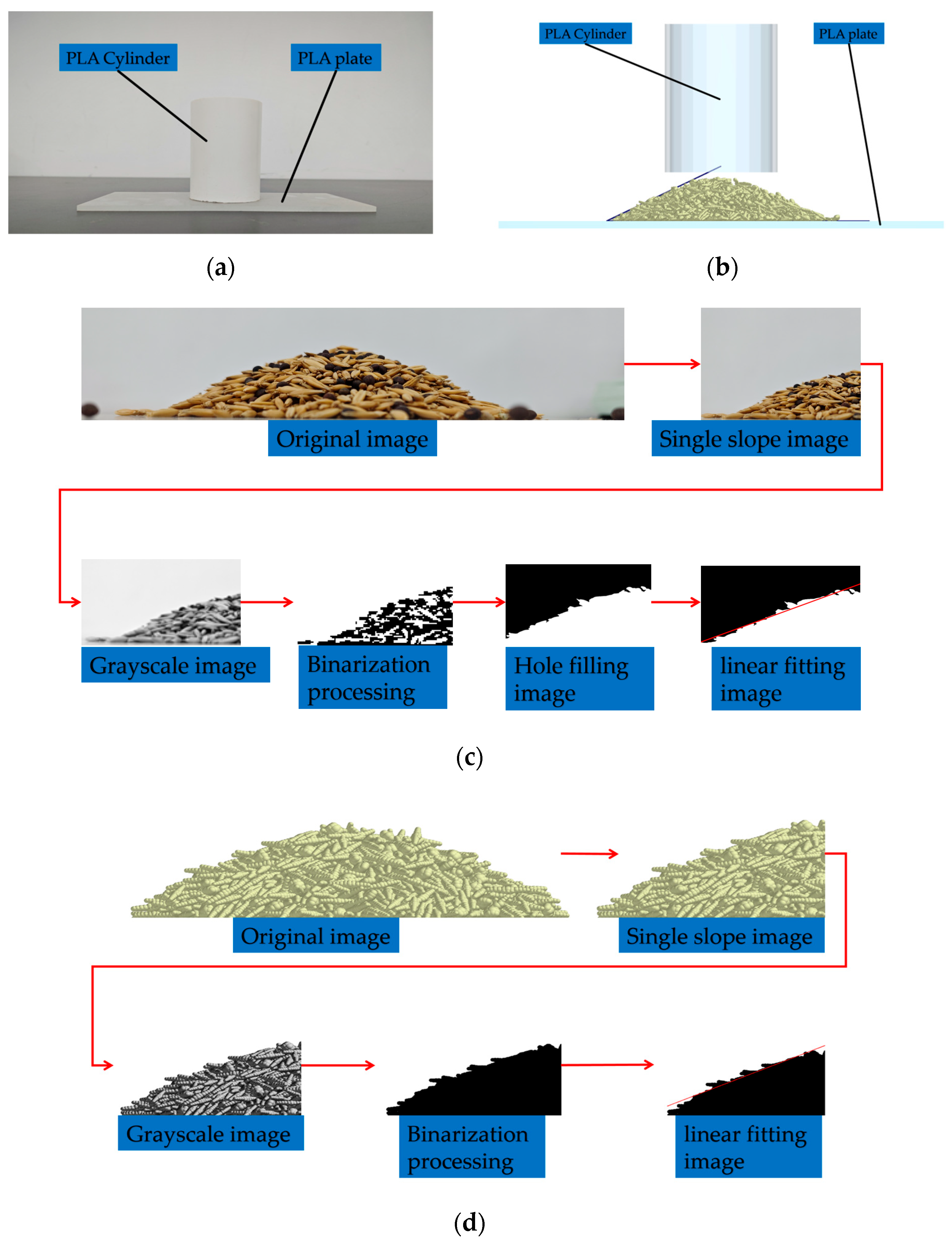
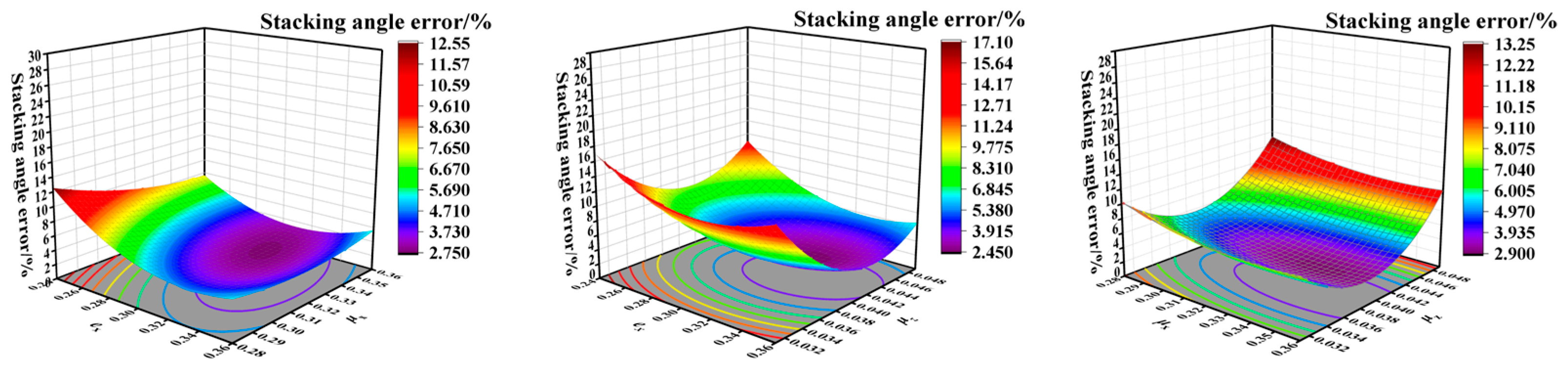
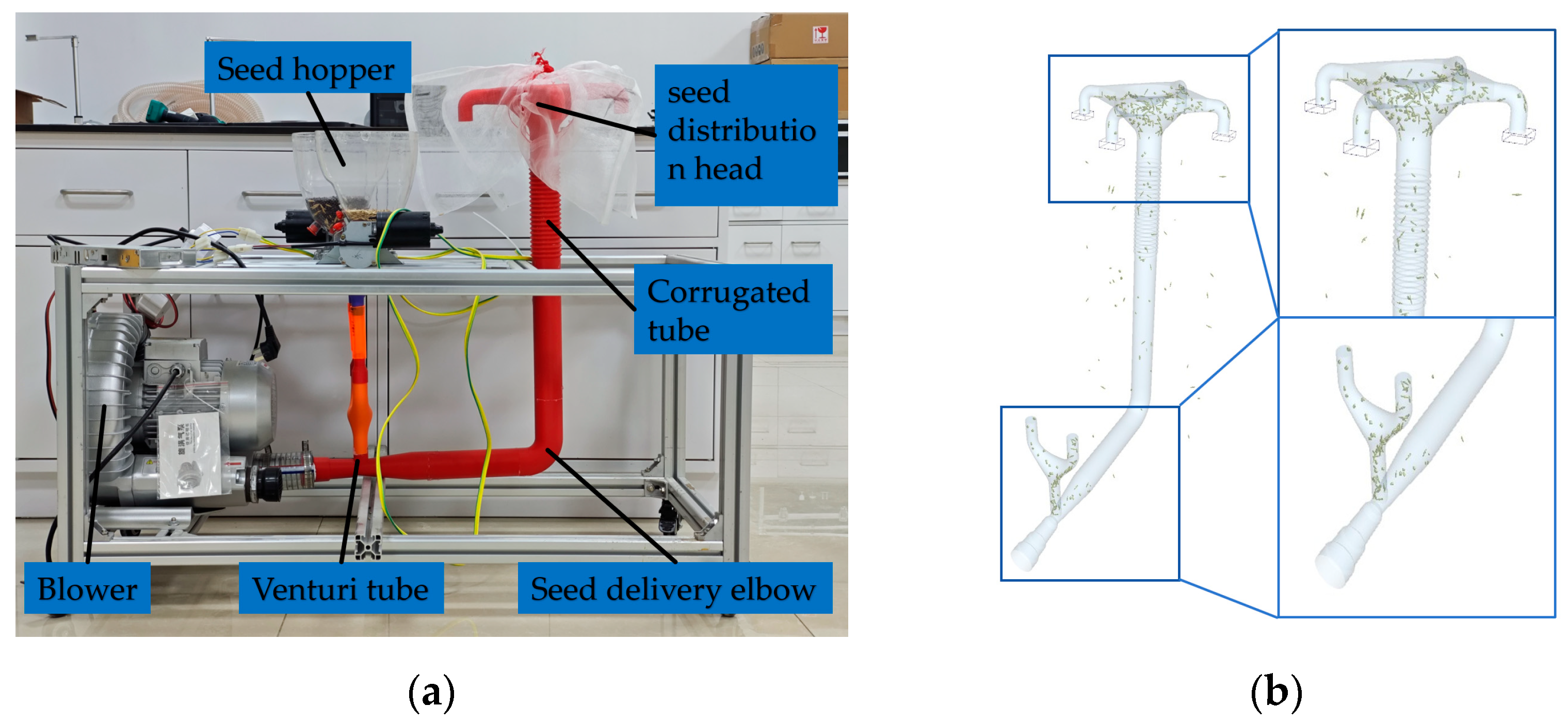
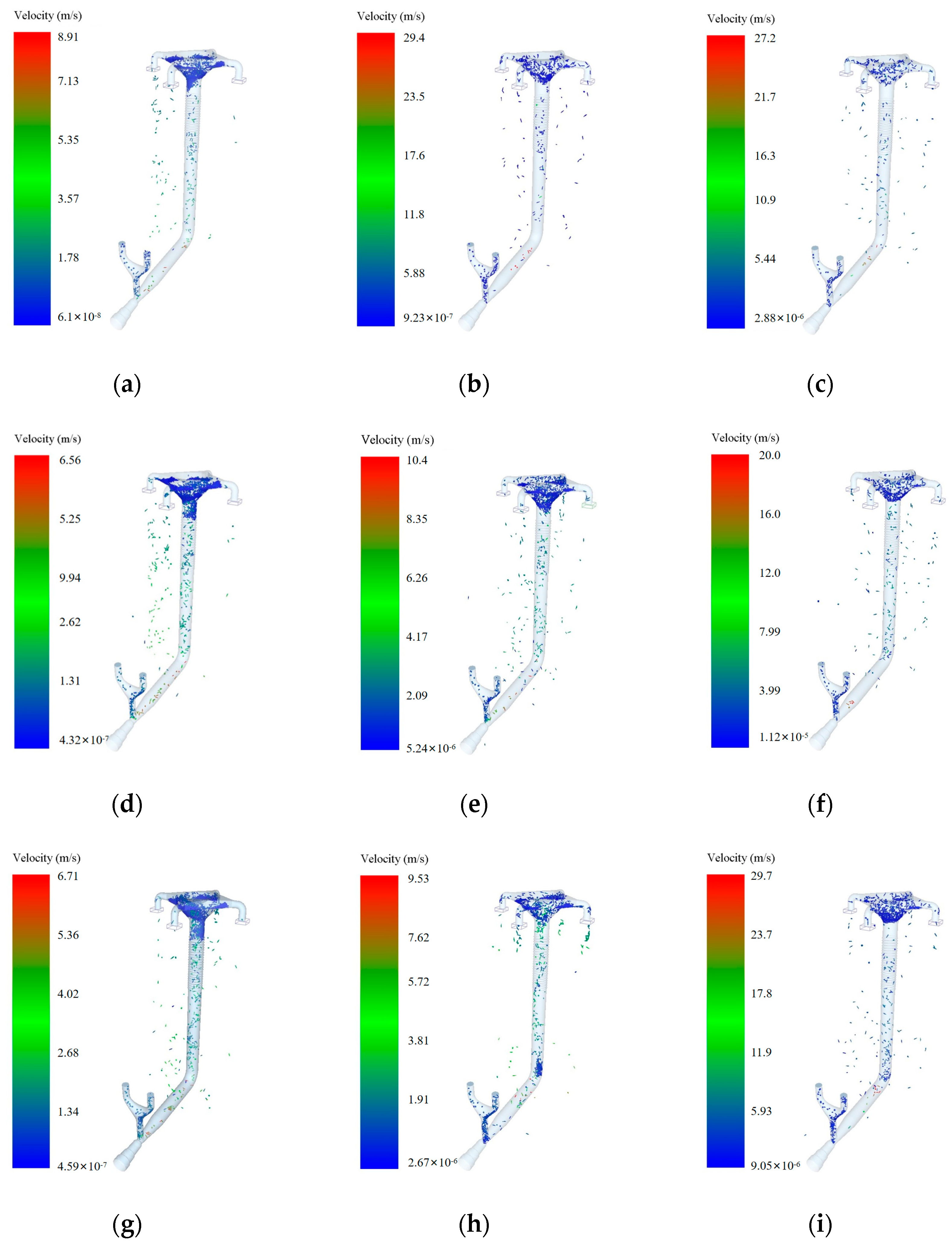
Based on the current research and technological needs, this study focuses on Malva sylvestris and oat seeds as research subjects. First, physical parameters such as triaxial dimensions, thousand-grain weight, density, moisture content, Poisson’s ratio, and shear modulus are measured to provide empirical data for the setting of particle geometry and elastic variables in the DEM model. Second, free fall, inclined plane sliding, and inclined plane rolling tests are conducted to calibrate the restitution coefficient, static friction coefficient, and rolling friction coefficient between the seeds and PLA material. Additionally, angle of repose tests and a two-level factorial design are used to optimize the response surface of contact parameter combinations for mixed seeds, with the goal of minimizing the relative error between simulated and measured values of the angle of repose to determine the optimal parameter set. On this basis, the DEM models of Malva sylvestris and oats are established using the multi-sphere manual packing method. These models are coupled with Fluent for gas–solid interaction simulations, and the calibrated contact parameters are applied to the simulation of air-assisted, collective seeders. The flow behavior of mixed seeds in the distributor under various inlet wind speeds and mass flow rate conditions, as well as the consistency of seed placement across rows, are systematically analyzed. Finally, by comparing with bench tests, the model’s predictive capability for key response variables such as angle of repose and seed placement variation coefficient is validated. This provides theoretical guidance and data support for the selection of DEM parameters and the structural optimization of pneumatic seeders for seed systems with significant morphological differences in legume–grass mixed sowing.

2. Materials and Methods

2.1. Intrinsic Parameter Determination and Model Establishment

2.1.1. Measurement of the Physical Parameters of Vetch (Vicia villosa) and Oat (Avena sativa) Seeds

The experimental materials used in this study include vetch variety “Xushao No. 1” and oat variety “Menglong,” both provided by Beijing Best Grass Industry Co., Ltd. (Beijing, China). These varieties are commonly used in legume–grass mixed-seeding combinations for pasture and green manure, characterized by high yield and strong disease resistance. The physical parameters of vetch and oat seeds primarily include shape and size (length × width × thickness), thousand-grain weight, density, moisture content, Poisson’s ratio, and shear modulus. These physical parameters were measured using instruments such as an electron microscope (TD-4KHU, Chinese San Jiang Tai Da company, Wenzhou, China), electronic balance (LPS-5003, Chinese Lianpusen company, Shenzhen, China), graduated cylinder, and inclinometer (HG-810, Wuhan Huaguang Optoelectronic Company, Wuhan, China), while the shear modulus and Poisson’s ratio were measured using a texture analyzer (TMS-Pro, American FTC Company, Sterling, VA, USA).

A random sample of 100 seeds each of vetch and oat was selected. The tri-axial dimensions were measured using a (Chinese San Jiang Tai Da company, TD-4KHU)electron microscope; the mean tri-axial dimensions were 3.45 mm × 3.31 mm × 3.16 mm for Vetch and 11.86 mm × 3.11 mm × 2.51 mm for Oat. For mass determination, 1000 seeds of each species were weighed on an electronic balance (precision 0.001 g) with five replicates; the mean thousand-seed mass was 69.06 g for Vetch and 43.77 g for Oat. Seed density was measured by the displacement method, with five replicates averaged; the mean densities were 1316.4 kg/m³ for Vetch and 1032.1 kg/m³ for Oat. The moisture content of the seeds was measured using a digital blast drying oven (GZX-9246 MBE, Chinese Shanghai Bosun Medical Biological Instrument Co., Ltd., Shanghai, China). The seeds were dried at 105 °C for 12 h, and the change in seed mass before and after drying was measured. The experiment was repeated five times, resulting in a moisture content of 3.10% for vetch seeds and 3.68% for oat seeds, as shown in

Table 1. Comparison of Physical Parameters Between Hairy Vetch and Oat Seeds.

Types	Vetch (Vicia villosa)	Oat (Avena sativa)
Triaxial Dimensions/mm	3.45 × 3.31 × 3.16	11.86 × 3.11 × 2.51
Thousand-grain weight/g	69.06	43.77
Density/(kg·m−3)	1316.4	1032.1
Moisture content/%	3.10	3.68

.

2.1.2. Poisson Ratio

Poisson’s ratio is one of the key parameters in the simulation process, representing the ratio of lateral strain to longitudinal strain when a material is subjected to tensile or compressive forces. It plays a significant role in revealing the elastic behavior of seeds under mechanical stress [13,14]. A uniaxial compression test was performed using a texture analyzer (type: TMS-Pro) to measure the Poisson’s ratio of vetch and oat seeds, as shown in Figure 1. During the experiment, a 36 mm diameter aluminum circular probe was applied along the seed thickness direction. The initial force was set at 1 N, with a loading speed of 10 mm/min and a compression distance of 0.25 mm. After compression, the width and thickness of the seeds were measured using a digital vernier caliper with an accuracy of 0.01 mm. The test was repeated five times, and the average values were calculated. Using Equation (1), the Poisson’s ratios of vetch and oat seeds were determined to be 0.23 and 0.35, respectively.

$${\mu }_m=\left|{\displaystyle \frac{{\epsilon }_x}{{\epsilon }_y}}\right|={\displaystyle \frac{∆L/L}{∆H/H}}$$

(1)

In the equation, μ_m represents Poisson’s ratio, εₓ is the lateral strain of the seed, ε_y is the longitudinal strain of the seed particle, with units in mm; ∆L is the lateral absolute deformation of the seed, with units in mm, and ∆H is the absolute deformation of the seed in the thickness direction, with units in mm; L is the original lateral length of the seed before compression, with units in mm; H is the original height of the seed in the thickness direction before compression, with units in mm.

2.1.3. Shear Modulus

When the vetch and oat seeds come into contact with the seed metering device, they are subjected to shear forces. Therefore, determining the shear modulus is crucial for preventing seed damage in the seed metering device. Compression tests on the seeds were conducted using a texture analyzer (type: TMS-Pro), as shown in Figure 1. An aluminum 36 mm circular probe was used to compress the seeds along their thickness direction. The probe’s detection speed was set at 10 mm/min, and the load-displacement data were obtained through the texture analyzer software (TL-Pro 1 15-408) processing module [15,16]. The test was repeated five times. Using Equation (2), the elastic modulus for vetch and oat seeds was determined, and the shear modulus was then calculated using Equation (3). The elastic modulus of vetch was 2.60 × 10⁷ Pa, with a shear modulus of 1.06 × 10⁷ Pa, while the elastic modulus of oat was 5.88 × 10⁶ Pa, with a shear modulus of 2.27 × 10⁶ Pa.

$$E={\displaystyle \frac{f/s}{\epsilon }}$$

(2)

In the formula, E is the elastic modulus, measured in Pa; f is the maximum applied pressure, measured in N; s is the contact area, measured in m²; ε is the linear strain.

$$G={\displaystyle \frac{E}{2(1+\mu )}}$$

(3)

In the formula: G denotes the shear modulus of the seed, Pa; E denotes the elastic modulus of the seed, Pa.

2.1.4. Establishment of a Seed Discrete Element Model

The Discrete Element Method (DEM) models for vetch and oat seeds were established using EDEM 2022 software. Since vetch and oat seeds are irregular particles, it is challenging to construct a DEM model using individual particles. Therefore, a multi-sphere particle aggregation approach was employed to build the simulation model, which allows for a more accurate representation of the seed shape. The physical and DEM simulation models of vetch and oat seeds are shown in Figure 2. Due to the relatively low adhesive forces on the seed surface, the Hertz–Mindlin (no slip) contact model was selected for the seed particle contact model.

2.2. Calibration of Contact Parameters Between Seeds and PLA Material

2.2.1. Determination of Simulation Test Parameters

EDEM 2022 (Discrete Element Method) is a software specifically designed for simulating and analyzing particulate materials, widely used in the study of particle mechanical properties, flow characteristics, and mixing processes. The software is based on the Discrete Element Method (DEM), and by accurately simulating the interactions between particles, it can precisely reproduce behaviors such as motion, collisions, and friction under varying physical conditions. In this study, EDEM software is employed to simulate the state of seeds within the seed dispenser and the seeding process. By adjusting mechanical parameters of the particles (e.g., elastic modulus, friction coefficient, and density) and fluid dynamic parameters (e.g., collision and adhesion forces between particles), the flow and discharge of seeds within the dispenser are precisely analyzed. Such simulation analyses provide a scientific basis for optimizing the design of seed dispensers and improving crop planting efficiency. In the simulation experiments, both the PLA cylinder and PLA sheets used were modeled in 3D using SolidWorks 2020. During the experiment, in addition to the particle-to-particle contact between the mixed vetch and oat seeds, there was also interaction between these two seed types and the experimental materials. The contact materials selected for this study were PLA, a common material in 3D printing technology. The characteristic parameters for the interactions between vetch and oat seeds and the contact materials are shown in

Table 2. Simulation test parameters.

Materials	Parameter	Value
Vetch (Vicia villosa)	Poisson ratio	0.23
	Density/(kg·m−3)	1316.4
	Shear modulus/Pa	1.06 × 106
Oat (Avena sativa)	Poisson ratio	0.35
	Density/(kg·m−3)	1032.1
	Shear modulus/Pa	2.27 × 107
PLA	Poisson ratio	0.34
	Density/(kg·m−3)	1260.0
	Shear modulus/Pa	3 × 109

. The Poisson’s ratio and shear modulus for vetch and oat seeds were measured using a texture analyzer (type: TMS-Pro).

2.2.2. Collision Recovery Coefficient Calibration

The coefficient of restitution is an important parameter in particle studies, reflecting a particle’s ability to recover its original shape after a collision. In this experiment, the coefficient of restitution was determined using the free fall method [13]. During the experiment, tweezers were used to release the seeds at a height of H = 150 mm above the PLA plastic sheet. Upon contact with the PLA plastic sheet, the seeds rebounded, and the maximum rebound height h_max was recorded using a high-speed camera. According to Newton’s law of collision, the coefficient of restitution (e) is the ratio of the normal separation velocities at the contact point, v₁ and v₂. It can be calculated using the ratio of the maximum rebound height h_max to the initial fall height H, as given by the following formula:

$$e={\displaystyle \frac{v_1}{v_2}}=\sqrt{{\displaystyle \frac{{2gh}_{max}}{2gH}}}=\sqrt{{\displaystyle \frac{h_{max}}{H}}}$$

(4)

where e is the collision recovery coefficient, v₁ and v₂ are the seed velocity before and after collision, respectively, in m/s.

The coefficient of restitution between the seeds and the PLA plastic sheet was calibrated using the seed free fall collision method. The PLA plastic sheet was placed horizontally beneath the seeds, with graph paper used as a reference. The seeds were released naturally from a height of H = 150 mm. When the seeds made contact with the PLA plastic sheet and began to rebound, the maximum rebound height (h_max) was captured using a high-speed camera (Chinese, Shenzhen Sresen Electromechanical Equipment Co., Ltd., Shenzhen, China, Fastec TS3-100S). This process was repeated five times to calculate the average value. The experiment is shown in Figure 3.

Through actual experiments, the maximum rebound heights of vetch and oat seeds were found to be 9.7 cm and 7.8 cm, respectively. In the EDEM simulation experiments, to avoid interference from other factors, the coefficient of restitution for the seeds was set as the primary experimental variable, while all other contact parameters were set to zero. In the computer simulation experiments, the range for the coefficient of restitution between vetch and oat seeds and the PLA plastic sheet was set from 0.5 to 0.8, with an interval of 0.05. The simulation test design and results for the coefficient of restitution are detailed in

Table 3. Collision recovery coefficient between seeds and PLA plastic plates.

Serial Number	Collision Recovery Coefficient e	Maximum Rebound Height of Vetch (Vicia villosa) Seeds hmax1/mm	Maximum Rebound Height of Oat (Avena sativa) Seeds hmax2/mm
1	0.5	39.96	39.08
2	0.55	48.05	47.34
3	0.6	56.97	56.53
4	0.65	66.72	65.88
5	0.7	76.74	76.58
6	0.75	88.03	87.44
7	0.8	99.7	99.41

. Each experiment was repeated five times, and the average value was calculated.

The simulation results from Table 3 were plotted as a scatter plot using Origin 2024 and fitted accordingly. The resulting fitted curve is shown in Figure 4. The fitting equations for the coefficient of restitution between vetch and oat seeds and the PLA plastic sheet, in relation to the maximum rebound heights h_max1 and h_max2, are as follows:

$$h_{max1}=144.24{e_1}^2+11.74e_1-1.99(R^2=0.99)$$

(5)

$$h_{max2}=140.95{e_2}^2+17.65e_2-4.97(R^2=0.99)$$

(6)

In the equation, h_max1 and h_max2 represent the maximum rebound heights of vetch and oat seeds when colliding with PLA material, measured in millimeters. e₁ and e₂ represent the restitution coefficients of vetch and oat seeds when colliding with PLA material.

From the fitting equations, it can be observed that the coefficient of determination (R²) is close to 1, indicating a high degree of fitness for the equations. By substituting the actual measured maximum rebound heights into Equations (5) and (6), the coefficients of restitution e₁ = 0.76 and e₂ = 0.70 were calculated. Simulation experiments were then conducted using these coefficients of restitution (e₁ and e₂), and each was repeated five times to obtain average values. The resulting maximum rebound heights were 8.9 cm and 7.5 cm, respectively. The relative errors between the simulation and actual experiments were 5.32% and 3.85%, respectively. The experimental results indicate that the simulation results are in good agreement with the actual test results. Therefore, the coefficients of restitution between vetch and oat seeds and the PLA plastic sheet are 0.76 and 0.70, respectively.

2.2.3. Calibration of Static Friction Coefficient

The coefficient of static friction is the ratio of the maximum static frictional force to the normal force and is used to characterize the frictional properties between a material and its contact surface [13,14]. In this study, the static friction coefficient μ_m between vetch and oat seeds and the PLA plastic sheet was measured using the inclined plane method. The calculation equation is as follows:

$${\mu }_m={\displaystyle \frac{f}{F}}={\displaystyle \frac{mgsin\alpha }{mgcos\alpha }}=tan\alpha$$

(7)

μ_m is the coefficient of static friction; f is the static frictional force, measured in newtons N; F is the supporting force perpendicular to the contact surface, also measured in newtons N; m is the mass of the seed, measured in kilograms kg; g is the acceleration due to gravity, measured in meters per second squared m/s²; α is the angle of inclination, measured in degrees °.

The static friction coefficient μ_m between the seeds and the PLA plastic sheet was measured using an inclined plane apparatus. The red arrow represents the force acting on the seed, and the blue arrow represents the component force of the seed’s gravity, as shown in Figure 5. At the start of the experiment, the inclined plane was placed horizontally. To minimize the effect of rolling friction on the results, four seeds were fixed to a piece of paper using double-sided tape to form a rectangular seed block. The seed block was then placed on one side of the inclined plane. The plane was gradually and uniformly raised until the seeds began to slide. At this point, the raising of the plane was immediately stopped, and the angle α between the inclined plane and the horizontal surface was measured using an electronic inclinometer. The experiment was repeated five times for both vetch and oat seeds, yielding angles of 31.21° and 27.66°, respectively.

The model of the static friction coefficient measuring device was simplified and imported into EDEM software. During the EDEM simulation experiments, the static friction coefficient between the seeds and the PLA plastic plate was set to range from 0.1 to 0.7, with an interval of 0.1. To minimize the influence of other contact parameters on the simulation results, all other parameters were set to 0. Each set of simulation experiments was repeated five times, and the average value was taken to determine the relationship between the inclined angle of the slope meter (type: HG-810) and the static friction coefficient. The experimental results are shown in

Table 4. Results of static friction simulation tests.

Test Number	Coefficient of Static Friction	Avena sativa Sliding Angle (°)	Vicia villosa Sliding Angle (°)
1	0.5	5.9	5.7
2	0.55	11.6	11.6
3	0.6	17.1	16.8
4	0.65	22.2	22.3
5	0.7	26.6	24.4
6	0.75	31.5	30.5
7	0.8	35.4	35.0

.

The experimental results were fitted using Origin 2024 software, and the fitted curve is shown in Figure 6. The curve fitting equations for the static friction coefficients μ_m1 and μ_m2 between vetch and oat seeds and the PLA plastic sheet, in relation to the angles of inclination α₁ and α₂, are as follows:

$${\alpha }_1=-10.98{{\mu }_{m1}}^2+56.38{\mu }_{m1}+0.54(R^2=0.99)$$

(8)

$${\alpha }_2=-15.98{{\mu }_{m1}}^2+62.07{\mu }_{m1}-0.15(R^2=0.99)$$

(9)

Here, α₁ and α₂ represent the inclined angles of vetch and oat seeds with respect to PLA, measured in degrees. μ_m1 and μ_m2 are the static friction coefficients between vetch and oat seeds and PLA.

From the fitting results, it can be seen that the coefficient of determination (R²) for the fitting equations is close to 1, indicating a good fit. By substituting the actual measured angles of inclination from the experimental setup into the fitting Equations (8) and (9), the static friction coefficients were calculated as μ_m1 = 0.619 and μ_m2 = 0.517. Simulation experiments were then conducted, repeated five times, and the average values were calculated. The resulting angles of inclination were 30.55° and 28.35°, with relative errors of 2.11% and 2.50%, respectively, compared to the measured values. These results show that the simulation values after calibration are in good agreement with the actual experimental results, with a small error. Therefore, the static friction coefficients between vetch and oat seeds, and the PLA plastic sheet are determined to be 0.619 and 0.517, respectively.

2.2.4. Rolling Friction Coefficient Calibration

Rolling friction refers to the ratio of the frictional force between the surface of a rolling object and the rolling surface to the weight of the object, occurring when an object rolls over another surface without slipping. In the rolling friction experiment, the seeds are subjected to rolling friction as they roll down the inclined plane until they come to rest on the horizontal surface [17]. According to the law of conservation of energy, the calculation formula for the rolling friction coefficient is as follows:

$$\left\{\begin{array}{c}mgSsin\beta =mg(Scos\beta +L){\mu }_s\\ {\mu }_n={\displaystyle \frac{Ssin\beta }{Scos\beta +L}}\end{array}\right.$$

(10)

where μ_n is the rolling friction coefficient; S is the rolling distance of the seed on the inclined plate, mm; β is the inclination angle of the inclined plate, °; L is the rolling distance of the cabbage on the horizontal plate, mm.

The rolling friction coefficient is a key influencing factor in EDEM simulations. To calibrate the rolling friction coefficient μ_n between the seeds and the plastic sheet, the inclined plane rolling method was used for the experiments. The process for both the actual and simulation experiments is shown in Figure 7. In the actual experiment, the angle between the inclined plane and the horizontal surface was set to β = 35°, and the seeds were released with an initial velocity of 0 m/s at a fixed position (L) on the inclined plane, allowing them to roll down. After the seeds came to rest on the horizontal surface, the rolling distance (S) was measured. Each experiment was repeated five times, and the average value was calculated. The results showed that the horizontal rolling distances for vetch and oat seeds on the PLA plastic sheet were 55.8 mm and 54.0 mm, respectively.

In the EDEM simulation experiments, the rolling friction coefficient was set within the range of 0.01 to 0.09, with intervals of 0.01, based on the experimentally calibrated coefficients of restitution and static friction. To minimize interference from other contact parameters, all other parameters were set to zero. Each set of experiments was repeated five times, and the average value was taken. The experimental design and results for the rolling friction coefficient simulation are detailed in

Table 5. Test results of rolling friction simulation.

Test Number	Coefficient of Rolling Friction	Vicia villosa Rolling Distance (mm)	Avena sativa Rolling Distance (mm)
1	0.01	70.3	77.7
2	0.02	51.3	62.4
3	0.03	44.6	53.2
4	0.04	36.6	48.5
5	0.05	32.4	38.9
6	0.06	30.3	34.2
7	0.07	27.3	24.5
8	0.08	25.2	21.4
9	0.07	23.7	19.4

, with each experiment repeated five times and averaged.

The resulting fitted curve is shown in Figure 8. The fitting equations for the rolling friction coefficients μ_n1 and μ_n2 between vetch and oat seeds and the PLA plastic sheet, in relation to the horizontal rolling distances (S₁ and S₂), are as follows:

$$S_1=8749.20{{\mu }_{n1}}^2-1383.32{\mu }_{n1}+79.41(R^2=0.97)$$

(11)

$$S_2=5416.49{{\mu }_{n1}}^2-1254.08{\mu }_{n1}+87.81(R^2=0.99)$$

(12)

In the equation, S₁ and S₂ represent the maximum rolling distances of vetch and oat seeds on PLA, measured in millimeters. μ_n1 and μ_n2 are the rolling friction coefficients of vetch and oat seeds on PLA.

From the fitting results, it can be seen that the coefficients of determination (R²) for both fitting equations are close to 1, indicating a high reliability of the fitting results. By substituting the average horizontal rolling distances measured in the actual experiments into Equations (11) and (12), the rolling friction coefficients were calculated as μ_n1 = 0.019 and μ_n2 = 0.034. Subsequently, these rolling friction coefficients were used in EDEM for simulation experiments, which were repeated five times, and the average values were calculated. The resulting horizontal rolling distances were 53.8 mm and 56.8 mm, with relative errors of 3.58% and 5.18%, respectively, compared to the actual experimental values. These results show that the calibrated simulation results are in good agreement with the actual experimental results. Therefore, the rolling friction coefficients between vetch and oat seeds and the PLA plastic sheet are determined to be 0.019 and 0.034, respectively.

2.3. Calibration of Seed-to-Seed Contact Parameters

2.3.1. Calibration of Interspecies Contact Parameters

During actual sowing, vetch and oat seeds are present as a mixture within the seed-metering device. Under these conditions, inter-seed contact parameters comprise intra-species contacts for vetch, intra-species contacts for oat, and inter-species contacts between the two species [19]. However, separate estimation of these three categories is unnecessary; instead, the overall contact parameters of the seed mixture within the metering device are considered [18,29]. In the experiments, the relative error between measured and simulated angles of repose for the mixed seeds was used as the performance metric. The coefficient of restitution, static friction coefficient, and rolling friction coefficient between mixed seeds were treated as experimental factors. A steepest-ascent procedure and a three-factor quadratic orthogonal rotatable design were employed to optimize the inter-seed contact parameters, thereby determining the simulation parameters applicable to the mixed seeds.

2.3.2. Angle of Repose Test

The seed-drop test apparatus consisted of a polylactic acid (PLA) cylinder, a PLA plate, and a digital protractor; the PLA cylinder measured 70 mm in diameter and 100 mm in height and contained 100 g of mixed seeds, as shown in Figure 9a. During the test, the PLA plate was placed horizontally, the bottom of the PLA cylinder was aligned with the plate center, and a 4.5:5.5 mixture of seeds was filled to the specified height; the cylinder was then withdrawn vertically at a slow, constant speed, allowing the seeds to slide and accumulate naturally on the plate. Once the heap stabilized, the angle of repose was measured with a ruler and the digital protractor. The test was repeated five times, and the mean value was reported, yielding an angle of repose of 21.34° for the mixed seeds.

2.3.3. Steepest Climb Test

Based on preliminary experimental results and relevant literature, the inter-particle coefficient of restitution for the mixed seeds was in the range of 0.1–0.7, the static friction coefficient ranged from 0.18 to 0.6, and the rolling friction coefficient ranged from 0.01 to 0.1; a steepest-ascent experiment was conducted to locate the center point and the neighborhood of the optimum for the rotatable quadratic orthogonal design (central composite design, CCD), and the plan and results are summarized in

Table 6. Steepest Climb Test Protocol and Results.

Serial Number	The Inter-Seed Collision Restitution Coefficient/ex	The Inter-Seed Static Friction Coefficient/μx	The Inter-Seed Rolling Friction Coefficient/μz	Angle of Repose θ/°	Relative Error δ/%
1	0.1	0.18	0.01	20.34	28.93%
2	0.2	0.25	0.025	24.16	14.52%
3	0.3	0.32	0.040	29.41	5.28%
4	0.4	0.39	0.055	34.35	23.92%
5	0.5	0.46	0.070	36.09	30.48%
6	0.6	0.53	0.085	42.88	56.09%
7	0.7	0.6	0.100	43.39	58.02%

. From the results in Table 6, the relative error of the angle of repose initially decreased and then increased, and the minimum error was observed in Trial 3. Accordingly, Trial 3 was selected as the center point for the three-factor rotatable CCD, Trials 2 and 4 were set as the low and high levels, respectively, and regression modeling was subsequently performed. For the mixed seeds of vetch and oat, the optimized ranges of the coefficient of restitution, static friction coefficient, and rolling friction coefficient were 0.02–0.04, 0.25–0.39, and 0.025–0.055, respectively.

2.3.4. Second-Order Orthogonal Rotational Combination Experiments, Response Surface Optimization Experiments, and Regression Model Establishment

Because a rotatable quadratic orthogonal combination design is commonly used to obtain optimal parameters, it was employed here to optimize the inter-seed contact parameters. The inter-seed coefficient of restitution, static friction coefficient, and rolling friction coefficient between vetch and oat were treated as experimental factors, and the response variable was the relative error between the measured and simulated angles of repose. A three-factor rotatable central composite design (CCD) was adopted; the coding of simulation factors is provided in

Table 7. Simulation Test Factor Coding.

Encoding	Factor
	A	B	C
−1.62	0.20	0.25	0.025
−1	0.24	0.28	0.031
0	0.30	0.32	0.04
1	0.36	0.36	0.049
1.62	0.40	0.39	0.055

, and the design matrix and results are summarized in

Table 8. Experimental Protocol and Results.

Serial Number	Factor			Relative Error δ/%
	A	B	C
1	−1	−1	−1	19.71
2	1	−1	−1	12.78
3	−1	1	−1	15.75
4	1	1	−1	16.21
5	−1	−1	1	15.63
6	1	−1	1	7.5
7	−1	1	1	11.53
8	1	1	1	6.5
9	−1.682	0	0	16.67
10	1.68	0	0	10
11	0	−1.682	0	11.1
12	0	1.68	0	4.39
13	0	0	−1.682	26.03
14	0	0	1.68	16.1
15	0	0	0	4.89
16	0	0	0	1.18
17	0	0	0	3.18
18	0	0	0	4.18
19	0	0	0	3.21
20	0	0	0	1.36
21	0	0	0	4.46
22	0	0	0	2.93
23	0	0	0	4.14

, where A, B, and C denote the coded factor levels. In Table 7, Table 8 and

Table 9. Analysis of Variance.

Sources of Variance	Sum of Squares	Degree of Freedom	Mean Square Sum	F	p
Model	983.2	9	109.24	48.1	0.0001 **
A	69.68	1	69.68	30.68	0.0001 **
B	20.95	1	20.95	9.22	0.0095 **
C	117.1	1	117.1	51.56	0.0001 **
AB	13.76	1	13.76	6.06	0.0286 *
AC	5.59	1	5.59	2.46	0.1405
BC	2.61	1	2.61	1.15	0.3032
A2	167.16	1	167.16	73.6	0.0001 **
B2	25.51	1	25.51	11.23	0.0052
C2	567.54	1	567.54	249.89	0.0001 **
residual	29.53	13	2.27
Lack of Fit	15.76	5	3.15	1.83	0.2129
Pure error	13.77	8	1.72
Total	1012.72	22

Note: * Indicates significant effect (0.01 < p ≤ 0.05), ** indicates extremely significant effect (p ≤ 0.01).

, A, B, and C represent the coefficient of restitution, the coefficient of static friction, and the coefficient of rolling friction between seeds, respectively.

The experimental data were fitted by regression in Design-Expert 13, and the significance analysis of the regression model (ANOVA) is presented in Table 9. According to the fitted model, the inter-seed coefficient of restitution, static friction coefficient, and rolling friction coefficient were found to have highly significant effects on the angle of repose; in particular, the AB interaction (coefficient of restitution × static friction) was especially significant for the angle-of-repose error. Response surfaces were generated (Figure 10). As shown in Figure 10, the relative error of the angle of repose decreased initially and then increased as the inter-seed coefficient of restitution, static friction coefficient, and rolling friction coefficient increased. The AC and BC interactions were not significant with respect to the relative error of the angle of repose, possibly because the rolling friction coefficient exerted a strong main effect, thereby weakening the interaction terms. Analysis of the response surfaces indicated that when the inter-seed coefficient of restitution, static friction coefficient, and rolling friction coefficient were within 0.24–0.36, 0.28–0.36, and 0.031–0.049, respectively, the relative error of the angle of repose was relatively small.

After removing insignificant terms from the regression equation, the new fitted equation is obtained as follows:

$$\delta =3.31-2.26A-1.24B-2.93C+1.31AB-0.8362AC-0.5172BC+3.24A^2+1.27B^2+5.98C^2$$

(13)

A p-value of less than 0.01 was obtained for the regression model, indicating that the regression equation was highly significant. The lack-of-fit term had a p-value greater than 0.05, indicating no significant lack of fit for Equation (13) and suggesting no evidence of additional influential factors. The coefficient of determination (R²) was 0.97, indicating a high degree of fit and accurate characterization of the relationship between the experimental factors and the relative error of the angle of repose; therefore, the model can be used for predictive analysis of the angle of repose.

2.3.5. The Influence of Various Factors on Test Indicators and Parameters

The optimization module of Design-Expert 13 was utilized to solve the regression equation, analyze the response surfaces, and determine the optimal combination of model parameters. Genetic algorithms, as an optimization technique, were employed within the module to simulate the principles of biological evolution. The process involves several key steps, including population initialization, fitness evaluation, selection, crossover, mutation, and iterative optimization. In this context, each candidate solution is represented as a chromosome, which evolves through genetic operations such as crossover and mutation. Unfit solutions are eliminated, while those with higher fitness are preserved and allowed to reproduce. After multiple iterations, the chromosome with the highest fitness is identified as the optimal solution, providing the desired model parameters.

The optimization module of Design-Expert 13 was used to solve the regression equation, analyze the response surfaces, and determine the optimal combination of model parameters. The optimization objective is to minimize the stacking angle error, with the static friction coefficient and rolling friction coefficient between the seeds as the optimization variables. The objective function and constraints were defined as follows:

$$\left\{\begin{array}{c}\mathrm{m}\mathrm{i}\mathrm{n}\mathsf{\delta }(A,B,C)\\ s.t.\left\{\begin{array}{c}0.20\le e_x\le 0.40\\ 0.25\le {\mu }_x\le 0.39\\ 0.025\le {\mu }_z\le 0.055\end{array}\right.\end{array}\right.$$

(14)

Through optimization of the regression model, the optimal parameter combination was obtained: an inter-seed coefficient of restitution of 0.312, a static friction coefficient of 0.328, and a rolling friction coefficient of 0.032. The calibrated contact parameters were imported into EDEM, and angle-of-repose tests were performed five times; the mean angle of repose was 20.96°, and the relative error was 1.78% compared with the physical test results. Therefore, the optimal parameter combination was highly consistent with the measured values and can be used effectively for subsequent EDEM–Fluent coupled simulations.

3. Results and Discussion

3.1. Verification Results and Methods

3.1.1. Validation Test

To further validate the accuracy of the vetch and oat seeds mixed discrete element model and the reliability of the contact parameters, an air-assisted, collective seeder was used for the seed placement tests. The seed placement device was manufactured using 3D printing technology, as shown in Figure 11. It mainly consists of a fan (Zhejiang Asba Motor Co., Ltd., Zhejiang, China, XGB510-15BS5), a seeding box, a venturi tube, a seed transport tube, a pressurization tube, and a distributor. The device’s structure and key dimensions are consistent with the previously described simulation model to ensure the comparability of the numerical simulations and physical tests. The test seeds consisted of vetch (Fabaceae) and oat (Poaceae), which were mixed in a ratio of 4.5:5.5 and introduced into the pneumatic seed dispensing system. The seed placement rate was controlled by adjusting the motor speed. The moisture content and particle size distribution of the seeds were measured prior to the experiment and controlled within the range of 3–8% to minimize the effect of material property variations on the test results. The bench tests were conducted in the Key Laboratory of Modern Agricultural Engineering at Tarim University, where the indoor environment remained relatively stable during the experiment.

3.1.2. Experiment Design and Treatment

This experiment is an indoor bench validation test, employing a two-factor full factorial design. The experimental factors include fan outlet wind speed and seed delivery efficiency. The wind speed factor is set at three levels: 20, 25, and 30 m·s⁻¹, with the fan speed adjusted using a variable frequency drive and verified by an anemometer. The seed delivery efficiency factor is based on the mass flow rate of vetch, with three levels: 5, 7, and 9 g·s⁻¹. The corresponding oat mass flow rates are 7.5, 10.5, and 13.5 g·s⁻¹, respectively. The specific combinations are shown in

Table 10. Measured and simulated results of the experimental indicators.

Conveying Efficiency/g·s−1		Wind Speed/(m·s−1)	Coefficient of Variation of the Uniformity of Seed Discharge in Each Row/%
Vetch (Vicia villosa)	Oat (Avena sativa)		Actual Measured Value	Simulation Value
5	7.5	20	5.44%	3.53%
		25	3.80%	5.34%
		30	6.41%	5.15%
7	10.5	20	5.23%	6.80%
		25	5.71%	4.54%
		30	5.57%	6.68%
9	13.5	20	4.91%	3.44%
		25	4.58%	3.64%
		30	7.20%	6.01%

. The wind speed and seed delivery efficiency are arranged in a full combination manner, resulting in a total of 9 treatment conditions (3 × 3 = 9). Each treatment condition is repeated three times. Between repetitions, the seed delivery tube and distribution head are completely emptied of residual seeds, and the mixed seeds are re-prepared according to the set proportions to avoid the carryover effect from the previous trial.

3.1.3. Experimental Methods and Measurement Indicators

Prior to the experiment, the fan speed and seed delivery device are adjusted according to the set conditions to achieve and maintain stable seed delivery efficiency at the target value. Once the system stabilizes, a timer is started, and during continuous operation for 30 s, mixed seeds are collected from each seed outlet of the distribution head using a mesh net. After the experiment, the mass of the seeds discharged from each row is measured using an electronic balance, and the coefficient of variation of seed discharge consistency is used as the evaluation index. The calculation method is shown in Equation (15).

$$Y_1={\displaystyle \frac{\sqrt{\frac{1}{i-1}\sum {\left(\sum m_i-\overline{m}\right)}^2}}{\overline{m}}}\times 100\%$$

(15)

In the equation, Y₁ represents the coefficient of variation of seed discharge consistency for each row, expressed as a percentage; i denotes the number of distribution outlets, and mi represents the mass of seeds passing through the i-th distribution outlet, where i = 1, 2, 3, 4; $\overline{m}$ represents the average mass of seeds discharged from each seed delivery tube.

A smaller value of Y₁ indicates a more uniform seed discharge across the rows. The statistical results of the measured Y₁ values under different combinations of wind speed and seed delivery efficiency are presented in Table 10.

Bench tests were conducted on vetch and oat to investigate the motion of mixed seeds in a pneumatic centralized seed-distribution metering device under different seed delivery rates and inlet air velocities. With increasing inlet air velocity, blockage at the distribution head decreased, and the coefficient of variation (CV) of per-row discharge likewise decreased. By contrast, the CV of per-row discharge showed no obvious change with increasing seed delivery rate. The device was applicable to legume and cereal seeds and enabled thorough mixing, ensuring that the mixed seeds were discharged uniformly and continuously. The CV of per-row seeding uniformity was used as the performance metric, and simulation and physical tests were conducted under varying seeding rates and air velocities; the CVs from measured and simulated results were compared. In the tests, seeds of vetch and oat were placed into two seed hoppers according to the preset mixing ratio, and different inlet air velocities and seeding rates were set based on agronomic requirements and machine forward speed. After the air pressure and seed feed rate had stabilized, the CV of per-row discharge was calculated; the results are shown in Table 10. The results indicated that, at fan air velocities of 20–30 m/s and seed delivery rates of 17.5–27.5 g/s, the CV of per-row seeding uniformity ranged from 3.44% to 7.20%. The experimental process is shown in Figure 12, where different subfigures (a–i) display the variation in seed velocity under wind speeds of 20 m/s, 25 m/s, and 30 m/s. The color scale in the figure represents the seed velocity (units: m/s), ranging from red (indicating high speed) to blue (indicating low speed). The simulation results indicate that with increasing wind speed, the seed velocity significantly increases. At lower wind speeds (e.g., 20 m/s), the seed velocity is relatively uniform and low, with more pronounced seed accumulation in the distributor. In contrast, at higher wind speeds (e.g., 30 m/s), the seed velocity exhibits greater variation, with an expanded speed distribution range and improved seed flowability.

3.2. Discussion

3.2.1. Calibration of the Physical Properties of Mixed Seeds and Optimization of the Discrete Element Models

Measurement of seed physical parameters is fundamental to discrete element method (DEM) simulations, and the reliability of the simulation results is directly affected by their accuracy. Accordingly, the determination of seed physical parameters is regarded as an essential component of DEM simulations. In this study, key physical parameters of vetch and oat seeds were measured by physical testing—including triaxial dimensions (length, width, and thickness), density, moisture content, Poisson’s ratio, and shear modulus—thereby providing a basis for the development and optimization of the DEM model. Significant differences were observed between the two seed types in morphology, density, and mechanical properties; these differences have important implications for simulations of mixed seeds, particularly for inter-particle contact and interaction behavior.

The triaxial dimensions of vetch seeds were 3.45 mm × 3.31 mm × 3.16 mm, whereas those of oat seeds were 11.86 mm × 3.11 mm × 2.51 mm. Oat seeds exhibited a more flattened profile and greater length, which may influence seed-to-seed and seed-to-polylactic acid (PLA) plate contact characteristics. In addition, the density of vetch seeds was 1316.4 kg/m³, whereas that of oat seeds was 1032.1 kg/m³. This difference suggests that oat seeds may be more susceptible to aerodynamic forcing during metering, altering their trajectories within the seeding unit. The higher density of vetch was associated with greater stability during contact, and differences in seed-coat properties were associated with lower friction and higher coefficients of restitution. Yan et al. [11] evaluated contact parameters for soybean seeds with three levels of sphericity and reported that seeds with higher density exhibited higher coefficients of restitution, consistent with the present findings.

The angle of repose is a key indicator of macroscopic granular packing; therefore, the mixed-seed angle of repose was used as the starting point to systematically optimize the contact parameters. With respect to DEM model construction, a variety of modeling strategies have been proposed. Wang et al. [25] developed a DEM approach for individual sunflower kernels that combined sphere- and polyhedron-based packing to represent kernel geometry realistically. Shi et al. [26] calibrated the rolling friction coefficient for maize kernels of different shapes to improve simulation accuracy; the relative error between experiment and simulation was 0.72%, and that of an additional angle-of-repose test was 0.20%. During simulation modeling, insights from related studies were adopted in the present work. Li et al. [27] investigated DEM construction for buckwheat seeds, creating particle models by manual and automated packing and validating both approaches experimentally. They reported that, using mass as the evaluation metric, the relative errors between measured and simulated results were 1.04% for the manual-packing model and 0.50% for the automated-packing model, both within a narrow range. These findings indicate that either packing method yields credible models; however, manual packing requires fewer computational resources and reduces computation time. On this basis, manual particle packing was preferentially employed to construct the DEM model of mixed seeds for the pneumatic metering process, thereby lowering computational requirements and shortening runtime to enhance simulation efficiency. Model parameters were iteratively adjusted by comparing physical tests with simulation outputs so that seed behavior was reproduced satisfactorily. Regarding mechanical properties, the Poisson’s ratio of vetch was 0.23, whereas that of oat was 0.35, indicating greater lateral strain in oat seeds and hence a greater tendency to deform under load. For the shear modulus, vetch exhibited 1.06 × 10⁷ Pa, whereas oat exhibited 2.27 × 10⁶ Pa; this lower stiffness of oat seeds implies larger deformations during contact and greater energy dissipation. These microstructural/property differences help explain why oat seeds exhibited a lower coefficient of restitution (0.707) and higher static (0.517) and rolling (0.197) friction coefficients. The shear-modulus characteristics are comparable to those reported by Liu [1] for adzuki bean seeds. Ma et al. [30] examined contact parameters between red clover seeds and coating powders; accounting for differences among particulate materials and using particle-scaling theory, they selected models to calibrate seed–particle contact parameters, thereby informing the determination of inter-seed contact parameters in the present study.

Compared with the work of Chen et al. [12], which also optimized granular contact parameters within a discrete element method (DEM) framework, their study focused primarily on static contact parameters and was not validated using dynamic simulations. In contrast, the NSGA-II genetic algorithm [31] was incorporated during optimization, with minimization of the discrepancy between simulated and measured mixed-seed angles of repose as the objective. Contact–parameter combinations were automatically searched and subsequently validated for suitability in the dynamic seed-metering process. The results indicated that the inter-seed coefficient of restitution, static friction coefficient, and rolling friction coefficient had significant effects on the angle of repose, and that interaction terms involving static friction were particularly significant; these findings are consistent with those reported by Adilet Sugirbay [23] for DEM calibration of wheat seeds. The coefficient of determination (R²) of the regression model was 0.97, indicating that the model accurately captured the relationship between the experimental factors and the angle of repose. Specifically, the optimal values of the coefficient of restitution, static friction coefficient, and rolling friction coefficient were 0.312, 0.328, and 0.032, respectively; this parameter set exhibited good adaptability during simulation validation, and the error between the simulated and measured angles of repose was only 1.32%, further confirming the model’s accuracy and reliability. These results provide a foundation for subsequent EDEM–Fluent coupled simulations. Given the complexity of aerodynamic–particle interactions during pneumatic seeding, reliable contact parameters are critical for ensuring the credibility of the coupled simulations. Likewise, the above calibration results can inform simulation-based optimization of the pneumatic centralized seed-distribution planter, enabling more accurate and reliable DEM-based predictions of seeding performance.

3.2.2. Numerical Simulation and Experimental Validation of a Pneumatic Centralized Seed–Distribution Device

In this study, the optimized discrete element method (DEM) simulation model was applied to the simulation and validation of the pneumatic centralized seed-distribution planter. The study involved inputting the calibrated contact parameters into the EDEM simulation software to simulate the mixed-seed discharge process under varying wind speeds and delivery efficiencies, which were then compared with physical bench test results. The bench test results indicated that, with variations in wind speed and delivery efficiency, the coefficient of variation (CV) of per-row seeding exhibited fluctuations, with the CV deviation between the simulated and physical tests ranging from 1.24% to 3.94%, suggesting that the optimized simulation model was able to predict seed uniformity differences in the actual seeding process with reasonable accuracy. This result validated the effectiveness and reliability of the DEM simulation model in dynamic seed-metering processes. Liao et al. [32] employed the EDEM–Fluent coupling method to study the gas–solid flow model of mixed oat and vetch seeds. Although their research also involved mixed-seed simulations, the discussion of inter-seed contact characteristics was relatively limited, focusing primarily on the dynamic behavior of the gas–solid coupling. In contrast, this study not only considers the impact of pneumatic conditions on the motion of mixed seeds but also takes a systematic approach to calibrating physical parameters, analyzing how seed morphology differences affect contact parameters, and revealing the mechanisms of inter-seed interactions at the microscopic structural level, providing a more comprehensive understanding.

Microscopic structural analysis further reveals the impact of seed morphology differences on the seed-metering process. The higher density and lower friction of vetch seeds provide greater stability during seeding, while the larger morphological differences and higher friction of oat seeds make them more susceptible to disturbance under wind influence. This difference is manifested in the distinct trajectories of mixed seeds within the seed-metering device, particularly under conditions of high wind speed and low delivery efficiency, where oat seeds are more likely to deviate from stable discharge patterns. By optimizing the contact parameters between seeds, the simulation results effectively replicate the motion of different seeds within the seed-metering device, providing a reliable basis for further optimization of the planter design and improving seeding accuracy.

Additionally, research by Chen et al. [28] has shown that seed shape differences are one of the key factors influencing the accuracy of discrete element method (DEM) simulations. They classified maize seeds into five shapes: dent, conical, spherical, pyramidal, and irregular, and constructed DEM models for each shape accordingly. This approach is instructive for mixed-seed simulations: in mixed sowing scenarios, there may be various shapes and sizes of seeds both between different species and within the same species. If the model can categorize particles based on morphological features, it would enhance both the accuracy of the simulation and the generalizability of the model. Considering the specifics of this study, while there are shape differences between vetch and oat seeds, this research primarily uses a spherical equivalent model for simulation. Future research could further explore the use of polyhedral or non-spherical models to represent the true shape characteristics of seeds and calibrate model parameters for seeds of varying sizes, thus improving the model’s adaptability to a wider range of crop seeds. By incorporating a more diverse range of particle shapes and parameter combinations into the model, it may reduce the dependency on specific crops and improve the accuracy of the model in describing mixed-seed systems. This would contribute to the broader applicability of DEM models in simulating complex crop seeding and delivery systems.

In summary, this study provides a comprehensive analysis of the calibration and application of the mixed-seed discrete element method (DEM) model parameters, incorporating both prior research and the experimental data from this work. The results indicate that, through rigorous experimental calibration and optimization methods, reliable mixed-seed contact parameters can be obtained, enabling simulation results to align closely with actual conditions in both static packing and dynamic seed-metering processes. This not only validates the accuracy of the model but also provides a scientific basis for the design improvements of pneumatic centralized mixed-seed planters. The discussion above lays the foundation for subsequent EDEM–Fluent coupled simulations and further studies on mixed-seeding of different crop species, demonstrating the potential and value of the mixed-seed DEM model in the field of agricultural engineering.

4. Conclusions

This study establishes a discrete element simulation model by measuring the physical parameters of vetch and oat seed mixtures. The experimental results demonstrate that, through a precise calibration process, including collision, inclined plane sliding, and rolling tests, the restitution coefficient, static friction coefficient, and rolling friction coefficient between vetch and oat seeds and the PLA plastic plate were determined. Specifically, the restitution coefficient for vetch seeds is 0.763, while for oat seeds it is 0.707; the static friction coefficients are 0.619 and 0.517, respectively; and the rolling friction coefficients are 0.139 and 0.197, respectively.

Based on these contact parameters, further experiments on the angle of repose of the seed mixture were conducted, and the contact parameters were optimized through a three-factor, quadratic rotation orthogonal experiment. The optimal combination of contact parameters is as follows: inter-seed restitution coefficient of 0.312, static friction coefficient of 0.327, and rolling friction coefficient of 0.042. The relative error between the simulated and measured angle of repose is 1.32%, confirming the validity of the selected contact parameters.

Furthermore, a practical bench test using an air-blown seed collector confirmed the reliability of the simulation model. The deviation between the simulation and experimental results ranged from 1.24% to 3.94%, indicating that the optimized discrete element model effectively replicates the seed movement behavior in the seed dispenser under varying wind speed and seed delivery efficiency conditions. This study not only provides a reliable simulation model for the seed dispensing process of vetch and oat seed mixtures but also offers data support for the optimization design of air-blown seed dispensers.