Design of Highway Maintenance Unmanned Vehicles Based on the Double-Circulation Double-Diamond Model

Featured Application

The “Double Circulation Double Diamond” design model that is the subject of this paper provides a systematic framework for the development of unmanned vehicles for the maintenance of highways. The model supports the identification of demand, the mapping of technology, and the optimisation of solutions to enhance both operational efficiency and safety.

Abstract

The objective of this study is to construct a “Double-Circulation Double-Diamond” model integrating AHP, QFD, and TRIZ. This will enable the resolution of contradictions between user requirements and technical solutions in the design of highway maintenance unmanned vehicles. The construction of an efficient, safe, and iterative systematic design framework will be achieved by following these steps. The model incorporates both internal and external feedback loops into the conventional Double-Diamond framework, thereby establishing a dynamic closed-loop process of “requirement identification—technical transformation—contradiction resolution—feedback optimization.” AHP is employed to conduct a hierarchical analysis of user requirements; QFD is utilized to map these requirements to technical characteristics; and TRIZ is integrated to facilitate innovative problem-solving and solution generation. The proposed model has been demonstrated to be an effective means of achieving requirement hierarchy decomposition, technical translation, and resolution of key contradictions. MATLAB R2025b (version 25.2.0) simulations were employed to verify the role of the external feedback loop in scheme iteration and optimization. This confirmed the A* algorithm as the optimal path planning approach, which achieves a balance between efficiency and safety. The fuzzy comprehensive evaluation yielded a score of 3.142, indicating performance between “well achieved” and “fully achieved”. In comparison with conventional linear development methodologies, the “Double-Circulation Double-Diamond” model has been shown to markedly enhance the systematicness and dynamic adaptability of complex equipment design through the utilization of cross-phase feedback and methodological coupling. This approach provides a transferable design framework applicable to highway maintenance, unmanned vehicles, and other complex engineering systems.

1. Introduction

With China’s expressway mileage now exceeding 160,000 km, the traditional maintenance mode that relies on manual inspection and mechanical operations has shown significant deficiencies in terms of efficiency, informatization, and safety [1,2]. The unmanned vehicle for highway maintenance, equipped with LiDAR, cameras and inertial navigation systems, represents a new type of intelligent equipment. It is capable of performing environmental perception, path planning, obstacle avoidance and remote monitoring. It offers significant advantages in terms of enhancing operational efficiency and safety [3].

In relation to the present state of research concerning the utilization of unmanned vehicles for the purpose of highway maintenance, scholars within the domestic and international research communities have achieved a certain degree of advancement. However, the majority of studies to date have been confined to specific technological advancements. For instance, Xu et al. proposed the concept of an automated maintenance system based on digital twins, while some domestic “intelligent inspection systems” have achieved automatic route planning and damage detection [4,5]. Nevertheless, in extreme conditions such as nocturnal periods, precipitation, or snowfall, challenges persist, including diminished recognition accuracy, unstable path planning, and delayed execution. It is evident that, at the system level, a mature architecture for multi-module collaboration and adaptability has yet to be established [6].

The design of highway maintenance unmanned vehicles involves multiple subsystems, including energy supply, driving mechanisms, transmission systems, control systems, and operational components, making it a highly complex process of system integration. According to the TRIZ Law of System Completeness, a technical system must include these elements to achieve functional integrity. However, existing studies have largely focused on individual modules, such as control or perception, and have paid insufficient attention to the holistic lifecycle perspective covering manufacturing, operation, maintenance, and decommissioning. This lifecycle perspective has been systematically elaborated in the context of autonomous buses; for example, Langner et al. proposed a comprehensive lifecycle model encompassing planning, development, operation, and retirement [7].

In recent years, lifecycle-oriented design frameworks have emphasized the integration of economic, environmental, and regulatory considerations throughout the product lifecycle. For instance, Ulrich et al. demonstrated how these factors can be incorporated into the early design stages of modular vehicle concepts [8]. Moreover, Malak et al. proposed a resource-efficiency–oriented lifecycle assessment approach in the commercial vehicle industry, further illustrating the applicability of this methodology to complex transportation equipment [9]. In the field of unmanned systems and robotics, Gupta et al. also demonstrated the feasibility of integrating lifecycle assessment into product–service system design [10].

Nevertheless, research on highway maintenance unmanned vehicles has primarily focused on algorithm optimization and user-centered design, with limited attention to system-level and lifecycle-oriented approaches. This research gap is particularly noteworthy, as a digitalized lifecycle framework has been proposed for highway infrastructure [11], providing guidance for extending lifecycle thinking to maintenance equipment.

Based on these insights, this study first uses the control and path-planning subsystems as representative research objects to validate the proposed methodological framework within a broader lifecycle context. These subsystems serve as effective testbeds for assessing the feasibility, adaptability, and iterative potential of the Double-Circulation Double-Diamond model, which will subsequently be extended to the full vehicle lifecycle design.

Methodologically, the Double Diamond Model was proposed by the British Design Council in 2005. The core logic of the process under discussion here follows a divergent–convergent process across the “problem space” and “solution space” [12]. This is a process which has been widely applied in the context of product innovation and service design, and which has gradually been extended to intelligent transportation and medical equipment design [13,14]. In the seminal paper by Nana Yaa Serwaah Sarpong et al., a pioneering approach was adopted by the introduction of an iterative feedback mechanism into the model [15]. This seminal innovation was undertaken with the objective of enhancing the model’s adaptability to complex systems. Researchers of Chinese origin have also endeavored to combine this model with user research and prototype iteration with a view to optimizing designs for kitchen appliances and campus unmanned vehicles [16,17]. Nevertheless, these explorations are generally confined to the single-product level. The absence of seamless stage transitions and feedback loops within the model gives rise to elevated costs associated with post hoc corrections, consequent to deviations in early-stage requirement definitions, thereby constraining its applicability in the domain of complex equipment system design.

The design of complex equipment is a multifaceted process that typically encompasses a multitude of objectives, constraints, and interdisciplinary interactions. This complexity necessitates the integration of diverse systematic methodologies to ensure optimal synergy and the effective management of the aforementioned challenges. The Analytic Hierarchy Process (AHP), Quality Function Deployment (QFD), and the Theory of Inventive Problem Solving (TRIZ) are among the most commonly used methods [18]. Previous studies have applied the integration of AHP, QFD and TRIZ in the design of complex products, including rescue robots and snow vehicles. For instance, Li Xiaojie et al. effectively resolved conflicts between requirements and technology in the design of earthquake rescue robots [19], while Huang Shiwen et al. verified the feasibility of this approach in the development of dual-purpose snow vehicles [20]. However, the aforementioned studies predominantly adopted a one-way cascading logic paradigm, exhibiting a paucity of cross-phase iteration and feedback mechanisms. Consequently, the system’s adaptability and dynamic optimization capabilities remain constrained, impeding the facilitation of continuous improvement in intelligent equipment within complex environments.

In summary, extant research is subject to three main limitations:

(1) The conventional Double Diamond Model is deficient in terms of stage coupling and feedback mechanisms, which impedes dynamic iteration in complex systems.

(2) It is evident that methodologies such as AHP, QFD and TRIZ are predominantly implemented in a linear sequence, exhibiting a lack of cross-phase linkage and information feedback.

(3) The extant research on unmanned vehicles for highway maintenance has primarily focused on single-module optimisation, with a paucity of attention being given to the development of a systematic, closed-loop design framework.

In order to address the aforementioned issues, this study proposes a “Double-Circulation Double-Diamond” model. This model integrates multiple methodologies and feedback mechanisms in order to establish a dynamic closed-loop process from requirement identification to solution verification. The integration of AHP, QFD and TRIZ within the model facilitates effective requirement transformation and contradiction resolution, thereby providing a systematic design pathway for complex engineering equipment systems.

2. Methodology

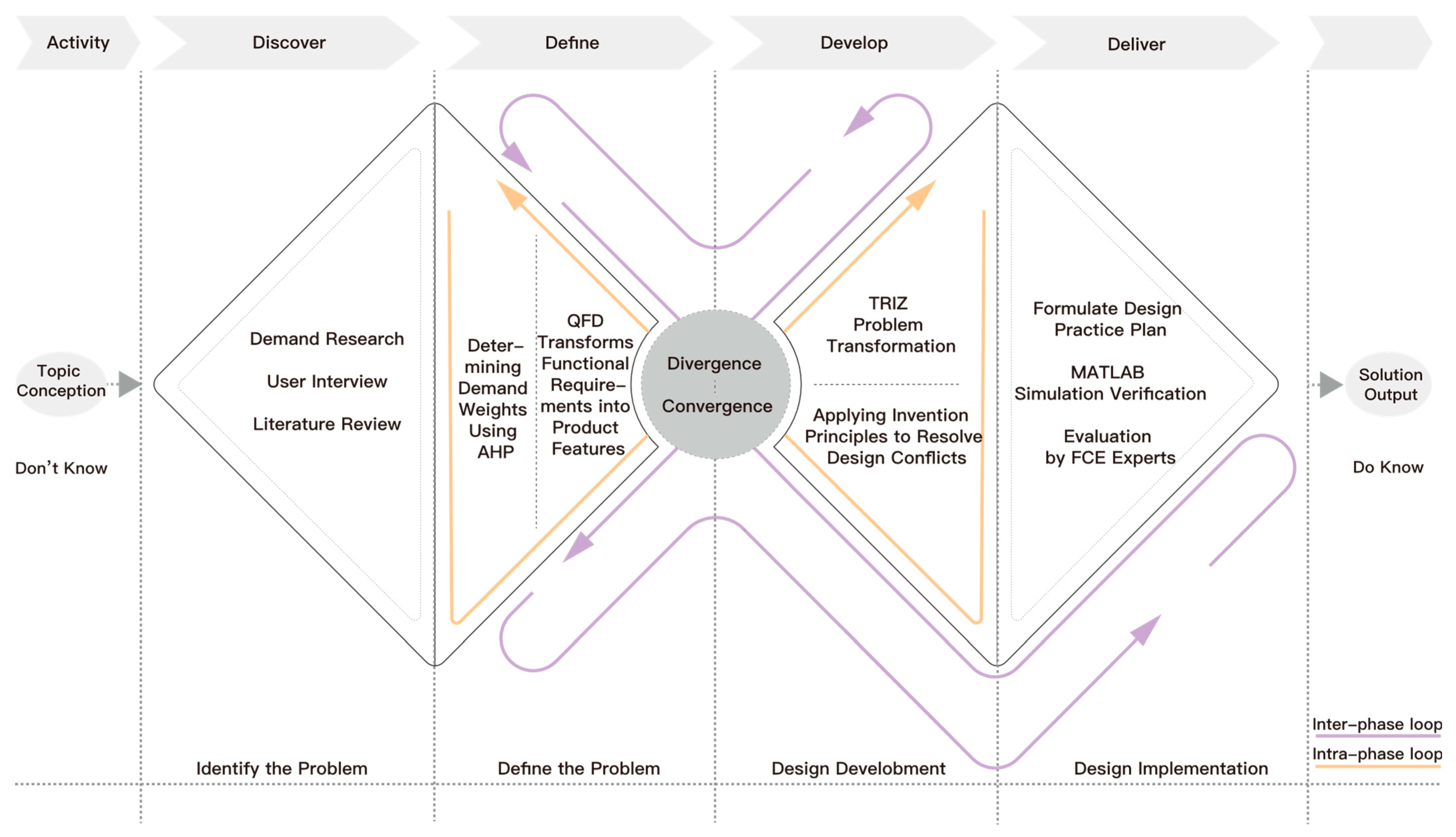
The “Double-Circulation Double-Diamond” model is a systematic approach to the design process, which is divided into four stages: Discovery, Definition, Development, and Delivery. This model incorporates feedback loops from both internal and external sources at each stage of the process. The internal loop facilitates real-time correction within a single phase, with this correction being based on data or validation results. In contrast, the external loop enables cross-phase retrospection and redefinition, thereby forming a dynamic and adaptive closed-loop system. The structure under discussion has been demonstrated to endow the design process with continuous optimization and self-correction capabilities. This renders it suitable for use in multi-constraint complex equipment systems, as illustrated in Figure 1.

This study specifically focuses on the control and path-planning subsystem of highway maintenance unmanned vehicles within the broader lifecycle design process. The proposed model is therefore applied to the design and optimization of key functional subsystems rather than the entire vehicle system.

(1) Discovery phase: The identification of core issues in maintenance operations is achieved through the utilization of questionnaires, interviews, and field research. This approach serves to elucidate the design requirements and functional boundaries of the unmanned vehicle. A comprehensive requirement list is established through the integration of literature and industry standards.

(2) Define phase: A mind-mapping approach is adopted to organize user needs and maintenance tasks, constructing a hierarchical structure of requirements. The AHP is a methodological framework employed to ascertain the relative importance of each requirement, while QFD facilitates the translation of high-priority needs into specific technical characteristics. The internal loop has been demonstrated to optimize weight distribution and indicator relationships, thereby achieving quantitative mapping from user needs to technical metrics.

(3) Develop phase: The results of the QFD analysis have enabled the identification of key conflicts. TRIZ is a method that is applied to establish contradiction function groups and generate innovative solutions. The external loop facilitates retrospection of the definition phase, enabling the refinement of requirements or technical indices. This process enables dynamic adjustment of innovative schemes.

(4) Delivery phase: The outcomes of preceding stages are integrated to complete the design of core modules. The external loop employs MATLAB R2025b (version 25.2.0) simulations to verify path planning and obstacle avoidance performance, while a fuzzy comprehensive evaluation is conducted to assess the overall design effectiveness. Should the results deviate from the target, scheme adjustments are made to ensure the feasibility and reliability of the design.

A comparison of the “Double-Circulation Double-Diamond” model with traditional linear processes and the standard Double Diamond model demonstrates significant advantages in iteration depth, requirement responsiveness, multi-method integration, and conflict resolution, as summarized in

Table 1. Comparative Analysis of Different Design Models.

Dimension	Traditional Linear Process	Standard Double Diamond Model	Double-Circulation Double-Diamond Model
Iteration capability	Each stage is completed once; rework cost is high	Emphasizes divergence–convergence, but overall process remains one-way	Internal loop ensures intra-phase iteration; external loop enables cross-phase dynamic retrospection
Requirement change responsiveness	Weak adaptability to requirement changes	Allows limited mid-term adjustments but lacks a complete feedback chain	Provides cross-phase dynamic retrospection, supporting iterative calibration of requirements and solutions
Multi-method integration	Methods used independently, lacking systematic linkage	Allows partial tool embedding, but integration is limited	Deeply integrates with AHP, QFD, and TRIZ to form a systematic framework
Conflict resolution mechanism	Relies on experiential judgment without systematic theory	No explicit mechanism for conflict resolution	TRIZ combined with external loop enables a closed loop of conflict identification–verification–optimization
Applicable scenarios	Simple, single-task system design	Medium or low complexity product and service development	Highly complex, multi-task, multi-condition equipment design and system development

. The system’s internal and external loops facilitate intra-phase optimization and cross-phase retrospection, thereby circumventing design rigidity. Moreover, it facilitates extensive integration with AHP, QFD, TRIZ, and other methodologies, thereby providing systematic support for the design of complex systems. In scenarios involving multiple tasks and multiple conditions, such as the maintenance of highways by unmanned vehicles, the model achieves a balance between flexibility and overall coherence.

3. Exploration Phase of the “Double-Circulation Double-Diamond” Model

The identification of the key issues in highway maintenance was the objective of the present study. To this end, contextual research was conducted, in addition to the administration of questionnaires and the analysis of accident data. The findings of the study indicate that manual inspection carries with it a number of significant safety risks and inefficiencies when undertaken in conditions of heavy traffic, during night-time operations, and in the presence of adverse weather conditions. Existing maintenance equipment is predominantly single-functional, with limited capacity to support multi-task operations or adapt to complex working environments.

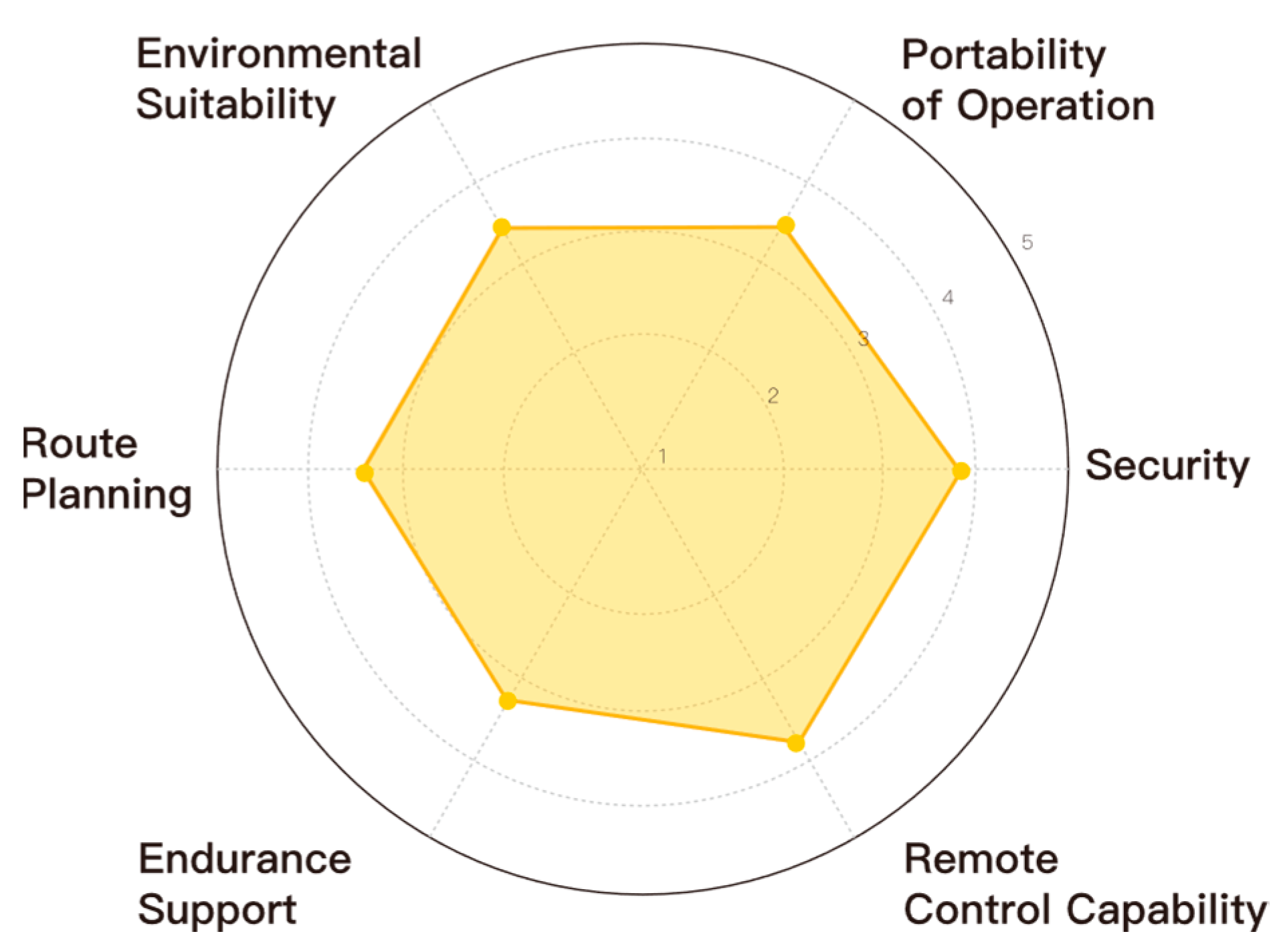
The findings from the interviews and questionnaires indicate that users primarily prioritize safety and remote control, while also anticipating that the unmanned vehicle should possess functions such as automatic obstacle avoidance, path planning, task switching, and status reporting. In the analysis of the 34 valid responses to the questionnaire, it was found that safety and remote control received the highest scores. However, it was also determined that there was still room for improvement with regard to operational convenience, endurance capability and path planning, as illustrated in Figure 2.

The validity of these findings is further supported by accident statistics. Rear-end collisions caused by road debris account for 16% of total incidents. Furthermore, the accident rate during rain, snow, and nighttime is 2.3 times higher than during daytime, and the average emergency handling time exceeds 35 min. The findings of this study demonstrate the inherent limitations of manual maintenance when conducted in extreme environments or during emergency scenarios.

In summary, the exploration phase reveals the core design contradiction of highway maintenance unmanned vehicles: the system must ensure high reliability across all weather and road conditions, while simultaneously achieving multi-task collaboration and operational efficiency. These insights provide critical guidance for constructing the subsequent design framework.

4. Definition Phase of the “Double-Circulation Double-Diamond” Model

The objective of the definition phase is to translate user requirements into actionable design criteria that serve as the foundation for subsequent technical solutions. This is a process that builds on the key issues identified during the exploration phase. The present study proposes a novel integrated model that combines mind mapping, AHP, and QFD to establish a closed-loop pathway for systematic requirement structuring and technical mapping. Specifically, the Mind Mapping method is employed to categorize and hierarchize user needs; the AHP quantifies and ranks these needs to clarify priorities; and QFD maps the requirements to technical characteristics while revealing potential conflicts. In instances where discrepancies arise in weight calculation or mapping relationships, the internal feedback loop facilitates the correction of expert judgments and parameter settings, thereby achieving dynamic iteration between requirement structuring and technical translation.

4.1. Functional Requirement Analysis Based on the Mind Mapping Method

During the user research phase, this study first constructed a questionnaire based on six primary dimensions—safety, operational convenience, environmental adaptability, path planning, range assurance, and remote control—to gather intuitive feedback from frontline operators. Concurrently, through literature review and industry standard analysis, key constraints for unmanned high-speed maintenance vehicles were supplemented regarding regulations, safety requirements, and typical usage scenarios (e.g., Highway Maintenance Safety Procedures, FHWA Maintenance Guidelines), forming an initial pool of requirements.

Building on this foundation, semi-structured interviews were conducted with 10 experts possessing experience in road operation and maintenance and equipment manufacturing to supplement and refine the preliminary requirements set. Subsequently, mind mapping techniques were employed to categorize and structure the multi-source requirements, systematically organizing generic requirements from literature sources, compliance requirements from standards, and authentic operational needs derived from questionnaires and interviews [21].

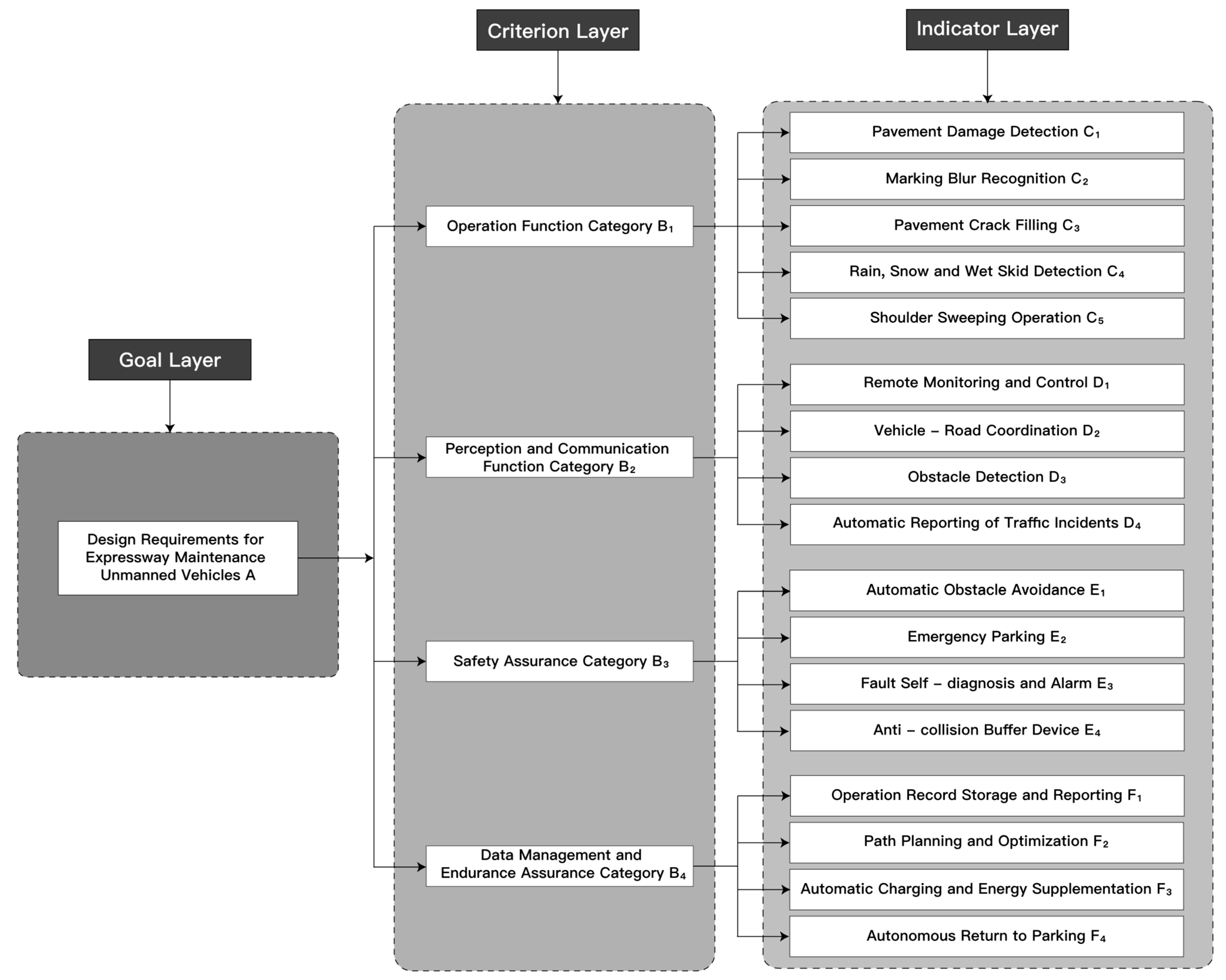
Ultimately, through multiple rounds of expert consensus discussions, a hierarchical structure comprising four principal layers and 17 functional requirement indicators was established, as shown in

Table 2. Design Requirements List for Unmanned Vehicles for Expressway Maintenance.

No.	Primary Functional Category	Secondary Functional Indicator	Description
1	Operational functions	Pavement damage detection	Real-time detection of pavement distress types
2		Fuzzy lane marking recognition	Detection of lane marking clarity
3		Pavement crack filling	Automatic filling and curing of cracks
4		Wet/slippery surface detection	Detect road surface condition and adjust operation strategy
5		Shoulder cleaning operation	Automatic cleaning of shoulders and edge areas
6	Perception and Communication Functions	Realize remote video monitoring and management	Realize remote video monitoring and control
7		Vehicle-road coordination	Interconnect with platform and obtain real-time traffic data
8		Obstacle detection	Detect obstacles around the vehicle body
9		Automatic traffic incident reporting	Automatically identify and report incidents
10	Safety assurance	Automatic obstacle avoidance	Intelligently plan avoidance paths
11		Emergency stop	Automatically stop safely in emergency situations
12		Fault self-diagnosis and alarm	Abnormality alarm and upload to platform
13		Collision buffer device	Rear-end buffer structure for energy absorption and deceleration
14	Data management and endurance	Operation recording and reporting	Automatically record and upload operation data
15		Path planning and optimization	Automatically generate optimal operation paths
16		Automatic charging	Identify charging stations and perform autonomous recharging
17		Autonomous return and parking	Safely return to parking area after operation

. To enhance research reproducibility, Appendix A provides supplementary explanations on the source categories and rationale for each requirement.

4.2. Functional Requirement Weight Analysis Based on AHP

Based on the functional hierarchy established through the mind mapping method, the AHP was applied in this phase to quantitatively rank the design requirements [22]. The nine-level scale method was adopted in order to perform pairwise comparisons among the requirements and their sub-items, as illustrated in

Table 3. 9-Level Scale Method [23].

Importance Level	Meaning	Description
1	Equally important	Both indicators are of equal importance.
3	Slightly more important	One indicator is slightly more important than the other.
5	Clearly more important	One indicator is clearly more important than the other
7	Much more important	One indicator is significantly more important than the other
9	Extremely more important	One indicator is extremely more important than the other
2, 4, 6, 8	----	Intermediate values between the adjacent judgments above

[23]. The relative priority of each requirement within the overall design framework was determined by constructing the judgment matrix and calculating the corresponding weight coefficients. In order to guarantee the scientific validity and consistency of the results, a consistency ratio (CR) test was conducted. In this context, a CR of less than 0.1 was deemed to be acceptable. In instances where the CR exceeded the designated threshold or where substantial discrepancies were observed among the expert assessments, the process underwent iterative refinement through the inner feedback loop until stable and consistent results were attained. The resulting weights functioned as pivotal input parameters for the subsequent QFD-based requirement–technology mapping.

Step 1: Construct the judgment matrix A, where the set of factors is defined as $A=\{a_1,a_2,\dots ,a_n\},$ and the matrix $A=(a_{ij}{)}_{n\times n}$ represents the relative importance between factor $i$ and factor $j$, satisfying $a_{ij}>0$, $a_{ii}=1$, and $a_{ij}=1/a_{ji}$, as shown in Equation (1).

$$A=(a_{ij}{)}_{n\times n}=\left[\begin{array}{cccc}1& a_{12}& \cdots & a_{1n}\\ {\displaystyle \frac{1}{a_{12}}}& 1& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{1}{a_{1n}}}& {\displaystyle \frac{1}{a_{2n}}}& \cdots & 1\end{array}\right]$$

(1)

Step 2: Calculate the sum of each column of the judgment matrix A, as shown in Equation (2), where $n$ represents the matrix dimension and $a_{ij}$ denotes the element in the ${ i}^{th}$ row and $j^{th}$ column.

$${\stackrel{\text{-}}{a}}_{ij}={\displaystyle \frac{a_{ij}}{\sum _{k=1}^n{a}_{kj}}},(i,j=\mathrm{1,2},\dots ,n)$$

(2)

Step 3: Compute the normalized weights of the requirement indices, as shown in Equation (3).

$${\overline{\omega }}_i=\sum _{j=1}^n{\overline{a}}_{ij},(i,j=\mathrm{1,2},\dots ,n)$$

(3)

Step 4: Perform the consistency check by calculating the maximum eigenvalue of the matrix, as shown in Equations (4) and (5).

$${\lambda }_{max}={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{(A\omega {)}_i}{{\omega }_i}}$$

(4)

$${\omega }_i={\displaystyle \frac{{\overline{\omega }}_i}{n}}$$

(5)

The product of the judgment matrix A and the weight vector w is calculated to obtain $A\omega$, where ${\left(A\omega \right)}_i$ denotes the i-th element of the resulting vector $A\omega$, and $w_i$ represents the i-th element of the weight vector w, as shown in equation.

Step 5: Conduct the consistency verification by evaluating the calculation results, as presented in Equation (6).

$$CI={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}$$

(6)

Refer to the average random consistency index RI shown in

Table 4. 1–9 Consistency indicators of the judgment matrix [23].

The Order of the Matrix n	1	2	3	4	5	6	7	8	9	10
RI	0	0	0.58	0.90	1.12	1.24	1.32	1.41	1.45	1.49

. For a judgment matrix of order $n$, obtain the corresponding RI value from the table.

The consistency ratio (CR) was calculated according to Equation (7).

$$CR={\displaystyle \frac{CI}{RI}}$$

(7)

As illustrated in Figure 3, the requirements are arranged into a three-tier hierarchical structure. The goal layer signifies the overarching design objective, whilst the criteria layer is divided into four categories: operational functions, perception and communication, safety assurance, and data management. The indicator layer further refines these into 17 specific requirements. This hierarchical structure provides the foundation for subsequent AHP weight calculations.

4.3. Iterative Application of the Internal Loop

During the weight elicitation process, a total of ten domain experts were invited to provide ratings. In the initial round of calculation, the consistency ratio (CR) of the criterion “Perception and Communication Functions” was determined to be 0.13, which exceeded the acceptable threshold of 0.1. Consequently, a requirement for revision through the internal loop was identified. The disagreement primarily stemmed from differing perceptions regarding the importance of “Remote Monitoring and Coordination.” Management emphasized its critical role in safety assurance. Conversely, some engineers considered the technology to be sufficiently mature and argued that it should not be assigned an excessively high weight.

In order to resolve the discrepancy, further illustration was provided to the expert panel of representative emergency takeover scenarios, thereby facilitating a shared understanding. Subsequent to this clarification, a consensus was reached, and the second-round calculation yielded a CR of 0.091 (<0.1), thereby successfully meeting the consistency criterion. The CR values of the remaining judgment matrices were all below 0.1, indicating satisfactory overall consistency (

Table 5. Overall target layer A judgment matrix.

Item	B1	B2	B3	B4	Weight	λmax	CR
B1	1	3	5	7	0.512	4.162	0.043 < 0.1
B2	1/3	1	3	5	0.284
B3	1/5	1/3	1	3	0.142
B4	1/7	1/5	1/3	1	0.062

,

Table 6. Criterion layer B₁ judgment matrix.

Item	C1	C2	C3	C4	C5	Weight	λmax	CR
C1	C1	3	5	7	7	0.499	5.296	0.065 < 0.1
C2	1/3	1	3	5	5	0.254
C3	1/5	1/3	1	3	3	0.125
C4	1/7	1/5	1/3	1	3	0.074
C5	1/7	1/5	1/3	1/3	1	0.045

,

Table 7. Criterion layer B₂ judgment matrix.

Item	D1	D2	D3	D4	Weight	λmax	CR
D1	1	5	7	7	0.216	4.089	0.091 < 0.1
D2	1/5	1	3	5	0.105
D3	1/7	1/3	1	3	0.623
D4	1/7	1/5	1/3	1	0.054

,

Table 8. Criterion layer B₃ judgment matrix.

Item	E1	E2	E3	E4	Weight	λmax	CR
E1	1	4	5	4	0.608	4.259	0.078 < 0.1
E2	1/4	1	3	3	0.198
E3	1/5	1/3	1	2	0.120
E4	1/4	1/3	1/2	1	0.073

and

Table 9. Criterion layer B₄ judgment matrix.

Item	F1	F2	F3	F4	Weight	λmax	CR
F1	1	3	5	5	0.543	4.203	0.075 < 0.1
F2	1/3	1	3	3	0.244
F3	1/5	1/3	1	3	0.136
F4	1/5	1/3	1/3	1	0.076

).

Finally, the weights of the criterion and indicator layers were multiplied and ranked to identify high-priority indicators, with the results summarized in

Table 10. Comprehensive weight and ranking of highway maintenance unmanned vehicle design demand indicators.

First-Level Requirement	First-Level Weight	Second-Level Requirement	Second-Level Weight	Composite Weight	Ranking
Operational Function Category (B1)	0.512	Pavement Damage Monitoring (C1)	0.499	0.2554	1
		Faded Lane Marking Recognition (C2)	0.254	0.1301	3
		Pavement Crack Repair (C3)	0.125	0.0640	5
		Rain/Snow Slippery Surface Monitoring (C4)	0.074	0.0379	7
		Shoulder Cleaning Operations (C5)	0.045	0.0230	9
Perception and Communication Function Category (B2)	0.284	Remote Monitoring and Control (D1)	0.216	0.0613	6
		Vehicle-Road Coordination (D2)	0.105	0.0298	11
		Obstacle Detection (D3)	0.623	0.1769	2
		Automatic Traffic Event Reporting (D4)	0.054	0.0153	13
Safety Assurance Category (B3)	0.142	Autonomous Obstacle Avoidance (E1)	0.608	0.0864	4
		Emergency Braking (E2)	0.198	0.0281	10
		Fault Self-Diagnosis and Alarm (E3)	0.120	0.0170	12
		Collision-Buffer Device (E4)	0.073	0.0104	15
Data Management and Endurance Assurance Category (B4)	0.062	Operation Data Logging and Reporting (F1)	0.543	0.0337	8
		Path Planning and Optimization (F2)	0.244	0.0151	14
		Automatic Charging and Energy Replenishment (F3)	0.136	0.0084	16
		Autonomous Return and Parking (F4)	0.076	0.0047	17

.

4.4. Transformation of Technical Requirements Based on QFD

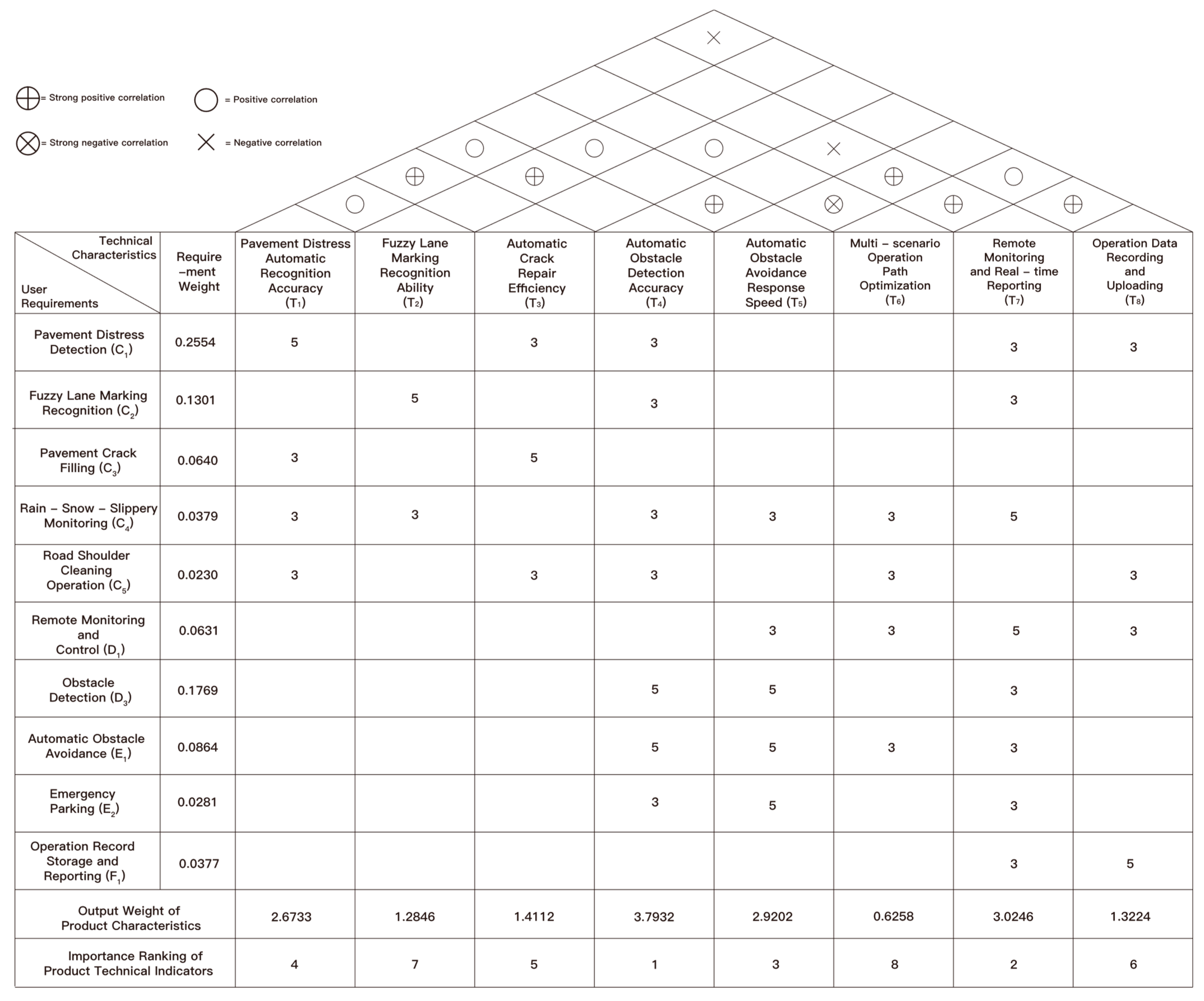
The QFD method is employed to translate user requirements into technical characteristics [24]. This is achieved by systematically mapping user needs to technical features, on the basis of the AHP weighting results. In the QFD House of Quality, the function of the ‘left wall’ is to select the top 10 core requirements; the ‘ceiling’ lists 8 representative technical features; and the ‘roof’ indicates positive, negative or no correlation between features using symbols. The matrix cells are assigned values (1, 3, 5) according to the strength of the requirement–feature relationship, and are combined with requirement weights to calculate the importance of each technical feature [25].

Step 1: Let $K_i$ denote the weight of the $i$-th requirement, and $P_{ij}$ represent the correlation strength between the $i$-th requirement and the $j$-th technical feature. The weighted value of the $j$-th feature is then calculated as shown in Equation (8).

$$Q_j={\displaystyle \sum _{i=1}^n}{K}_i{P}_{ij}$$

(8)

Step 2: Normalize the weighted values to obtain the final importance weights.

$$H_j={\displaystyle \frac{Q_j}{\sum _{j=1}^m{Q}_j}}$$

(9)

4.5. Second Iteration of the Inner Loop: Application Example

In the initial QFD analysis, noticeable discrepancies were found in the weighting of technical characteristics, and the “roof” correlation matrix revealed distinct negative correlations, leading to expert disagreement over their interpretation and the corresponding weight allocation. To address this issue, a second internal iteration was conducted during the technical requirement transformation stage. Typical conflict scenarios were introduced, and expert re-evaluation was carried out to revise key parameters and ensure consistency.

The results indicate the presence of functional conflicts and resource competition among several technical characteristics. Automatic Obstacle Avoidance Response Speed (T₅) and Multi-Scenario Path Optimization (T₆) exhibited a strong negative correlation (−0.64) between real-time responsiveness and global optimization. Obstacle Detection Accuracy (T₄) and Remote Monitoring and Reporting (T₇) showed a moderate negative correlation (−0.52), reflecting the trade-off between accuracy and communication load, while Pavement Damage Recognition Accuracy (T₁) and Data Recording and Upload (T₈) presented a slight negative correlation (−0.47), implying a balance between system latency and data completeness. The strong negative correlation primarily represents a structural contradiction between real-time decision-making and global optimization, whereas the moderate and slight negative correlations stem from trade-offs in resource allocation and data transmission capacity. These relationships uncover the inherent interdependencies among multiple performance objectives and provide a logical basis for subsequent TRIZ-based contradiction resolution.

As shown in Figure 4, after adjustment, the importance levels of Obstacle Detection Accuracy (T₄), Remote Monitoring and Reporting (T₇), and Automatic Obstacle Avoidance Response Speed (T₅) increased significantly, highlighting the dominant roles of safety monitoring and communication performance. The overall weight distribution became more balanced, and the model input was refined through iteration, offering more targeted data support for constructing the contradiction matrix in the TRIZ phase.

5. Development Stage of the Double-Circulation Double-Diamond Model

During the definition phase, AHP and QFD had already translated user requirements into technical features and revealed three critical conflict pairs (T₅–T₆, T₄–T₇, T₁–T₈) that, if unresolved, could constrain overall system performance. In order to address these conflicts, the development phase integrates the TRIZ. Specifically, the identified conflicts are mapped to 39 engineering parameters, and the corresponding inventive principles are selected using the TRIZ contradiction matrix. The results of this process are summarized in

Table 11. TRIZ Problem Transformation and Solution Acquisition.

No.	Functional Conflict Pair	TRIZ Parameter Transformation	Corresponding Solutions
1	Autonomous Obstacle Avoidance (T5) ↔ Path Optimization (T6)	Improvement: No. 40 Degree of Automation Worsening: No. 35 Adaptability	No. 10 Preliminary Action No. 15 Dynamization
2	Obstacle Detection (T4) ↔ Remote Monitoring & Reporting (T7)	Improvement: No. 28 Accuracy Worsening: No. 33 Ease of Operation	No. 19 Periodic Action No. 34 Discarding and Recovering
3	Pavement Damage Recognition (T1) ↔ Data Logging & Upload (T8)	Improvement: No. 28 Accuracy Worsening: No. 26 Quantity of Substance	No. 34 Discarding or Recovering No. 1 Segmentation

[26,27].

Despite specific environmental constraints and operational characteristics of unmanned high-speed maintenance equipment, this study confirms that all key functional requirements can be reasonably mapped within the traditional framework of 39 engineering parameters through a systematic comparison with TRIZ engineering parameters. Consequently, no expansion or adjustment to the original parameter set or contradiction matrix structure is required. This mapping outcome not only demonstrates the applicability of the classic TRIZ contradiction matrix in the field of road maintenance equipment but also provides a reference path for applying TRIZ methods across scenarios in other engineering systems.

5.1. Resolving Design Conflicts Through the Application of Inventive Principles

The findings suggest that the discordance between Autonomous Obstacle Avoidance and Path Optimization (T₅–T₆) can be mitigated by a harmonization of immediacy and global path planning through the implementation of the Preliminary Action (No. 10) and Dynamization (No. 15) principles. In the context of the Obstacle Detection and Remote Reporting (T₄–T₇) pair, the coordination of detection accuracy and communication bandwidth is facilitated by the Periodic Action (No. 19) and Discarding and Recovering (No. 34) principles. In the case of Pavement Damage Recognition and Data Upload (T₁–T₈), the Segmentation (No. 1) and Recovering (No. 34) principles serve to reduce redundancy and enhance data utilization. Overall, TRIZ provides a systematic approach for resolving design conflicts; however, further validation at the system level is required to ensure feasibility.

5.2. Solution Refinement and Validation Driven by the Outer Loop

The outer loop focuses on embedding TRIZ principles within the system context for iterative optimization, facilitating the transformation from theoretical solutions to engineering-feasible implementations. In the T₅–T₆ conflict, the Dynamization and Preliminary Action principles effectively balance real-time responsiveness with global path planning. However, this results in increased energy consumption, necessitating integration with smooth control strategies and redundancy design to enhance system stability. In the context of the T₄–T₇ conflict, the Periodic Action and Recovering strategies have been shown to alleviate bandwidth pressure. However, these strategies have also been observed to introduce potential delays under high-risk scenarios. Consequently, layered communication channels have been implemented to ensure the real-time reporting of critical information. In the T₁–T₈ conflict, Segmentation and Recovering reduce data volume, but over time, this may lead to congestion; this can be mitigated by adopting edge computing, transmitting only feature vectors to reduce communication load effectively.

In summary, the outer-loop feedback has been demonstrated to serve two primary functions. Firstly, it has been shown to address the limitations of TRIZ principles in practical implementation. Secondly, it has been demonstrated to effect a shift from single-conflict resolution towards system-level adaptability optimization. These functions provide a solid foundation for subsequent simulation and empirical studies.

5.3. Applicability and Comparative Analysis of Models

Compared to the V-model, spiral model, and systems engineering processes commonly used in autonomous vehicles, the “dual-loop double-diamond” model demonstrates greater efficiency in handling multi-demand coupling and technical conflicts. By introducing dual loops between demand convergence and technical resolution, this model exposes critical conflicts earlier and enables rapid iteration, making it particularly suitable for high-complexity projects such as multi-vehicle coordination, cross-scenario operations, and high-safety requirements. For maintenance fleets with stable requirements, limited budgets, or highly standardized tasks, the model’s full workflow may appear overly comprehensive. It can be simplified by trimming certain modules. Overall, this model demonstrates distinct advantages in complex system design scenarios while maintaining broad applicability and flexibility.

6. Delivery Phase of the Double-Circulation Double-Diamond Model

In the course of the delivery phase, the outcomes of the preceding stages—namely, requirement analysis, technical transformation, and conflict resolution—are integrated into a systematic design scheme. The implementation of high-priority functions is initiated through a weighting analysis, with subsequent refinement of conflict-resolution strategies through outer-loop feedback, resulting in the formulation of executable engineering measures. It is imperative to note that the inner loop persists in its operation during the validation of the prototype, thereby ensuring the feasibility and reliability of the design.

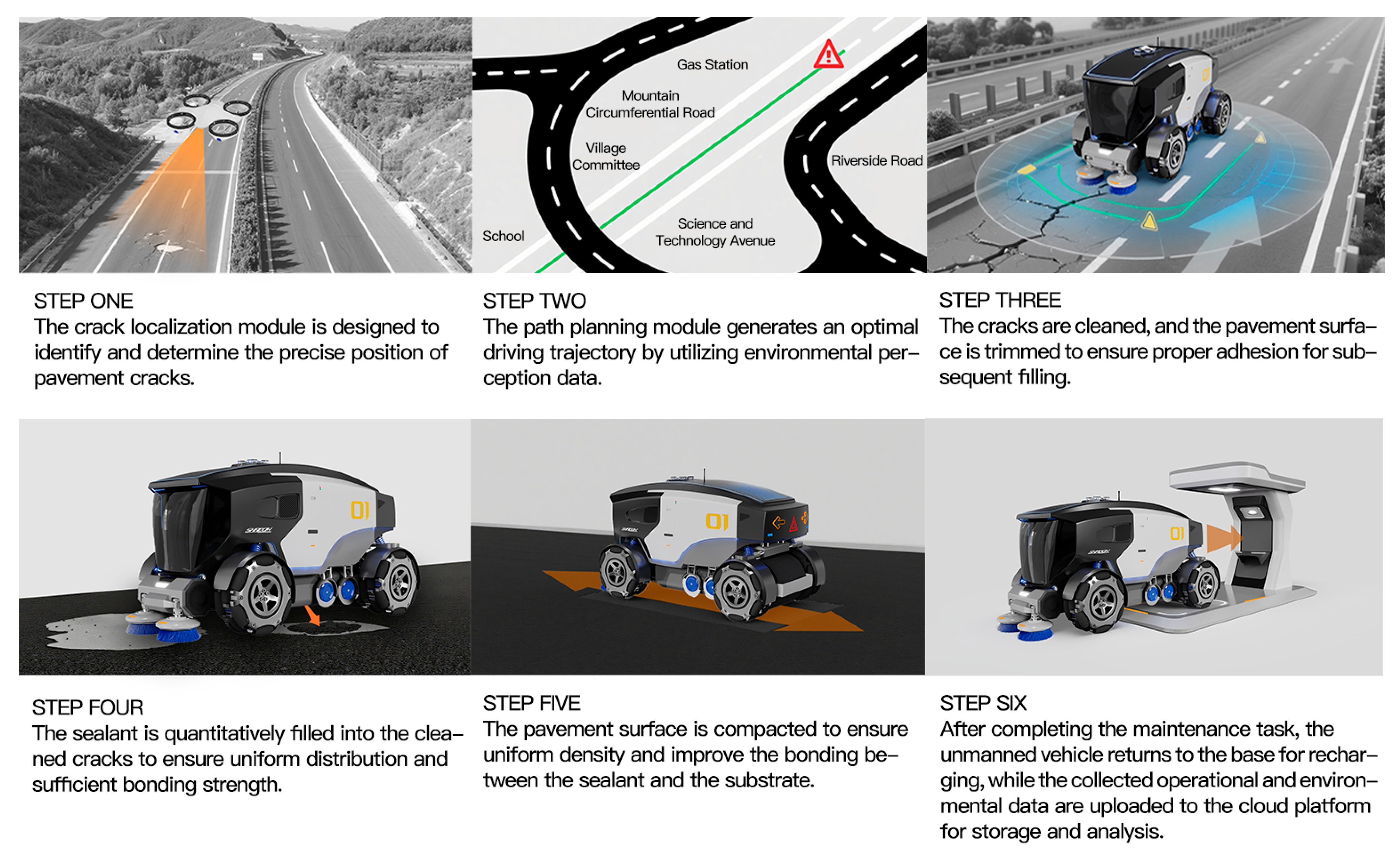
The development of an unmanned vehicle system for highway maintenance has been achieved. The system incorporates core capabilities, including autonomous navigation, environmental perception, and remote control. The vehicle is capable of performing diverse maintenance tasks, including crack sealing, shoulder cleaning, and rain–snow condition monitoring. As demonstrated in Figure 5, Figure 6 and Figure 7, the overall system performance and operational workflow validate the practical applicability and effectiveness of the Double-Circulation Double-Diamond model in the design of complex engineering equipment.

6.1. Design Optimization and System Integration

In the delivery phase, the engineering solutions for various functional conflicts are integrated into a holistic design scheme. The system’s dynamic hierarchical obstacle avoidance is achieved through multi-sensor fusion, and it employs a dual-mode operation of cruise and fine-scan to balance task precision and efficiency. Core data are transmitted in real time, while auxiliary data are processed via edge computing and transmitted through layered channels to optimize bandwidth utilization.

In addition, the incorporation of outer-loop feedback has been demonstrated to introduce redundancy mechanisms and health-diagnosis functions, thereby enhancing system reliability. It is evident that the proposed framework has been shown to successfully transform theoretical design concepts into an engineering-feasible solution through multiple iterative verifications under the Double-Circulation Double-Diamond model. This highlights both methodological innovation and practical applicability.

6.2. Outer-Loop Verification Through MATLAB Simulation

After completing the requirements analysis, technology mapping, and conflict identification, this chapter constructs static and dynamic scenarios using MATLAB R2025b (version 25.2.0) to validate the effectiveness of the “Dual-Circulation Dual-Diamond Model” in optimizing path planning solutions. Multiple algorithms are compared through simulation to verify whether the key technology weights and conflict pairs derived from the model align with actual performance. Through a combined static and dynamic validation process, a closed-loop demonstration is achieved, bridging theoretical analysis and engineering simulation.

6.3. Static Scenario Simulation Construction

To evaluate the fundamental performance of different path planning algorithms under conditions without traffic flow interference, this study constructed a 50 × 50 static two-dimensional grid environment and completed simulations on the MATLAB R2025b (version 25.2.0) platform. Several fixed obstacles were placed on the map, with vehicles simplified as uniform-speed point mass models. The starting point and destination were located at the bottom-left and top-right corners, respectively. To objectively measure algorithm performance, this section evaluates four aspects: path length, smoothness, computational efficiency, and feasibility. 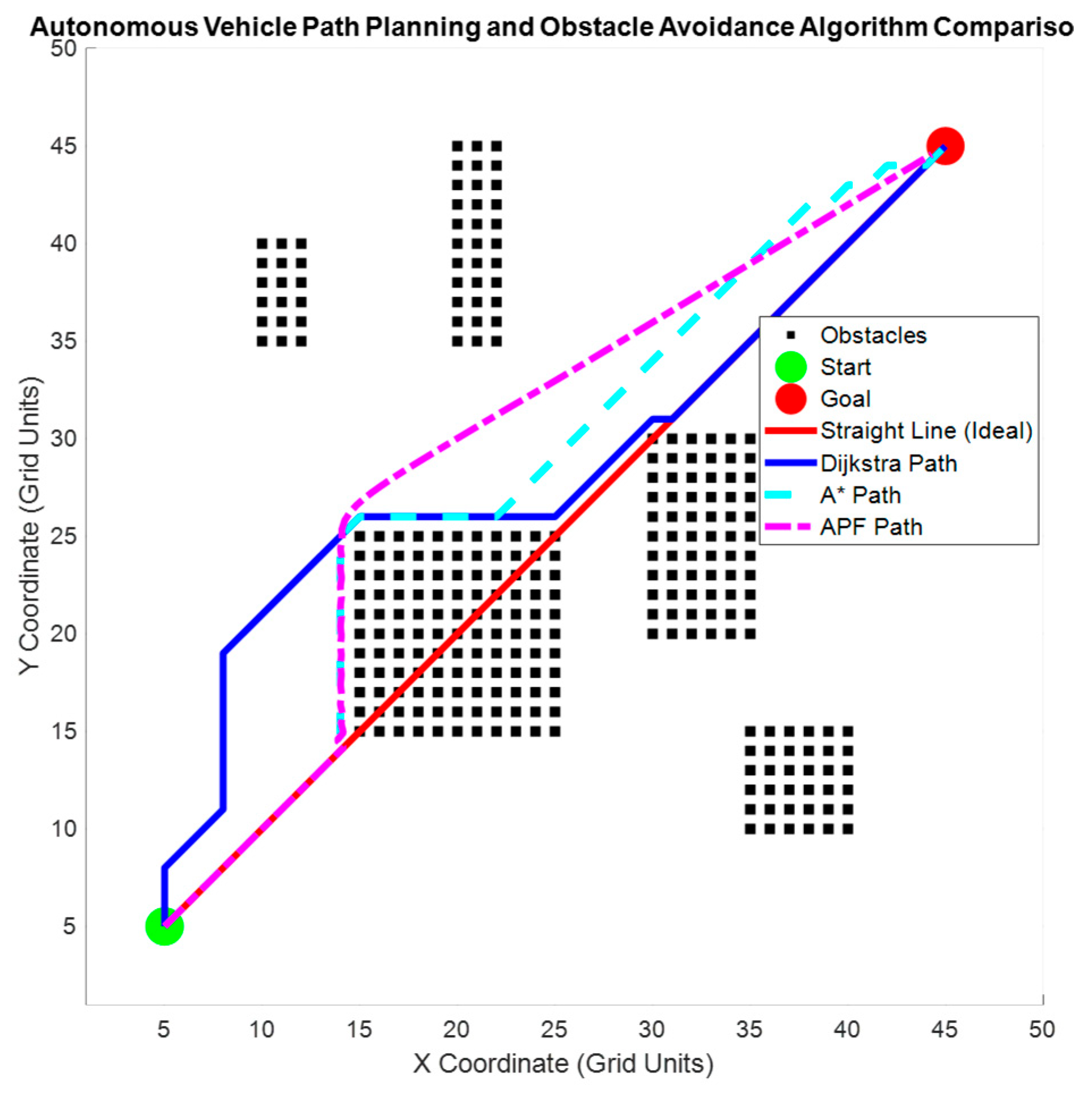Figure 8 displays the planning results of Dijkstra, A*, and the Artificial Potential Field (APF) method in this static environment. An ideal straight path is plotted for comparison, highlighting differences in deviation characteristics and smoothness during obstacle avoidance among the algorithms.

6.4. Analysis of Static Scenario Simulation Results

As shown in Figure 8, all three algorithms can generate feasible paths in static obstacle environments, but their performance differs significantly. Dijkstra’s algorithm achieves globally optimal paths but involves extensive search coverage, high computational cost, and paths with numerous abrupt turns, resulting in poor smoothness. A* significantly enhances search efficiency through heuristic functions, produces smoother paths, and offers the most balanced trade-off between path length and computational efficiency. APF exhibits the fastest computation speed but tends to oscillate or get stuck in local minima in densely obstructed areas, resulting in insufficient path stability. 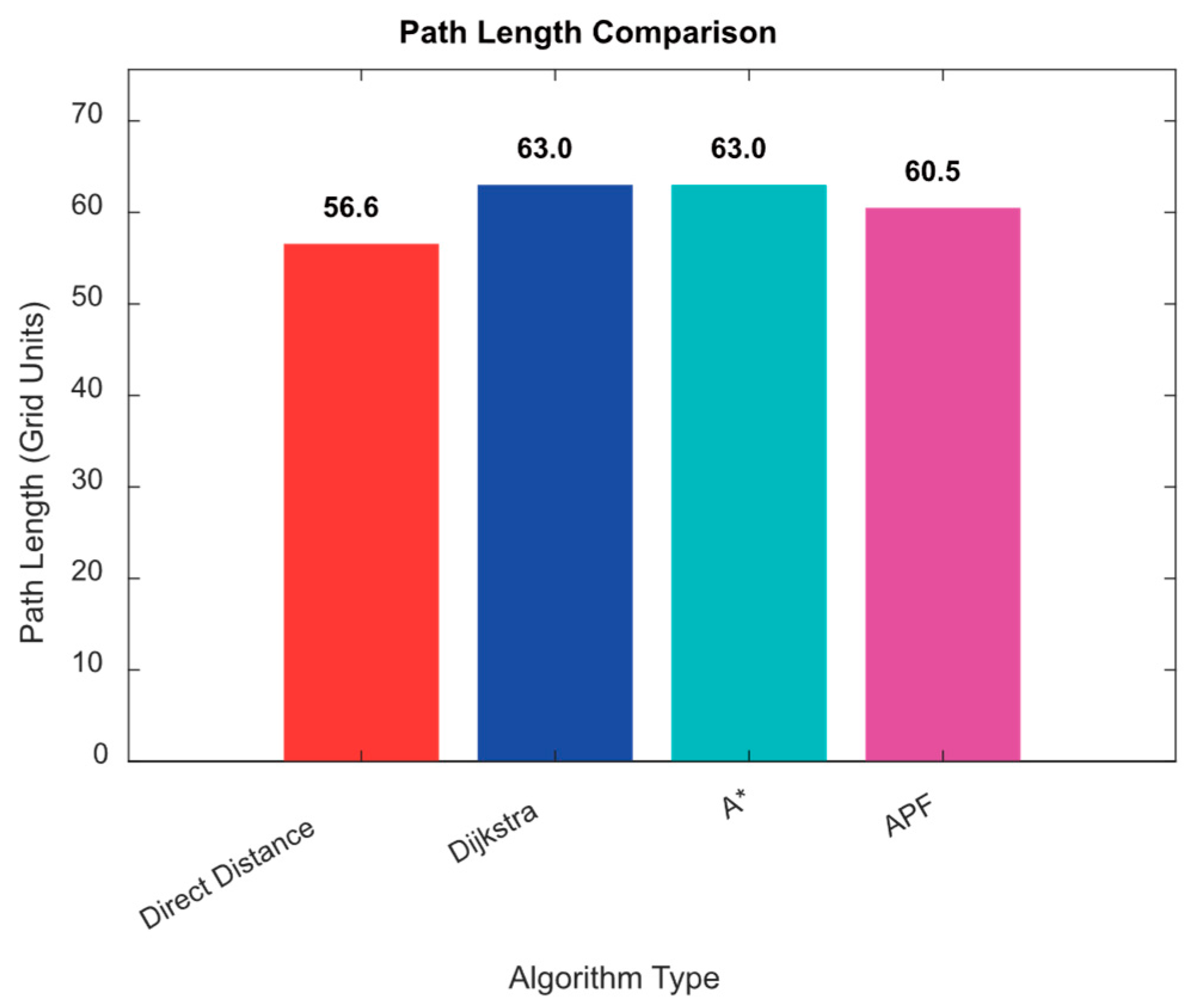The path length results in Figure 9 further indicate that A* and Dijkstra produce similar path lengths, while APF yields slightly shorter paths. However, its instability limits its reliability for global path planning tasks.

In summary, A* achieves the optimal balance between path quality and computational efficiency, making it the most effective algorithm in static scenarios. Consequently, subsequent dynamic scenario simulations adopt A* as the primary reference to evaluate its adaptability under complex conditions such as multi-vehicle interactions and speed variations.

6.5. Dynamic Multi-Vehicle Interaction Simulation

To validate the adaptability of path planning solutions in real-world highway maintenance scenarios, this section constructs a dynamic traffic environment featuring multi-vehicle interactions, speed variations, and static obstacles. The focus is on evaluating the safety, stability, and trajectory convergence capabilities of different algorithms under complex conditions. Compared to static scenarios, dynamic traffic flows better demonstrate the role of external loops in solution optimization and feedback-driven processes. This also provides a foundation for engineering validation of TRIZ invention principles such as “pre-action” and “dynamicization”.

6.6. Dynamic Simulation Construction

To validate the adaptability of path planning algorithms under multi-vehicle interaction conditions, this study constructed a two-dimensional dynamic traffic simulation environment in MATLAB R2025b (version 25.2.0), comprising a lead vehicle, dynamic obstacle vehicles, and static obstacles (as shown in Figure 10, Figure 11 and Figure 12). The simulation area measures 100 m × 50 m. The lead vehicle travels from the left starting point toward the target point in the upper right, employing a point-mass model with limited acceleration.

Three dynamic obstacle vehicles are positioned at their initial locations as shown in the figure, moving uniformly at different speeds along the longitudinal direction to simulate random traffic flow in high-speed maintenance scenarios. Two rectangular static obstacles, representing roadside facilities or work zone protective structures, are also placed to form impassable zones.

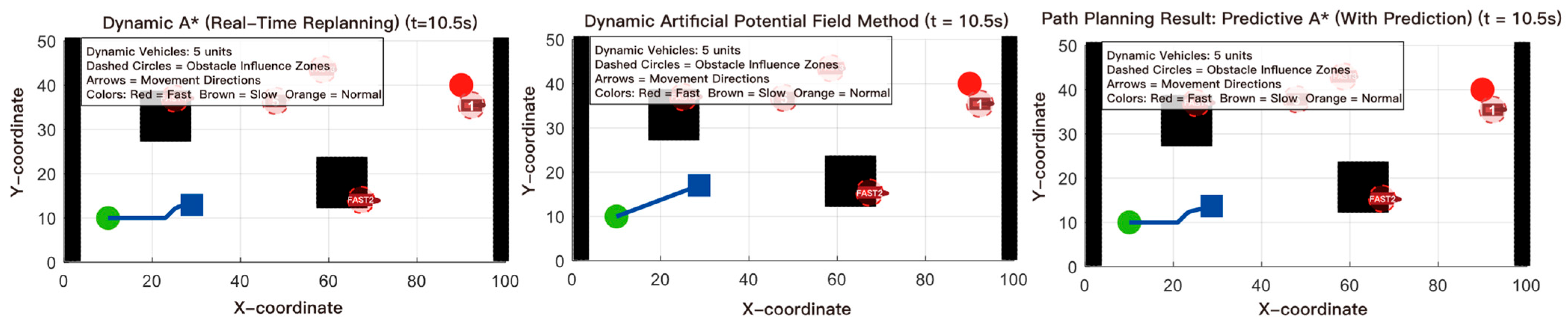
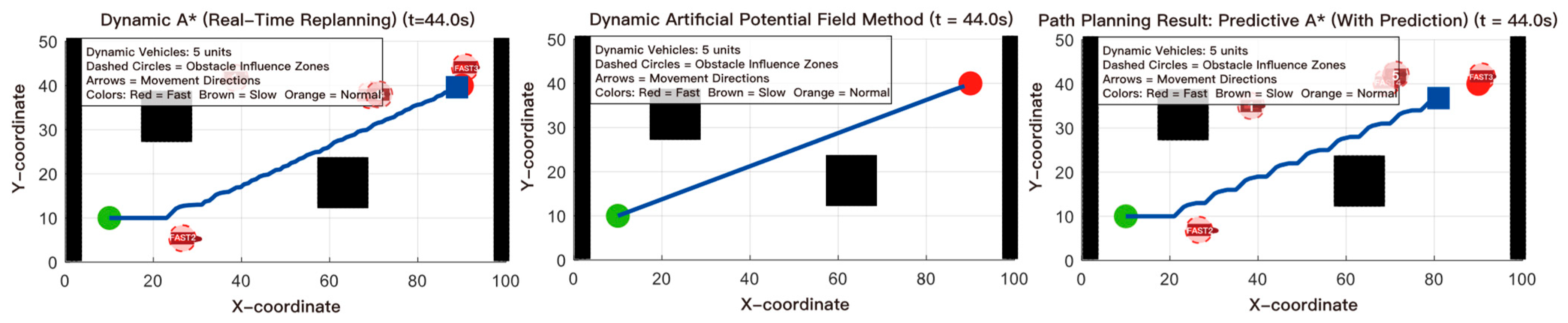
The simulation runs for 50 s, with key observation points at t = 10.5 s and t = 44.0 s to demonstrate the algorithm’s path planning performance during early, late, and full-process stages, as shown in Figure 10, Figure 11 and Figure 12.

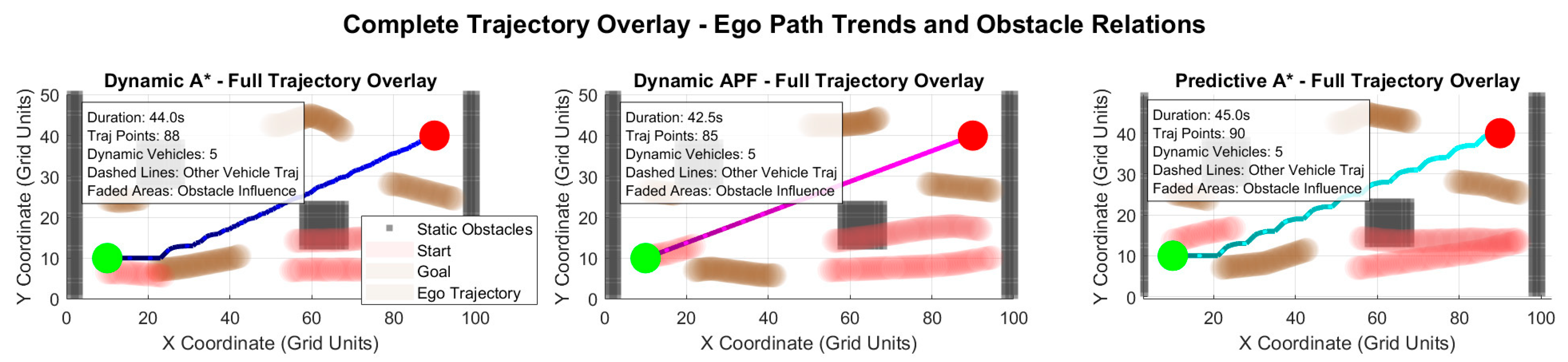
6.7. Analysis of Dynamic Scenario Simulation Results

Figure 10, Figure 11 and Figure 12 illustrate the planning results of the three algorithms at different stages within the dynamic scene, while

Table 12. Comparative Analysis of Dynamic Performance of Three Path Planning Algorithms at Three Critical Moments.

Time	Dynamic A*	Dynamic APF	Predictive A*	Overall Evaluation
Early stage (t = 10.5 s)	Feasible avoidance, but the trajectory contains noticeable zig-zag segments; local curvature exhibits sudden changes; delayed response to future obstacle motion	The trajectory is continuous, but field superposition leads to lateral deviation and slight oscillation	Utilizes predicted obstacle motion to avoid potential conflicts in advance; trajectory remains smooth with stable safety margins	Predictive A* shows the best early-stage dynamic interaction capability
Late stage (t = 44.0 s)	After multiple re-plannings, the path shows oscillations and reduced continuity	Field resonance causes local oscillations; the vehicle approaches obstacles at certain moments	Trajectory exhibits the highest stability; maintains safe spacing even in complex multi-vehicle merging regions	Predictive A* demonstrates significantly greater robustness in mid-to-late dynamic scenarios
Full-trajectory performance (0–50 s)	Path is relatively long with multiple sharp turns; frequent re-planning occurs	Path is shorter but includes segments where the vehicle travels close to obstacles	Trajectory is the smoothest, with uniform curvature variation; maintains stable safety distance throughout the entire process	Predictive A* achieves the best overall performance, suitable for complex dynamic environments

provides a structured comparison of their performance.

Results indicate that Dynamic A* exhibits path oscillation during complex interactions, while Dynamic APF demonstrates deviation and oscillation under potential field interference. Predictive A*, however, maintains a more stable and smoother trajectory throughout the entire journey, including both early and late stages. Overall, Predictive A* demonstrates higher robustness and consistency in handling multi-vehicle dynamic interference.

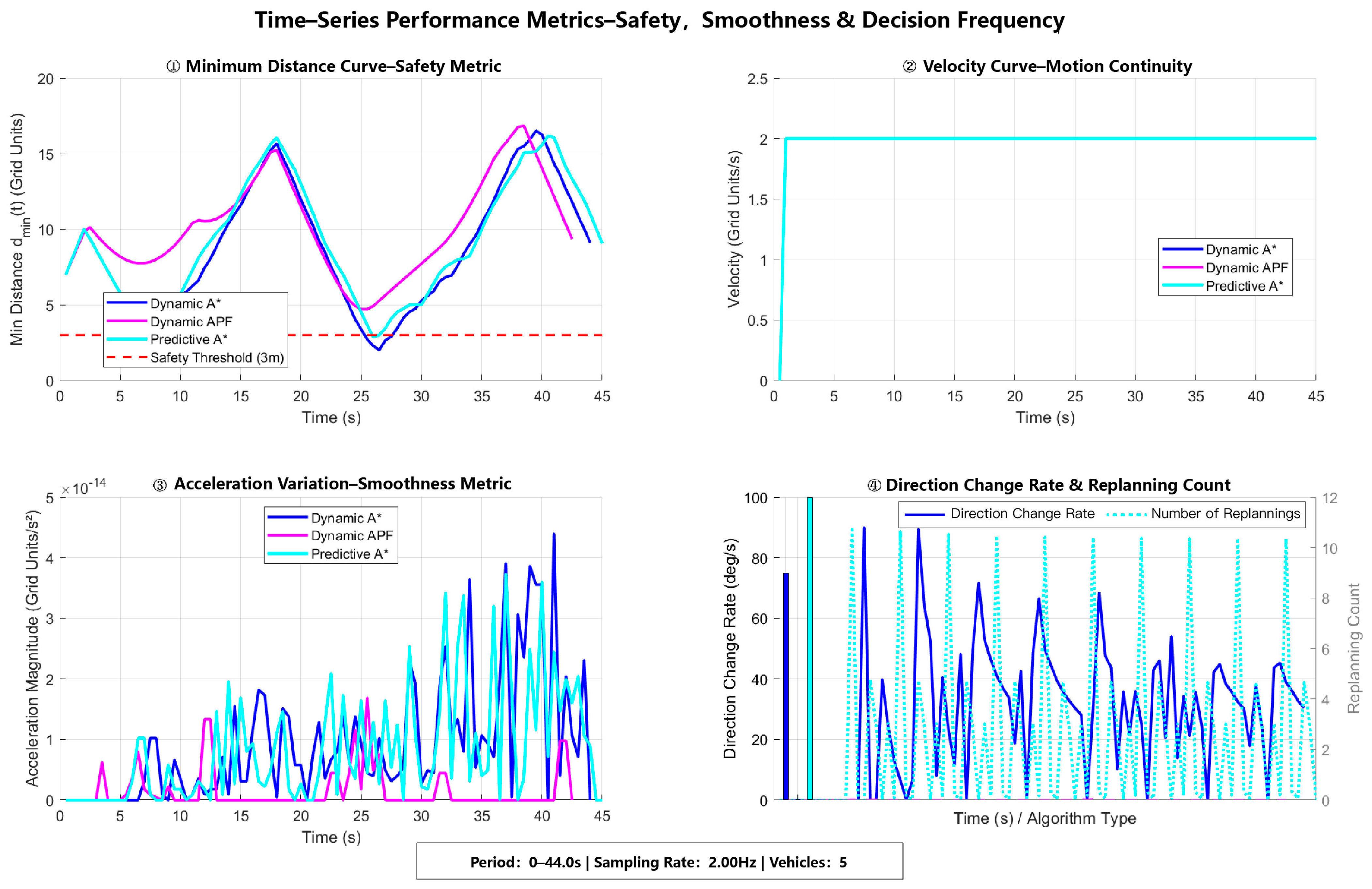
6.8. Dynamic Closed-Loop Performance Metrics Analysis

Figure 13 presents key timing metrics for the three algorithms in closed-loop simulation, including minimum safe distance, velocity and acceleration changes, rate of direction change, and number of replanings. These metrics quantify their safety, smoothness, and real-time performance in dynamic scenarios.

Results indicate that Predictive A* achieves optimal performance across metrics, including safety distance, velocity/acceleration fluctuations, and rate of direction change. In contrast, Dynamic A* and Dynamic APF exhibit instability during multi-vehicle interactions, manifesting as reduced safety distances and abrupt acceleration changes. Additionally, Predictive A* requires the fewest replanings, demonstrating superior trajectory consistency and computational efficiency.

In summary, the closed-loop metrics align with the trajectory comparison analysis, further validating that Predictive A* simultaneously achieves safety (T5), smoothness (T6), and real-time performance advantages in dynamic traffic scenarios.

6.9. Fuzzy Comprehensive Evaluation of the Design Method

After multiple iterations of internal and external cycles, the path planning scheme ultimately converged on a design strategy centered around Predictive A*. To further quantitatively assess the achievement level of this scheme, this paper employs the Fuzzy Comprehensive Evaluation (FCE) method, combined with indicator weights derived from the Analytic Hierarchy Process (AHP), to conduct a comprehensive evaluation of the overall design scheme [28].

This study invited six domain experts to score 17 secondary indicators using a four-point scale (4 indicates full achievement, 3 indicates good achievement, 2 indicates basic achievement, 1 indicates no achievement). A fuzzy evaluation matrix was constructed, and fuzzy operations were performed in conjunction with the weight vector to obtain the comprehensive membership degree and overall evaluation results for the scheme. The evaluation results are shown in

Table 13. Summary of Indicator Item Evaluation.

Requirement Indicator	Comprehensive Weight	Fully Achieved	Well Achieved	Partially Achieved	Not Achieved
C1	0.2554	4	2	0	0
C2	0.1301	3	2	1	0
C3	0.0640	5	1	0	0
C4	0.0379	3	2	1	0
C5	0.0230	4	1	1	0
D1	0.0613	3	2	1	0
D2	0.0298	2	3	1	0
D3	0.1769	4	1	1	0
D4	0.0153	3	2	1	0
E1	0.0864	5	1	0	0
E2	0.0281	4	2	0	0
E3	0.0170	3	2	1	0
E4	0.0104	2	3	1	0
F1	0.0337	2	2	2	0
F2	0.0151	4	1	1	0
F3	0.0084	2	3	1	0
F4	0.0047	3	2	1	0

.

Based on the aforementioned results, a weighted matrix of indicators and evaluation linguistic terms was constructed, and the membership degrees of each indicator were computed using a weighted averaging operator, as defined in Equation (10).

$$M(.,+):S_k=\min \left(1,\sum _{j=1}^m{\mu }_j{r}_{jk}\right),k=\mathrm{1,2},\dots ,n$$

(10)

Consequently, the weights of the four evaluation linguistic terms were obtained, as presented in

Table 14. Weight calculation results.

Membership Degree	Fully Achieved	Well Achieved	Partially Achieved	Not Achieved
Weight	0.436	0.328	0.178	0.058
Normalized Weight	0.436	0.328	0.178	0.058

, and the comprehensive scores of the evaluations were subsequently calculated, as shown in

Table 15. Comprehensive score calculation.

Comprehensive Score	Fully Achieved	Well Achieved	Partially Achieved	Not Achieved
3.142	4	3	2	1

.

The findings suggest that the maximum membership level of the scheme has been fully achieved, with a comprehensive score of 3.142, indicating a high level of accomplishment. The majority of high-weight requirements, such as pavement damage monitoring, obstacle detection and autonomous obstacle avoidance, have been successfully met. However, certain low-weight indicators, including automatic energy replenishment and autonomous return, still offer potential for enhancement. The scheme under review achieves a balance between core requirements and engineering feasibility. It also serves to validate the methodological value of the “Double Circulation Double Diamond” model in feedback-driven iteration and solution optimization.

7. Conclusions

In the context of the growing intricacy of highway maintenance tasks and mounting demands for safety and efficiency, conventional design methodologies encounter notable limitations when it comes to the design of complex equipment such as unmanned vehicles for highway maintenance. These challenges include the management of multi-source requirements, the resolution of technical conflicts, and the achievement of system integration. In order to address this issue, the present paper puts forward a “Double-Circulation Double-Diamond” design model that integrates AHP, QFD, and TRIZ. This approach provides a systematic and dynamic framework for addressing the design challenges associated with the use of unmanned vehicles in highway maintenance.

The model establishes a dynamic closed-loop design process—“demand identification—technology transformation—conflict resolution—solution validation”—by introducing dual internal and external feedback loops within the traditional double-diamond framework. Specifically, the AHP is employed to hierarchically analyze user demands and determine their weights; QFD maps high-priority demands to technical features, identifying key conflicting pairs; TRIZ systematically resolves technical contradictions to generate innovative solutions; MATLAB R2025b (version 25.2.0) simulation and fuzzy comprehensive evaluation further validate the feasibility and superiority of the solution in path planning and system performance. The simulation and evaluation results demonstrate that this design model exhibits significant advantages in terms of demand response, conflict coordination, and system integration.

The theoretical contributions of this study are primarily reflected in the following four aspects:

(1) Innovative Model Architecture: The proposed “Dual-Cycle Dual-Diamond” design framework integrates structured phase segmentation with dynamic feedback loops, enhancing the systematic approach and iterative capability in complex equipment design.

(2) Method Integration Mechanism: The integration of AHP, QFD, and TRIZ methodologies into distinct design phases systematically bridges the transformation pathways from requirement analysis to technical considerations and solution implementation.

(3) Feedback Loop Design: The model’s adaptability and feasibility in complex scenarios are enhanced by achieving intra-phase refinement and inter-phase optimization through internal and external cycles.

(4) System Validation Framework: The integration of simulation experiments with fuzzy comprehensive evaluation is a key aspect of the methodology, with the objective being to achieve practical verification from theoretical design to engineering feasibility.

From a methodological perspective, this integrated model exhibits a clear hierarchical structure: the internal cycle ensures information consistency within each stage, while the external cycle enables cross-stage requirement tracing and solution iteration. This configuration not only enhances the interpretability of the model but also provides a foundation for its extension to other complex system designs.

Although this study established a comprehensive design framework and validated its effectiveness, several limitations remain that warrant further investigation. First, AHP, QFD, and FCE rely on expert judgments, which inevitably introduce subjectivity. While the internal loop improves the consistency ratio (CR) of AHP, this primarily enhances agreement among experts rather than the objectivity of the evaluation. Future research could address this by: (1) integrating digital twin technology or high-fidelity vehicle dynamics models to construct engineering simulations that better reflect real-world conditions, and (2) incorporating data-driven approaches, such as accident statistics, sensor data, or machine learning-based dynamic weight adjustment, to reduce dependence on expert experience.

Furthermore, although the simulation environment reflects typical operational conditions, it simplifies dynamic traffic flow, vehicle interactions, and complex scenarios, limiting its representation of actual highway environments. Future work could leverage real traffic data or more sophisticated scenario modeling to improve the generalizability and reliability of the results. Finally, the current framework does not yet consider life-cycle indicators such as cost, energy consumption, and long-term operation and maintenance. Incorporating these factors would support a more comprehensive decision-making system for practical applications.

In summary, the “Double-Circulation Double-Diamond” design model proposed in this paper provides systematic, iterative, and integrated verification methodological support for the development of complex intelligent equipment such as unmanned highway maintenance vehicles. The product under discussion combines theoretical innovation with practical engineering value.