Next Article in Journal
Development of a Monitoring Method for Powered Roof Supports
Previous Article in Journal
Function-Centered Modeling of Complex Non-Physical Systems: An Exploratory GTST-MLD Application to an Unstructured System for Transformative Change
Previous Article in Special Issue
Kinematic and Dynamic Behavior of a Coastal Colluvial Landslide in a Low-Elevation Forest
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 15
Issue 23
10.3390/app152312829
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental and Numerical Study on the Influence of Forest Spatial Structure on Rockfall Protection Efficacy

by
Haiyang Liu
1,2,
Chunling Liu
1,2,*,
Jian Zhou
3,4,
Juanjuan Sun
5,6,*,
Kuiyu Shao
1,2,
Zhaocheng Guo
1,2 and
Xueliang Wang
7,8
1
China Aero Geophysical Survey and Remote Sensing Center for Natural Resources, Beijing 100083, China
2
Technology Innovation Center for Geohazards Identification and Monitoring with Earth Observation System, Ministry of Natural Resources of the People’s Republic of China, Beijing 100083, China
3
Key Laboratory of Urban Security and Disaster Engineering of Ministry of Education, Beijing University of Technology, Beijing 100124, China
4
College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China
5
State Key Laboratory of Precision Blasting, Jianghan University, Wuhan 430056, China
6
Hubei Key Laboratory of Blasting Engineering, Jianghan University, Wuhan 430056, China
7
State Key Laboratory of Lithospheric and Environmental Coevolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
8
College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing 100049, China
*
Authors to whom correspondence should be addressed.
Appl. Sci. 2025, 15(23), 12829; https://doi.org/10.3390/app152312829
Submission received: 29 October 2025 / Revised: 28 November 2025 / Accepted: 2 December 2025 / Published: 4 December 2025
(This article belongs to the Special Issue A Geotechnical Study on Landslides: Challenges and Progresses)
Browse Figures
Versions Notes

Abstract

With the growing emphasis on bio-engineering techniques, the sustainable advantages of using trees as barriers against rockfalls have become increasingly evident. The key mechanism for forest protection against rockfalls is the dissipation of block kinetic energy during impacts. However, previous studies have primarily focused on the overall attributes of protection forests, with limited attention to the quantitative relationship between internal spatial structural parameters and protective effectiveness. This study systematically investigated the effects of tree diameter, plant spacing, and arrangement pattern on rockfall energy dissipation through physical experiments. The results indicate that: (1) The energy dissipation capacity of trees increases with tree diameter; however, the rate of increase declines significantly when the relative diameter (the ratio of tree diameter to block size) exceeds 0.4. (2) Rockfall energy dissipation increases with reduced plant spacing, but the resultant gain exhibits a diminishing trend. (3) Under otherwise identical conditions, the rhombus arrangement pattern achieved a significantly higher rockfall energy dissipation rate (82.67%) than the square pattern (49.28%). Based on the experimental findings, an optimized protection scheme was designed for a typical rockfall on the slope of the Lehong Tunnel in Yunnan Province, southwestern China. Three-dimensional numerical simulation validated the designed scheme. The designed protection forests dissipated 89.49% of the kinetic energy from 0.5 m blocks, demonstrating the practical efficacy of the parameters derived from experiments. This study quantifies the influence of internal spatial structure parameters on the protective effectiveness of forests against rockfalls, providing a valuable theoretical basis and practical guidance for the design of ecological prevention measures against rockfall hazards.

1. Introduction

Rockfalls represent one of the most prevalent geological hazards in mountain areas. Traditional protection strategies primarily rely on engineering measures, such as flexible protection nets, retaining walls, and open-cut tunnels, to mitigate the impact and damage caused by falling rocks. With growing awareness of ecological and environmental protection, the concept of using bio-engineering measures for hazard mitigation has gained increasing attention [1,2,3,4]. Compared to geotechnical measures, ecological protection against geological hazards is characterized by self-repairing capabilities, long-lasting effects, low energy consumption, minimal material usage, and environmental compatibility. Forests on slopes function as natural barriers against instability phenomena, such as rockfall and shallow landslides [5,6]. Developing rockfall prevention technologies based on the protective effect of forests is crucial for enhancing the long-term efficacy of mitigation works. The utilization of forests for protection against mountain disasters was documented in Switzerland as early as the 14th century. Since then, Switzerland has consistently prioritized the planning and management of protection forests against mountain disasters [5].
The protective effect of forests against rockfalls is primarily reflected in the dissipation of the kinetic energy of falling blocks during block-tree impacts. The interactions between rockfalls and trees have been intensively studied through various methods, including field surveys, in situ and laboratory physical experiments, and numerical simulations [7,8,9,10,11,12,13]. The protective capacity of forests is largely determined by the stand structure. Consequently, considerable research has focused on how overall stand structural parameters, such as diameter at breast height (DBH), basal area (sum of the cross-sectional areas of all trees in a given area, measured at breast height), stand density, and species composition, influence protective effectiveness. For instance, Berger and Dorren [14] concluded that a basal area of at least 10 m2/ha is required for forests to effectively prevent rockfalls. Jancke et al. [10] and Song et al. [15] further demonstrated that protective capacity increases significantly with stand density and DBH. Additionally, researchers have found that slope gradient and block size also exert significant influence on the effectiveness of forests in preventing rockfalls [9,10].
Physical experiments have always been the fundamental method for investigating natural phenomena. Field experiments are regarded as the most effective approach for replicating actual rockfall events [16,17,18], whereas laboratory experiments offer higher repeatability and enable more precise control over variables [19,20,21]. In both methods, researchers investigate the kinematic characteristics of rockfalls by recording the motion process and extracting parameters such as velocity and trajectory [22,23,24,25,26]. Despite necessary simplifications, physical simulation remains a fundamental and reliable method for investigating rockfall phenomena.
Numerical simulation has greatly facilitated the rapid analysis of rockfall kinematic characteristics, complementing experimental methods. Based on extensive field surveys and experiments, researchers have statistically analyzed the height and frequency of impact marks on tree trunks to reconstruct the rockfall events [27,28]. These studies have not only enhanced the understanding of rockfall-forest interactions but also promoted the development and refinement of computational models in numerical simulation software to account for the influence of trees during rockfall processes [29,30]. These models have subsequently been applied to analyze rockfall hazards in forested areas, enabling the delimitation of hazard indication zones and the evaluation of forest management strategies for rockfall protection [31,32].
While previous studies have extensively investigated the protection effectiveness of forests against rockfalls through field surveys and experiments, a distinct research gap remains. Most of the studies treated the forests either as a unified entity or divided them into small units, leading to conclusions based on the average characteristics of the forest. Consequently, the influence of specific internal spatial structural parameters on protective effectiveness has received limited attention, despite its critical importance for the precise design of protection forests. To address this gap, this study aims to systematically quantify the effects of key internal spatial structural parameters on rockfall protection efficacy. The research objectives are twofold: (1) to determine the individual effects of tree diameter (characterized by DBH), plant spacing, and arrangement pattern on rockfall energy dissipation through controlled laboratory experiments; and (2) to develop an optimized protection forest scheme for a specific rockfall hazard based on the experimental trends and evaluate its protective effectiveness through numerical simulation. This research could provide a quantitative basis for the design of protection forests, thereby advancing the ecological mitigation of rockfall hazards.

2. Materials and Methods

2.1. Laboratory Experiment

2.1.1. Experimental Platform

The objective of this study was an exploratory investigation into the influence of forest spatial structure on rockfall protection capacity, aiming to provide a conceptual reference for practical protection forest design. Rather than adhering to strict similitude principles for field-scale replication, the experimental design prioritized the target parameters. Similitude considerations were therefore intentionally confined primarily to the relative scale between block and tree diameters. To further neutralize confounding variables, an idealized setup (a horizontal platform and spherical blocks) was employed. Consequently, analysis of slope angle, block size, and tree species was beyond the scope of this experiment.
The experimental platform (Figure 1) consists of the following five components: the slope surface, the release device, the image acquisition device, the support frame, and the image acquisition control system.
The relative scale between blocks and trees in the experiment was determined based on an extensive analysis of typical rockfall sites and previous physical experiments [17,24,33]. Accordingly, the reference block size was set at 0.5 m, and the reference tree diameter at breast height (DBH) was set at 20 cm. Since the objective of this experiment was to preliminarily explore the influence of internal spatial structural parameters of forests on protective effectiveness, the mass and strength of the blocks, as well as the strength of the tree trunks, were not rigorously controlled here.
Based on the experimental site conditions and the aforementioned reference dimensions, the geometric scales of rock blocks and tree diameters were determined. In the model, the rock block size was set to 2.5 cm, and the basic tree diameter was set to 1 cm. To minimize the influence of block shape on the protective effectiveness of forests, spherical blocks were adopted. As shown in Figure 2, four gypsum spheres with a diameter of 2.5 cm and a mass of 15.2 g were used to simulate falling rocks. The slope surface was constructed from wood and consisted of two distinct sections. The first section was a 30° inclined slope, which ensured that the blocks attained sufficient initial velocity before entering the protection forest area. The second section was a horizontal platform, where the wooden poles with a height of 10 cm were wedged into pre-drilled holes (as shown in Figure 1a) to simulate the forest stand on the slope.
In each trial, four gypsum spheres were released simultaneously from a height of 50 cm along the slope. Two high-speed cameras recorded the movements of the gypsum spheres from the front and side perspectives, respectively. The recorded footages were analyzed to extract the kinetic energy of the spheres immediately before they entered and after they exited the forest model. The energy dissipation attributable to tree impacts was then calculated as the difference in kinetic energy between these two time points.

2.1.2. Experimental Scheme

Three experimental scenarios were designed to examine the effects of tree diameter, plant spacing, and arrangement pattern on the protective effectiveness of forests against rockfalls. The configurations for these scenarios were as follows:
(1) Tree Diameters
Three diameters were tested for the wooden poles: 0.5 cm, 1.0 cm, and 1.5 cm. All poles were arranged in a rhombus pattern with uniform 10 cm spacing between rows and columns (Figure 3).
(2) Plant Spacing
Wooden poles with a diameter of 1 cm were arranged in a rhombus pattern. The row and column spacing, maintained at a 1:1 ratio, was set to 5 cm, 10 cm, and 20 cm for the three test conditions. (Figure 4).
(3) Arrangement Patterns
Wooden poles with a diameter of 1 cm were arranged in square and rhombus patterns, respectively, with 10 cm of uniform spacing between the rows and columns (Figure 5).
Following the experimental design, four gypsum spheres were placed at a fixed height of 50 cm on the slope surface and held in place by a robotic manipulator prior to each test. At the start of each trial, the manipulator opened, releasing all spheres to roll down the slope simultaneously.
Two high-speed cameras were used to capture the motion of each sphere as it entered and exited the forest stand (wooden pole area), based on which the velocity and kinetic energy could be extracted. The energy dissipation rate (EDR) was used to quantify the protective capacity of the forest, which is defined as the ratio of the total kinetic energy dissipation of rock blocks during their passage through the forest to their initial kinetic energy upon entry. The experimental procedure was repeated six times for each configuration. The average value of these replicates was calculated and adopted as the final result to minimize the influence of random errors.

2.1.3. Data Acquisition Process

The high-speed camera type used for image recording during the experiment was ORPIX FR-800 (NorPix, Inc., Montreal, QC, Canada). The recording rate was set to 300 frames per second. The recorded footages were analyzed using TEMA (V4.1) motion analysis software (Image Systems AB, Linköping, Sweden) to extract the kinematic characteristics of the blocks. This software enables comprehensive motion analysis by processing sequential images. Through automated target tracking, it quantifies the kinematic parameters, such as displacement, velocity, and acceleration.
The initial step in obtaining the kinematic parameters entailed pre-experiment setup, including camera calibration and parameter configuration (e.g., frame rate). Subsequently, a reference coordinate system was established, and the spatial scale was calibrated using the marked reference points (Points 1–4 in Figure 6).
A sequence of footage of the gypsum spheres was captured during testing. The four gypsum spheres in the kinematic images were labeled as tracking points A, B, C, and D (in Figure 6). When automated tracking deviated at any point, the process was paused for manual correction before resuming. After completion of entire motion tracking, the software generated a series of charts depicting the position, velocity, and acceleration of each tracked sphere. These charts visualized the kinematic trajectory and the variation in velocity and acceleration over time.

2.2. Numerical Simulation

Rockyfor3D (V6.0) (EcorisQ, Bern, Switzerland) is a three-dimensional (3D) numerical simulation program that is widely used to analyze the kinematic characteristics of rockfalls, especially in forested areas [34,35,36]. Its algorithms are based on extensive field surveys and experiments. By inputting parameters of slope surface and rockfall source areas into the software, the key kinematic characteristics of falling blocks can be obtained, including velocity, kinetic energy, arrival probability, and passing height. Additionally, the software enables the analysis in the presence of protection forests and flexible protection nets. This study primarily utilizes Rockyfor3D (V6.0) to comparatively analyze the kinematic characteristics of rockfalls before and after the implementation of designed protection forests and protection nets in a typical case, thereby assessing the protective effectiveness of rockfall mitigation strategies that incorporate protection forests.

2.2.1. Rockfall Case

The rockfall case is located in Lehong Township, Yunnan Province, in southwestern China (Figure 7b). Based on the field investigations and topographic data (with a resolution of 2 m) acquired via unmanned aerial vehicle (UAV), the slope gradient ranges from approximately 25° to 50°. The ground elevation ranges from 1325 m to 1540 m, resulting in a relative relief of about 215 m (Figure 7a). The upper section of slope is composed primarily of dolomite and dolomitic limestone, underlain by interbedded mudstone, shale, and siltstone. The lower section of slope comprises gray-green shale interbedded with siltstone. The slope vegetation consists primarily of shrubs and grasses, with scattered arbors. The slope toe area contains the entrance and exit portals of a highway tunnel, with access ramps located downslope.
Multiple unstable rock masses were identified along the steep cliff within the upper slope section based on field surveys and three-dimensional modeling obtained by UAV. Consequently, 15 rockfall source areas were identified and labeled as A through O (Figure 8). Field investigations and analysis of 3D model were conducted to assess the joint spacing, joint density in each rockfall source area, and the size of blocks in the downslope deposition zone. Based on these measurements, the representative block size was determined to be 0.5 m, with a cuboid shape.

2.2.2. Simulation Parameters

To evaluate the potential impact zone and kinematic parameters of the rockfalls, this study performed numerical simulations using Rockyfor3D (V6.0). The slope material parameters were calibrated through back analysis of historical rockfall events in adjacent areas. Zone ① corresponds to the bedrock exposure area, while Zone ② represents the highly weathered soil zone (Figure 7a). The specific parameters of the slope are detailed in Table 1. The distribution of rockfall source areas and the characteristics of unstable rock masses were determined as described in Section 2.2.1. The representative block size was set to 0.5 m, with additional parameters of rockfall sources listed in Table 2. In the simulation, 100 blocks were released from each grid point within the source areas.

3. Experimental Results

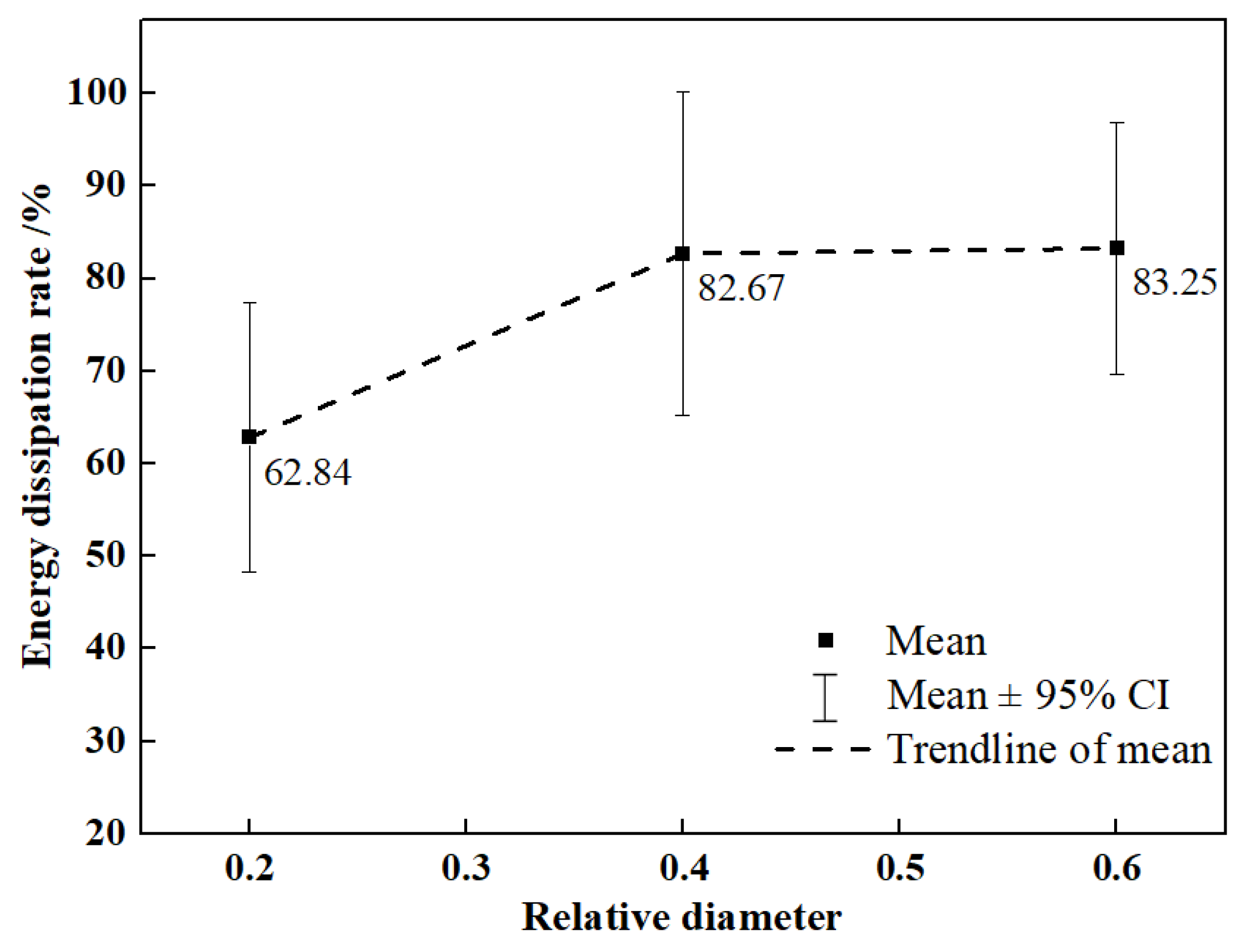
3.1. Different Tree Diameters

The kinematic parameters of the falling blocks were obtained by analyzing the image sequences captured with high-speed cameras. In the analysis, relative diameter was used to represent the relative size of tree diameter, defined as the ratio of tree trunk diameter to block size, which refers to the ratio of wooden pole diameter to gypsum block diameter in the experiment. To compare the changes in EDR of falling blocks corresponding to unit changes in tree spatial structure parameters, the concept of EDR variation rate (EDRVR) was introduced. For analyzing the effects of tree diameter, the EDRVR corresponds to the variation in EDR resulting from a unit change in the relative diameter.
The analysis results are presented in Figure 9. The EDR values for relative diameters of 0.2, 0.4, and 0.6 were 62.84%, 82.67%, and 83.25%, respectively. As the relative diameter increased from 0.2 to 0.4, the EDR rose by 19.83 percentage points. This corresponds to an EDRVR of 99.15%, which means that for every increment of the relative diameter, the energy dissipation increased by an additional 99.15%. However, when the relative diameter increased from 0.4 to 0.6, the EDR increased by only 0.58 percentage points, with a much lower corresponding EDRVR of 2.90%. This EDRVR was significantly lower than that observed when the relative diameter increased from 0.2 to 0.4. The analysis indicates that the energy dissipation of falling blocks increases with the relative diameter. However, beyond a relative diameter of approximately 0.4, further increases in relative diameter produce diminishing returns in energy dissipation capacity.
These experimental findings indicate that for the design of protection forests under similar slope conditions, optimal protective effectiveness can be achieved at a relative diameter of approximately 0.4. This value ensures sufficient protection effect while avoiding unnecessary costs.

3.2. Different Plant Spacing

In this analysis, the relative spacing was proposed to represent the relative magnitude of tree spacing, defined as the ratio of plant spacing to block diameter. In this section, EDRVR represents the variation in EDR per unit change in relative spacing.
The analysis results are illustrated in Figure 10. Corresponding to relative spacing values of 2, 4, and 8, the EDR values were determined to be 91.53%, 82.67%, and 52.17%, respectively. The results show that when the relative spacing decreased from 8 to 4, the EDR increased by 30.50 percentage points, corresponding to an EDRVR of 7.63%. When the relative spacing decreased from 4 to 2, the EDR increased by 8.86 percentage points, with a corresponding EDRVR of 4.43%. This EDRVR is lower than that observed for the decrease from 8 to 4. The analysis reveals that the protective effectiveness of forests increases as relative spacing decreases. However, the rate of this increase exhibits a decelerating trend as the relative spacing continues to diminish.

3.3. Different Arrangement Patterns

The results for this group of experiments are presented in Figure 11. The average EDR of the forest arranged in a rhombus pattern was 82.67%, while that in a square pattern was only 49.28%. This result clearly demonstrates that the protective effectiveness of the rhombus pattern is significantly superior to the square pattern. Therefore, the rhombus arrangement is the recommended configuration for practical protection forest design.

4. Protection Forest Scheme for the Rockfall Case

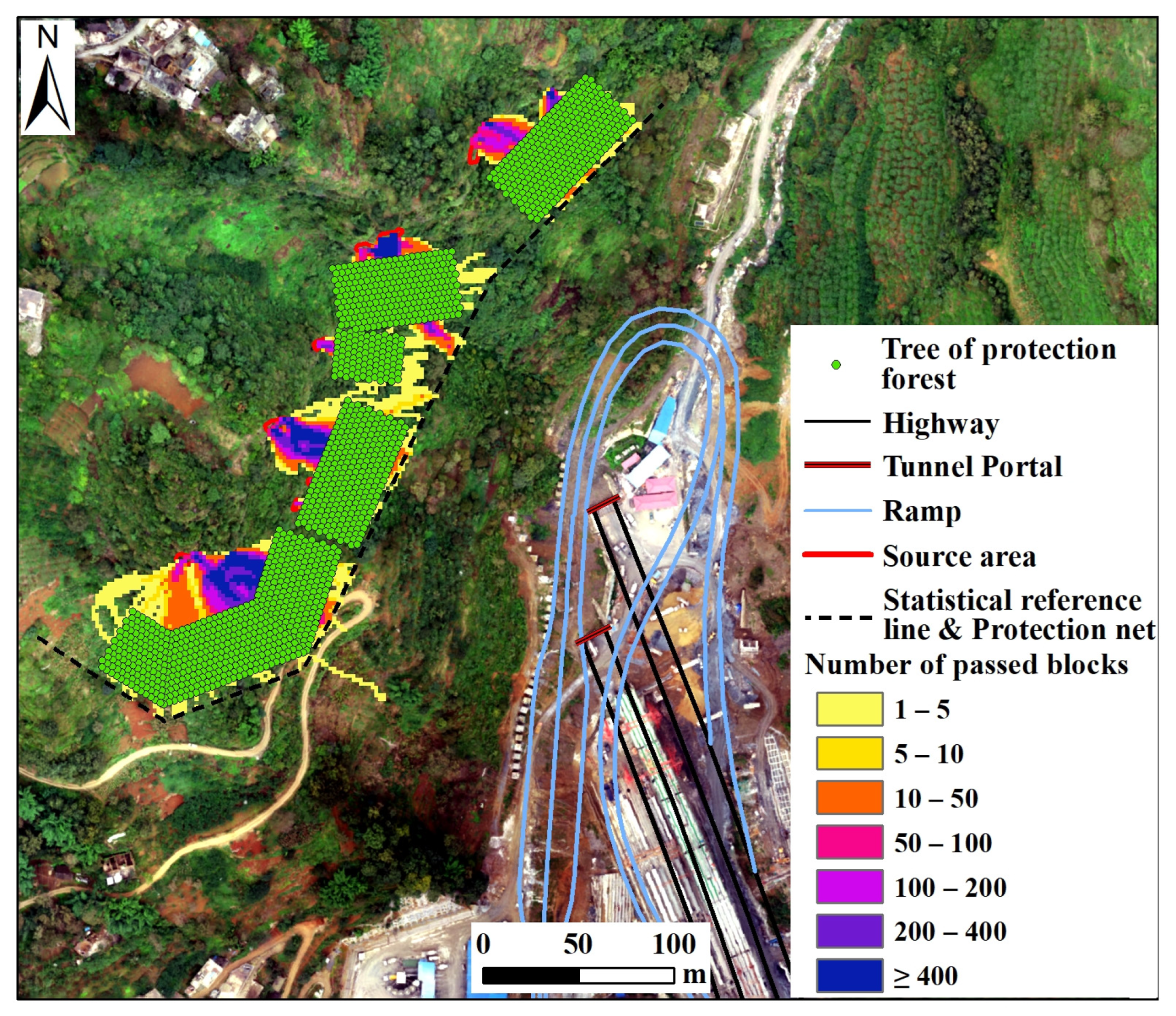
4.1. Simulation Without the Protection Forest

Before designating a forest protection scheme, it is necessary to determine the kinematic characteristics of rockfalls without the protection forest. This provides the basis for determining the distribution range of the protection forest.
Based on the parameter values specified in Section 2.2.2, simulations were conducted to analyze the kinematic characteristics of rockfalls within the study area. The simulation results are summarized in Figure 12. The results indicate that rock blocks falling from the identified source areas pose a direct threat to the tunnel portals and the access ramps.

4.2. Protection Scheme Design and Simulation

Based on the physical experiment results, a protection forest scheme was developed to mitigate the rockfall hazard on Lehong Tunnel slope. Field investigations confirmed that the characteristic block size and the slope condition at this site were consistent with the reference standard used in the physical experiments. Therefore, the internal structural parameters obtained from the physical experiments were directly applied in the protection forest design.
According to the analysis results in Section 3, the protective capacity of the forest arranged in a rhombus pattern was significantly higher than that of the forest arranged in a square pattern. Therefore, the rhombus arrangement was selected as the optimal configuration for the protection forest. Although larger basal areas enhance protective effectiveness, constraints such as economic costs, slope conditions, and canopy growth space must be considered in the design. Accordingly, the relative diameter and relative spacing were set to 0.4 and 6, respectively. For the characteristic block size of 0.5 m, we set the DBH to 20 cm and the plant spacing to 3 m. The design comprises 12 rows of trees, with the row lengths determined according to the specific slope conditions and the rockfall trajectories simulated in Section 4.1. Based on these parameter settings, the protective effectiveness of the forest scheme was assessed through 3D numerical simulation. A total of 6700 blocks were released from source areas in the simulation, with 100 blocks released from each source grid.
A statistical reference line was established at the location shown in Figure 12 and Figure 13 to facilitate statistical analysis of the number, kinetic energy and jump height of blocks reaching the same location under conditions with and without protective forests. In this case, the EDR is defined differently from that in physical experiments. It is defined as the difference between the kinetic energy without the forest and the kinetic energy with the forest at the reference line, divided by the kinetic energy without the forest. Both metrics effectively quantify the energy dissipation effect of the protection forests on the falling blocks. Simulation results are illustrated in Table 3 and Figure 14.
The analysis demonstrated that the designed protection forest significantly reduced the rockfall hazard for blocks with a characteristic size of 0.5 m. Compared to the condition without the protection forest, the EDR value increased to 89.49% with the protection forest in place. Most of the blocks at the reference line had passing heights below 3 m (Figure 14). Specifically, 80.62% of heights were below 1 m and 96.21% were below 3 m.
Currently, the maximum energy value that the passive flexible protection net can intercept reaches 8000 kJ [37,38]. Accordingly, a 3 m-high passive protection net was designed and employed beneath the protection forest. Numerical simulations were subsequently performed to reassess the rockfall kinematic characteristics in the study area. The simulation results are presented in Figure 15.
As shown in Figure 15, the integrated protective system, combining the protection forest and passive flexible net intercepted nearly all of the blocks. For the few blocks that penetrated the protective system, supplementary measures such as planting shrubs, constructing retaining walls or excavating interception trenches could be implemented in critical zones to enhance protection.

5. Discussion

5.1. Influence of Spatial Structure on Energy Dissipation

The experimental results demonstrate a nonlinear relationship between relative diameter and the rockfall protection efficacy of forests. This finding aligns with the work of Song et al. (2023) [15], who reported diminishing protective effects with increasing block size relative to tree dimensions. Furthermore, a critical threshold for the relative diameter was identified at approximately 0.4. Beyond this threshold, the EDR gains diminish significantly. Regarding plant spacing, the results indicate that reducing it enhances protective effectiveness, though EDR gains decline as it decreases. This observation is consistent with that of Jancke et al. (2009) [10], who found that stand density is the predominant factor for small blocks, while influence efficacy plateaus once a critical density is reached to ensure a high probability of impact. The underlying mechanism governing the enhanced protection capacity with increasing relative diameter and decreasing plant spacing is that both larger diameters and closer spacing increase the total cross-sectional area of trees per unit area. This increased cross-sectional coverage raises the probability of impacts between blocks and trees, thereby enhancing the forest’s protective capacity.
The movement of falling blocks is primarily influenced by their initial kinematic conditions and gravity, resulting in a predominant downward motion along the slope. For the forests in the rhombus arrangement, trees in the subsequent rows exactly fill the gaps between trees in preceding rows along the expected rockfall trajectories. This staggered arrangement forms a more continuous barrier, which significantly increases the impact probability compared to the square arrangement, thereby enhancing the overall protection efficacy of the forest.
The experimental results demonstrate that tree diameter, plant spacing, and arrangement pattern are critical factors influencing the protective effectiveness of forests. Therefore, in practical protection forest design, these structural parameters should be optimized while also considering slope conditions and economic feasibility.

5.2. Engineering Applications

The numerical simulation results indicated that the designed protection forest, incorporating the optimal relative diameter of 0.4 and the rhombus arrangement identified in laboratory experiments, dissipated 89.49% of the kinetic energy from 0.5 m blocks. This high interception effectiveness corroborates the Barrier Effect (BARI) index proposed by Dupire et al. (2016) [12], which quantifies the capacity of forest stands to intercept blocks based on geometric probability.
The simulation confirms that optimally configured forests serve as primary energy dissipators, significantly reducing impact loads on downstream infrastructure. This finding supports hybrid protection systems that integrate ecological barriers with engineering structures. As demonstrated by Moos et al. (2018) [39], incorporating the mitigating effect of forests into quantitative risk analysis can effectively reduce residual risk and enable downscaling of technical protection measures. Furthermore, Getzner et al. (2017) [40] emphasized that nature-based solutions provide substantial economic advantages, pointing out that engineering measures incur considerably higher costs than maintaining protection forests. By reducing the energy capacity requirements for passive protection nets, the optimized forest not only enhances safety but also potentially improves the cost-effectiveness of the overall mitigation project.

5.3. Limitations

Although this study provides valuable quantitative insights, several limitations inherent in the experimental design should be acknowledged. The physical experiments employed wooden poles and spherical blocks on a uniform slope, thereby simplifying the complex interactions occurring in natural environments. Specifically, rock fragmentation upon impact was not incorporated in the model. As demonstrated by Lanfranconi et al. (2023) [13], fragmentation can significantly alter the trajectories and residual hazards of rockfalls, a factor that simple restitution coefficients may fail to capture. Additionally, complex biomechanical behaviors of real trees, such as root rotation and stem damping [41], were not considered in this study. Future research should focus on establishing more realistic experimental protocols, such as considering rock fragmentation and the biomechanical properties of different species, to clarify how additional factors influence forest protection effectiveness and optimize forest designs for diverse environmental conditions.

6. Conclusions

This study systematically investigated the influence of key internal spatial structural parameters–tree diameter, plant spacing, and arrangement pattern-on the protective effectiveness of forests against rockfalls. Through a combination of physical experiments and numerical simulations, this research bridges the gap between theoretical understanding and practical design. The main findings are summarized as follows:
(1)
The protection efficacy of forests increases with tree diameter, while the gains plateau after the relative diameter reaches a certain threshold. For slopes with conditions analogous to this study, a relative diameter of 0.4 is recommended as the optimal parameter value for the protection forest design.
(2)
Protective effectiveness is enhanced by reducing plant spacing. However, the marginal gains exhibit a diminishing trend with closer spacing. The plant spacing design should integrate considerations of both tree growth space and economic constraints.
(3)
The rhombus arrangement enhances the probability of block-tree impact, achieving a substantially higher protective effectiveness compared to the square pattern.
(4)
An integrated protection scheme combining protection forests with flexible protection nets was designed based on the experimental results for the rockfall hazard at the Lehong Tunnel slope. Numerical simulations validated the scheme’s effectiveness, demonstrating its capacity to intercept nearly all falling blocks and dissipate 89.49% of the kinetic energy.
This study highlights the practical potential of the proposed optimization of forest spatial structure parameters in slope protection engineering, providing valuable design guidance for integrating ecological and engineering measures to prevent geological disasters.

Author Contributions

Conceptualization, H.L., C.L. and X.W.; methodology, H.L., C.L. and X.W.; software, H.L. and J.Z.; validation, J.Z. and J.S.; formal analysis, H.L., C.L. and J.S.; investigation, J.Z., J.S., K.S. and X.W.; resources, C.L. and Z.G.; data curation, H.L., J.S. and K.S.; writing—original draft preparation, H.L.; writing—review and editing, J.Z., J.S. and K.S.; visualization, H.L.; supervision, C.L. and Z.G.; project administration, C.L. and Z.G.; funding acquisition, C.L. and Z.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Second Tibetan Plateau Scientific Expedition and Research Program (STEP) (No. 2019QZKK0904), the Geological Survey Project of China Geological Survey (Comprehensive Remote Sensing Identification for Geohazards No. DD20230083; Operation and Maintenance of the National Geological Safety Monitoring and Early Warning Network No. DD20251300205), and the Key Laboratory of Airborne Geophysics and Remote Sensing Geology Foundation (No. 2023YFL22).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors on request.

Acknowledgments

The authors thank faculty and students of College of Civil Engineering and Architecture, Quzhou University, for their support of the physical experiment. Especially, the authors wish to thank Xiaohui Liao for providing access to testing equipment, facilities, and test site support.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
DBHDiameter at Breast Height
3DThree-dimensional
UAVUnmanned Aerial Vehicle
EDREnergy Dissipation Rate
EDRVRVariation Rate of Energy Dissipation Rate

References

  1. Liu, X.; Hao, G.; Zhang, Y.; Xiang, L.; Wang, L. Study on improvement effect of herb plants on slope stability of dumping site. J. Saf. Sci. Technol. 2021, 17, 103–108. [Google Scholar] [CrossRef]
  2. Faruqi, A.; Hall, C.; Kendall, A. Sustainability of bio-mediated and bio-inspired ground improvement techniques for geologic hazard mitigation: A systematic literature review. Front. Earth Sci. 2023, 11, 1211574. [Google Scholar] [CrossRef]
  3. Giupponi, L.; Borgonovo, G.; Giorgi, A.; Bischetti, G.B. How to renew soil bioengineering for slope stabilization: Some proposals. Landsc. Ecol. Eng. 2019, 15, 37–50. [Google Scholar] [CrossRef]
  4. Mickovski, S.B. Re-Thinking Soil Bioengineering to Address Climate Change Challenges. Sustainability 2021, 13, 3338. [Google Scholar] [CrossRef]
  5. Jonsson, M.J. Energy Absorption of Trees in a Rockfall Protection Forest. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2007. [Google Scholar] [CrossRef]
  6. Reubens, B.; Poesen, J.; Danjon, F.; Geudens, G.; Muys, B. The role of fine and coarse roots in shallow slope stability and soil erosion control with a focus on root system architecture: A review. Trees 2007, 21, 385–402. [Google Scholar] [CrossRef]
  7. Corona, C.; Lopez-Saez, J.; Favillier, A.; Mainieri, R.; Eckert, N.; Trappmann, D.; Stoffel, M.; Bourrier, F.; Berger, F. Modeling rockfall frequency and bounce height from three-dimensional simulation process models and growth disturbances in submontane broadleaved trees. Geomorphology 2017, 281, 66–77. [Google Scholar] [CrossRef]
  8. Moos, C.; Khelidj, N.; Guisan, A.; Lischke, H.; Randin, C.F. A quantitative assessment of rockfall influence on forest structure in the Swiss Alps. Eur. J. For. Res. 2021, 140, 91–104. [Google Scholar] [CrossRef]
  9. Perret, S.; Dolf, F.; Kienholz, H. Rockfalls into forests: Analysis and simulation of rockfall trajectories—Considerations with respect to mountainous forests in Switzerland. Landslides 2004, 1, 123–130. [Google Scholar] [CrossRef]
  10. Jancke, O.; Dorren, L.K.A.; Berger, F.; Fuhr, M.; Köhl, M. Implications of coppice stand characteristics on the rockfall protection function. For. Ecol. Manag. 2009, 259, 124–131. [Google Scholar] [CrossRef]
  11. Dupire, S.; Bourrier, F.; Monnet, J.M.; Bigot, S.; Borgniet, L.; Berger, F.; Curt, T. The protective effect of forests against rockfalls across the French Alps: Influence of forest diversity. For. Ecol. Manag. 2016, 382, 269–279. [Google Scholar] [CrossRef]
  12. Dupire, S.; Bourrier, F.; Monnet, J.M.; Bigot, S.; Borgniet, L.; Berger, F.; Curt, T. Novel quantitative indicators to characterize the protective effect of mountain forests against rockfall. Ecol. Indic. 2016, 67, 98–107. [Google Scholar] [CrossRef]
  13. Lanfranconi, C.; Frattini, P.; Sala, G.; Dattola, G.; Bertolo, D.; Sun, J.; Crosta, G.B. Accounting for the Effect of Forest and Fragmentation in Probabilistic Rockfall Hazard. Nat. Hazards Earth Syst. Sci. 2023, 23, 2349–2363. [Google Scholar] [CrossRef]
  14. Berger, F.; Dorren, L.K. Principles of the tool Rockfor.net for quantifying the rockfall hazard below a protection forest. Schweiz. Z. Forstwes. 2007, 158, 157–165. [Google Scholar] [CrossRef]
  15. Song, K.; Yang, H.; Liang, D.; Chen, L.; Qu, L.; Chen, C. Assessment and Mechanism Analysis of Forest Protection against Rockfall in a Large Rock Avalanche Area. Forests 2023, 14, 1982. [Google Scholar] [CrossRef]
  16. Okura, Y.; Kitahara, H.; Sammori, T.; Kawanami, A. The effects of rockfall volume on runout distance. Eng. Geol. 2000, 58, 109–124. [Google Scholar] [CrossRef]
  17. Okada, Y.; Uchida, I. Dependence of runout distance on the number of rock blocks in large-scale rock-mass failure experiments. J. For. Res. 2014, 19, 329–339. [Google Scholar] [CrossRef]
  18. Lan, H.; Li, L.; Wu, Y. Stochasticity of Rockfall Tracjectory Revealed by a Field Experiment Repeated on a Single Sample. In Engineering Geology for Society and Territory; Springer International Publishing: Cham, Switzerland, 2015; Volume 2, pp. 1713–1721. [Google Scholar] [CrossRef]
  19. Piteau, D.R.; Clayton, R. Proceedings of the meeting on rockfall dynamics and protective works effectiveness. In Computer Rockfall Model; ISMES Publication No. 90; ISMES: Bergamo, Italy, 1976; pp. 123–125. [Google Scholar]
  20. Chau, K.; Wong, R.; Wu, J. Coefficient of restitution and rotational motions of rockfall impacts. Int. J. Rock Mech. Min. Sci. 2002, 39, 69–77. [Google Scholar] [CrossRef]
  21. Buzzi, O.; Giacomini, A.; Spadari, M. Laboratory Investigation on High Values of Restitution Coefficients. Rock Mech. Rock Eng. 2011, 45, 35–43. [Google Scholar] [CrossRef]
  22. Huang, R.; Liu, W.; Zhou, J.; Pei, X. Rolling tests on movement characteristics of rock blocks. Chin. J. Geotech. Eng. 2007, 29, 1296–1302. [Google Scholar] [CrossRef]
  23. Giacomini, A.; Thoeni, K.; Lambert, C.; Booth, S.; Sloan, S.W. Experimental study on rockfall drapery systems for open pit highwalls. Int. J. Rock Mech. Min. Sci. 2012, 56, 171–181. [Google Scholar] [CrossRef]
  24. Asteriou, P.; Tsiambaos, G. Effect of impact velocity, block mass and hardness on the coefficients of restitution for rockfall analysis. Int. J. Rock Mech. Min. Sci. 2018, 106, 41–50. [Google Scholar] [CrossRef]
  25. Lin, Q.; Cheng, Q.; Li, K.; Xie, Y.; Wang, Y. Contributions of Rock Mass Structure to the Emplacement of Fragmenting Rockfalls and Rockslides: Insights From Laboratory Experiments. J. Geophys. Res. Solid Earth 2020, 125, e2019JB019296. [Google Scholar] [CrossRef]
  26. Huang, J.; Huang, X.; Wang, H.; Liao, J.; He, Z. Experimental study on physical model of dynamic fragmentation process in high-locality rockfall. Chin. J. Rock Mech. Eng. 2023, 42, 2164–2174. [Google Scholar] [CrossRef]
  27. Dorren, L.K.A.; Berger, F.; Hir, C.L.; Mermin, E.; Tardif, P. Mechanisms, effects and management implications of rockfall in forests. For. Ecol. Manag. 2005, 215, 183–195. [Google Scholar] [CrossRef]
  28. Perret, S.; Stoffel, M.; Kienholz, H. Spatial and temporal rockfall activity in a forest stand in the Swiss Prealps—A dendrogeomorphological case study. Geomorphology 2006, 74, 219–231. [Google Scholar] [CrossRef]
  29. Dorren, L.K.A.; Seijmonsbergen, A.C. Comparison of three GIS-based models for predicting rockfall runout zones at a regional scale. Geomorphology 2003, 56, 49–64. [Google Scholar] [CrossRef]
  30. Rammer, W.; Brauner, M.; Dorren, L.K.A.; Berger, F.; Lexer, M.J. Evaluation of a 3-D rockfall module within a forest patch model. Nat. Hazards Earth Syst. Sci. 2010, 10, 699–711. [Google Scholar] [CrossRef]
  31. Dorren, L.K.A.; Schaller, C.; Erbach, A.; Moos, C. Automated Delimitation of Rockfall Hazard Indication Zones Using High-Resolution Trajectory Modelling at Regional Scale. Geosciences 2023, 13, 182. [Google Scholar] [CrossRef]
  32. Bigot, C.; Dorren, L.K.A.; Berger, F. Quantifying the protective function of a forest against rockfall for past, present and future scenarios using two modelling approaches. Nat. Hazards 2009, 49, 99–111. [Google Scholar] [CrossRef]
  33. Han, Z.; Chen, X.; Wang, X.; Zhao, T.; Zhou, J.; Zhang, L. Risk Assessment for Luojiaqinggangling Rockfall. J. Eng. Geol. 2017, 25, 520–530. [Google Scholar] [CrossRef]
  34. Dorren, L.K.A. Rockyfor3D (V6.0) Revealed—Transparent Description of the Complete 3D Rockfall Model. EcorisQ Manual. 2025. Available online: www.ecorisq.org (accessed on 5 October 2025).
  35. Stoffel, M.; Wehrli, A.; Kühne, R.; Dorren, L.K.A.; Perret, S.; Kienholz, H. Assessing the protective effect of mountain forests against rockfall using a 3D simulation model. For. Ecol. Manag. 2006, 225, 113–122. [Google Scholar] [CrossRef]
  36. Moos, C.; Dorren, L.K.A.; Stoffel, M. Quantifying the effect of forests on frequency and intensity of rockfalls. Nat. Hazards Earth Syst. Sci. 2017, 17, 291–304. [Google Scholar] [CrossRef]
  37. Zhao, S.; Yu, Z.; Zhao, L.; Qi, X.; Wei, T. Damage mechanism of rockfall barriers under strong impact loading. Eng. Machenics 2016, 33, 24–34. [Google Scholar] [CrossRef]
  38. European Organization for Technical Approvals (EOTA). Guideline for European Technical Approval of Falling Rock Protection Kits—ETAG 27; European Commission: Brussels, Belgium, 2008. [Google Scholar]
  39. Moos, C.; Fehlmann, M.; Trappmann, D.; Stoffel, M.; Dorren, L. Integrating the mitigating effect of forests into quantitative rockfall risk analysis—Two case studies in Switzerland. Int. J. Disaster Risk Reduct. 2018, 32, 55–74. [Google Scholar] [CrossRef]
  40. Getzner, M.; Gutheil-Knopp-Kirchwald, G.; Kreimer, E.; Kirchmeir, H.; Huber, M. Gravitational natural hazards: Valuing the protective function of Alpine forests. For. Policy Econ. 2017, 80, 150–159. [Google Scholar] [CrossRef]
  41. Dorren, L.K.; Maier, B.; Putters, U.S.; Seijmonsbergen, A.C. Combining field and modelling techniques to assess rockfall dynamics on a protection forest hillslope in the European Alps. Geomorphology 2004, 57, 151–167. [Google Scholar] [CrossRef]
Applsci 15 12829 g001
Figure 1. Structure of experimental platform: (a) Slope surface, (b) Release device, (c) Image acquisition device, (d) Support frame, (e) Image acquisition control system.
Figure 1. Structure of experimental platform: (a) Slope surface, (b) Release device, (c) Image acquisition device, (d) Support frame, (e) Image acquisition control system.
Applsci 15 12829 g001
Applsci 15 12829 g002
Figure 2. The gypsum spheres used in the experiment.
Figure 2. The gypsum spheres used in the experiment.
Applsci 15 12829 g002
Applsci 15 12829 g003
Figure 3. Wooden poles of different diameters: (a) 0.5 cm, (b) 1.0 cm, (c) 1.5 cm.
Figure 3. Wooden poles of different diameters: (a) 0.5 cm, (b) 1.0 cm, (c) 1.5 cm.
Applsci 15 12829 g003
Applsci 15 12829 g004
Figure 4. Wooden poles of different plant spacing: (a) 5 cm, (b) 10 cm, (c) 20 cm.
Figure 4. Wooden poles of different plant spacing: (a) 5 cm, (b) 10 cm, (c) 20 cm.
Applsci 15 12829 g004
Applsci 15 12829 g005
Figure 5. Wooden poles of different arrangement patterns: (a) Square pattern, (b) Rhombus pattern.
Figure 5. Wooden poles of different arrangement patterns: (a) Square pattern, (b) Rhombus pattern.
Applsci 15 12829 g005
Applsci 15 12829 g006
Figure 6. Calibration of the coordinate system.
Figure 6. Calibration of the coordinate system.
Applsci 15 12829 g006
Applsci 15 12829 g007
Figure 7. Topography (a) and location (b) of the rockfall case.
Figure 7. Topography (a) and location (b) of the rockfall case.
Applsci 15 12829 g007
Applsci 15 12829 g008
Figure 8. The site photo of rockfall source areas.
Figure 8. The site photo of rockfall source areas.
Applsci 15 12829 g008
Applsci 15 12829 g009
Figure 9. Energy dissipation rates for different relative diameters.
Figure 9. Energy dissipation rates for different relative diameters.
Applsci 15 12829 g009
Applsci 15 12829 g010
Figure 10. Energy dissipation rates for different relative spacing.
Figure 10. Energy dissipation rates for different relative spacing.
Applsci 15 12829 g010
Applsci 15 12829 g011
Figure 11. Energy dissipation rates for different arrangement patterns.
Figure 11. Energy dissipation rates for different arrangement patterns.
Applsci 15 12829 g011
Applsci 15 12829 g012
Figure 12. Rockfall numerical simulation result without a protection forest.
Figure 12. Rockfall numerical simulation result without a protection forest.
Applsci 15 12829 g012
Applsci 15 12829 g013
Figure 13. Rockfall numerical simulation result with the designed protection forest.
Figure 13. Rockfall numerical simulation result with the designed protection forest.
Applsci 15 12829 g013
Applsci 15 12829 g014
Figure 14. Passing heights of blocks reaching the reference line (with designed protection forest).
Figure 14. Passing heights of blocks reaching the reference line (with designed protection forest).
Applsci 15 12829 g014
Applsci 15 12829 g015
Figure 15. Rockfall numerical simulation result with a protection forest and net.
Figure 15. Rockfall numerical simulation result with a protection forest and net.
Applsci 15 12829 g015
Table 1. Back analysis results of slope parameters.
Table 1. Back analysis results of slope parameters.
Zone NumberRg70 aRg20Rg10Soiltype b
①00.050.15
②0.030.030.033
a Rg70 corresponds to the height of a representative obstacle in m that a falling block encounters in resp. 70%. Analogously, Rg20 and Rg10 represent the corresponding values. b Soil type corresponds to the type of soil. In this study, 5 represents bedrock with thin weathered material, and 3 represents medium compact soil with small rock fragments [34].
Table 2. Parameters of rockfall sources.
Table 2. Parameters of rockfall sources.
ParametersValue
Block size (m3)0.5 × 0.5 × 0.5
Calculation times100
Block shape/blshapeCuboid/1
Rock mass density (kg/m3)2800
Table 3. The simulation results with and without the protection forest.
Table 3. The simulation results with and without the protection forest.
Without Protection ForestWith Protection ForestEDR/%
Number of Reaching BlocksTotal Kinetic Energy
/kJ		The Maximum Kinetic Energy of the Blocks/kJNumber of Reaching BlocksTotal Kinetic Energy
/kJ		The Maximum Kinetic Energy of the Blocks/kJ
581596,355.9161.871210,12772.189.49
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Liu, H.; Liu, C.; Zhou, J.; Sun, J.; Shao, K.; Guo, Z.; Wang, X. Experimental and Numerical Study on the Influence of Forest Spatial Structure on Rockfall Protection Efficacy. Appl. Sci. 2025, 15, 12829. https://doi.org/10.3390/app152312829

AMA Style

Liu H, Liu C, Zhou J, Sun J, Shao K, Guo Z, Wang X. Experimental and Numerical Study on the Influence of Forest Spatial Structure on Rockfall Protection Efficacy. Applied Sciences. 2025; 15(23):12829. https://doi.org/10.3390/app152312829

Chicago/Turabian Style

Liu, Haiyang, Chunling Liu, Jian Zhou, Juanjuan Sun, Kuiyu Shao, Zhaocheng Guo, and Xueliang Wang. 2025. "Experimental and Numerical Study on the Influence of Forest Spatial Structure on Rockfall Protection Efficacy" Applied Sciences 15, no. 23: 12829. https://doi.org/10.3390/app152312829

APA Style

Liu, H., Liu, C., Zhou, J., Sun, J., Shao, K., Guo, Z., & Wang, X. (2025). Experimental and Numerical Study on the Influence of Forest Spatial Structure on Rockfall Protection Efficacy. Applied Sciences, 15(23), 12829. https://doi.org/10.3390/app152312829

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop