Research on the Short-Term Compressive Creep Behavior of the Bamboo Scrimber Based on Different Zener Models

Abstract

For the gluing process of natural fiber-reinforced composite materials like bamboo scrimber, an obvious creep behavior can be found during the working stage, which must be seriously considered in safety and reliability design. In this paper, the compressive creep performance of the bamboo scrimber, a kind of plywood material, was chosen as the research object. Several groups of compressive creep tests were conducted with various stress levels and samples to record the respective processes of creep strain evolution. Furthermore, different types of models were adopted in studying the compressive viscoelastic behavior of the material. The creep growth is sensitive to the stress level of the creep test, according to the results. Furthermore, the conventional Zener model can work well for simulating the compressive creep strain growth behavior of the bamboo scrimber at high stress levels, but obvious errors can sometimes occur when it is applied to analyze this property under low stress levels. At the same time, using MD (memory-dependent) theory to define the Zener model can pertain to the requirement of accuracy in analyzing the compressive creep property under all load conditions and is more practically useful.

1. Introduction

Nowadays, plywood materials made using natural fibers, such as bamboo scrimber, have been widely used in various fields of modern industry [1,2]. Compared with metal and synthetic materials, this kind of material made with natural bamboo fiber is superior due to the following factors: lower costs, more abundant resources, shorter life cycles, and so on. Meanwhile, the application scenarios of this material in real life are usually the construction or furniture engineering. Due to this fact, some important factors of the material, such as the mechanical property, should be accurately evaluated before application [3].

Focused on this topic, a large amount of corresponding research has been carried out in recent years. Among these, Huang experimented with several kinds of flexural tests based on different beam models to accurately compute the key strength parameters of the material [4,5]. Li conducted the experimental evaluation on the axial crushing performance of the BFRP-bamboo winding composite hollow components, and the test results showed that this type of bamboo material had superior crushing resistance with a lighter weight than some other commonly used materials [6,7,8]. Liu studied the low-velocity impact performance of two kinds of bamboo-based laminated composites and found that, compared with the BGFLC (bamboo/glass fiber laminated composite), the BPLC (bamboo/poplar laminated composite) showed a better impact property [9]. Cui conducted both experimental and theoretical studies on the mechanical performance of the bolt steel-to-laminated bamboo connection structures, based on which the bearing capacity of the component under the given load conditions can be determined [10,11]. Chen studied the mechanical properties of the laminated bamboo lumber based on different kinds of tests and proposed two simplified models for analyzing the compressive cases. The analysis results are in good agreement with the actual data [12]. Ma researched the flexural fatigue property of the bamboo scrimber under high-cycle fatigue life and found that the alternating load’s stress level obviously affects the specimen’s residual stiffness [13].

During the earlier years in the research process of bamboo scrimber, the material was usually considered as a typical kind of elastic material. According to the manufacturing process, the ingredients of the material are the selected glue and bamboo fiber, which both show creep properties. As a result of this, the bamboo scrimber itself will also exhibit obvious creep properties if an external load is applied on it [14]. In view of this phenomenon, Wei applied the Burgers model in researching the various types of creep behavior of the bamboo scrimber (tensile, compressive, and bending); in this way, not only the stress level effect can be expressed accurately, but also the percentage of different types of strain (elastic, viscos, viscoelastic) among the whole strain can be measured in detail [15,16]. Ma studied the creep property of the columns made by bamboo scrimber and found out that both the temperature and humidity affected the creep strain growth property obviously during the long-term experiment process, and the proposed three-parameter Kelvin model can accurately fit the law of the creep strain growth [17]. Liu studied the creep performance of the material and proposed the accelerated creep experiment method to quicken the test process; in this way, more experiment time and cost can be saved [18]. Luo studied the mechanical property of the bamboo scrimber during a relatively longer period based on both a macroscopical creep experiment and microstructure detection approaches, and in this way, the creep damage mechanism of the bamboo scrimber can be determined [19].

At present, one of the most commonly applied viscoelastic mechanical constitutive models in the creep property research field is the classical Zener model [20]. This model can accurately simulate and express the growth property of the creep strain under most conditions, but the viscoelastic property of the model is provided by the shunt-wound standard Newtonian fluid body and spring body. In addition, the model parameters during the creep process usually remain unchanged. These may be different from the actual engineering performance.

In this paper, the framework of memory-dependent (MD) derivative theory, a typical kind of time-variant model, was adopted in the compressive creep study of bamboo scrimber. The dashpot body of the Zener model was modified based on this approach, based on which the creep strain response function can be derived under the given stress condition. In addition, several groups of compressive creep tests under various stress levels were conducted to supply the verification data. The results demonstrated that this modified model was able to characterize the creep performance of the bamboo scrimber accurately under all the given load conditions for all the specimens, which makes it far superior to the traditional Zener model for promotion.

2. Materials and Methods

2.1. The Test Material

In this paper, the bamboo scrimber was selected to be the research subject. For this kind of typical composite material made from natural fibers, the manufacturing process can usually be divided into three steps: Firstly, the bamboo fibers were extracted from the raw bamboo based on the given chemical or physical approaches. Secondly, the fibers were recombined with the glue (phenolic resin or some other kinds of bakelite) and mixed. Finally, the mixture was compressed under the given pressure until the specimen was recombined into a solid piece. The specimen of the material in this paper was produced by the Taohua Jiang Company Ltd. (Yiyang, China). The raw bamboo fibers were extracted from 4- to 5-year-old Phyllostachys bamboo trees in Hunan province. The density of the bamboo scrimber produced by this company was 1280 Kg/m³, and the glue content was 8.5%. Figure 1 shows the prism specimen for the experimental study in this paper, from which it can be found that the longer side of the sample was cut from the fiber direction. In addition, the serial number of the standard in guiding the test material preparation process is ASTMD143-94 [21]. The values of the compressive strength and modulus of the material are 78.5 MPa and 9.9 GPa, respectively. The serial number of the compressive strength and modulus is GB T1041-2008 [22]. In addition, the experiment was conducted by the STANDARD Testing Group Co., Ltd. (Xi’an, China), and the test was conducted with the UTM5504-GD microcomputer-controlled test equipment (Jinan Huikai Testing Instrument Co., Ltd., Jinan, China).

2.2. The Experiment Method

At present, the most commonly used parameter in monitoring the creep behavior is the strain. According to a previous study, when the strain of the bamboo scrimber is recorded under the compressive load, the electronic extensometer is a suitable choice due to the high stability in this condition. Figure 2 shows the corresponding equipment for this test, from which it can be found that the electronic extensometer is installed at the central part of the test piece. In addition, the length of the equipment applied in this paper is 50 mm. Thus, the compressive creep strain value recorded during the test process can be determined as follows [23]:

$$\epsilon ={\displaystyle \frac{∆L}{50}}$$

(1)

where $∆L$ is the offset variable of the extensometer. The serial number of the creep test criteria in this paper is ASTM D2990-17 [23]. The brand name of the electronic is Reliant, and the serial number is SN: R2489. This type of electronic extensometer has no obvious zero drift property within a relatively short creep experiment process (no more than 10 days). In addition, the temperature and humidity during the experiment are generally steady based on the operation of the condition control system of the test room. Thus, the accuracy of the recorded strain can be guaranteed.

As shown in Figure 2a, the pressing head was installed on a steel beam connected with two arms. Before the experiment process, the levelness of both the beam and the bottom plate was checked to ensure that they were parallel to each other. In addition, the upper and bottom surfaces of the specimen were also parallel to each other due to the cutting technology. In this way, the eccentric compression can be avoided in advance.

During the test process, the sampling frequency throughout the whole experiment process was 1 min⁻¹. According to a previous study [24,25], some other factors, such as the temperature and humidity, may affect the performance of the engineering equipment. In this paper, the temperature of the experiment was set to 25 °C, and the humidity was set to 40% throughout all the experiment cases.

On the other hand, according to a previous study [26], the tiny gaps between the specimen and the test equipment (both the press head and the steel platform) may affect the testing results. In order to solve this problem in advance, a pretreatment load history was applied to the specimen to eliminate the gaps. The detailed information of the load history is shown in Figure 3 [27].

In this paper, there are twelve groups of compressive creep experiments carried out in all. In addition, the stress level of the compression of the experiment is defined according to the material’s compressive strength. The detailed information is shown in

Table 1. Parameters of the compressive creep experiment.

Specimen Number	Stress Level/%	Stress/MPa
C-101, C-102, C-103	10	7.85
C-201, C-202, C-203	20	15.7
C-301, C-302, C-303	30	23.55
C-401, C-402, C-403	40	31.4

.

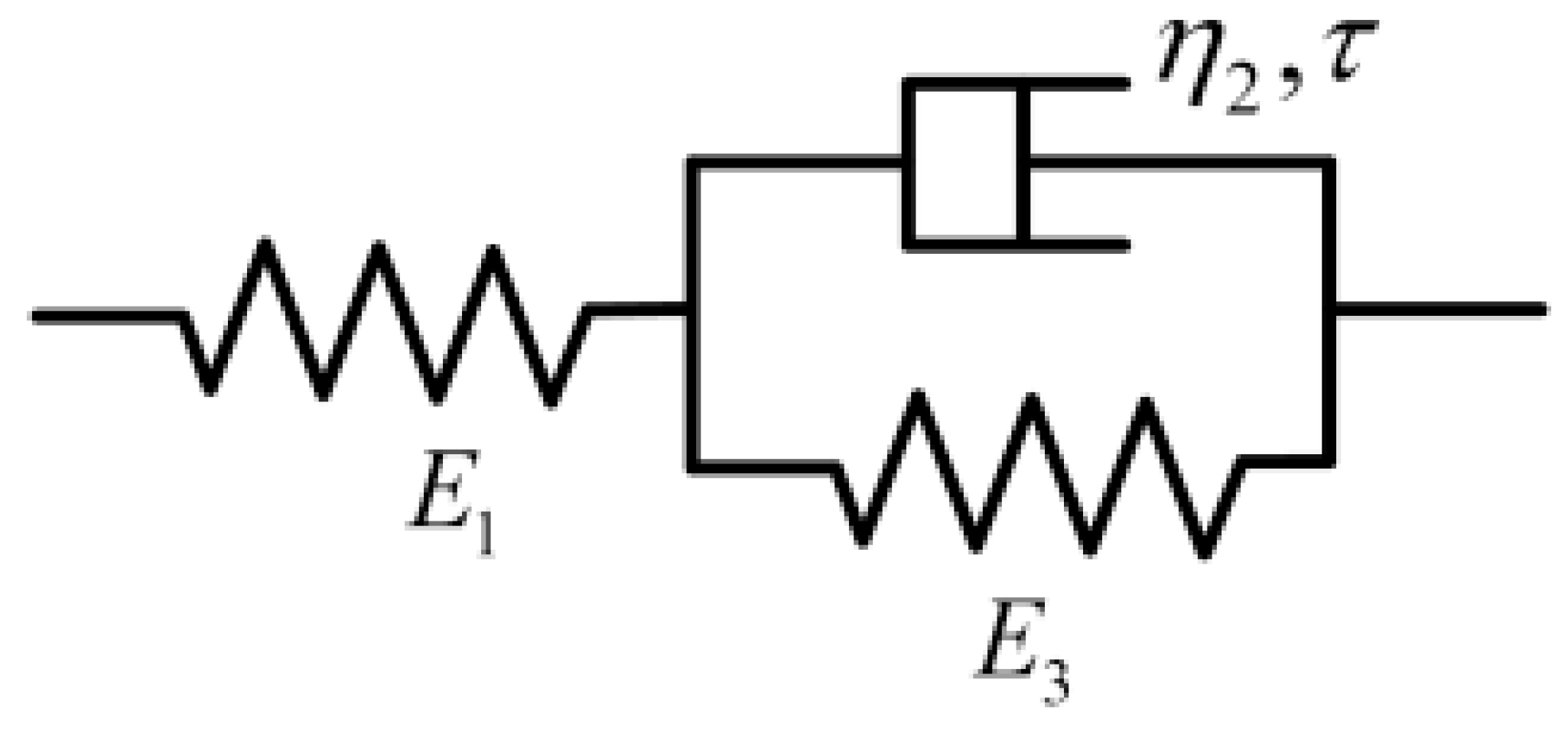
2.3. The MD-Defined Zener Model

According to the published related study, a suitable viscoelastic mechanical constitutive model is an indispensable factor in the creep performance research process of composite materials. Up to now, there are several corresponding models proposed in this field, among which the Zener model is usually considered to be an effective choice [20]. The main components and structural features of the model are shown in Figure 2.

As shown in Figure 4, the Zener model is mainly composed of three parts: the spring body $E_1$ and the Kelvin body, which is made up of a parallel connected spring body $E_3$ and dashpot body ${\eta }_2$. According to previously published papers, when the dashpot body is considered as a typical Newtonian fluid type, the strain response of this model can be expressed as follows:

$$\epsilon ={\displaystyle \frac{{\sigma }_0}{E_1}}+{\displaystyle \frac{{\sigma }_0}{E_3}}(1-\exp (-{\displaystyle \frac{E_3}{{\eta }_2}}t))$$

(2)

where $\epsilon$ is the total strain provided by the Zener model, ${\sigma }_0$ is the stress applied on the model, $E_1$ and $E_3$ are the elastic moduli of the spring body, and ${\eta }_2$ is the viscosity coefficient of the Newtonian fluid body. In a previous study, the model parameters of the Zener model are usually treated as material constants and are not influenced by the stress level and the related condition. In recent years, some experts discovered that the model may have a combined nonlinear and time-variant characteristic.

According to the related published paper, the memory-dependent (MD) derivative model usually shows an obvious time-variant property. For the dashpot body defined based on this approach, the stress–strain relationship can be expressed as follows [28]:

$$\sigma \left(t\right)={\eta }_m{D}_{\tau }^2\epsilon \left(t\right)={\eta }_m{\displaystyle \frac{1}{\tau }}{\displaystyle \underset{t-\tau }{\overset{t}{\int }}{K}_n(s-t)}{\epsilon }^{″}\left(s\right)ds$$

(3)

where $\sigma \left(t\right)$ is the stress, $\epsilon \left(t\right)$ is the strain, ${\eta }_m$ is the viscosity coefficient of the dashpot body, $\tau$ is the duration of the memory-dependent time, and $K_n(s-t)$ is the weight function. When the weight function is equal to 1, the model is converted into a simple nonlinear Newton fluid body. In a previous study, several experts proposed corresponding weight function models, among which the model carried out by Zhang is considered to be an effective choice [29]. The definition of this kind of function can be expressed as follows:

$$K\left(s-t\right)={\displaystyle \frac{s-t}{\tau }}+1$$

(4)

As shown in Equations (3) and (4), it is obvious that the MD approach has a similar expression to the fractional-order model. The main differences between them are that the memory-dependent derivative comprises intuitive physical meanings and is expressed as a weighted average of ordinary derivatives over a certain period of time. It corrects the defect that the memory effect of the fractional derivative was weakened with time. By taking Equation (3) into Equation (2), the stress–strain relationship can be rewritten as follows:

$$\sigma \left(t\right)={\eta }_3{D}_{\tau }^2\epsilon \left(t\right)={\eta }_3{\displaystyle \frac{1}{\tau }}{\displaystyle \underset{t-\tau }{\overset{t}{\int }}\left(\frac{s-t}{\tau }+1\right)}{\epsilon }^{″}\left(s\right)ds={\eta }_3{\displaystyle \frac{1}{\tau }}\left[{\epsilon }^{\prime }\left(t\right)-{\displaystyle \frac{1}{\tau }}{\displaystyle \underset{t-\tau }{\overset{t}{\int }}{\epsilon }^{\prime }\left(s\right)ds}\right]$$

(5)

By solving Equation (4), the strain of the dashpot body under the given stress can be determined as follows:

$${\epsilon }^{\prime }(t)-{\displaystyle \frac{1}{\tau }}\left[\epsilon (t)-\epsilon (t-\tau )\right]={\displaystyle \frac{\sigma \tau }{{\eta }_3}}$$

(6)

$$\epsilon (t)=e^{{\displaystyle \raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.}}\left[{\displaystyle \underset{0}{\overset{t}{\int }}(\frac{\sigma \tau }{{\eta }_3}-\frac{\epsilon (t-\tau )}{\tau })}\right]e^{{\displaystyle \raisebox{1ex}{$-s$}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.}}ds+C$$

(7)

According to the theory of viscoelastic mechanics, the strain of the dashpot is zero before the stress has been applied to it. Based on this, the strain provided by the MD-defined dashpot body can be expressed as follows:

$$\epsilon (t)={\displaystyle \frac{\sigma {\tau }^2}{{\eta }_3}}(e^{t/\tau }-1)$$

(8)

For the Kelvin body established in Figure 4, the MD-defined dashpot body is connected to the spring body side by side. The stress–strain of the body can be expressed as follows:

$${\sigma }_0={\sigma }_2+{\sigma }_3$$

(9)

$${\epsilon }_3(t)={\displaystyle \frac{{\sigma }_3(t)}{E_3}}$$

(10)

$${\epsilon }_2(t)={\epsilon }_3(t)={\displaystyle \frac{{\sigma }_2(t){\tau }^2}{{\eta }_2}}(e^{t/\tau }-1)$$

(11)

where ${\sigma }_0$ is the total stress of the Kelvin body, ${\sigma }_3$ and ${\sigma }_2$ are the stress provided by the spring body and dashpot body, respectively, and ${\epsilon }_3$ and ${\epsilon }_2$ are the strain of the spring body and the dashpot body, respectively. In addition, according to the structure feature of the Kelvin body, the strain provided by the spring body is equal to that provided by the MD dashpot body. Based on this assumption, the total strain provided by the Kelvin body under the given stress level ${\sigma }_0$ can be determined as follows:

$${\epsilon }_3(t)={\epsilon }_2(t)={\displaystyle \frac{{\sigma }_0}{E_2+{\eta }_3/[{\tau }^2(e^{t/\tau }-1)]}}$$

(12)

For the whole Zener model defined by the MD derivative approach, the response strain can be defined as follows:

$$\epsilon ={\displaystyle \frac{{\sigma }_0}{E_1}}+{\displaystyle \frac{{\sigma }_0}{E_2+{\eta }_3/[{\tau }^2(e^{t/\tau }-1)]}}$$

(13)

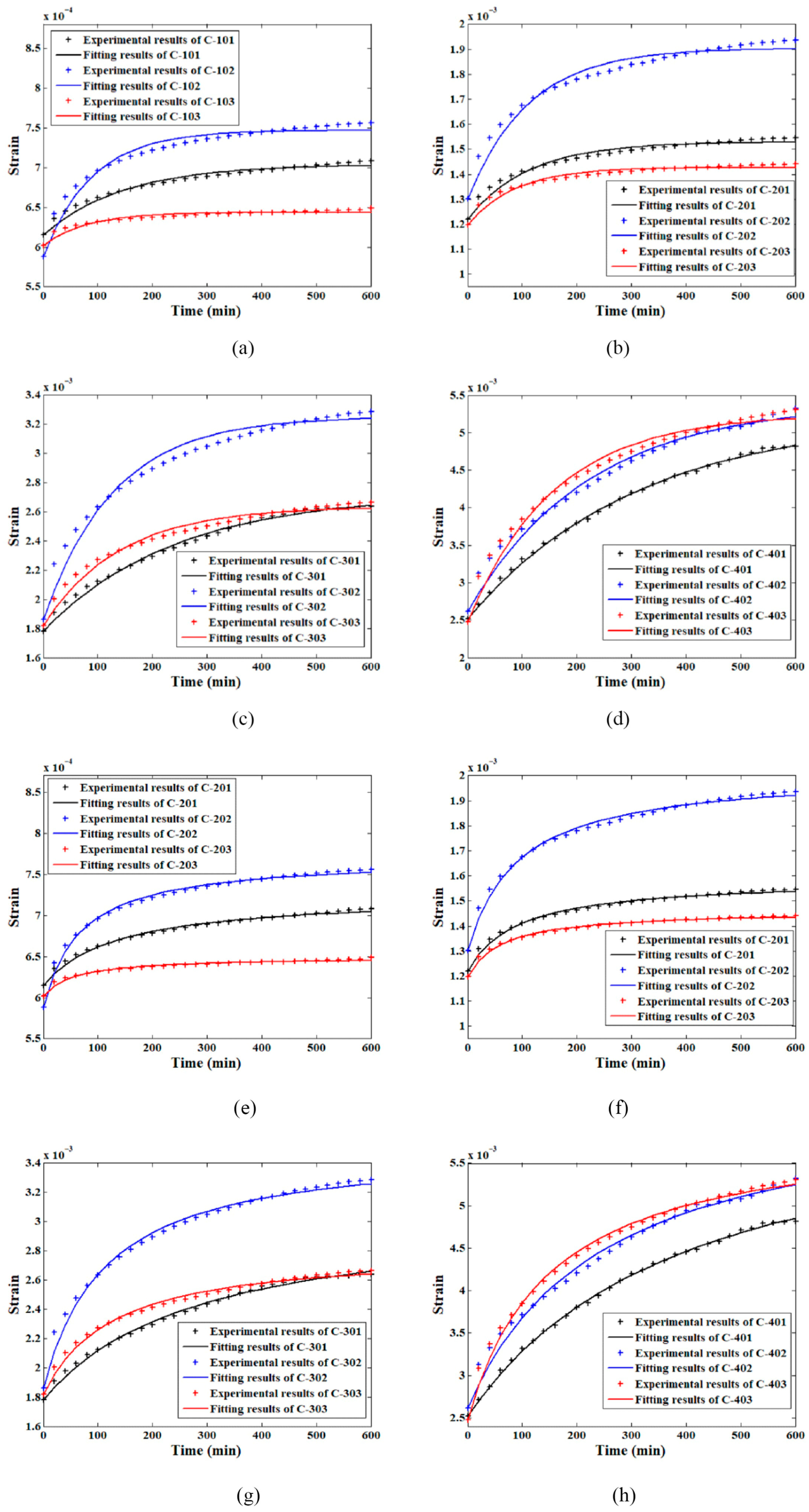
3. Results

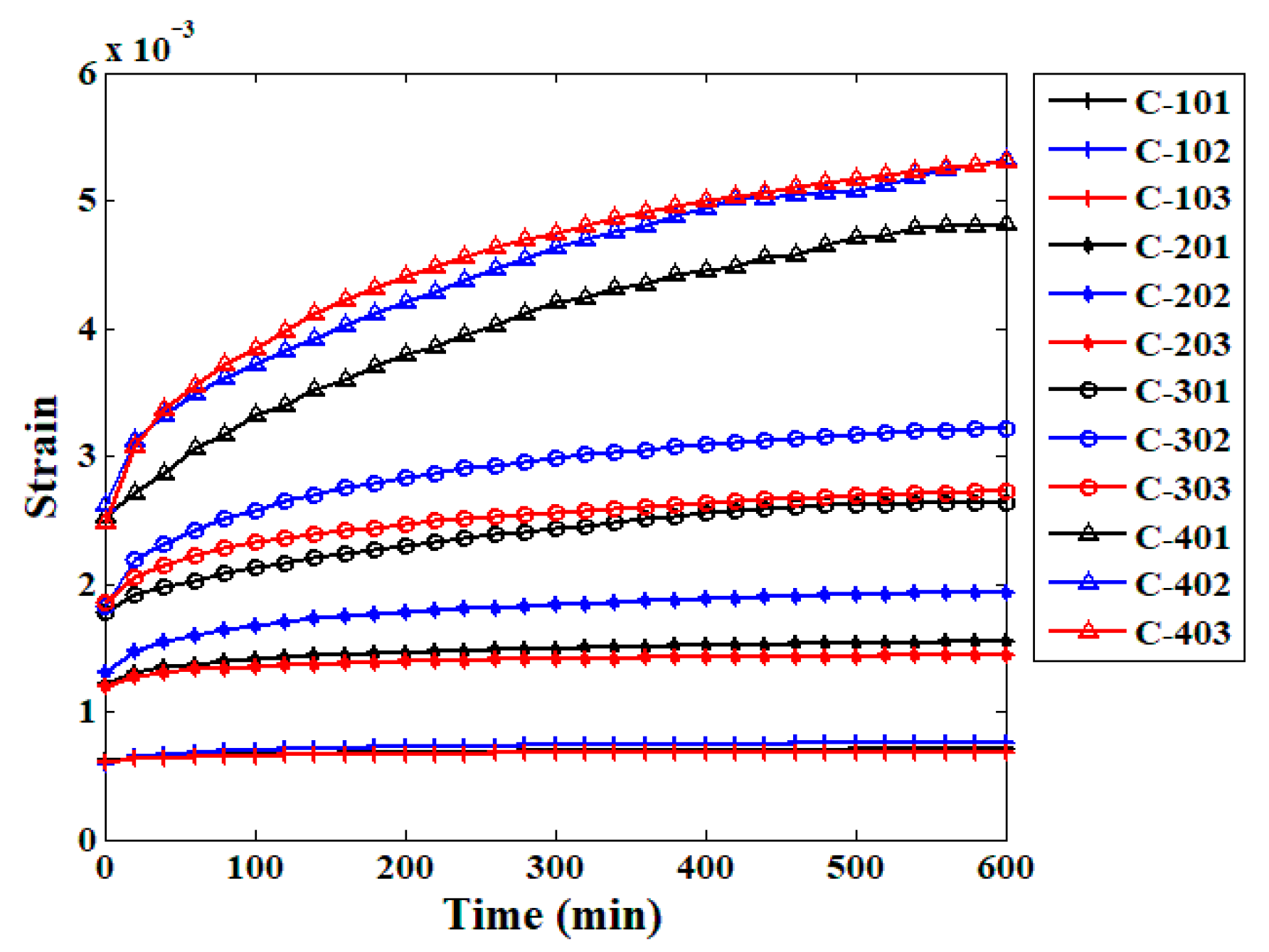
3.1. The Creep Test Results

Based on the experiment method mentioned and the analysis models above, the compressive creep behavior of the bamboo scrimber can be studied in detail. In this paper, the compressive creep test for each specimen lasts for 10 h. The detailed experiment results of all the specimens are shown in Figure 5.

As shown in Figure 5, when the lowest stress level (the corresponding serial numbers are C-101, C-102, and C-103, respectively) is applied on the specimen, the creep strain growth rate obtained from the figure is not obvious; the curves of all the specimens are almost straight lines and parallel to the axial direction. The values of the relative increment of the compressive creep strain of all three specimens are less than 10%, which means that the strain under this stress level is mainly made up by the elastic property of the bamboo scrimber. While for the specimens under the second stress level, the corresponding serial numbers are C-201, C-202, and C-203, respectively, and a more obvious creep strain can be found from the recorded experiment data, especially for the second specimen (C-202). For the three specimens under the third stress level, it is obvious that the slopes of the curves are much larger, which means that more creep strain has been created under this stress level. When the highest stress level is applied, the most obvious growth rate can be found (the relative increment is over 100% or more).

Meanwhile, another feature of the compressive creep behavior of the bamboo material is that the values of the creep strain growth speed from different specimens are also different, even if the same load amplitude is applied to them. In addition, the rate of rise in the compressive creep strain throughout the experiment process is not changeless. For the three specimens under the highest stress level, the values of the creep strain of the second and third specimens are generally the same during the earlier stage of the experiment (about 60 min). Then, their growth speeds gradually become different during the middle stage (from about 60 min to 440 min). While in the final stage, their growth speeds become similar again. This phenomenon can be explained by the dispersion characteristic of the material’s mechanical property, as well as the uneven structural property of the material. Among the inner parts of the specimen, there are many defects randomly distributed everywhere. During the creep deformation process, these defects will gradually grow and coalesce into a larger size until the final fracture. Thus, the time of duration of this process is certainly influenced by the location and size of these defects, which will also show an obvious dispersion property.

3.2. The Model Validation Results

Based on the different kinds of Boltzmann models and the compressive creep experiment results, it is probable to analyze the compressive creep performance of the material by fitting the experiment data. Among the fitting approaches, the goal is to reduce the relative differences between the response function and the experimental data as little as possible by adjusting the values of the model parameters. In order to make a comprehensive comparison, in this paper, both the traditional and memory-dependent-approach-defined Zener models were selected for analyzing the creep test results. In addition, the fitting method is achieved using the Levenberg–Marquardt algorithm. The fitting results of the experimental data based on this method and both kinds of Zener models are shown in Figure 6.

As shown in Figure 7a, when the traditional Zener model was selected for analyzing the compressive creep strain obtained under the lowest stress level (7.85 MPa), an obvious error can be found among the fitting curves and the experiment data points, especially for the second specimen (C-102). For the fitting results in Figure 7b, similar conclusions can be proposed according to the obvious distance between the experimental data points and the fitted curves. Figure 6c shows the analysis results under the third stress level (23.55 MPa), with higher accuracy than the fitting results in Figure 6b. In this case, only the fitting results of the third specimen show obvious differences from the original experiment data. In Figure 6d, when the highest stress level (31.4 MPa) is applied, all the fitting results of the four specimens are quite close to the exact experimental data.

Table 2. The $R^2$ of the fitting results in all cases based on the traditional Zener model.

Specimen Number	Value	Mean Value
C-101	0.9785	0.9584
C-102	0.9655
C-103	0.9312
C-201	0.9718	0.9695
C-202	0.9716
C-203	0.9651
C-301	0.9942	0.9831
C-302	0.9772
C-303	0.9779
C-401	0.9986	0.9906
C-402	0.9876
C-403	0.9855

shows the detailed information of the correlation coefficient under all the stress levels and specimens, from which it can be found that for the traditional Zener model, the higher stress level will result in higher accuracy in fitting the creep strain evolution history. For the evolution history under the lower stress levels, the fitting results carried out from the traditional Zener model usually show obvious error, which makes corresponding modification and improvement necessary.

Figure 6e–h show the fitting results of the same experiment data based on the Zener model defined by the memory-dependent approach. As shown in Figure 6e, when the first stress level (7.85 MPa) is applied, compared with the fitting results based on the conventional Zener model in Figure 6a, the fitting results based on the memory-dependent-derivative-defined Zener model are obviously much closer to the original experiment data points. Similar situations can also be found from the fitting curves in Figure 6f, which means that this memory-dependent-derivative-defined Zener model can also provide high enough accuracy in analyzing the compressive creep strain under this stress level (15.7 MPa). Figure 6g shows the analysis results under the third stress level (23.55 MPa). It can be found that when the proposed model is applied in this case, the fitting results and the original experiment data are similar. In Figure 6h, when the highest stress level (31.4 MPa) is applied, all the fitting results are quite close to the exact experimental data.

Table 3. The $R^2$ of the fitting results in all cases based on the modified Zener model.

Specimen Number	Value	Mean Value
C-101	0.9916	0.9919
C-102	0.9926
C-103	0.9917
C-201	0.9921	0.9924
C-202	0.9924
C-203	0.9926
C-301	0.9956	0.9937
C-302	0.9911
C-303	0.9945
C-401	0.9991	0.9948
C-402	0.9941
C-403	0.9911

shows the detailed information of the correlation coefficient of all the specimens based on the memory-dependent-derivative-approach-defined Zener model. It is clear that the fitting accuracy based on the proposed memory-dependent-derivative-approach-defined Zener model is much higher than that based on the conventional Zener model under the two relatively lower stress levels, and the relative errors in these conditions have been significantly reduced, while for the relatively higher stress levels, the accuracy of the fitting results is still high enough to meet the engineering application requirements in the corresponding cases (more than 99%). Based on the comprehensive comparison between the fitting results based on different models and the actual experiment data, it is obvious that the memory-dependent-derivative-approach-defined Zener model is more suitable to be selected in the creep performance analysis of the bamboo scrimber, especially for the relatively lower stress level cases.

3.3. Model Parameter Analysis Results

From the above research, it is clear that the proposed modified Zener model can provide satisfactory accuracy in analyzing the creep property of the bamboo scrimber under various load conditions, no matter whether a high or low stress level is applied to the specimen. In addition, another feature of the model is that an obvious relative difference can be found among the fitting results, even if the stress levels applied to different specimens are the same in some cases. The main reason for this could also be the diversity of the material’s mechanical properties. As a result of this, a corresponding parameter sensitivity analysis of the main model parameters is necessary. On the other hand, among the main model parameters, the stress level on the elastic modulus of the spring body $E_1$ has already been studied in detail. Thus, the effect of the other three parameters on the relative creep should be discussed in detail. The results are shown in Figure 7.

Figure 7. The parameter sensitivity analysis results: (a) the elastic modulus; (b) the viscosity coefficient; (c) the duration of the memory-dependent time.

Figure 7. The parameter sensitivity analysis results: (a) the elastic modulus; (b) the viscosity coefficient; (c) the duration of the memory-dependent time.

As shown in Figure 7, it is obvious that among the three parameters, only the duration of the memory-dependent time has a positive effect on the rate of increase for the relative creep. In a word, the larger the value of the duration time, the quicker the growth speed of the strain provided during the creep process. The effects of the other two parameters are both negative. In addition, the effect of the duration time is also the most obvious within the definition ranges.

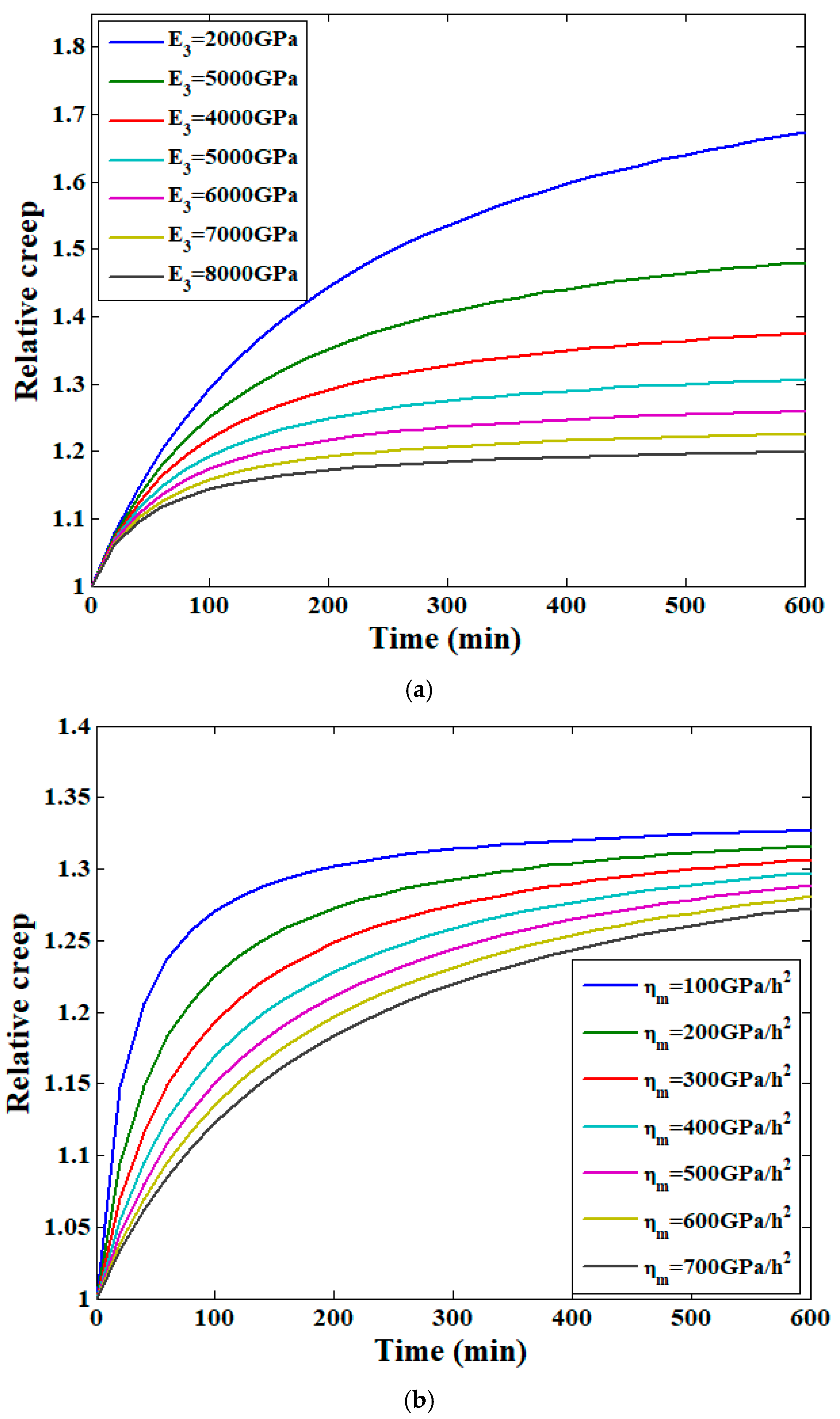
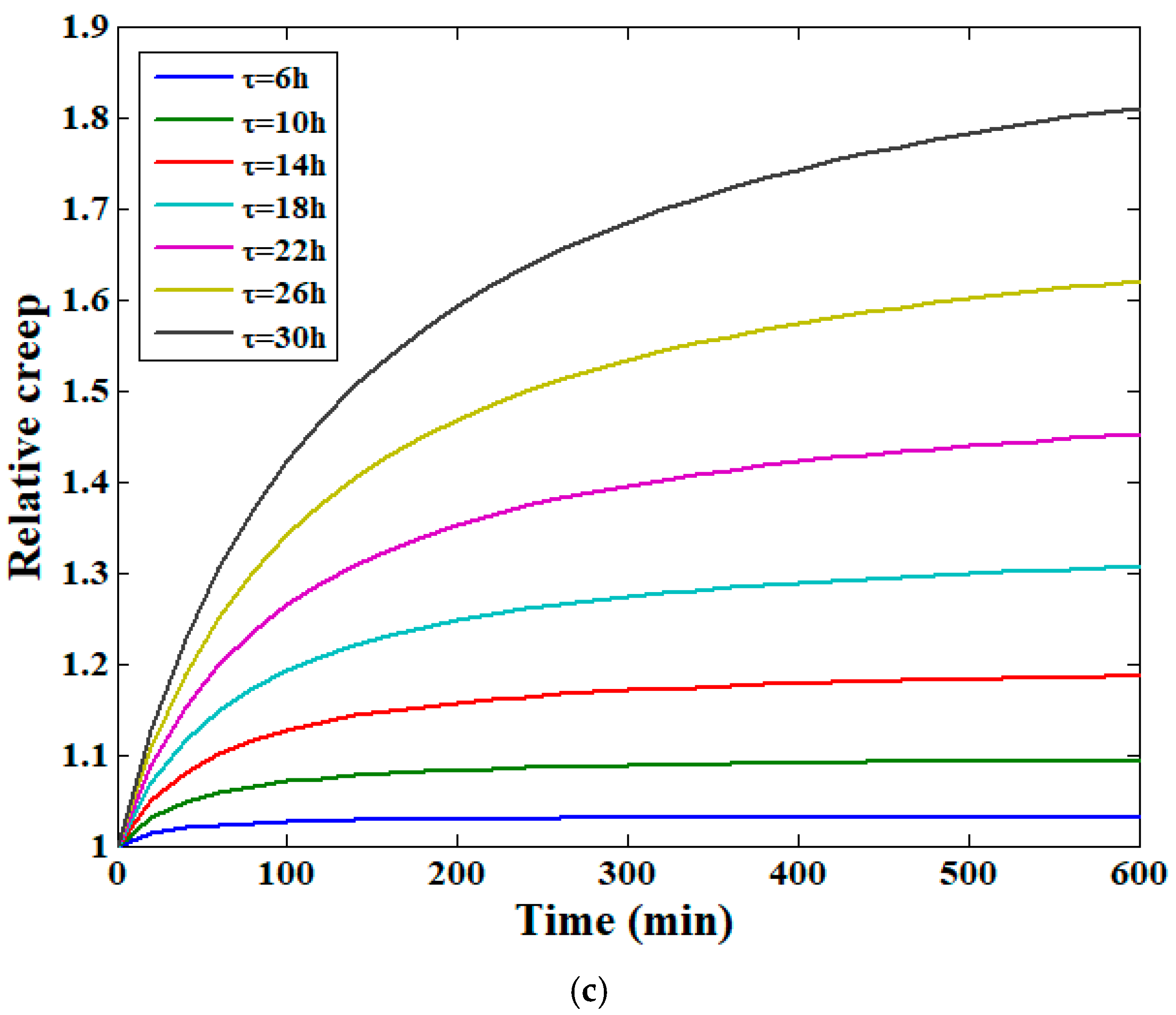
3.4. Discussion

From the research above, it is obvious that compared with the traditional Zener model, the modified Zener model based on the MD approach can more accurately analyze the compressive creep performance of the bamboo scrimber. On the other hand, in a previous study, the most commonly used model in research on the creep performance of the bamboo materials is the classic Burgers model, which has four elements in all, while for the proposed Zener model, there are three elements. In addition, the dashpot body in a previous related study is usually considered as the standard Newtonian fluid body, which is not suitable for researching the mechanical performance of a solid component. These advantages make this proposed model more suitable for engineering applications.

4. Conclusions

Due to the safety and reliability requirements, the obvious creep property of the composite material in the working period should be evaluated and researched. In the paper, it was chosen as a research object of compressive creep performance of the bamboo scrimber. To yield the data required for this analysis, we carried out several groups of compressive creep experiments with different stress levels. In addition, various types of Zener models were chosen in the study of compressive creep behavior of this type of fiber-reinforced material. The research’s main conclusions are drafted as follows:

(1)

Obvious creep behavior can be observed when the static compressive load is applied on the specimen for hours, and the stress level has a significant effect on the growth rate of compressive creep strain. The larger the stress level acted on the material, the later the change point of the creep strain curve appeared.

(2)

The original Zener model might introduce some errors in the bamboo scrimber compressive creep strain evolution process, especially for the compressive creep at a relatively low stress level. In this paper, the memory content of the definition of a Zener model for creep-type behavior can be used to accurately simulate the evolution curves for the compositional creep strain of the bamboo scrimber under various levels of stress, indicating its merit for adoption of the model in practice.

(3)

As for the main parameters in the proposed Zener model, the influence of the duration time on the speed of the creep strain growth is positive and the most significant. Both the viscosity coefficient and elastic modulus have a differential detrimental impact on creep strain growth speed.