Preview Control with Virtual Disturbance for Active Suspension Systems

Abstract

This paper presents a method to design a preview controller with virtual disturbance and an active suspension system for ride comfort improvement and motion sickness mitigation. Quarter-car and half-car models are selected as the vehicle model. With those models, an LQ optimal preview controller is designed in the discrete-time domain. In the controller, feedback controllers are designed with LQ static output feedback (SOF) control. In real driving environments, it is hard to exactly measure a bump profile, which causes performance deterioration. To cope with difficulties and uncertainties in measuring a real bump, a virtual disturbance is used instead of a real bump. In the LQ optimal preview controller, the virtual disturbance, used for the feedforward control, is optimized with a simulation-based optimization method. To show the effectiveness of the proposed method, a simulation is performed on a vehicle simulation package. The simulation results show that the LQ SOF controller decreases the vertical acceleration and pitch rate of the sprung mass by 28% and 66%, respectively, whereas the preview controllers with the optimized virtual disturbance yield reductions of 41% and 84%, respectively. Those results demonstrate that the proposed preview controller with the optimized virtual disturbance can effectively enhance ride comfort and mitigate motion sickness.

1. Introduction

It has been known that there are three primary objectives in the area of suspension control: ride comfort, road holding, and suspension travel management [1,2,3,4,5,6]. Ride comfort is achieved by attenuating the vertical acceleration of sprung mass (SPM), a_z, transmitted to occupants across a 0.5–20 Hz band, specified in ISO2631-1:1997, where human sensitivity is highest [7]. Road holding is achieved by maintaining a sufficiently high tire-road normal force so that steering, braking, and traction remain predictable [8]. Suspension travel management, or rattle-space protection, is achieved by preventing mechanical end-stops, limiting structural loads, and preserving component durability [2]. Among those objectives, ride comfort and road holding are known to conflict with each other [1,2,3,4]. When designing a suspension controller for a real vehicle, those goals should be balanced. However, ride comfort is the primary consideration in routine straight-line driving. For this reason, most of the studies on suspension control have tried to improve ride comfort by reducing a_z with an active or semi-active actuator [1,2,3,4,5,6].

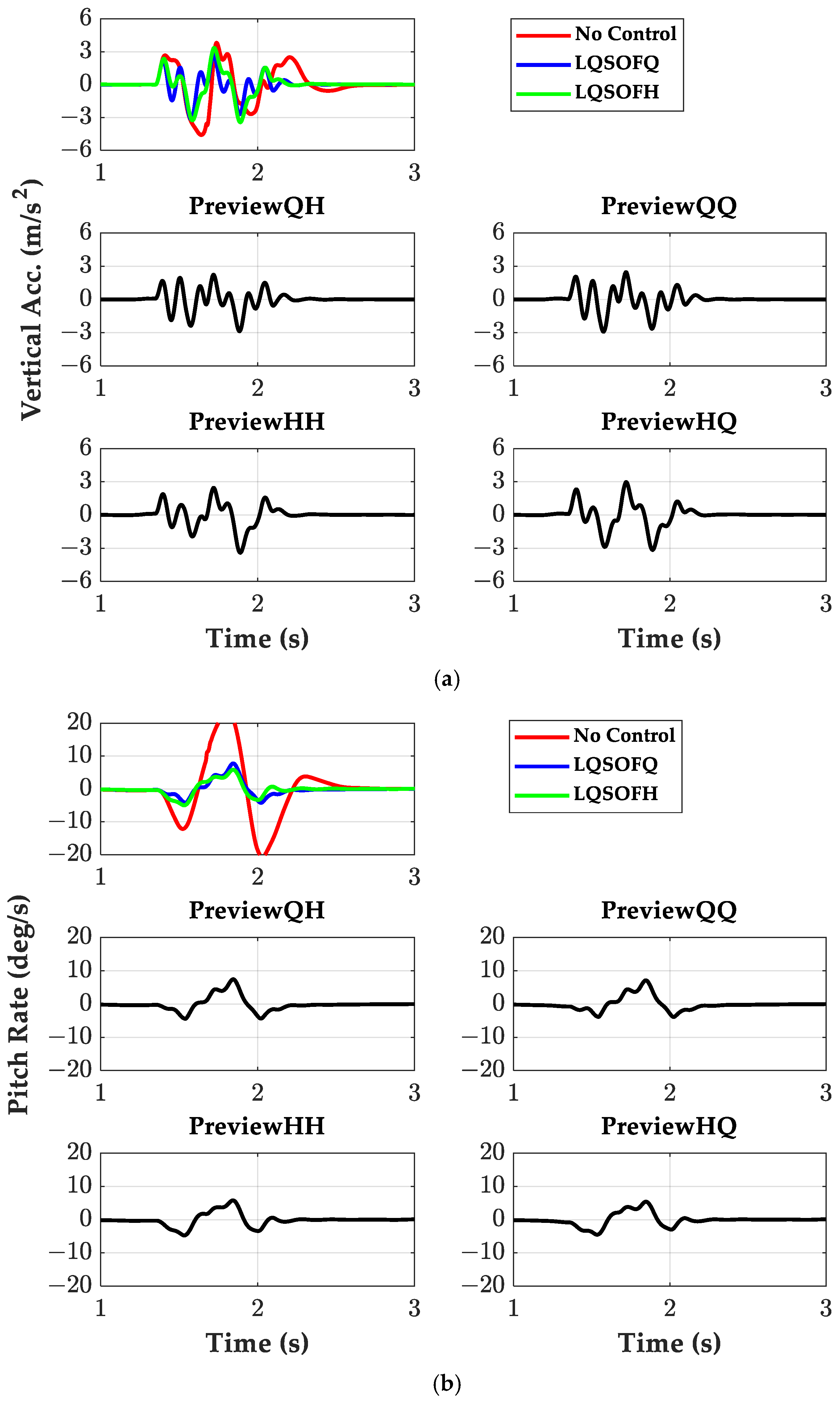
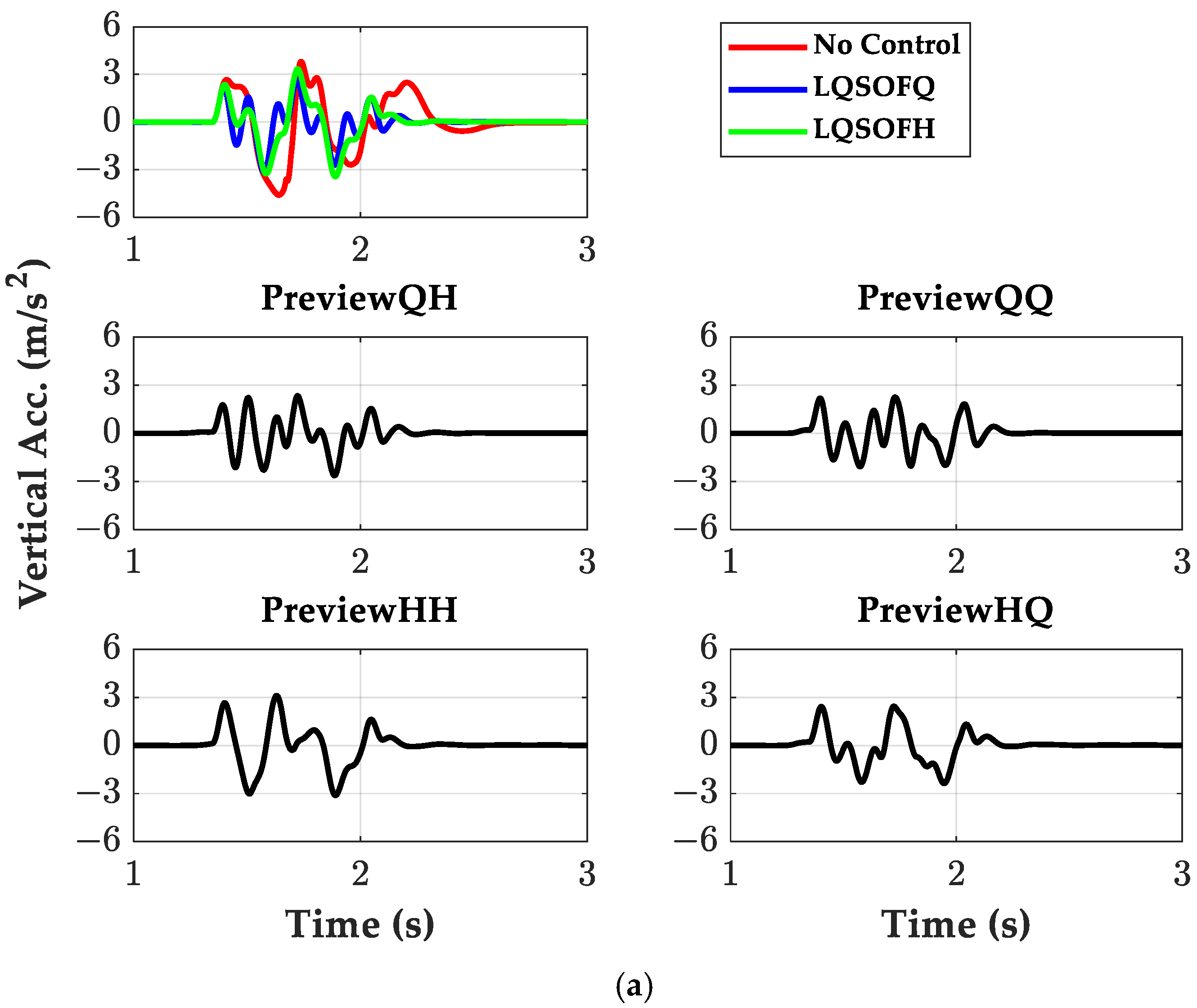
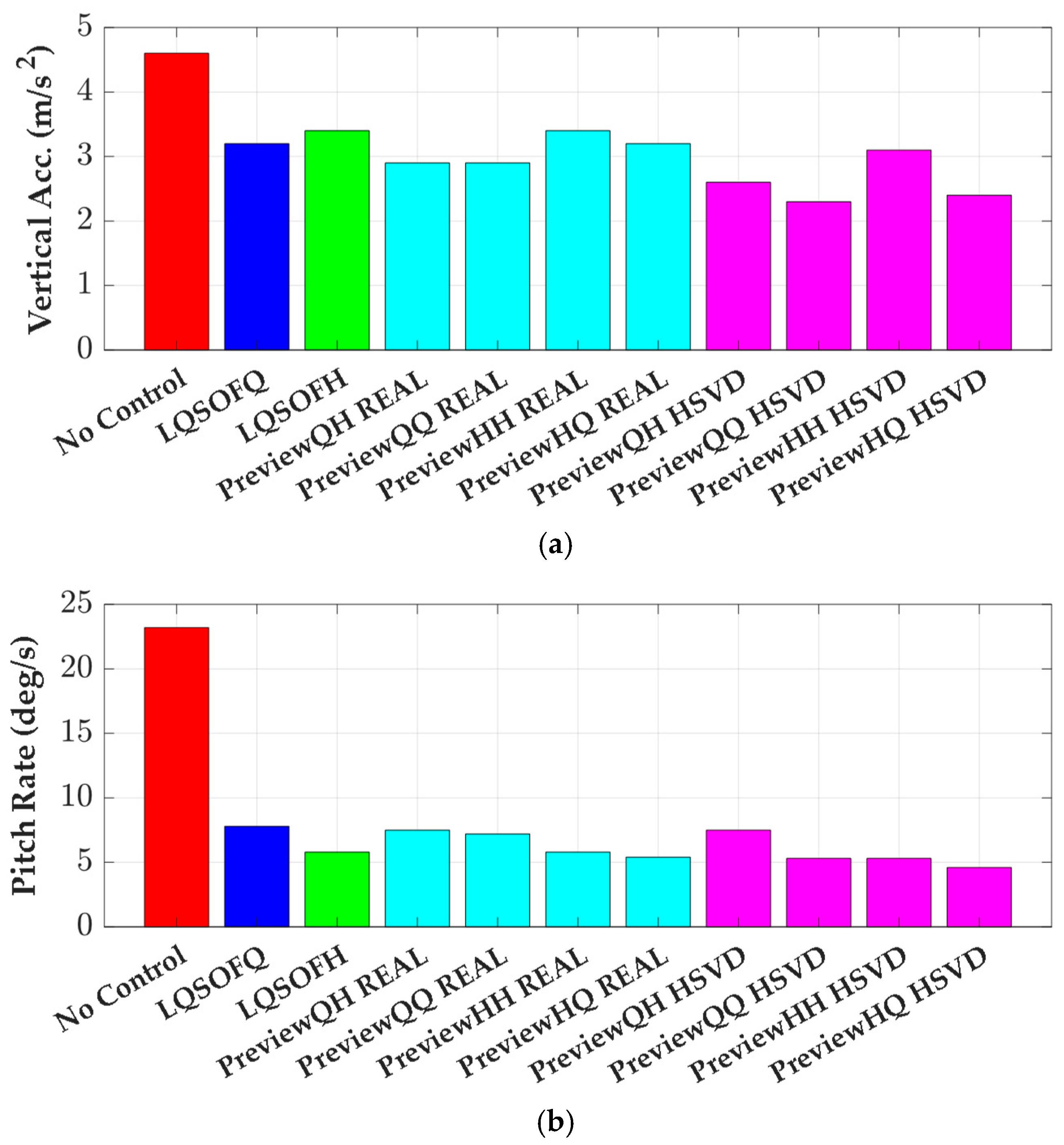
Three primary objectives in suspension control are evaluated with time- and frequency-domain metrics tailored to each goal. Generally, ride comfort is assessed via RMS or frequency-weighted RMS of a_z, absorbed-power indices, and motion-sickness dose value (MSDV) for longer exposures [7,9,10]. According to a recent study, motion sickness is attributable to the combined effects of a_z and pitch rate of the SPM, ω_y [11]. Accordingly, reducing a_z and ω_y is necessary for ride-comfort enhancement and motion-sickness mitigation. Road holding is evaluated by dynamic tire load measures, RMS tire deflection, and contact patch force variation [12]. Suspension travel management is evaluated with peak and RMS suspension deflection, end-stop hit counts, and probabilistic exceedance of bump/rebound limits [2].

A wide spectrum of suspension control strategies has been proposed to improve ride comfort while respecting road holding and travel limits. Those strategies can be classified into active and semi-active approaches. Semi-active approaches such as skyhook, groundhook, hybrid sky/ground, and acceleration-driven damper modulate damping to emulate desirable force laws with low energy cost [3,4,5,6]. Recent reviews on semi-active suspension control report that, compared with passive suspensions, several semi-active control approaches, such as skyhook, robust, MPC, and rule-based ones, can deliver clear gains in ride comfort and road holding and can approach active-suspension performance in various road scenarios [4]. Because those approaches require smaller actuators and modest electrical power, semi-active systems are cheaper, easier to package, and more reliable for production, which explains their wide commercial adoption (especially MR/CDC dampers) over the last decade [13,14]. However, since semi-active actuators cannot inject net energy into the suspension, their achievable control authority is fundamentally bounded, so performance deteriorates in severe disturbances or when severely aggressive body control is required [4].

As fully active strategies, linear quadratic regulator (LQR) and linear quadratic Gaussian (LQG), H_∞/μ-synthesis, sliding-mode, model predictive control (MPC), and disturbance-observer-based control have been applied to date [2,3,4,5,6]. A recent study integrates multi-actuator coordination (heave/roll/pitch) and explicit constraint handling via MPC to respect travel, tire force, and actuator limits [5]. Data-driven and adaptive extensions refine parameters online to accommodate speed/load variability and changing road roughness [15,16]. Road-preview layers such as wheelbase, LiDAR/camera, and map-based augment these feedback cores by turning upcoming road inputs into anticipatory control actions [17,18,19]. In this paper, an active suspension is selected as an actuator because the goal of this paper is to propose a new method for preview controller design.

Among those control strategies for suspension control, LQR with active suspension provides a systematic tuning framework through the LQ performance index (LQPI) and yields stabilizing feedback for controllable systems [1,2,4,20]. LQG extends LQR with Kalman filtering, enabling output-feedback designs while preserving the separation principle [21]. In suspension applications, LQ-based designs have historically delivered strong baselines and insight into achievable comfort/handling trade-offs [2,3,4,5,6]. Advantages of LQ-based design include smooth control actions, analytic performance interpretation, and low online computational demand once gains are computed offline [21]. However, classic LQR/LQG does not natively enforce hard constraints on travel, actuator stroke/force, or tire loads, which motivates MPC or constrained extensions [22].

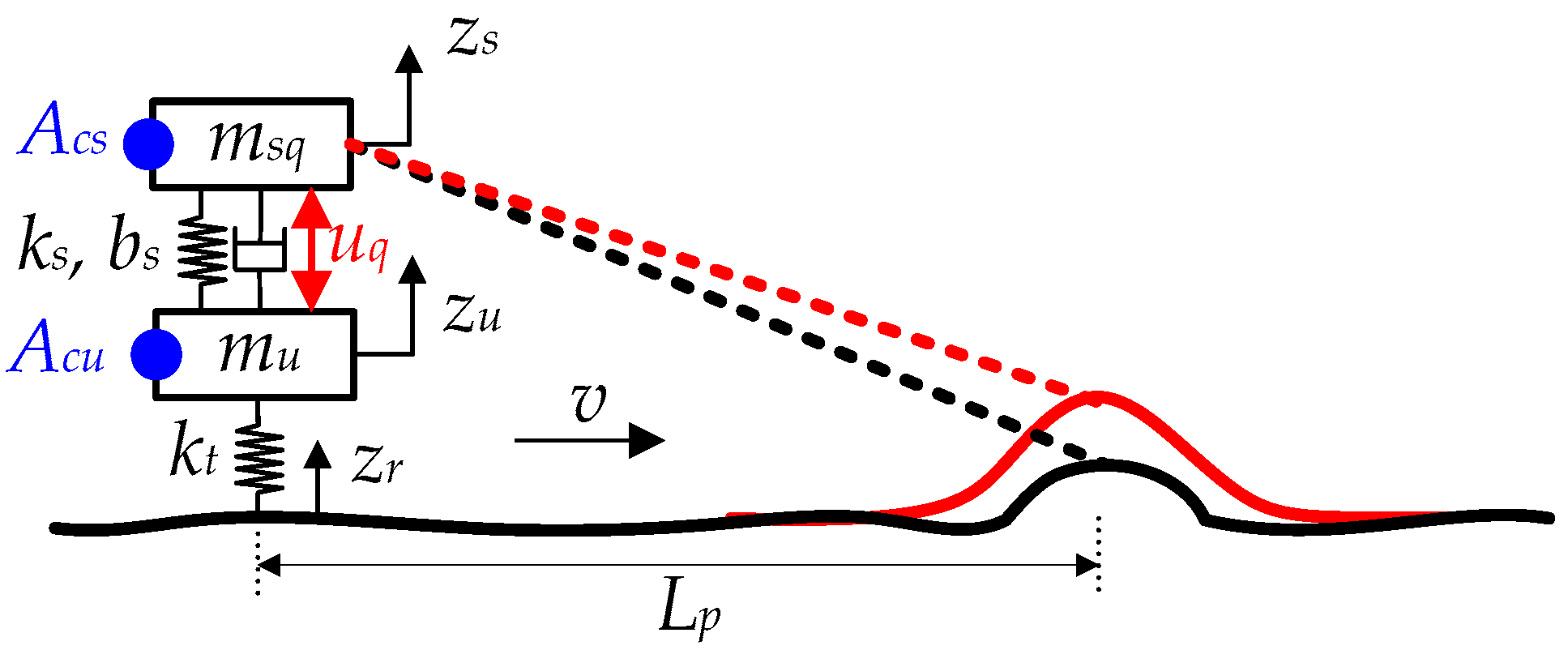
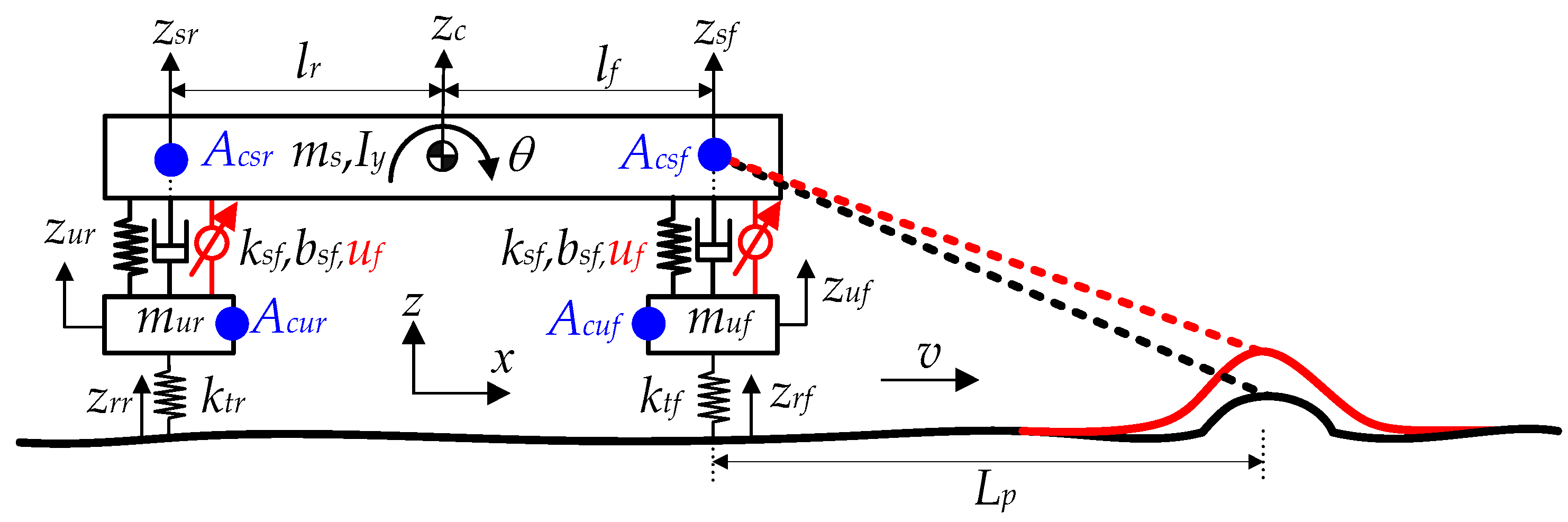
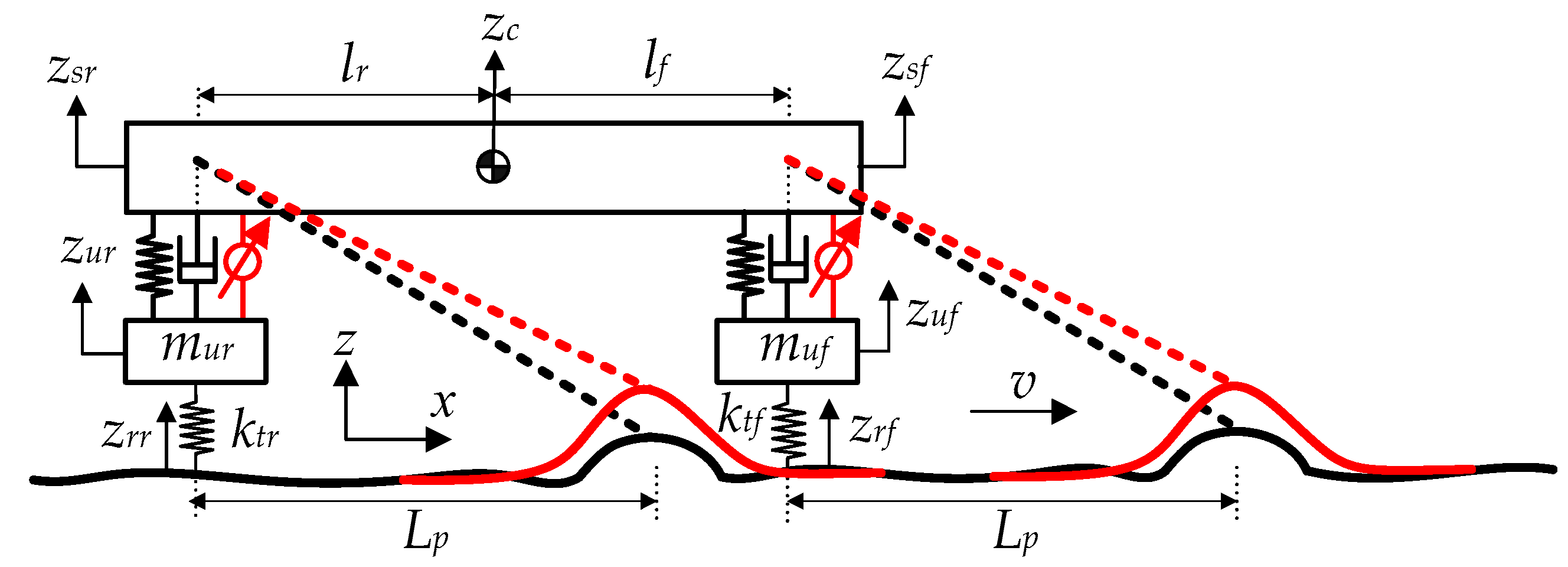
To apply LQ methods to suspension control, a state-space representation of a vehicle model is required. Prior studies have primarily employed three canonical formulations for active-suspension control synthesis: the 2-DOF quarter-car, the 4-DOF half-car, and the 7-DOF full-car models [23,24,25,26]. Among these, the quarter-car model is the most widely used owing to its simplicity and analytical tractability. In this paper, an active-suspension controller is designed using a half-car model, which explicitly captures the SPM heave (vertical) and pitch motions. Because the half-car model can be viewed as two coupled quarter-car ones, controllers designed with the quarter-car model can often be embedded within the half-car or full-car model with minor modifications [23,24,25]. For example, in 2024, the quarter-car-based controller was designed and validated with the semi-active suspension or on a real vehicle [25]. In this study, an active suspension is adopted as the actuator for control force generation, as it can be represented in the vehicle model with a relatively simple structure, and its control bandwidth can be modeled in a straightforward manner.

From a structural standpoint, LQR implements full-state feedback (FSF) and therefore requires all state variables to be either measured or estimated via a state observer or estimator. In a real vehicle, however, direct measurement of the half-car state vector is impractical. To circumvent this requirement in this paper, a static output-feedback (SOF) architecture is adopted instead of observer-based FSF control [4]. Specifically, the SPM vertical velocity and the suspension stroke rate are selected as sensor outputs for the SOF control in this paper; these outputs arise naturally from both quarter-car and half-car models, which enables an SOF controller synthesized on the quarter-car model to be ported to the half-car or full-car one with minimal modification [23,24,25]. The LQ SOF controller is obtained by minimizing an LQPI subject to the selected output structure. In this paper, two LQ SOF controllers are proposed as feedback controllers: (i) one designed with the quarter-car model and deployed on the half-car model, and (ii) one designed directly with the half-car model. Within the preview-control framework, each SOF controller is augmented by a feedforward path to use measured/previewed road inputs. To date, only a few studies have investigated preview control that employs LQ SOF control as the feedback controller [17,18]. This is the main contribution of this study.

Feedforward control acts with known or measured disturbances before these enter the plant, thereby reducing the burden on feedback and lowering tracking or regulation error [27,28]. Because it bypasses plant phase lags, properly timed feedforward control can attenuate incoming disturbances at the input and improve transient response without requiring higher feedback gains. In combination, feedback control cleans up model errors and unmeasured disturbances, while feedforward control cancels the predictable component, increasing effective bandwidth and robustness margins.

In the area of suspension control, preview control is the sum of feedback and feedforward controls [17,18,19]. Previewed signals can come from wheelbase preview (front-to-rear delay), perception sensors such as LiDAR or stereo cameras, or map/V2X sources aligned to vehicle speed [29,30,31,32,33,34,35]. Optimal preview control augments the plant with future disturbance samples and computes anticipatory actions—often within LQG or H₂/H_∞ frameworks—to reduce body acceleration and suspension travel [16,17]. MPC variants use predicted road inputs over a finite horizon to enforce travel, tire-load, and actuator constraints explicitly [36]. Practical implementations must address speed-dependent preview time, sensor latency/noise, and alignment/registration between sensed profile and wheel contact points [17,18,19].

Preview control performance depends critically on accurate and timely road-profile estimation; sensor noise, latency, and calibration misalignment can substantially degrade effectiveness, particularly in vision-based approaches. In practice, robust reconstruction of bump profiles from onboard cameras remains challenging across diverse operating conditions, and discrepancies between the reconstructed and true profiles have been reported [37]. To address these limitations in this paper, instead of measuring a real bump, a parameterized virtual disturbance is adopted and embedded in the preview path [38,39]. 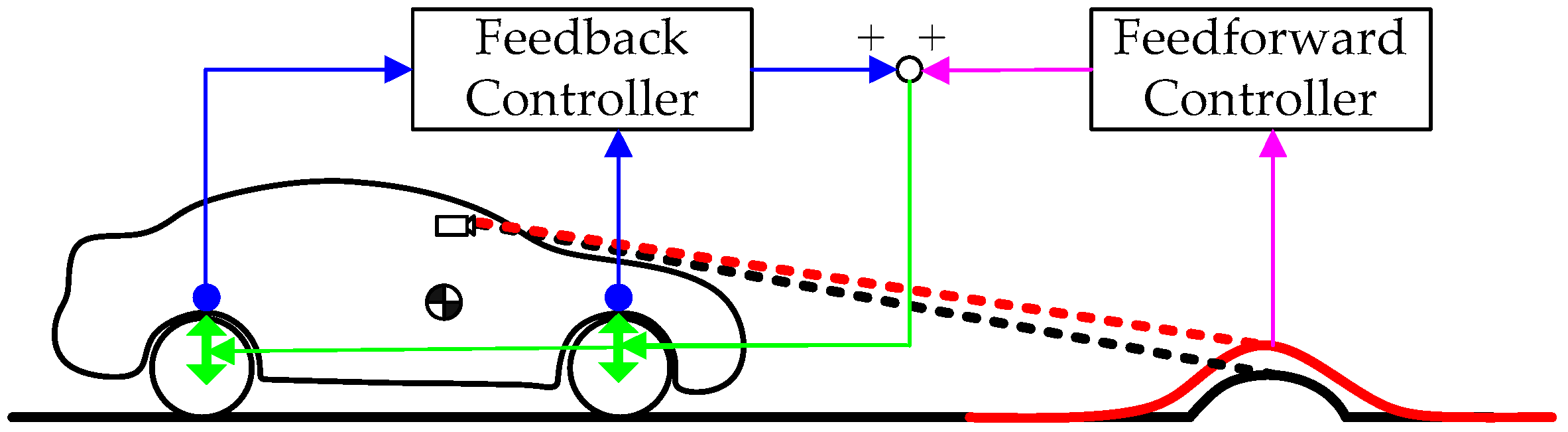The resulting architecture—illustrated in Figure 1 (highlighted with a red solid line)—eliminates the need for real-time bump measurement while enabling deliberate shaping of the feedforward signal to enhance closed-loop performance [39]. The virtual-disturbance parameters are optimized via a simulation-based optimization method (SBOM) for better control performance. The complete preview-control system is realized in a MATLAB2019a/Simulink–CarSim8.0 co-simulation environment in this paper.

The objective of this paper is to design a preview controller augmented with a virtual disturbance to enhance ride comfort and to mitigate motion sickness. The main contributions are as follows:

• Feedback and preview synthesis. As a feedback part of the preview controller, two LQ SOF controllers are designed using the quarter-car and half-car models in the discrete-time domain, respectively. In parallel, two feedforward schemes are derived from the same models. Pairwise combination of feedback and preview designs yields four discrete-time preview controllers. Existing literature on preview control with an LQ SOF controller is scarce [17,18]. For this reason, this is the key contribution of this paper.
• Virtual disturbance and optimization. The feedforward path employs a virtual disturbance instead of a real bump, eliminating explicit road-profile sensing. For better control performance, the virtual disturbance is optimized via SBOM on a MATLAB2019a/Simulink–CarSim8.0 co-simulation environment. The optimized virtual disturbance can enhance the performance of the preview controller and reduce sensitivity to mismatch between assumed and actual bump profiles.
• Simulation-based validation. Performance is assessed in CarSim8.0 by evaluating the two LQ SOF controllers and the four preview controllers augmented with their optimized virtual disturbances.

This paper is organized as follows. Section 2 formulates the quarter-car and half-car models and derives their state-space equations. Building on these models, active-suspension controllers are synthesized using LQ SOF and LQ optimal preview control. In Section 3, the virtual disturbance is introduced and employed in the feedforward path, and its parameters are optimized. Section 4 presents the simulation setup and evaluates the closed-loop performance of the designed preview controllers. Section 5 concludes the paper.

2. Design of Preview Controller

This section presents the design of LQ optimal preview controllers using discrete-time state-space representations derived from the quarter-car and half-car models. Within the preview architecture, the feedback controller is designed with LQ SOF control, while the feedforward path uses previewed road inputs. All designs are carried out directly in the discrete-time domain to facilitate digital implementation.

When using the quarter-car and half-car models for controller design, the following premises are needed: (i) There are no cornering or other movements except vertical and pitch motions. (ii) The elastic deformation caused by the wheel and road adhesion is ignored. (iii) The vertical excitation of the vehicle is less affected by the coupling of lateral and longitudinal dynamics.

2.1. Vehicle Models

Figure 2 depicts the 2-DOF quarter-car model, which represents the vertical (heave) motions of the SPM and the unsprung mass (USPM) [23,24,25]. The control input, u_q, generated by an active actuator, acts between the SPM, m_sq, and USPM, m_u. The external disturbance is the road profile, z_r. The vehicle speed is denoted by v, and the preview distance by L_p. As indicated in Figure 2, the accelerometers, A_cs and A_cr, are mounted on the SPM and USPM, respectively.

The suspension force, f_q, is defined in Equation (1), characterizing the coupling between m_sq and m_u via the suspension elements such as spring and damper [23,24,25]. With f_q, the equations of vertical (heave) motions of the SPM and USPM are then derived as in Equation (2). Combining Equations (1) and (2), and recasting the result into a compact vector–matrix form yields Equation (3).

$$f_q=-k_s(z_s-z_u)-b_s({\dot{z}}_s-{\dot{z}}_u)+u_q$$

(1)

$$\left\{\begin{array}{l}{m}_{sq}{\ddot{z}}_s=f_q\hfill \\ m_u{\ddot{z}}_u=-f_q-k_t\left(z_u-z_r\right)\hfill \end{array}\right.$$

(2)

$$\left[\begin{array}{cc}{m}_{sq}& 0\\ 0& m_u\end{array}\right]\left[\begin{array}{c}{\ddot{z}}_s\\ {\ddot{z}}_u\end{array}\right]=\left[\begin{array}{cc}-k_s& k_s\\ k_s& -k_s-k_t\end{array}\right]\left[\begin{array}{c}{z}_s\\ z_u\end{array}\right]+\left[\begin{array}{cc}-b_s& b_s\\ b_s& -b_s\end{array}\right]\left[\begin{array}{c}{\dot{z}}_s\\ {\dot{z}}_u\end{array}\right]+\left[\begin{array}{c}1\\ -1\end{array}\right]u_q+\left[\begin{array}{c}0\\ k_t\end{array}\right]z_r$$

(3)

To derive the state-space equation for the quarter-car model, new vectors and matrices are introduced as Equation (4) [23,24,25]. By incorporating these definitions, the dynamic formulation in Equation (3) can be reformulated into the matrix form expressed in Equation (5). The state vector of the quarter-car model is defined in Equation (6). With additional matrices defined in Equation (7), the complete state-space equation for the quarter-car model is derived and presented in Equation (8) [23,24,25].

$$\begin{array}{c}{z}_q\triangleq \left[\begin{array}{c}{z}_s\\ z_u\end{array}\right],M_q\triangleq \left[\begin{array}{cc}{m}_{sq}& 0\\ 0& m_u\end{array}\right], K_q\triangleq \left[\begin{array}{cc}-k_s& k_s\\ k_s& -k_s-k_t\end{array}\right], B_q\triangleq \left[\begin{array}{cc}-b_s& b_s\\ b_s& -b_s\end{array}\right], \\ U_q\triangleq \left[\begin{array}{c}1\\ -1\end{array}\right], L_q\triangleq \left[\begin{array}{c}0\\ k_t\end{array}\right]\end{array}$$

(4)

$$M_q{\ddot{z}}_q=K_q{z}_q+B_q{\dot{z}}_q+U_q{u}_q+L_q{z}_r$$

(5)

$$x_q\triangleq \left[\begin{array}{c}{z}_q\\ {\dot{z}}_q\end{array}\right]={\left[\begin{array}{cccc}{z}_s& z_u& {\dot{z}}_s& {\dot{z}}_u\end{array}\right]}^T$$

(6)

$$A_q\triangleq \left[\begin{array}{cc}{0}_{2\times 2}& I_{2\times 2}\\ M_q^{-1}{K}_q& M_q^{-1}{B}_q\end{array}\right], B_{1q}\triangleq \left[\begin{array}{c}{0}_{2\times 1}\\ M_q^{-1}{L}_q\end{array}\right], B_{2q}\triangleq \left[\begin{array}{c}{0}_{2\times 1}\\ M_q^{-1}{U}_q\end{array}\right]$$

(7)

$${\dot{x}}_q=A_q{x}_q+B_{1q}{z}_r+B_{2q}{u}_q$$

(8)

Figure 3 depicts the 4-DOF half-car model, which captures the vertical and pitch motions of the SPM [26]. The model consists of the front/rear suspension subsystems, where u_f and u_r represent the control inputs, i.e., the vertical control forces generated by the active actuators located in the front/rear suspensions. The variables z_sf and z_sr denote the vertical displacements of the front/rear corners of the SPM, respectively. As shown in Figure 3, the accelerometers A_csf, A_csr, A_cuf, and A_cur are mounted at the front/rear corners of the SPM and at the front/rear wheel centers, respectively, to obtain measurable signals for controller implementation.

In Figure 3, the forces at the front/rear suspensions, f_f and f_r, are derived as Equation (9) [26]. With Equation (9) and the geometric relationship between the SPM and front/rear suspensions shown in Figure 3, the equations of motions of the SPM, m_s, and the USPMs, m_uf and m_ur, are derived as Equation (10). The vertical displacements, z_sf and z_sr, at the front and rear corners of the SPM are calculated as Equation (11) from the geometric relationship between the SPM and front/rear suspensions. New vectors and a matrix are defined as Equation (12), where the vectors of state variables, disturbances and control inputs, i.e., x, w, u, are defined. With those definitions in (12), the state-space equation of the half-car model is obtained as Equation (13). The detailed derivation procedure of the state-space Equation (13) can be found in the previous study [26].

$$\left\{\begin{array}{l}{f}_f=-k_{sf}\left(z_{sf}-z_{uf}\right)-b_{sf}\left({\dot{z}}_{sf}-{\dot{z}}_{uf}\right)+u_f\\ f_r=-k_{sr}\left(z_{sr}-z_{ur}\right)-b_{sr}\left({\dot{z}}_{sr}-{\dot{z}}_{ur}\right)+u_r\end{array}\right.$$

(9)

$$\left\{\begin{array}{l}{m}_s{\ddot{z}}_c=f_f+f_r\hfill \\ I_y\ddot{\theta }=-l_f{f}_f+l_r{f}_f\hfill \end{array}\right.\hspace{1em}\hspace{1em}\left\{\begin{array}{l}{m}_{uf}{\ddot{z}}_{uf}=-f_f-k_{tf}(z_{uf}-z_{rf})\hfill \\ m_{ur}{\ddot{z}}_{ur}=-f_r-k_{tr}(z_{ur}-z_{rr})\hfill \end{array}\right.$$

(10)

$$\left\{\begin{array}{c}{z}_{sf}=z_c-l_f\sin \theta \simeq z_c-l_f\theta \\ z_{sr}=z_c+l_r\sin \theta \simeq z_c+l_r\theta \end{array}\right.$$

(11)

$$\begin{array}{c}{p}_h\equiv \left[\begin{array}{c}{z}_c\\ \theta \end{array}\right], z_s\equiv \left[\begin{array}{c}{z}_{sf}\\ z_{sr}\end{array}\right], z_u\equiv \left[\begin{array}{c}{z}_{uf}\\ z_{ur}\end{array}\right], z_h\equiv \left[\begin{array}{c}{p}_h\\ z_u\end{array}\right], f\equiv \left[\begin{array}{c}{f}_f\\ f_r\end{array}\right], H\equiv \left[\begin{array}{cc}1& 1\\ -l_f& l_r\end{array}\right]\\ x_h\equiv \left[\begin{array}{c}{z}_h\\ {\dot{z}}_h\end{array}\right] , w_h=z_r\equiv \left[\begin{array}{c}{z}_{rf}\\ z_{ru}\end{array}\right] , u_h\equiv \left[\begin{array}{c}{u}_f\\ u_r\end{array}\right]\end{array}$$

(12)

$${\dot{x}}_h=A_h{x}_h+B_{1h}{w}_h+B_{2h}{u}_h$$

(13)

In this paper, all feedback and preview controllers are designed in the discrete-time domain. Accordingly, the continuous-time state-space equations in Equations (8) and (13) are discretized into Equation (14) with sampling period T_s, where the discrete-time system and input matrices, Φ, Γ and Σ, are computed using the formulas in Equation (15) [30]. For discretization, the zero-order hold method is selected. The subsequent controller synthesis is carried out exclusively on these discrete-time state-space representations as given in Equation (14).

$$x_i\left(k+1\right)={\Phi }_i{x}_i\left(k\right)+{\Gamma }_i{w}_i\left(k\right)+{\Sigma }_i{u}_i\left(k\right),\hspace{1em}i\in \left\{q,h\right\}$$

(14)

$${\Phi }_i\left(T_s\right)\equiv e^{A_i{T}_s}, {\Gamma }_i\equiv \left({\displaystyle {\int }_0^{T_s}{\Phi }_i\left(\tau \right)d\tau }\right)B_{1i}, {\Sigma }_i=\left({\displaystyle {\int }_0^{T_s}{\Phi }_i\left(\tau \right)d\tau }\right)B_{2i},\hspace{1em}i\in \left\{q,h\right\}$$

(15)

2.2. Design of LQR

In the discrete-time domain, the linear quadratic performance index (LQPI) for the quarter-car model is specified in Equation (16). Task priorities are encoded by adjusting the associated weighting factors while holding the remaining weights fixed. The weight ρ_i is tuned via Bryson’s rule, as in Equation (17), where ξ_i denotes the maximum allowable value (MAV) for the i-th term in J_q [40]. For ride-comfort enhancement, the MAV ξ₁ on a_z is selected to be as small as practicable. Note that the LQPI for the quarter-car model, Equation (16), does not include pitch-related terms. By standard algebraic manipulations, Equation (16) is recast into the equivalent quadratic form, Equation (18) [41]. With the matrices Φ_q, Σ_q, Q_q, N_q and R_q defined in (18), the LQR for the quarter-car model yields the full-state feedback law of Equation (19). Let denote K_q as LQRQ.

$$J_q={\displaystyle \sum _{k=0}^{\infty }\left\{{\rho }_1{\ddot{z}}_s^2\left(k\right)+{\rho }_2{\left(z_s\left(k\right)-z_u\left(k\right)\right)}^2+{\rho }_3{\left(z_u\left(k\right)-z_r\left(k\right)\right)}^2+{\rho }_4{u}_q^2\left(k\right)\right\}}$$

(16)

$${\rho }_i={\displaystyle \frac{1}{{\xi }_i^2}},\hspace{1em}i=1,2,3,4$$

(17)

$$J_q={\displaystyle \sum _{k=0}^{\infty }\left\{{\left[\begin{array}{c}{x}_q\left(k\right)\\ u_q\left(k\right)\end{array}\right]}^T\left[\begin{array}{cc}{Q}_q& N_q\\ N_q^T& R_q\end{array}\right]\left[\begin{array}{c}{x}_q\left(k\right)\\ u_q\left(k\right)\end{array}\right]\right\}}$$

(18)

$$u_q\left(k\right)=-K_q{x}_q\left(k\right)$$

(19)

The LQPI for the half-car model is defined in Equation (20). The weight ρ_i is tuned using Bryson’s rule, as given in Equation (17). For ride-comfort enhancement, the MAV ξ₁ on a_z is chosen to be as small as practicable; for motion-sickness mitigation, the MAV ξ₃ on ω_y is likewise minimized. By standard transformations, Equation (20) is recast into the quadratic form Equation (21) [41]. Following the procedure in Equation (19), the LQR synthesis for the half-car model yields the full-state feedback law in Equation (22), with matrices Φ_h, Σ_h, Q_h, N_h and R_h. Let denote K_h as LQRH.

$$J_h={\displaystyle \sum _{k=0}^{\infty }\left\{\begin{array}{c}{\rho }_1{\ddot{z}}_c^2\left(k\right)+{\rho }_2{\ddot{\theta }}^2\left(k\right)+{\rho }_3{\dot{\theta }}^2\left(k\right)+{\rho }_4{\theta }^2\left(k\right)\\ +{\rho }_5{\displaystyle \sum _{i=f,r}{\left\{z_{si}\left(k\right)-z_{ui}\left(k\right)\right\}}^2}+{\rho }_6{\displaystyle \sum _{i=f,r}{\left\{z_{ui}\left(k\right)-z_{ri}\left(k\right)\right\}}^2}+{\rho }_7{\displaystyle \sum _{i=f,r}{u}_i^2\left(k\right)}\end{array}\right\}}$$

(20)

$$J_h={\displaystyle \sum _{k=0}^{\infty }\left\{{\left[\begin{array}{c}{x}_h\left(k\right)\\ u_h\left(k\right)\end{array}\right]}^T\left[\begin{array}{cc}{Q}_h& N_h\\ N_h^T& R_h\end{array}\right]\left[\begin{array}{c}{x}_h\left(k\right)\\ u_h\left(k\right)\end{array}\right]\right\}}$$

(21)

$$u_h\left(k\right)=-K_h{x}_h\left(k\right)$$

(22)

2.3. Design of LQ SOF Controller

In this paper, a static output-feedback (SOF) control is employed within the preview-control architecture to eliminate the need for full-state measurement required by conventional FSF of LQR [23,24,25,26,41]. An SOF controller is designed for the quarter-car and half-car models, providing implementable feedback laws that rely solely on measurable outputs while preserving the optimality structure of the LQ formulation.

For the quarter-car model, the measurable output vector, y_q, is defined as Equation (23). As indicated in Equation (23), the available outputs comprise the SPM vertical velocity and the suspension stroke rate. These quantities are computed by processing the accelerometer measurements, A_cs and A_cu, as illustrated in Figure 2 [26,41]. The SOF control law is specified by Equation (24). To find an optimal feedback gain matrix, K_SOFq, minimizing the LQPI, J_q, the optimization problem is formulated as Equation (25). In Equation (25), the constraint A represents the closed-loop stability condition, indicating the closed-loop poles should be in a unit circle for stability. The constraint B is the Lyapunov equation for a particular K_SOFq. For a K_SOFq satisfying A, the solution P of the constraint B can be obtained. This problem is solved using the derivative-free Nelder–Mead simplex algorithm, fminsearch(), provided in MATLAB. Let us denote the optimum K_SOFq as LQSOFQ.

$$y_q\left(k\right)\equiv \left[\begin{array}{c}{\dot{z}}_s\left(k\right)\\ {\dot{z}}_s\left(k\right)-{\dot{z}}_u\left(k\right)\end{array}\right]=\left[\begin{array}{cccc}0& 0& 1& 0\\ 0& 0& 1& -1\end{array}\right]x_q\left(k\right)=C_q{x}_q\left(k\right)$$

(23)

$$u_q\left(k\right)=K_{SOFq}{y}_q\left(k\right)=\left[\begin{array}{cc}{k}_1& k_2\end{array}\right]y_q\left(k\right)$$

(24)

$$\begin{array}{ll}\underset{K_{SOFq}}{\min }\hfill & J={\displaystyle \frac{1}{2}}\mathrm{trace}\left(P\right),\hspace{1em}P=P^T>0\hfill \\ \begin{array}{c}s.t.\\ \\ \end{array}\hfill & \left\{\begin{array}{l}\mathrm{A}. \max \left\{\mathrm{abs}\left(\mathrm{eig}\left[{\Phi }_q+{\Sigma }_q{K}_{SOFq}{C}_q\right]\right)\right\}<1\\ \mathrm{B}. {\left({\Phi }_q+{\Sigma }_q{K}_{SOFq}{C}_q\right)}^{T}P\left({\Phi }_q+{\Sigma }_q{K}_{SOFq}{C}_q\right)-P\\ \hspace{1em}\hspace{1em}+Q_q+K_{SOFq}^T{N}_q^T+N_q{K}_{SOFq}+K_{SOFq}^T{R}_q{K}_{SOFq}=0\end{array}\right.\hfill \end{array}$$

(25)

For the half-car model, two candidate output vectors, y_h1 and y_h2, are defined in Equation (26). In y_h1, the measurable outputs comprise the vertical velocity and the pitch rate of the SPM and the front/rear suspension stroke rates. In y_h2, the measurable outputs comprise the front/rear corner vertical velocities of the SPM together with the front/rear suspension stroke rates. These signals are readily computed from the accelerometer measurements, A_csf, A_csr, A_cuf and A_cur, as shown in Figure 3 [26,40]. Notably, y_h2 is equivalent to y_q in Equation (23); that is, y_h2 corresponds to the concatenation of the front and rear y_q vectors [23,24,25]. The associated SOF control laws for y_h1 and y_h2 are given in Equation (27), where the gain matrices, K_SOFh1 and K_SOFh2, adopt structured forms. Since K_SOFh2 is identical to K_SOFq, the elements k₁ and k₂ of K_SOFq can be directly mapped to q₁ and q₂ in K_SOFh2, as given in Equation (28).

$$\left\{\begin{array}{l}{y}_{h1}\left(k\right)\equiv \left[\begin{array}{c}{\dot{z}}_c\left(k\right)\\ \dot{\theta }\left(k\right)\\ {\dot{z}}_{sf}\left(k\right)-{\dot{z}}_{uf}\left(k\right)\\ {\dot{z}}_{sr}\left(k\right)-{\dot{z}}_{ur}\left(k\right)\end{array}\right]=\left[\begin{array}{cccccccc}0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& -l_f& -1& 0\\ 0& 0& 0& 0& 1& l_r& 0& -1\end{array}\right]x_h\left(k\right)=C_{h1}{x}_h\left(k\right)\\ y_{h2}\left(k\right)\equiv \left[\begin{array}{c}{\dot{z}}_{sf}\left(k\right)\\ {\dot{z}}_{sf}\left(k\right)-{\dot{z}}_{uf}\left(k\right)\\ {\dot{z}}_{sr}\left(k\right)\\ {\dot{z}}_{sr}\left(k\right)-{\dot{z}}_{ur}\left(k\right)\end{array}\right]=\left[\begin{array}{cccccccc}0& 0& 0& 0& 1& -l_f& 0& 0\\ 0& 0& 0& 0& 1& -l_f& -1& 0\\ 0& 0& 0& 0& 1& l_r& 0& 0\\ 0& 0& 0& 0& 1& l_r& 0& -1\end{array}\right]x_h\left(k\right)=C_{h2}{x}_h\left(k\right)\end{array}\right.$$

(26)

$$\left\{\begin{array}{l}{u}_{h1}\left(k\right)=K_{SOFh1}{y}_{h1}\left(k\right)=\left[\begin{array}{cccc}{g}_1& g_1& g_3& 0\\ g_1& -g_2& 0& g_4\end{array}\right]y_{h1}\left(k\right)\\ u_{h2}\left(k\right)=K_{SOFh2}{y}_{h2}\left(k\right)=\left[\begin{array}{cccc}{q}_1& q_2& 0& 0\\ 0& 0& q_1& q_2\end{array}\right]y_{h2}\left(k\right)\end{array}\right.$$

(27)

$$K_{SOFh2}=\left[\begin{array}{cccc}{q}_1& q_2& 0& 0\\ 0& 0& q_1& q_2\end{array}\right]=\left[\begin{array}{cc}{K}_{SOFq}& \begin{array}{cc}0& 0\end{array}\\ \begin{array}{cc}0& 0\end{array}& K_{SOFq}\end{array}\right]=\left[\begin{array}{cccc}{k}_1& k_2& 0& 0\\ 0& 0& k_1& k_2\end{array}\right]$$

(28)

To find the gain matrices, K_SOFh1 and K_SOFh2, minimizing J_h, the optimization problem is formulated in the same manner as Equation (25). This optimization problem is also solved using the derivative-free Nelder–Mead simplex algorithm, fminsearch(), provided in MATLAB. Because K_SOFh2 is equivalent to K_SOFq, the optimal gain elements obtained from K_SOFq are directly reused for K_SOFh2. Let denote the optimum K_SOFh1 and K_SOFh2 as LQSOFH and LQSOFQ.

2.4. Design of LQ Preview Controller

For preview control, the road disturbance (i.e., the forward bump profile) is assumed measurable by a sensor at uniform sampling instants with the sampling period, T_s. The preview horizon is specified by T_p, yielding p = T_p/T_s preview steps, and, consequently, there are (1 + p) disturbance samples, including the current one. These previewed disturbance signals are collected in the vector, υ(k), defined in Equation (29). Using υ(k), the discrete-time state-space equation is obtained as in Equation (30). Two vectors, x_i(k) and υ(k), are then stacked to form the augmented vector φ(k) as specified in Equation (31). With this augmented state vector, (14) and (30) are combined into the augmented state-space equation as given in Equation (32), where the matrix Λ is defined in Equation (33) [30,31].

$$\upsilon \left(k\right)\equiv {\left[\begin{array}{cccc}{z}_r\left(k\right)& z_r\left(k+1\right)& \dots & z_r\left(k+p\right)\end{array}\right]}^T$$

(29)

$$\begin{array}{l}\upsilon \left(k+1\right)=\left[\begin{array}{ccccc}0& 1& 0& \dots & 0\\ 0& 0& 1& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \ddots & 1\\ 0& 0& 0& \dots & 0\end{array}\right]\upsilon \left(k\right)+\left[\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 1\end{array}\right]z_r\left(k+p+1\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\Pi \upsilon \left(k\right)+\Xi z_r\left(k+p+1\right)\end{array}$$

(30)

$${\phi }_i\left(k\right)\equiv \left[\begin{array}{c}{x}_i\left(k\right)\\ {\upsilon }_i\left(k\right)\end{array}\right],\hspace{1em}i\in \left\{q,h\right\}$$

(31)

$$\begin{array}{l}{\phi }_i\left(k+1\right)=\left[\begin{array}{cc}{\Phi }_i& {\Lambda }_i\\ 0& \Pi \end{array}\right]{\phi }_i\left(k\right)+\left[\begin{array}{c}0\\ \Xi \end{array}\right]z_r\left(k+p+1\right)+\left[\begin{array}{c}{\Sigma }_i\\ 0\end{array}\right]u\left(k\right)\hfill \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=F_i{\phi }_i\left(k\right)+G{z}_r\left(k+p+1\right)+H_{i}u\left(k\right)\hfill \end{array},\hspace{1em}i\in \left\{q,h\right\}$$

(32)

$${\Lambda }_i\equiv \left[\begin{array}{cccc}{\Gamma }_i& 0& \dots & 0\end{array}\right],\hspace{1em}i\in \left\{q,h\right\}$$

(33)

For the augmented system of Equation (32), the LQPIs—cf. Equation (18) or (21)—is reformulated as Equation (34), with the associated weighting matrices specified in Equation (35). Using Equations (32) and (34), the LQ optimal preview controller is obtained via the standard LQR procedure, yielding Equation (36) [30,31]. As indicated in Equation (36), the control input, u_p, of the preview controller decomposes into feedback and feedforward components, K_FB and K_FF, respectively, where K_FB is a full-state feedback gain. Notably, K_FBq and K_FBh coincide with K_q and K_h given in Equations (19) and (22), respectively.

$$J_{ai}={\displaystyle \sum _{k=0}^{\infty }\left\{{\left[\begin{array}{c}{\phi }_i\left(k\right)\\ u_i\left(k\right)\end{array}\right]}^T\left[\begin{array}{cc}{\overline{Q}}_i& {\overline{N}}_i\\ {\overline{N}}_i^T& {\overline{R}}_i\end{array}\right]\left[\begin{array}{c}{\phi }_i\left(k\right)\\ u_i\left(k\right)\end{array}\right]\right\}},\hspace{1em}i\in \left\{q,h\right\}$$

(34)

$${\overline{Q}}_i\equiv \left[\begin{array}{cc}{Q}_i& 0\\ 0& 0\end{array}\right], {\overline{N}}_i\equiv \left[\begin{array}{c}{N}_i\\ 0\end{array}\right], {\overline{R}}_i\equiv R_i,\hspace{1em}i\in \left\{q,h\right\}$$

(35)

$$u_{pi}\left(k\right)=-{\overline{K}}_i{\phi }_i\left(k\right)=-\left[\begin{array}{cc}{K}_{FBi}& K_{FFi}\end{array}\right]\left[\begin{array}{c}{x}_i\left(k\right)\\ \upsilon \left(k\right)\end{array}\right],\hspace{1em}i\in \left\{q,h\right\}$$

(36)

2.5. Combinations of Feedback and Feedforward Controllers in the Preview Controller

In a real vehicle, direct sensing of all state variables in x_q and x_h is impractical. Accordingly, the full-state feedback gains K_q and K_h of the LQR are replaced with LQ SOF controllers, LQSOFQ and LQSOFH, that rely solely on measurable outputs. While this substitution enables implementable preview control without state reconstruction, the strict optimality guaranteed under the full-state feedback assumption is broken. The resulting preview controller should therefore be interpreted as a practically realizable, near-optimal implementation conditional on the selected output set.

The feedforward gains, K_FFq and K_FFh, are computed from the quarter-car and half-car models in Equation (36). When driven by the preview vector υ(k), K_FFq yields a single control input for the quarter-car model, whereas K_FFh produces two control inputs for the front and rear suspensions in the half-car model. Noting that a half-car model can be viewed as two front/rear quarter-car ones [23,24,25], K_FFq can be deployed per axle instead of K_FFh. In this configuration, each axle receives its own previewed disturbance and the corresponding feedforward command, as illustrated in Figure 4. To formalize this implementation, the axle-wise quarter-car feedforward is aggregated into the block-structured gain K_FFQ defined in Equation (37). Let denote K_FFh and K_FFQ as HPreview and QPreview, respectively. Graphically, Figure 3 illustrates the HPreview scheme, and Figure 4 illustrates the QPreview one. Especially, QPreview is the combination of two preview controllers designed with the quarter-car model given in Figure 2.

$$K_{FFQ}=\left[\begin{array}{c}{K}_{FFq}\\ K_{FFq}\end{array}\right]$$

(37)

Multiple configurations can be assembled for the preview controller. On the feedback side, either K_SOFh1 (LQSOFH) or K_SOFq (LQSOFQ) may be selected. On the feedforward side, either K_FFh (HPreview) or K_FFQ (QPreview) may be selected.

Table 1. Feedback and feedforward controllers for the half-car model.

Controller	Feedback	Feedforward
LQRH	Kh
LQSOFH	KSOFh1
LQSOFQ	KSOFq
PreviewHH	LQSOFH (KSOFh1)	HPreview (KFFh)
PreviewQH	LQSOFQ (KSOFq)	HPreview (KFFh)
PreviewHQ	LQSOFH (KSOFh1)	QPreview (KFFQ)
PreviewQQ	LQSOFQ (KSOFq)	QPreview (KFFQ)

summarizes the admissible pairings for the half-car model, enumerating the combinations of feedback and feedforward components that define each controller variant.

3. Design of Virtual Disturbance with SBOM

In the prior works, a normal-distribution–shaped virtual reference (NDVR) was introduced to emulate road bumps for feedforward control [38,39]. Following the idea of the prior works, this paper adopts the same principle that eliminates direct measurement or estimation of a physical bump profile. In this paper, this concept is extended to preview control by replacing a real bump signal with a virtual disturbance.

The NDVR proposed in the previous work is given in Equation (38) [39]. In Equation (38), there are three parameters in NDVR: the height h, width σ, and the center position μ. However, it is not easy to tune those parameters due to the nonlinear term, h/σ. In other words, it is not intuitive to shape NDVR with those parameters. Moreover, due to the nonlinear term, increasing the temporal width unavoidably distorts the peak magnitude, making it difficult, for example, to generate a wider reference with a smaller height. To cope with the problem, a half-sine virtual disturbance (HSVD), defined in Equation (39), is adopted as the previewed one in this paper. This choice preserves key temporal and amplitude characteristics of typical bump excitations while enabling a compact parametric description compatible with the preview horizon.

$$z_{rv}\left(x\right)={\displaystyle \frac{h}{\sigma \sqrt{2\pi }}}\exp \left(-{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{x-\mu }{\sigma }}\right)}^2\right)$$

(38)

$$z_{rv}\left(x\right)={\displaystyle \frac{h}{2}}\left\{1-\sin {\displaystyle \frac{2\pi }{w}}\left(x-c-0.25·w\right)\right\}$$

(39)

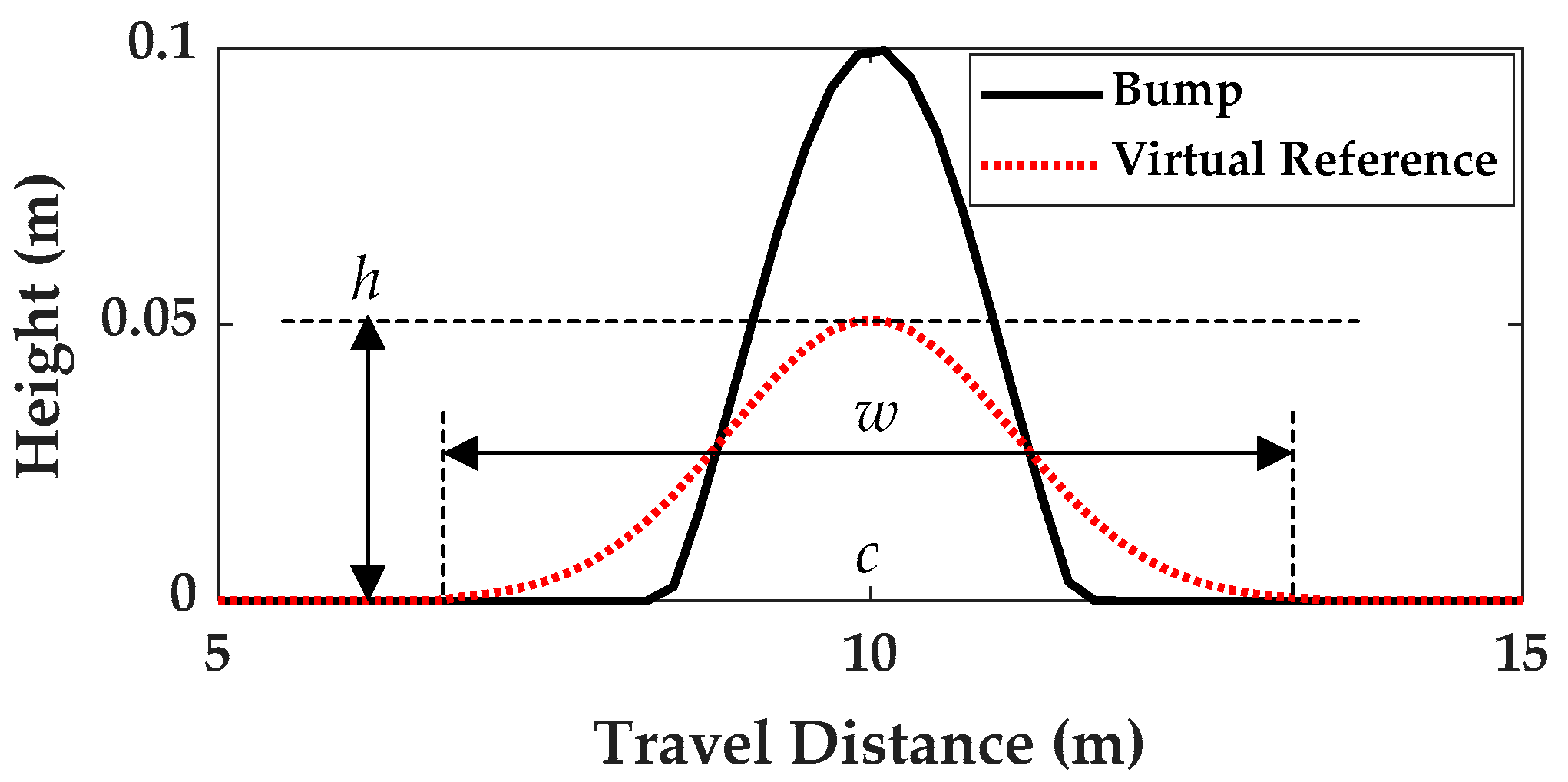
Figure 5 depicts the HSVD adopted in this paper. The HSVD is parameterized by three scalars—h, w, and c—representing the height (amplitude), width (effective duration), and center position, respectively. The center position, c, is anchored to the midpoint of the corresponding physical bump; consequently, if c is included in the decision vector, it quantifies the phase offset from a true bump center. To maximize the performance of the preview controller, the HSVD parameters (h,w,c) are optimized with respect to a particular performance criterion.

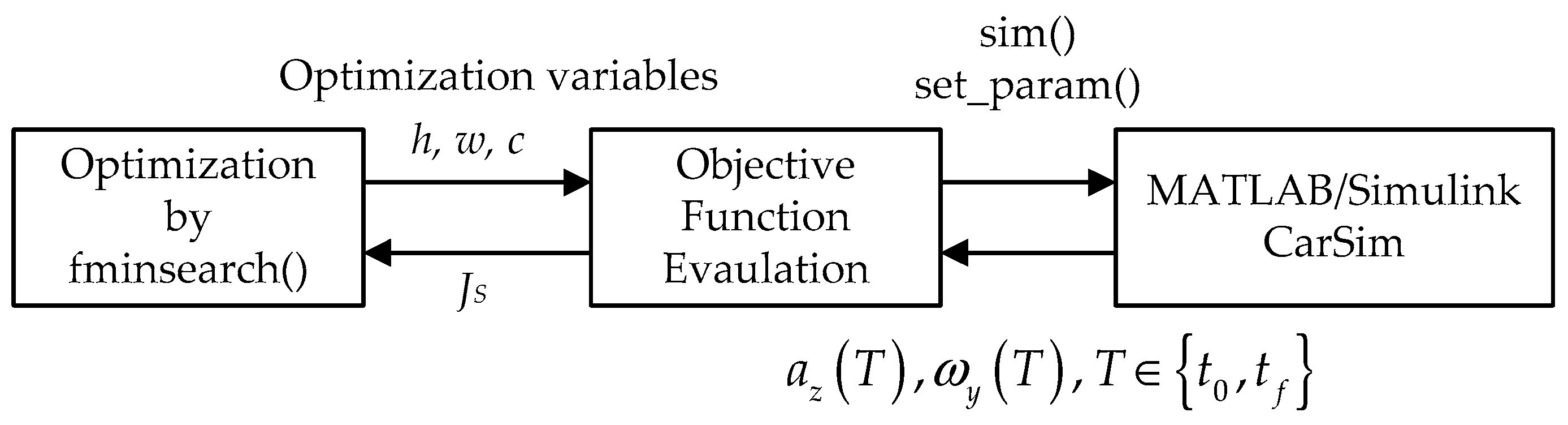
In this paper, a simulation-based optimization method (SBOM) is adopted to optimize the HSVD parameters [26,39]. To jointly address ride-comfort improvement and motion-sickness mitigation, the objective function of SBOM is defined in Equation (40) as a composite of a_z and ω_y responses, evaluated over the simulation horizon T on a co-simulation environment of MATLAB2019a/Simulink and CarSim8.0 [26,42]. In Equation (40), R2D denotes the radians-to-degrees conversion factor, and α is a parameter used to tune the relative importance of a_z to ω_y; in this paper, α = 0.3. The derivative-free Nelder–Mead simplex algorithm, fminsearch(), provided in MATLAB, is selected as an optimizer for SBOM in this paper. The SBOM workflow is illustrated in Figure 6. Once the HSVD parameters are optimized via SBOM, the resulting virtual disturbance replaces the physical bump signal in all subsequent simulations.

$$J_S=\max \left|a_z\left(T\right)\right|+\alpha ·\mathrm{R}2\mathrm{D}·\max \left|{\omega }_y\left(T\right)\right|,\hspace{1em}T\in \left\{t_0,t_f\right\}$$

(40)

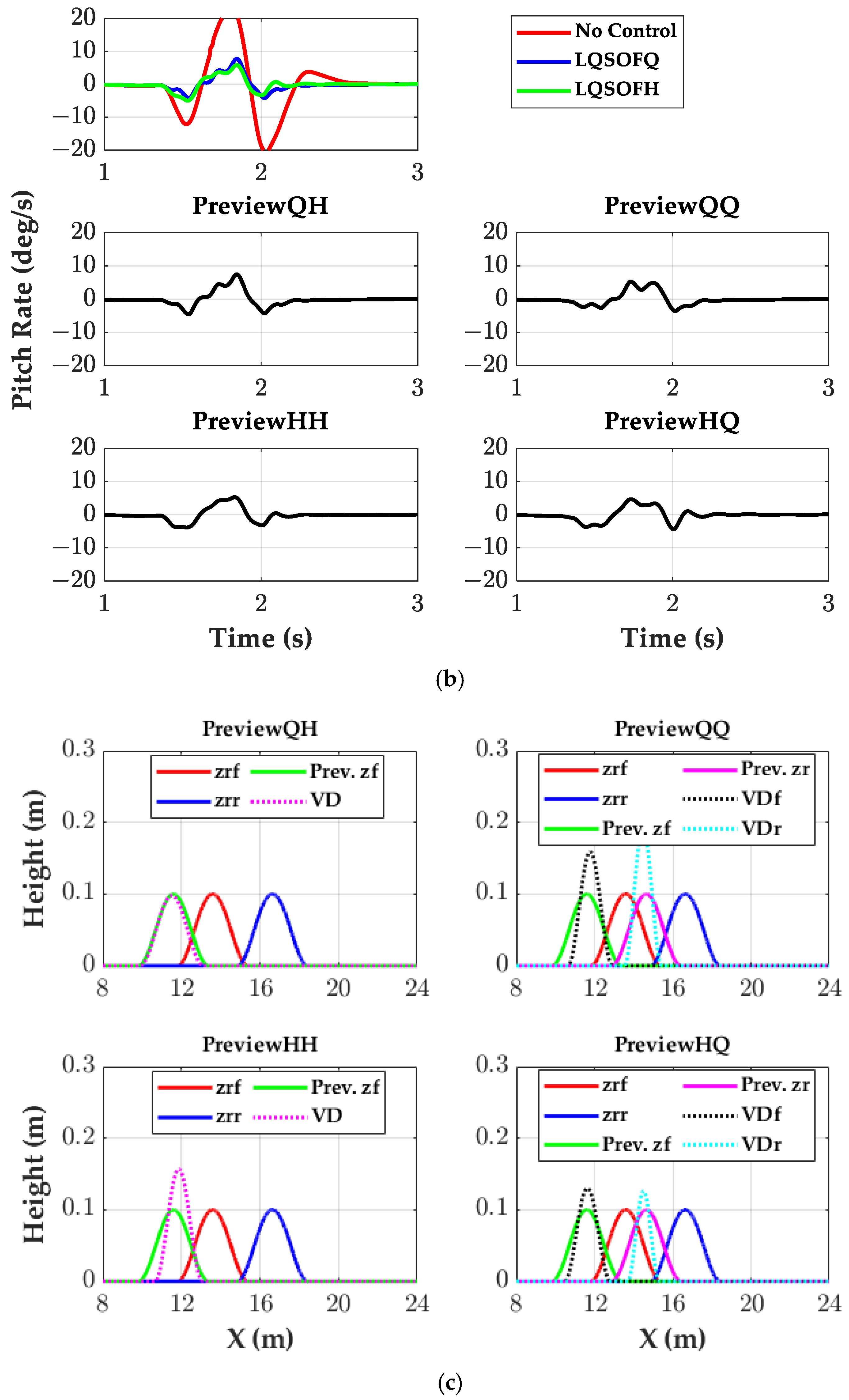
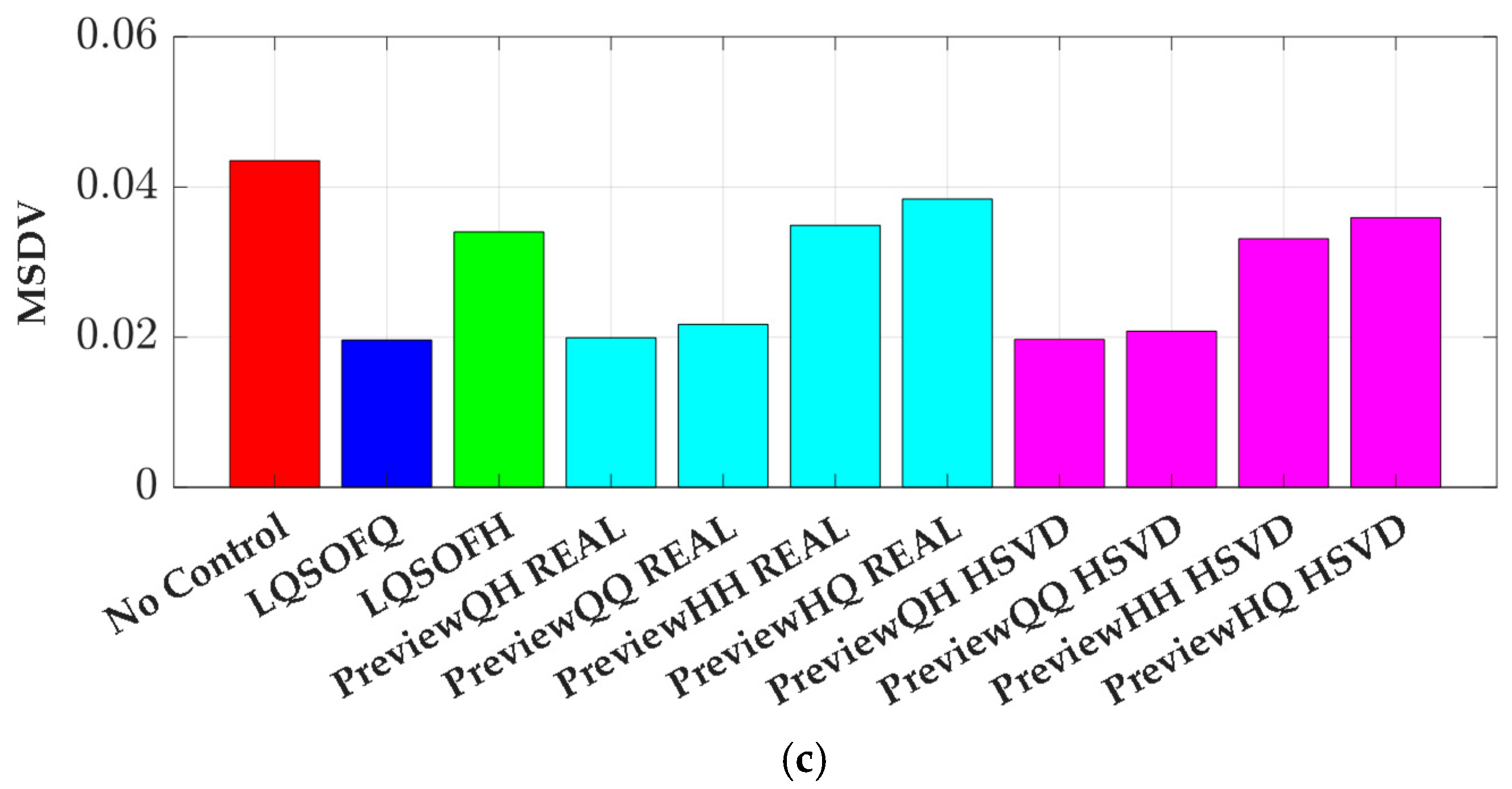
As summarized in Table 1 and Figure 3, preview controllers employing HPreview (i.e., K_FFh) utilize a single set of previewed signals associated with one bump; consequently, a single HSVD, as shown with a red line in Figure 3, is required, and its three parameters (h, w, c) are optimized by SBOM. By contrast, as illustrated in Figure 4, preview controllers employing QPreview (i.e., K_FFQ) require two distinct preview signal sets for a single bump, since the rear suspension encounters a phase-shifted disturbance relative to the front. Accordingly, two—front/rear—HSVD profiles, as shown with red lines in Figure 4, are introduced, yielding six decision variables (h_f, w_f, c_f, h_r, w_r, c_r) where subscripts, f and r, denote the front and rear axles, respectively. Noting that the wheelbase specifies the spatial offset between axles, c_r represents the deviation of the rear HSVD center from the wheelbase-aligned position.

4. Simulation and Discussion

In this section, a simulation is conducted to evaluate the performance of the preview controllers and their pairings with the virtual disturbance configurations summarized in Table 1.

4.1. Simulation Condition

The parameters of the quarter- and half-car models used in this paper are summarized in

Table 2. Parameters and values of the quarter-car and half-car models.

Parameter	Value	Parameter	Value
ms	1623 kg	mu	40 kg
Iy	2765 kg⋅m2	kt, ktf, ktr	230,000 N/m
lf	1.40 m	lr	1.65 m
ks, ksf, ksr	34,000 N/m	bs, bsf, bsr	3500 Ns/m
msq	ms/4

and are drawn from the CarSim E-class sedan dataset [42]. The vehicle dynamics are represented using a 27-degree-of-freedom (DOF) nonlinear model implemented in CarSim8.0, which consists of a single sprung mass, four wheels, four suspension units, and a steering mechanism. The suspension system is modeled with independent suspensions on the front and rear axles [42].

The weighting factors for the LQPIs, J_q and J_h, were selected on the basis of the MAVs listed in

Table 3. MAVs in LQ cost functions.

LQPI	MAV	Value	MAV	Value	MAV	Value	MAV	Value
Jq	ξ1	0.5 m/s2	ξ2	0.1 m	ξ3	0.1 m	ξ4	5000 N
Jh	ξ1	0.1 m/s2	ξ2	30.0 deg/s2	ξ3	1.0 deg/s	ξ4	5.0 deg
	ξ5	0.1 m	ξ6	0.1 m	ξ7	10,000 N

. As shown in Table 3, the MAV associated with a_z, ξ₁, was set to a relatively low value to prioritize ride-comfort improvement; for the half-car model, the MAV for ω_y, ξ₃, was likewise reduced to reflect its importance for motion-sickness mitigation. An actuator bandwidth was set to 10 Hz to ensure the resulting controllers remain feasible under practical actuation limits.

For simulation on CarSim, a large half-sine bump (LHSB) with a height of 0.10 m and a width of 3.6 m was selected as the road excitation. The vehicle speed was fixed and maintained at 10 m/s by the built-in speed controller in CarSim. Sensor and controller sampling periods, T_s, were set to 1 ms, and the preview interval, T_p, was set to 0.2 s. Consequently, the preview distance equals 2 m, and the number of previewed disturbance samples is 1 + p = 201 with p = T_p/T_s = 200.

When applying SBOM to HSVD, the ranges of HSVD parameters for HPreview and QPreview were set as given in

Table 4. Ranges of the HSVD parameters for HPreview and QPreview.

Preview Scheme	Front	Rear
HPreview	0.01 ≤ h ≤ 0.2
	0.05 ≤ w ≤ 4.0
	−2.0 ≤ c ≤ 2.0
QPreview	0.01 ≤ hf ≤ 0.2	0.01 ≤ hr ≤ 0.2
	0.05 ≤ wf ≤ 4.0	0.05 ≤ wr ≤ 4.0
	−2.0 ≤ cf ≤ 2.0	2.0 ≤ cr ≤ 5.0

. As summarized in Table 4, the HSVD for HPreview comprises three parameters because HPreview relies solely on front preview signals, whereas the HSVD for QPreview comprises six parameters, reflecting the use of both front and rear preview signals.

4.2. Frequency Response Analysis with the Preview Controllers

In this subsection, frequency-response analyses are conducted for the half-car discrete-time state-space equation with four controllers: LQRH and LQ Preview, defined in Equations (22) and (36), respectively, together with LQSOFQ and LQSOFH.

The frequency response plots are presented in Figure 7. As observed in Figure 7, LQSOFQ yields the lowest a_z, whereas LQ Preview achieves the most favorable attenuation in the pitch-rate channel ω_y. Notably, LQSOFQ surpasses both LQRH and LQ Preview in the vicinity of 1 Hz. In addition, LQRH and LQ Preview exhibit nearly indistinguishable behavior below 1 Hz, while LQ Preview provides superior attenuation relative to LQRH over the 1–10 Hz band.

Figure 8 presents the frequency response plots of the five preview-controller variants summarized in Table 1—namely, LQ Preview, LQSOFQ, and LQSOFH, combined with HPreview and QPreview. As evidenced in Figure 8, inclusion of the feedforward component enhances the response when paired with LQSOFQ feedback. By contrast, the feedforward term exerts only a marginal influence when combined with LQSOFH. Furthermore, QPreview and HPreview exhibit only minor differences across the examined frequency range. Collectively, these results indicate that the feedforward control yields performance gains primarily for preview configurations that employ LQSOFQ as the feedback controller.

4.3. Simulation on CarSim

In this subsection, numerical simulations are conducted using the controller configurations summarized in Table 1. The resulting time responses are depicted in Figure 9, and the corresponding peak metrics—maximum absolute values of a_z and ω_y—RMS and MSDV are listed in

Table 5. Maximum absolute a_z and ω_y calculated from the simulation results given in Figure 9.

Controller	Max |az| (m/s2)	RMS(az)	MSDV(az)	Max |ωy| (deg/s)	RMS (ωy)
No Control	4.6	0.0194	0.0435	23.2	0.1012
LQSOFQ	3.2 (31%)	0.0088	0.0196	7.8 (67%)	0.0504
LQSOFH	3.4 (25%)	0.0152	0.0340	5.8 (75%)	0.0820
PreviewQH	2.9 (38%)	0.0089	0.0199	7.5 (68%)	0.0498
PreviewQQ	2.9 (38%)	0.0097	0.0217	7.2 (69%)	0.0541
PreviewHH	3.4 (26%)	0.0156	0.0349	5.8 (75%)	0.0754
PreviewHQ	3.2 (31%)	0.0172	0.0384	5.4 (77%)	0.0901

. In Table 5, RMS and MSDV are computed with frequency-weighted signals as given in the previous study [10].

As evidenced in Figure 9 and Table 5, both LQSOFQ and LQSOFH enhance ride comfort and attenuate motion-sickness–related responses relative to the uncontrolled baseline. For LQSOFQ, the addition of feedforward action, HPreview or QPreview, further suppresses a_z with only minor influence on ω_y. Conversely, for LQSOFH, HPreview and QPreview primarily reduce ω_y while exerting a limited effect on a_z; notably, HPreview yields negligible benefit when paired with LQSOFH. These results were expected from the frequency response analysis of the previous subsection. Based on these results, it can be anticipated that the control performance of the preview controllers with LQSOFQ would be further enhanced by the optimized HSVD.

4.4. Simulation with HSVD on CarSim

In this subsection, numerical simulations are performed for the preview controllers augmented with the optimized HSVD. The HSVD parameters are first optimized for the four preview configurations considered in the preceding subsection. Using these optimized HSVD profiles, closed-loop evaluations are carried out on the LHSB scenario in CarSim. The resulting time-domain responses are presented in Figure 10, and the corresponding peak performance metrics—maximum absolute a_z and ω_y—RMS, and MSDV are summarized in

Table 6. Maximum absolute a_z and ω_y calculated from the simulation results given in Figure 10.

Controller	Max |az| (m/s2)	RMS(az)	MSDV(az)	Max |ωy| (deg/s)	RMS (ωy)
No Control	4.6	0.0194	0.0435	23.2	0.1012
LQSOFQ	3.2 (31%)	0.0088	0.0196	7.8 (67%)	0.0504
LQSOFH	3.4 (25%)	0.0152	0.0340	5.8 (75%)	0.0820
PreviewQH	2.6 (43%)	0.0088	0.0197	7.5 (68%)	0.0504
PreviewQQ	2.3 (51%)	0.0093	0.0208	5.3 (77%)	0.0522
PreviewHH	3.1 (32%)	0.0148	0.0331	5.3 (77%)	0.0659
PreviewHQ	2.4 (47%)	0.0160	0.0359	4.6 (80%)	0.0925

.

As evidenced in Figure 10 and Table 6, QPreview equipped with an optimized HSVD outperforms HPreview with its corresponding optimized HSVD. This performance gap arises from the greater parametric flexibility of QPreview: its HSVD comprises six decision variables, i.e., front/rear (h,w,c), whereas HPreview employs only three, enabling more precise amplitude–duration–phase shaping per axle (cf. Figure 10c). Across the reported metrics, the reduction in a_z is more pronounced than that of ω_y, indicating that QPreview primarily enhances heave attenuation. This behavior is consistent with the fact that quarter-car–based designs exert limited direct authority over the SPM pitch dynamics. Overall, the combination of LQSOFQ with QPreview and an optimized HSVD delivers the most favorable trade-off between ride-comfort improvement and motion-sickness mitigation in the tested scenario.

4.5. Summary and Discussion

Figure 11 illustrates the simulation outcomes, Max|a_z|, Max |ω_y|, and MSDV(a_z), summarized in Figure 9 and Figure 10 and Table 5 and Table 6. In Figure 11, the controller labels suffixed with “REAL” and “HSVD” denote the preview controllers given in Table 5 and Table 6, respectively.

As shown in Figure 11a,b, the preview controllers employing the optimized HSVD yield the most favorable ride-comfort outcomes; among them, the PreviewQQ–HSVD configuration attains the lowest a_z metrics. This superiority is attributable to the comparatively strong baseline performance of LQSOFQ and the use of two preview channels in PreviewQQ. By contrast, inter-controller differences in pitch-rate responses are modest; however, controllers synthesized with the half-car model exhibit slightly better pitch-rate attenuation. Consistent with Figure 11c, LQSOFQ—and the preview schemes constructed upon it—deliver the best motion-sickness performance, while the incremental benefit attributable to preview action on motion-sickness indices remains limited.

5. Conclusions

This paper presents the design method for preview controllers with active suspension systems. Instead of full-state feedback within the preview loop, two LQ SOF controllers—LQSOFQ and LQSOFH—are designed using quarter-car and half-car models, respectively, to provide implementable feedback laws based solely on measurable outputs. On the feedforward side, two alternatives are constructed: HPreview, derived from the half-car model, and QPreview, assembled from axle-wise quarter-car feedforward blocks. To enhance the performance of the feedforward loop in the preview controller, a half-sine virtual disturbance (HSVD) is adopted and optimized via a simulation-based optimization method. Comparative evaluations focusing on ride comfort and motion-sickness proxies are performed in CarSim. The analysis of the simulation results reveals the following key findings:

• The static output-feedback controller derived from the quarter-car model (LQSOFQ) consistently surpasses its half-car counterpart (LQSOFH), including within the preview-control configurations.
• The quarter-car-based feedforward scheme (QPreview) outperforms the half-car–based alternative (HPreview), attributable to its utilization of two axle-specific previewed disturbance signals. The simulation results show that the LQ SOF controller decreased the vertical acceleration and pitch rate of the sprung mass by 25% and 75%, respectively, whereas the preview controller with QPreview yielded reductions of 38% and 69%, respectively.
• The simulation-based optimized virtual disturbance (HSVD via SBOM) markedly attenuates the SPM vertical acceleration while exerting only a modest influence on the SPM pitch-rate response. The simulation results show that the LQ SOF controller decreased the vertical acceleration and pitch rate of the sprung mass by 25% and 75%, respectively, whereas the preview controller with QPreview and NSVD yielded reductions of 47% and 80%, respectively.

The virtual disturbance adopted in this paper is not directly applicable to sinusoidal road profiles or ISO random road excitations. Accordingly, future work should develop virtual-disturbance parameterizations that are well matched to periodic and broadband stochastic road excitations. In addition, experimental validation on a real vehicle should be performed to substantiate the simulation findings. From experiments, some problems regarding potential real-time implementation issues, such as sensor delays and preview horizon accuracy, can be identified. To this end, as given in the previous study, tests on a real vehicle platform or a quarter-car hardware-in-the-loop (HIL) rig are planned to assess controller robustness and implementability under real-world sensing and actuator constraints [25].