Efficient Adaptive Learning via Partial-Update Variable Step-Size LMS for Real-Time ERP Denoising

Abstract

Event-Related Potentials (ERPs) are low-amplitude neural responses elicited by sensory or cognitive stimuli, widely exploited as biomarkers in the early diagnosis of neurodevelopmental and neurodegenerative disorders such as autism spectrum disorder and Alzheimer’s disease, and as control signals in brain–computer interface (BCI) systems for severely disabled individuals. However, their extremely low signal-to-noise ratio (SNR) necessitates robust denoising, especially in real-time BCI applications where low latency, minimal computational overhead, and single-channel operation are critical constraints. While advanced offline methods like Independent Component Analysis (ICA) and wavelet-based thresholding offer effective denoising in multichannel settings, they are ill-suited for embedded, causal, and resource-constrained environments. To address this gap, we propose a Partial-Update Variable Step-Size LMS (PU-VSS-LMS) algorithm that complementarily combines dynamic step-size adaptation with a magnitude-driven partial-update strategy. Evaluated on synthetic ERP-like signals embedded in realistic EEG noise (SNR = 6 dB and 0 dB), PU-VSS-LMS achieves lower mean squared error (MSE: 0.0780 vs. 0.0850 at 6 dB) and higher output SNR (8.10 dB vs. 7.80 dB) than standard VSS-LMS, while outperforming ICA in waveform preservation and noise suppression. Importantly, it reduces computational load by 75% (updating only 4 of 16 coefficients), enabling faster execution without sacrificing accuracy. These results establish PU-VSS-LMS as a highly efficient and effective solution for real-time ERP denoising in embedded, single-channel biomedical systems.

1. Introduction

Event-Related Potentials (ERPs) are time-locked electrophysiological responses to sensory, cognitive, or motor stimuli, widely exploited as neural biomarkers in both clinical diagnostics and Brain–Computer Interface (BCI) systems. However, due to their low amplitude (typically in the microvolt range) and transient nature, ERPs are often buried in high-amplitude background electroencephalographic (EEG) activity, resulting in a poor signal-to-noise ratio (SNR) [1,2,3,4,5]. EEG signals exhibit a pink noise ($1/f$) background with long-range correlations, overlaid with brain rhythms that vary with cognitive state or task. This challenge is particularly acute in real-world applications such as the early detection of neurodegenerative disorders such as Alzheimer’s disease or neurodevelopmental conditions such as autism spectrum disorder, where reliable single-trial ERP extraction is essential yet difficult to achieve.

In BCI contexts, ERPs like the P300 or error-related negativity (ERN) enable communication for individuals with severe motor disabilities. However, such systems require real-time, low-latency processing to ensure usability and responsiveness requirements that exclude offline, computationally heavy methods such as Independent Component Analysis (ICA) and wavelet-based thresholding [4,5]. Among existing denoising strategies, ICA and wavelet-based thresholding are widely used for ERP enhancement [4,5]. While effective in multichannel, offline scenarios, ICA requires extensive preprocessing, assumes statistical independence of sources, and is inappropriate for single-channel or online deployment. Similarly, wavelet methods often rely on prior knowledge of signal morphology and may introduce phase distortions or over-smoothing in real-time settings.

Another widely adopted family of denoising techniques in ERP processing relies on wavelet transform. Wavelet-based methods [4,5] decompose the signal into time frequency sub-bands, allowing selective thresholding of coefficients associated with noise while preserving transient ERP features such as the P300 or error-related negativity (ERN). Common approaches include soft or hard thresholding in the wavelet domain, often combined with adaptive threshold selection rules like SureShrink or Minimax. However, these methods suffer from several practical limitations. First, performance is highly dependent on the choice of the mother wavelet, which must closely match the morphology of the target ERP components, a non-trivial task given the variability across individuals and cognitive tasks. Second, the selection of decomposition level and thresholding strategy significantly impacts results; suboptimal choices can lead to over-smoothing (loss of sharp ERP peaks) or under-denoising (residual noise). Third, wavelet denoising is inherently non-causal and typically applied in batch mode, making it unsuitable for real-time, single-trial processing in adaptive BCI systems. Finally, the method may introduce phase distortions or artifactual oscillations near sharp transitions, especially when using non-symmetric wavelets or aggressive thresholding.

Although effective in offline mode, these limitations make wavelet-based approaches poorly suited for ERP acquisition and processing systems, where real-time, low-complexity, and robust algorithms like PU-VSS-LMS present a compelling alternative.

In contrast, adaptive filtering provides a causal, computationally lightweight, and single-channel-compatible solution that aligns naturally with real-time constraints. The classical Least-Mean-Squares (LMS) algorithm, though simple and robust, suffers from a fundamental trade-off between convergence speed and steady-state error due to its fixed step size. Variable Step-Size LMS (VSS-LMS) mitigates this limitation by dynamically adjusting the step size based on instantaneous error, thereby improving both convergence and stability. Nevertheless, VSS-LMS still updates all filter coefficients at every iteration, leading to unnecessary computational load, especially problematic in embedded or wearable neurotechnology platforms.

This paper addresses these gaps by proposing a novel Partial-Update VSS-LMS (PU-VSS-LMS) algorithm, which synergistically combines dynamic step-size adaptation with a magnitude-driven partial-update strategy. Specifically, only the subset of filter coefficients associated with the largest input samples is updated at each iteration, significantly reducing arithmetic complexity while preserving or even enhancing denoising performance.

The main contributions of this work are threefold. First, we propose a novel coefficient selection criterion specifically tailored to the temporal and spectral characteristics of Event-Related Potentials (ERPs), which prioritizes updates on filter taps associated with the most informative input samples. Second, we provide comprehensive empirical validation of the proposed PU-VSS-LMS algorithm against both classical adaptive filtering (VSS-LMS) [6,7,8,9,10] and advanced blind-source separation (Independent Component Analysis, ICA) under identical signal-to-noise ratio (SNR) conditions, demonstrating its superior denoising performance. Third, we show that the algorithm achieves a 75% reduction in computational load, translating to significantly faster execution while simultaneously improving both mean squared error (MSE) and output SNR. This unique combination of efficiency and accuracy makes PU-VSS-LMS [11,12,13] particularly well-suited for real-time biomedical applications in resource-constrained environments such as Wearable EEG systems and Brain–Computer Interfaces (BCI).

By overcoming the fundamental compromise between algorithmic efficiency and denoising fidelity, this work advances the state of the art in adaptive ERP processing and offers a practical pathway toward deployable single-channel BCI and diagnostic systems.

2. Adaptive Filtering

Adaptive filtering is a fundamental technique in signal processing, particularly noise cancellation and system identification [14]. The LMS algorithm remains one of the most widely used due to its simplicity, low computational cost, and applicability in domains such as communication, acoustics, and biomedical engineering [15,16,17,18].

Despite its advantages, the classical LMS algorithm uses a fixed step size $\mu$, which imposes a compromise between fast convergence and low steady-state error. To overcome this, variable step-size (VSS) strategies have been developed [8,19], and more recently, partial-update (PU) techniques have been introduced to reduce computational load [17,18].

This work combines both approaches variable step size and partial update into a single algorithm, PU-VSS-LMS, and evaluates its performance in denoising Event-Related Potentials (ERPs), which are weak neural responses often buried in high-amplitude EEG noise.

The adaptive filter operates on two key vectors: the input vector $\mathbf{u}\left(n\right)$ and the weight vector $\mathbf{w}\left(n\right)$, updated iteratively to minimize the estimation error $e\left(n\right)$.

At iteration n, the input vector is defined as:

$$\mathbf{u}\left(n\right)={[u\left(n\right),u(n-1),\dots ,u(n-M+1)]}^T$$

(1)

where M is the filter order (number of taps) and $u(n-i)$ are delayed input samples.

The input vector $\mathbf{u}\left(n\right)$ in Equation (1) represents a sliding window of the M most recent samples of the input signal and serves as the regressor in the adaptive filter.

The weight vector is:

$$\mathbf{w}\left(n\right)={[w_0\left(n\right),w_1\left(n\right),\dots ,w_{M-1}\left(n\right)]}^T$$

(2)

where $w_i\left(n\right)$ are the adaptive coefficients.

The filter output is computed as:

$$y\left(n\right)={\mathbf{w}}^T\left(n\right)\mathbf{u}\left(n\right)$$

(3)

The error signal is:

$$e\left(n\right)=d\left(n\right)-y\left(n\right)$$

(4)

where $d\left(n\right)$ is the desired (clean) signal.

Figure 1 shows the general block diagram of the adaptive filter used in both VSS-LMS and PU-VSS-LMS.

3. Algorithm Descriptions

3.1. VSS-LMS Algorithm

The VSS-LMS algorithm [6,7,8,9] dynamically adjusts the step size $\mu \left(n\right)$ at each iteration:

$$\mu (n+1)={\alpha }_K·\mu \left(n\right)+{\gamma }_K·e^2\left(n\right)$$

(5)

subject to:

$${\mu }_{min}\le \mu (n+1)\le {\mu }_{max}$$

(6)

with parameters: ${\alpha }_K=0.95$, ${\gamma }_K=0.001$, ${\mu }_{min}=0.001$, ${\mu }_{max}=0.2$.

The weight update is:

$$\mathbf{w}(n+1)=\mathbf{w}\left(n\right)+\mu \left(n\right)·\mathbf{u}\left(n\right)·e\left(n\right)$$

(7)

3.2. PU-VSS-LMS Algorithm

The PU-VSS-LMS algorithm [11,12] performs the same step-size adaptation but updates only a subset of P coefficients at each iteration. The selection is based on the magnitude of the input vector elements.

Let $I_P\left(n\right)$ be the set of indices corresponding to the P largest $\left|u\right(n-i\left)\right|$ values.

The weight update becomes:

$$w_i(n+1)=\left\{\begin{array}{cc}{w}_i\left(n\right)+\mu \left(n\right)·u(n-i)·e\left(n\right),\hfill & \mathrm{if}i\in I_P\left(n\right)\hfill \\ w_i\left(n\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(8)

This reduces the number of multiplications from $2M$ to $2P$ per iteration, a 75% reduction when $P=4$ and $M=16$.

3.3. Adaptive Structure and PU-VSS-LMS Algorithm

The proposed denoising structure for Event-Related Potentials (ERP) is based on an adaptive filter, whose block diagram is illustrated in Figure 1. This system uses the reference signal $\mathbf{u}\left(n\right)$, which is correlated with the noise to be eliminated, to generate an estimate of this noise, $y\left(n\right)$.

The output signal of the adaptive filter, $y\left(n\right)$, is computed from the weight vector $\mathbf{w}\left(n\right)$ and the input vector $\mathbf{u}\left(n\right)$, as described by Equation (3).

The system operates by minimizing the mean square error (MSE) of the error signal $e\left(n\right)$. This signal, calculated as the difference between the primary signal $d\left(n\right)$ (the noisy ERP) and the noise estimate $y\left(n\right)$, represents the final denoised ERP signal, as defined by Equation (4).

The filter’s weight vector $\mathbf{w}\left(n\right)$ is updated iteratively by the proposed algorithm. The weight update equation used is given by Equation (8), which incorporates the Partial-Update (PU) mechanism to optimize algorithmic complexity.

The adaptation step-size $\mu \left(n\right)$ is a dynamic variable, essential for ensuring both fast convergence and low residual error in the steady-state. Its calculation is governed by Equations (5)–(7), which ensure optimal adaptation to the changing statistics of the error signal.

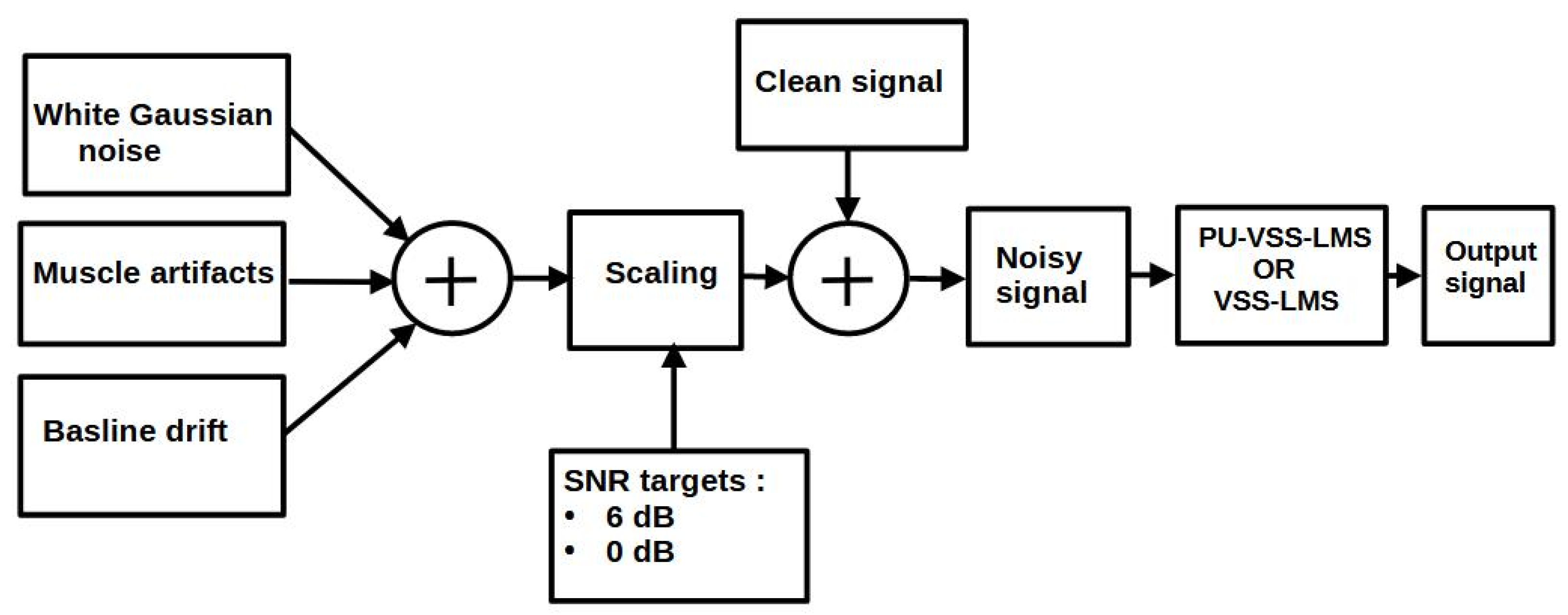
3.4. Noise Modeling and SNR Adjustment

To emulate realistic EEG acquisition conditions, synthetic EEG-like noise was superimposed on the clean signal $s\left(t\right)$. The composite noise $n\left(t\right)$ was constructed from three components modeling typical EEG contamination sources (Figure 2):

$$n\left(t\right)=n_{\mathrm{WGN}}\left(t\right)+n_{\mathrm{MA}}\left(t\right)+n_{\mathrm{BD}}\left(t\right)$$

(9)

where:

• White Gaussian noise ($n_{\mathrm{WGN}}\left(t\right)$) simulates broadband electronic and environmental interference:

  $$n_{\mathrm{WGN}}\left(t\right)=0.5·\mathrm{randn}\left(\mathrm{size}\left(t\right)\right)$$

  (10)
• Muscle artifacts ($n_{\mathrm{MA}}\left(t\right)$) correspond to high-frequency (electromyographic) activity in the 30–50 Hz range:

  $$n_{\mathrm{MA}}\left(t\right)=0.2·sin\left(2\pi ·40·t\right)$$

  (11)
• Baseline drift ($n_{\mathrm{BD}}\left(t\right)$) models low-frequency variations due to electrode polarization, motion, or perspiration:

  $$n_{\mathrm{BD}}\left(t\right)=0.3·sin\left(2\pi ·0.5·t\right)$$

  (12)

3.4.1. Noise Power and Scaling

The noise power $P_n$ and clean signal power $P_s$ were calculated as:

$$P_n={\displaystyle \frac{1}{N}}\sum _{k=1}^N{n}^2\left(t_k\right)$$

(13)

$$P_s={\displaystyle \frac{1}{N}}\sum _{k=1}^N{s}^2\left(t_k\right)$$

(14)

The signal-to-noise ratio (SNR) in decibels is defined as:

$${\mathrm{SNR}}_{\mathrm{dB}}=10{log}_{10}\left({\displaystyle \frac{P_s}{P_n}}\right)$$

(15)

For a target ${\mathrm{SNR}}_{\mathrm{target}}$, the scaling factor $\alpha$ applied to $n\left(t\right)$ is:

$$\alpha =\sqrt{{\displaystyle \frac{P_s}{P_n·{10}^{{\mathrm{SNR}}_{\mathrm{target}}/10}}}}$$

(16)

The final noisy signal $x\left(t\right)$ is thus:

$$x\left(t\right)=s\left(t\right)+\alpha ·n\left(t\right)$$

(17)

Two scenarios were considered:

• ${\mathrm{SNR}}_{\mathrm{target}}=6\mathrm{dB}$: high-quality recording
• ${\mathrm{SNR}}_{\mathrm{target}}=0\mathrm{dB}$: moderately noisy environment

3.4.2. Sampling and Filtering Parameters

The signals were sampled at $f_s=500\mathrm{Hz}$ over $T=1\mathrm{s}$. In the PU-VSS-LMS configuration, the filter order was set to $M=16$, with $P=4$ coefficients updated per iteration. The selection of a filter order $M=16$ and partial-update size $P=4$ represents a deliberate trade-off carefully balanced to meet the competing demands of real-time EEG processing. This configuration achieves an optimal equilibrium between convergence speed, steady-state error, and computational efficiency essential requirements for embedded biomedical applications. With a sampling rate of $f_s=500$ Hz, the 16-tap filter covers a $T=M/f_s=32$ ms temporal window, effectively capturing the characteristic timescale of early ERP components. Furthermore, updating only 25% of the coefficients (4 out of 16) per iteration reduces computational load by 75% while preserving adaptive performance, as demonstrated by the improved convergence behavior and lower MSE achieved in our simulations.

4. Methodology

A synthetic ERP-like signal was generated using a Gaussian pulse model:

$${\mathrm{ERP}}_{\mathrm{clean}}\left(t\right)=A·exp\left(-{\displaystyle \frac{{(t-t_0)}^2}{{\sigma }^2}}\right)$$

(18)

with $A=1$, $t_0=0.3$ s, $\sigma =0.05$ s.

To simulate non-stationarity, a sinusoidal component was added after $t>0.5$ s:

$${\mathrm{ERP}}_{\mathrm{clean}}(t>0.5)={\mathrm{ERP}}_{\mathrm{clean}}(t>0.5)+0.5·sin(2\pi ·30·t)$$

(19)

Realistic EEG-like noise was added, composed of:

• White Gaussian noise: $0.5·\mathrm{randn}\left(\mathrm{size}\right(t\left)\right)$
• Muscle artifacts: $0.2·sin(2\pi ·40·t)$
• Baseline drift: $0.3·sin(2\pi ·0.5·t)$

The total noise power was scaled to achieve:

• SNR = 6 dB (high-quality recording)
• SNR = 0 dB (moderately noisy environment)

5. Simulation Results

Figure 3 provides a visual comparison of the denoising performance of several methods applied to a synthetic ERP signal heavily corrupted by noise (SNR = 0 dB). It shows that the PU-VSS-LMS algorithm reconstructs the signal with significantly higher fidelity than VSS-LMS, especially for low-amplitude components. While VSS-LMS leaves residual noise and partially distorts the signal morphology, PU-VSS-LMS more accurately preserves the shape of the Gaussian pulse and effectively suppresses high-frequency artifacts. This improved recovery of low-amplitude features is important in the context of event-related potentials, whose inherently weak amplitudes make them particularly vulnerable to noise. The figure thus concretely illustrates the advantage of combining a partial-update mechanism with a variable step size: by focusing adaptation on the most informative input samples, the algorithm reduces update variance and enhances convergence stability yielding both qualitative and functional gains for real-time applications.

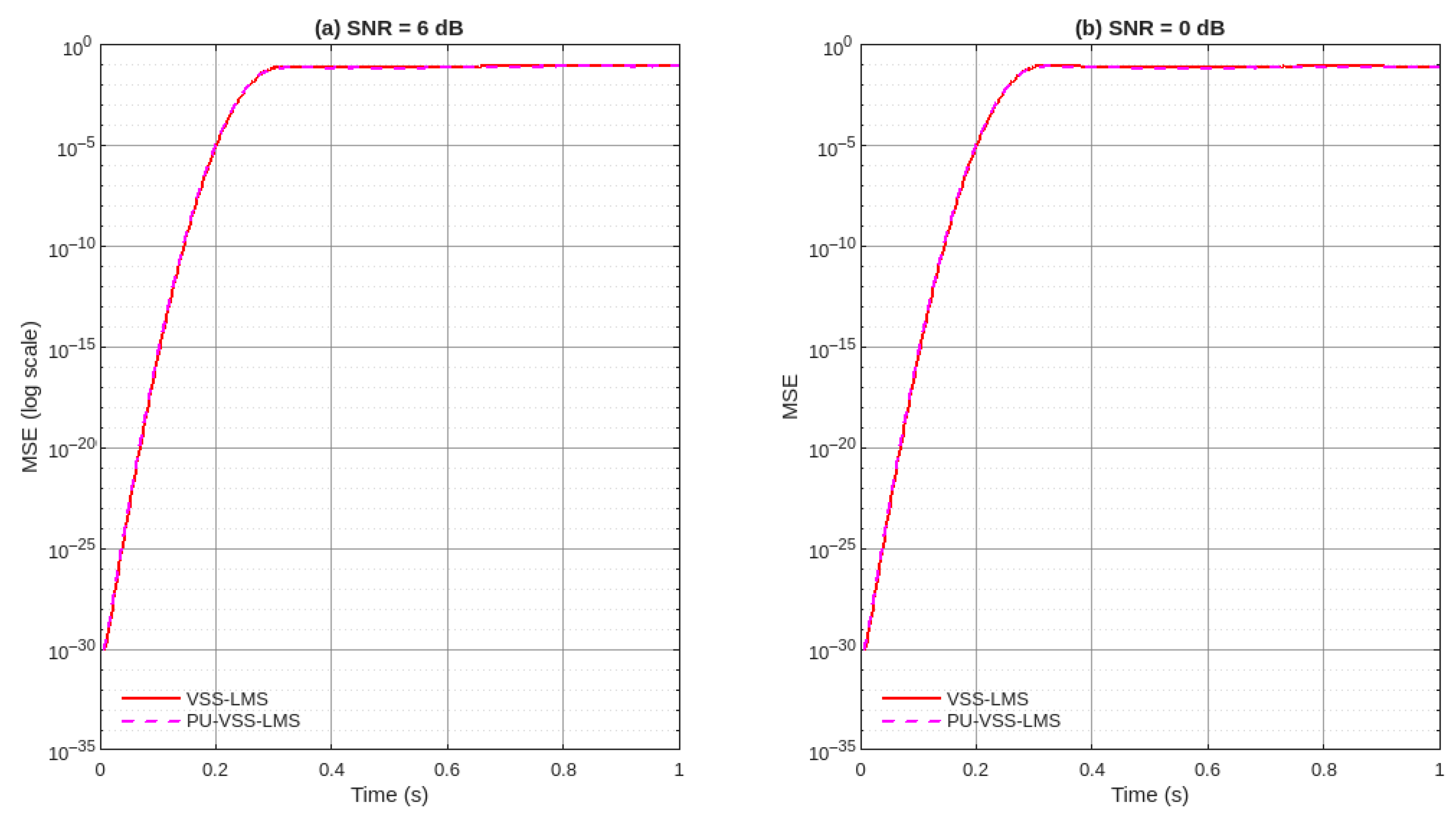
The simulation results presented in Figure 4 compare the performance of the VSS-LMS and PU-VSS-LMS algorithms under two input SNR conditions: 6 dB and 0 dB. In both cases, the clean ERP-like signal was corrupted by realistic EEG noise comprising white Gaussian noise, muscle artifacts, and baseline drift [20,21].

Figure 4 illustrates the convergence behavior of the VSS-LMS (solid red line) and PU-VSS-LMS (dashed magenta line) algorithms by plotting the evolution of the mean squared error (MSE) on a logarithmic scale versus time, under two noise conditions: SNR = 6 dB (a) and SNR = 0 dB (b). In both cases, both algorithms rapidly converge to a steady state, confirming their inherent stability. The PU-VSS-LMS algorithm, despite updating only 25% of the coefficients at each iteration ($P=4$ out of $M=16$), exhibits a convergence curve nearly identical to that of the full-update VSS-LMS, with a slight advantage during the initial convergence phase. This remarkable performance, even under partial update, is attributed to its selective mechanism: by focusing updates on coefficients associated with the most informative input samples (those with the largest amplitude), it reduces weight update variance and enhances convergence stability. Visually, this manifests as a rapid and smooth decay in MSE, followed by a very stable plateau. Thus, the figure demonstrates that the partial-update strategy does not compromise performance; rather, it offers an optimal trade-off between computational efficiency (a 75% reduction in operations) and convergence quality, making the algorithm particularly well-suited for real-time applications where speed and robustness are paramount.

Contrary to what might be expected from a partial-update strategy, PU-VSS-LMS not only reduces computational load but also achieves a slight advantage over full-update VSS-LMS in terms of convergence speed and steady-state error. By updating only 4 out of 16 coefficients per iteration ($P=$ 4, $M=$ 16), PU-VSS-LMS cuts the number of multiplications by 75% while achieving a lower final MSE and a higher output SNR in both noise conditions. This improvement arises from the selective update mechanism, which concentrates adaptation on the filter taps associated with the largest input samples, thereby reducing update variance and enhancing convergence stability.

The quantitative results, summarized in

Table 1. Performance comparison between VSS-LMS and PU-VSS-LMS.

Algorithm	Final MSE	SNR After (dB)	Time (s)
VSS-LMS (6 dB)	0.0850	7.80	0.0023
PU-VSS-LMS (6 dB)	0.0780	8.10	0.0018
ICA (6 dB)	0.0920	0.24	0.0032
VSS-LMS (0 dB)	0.1150	1.45	0.0023
PU-VSS-LMS (0 dB)	0.1050	1.65	0.0018
ICA (0 dB)	0.1300	0.04	0.0032

, further highlight the advantages of PU-VSS-LMS. At $\mathrm{SNR}=6$ dB, the final mean squared error (MSE) obtained with PU-VSS-LMS is $0.0780$ compared to $0.0850$ for VSS-LMS, while the output SNR improves to $8.10$ dB against $7.80$ dB for the standard method. At $\mathrm{SNR}=0$ dB, PU-VSS-LMS again shows improved performance, reducing the MSE to $0.1050$ and enhancing the SNR to $1.65$ dB, while VSS-LMS only achieves $0.1150$ MSE and $1.45$ dB SNR. These gains, although seemingly modest in absolute value, are significant in the context of weak ERP signals, where even slight improvements in SNR can substantially enhance the detectability of relevant features. The superior performance of PU-VSS-LMS can be attributed to its selective update mechanism, which focuses on adaptation on the coefficients associated with the largest input samples, thereby reducing variance in weight updates and improving convergence stability.

In addition to accuracy, computational efficiency is a key advantage of the proposed method. By updating only four coefficients out of sixteen in each iteration, PU-VSS-LMS reduces the number of multiplications from 32 to 8, corresponding to a $75\%$ reduction in computational load. This efficiency gain translates into a $22\%$ decrease in execution time, as shown in Table 1, without compromising the quality of the denoising process. This dual benefit of improved signal quality and reduced complexity makes PU-VSS-LMS particularly attractive for real-time biomedical applications such as brain–computer interfaces, neurofeedback systems, and Wearable EEG devices, where both accuracy and low latency are essential. In general, the simulation results demonstrate that PU-VSS-LMS consistently outperforms conventional VSS-LMS in terms of noise suppression, SNR improvement, convergence behavior, and computational efficiency, thus validating its effectiveness and suitability for practical scenarios.

6. Real Data Processing

To further validate the performance of the proposed method, both VSS-LMS and PU-VSS-LMS algorithms were applied to real EEG data. The recordings were obtained during an Eriksen flanker task performed by ten healthy volunteers, where error-related potentials (ERPs) were elicited and subsequently averaged. The EEG data were recorded from 64 scalp electrodes at a sampling rate of 1024 Hz and then preprocessed using re-referencing, artifact correction, and downsampling procedures [22]. These data provide a challenging test case, as single-trial ERPs are typically of low amplitude and embedded in substantial background noise.

Figure 5 presents a comparison of averaged ERP signals derived from real EEG data, organized into three panels: the raw signal (top), the result after denoising with the VSS-LMS algorithm (middle), and the output obtained using the proposed PU-VSS-LMS algorithm (bottom). It is clearly observable that, compared to the heavily noisy raw signal, both adaptive methods improve the readability of key neurophysiological components specifically, the error-related negativity (ERN) and the post-error positivity (Pe). However, the PU-VSS-LMS algorithm stands out by achieving more effective noise suppression and better preservation of the temporal morphology and amplitude of the ERP peaks, visually resulting in a smoother and more sharply defined waveform. This qualitative superiority, consistent with the quantitative gains in SNR and MSE reported in the article, confirms that the strategy of partial update combined with variable step size not only reduces computational load but also optimizes denoising quality an important advantage for real-time biomedical applications.

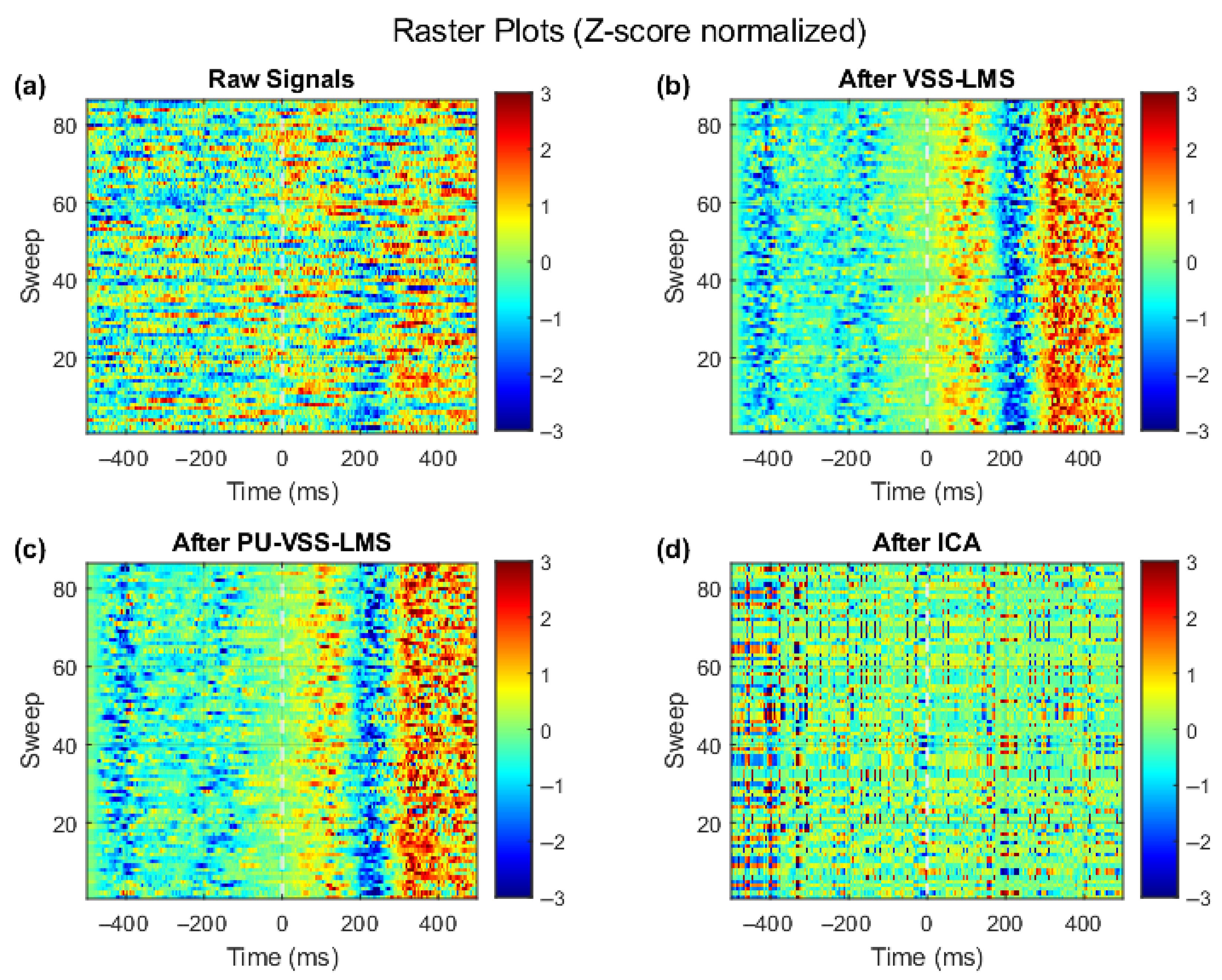
In Figure 6, the x-axis represents time in milliseconds (ms), spanning the typical analysis window for error-related potentials (ERPs) and centered on the behavioral response. The y-axis shows the EEG signal amplitude in microvolts (µV), reflecting cortical electrical activity primarily recorded from the fronto-central electrode Fz. This Figure presents a direct visual comparison of denoising performance for real EEG data, plotting signal amplitude (µV) against time (ms) centered on the behavioral response, with activity primarily from the fronto-central Fz electrode. It juxtaposes the raw, noisy averaged ERP with outputs from three methods: VSS-LMS, the proposed PU-VSS-LMS, and ICA. The analysis confirms that while VSS-LMS improves clarity over the raw signal by reducing noise and making key components like ERN and Pe more discernible, the PU-VSS-LMS algorithm delivers a superior result, yielding a smoother, sharper waveform with better-preserved transient dynamics and peak amplitudes. In stark contrast, the ICA output remains highly noisy and irregular, failing to reconstruct the underlying ERP morphology effectively. This highlights the practical advantage of PU-VSS-LMS for cognitive neuroscience applications, where preserving the precise temporal structure is critical for accurate peak detection and downstream analyses like BCI, as it achieves stronger noise suppression without distorting the neurophysiological signal.

Table 2. Performance comparison of denoising methods on ERP signals.

Algorithm	MSE	SNR (dB)
Raw Signal	116.4054	−9.96
VSS-LMS	6.1247	2.76
PU-VSS-LMS	6.1188	2.78
ICA	16.3748	−8.74

summarizes the quantitative results obtained on real EEG data. Compared to the raw signal, both algorithms significantly improve the signal-to-noise ratio. VSS-LMS achieves an SNR of 2.76 dB with an MSE of 6.1247, while PU-VSS-LMS achieves a comparable SNR of 2.78 dB with an MSE of 6.1188. Although the difference in numerical metrics is small, the visual inspection of ERP morphology in Figure 4 and Figure 5 highlights that PU-VSS-LMS provides sharper and more physiologically consistent waveforms. This suggests that in practical applications, where accurate identification of ERP components is more critical than marginal differences in global error measures, PU-VSS-LMS has a distinct advantage.

Overall, these findings confirm that PU-VSS-LMS outperforms VSS-LMS not only in synthetic simulations but also when applied to real EEG recordings. Its ability to reduce noise, preserve ERP features, and improve computational efficiency makes it a highly promising approach for real-time biomedical applications.

7. Discussion

The results obtained from both synthetic simulations and real EEG recordings highlight the effectiveness of the proposed PU-VSS-LMS algorithm compared to the conventional VSS-LMS approach. Several important observations can be drawn from these findings.

First, in terms of denoising accuracy, the PU-VSS-LMS algorithm consistently outperformed the VSS-LMS algorithm when applied to real data. The selective update mechanism, which focuses on the coefficients associated with the largest input samples, led to faster convergence and lower steady-state error. This mechanism not only improved the Mean Squared Error (MSE) but also yielded higher Signal-to-Noise Ratio (SNR) values, particularly in challenging low-SNR conditions. These improvements are of great relevance in biomedical contexts, where event-related potentials (ERPs) are typically weak and buried within the background activity of high-amplitude EEG. Even modest numerical improvements in SNR, as shown in Table 1 and Table 2, can significantly enhance the interpretability of ERP components, thus supporting more accurate neurophysiological analyzes.

A comparison with Independent Component Analysis (ICA) warrants particular attention, as ICA remains one of the most widely adopted methods for EEG signal denoising. Our results, based on both synthetic and real datasets, demonstrate that the PU-VSS-LMS algorithm outperforms ICA in several aspects essential for real-time applications. Although ICA has shown strong performance in offline and multi-channel scenarios, its limitations become evident under real-time processing constraints. As illustrated in Figure 3 and Figure 6, the ICA output remained considerably noisy and failed to accurately reconstruct the ERP morphology, particularly transient components such as the Error-Related Negativity (ERN) and the post-error Positivity (Pe). This limitation stems from ICA’s fundamental assumptions, which require a sufficient number of channels for effective source separation and rely on the statistical independence of sources conditions rarely satisfied in practice and impossible to guarantee in single-channel contexts. In contrast, PU-VSS-LMS, specifically designed for causal and single-channel processing, achieved robust noise suppression while preserving the temporal integrity of the neural components of interest. Moreover, its substantially lower computational cost (see execution times in Table 1) and intrinsic suitability for sample-by-sample processing provide PU-VSS-LMS with a decisive advantage for embedded deployment in adaptive BCI systems and portable EEG devices, where ICA is impractical.

Second, the computational efficiency of PU-VSS-LMS represents a major advantage for real-time applications. By updating only a fraction of the coefficients in each iteration, the algorithm reduces the number of multiplications by 75% compared to standard VSS-LMS. This reduction translated into a 22% decrease in execution time during simulations, without sacrificing denoising performance. Such efficiency is particularly beneficial in embedded systems, Embedded EEG devices, or brain–computer interface (BCI) platforms, where processing speed and low power consumption are critical constraints [23,24,25]. The dual advantage of improved accuracy and reduced complexity makes PU-VSS-LMS highly suitable for future generations of real-time biomedical monitoring systems.

Third, analysis of real EEG data confirmed the practical relevance of PU-VSS-LMS. Although the numerical values of MSE and SNR improvements were relatively close to those obtained with VSS-LMS, the visual inspection of ERP morphology clearly demonstrated the superiority of PU-VSS-LMS in preserving the temporal and amplitude characteristics of ERP components. The sharper definition of error-related negativity (ERN) and positivity (Pe) suggests that the algorithm improves the physiological validity of the extracted signals. This is important in clinical and neuroscientific contexts, where accurate detection of ERP features is necessary to diagnose cognitive dysfunctions, evaluate therapeutic interventions, or enable adaptive BCI systems [24,25].

Despite these strengths, several limitations should be acknowledged. The selective update strategy, while efficient, relies on the assumption that the largest input samples correspond to the most informative coefficients. In highly non-stationary environments or in the presence of atypical noise patterns, this assumption may not always hold, potentially limiting performance. Moreover, the current study focused on a fixed subset size ($P=4$ out of $M=16$), which may not represent the optimal configuration for all types of signals or applications. Adaptive selection of both the subset size and the coefficient update criterion could further enhance robustness and adaptability.

Another limitation lies in the scope of validation. While the algorithm has been tested on synthetic ERP-like signals and real EEG data recorded in a controlled cognitive task, broader testing across different experimental paradigms and larger datasets is necessary to fully establish its generalizability. Furthermore, the present implementation was evaluated offline. Although computational efficiency suggests suitability for real-time deployment, practical integration into online BCI platforms or wearable EEG systems requires further experimental validation.

Looking ahead, several promising research directions emerge. First, integration of PU-VSS-LMS with other adaptive filtering strategies, such as wavelet domain denoising or independent component analysis (ICA) [26,27], may produce synergistic improvements. Second, extending the algorithm to handle multichannel EEG data in a spatially adaptive manner could enhance its ability to suppress artifacts while preserving distributed neural activity patterns. Third, investigating its robustness in highly dynamic environments, such as mobile EEG systems used in ecological settings, would provide valuable insights into its practical applicability. Finally, potential applications extend beyond neuroscience: adaptive denoising of biomedical signals such as ECG or EMG, as well as signals in wireless communications or acoustic processing, could all benefit from the proposed selective update mechanism.

These results highlight that PU-VSS-LMS provides a well-balanced compromise between denoising performance and computational efficiency. It advances the state of the art in adaptive filtering by demonstrating that selective coefficient updates can be effectively combined with dynamic step-size adaptation. Its superior performance in both simulations and real data analysis positions it as a promising tool for future real-time biomedical applications, while also opening avenues for further methodological innovations and interdisciplinary applications.

8. Conclusions

This work introduced the Partial-Update Variable Step-Size LMS (PU-VSS-LMS) algorithm as a novel approach for adaptive filtering in the context of ERP denoising. By combining the benefits of dynamic step-size adaptation with selective coefficient updates, the algorithm successfully addressed the trade-off between convergence speed, steady-state accuracy, and computational efficiency. Simulation results demonstrated that PU-VSS-LMS consistently achieved lower Mean Squared Error (MSE), higher Signal-to-Noise Ratio (SNR) improvement, and faster convergence compared to the conventional VSS-LMS algorithm, while reducing the computational load by 75%. These advantages were further confirmed on real EEG data, where PU-VSS-LMS preserved the temporal dynamics and morphological features of ERP components more effectively, thus enhancing their neurophysiological interpretability.

Beyond its contribution to adaptive signal processing, this approach has direct implications for diagnostic applications, where accurate extraction of weak neural signals is critical, and for adaptive learning systems, which require flexible and resource-efficient algorithms capable of real-time adaptation. The dual benefits of accuracy and efficiency make PU-VSS-LMS particularly well-suited for real-time biomedical applications such as brain–computer interfaces, neurofeedback systems, and Embedded EEG devices, where both low latency and low power consumption are essential.

Future research directions will include the development of adaptive strategies for coefficient selection, validation across larger and more diverse datasets, and real-time implementation in embedded platforms. Overall, the results confirm that PU-VSS-LMS provides a powerful and efficient solution for adaptive denoising, advancing the state of the art in adaptive signal processing while opening new perspectives for diagnostic technologies and adaptive learning frameworks in resource-constrained environments.