CAD–FEA Integrated Automation Platform for Structural Design, Deformation Simulation, and Size Optimization of Housings in External Gear Pumps

Abstract

External spur gear pumps are widely employed in hydraulic systems for their simplicity, efficiency, and cost-effectiveness; however, the conventional CAD-based methods used to design these components remain time-intensive and prone to inconsistencies, particularly during iterative structural analysis and optimization. To address these limitations, this study presents a parametric, automated design platform for external spur gear pumps by integrating the SOLIDWORKS API with a custom C# desktop application. The tool automatically generates 3D solid models and facilitates strength analysis and housing wall-thickness optimization through a user-friendly interface. Geometric and hydraulic inputs are used to define model parameters and simulation conditions, into which an empirical pressure distribution model, derived from prior experimental data, is embedded to establish accurate boundary conditions. This integrated configuration enables structural analysis in SOLIDWORKS Simulation, allowing systematic variation of wall thickness and geometry within prescribed constraints. Results from the case study yielded a configuration achieving an 18.42% reduction in housing mass while maintaining a minimum factor of safety of 3.948 and a maximum deformation of 0.012 mm. The system effectively reduces design time, improves repeatability, and minimizes human error, while demonstrating robustness across varied design scenarios. Overall, the proposed approach provides a practical and efficient solution for automated design and optimization of external gear pumps, supporting parametric flexibility and advancing CAD/CAE integration in hydraulic component design workflows.

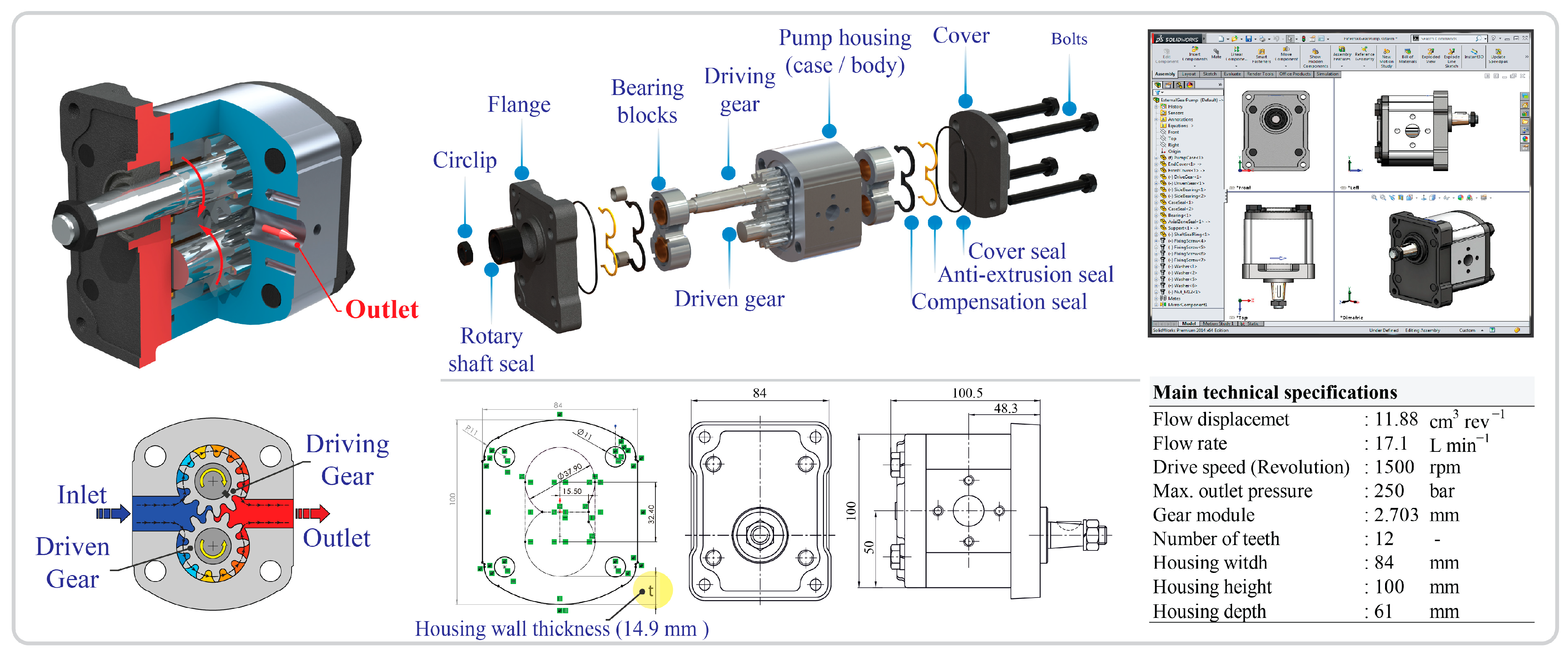
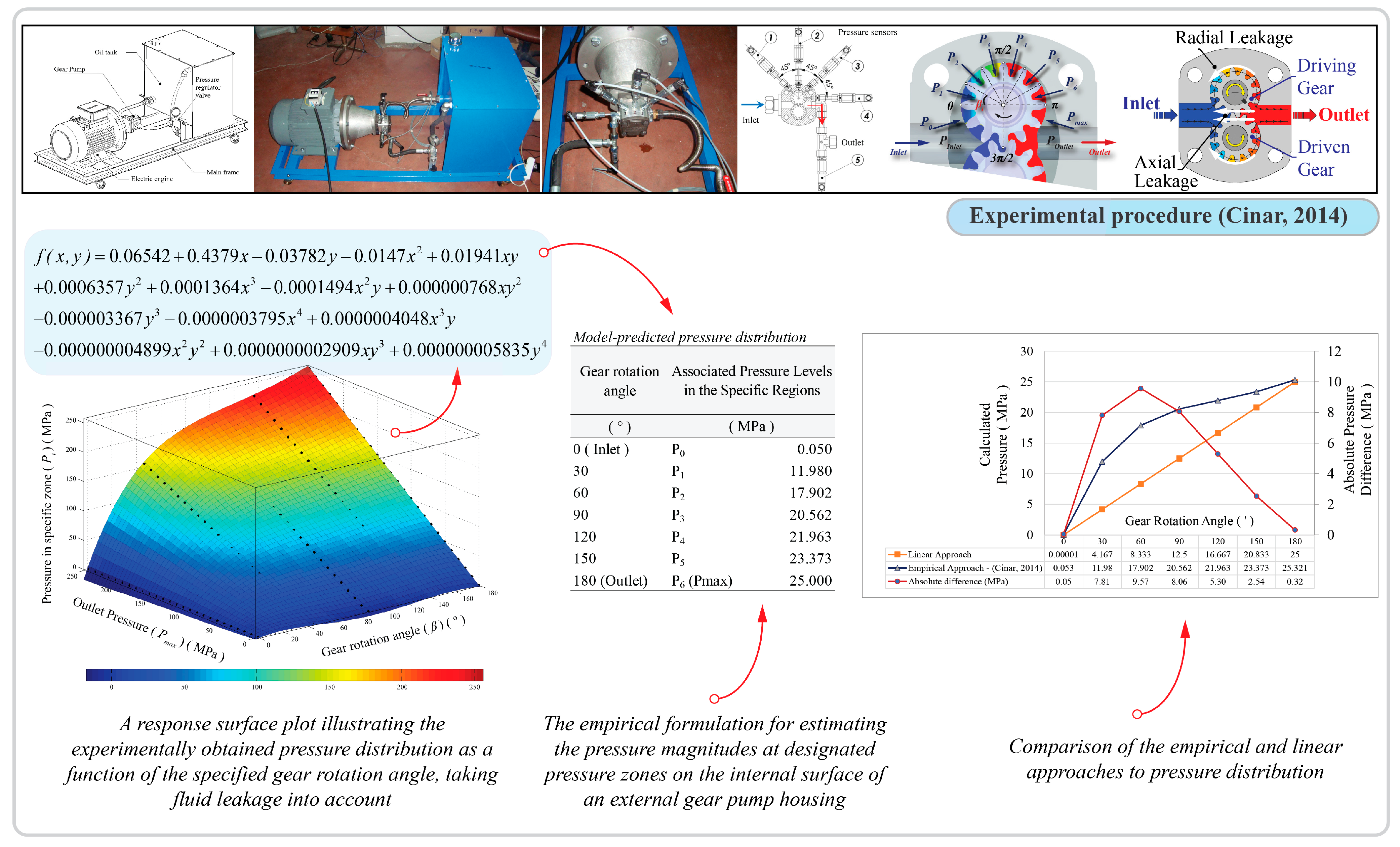
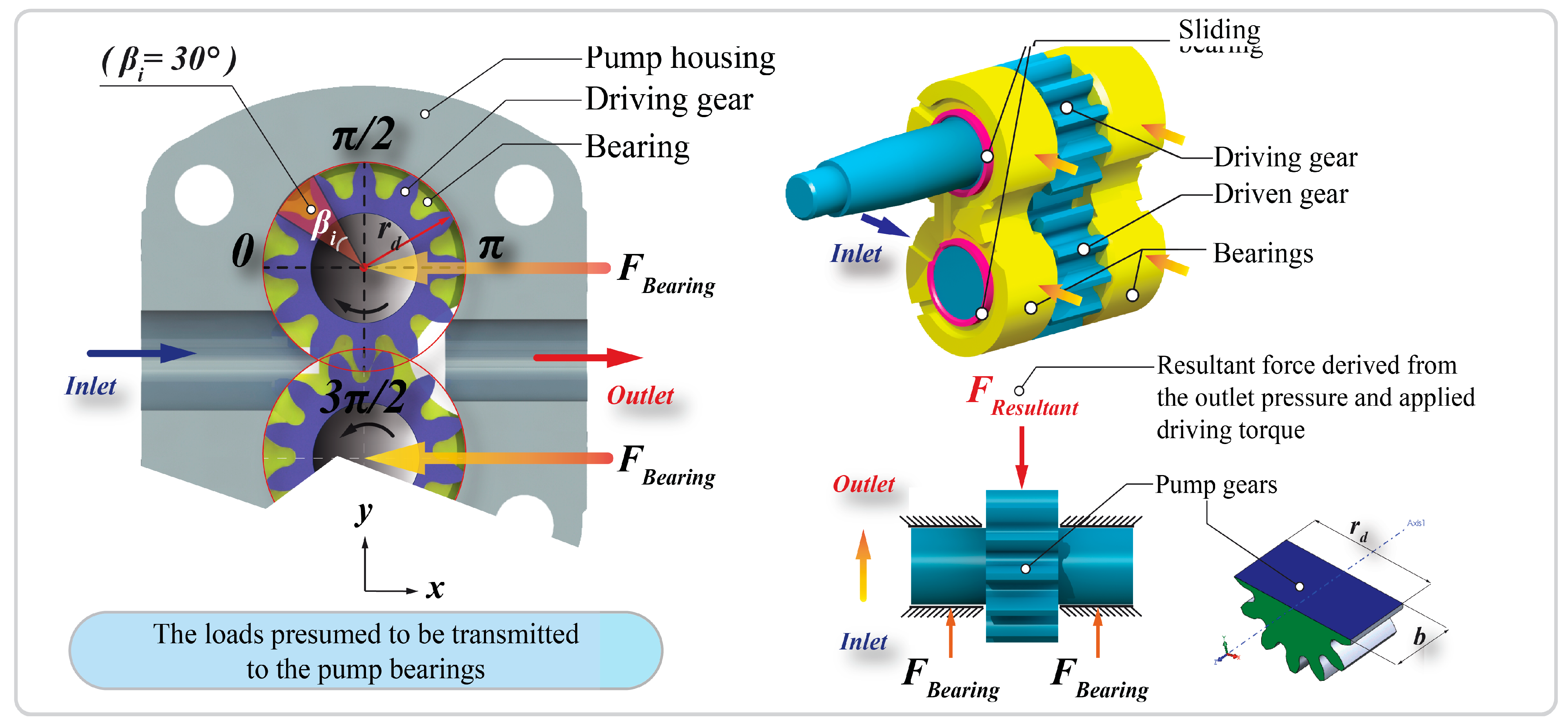
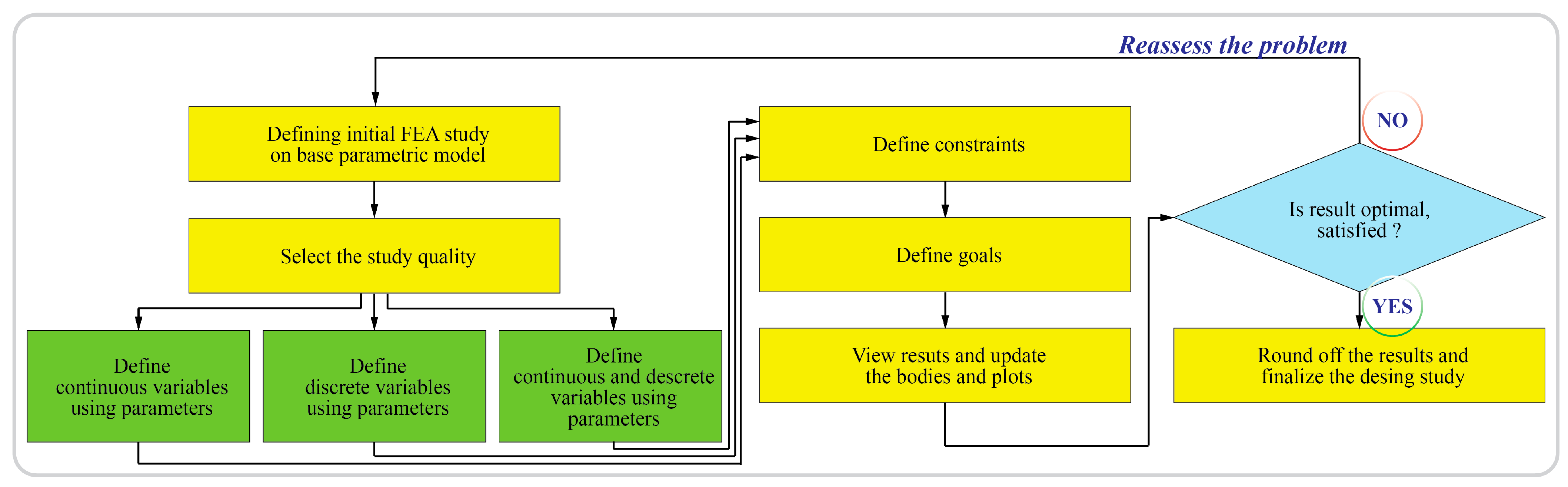
1. Introduction

The external gear pumps represent one of the most extensively used positive displacement pumps in fluid power systems due to their simplicity, cost-effectiveness, robustness, and wide range of industrial applications. These pumps operate by meshing gear pairs that transport fluid from the suction to the discharge side without the need for valves, making them highly reliable even in harsh operating conditions [1,2,3]. They find critical usage in sectors such as automotive, aerospace, agricultural machinery, construction equipment, and industrial hydraulics [4,5,6,7]. The primary reason for their popularity lies in their favourable attributes: compact design, high-pressure capabilities, self-priming operation, and tolerance to contamination. These characteristics make them particularly suitable for applications involving power steering systems, lubrication circuits, and transmission control in mobile machinery [6,8]. Despite their structural simplicity, external gear pumps are increasingly being subjected to performance optimization and durability enhancements to meet stringent energy efficiency, noise emission, and service life requirements.

One of the significant challenges in external gear pump design is optimizing the pump housing structural integrity, a component that must provide sufficient structural stiffness to withstand pressure fluctuations and gear-induced dynamic loads while also contributing to mass minimization. Housing size and wall thickness have a direct impact on pump mass, manufacturing cost, and overall system compactness. Therefore, designers are faced with a fundamental trade-off between mass reduction and mechanical strength, particularly in lightweight or energy-sensitive applications such as aerospace and electric vehicles [9,10].

The structural optimization of gear pump housings is further complicated by the non-uniform and dynamic internal pressure distribution arising from the meshing of gear teeth, pressure pulsations, and fluid leakage paths. Traditional approaches often adopt conservative design margins, which tend to result in over-dimensioned housings. However, recent studies have employed finite element analysis (FEA) in conjunction with empirical or analytical pressure models to more accurately assess stress distributions within the housing [2,11]. Furthermore, the integration of automated design tools, such as CAD software application programming interfaces (APIs), with FEA solver codes represents a significant advancement in parametric design optimization. These frameworks facilitate the rapid iteration of housing geometries under defined boundary conditions and performance constraints, thereby enabling efficient exploration of the design space [12,13,14]. Such approaches have demonstrated potential in reducing mass while preserving structural integrity, and in aligning mechanical design processes with digital twin paradigms [15].

Recent advancements in gear pump design and optimization have been largely influenced by innovations in computational modelling, design automation, and simulation-driven engineering [16]. As external gear pumps continue to be essential components in fluid power systems across industries, ranging from automotive and aerospace to heavy machinery and agriculture, research has increasingly focused on improving their volumetric efficiency, reducing flow pulsation and noise, and enhancing structural robustness [4,5,8]. A significant area of research has centred on the internal geometry of gear pumps, particularly the design of gear tooth profiles to improve displacement characteristics and reduce pressure pulsation. Zhao and Vacca (2017) developed a multi-objective optimization framework for external spur gear pumps, using analytical expressions for flowrate and non-uniformity, integrated into a parametric model [4]. Their work demonstrated that asymmetric gear teeth profiles, designed through variation in pressure angle, profile shift, and addendum modification, can significantly reduce flow irregularities, which are major contributors to noise and vibration in hydraulic systems. This methodology is especially relevant in the context of high-precision applications where smooth flow delivery is critical. In addition to flow uniformity, recent studies have explored the impact of gear geometry on volumetric efficiency and internal leakage. For example, Mitov et al. (2024) conducted a combined computational fluid dynamics (CFD)–experimental validation study, analyzing transient flow behaviour in gear pumps under varying rotational speeds and pressures [1]. Their findings highlighted the critical role of gear clearances and tooth engagement dynamics on flow pulsation and pressure recovery, indicating opportunities for further performance improvements through profile refinement. The integration of numerical methods such as CFD and FEA has enabled comprehensive performance predictions under realistic operating conditions. Zharkevich et al. (2023) [17] proposed a parametric optimization strategy for a newly designed five-gear pump casing using FEA. The study compared structural performance under specific pressure using aluminum, cast iron, and polycarbonate materials. Stress analysis identified high-stress zones at casing grooves, and optimized designs, achieved by geometric alterations and rounding stress concentrators, led to significant mass reductions (up to 16%) without compromising safety or fatigue strength. The aluminum version showed the most favourable trade-off between mass and strength, making it the optimal material for lightweight pump designs [17]. Cinar (2014) conducted a research study combining experimental methods with engineering simulations to develop an empirical alternative to linear approximation in defining the internal pressure zones of pump housings [18]. The study consequently offered clearly defined guidelines and outputs for simulating structural deformation in gear pump housings [9]. Zharkevich et al. (2024) presented a coupled CFD-FEM approach for multi-gear pumps, assessing not only the internal flow field but also the resulting stress distributions and displacement of structural components under hydraulic loading [15]. This dual analysis confirmed that torque-induced deformations, rather than fluid pressure alone, are the dominant factor in structural fatigue and failure, thereby underscoring the importance of integrated design-validation frameworks. Similarly, Castilla et al. (2015) developed a three-dimensional CFD model of an external gear pump, accounting for dynamic meshing contact and decompression slot effects [2]. Their simulations revealed complex flow interactions at gear tooth interfaces, which were not captured in earlier two-dimensional studies. This highlighted the necessity of high-fidelity 3D models for accurate flow prediction, especially in regions where cavitation or trapped volumes may occur. The study also reinforced the importance of incorporating pressure relief features in the housing design to mitigate peak loading during meshing transitions.

Complementing advances in simulation, the automation of CAD modelling using parametric design frameworks has become increasingly prevalent. Modern computer-aided design environments such as SOLIDWORKS offer powerful API’s that facilitate automated geometry generation and iterative design workflows [19]. Chowdhury (2020) and Balachandar et al. (2020) demonstrated how CAD macros and “Visual Basic” language scripts can be employed to automate the creation and modification of part geometries based on predefined input parameters [12,13]. This capability drastically reduces design cycle time and enables rapid prototyping of multiple design variants for structural or performance optimization. In the context of gear pump housing design, such automation is particularly useful when integrated with FEA solvers, allowing automated evaluation of stress responses under different geometrical configurations. The use of design automation not only ensures consistency and repeatability in the modelling process but also supports optimization routines, such as those involving genetic algorithms or response surface methods, to identify optimal geometries under multi-objective constraints [10]. The convergence of digital tools, parametric CAD modelling, high-fidelity CFD/FEA simulation, and design-of-experiments (DoE) based optimization, has paved the way for comprehensive, simulation-driven design of external gear pumps. Recent frameworks allow for automatic iteration of geometry, real-time performance evaluation, and multi-disciplinary optimization. Such approaches have the potential to substantially enhance traditional trial-and-error methods, paving the way for the development of lightweight, efficient, and application-specific gear pump designs [5,11,20]. The state-of-the-art in gear pump design has evolved toward highly integrated digital workflows that leverage advanced geometry modelling, simulation fidelity, and design automation. These technologies collectively enable more informed design decisions, shorter development cycles, and, ultimately, higher-performance pump systems.

Despite the significant advancements in gear pump modelling and performance analysis over the last decade, a notable shortcoming persists in the holistic integration of CAD and FEA for automated structural optimization of external gear pump housings. The literature has largely focused on either fluid dynamic simulation of internal pump flows or isolated structural analyses, with few studies advancing a parametric CAD-FEA pipeline that can drive iterative, geometry-based size optimization [1,2,4,21]. While several researchers have proposed analytical or computational methods to investigate gear tooth profiles and internal flow behaviour [4,10,22], these are typically decoupled from structural performance evaluations of the housing components. Moreover, pressure boundary conditions used in most FEA studies are often simplified or assumed uniform [2], whereas real internal pressure distributions are non-uniform and transient [9,11]. Although Cinar et al. (2016) proposed a methodology for applying experimentally derived pressure distribution to FEA for stress analysis of a pump housing, the automation and iterative optimization of the design process based on this approach remains unexplored [9]. Recent studies have shown the potential of integrating CAD macros and API-based automation tools with parametric modelling environments yet these have largely been applied to simpler geometries or mechanical components (e.g., pistons and brackets), without extending to pressure-bearing components such as hydraulic pump housings [12,13]. Furthermore, although the use of genetic algorithms for pump performance optimization has been demonstrated, these have not been combined with parametric CAD-FEA models for size optimization under structural constraints [10]. There is also a scarcity of literature addressing optimization strategies that balance mass reduction with structural integrity and manufacturability. Most design improvements reported in gear pump literature target fluid efficiency or noise reduction [5,8], often neglecting structural mass and material usage, factors that are increasingly important for aerospace and mobile machinery applications.

In response to the limitations identified in the existing literature, this study proposes a systematic and automated framework for the lightweight structural design of external spur gear pump housings, an area that remains critically important and limitedly explored in automated mechanical design optimization research. The methodology integrates parametric 3D CAD modelling, experimentally informed boundary conditions, static structural FEA simulations, and size optimization routines aimed at reducing material usage while ensuring mechanical robustness in a single user interface (UI). The approach is grounded in validated pressure models and experimental data from previous investigations and doctoral research, thereby enhancing its practical applicability and industrial relevance.

2. Materials and Methods

2.1. Reference Model

In this study, a HEMA-branded (Tekirdag, Turkey), 1P series, model N-119 external spur gear-type hydraulic pump with a flow rate of 17.1 L min⁻¹ (volumetric flow displacement is 11.9 cm³ rev⁻¹) was employed as the reference model (https://www.hemaendustri.com.tr/1pn-serisi (accessed on 1 April 2025)). This specific model was selected owing to the widespread use of spur gear pumps with similar geometric configurations in industry, as well as their domestic manufacture in Turkey. The template solid model of the pump was developed through the application of reverse engineering approach. Dimensional measurements were taken directly from the original pump, and a parametric 3D solid model was subsequently constructed using the SOLIDWORKS 3D parametric CAD software (SOLIDOWRKS-Premium v2025 SP.1.0). In generating the UI linkable parametric model, both dimensional parameters, such as housing wall thickness and gear parametric dimensions, and key hydraulic parameters, including effective flow rate, rotational (drive) speed, and volumetric efficiency, were employed. The interrelationships among these parameters were established with reference to Equations (1) and (2) and spur gear design standards such as ANSI/AGMA 2001-D04 [5,23,24,25,26,27,28,29].

$$V=\left({\displaystyle \frac{Q_e}{n\cdot {\eta }_v}}\right)$$

(1)

$$b={\displaystyle \frac{V\cdot {10}^6}{2\cdot \pi \cdot m^2\cdot \left(z+\left(1+\frac{{\pi }^2\cdot {\cos }^2\cdot {\alpha }_0}{12}\right)\right)}}$$

(2)

Here, V: Flow displacement (L rev⁻¹), Q_e: effective flow rate (L min⁻¹), n: Drive speed (rpm), ƞ_v: Volumetric efficiency (%), m: Gear module (mm), z: Number or gear teeth, α₀: Tooth pressure angle (°), and b: gear tooth face width (mm).

In the parametric model, the pump’s fluid displacement volume can be derived by substituting the defined effective flow rate, operating drive speed, and volumetric efficiency into Equation (1). This calculated displacement volume is then used in Equation (2) to parametrically determine the gear tooth face width, hence, the housing effective pressure width, of an external spur gear pump with a fixed module and number of teeth parameters.

One of the principal criteria for evaluating how accurately a modelled structure represents its physical counterpart is the accuracy of its material mass. In solid modelling software, the mass of a digital model can be determined by assigning appropriate material properties. The software calculates the mass by multiplying the user-defined material density by the automatically computed total volume of the solid geometry. For the solid model of the pump housing, this calculation yielded a mass of 0.741 kg. By comparison, the mass of the actual pump housing, measured physically, was found to be 0.734 kg. The close correspondence between these values (relative difference: 0.95%) suggests that the geometric representation within the modelling environment is highly accurate (with correct material density assignment). The principal dimensions of the pump assembly, along with selected technical specifications, are presented in Figure 1.

2.2. Pressure Distribution in External Gear Pump Housings and FEA Pre-Processing

A widely adopted approach in the literature for representing pressure distribution in external spur gear pumps is the linear model, which relates internal pressure to the gear’s angular rotation and the pump’s maximum operating pressure. This model presumes a constant outlet pressure and posits that the internal pressure rises linearly as a function of the gear’s angular position. Within this framework, the pressure at a specific angular position (P_i) is defined by Equation (3) [25].

$$P_i=P_{\max }\cdot {\displaystyle \frac{\beta }{\pi }}$$

(3)

Here, P_max: Maximum pressure at outlet (bar), P_i: Pressure at specific zone (bar), and β: Gear rotation angle (Rad).

Crucially, this approximation is based on the assumption of ideal operational conditions, notably the complete absence of internal leakage and other unpredicted physical conditions throughout the pumping process. In this context, Cinar (2014) reported an empirical equation based on experimental data to estimate the pressure distribution within a specific region of the pump housing [18]. The pressure values obtained from this empirical equation demonstrated a relatively reasonable degree of deviation; however, they claim more accurately represented real-operation conditions in comparison to those derived from Equation (3). Hence, in the present study, the internal surface pressure of the housing, exposed to varying levels of pressure from the inlet to the outlet, was modelled using the aforementioned empirical equation, which stems from the author’s previous experimental investigations. Figure 2 presents the resulting response surface pressure distribution chart, incorporating data from the experimental results, the empirical equation, and the pressure magnitudes determined for specific regions according to the angular position of the pump gear, together with an additional comparative plot illustrating the deviation between the empirical and linear pressure distributions.

The empirical pressure model adopted in this study was experimentally established and validated in our previous work (Cinar, 2014 [18], Cinar et al., 2016 [9]), where detailed test rig design, measurement procedure, and correlation analyses between recorded pressure signals and finite element simulations were comprehensively reported. This prior experimental verification included deformation and strain measurements on physical gear pump housings, providing direct validation of the pressure field subsequently utilized within the current automated FEA framework. In the present research, this experimentally derived equation is not re-validated but directly integrated within the automation framework as a functional module. Through the developed C#-based API routines, the empirical model acts as the governing function that automatically computes and assigns nodal pressure magnitudes to each of the seven angular pressure zones during FEA pre-processing, ensuring that experimental realism is embedded within every automated simulation cycle rather than treated as a separate input stage.

In the preliminary phase of this study, a finite element method-based stress analysis was conducted to examine the stress distribution and structural deformation within the pump’s housing. This served as a foundational step prior to implementing an automated optimization process. The three-dimensional solid model of the pump used in the analysis was evaluated using SOLIDWORKS Simulation, a general-purpose FEA commercial code. The accuracy of results obtained through FEA is inherently linked to the boundary and loading conditions defined during the simulation process. Accordingly, the boundary conditions in this study were established based on reasonable assumptions and in line with best practices recommended in the literature, with the aim of replicating actual operating conditions as closely as possible. The FEA was conducted to investigate the extent of deformation in the pump body under its maximum outlet pressure (250 bar ≈ 25 MPa), which was obtained from manufacturer product catalogue, as well as to assess the resulting stress distribution. Within the simulation environment, this pressure variation was implemented by dividing the internal surface of the pump housing into seven equally spaced angular pressure zones, spanning from the inlet to the outlet (Figure 3). The pressure values corresponding to each designated zone were calculated using the empirical equation previously described and subsequently incorporated into the FEA model.

In addition to the general configuration, the fluid pressure acting on the pump’s bearing components and the reaction loads transmitted from the gear shafts have also been specified. In this type of gear pumps, it is widely recognized that the region most susceptible to maximum pressure and resulting bearing loads lies between the angular positions of π and 3π/2—commonly referred to as Region IV, near the outlet port. The elevated pressure in this region tends to force the gears towards the inlet side, thereby generating substantial bearing loads. These loads are effectively transferred to the pump housing through the bearings, directed from the outlet to the inlet side at an appropriate force angle. To account for complex and often unpredictable dynamic loading conditions, the structural analysis has adopted a conservative approach by simulating the pump housing under worst-case loading scenarios. Accordingly, it was assumed that the maximum pressure acts upon the gears in the π/2 to 3π/2 region. In line with this assumption, the bearing loads on the housing were modelled as direct forces with no angular offset, acting from outlet to inlet, as illustrated in Figure 4 [25,30].

Based on calculations that incorporate the gear tooth geometry and pressure distribution across each tooth space, the resultant total radial force acting on the gear was estimated and given the symmetrical configuration of the gear bearings, each bearing was subjected to a load of 5 868.8 N (flow rate configuration is 17.1 L min⁻¹). The FEA model further included frictional contact interactions (defined as ‘no penetration’) between the pump housing, covers, and bearings, thereby allowing for relative movement of the covers under loading conditions. A bolted connection with a tightening torque of 60 Nm was applied to couple the rear cover, housing, and front cover. To maintain alignment of the gear bearings along a shared axis, a pin connector was used between the front and rear bearings. Additionally, the holes used to mount the pump to the electric motor bell housing were constrained by applying a cylindrical face boundary condition. A separate planar face constraint (on flat faces) was also defined to simulate the sliding interaction between the front cover and the flange of the motor bell housing [31].

In assigning materials for the pump assembly, the housing was modelled using a high-strength aluminum alloy from the 7000 series (7020-T6). Cast carbon steel was chosen for the covers, while high-lead bronze was utilized for the bushings, and a stainless steel-based material was employed for the bearings, as specified by the manufacturer [32,33]. The FEA model of the pump was constructed as a three-dimensional static configuration, assuming a linear elastic, homogeneous, and isotropic material model. The finite element (FE) model (mesh structure) of the gear pump components was generated using the meshing functionality provided within SOLIDWORKS Simulation software (SOLIDOWRKS-Premium v2025 SP.1.0). Figure 5 illustrates the mesh configuration alongside the material properties applied in the FEA model.

2.3. Size Optimization and Automation Workflow

Size optimization in product design, particularly in gear pump housing design, revolves around identifying the geometric configuration that best satisfies functional, structural, and manufacturing constraints while minimizing or maximizing an objective function (e.g., volume, mass, stress, deformation or cost) [34]. This is typically achieved through constrained nonlinear optimization, where design variables such as wall thickness, gear centre distance, and housing dimensions are optimized using analytical models, numerical simulations, and/or experimental validation. Ideally, pump housings should be capable of withstanding internal pressures while simultaneously minimizing both mass and manufacturing costs. Conventional designs, often oversized to ensure safety, tend to compromise overall system efficiency. To overcome this limitation, a systematic methodology was followed to optimize wall thickness through FEA integrated with parametric CAD modelling. This approach, informed by actual pressure measurements and empirical equations derived from the aforementioned experimental studies, enables a well-founded balance between structural integrity and material efficiency.

2.3.1. Optimization Problem

The initial step in applying size optimization theory in product design is to define the problem and objectives clearly. The objectives often encompass minimizing mass and size while maximizing performance and functionality [34,35,36,37]. In this context, mathematical formulation of size optimization (generic) can be described as follows (Equation (4)):

x = [x₁, x₂, …, x_n]^T represents the vector of design variables;

f(x) represents the objective function to be minimized;

g_i(x) ≤ 0 represents inequality constraints;

h_j(x) = 0 represents equality constraints.

Then the general size optimization problem is:

$$\begin{array}{l}\underset{x}{\min } \hspace{1em}\hspace{1em}\hspace{1em}f(x)\\ \mathrm{subject} \mathrm{to} \hspace{1em}{g}_i(x)\le 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}i=1,\dots ,m\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{h}_j(x)=0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}j=1,\dots ,p\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{x}_k^{\min }\le x_k\le x_k^{\max },\hspace{1em}\hspace{1em}k=1,\dots ,n\end{array}$$

(4)

This general formulation can be adapted to the specific objective of minimizing housing mass by optimizing wall thickness, as follows (Equations (5)–(8)):

Design Variable:

t = wall thickness of the gear pump housing (mm).

Objective Function:

The mass of the housing M(t) is given by:

$$f(t)=\rho \cdot V_H(t)$$

(5)

where

ρ: density of the material (kg mm⁻³);

V_H(t): Volume of the housing as a function of wall thickness (mm³).

Constraints:

Maximum von Mises stress constraint:

$${\sigma }_{von-mises}(t)\le {\sigma }_{allowed} (\mathrm{M}\mathrm{P}\mathrm{a})$$

(6)

Maximum displacement constraint:

$$U_{\max }(t)\le U_{allowed} (\mathrm{m}\mathrm{m})$$

(7)

Variable bounds on the wall thickness:

$$t_{\min }(t)\le t\le t_{\max } (\mathrm{m}\mathrm{m})$$

(8)

The framework for size optimization utilized in this study integrates parametric solid modelling with FEA procedures by employing the “Design Studies” approach [19]. This approach enables a streamlined workflow for both optimization processes and the assessment of specific design scenarios. A “Design Study” can be configured either to execute an optimization task or to explore alternative design configurations. To initiate a “Design Study”, it is necessary to define at least one preliminary analysis, which subsequently serves as the foundation for further optimization or evaluation activities. During each iteration, the software recalculates these analyses by adjusting the values of the designated variables. This approach was implemented in the current study, and the principal workflow adopted is depicted in Figure 6.

2.3.2. Development of the Desktop Application User Interface and the Workflow

This study establishes a parametric modelling framework demonstrating that, when gear module, number of teeth, and pressure angle remain constant, ideal fluid displacement exhibits direct proportionality to gear width. This principle aligns with design strategies widely adopted by commercial manufacturers producing variable-displacement pumps. Rather than modifying core gear dimensions (which would alter housing geometry), hydraulic gear pump manufacturers typically adjust gear width. This method enables the creation of pumps with varying displacement capacities through housing depth modifications, eliminating the need for comprehensive geometric redesign. The automated structural optimization process for housing development integrates this design principle.

In order to automatically generate pump’s housing solid models with varying flow rates and outlet pressures without the need for repeated redrawing, and to optimize the generated models, a desktop application was developed using the .NET Framework 4.5 development platform. The application was implemented using Microsoft Visual Studio, the most commonly used integrated development environment, and the object-oriented programming language C#. To enable intervention in both the dimensions of the pump CAD model and the boundary conditions defined during optimization analyses, the application leverages the Application Programming Interfaces (APIs) of SOLIDWORKS and SOLIDWORKS Simulation. The API contains hundreds of functions that you can call from Visual Basic for Applications (VBA), VB.NET, Visual C#, Visual C++ 6.0, and Visual C++/CLI. These functions provide direct access to SOLIDWORKS functionality such as creating a line, inserting an existing part into a part/assembly document, or verifying the parameters of a surface [19,38]. Within this context, the dynamic link library (DLL) files SOLIDWORKS.Interop.sldworks.dll and solidworks.Interop.swconst.dll, which were added to the project references in the Visual Studio environment, provide functionality for launching the SOLIDWORKS application and manipulating model parameters. Similarly, the solidworks.Interop.cosworks.dll file enables access to the parameters of boundary conditions defined within SOLIDWORKS Simulation, as well as to analysis-related functions. The automation tool comprises a custom-built UI, through which design parameters, specifically the housing wall thickness of an external gear pump, can be defined and manipulated.

In the designed interface, functional relationships have been established between the control elements and the pump parameters. Utilizing Equations (1) and (2), the gear width (b) of a pump with fixed module and number of teeth is determined based on the user-defined input parameters, namely, effective flow rate, rotational speed, and efficiency. When the user inputs these parameters, along with the wall thickness value, and clicks the “Configure Pump Housing in Assembly” button, SOLIDWORKS is automatically launched and generates the required solid model of the pump in accordance with the specified parameters. Should the user subsequently modify any of the parameters and click the same button again, the pump body model is automatically updated to reflect the new values.

By entering the pump’s operating pressure and overall efficiency under the “3D CAD Input Parameters” for FEA group box, FEA can be performed on the pump model. The power (N) required to drive the electric motor is calculated based on the effective flow rate, operating pressure, and total efficiency parameters [25]. To estimate the pressure distribution within the pump housing, the predictive model specified through aforementioned empirical equation is employed. When the operating pressure is entered via the input parameters section, the pressure values to be applied to the pressure surfaces (P0–Pmax) from inlet to outlet are automatically calculated.

The bearing load (F) applied to each bearing is determined using several parameters, including the module, number of teeth, addendum diameter, tooth width, operating pressure, motor power, and rotational speed [30]. The calculated pressure and bearing load values are displayed under the “Calculated Boundary Conditions” for FEA group box and are subsequently utilized in the definition of boundary conditions within the FEA. Once all input parameters have been entered, the “Perform Static Analysis” button can be clicked to execute a FEA based on the pre-defined parameters. The resulting outputs are then listed beneath the Scenario Outputs group box.

If a dimensional optimization study is to be carried out for the pump body wall thickness, additional optimization scenario parameters must also be entered via the interface. These parameters include the lower and upper bounds of the wall thickness, as well as the increment step. By default, the software displays a range that spans 3 mm below and above the initially entered wall thickness (optional). The user may adjust these values to define their own desired lower and upper bounds. The Step parameter specifies the increment, in millimetres, by which the wall thickness will be increased in each successive solution within the defined range.

Once all necessary parameters for the dimensional Optimization have been specified, the Solve Scenarios button can be used to execute all Optimization scenarios. The application begins by setting the wall thickness of the pump body’s solid model to the defined lower bound. It then incrementally increases the wall thickness according to the step size, solving each scenario in sequence.

Upon completion, the results for each scenario, namely, wall thickness, maximum equivalent stress, maximum deformation, safety factor, and pump housing mass, are listed under the “Scenario Outputs” section. Subsequently, the wall thickness of the lightest pump body that does not exceed the defined design limits (i.e., threshold equivalent stress and displacement) is displayed on the interface beside the label “Optimal Wall Thickness”. Through this process, the optimum wall thickness for the pump body, suitable for delivering the required flow rate under the specified operating conditions, is determined.

The automation tool comprises a custom-built UI, through which design parameters, specifically the housing wall thickness of an external gear pump, can be defined and manipulated. The underlying optimization algorithm follows a deterministic iterative scheme, whereby the input parameter is varied systematically within predefined bounds. At each iteration, a SOLIDWORKS model is regenerated through the SOLIDWORKS API, ensuring that the geometry remains fully associative and parametrically consistent. The algorithm incorporates conditional logic to assess whether the resulting geometry satisfies structural, spatial, and manufacturing constraints. If a candidate solution fails to meet the criteria, the algorithm advances to the next iteration. This process continues until convergence is achieved on an optimal configuration, as determined by an objective function tailored to mechanical performance and material economy. Algorithmic expression of the application procedure and the UI of the developed desktop application is presented in Figure 7, while the corresponding software code is provided in Supplementary File S1.

2.4. Case Study: Wall Thickness Optimization of the Reference Model Housing

In this case study, an automated optimization analysis sample was carried out for the reference pump model utilized int this research. The user-defined input parameters based on manufacturer’s catalogue for generating the automated solid model were as follows: an operating pressure of 250 bar, an effective flow rate of 17.1 L min⁻¹, the electric motor’s drive speed of 1500 rpm, an initial wall thickness of 14.9 mm, a volumetric efficiency of 96%, and an overall efficiency of 85%. For the automated FEA setup, a global element size of 6 mm (min. local mesh control size: 1 mm, defeature tolerance: 0.125 mm), utilizing a second-order, high-quality mesh were specified. For the optimization configuration, the design constraints included an allowed equivalent stress of 280 MPa for the housing (corresponding to the material’s yield strength). As with any mechanical device containing moving components, there exist finite clearances that separate dynamic elements, in this case, the gears, from the pump housing or the wear/cover plates. The pressure differential between the suction and discharge sides of the pump induces leakage flow through these clearances, thereby affecting the volumetric efficiency of the system. Two principal leakage paths may be identified: radial leakage, occurring between the gear tooth tips and the internal side walls of the housing, and axial leakage, taking place between the gear faces and the wear plates [16,23,26]. In the reference model utilized in this case study, the distance between the centres of the gear shafts is fixed. The current clearance between the gear tooth tips and the housing wall is 0.030 mm. According to the relevant literature, the recommended clearance between the gear teeth and the internal housing surfaces lies within the range of 0.001 inch (≈0.0254 mm) to 0.002 inch (≈0.0508 mm) [26,39].

In this context, assuming an allowable maximum clearance of 0.050 mm between the gear teeth tip and the internal surfaces of the housing during operation, it is postulated, within the scope of this case study, that this clearance may vary and locally increase in regions subjected to elevated pressure during pumping. Based on empirical observations and experiences, it is further assumed that the maximum clearance between the gear tip and the inner housing surface is attributable to deformation distributed in a ratio of approximately one-third due to gear shaft bending and two-thirds due to housing extension. Under this predictive assumption, the maximum allowable deformation is set at 0.020·(2/3) ≈ 0.013 mm, which serves as a critical design constraint in the analysis. Notably, this constraint aligns closely with the value (0.04 mm) recommended in the most recent relevant literature [40].

For the design variable under consideration, wall thickness (initially set at 14.9 mm), the allowable range was defined between 11 mm and 18 mm, with increments of 1 mm. The UI subsequently calculated the relevant values accordingly. The objective is minimizing the mass of the housing through optimizing the design variable of wall thickness (t).

This case study specifically focuses on the objective of reducing the housing mass by optimizing the wall thickness, as formulated below (Equation (9)):

$$\begin{array}{l}\underset{t}{\min }\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}f(t)=\rho \cdot V_H(t)\hspace{1em}(kg)\\ \mathrm{subject} \mathrm{to} \hspace{1em}\hspace{1em}{\sigma }_{von-mises}(t)\le {\sigma }_{allowed}\hspace{1em} ({\sigma }_{allowed}={\sigma }_{yield}=280 \mathrm{MPa})\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{U}_{\max }(t)\le U_{allowed}\hspace{1em}\hspace{1em}\hspace{1em}(U_{allowed}=0.013 \mathrm{mm})\\ \hspace{1em} \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{t}_{\min }\le t\le t_{\max }\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}(11 \mathrm{mm}\le t \le 18 \mathrm{mm})\end{array}$$

(9)

3. Results and Discussion

3.1. Confirmation for Mass Reduction Goal: Initial FEA Outputs

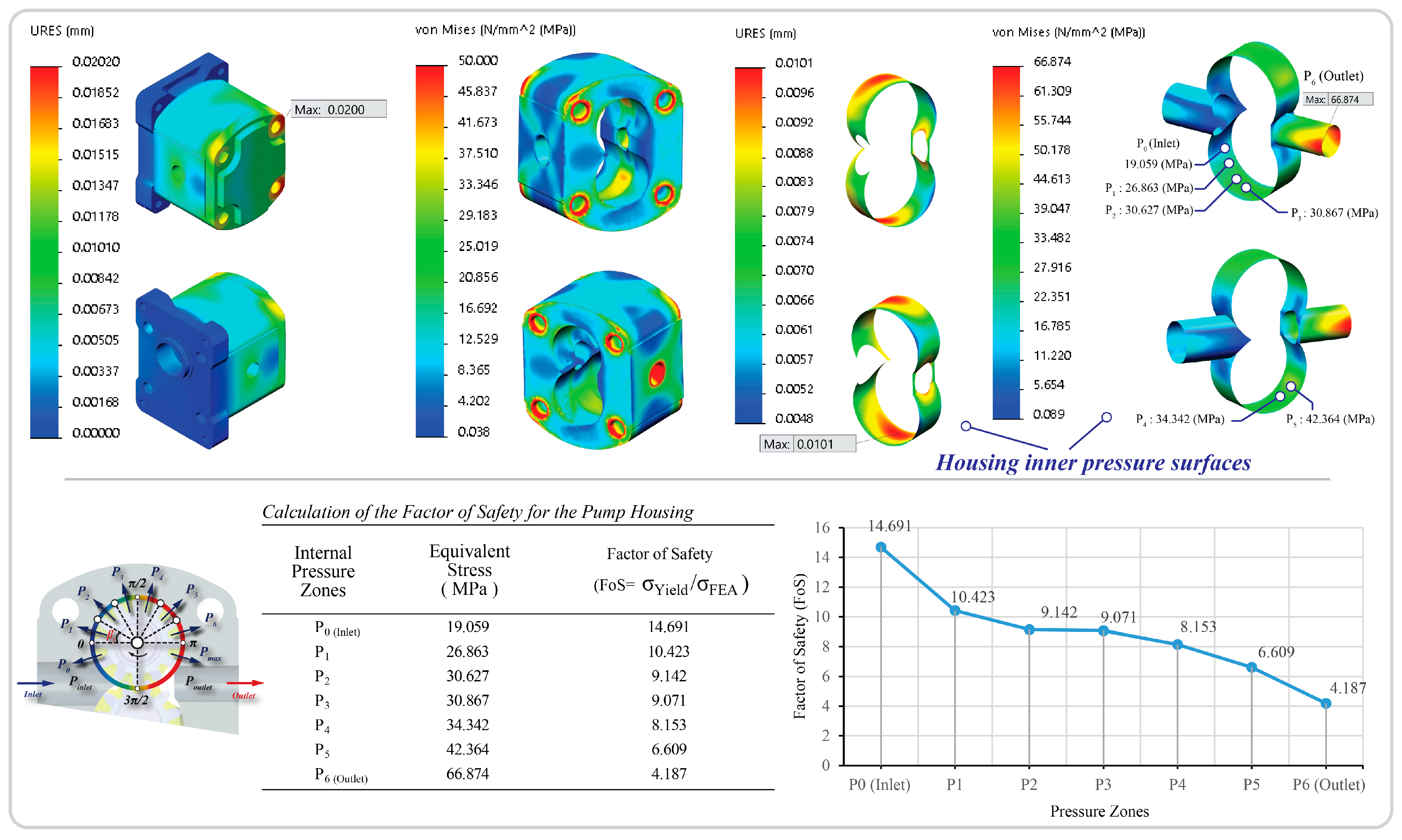
Following the completion of the pre-processing stage of the FEA workflow, a structural simulation was performed to assess the behaviour of the reference gear pump model under operating pressure loads. The primary objective was to inform subsequent structural optimization, particularly with regard to reducing housing mass while preserving mechanical integrity. The simulation assessed both global displacement responses (URES) and localized stress concentrations (via von Mises equivalent stress), spanning the outer housing structure and the internal fluid domain. As illustrated in Figure 8, the housing exhibited low overall displacement, with a maximum deformation of 0.020 mm occurring at the front flange interface—an expected outcome given the application of mechanical boundary constraints at these regions. This low deflection behaviour at the outer body component confirms the geometric rigidity of the design and supports the retention of internal alignment tolerances essential for volumetric efficiency and long-term wear resistance in gear-driven systems. The equivalent stress distribution revealed peak stress values localized primarily around bolt holes and internal cavity transitions. However, it is critical to interpret these results within the context of the modelling approach: notably, the SOLIDWORKS Simulation “Spider Bolt” technique, which employs rigid link beam elements and preload simulation via thermal contraction, introduced artificially high stress artefacts near the bolt heads. As established in existing literature, these stress concentrations are non-physical and were therefore excluded from further interpretation to maintain analytical integrity [31,41,42].

In the internal domain, the housing was subjected to a realistic fluid pressure regime ranging from 19.059 MPa at the inlet (P₀) to 42.364 MPa at the outlet (P₅), peaking at 66.874 MPa equivalent stress near the outlet port (P₆). These stress concentrations were primarily located on the inner curved surfaces and outlet channel where the abrupt pressure transition interacts with geometric complexity. Despite these localized stress peaks, the results remain comfortably within the material’s yield strength limit of 280 MPa, with a minimum factor of safety (FoS) of 4.187 observed at the most critical point (P₆). The calculated FoS values, shown in the accompanying table and trend plot, exhibit a gradual decline from inlet to outlet, corresponding with the increasing internal pressure. This gradient provides a valuable insight into the progressive load transmission through the housing and highlights potential zones for structural refinement.

Importantly, the displacement results in the internal fluid geometry were also modest, with a maximum of 0.010 mm, further confirming the stability of the structure under operational pressures. No abnormal deformation modes or signs of incipient failure sign were observed, validating the adequacy of the current geometry. Given the conservative stress distribution, particularly in regions where the FoS significantly exceeds design minimums, a clear opportunity exists for structural size optimization. Specifically, the housing wall thickness could be reduced in areas exhibiting low stress without compromising safety margins. Such a strategy would reduce the total mass of the housing, thereby improving material utilization and reducing production costs, an especially valuable improvement for mass-manufactured hydraulic components. However, the implementation of any wall thickness reduction must be executed cautiously, supported by a detailed parametric sensitivity study to ensure the retention of structural robustness, particularly in regions exposed to dynamic or fatigue-critical loading conditions. To maintain a clear methodological scope, a full sensitivity study was not undertaken; however, examining how variations in the empirical pressure distribution influence the optimization outcome (e.g., outlet-region stress gradients and selected wall-thickness values) would be particularly informative.

From a CAD and product development standpoint, it may be recommended that a parametric optimization strategy be pursued, leveraging a CAD-FEA integration loop capable of automating geometry variation and performance evaluation. Techniques such as design-of-experiments, gradient-based solvers, and topology-sensitive refinement algorithms should be employed to systematically explore and converge on an optimized wall profile. Special focus should be given to sidewall regions, flange bases, and bearing support surfaces, zones that current analysis identifies as structurally over-conservative. In these regards, the current design provides a structurally sound baseline with favourable stress and displacement characteristics under realistic pressure loading. However, the updated simulation results and factor of safety analysis reveal significant untapped optimization potential. As such, the next phase of development will adopt a CAD-FEA automated design workflow to guide the creation of a lightweight, manufacturable, and mechanically efficient gear pump housing architecture.

The integration between the empirical pressure formulation and the automated analysis loop is achieved programmatically: when the user specifies the operating pressure within the interface, the empirical equation is invoked by the backend solver module to generate the corresponding spatial pressure field. These calculated pressure values are then transmitted through the SOLIDWORKS Simulation API to update boundary conditions for each iteration. In this way, the experimentally validated model and the CAD–FEA automation operate as a deeply coupled, single workflow rather than two independent procedures. The scientific basis and experimental derivation of this model were fully detailed in our earlier publication [9].

3.2. Interpretation of Application User Interface

The developed desktop application represents a pivotal advancement in automating the design optimization process for external gear pump housings. Its design demonstrates adherence to user experience and software engineering principles, with a clear separation of functionality across discrete UI panels that correspond logically to user tasks—namely, geometric input, boundary condition specification, FEA execution, and design optimization. This modularity significantly enhances usability, particularly for design engineers and researchers without specialist knowledge of CAD scripting or FEA solvers. From a user-friendly standpoint, the interface facilitates intuitive data entry through parameter-specific input fields and command buttons. The interface hierarchy mirrors the sequential nature of the design workflow, thereby reducing the cognitive load associated with navigating between operations. By providing real-time visual and numerical feedback on entered parameters and resulting outputs, the UI improves transparency and reinforces user confidence in simulation fidelity. This is consistent with established heuristics in user-centred interface design [43], particularly the principles of feedback and visibility of system status. Technically, the interface capitalizes on the SOLIDWORKS API ecosystem to bridge parametric geometry manipulation and FEA setup, a non-trivial integration given the complex nature of boundary condition assignment and mesh control. The use of Visual Studio (Microsoft Visual Studio Community 2022) and .NET Framework v4.8 ensures platform stability, while the integration of SOLIDWORKS Interop libraries allows programmatic access to geometric features and simulation entities. This streamlines iterative design exploration and enables deterministic, reproducible simulation cycles. Notably, the system architecture adopts a closed-loop Optimization workflow where updated geometric variables, primarily wall thickness, are automatically re-evaluated under defined constraints. This approach aligns with modern practices in simulation-driven design [17,44], wherein the CAD-FEA pipeline is rendered executable through scripting and procedural automation. From a software engineering perspective, the deterministic iteration strategy employed in the wall thickness Optimization routine enhances solution convergence and eliminates the subjectivity inherent in manual model adjustments. Moreover, by exposing functional relationships such as flow rate versus housing depth via parametric control, the UI reflects sound object-oriented design. The inclusion of fail-safe mechanisms, such as boundary checks for stress and displacement constraints, ensures that only structurally valid solutions are considered for final selection, adhering to robustness principles in design optimization.

3.3. Case Study Outputs

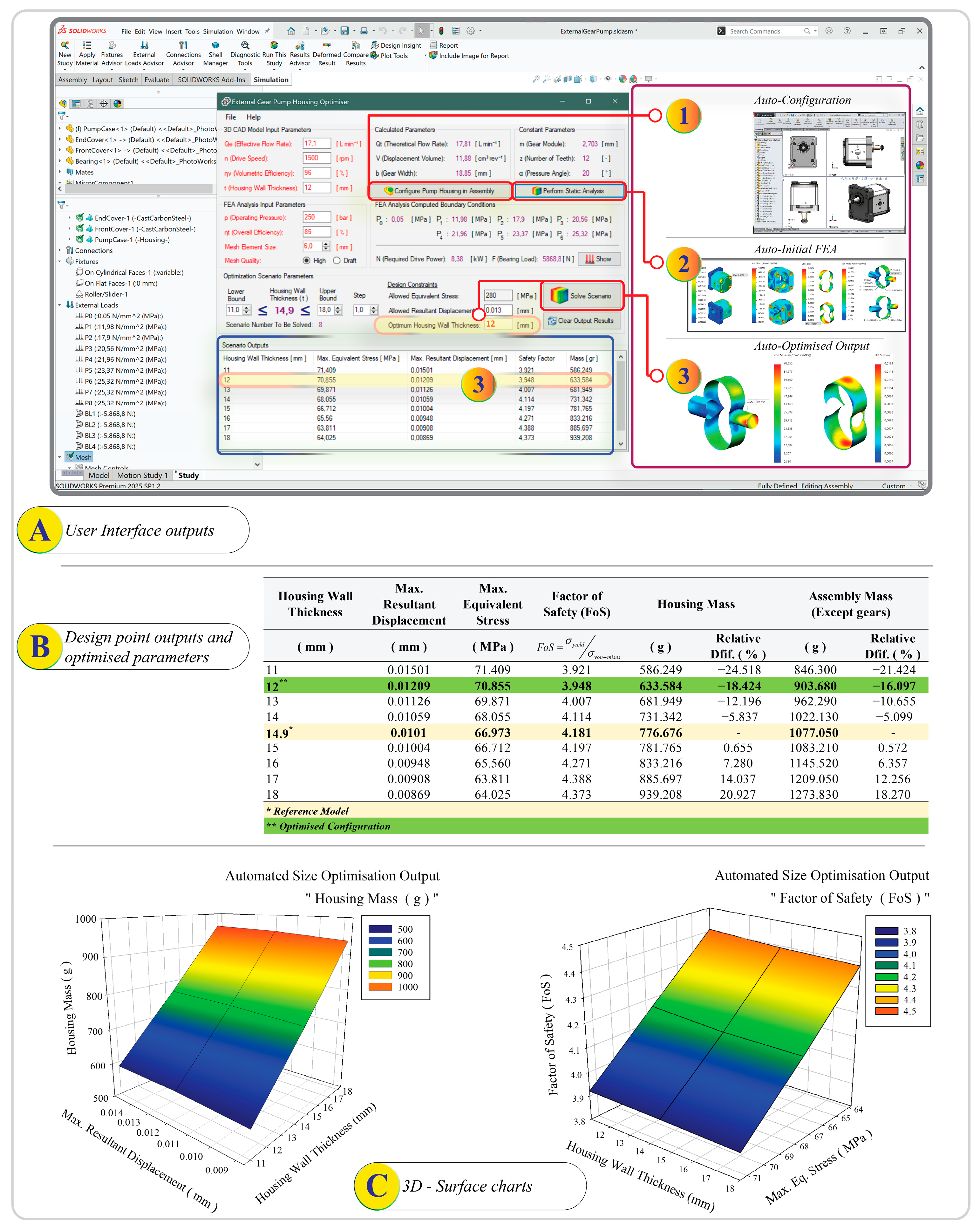
Using the custom CAD-FEA optimization environment, a series of design iterations was executed to evaluate pump housing performance across a range of wall thickness values from 11 mm to 18 mm (in 1 mm increments). This automated, CAD-integrated workflow proved highly effective in performing a rapid multi-objective exploration of the design space, simultaneously assessing structural criteria and mass for each variant. Figure 9 provides a detailed view of the optimization interface and outputs, including the scenario setup and results. Steps 1–3 shown in Figure 9 correspond, respectively, to (1) the CAD model parameter definition and import stage, (2) the automatic FEA setup and boundary condition assignment executed by the API, and (3) the optimization and result visualization phase within the integrated interface.

Comparable optimization studies in the field, such as Zharkevich et al. (2023), who reported mass reductions up to 16% through geometric alteration and stress concentrator rounding, corroborate the efficacy of simulation-driven size reduction strategies [17]. However, the current work distinguishes itself through its integration of experimentally validated pressure models, parametric automation, and iterative constraint evaluation within a unified desktop interface. This represents a more holistic and scalable methodology compared to previous studies that often relied on fixed-pressure assumptions and manual geometry updates [1,2].

Similarly, Ghionea (2013) demonstrated the effectiveness of CAD-integrated FEA tools in enabling rapid, iterative optimization of mechanical components [45]. The current system distinguishes itself by offering a fully automated optimization workflow within the design environment, a feature particularly beneficial in digital twin development and mass customization strategies.

Key advantages of this method include the integration of automated routines, support for visual trade-off analysis via surface charts, and the ability to reduce component mass without compromising structural safety. These outcomes contribute to eco-design and lightweighting efforts, aligning with sustainability objectives. Furthermore, the customizable interface facilitates quick scenario switching and parameter adjustments, enhancing usability during iterative development cycles. However, certain limitations must be acknowledged. The current simulations assume static loading conditions, which may not accurately reflect the dynamic or transient operational stresses encountered in actual pump service. Material behaviour is modelled as linear elastic, omitting potential effects of fatigue or creep. Although dynamic loading and material fatigue effects were not explicitly simulated, their potential influence on local stress peaks and long-term structural integrity is acknowledged. Consequently, under cyclic and thermally varying operational conditions, actual stress and strain responses may differ from the present static predictions due to transient load redistribution and progressive material softening, which are recognized as inherent limitations of the current model. Additionally, manufacturing constraints, such as casting feasibility for thinner walls, are not directly integrated into the optimization loop. The use of parametric sweeping, while straightforward, may not achieve globally optimal solutions as effectively as multi-objective evolutionary algorithms like NSGA-II [46].

To enhance the framework’s applicability, future work could incorporate dynamic FEA simulations, topological optimization strategies, and AI-driven surrogate models to accelerate performance predictions. Integrating cost and manufacturability assessments would further extend the system toward a comprehensive design for manufacturing (DfM) solution.

3.4. Overall Discussion

The study successfully demonstrates an integrated and automated methodology for the structural design optimization of external spur gear pump housings. By combining empirical pressure modelling, parametric CAD geometry, static structural FEA, and an intuitive desktop application interface, it offers a cohesive framework that addresses several longstanding challenges in mechanical component design, namely, the trade-off between mass reduction and structural reliability. Technically, the research advances the field by enabling realistic pressure distribution modelling within the housing, surpassing traditional simplifications such as uniform or linearly distributed loads. The adoption of an empirically derived pressure function, validated through prior experimental work, introduces a higher degree of physical fidelity into the simulation process, thereby enhancing the relevance of the FEA results. This represents a notable contribution, as earlier works [2,11] either employed overly simplified boundary conditions or failed to integrate such empirical insights into automated workflows.

The study’s novelty is further exemplified by the seamless integration of CAD and FEA through SOLIDWORKS API scripting, which enables dynamic model regeneration and real-time simulation. This stands in contrast to prior literature, where CAD-FEA interoperability remains largely manual or is restricted to static geometry evaluations [13]. Moreover, the deterministic optimization routine employed here avoids the stochastic nature of genetic algorithms, offering faster convergence and improved traceability of design decisions. The UI developed as part of this study further enhances the practicality and accessibility of the automated design process. By providing a user-friendly environment for inputting design parameters and visualizing simulation results, the system lowers the barrier to adoption for engineers and designers. This is particularly relevant in industries where rapid customization and prototyping are essential [47,48,49].

From a theoretical standpoint, the framework contributes to design methodology by formalizing a parametric optimization problem for gear pump housings, incorporating constraint handling and objective function formulation. It also provides a realistic and quantifiable pathway to lightweight design—a critical requirement in sectors such as aerospace, automotive, and mobile hydraulics. These results align with contemporary literature, which increasingly prioritizes multi-objective optimization for both fluid performance and mechanical resilience [4,10,21]. While this approach offers numerous advantages, certain limitations must be acknowledged. These include potentially high computational demands when a large number of FEA simulations are required, a strong reliance on the accuracy of input data to ensure reliable outcomes, and the inherent opacity of the optimization algorithm, which may be perceived by users as a ‘black box’. Although a formal timing and scaling analysis was outside the present scope, identifying principal efficiency constraints (e.g., sequential FEA execution and re-meshing overhead) and benchmarking iteration cost would be beneficial for strengthening the platform’s performance characterization. In addition, the structural simulation within the application is currently restricted to static conditions and assumes a linear elastic material model. In reality, gear pumps are subjected to dynamic loading, cyclic fatigue, and thermal gradients. These factors warrant future extension of the simulation environment to include dynamic FEA or coupled multiphysics analysis. Another limitation is that, while the use of deterministic stepwise optimization provides robustness, it may fail to identify global optima in complex design spaces, a shortcoming that could potentially be addressed through hybrid methods combining deterministic and metaheuristic techniques. Furthermore, the current study does not explicitly address manufacturability constraints such as casting tolerances or machining allowances, which may affect the real-world viability of the optimized geometries. Incorporating manufacturing cost models into the objective function could further enhance the tool’s industrial applicability. Future comparative studies incorporating metaheuristic algorithms such as genetic or particle-swarm optimization may be undertaken to evaluate the computational efficiency and solution quality relative to the present deterministic framework.

4. Conclusions

This study presents a comprehensive and automated design framework for the structural optimization of external spur gear pump housings, integrating parametric CAD modelling with FEA via SOLIDWORKS API and a custom-developed desktop application. The core objective was to minimize housing mass while maintaining mechanical integrity under realistic operational pressures in the presented case study. Unlike traditional approaches, which often rely on static geometry and idealized loading assumptions, this research embeds an empirically derived pressure distribution model into the automated simulation loop, thus achieving a higher degree of physical fidelity. The developed platform enables rapid parametric model generation, automated assignment of realistic boundary conditions, and iterative size optimization based on predefined stress and displacement constraints. A case study conducted on a reverse-engineered reference pump demonstrated the system’s efficacy, yielding a wall thickness configuration that achieved an 18.42% reduction in housing mass without compromising safety factors (3.948) or inducing excessive deformation (0.012 mm). The automation of the CAD-FEA workflow significantly enhances design repeatability, reduces user intervention, and streamlines the optimization process, making it particularly suitable for industrial applications requiring rapid customization and prototyping.

Key contributions of this research include (i) the integration of empirical pressure modelling with FEA for more accurate representation of internal loads; (ii) the development of a fully automated design optimization interface enabling deterministic convergence on optimal configurations; and (iii) the validation of the approach through a practical case study, showing notable improvements in structural efficiency and material utilization.

Despite its promising outcomes, the current framework is limited to static structural conditions and assumes linear elastic material behaviour. Furthermore, although a user-friendly interface has been developed to simplify complex design processes, several limitations remain. These include potentially high computational costs arising from the large number of FEA required due to the broad range of design variables, reliance on the accuracy of input data to ensure reliable results, and the opaque nature of the optimization algorithm, which may appear as a “black box” to users. Future developments may therefore focus on enhancing the UI, incorporating dynamic and fatigue loading conditions, integrating manufacturing constraints, and employing advanced optimization strategies such as topology optimization or AI-driven surrogate modelling. These improvements would contribute to increased design robustness and industrial applicability. Here, the proposed methodology represents a significant advancement in the automated design and optimization of hydraulic components, offering a scalable and efficient solution to the complex trade-offs between mass, structural integrity, and manufacturability in gear pump housing design.