Factors Influencing the Seismic Collapse of Stratified Steep Cliffs Based on Analytic Hierarchy Process (AHP)
Abstract
1. Introduction
2. Small Shaker Model Tests
2.1. Test Equipment and Materials
2.2. Test Methods
2.3. Test Scheme
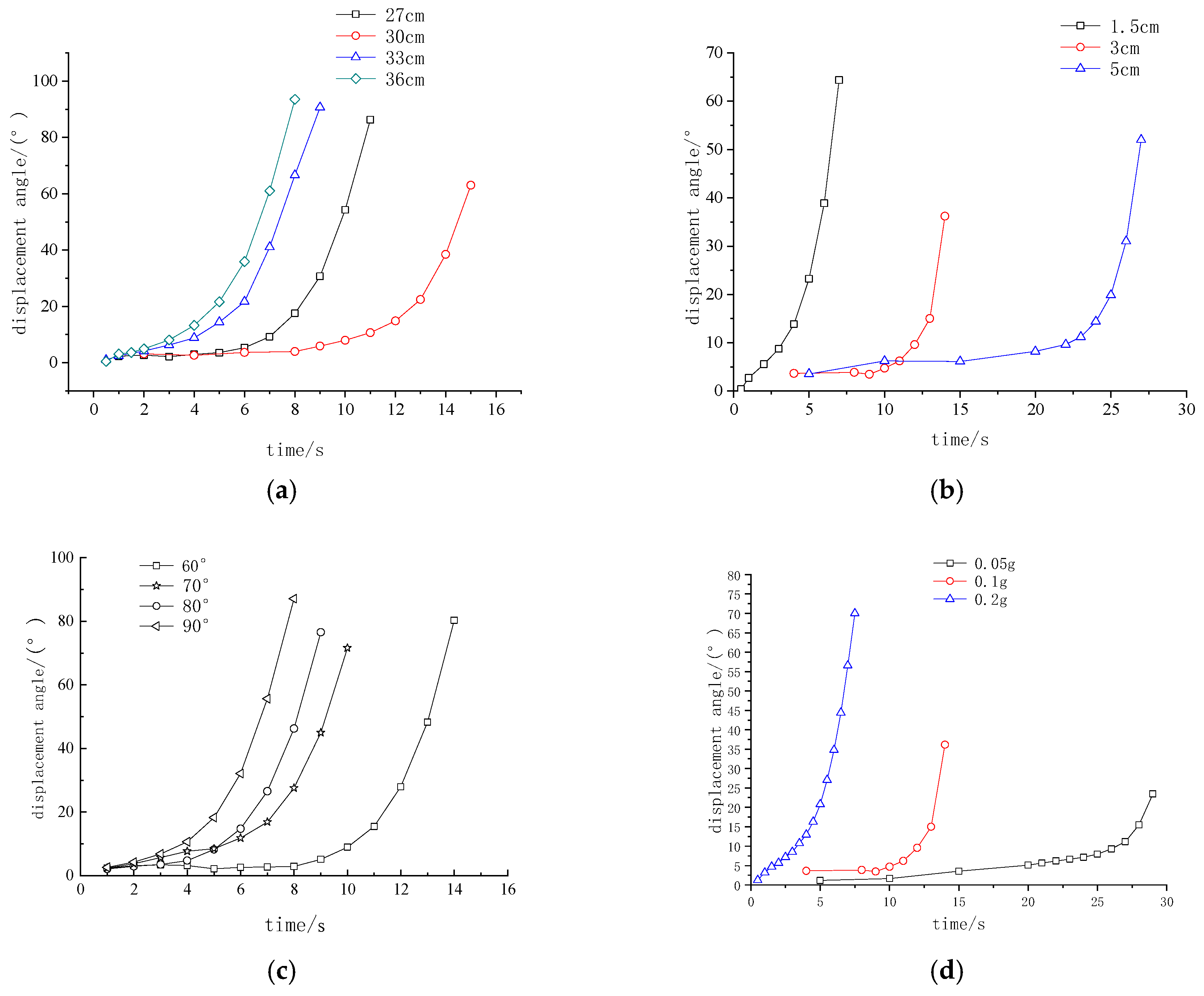
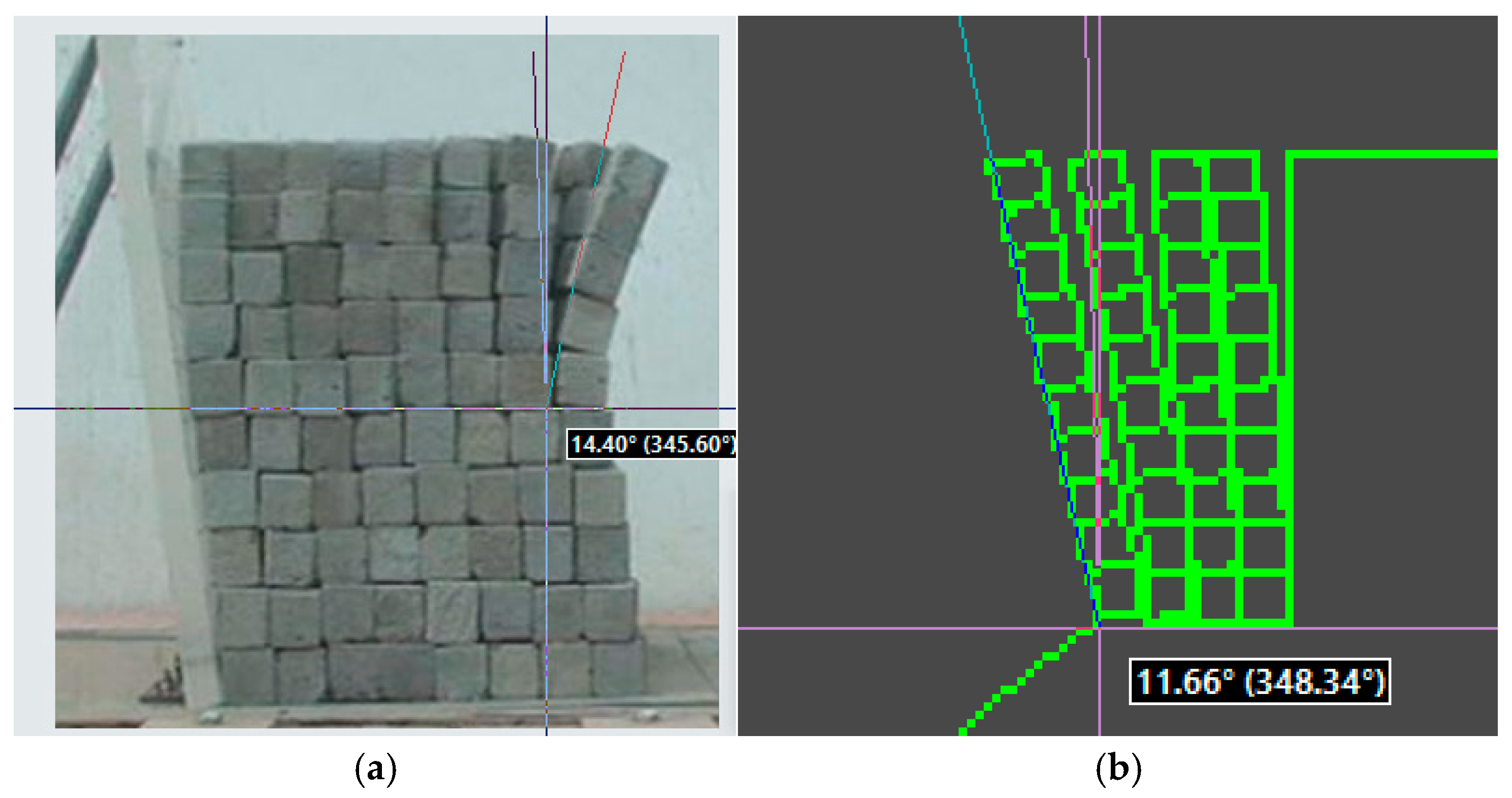
2.4. Test Analyses
3. Two-Dimensional (2D) UDEC Numerical Simulation
3.1. Generalization of Geometric Models and Parameter Selection
3.2. Model Validation Against Experimental Results
3.3. Research on Influencing Factors in Rockfall
3.4. Criteria for Determining the Critical Threshold of Collapse
3.5. Analysis of the Impact Mechanisms of Collapse Factors
3.6. Precursors to Rock Collapse
4. Weight Analysis of Various Factors Based on AHP
4.1. The Principle of the Analytic Hierarchy Process (AHP)
4.2. Selection of Evaluation Factors
4.3. Evaluation Process
5. Discussion: Engineering Implications and Limitations
5.1. Model Application and Scale Justification
5.2. Limitations and Scale Effects
5.3. Validation with Field Evidence
5.4. Representativeness of the Assumed Lithology and Materials
6. Conclusions
- (1)
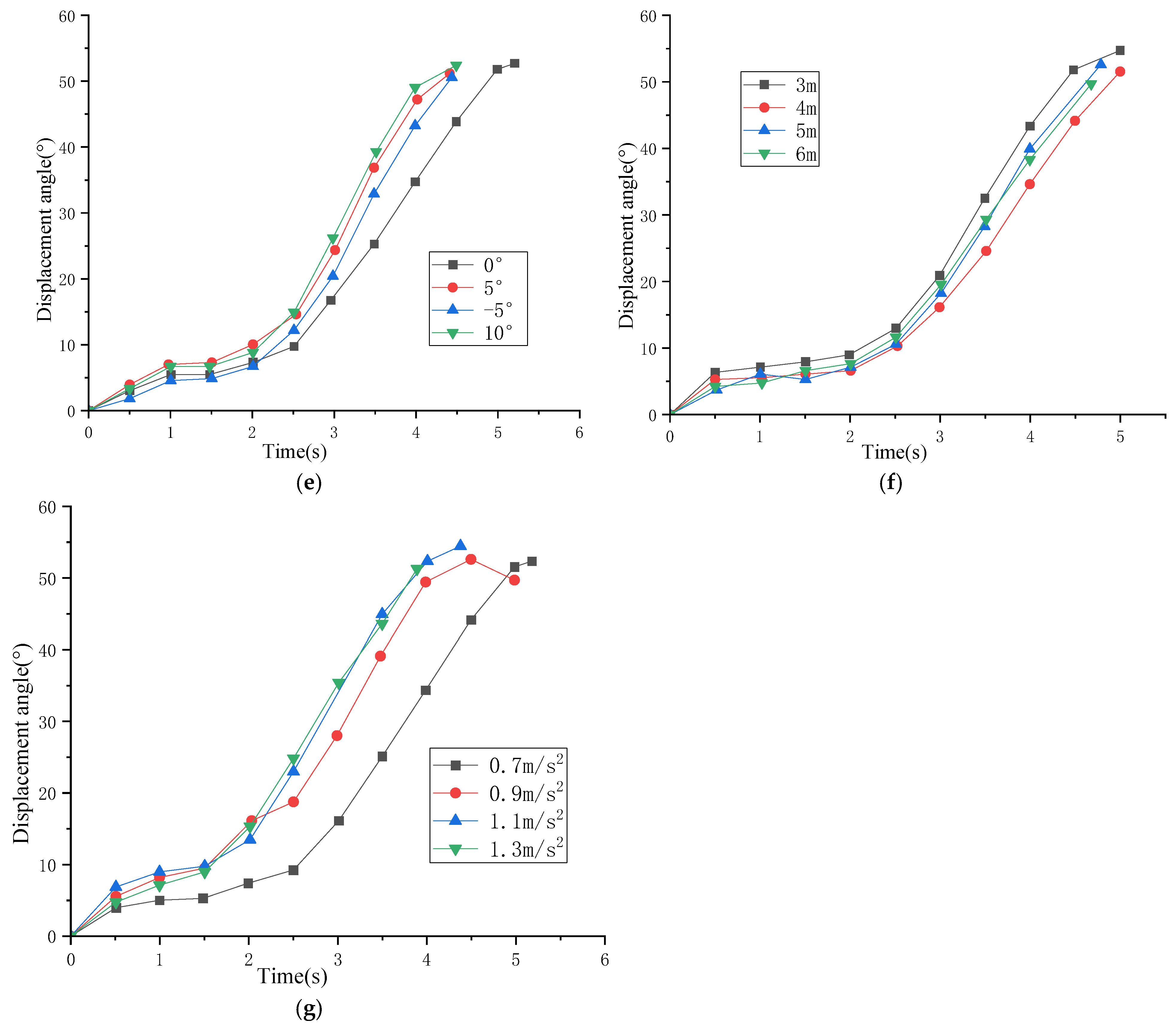
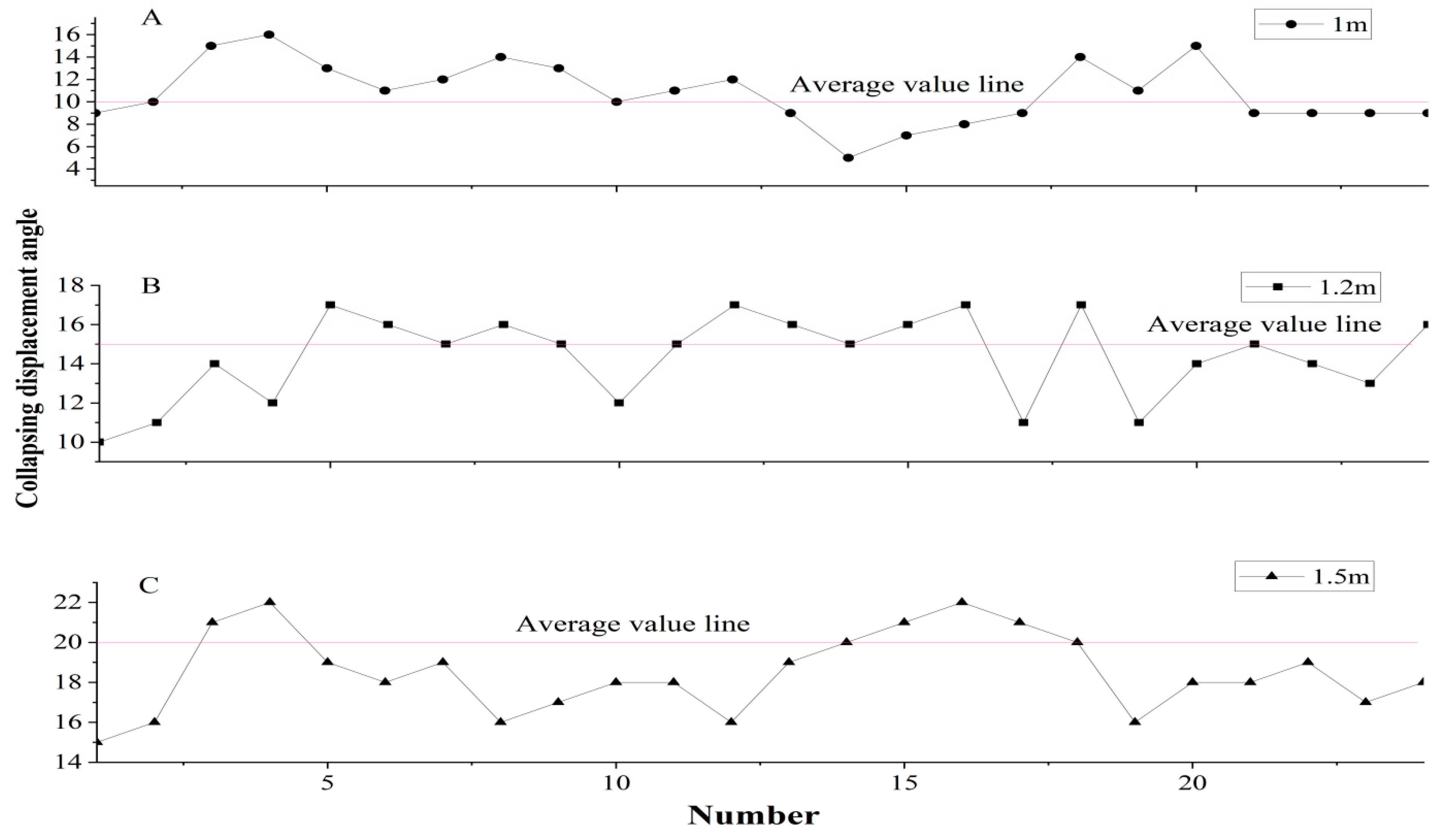
- Collapse displacement angle is strongly correlated with joint spacing. Quantitative result: The collapse displacement angle ranged from 9 to 15°, 12 to 17°, and 16 to 21° for joint spacings of 1.0 m, 1.2 m, and 1.5 m, respectively. Interpretation: Larger joint spacing (i.e., lower fragmentation) increases the critical angle required for collapse initiation. Engineering implication: The displacement angle serves as a quantifiable precursor for early-warning systems; monitoring tilt beyond these thresholds can signal imminent collapse.
- (2)
- Degree of rock mass fragmentation is the most influential factor. Quantitative result: AHP weighting assigned the highest priority to fragmentation degree (weight = 0.278), followed by seismic amplitude (0.222) and cliff slope angle (0.167). Interpretation: Fragmentation governs both the failure mode and the displacement angle threshold. Engineering implication: Mitigation measures should prioritize reducing weathering and sealing joints to minimize fragmentation progression.
- (3)
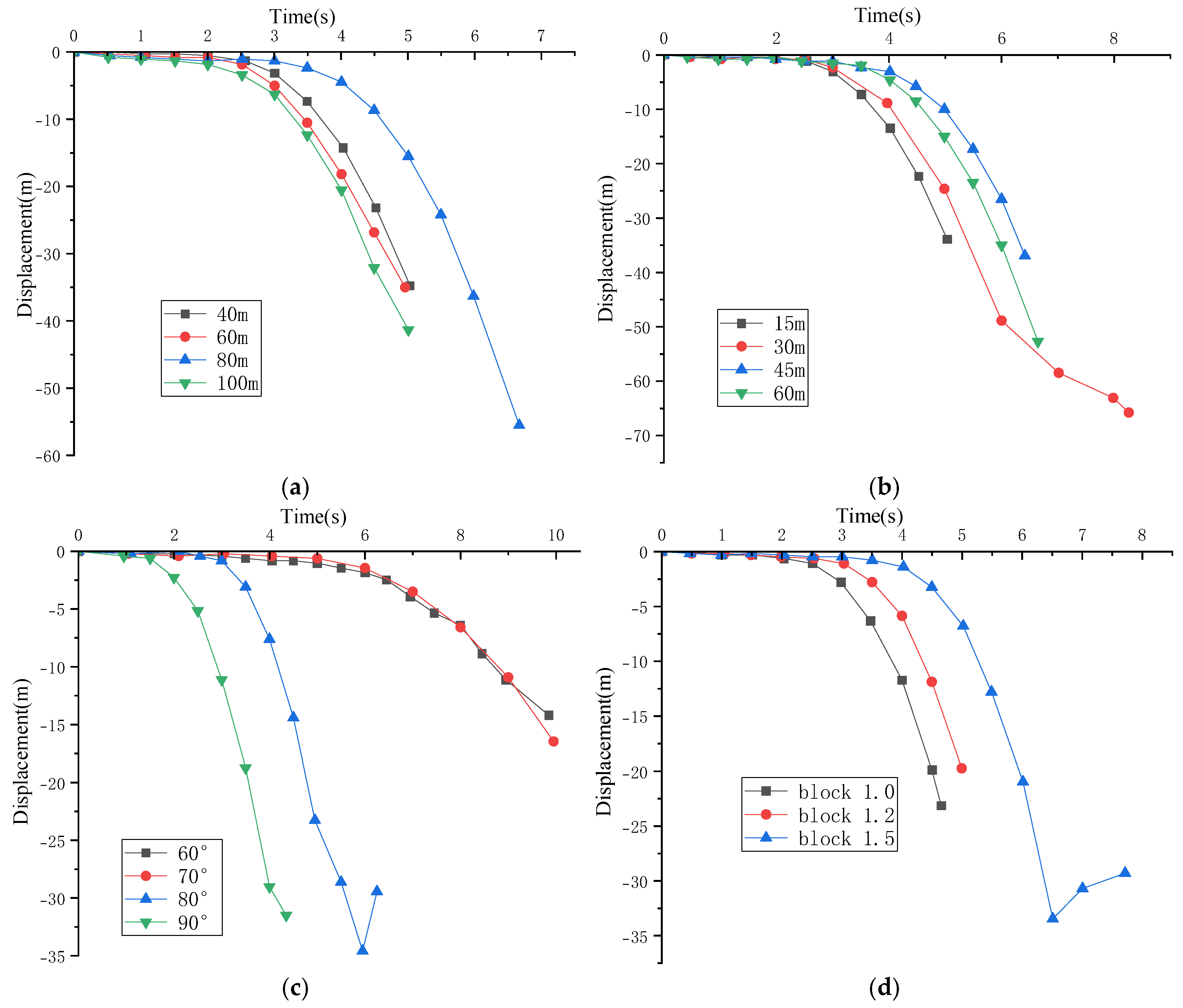
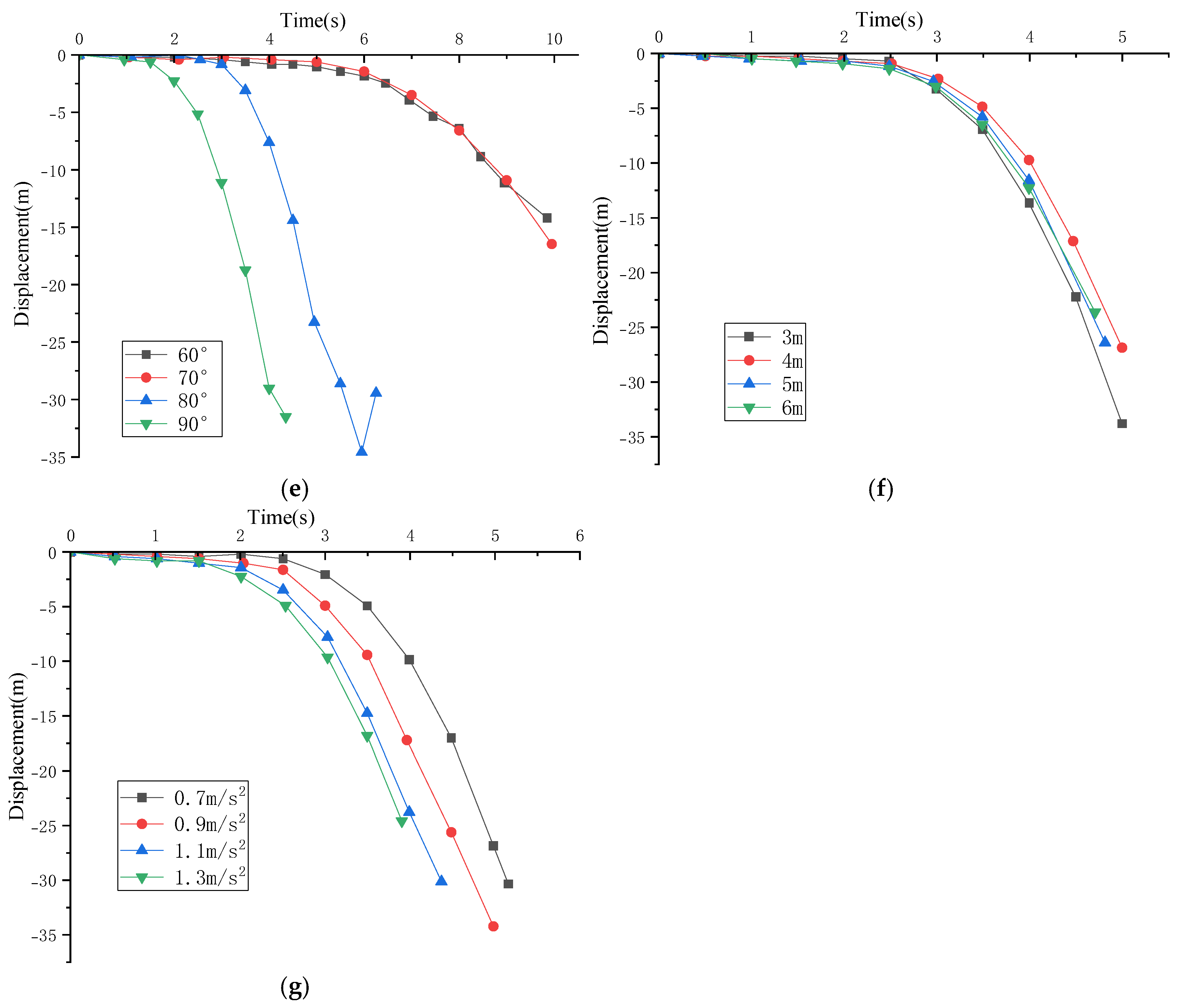
- Nonlinear thresholds govern collapse timing and mode. Quantitative result: Critical thresholds include H1 = 80 m (transition in collapse timing), H2 = 45 m (block height stability limit), and β ≈ 70° (slope angle influence saturation). Interpretation: Collapse behavior shifts from self-stabilizing to destabilizing beyond these thresholds. Engineering implication: Slope design and reinforcement should account for these thresholds to avoid abrupt stability loss.
- (4)
- Seismic amplitude and slope angle significantly affect collapse initiation. Quantitative result: Seismic amplitude showed a positive correlation with collapse time, while slope angle exhibited a negative correlation until β ≈ 70°. Interpretation: Higher PGA delays collapse by prolonging the rocking phase, whereas steeper slopes accelerate it. Engineering implication: Slope angle reduction or seismic retrofitting may be effective in high-seismicity regions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, R.; Liu, W.; Zhou, J.; Pei, X. Experimental Field Study of Movement Characteristics of Rock Blocks Falling down a Slope. J. Earth Sci. 2010, 21, 330–339. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Crosta, G.B.; Agliardi, F. Failure forecast for large rock slides by surface displacement measurements. Can. Geotech. J. 2003, 40, 176–191. [Google Scholar] [CrossRef]
- Zhou, F.; Liu, X.; Tang, H.; Miao, M.; Xu, B.; Guo, X. Analysis of the frequency–response stability and reliability of a tower-column unstable rock mass on a high and steep slope. Sci. Rep. 2024, 14, 20308. [Google Scholar] [CrossRef] [PubMed]
- Berrett, B.; Fulmer, E.; Leshchinsky, B.; Olsen, M.; Massey, C.; Wartman, J. Simplified analysis of coseismic slope displacement and hillslope weakening. Eng. Geol. 2025, 352, 108058. [Google Scholar] [CrossRef]
- Najib, F.D.; Kodama, J.; Fujii, Y. The Deformation modes of rock slopes due to excavation in mountain-type mines. Mater. Trans. 2015, 56, 1159–1168. [Google Scholar] [CrossRef]
- Mufundirwa, A.; Fujii, Y.; Kodama, N.; Kodama, J.I. Analysis of natural rock slope deformations under temperature variation: A case from a cool temperate region in Japan. Cold Reg. Sci. Technol. 2011, 65, 488–500. [Google Scholar] [CrossRef]
- Ning, Y.; Shen, Y.; Ding, T.; Xu, P.; Duan, F.; Zhang, B.; Zhang, B.; Smith, J.V. Evolution Process of Toppling Deformations in Interbedded Anti-Inclined Rock Slopes. Appl. Sci. 2025, 15, 7727. [Google Scholar] [CrossRef]
- Ning, Y.B.; Zhang, G.C.; Tang, H.M.; Shen, W.C.; Shen, P.W. Process analysis of toppling failure on anti-dip rock slopes under seismic load in southwest China. Rock Mech. Rock Eng. 2019, 52, 4439–4455. [Google Scholar] [CrossRef]
- Tai, D.; Qi, S.; Zheng, B.; Luo, G.; He, J.; Guo, S.; Zou, Y.; Wang, Z. Effect of excitation frequency and joint density on the dynamic amplification effect of slope surface on jointed rock slopes. Eng. Geol. 2024, 330, 107385. [Google Scholar] [CrossRef]
- Antwi Buah, P.; Zhang, Y.; He, J.; Yu, P.; Xiang, C.; Fu, H.; He, Y.; Liu, J. Evaluating the dynamic response and failure process of a rock slope under pulse-like ground motions. Geomat. Nat. Hazards Risk 2023, 14, 2167613. [Google Scholar] [CrossRef]
- Zhou, H.X.; Che, A.L.; Zhu, R.J. Damage evolution of rock slopes under seismic motions using shaking table test. Rock Mech. Rock Eng. 2022, 55, 4979–4997. [Google Scholar] [CrossRef]
- Zang, M.; Yang, G.; Dong, J.; Qi, S.; He, J.; Liang, N. Experimental study on seismic response and progressive failure characteristics of bedding rock slopes. J. Rock Mech. Geotech. Eng. 2022, 14, 1394–1405. [Google Scholar] [CrossRef]
- Miao, S.; Su, L.; Zhang, C.; Liu, Z.; Wang, B.; Dong, Z. Dynamic response characteristics and damage failure process of bedding rock slope in shaking table test. Bull. Eng. Geol. Environ. 2024, 83, 358. [Google Scholar] [CrossRef]
- Negi, R.; Sati, S.P.; Sharma, V.; Samanta, M.; Kumar, V.; Puniya, M.K.; Rana, S.S.; Kanungo, D.P. Evaluating instability & failure pattern of landslides, Giri valley, Northwest Himalaya, India. Bull. Eng. Geol. Environ. 2024, 83, 271. [Google Scholar] [CrossRef]
- Bolla, A.; Paronuzzi, P. Geomechanical field survey to identify an unstable rock slope: The Passo della Morte case history (NE Italy). Rock Mech. Rock Eng. 2020, 53, 1521–1544. [Google Scholar] [CrossRef]
- Luo, W.; Liu, S.; Tao, Z.; Wang, H.; Gan, X. Nonlinear energy consumption analysis of shallow-buried bias tunnel stability with improvement of failure mode. Sci. Rep. 2025, 15, 25965. [Google Scholar] [CrossRef]
- Zhan, Z.; Qi, S.; He, N.; Zheng, B.; Ge, C. Shaking table test study of homogeneous rock slope model under strong earthquake. J. Eng. Geol. 2019, 27, 946–954. [Google Scholar]
- Frodella, W.; Ciampalini, A.; Gigli, G.; Lombardi, L.; Raspini, F.; Nocentini, M.; Scardigli, C.; Casagli, N. Synergic use of satellite and ground based remote sensing methods for monitoring the San Leo rock cliff (Northern Italy). Geomorphology 2016, 264, 80–94. [Google Scholar] [CrossRef]
- Arnold, L.; Wartman, J.; MacLaughlin, M. Seismically-induced failure mechanisms in massive rock slopes. Eng. Geol. 2025, 352, 108046. [Google Scholar] [CrossRef]
- Liu, W.L.; Dong, J.X.; Xu, H.H.; Sui, S.G.; Yang, R.X.; Zhou, L.S. Trajectory analysis and risk evaluation of dangerous rock mass instability of an overhang slope, southwest of China. Adv. Civ. Eng. 2021, 2021, 7153535. [Google Scholar] [CrossRef]
- Akin, M.; Dinçer, İ.; Orhan, A.; Varol, O.O. A comparative study on rockfall block motion characteristics using 3-D and 2-D rockfall simulations: A case study from Cappadocia (Mazı, Türkiye). Nat. Hazards 2025, 121, 2265–2291. [Google Scholar] [CrossRef]
- Zhu, H.; Yang, Z.; Cheng, L.; Luo, R.; Liu, Z. Study on rockfall trajectory of dangerous rocks based on rocfall numerical simulation: A case study of a section of dangerous rocks in the three gorges reservoir area. Sci. Technol. Innov. 2020, 19, 45–46. [Google Scholar]
- Jianqun, H. Application of Rocfall software in engineering design of geological disaster prevention and control of collapse. Eng. Constr. Des. 2020, 12, 33–34. [Google Scholar]
- Zhang, S.; Luo, Y. Discussion on prevention and control method of boulder falling in high and steep building slope based on rocfall simulation. Guangdong Civ. Eng. Archit. 2019, 26, 54–63. [Google Scholar]
- Luo, C.; Xiang, Z.; Chen, R. Rockwall design based on Rocfall. Nonferrous Met. Des. 2018, 45, 12–23. [Google Scholar]
- Fu, X.; Sheng, Q.; Zhang, Y.; Chen, J.; Leng, X. Extension of discontinuous deformations analysis method to simulate seismic response of large rock cavern complex. Int. J. Geomech. (ASCE) 2017, 17, E4016008. [Google Scholar] [CrossRef]
- Wang, L.; Yongfeng, C.; Xingxin, N. Calculation and application of blasting force transport distance based on rocfall numerical simulation. Min. Res. Dev. 2015, 35, 8–11. [Google Scholar]
- Fu, X.; Sheng, Q.; Tang, H.; Chen, J.; Du, Y.; Zhang, Z.; Mei, H. Seismic stability analysis of a rock block using the block theory and Newmark method. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 1392–1409. [Google Scholar] [CrossRef]
- Zeng, S. Application of rocfall software in the design of dangerous rock collapse. China Water Transp. (Second. Mon.) 2011, 11, 211–212. [Google Scholar]
- Xu, J.; Zhang, M.; Fan, W. A review of geological hazard risk evaluation. Disaster 2015, 30, 130–134. [Google Scholar]
- Xiang, X.; Huang, R. Risk evaluation and risk management of geological hazards. Geol. Hazards Environ. Prot. 2000, 11, 38–41. [Google Scholar]
- Xu, B.; Liu, X.; Zhou, X.; Liang, Y.; Cai, P.; Han, Y.; Tu, Y.; Deng, Z.; Xie, Y.; Huang, J. Investigation of the dynamic response pattern and instability mechanism of a bedding rock slope subjected to frequent seismic loads. Int. J. Geomech. 2024, 24, 04024117. [Google Scholar] [CrossRef]
- Borgeat, X.; Glueer, F.; Häusler, M.; Hobiger, M.; Fäh, D. On the variability of the site-response parameters of the active rock slope in Brienz/Brinzauls (Switzerland). Geophys. J. Int. 2025, 240, 779–790. [Google Scholar] [CrossRef]
- Fattahi, H.; Hematian, M. Integrating Block Theory and Reliability Methods for Enhanced Stability in Underground Construction: A Case Study. Min. Metall. Explor. 2025, 42, 1693–1715. [Google Scholar] [CrossRef]
- Liu, W.L.; Dong, J.X.; Sui, S.G.; Xu, H.H.; Yang, R.X.; Shen, Z.L. Stability assessment of dangerous rock mass of an overhanging slope in Puerdu Town, Southwestern China. Adv. Civ. Eng. 2021, 2021, 6526417. [Google Scholar] [CrossRef]
- Ishizaka, A.; Labib, A. Review of the main developments in the analytic hierarchy process. Expert Syst. Appl. 2011, 38, 14336–14345. [Google Scholar] [CrossRef]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Deng, F.; Pu, J.; Huang, Y.; Han, Q. 3D geological suitability evaluation for underground space based on the AHP-cloud model. Undergr. Space 2023, 8, 109–122. [Google Scholar] [CrossRef]
- Liu, Y.; Ouyang, Z.; Yi, H.; Qin, H. Study of the multilevel fuzzy comprehensive evaluation of rock burst risk. Sustainability 2023, 15, 13176. [Google Scholar] [CrossRef]
- Zhang, R.; Tian, D.; Wang, H.; Kang, X.; Wang, G.; Xu, L. Risk assessment of compound dynamic disaster based on AHP-EWM. Appl. Sci. 2023, 13, 10137. [Google Scholar] [CrossRef]
- Dong, F.; Wang, S.; Yang, Y.; Ren, M.; Demisa, M.G.; Zhang, R. Research on dynamic fuzzy prediction method for surrounding rock stability of mountain tunnels throughout the construction period. Tunn. Undergr. Space Technol. 2025, 158, 106390. [Google Scholar] [CrossRef]
- Liu, X.; Lang, Q.; Zhang, J.; Zhang, Y.; Yu, C.; Jin, Q.; Liu, Y.; Liu, Z.W.P. Dynamic failure mechanisms and hazard evaluation of rock collapse induced by extreme rainfall in Changbai County highways. Sci. Rep. 2025, 15, 9794. [Google Scholar] [CrossRef]
- Xu, C.S.; Jiang, Z.W.; Du, X.L.; Shen, Y.Y.; Chen, S. 1-g shaking table tests of precast horseshoe segmental tunnel: Experimental design, dynamic properties, deformation mode and damage pattern. Tunn. Undergr. Space Technol. 2021, 113, 103976. [Google Scholar] [CrossRef]
- Yang, Y.S.; Yu, H.T.; Yuan, Y.; Sun, J. 1 g Shaking table test of segmental tunnel in sand under near-fault motions. Tunn. Undergr. Space Technol. 2021, 115, 104080. [Google Scholar] [CrossRef]
- Srilatha, N.; Latha, G.M.; Puttappa, C.G. Effect of frequency on seismic response of reinforced soil slopes in shaking table tests. Geotext. Geomembr. 2013, 36, 27–32. [Google Scholar] [CrossRef]
- Yang, G.X.; Qi, S.W.; Wu, F.Q.; Zhan, Z.F. Seismic amplification of the anti-dip rock slope and deformation characteristics: A large-scale shaking table test. Soil Dyn. Earthq. Eng. 2017, 115, 907–916. [Google Scholar] [CrossRef]
- Yang, Z.P.; Tian, X.; Jiang, Y.W.; Liu, X.R.; Hu, Y.X.; Lai, Y.L. Experimental study on dynamic characteristics and dynamic responses of accumulation slopes under frequent microseisms. Arab. J. Geosci. 2020, 13, 770. [Google Scholar] [CrossRef]
- Panah, A.K.; Eftekhari, Z. Shaking table tests on polymeric-strip reinforced-soil walls adjacent to a rock slope. Geotext. Geomembr. 2021, 49, 737–756. [Google Scholar] [CrossRef]
- Dong, J.Y.; Wang, C.; Huang, Z.Q.; Yang, J.H.; Xue, L. Shaking table model test to determine dynamic response characteristics and failure modes of steep bedding rock slope. Rock Mech. Rock Eng. 2022, 55, 3645–3658. [Google Scholar] [CrossRef]
- Kuo, C.-Y.; Chang, K.-J.; Tsai, P.-W.; Wei, S.-K.; Chen, R.-F.; Dong, J.-J.; Yang, C.-M.; Chan, Y.-C.; Tai, Y.-C. Identification of co-seismic groundmotion due to fracturing and impact of the Tsaoling landslide, Taiwan. Eng. Geol. 2015, 196, 268–279. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek–Brown failure criterion and GSI–2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Jaeger, J.C.; Cook, N.G.W.; Zimmerman, R. Fundamentals of Rock Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Bahaaddini, M.; Hagan, P.C.; Mitra, R.; Hebblewhite, B.K. Scale effect on the shear behaviour of rock joints based on a numerical study. Eng. Geol. 2014, 181, 212–223. [Google Scholar] [CrossRef]
- Goodman, R.E. Block theory and its application. Geotechnique 1995, 45, 383–423. [Google Scholar] [CrossRef]
- Sewnun, D.; Joughin, W.C.; Armstrong, R.; Cooper, A. Keyblock stability analysis of longhole stopes. In Proceedings of the ISRM AfriRock-Rock Mechanics for Africa, Cape Town, South Africa, 3–5 October 2017. ISRM-AFRIROCK-2017-087. [Google Scholar]
- Agliardi, F.; Crosta, G.B.; Meloni, F.; Valle, C.; Rivolta, C. Structurally-controlled instability, damage and slope failure in a porphyry rock mass. Tectonophysics 2013, 605, 34–47. [Google Scholar] [CrossRef]






| Property | Value | Unit | Remarks |
|---|---|---|---|
| Primary Composition | Ordinary Cement, Fine Sand, Water | - | Typical cement–mortar mixture |
| Mixture Proportion (by weight) | 1:2:0.45 | - | Cement:Sand:Water |
| Density (ρ) | 2250 ± 50 | kg/m3 | Measured |
| Uniaxial Compressive Strength (UCS, σc) | 18 ± 2 | MPa | Tested on 50 mm cubes |
| Young’s Modulus (E) | 18 ± 2 | GPa | Secant modulus at 50% of peak UCS |
| Cohesion (c) | 3.5 ± 0.5 | MPa | Derived from direct shear test on mortar specimens |
| Internal Friction Angle (φ) | 35 ± 2 | ° | Derived from direct shear test on mortar specimens |
| Category | Physical Quantity | Symbol | Scale Factor | Value |
|---|---|---|---|---|
| Geometry | Length | 1/100 | ||
| Angle | 1 | 1 | ||
| Material | Density | 1 | ||
| Unit Weight | 1 | |||
| Elastic Modulus | 1 | |||
| Poisson’s Ratio | 1 | 1 | ||
| Dynamic Loading | Acceleration | 1 | 1 | |
| Time | 1/10 | |||
| Frequency | 10 | |||
| Velocity | 1/10 | |||
| Displacement | 1/100 |
| Earthquake Intensity Accelerations | Frequency f (Hz) | Amplification A (mm) | |
|---|---|---|---|
| 8 | 0.2 g | 3 | 5.5 |
| 3.5 | 4 | ||
| 7 | 0.1 g | 3 | 2.76 |
| 2 | 6.2 | ||
| 6 | 0.05 g | 2 | 3.1 |
| 1.5 | 5.5 | ||
| Case ID | Block Size (cm) | Stacking Height (cm) | Nodal Angle (°) | PGA (g) | Primary Factor Investigated | |
|---|---|---|---|---|---|---|
| B | 3 | 30 | 80 | 0.1 | Baseline | |
| Variation in Block Size (Fragmentation Degree) | S1 | 1.5 | 30 | 80 | 0.1 | Block Size |
| S2 | 5 | 30 | 80 | 0.1 | ||
| Variation in Stacking Height | H1 | 3 | 27 | 80 | 0.1 | Stacking Height |
| H2 | 3 | 33 | 80 | 0.1 | ||
| H3 | 3 | 36 | 80 | 0.1 | ||
| Variation in Nodal Angle | A1 | 3 | 30 | 60 | 0.1 | Nodal Angle |
| A2 | 3 | 30 | 70 | 0.1 | ||
| A3 | 3 | 30 | 90 | 0.1 | ||
| Variation in Seismic Intensity (PGA) | P1 | 3 | 30 | 80 | 0.05 | PGA |
| P2 | 3 | 30 | 80 | 0.2 | ||
| Component | Parameter | Symbol | Value | Unit | Remarks/Source |
|---|---|---|---|---|---|
| Intact Rock | Density | ρ | 2650 | kg/m3 | Typical for sandstone/siltstone [52] |
| Young’s Modulus | E | 15 GPa | GPa | Estimated based on UCS and typical values for weak rock [52] | |
| Poisson’s Ratio | ν | 0.25 | - | Typical value [52] | |
| Uniaxial Compressive Strength (UCS) | σc | 40 | MPa | Representative of weak to medium rock [52] | |
| Discontinuities | Normal Stiffness | kn | 50 | GPa/m | Estimated based on joint properties and rock modulus [53] |
| Shear Stiffness | ks | 20 | GPa/m | Estimated based on joint properties and rock modulus [53] | |
| Cohesion | cj | 0.1 | MPa | Assumed low value for clean, non-persistent joints | |
| Friction Angle | ϕ | 30 | ° | Typical residual friction for rock joints [53] | |
| Tensile Strength | σt | 0 | MPa | Assumed zero for open/weathered joints | |
| Simulation Settings | Rayleigh Damping Ratio | ξ | 0.02 (2%) | – | Common value for geotechnical dynamic analysis [53] |
| Mesh Size (average) | - | 0.5 | m | Determined from mesh sensitivity analysis |
| Symbol | H1 (m) | H2 (m) | β (o) | d1 (m) | d2 (m) | b (m) | α (o) | λ (m/s2) |
|---|---|---|---|---|---|---|---|---|
| Significance | occurrence height of unstable rock mass | height of unstable rock mass | cliff slope angle | Interlayer spacing | Joint spacing | thickness of unstable rock mass | bedding plane inclination angle | seismic wave amplitude |
| Value range | 40~100 | 15~60 | 60~90 | 1~2 | 1~2 | 3~6 | −5~10 | 0.7~1.3 |
| No | H1 (m) | H2 (m) | β (o) | d1 (m) | d2 (m) | b (m) | α (o) | λ (m/s2) |
|---|---|---|---|---|---|---|---|---|
| 1–4 | 40, 60, 80, 100 | 15 | 0 | 1 | 1 | 3 | 0 | 0.9 |
| 5–8 | 40 | 15, 30, 45, 60 | 0 | 1 | 1 | 3 | 0 | 0.9 |
| 9–12 | 40 | 15 | 60, 70, 80, 90 | 1 | 1 | 4 | 0 | 0.9 |
| 12–16 | 100 | 15 | 0 | 1, 1.2, 1.5, 2 | 1, 1.2, 1.5, 2 | 6 | 0 | 0.9 |
| 17–20 | 40 | 15 | 90 | 1 | 1 | 6 | 0, 5, 10, −5 | 0.9 |
| 21–24 | 40 | 15 | 0 | 1 | 1 | 3, 4, 5, 6 | 0 | 0.9 |
| 25–28 | 60 | 15 | 0 | 1 | 1 | 3 | 0 | 0.7, 0.9, 1.1, 1.3 |
| Factors | Symbol | Observed Effect on Failure Mode | Failure Type Transition |
|---|---|---|---|
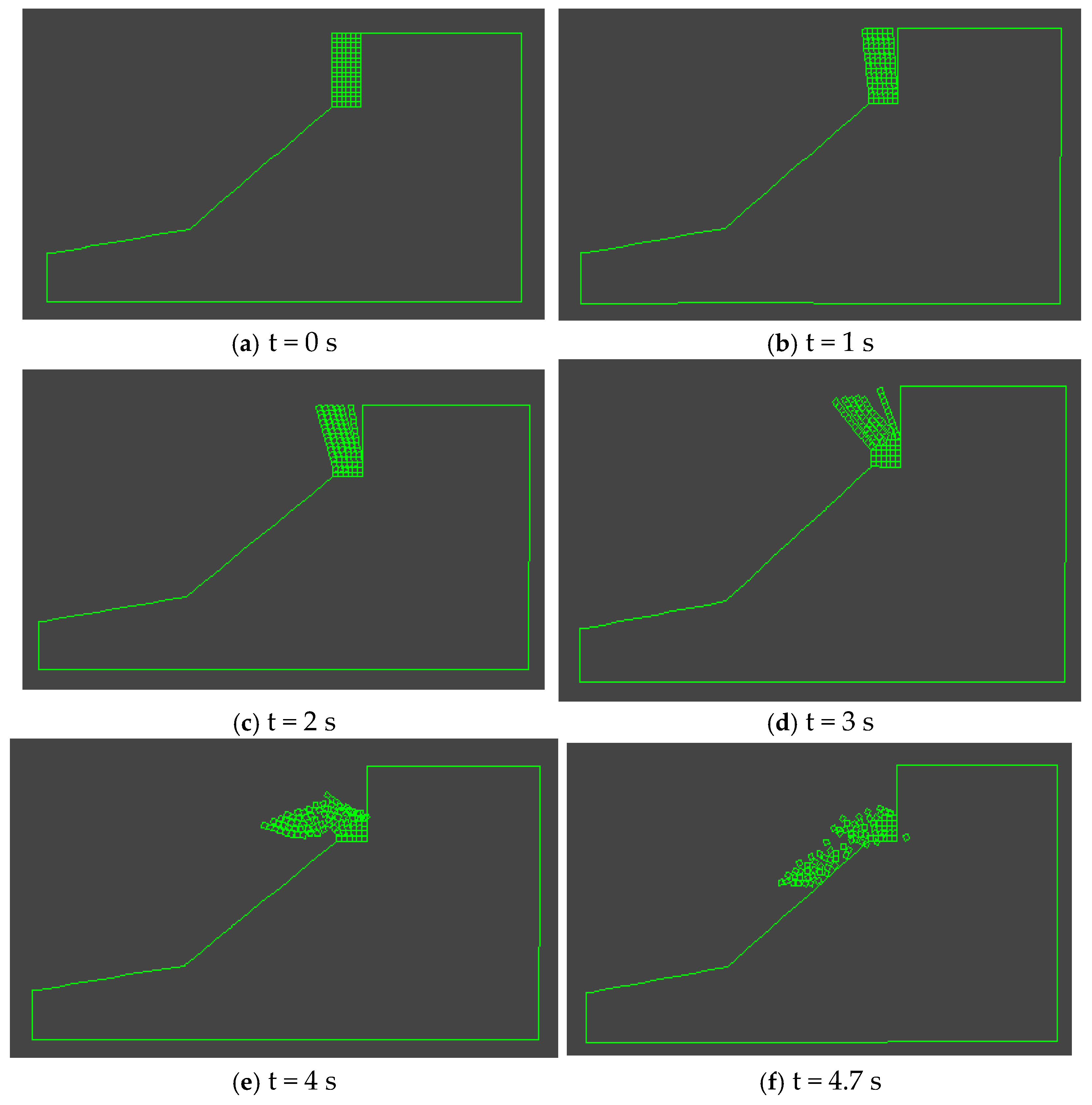
| Occurrence Height | H1 | The rock mass undergoes integral toppling failure above the one-third height point, while secondary collapse occurs below it, resulting in minimal residual blocks. | No |
| Block Height | H2 | H2 < 45 m: The upper section above the inflection point experiences integral toppling failure, while the lower section undergoes secondary collapse. H2 > 45 m: The failure pattern exhibits two inflection points, resulting in an S-shaped collapse trajectory. | Yes |
| Cliff Slope Angle | β | β > 80°: No significant relative displacement is observed between columns. The upper section experiences integral toppling failure, and the completeness of the collapse increases with the slope angle. β ≤ 80°: The slope exhibits relatively good stability. The outermost column develops an inflection point and undergoes toppling failure, followed by the second and third columns, resulting in progressive spalling-type collapse from the exterior inward. | Yes |
| Degree of Fragmentation | d1, d2 | When the rock mass is fragmented, it collapses in an irregular, granular manner, with a significant number of blocks remaining at the base, while the upper sections experience more complete collapse. When the rock mass is intact, it undergoes strip-shaped toppling failure along vertical joints, spalling from the free surface. Few blocks remain at the base, though those adjacent to the bedrock may remain stable without collapsing. | Yes |
| Rock Layer Thickness | b | b < 6 m: The upper section experiences integral toppling failure with no relative displacement between columns. b ≥ 6 m: Relative displacement occurs between columns. | Yes |
| Bedding Plane Inclination | α | The section above the inflection point experiences integral toppling failure. A lower dip angle results in a greater volume of residual blocks. | No |
| Seismic Wave Amplitude | λ | The integral toppling failure in the upper section triggers secondary collapse in the lower part. | No |
| Factors | Symbol | Starting Time of Collapse | Induces Change in Time |
|---|---|---|---|
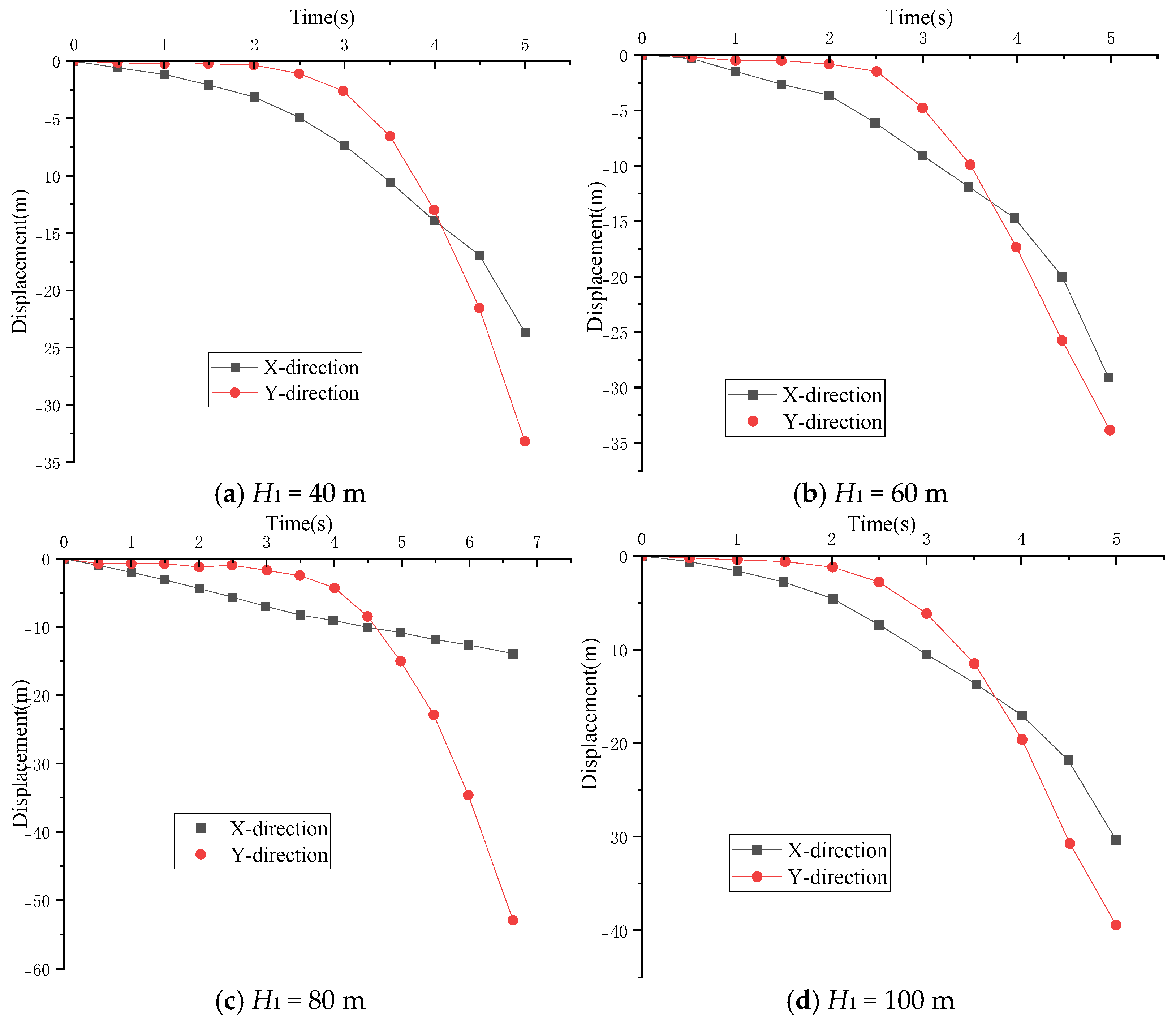
| Occurrence Height | H1 | H1 < 80 m, H1 is positively correlated with collapse time. H1 > 80 m, H1 is negatively correlated with collapse time. | Yes |
| Block Height | H2 | h < 45 m, h is positively correlated with collapse time. h > 45 m, No correlation between h and collapse time. | Yes |
| Cliff Slope Angle | β | β is negatively correlated with collapse time; A slope threshold exists between 60° and 70°. | Yes |
| Degree of Fragmentation | d1, d2 | The more fragmented the rock mass, the earlier the collapse initiation time. | Yes |
| Rock Layer Thickness | b | b shows no significant correlation with collapse time. | No |
| Bedding Plane Inclination | α | No Significant Impact. | No |
| Seismic Wave Amplitude | λ | Amplitude is positively correlated with collapse time. | Yes |
| Factors | Occurrence Height of Unstable Rock Mass | Height of Unstable Rock Mass | Thickness of Unstable Rock Mass | Degree of Rock Mass Fragmentation | Cliff Slope Angle | Bedding Plane Inclination Angle | Seismic Wave Amplitude |
|---|---|---|---|---|---|---|---|
| Symbol | H1 (m) | H2 (m) | β (o) | d1, d2 (m) | b (m) | α (o) | λ (m/s2) |
| Denoted as | F1 | F2 | F3 | F4 | F5 | F6 | F7 |
| Weight Value | 0.2778 | 0.2222 | 0.1667 | 0.1111 | 0.1111 | 0.0556 | 0.0556 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maimaiti, N.; Liu, R.; Zhang, P.; Qu, J. Factors Influencing the Seismic Collapse of Stratified Steep Cliffs Based on Analytic Hierarchy Process (AHP). Appl. Sci. 2025, 15, 12485. https://doi.org/10.3390/app152312485
Maimaiti N, Liu R, Zhang P, Qu J. Factors Influencing the Seismic Collapse of Stratified Steep Cliffs Based on Analytic Hierarchy Process (AHP). Applied Sciences. 2025; 15(23):12485. https://doi.org/10.3390/app152312485
Chicago/Turabian StyleMaimaiti, Naman, Ruiming Liu, Peng Zhang, and Jili Qu. 2025. "Factors Influencing the Seismic Collapse of Stratified Steep Cliffs Based on Analytic Hierarchy Process (AHP)" Applied Sciences 15, no. 23: 12485. https://doi.org/10.3390/app152312485
APA StyleMaimaiti, N., Liu, R., Zhang, P., & Qu, J. (2025). Factors Influencing the Seismic Collapse of Stratified Steep Cliffs Based on Analytic Hierarchy Process (AHP). Applied Sciences, 15(23), 12485. https://doi.org/10.3390/app152312485





