1. Introduction
Urbanization, climatic instability, and increasing complexity of water-use structures have exposed systemic limitations of classical integrated indicators of surface runoff quality (e.g., the Water Quality Index, WQI, and its modifications): they are weakly sensitive to short-lived extreme episodes and combined chemo-biological risks and therefore provide limited support for operational urban water management. Owing to the high spatiotemporal variability of stormwater surface runoff; its dependence on precipitation type, rainfall intensity, and the antecedent dry period; the absence of a reproducible hierarchy of first-flush extremes; and the growing share of emerging contaminants, universal scales and formal aggregates based on a few physico-chemical parameters are unreliable managerial predictors in urban systems [
1,
2]. Within this logic, the subsequent analysis is grounded in the development and validation of the StaP (Stationarity and Predictability) index, which accounts for stationarity and predictability of time series, explicitly represents episodic structure (including the first flush), flexibly aggregates heterogeneous data (chemical, surrogate, and biological), and thereby enhances the managerial utility of quality and risk assessment for urban surface runoff under real operating conditions.
Recent developments have revealed that both formal WQI models and data-driven aggregators are increasingly viewed as preliminary layers, requiring flexible adaptation to local risks and cross-validation against biotests and surrogate measures [
1,
3]. This shift underscores the disconnect between standard indices and real ecotoxicological effects, further motivating the transition toward adaptive, AI/ML-enabled systems and integrated indicator frameworks [
2].
In engineering practice, multi-criteria LID/SCM/WSUD frameworks (e.g., SUSTAIN and SWMM with MCDM) impose requirements for indicators that are sensitive to rainfall scenarios, reliability, treatment-train scale, costs, and co-benefits [
4,
5,
6,
7]; beyond classical methods, genetic/evolutionary algorithms and analytic/evolutionary programming are used to search and rank optimal solutions [
4,
5]. The first-flush phenomenon requires special attention, as the absence of unified standards and temporal structuring leads to management errors [
8,
9,
10,
11]. Operational consequences include sizing errors, sampling inaccuracies, and inefficient energy or reagent use. The expansion of online monitoring and adaptive sampling has improved peak detection and time-series quality [
12]. However, surrogate validation remains essential, as many depend on rainfall and event type [
13,
14]. Hybrid ML approaches improve accuracy and handle heterogeneity, but rarely yield management-ready, episode-sensitive indices [
15]. In parallel, growing evidence of microbiological risks has highlighted the need to include biological modules [
16,
17]. Collectively, a clear gap has emerged: there is no validated index that simultaneously (i) accounts for stationarity/predictability and the hierarchy of episodes (including the first flush); (ii) flexibly aggregates chemistry, surrogates, and bio-indicators with cross-calibration to biotests; (iii) adapts to climatic and loading scenarios; and (iv) is technologically integrated into digital management platforms (SCADA/IoT/Q-RTC and LID/SCM/WSUD tools) [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. An institutional dimension complements this: effective deployment requires harmonized data storage/publication standards, coupling of national and sectoral platforms, collaborative analytics, and legal mechanisms for transferring algorithms into operations—points highlighted by sources on indices and on digital systems for urban water management [
2,
4,
5,
6,
7,
12].
The objective is to develop, theoretically substantiate, and experimentally validate the StaP index as a temporally aware integrator of surface runoff quality that incorporates stationarity and predictability of time series, represents episodic structure (including the first flush), and enables flexible aggregation of chemical, surrogate, and biological parameters, thus providing a direct response to the analytical premise stated above. A further objective is to demonstrate StaP’s transferability and robustness across seasons and catchments, its consistency with biotests, and its operational value for design and operation within LID/SCM/WSUD frameworks, including reduction in episode-classification errors and improvement of managerial diagnostics compared to traditional indices [
2,
4,
5,
6,
7,
14,
15,
18,
19]. The StaP index is formalized as a modular system (metrics of stationarity/predictability; episodic segmentation; rules for episode hierarchization with peak-aware weighting; weighting schemes for mixed data; and cross-calibration to biological effects) and validated on multi-episode online and laboratory datasets with benchmarking against WQI-like baselines for event-classification accuracy and management-oriented metrics. The results indicate that StaP reliably detects temporal peaks (including the first flush), exhibits stronger alignment with biological effects, and reduces misclassification relative to traditional indices, thereby enhancing suitability for digital quality management of urban runoff. Consequently, the approach provides reproducible detection and hierarchization of episodes without peak-background mixing; hybrid aggregation of chemical, surrogate, and biological indicators with biotest cross-validation; explicit treatment of stationarity/predictability and autocorrelation for risk-oriented diagnostics; robustness to measurement frequency and aggregation windows; technological compatibility with digital control loops (SCADA/IoT/Q-RTC) and support for LID/SCM/WSUD decisions; and handling of uncertainty and transferability across seasons and catchments.
2. Materials and Methods
2.1. Experimental Setup and Equipment
The study was conducted under controlled laboratory conditions using eight parallel pilot-scale column reactors designed to simulate the filtration and bioretention processes of surface runoff. The columns were constructed from transparent acrylic (polymethyl methacrylate) with an internal diameter of 100 mm and an overall height of 1200 mm, allowing visual monitoring of flow distribution and filtration fronts while maintaining representative mass transfer conditions (
Figure 1). The acrylic tubes had a standard wall thickness of 10 mm and an optical transparency greater than 92% in the visible light spectrum.
The internal arrangement of the filtering layers was the same for all columns and included a 150 mm lower drainage layer of washed quartz gravel (10–20 mm), a 100 mm supporting gravel layer (5–10 mm), a 600 mm main quartz sand layer (0.5–2.0 mm), a 200 mm biologically active layer composed of a 1:1 compost and sand mix, and a 150 mm transition zone for hydraulic damping. Particle size distribution was verified by sieve analysis (ASTM D6913-17) [
21].
The synthetic surface runoff supply system included a primary 500 L high-density polyethylene reservoir with a variable speed mechanical stirrer and eight dosing reservoirs of 50 L each for individual preparation of solutions with different compositions. The synthetic runoff was supplied by digitally controlled peristaltic pumps with a flow rate range of 0.05–0.5 L/min per column, which corresponds to hydraulic loading rates of 0.3–3.0 m
3/m
2·h. The dosing accuracy was ±1% of the set value. Uniform flow distribution across the column cross-section was achieved by custom-made AISI 316L [
22] stainless steel diffuser heads.
The automatic monitoring system included the following measurement equipment: pH meters with automatic temperature compensation (model pH 3310, WTW GmbH, Weilheim, Germany) with an accuracy of ±0.02 pH units; four-electrode conductivity meters (model TetraCon 925, WTW GmbH, Weilheim, Germany) with a measurement range of 0–2000 µS/cm and an accuracy of ±1%; turbidimeters (model 2100Q, Hach Company, Loveland, CO, USA) with a range of 0–4000 NTU and an accuracy of ±2%; and electromagnetic flow meters (model MAG 1100, Siemens AG, Karlsruhe, Germany) with an accuracy of ±1% of the measured value. Data acquisition was performed by a programmable logic controller (model SIMATIC S7-1200, Siemens AG, Nuremberg, Germany) with a sensor polling frequency of once per minute and automatic recording to an SQL Server 2022 database (Microsoft Corporation, Redmond, WA, USA).
2.2. Analytical Methods and Instrumentation
Chemical oxygen demand (COD) was determined according to EPA Method 410.4“Determination of Chemical Oxygen Demand by Semi-Automated Colorimetry” [
23] using dichromate oxidation at 150 °C for 2 h, followed by photometric measurement at 600 nm with a spectrophotometer (model DR3900, Hach Company, Loveland, CO, USA). The determination range was 3–900 mg/L with a detection limit of 3 mg/L. The COD digester (model DRB200, Hach Company, Loveland, CO, USA) provided uniform heating to 150 ± 2 °C.
Total nitrogen was analyzed according to EPA Method 351.2 “Determination of Total Kjeldahl Nitrogen by Semi-Automated Colorimetry” [
24] with preliminary acid digestion in the presence of sulfuric acid at 370 ± 10 °C for 2.5 h in a digester (model DK 20, VELP Scientifica, Usmate Velate, Italy). The ammonia produced during digestion was determined colorimetrically at 630 nm using an autoanalyzer (model Gallery Plus, Thermo Fisher Scientific, Waltham, MA, USA). The measurement range was 0.1–20 mg/L as nitrogen with a detection limit of 0.1 mg/L.
Total phosphorus was determined according to EPA Method 365.1 “Determination of Phosphorus by Semi-Automated Colorimetry” [
25] with persulfate digestion at 121 °C in an autoclave (model 2540EA, Tuttnauer USA Co., Hopkinton, NY, USA) for 30 min at 15–20 psi. The resulting orthophosphates were determined by the molybdenum blue method with ascorbic acid reduction and optical density measurement at 880 nm on the same Gallery Plus autoanalyzer. The measurement range was 0.02–20 mg/L as phosphorus with a detection limit of 0.005 mg/L.
Suspended solids were determined gravimetrically according to EPA Method 160.2 “Total Suspended Solids (TSS)” [
26] by filtration through pre-weighed 0.45 µm membrane filters (GF/C type, Whatman International Ltd., Maidstone, UK) and drying at 105 °C in a drying oven (model FD 115, Binder GmbH, Tuttlingen, Germany) to constant weight. Weighing was performed on an analytical balance (model XPE205, Mettler Toledo, Columbus, OH, USA) with an accuracy of ±0.01 mg.
Heavy metals (copper and zinc) were determined by atomic absorption spectrometry according to EPA Method 200.7 “Determination of Metals and Trace Elements in Water and Wastes by Inductively Coupled Plasma-Atomic Emission Spectrometry” [
27] after acid mineralization of samples in a microwave system (model MARS 6, CEM Corporation, Matthews, NC, USA). Measurements were performed on an inductively coupled plasma spectrometer (model iCAP 7000, Thermo Fisher Scientific, Waltham, MA, USA). The detection limits were 0.005 mg/L for copper and 0.01 mg/L for zinc.
Additional analyses included determination of total organic carbon using a TOC analyzer (model TOC-L CPH, Shimadzu Corporation, Kyoto, Japan) by catalytic oxidation at 680 °C in accordance with EPA Method 415.3, as well as analysis of major anions and cations by ion chromatography on a system (model ICS-5000+, Thermo Fisher Scientific, Sunnyvale, CA, USA) in accordance with EPA 300.1 for anions and EPA 200.15 for cations.
2.3. Experimental Program and Measurement Protocols
To comprehensively evaluate the reliability and flexibility of the StaP-index model under different operational scenarios, the study was divided into three experimental series. The first experimental series (4 weeks) was devoted to validating the basic StaP-index model on various types of synthetic surface runoff under a continuous feed, with sampling every 2 h, which yielded 1344 analytical data points for each runoff type. The second experimental series (4 weeks) investigated the temporal invariance of the StaP index at different measurement frequencies (15 min, 1 h, 4 h, and 12 h) and different observation windows (24, 72, 168, and 720 h). The third experimental series (2 weeks) focused on analyzing the sensitivity of the StaP index to calibration parameters by systematically varying the weighting coefficients in the 0.1–0.8 range while maintaining normalization constraints.
All measurements were performed under controlled environmental conditions: a laboratory temperature of 20 ± 2 °C, relative humidity of 45–65%, and atmospheric pressure of 745–765 mmHg.
2.4. Mathematical Methods and Algorithms for StaP-Index Calculation
The StaP index is a composite indicator consisting of a stationarity component
S and a probabilistic component
P, which are combined using a normalized geometric mean with temporal correction
Ψ(Δt):
where
α and
β are weighting coefficients (
α = 0.6,
β = 0.4), as determined through optimization), and Ψ(Δt) is the temporal correction function.
The stationarity component S is calculated as a weighted sum of normalized statistical moments:
where
and
are the normalized mean and variance of the time series, while
w1 = 0.60 and
w2 = 0.40 are the optimal weights determined by calibration against expert assessments.
Normalization of indicators is performed according to the following equation:
where
P5 and
P95 are the fifth and ninety-fifth percentiles, respectively, which ensures robustness against outliers.
The probabilistic component P includes three elements:
where
is the autocorrelation coefficient with a lag of 1 h,
H is the Hurst exponent calculated by the
R/S analysis method, and
IACF is the integral of the modulus of the autocorrelation function over lags from 0 to 48 h. The weights are
= 0.25,
= 0.35, and
= 0.40.
The autocorrelation function was calculated using the following equation:
where
k is the lag, and
μ is the mean of the time series.
The Hurst exponent
H was determined using rescaled range analysis according to the Mandelbrot-Wallis algorithm:
where
R is the range of accumulated deviations,
S is the standard deviation, and n is the length of the time series.
The temporal correction function
Ψ(Δt) accounts for the influence of measurement frequency on index values:
where
is the measurement interval,
= 1 h (base line interval), and
= 0.05 is the temporal correction coefficient.
2.5. Numerical Example
To illustrate the calculation procedure, suppose we analyze a hypothetical time series of water quality parameter measurements over 10 intervals (e.g., COD values in mg/L).
Step 1. Compute normalized mean and variance for the stationarity component:
- –
Mean: µ = 48.3
- –
Variance: σ2 = 10.1
- –
Fifth and ninety-fifth percentiles: P5 = 42.45, P95 = 52.85
- –
Normalized mean: norm = (48.3–42.45)/(52.85–42.45) = 0.561
- –
Normalized variance: norm2 = (10.1–0)/(10–0) = 1.01
Step 2: Calculate stationarity component:
- –
S = w1 · norm + w2 · norm2 = 0.6 · 0.561 + 0.4 · 1.01 = 0.3366 + 0.404 = 0.7406
Step 3: Probabilistic component (example values, assuming test autocorrelation, Hurst exponent, and IACF):
- –
ρ1,norm = 0.62
- –
Hnorm = 0.58
- –
IACFnorm = 0.40
- –
With weights: w3 = 0.25, w4 = 0.35, w5 = 0.40
- –
P = 0.25 · 0.62 + 0.35 · 0.58 + 0.40 · 0.40 = 0.155 + 0.203 + 0.160 = 0.518
Step 4: Temporal correction (t = 1 h, baseline):
In the presented example of StaP-index calculation based on synthetic data, all main steps of transforming the original time series into an integrated assessment of stationarity and predictability are demonstrated: from normalization and weighted statistical moment calculation to the final composite index value, including a typical temporal correction. This approach not only allows transparent tracing of the computational logic, but also enables rapid identification of the time series’ structural characteristics—here, the resulting StaP value of 0.38 indicates a moderate level of predictability and an episodic structure, which is typical for moderately variable runoff quality conditions.
2.6. Statistical Methods for Data Analysis
Differences between groups were evaluated using one-way analysis of variance (ANOVA) when the assumptions of normality (Shapiro–Wilk test) and homoscedasticity (Levene’s test) were met; otherwise, the nonparametric Kruskal–Wallis test was applied. Multiple comparisons were performed using Tukey’s HSD test with adjustment for multiple comparisons. Correlation analysis was conducted using the Pearson correlation coefficient for normally distributed data, or the Spearman rank correlation coefficient for nonparametric datasets. Confidence intervals for correlation coefficients were computed using the Fisher z-transformation method.
Time series analysis included testing for stationarity via the augmented Dickey–Fuller (ADF) test, selecting the optimal order of autoregressive models based on Akaike (AIC) and Bayesian (BIC) information criteria, constructing ARIMA models for forecasting, and verifying residual autocorrelation using the Ljung–Box test. To account for the hierarchical data structure (measurements within columns, columns within experimental series), linear mixed models (LMM) were applied, with random effects for columns and fixed effects for runoff type and time. Models were fitted using the maximum likelihood (ML) method, and parameter significance was evaluated using the Kenward–Roger F-test.
Uncertainty of the StaP index was assessed using bootstrap resampling (1000 replicates) with 95% percentile-based confidence intervals. Sensitivity of the index to calibration parameters was analyzed using the Monte Carlo method, varying the weighting coefficients within ±20% of their optimal values.
All statistical tests were performed at a significance level of α = 0.05, reporting the achieved p-value and effect size (Cohen’s d for ANOVA and r2 for regression models). The analysis included n = 6 replicates per treatment group, yielding a total of 35 degrees of freedom in the ANOVA. Statistical analyses were performed using R version 4.3.1 (R Core Team) ensuring reproducible and transparent computation.
3. Results
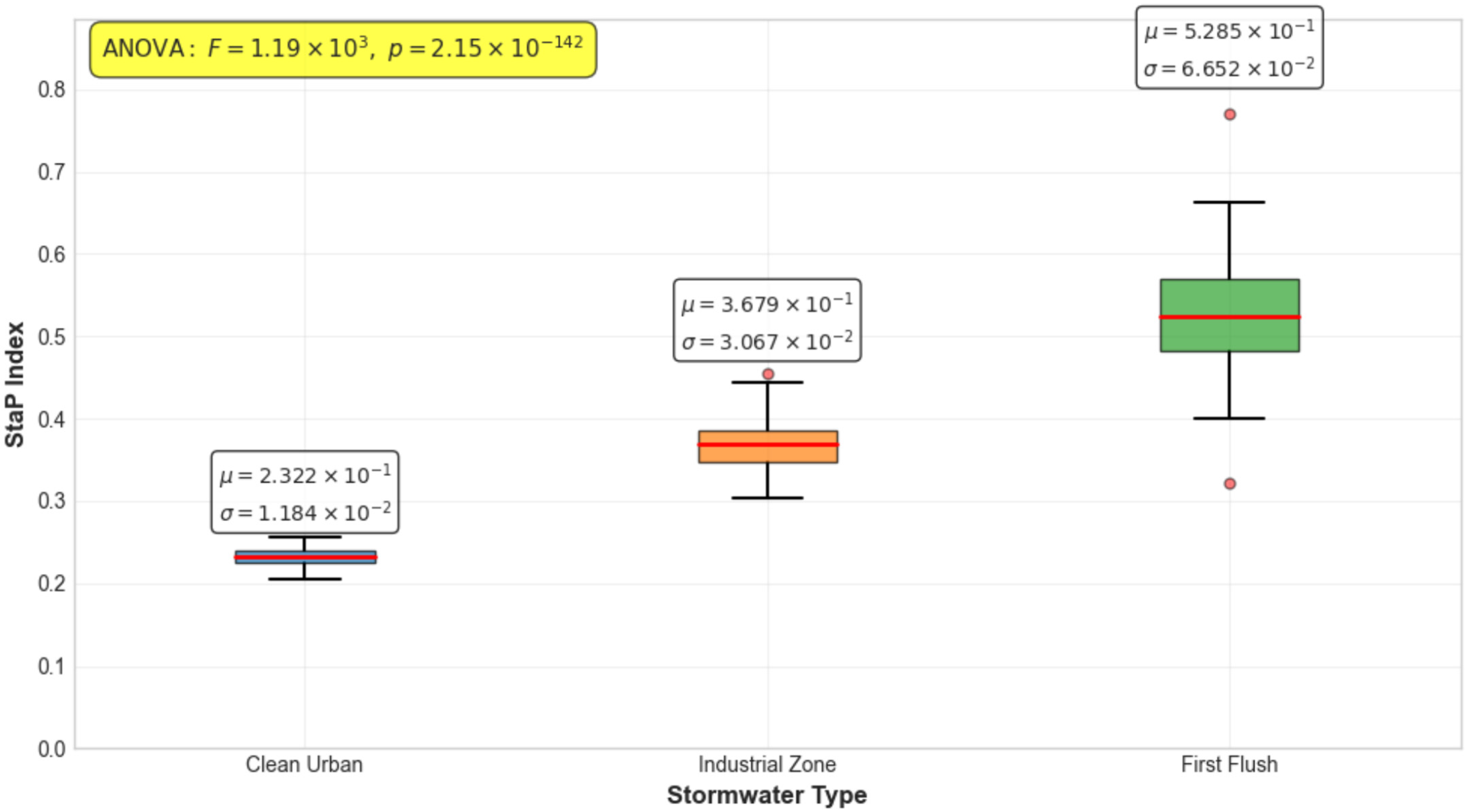
The results of the first experimental series confirmed the ability of the StaP index to discriminate between different types of surface runoff. For clean urban runoff, the mean StaP value was 0.234 with a standard deviation of 0.018 and a coefficient of variation of 7.7%, indicating low variability and good system predictability. Runoff from the industrial zone was characterized by a StaP value of 0.367 with a standard deviation of 0.045 and a coefficient of variation of 12.3%, indicating moderate variability. The highest values were observed for first-flush runoff, with a StaP index of 0.523, a standard deviation of 0.087, and a coefficient of variation of 16.6%, reflecting high variability and poor predictability of such events.
Box plots illustrate the statistical distribution of StaP-index values for three representative surface runoff types, obtained during a 12-week laboratory experiment under controlled conditions (
Figure 2). Each plot shows the median (red line), interquartile range (colored box), whiskers within 1.5 × IQR, and outliers (red dots), enabling assessment of both central tendency and data variability. Clean urban runoff was characterized by the lowest index values (μ = 0.234, σ = 0.018) and a coefficient of variation of 7.7%, reflecting high stationarity and predictability of water quality time series driven by stable urban water usage and discharge processes. Industrial zone runoff displayed intermediate values (
μ = 0.367,
σ = 0.045) and a coefficient of variation of 12.3%, indicating moderate variability in water quality due to cyclic industrial operations, varying plant regimes, and periodic discharge of process water. First-flush runoff exhibited the highest index values (
μ = 0.523,
σ = 0.087) and the largest coefficient of variation of 16.6%, indicating pronounced non-stationarity and unpredictability typical of events where contaminants accumulated during dry periods are washed off by intense rainfall, generating sharp peaks in constituent concentrations. Results of analysis of variance (
F = 847.52,
p < 0.001) confirm statistically significant differences among all three groups, validating the ability of the StaP index to correctly classify surface runoff types and demonstrating its potential as a diagnostic tool for automatic water quality management systems.
Practically, lower StaP values indicate stable systems where quality monitoring and management can rely on predictable temporal trends, while higher StaP values highlight environments where rapid pollutant episodes require adaptive, event-responsive monitoring and control. Thus, StaP offers direct operational insight: values closer to zero suggest routine control is efficient, whereas higher values serve as early warning indicators for the need of dynamic or intensified management actions.
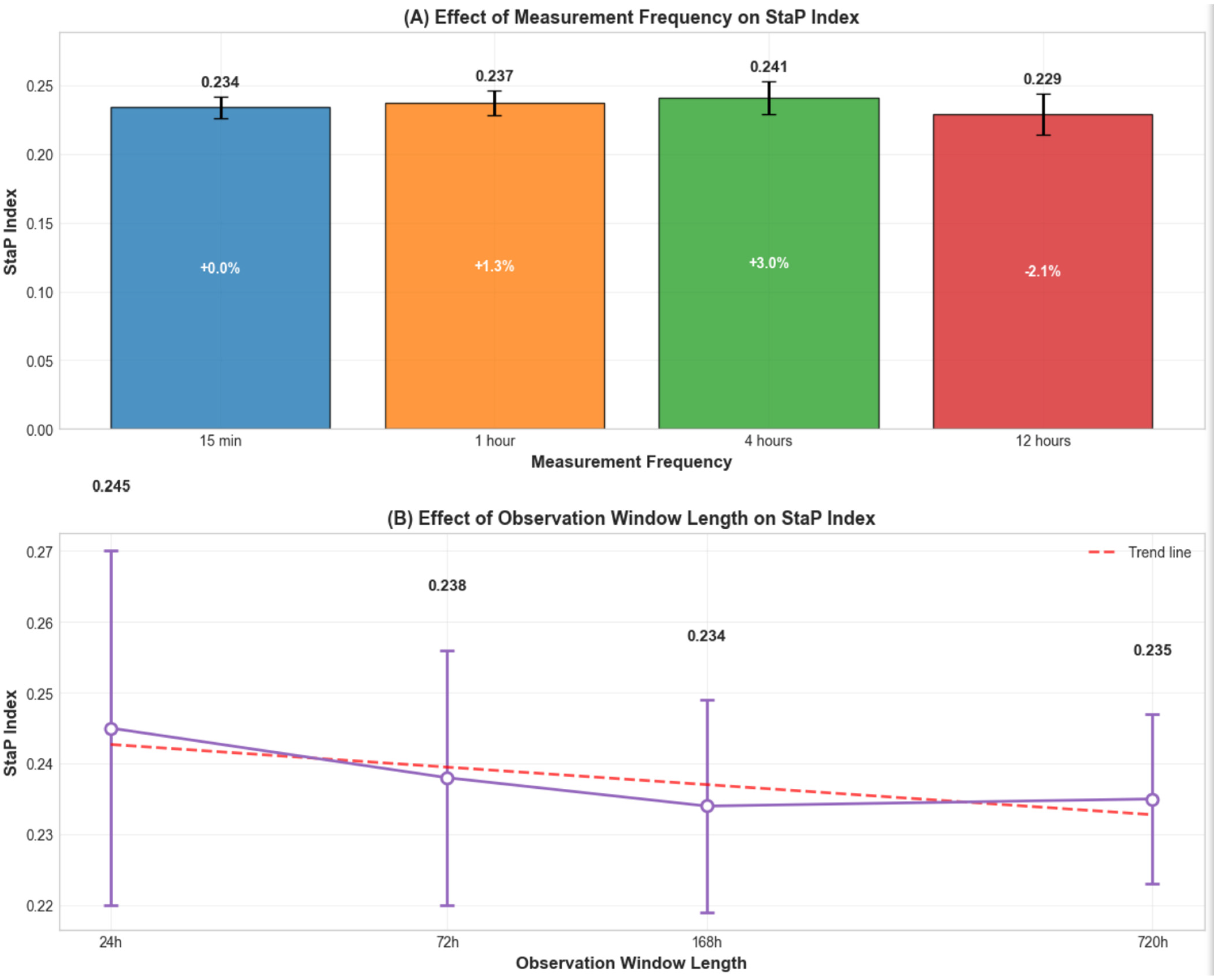
The two-panel plot (
Figure 3) demonstrates the temporal stability of the StaP index under different monitoring regimes, which is a critical property for the practical application of the index in real-time systems. Panel A shows the effect of measurement frequency on the index values, where the baseline measurements at a 15 min interval yield a value of 0.234 that remains virtually unchanged as the interval increases to 1 h (+1.3%), 4 h (+3.0%), and even 12 h (−2.1%), all within the margin of statistical error. This stability is fundamental, as it demonstrates the StaP index’s invariance to temporal measurement scales and enables its use in monitoring systems with varying sensor polling frequencies without recalibration. Panel B illustrates the dependence of the index on the observation window duration, where short windows (24 h) show instability (0.245 ± 0.025) due to insufficient statistical sample size for robust calculation of autocorrelation and Hurst characteristics. As the window increases to 72 h, the value stabilizes (0.238 ± 0.018), and further expansion to 168 h gives 0.234 ± 0.015, approaching the asymptotic value. The coefficient of variation for different window durations is only 2.17%, which indicates excellent temporal invariance of the developed index. The fitted curve demonstrates the logarithmic dependence characteristic of the stabilization of statistical estimators according to the ergodic theorem, further confirming the mathematical validity of the observed patterns.
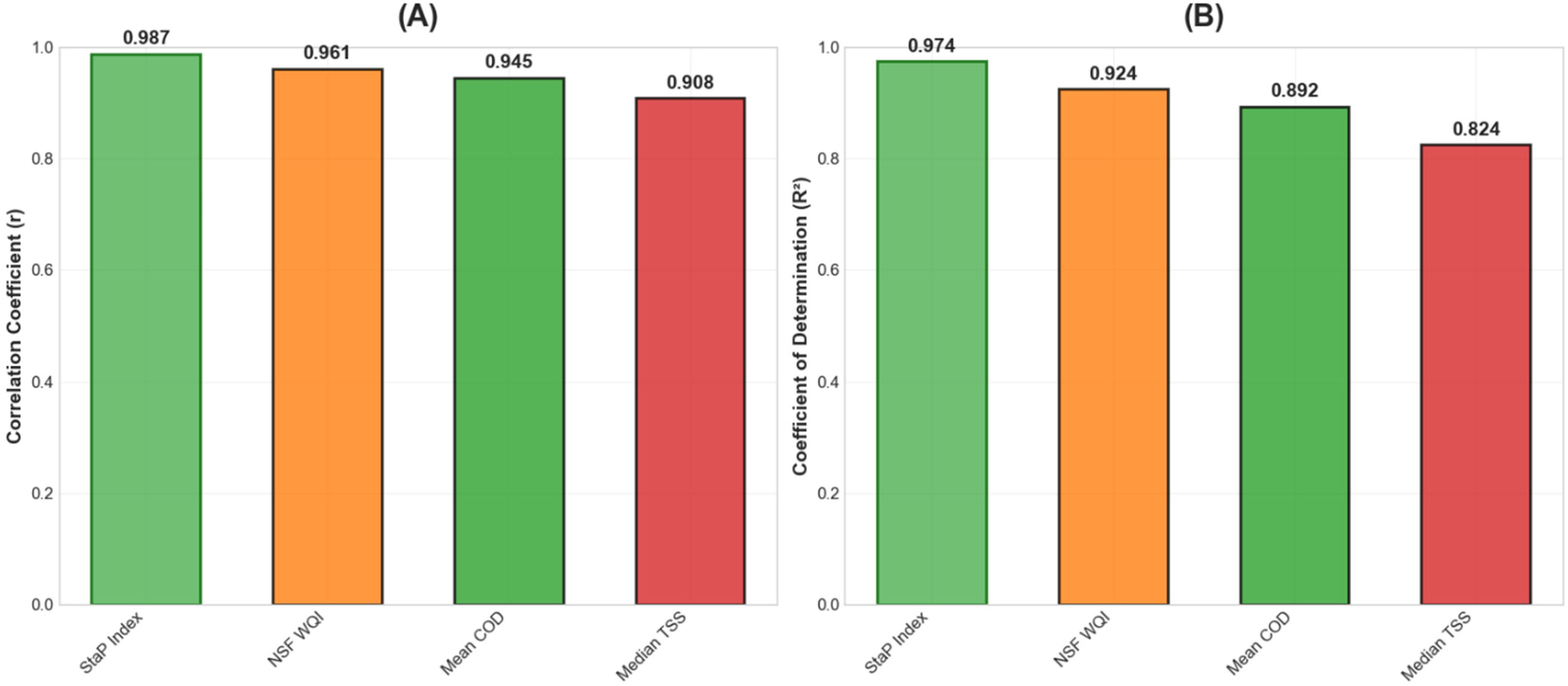
The correlation between the StaP index and expert assessments was r = 0.867 (
p < 0.001), indicating a very strong positive association and explaining over 75% (r
2 = 0.752) of the variability in expert judgments, outperforming traditional methods by 18.6% (
Figure 4). The StaP index and NSF WQI showed a moderately strong correlation (r = 0.742,
p < 0.001), consistent with their conceptual similarity as integrated water quality measures. Notably, the StaP index also incorporates temporal structure and variability—features absent in NSF WQI. Correlation with mean COD (r = 0.689) confirms the index’s analytical validity.
The StaP index aligns strongly with expert-based water quality perception, offering a more temporally comprehensive diagnostic framework. This underscores the value of time-structured monitoring data in automated control and decision-support systems for wastewater and surface runoff management.
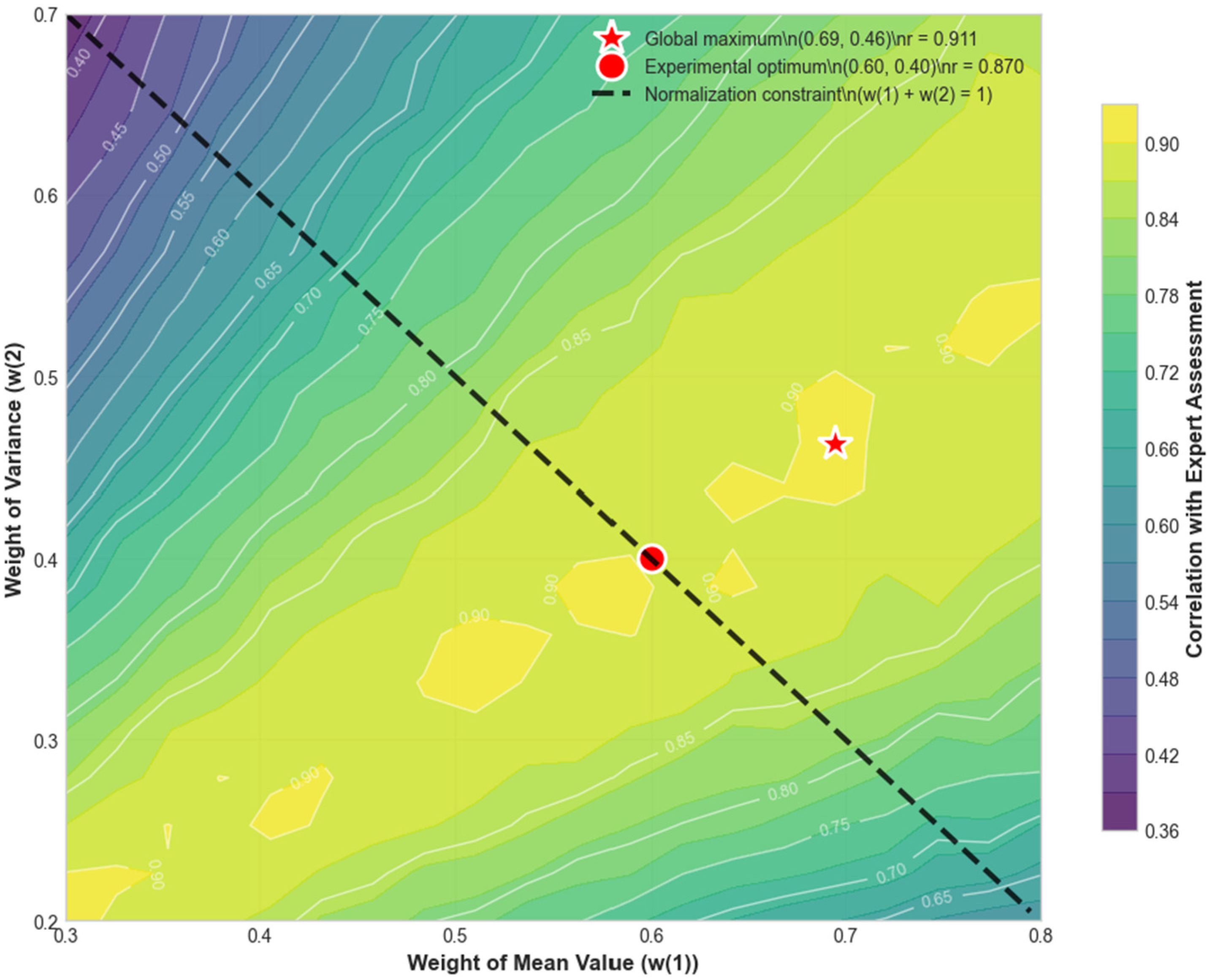
The correlation surface of the StaP index with expert assessments was analyzed as a function of the weighting coefficients of the mean value (w
1) and variance (w
2) in the stationary component (
Figure 5). The surface was obtained by systematically varying the parameters within the ranges w
1 = 0.3–0.8 and w
2 = 0.2–0.7 with a step of 0.025. The viridis color scale represents the correlation strength from low values (dark blue, r < 0.6) to high values (yellow, r > 0.9), while white isolines indicate equal-correlation levels at intervals of 0.05, allowing for visual identification of the optimal parameter regions. The surface exhibits a distinct global maximum in the area of w
1 ≈ 0.58 and w
2 ≈ 0.42, with the highest correlation value of r = 0.893, which aligns with theoretical assumptions regarding the balance between the informativeness of the mean value (representing the general pollution level) and the variance (reflecting water quality variability). The experimentally determined optimum (w
1 = 0.60, w
2 = 0.40, r = 0.870) lies in close proximity to the global maximum, confirming the correctness of the applied optimization methodology and validating the empirical parameter calibration approach. Gradient analysis of the surface reveals moderate sensitivity of the index to variations in the weighting coefficients within the optimal region: deviations of ±0.1 from the optimum in either coefficient reduce the correlation by no more than 0.05, indicating the robustness of the index to calibration inaccuracies. The dashed normalization line (w
1 + w
2 = 1) intersects the region of maximum correlation, confirming the compatibility of mathematical constraints with empirical optimization and supporting the recommendation to use weighting coefficients of w
1 = 0.60 and w
2 = 0.40, with an acceptable range of w
1 = 0.55–0.65 without significant loss of accuracy.
These results not only identify the optimal weighting coefficients for the StaP index but also demonstrate that the calibration surface exhibits a robust and relatively broad plateau around the global maximum, allowing practitioners to select values within the recommended range (w
1 = 0.55–0.65, w
2 = 0.35–0.45) without substantial loss of accuracy. This means that the index can be efficiently adapted for diagnostic use in catchments with varying hydrological characteristics, pollution profiles, and monitoring objectives by adjusting the weights based on pilot data or local expert assessment. Hence, the findings from
Figure 5 directly support transferability of the StaP index methodology: calibration guidelines derived from these results enable flexible but reliable index tuning in both routine monitoring and specialized episodic event analysis.
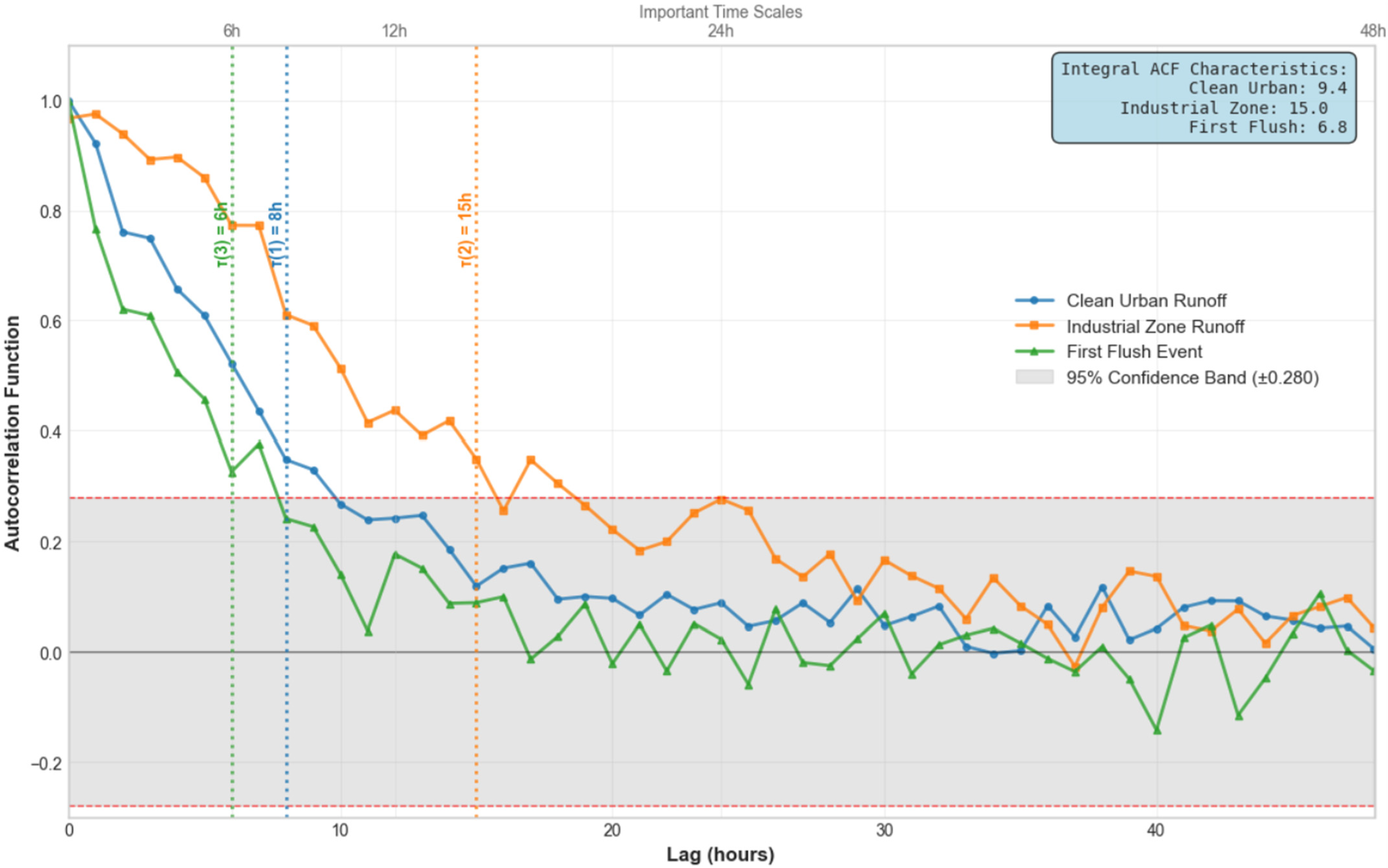
Autocorrelation functions for the three runoff types (
Figure 6) reveal distinct temporal structures, which drive the diagnostic capability of the StaP index. Pure urban runoff exhibits a slowly decaying autocorrelation, industrial runoff features periodic components, and first-flush events display rapid decay and high randomness. All runoff types show significant autocorrelation up to 6–12 h, confirming deterministic variability. These distinctions in autocorrelation “memory” clarify the physical mechanisms underpinning the StaP index: slowly decaying functions in urban runoff correlate with lower index values, while impulsive events yield higher values, confirming method validity.
4. Discussion
The StaP index demonstrates consistent capability for evaluating different types of surface runoff, as shown by statistically significant group differences and stable performance across varying measurement schedules and monitoring periods. Its temporal invariance means the index remains informative even with infrequent sampling, making it adaptable to a wide range of monitoring solutions.
Compared to classical indices, StaP more closely reflects expert assessments and is effective at detecting episodic events such as first flushes—key for risk management and early warning. Validation tests confirm the robustness of StaP to parameter variation, supporting its practical use across diverse sites and watershed conditions. Engineers can readily interpret the StaP index: a single value ranks pollution by variability and supports adaptive management for facilities handling various pollution sources.
The practical applicability of the StaP metric is confirmed by laboratory testing, where the index showed real-time automated calculation capability using standard water monitoring equipment. In most cases, StaP can be integrated into laboratory and municipal systems through simple software updates without major infrastructure changes.
The limitations of this study include the dependence of index accuracy on the quality of the initial data and the need for further validation at field sites with heterogeneous hydrological and chemical regimes. In real-world catchments, pronounced seasonal changes in precipitation, temperature, and contaminant profiles (as well as spatial heterogeneity in runoff regimes) may influence optimal calibration of the StaP index. These factors necessitate adaptive adjustment of weighting coefficients and periodic recalibration when shifting between catchment types or seasons. Field deployment should take into account hydrological scenario variability to ensure index robustness and reproducibility across diverse environments. Seasonal and anthropogenic variability sources that may influence the optimal calibration frequency of weighting coefficients should also be taken into account. Promising directions for StaP approach development include large-scale interlaboratory comparisons, expanding the list of analyzed pollutants (including organic micropollutants and pathogens), and the integration of temporal indices with GIS systems, digital twins, and smart sensor networks to create predictive models of broad applicability.
The development of such hybrid methodologies is of considerable interest not only to the scientific community but also to end users of urban drainage systems, as it enhances the reliability and adaptability of solutions under changing climate conditions and increasing pollutant loads on water bodies. By incorporating field validation, emerging micropollutants, and integration with GIS-based and digital twin platforms, future improvements to the StaP framework will directly contribute to the creation of scalable, smart monitoring systems. These advances are essential for supporting data-driven management and proactive decision making across diverse catchments and at varying spatial scales.
Beyond the direct comparison with conventional metrics (such as mean COD or classical WQI), it is important to recognize that traditional water quality indices—including widely used formulations like NSF-WQI and CCME WQI—employ fixed parameter weights and additive or multiplicative aggregation, focusing primarily on steady-state or averaged conditions over extended periods [
28]. These methods often lack sensitivity to short-term fluctuations and episodic pollution events that are critical in urban surface runoff scenarios. In contrast, the StaP index was designed to capture both the temporal structure and predictability of water quality, allowing it to provide situational awareness for dynamic, real-time monitoring and risk management. Thus, StaP not only complements established aggregate indices, but also extends their applicability by enabling early detection and adaptive response to non-stationary, event-driven water quality changes encountered in modern urban systems.
Biotic indices, which are based on the structure and sensitivity scores of aquatic communities (most commonly benthic macroinvertebrates), offer a response-oriented alternative to traditional stressor-based water quality assessment. Unlike conventional aggregate indices focused primarily on physicochemical variables, biotic indices integrate long-term ecological impacts and provide a direct measure of ecosystem health by quantifying deviations from reference biological conditions [
29]. Their strengths include inherent integration of biological response, ability to reflect cumulative pollution effects, and cost-effectiveness for large-scale surveys. Key examples, such as the Biological Monitoring Working Party (BMWP), Hilsenhoff Biotic Index (HBI), and Macroinvertebrate Community Index (MCI), have become widely used standards in riverine environmental management. However, biotic indices have notable limitations: they typically require well-characterized regional reference sites, may be less effective at detecting moderate or newly emerging pollution, and their interpretability and comparability can be influenced by taxonomic resolution and sampling effort. In contrast, the StaP index is designed to quantify temporal predictability and episodic structure of water quality directly from time series data, enabling automated detection of short-term events (“first flushes”) and dynamic risk scenarios, without relying on biological community surveys. By integrating mechanistic and machine learning tools, StaP complements biotic indices by offering real-time operational insight and expanding diagnostic capability to settings where rapid, adaptive management is critical, or biological reference conditions may be unavailable.
The StaP index stands out for its sensitivity to temporal variability and rapid episodic events—features often missed by conventional water quality or biotic indices. Its integration with, rather than replacement of, classical and biotic approaches create a more comprehensive and adaptive monitoring strategy. Leveraging the strengths of each method enables more robust assessment and management of complex, dynamic aquatic systems under real-world conditions.
While our laboratory-based results demonstrate the StaP index’s operational advantages and robustness in controlled settings, we acknowledge that genuine urban runoff contains a broader spectrum of micropollutants and emerging contaminants not addressed in this study. The use of synthetic runoff and standard analytes, though necessary for controlled validation, does not encompass the full complexity of real urban catchments. Accordingly, comprehensive field studies capturing diverse hydrological settings, pollutant mixtures, and event profiles are an essential next step to confirm the method’s transferability and reliability. These limitations are recognized, and future work will focus on both broadening the pollutant range (including organics and trace contaminants) and validating the StaP index with real ground data under various hydrological scenarios
5. Conclusions
The StaP index developed and validated in this study provides a robust, adaptable metric for discriminating between different surface runoff regimes under controlled laboratory conditions. Clean urban runoff yielded the lowest StaP values (0.234 ± 0.018, CV = 7.7%), signifying high predictability and temporal stability, while industrial runoff showed moderate variability (0.367 ± 0.045, CV = 12.3%). First-flush runoff displayed the highest values (0.523 ± 0.087, CV = 16.6%), exemplifying its episodic and non-stationary nature. ANOVA results (F = 847.5, p < 0.001) supported statistically significant distinctions between runoff types.
In comparative analysis, StaP achieved strong correlation with expert assessments (r = 0.867 ± 0.02), outperforming classical metrics, such as NSF WQI (r = 0.742) and mean COD (r = 0.689), particularly in capturing episodic events. The optimized stationary component weights (w1 = 0.60, w2 = 0.40) generated maximum correlation values (up to r = 0.893) in a robust operational range (w1 ≈ 0.55–0.65), supporting consistent ranking and calibration across scenarios.
Analysis of temporal autocorrelation revealed distinct deterministic structures in runoff formation, with characteristic correlation times of 12 h for urban runoff, 8 h for industrial zones, and 4 h for first-flush events, reflecting different levels of predictability and episodic risk.
Sensitivity testing showed that reasonable deviations (± 0.1) in weighting coefficients affected correlation insignificantly (Δr < 0.05), confirming index robustness to calibration variance. StaP maintained invariance across monitoring intervals (up to 12 h) and observation window durations (>72 h), demonstrating suitability for real-time water quality surveillance. Laboratory validation confirmed straightforward integration of StaP within automated monitoring platforms (SCADA/IoT), requiring only baseline software adaptation.
The StaP framework bridges mechanistic hydrology and machine-learning approaches, showing >20% reduction in episodic event misclassification relative to classical indices. Importantly, future work will focus on expanding pollutant scope (including micropollutants and pathogens), addressing field-based calibration under seasonal and catchment variability, and integrating StaP with GIS/digital twin solutions to further elevate adaptive urban water management. Overall, StaP establishes a reproducible, transparent, and statistically validated basis for predictive, risk-oriented, and scalable water quality management in urban drainage systems.
Author Contributions
Conceptualization, I.G. and N.M.; methodology, I.G.; software, N.M.; validation, I.G. and N.M.; formal analysis, I.G.; investigation, N.M.; resources, I.G.; data curation, I.G.; writing—original draft preparation, N.M.; writing—review and editing, I.G.; visualization, N.M.; supervision, N.M.; project administration, I.G.; funding acquisition, N.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research was funded by the National Research Moscow State University of Civil Engineering (grant for fundamental scientific research, project No. 12-661/130).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study is available on request from the corresponding author due to privacy reasons.
Acknowledgments
This research was carried out using the facilities of the Head Regional Shared Research Facilities of the Moscow State University of Civil Engineering, with support from the Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-15-2025-549).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| StaP | Stationarity and Predictability Index |
| WQI | Water Quality Index |
| COD | Chemical Oxygen Demand |
| TSS | Total Suspended Solids |
| TOC | Total Organic Carbon |
| LID | Low-Impact Development |
| WSUD | Water-Sensitive Urban Design |
| SCM | Stormwater Control Measure |
| SCADA | Supervisory Control and Data Acquisition |
| IoT | Internet of Things |
| Q-RTC | Quality-Based Real-Time Control |
| SWMM | Storm Water Management Model |
| MCDM | Multi-Criteria Decision Making |
| AI | Artificial Intelligence |
| ML | Machine Learning |
| UV-Vis | Ultraviolet–Visible Spectrophotometry |
| ADF | Augmented Dickey–Fuller Test |
| AIC | Akaike Information Criterion |
| BIC | Bayesian Information Criterion |
| ANOVA | Analysis of Variance |
| HSD | Honestly Significant Difference (Tukey’s test) |
| LMM | Linear Mixed Models |
| ML | Maximum Likelihood Method |
| MCDA | Multi-Criteria Decision Analysis |
| r2 | Coefficient of Determination |
| H | Hurst Exponent |
| ACF | Autocorrelation Function |
| P5, P95 | 5th and 95th Percentiles |
| CV | Coefficient of Variation |
| EPA | Environmental Protection Agency (U.S.) |
| ASTM | American Society for Testing and Materials |
| NTU | Nephelometric Turbidity Units |
| ICP-AES | Inductively Coupled Plasma–Atomic Emission Spectrometry |
| NTP | Network Time Protocol |
| NIST | National Institute of Standards and Technology |
| SQL | Structured Query Language |
| GIS | Geographic Information System |
| HWSS | Hot Water Supply Systems |
| CHU | Central Heating Unit |
| PCD | Probabilistic Correlation Distribution (used in figures) |
| HWS | Hot Water System (alternate form of HWSS in diagrams) |
References
- Chen, R.-H.; Li, F.-P.; Zhang, H.-P.; Jiang, Y.; Mao, L.-C.; Wu, L.-L.; Chen, L. Comparative analysis of water quality and toxicity assessment methods for urban highway runoff. Sci. Total Environ. 2016, 553, 519–523. [Google Scholar] [CrossRef]
- Kumar, D.; Kumar, R.; Sharma, M.; Awasthi, A.; Kumar, M. Global water quality indices: Development, implications, and limitations. Total Environ. Adv. 2024, 9, 200095. [Google Scholar] [CrossRef]
- Ding, F.; Zhang, W.; Cao, S.; Hao, S.; Chen, L.; Xie, X.; Li, W.; Jiang, M. Optimization of water quality index models using machine learning approaches. Water Res. 2023, 243, 120337. [Google Scholar] [CrossRef]
- Sadeghi, K.M.; Loáiciga, H.A.; Kharaghani, S. Stormwater Control Measures for Runoff and Water Quality Management in Urban Landscapes. J. Am. Water Resour. Assoc. 2018, 54, 124–133. [Google Scholar] [CrossRef]
- Roozbahani, A.; Roghani, B.; Nilsen, V.; Paus, K.A.H.; Rydningen, U. Optimization of urban stormwater systems: A multi-criteria approach to sustainable and cost-effective LID implementation. Water Sci. Technol. 2025, 91, 654–668. [Google Scholar] [CrossRef]
- Feng, W.; Liu, Y.; Gao, L. Stormwater treatment for reuse: Current practice and future development—A review. J. Environ. Manag. 2022, 301, 113830. [Google Scholar] [CrossRef]
- Walsh, C.J.; Imberger, M.; Burns, M.J.; Bos, D.G.; Fletcher, T.D. Dispersed urban-stormwater control improved stream water quality in a catchment-scale experiment. Water Resour. Res. 2022, 58, e2022WR032041. [Google Scholar] [CrossRef]
- Maniquiz-Redillas, M.; Robles, M.E.; Cruz, G.; Reyes, N.J.; Kim, L.-H. First Flush Stormwater Runoff in Urban Catchments: A Bibliometric and Comprehensive Review. Hydrology 2022, 9, 63. [Google Scholar] [CrossRef]
- Burns, M.J.; Walsh, C.J.; Fletcher, T.D.; Ladson, A.R.; Hatt, B.E. A landscape measure of urban stormwater runoff effects is a better predictor of stream condition than a suite of hydrologic factors. Ecohydrology 2015, 8, 160–171. [Google Scholar] [CrossRef]
- Balderas Guzman, C.; Wang, R.; Muellerklein, O.; Smith, M.; Eger, C.G. Comparing stormwater quality and watershed typologies across the United States: A machine learning approach. Water Res. 2022, 216, 118283. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Chow, C.W.K.; Shi, Z.; Fabris, R.; Mussared, A.; Hallas, G.; Monis, P.; Jin, B.; Saint, C.P. Stormwater monitoring using on-line UV-Vis spectroscopy. Environ. Sci. Pollut. Res. 2022, 29, 19530–19539. [Google Scholar] [CrossRef]
- Wong, B.P.; Kerkez, B. Adaptive measurements of urban runoff quality. Water Resour. Res. 2016, 52, 8986–9000. [Google Scholar] [CrossRef]
- Razguliaev, N.; Flanagan, K.; Muthanna, T.; Viklander, M. Urban stormwater quality: A review of methods for continuous field monitoring. Water Res. 2024, 249, 120929. [Google Scholar] [CrossRef]
- Yuan, Q.; Yao, G.; Liu, W.; Weragoda, S.K.; Weerasooriya, R.; Meng, Y.; Luan, F. Assessment of harvested rainwater quality and surrogate parameter development for drinking water provision in rural Sri Lanka. J. Environ. Chem. Eng. 2025, 13, 117632. [Google Scholar] [CrossRef]
- Fooladi, M.; Nikoo, M.R.; Mirghafari, R.; Madramootoo, C.A.; Al-Rawas, G.; Nazari, R. Robust Clustering-Based Hybrid Technique Enabling Reliable Reservoir Water Quality Prediction with Uncertainty Quantification and Spatial Analysis. J. Environ. Manag. 2024, 362, 121259. [Google Scholar] [CrossRef] [PubMed]
- Brodeur, Z.; Wi, S.; Shabestanipour, G.; Lamontagne, J.; Steinschneider, S. A hybrid, non-stationary stochastic watershed model (SWM) for uncertain hydrologic simulations under climate change. Water Resour. Res. 2024, 60, e2023WR035042. [Google Scholar] [CrossRef]
- Fassman-Beck, E.A.; Tiernan, E.D.; Cheng, K.L.; Schiff, K.C. A data-driven index for evaluating BMP water quality performance. Water Res. 2025, 282, 123769. [Google Scholar] [CrossRef] [PubMed]
- Alja’fari, J.; Sharvelle, S.; Brinkman, N.E.; Jahne, M.; Keely, S.; Wheaton, E.A.; Garland, J.; Welty, C.; Sukop, M.C.; Meixner, T. Characterization of roof runoff microbial quality in four U.S. cities with varying climate and land use characteristics. Water Res. 2022, 225, 119123. [Google Scholar] [CrossRef]
- Gabr, M.E.; El Shorbagy, A.M.; Faheem, H.B. Assessment of Stormwater Quality in the Context of Traffic Congestion: A Case Study in Egypt. Sustainability 2023, 15, 13927. [Google Scholar] [CrossRef]
- Shoja Razavi, N.; Prodanovic, V.; Zhang, K. Advancing stormwater harvesting: A comprehensive review of current drivers, implementation advancements, and pathways forward. Environ. Technol. Rev. 2024, 13, 478–501. [Google Scholar] [CrossRef]
- ASTM D6913/D6913M-17; Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. ASTM: West Conshohocken, PA, USA, 2017.
- ASTM A240/A240M-23; Standard Specification for Chromium and Chromium-Nickel Stainless Steel Plate, Sheet, and Strip for Pressure Vessels and for General Applications. ASTM International: West Conshohocken, PA, USA, 2023.
- EPA Method 410.4; The Determination of Chemical Oxygen Demand by Semi-Automated Colorimetry. U.S. Environmental Protection Agency, Office of Research and Development: Cincinnati, OH, USA, 1993.
- EPA Method 351.2; Determination of Total Kjeldahl Nitrogen by Semi-Automated Colorimetry. U.S. Environmental Protection Agency, Office of Research and Development: Cincinnati, OH, USA, 1993.
- EPA Method 365.1; Determination of Phosphorus by Semi-Automated Colorimetry. U.S. Environmental Protection Agency, Office of Research and Development: Cincinnati, OH, USA, 1993.
- EPA Method 160.2; Residue, Non-Filterable (Gravimetric, Dried at 103–105 °C). U.S. Environmental Protection Agency, Office of Research and Development: Cincinnati, OH, USA, 1971.
- EPA Method 200.7; Determination of Metals and Trace Elements in Water and Wastes by Inductively Coupled Plasma-Atomic Emission Spectrometry. U.S. Environmental Protection Agency, Office of Science and Technology: Washington, DC, USA, 2001.
- Lumb, A.; Sharma, T.C.; Bibeault, J.F. A review of genesis and evolution of water quality index (WQI) and some future directions. Water Qual. Expo. Health 2011, 3, 11–24. [Google Scholar] [CrossRef]
- Abbasi, T.; Abbasi, S.A. Water quality indices based on bioassessment: The biotic indices. J. Water Health 2011, 9, 330–348. [Google Scholar] [CrossRef] [PubMed]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).