Study on the Stress Response and Deformation Mechanism of Pipe Jacking Segments Under the Coupling Effect of Defects and Deflection
Abstract
1. Introduction
2. Project Overview
3. Test System and Scheme
3.1. Comprehensive Experimental Design for the Indoor Pipe Jacking Model Test
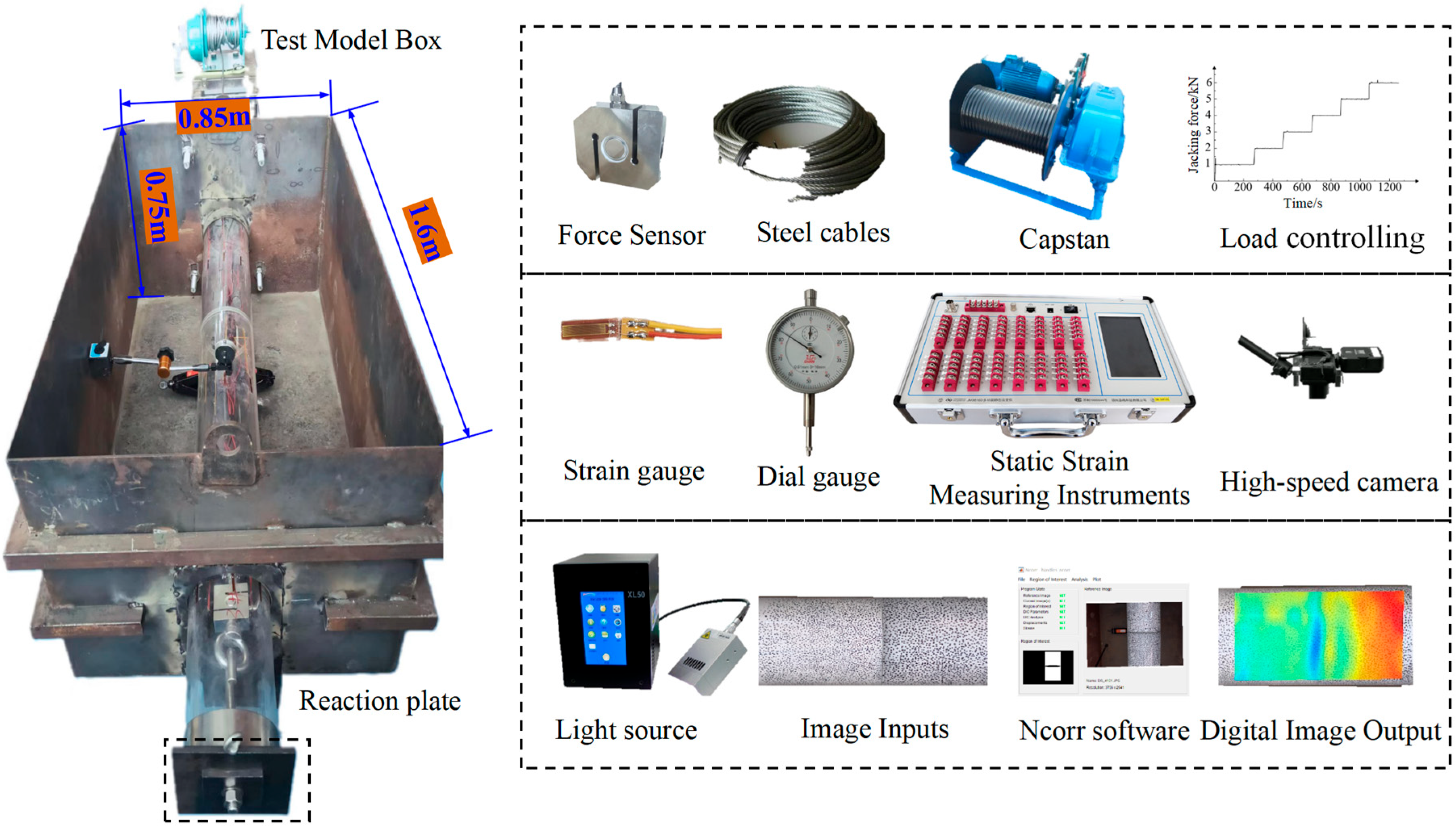
3.2. Test Setup
3.3. Deflection Test Scheme
3.3.1. Segment Deflection Simulation Test
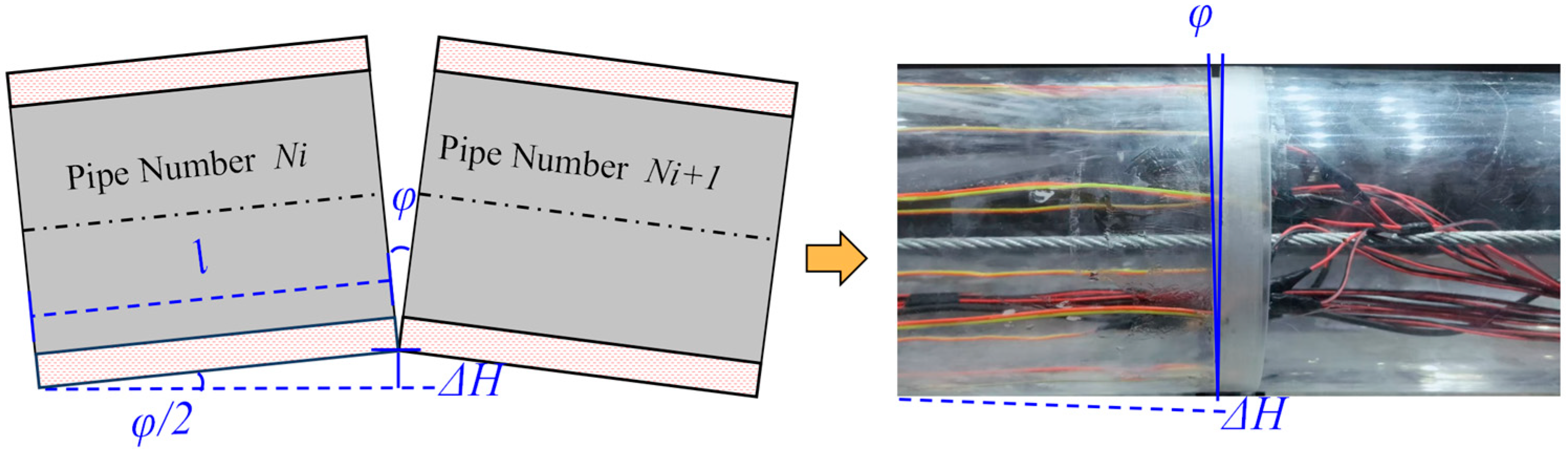
3.3.2. Monitoring Point Layout
3.4. Deformation Test Scheme
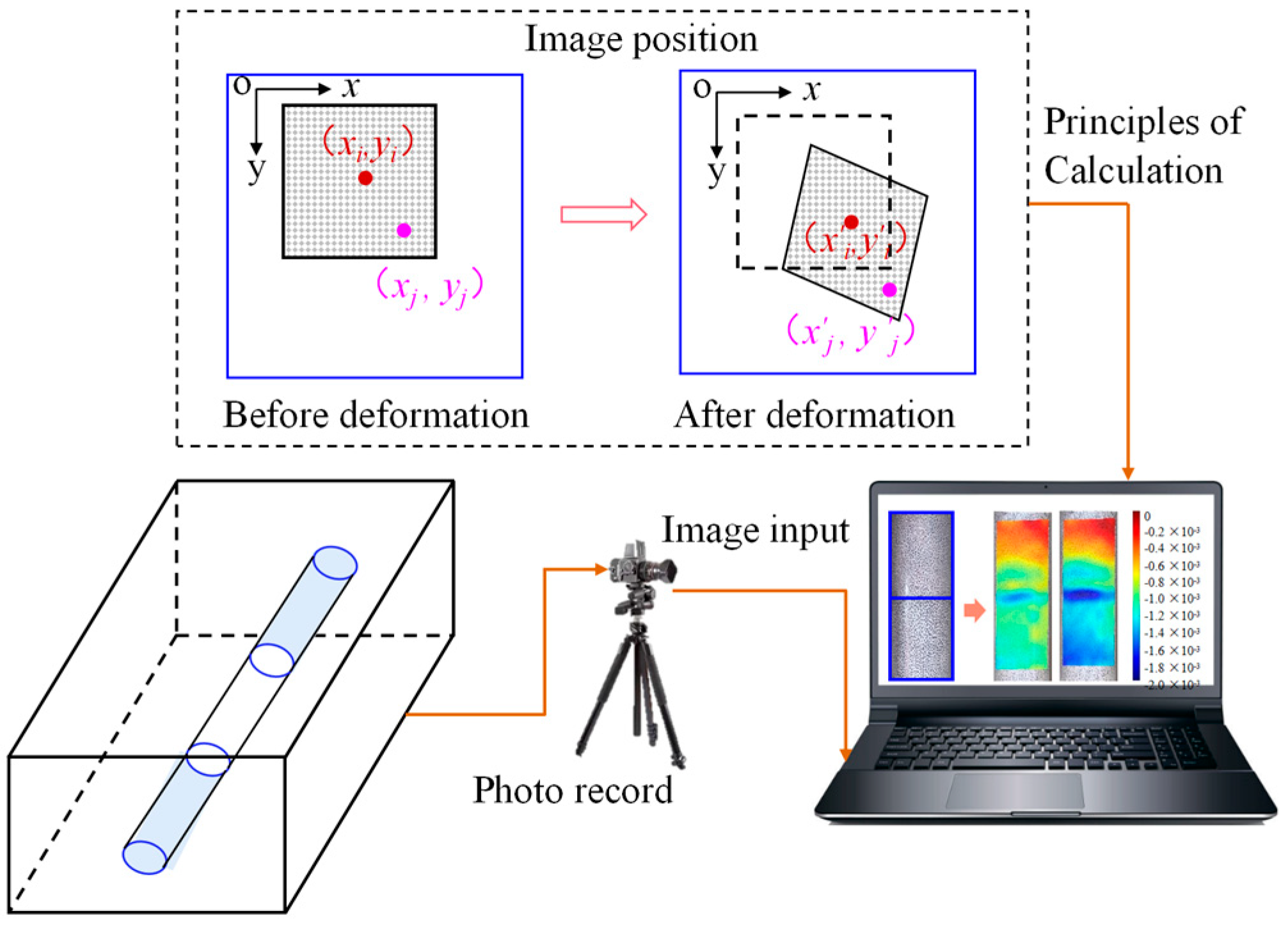
3.5. Segment Defect Test Scheme
4. Analysis of Test Results
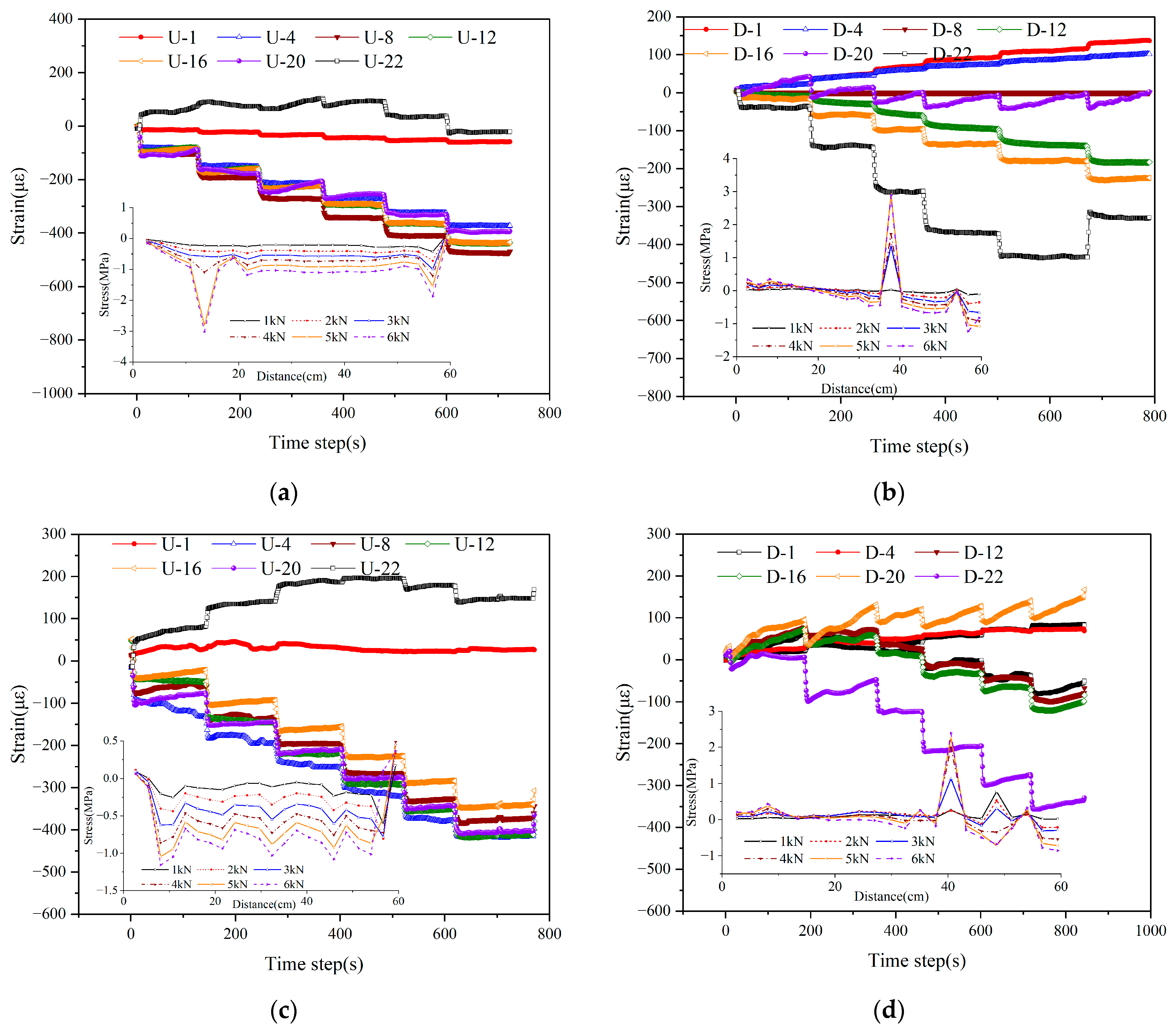
4.1. Characteristics of Segment Stress and Deformation Fields
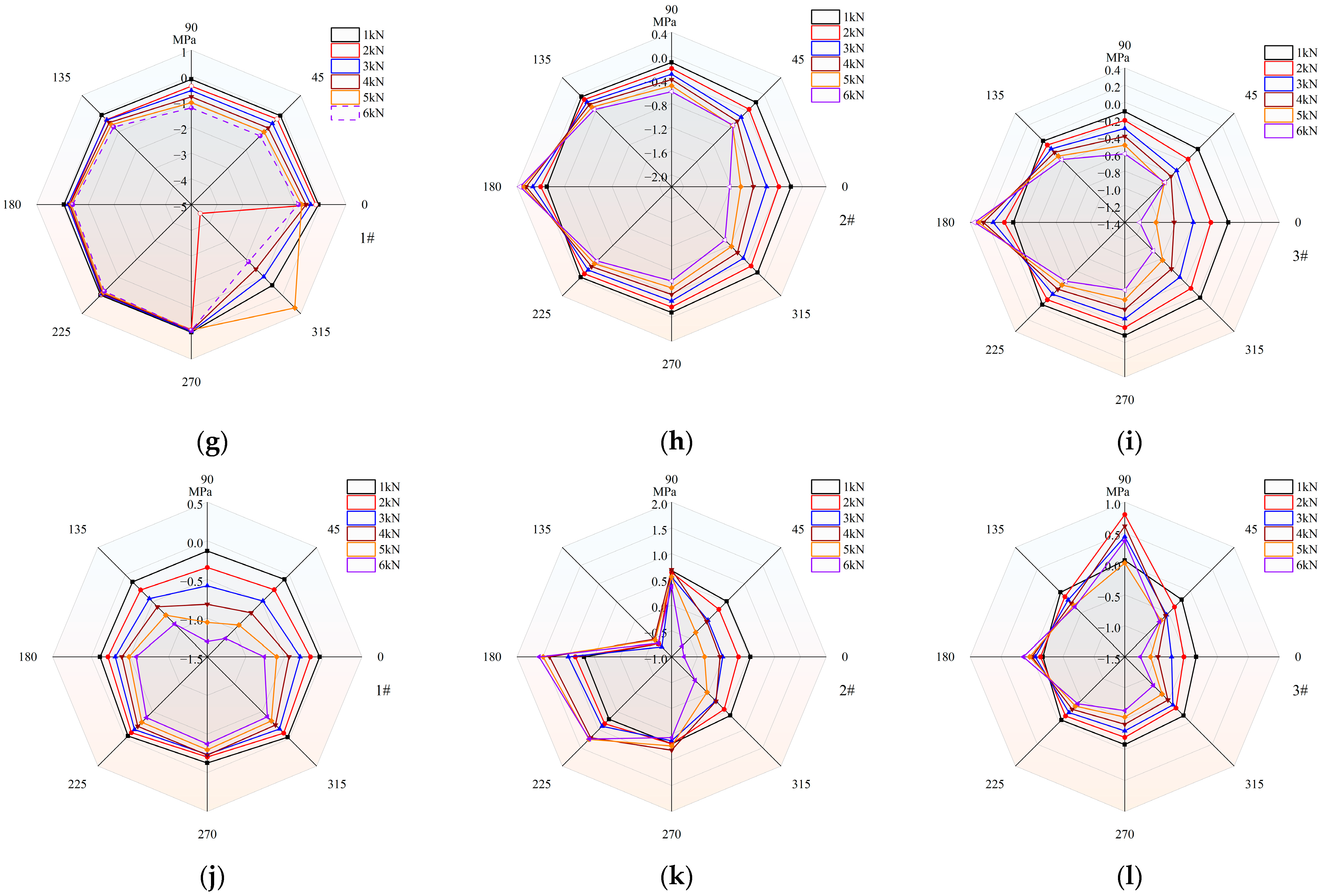
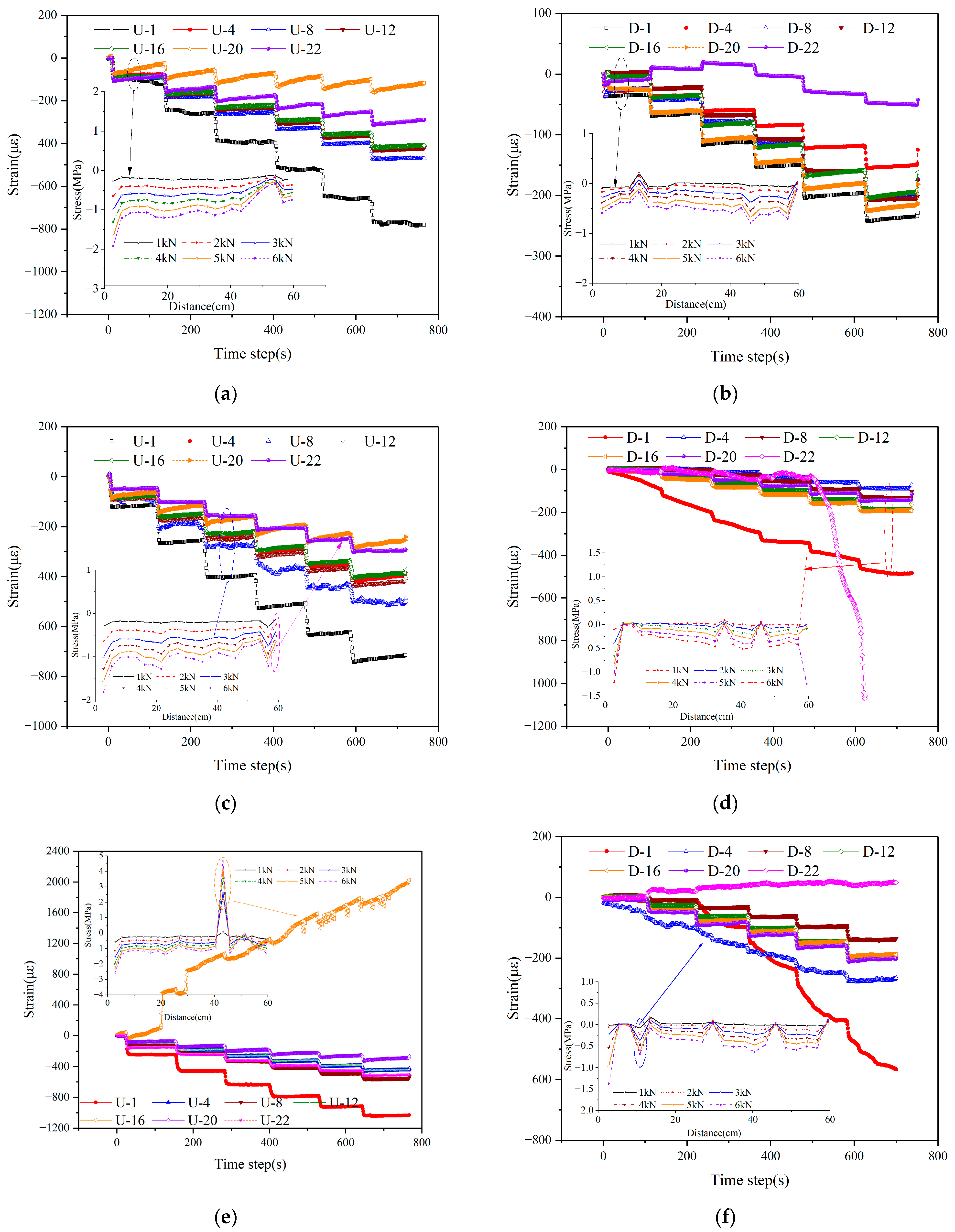
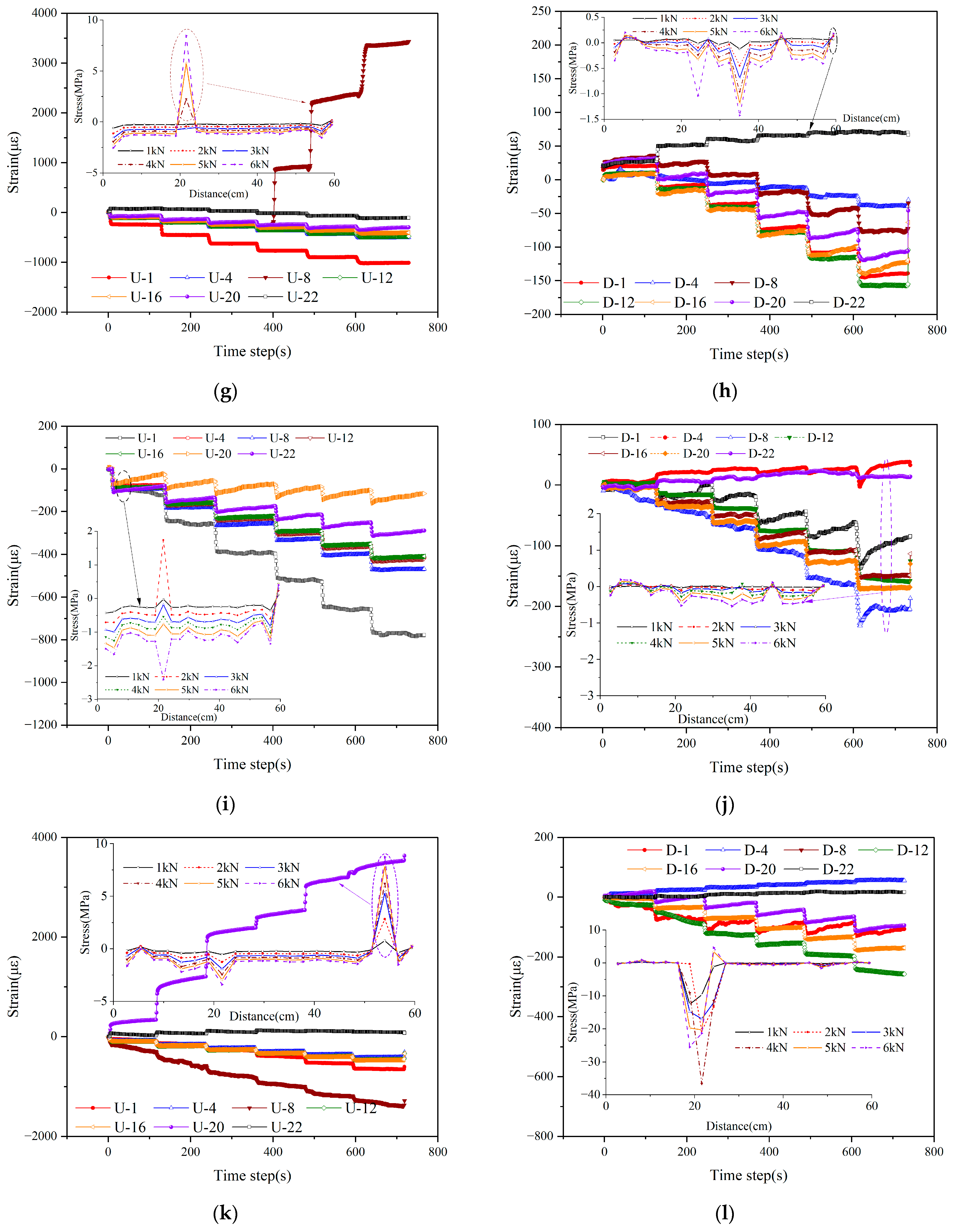
4.1.1. Co-Directional Deflection and Axial Stress Response
4.1.2. Diagonal Deflection and Axial Stress Response
4.2. Joint Deformation Characteristics
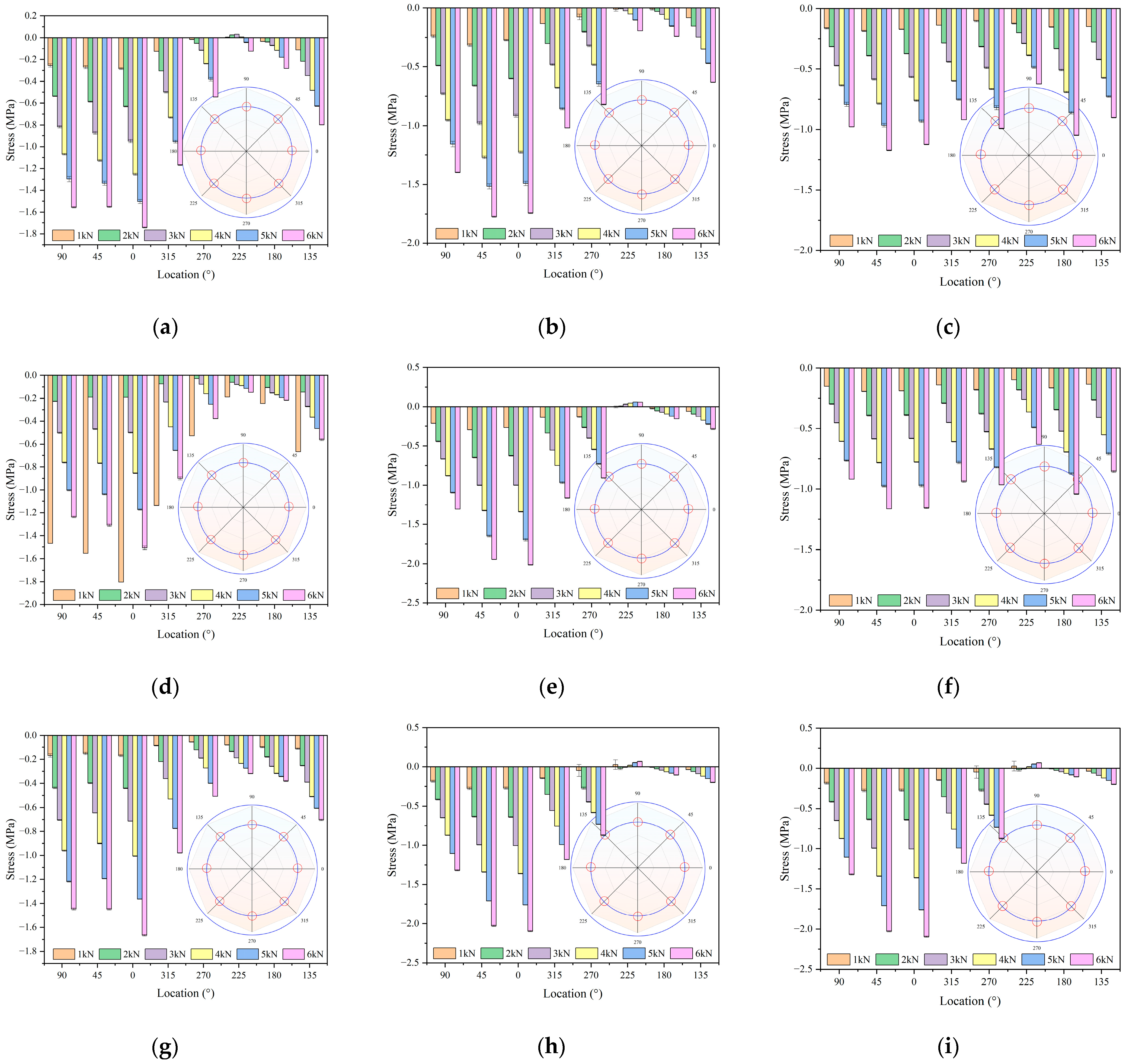
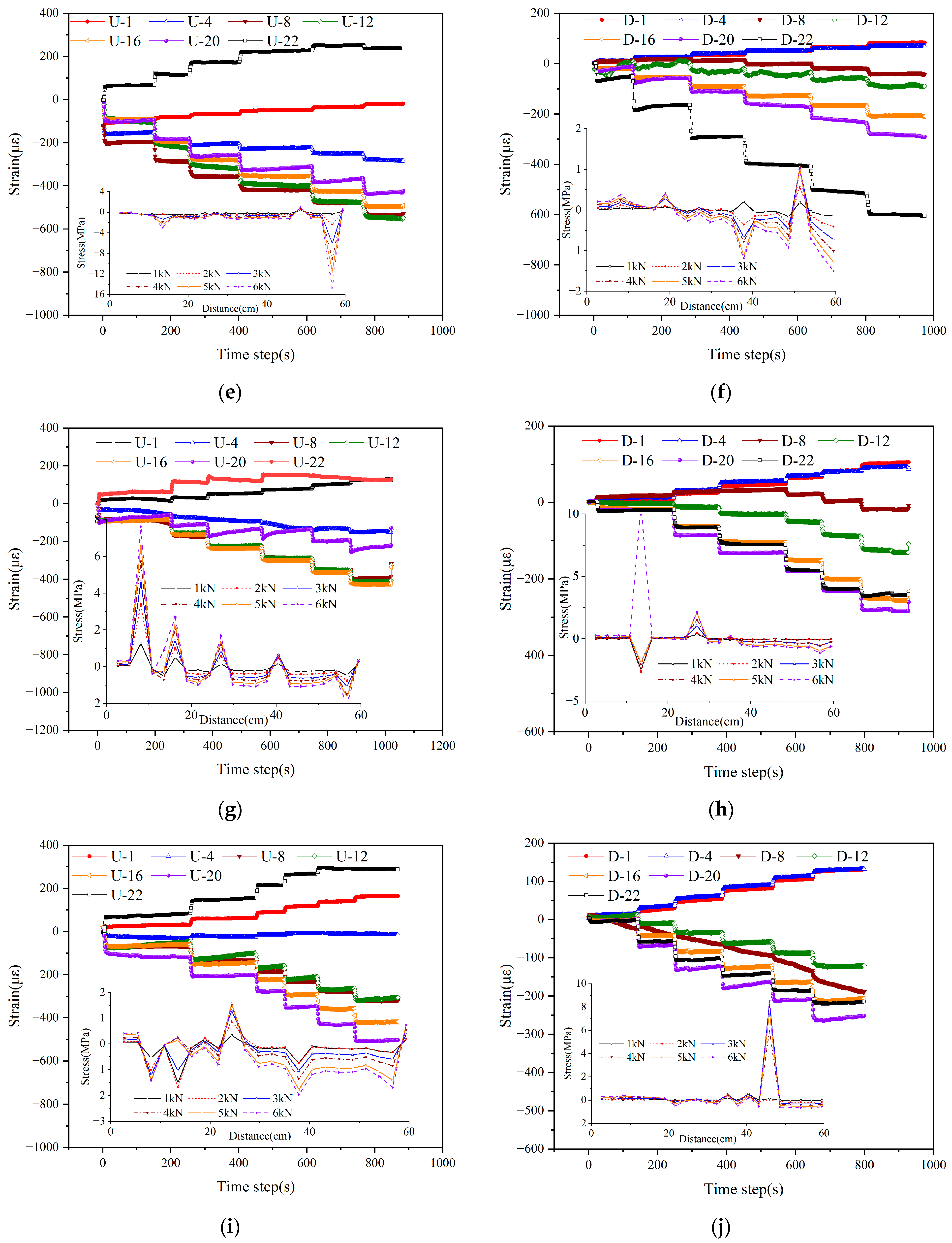
4.3. Axial Stress Response Induced by Defects
4.3.1. Mechanical Characteristics Under Single Defect Conditions
4.3.2. Mechanical Characteristics of Segments Under Combined Vault and Bottom Defects
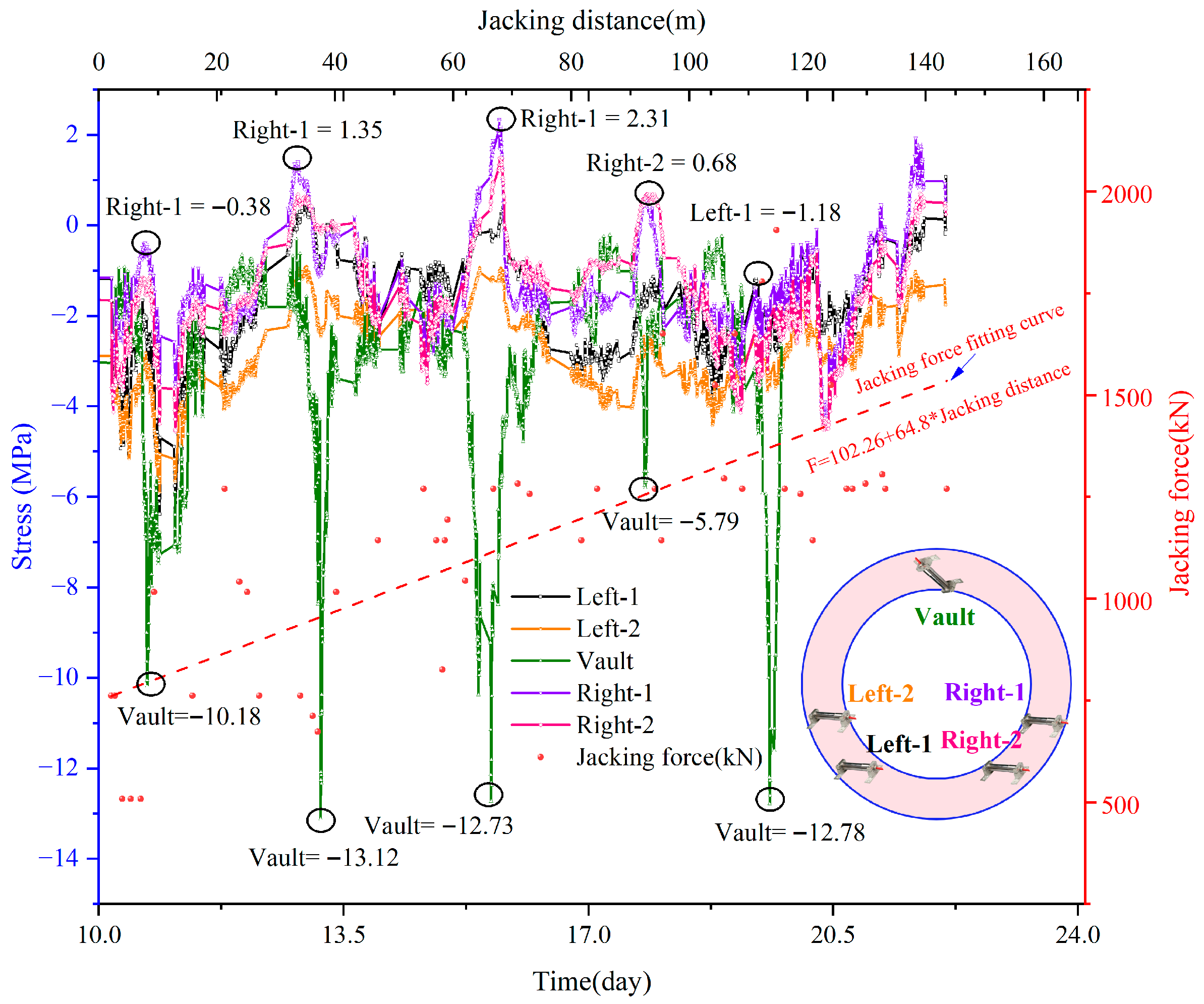
5. Discussion
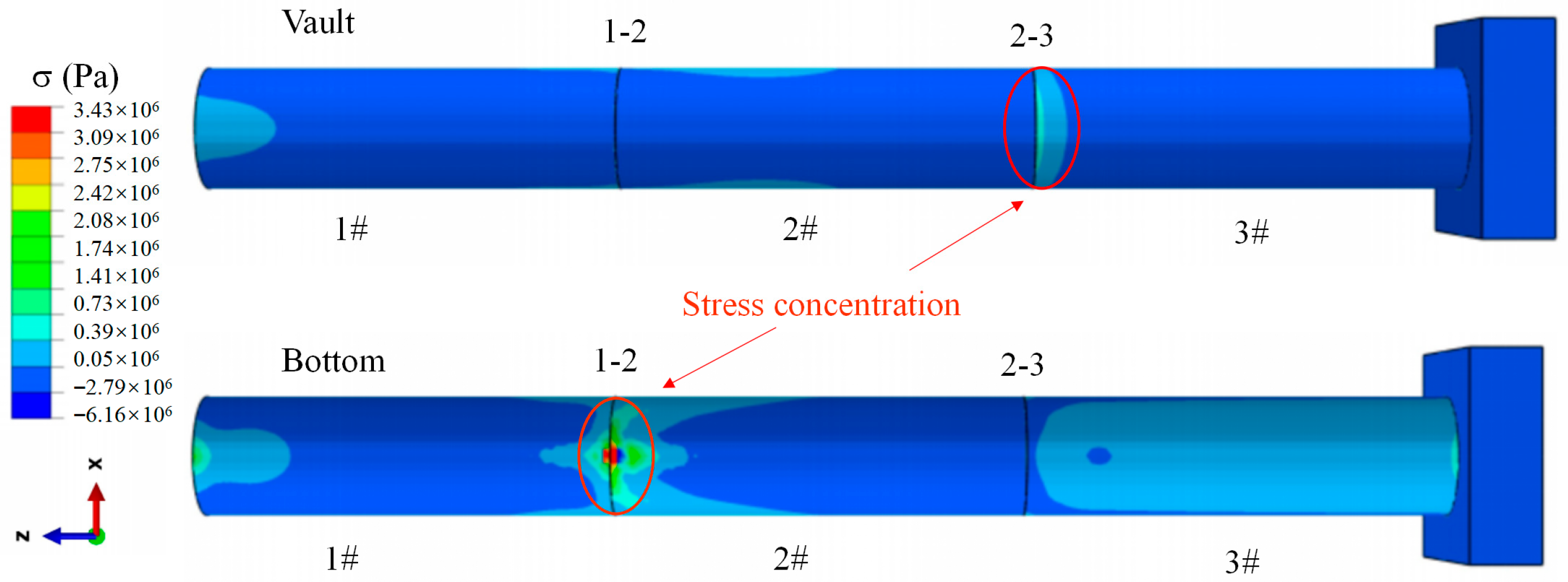
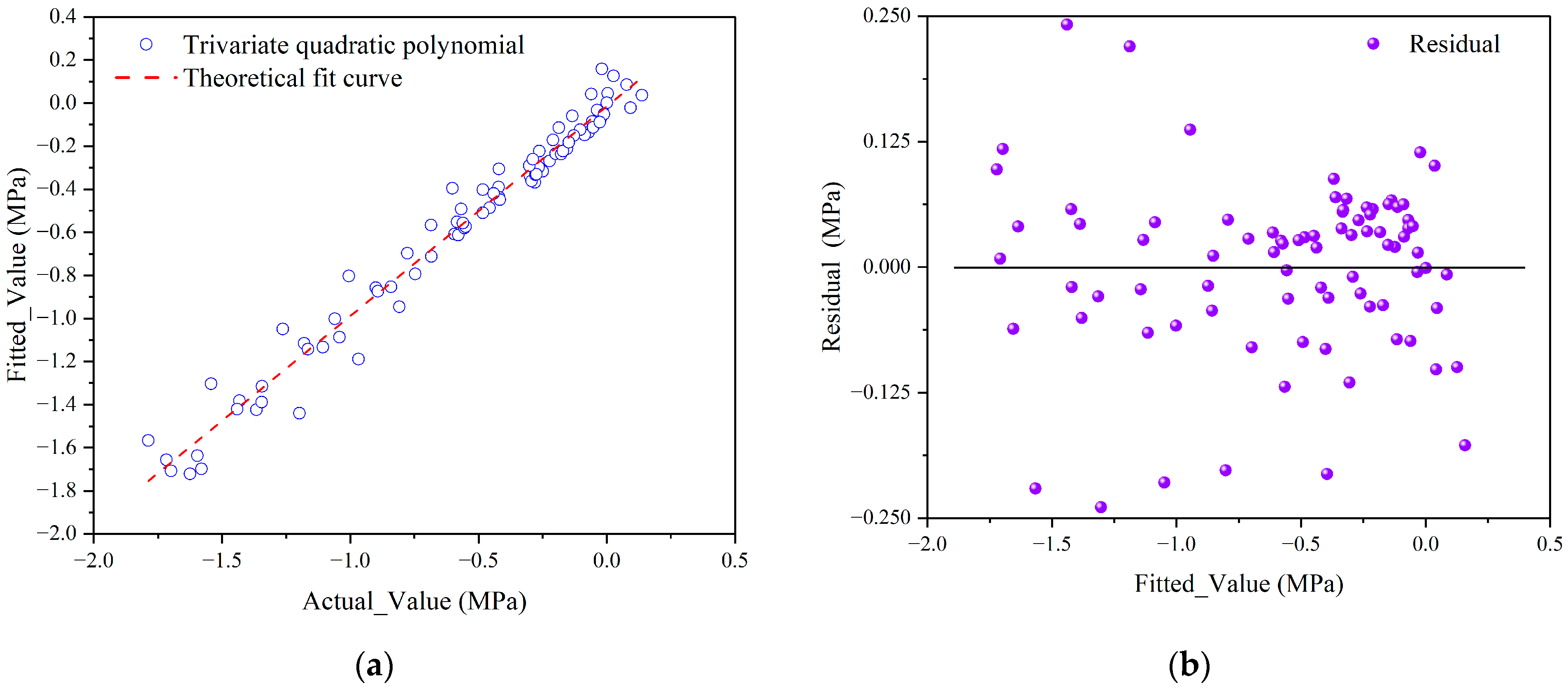
5.1. Theoretical Validation
5.2. Numerical Model Validation
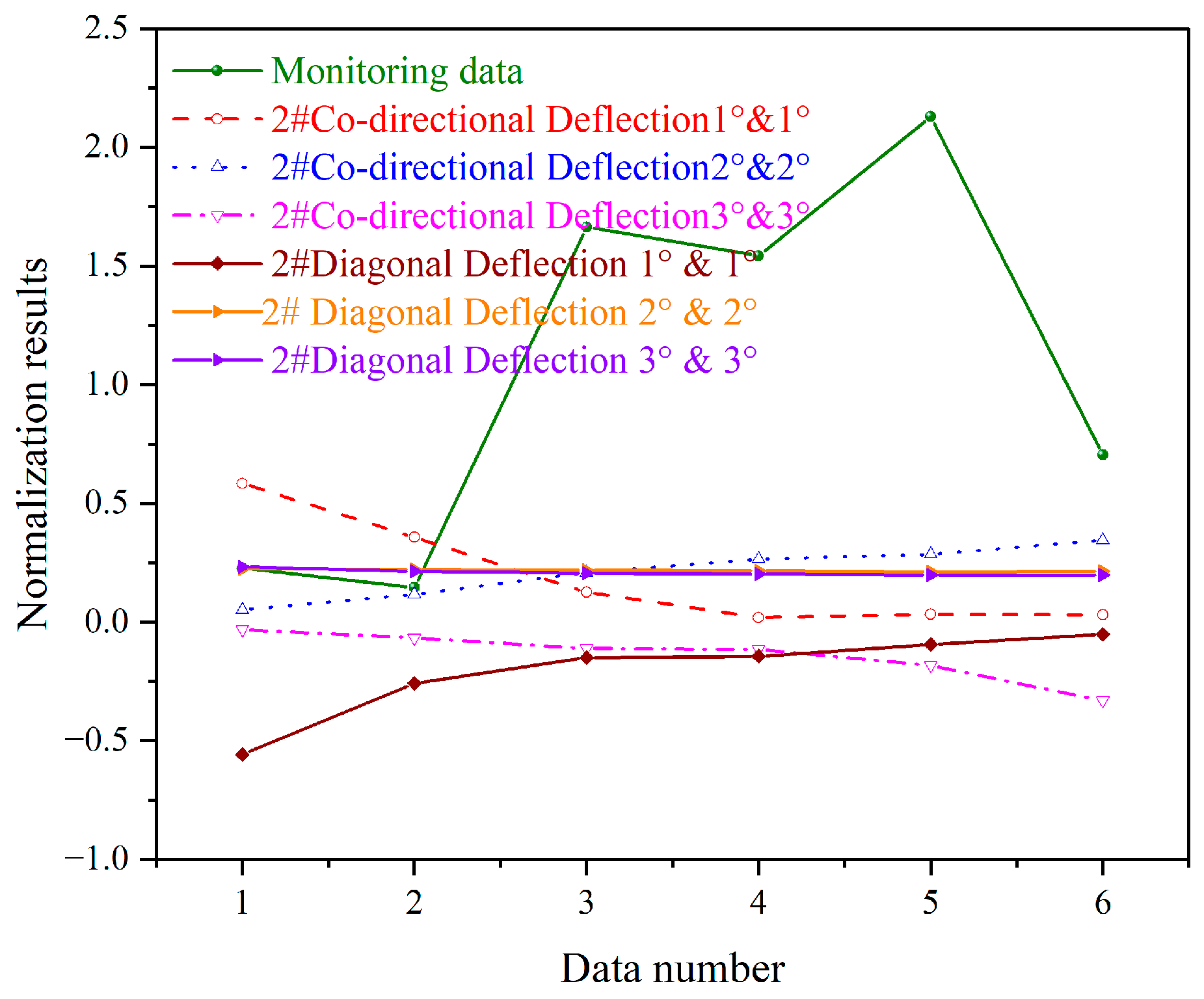
5.3. Normalization Analysis
5.4. Analysis and Recommendations for the Mechanical Response of Pipe Jacking Structures
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ong, D.E.L.; Barla, M.; Cheng, J.W.C.; Choo, C.S.; Sun, M.; Peerun, M.I. Sustainable Pipe Jacking Technology in the Urban Environment: Recent Advances and Innovations; Springer: Singapore, 2022. [Google Scholar] [CrossRef]
- Thakre, G.; Kaushal, V.; Karkhanis, E.; Najafi, M. A Data-Driven Visualization Approach for Life-Cycle Cost Analysis of Open-Cut and Trenchless CIPP Methods for Sanitary Sewers: A PRISMA Systematic Review. Appl. Sci. 2025, 15, 1765. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.; Su, D.; Liu, S.; Liu, X.; Jiang, S.; Gao, H.; Yang, W. Mechanical performance of a prefabricated subway station structure constructed by twin closely-spaced rectangular pipe-jacking boxes. Tunn. Undergr. Space Technol. 2023, 135, 105062. [Google Scholar] [CrossRef]
- Zhang, X.; Fang, H.; Hu, Q.; Ma, B.; Hu, S.; Du, M.; Du, X.; Yang, K.; Li, B.; Shi, M. Mechanical performance of corroded reinforced concrete pipelines rehabilitated with sprayed-on cementitious liners subjected to combined loads. Tunn. Undergr. Space Technol. 2022, 120, 104266. [Google Scholar] [CrossRef]
- Zhen, L.; Chen, J.-J.; Qiao, P.; Wang, J.-H. Analysis and remedial treatment of a steel pipe-jacking accident in complex underground environment. Eng. Struct. 2014, 59, 210–219. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, P.; Chen, X.; Zhang, Y.; Ma, B.; Liu, K.; Xu, T.; Zeng, C. Field mechanical properties of large section concrete pipes during jacking in fractured moderately weathered siltstone. Tunn. Undergr. Space Technol. 2023, 131, 104818. [Google Scholar] [CrossRef]
- Chen, Q.; Ni, P.; Qin, X. Numerical investigation on failure modes of bell-spigot jointed ductile iron pipelines subjected to dip-slip faults with different dip angles. Tunn. Undergr. Space Technol. 2023, 133, 104982. [Google Scholar] [CrossRef]
- Yu, B.; Shimada, H.; Sasaoka, T.; Hamanaka, A.; Matsumoto, F.; Morita, T. A jacking force study based on interpretation of box jacking records: A case study of curved rectangular box jacking in soft soil in Saitama, Japan. Tunn. Undergr. Space Technol. 2023, 139, 105228. [Google Scholar] [CrossRef]
- Becerril García, D.; Moore, I.D. Behaviour of bell and spigot joints in buried reinforced concrete pipelines. Can. Geotech. J. 2014, 52, 609–625. [Google Scholar] [CrossRef]
- Ma, P.; Zhao, Y.; Song, Z.; Shimada, H.; Zhou, H.; Ma, B. Experimental Study and Performance Comparison of Different Jacking Pipes under the Effects of Concentrated Loads. J. Pipeline Syst. Eng. Pract. 2025, 16, 04025054. [Google Scholar] [CrossRef]
- Zheng, S.; Wang, C.; Luo, Z.; Zhang, Y.; Chen, J.; Li, X. Factors Influencing Pipe Stress Responses in Pipe Jacking in Bedrock: Field Monitoring and Numerical Simulation. J. Pipeline Sci. Eng. 2025; 100320, in press. [Google Scholar] [CrossRef]
- Nyrkova, L. Stress-corrosion cracking of pipe steel under complex influence of factors. Eng. Fail. Anal. 2020, 116, 104757. [Google Scholar] [CrossRef]
- Li, B.; Wang, F.; Fang, H.; Yang, K.; Zhang, X.; Ji, Y. Experimental and numerical study on polymer grouting pretreatment technology in void and corroded concrete pipes. Tunn. Undergr. Space Technol. 2021, 113, 103842. [Google Scholar] [CrossRef]
- Becerril García, D.; Moore, I.D.; Cortés-Pérez, J. Modeling and Parametric Study of Gasketed Bell and Spigot Joint in Buried RC Pipeline. J. Pipeline Syst. Eng. Pract. 2019, 10, 04019015. [Google Scholar] [CrossRef]
- Zhang, P.; Behbahani, S.S.; Ma, B.; Iseley, T.; Tan, L. A jacking force study of curved steel pipe roof in Gongbei tunnel: Calculation review and monitoring data analysis. Tunn. Undergr. Space Technol. 2018, 72, 305–322. [Google Scholar] [CrossRef]
- Wang, L.; Wu, Z.; Chen, Y.; Wang, Z.; Yan, C.; Tong, T. Pipe for Pipe Jacking. Technology Standard of Pipe Jacking; Springer Nature: Singapore, 2024; pp. 23–59. [Google Scholar]
- DeGrande, V.; Nervik, A.; Fogg, D.; Mah, R. Fabrication of Large-Diameter, Thick-Walled Pipe to Meet Special Fault-Crossing Design Requirements for San Francisco Hetch Hetchy Water System. Pipelines 2013, 576–587. [Google Scholar] [CrossRef]
- Ong, D.E.L.; Barla, M.; Cheng, J.W.-C.; Choo, C.S.; Sun, M.; Peerun, M.I. Deep Shaft Excavation: Design, Construction, and Their Challenges. Sustainable Pipe Jacking Technology in the Urban Environment: Recent Advances and Innovations; Springer: Singapore, 2022; pp. 103–145. [Google Scholar]
- Wang, L.; Chen, X.; Su, D.; Zhou, W.; Sun, B.; Pan, J.; Wu, Y.; Feng, M. Construction of a super-large prefabricated rectangular tunnel beneath a box culvert using pipe jacking: A case study. Tunn. Undergr. Space Technol. 2024, 152, 105913. [Google Scholar] [CrossRef]
- Hu, F.; Yang, T.; Adagunodo, T.A.; Zhu, D.; Huang, R. Practice and theoretical analysis of ground penetrating radar in voids detection of urban underground pipe-jacking. J. Appl. Geogr. 2025, 233, 105639. [Google Scholar] [CrossRef]
- Lin, Y.; Qiu, H.; He, Y.; Huang, R.; Wei, J.; Zhou, W. Current Status of Inspection and Repair of Difficult Drainage Pipelines in China. J. Pipel. Syst. Eng. Pract. 2024, 15, 03124002. [Google Scholar] [CrossRef]
- Su, D.; Chen, J.; Chen, P.; Wang, L.; Zhou, J.; Chen, X. Real-time attitude control of large rectangular pipe-jacking machines using a mechanics-informed digital twin. Autom. Constr. 2025, 177, 106373. [Google Scholar] [CrossRef]
- Qiu, D.; Wang, L.; Zu, Y.; Qing, Y. The Development of the Pipe Jacking Guidance Technology. Appl. Sci. 2025, 15, 2137. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, C.; Zhang, C.; Zhang, X. Experimental and numerical study on the mechanical properties of F type socket joints for rectangular pipe jacking with steel screw connection. Sci. Rep. 2024, 14, 30952. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, Y.; Ariaratnam, S.T.; Yan, X. Study on the impact of ovality defect on structural stability of CIPP liner of drainage pipeline. Tunn. Undergr. Space Technol. 2023, 140, 105338. [Google Scholar] [CrossRef]
- Arumugam, T.; Vijaya Kumar, S.D.; Karuppanan, S.; Ovinis, M. The Influence of Axial Compressive Stress and Internal Pressure on a Pipeline Network: A Review. Appl. Sci. 2023, 13, 3799. [Google Scholar] [CrossRef]
- Faisal, A.; Abbas, S.; Ahmed, A. Mechanical performance of spun-cast full-scale precast pipes incorporating hybrid conventional rebar cage and steel fibers. Structures 2023, 52, 104–116. [Google Scholar] [CrossRef]
- Zhai, K.; Fang, H.; Fu, B.; Wang, F.; Hu, B. Mechanical response of externally bonded CFRP on repair of PCCPs with broken wires under internal water pressure. Constr. Build. Mater. 2020, 239, 117878. [Google Scholar] [CrossRef]
- Li, B.; Fang, H.; Zhang, X.; Yang, K.; Dong, B.; Pang, G.; Zhai, K. Prediction model for maximum shear displacement of pipe joints with preexisting defects based on finite element–multiple nonlinear regression method. Struct. Concr. 2021, 22, 3727–3745. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, S.; Ma, B.; Zhao, Y.; Tan, X.; Zhang, H. Prestressed steel wires impact on axial bearing capacity of ultra-large section jacking prestressed concrete cylinder pipe (JPCCP): Field experiment and simulation. Eng. Fail. Anal. 2025, 167, 109046. [Google Scholar] [CrossRef]
- Shen, Y.; Ling, J.; Lu, X.; Zhang, Y.; Yan, Z. Steel wire prestress analysis of large section jacking prestressed concrete cylinder pipe (JPCCP): Site experiment and numerical investigation. Thin-Walled Struct. 2023, 184, 110420. [Google Scholar] [CrossRef]
- Jibreen, A.; Najafi, M.; Aljaberi, M.; Mohammadagha, M. Study of Rehabilitation of Broken Wires in Prestressed Concrete Cylinder Pipe (PCCP) and Its Effect on the Structural Continuity of the Pipe. Pipelines 2025, 82–90. [Google Scholar] [CrossRef]
- Dong, X.; Dou, T.; Dong, P.; Su, Y.; Li, Y.; Ning, J.; Wei, J.; Li, K.; Cheng, B. Experimental study on the influence of scattered broken wires on the structural performance of prestressed concrete cylinder pipe. Structures 2023, 47, 52–62. [Google Scholar] [CrossRef]
- Fang, H.; Tan, P.; Du, X.; Li, B.; Yang, K.; Zhang, Y. Mechanical response of buried HDPE double-wall corrugated pipe under traffic-sewage coupling load. Tunn. Undergr. Space Technol. 2021, 108, 103664. [Google Scholar] [CrossRef]
- Zhai, K.; Zhang, C.; Fang, H.; Ma, H.; Ni, P.; Wang, F.; Li, B.; He, H. Mechanical responses of bell-and-spigot joints in buried prestressed concrete cylinder pipe under coupled service and surcharge loads. Struct. Concr. 2021, 22, 827–844. [Google Scholar] [CrossRef]
- Rakitin, B.; Xu, M. Centrifuge testing to simulate buried reinforced concrete pipe joints subjected to traffic loading. Can. Geotech. J. 2015, 52, 1762–1774. [Google Scholar] [CrossRef]
- Wu, H.; Zhai, K.; Fang, H.; Wang, F.; Yu, X.; Li, B. Bell-and-spigot joints mechanical properties study of PCCP under the uneven settlement of foundation: Simulation and full-scale test. Structures 2022, 43, 1692–1703. [Google Scholar] [CrossRef]
- Batsaikhan, U.; Hashikawa, H.; Shimada, H.; Sasaoka, T.; Hamanaka, A. Numerical Study on the Applicability of the Pipe-Jacking Method for the Main Gate of an Underground Coal Mining in Weak Rock Mass. Appl. Sci. 2022, 12, 1719. [Google Scholar] [CrossRef]
- Chen, Q.; Ni, P. Three-dimensional modeling of joint kinematic of ductile iron pipelines subjected to normal faulting. Tunn. Undergr. Space Technol. 2023, 132, 104863. [Google Scholar] [CrossRef]
- Kalisz, P.; Zięba, M. Influence of Soil Deformation Caused by Mining on Sewage Pipelines Built Using the Pipe Jacking Method. Stud. Geotech. Mech. 2018, 40, 147–153. [Google Scholar] [CrossRef]
- Ye, M.; Ni, P.; Maitra, S. Response of flexible pipes buried in sand under multi-directional movement: Understanding fault-pipeline interaction. Soil Dyn. Earthq. Eng. 2024, 187, 108978. [Google Scholar] [CrossRef]
- Robert, D.J.; Rajeev, P.; Kodikara, J.; Rajani, B. Equation to predict maximum pipe stress incorporating internal and external loadings on buried pipes. Can. Geotech. J. 2016, 53, 1315–1331. [Google Scholar] [CrossRef]
- Chen, Y.; Li, J.; Chen, Q.; Lin, C.; Ni, P.; Lu, Z. Simplified analytical method for bell-spigot jointed pipeline response to normal faults using two-layer Winkler foundation model. Tunn. Undergr. Space Technol. 2026, 168, 107063. [Google Scholar] [CrossRef]
- Lin, W.; Li, P.; Xie, X. A Novel Detection and Assessment Method for Operational Defects of Pipe Jacking Tunnel Based on 3D Longitudinal Deformation Curve: A Case Study. Sensors 2022, 22, 7648. [Google Scholar] [CrossRef]
- Liu, W.; Tan, J.; Shi, J.; Huang, X.; Chen, W. A Method for calculating jacking force of parallel pipes considering Soil Arching Effect and Pipe-Slurry-Soil Interaction. Comput. Geotech. 2024, 173, 106528. [Google Scholar] [CrossRef]
- Zhang, Y.; Tao, L.; Zhao, X.; Liu, J.; Liao, W.; Guo, F.; Yang, X.; Zhong, R. Analytical model of vertical load acting on jacked pipe considering soil arching effect in cohesionless soil. Undergr. Space 2024, 14, 263–284. [Google Scholar] [CrossRef]
- Sheil, B. Prediction of microtunnelling jacking forces using a probabilistic observational approach. Tunn. Undergr. Space Technol. 2021, 109, 103749. [Google Scholar] [CrossRef]
- Sheil, B.B.; Suryasentana, S.K.; Templeman, J.O.; Phillips, B.M.; Cheng, W.-C.; Zhang, L. Prediction of Pipe-Jacking Forces Using a Bayesian Updating Approach. J. Geotech. Geoenviron. Eng. 2022, 148, 04021173. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, P.; Xu, Y.; Mei, J. Model Test on Excavation Face Stability of Shallow-Buried Rectangular Pipe Jacking in Sand Layer. Appl. Sci. 2025, 15, 7847. [Google Scholar] [CrossRef]
- Tang, J.; Xu, J.; Zhou, D.; Huang, D.; Zeng, K.; Li, Y.; Chen, Z. Ground Surface Deformation Caused by Pipe Jacking Construction in a Soft Soil Area: An Experiment-Based Study. Buildings 2023, 13, 1628. [Google Scholar] [CrossRef]
- Shahin, H.M.; Nakai, T.; Ishii, K.; Iwata, T.; Kuroi, S. Investigation of influence of tunneling on existing building and tunnel: Model tests and numerical simulations. Acta Geotech. 2016, 11, 679–692. [Google Scholar] [CrossRef]
- Guo, W.; Feng, K.; Lu, X.; Qi, M.; Liu, X.; Fang, Y.; He, C.; Xiao, M. Model test investigation on the longitudinal mechanical property of shield tunnels considering internal structure. Tunn. Undergr. Space Technol. 2023, 140, 105293. [Google Scholar] [CrossRef]
- Ashoor, F.; Abdollahipour, A.; Khosravi, M.H. Numerical and experimental analysis of contact pressure in rock-disc cutter interaction using displacement discontinuity method and digital image correlation. Transp. Geotech. 2025, 52, 101583. [Google Scholar] [CrossRef]
- Peshave, A.; Pierron, F.; Lava, P.; Moens, D.; Vandepitte, D. Practical Uncertainty Quantification Guidelines for DIC-Based Numerical Model Validation. Exp. Tech. 2025, 49, 437–457. [Google Scholar] [CrossRef]
- Huang, X.; Li, S.; Zhu, G.; Xu, D.; Feng, Z. Internal Pressure Drives Tensile-to-Shear Transition in Time-Dependent Failure of Deep-Buried Pressurized Tunnels: An AE–DIC Physical Modeling. Rock Mech. Rock Eng. 2025, 1–24. [Google Scholar] [CrossRef]
- Dong, X.; Dou, T.; Dong, P.; Wang, Z.; Li, Y.; Ning, J.; Wei, J.; Li, K.; Cheng, B. Failure experiment and calculation model for prestressed concrete cylinder pipe under three-edge bearing test using distributed fiber optic sensors. Tunn. Undergr. Space Technol. 2022, 129, 104682. [Google Scholar] [CrossRef]
- Liu, K.; Chen, X.; Zhang, P.; Ma, B.; Feng, X.; Zhang, Y.; Liu, H.; Tan, X.; Xu, T. Axial mechanical response of concrete pipe jacking considering the deflection of the bell-and-spigot joint: Full-scale test and numerical simulation. Tunn. Undergr. Space Technol. 2024, 149, 105805. [Google Scholar] [CrossRef]
- Li, C.; Zhong, Z.; Bie, C.; Liu, X. Field performance of large section concrete pipes cracking during jacking in Chongqing—A case study. Tunn. Undergr. Space Technol. 2018, 82, 568–583. [Google Scholar] [CrossRef]
- Kiriella, S.; Manalo, A.; Tien, C.M.T.; Ahmadi, H.; Wham, B.P.; Salah, A.; Tafsirojjaman, T.; Karunasena, W.; Dixon, P.; O’Rourke, T.D. Lateral deformation behaviour of structural internal replacement pipe repair systems. Compos. Struct. 2023, 319, 117144. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, P.; Chen, Y.; Liu, K.; Yan, X.; Ma, B.; Wang, F. Stability assessment of CIPP liner under varied boundary conditions: A theoretical and simulation study. Results Eng. 2024, 22, 102187. [Google Scholar] [CrossRef]
- Zhao, Y.; Ma, B.; Ariaratnam, S.T.; Zeng, C.; Yan, X.; Wang, F.; Wang, T.; Zhu, Z.; He, C.; Shi, G.; et al. Structural performance of damaged rigid pipe rehabilitated by centrifugal spray on mortar liner. Tunn. Undergr. Space Technol. 2021, 116, 104117. [Google Scholar] [CrossRef]
- Deng, Z.; Liu, X.; Zhou, X.; Yang, Q.; Chen, P.; de la Fuente, A.; Ren, L.; Du, L.; Han, Y.; Xiong, F.; et al. Main engineering problems and countermeasures in ultra-long-distance rock pipe jacking project: Water pipeline case study in Chongqing. Tunn. Undergr. Space Technol. 2022, 123, 104420. [Google Scholar] [CrossRef]
- Zare, M.R.; Iseley, D.T.; Najafi, M. Trenchless Limitations on Postearthquake Repair and Rehabilitation of Unpressurized Networks: Christchurch, New Zealand. J. Pipeline Syst. Eng. Pract. 2019, 10, 05019002. [Google Scholar] [CrossRef]
- Jia, P.; Guan, Y.; Lu, B.; Zhao, W.; Bai, Q.; Du, X. Flexural performance of steel tube roof slab and parameter optimization. Case Stud. Constr. Mater. 2023, 18, e01726. [Google Scholar] [CrossRef]
- Sterling, R.L. Developments and research directions in pipe jacking and microtunneling. Undergr. Space. 2020, 5, 1–19. [Google Scholar] [CrossRef]
- GB/T 11836-2009; Concrete and Reinforced Concrete Sewer Pipes. Standardization Administration of China: Beijing, China, 2009.
- Hebert, J.; Khonsari, M. The application of digital image correlation (DIC) in fatigue experimentation: A review. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 1256–1299. [Google Scholar] [CrossRef]
- Huang, F.; Wu, C.; Ni, P.; Wan, G.; Zheng, A.; Jang, B.-A.; Karekal, S. Experimental analysis of progressive failure behavior of rock tunnel with a fault zone using non-contact DIC technique. Int. J. Rock Mech. Min. Sci. 2020, 132, 104355. [Google Scholar] [CrossRef]
- Zaletelj, K.; Slavič, J.; Boltežar, M. Full-field DIC-based model updating for localized parameter identification. Mech. Syst. Signal Process. 2022, 164, 108287. [Google Scholar] [CrossRef]







| Test Condition | Deflection Angle | ||||||
|---|---|---|---|---|---|---|---|
| Co-directional Deflection | α | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| β | 0.5~3.0 | 0.5~3.0 | 0.5~3.0 | 0.5~3.0 | 0.5~3.0 | 0.5~3.0 | |
| Diagonal Deflection | α′ | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| β′ | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | |
| Test Conditions | Central Angle/° | Defect Location | |||||
|---|---|---|---|---|---|---|---|
| Defect Angles | 30 | 45 | 60 | 75 | 90 | ||
| Scope of Defects | 8.33% | 12.5% | 16.7% | 20.8% | 25% | ||
| Single Defect Angle | 30 | 45 | 60 | 75 | 90 | Vault | |
| Combined Defect Angle | 90 | 90 | 90 | 90 | 90 | Vault & | |
| 30 | 45 | 60 | 75 | 90 | Bottom | ||
| Load /kN | Theoretical Values/MPa | 1# 90°Testing/MPa | 1# 135°Testing/MPa | 1# 180°Testing/MPa |
|---|---|---|---|---|
| 1 | −0.20 | −0.22 | −0.25 | −0.22 |
| 2 | −0.40 | −0.46 | −0.46 | −0.35 |
| 3 | −0.60 | −0.68 | −0.65 | −0.45 |
| 4 | −0.80 | −0.81 | −0.74 | −0.47 |
| 5 | −0.99 | −0.97 | −0.88 | −0.57 |
| 6 | −1.19 | −1.20 | −1.09 | −0.75 |
| Average error rate (%) | 0 | 6.74 | 3.73 | −24.27 |
| Fitting Parameters | |||||||||
| Values | −0.296 | −0.106 | −0.001 | −0.004 | 0.075 | 0.000008 | −0.023 | 0.01 | −0.0005 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Chen, J.; Zhang, Y.; Wu, H.; Zhang, X. Study on the Stress Response and Deformation Mechanism of Pipe Jacking Segments Under the Coupling Effect of Defects and Deflection. Appl. Sci. 2025, 15, 12465. https://doi.org/10.3390/app152312465
Luo Z, Chen J, Zhang Y, Wu H, Zhang X. Study on the Stress Response and Deformation Mechanism of Pipe Jacking Segments Under the Coupling Effect of Defects and Deflection. Applied Sciences. 2025; 15(23):12465. https://doi.org/10.3390/app152312465
Chicago/Turabian StyleLuo, Zhimin, Jianhua Chen, Yongjie Zhang, Hanghui Wu, and Xinyu Zhang. 2025. "Study on the Stress Response and Deformation Mechanism of Pipe Jacking Segments Under the Coupling Effect of Defects and Deflection" Applied Sciences 15, no. 23: 12465. https://doi.org/10.3390/app152312465
APA StyleLuo, Z., Chen, J., Zhang, Y., Wu, H., & Zhang, X. (2025). Study on the Stress Response and Deformation Mechanism of Pipe Jacking Segments Under the Coupling Effect of Defects and Deflection. Applied Sciences, 15(23), 12465. https://doi.org/10.3390/app152312465






