Research on the Stability and Support Effect of a Tunnel Excavated by a Mechanical Drilling Method: Insights from a PFC3D-FLAC3D Coupling Simulation
Abstract
1. Introduction
2. Methodology
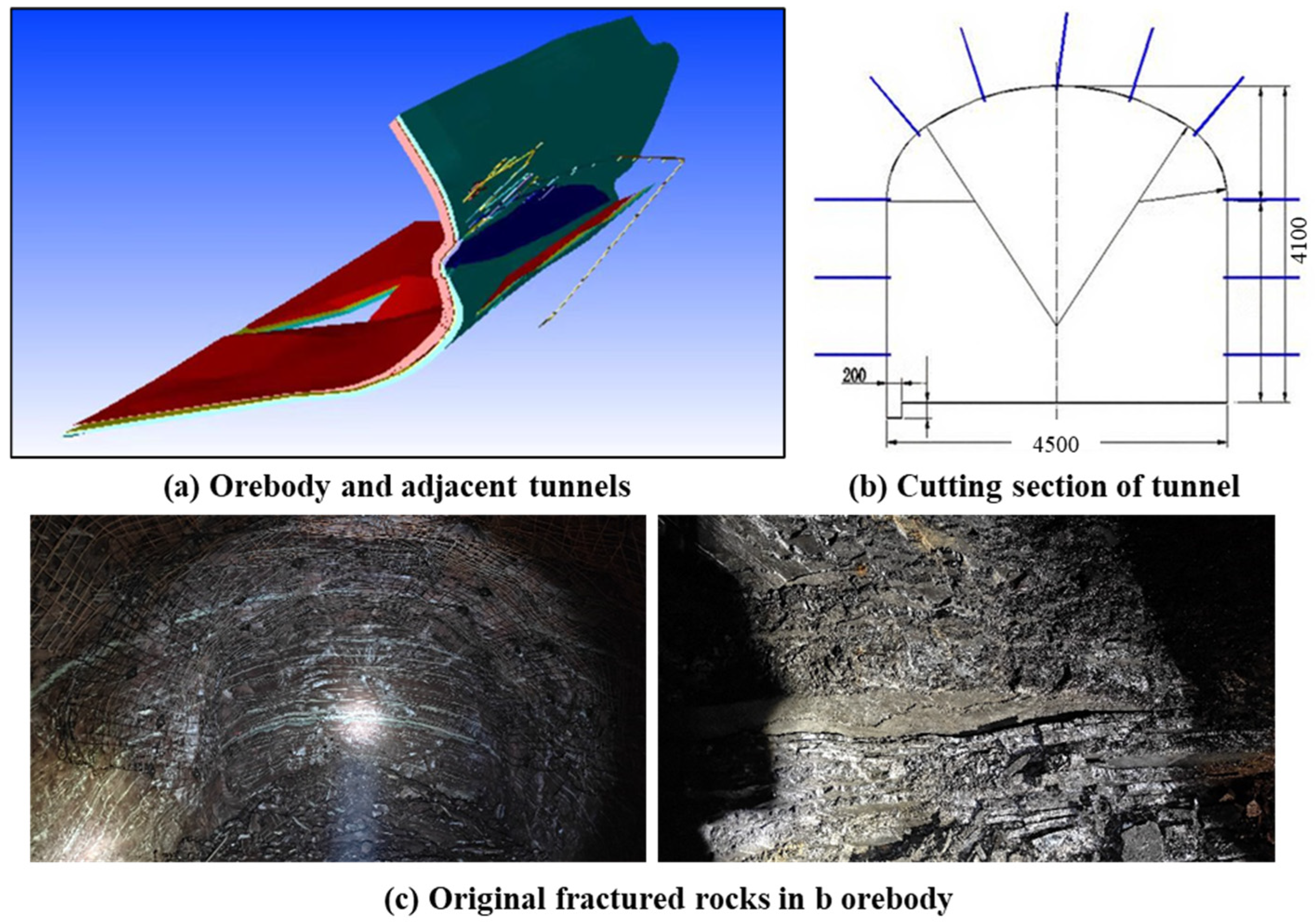
2.1. Engineering Background
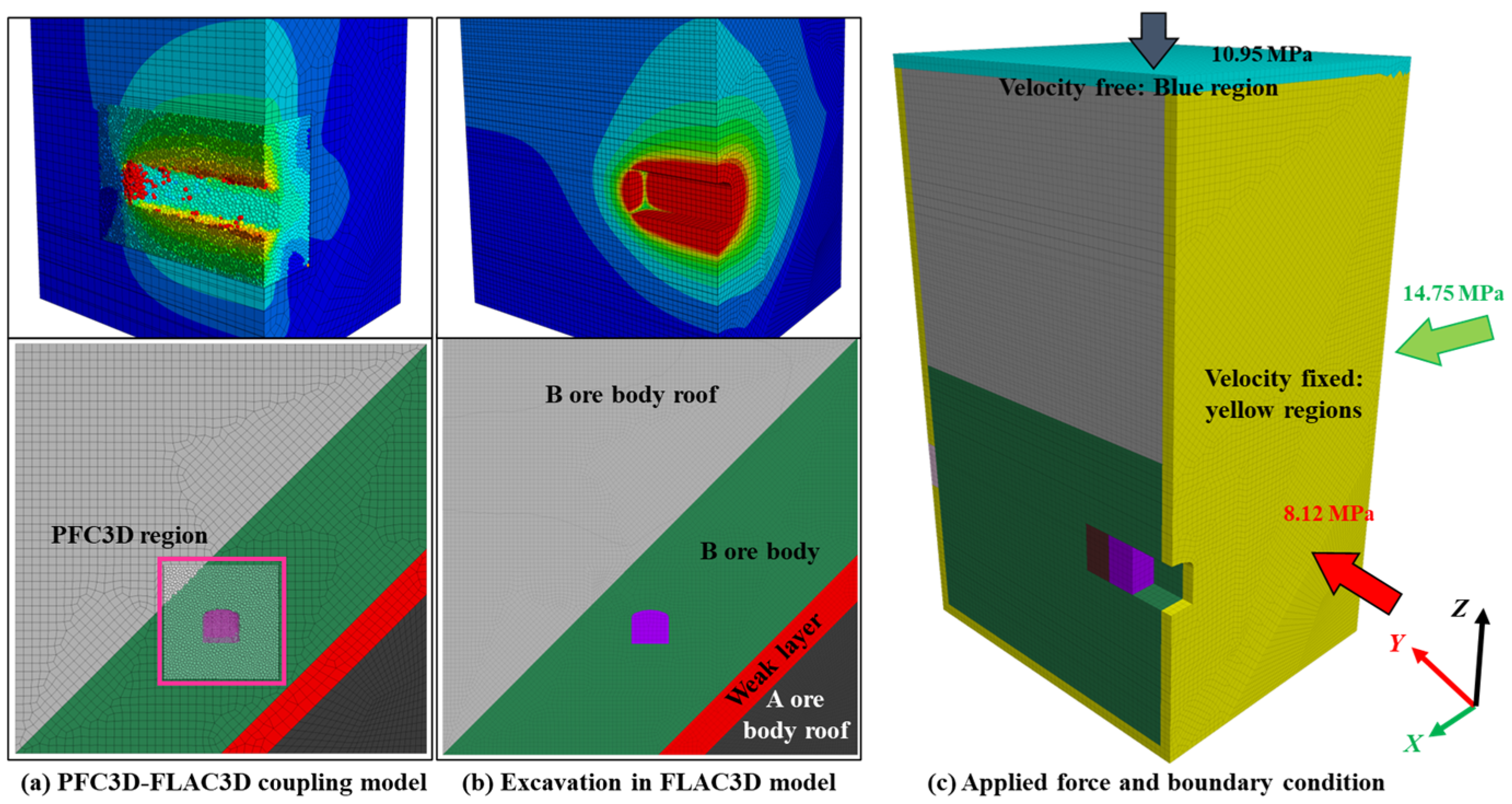
2.2. Modeling of the Inclined Strata
- (1)
- Micro–macro cross-scale analysis capability: PFC3D can simulate micro-mechanical behaviors such as rock fragmentation and particle flow within a discrete particle system, while FLAC3D efficiently models large-scale deformation and stress propagation using continuum theory. Coupling these two approaches allows for the synchronous analysis of local failure mechanisms and overall mechanical responses through the exchange of interface data.
- (2)
- Efficient computation and parameter optimization: By employing a partitioned coupling strategy, FLAC3D handles macroscopic calculations in regions of low strain, whereas PFC3D focuses on microscopic simulations in areas of high deformation gradients. This division substantially reduces the computational cost compared with purely discrete element models.
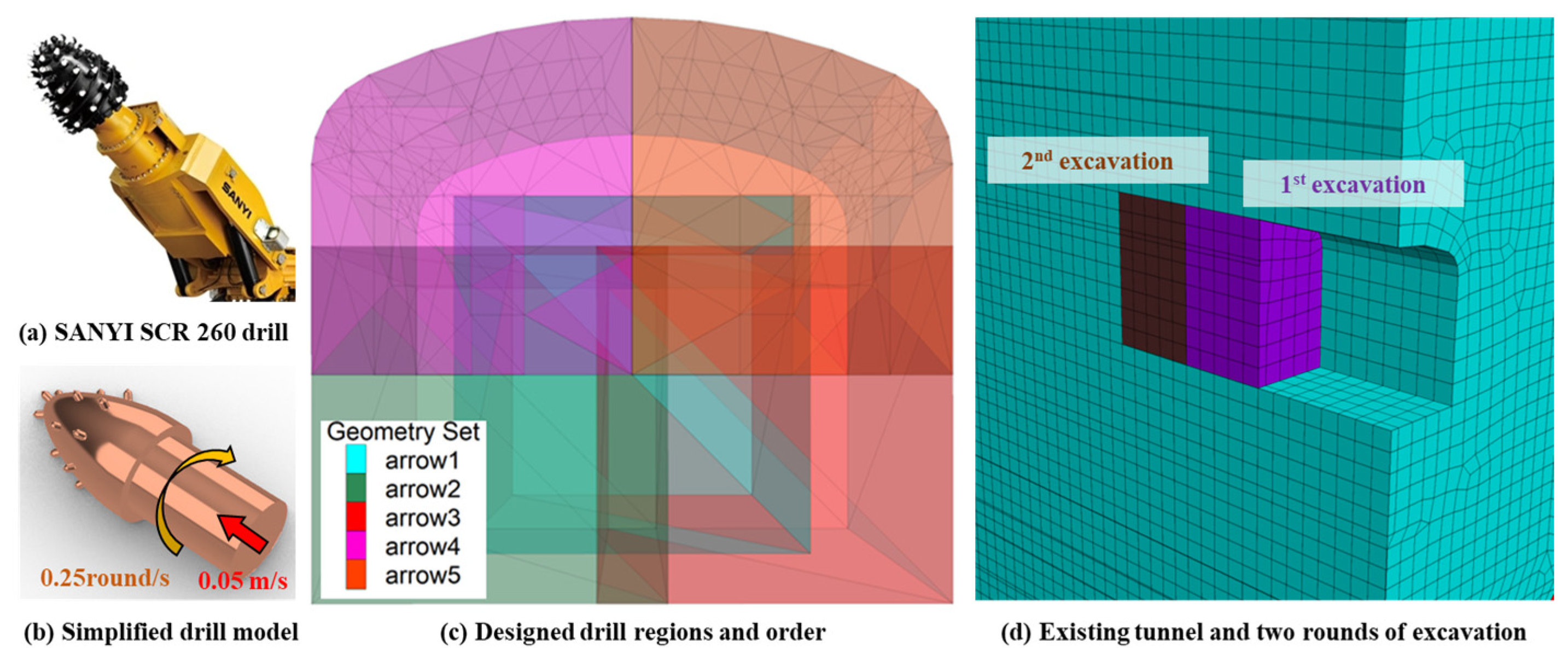
2.3. Simulation of Excavation and Supporting System
3. Tunnel Stability Analysis Based on a Traditional FLAC3D Simulation
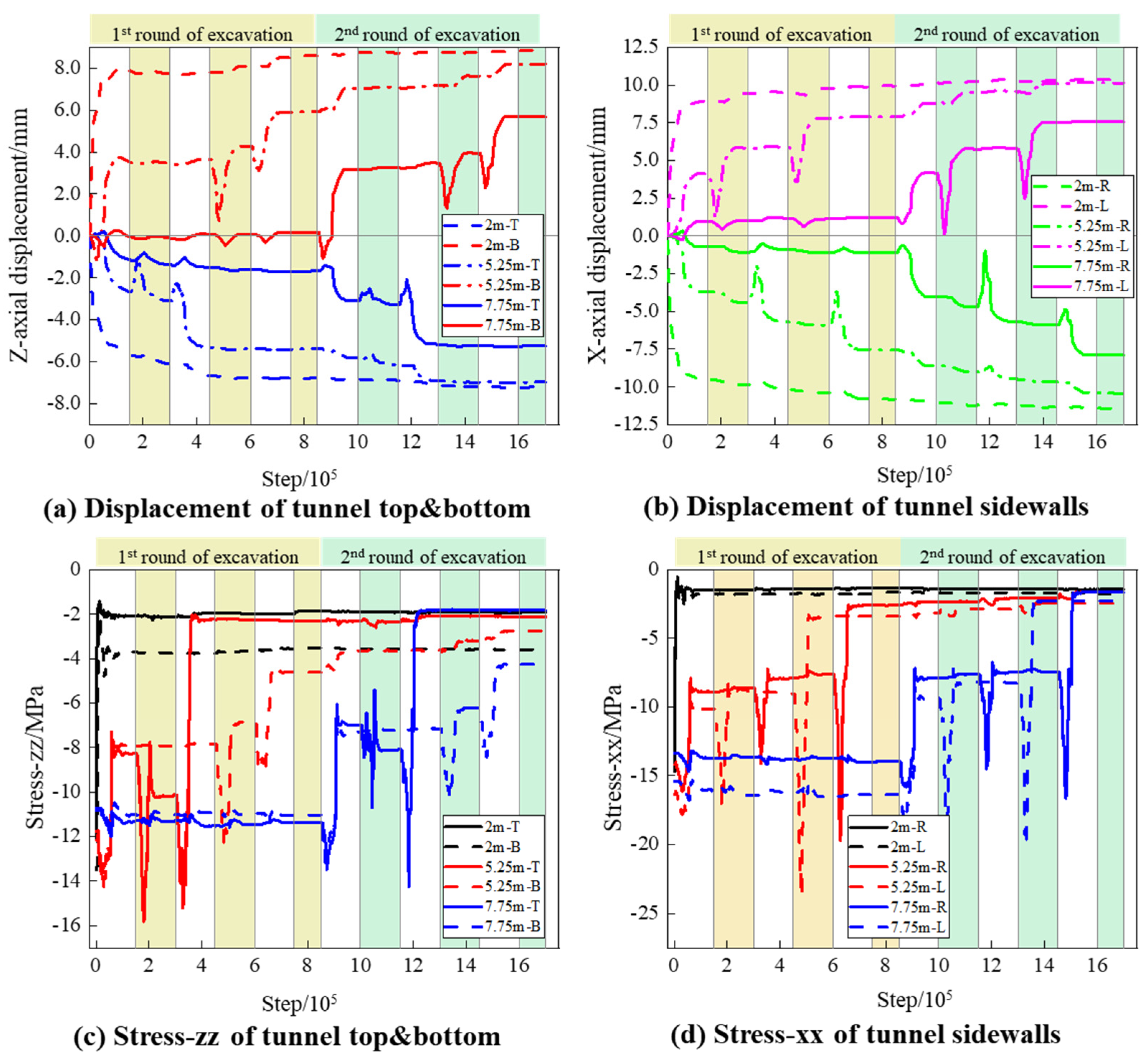
3.1. Physical Responses During the Excavation
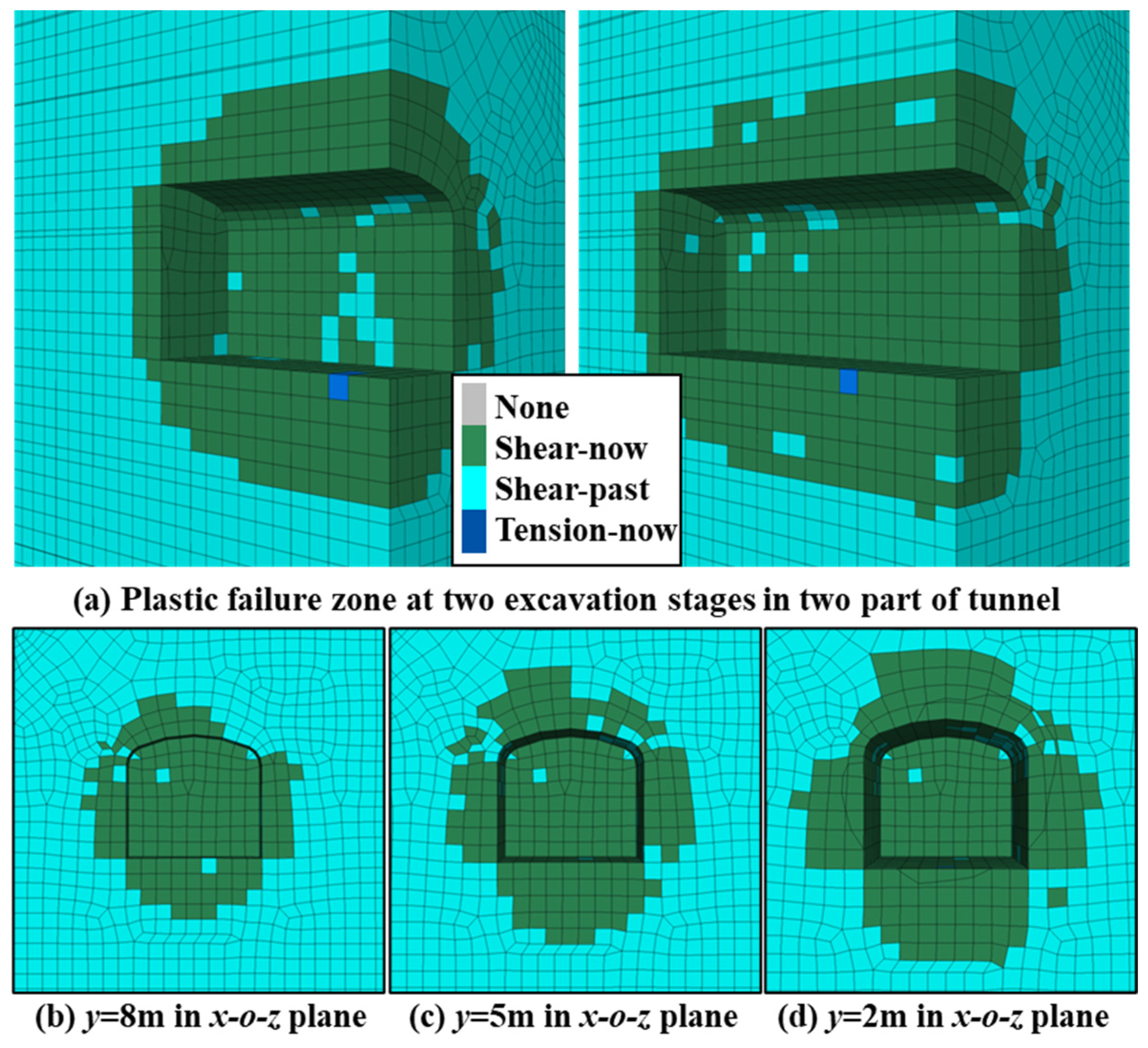
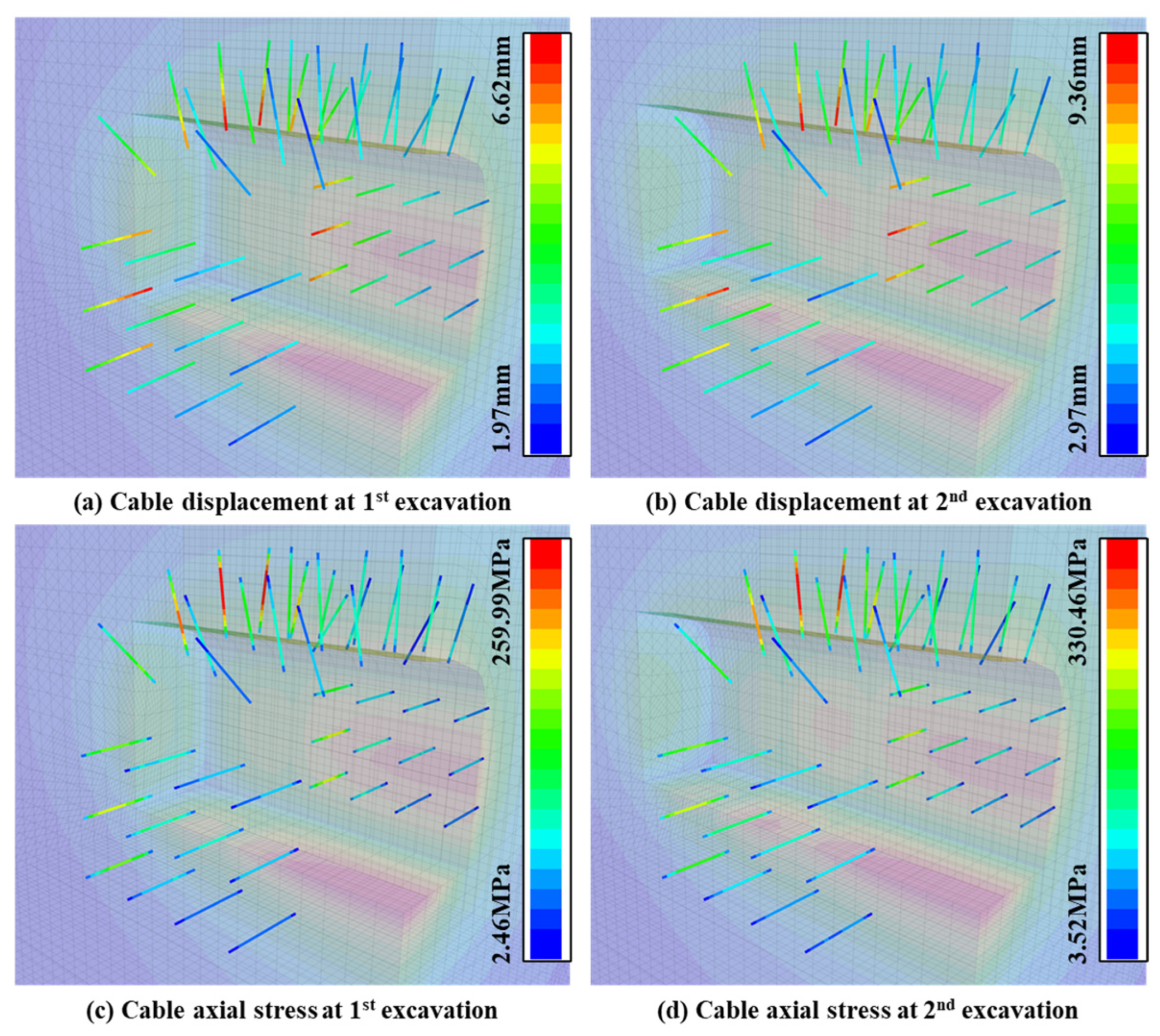
3.2. Responses of the Structural Elements
3.3. Limitations of the Finite Element Method When Simulating Tunnel Excavation
4. Application of the PFC3D-FLAC3D Simulation to the Mechanical Drilling and Excavation of a Tunnel
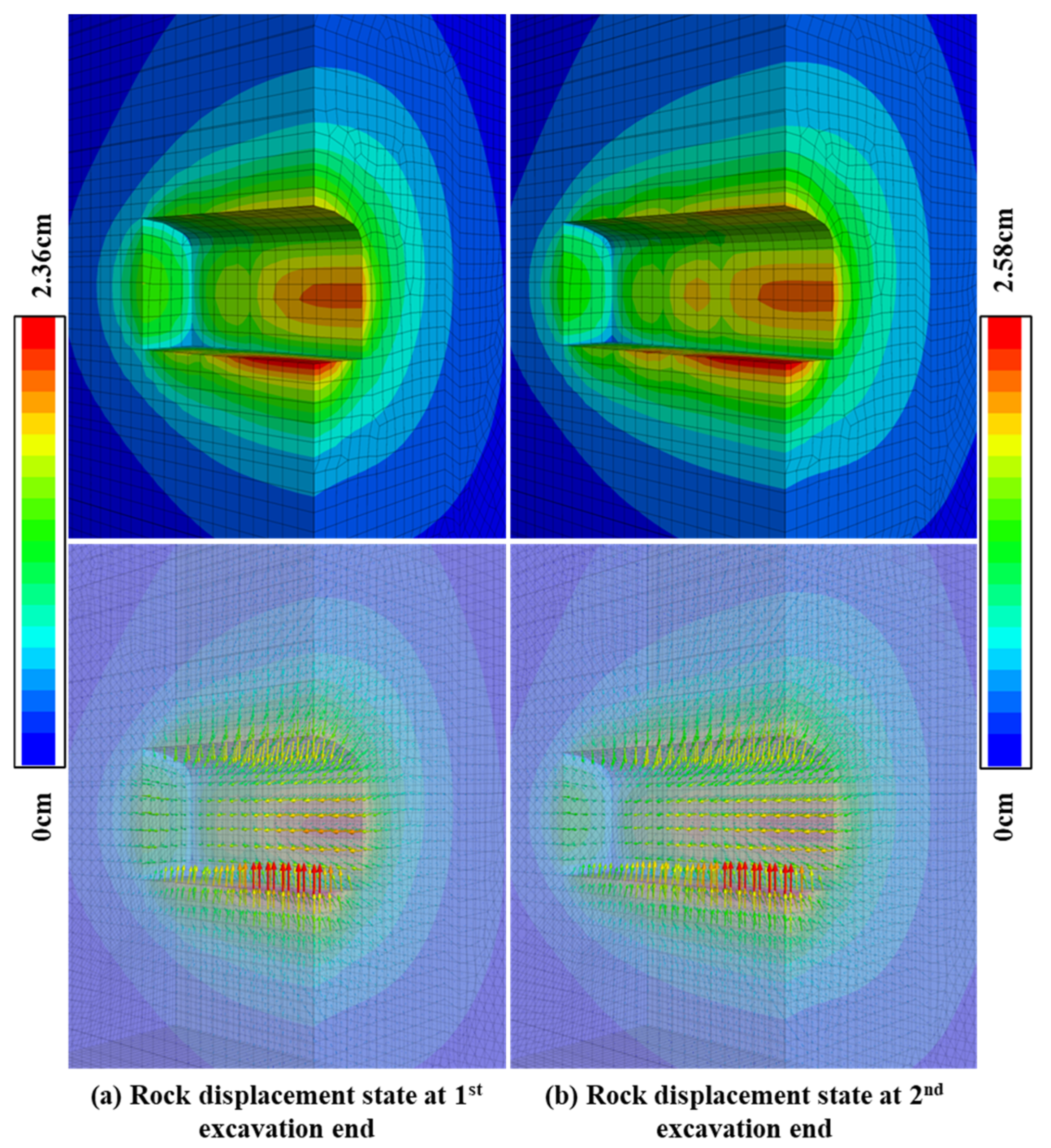
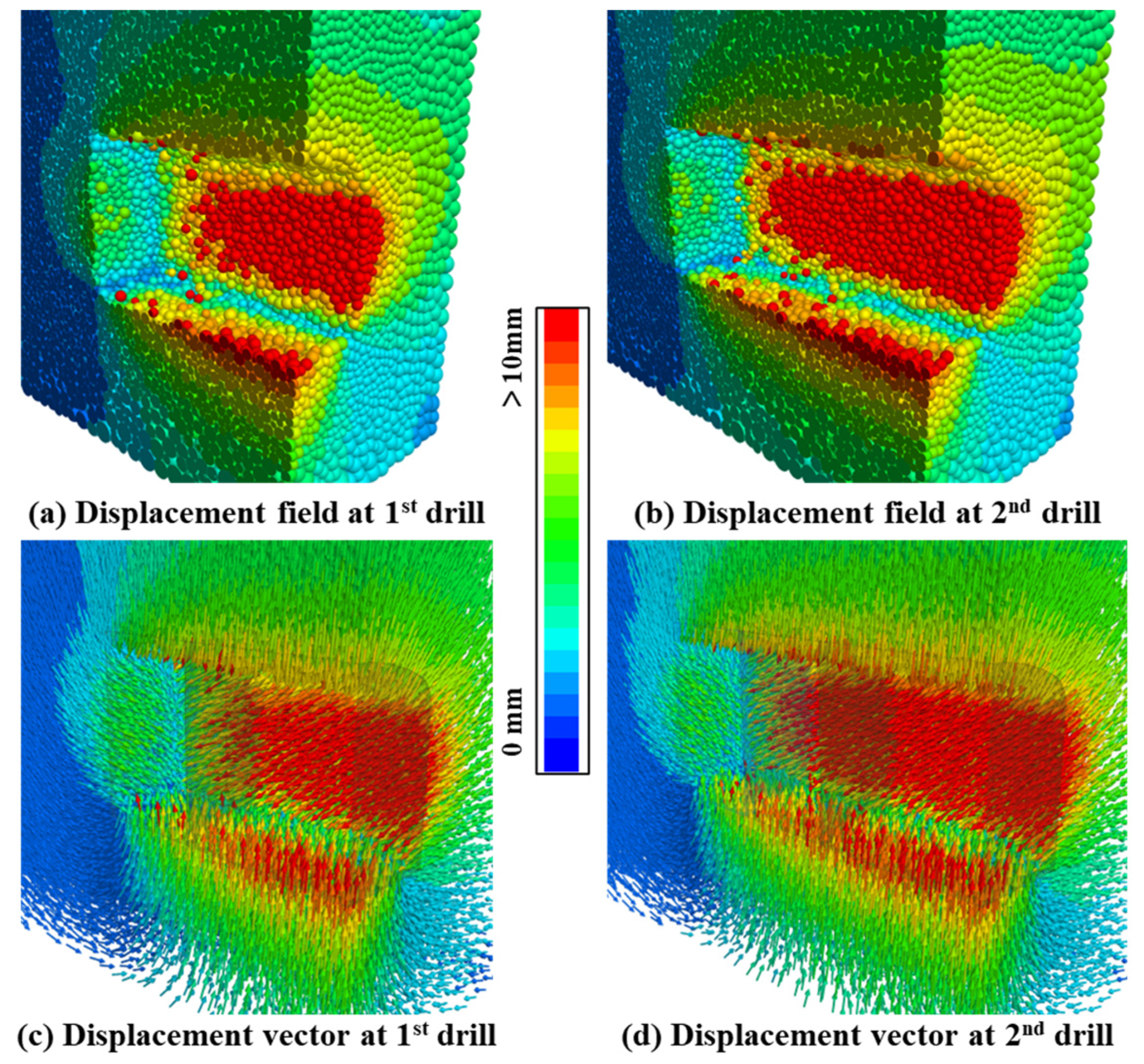
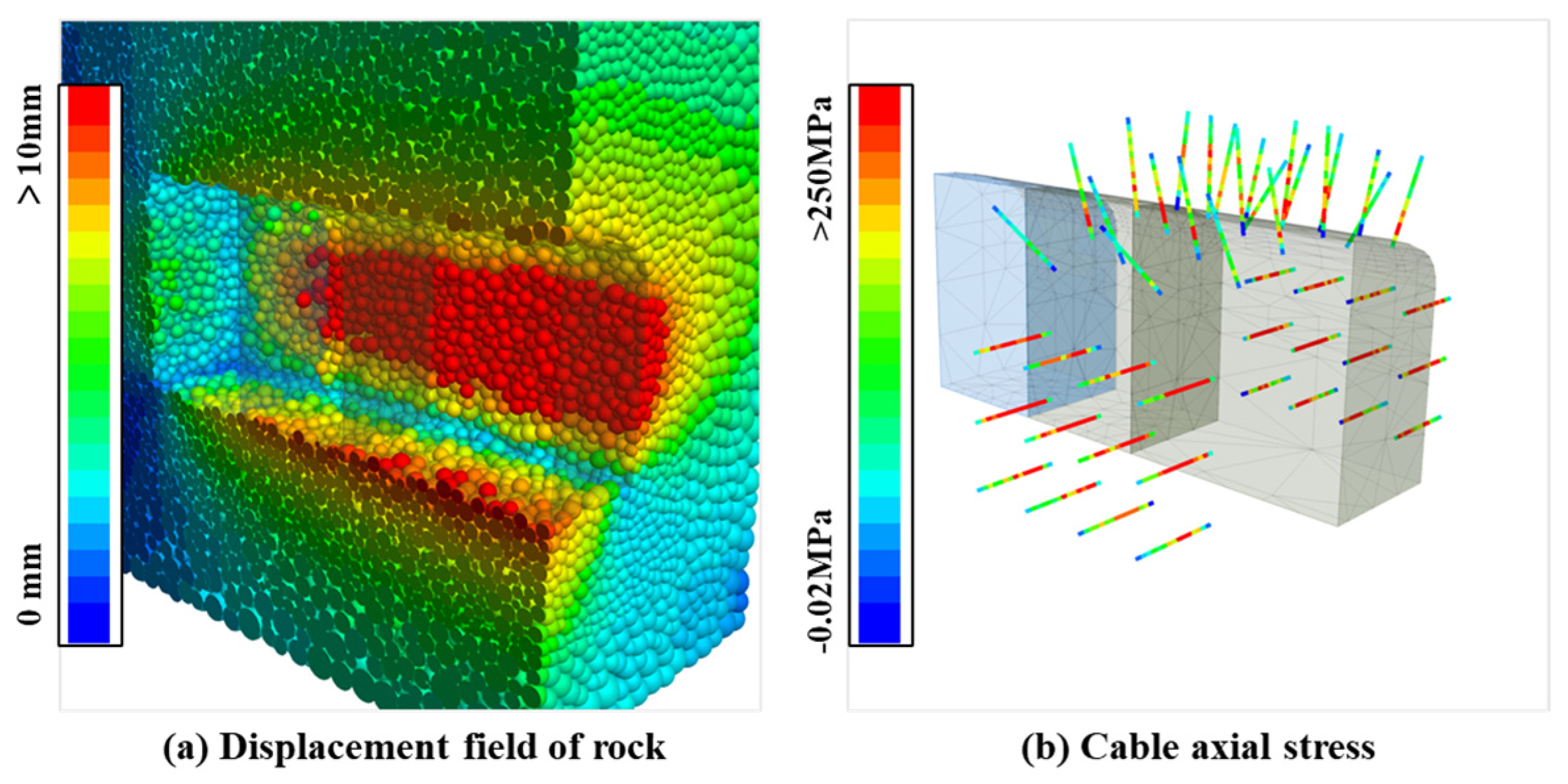
4.1. Deformation and Stress Characteristics of the Surrounding Rock
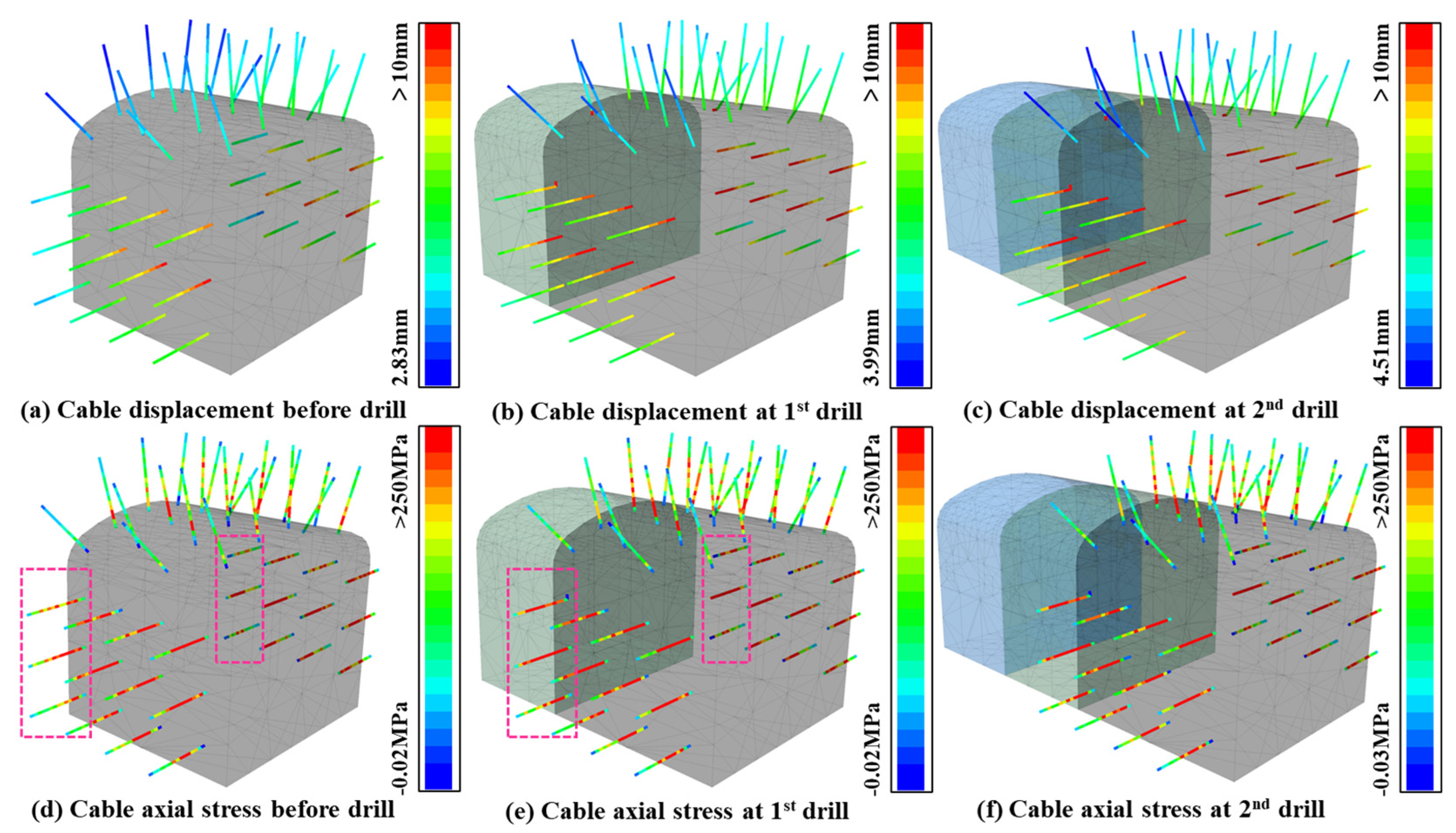
4.2. States of the Structural Elements
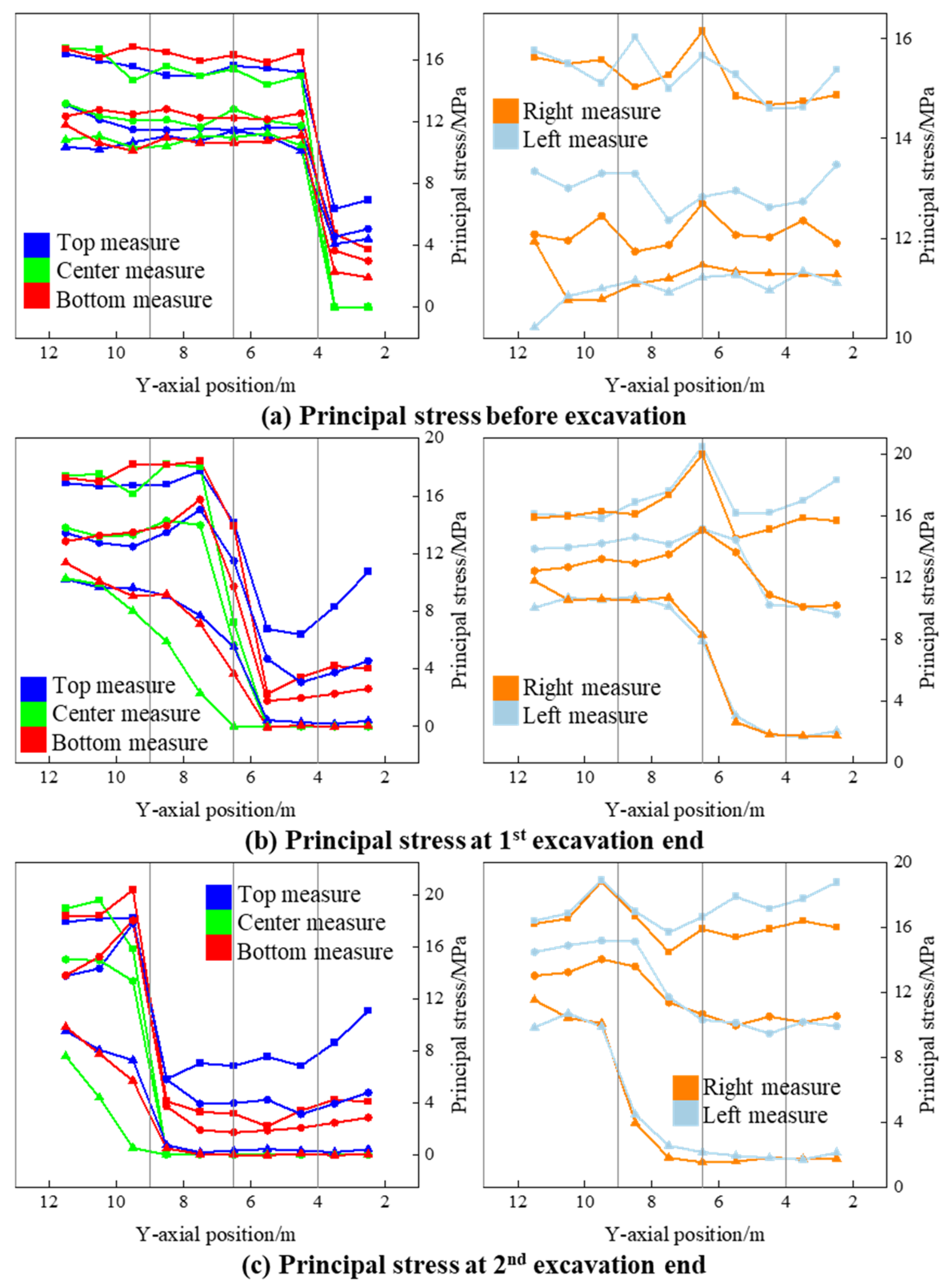
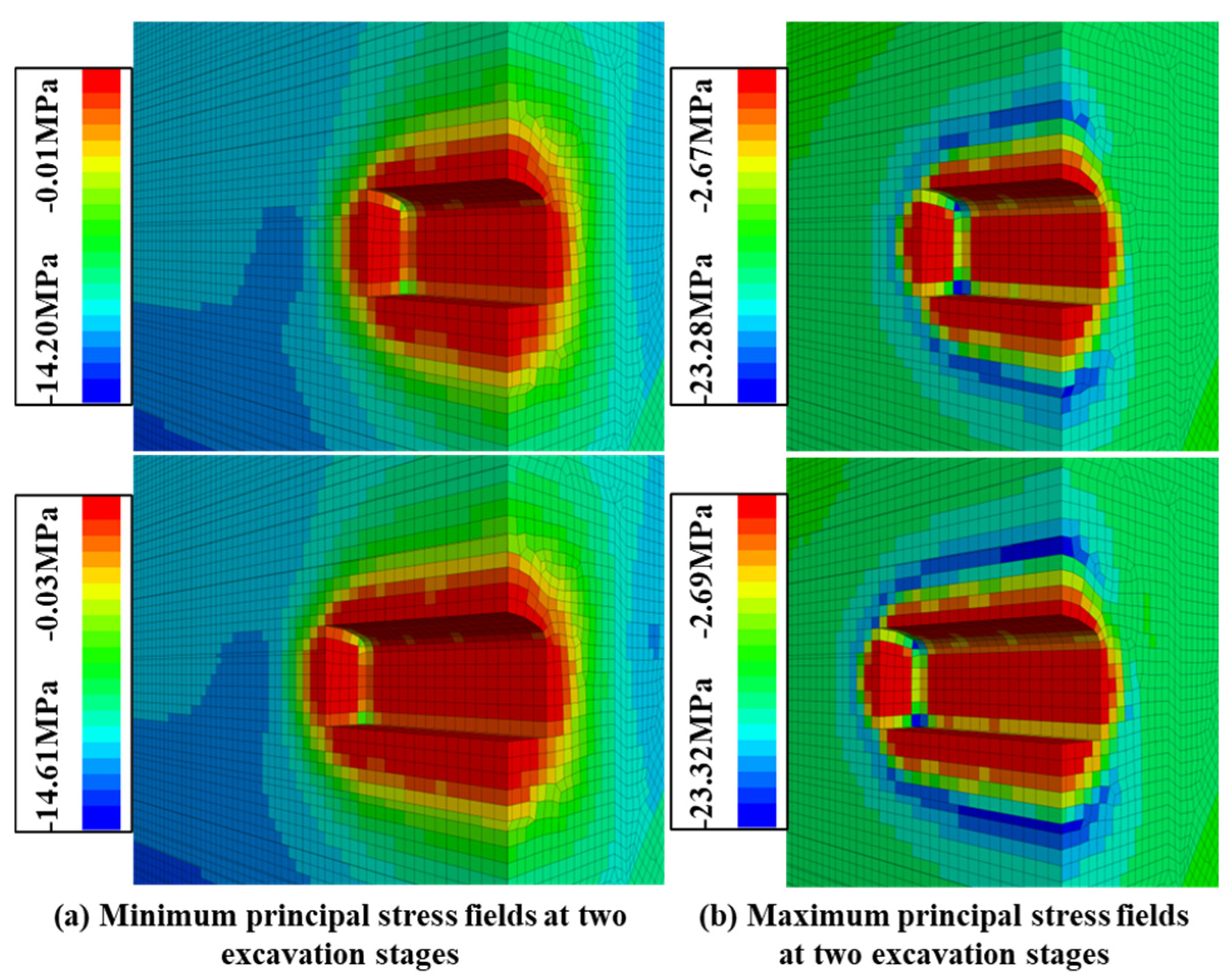
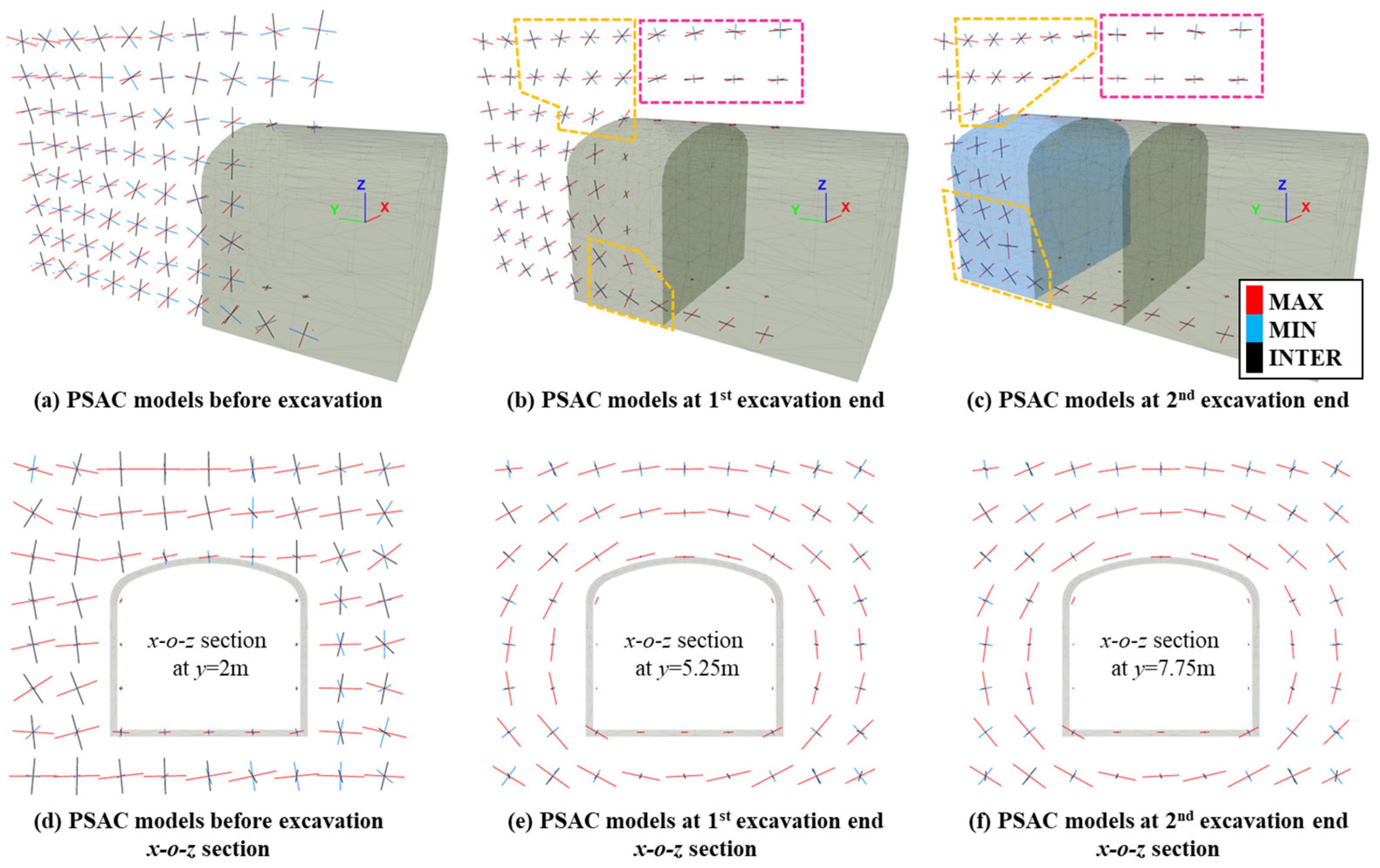
4.3. Local Concentration and Axis Rotation of Principal Stress in the Near-Field
- (1)
- In the initial state (subgraph a), the principal stress at the top center bottom measuring point is relatively small (0–4 m) in the constructed tunnel, while the triaxial principal stress values in the unexcavated rock mass remain stable. From the stress-monitoring curves on the left and right sides, it can be observed that there is not much difference between the two in terms of maximum and minimum principal stresses. However, the principal stress in the middle of the right side is significantly lower than that on the left side (averaging 10% lower). This may be due to uneven convergence on both sides of the tunnel, and the deeper reason is the uneven deformation caused by the inclined rock layers.
- (2)
- After the first excavation is completed (subfigure b), the principal stress of the top center bottom measuring points at the four positions on the right (y = 2.5 m − 5.5 m) remains basically stable; however, the maximum principal stress at the top measuring point showed a significant increase in the early stage of the tunnel, while the minimum principal stress at the top and bottom measuring points dropped from around 2 MPa to 0. The stress of the surrounding rock on the excavation face quickly recovered, and the top and bottom measuring points returned to the far-field stress state at y = 7.5 m, while the center measuring point only fully recovered the stress at y = 12 m. According to the monitoring results of the horizontal measuring points, the minimum principal stress is maintained at around 1 MPa in the excavated tunnel, the middle principal stress slightly decreases, and the maximum principal stress increases significantly compared to the initial state. The maximum principal stress in the horizontal measuring point reaches its peak near the excavation surface, indicating a significant stress concentration at that location; The surrounding rock 1 m deep in front of the excavation has been restored to the far-field stress state.
- (3)
- After the second excavation is completed (subfigure c), the maximum principal stress at the top center bottom measuring point of the surrounding rock in front of the excavation face quickly recovers, while the middle and minimum principal stresses continue to rise; the maximum principal stress at the left and right measuring points remains basically unchanged, while the middle principal stress recovers to the initial ground stress. The minimum principal stress begins to recover at y = 7.5 m and reaches a stable value at y = 10.5 m.
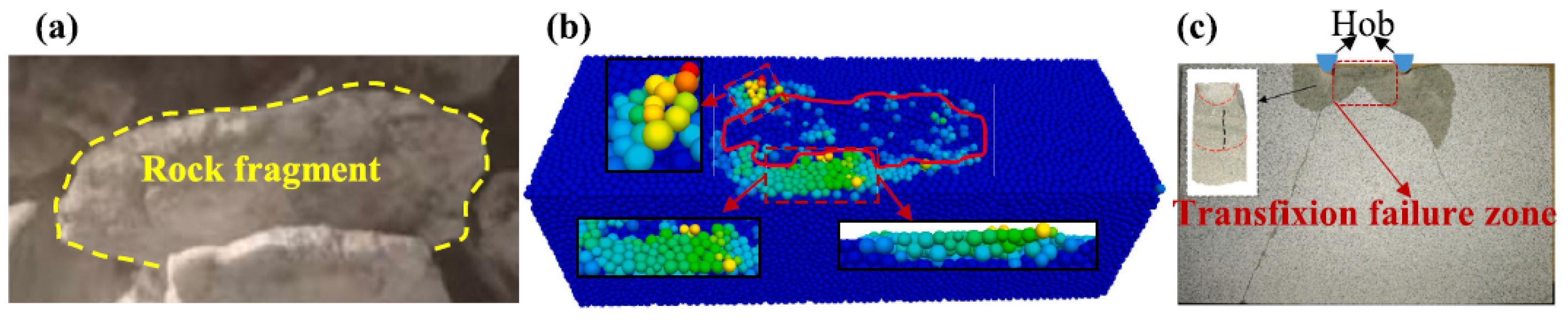
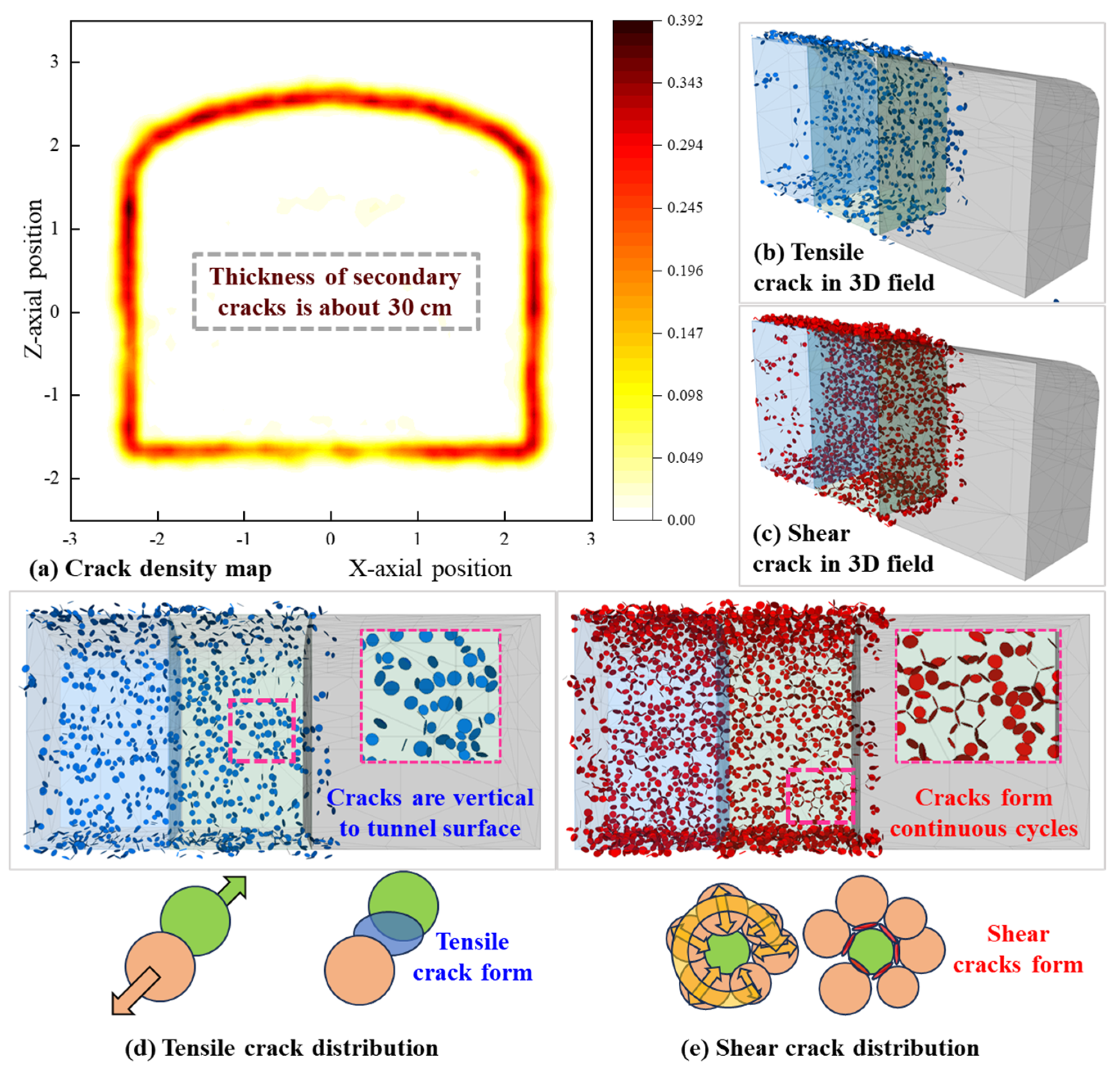
4.4. Distribution and Fundamental Mechanics of Secondary Failures
4.5. Comparison Between Excavation and Simulation Methods
- (1)
- The real mechanical excavation simulation of a new tunnel cannot be completed in FLAC3D models, and the “undisturbed” excavation process can only be achieved using the direct deletion method. The deformation of the surrounding rock, anchor deformation, and displacement obtained by this method are slightly larger than those of the PFC3D model, and the difference is due to the different parameter selection principles of the two numerical simulation methods.
- (2)
- The application of the PFC3D-FLAC3D coupled model can significantly reduce the number of particles and improve computational efficiency. The PFC3D model in this article accounts for 5.2% of the total model volume and contains over 290,000 particles. It is reasonable to speculate that using the large-scale PFC3D model would require at least 2 million particles.
- (3)
- The direct deletion method can form uniform deformation fields in both FLAC3D and PFC3D tunnel models, ignoring any external disturbances to ensure that the surrounding rock and support structures are in a safer state. On the other hand, the mechanical excavation method in the PFC3D model will result in a certain range of secondary damage and un-stripped rock blocks in the surrounding rock, which is more in line with engineering practice and the previous numerical simulation results of small-scale blade-head rock-breaking. It is recommended to use the FLAC3D and PFC3D coupled models for other types of mechanical rock breaking (such as cross cutters, coal automatic cutters) or hard-rock TBM excavation simulations.
5. Conclusions
- (1)
- Whether in traditional FEM simulations or DEM models, if the direct deletion method is used to simulate undisturbed or low-disturbance excavation of tunnels, the simulation results cannot reasonably reproduce the damage caused by mechanical cutting to the surrounding rock in real engineering, resulting in tunnels being “safer” in numerical models (because the influence of mechanical cutting process is whole ignored).
- (2)
- The true triaxial compression stress state constrains the potential impact of weak strata on the tunnel, resulting in a symmetrical distribution of deep displacement and stress fields.
- (3)
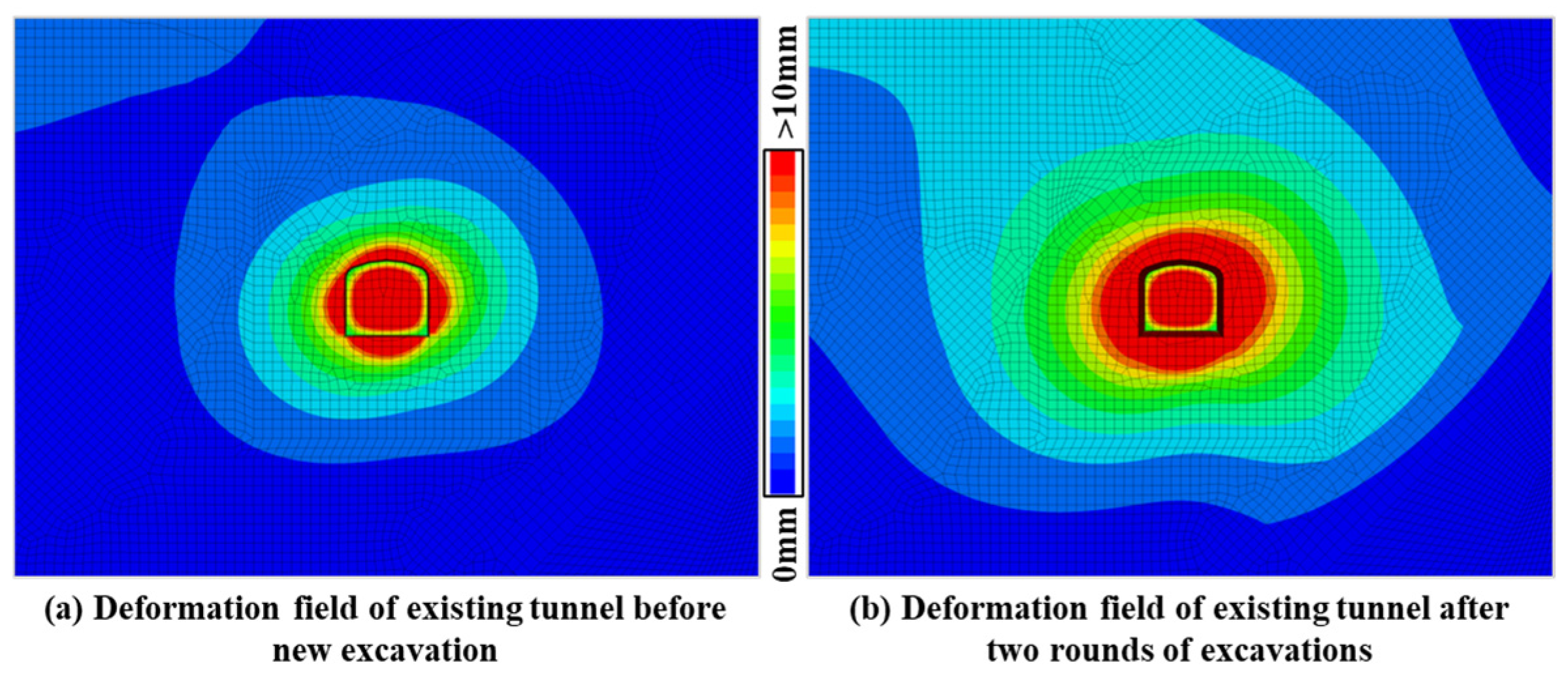
- Due to the maximum external load applied in the horizontal direction, the deformation of the side walls of the tunnel (greater than 10 mm) is significantly greater than that of the surrounding rock of the roof and floor (4–8.5 mm). At the end of the mechanical excavation process, there are still some large deformation particles (with more than 4 cm of movement) remaining on the surface of the tunnel, so these “floating stones” need to be handled carefully in the project. In addition, although the support structure can suppress the deformation of the surrounding rock in the area, the new excavation area needs to complete the support operation in a timely manner (unsupported rock shows a faster deformation rate) to prevent the extreme deformation of the surrounding rock.
- (4)
- When the first excavation finished, the nodes of the structural element in a yielding state gradually increased (the proportion of the yield region in the tunnel side walls rose from 61.9% to 73.5%), especially the anchor rods in the left and right walls, which were adjacent to the new tunnel surface. The second round of excavation had almost no impact on the state of the supporting structure. Although many anchor rods reached the yield stress after two excavations, their axial stress was still less than the tensile strength, and the anchoring system still worked. However, it is necessary to promptly install new anchor rods in the new tunnel to prevent the existing anchor rods from being subjected to stress that exceeds the threshold.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, S.; Kim, J.-S.; Kwon, S. Investigation of the development of an excavation damaged zone and its influence on the mechanical behaviors of a blasted tunnel. Geosystem Eng. 2017, 21, 165–181. [Google Scholar] [CrossRef]
- Mollo, T.; Sengani, F.; Mahachi, J. Experimental and Numerical Analysis on the Static and Dynamic Performance of Adhesive Bolts in Various Ground Conditions. Appl. Sci. 2025, 15, 10293. [Google Scholar] [CrossRef]
- Godio, A.; Oggeri, C.; Seccatore, J. An Analysis of Rock Bolt Dynamic Responses to Evaluate the Anchoring Degree of Fixation. Appl. Sci. 2025, 15, 1513. [Google Scholar] [CrossRef]
- Gholipour, M.; Narimani, S.; Davarpanah, S.M.; Vásárhelyi, B. Evaluating Minimum Support Pressure for Tunnel Face Stability: Analytical, Numerical, and Empirical Approaches. J. Exp. Theor. Anal. 2025, 3, 2. [Google Scholar] [CrossRef]
- Imashev, A.; Mussin, A.; Adoko, A.C. Investigating an Enhanced Contour Blasting Technique Considering Rock Mass Structural Properties. Appl. Sci. 2024, 14, 11461. [Google Scholar] [CrossRef]
- Hashemnejad, A.; Aghda, S.M.F.; Talkhablou, M. Mechanized tunnelling in hydrothermally altered grounds: The effect of hydrothermal fluids on the rock behaviour in the central Iran. Tunn. Undergr. Space Technol. 2020, 99, 103340. [Google Scholar] [CrossRef]
- Deng, K.; Gao, J.; Fan, Y.; Yang, G.; Chen, M.; Lu, W. Experimental Investigation on the Mechanical Characteristics of Cement-Filled Joint under Blasting Load. Arab. J. Sci. Eng. 2025, 1–18. [Google Scholar] [CrossRef]
- Hekmatnejad, A.; Muñoz, F.; Prado, J.; Saavedra, C.; Roja, E.; Crespin, B.; Aguilar, B. Comprehensive Investigation of the Role of the Geometrical, Topological, and Mechanical Properties of Discrete Fracture Network, Rock Type, and In-Situ Stress on Over-Excavation Around a Tunnel of El Teniente Mine. In Recent Research on Geotechnical Engineering, Remote Sensing, Geophysics and Earthquake Seismology; Springer Nature: Cham, Switzerland, 2024; pp. 69–72. [Google Scholar] [CrossRef]
- Parisio, F.; Vilarrasa, V.; Laloui, L. Hydro-mechanical modeling of tunnel excavation in anisotropic shale with coupled damage-plasticity and micro-dilatant regularization. Rock Mech. Rock Eng. 2018, 51, 3819–3833. [Google Scholar] [CrossRef]
- Cho, G.-C.; Joo, G.-W.; Oh, T.-M.; Hong, E.-S. New hydro-mechanical tunnel excavation method using an abrasive waterjet system. Jpn. Geotech. Soc. Spec. Publ. 2016, 4, 132–137. [Google Scholar] [CrossRef]
- Mussin, A.; Imashev, A.; Matayev, A.; Khussan, B.; Abdrashev, R. Probabilistic analysis application to substantiate support parameters in seismically active and fractured rock masses. Min. Miner. Deposits 2025, 19, 66–75. [Google Scholar] [CrossRef]
- Bai, Y.; Li, X.; Yang, W.; Xu, Z.; Lv, M. Multiscale analysis of tunnel surrounding rock disturbance: A PFC3D-FLAC3D coupling algorithm with the overlapping domain method. Comput. Geotech. 2022, 147, 104752. [Google Scholar] [CrossRef]
- Hou, R.; Cui, Q.; Guo, Y.; Shi, Y.; Fu, J. A new elasto-visco-plastic damage model and numerical simulation method used for time-dependent behavior prediction of deep tunnel. Comput. Geotech. 2024, 168, 106129. [Google Scholar] [CrossRef]
- Min, G.; Fukuda, D.; Oh, S.; Cho, S. Investigation of the dynamic tensile fracture process of rocks associated with spalling using 3-D FDEM. Comput. Geotech. 2023, 164, 105825. [Google Scholar] [CrossRef]
- Zheng, Z.; Li, S.; Zhang, Q.; Tang, H.; Liu, G.; Pei, S.; Lu, G. True triaxial test and DEM simulation of rock mechanical behaviors, meso-cracking mechanism and precursor subject to underground excavation disturbance. Eng. Geol. 2024, 337, 107567. [Google Scholar] [CrossRef]
- Song, Y.; Yang, S.-Q.; Li, K.-S.; Yin, P.-F.; Pan, P.-Z. Mechanical Behavior and Fracture Evolution Mechanism of Composite Rock Under Triaxial Compression: Insights from Three-Dimensional DEM Modeling. Rock Mech. Rock Eng. 2023, 56, 7673–7699. [Google Scholar] [CrossRef]
- Sun, Y.; Kwok, C.Y.; Duan, K. Size effects on crystalline rock masses: Insights from grain-based DEM modeling. Comput. Geotech. 2024, 171, 106376. [Google Scholar] [CrossRef]
- Xu, C.; Liu, Q.; Tang, X.; Sun, L.; Deng, P.; Liu, H. Dynamic stability analysis of jointed rock slopes using the combined finite-discrete element method (FDEM). Comput. Geotech. 2023, 160, 105556. [Google Scholar] [CrossRef]
- Zhao, Y.; Qi, Q.; Chen, C.; Chen, L. Spalling characteristics of sandstone containing rectangle hole with gradient cavity height: An experimental and DEM numerical study. Theor. Appl. Fract. Mech. 2024, 133, 104550. [Google Scholar] [CrossRef]
- Si, X.; Luo, Y.; Luo, S. Influence of lithology and bedding orientation on failure behavior of “D” shaped tunnel. Theor. Appl. Fract. Mech. 2023, 129, 3017–3038. [Google Scholar] [CrossRef]
- Zhang, X.-P.; Zhang, P.-Y.; Ji, P.-Q.; Zhang, H.; Zhang, Q. The Applicability of Brazilian Test Loading with Different Platens to Measure Tensile Strength of Rock: A Numerical Study. Rock Mech. Rock Eng. 2023, 57, 233–260. [Google Scholar] [CrossRef]
- An, M.; Elsworth, D.; Zhang, W.; Wang, T.; Huang, R.; Huang, L.; Zhang, F. Role of Chlorite on the Friction and Stability of Granite Faults and Implications for Seismicity in Deep Geothermal Reservoirs. Rock Mech. Rock Eng. 2025. [Google Scholar] [CrossRef]
- Chen, J.; Ma, J.; Zeng, X.; Zeng, B.; Skrzypkowski, K.; Zagórski, K.; Zagórska, A.; Wu, S. An Enhanced Numerical Calculation Method to Study the Anchorage Performance of Rebars. Materials 2024, 17, 3987. [Google Scholar] [CrossRef] [PubMed]
- Takhanov, D.; Zhienbayev, A.; Zharaspaev, M. Determining the parameters for the overlying stratum caving zones during re-peated mining of pillars. Min. Miner. Deposits 2024, 18, 93–103. [Google Scholar] [CrossRef]
- Tahmasebinia, F.; Yang, A.; Feghali, P.; Skrzypkowski, K. A Numerical Investigation to Calculate Ultimate Limit State Capacity of Cable Bolts Subjected to Impact Loading. Appl. Sci. 2022, 13, 15. [Google Scholar] [CrossRef]
- Huang, H.; Wang, P.; Huang, B.; Jing, G.; Cai, M. Fracturing characteristics of unconfined rock plate subjected to point-plate loading. Eng. Fract. Mech. 2025, 319, 111047. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, X.; Wang, B.; Zhuo, X.; Jia, L. Investigation into the Rock-Breaking Forces of TBM Disc Cutters with Diverse Edge Shapes. Rock Mech. Rock Eng. 2025. [Google Scholar] [CrossRef]
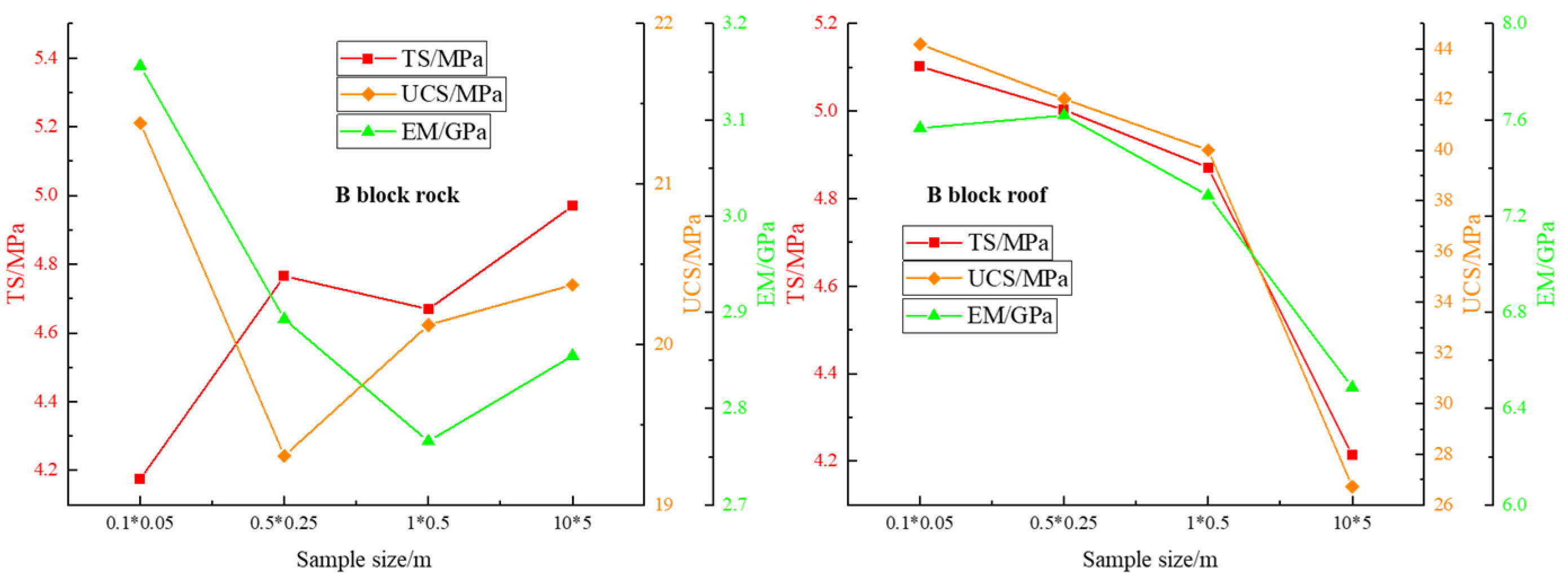

| Rock Strata | Dry Density (g/cm3) | Saturation Rate (%) | UCS (MPa) | Elastic Modulus E/GPa | Poisson’s Ratio μ | Tensile Strength (MPa) | Cohesion c/MPa | Internal Friction Angle φ/(°) |
|---|---|---|---|---|---|---|---|---|
| B orebody roof | 2.67 | 1.11% | 45.37 | 7.50 | 0.21 | 4.63 | 7.25 | 54.57 |
| B orebody | 2.80 | 14.24% | 21.35 | 3.10 | 0.22 | 4.13 | 4.70 | 42.52 |
| Week layer | 2.81 | 5.45% | 28.95 | 3.60 | 0.23 | 4.74 | 5.86 | 45.94 |
| A orebody | 3.00 | 0.77% | 72.61 | 8.50 | 0.28 | 11.21 | 14.26 | 47.10 |
| A orebody bottom | 2.86 | 0.35% | 144.68 | 76.24 | 0.13 | 8.08 | 16.28 | 63.4 |
| Parameters | A Orebody Bottom | A Orebody | Week Layer | B Orebody | B Orebody Roof |
|---|---|---|---|---|---|
| Density (g/cm3) | 3.00 | 2.86 | 2.81 | 2.80 | 2.67 |
| Bulk modulus (GPa) | 18.31 | 5.33 | 1.74 | 5.56 | 5.26 |
| Shear modulus (GPa) | 13.82 | 3.20 | 0.45 | 1.85 | 2.29 |
| Cohesion (MPa) | 2.10 | 1.50 | 0.19 | 0.65 | 0.70 |
| Fric | 57 | 47 | 26 | 38 | 39 |
| Mirco-Parameters | B Block Rock (Values) | B Block Roof (Values) |
|---|---|---|
| Particle minimum radius Rmin | 0.15 m | 0.15 m |
| Ratio of the particle maximum-to-minimum radius Rrat | 1.66 | 1.66 |
| Particle assembly porosity | 0.08 | 0.08 |
| Damping coefficient | 0.7 | 0.7 |
| Particle density ρ | 2800 kg/m3 | 2670 kg/m3 |
| Young’s modulus of particles | 1.0 GPa | 1.0 GPa |
| Young’s modulus of parallel bonds | 3.0 Pa | 3.0 Pa |
| Normal-to-shear stiffness ratio of the parallel bond kn/ks | 1.0 | 1.0 |
| Parallel bond tensile strength | 8.1 MPa | 6.5 MPa |
| Parallel bond cohesion strength | 9.05 MPa | 20.1 MPa |
| Friction angle between particles φ | 42.5 | 54.5 |
| Group | Properties |
|---|---|
| Cross-sectional area of the anchor rod | 3.8 × 10−4 m2 |
| Cross-sectional area of the drilling hole | 12.57 × 10−4 m2 |
| Young (combined status of steel and cement-based material) | 98.6 × 109 Pa |
| Yield–tension | 310 × 103 Pa |
| Grout stiffness | 2 × 107 Pa |
| Crout cohesion | 10 × 105 Pa |
| Length of the anchor rod | 1.5 m |
| Diameter of the anchor rod | 22 mm |
| Type of material | Q235 |
| Tensile strength of the anchor rod | 400 MPa |
| Yield strength of the anchor rod | 250 MPa |
| Element number in one cable | 15 |
| Grout length | Full length |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Zheng, Z.; Zhao, Y. Research on the Stability and Support Effect of a Tunnel Excavated by a Mechanical Drilling Method: Insights from a PFC3D-FLAC3D Coupling Simulation. Appl. Sci. 2025, 15, 12309. https://doi.org/10.3390/app152212309
Huang D, Zheng Z, Zhao Y. Research on the Stability and Support Effect of a Tunnel Excavated by a Mechanical Drilling Method: Insights from a PFC3D-FLAC3D Coupling Simulation. Applied Sciences. 2025; 15(22):12309. https://doi.org/10.3390/app152212309
Chicago/Turabian StyleHuang, Dan, Zhijie Zheng, and Yusong Zhao. 2025. "Research on the Stability and Support Effect of a Tunnel Excavated by a Mechanical Drilling Method: Insights from a PFC3D-FLAC3D Coupling Simulation" Applied Sciences 15, no. 22: 12309. https://doi.org/10.3390/app152212309
APA StyleHuang, D., Zheng, Z., & Zhao, Y. (2025). Research on the Stability and Support Effect of a Tunnel Excavated by a Mechanical Drilling Method: Insights from a PFC3D-FLAC3D Coupling Simulation. Applied Sciences, 15(22), 12309. https://doi.org/10.3390/app152212309






