Rock Cutting and Crack Propagation of Jointed Rock Mass Within Rough Fractures Based on Point-Splitting Process
Abstract
1. Introduction
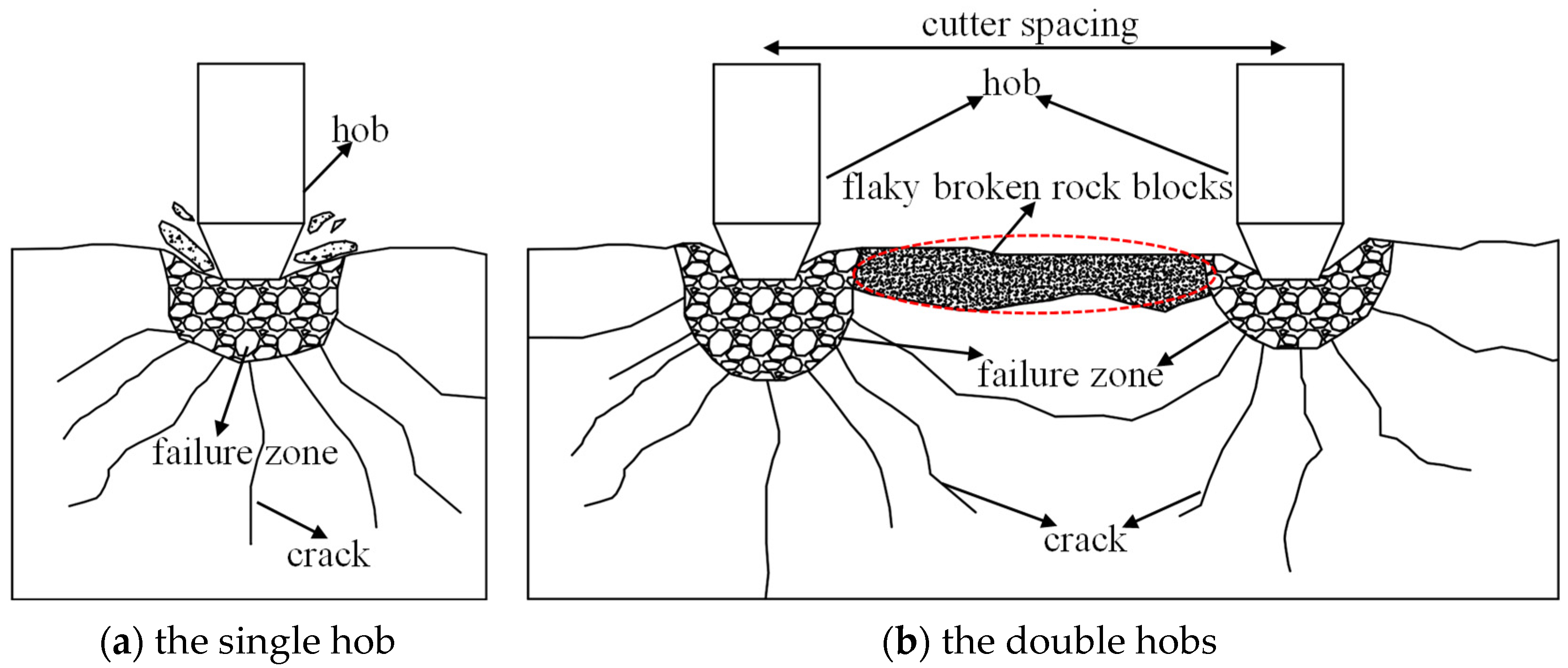
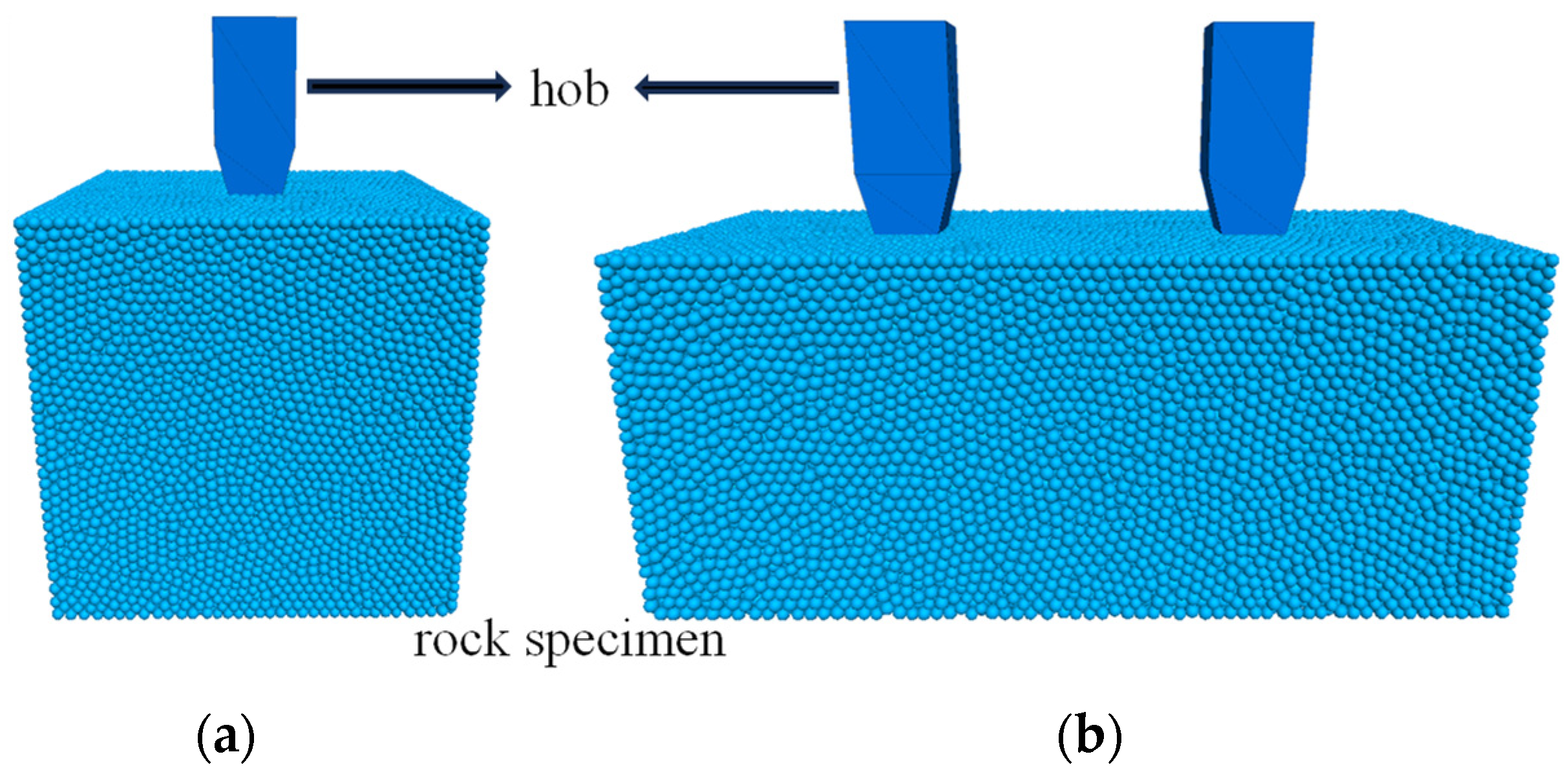
2. Establishment of Rock Breaking Model
3. Complete Rock Breaking
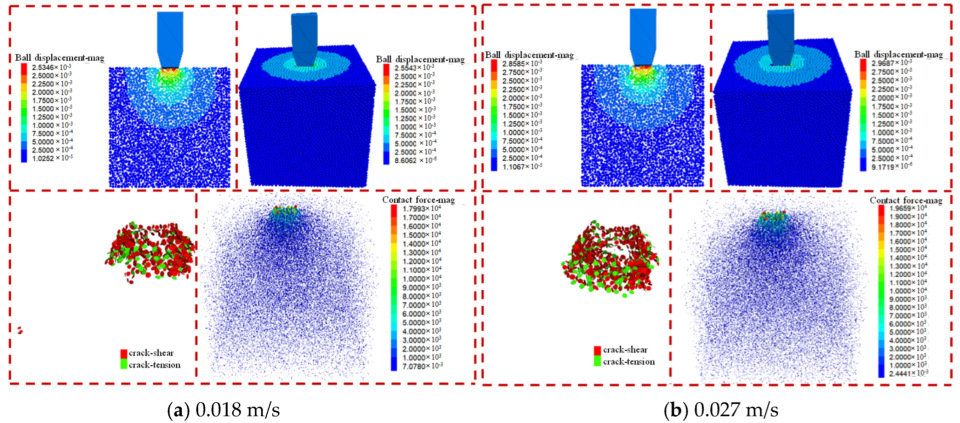
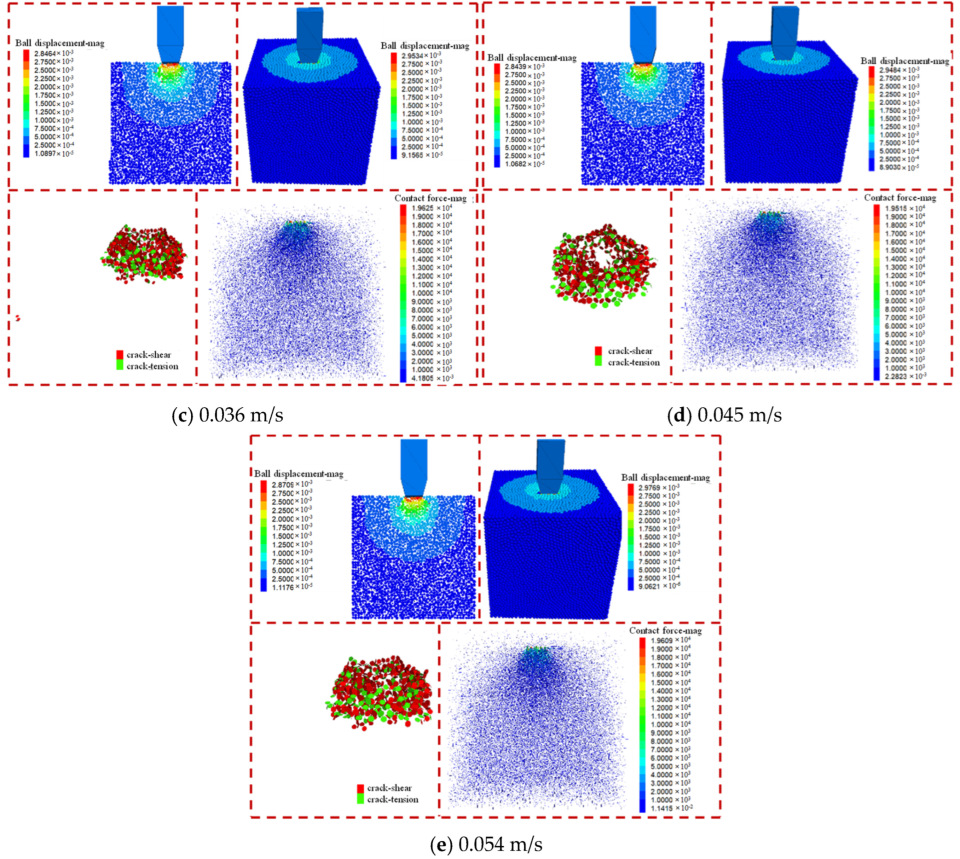
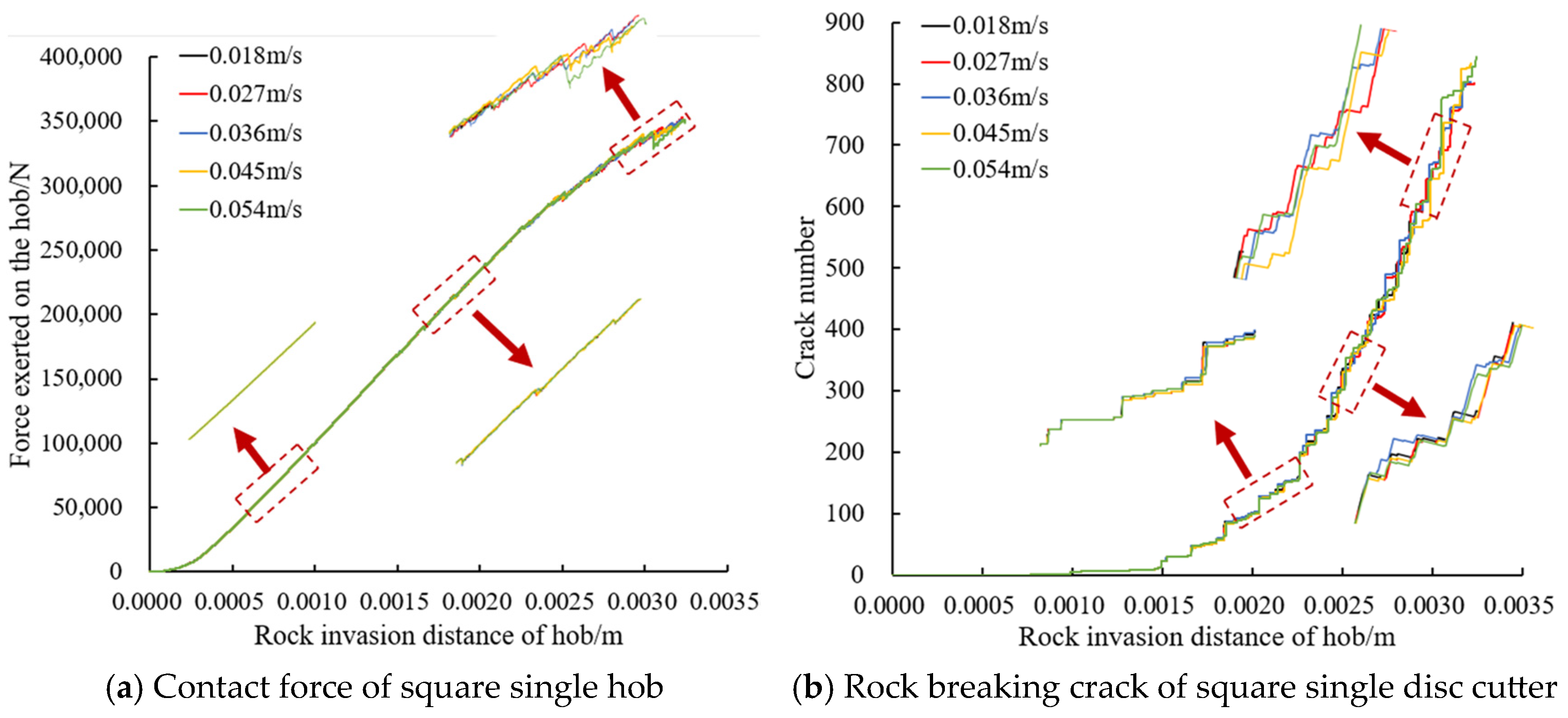
3.1. Hob Speed
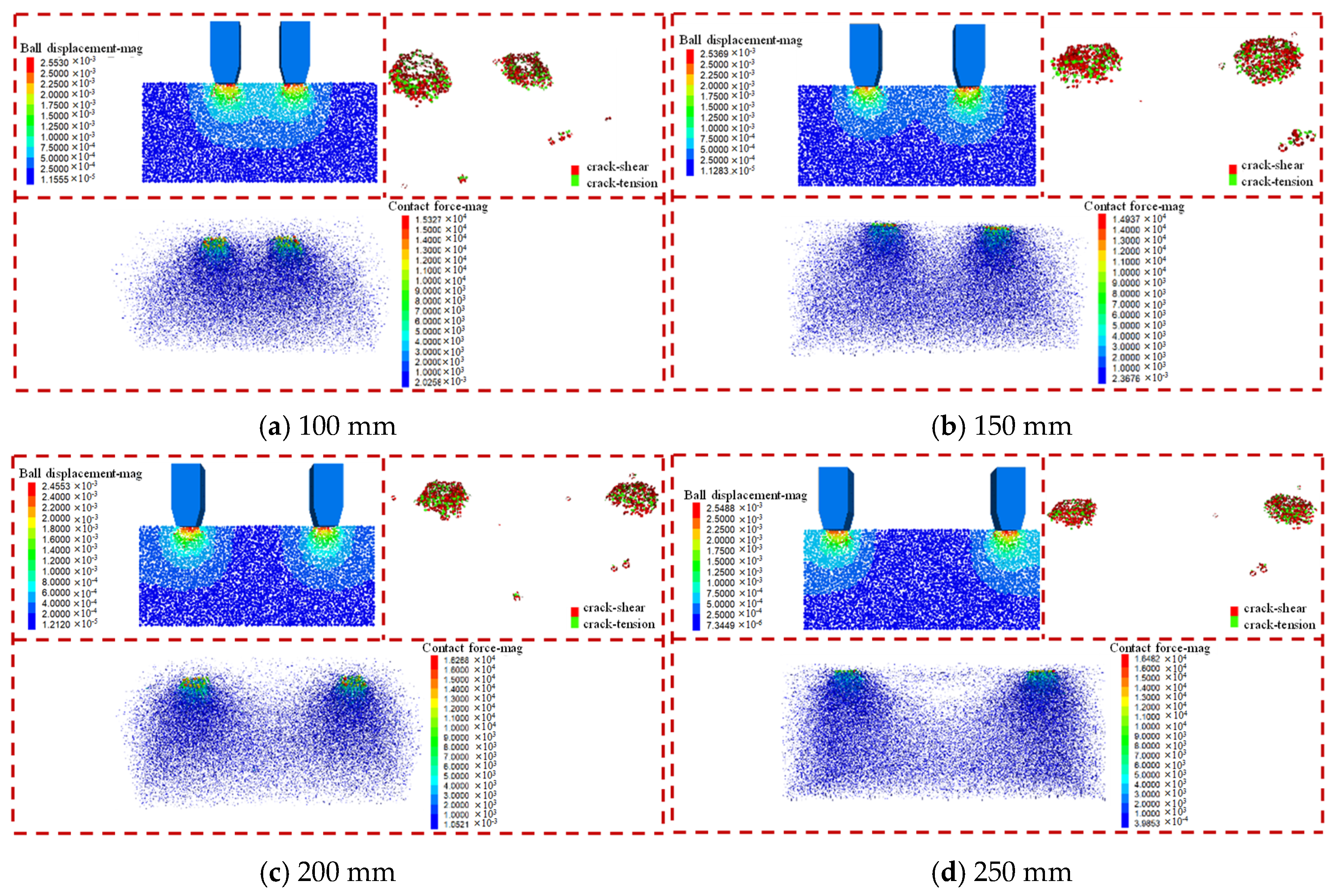
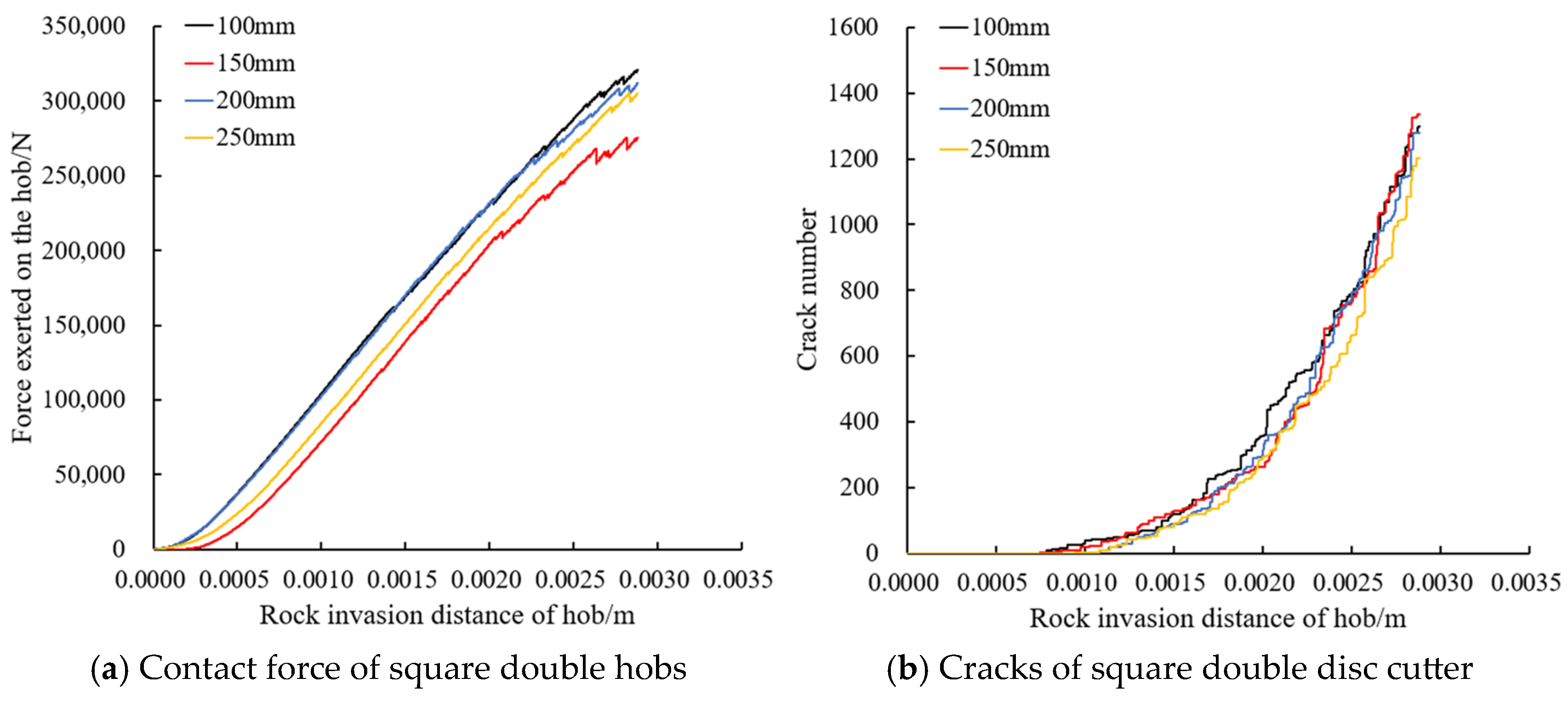
3.2. Hob Spacing
4. Rock-Breaking of Jointed Rock Mass
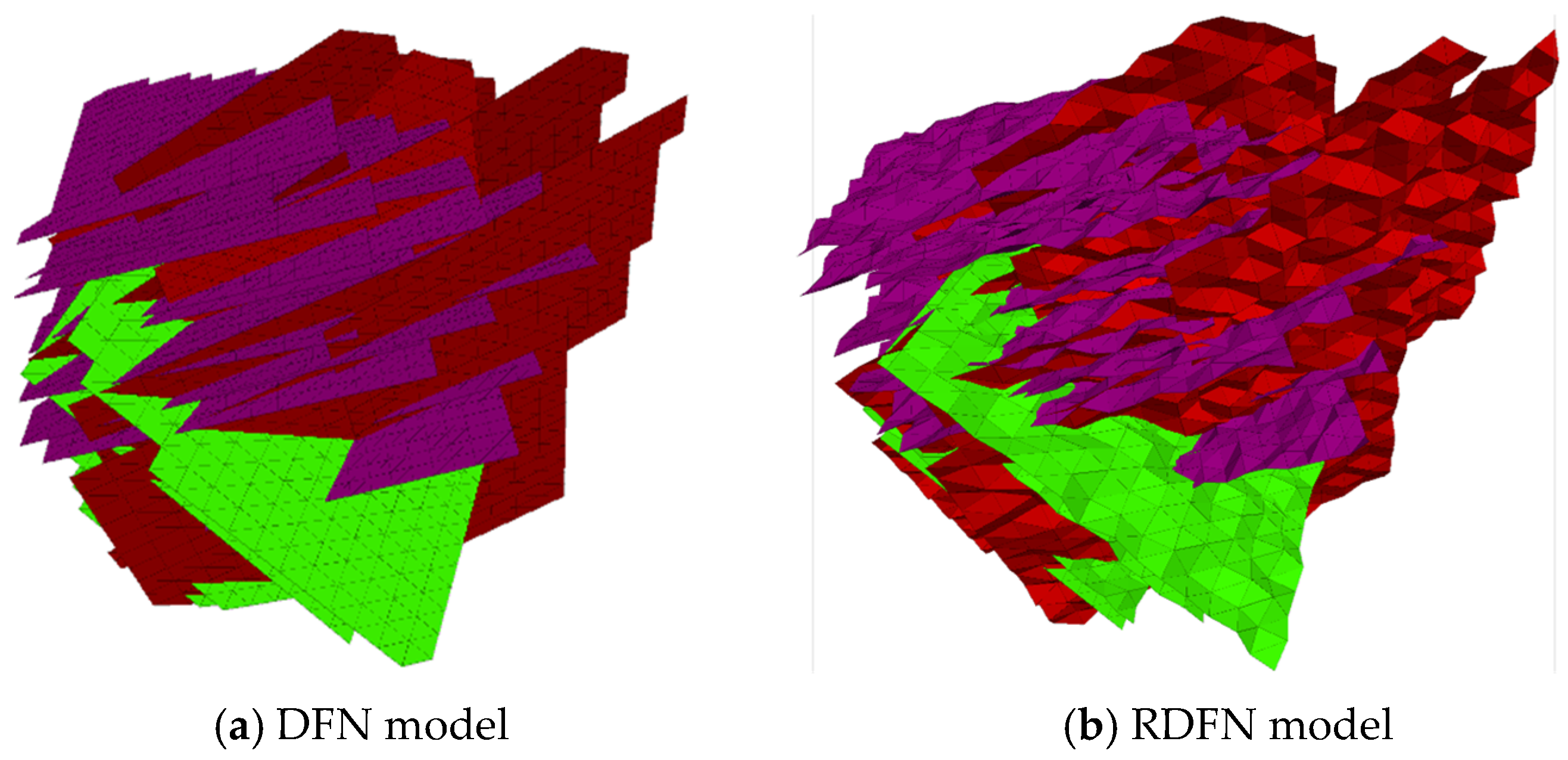
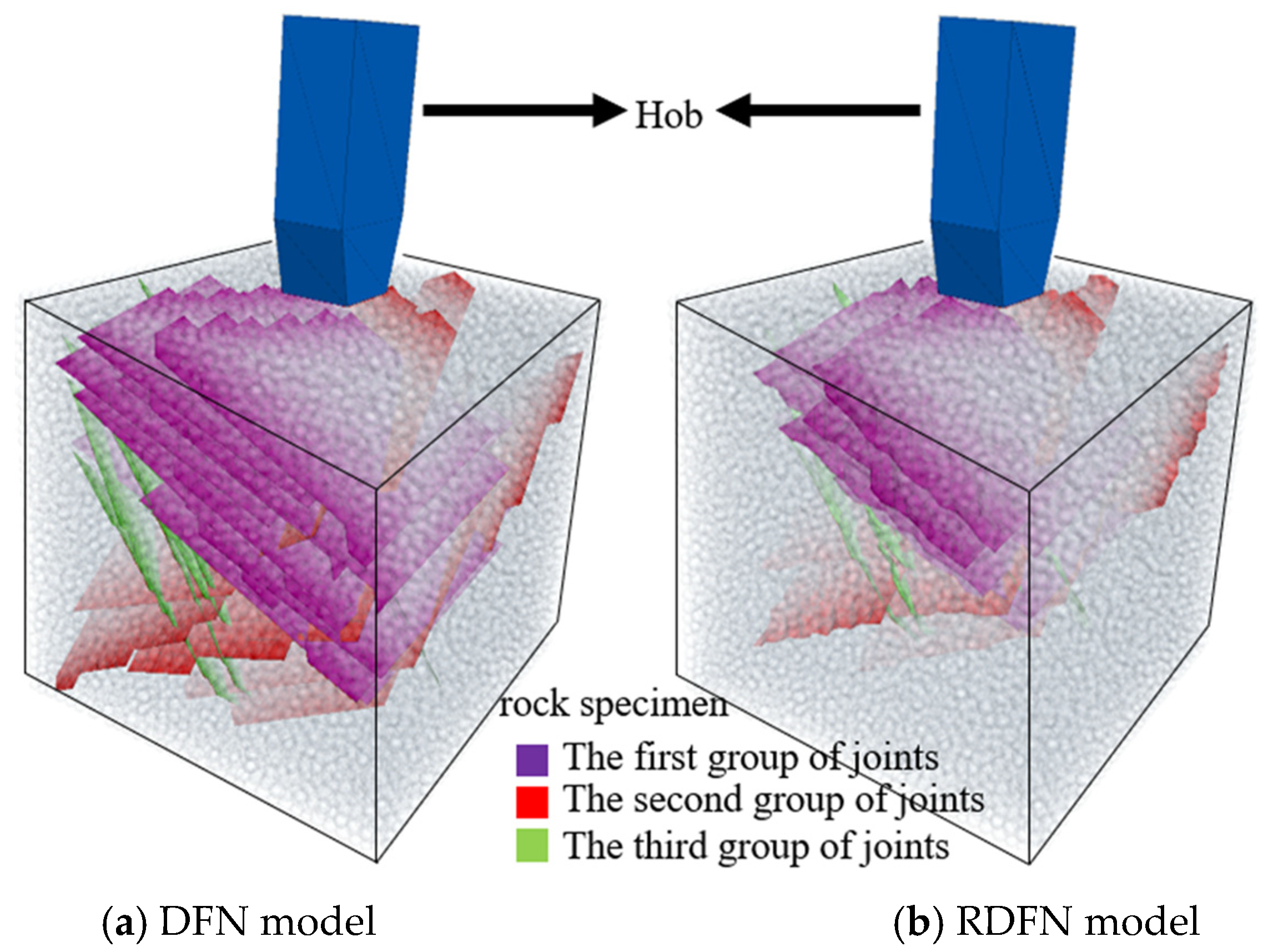
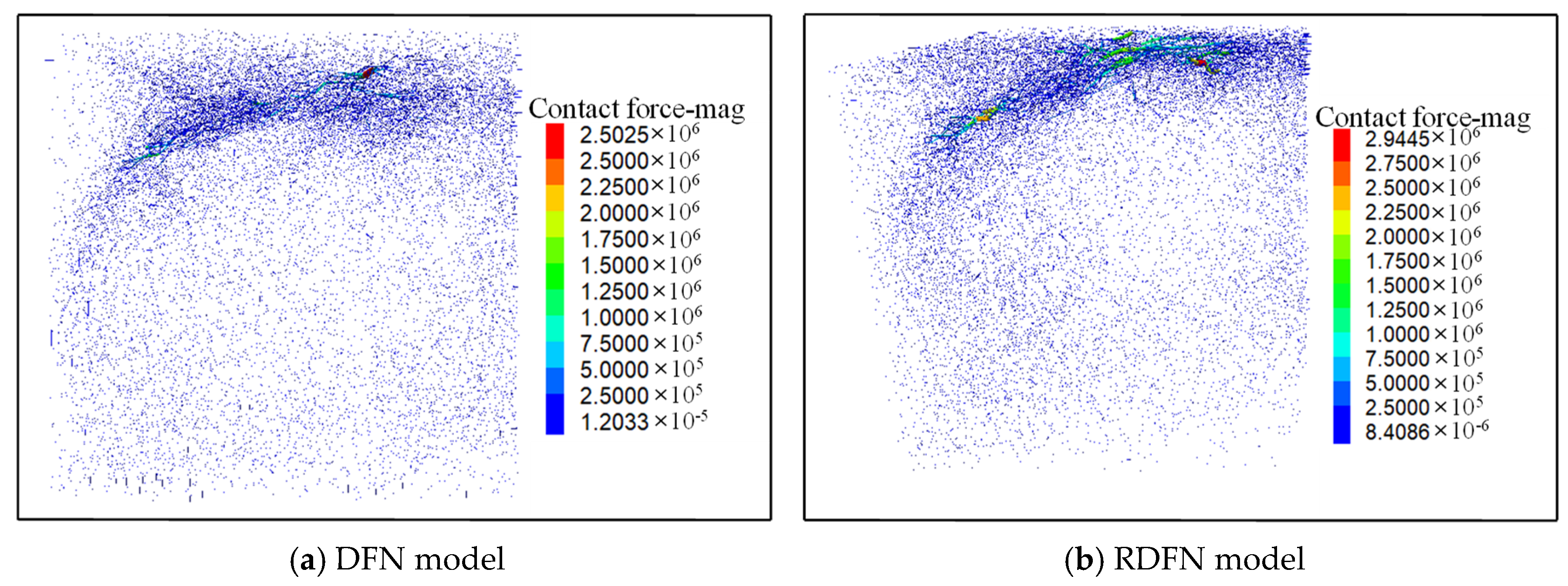
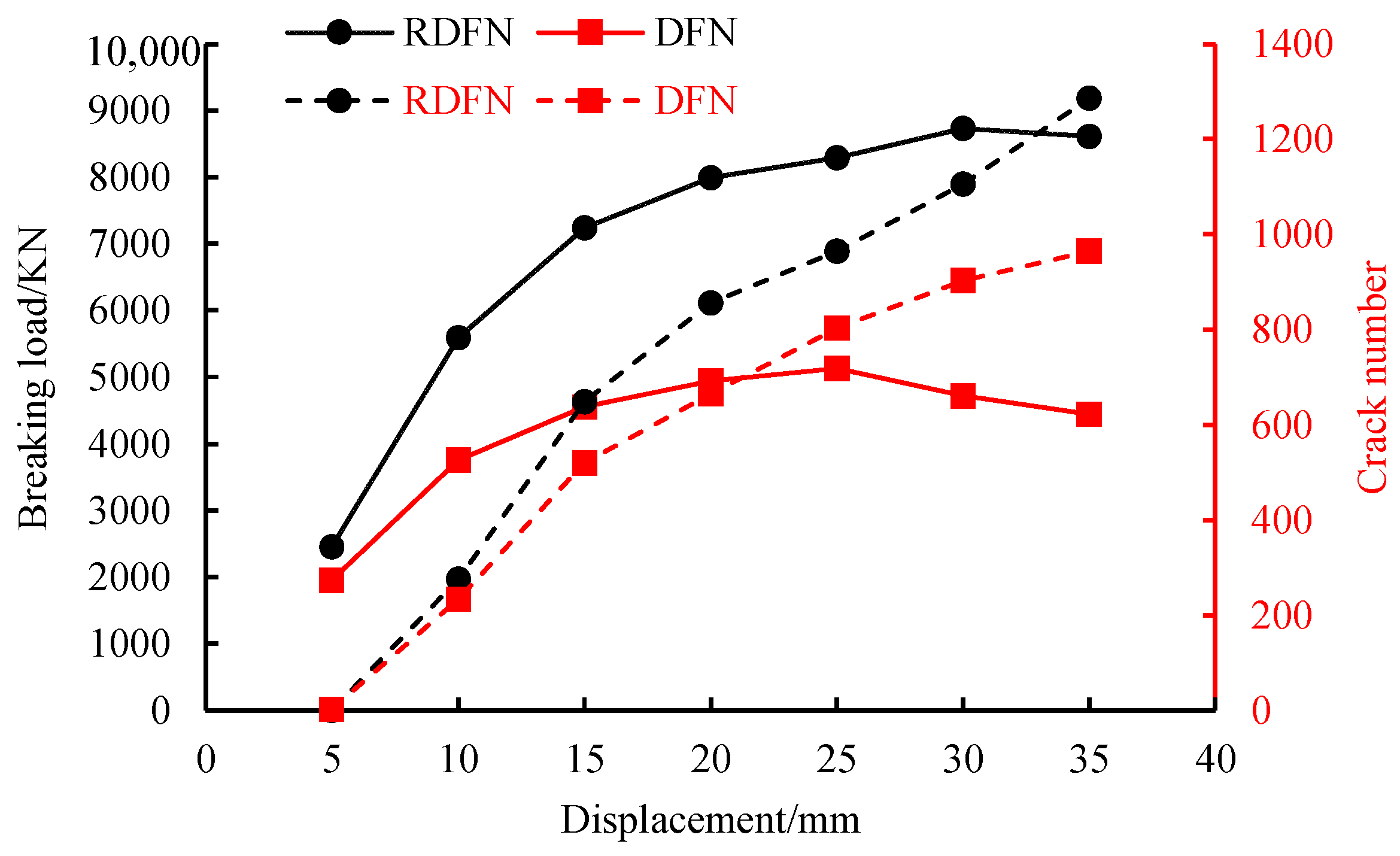
4.1. DFN Model
4.2. RDFN Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shao, X.; Li, H.; Qian, H.; Niu, Y.; Zhu, X.; Ye, S. Optimal TBM cutter penetration and spacing for varying rock strengths: Field tests and numerical modeling. Geotech. Geol. Eng. 2025, 43, 201. [Google Scholar] [CrossRef]
- Xu, F.; Lu, J.; Zhuo, H.; Xiao, J.C.; Zhang, C.Q.; Qiu, H.Q. Research on combined rock-breaking mode of pre-cutting groove and TBM mechanical cutter. Rock Soil Mech. 2021, 42, 1363–1372. [Google Scholar]
- Zhang, X.H.; Xia, Y.M.; Zeng, G.Y.; Tan, Q.; Guo, B. Numerical and experimental investigation of rock breaking method under free surface by TBM disc cutter. J. Cent. South Univ. 2018, 25, 2107–2118. [Google Scholar] [CrossRef]
- Liu, S.; Li, H.; Jiang, H.; Zhang, Q.; Cui, Y.; Liu, X. Research progress and prospect of coal-rock breaking methods in mines. J. China Coal Soc. 2023, 48, 1047–1069. [Google Scholar] [CrossRef]
- Liu, X.; Sun, H.; Dong, Q.; Su, Y.; Zhou, J. Extremely hard rock mass excavation using rock breakdown methods to assist TBM in a deep, long diversion tunnel in the Qinling Mountains. J. Tsinghua Univ. 2022, 62, 1292–1301. [Google Scholar]
- Zhang, K.; Liu, W.; Yao, X.; Peng, C.; Liu, J.; Zheng, X. Investigation on two-step simulation modeling method for rock breaking by TBM disc cutters assisted with laser. KSCE J. Civ. Eng. 2022, 26, 2966–2978. [Google Scholar] [CrossRef]
- Fu, S.Y.; Li, H.B.; Li, X.F. Research on the range of fracture process zone of granite based on DIC and acoustic emission. Chin. J. Rock Mech. Eng. 2022, 41, 2497–2508. [Google Scholar]
- Yang, J.; Chai, J.; Zhang, D.; Zhang, Y.X. Study on ductile fracture mechanism of coal and rock mass based on cohesive crack model. Chin. J. Rock Mech. Eng. 2021, 40, 3014–3023. [Google Scholar]
- Wen, S.; Liao, C.; Yan, S.; Liang, N.; Jin, T. Damage mechanism and amplification effect of compression failure in soft rock with initial cracks. J. Theor. Appl. Mech. 2025, 63, 375–385. [Google Scholar] [CrossRef] [PubMed]
- Gao, M.-Z.; Xie, J.; Yang, B.-G.; Tang, R.-F.; Deng, H.-C.; Liu, Y.-T.; Wang, S.-L. Characteristics and mechanism of rock 3D volume fracturing in microwave field. J. China Coal Soc. 2022, 47, 1122–1137. [Google Scholar]
- Liu, R.; Zhu, Z.; Du, Y.; Li, M.; Liu, B.; Wan, D. Study on dynamic propagation law of cracks with different lengths under blasting. Chin. J. Rock Mech. Eng. 2022, 41, 3114–3123. [Google Scholar]
- Zhang, X.; Zhang, S.; An, D. Experimental study on the size effect of crack propagation process of disk samples containing parallel double pre-existing flaws. Chin. J. Rock Mech. Eng. 2023, 42, 115–128. [Google Scholar] [CrossRef]
- Li, Z.; Zhou, W.; Wang, L.; Li, W.; Ren, B. Numerical simulation of true triaxial fracture evolution of rocks with random fracture. J. China Univ. Min. Technol. 2023, 52, 43–51. [Google Scholar]
- Zhang, H.; Yuan, C.; Chen, S.; Yang, G.; Xia, H. Experimental study of fracture geometry characteristics on rock mass strength and crack propagation evolution law. Eur. J. Environ. Civ. Eng. 2022, 26, 7972–8001. [Google Scholar] [CrossRef]
- Cheng, L.; Chang, X.; Wang, S.; Wang, Y.; Zhang, M. Effect analysis of bedding plane and fracture distribution on crack propagation process in layered fractured rock mass. J. Eng. Sci. Technol. Rev. 2021, 14, 90–99. [Google Scholar] [CrossRef]
- Su, H.; Jiang, Y.; Yu, L.; Wang, W.; Guo, Q. Dynamic fracture and deformation responses of rock mass specimens containing 3D printing rough joint subjected to impact loading. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 186. [Google Scholar] [CrossRef]
- Xie, Z.; Qiu, S.; Li, S.; Jiang, Q.; Xu, D.; Zheng, M. Excavation damage mechanism of deep buried layered fractured rock mass based on three-dimensional bonded block damage model. Comput. Geotech. 2025, 180, 107101. [Google Scholar] [CrossRef]
- Herrero, M.J.; Pérez-Fortes, A.P.; Escavy, J.I.; Insua-Arévalo, J.M.; De la Horra, R.; López-Acevedo, F.; Trigos, L. 3D model generated from UAV photogrammetry and semi-automated rock mass characterization. Comput. Geosci. 2022, 163, 105121. [Google Scholar] [CrossRef]
- Buyera, A.; Aichingerb, S.; Schuberta, W. Applying photogrammetry and semi-automated joint mapping for rock mass characterization. Eng. Geol. 2022, 264, 105332. [Google Scholar] [CrossRef]
- Vlachopoulos, N.; Vazaios, I.; Forbes, B.; Carrapatoso, C. Rock mass structural characterization through DFNLiDAR–DOS methodology. Geotech. Geol. Eng. 2020, 38, 6231–6244. [Google Scholar] [CrossRef]
- Li, J.; Caspari, E.; Greenwood, A.; Pierdominici, S.; Lemke, K.; Venier, M.; Kück, J.; Baron, L.; Pistone, M.; Petri, B.; et al. Integrated rock mass characterization of the lower continental crust along the ICDP-DIVE 5071_1_B borehole in the IVREA-VERBANO zone. Geochem. Geophys. Geosyst. 2024, 25, e2024GC011707. [Google Scholar] [CrossRef]
- Pola, A.; Herrera-Díaz, A.; Tinoco-Martínez, S.R.; Macias, J.L.; Soto-Rodríguez, A.N.; Sereno, H.; Avellán, D.R. Rock characterization, UAV photogrammetry and use of algorithms of machine learning as tools in mapping discontinuities and characterizing rock masses in Acoculco Caldera Complex. Bull. Eng. Geol. Environ. 2024, 83, 260. [Google Scholar] [CrossRef]
- Fatolahzadeh, S.; Sepúlveda, S.; Singh, J. Applicability and limitations of terrestrial and UAV-based remote sensing techniques for slope rock mass characterization. In Proceedings of the 59th US Rock Mechanics/Geomechanics Symposium, Santa Fe, NM, USA, 8–11 June 2025. [Google Scholar]
- Li, L.; Wu, W.; El Naggar, M.H.; Mei, G.; Liang, R. Characterization of a jointed rock mass based on fractal geometry theory. Bull. Eng. Geol. Environ. 2019, 78, 6101–6110. [Google Scholar] [CrossRef]
- Li, N.; Zhang, K.; Luo, G.; Zhang, K. Experimental study on the size effect and anisotropy in mechanical properties of fractured rock mass based on 3D printing. Theor. Appl. Fract. Mech. 2024, 129, 104224. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Zhang, S. Influence Mechanism of Loading Rate and Size Effect on Altered Rock Mechanical Properties. Adv. Transdiscipl. Eng. 2024, 62, 855–860. [Google Scholar]
- Wang, P.; Qi, Z.; Ma, C.; Cai, M. Mechanical behavior and failure modes of jointed rock mass based on rough discrete fracture network models. Environ. Earth Sci. 2022, 81, 543. [Google Scholar] [CrossRef]
- Wang, P.; Liu, C.; Qi, Z.; Liu, Z.; Cai, M. A rough discrete fracture network model for geometrical modeling of jointed rock masses and the anisotropic behaviour. Appl. Sci. 2022, 12, 1720. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, D.F.; Jin, A.B.; Chen, S.J. Failure characteristics and crack evolution laws of hard rock under nonlinear unloading rates. J. Northeast. Univ. 2022, 43, 1010–1018. [Google Scholar]
- Sun, C.; Ao, Y.H.; Zhang, J.M.; Wang, S. Particle flow of meso-fracture characteristics and macro-scale effect of granites. Chin. J. Geotech. Eng. 2020, 42, 1687–1695. [Google Scholar]

| Parameter | Mechanical Analysis Model of Rock Breaking by Square Hob [29,30] | DFN Model and RDFN Model | |
|---|---|---|---|
| Strength of Rock Specimen | Fracture Intensity | ||
| Ball Rmin/mm | 2.5 | 50 | |
| Ball Rmax/mm | 3 | 80 | |
| Particle damping coefficient | 0.7 | 0.7 | |
| particle density/kg·m−3 | 2700 | 2650 | |
| effective modulus E/GPa | 2 | 15 | |
| kn/ks | 2 | 1 | |
| Bond effective modulus E/GPa | 2 | 15 | |
| 2 | 1 | ||
| tension bond strength /MPa | 32 | 25 | 5 |
| Bonding cohesion /MPa | 24 | 50 | 5 |
| internal friction ƒ/(°) | 32 | 57 | 30 |
| friction coefficient/µ | 0.2 | 0.4 | 0.5 |
| /Pa | 55,000 | ||
| /Pa | 55,000 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, G.; Huang, H.; Wang, P.; Cai, M. Rock Cutting and Crack Propagation of Jointed Rock Mass Within Rough Fractures Based on Point-Splitting Process. Appl. Sci. 2025, 15, 12312. https://doi.org/10.3390/app152212312
Jing G, Huang H, Wang P, Cai M. Rock Cutting and Crack Propagation of Jointed Rock Mass Within Rough Fractures Based on Point-Splitting Process. Applied Sciences. 2025; 15(22):12312. https://doi.org/10.3390/app152212312
Chicago/Turabian StyleJing, Guoye, Hao Huang, Peitao Wang, and Meifeng Cai. 2025. "Rock Cutting and Crack Propagation of Jointed Rock Mass Within Rough Fractures Based on Point-Splitting Process" Applied Sciences 15, no. 22: 12312. https://doi.org/10.3390/app152212312
APA StyleJing, G., Huang, H., Wang, P., & Cai, M. (2025). Rock Cutting and Crack Propagation of Jointed Rock Mass Within Rough Fractures Based on Point-Splitting Process. Applied Sciences, 15(22), 12312. https://doi.org/10.3390/app152212312







