Modification and Application of Söhne, McKyes, and Perumpral Models for Predicting Draught Forces in a Duckfoot Tool

Abstract

The study aimed to modify the models of Söhne, McKyes, and Perumpral to predict the draught force acting on duckfoot tools. Classic models, developed for narrow tools, do not consider the specific geometry of the wide duckfoot wings or the dynamic soil–tool interactions. In laboratory studies, duckfoots with widths of 105, 133, and 202 mm were used in the soil bin, operating at depths of 0.03–0.07 m at speeds of 0.84–2.31 m·s⁻¹ in soils with 10% and 14% moisture content. The results showed that the modified models predicted a draught force with a global error δ_g of 23–25% for the whole data, while the classical solutions achieved higher values (25–62%). The best fit and highest prediction were obtained for the Perumpral model (RMSE = 58 N), confirming its suitability for analysing wide tools. The developed modifications increase the reliability of predictions and performance of tillage implements, particularly in compacted soils. The falsification of hypotheses showed that while modifications improve accuracy, they do not eliminate limitations under varying operating conditions. It is necessary to improve the models by considering the three-dimensional effects of soil deformation, the variability of its properties over time, and random terms describing field factors.

1. Introduction

1.1. Development of Predictive Models

Modelling soil–tool interactions is a key element in optimising tool performance and improving the efficiency of agricultural machinery. In recent decades, numerous approaches have been developed to describe soil behaviour under tool loading, including analytical, empirical, and numerical models (Finite Element Method, Discrete Element Method, DEM), as well as newer methods based on Machine Learning, ML. Numerical methods enable the analysis of stress and displacement fields with minimal assumptions about soil homogeneity [1], while DEM allows for modelling soil flow and fracture at the particle level [2]. Simultaneously, ML methods are being developed and utilised, among other applications, in geotechnical engineering to predict forces in soil-to-object structures [3]. Although these approaches expand the range of modelling possibilities, classical analytical models based on the soil wedge theory are still widely used in agricultural engineering practice.

To optimise the technical parameters of machine design and performance, several analytical models have been developed to predict the forces acting on tillage implements. The most frequently cited are those created by Söhne [4], McKyes [5], and Perumpral [6]. These models are also used to predict draught forces in wide implements, which are defined as those with a width-to-depth ratio of 2 or more, but there are also suggestions that, in some cases, this ratio may be less. However, none of these models have been directly applied to the duckfoot tool, a commonly used implement for shallow tillage, especially with weeders or row cultivators. The specific geometry of the wide duckfoot blades causes significant lateral soil displacement and a different stress distribution compared to the straight-edged implements for which these models were initially developed. Therefore, it is necessary to modify existing analytical models to enable the accurate prediction of the draught force acting on duckfoots, taking into account the characteristic geometry of these tools and the specificity of their operation in the subsurface soil layer.

The basic model for predicting the draught forces acting on tillage tools assumes that the tool cutting through the soil creates a soil wedge, leading to the displacement of the cut soil pile [4]. Söhne’s model is widely regarded as a pioneering approach, enabling scientists to predict forces using the basic principles of soil mechanics. The model assumes that the soil behaves rigidly and requires several simplistic assumptions, such as soil homogeneity and constant contact conditions between the soil and the tool. The model validates well for narrow tools but is less effective for wide tools with complex geometries.

The theoretical foundations of draught force prediction developed by Söhne were created by integrating more detailed parameters related to tool geometry, such as the cutting-edge angle of the tool and soil consistency [5]. McKyes’ model is commonly used to predict the forces acting on wide tools. McKyes’ model is one of the most widely accepted in agricultural engineering due to its versatility for predicting horizontal forces acting on tools. However, the model’s assumptions are adapted to narrow tools with straight edges, which limits its direct application to tools such as duckfoot.

Another improved model of soil–tool interaction considers both draught and vertical forces, providing a more comprehensive understanding of tool behaviour in different soil conditions [6]. This model emphasises the significance of soil parameters, including moisture content and bulk density, as well as the impact of soil adhesion and cohesion on tool resistance. However, like the Söhne and McKyes models, the Perumpral model has been limited due to its application to tools with simpler geometries and narrow cutting edges.

Until the end of the 1990s, most of the analysed models were two-dimensional, which explained the operation of wide tools [4,7,8]. Based on the assumption that the cross-section of the plane parallel to the direction of motion of the surface separating the detached soil from the monolith is a logarithmic spiral [9], a system of equations of force equilibrium acting on a deformed soil block was developed, the vertical cross-section of which is represented in the form of a connection between a logarithmic spiral and a straight line [10]. Based on this theory, Reece [11] developed a universal equation (Equation (1)), which describes the specific force of the tool’s pressure on the soil, as detailed in the publication by Hettiaratchi, Witney, and Reece [12].

$$F_1=\gamma d^2{N}_{\gamma }+cd{N}_c+c_{a}d{N}_{ca}+qd{N}_q$$

(1)

where F₁—specific force of the tool pressure on the soil, converted to working width, N·m⁻¹; γ—volumetric weight of the soil, N·m⁻³; d—depth of tool work, m; c—cohesion, N·m⁻²; c_a—adhesion of the soil to the surface of the tool, N·m⁻²; q—external pressure exerted on the soil surface, N·m⁻²; N_γ, N_c, N_ca, N_q—dimensionless coefficients determined experimentally, read from graphs for different tool rake angles and angles of internal friction of the soil and external soil–tool.

Four expressions in the model (Equation (1)) represent, in order, the gravitational, cohesive, adhesive, and additional (from the embankment) components of the soil reaction, without taking into account the forces of inertia, due to the relatively small deformations of the soil. Therefore, the influence of the speed of tool movement was omitted. From studies carried out in cohesive and frictional soils, it has been confirmed that the effects of inertia on the draught force for tine are not significant below the speed $\sqrt{5gw}$ and are limited to the speed $\sqrt{5g\left(w+0.6d\right)}$, where g is the acceleration in m·s⁻², w is the width of the tool in m, and d is the depth of tool work in m [13]. It was also found that the effects of the tool’s speed of movement are less significant compared to its working depth [14].

The cited model (Equation (1)) is a slight extension of the Terzaghi equation [8], to which an expression with adhesion resistance has been added. Because soil–tool adhesion has little effect on specific force F₁, its authors combined the expressions of adhesion with cohesion, introducing the concept of conjugated adhesion [12], thus returning to the Terzaghi equation [8], Equation (2).

$$F_1=\gamma d^2{N}_{\gamma }+cd{N}_c+qd{N}_q$$

(2)

where F₁—specific force of the tool pressure on the soil, converted to working width, N·m⁻¹; γ—volumetric weight of the soil, N·m⁻³; d—depth of tool work, m; c—cohesion, N·m⁻²; q—external pressure exerted on the soil surface, N·m⁻²; N_γ, N_c, N_q—dimensionless coefficients.

In McKyes’ fundamental textbook [5], the analysed model (Equation (1)) is represented by the tool’s force on the soil (Equation (3)), which was obtained by multiplying Equation (1) by the tool width w, and the components of the force were determined: draught (horizontal) (Equation (4)) and vertical (Equation (5)).

$$F=\left(\gamma d^2{N}_{\gamma }+cd{N}_c+c_{a}d{N}_{ca}+qd{N}_q\right)w$$

(3)

$$F_x=F\sin \left(\alpha +\delta \right)+c_{a}dw\cot \alpha$$

(4)

$$F_y=F\cos \left(\alpha +\delta \right)-c_{a}dw$$

(5)

where F—resultant force of the tool’s pressure on the soil, N; γ—volumetric weight of the soil, N·m⁻³; d—depth of tool work, m; c—cohesion, N·m⁻²; c_a—adhesion of the soil to the surface of the tool, N·m⁻²; q—external pressure exerted on the soil surface, N·m⁻²; w—width of the tool, m; N_γ, N_c, N_ca, N_q—dimensionless coefficients; F_x—draught force, component of horizontal force, N; α—angle of the tool, °; δ—angle of external friction soil–steel, °; F_y—component of vertical force, N.

The universal equation of soil motion was used to analyse the work of the subsoiler’s tine with the wings, and it was found that the results did not always correlate well with the experimental values for different rake angles of the wings [15].

In developing the model under consideration (Equation (1)), the slip lines in the soil were determined [12], and the mechanical determinants of agricultural soil deformation were presented [16]. Thought experiments were conducted, confirmed by empirical research, and a model (Equation (6)) was developed to optimise the working conditions of tools in terms of energy [17].

$$E^{\prime }=\left({\displaystyle \frac{k_a}{d}}+k^{\prime }\right)w^{1-{\displaystyle \frac{k}{2}}}{d}^{2-{\displaystyle \frac{k}{2}}}{\gamma }^2{v}^{k-1}$$

(6)

where E′—specific energy needed to deform the soil, J·m⁻³; d—depth of tool work, m; w—working width of the tool, m; γ—volumetric weight of the soil, N·m⁻³; v—speed of tool movement, m·s⁻¹; k_a, k′, k—empirical coefficients.

In the discussed models, it was assumed that the tool moves in progressive motion in different directions relative to the level, without considering the momentary oscillations of forces and the cross-section of the loosened soil.

1.2. Wide Tools and Challenges in Duckfoot Modelling

Duckfoots, known for their wide, triangular blades, pose a unique challenge because their wing geometry significantly affects the distribution of forces. Current models, such as those by Söhne, McKyes, and Perumpral, do not consider such geometries or complex soil–tool interactions with work elements that have large side spans of cutting edges, particularly in relation to the working depth. These models assume a relatively simple geometry, with straight or slightly curved blades that cannot capture the complex interaction between the duckfoots’ wide wings and the soil. The lateral displacement caused by duckfoot wings requires modification of existing models to accommodate different shear and cracking patterns in the soil. These models do not account for changes in soil strength, moisture content, and cohesion, which can dynamically change during fieldwork. This gap is particularly pronounced in compacted soils, where these variables fluctuate significantly.

Empirical studies on duckfoots show that their interaction with the soil differs from that of narrow tools, due to their wide cutting edges and ability to work efficiently at shallow depths. The forces acting on these tools depend highly on soil properties such as moisture content, density, and the elastic properties of the tines to which the duckfoots are attached. Therefore, using models developed for narrow chisel tools is impossible without significant modifications.

Given the limitations of existing models for predicting forces acting on duckfoots, there is a clear need to modify and adapt the Söhne, McKyes, and Perumpral models to more accurately reflect the actual operating conditions of these wide tools. In particular, it is necessary to create modified models that account for the unique geometry of the duckfoot, which results in significant vertical and lateral displacement of the soil, while considering soil properties and operating conditions.

The study’s primary goal is to modify the Söhne, McKyes, and Perumpral models to enable more accurate prediction of the draught force acting on the duckfoot. These modifications are designed to eliminate the limitations of current models, particularly in relation to wide tools and the impact of soil properties. The modified models will be validated with empirical data collected from laboratory experiments to confirm their effectiveness.

Based on these considerations, explanatory hypotheses were formulated: H1: Modification of the Söhne, McKyes, and Perumpral models to include the unique duckfoot geometry will significantly improve the accuracy of draught force prediction; H2: The modified models, experimentally verified, will allow for reliable and stable predictions of draught force under different operating conditions, taking into account variability in soil moisture content and compaction.

The novelty of this article lies in the modification of established models (Söhne, McKyes, and Perumpral) to predict the draught force for wide tools, such as duckfoots. While these models have been widely used for narrow tools with simple shapes, their use for wide tools has been limited. This paper presents innovative solutions in the first adaptation of these three models for duckfoot, which has a significantly different geometry than the tools for which these models were initially developed. These creative modifications of the models aim to fill a significant gap in the current knowledge of models that consider soil–tool interactions by adapting existing theoretical frameworks to duckfoots. This will enable the improved design and optimisation of tools in agricultural engineering.

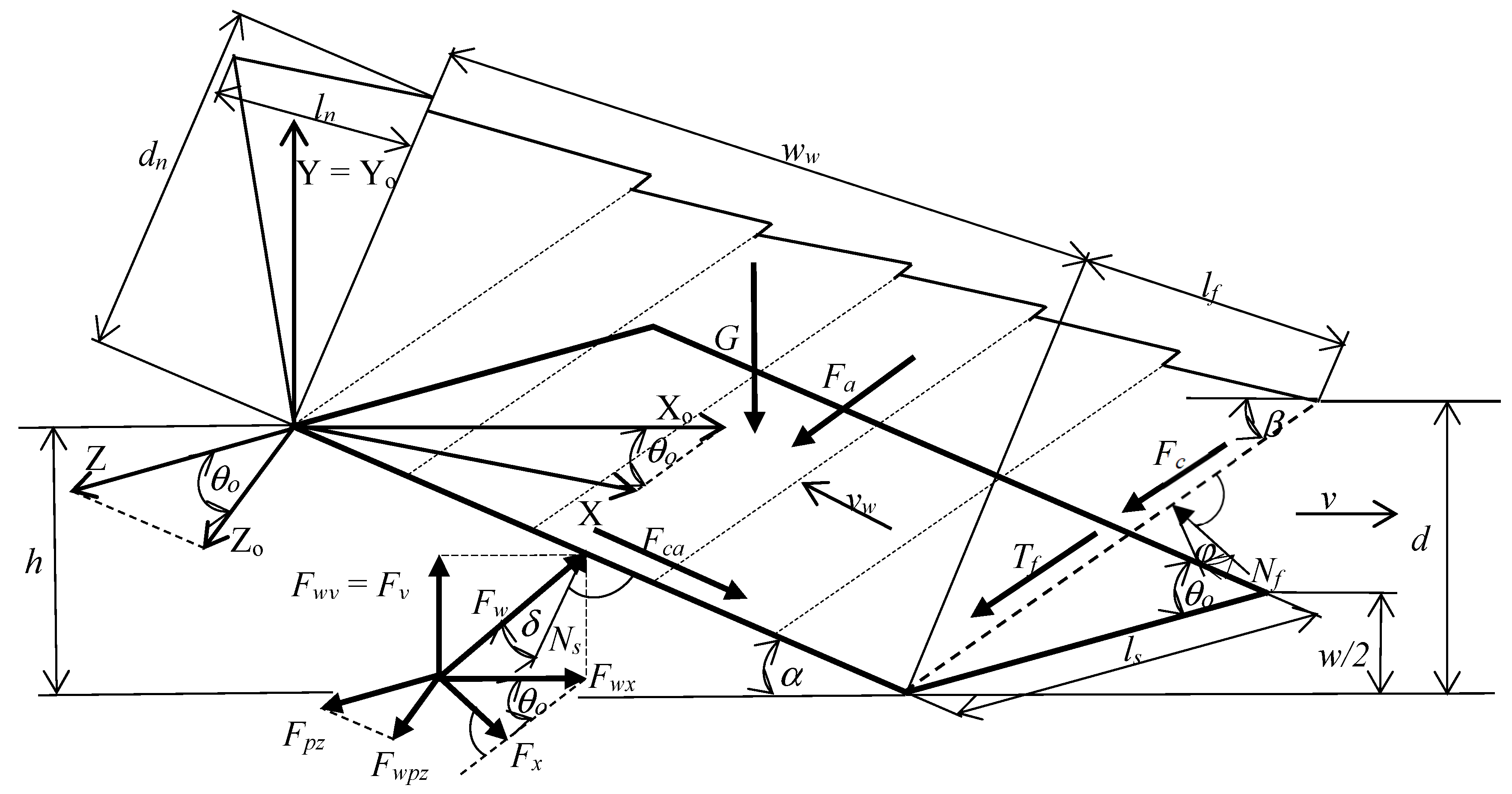
2. Theoretical Model of Duckfoot Work in Soil

2.1. General Data and Assumptions

The analysis was carried out in a 2D system, excluding lateral deformations relative to the cutting edge of the duckfoot. Since the throw from the top of the knife resembles two elements connected in a triangle, the calculations were made for one side perpendicular to the edge. The results were then doubled, and after rotating the X_oY_oZ_o system by the angle of the duckfoot wing, the components of the forces in the XYZ system were determined (Figure 1). The structural model took into account the shape and dimensions of the deformed soil pile and soil–duckfoot forces, using the laws and theorems of mechanics.

The same assumptions were introduced when modifying mathematical models: 1. The soil is homogeneous and isotropic; 2. Deformation is considered in 2D (tool width > tool working depth); 3. Soil cracking meets the Coulomb–Mohr criterion; 4. Soil parameters: bulk density (volumetric weight), angle of internal friction (soil–soil), angle of external friction (soil–steel), cohesion, and adhesion depend only on soil moisture content; 5. The width of the soil pile is equal to the length of the blade edge; 6. The cutting resistance of the blade’s sharp edge is omitted; 7. Duckfoot operates at a constant depth, and the angles of setting and clearance remain unchanged, despite the use of elastic tines; 8. The movement of the tool is uniform.

The mathematical models were modified to a 2D space and duckfoot geometry, and the existing designations were considered [18,19] to ensure consistency in deliberations and analysis.

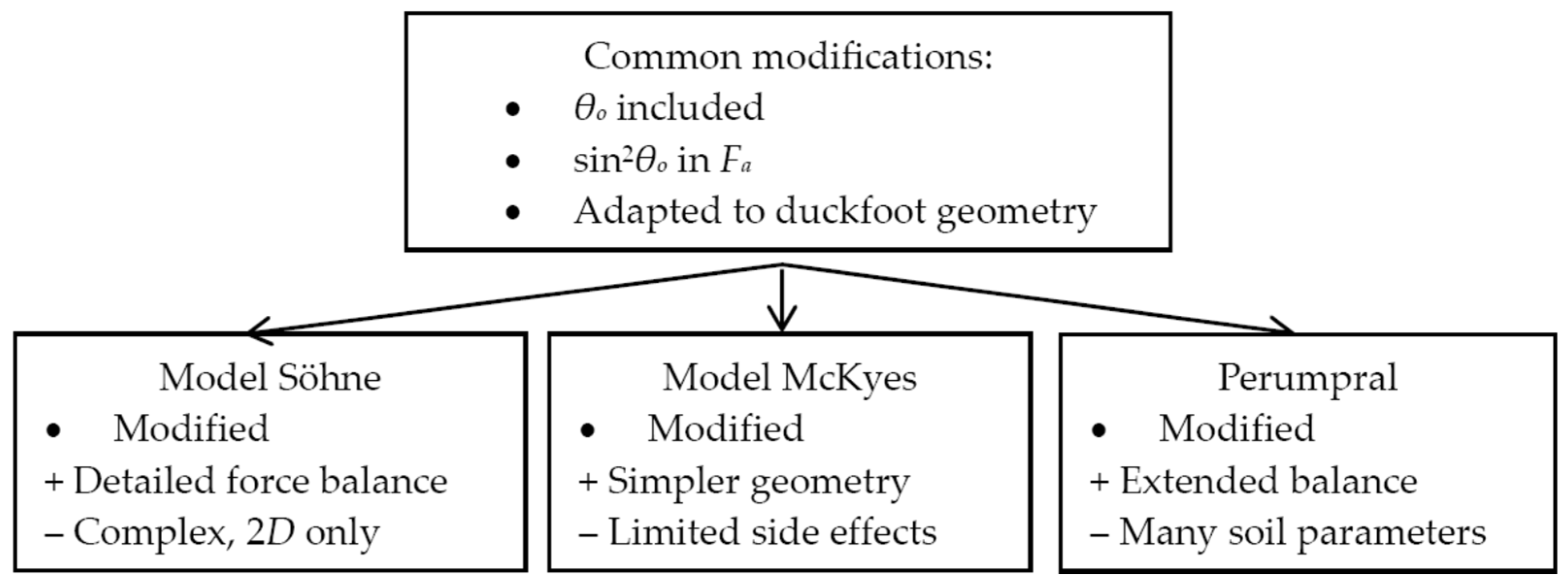
2.2. Model 1 Söhne

The soil cracking pattern for model 1 Söhne in 2D space assumes stepped cracking of the soil as shown in Figure 1. Model 1 for 2D was presented by Söhne [4] and modified by Rowe and Barnes [20]. The coupled forces in the soil–tool system include the weight of the soil pile (soil wedge) G, the cohesion force at the surface of soil cracking due to soil pile shear F_c, the standard component of the soil reaction on the fracture surface N_f, the tangential component of the soil reaction at the fracture surface T_f = μ_fN_f, adhesion force at the soil–duckfoot boundary F_ca, a normal component of soil surface reaction N_s, and the tangential component of the soil response to duckfoot T_s = μ_sN_s, inertia force F_a, vertical force F_y and draught F_x. Soil–steel friction coefficient μ_s is equal to tanδ, where δ is the angle of external friction of soil–steel, while the coefficient of friction of soil–soil pile μ_f is equal to tanφ, where φ is the angle of internal friction of the soil.

After adding the horizontal and vertical forces and comparing them to zero, and eliminating the reaction components N_f and N_s obtained by the horizontal component, which is the draught force for duckfoot [21], Equation (7), and the vertical component of duckfoot pressure on the soil, Equation (8).

$$F_x=2\left({\displaystyle \frac{G}{Z}}+{\displaystyle \frac{c{A}_f+F_a}{Z\left(\sin \beta +\tan \phi \cos \beta \right)}}+{\displaystyle \frac{c_a{A}_w}{Z\left(\sin \alpha +\tan \delta \cos \alpha \right)}}\right)\sin {\theta }_o$$

(7)

$$F_y={\displaystyle \frac{F_x\left(\cos \alpha -\tan \delta \sin \alpha \right)}{\sin \alpha +\tan \delta \cos \alpha }}$$

(8)

where Z is the auxiliary variable described by Equation (9).

$$Z={\displaystyle \frac{\cos \alpha -\tan \delta \sin \alpha }{\sin \alpha +\tan \delta \cos \alpha }}+{\displaystyle \frac{\cos \beta -\tan \phi \sin \beta }{\sin \beta +\tan \phi \cos \beta }}$$

(9)

where F_x—draught force, N; F_y—vertical component of the pressure force of the duckfoot on the soil, N; G—weight of the soil pile, N; Z—auxiliary variable; c—cohesion, N·m⁻²; A_f—shear area of the soil pile, m²; F_a—inertia force of the soil pile, N; c_a—adhesion of the soil to the surface of the tool, N·m⁻², A_w—area of the surface of the soil pile on the duckfoot wing, m²; α—duckfoot wing angle, °; β—soil shear angle, °; δ—angle of external friction soil–steel, °; φ—angle of internal friction of the soil, °; θ_o—lateral angle of the duckfoot wing, °.

Other variables found in Equations (7)–(9) were designated with Equations (10)–(13).

$$G={\gamma l}_s{\displaystyle \frac{d\mathrm{s}\mathrm{i}\mathrm{n}\left(\alpha +\beta \right)}{\sin \beta }}\left(w_w+{\displaystyle \frac{d\cos \beta }{2\cos \alpha \mathrm{s}\mathrm{i}\mathrm{n}\beta }}\right)$$

(10)

$$F_a={\displaystyle \frac{\gamma l_{s}d}{g}}{v}^2{\mathrm{s}\mathrm{i}\mathrm{n}}^2{\theta }_o{\displaystyle \frac{\sin \alpha }{\sin \left(\alpha +\beta \right)}}$$

(11)

$$A_w=l_s{w}_w$$

(12)

$$A_f=l_s{\displaystyle \frac{d}{\sin \beta }}$$

(13)

where G—weight of the soil pile, N; γ—volumetric weight of the soil, N·m⁻³; l_s—duckfoot blade length, m; w_w—wing width of duckfoot, m; α—duckfoot wing angle, °; β—soil shear angle, °; φ—angle of internal friction of the soil, °; F_a—inertia force of the soil pile, N; d—depth of work duckfoot, m; v—speed of tool movement, m·s⁻¹; g—acceleration of gravity, m·s⁻²; A_w—area of the soil pile on the duckfoot wing, m²; A_f—shear area of the soil pile, m².

After the modification, the Söhne’s model has been adapted to the specifics of duckfoot work, providing a better description of the actual direction of soil movement and its dynamic interaction with the tool. It takes into account the lateral angle of application of the wings, the weight of the soil wedge, cohesion, adhesion, internal and external friction, and components of the soil reaction.

2.3. Model 2 McKyes

The geometry of the soil pile in model 2 is in the shape of a soil wedge, attributed to McKyes [5,22]. For 2D spaces and wide tools, it consists only of a central part, a flat wedge inclined at an angle α for the tool position and sliding on the soil surface at a shear angle β. The interaction of the forces related to the action of the duckfoot on the soil involves the weight of the soil wedge G, soil reaction N_f, cohesion c, adhesion c_a, and specific cutting force F₁. Specific cutting force F₁ is the force per unit length of the blade and is given in the form of the universal equation of soil motion, Equation (1) [11].

As mentioned, the specific cutting force F₁ can be multiplied by the width of the duckfoot w, considering the lateral angle of the duckfoot wing θ_o. In this way, the resultant pressure force of the duckfoot on the soil is obtained, with a dynamic expression that considers the speed of soil movement on the wings of the duckfoot, but without external pressure on the soil surface q, Equation (14).

$$F=\left(\gamma d^2{N}_{\gamma }+cd{N}_c+c_{a}d{N}_{ca}+\gamma v^2{\mathrm{s}\mathrm{i}\mathrm{n}}^2{\theta }_{o}d{N}_a/g\right)w\sin {\theta }_o$$

(14)

where F—resultant force of the tool’s pressure on the soil, N; γ—volumetric weight of the soil, N·m⁻³; d—depth of work duckfoot, m; w—width of duckfoot, m; c—cohesion, N·m⁻²; c_a—adhesion of the soil to the surface of the tool, N·m⁻²; v—speed of tool movement, m·s⁻¹; g—acceleration of the earth, m·s⁻²; N_γ, N_c, N_ca, N_a—dimensionless coefficients; θ_o—lateral angle of the duckfoot wing, °.

Dimensionless coefficients, related to the weight of the soil pile N_γ, soil cohesion N_c, soil–duckfoot adhesion N_ca, and the inertia of the soil pile N_a, were assigned with Equations (15)–(18) [21].

$$N_{\gamma }={\displaystyle \frac{r/2d}{\cos \left(\alpha +\delta \right)+\sin \left(\alpha +\delta \right)\cot \left(\beta +\phi \right)}}$$

(15)

$$N_c={\displaystyle \frac{1+\cot \beta \cot \left(\beta +\phi \right)}{\cos \left(\alpha +\delta \right)+\sin \left(\alpha +\delta \right)\cot \left(\beta +\phi \right)}}$$

(16)

$$N_{ca}={\displaystyle \frac{1+\cot \beta \cot \left(\beta +\phi \right)}{\cos \left(\alpha +\delta \right)+\sin \left(\alpha +\delta \right)\cot \left(\beta +\phi \right)}}$$

(17)

$$N_a={\displaystyle \frac{\tan \beta +\cot \left(\beta +\phi \right)}{\left[\cos \left(\alpha +\delta \right)+\sin \left(\alpha +\delta \right)\cot \left(\beta +\phi \right)\right]\tan \beta \cot \alpha }}$$

(18)

where N_γ, N_c, N_ca, N_a—dimensionless coefficients; d—depth of work duckfoot, m; r—extent of the soil pile cracking, m; α—duckfoot wing angle, °; β—soil shear angle, °; δ—angle of external friction soil–steel, °; φ—angle of internal friction of the soil, °.

The breakage range of the soil pile was determined from Equation (19).

$$r=d\left(\cot \alpha +\cot \beta \right)$$

(19)

where r—range of cracking of the soil pile, m; d—depth of work duckfoot, m; α—duckfoot wing angle, °; β—soil shear angle, °.

The draught force and vertical component of the duckfoot pressure on the soil were obtained by combining the resultant contact force with the adhesion force, Equations (20) and (21), respectively.

$$F_x=F\sin \left(\alpha +\delta \right)+{2c}_a{w}_w\cos \alpha l_s\sin {\theta }_o$$

(20)

$$F_y=F\cos \left(\alpha +\delta \right)-{2c}_a{w}_w\sin \alpha l_s$$

(21)

where F_x—draught force, horizontal component of the pressure force of duckfoot on the soil, N; F_y—vertical component of the pressure force of the duckfoot on the soil, N; F—resultant pressure force of the duckfoot on the soil, N; c_a—adhesion of the soil to the surface of the tool, N·m⁻², w_w—width of the duckfoot wing, m; l_s—duckfoot blade length, m; α—duckfoot wing angle, °; δ—angle of external friction soil–steel, °; θ_o—lateral angle of the duckfoot wing, °.

After modification, McKyes’ model 2 was adapted to work with duckfoots by introducing a lateral angle of application θ_o and taking into account the dynamic influence of the speed of soil movement along the wings of the tool. The model describes the soil wedge as a flat wedge sliding on the soil surface at an angle of shear β. In the balance of forces, it takes into account the weight of the pile, cohesion, adhesion, friction, and the inertia force, incorporating the sin²θ_o factor. As a result, it allows for the determination of the resultant pressure force on the soil and its distribution into the draught force F_x and the vertical component F_y, better reflecting the real working conditions of wide duckfoot tools.

2.4. Model 3 Perumpral

Model 3, presented by Swick and Perumpral [6], assumes the same soil fracture wedge and force system as model 2 by McKyes. Analysing the balance of forces acting on the middle soil wedge gave expressions for the resultant soil cutting force by duckfoot F, Equation (22).

$$F=2{\displaystyle \frac{F_{ca}\cos \left(\alpha +\phi +\beta \right)+G\sin \left(\phi +\beta \right)+\left(F_c+F_a\right)\cos \phi }{\sin \left(\alpha +\phi +\beta +\delta \right)}}\sin {\theta }_o$$

(22)

where F—resultant force of the tool’s pressure on the soil, N; F_c—cohesion force on the soil shear surface, N; F_ca—adhesion force at the contact surface of the soil pile with the duckfoot wing, N; G—weight of the soil pile, N; F_a—inertia force of the soil pile, N; α—duckfoot wing angle, °; β—soil shear angle, °; δ—angle of external friction soil–steel, °; φ—angle of internal friction of the soil, °; θ_o—lateral angle of the duckfoot wing, °.

The other variables were calculated from Equations (23)–(27).

$$F_c=c{l}_s{\displaystyle \frac{d}{\sin \beta }}$$

(23)

$$F_{ca}=c_a{l}_s{w}_w$$

(24)

$$G={\displaystyle \frac{{\gamma l}_{s}dr}{2}}$$

(25)

$$F_a={\displaystyle \frac{\gamma l_{s}d}{g}}{v}^2{\mathrm{s}\mathrm{i}\mathrm{n}}^2{\theta }_o{\displaystyle \frac{\sin \alpha }{\sin \left(\alpha +\beta \right)}}$$

(26)

$$r=d\left(\cot \alpha +\cot \beta \right)$$

(27)

where F_c—cohesion force on the soil shear surface, N; F_ca—adhesion force at the contact surface of the soil pile with the duckfoot wing, N; G—weight of the soil pile, N; F_a—inertia force of the soil pile, N; r—extent of the soil pile cracking, m; c_a—adhesion of the soil to the surface of the tool, N·m⁻², c—cohesion, N·m⁻²; l_s—duckfoot blade length, m; w_w—wing width of duckfoot, m; d—depth of work duckfoot, m; γ—volumetric weight of the soil, N·m⁻³; v—speed of tool movement, m·s⁻¹; g—acceleration of gravity, m·s⁻²; α—duckfoot wing angle, °; β—soil shear angle, °.

The draught force and vertical component of the duckfoot pressure on the soil were obtained, as given in model 2, by combining the resultant contact force with the adhesion force, Equations (28) and (29), respectively, were rewritten to create the complete algorithm.

$$F_x=F\sin \left(\alpha +\delta \right)+{2c}_a{w}_w\cos \alpha l_s\sin {\theta }_o$$

(28)

$$F_y=F\cos \left(\alpha +\delta \right)-{2c}_a{w}_w\sin \alpha l_s$$

(29)

where F_x—draught force, horizontal component of the pressure force of duckfoot on the soil, N; F_y—vertical component of the pressure force of the duckfoot on the soil, N; F—resultant pressure force of the duckfoot on the soil, N; c_a—adhesion of the soil to the surface of the tool, N·m⁻², w_w—width of the duckfoot wing, m; l_s—duckfoot blade length, m; α—duckfoot wing angle, °; δ—angle of external friction soil–steel, °; θ_o—lateral angle of the duckfoot wing, °.

In the modified model 3 of Perumpral, the wedge geometry and the system of forces, similar to those of the McKyes model, were retained. Still, the equilibrium equations were developed to determine the cutting force of the soil directly.

In the summary of the changes, a comparative diagram of the three modified analytical models for duckfoots (Söhne, McKyes, Perumpral) is provided in Figure 2, which illustrates the common modifications and the advantages and limitations of each approach. The inclusion of the factor sin² θ_o in the inertial term was a direct consequence of projecting the tool motion velocity onto the direction related to the tool wing edge.

The mathematical models were validated for the draught force F_x using experimental data for the same technical parameters.

3. Materials and Methods

3.1. Soil Properties

Soil bin tests were conducted at the Department of Biosystems Engineering, Institute of Mechanical Engineering, Warsaw University of Life Sciences, to obtain data for verifying the analytical model. The soil bin was filled with light loamy sand, comprising clay, silt, and sand fractions of 2%, 36%, and 62%, respectively, as determined by the sieve separation method. The dry soil volume density was 1535 ± 11 kg·m⁻³, and the compaction of 486 ± 25 kPa was determined using a 30° cone penetrometer with a base diameter of 20.27 mm, in accordance with the ASAE S 313.2 standard [23]. The drying-weighing method determined soil moisture contents of 10% and 14% (wet basis), in accordance with the ISO 11465 standard [24].

For both moisture contents, the mechanical properties of the soil were investigated in the annular rotary Schulze shear apparatus at the Institute of Agrophysics of the Polish Academy of Sciences in Lublin [25]. The soil was pre-consolidated at pressures of 10, 20, 30, 40, and 50 kPa [26]. For moisture content levels of 10% and 14%, the values of the angle of internal friction were 37° and 32°, respectively. The values of the angle of friction for soil–steel were 24° and 22°, respectively. The cohesion was 17 kPa and 18 kPa, and adhesion was 10 kPa and 12 kPa, respectively. The index of flowability, ff_c, was 1.50 and 1.60, respectively. According to the classification [27], this soil was classified as a cohesive material, because the value of ff_c was within the range of 1 < ff_c < 2.

3.2. Test Objects

Three duckfoots with widths of 105, 133, and 202 mm, labelled A105, B135, and C200, were used in the study. Duckfoot was attached to S-type and VCO-type tines, with stiffnesses of 5.3 kN·m⁻¹ and 8.3 kN·m⁻¹, respectively. Although the shape and characteristic angles of duckfoots were similar, when combined with the S and VCO tines, the landing angles were 8° and 2°, respectively [28].

3.3. Soil Bin with Measuring Equipment

The tine with a duckfoot was attached to the frame of a tool trolley pulled by a rope system driven by a 22.0 kW WAR 1M4 TF electric motor, coupled to a FUA 85A 16 1M4 TF gearbox. The rotational speed was determined by a V2500-0220 TFW1 inverter (Watt Drive, Markt Piesting, Austria). The trolley’s movement speed with working elements was monitored by an optical sensor (CS3D, ZEPWN, Marki, Poland). The depth of duckfoot work was determined and controlled using a laser distance meter (LDS 100-500P-S, Beta Sensorik, Dresden, Germany) combined with a 3000 mm horizontal displacement indicator, with a sensitivity of 0.3163 mV V⁻¹ mm⁻¹ (WS12-3000-R1K-L10-M, ASM GmbH, Moosinning, Germany). The measurement data were recorded on a computer via a high-speed digital interface board (Hottinger Brüel & Kjaer GmbH, Darmstadt, Germany), specifically the DMCplus. The measurement and control system was controlled by the CATMAN 2.1 software, which provided simultaneous data acquisition and motion control, with a sampling rate of 50 Hz.

3.4. Measurement Procedure

The soil at a depth of 0.6 m was loosened with tines using a subsoiler to a depth of 0.22 ± 0.02 m, levelled with a scraper, and compacted with a roller weighing 360–520 kg, according to a verified procedure [28]. The research was conducted at three duckfoot working depths: 30, 50, and 70 mm, and at three movement speeds: 0.84, 1.67, and 2.31 m·s⁻¹. These variables were combined into a factorial experiment with the following design: 3 × 2 × 3 × 3 × 2 (duckfoot width × tine × working depth × movement speed × soil moisture content, respectively), with three or four blocks (replications).

3.5. Statistical Analysis

Separately, for soil moisture contents of 10% and 14%, the optimal values of internal φ and external δ friction angles and soil shear β were determined, using the method of minimising differences between empirical values of draught force (F_xe) and values calculated from theoretical models (F_xp), Equation (30) and using the open-source Python software’s v. 3.11.5 (https://www.python.org, accessed on 10 October 2025).

$$SSE(\phi ,\delta ,\beta )=\sum _{i=1}^N{(F_{xei}-F_{xpi}(\phi ,\delta ,\beta \left)\right)}^2$$

(30)

where F_xei—ith empirical value of the draught force, N; F_xpi(φ, δ, β)—ith value of the force calculated from the model at given angles, N; N—number of observations

Based on the minimisation of this function (Equation (30)), a set of angle values (φ, δ, β) was determined that reproduces the experimental data the best. The L-BFGS-B algorithm was used for optimisation, which allows the constraints for individual angles to be considered. The boundaries were adopted in accordance with the literature data: φ ∈ [30°, 40°], δ ∈ [20°, 30°], β ∈ [27°, 45°] [5,29,30]. The angle ranges were taken from the agricultural soil mechanics literature, which describes these typical friction and shear angles. These angle values are consistent with soil–tool interaction models and reflect the physical properties of light sandy loam soils. The assumed limits for φ, δ, and β are valid for the light loam studied and should be redefined when applying the models to soils with significantly different mechanical properties.

The fit of analytical models to the empirical data was assessed based on the mean squared error RMSE—Equation (31), mean relative error—Equation (32), and global error—Equation (33).

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{(F_{xei}-F_{xpi})}^2}$$

(31)

$${\delta }_r={\displaystyle \frac{100}{N}}{\sum }_{i=1}^N\left({\displaystyle \frac{F_{xei}-F_{xpi}}{F_{xei}}}\right)$$

(32)

$${\delta }_g={\displaystyle \frac{\sqrt{{\sum }_{i=1}^N{\left(F_{xei}-F_{xpi}\right)}^2}}{\sqrt{\left({\sum }_{i=1}^N{\left(F_{xei}\right)}^2\right)}}}100$$

(33)

where RMSE—mean squared error, N; δ_r—relative match error, %; δ_g—global model error, %; F_xei—ith experimental value of the draught force, N; F_xpi—ith value calculated from the predictive model, N; N—number of observations in a given case (whole—values for all data; soil moisture contents of 10% and 14%; tine S and VCO; duckfoot A105, B135 and C200; duckfoot working depth 0.030 m, 0.050 m and 0.070 m; tool movement speed 0.84 m·s⁻¹, 1.67 m·s⁻¹ and 2.31 m·s⁻¹).

Selected error rates allow for a comprehensive evaluation of the model. Mean squared error RMSE measures the average magnitude of the deviation of the values calculated from the model from the experimental values, expressed in units of the analysed value, in this case, in Newtons. This error allows for direct physical interpretation, indicating how much the model differs from the measurement data on average. RMSE is sensitive to large deviations because Equation (31) errors are squared, so it works exceptionally well when evaluating models for outliers and significant local differences.

The advantage of the mean relative error δ_r is that it takes both positive and negative values, which allows for the identification of the direction of deviation of the model. A positive value indicates an underestimation, while a negative value indicates an overestimation of the model relative to experimental data. Thanks to this, the relative error analysis provides information about the size of the error and its nature.

The global error δ_g is a normalised version of the mean squared error and is a measure of the total deviation of the model from the experimental values. This indicator enables the evaluation of the overall precision of the model fit, regardless of the units of measurement and the scale of the draught force value.

All three error rates were calculated for the entire dataset and separately for different test conditions (soil moisture content, tine type, duckfoot width, duckfoot working depth, tool movement speed) to compare error values and assess under which conditions the models perform the best. The analysis aimed to obtain the smallest possible error values of RMSE, δ_r (in absolute terms), and δ_g, which would indicate high accuracy of the model and its good compatibility with experimental data. The evaluated models should have the lowest values of these error rates.

4. Research Results and Discussion

Analysis of the results for the modified Söhne model indicates that the friction angle values obtained during the fitting process were slightly lower than those observed in the shear tests. For the entire dataset, the model optimised φ to 30° and δ up to 20° at β = 35° (

Table 1. The optimal values of φ and external friction angles of δ and shear β for modified Söhne, McKyes, and Perumpral models. For comparison, the angles from the shear test; for soil moisture content MC = 10% were φ = 37.0°, δ = 24.0°, and β = 31.4°, and for MC = 14%, they were φ = 32.0°, δ = 22.0°, and β = 30.1°.

Feature	Söhne			McKyes			Perumpral
	φ, °	d, °	b, °	φ, °	d, °	b, °	φ, °	d, °	b, °
All data	30.00	20.00	35.00	40.00	24.38	39.64	40.00	28.77	45.00
MC = 10%	30.00	20.32	33.66	40.00	29.05	40.00	37.03	29.42	45.00
MC = 14%	30.00	20.00	35.00	40.00	20.79	40.00	40.00	27.84	45.00

). Meanwhile, in the shear apparatus tests for a moisture content of 10%, the values were φ = 37°, δ = 24°, and β = 31.4°, and for a moisture content of 14%, φ = 32°, δ = 22°, β = 30.1°. This means that some of the physical effects not included in the model (i.e., simplification to 2D space, omitting the blade resistance or assuming fixed working angles) were absorbed by reduced values of friction angles, which allowed for a better balance the system of forces shown in Figure 1. Despite some differences, and taking into account the influence of compaction, moisture content and mineral fractions, the optimal values of friction and shear angles correlated well with the range of angles for mineral soils [5,29]. The optimal values of friction angles φ and δ were within the range of values measured in shear tests but were smaller. The differences in φ and δ angle values were higher for soil with a moisture content of 10% compared to 14%, which may indicate a lower proportion of soil-to-soil resistance under dynamic conditions and complex contacts within the soil. They could result from the plasticization effect and flow processes in moist soil. The optimal angles of external friction δ, which measure the interaction of soil with the tool surface, were at the lower end of the range reported by de Melo Ferreira et al. [30], specifically 20–30%.

A comparison of fit errors shows clear trends in the tool’s working conditions. For 10% moisture content, the relative error was small (δ_r about −4%), at RMSE = 47 N, while for 14% moisture content, δ_r increased to about −19%, and RMSE reached 78 N, which indicates a systematic overestimation of the draught force in wetter soils (

Table 2. Mean values of draught force, experimental F_xe and predictive from the F_xp models, and mean values of mean square errors RMSE, relative δ_r, and global δ_g evaluating modified analytical models Söhne, McKyes, and Perumpral.

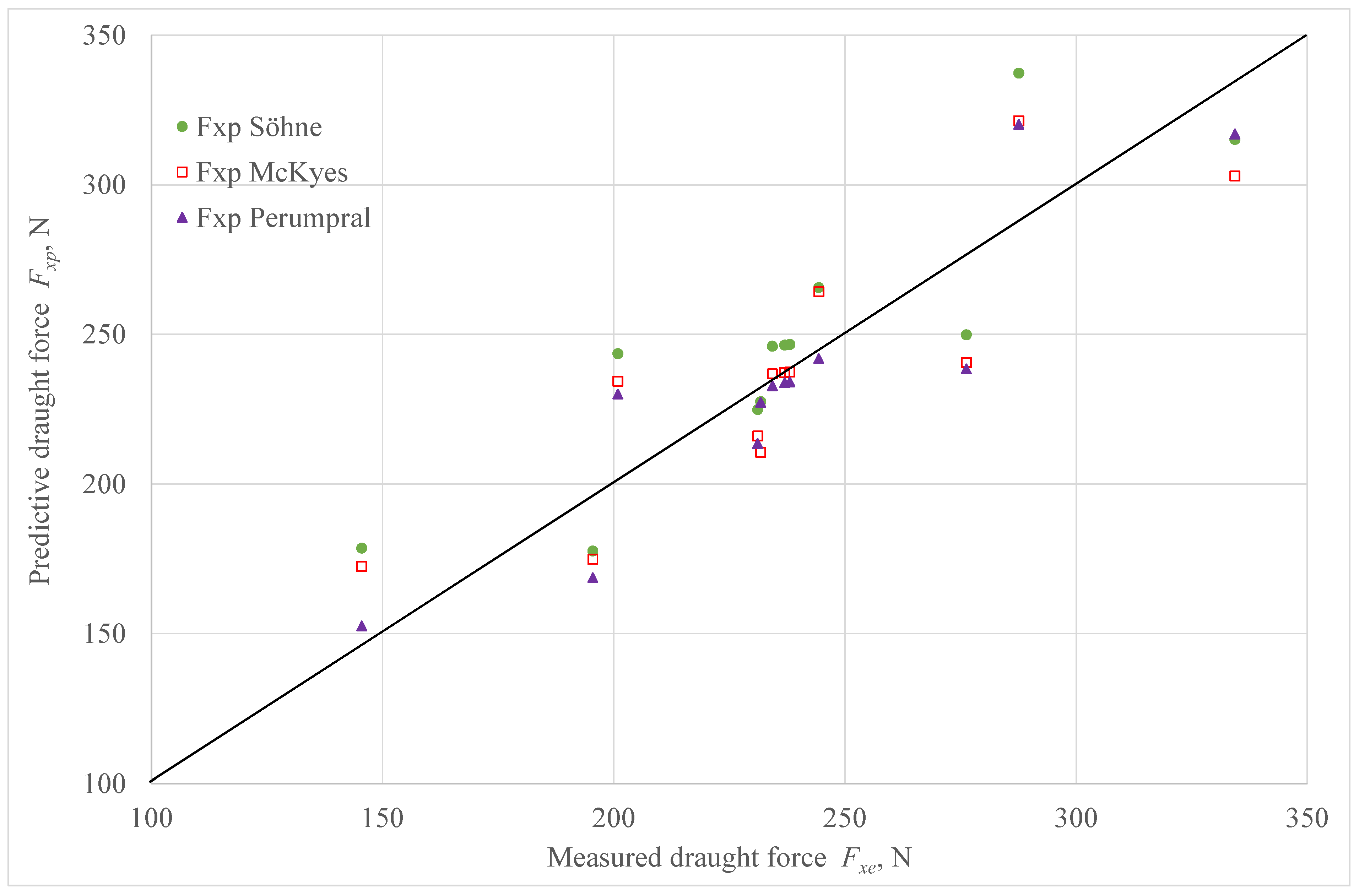
Model	Söhne
Feature	Fxe, N	Fxp, N	RMSE, N	δr, %	δg, %
All data	238.04	246.57	64.37	−11.58	24.95
MC = 10%	231.78	227.48	46.76	−3.94	18.78
MC = 14%	244.30	265.66	78.12	−19.22	29.29
Duckfoot = A105	195.45	177.56	57.59	−4.54	26.81
Duckfoot = B135	231.13	224.86	52.83	−4.77	21.30
Duckfoot = C200	287.56	337.29	79.53	−25.44	26.21
d = 0.03 m	145.50	178.55	56.92	−33.23	36.64
d = 0.05 m	234.31	246.01	53.13	−6.01	22.06
d = 0.07 m	334.33	315.15	79.80	4.49	23.28
v = 0.84 m·s−1	200.89	243.53	65.39	−27.94	30.45
v = 1.67 m·s−1	236.97	246.36	55.67	−10.46	21.85
v = 2.31 m·s−1	276.27	249.82	71.11	3.65	23.88
Model	McKyes
All data	238.04	237.38	64.39	−7.68	24.96
MC = 10%	231.78	210.52	50.61	3.31	20.32
MC = 14%	244.30	264.24	75.70	−18.66	28.39
Duckfoot = A105	195.45	174.78	58.53	−2.49	27.25
Duckfoot = B135	231.13	216.0	57.4	−0.78	23.15
Duckfoot = C200	287.56	321.35	75.62	−19.76	24.93
d = 0.03 m	145.50	172.44	55.08	−29.09	35.45
d = 0.05 m	234.31	236.77	52.96	−2.20	21.99
d = 0.07 m	334.33	302.92	81.24	8.26	23.70
v = 0.84 m·s−1	200.89	234.35	59.99	−23.49	27.93
v = 1.67 m·s−1	236.97	237.17	54.98	−6.51	21.58
v = 2.31 m·s−1	276.27	240.61	76.27	6.97	25.61
Model	Perumpral
All data	238.04	234.11	58.41	−3.38	22.64
MC = 10%	231.78	227.29	45.13	−2.00	18.12
MC = 14%	244.30	241.91	68.73	−5.70	25.77
Duckfoot = A105	195.45	168.68	56.54	3.44	26.32
Duckfoot = B135	231.13	213.46	49.28	2.93	19.87
Duckfoot = C200	287.56	320.20	67.89	−16.52	22.38
d = 0.03 m	145.50	152.57	42.43	−13.75	27.31
d = 0.05 m	234.31	232.83	47.06	−0.28	19.54
d = 0.07 m	334.33	316.94	78.86	3.89	23.00
v = 0.84 m·s−1	200.89	230.03	53.81	−18.00	25.06
v = 1.67 m·s−1	236.97	233.83	49.56	−2.38	19.46
v = 2.31 m·s−1	276.27	238.48	69.87	10.23	23.47

). When analysing the width of the tool, Söhne’s model well mapped the force for narrower duckfoots (A105 and B135, δ_r error of −5%), but at 200 mm wide, the overestimation was apparent (δ_r ≈ −25%, RMSE ≈ 80 N). A similar effect was visible depending on the working depth—for 0.03 m the model strongly overestimates (δ_r ≈ −33%), for 0.05 m the result was much better (δ_r about −6%), while at 0.07 m, there was a change in the sign and an underestimation appeared (δ_r ≈ +4%). This means that the proportion of geometric and dynamic forces in the Söhne model scaled inversely with increasing depth. Dynamic effects were more important at shallow depths, as low-mass soil moved easily and accelerated at low speeds. At a greater depth, a larger volume of soil was cut and shifted, and then geometric forces prevailed, with the influence of velocity (dynamic effect) being relatively small. When analysing the speed of the tool, it can be seen that at 0.84 m·s⁻¹ the error was significant and negative (δ_r = −28%), at 1.67 m·s⁻¹ it was still negative, but more minor (δ_r = −10%), and at 2.31 m·s⁻¹ it became positive (δ_r = +3.7%). This behaviour suggests that the dynamic term of the inertial force was overestimated at low speeds and underestimated at the highest speeds. This phenomenon results from the non-linear nature of soil displacements and the variable soil–tool contact: at low speeds, the soil moves quasi-continuously with the tool, while at high speeds, it is partially detached, which reduces the effective contribution of inertial forces to the total draught force.

From the perspective of modifying the Söhne model and introducing the projection of forces from the X_oY_oZ_o to the XYZ system, as well as the dynamic correction of sin²θ_o, it can be observed that scaling with width, depth, and velocity still yields underestimates and overestimations, depending on the tool’s operating conditions. They are quite symmetrical with respect to the diagonal (line of perfect conformity), which is a proof that the determined values of the optimal angles were correct (Figure 3). The values of the friction angles were reduced in the optimisation compared to the values from the shear tests, which is a typical sign that they compensate for the simplification of the model design and average the technical parameters. In practice, additional constraints for φ and δ close to the measured values can be considered, which would transfer more of the correction to geometric and dynamic parameters. It would also be helpful to adjust the ratio of the inertial term to different velocity ranges and verify the active surface’s scaling for wide tools, thereby improving the accuracy of field conditions.

Lower optimal values of friction angles φ and δ, compared to laboratory measurements, may also be the result of adhesion phenomena that are difficult to separate unambiguously, friction with adhering soil, and local deformations of the tool and soil, which do not occur in the conditions of the shear apparatus where the soil tests were performed. In addition, in real situations, the steel–soil contact could be interrupted by a layer of soil adjacent to the duckfoots, which increases the adequate soil–soil friction. In the Söhne model, better matching to the values of F_x obtained at the lowest values of φ and δ may be the result of geometric assumptions in the model, including static force equilibria on the two sliding surfaces. This suggests that differences in optimal angles do not necessarily indicate inconsistencies but rather result from the distinct structures of models and the distribution of forces in the soil. The fit to empirical data confirms the usefulness of the adopted values.

For shear angles β, optimal values were 35.0° (global), 33.7° for MC = 10% and 35.0° for MC = 14%, also within the typical range observed in wedge models [29]. The differences between measured and calculated values should be interpreted as a natural result of the adopted simplified description of the soil–tool space, in which the mathematical model averages many interdependent physical phenomena—such as deformations, friction, adhesion, and contact variables—over time.

In conclusion, for the Söhne model, the best experimental fit was achieved at the minimum limiting values of the internal friction angle φ and external friction angle δ, with shear angles at the same time β (33.7–35.0°) in the lower half of the range (27°, 45°) reported in the literature [5,29,30]. The interpretation of these results suggests that Söhne’s model simplifies real phenomena, describes them most accurately under conditions of limited friction, and assigns a greater role to the geometry and system of forces in the wedge.

For the McKyes model, the optimal values of the friction and shear angles were determined at the level of φ 40°, δ between 20,8° and 29,0°, and β = 39.6–40° (Table 1), which means that both the internal friction and the shear angle reached values close to the limit values assumed in optimisation. The values φ and β were consistent with the literature, where the reported range of internal friction for mineral soils is 30–40° 2, 25], and β is usually close to φ, as confirmed by the optimisation results. The external friction angle δ was within the typical range of 20–30° [26], with a moisture content of 10% reaching a value close to the upper limit and a minimum of 14% of the permitted moisture content, which well reflects the decrease in adequate friction as the soil moisture content increases. In terms of fit to the empirical data, the McKyes model achieved significantly better results for MC = 10% (δ_g = 20.3%, RMSE = 51 N), and weaker results for MC = 14% (δ_g = 28.4%, RMSE = 76 N), which confirms the observations from the Söhne model that wedge models better describe the behaviour of dry soil with higher rigidity. At the same time, under conditions of increased moisture content, plastic and viscous phenomena appear, which reduce the accuracy of prediction. Analysis by factor groups showed that the McKyes model correctly reflected the average level of draught force. Still, it was characterised by apparent discrepancies for extreme conditions: at a shallow depth of 0.03 m, the model significantly overestimated the force (δ_r = −29%, δ_g = 35.5%), and for the wide C200 duckfoot and high speeds, the discrepancies have also intensified. The best fit was obtained for an intermediate depth of 0.05 m and a mean width (duckfoot B135), indicating that the model most accurately describes the mean conditions under which the soil wedge develops, in accordance with the assumptions of the wedge theory and the results of the optimisation method. Comparing the results of the Söhne and McKyes models, it can be concluded that the global errors of both models were similar; however, the relative error for the entire dataset was smaller for the McKyes model. Both models (Söhne, McKyes) confirm that the effective angles of external friction decreased with increased soil moisture content (MC = 14%). The differences between the results of laboratory measurements and optimal values result from the nature of averaging in wedge models, which simultaneously integrate the interactions of friction, adhesion, and dynamic soil deformations. In summary, it can be stated that the McKyes model preferred the values of φ and β close to the upper limits (about 40°), which corresponds to the typical values of internal friction for mineral soils reported in the literature (30–40°) and close to the cover β and φ. According to the literature data, the external friction angle δ is assumed to be 20–30° for soil moisture content.

In the Perumpral model, a behaviour similar to the McKyes model was observed, with the shear angle of β kept at the highest allowable level (45°), indicating an increased role for geometry in this approach and a tendency to describe the soil as more compact. The angle of internal friction of φ was near the upper limit (especially globally and for MC = 14%). The external friction of δ was greater at MC = 10% and smaller at MC = 14%, which is consistent with the literature (φ ≈ 30–40°, δ ≈ 20–30°) and is intuitive, given the decrease in adequate external friction at higher soil moisture content. The fit quality of the Perumpral model was the best for MC = 10% (δ_g ≈ 18%) and weaker for MC = 14% (δ_g ≈ 26%), as in the Söhne and McKyes models: moist soil introduces plastic-viscous effects that wedge models describe only approximately. Analysis by factor groups reveals the best fit of the Perumpral model for B135 and d = 0.05 m, with clearer discrepancies for the duckfoot C200 at extreme working depths and movement speeds. The improved accuracy of Perumpral’s model results from its force balance equation having a different structure, which incorporates the dynamic component of the soil pile inertia, F_a. The term of v²sin²θ_o is a direct result of the projection of the velocity component along the edge of the duckfoot wing, rather than an arbitrary correction factor. This form of the equation better reflects the actual direction of soil flow on the wing, especially in the presence of a lateral relief angle, θ_o, and allows for the inclusion of the interaction between geometric parameters (α, β) and flow dynamics. In McKyes’s model, the effect of inertia is captured in a more simplified way, through the dimensionless coefficient N_a. Perumpral’s model is consistent with the classical Söhne approach, but its inertial formulation better balances the geometric, gravity, and dynamic terms and includes more parameters. For this reason, the Perumpral model exhibits a more stable fit over a wide range of speeds and working depths, particularly for soils with lower moisture content (MC = 10%), where soil displacements exhibit a more plastic–elastic character.

From the point of view of the quality of the fit to the empirical data, all three models were characterised by a relatively good error rating at a moisture content of 10%, where the global errors δ_g were at the level of 18–20%, while significantly weaker results were recorded at a moisture content of 14%, where δ_g increased to 26–29%. This means that all three models correctly mapped soil behaviour with lower moisture content (10%), which is characterised by greater rigidity. At the same time, they have a limited ability to describe a higher moisture content (14%), plasticized soil, in which viscous and adhesive phenomena not included in classical wedge theories occur. When comparing the models, Söhne required the smallest values of φ and δ, which may be less intuitive from the perspective of the literature. In contrast, the McKyes and Perumpral models better reflected the empirical approach. In the analysis by factor groups, all models best reproduced the draught force for medium operating conditions (depth 0.05 m, duckfoot B135). In comparison, the most significant discrepancies appeared for the shallow depth of 0.03 m, the wide duckfoot C200, and the highest travel speed of 2.31 m·s⁻¹. The overestimation of the draught force for the wide C200 implement is likely due to a combination of unmodelled soil bulge between the wings and wing boundary effects, which may require extending the description to a 3D version or applying local correction factors for large implement widths. This means that the wedge assumptions used in all three models are more effective in moderate conditions than in extreme conditions, where the nature of real phenomena in the soil deviates from geometric idealisations.

The error values enable an upbeat assessment of the developed analytical models, particularly when compared to the literature, where the error values for the Söhne, McKyes, and Perumpral models are higher. For a 25.4 cm wide blade working at a depth of 10 cm, set at 45° angles [21]. The calculated relative prediction errors for draught force were 38%, 48%, and 62%, respectively. For a 200 mm wide tool, mounted on a rigid shank, working in light sand at depths of 35, 100, and 150 mm, the relative prediction errors of draught force for the McKyes model were 24.6%, 27.0% and 32.0%, respectively, with the model being overestimated [31]. Based on the cited evaluations of mathematical models presented in the literature, it can be concluded that the modified models in this article enable more accurate predictions of draught force for duckfoots under different soil conditions, which supports the H1 hypothesis.

In conclusion, the carried-out analyses showed that all three models—Söhne, McKyes, and Perumpral—reproduced the draught force well in soil conditions at a moisture content of 10% and for average values of width, depth, and speed of movement. At the same time, their accuracy clearly decreased at higher soil moisture content (14%) and extreme values of technical parameters, which only partially justifies the H2 hypothesis. Although soil moisture was not directly included as an independent variable in the analytical equations, its influence was partially accounted for by experimentally determined soil parameters, namely cohesion (c), adhesion (c_a), and internal and external friction angles (φ, δ). These parameters were measured separately for 10% and 14% soil moisture, and the models were validated independently for both conditions.

The results confirm the legitimacy of the wedge-shaped approach, while indicating the need for further modification of the models to capture the phenomena of adhesion and plastic-viscous deformations of the soil. The analysis of three theoretical models (Söhne, McKyes, Perumpral) describing the process of soil shear by duckfoot tools yielded results that allow for a comparison of both the quality of fit and the nature of the optimal angle values. These models are based on a similar concept of a soil wedge and the balance of forces but differ in the details of their description and the way in which individual components are considered. The models were formulated based on a 2D structure, which is typical for wide tools such as the duckfoot drills analysed. For duckfoot tools with a diameter of less than 100 mm, three-dimensional (3D) modelling should be used. Therefore, the models reflect the dominant soil reaction perpendicular to the cutting edge, including its main component (draught force) in the direction of tool movement. Future analyses may incorporate a 3D approach to explain the lateral forces that influence soil shedding.

5. Conclusions

The conducted research confirmed the legitimacy of the modifications to the classic models of Söhne, McKyes, and Perumpral, specifically regarding the operation of duckfoot tools. The introduced geometric and dynamic adaptation, including a scaled inertial term sin²θ_o, allowed for a significantly improved reproduction of the distribution of forces in the soil.

The research methods, including experiments in a soil bin at different moisture content levels (10% and 14%), working depths (0.03–0.07 m), and movement speeds (0.84–2.31 m·s⁻¹), allowed for a wider range of model verifications. An essential element was the method of optimising the angles of internal friction (φ), external friction (δ), and shear angle (β) using the L-BFGS-B algorithm. However, the results showed that the optimal angle values differed from those measured by the shear apparatus, indicating that the models’ simplifications (two-dimensionality, omitting blade resistance, and assuming fixed operating angles) are not fully compensated.

Comparing the three modifications, the Perumpral model was the most effective, with an average RMSE of 58 N for the total data and a global error of δg that remained within the 18–26% range, depending on the soil moisture content. The Söhne and McKyes models gave less favourable results (RMSE ≈ 64 N). They showed the most significant deviations under extreme operating conditions (RMSE up to 80–81 N) in a detailed balance of forces. These differences indicate that the structure of the balance of forces and how soil–tool interactions were captured significantly influenced the sensitivity of models to soil and geometric variables.

The falsification of the hypotheses showed that although H1 (modification of models increases accuracy) was confirmed, H2 in its original form was not fully verified—the models turned out to be sufficiently precise only under specific conditions, especially under medium conditions (duckfoot B135, working depth 0.05 m, movement speed 1.67 m·s⁻¹) and for moderate soil moisture content of 10%. For a soil moisture content of 14% and under extreme tool operating conditions, systematic overestimation or underestimation of the draught force was observed, which proves that the current modifications do not eliminate all limitations.

From a scientific perspective, the introduced method for optimising soil parameters must enable the capture of hidden interactions between friction, cohesion, adhesion, and tool geometry. At the same time, the error analysis (RMSE, δ_r, δ_g) indicates the need for further development of the models. Future research directions should include the following: (1) moving from 2D analysis to a full 3D description that allows for lateral soil displacements; (2) integration of variability of physical properties of the soil over time (moisture content, compaction, plasticization); (3) the introduction of random terms in statistical models to capture uncontrollable field factors and improve prediction; (4) extension of the study to other soil types and tines structures to confirm the versatility of the proposed modifications. Tool wear was not considered at this stage of model modification and represents a separate, important direction for further research. These future research directions stem from an awareness of the limitations of the presented model modifications. These limitations result from the modelling assumptions and the range of validation conditions, including soil type, moisture levels, and tool geometric and technical parameters. The presented results refer to controlled laboratory conditions, and complete translation to the field scale will require combining analytical models with methods for describing spatial and probabilistic variability. The developed modifications can help optimise the design of row crop weeding tools such as goosefoot cultivators by enabling prediction-based selection of working width, rake angle, and working speed in specific soil conditions.

Overall, the developed model modifications represent a crucial step towards the reliable prediction of duckfoot tool draught. Still, further theoretical and empirical improvements are needed to achieve stability and high reproduction precision across the full spectrum of field conditions.