An Indirect Method for Accurate Identification of Short-Pitch Rail Corrugation Using Vehicle Interior Noise and Vibration Measurements and Train–Track Transfer Functions
Featured Application
Abstract
1. Introduction
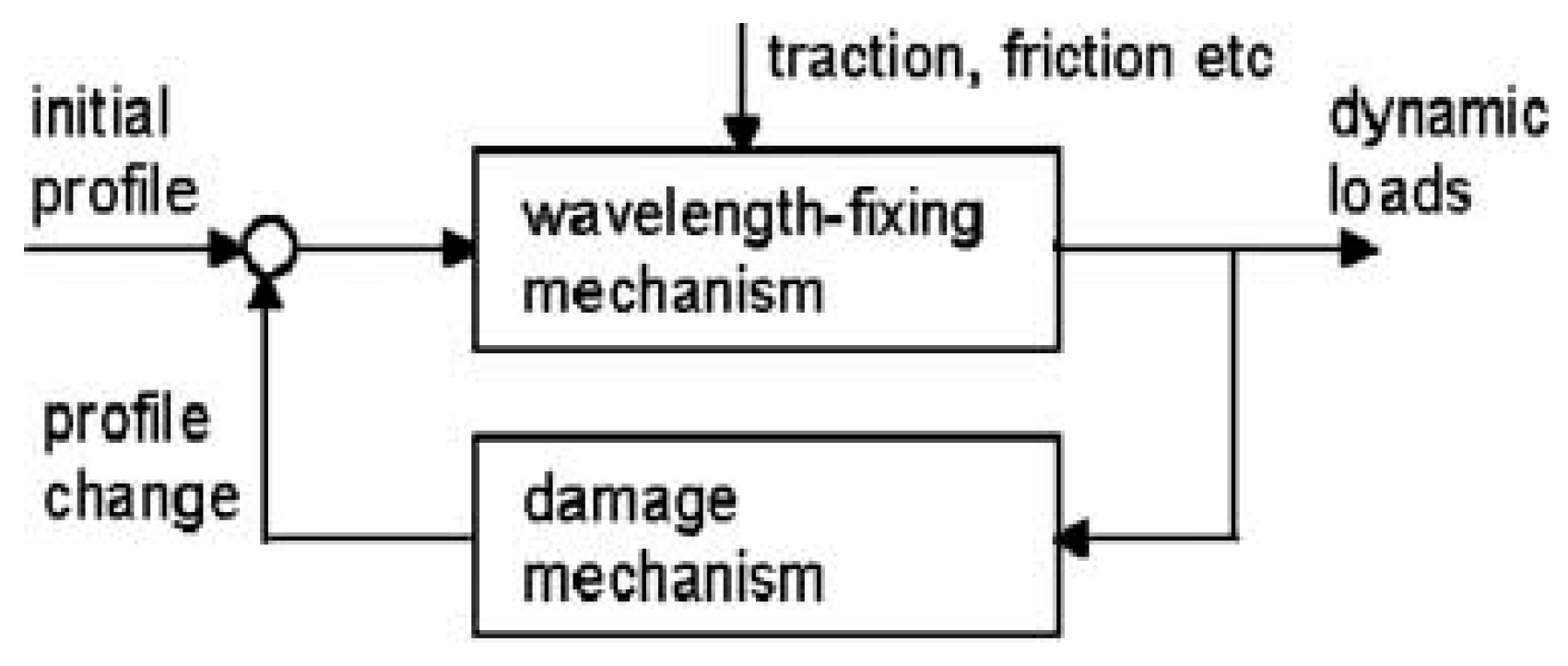
1.1. Rail Corrugation
1.2. Conventional Diagnosis Methods for Rail Corrugations
2. Research Methodology
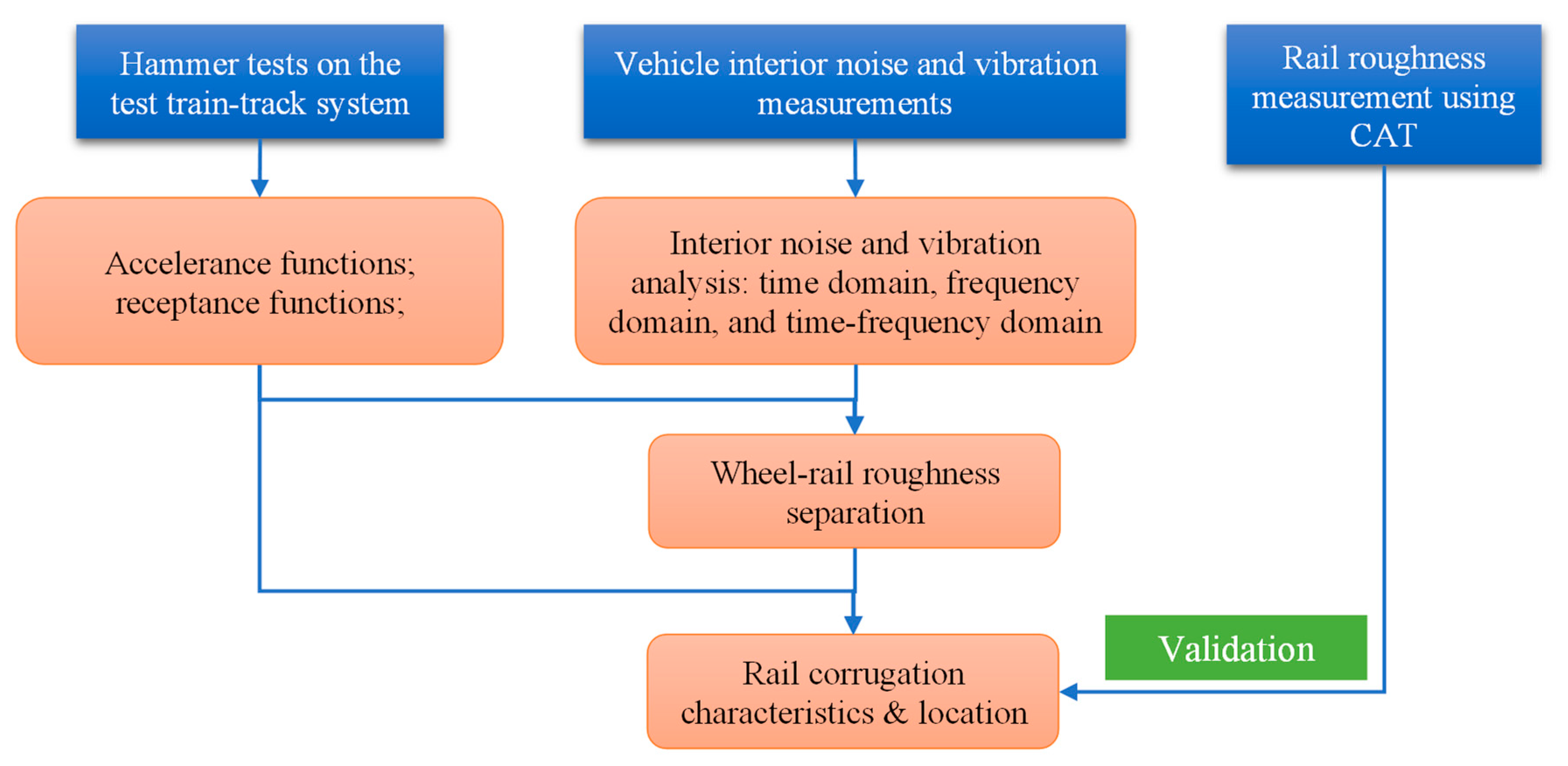
2.1. The Proposed Indirect Diagnosis Method
2.1.1. The Relationship Between Roughness and Wheel–Rail Force
2.1.2. The Relationship Between the Wheel–Rail Force and Vehicle Interior Responses
2.1.3. Rail Corrugation Diagnosis Using Interior Response and Transfer Functions
2.1.4. Separation of Wheel and Rail Roughness
2.2. Implementation of the Proposed Indirect Method and Validation
3. The Test Train–Track System
4. Transfer Functions of the Test Wheel–Rail System
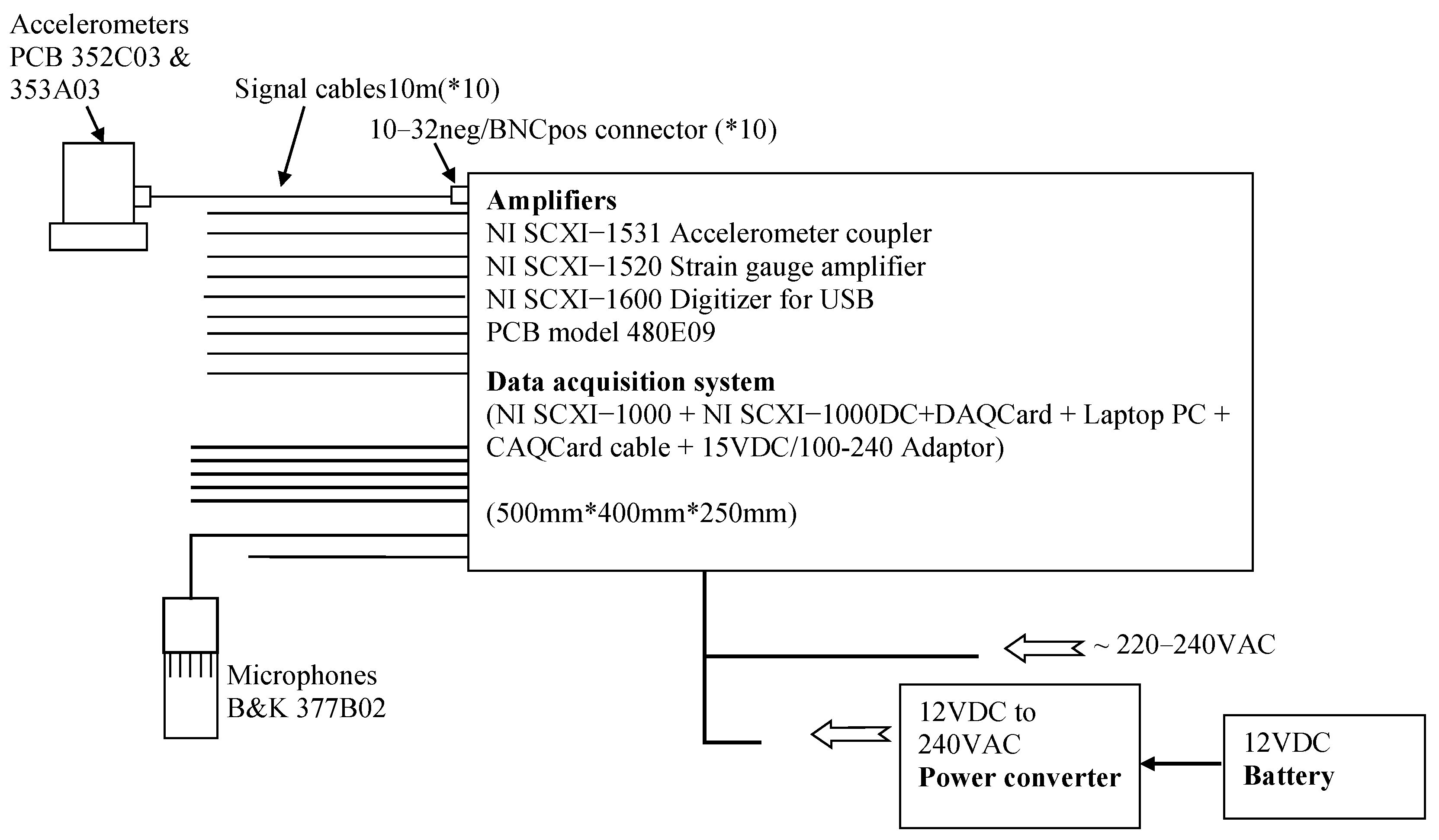
4.1. Experimental Setup
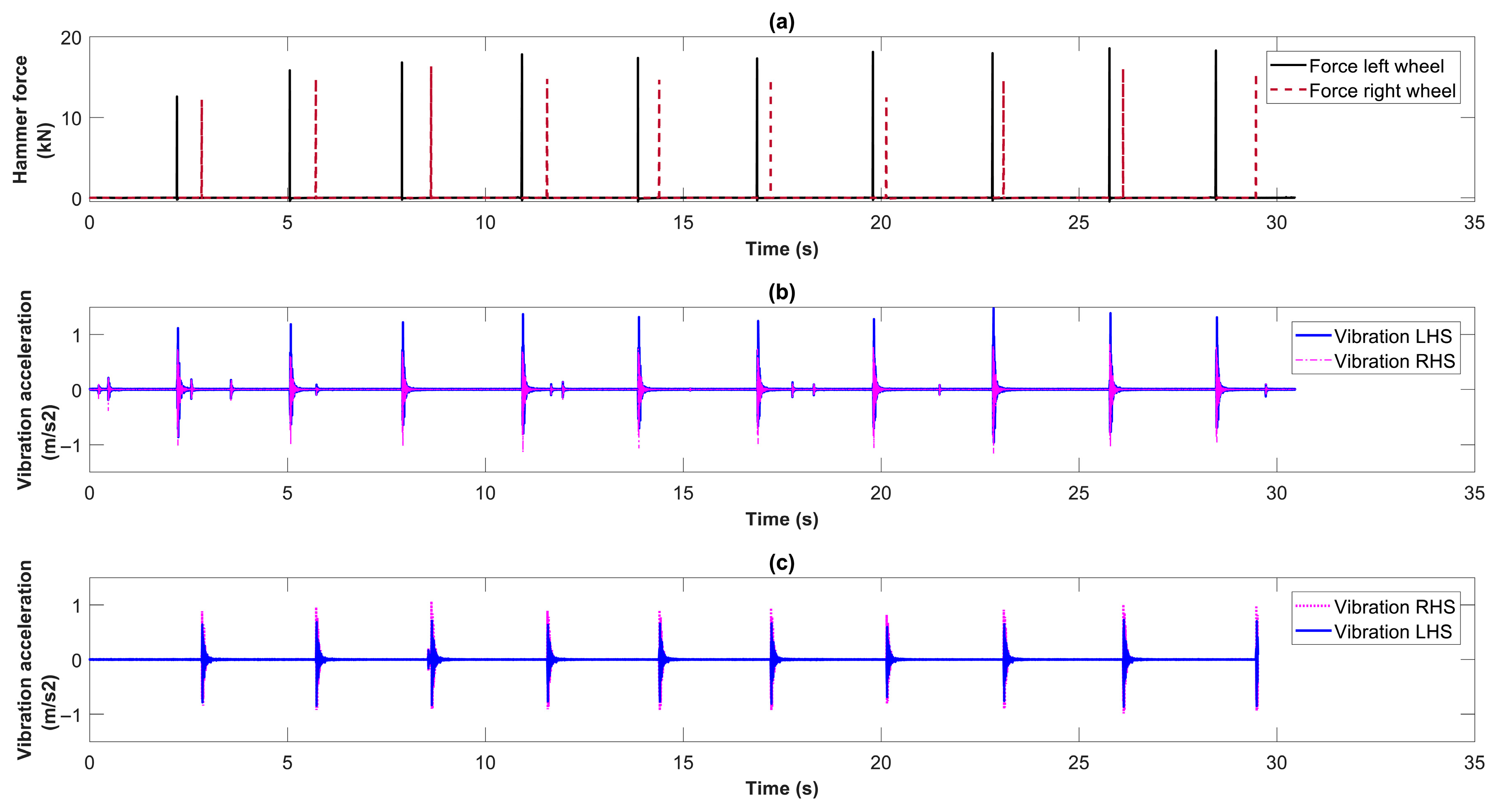
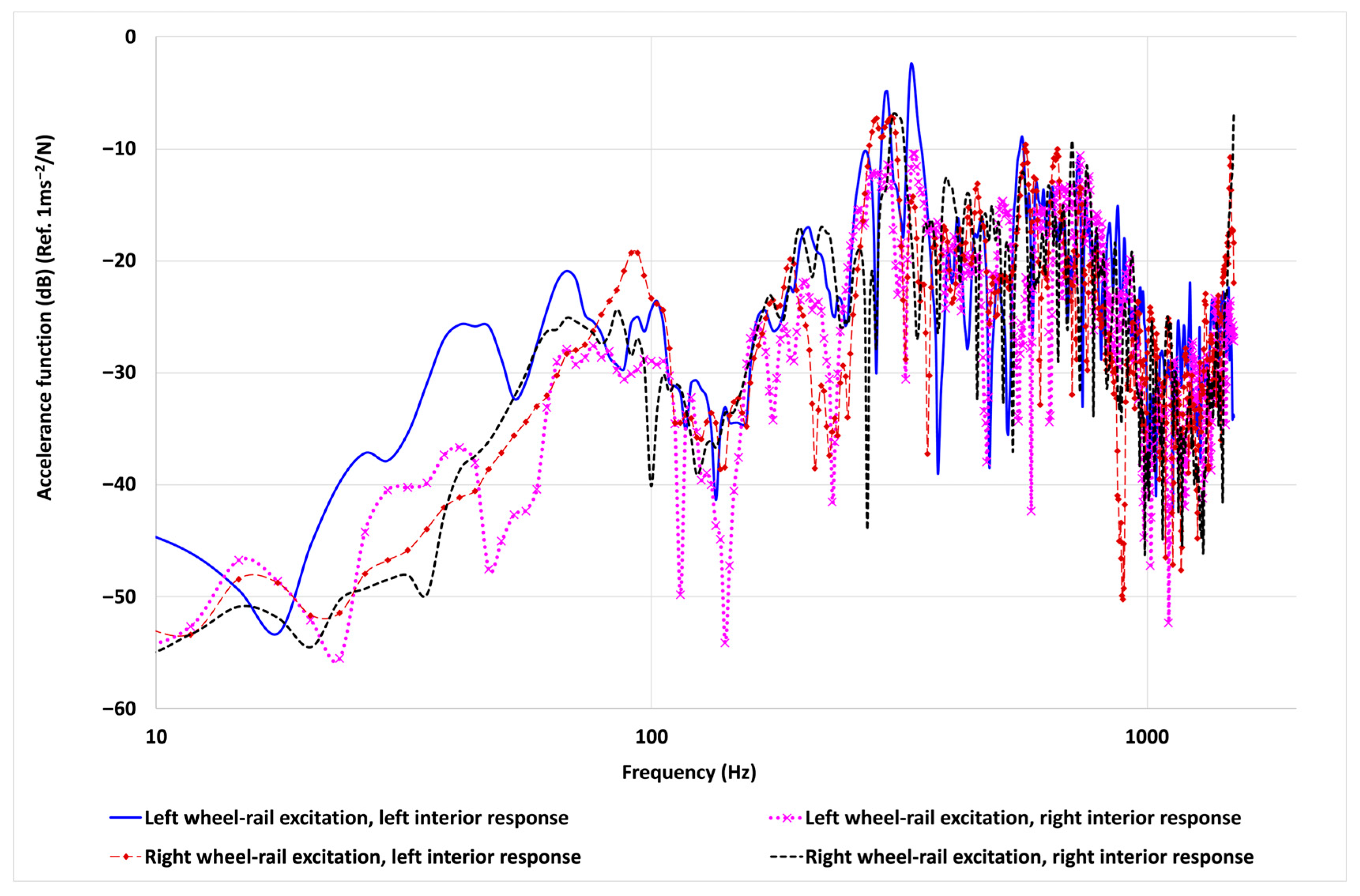
4.2. Accelerance
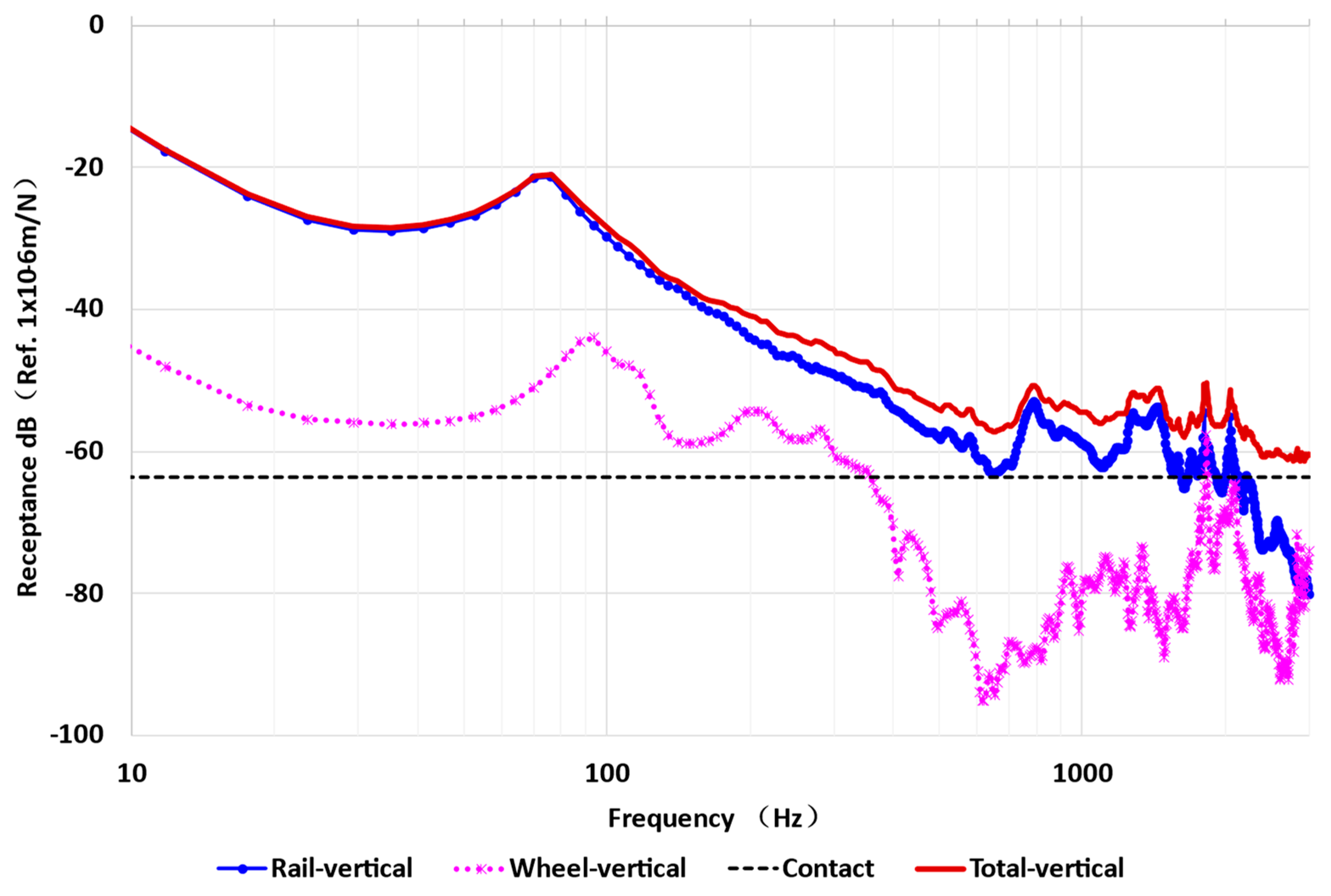
4.3. Receptance
5. Train Vehicle Interior Noise and Vibration Measurements
5.1. Site Inspection
5.2. Experimental Setup
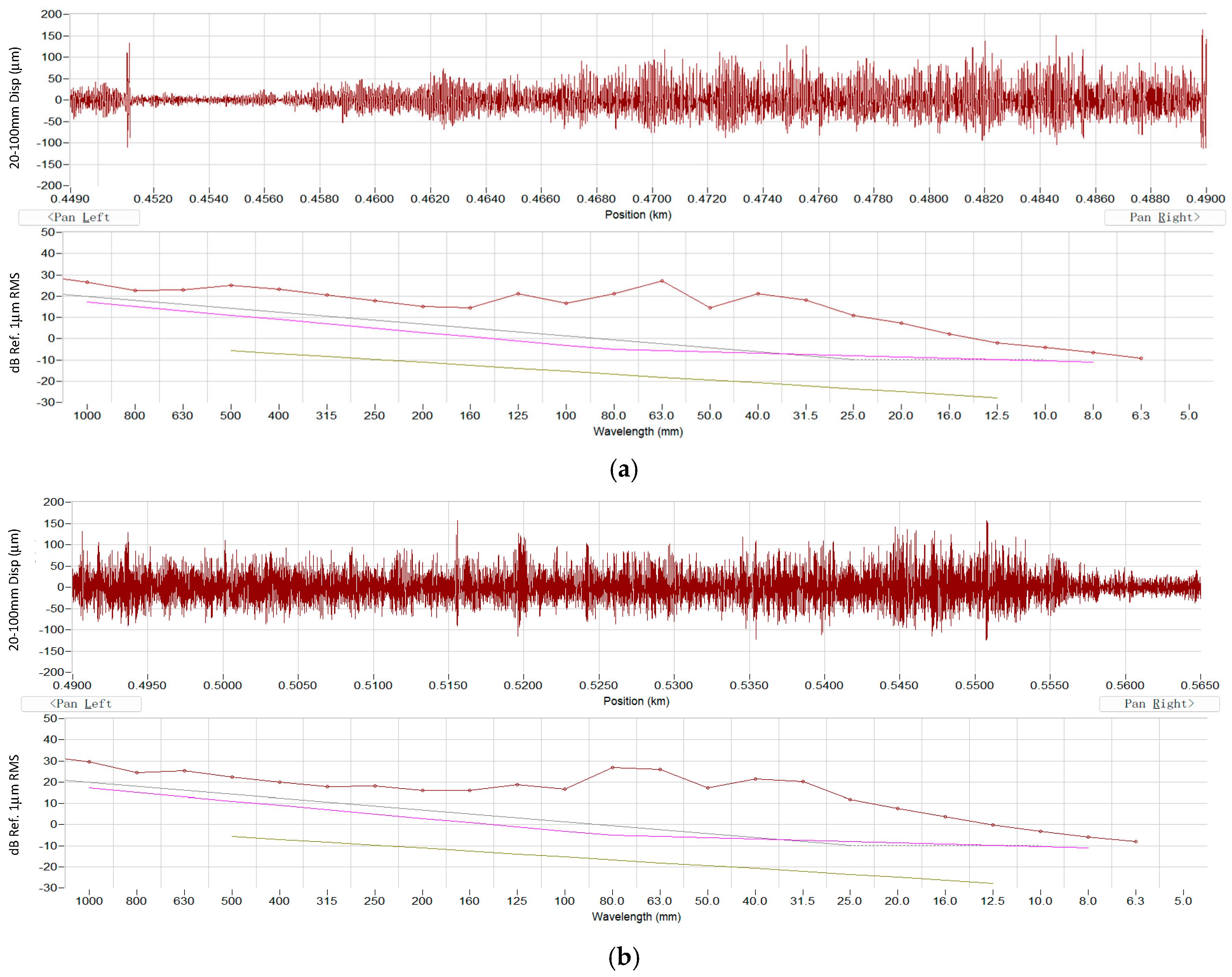
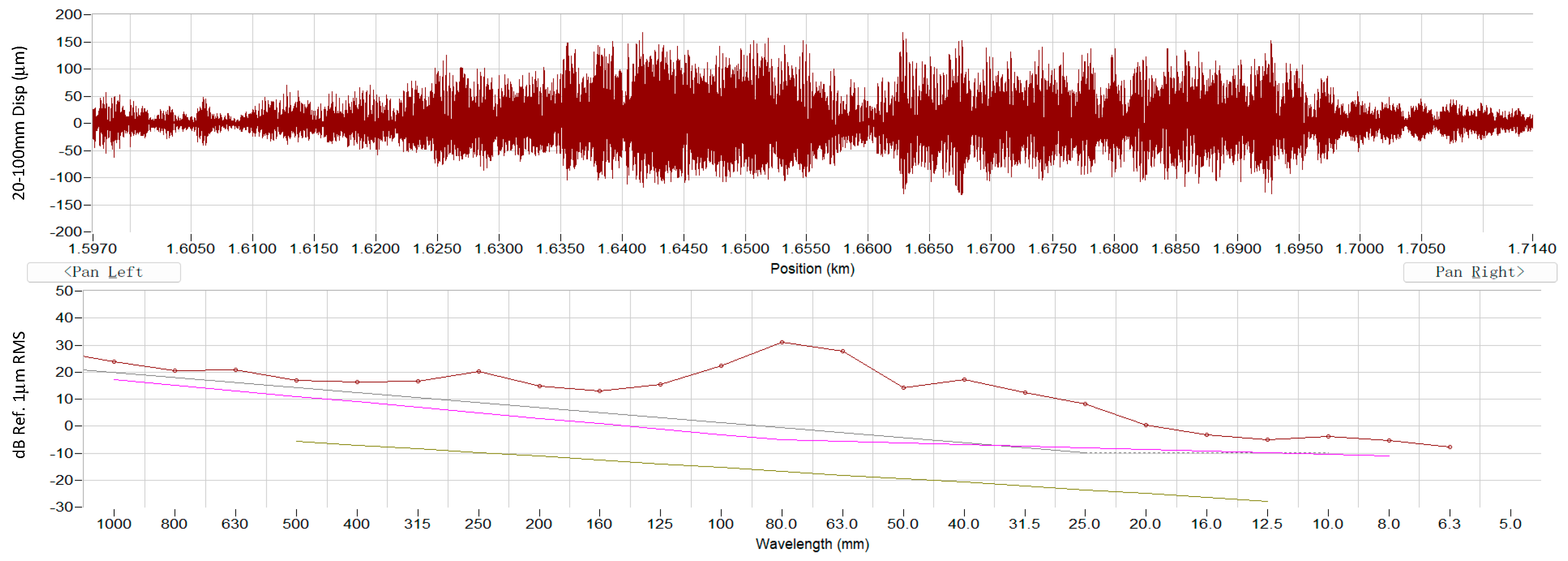
5.3. Time and Frequency Domain Analysis of Interior Responses
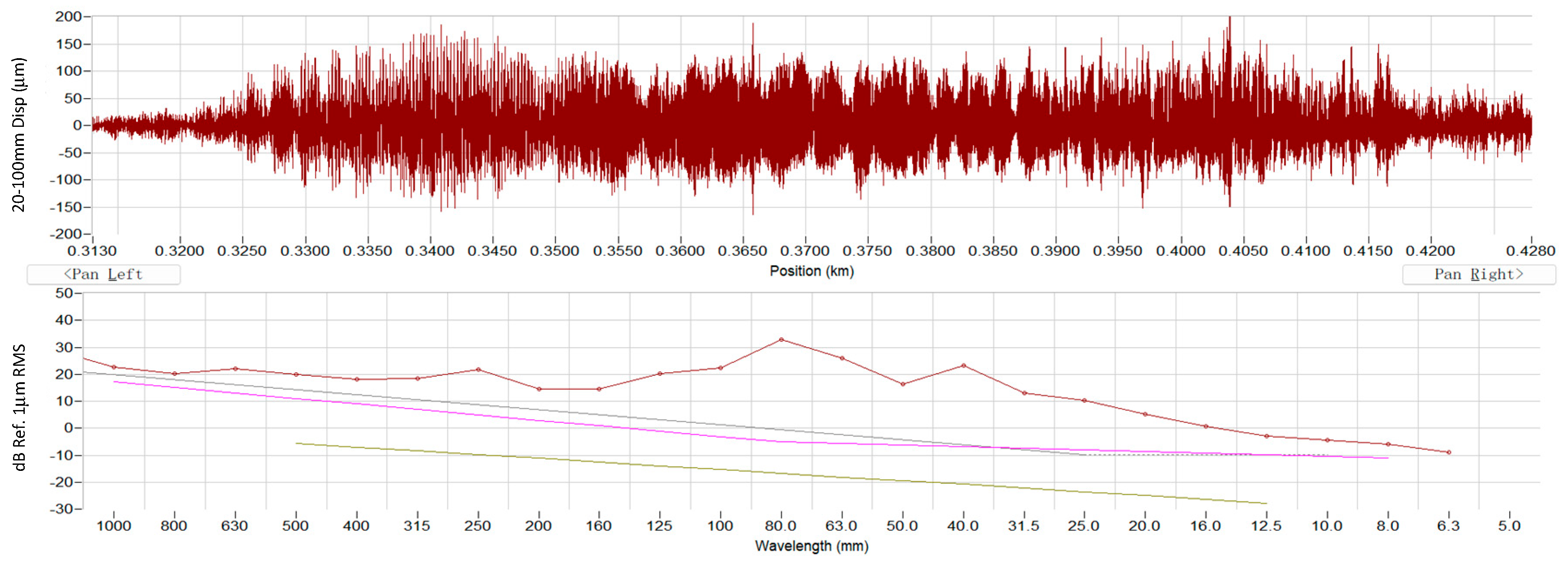
6. Direct Measurement of Rail Roughness Using CAT
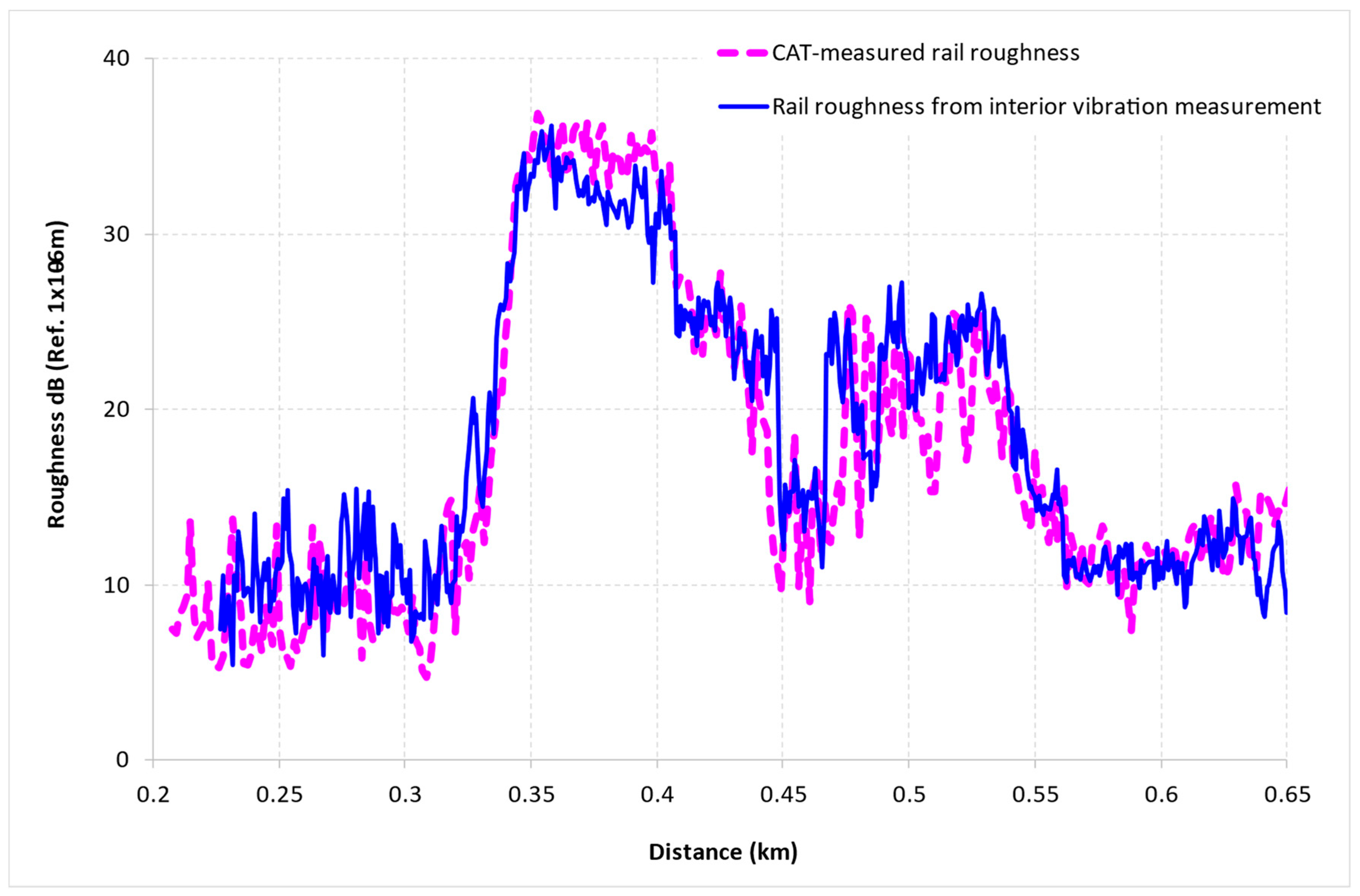
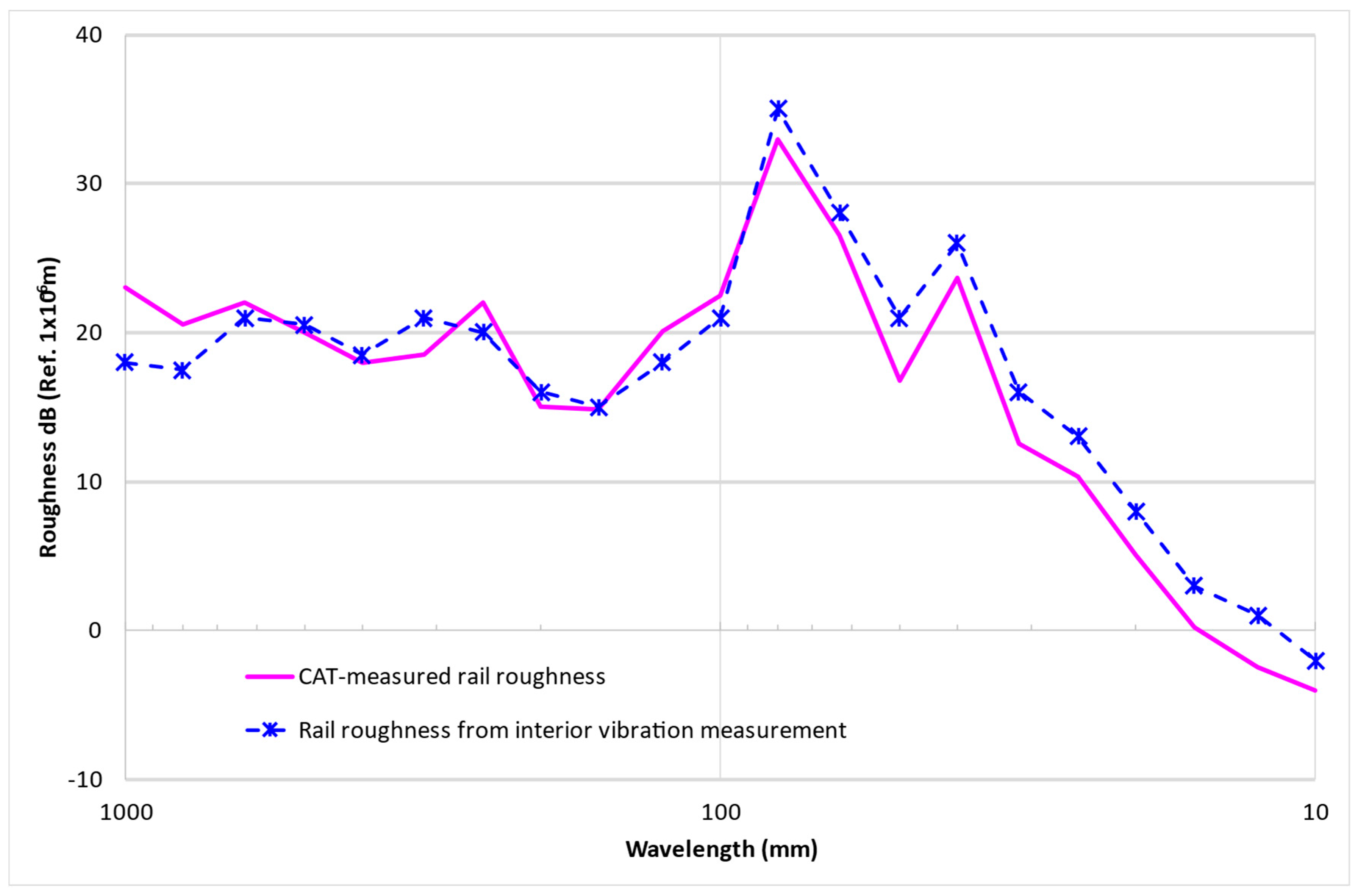
7. Validation and Discussions of the Indirect Diagnosis Method
7.1. Validation Using Direct CAT Measurement
7.2. Discussions
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jeong, W. Spectral characteristics of rail surface by measuring the growth of rail corrugation. Appl. Sci. 2021, 11, 9568. [Google Scholar] [CrossRef]
- Oostermeijer, K.H.H. Review on short pitch rail corrugation studies. Wear 2008, 265, 1231–1237. [Google Scholar] [CrossRef]
- Brockley, C.A.; Ko, P.L. An investigation of rail corrugation using friction-induced vibration theory. Wear 1988, 128, 99–106. [Google Scholar] [CrossRef]
- Ahlbeck, D.R.; Daniels, L.E. Investigation of rail corrugations on the Baltimore Metro. Wear 1991, 144, 197–210. [Google Scholar] [CrossRef]
- Tassilly, E.; Vincent, N. Rail corrugations: Analytical model and field tests. Wear 1991, 144, 163–178. [Google Scholar] [CrossRef]
- Grassie, S.L.; Kalousek, J. Rail Corrugation: Characteristics, Causes and Treatments. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 1993, 207, 57–68. [Google Scholar] [CrossRef]
- Grassie, S.L. Rail corrugation: Characteristics, causes, and treatments. Proc. Inst. Mech. Eng. F J. Rail Rapid Transit. 2009, 223, 581–596. [Google Scholar] [CrossRef]
- Grassie, S.L. Rail corrugation: Advances in measurement, understanding and treatment. Wear 2005, 258, 1224–1234. [Google Scholar] [CrossRef]
- Korpanec, I.; Pradier, H.P. Practical implementation of results of ORE-ERRI research on wheel-rail contact interaction on the European railways. Wear 1996, 191, 121–125. [Google Scholar] [CrossRef]
- Igeland, A.; Ilias, H. Rail head corrugation growth predictions based on non-linear high frequency vehicle/track interaction. Wear 1997, 213, 90–97. [Google Scholar] [CrossRef]
- Vadillo, E.G.; Tárrago, J.A.; Zubiaurre, G.G.; Duque, C.A. Effect of sleeper distance on rail corrugation. Wear 1998, 217, 140–145. [Google Scholar] [CrossRef]
- Jin, X.; Xiao, X.; Wen, Z.; Zhou, Z. Effect of sleeper pitch on rail corrugation at a tangent track in vehicle hunting. Wear 2008, 265, 1163–1175. [Google Scholar] [CrossRef]
- Ilias, H. The influence of railpad stiffness on wheelset/track interaction and corrugation growth. J. Sound Vib. 1999, 227, 935–948. [Google Scholar] [CrossRef]
- Egana, J.I.; Vinolas, J.; Seco, M. Investigation of the influence of rail pad stiffness on rail corrugation on a transit system. Wear 2006, 261, 216–224. [Google Scholar] [CrossRef]
- Meehan, P.A.; Bellette, P.A.; Horwood, R.J. “Does god play dice with corrugations?”: Environmental effects on growth. Wear 2014, 314, 254–260. [Google Scholar] [CrossRef]
- Bellette, P.A.; Meehan, P.A.; Daniel, W.J.T. Effects of variable pass speed on wear-type corrugation growth. J. Sound Vib. 2008, 314, 616–634. [Google Scholar] [CrossRef]
- Meehan, P.A.; Batten, R.D.; Bellette, P.A. The effect of non-uniform train speed distribution on rail corrugation growth in curves/corners. Wear 2016, 366–367, 27–37. [Google Scholar] [CrossRef]
- Batten, R.D.; Bellette, P.A.; Meehan, P.A.; Horwood, R.J.; Daniel, W.J.T. Field and theoretical investigation of the mechanism of corrugation wavelength fixation under speed variation. Wear 2011, 271, 278–286. [Google Scholar] [CrossRef]
- Brockley, C.A. The influence of track support structure and locomotive traction characteristics on short wavelength corrugations. Wear 1992, 153, 315–322. [Google Scholar] [CrossRef]
- Ishida, M.; Moto, T.; Takikawa, M. The effect of lateral creepage force on rail corrugation on low rail at sharp curves. Wear 2002, 253, 172–177. [Google Scholar] [CrossRef]
- Saulot, A.; Descartes, S.; Desmyter, D.; Levy, D.; Berthier, Y. A tribological characterization of the “damage mechanism” of low rail corrugation on sharp curved track. Wear 2006, 260, 984–995. [Google Scholar] [CrossRef]
- Suda, Y.; Hanawa, M.; Okumura, M.; Iwasa, T. Study on rail corrugation in sharp curves of commuter line. Wear 2002, 253, 193–198. [Google Scholar] [CrossRef]
- Suda, Y.; Komine, H.; Iwasa, T.; Terumichi, Y. Experimental study on mechanism of rail corrugation using corrugation simulator. Wear 2002, 253, 162–171. [Google Scholar] [CrossRef]
- Matsumoto, A.; Sato, Y.; Ono, H.; Tanimoto, M.; Oka, Y.; Miyauchi, E. Formation mechanism and countermeasures of rail corrugation on curved track. Wear 2002, 253, 178–184. [Google Scholar] [CrossRef]
- Sato, Y.; Matsumoto, A.; Knothe, K. Review on rail corrugation studies. Wear 2002, 253, 130–139. [Google Scholar] [CrossRef]
- Wu, T.X.; Thompson, D.J. An investigation into rail corrugation due to micro-slip under multiple wheel/rail interactions. Wear 2005, 258, 1115–1125. [Google Scholar] [CrossRef]
- Andersson, C.; Johansson, A. Prediction of rail corrugation generated by three-dimensional wheel-rail interaction. Wear 2004, 257, 423–434. [Google Scholar] [CrossRef]
- Jin, X.S.; Wen, Z.F. Effect of discrete track support by sleepers on rail corrugation at a curved track. J. Sound Vib. 2008, 315, 279–300. [Google Scholar] [CrossRef]
- Torstensson, P.T.; Schilke, M. Rail corrugation growth on small radius curves-Measurements and validation of a numerical prediction model. Wear 2013, 303, 381–396. [Google Scholar] [CrossRef]
- Torstensson, P.T.; Nielsen, J.C.O. Monitoring of rail corrugation growth due to irregular wear on a railway metro curve. Wear 2009, 267, 556–561. [Google Scholar] [CrossRef]
- Torstensson, P.T.; Pieringer, A.; Nielsen, J.C.O. Simulation of rail roughness growth on small radius curves using a non-Hertzian and non-steady wheel-rail contact model. Wear 2014, 314, 241–253. [Google Scholar] [CrossRef]
- Han, J.; Xiao, X.; Wu, Y.; Wen, Z.; Zhao, G. Effect of rail corrugation on metro interior noise and its control. Appl. Acoust. 2018, 130, 63–70. [Google Scholar] [CrossRef]
- Gu, X.P.; Ma, Z.; Wang, A.; Ju, L.; Chai, X.; Gao, X. Cost Effectiveness of Noise and Vibration Mitigation Measures Using Life-Cycle Cost Analysis. In Noise and Vibration Mitigation for Rail Transportation Systems; Springer: Cham, Switzerland, 2021; pp. 214–221. [Google Scholar] [CrossRef]
- Egana, J.I.; Vinolas, J.; Gil-Negrete, N. Effect of liquid high positive friction (HPF) modifier on wheel-rail contact and rail corrugation. Tribol. Int. 2005, 38, 769–774. [Google Scholar] [CrossRef]
- Maes, J.; Sol, H. A double tuned rail damper—Increased damping at the two first pinned–pinned frequencies. J. Sound Vib. 2003, 267, 721–737. [Google Scholar] [CrossRef]
- Thompson, D.J.; Jones, C.J.C.; Waters, T.P.; Farrington, D. A tuned damping device for reducing noise from railway track. Appl. Acoust. 2007, 68, 43–57. [Google Scholar] [CrossRef]
- Croft, B.E.; Jones, C.J.C.; Thompson, D.J. Modelling the effect of rail dampers on wheel–rail interaction forces and rail roughness growth rates. J. Sound Vib. 2009, 323, 17–32. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, A.; Gao, X.; Gu, X.; Ju, L.; Wang, Z. Rail Vibration and Rolling Noise Reduction Using Tuned Rail Damper for Vulcanized Bonded Baseplate. In Noise and Vibration Mitigation for Rail Transportation Systems; Springer: Cham, Switzerland, 2021; pp. 671–679. [Google Scholar] [CrossRef]
- RailMeasurement, Corrugation Analysis Trolley (CAT). Available online: https://www.railmeasurement.com/ (accessed on 21 August 2024).
- Gu, X.P.; Han, Y.; Shi, J.; Wang, A. Rail Corrugation Characteristics Deduced from a Wavelet Analysis of High-Speed Train Interior Noise and Vibration. Shock. Vib. 2024, 2024, 8810338. [Google Scholar] [CrossRef]
- ISO 3095-2013; Acoustics—Railway Applications—Measurement of Noise Emitted by Railbound Vehicles. International Organization for Standardization: Geneva, Switzerland, 2013.
- ISO 3095-2005; Railway Applications—Acoustics—Measurement of Noise Emitted by Railbound Vehicles. International Organization for Standardization: Geneva, Switzerland, 2005.
- ISO 3095:2025; Railway Applications—Acoustics—Measurement of Noise Emitted by Railbound Vehicles. International Organization for Standardization: Geneva, Switzerland, 2025.
- EN 13231-2:2020; Railway Applications—Track—Acceptance of Works—Part 2: Acceptance of Reprofiling Rails in Plain Line, Switches, Crossings and Expansion Devices. European Committee for Standardization (CEN): Brussels, Belgium, 2020.












| Direct Method | Level of Accuracy | Time and Cost |
|---|---|---|
| CAT | Good for short-pitch corrugation | Measurement speed: walking speed, typically 4–6 km/h; using less expensive hand-held devices. |
| Inspection vehicle | Insufficient for short-pitch corrugation | Measurement speed: 5–35 km/h; need to hire inspection vehicles. |
| Section Code | Starting Mileage | End Mileage | Geometry | Fastener Type |
|---|---|---|---|---|
| S1 | K0.0 | K0.313 | Straight line leaving the station | Non-resilient |
| C1 | K0.313 | K0.428 | Right-curve | Cologne eggs |
| T1 | K0.428 | K0.449 | Transition between 2 curves | Cologne eggs |
| C2 | K0.449 | K0.565 | Left-curve | Cologne eggs |
| T2 | K0.565 | K0.780 | Transition from curve to straight line | Cologne eggs |
| S2 | K0.780 | K1.410 | Straight line | Non-resilient |
| T3 | K1.410 | K1.597 | Transition from straight line to curve | Cologne eggs |
| C3 | K1.597 | K1.745 | Left-curve | Cologne eggs |
| S3 | K1.745 | K1.861 | Straight line entering the station | Non-resilient |
| Sensor Type | Measurement Points | Measurement Range | Sensitivity | Frequency Range |
|---|---|---|---|---|
| PCB 352C03 | Wheels and rails (Figure 8) | ±500 g pk | (±10%) 10 mV/g | (±5%) 0.5 to 10,000 Hz |
| PCB 353A03 | Floor inside train carriage (Figure 7a) | ±5 g pk | (±5%) 1000 mV/g | (±5%) 0.5 to 2000 Hz |
| B&K 377B02 | All noise measurement points | 146 dB | 48.4 mV/Pa | (±5%) 20 to 20,000 Hz |
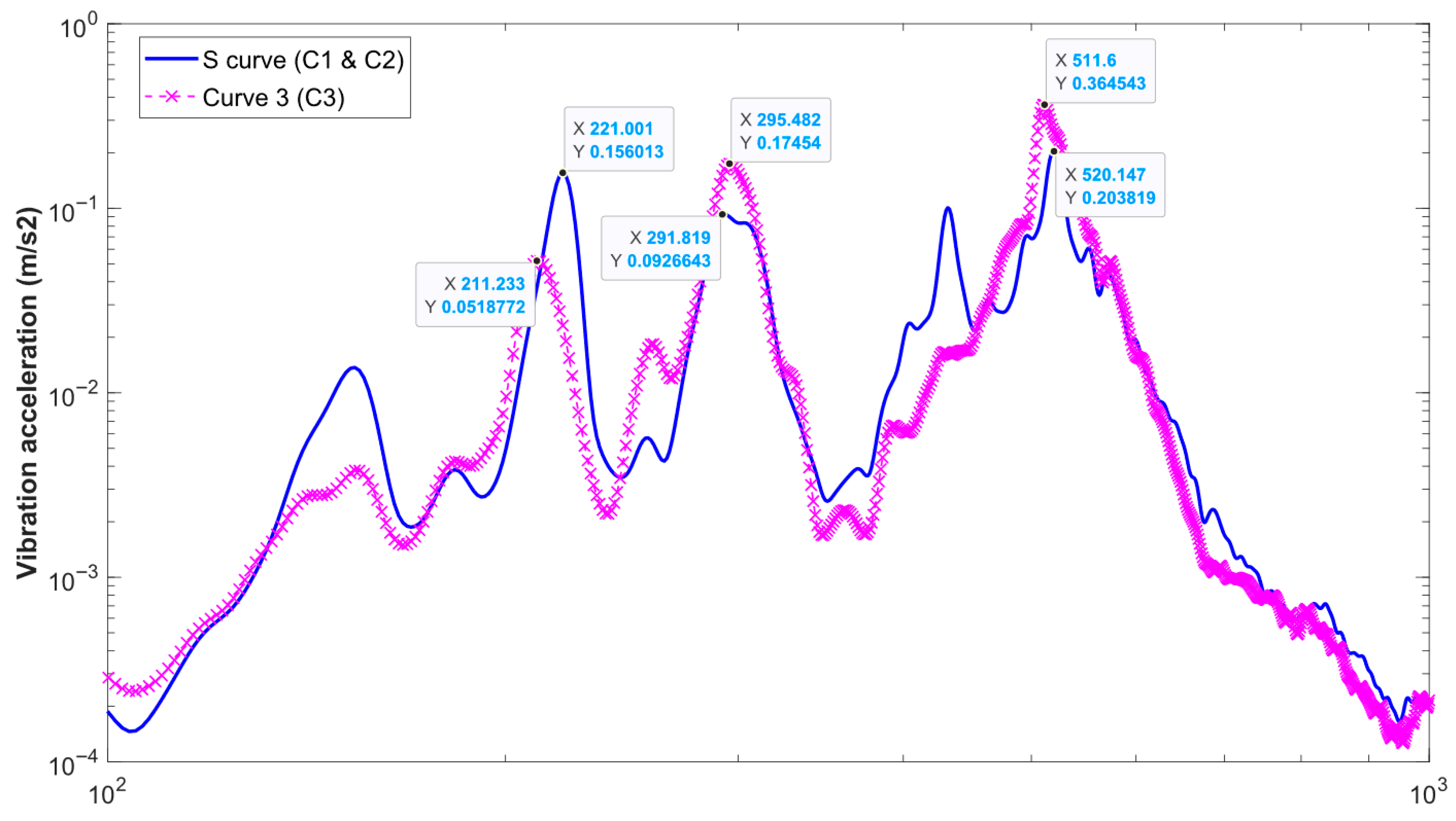
| Mode ID | Modal Frequency (Hz) | Fixed Wavelength (mm) |
|---|---|---|
| 1 | 221 | 82 |
| 2 | 295 | 61 |
| 3 | 520 | 35 |
| Mode ID | Fixed Wavelength (mm) (1/3 Octave Band) | Corrugation Depth (dB) (Ref. 1 × 10−6 m) | ||
|---|---|---|---|---|
| CAT–Measured | Computed from Interior Vibration | CAT–Measured | Computed from Interior Vibration | |
| 1 | 80 | 80 | 33 | 35 |
| 2 | 63 | 63 | 26.5 | 28 |
| 3 | 40 | 40 | 23.7 | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, X.P.; Wang, A.; Yan, Z.; Sun, L. An Indirect Method for Accurate Identification of Short-Pitch Rail Corrugation Using Vehicle Interior Noise and Vibration Measurements and Train–Track Transfer Functions. Appl. Sci. 2025, 15, 12262. https://doi.org/10.3390/app152212262
Gu XP, Wang A, Yan Z, Sun L. An Indirect Method for Accurate Identification of Short-Pitch Rail Corrugation Using Vehicle Interior Noise and Vibration Measurements and Train–Track Transfer Functions. Applied Sciences. 2025; 15(22):12262. https://doi.org/10.3390/app152212262
Chicago/Turabian StyleGu, Xiaohan Phrain, Anbin Wang, Ziquan Yan, and Linlin Sun. 2025. "An Indirect Method for Accurate Identification of Short-Pitch Rail Corrugation Using Vehicle Interior Noise and Vibration Measurements and Train–Track Transfer Functions" Applied Sciences 15, no. 22: 12262. https://doi.org/10.3390/app152212262
APA StyleGu, X. P., Wang, A., Yan, Z., & Sun, L. (2025). An Indirect Method for Accurate Identification of Short-Pitch Rail Corrugation Using Vehicle Interior Noise and Vibration Measurements and Train–Track Transfer Functions. Applied Sciences, 15(22), 12262. https://doi.org/10.3390/app152212262






