Many-Objective Edge Computing Server Deployment Optimization for Vehicle Road Cooperation
Abstract
1. Introduction
- A six-objective optimization model incorporating time delay, energy consumption, security, load balancing, and number and communication coverage areas is proposed for the RSU deployment optimization problem.
- The WGTwo_Arch2 algorithm is proposed to optimize the many-objective deployment model of RSUs. To enhance the algorithm’s ability to identify diverse solutions, Kent chaotic mapping data is applied to train the WGAN to generate random individuals covering the entire distribution space during the population initialization process, making the initial population distribution more uniform. A mating selection strategy based on the WGAN is designed to generate more diverse solutions for offspring generation.
- To improve the global search ability and convergence speed of the algorithm when dealing with many-objective problems, a polynomial variation strategy based on the Levy flight mechanism is proposed. The stochastic wandering mechanism of the Levy flight is used to generate variation probabilities, enabling better exploration of the global search space. An adaptive Lp-norm-based strategy for updating diversity archives is proposed to control exploration and exploitation. Finally, the effectiveness of the proposed algorithm in solving the RSU many-objective deployment optimization problem is experimentally verified.
2. Related Work
2.1. Large-Scale Many-Objective Optimization Problem (LSMaOP)
2.2. Two_Arch2 Algorithm
| Algorithm 1: The Two-Archive2 Algorithm |
 |
2.3. Research Status of RSU Deployment Optimization
3. Methods
3.1. System Model and Problem Formulation
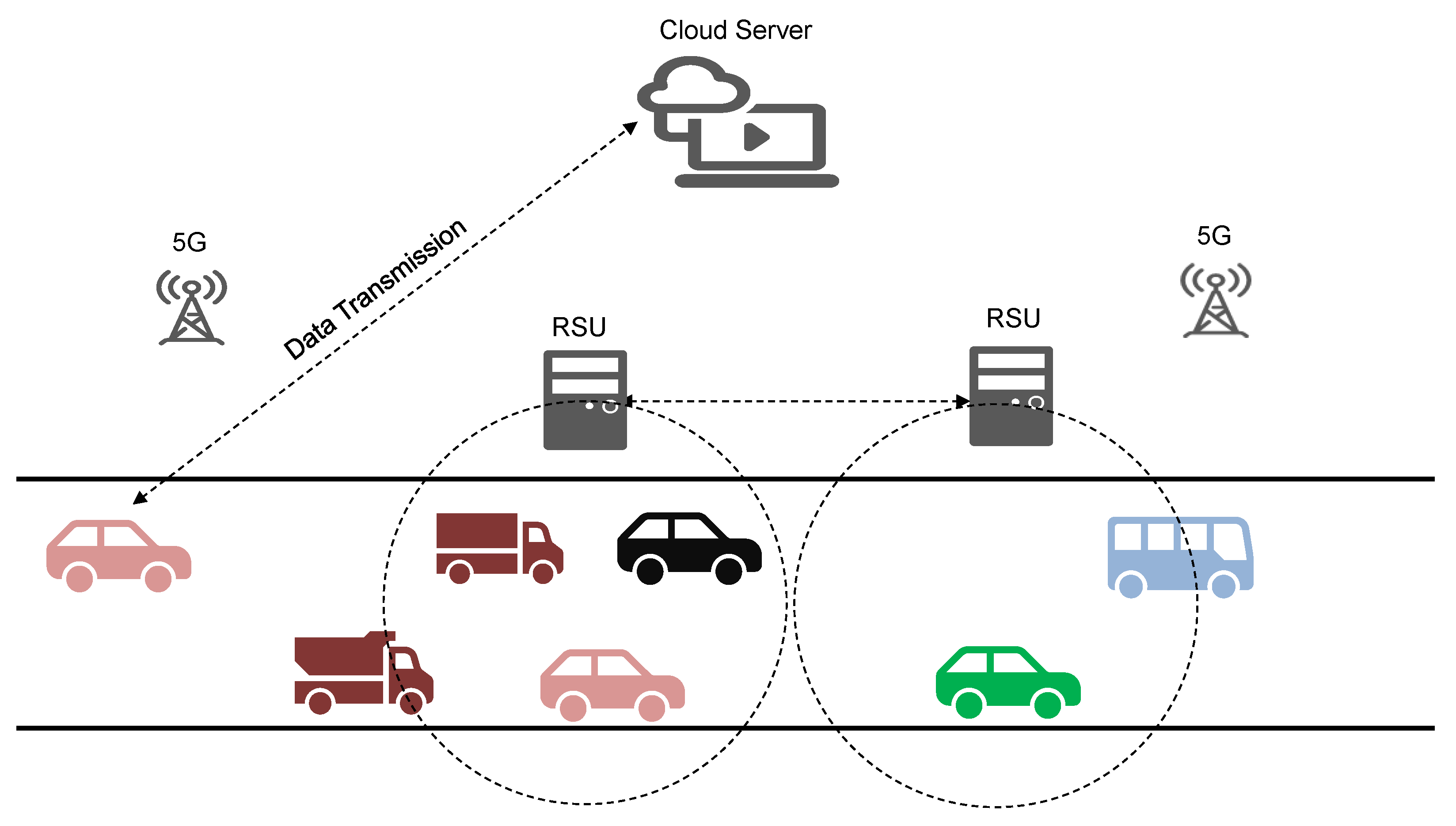
3.1.1. The Vehicle-Road Cooperation System for RSU-Based Deployment
3.1.2. The RSUs Deployment Optimization Model
- 1.
- Total delayIn computationally intensive applications, the output data of a computation are often significantly smaller than the input data. Therefore, the time required to return the computation results to the vehicle is negligible. If the vehicle transmits data to an RSU for processing, the user’s time delay mainly consists of the transmission delay, queuing delay, and computation delay of the data in the RSU. If the vehicle transmits data to the cloud server for processing, the queuing time and the computation processing time are negligible because the cloud server has sufficient computational resources, and only the transmission delay needs to be considered.The time delay of the vehicle transmits data to an RSU: when vehicle transmits task to RSU , the transmission delay is generated at this time as follows:where denotes the transmission rate (in bps) obtained by vehicle user when it offloads the task to RSU :where W is the channel bandwidth, which is set to 5 MHz. The transmission power of the vehicle determines the strength of the signal sent by the vehicle, and the transmit power and idle power are set to 500 mW and 100 mW, respectively. The small-scale fading coefficient accounts for the rapid variation in the signal over short distances due to multipath effects, etc. The distance between vehicle user n and base station m is expressed as , and denotes the path loss coefficient (a constant), which is set to 3. denotes the noise power spectral density, which is set to [28].The vehicle’s queuing delay in the RSUs: The vehicles in the set transmit messages to at the same time and wait in line to be processed. The waiting time of vehicle () in is computed as follows:The vehicle’s computation delay in the RSU: When a task arrives at the RSU, the RSU processes it, assuming that the computational power of the RSU is , which is set to 5 GHz. The average computation time for all the vehicles in the system isThe vehicle’s transmission delay in the cloud server: The time delay of the vehicle user who is processing the task in the cloud server can be calculated asTherefore, the average time delay for all vehicles isThe objective function for minimizing the time delay can be normalized and expressed as
- 2.
- Energy consumption of vehiclesWhen user transmits task to RSU , the transmission energy consumption iswhere is set to 500 mW. The transmission energy consumption when user transmits task to the cloud server is as follows:When the RSU processes the task of user , user is in the idle state, and the idle energy consumption of the vehicle can be calculated as follows:where is the power consumption in the idle state, which is set to 100 mW. The cloud server has sufficient computational resources to process the task very quickly, so the idle energy consumption of the vehicle assigned to the cloud server is ignored, and only the transmission energy is consumed. In the last step, user downloads the output data from the server. Since the size of the output data is much smaller than the size of the input data, the latency and energy consumption in this phase are intentionally ignored. The total energy consumption of the vehicle is defined asThe average energy consumption objective function for all vehicles isThe objective function for minimizing energy consumption can be normalized and expressed as:
- 3.
- SecuritySecure transmission is a key metric of QoS and is used to measure the probability of successful transmission. RSUs return data via multiple hops. Assuming that the probability that the link between two RSUs in the network is eavesdropped (i.e., transmitted packets may be intercepted) is , the probability of successful forwarding between RSUs between each hop is . When the number of hops in the path increases, the cumulative probability of successful eavesdropping on the end-to-end overall link will rise significantly, leading to a marked decline in the overall security of the path with more hops. In addition, a greater number of RSUs through which the data packets pass not only increases the delay but also means that the failure of any RSU in the path will cause the entire path becoming unavailable, thereby reducing the reliability of data transmission. Therefore, the number of RSU hops passed through when returning data is used as a measure of security. If the vehicle’s original and destination locations are within two RSUs and , respectively, and j RSUs need to be passed between and , the probability that forward the data successfully to vehicle is as follows:where .Therefore, the average safe forwarding rate for all vehicles is denoted as:The minimization objective function is expressed as follows:
- 4.
- Load balancing of RSUsLoad balancing improves both the availability of RSUs, by optimizing their resource allocation, and the reliability of the network by effectively handling congestion and failure events. The average load of the RSUs is denoted asThe vehicles covered by each RSU should be the same as possible. When an excessive number of vehicles are connected to certain RSUs, it often results in in a greater level of interference in vehicle data transmission. This also leads to stress overload in busy task RSUs and resource waste in idle RSUs. The standard deviation of the RSU load is used to denote the balanced load among them:The balanced load of the RSUs is normalized and expressed as a minimization objective function:
- 5.
- Cost of deploying RSUsThe RSU cost is related mainly to the number of RSUs, so the minimized RSU cost is denoted as
- 6.
- Coverage area of RSUsThe more vehicles that RSUs can communicate with, the greater the coverage of the car network. Therefore, the coverage should be maximized and denoted asThe objective function is expressed as follows:
- 7.
- Six-objective optimization modelIn summary, we construct a six-objective optimization model. That is, minimize total delay, energy consumption, balanced load, and deployment cost, and maximize security and coverage. The six-objective optimization model based on RSUs deployment is shown below:
3.2. The Proposed WGTwo_Arch2 Approach
| Algorithm 2: Population initialization strategy based on WGAN |
 |
3.2.1. WGAN-Based Population Initialization Strategy and Mating Selection Strategy
| Algorithm 3: The mating selection strategy based on WGAN |
|
3.2.2. Polynomial Variation Strategy Based on the Levy Distribution
3.2.3. Diversity Archive Update Based on the Adaptive Lp-Norm
4. Experimental Evaluation
4.1. Experimental Parameter Settings
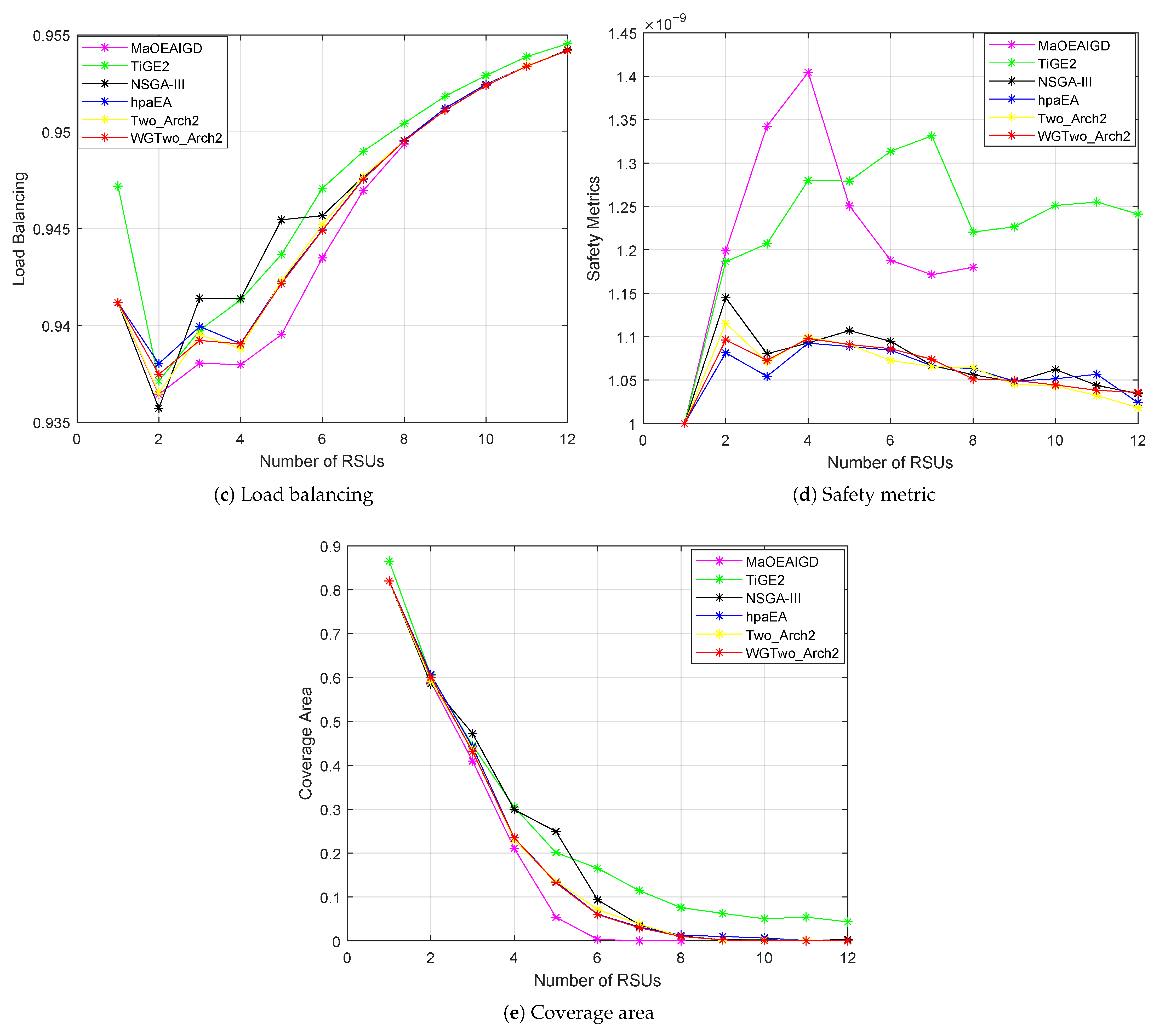
4.2. Comparison and Analysis of Experimental Results
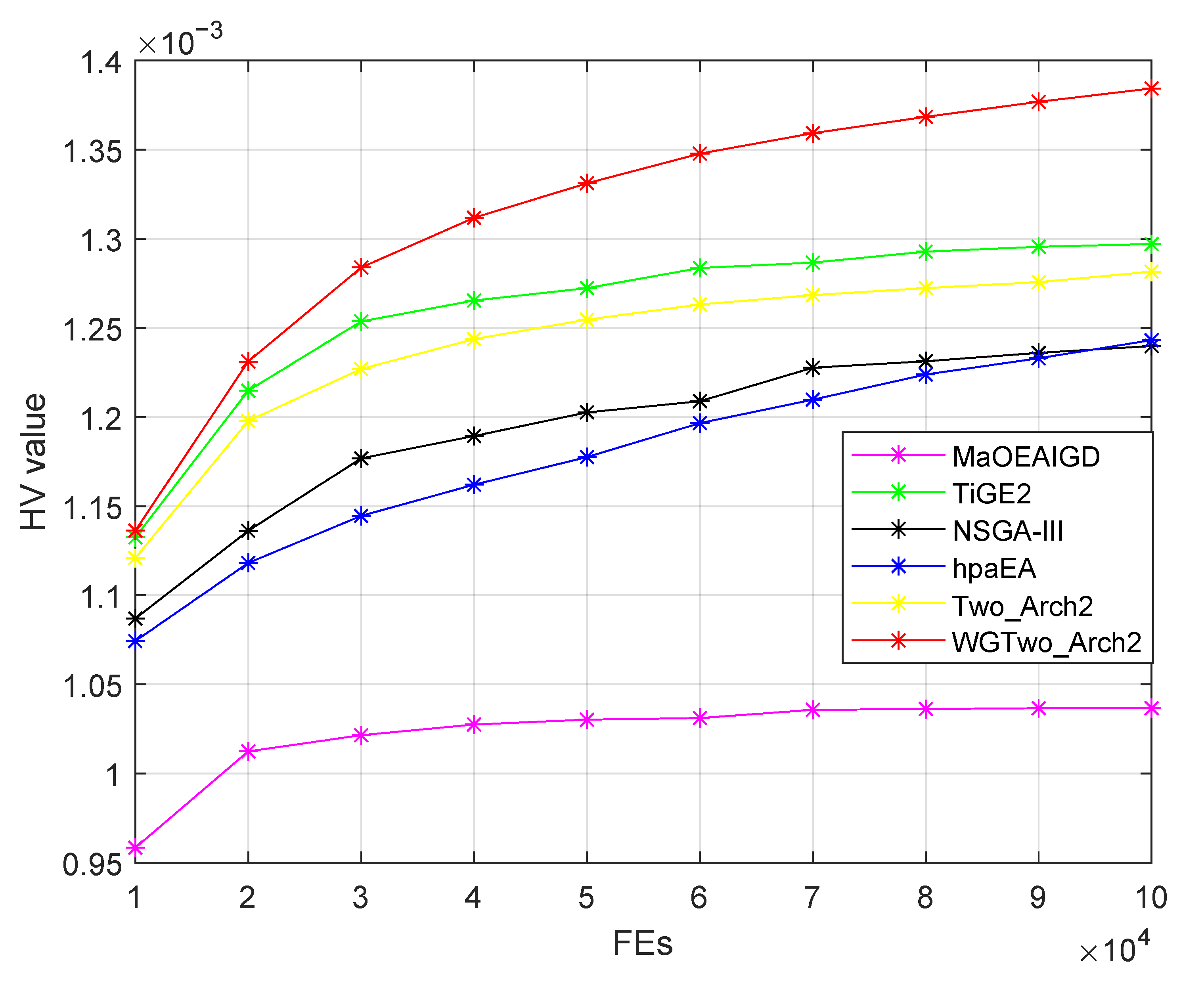
4.3. Comparison of HV Indicator Values
4.4. Time Complexity Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fan, X.; Gu, W.; Long, C.; Gu, C.; He, S. Optimizing task offloading and resource allocation in vehicular edge computing based on heterogeneous cellular networks. IEEE Trans. Veh. Technol. 2023, 73, 7175–7187. [Google Scholar] [CrossRef]
- Ning, Z.; Huang, J.; Wang, X.; Rodrigues, J.J.; Guo, L. Mobile edge computing-enabled internet of vehicles: Toward energy-efficient scheduling. IEEE Netw. 2019, 33, 198–205. [Google Scholar] [CrossRef]
- Huo, Y.; Yang, R.; Jing, G.; Wang, X.; Mao, J. A multi-objective Roadside Units deployment strategy based on reliable coverage analysis in Internet of Vehicles. Ad Hoc Netw. 2024, 164, 103630. [Google Scholar] [CrossRef]
- Massobrio, R.; Toutouh, J.; Nesmachnow, S.; Alba, E. Infrastructure deployment in vehicular communication networks using a parallel multiobjective evolutionary algorithm. Int. J. Intell. Syst. 2017, 32, 801–829. [Google Scholar] [CrossRef]
- Zhang, K.; Mao, Y.; Leng, S.; He, Y.; Zhang, Y. Mobile-edge computing for vehicular networks: A promising network paradigm with predictive off-loading. IEEE Veh. Technol. Mag. 2017, 12, 36–44. [Google Scholar] [CrossRef]
- Nikookaran, N.; Karakostas, G.; Todd, T.D. Combining capital and operating expenditure costs in vehicular roadside unit placement. IEEE Trans. Veh. Technol. 2017, 66, 7317–7331. [Google Scholar] [CrossRef]
- Yu, H.; Liu, R.; Li, Z.; Ren, Y.; Jiang, H. An RSU deployment strategy based on traffic demand in vehicular ad hoc networks (VANETs). IEEE Internet Things J. 2021, 9, 6496–6505. [Google Scholar] [CrossRef]
- Talpur, A.; Gurusamy, M. Drld-sp: A deep-reinforcement-learning-based dynamic service placement in edge-enabled internet of vehicles. IEEE Internet Things J. 2021, 9, 6239–6251. [Google Scholar] [CrossRef]
- Lin, M.; Huo, J.; Wang, L.; Yao, G.; Chen, Y.; Lu, Z. A Multi-Objective Optimization Approach for Roadside Unit Deployment Strategy in IoV. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 14–17 April 2024; pp. 1–6. [Google Scholar]
- Zhang, L.; Wang, L.; Zhang, L.; Zhang, X.; Sun, D. An RSU deployment scheme for vehicle-infrastructure cooperated autonomous driving. Sustainability 2023, 15, 3847. [Google Scholar] [CrossRef]
- Chaudhary, R.; Kumar, N. Secgreen: Secrecy ensured power optimization scheme for software-defined connected iov. IEEE Trans. Mob. Comput. 2023, 22, 2370–2386. [Google Scholar] [CrossRef]
- Wang, H.; Jiao, L.; Yao, X. Two_Arch2: An improved two-archive algorithm for many-objective optimization. IEEE Trans. Evol. Comput. 2014, 19, 524–541. [Google Scholar]
- Praditwong, K.; Yao, X. A new multi-objective evolutionary optimisation algorithm: The two-archive algorithm. In Proceedings of the 2006 International Conference on Computational Intelligence and Security, Guangzhou, China, 3–6 November 2006; pp. 286–291. [Google Scholar]
- Zitzler, E.; Künzli, S. Indicator-based selection in multiobjective search. In Proceedings of the International Conference on Parallel Problem Solving from Nature, Birmingham, UK, 18–22 September 2004; pp. 832–842. [Google Scholar]
- Deb, K.; Goyal, M. A combined genetic adaptive search (GeneAS) for engineering design. Comput. Sci. Inform. 1996, 26, 30–45. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; Volume 27. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein generative adversarial networks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 July 2017; pp. 214–223. [Google Scholar]
- Chen, F.; Zhou, J.; Xia, X.; Xiang, Y.; Tao, X.; He, Q. Joint optimization of coverage and reliability for application placement in mobile edge computing. IEEE Trans. Serv. Comput. 2023, 16, 3946–3957. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Kumrai, T.; Ota, K.; Dong, M.; Champrasert, P. RSU placement optimization in vehicular participatory sensing networks. In Proceedings of the 2014 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), Toronto, ON, Canada, 27 April–2 May 2014; pp. 207–208. [Google Scholar]
- Wang, F.; Wang, C.; Wang, K.; Jiang, Q.; Wang, B.; He, W. Multiobjective differential evolution with discrete elite guide in internet of vehicles roadside unit deployment. Wirel. Commun. Mob. Comput. 2021, 1, 4207130. [Google Scholar]
- Guerna, A.; Bitam, S. GICA: An evolutionary strategy for roadside units deployment in vehicular networks. In Proceedings of the 2019 International Conference on Networking and Advanced Systems (ICNAS), Annaba, Algeria, 26–27 June 2019; pp. 1–6. [Google Scholar]
- Wu, T.J.; Liao, W.; Chang, C.J. A cost-effective strategy for road-side unit placement in vehicular networks. IEEE Trans. Commun. 2012, 60, 2295–2303. [Google Scholar]
- Ghosh, D.; Katehara, H.; Rawlley, O.; Gupta, S.; Arulselvan, N.; Chamola, V. Artificial intelligence-empowered optimal roadside unit (RSU) deployment mechanism for internet of vehicles (IoV). In Proceedings of the 2022 IEEE 23rd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Belfast, UK, 14–17 June 2022; pp. 495–500. [Google Scholar]
- Lu, J.; Jiang, J.; Balasubramanian, V.; Khosravi, M.R.; Xu, X. Deep reinforcement learning-based multi-objective edge server placement in Internet of Vehicles. Comput. Commun. 2022, 187, 172–180. [Google Scholar] [CrossRef]
- Shen, B.; Xu, X.; Qi, L.; Zhang, X.; Srivastava, G. Dynamic server placement in edge computing toward internet of vehicles. Comput. Commun. 2021, 178, 114–123. [Google Scholar] [CrossRef]
- Deb, K.; Jain, H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints. IEEE Trans. Evol. Comput. 2013, 18, 577–601. [Google Scholar]
- Nath, S.; Li, Y.; Wu, J.; Fan, P. Multi-user multi-channel computation offloading and resource allocation for mobile edge computing. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar]
- Sun, Y.; Yen, G.G.; Yi, Z. IGD indicator-based evolutionary algorithm for many-objective optimization problems. IEEE Trans. Evol. Comput. 2018, 23, 173–187. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, M.; Wang, J.; Zhang, Z.; Xiang, Y.; Zhang, J. Tri-goal evolution framework for constrained many-objective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 3086–3099. [Google Scholar] [CrossRef]
- Chen, H.; Tian, Y.; Pedrycz, W.; Wu, G.; Wang, R.; Wang, L. Hyperplane assisted evolutionary algorithm for many-objective optimization problems. IEEE Trans. Cybern. 2019, 50, 3367–3380. [Google Scholar] [CrossRef]

| Symbol | Description | Value |
|---|---|---|
| n | the maximum number of RSUs | 12 |
| m | the number of the vehicles | 50 |
| W | channel bandwidth | 5 MHz |
| the size of the input data | [400, 600] kbits | |
| the required total number of CPU cycles | [900, 1100] megacycles | |
| vehicle transmission power | 500 mW | |
| vehicle transmission power | 100 mW | |
| small-scale fading coefficient | ||
| Path loss coefficient | 3 | |
| d | the maximum communication range | 250 m |
| the noise power spectral density | W | |
| Probability of being eavesdropped | ||
| Maximum evaluation times | 100,000 |
| Algorithm | HV |
|---|---|
| WGTwo_Arch2 | |
| Two_Arch2 | |
| NSGA-III | |
| hpaEA | |
| TiGE2 | |
| MaOEA-IGD |
| Algorithm | Computational Complexity |
|---|---|
| WGTwo_Arch2 | |
| Two_Arch2 | |
| NSGA-III | |
| hpaEA | |
| TiGE2 | |
| MaOEA-IGD |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.; Cao, B. Many-Objective Edge Computing Server Deployment Optimization for Vehicle Road Cooperation. Appl. Sci. 2025, 15, 12240. https://doi.org/10.3390/app152212240
Fan S, Cao B. Many-Objective Edge Computing Server Deployment Optimization for Vehicle Road Cooperation. Applied Sciences. 2025; 15(22):12240. https://doi.org/10.3390/app152212240
Chicago/Turabian StyleFan, Shanshan, and Bin Cao. 2025. "Many-Objective Edge Computing Server Deployment Optimization for Vehicle Road Cooperation" Applied Sciences 15, no. 22: 12240. https://doi.org/10.3390/app152212240
APA StyleFan, S., & Cao, B. (2025). Many-Objective Edge Computing Server Deployment Optimization for Vehicle Road Cooperation. Applied Sciences, 15(22), 12240. https://doi.org/10.3390/app152212240






