Comparative Study of Continuous Versus Discontinuous Numerical Models for Railway Vehicles Suspensions with Dry Friction

Abstract

Dry friction dampers are widely used in railway vehicle suspensions due to their simplicity, robustness, and cost-effectiveness compared to hydraulic alternatives. However, accurately modelling their behaviour remains challenging because of the discontinuous nature of friction forces. This paper presents a comparative study between two modelling approaches: continuous (regularized) models, which smooth out discontinuities, and discontinuous (switch-based) models, which explicitly capture stick–slip transitions. Using a two-degree-of-freedom suspension system, both models are implemented and analyzed under steady-state and transient conditions. Results show that while continuous models are easier to implement and integrate numerically, they fail to capture key physical phenomena such as zero relative velocity intervals and force discontinuities. In contrast, discontinuous models offer superior physical fidelity and significantly better computational efficiency, especially during static friction phases. This study highlights the trade-offs between modelling simplicity and accuracy, providing valuable insights for the simulation and design of railway suspension systems. The findings support the use of discontinuous models in safety-critical simulations and suggest avenues for hybrid modelling strategies.

1. Introduction

Suspension systems play a critical role in railway vehicles by ensuring stability, safety, and passenger comfort. Among the damping devices used, dry friction dampers are notable for being more robust and cost-effective than hydraulic dampers. However, their performance strongly depends on the complex nonlinear behaviour of frictional forces, which complicates both design and simulation. Traditional design practices often rely on empirical adjustments, but with increasing computational resources, numerical modelling has become essential for predicting suspension behaviour under realistic operating conditions [1,2,3,4,5,6].

The main difficulty in modelling dry friction arises from the stick–slip phenomenon, where contact elements alternately adhere and slide relative to one another. This results in discontinuous differential equations, which create significant challenges for numerical integration. Two main strategies have emerged to deal with these challenges: continuous (regularized) models, which replace discontinuities with smooth approximations, and discontinuous (non-smooth or switch) models, which explicitly treat stick and slip phases as separate regimes [7,8,9].

Previous studies on railway dynamics have explored both approaches in different contexts [10,11,12,13,14,15]. In particular, ref. [16] studied dry friction in braking train buffers using both continuous and discontinuous models, providing a systematic comparison of their accuracy and computational costs. Building on this methodology, the present paper extends the comparative study to suspension systems, where dry friction damping plays an important role. The objective is to evaluate the efficiency and physical fidelity of continuous versus discontinuous models for suspension dynamics and to draw conclusions relevant for both simulation and engineering design. The contents can be resumed as follows.

The Background chapter explores the physics of dry friction, differentiates static and kinetic friction, and explains the stick–slip phenomenon. It introduces continuous and discontinuous modelling strategies and their implications for simulation accuracy and efficiency.

The Modelling Approaches chapter describes the mechanical suspension model and details both continuous and discontinuous friction formulations. It explains how each model handles stick–slip transitions and outlines the comparative methodology used to evaluate them.

Numerical Simulation and Results present simulation setups and results for both models. It shows that the discontinuous model better captures stick–slip dynamics and is more computationally efficient, while the continuous model struggles with stiffness and numerical instability.

The Discussion analyzes the mathematical structure and implications of each modelling approach. It highlights the advantages of discontinuous models in terms of physical fidelity and computational performance, especially in capturing realistic suspension behaviour.

The Conclusions summarize the findings: discontinuous models are more accurate and efficient for simulating dry friction in railway suspensions, while continuous models are simpler but less reliable. This section suggests future research directions including hybrid models and experimental validation.

It is important to emphasize that the purpose of this work is methodological rather than experimental. The study does not introduce a new physical or friction model but instead applies, for the first time, a discontinuous numerical formulation to simulate a two-stage railway suspension system with dry friction. The focus lies on evaluating the numerical performance, stability, and accuracy of this discontinuous approach in comparison with the classical regularized method. Consequently, the “experiments” presented in the paper are numerical in nature, designed to assess computational efficiency and the capability to capture stick–slip behaviour, rather than to validate physical models against experimental vibration measurements.

2. Background

2.1. Dry Friction in Mechanical Systems

The interaction between contacting surfaces is inherently associated with dry friction, a phenomenon encompassing a wide spectrum of physical effects such as elastic and plastic deformation, surface roughness, asperity interactions, and interfacial third-body layers. Because surfaces are rarely ideal, phenomena like micro-asperity contact, plasticity, and interfacial contamination often play non-negligible roles [6]. This complexity explains the persistent attention friction has had in classical mechanical engineering and vehicle dynamics.

Frictional forces are typically classified into static (stick) and kinetic (slip) friction, which obey distinct physical laws. Static friction resists motion up to a limiting value, while kinetic friction opposes relative motion with a generally velocity-dependent magnitude. In the Coulomb model, the kinetic friction force is constant in magnitude but opposite in direction to the sliding velocity. More advanced models incorporate velocity dependence, hysteresis, or transitions between static and dynamic regimes [17].

In railway vehicle suspensions, friction is present in bearings, joints, dampers, wheel-rail contact, and other interfaces; its nonlinear behaviour is particularly challenging for simulation and control. Nonlinear friction can give rise to steady-state offsets, limit cycles, stick–slip behaviour, energy dissipation, and sometimes chaotic responses, all of which can degrade performance or damage components over time. Precise friction modelling is therefore essential for reliable numerical simulations, especially when comparing more elaborate models (e.g., discontinuous or non-smooth) versus classical ones [18,19,20,21,22,23,24].

2.2. Static vs. Kinetic Friction, Stick–Slip Transitions

A fundamental distinction must be made between static friction $F_{stick}$ (no relative motion) and kinetic (sliding) friction $Fslip$ (when surfaces slip relative to one another). In kinetic regimes, the friction force opposes the slip velocity and may depend on that velocity and other factors [17].

A general functional form can be:

$$Fslip=Fslip\left(v_{rel}\right)$$

(1)

where $v_{rel}$ is the relative velocity at the contact point.

Static friction adjusts to counter external forces up to a threshold—the maximum stick force. When that threshold is exceeded, sliding begins.

The simplest case is the Coulomb model, in which the slip force remains constant and independent of velocity [17].

$$F_f\in \left\{\begin{array}{c}{F}_{\mathit{slip}}\left(t, v_{rel}\right), \mathrm{if} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel}\right) > 0, \left(\mathrm{slip}\right)\\ F_{stick}\in \left[-F_{\mathit{sMax}} F_{\mathit{sMax}}\right] \mathrm{if} v_{rel}=0, \left(\mathrm{stick}\right)\end{array}\right.$$

(2)

The maximum possible value of the static friction force is $F_{\mathit{sMax}}$. However, this model introduces a discontinuity at zero velocity, which creates difficulties for standard solvers at low velocities.

To alleviate such issues, combined friction laws have been proposed, where viscous and Coulomb effects are superimposed [24,25,26]. A smooth alternative employs the hyperbolic tangent function, which approximates the transition between sticking and sliding states. Although easier to simulate, such models incorrectly predict zero friction at zero velocity, which can cause unrealistic drift and suppress true sticking phases.

2.3. Continuous and Discontinuous Approaches

Continuous or regularized models approximate frictional discontinuities with smooth mathematical functions, such as hyperbolic tangent functions [25]. This eliminates discontinuities and permits the use of standard stiff Ordinary Differential Equation (ODE) solvers. However, these models suffer from drawbacks, such as the absence of true sticking phases and artificial drift during low-velocity motion.

To smooth the transition between stick and slip, researchers use regularized laws: viscous plus Coulomb, Stribeck curves, or hyperbolic tangent approximations controlling transition steepness, viscous damping, etc. These models reduce numerical stiffness and help avoid pathological behaviour around zero velocity but may underrepresent true sticking [26,27].

Discontinuous or switch models explicitly handle stick–slip transitions by partitioning the system dynamics into separate regimes. During stick phases, the relative velocity is constrained to zero, while during slip phases, kinetic friction laws govern motion. This results in non-smooth dynamics, but the governing equations are non-stiff and can be integrated efficiently with standard solvers. Switch models have been successfully applied in the study of braking trains and are particularly suitable for suspension systems with dry friction damping [16].

From a broader perspective, two major approaches exist for modelling frictional contact:

• Regularized models, which ensure continuity but lead to stiff differential equations and neglect true stick phases.
• Non-smooth formulations, which retain discontinuities but provide a more realistic description of contact dynamics at the expense of higher modelling complexity [12,14].

In the context of railway vehicle suspensions, these modelling strategies play a decisive role in evaluating [16] the trade-off between classical continuous models (simpler but often computationally demanding and less accurate) and discontinuous formulations (modelling demanding yet physically consistent and computationally demanding). Section 2 provides the foundation for comparing their efficiency in large-scale simulations.

2.4. Event-Driven Algorithms

The event-driven method simulates contact dynamics by viewing the time evolution as a sequence of smooth dynamic modes (stick or slip) separated by discrete mode switches (events). The system is integrated over smooth subintervals described by ODEs where the friction law is fixed. A change in the friction regime requires a switch to a new set of governing equations because sticking constraints reduce the system’s Degrees of Freedom (DOFs) [28,29].

This method, however, suffers from a severe scalability limitation: its logical complexity increases exponentially with the number of contact points, making it impractical for large systems [29]. The functional alternative is to preserve the complete system dynamics (full slip) and solve for the appropriate static friction and constraint forces. This constrained dynamics approach relies on dedicated techniques for three tasks: precise switch detection, accurate mode determination, and reliable static friction calculations.

The algorithm includes the following stages [28]:

• Initialize the system, determine the next smooth mode, and update the equations.
• Integrate the smooth state vector with any ODE solver while constraints are not violated.
• Detect within imposed tolerance the moment of the next event.

In the implementation of this algorithm, two issues must be solved: event detection and static friction computation [27].

2.4.1. Event Detection

Systems using the Coulomb friction model transition from slip to stick when relative velocity approaches zero $v_{\mathit{rel}}\to 0$ and the friction force stays below the static limit $F_{stick}\in \left[-F_{\mathit{sMax}} F_{\mathit{sMax}}\right]$. Precisely locating these zero-crossings is a feature of highly accurate, but computationally intensive methods [28].

An efficient approach is the Karnopp method, which introduces a finite stick band defined by a small velocity threshold η: stick occurs for $\mathrm{a}\mathrm{b}\mathrm{s}\left(v_{\mathit{rel}}\right)<\eta$, while slip occurs outside this range. This approach avoids explicit zero velocity detection and enables efficient simulation of discontinuous dynamics. Nevertheless, it may suffer from long-term drift and the potential numerical instability of ODE solvers [26,27].

This method successfully bypasses the costly exact zero-crossing problem and allows for efficient simulation even with a relatively wide band $\eta$. A known downside, however, is that the slight, constant velocity offset within the stick band can cause a drift-off effect during long integrations, which may introduce numerical instability into the ODE solution [29]. Despite this trade-off, the method’s computational benefits led to its selection for generating all simulation results in this study.

Mode transition out of stick occurs when the static friction force, $F_{stick}$, reaches the maximum static limit $F_{\mathit{sMax}}$(Equation (2)), and an event that must be located via a root-finding procedure [27].

2.4.2. Mode Selection and Integration of a Smooth Mode

The computation of constraint forces (such as static friction) is central to non-smooth dynamics. The processes of event detection, mode selection, and integration are fundamentally coupled, with success relying on the precise determination of these constraints [29].

A significant challenge is the uniqueness and existence of solutions, which frequently break down in planar rigid body problems (e.g., “Painlevé paradoxes”). This problem is most acute when constraints are redundant, leading to a rank-deficient constraint matrix and thus, indeterminacy [27].

Methods that rely on simple conditional statements to define system modes, like the switch model, quickly become impractical as the logical complexity grows exponentially with the number of contacts [28,29].

Alternatives include the development of Impulse–Velocity methods and the use of statistical analysis to treat friction indeterminacy as a probability problem. A more rigorous mathematical framework is provided by convex analysis, which resolves set-valued laws using variational techniques and associated optimization problems [27,29].

The most widely adopted framework is the Linear Complementarity Problem (LCP). This approach models contact dynamics and friction using complementarity constraints, which mathematically enforce the stick/slip dichotomy. LCP solvers determine the constraint forces without relying on a costly analysis of conditional statements, benefiting from extensive research in mathematical programming [28,29].

It is important to note that while the LCP provides a coherent and mathematically consistent solution framework, the results often still require empirical correction to match physical reality. This suggests that the solution method must be carefully tailored to the specific application [29]. Being relatively simple, the model used in this paper is complementarity-free and the computation of static friction forces is straightforward.

3. Modelling Approaches

3.1. Suspension System Model

The mechanical configuration under study is represented schematically in Figure 1. The system consists of two sprung masses, m₁ and m₂, with corresponding vertical displacements y_i. Here, i = 1 denotes the primary suspension (bogie frame) and i = 2 denotes the secondary suspension (carbody). Track irregularities are introduced through the displacement x. This simplified representation of vertical dynamics is generally known as the quarter-car model and is commonly applied in both railway and road vehicle studies. In the railway case, the indices refer to bogie and carbody motions, while in the automotive context they correspond to wheel masses and tyre stiffnesses, e.g., [30,31].

The elastic forces transmitted through the suspensions are denoted by F_el1 and F_el2.

$$F_{el1}=-k_1\left(y_1-x\right) \mathrm{a}\mathrm{n}\mathrm{d}{ F}_{el2}=-k_2(y_2-y_1)$$

(3)

These are proportional to the respective spring stiffnesses, k_i, and the relative displacements between adjacent bodies, as defined in Equation (3).

The expression of the friction forces F_fi is essential for the model and will be discussed in the following paragraphs. The state-space formulation of the model, as shown in Equation (4), includes the displacements and velocities of the two masses.

$$\dot{Y}=\left[\begin{array}{c}\begin{array}{c}\dot{y_1}\\ \dot{y_2}\end{array}\\ \begin{array}{c}1/m_1\left(F_{el1}+F_{f1}-F_{f2}-F_{el2}\right)\\ 1/m_2\left(F_{f2}+F_{el2}\right)\end{array}\end{array}\right]$$

(4)

The state vector contains the vertical displacements and velocities of the two bodies.

$$\dot{Y}=\left[\begin{array}{cc}\begin{array}{cc}{y}_1& \dot{y_1}\end{array}& \begin{array}{cc}{y}_2& \dot{y_2}\end{array}\end{array}\right]$$

(5)

3.2. Continuous Model

In the continuous model, the friction force is expressed as a smooth function of relative velocity. A typical formulation uses a hyperbolic tangent approximation:

$$F_f\left(v_{rel}\right)=F_{\mathit{slipMax}}\cdot \tanh (C\cdot v_{rel})$$

(6)

where $F_{\mathit{slipMax}}$ is the slip force magnitude, $v_{rel}$ is the relative velocity, and $C$ is a large parameter controlling the steepness of the transition. This approach avoids discontinuities but introduces stiffness into the equations of motion, making numerical integration computationally expensive.

The more physically detailed friction models (including temperature, third body, and plastic shearing, etc.) improve realism but also increase complexity. Such models may be more appropriate in high-fidelity simulations (or for validating simpler models) [32], but less suited for real-time or large-scale parametric studies unless optimized.

In multibody dynamics, elements like clearance joints, Stribeck velocity laws, and realistic thresholds become important, especially in transitions (curves and changes in loading). The sensitivity to the friction model is much higher in those situations.

3.3. Discontinuous Model

The suspension characteristics are analytic only within limited intervals, while sliding contacts can alter the number of active degrees of freedom during operation [24]. Consequently, the switch model proves well suited for capturing the nonlinear dynamics of the system. Moreover, the presence of dry friction in the suspensions can generate stick–slip oscillations, which must be properly described within the governing equations. In this configuration, stiction can arise in both the primary and secondary suspension stages [33,34,35].

In the general case, dry friction forces F_fi act at both suspension stages. Their values may be either kinematic (F_slip1, F_slip2) or static (F_stick1, F_stick2), depending on whether slip occurs or not. Within the switch model, the logical complexity grows rapidly with the number of contact points [24], since evaluating inequalities and inclusions becomes increasingly challenging. However, in the present system, which involves only two frictional contacts, these conditions can be evaluated without resorting to advanced numerical techniques. Using the Karnopp method and choosing a constant slip friction force, $F_{\mathit{slip}}\left(t, v_{rel}\right)=F_{\mathit{sMax}}$, the dry friction forces can be expressed as described in the following paragraphs.

Equation (7) defines the slip phase, i.e., there is relative displacement between the bodies in contact and the slip friction force $F_{slip}$ (i.e., the saturated friction force), is described by a classical constitutive law.

$$\begin{gathered} \mathrm{i}\mathrm{f} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel1}\right)\ge \eta \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel2}\right)\ge \eta (\mathrm{slip} \mathrm{modes} \mathrm{in} \mathrm{both} \mathrm{suspension} \mathrm{stages}) \\ {F}_{f1}=F_{slip1}\left(v_{rel1}\right)=-F_{\mathit{sMax}1} \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(v_{rel1}\right) \\ {F}_{f2}=F_{slip2}\left(v_{rel2}\right)=-F_{\mathit{sMax}2} \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(v_{rel2}\right) \end{gathered}$$

(7)

Equations (8)–(10) define either the stick phase in the primary, secondary or both suspension stages, or the stick-to-slip transition in one of the mentioned configurations.

$$\begin{gathered} \mathrm{i}\mathrm{f} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel1}\right)<\eta \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel2}\right)\ge \eta (\mathrm{stick} \mathrm{mode} \mathrm{in} \mathrm{the} \mathrm{first} \mathrm{suspension} \mathrm{stage}) \\ {F}_{f1}=-\min (\mathrm{a}\mathrm{b}\mathrm{s}(F_{el1}-F_{el2}-m_1\ddot{x}),F_{\mathit{sMax}1})\cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(F_{el1}-F_{el2}-m_1\ddot{x}) \\ {F}_{f2}=F_{slip2}\left(v_{rel2}\right)=-F_{\mathit{sMax}2} \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(v_{rel2}\right) \end{gathered}$$

(8)

$$\begin{gathered} \mathrm{i}\mathrm{f} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel1}\right)\ge \eta \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel2}\right)<\eta (\mathrm{stick} \mathrm{mode} \mathrm{in} \mathrm{the} \mathrm{second} \mathrm{suspension} \mathrm{stage}) \\ {F}_{f1}=F_{slip1}\left(v_{rel1}\right)=-F_{\mathit{sMax}1} \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(v_{rel1}\right) \\ {F}_{f2}=-\min (abs\left(F_{el2}-m_2\ddot{x}\right), F_{\mathit{sMax}2})\cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(F_{el2}-m_2\ddot{x}) \end{gathered}$$

(9)

$$\begin{gathered} \mathrm{i}\mathrm{f} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel1}\right)<\eta \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{a}\mathrm{b}\mathrm{s}\left(v_{rel2}\right)<\eta (\mathrm{stick} \mathrm{mode} \mathrm{in} \mathrm{both} \mathrm{suspension} \mathrm{stages}) \\ {F}_{f1}=-\min (\mathrm{a}\mathrm{b}\mathrm{s}(F_{el1}-F_{el2}-m_1\ddot{x}),F_{\mathit{sMax}1})\cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(F_{el1}-F_{el2}-m_1\ddot{x}) \\ {F}_{f2}=-\min (\mathrm{a}\mathrm{b}\mathrm{s}(F_{el2}-m_2\ddot{x}),F_{\mathit{sMax}2})\cdot \mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}(F_{el2}-m_2\ddot{x}) \end{gathered}$$

(10)

The discontinuous model, also known as the switch model, distinguishes explicitly between the stick and slip phases. Stick occurs when the relative velocity is zero (or sufficiently small) and the external force does not exceed the static friction limit. Slip occurs otherwise, with the friction force opposing motion up to the kinetic friction level.

Transitions between modes (i.e., stick or slip) occur when the relative velocity drops below $\eta$, $\mathrm{a}\mathrm{b}\mathrm{s}\left(v_{reli}\right)<\eta$, (for slip to stick) and when the necessary static force should be greater than the maximum stick force, $\mathrm{a}\mathrm{b}\mathrm{s}(F_{el1}-F_{el2}-m_1\ddot{x})>F_{\mathit{sMax}1}$ or $\mathrm{a}\mathrm{b}\mathrm{s}\left(F_{el2}-m_2\ddot{x}\right)>F_{\mathit{sMax}2}$ (for stick to slip).

The governing equations for a suspension system with two degrees of freedom and two dry friction contacts can be written as piecewise functions, with each regime (stick, slip, or transition) represented by a different set of equations. This formulation accurately reproduces stick–slip oscillations and force discontinuities, which are essential features of dry friction damping [36].

3.4. Comparative Methodology

The comparison between continuous and discontinuous suspension models rests on techniques already used to compare similar descriptions [7,16]. In those works, the models were evaluated for their ability to simulate observed stick–slip phases, numerical stability, and computational efficiency. In this paper we apply the same approach to the suspension system.

The comparison criteria include the following:

• Physical representation: How well does the model capture stick–slip phases?
• Stability: Solver tolerance dependence, stiffness, and integration time.
• Computation time: Computational cost of simulating the system in execution time.
• Predictive power: Reproduce some stable and time-dependent oscillations with different parameters.

4. Numerical Simulation and Results

4.1. Simulation Setup

The parameters are within the typical range for railway vehicles. Simulations were conducted for various values of the track irregularities angular frequency $\mathsf{\omega }$ and amplitude $A$. The track irregularities variation is as follows:

$$x=A\mathrm{s}\mathrm{i}\mathrm{n}\left(\omega t\right)$$

(11)

Two classes of simulations were performed:

• Continuous model: friction represented by a tanh-based regularization.
• Discontinuous model: friction represented by a switch model with explicit stick–slip detection.

Minimum integration tolerances were carefully set to ensure the accurate detection of stick–slip intervals. Simulation data are defined in

Table 1. Model parameter values.

Description	Symbol	Value	Unit
Bogie mass	m1	3000	kg
Half carbody mass	m2	10,000	kg
Primary suspension rigidity	k1	2.5	kN/mm
Secondary suspension rigidity	k2	2.5	kN/mm
Saturation creep limit	η	10−4–10−6	m/s
Maximum static friction, primary suspension	$F_{\mathit{sMax}1}$	5000	N
Maximum static friction, secondary suspension	$F_{\mathit{sMax}2}$	5000	N
Friction parameter	C	9000	s/m
Regularized slip force magnitude, primary suspension	$F_{\mathit{slipMax}1}$	5000	N
Regularized slip force magnitude, secondary suspension	$F_{\mathit{slipMax}2}$	5000	N
Track irregularities amplitude	A	2/20	mm
Track irregularities frequency	ω	1–100	rad/s

.

The choice of the Matlab solver was driven by the attempt to provide a common and neutral comparison basis for two structurally different models: a stiff one and a non-stiff one. Consequently, a mildly stiff model-suited solver was chosen, i.e., ode23.

The simulation frequency range is typical for bogie rigid-body modes [37].

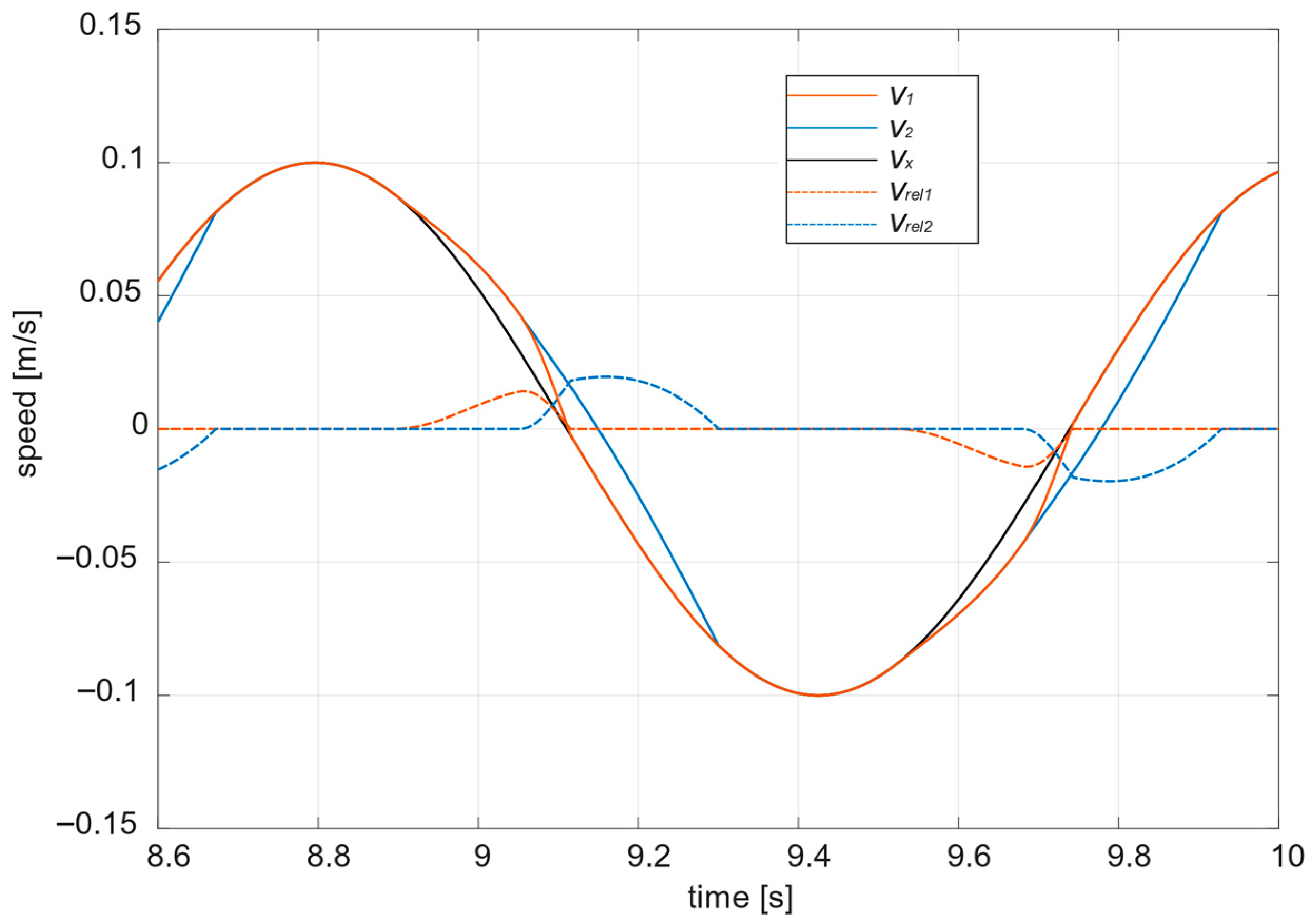
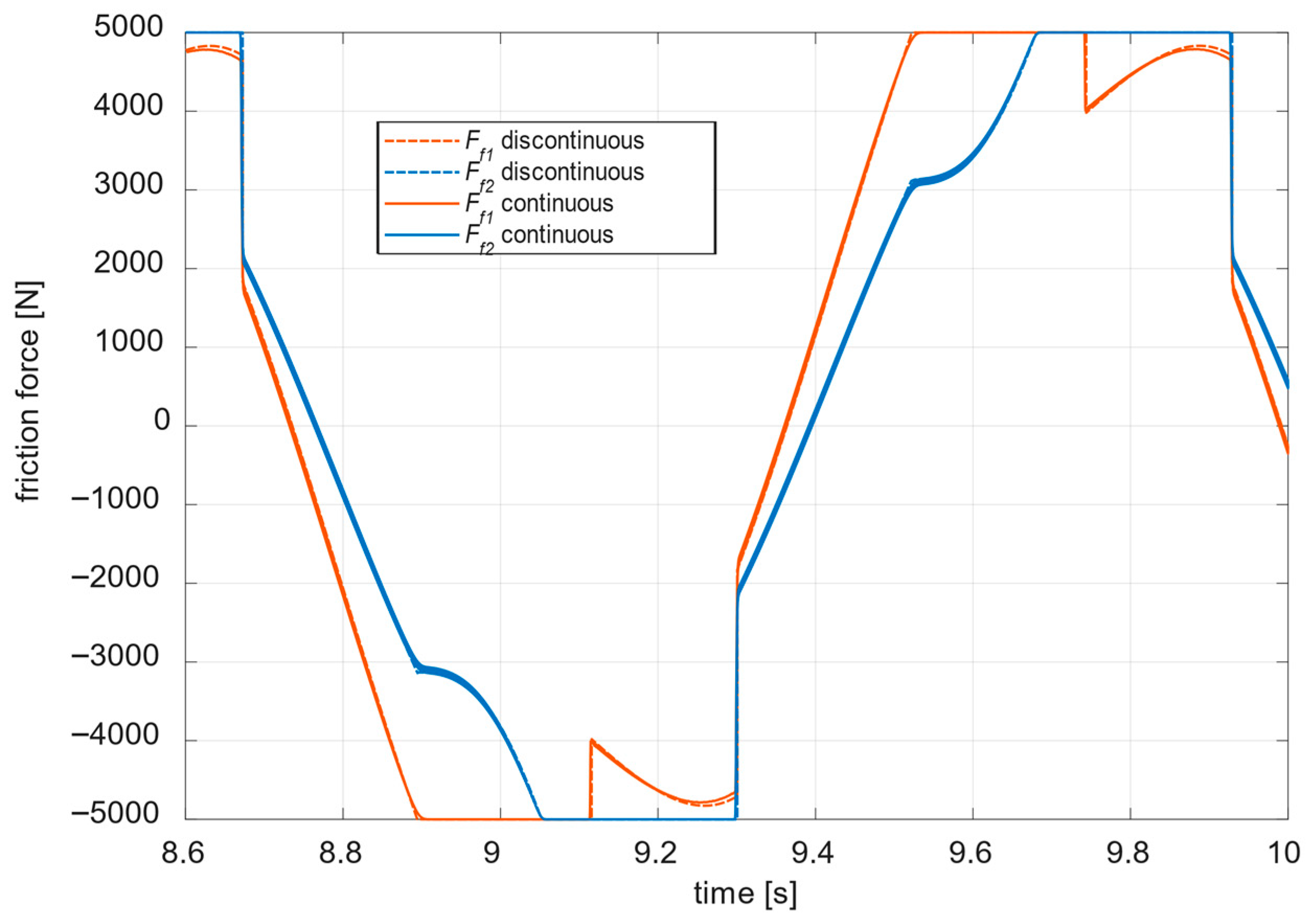
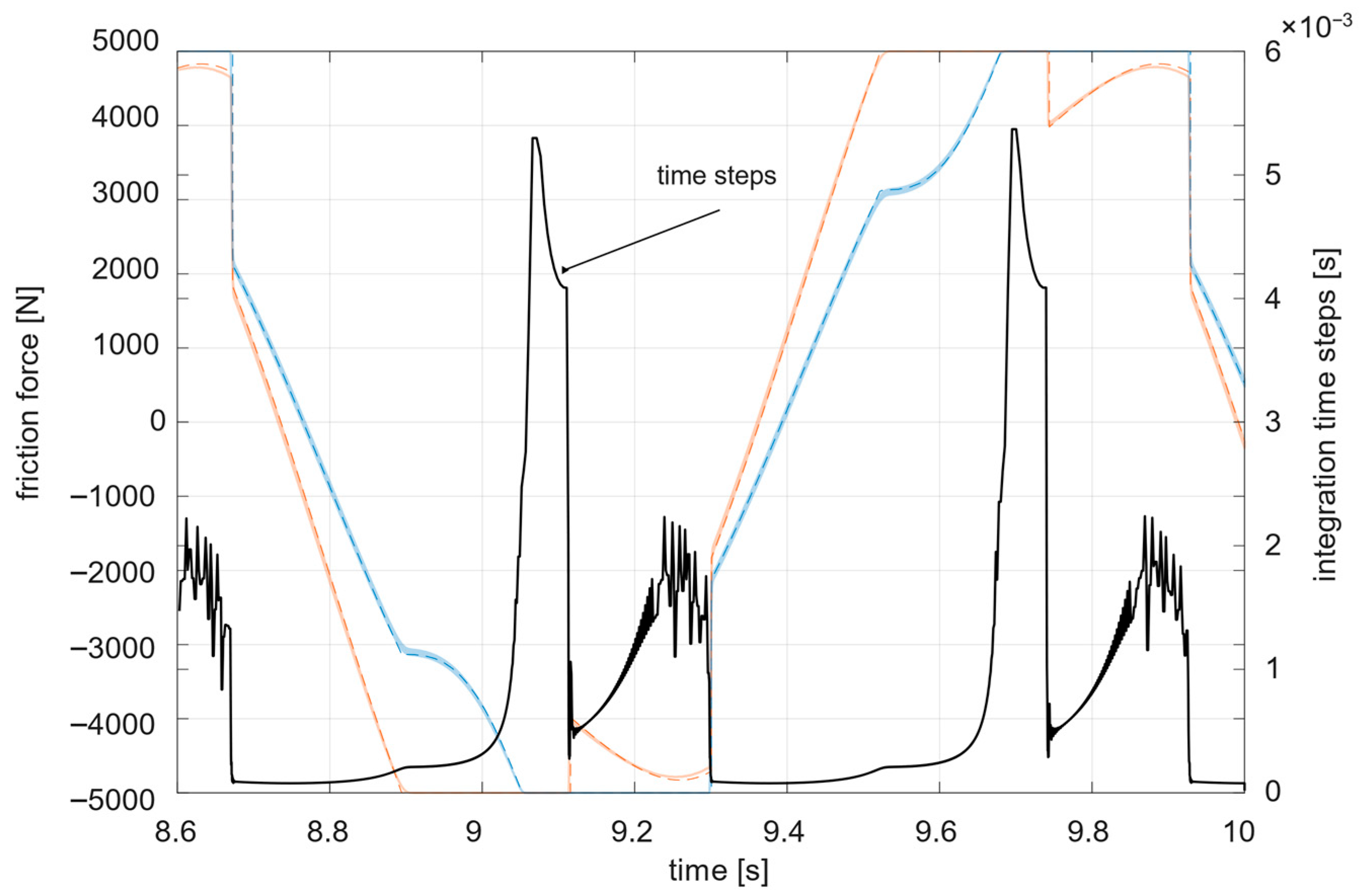
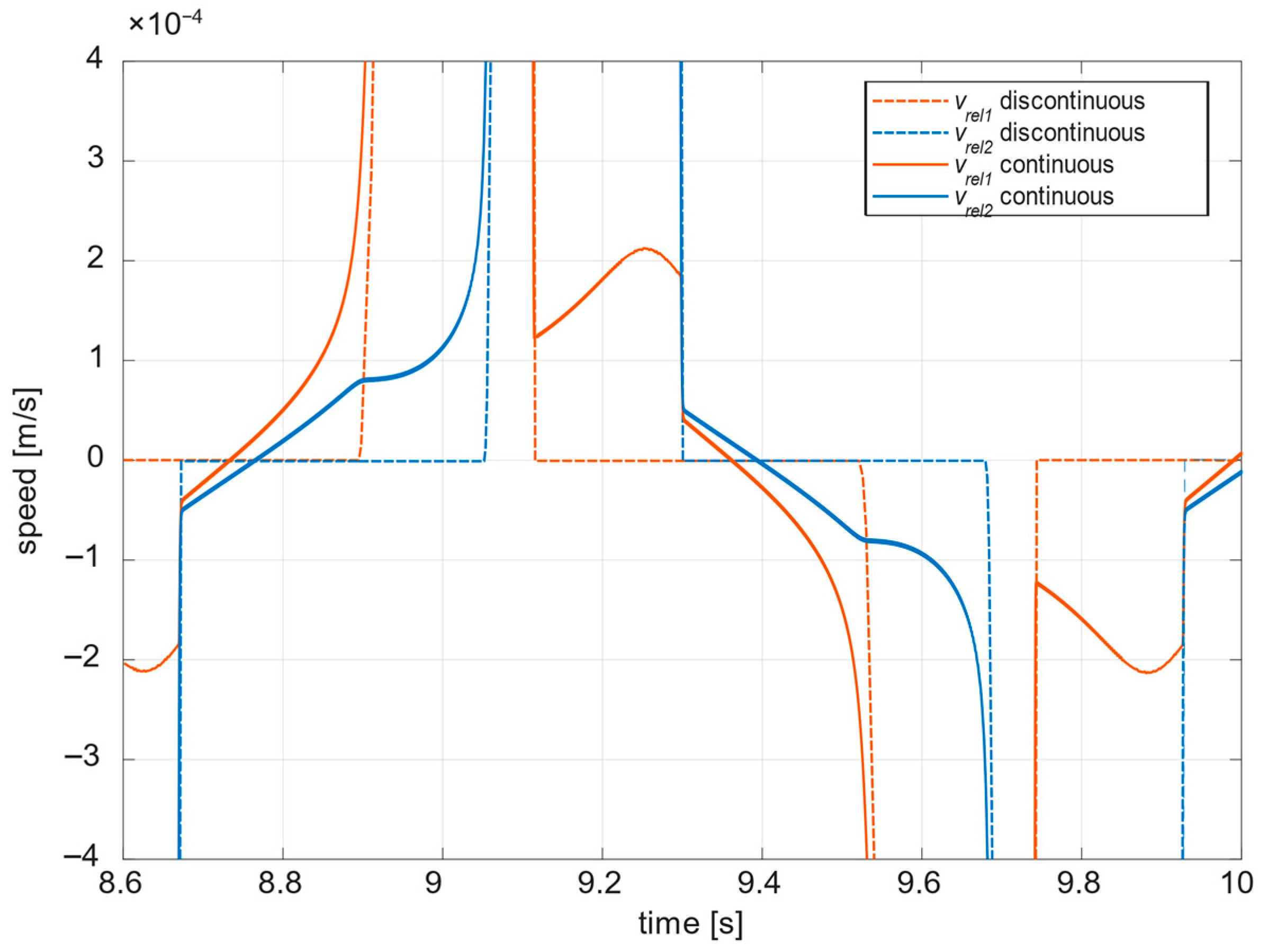
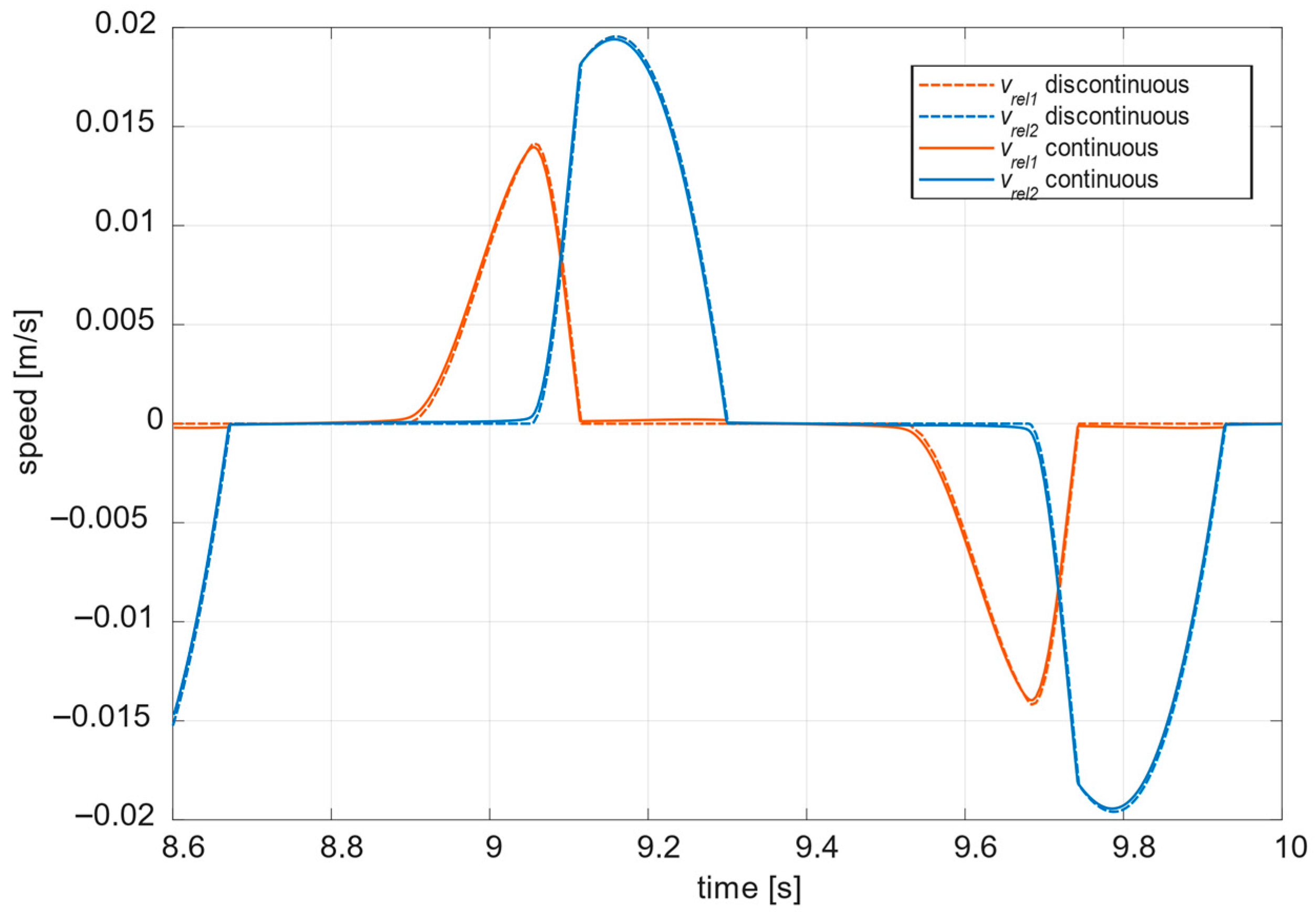
4.2. Results: Discontinuous Model

The discontinuous model successfully captured stick–slip intervals and force discontinuities. Time histories showed sharp transitions in both stick-to-slip and slip-to-stick, consistent with dry friction. The simulations revealed that the discontinuous model was more efficient, as it avoided stiffness and could be solved with standard ODE integrators, i.e., Matlab ode23 with RelTol value 10⁻⁸.

Absolute and relative vertical velocities of the masses and track profiles are depicted in Figure 2 for steady-state oscillations obtained at ω = 5 rad/s, A = 20 mm, and η = 10⁻⁶. All the possible situations defined by Equations (7)–(10) can be observed: both suspension stages in the stick phase (e.g., around 9.4 s), both in the slip phase (e.g., around 9.1 s), or one stage in slip and the other in stick phase (e.g., 8.8 s or 9.8 s), Figure 2. The phase transition is always obvious in the superposition or setting apart of the absolute velocities. The stick phases are also clearly highlighted by the zero relative velocity spans.

In the plotted time span, the bogie vertical velocity (orange) is superposed either on the carbody velocity (blue) or the wheel–rail contact point (black) most of the time. The lengths of the stick periods depend on the amplitude and frequency of the track irregularities, and they can be completely replaced by the slip mode as the amplitude A or frequency ω increases, or at resonances.

An interesting feature of the model is also that when one stage is slipping and the other sticking, the model behaves like a one-degree-of-freedom system and when both stages are blocked, the movement follows the track irregularities.

Along with the accurate simulation of the phenomenon, the discontinuous model’s numerical performance was found to be nearly independent of the saturation creep limit η. Simulations carried out with values of η between 10⁻⁶ and 10⁻⁴ had almost identical results both for values and numerical efficiencies. Accuracy and efficiency also proved independent of track irregularity parameters, i.e., amplitude A or frequency ω, and friction modes, i.e., stick or slip.

4.3. Results: Continuous Model

The continuous model produced smooth force–displacement curves and velocity responses. To match the values of the non-smooth model, the friction parameter C = 9000 s/m in Figure 3 was chosen to yield a reasonable simulation time.

The friction forces computed with the alternative methods are quite similar. In the slip phases, friction forces have maximum values for the discontinuous model, i.e., 5000 N and −5000 N, while for the regularized one, almost maximum values (the $tanh$ function will never have exactly the maximum value). But the most striking aspect is that the “regularized stick force”, in the interval (−5000 N, 5000 N), exhibits a numerical instability (the line is thickened due to the fast oscillations).

Figure 4 illustrates the numerical instability of the regularized model through the plotted time–integration steps. The friction force, also shown, helps distinguish between the stick and slip phases. During the stick phase, the solver drastically reduces the integration time step to maintain stability while solving the stiff equations generated by the smooth friction formulation. The ratio between the maximum slip time step and the minimum stick time step is approximately 100. In contrast, for the discontinuous model, although a similar variation in the time step is observed, the actual values differ significantly. The corresponding ratio is around 10, and the integration steps remain consistently larger than those of the regularized case.

Computed relative velocities also match well for the two approaches in the slip phase but they are several orders higher than the one obtained with the switch model in the stick phase, as shown in Figure 5. In theory, during stick modes, relative velocities should be zero, but, as explained before, searching for absolute zero would be inefficient, but the Karnopp method allows for a much better approximation.

However, a detailed image reveals that the stick–slip behaviour was blurred and replaced by gradual transitions in the regularized approach. While this avoided too long of an integration time, it led to inaccurate predictions, Figure 6.

A decrease in the friction parameter is not tolerable because the stick phases become indistinguishable while the increase in the friction parameter C leads to proportional lengthening of the integration time and unacceptable integration time spans. In contrast to the continuous solution, the discontinuous ones accurately indicate the zero relative velocity intervals.

5. Discussion

5.1. Alternative Approaches

To illustrate and evaluate the numerical methods considered in this study, we introduce a two-degree-of-freedom (2-DOF) model representing a simplified vertical suspension (Figure 1). The vehicle bogie and carbody are idealized as rigid bodies of mass m₁ and m₂, respectively, and the suspensions components are springs and buffers that provide both elastic (F_e) and dry friction damping (F_f) forces.

As outlined earlier, two main approaches exist:

• The regularized approach, which smoothens the discontinuity at zero slip velocity.
• The non-smooth approach, which retains discontinuities and better captures stick–slip transitions.

In the regularized approach, the dry friction force is approximated by a smooth, velocity-dependent function. In contrast, the stick discontinuous force can take any value between $-F_{\mathit{sMax} }$ and $F_{\mathit{sMax}}$ independent on the relative velocity, within the Karnopp stick band, Figure 7.

However, the suspension forces are only analytic within certain operating intervals, and sliding contact may induce changes in the effective number of degrees of freedom [26]. This feature makes the switch model particularly suitable for representing suspension systems with dry friction damping.

5.2. Stick–Slip Oscillations and Mathematical Structure

Dry friction gives rise to stick–slip oscillations whenever the external forces remain below the maximum stick threshold. In the stick regime, the coupled system effectively reduces to a single degree of freedom. Such switching alters the mathematical structure of the governing equations, which can no longer be assumed smooth.

To represent these effects, the frictional forces must be expressed as set-valued functions, typically written as inequalities or inclusions. Practical solutions involve complementarity formulations, often tackled via quadratic programming or iterative projection methods.

Recent advancements include the switch model, which distinguishes between attractive and repulsive sliding modes and guides the system towards the exact zero velocity state in the stick regime. This refinement enhances numerical stability and reduces integration errors.

The main aspects of the non-smooth approach can be summarized as follows:

• Set-valued/non-smooth models: these treat friction as a multivalued function at zero velocity (e.g., friction force in a range when velocity is zero), which is inherent in non-smooth mechanics.
• Switch models: models that switch laws depending on the regime (stick vs. slip), possibly also depending on additional state variables or thresholds. These are efficient in capturing realistic behaviour with reduced computational overhead when compared to finely regularized/hybrid continuous approximations.
• Karnopp model: introduces a finite “stick band” with threshold $\eta$. For $abs\left(v_{rel}\right)<\eta$, the state is “stick”; outside, slip. This allows for handling stick–slip without infinitely sharp transitions.

Each regime is described by its own governing equations, enabling consistent treatment of discontinuities. The resulting discontinuous force law has a more demanding modelling but provides a physically consistent description of suspension dynamics with dry friction elements.

5.3. Comparative Analysis

A direct comparison between continuous and discontinuous approaches shows that both yield similar global trends, with maximum force and displacement values differing by less than 10%. However, the discontinuous model provides a more realistic description of stick–slip behaviour that the continuous model cannot reproduce (e.g., zero relative velocity spans or discontinuities of the friction forces). From a computational perspective, the discontinuous model allowed for faster simulations. As can be seen in Figure 8, it can be even hundreds of times faster than the regularized approach. These findings mirror earlier results in braking buffer studies, confirming that discontinuous models offer better overall efficiency and accuracy.

Discontinuous (set-valued, event-driven) models tend to achieve significantly better computational efficiency in regimes with prolonged stick phases. In these cases, the smooth (regularized) model is stiff and, hence, is prone to numerical instability, whereas the non-smooth model is not stiff but may be prone to solutions that are non-unique or ambiguous if the model’s complexity increases.

Simulations were run for 500 angular frequencies distributed on a logarithmic scale between 1 and 100 rad/s, both for the regularized and the non-smooth model. The time ratio of the continuous system simulation time vs. the time of the discontinuous one is given in Figure 8 for two sets of simulations, with track irregularity amplitudes of A = 2 mm and A = 20 mm, respectively. The same initial conditions and time span were used for both modes. Both transient and steady-state periods are included in each simulation. The results obviously show that the continuous model is numerically inefficient compared to the discontinuous one. The reason is that in the stick phases the continuous model is “stiff” and requires intensive computing resources. This is also the reason why simulations time is increased in the regularized approach for a smaller perturbation amplitude, as the stick phases become longer. In contrast, the simulation time of the discontinuous model is almost insensitive to the increase in stick periods.

Classical regularized models offer continuous solutions but often require very small time-steps or stiff integrators when enforcing near-stick behaviour, which increases cost and may reduce accuracy in capturing stick phases. More than that, the regularized model exhibited numerical instability in the stick phase leading to additional computational overheads and reduced reliability. In addition to its detrimental impact on integration efficiency, the effort required to address this issue negates the benefits of the simple formulation. As illustrated in Figure 8, the integration time for the continuous model can be prohibitively higher than that of the discontinuous model. As expected, when the slip phases span almost the entire simulation time interval, e.g., as seen in Figure 8, with high frequencies, and $A$ = 20 mm, the regularized solution is faster because it is less complex.

The comparative analysis highlights the trade-offs inherent in suspension modelling with dry friction. Continuous models are appealing due to their mathematical smoothness, which simplifies implementation. However, they risk omitting essential physical features such as stick–slip oscillations, which are central to suspension performance. This omission can lead to overly optimistic predictions of ride comfort and system stability.

Discontinuous models, while more complex to formulate, provide superior physical fidelity, Figure 5. They explicitly account for the non-smooth nature of dry friction, thereby capturing the rich dynamics of railway suspensions. Importantly, they are not only more accurate but also more computationally efficient, since they avoid the stiffness inherent to regularized models.

From an engineering standpoint, these findings suggest that discontinuous models should be preferred when accurate prediction of vehicle dynamics is required, especially in safety-critical contexts. Continuous models may still be useful for large-scale system simulations or optimization studies, where computational simplicity outweighs the need for fine detail or computational efficiency.

5.4. Potential Implementations of Hybrid Modelling Strategies

As explained in Section 2.1, physical friction laws can reproduce effects such as elastic and plastic deformation, surface roughness, asperity interactions, and interfacial third-body layers. Because surfaces are rarely ideal, phenomena like micro-asperity contact, plasticity, and interfacial contamination often play non-negligible roles. Precise friction modelling is therefore essential for reliable numerical simulations, especially when comparing more elaborate models.

Additionally, a major problem of the calculation methods applied to solve non-smooth systems is the uniqueness and existence of the solution. Indeterminacy and inconsistency have been observed in many planar rigid body problems. Some of them are known as “Painleve paradoxes”. The problem comes to a climax when the static friction forces (or other constraint types) are redundant. In this case, indeterminacy is attended by a rank-deficient constraint matrix. The 2_DOF model proposed in this paper is always determined but any increase in complexity leads to the above-mentioned problem.

For modelling dry friction in railway vehicle suspensions, hybrid approaches are increasingly necessary as they merge the high physical fidelity of non-smooth dynamics with the computational tractability of continuous (regularized) models. The selection among existing hybrid implementations dictates the specific compromise achieved in terms of accuracy, solution stability, and overall computational cost. Two potential strategies result from these constraints:

• Firstly, a hybrid complementarity regularization which couples a mathematical programming-based (complementarity) solver for the discontinuous regime with a regularized ODE solver for smooth phases based on the following approach:
  • Express friction laws as inequalities.
  • Use a Mixed Linear Complementarity Problem formulation when discontinuities are active.
  • Otherwise, integrate with standard ODE solvers.
• Secondly, a machine learning-assisted hybrid model using data-driven algorithms to emulate parts of the friction law where analytical models fail or are computationally demanding. The implementation should include the following processes:
  • Train a neural network or regression model to approximate the friction–velocity relationship in transition regions.
  • Embed the learned model into a physics-based framework that governs overall system dynamics.

Such hybrid models could perform predictive modelling for modern railway suspensions with composite or adaptive friction materials in large-scale train dynamics or multi-car simulations with frequent transitions between static and sliding contacts.

6. Conclusions

This paper has presented a comparative study of continuous and discontinuous approaches to modelling railway suspensions with dry friction dampers. The analysis shows that:

• Continuous models are simple to implement but require stiff solvers, exhibit numerical instability, and fail to capture true stick–slip dynamics.
• Discontinuous models accurately reproduce stick intervals and allow for distinguishing stick and slip periods even with a wide stick band while being computationally efficient.

The choice of model should depend on the intended application: discontinuous models for design and safety studies and continuous models for large-scale system optimization where fine physical details may be less critical.

Future research should focus on hybrid modelling strategies that combine the robustness of continuous formulations with the accuracy of discontinuous ones. Experimental validation of the models under realistic suspension conditions would also be valuable. Moreover, extending the comparative framework to multi-bogie vehicles and more complex track excitations would provide deeper insights into railway vehicle dynamics and support the development of more reliable predictive tools for industry applications.