Gross Calorific Value Estimation in Coal Using Multi-Model FTIR and Machine Learning Approach
Abstract
1. Introduction
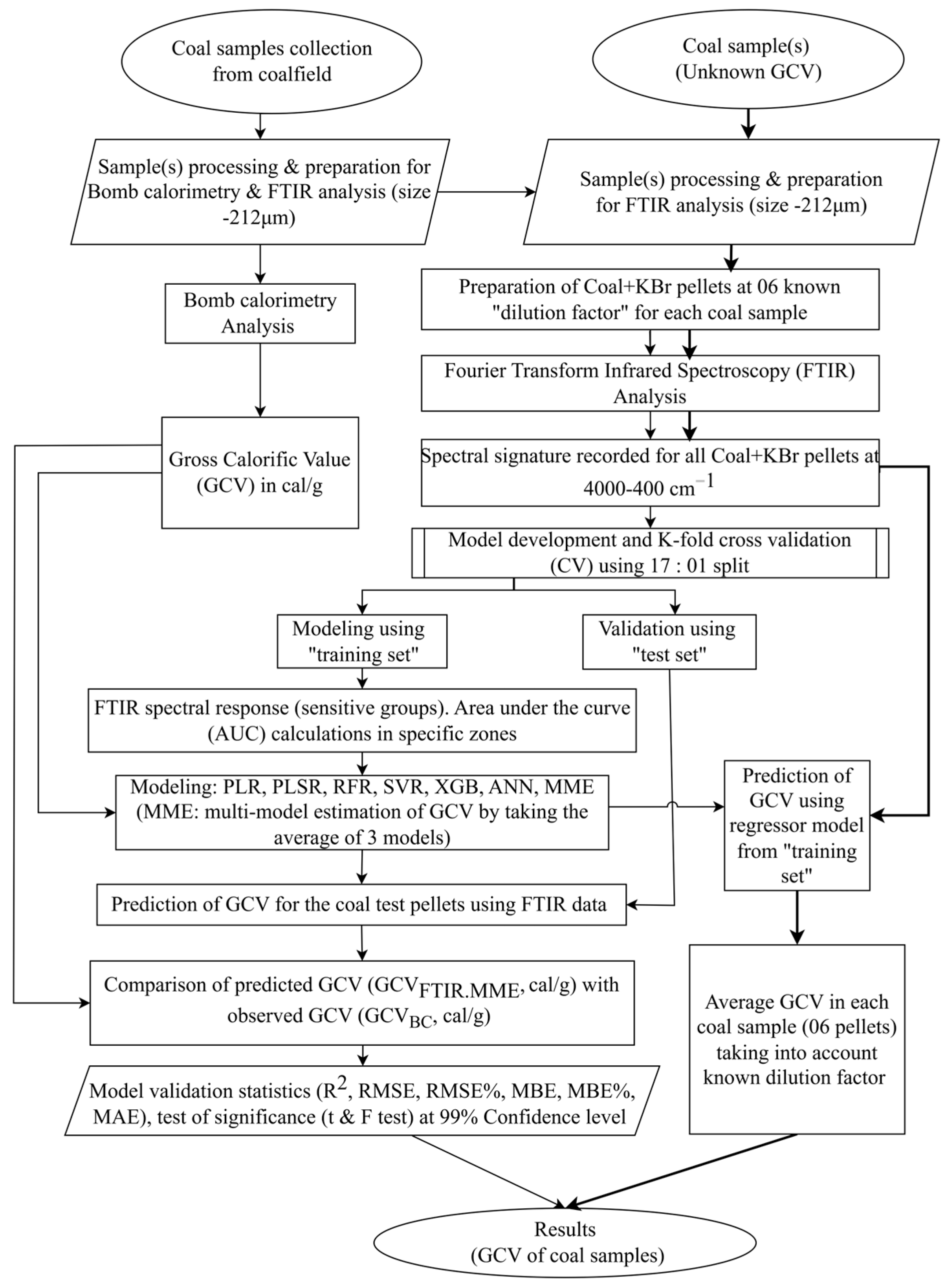
2. Materials and Methods
2.1. Coal Sample Data
2.2. Bomb Calorimetry Analysis
2.3. Fourier-Transform Infrared (FTIR) Spectroscopy
2.4. Proximate Analysis
2.5. Piecewise Linear Regression (PLR)
2.6. Partial Least Squares Regression (PLSR)
2.7. Random Forest Regression (RFR)
2.8. Support Vector Regression (SVR)
2.9. Extreme Gradient Boosting (XGB)
2.10. Artificial Neural Network (ANN)
3. Results
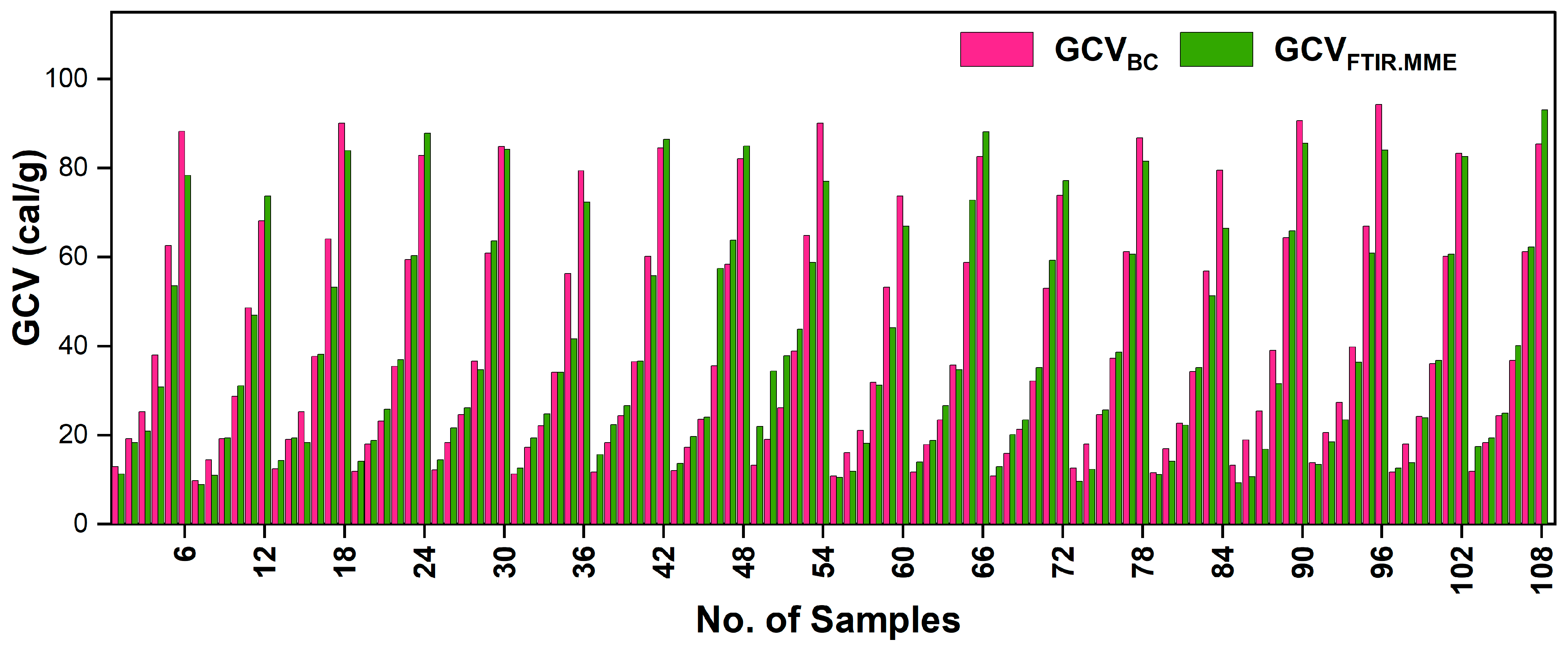
3.1. Gross Calorific Value of Coal Samples
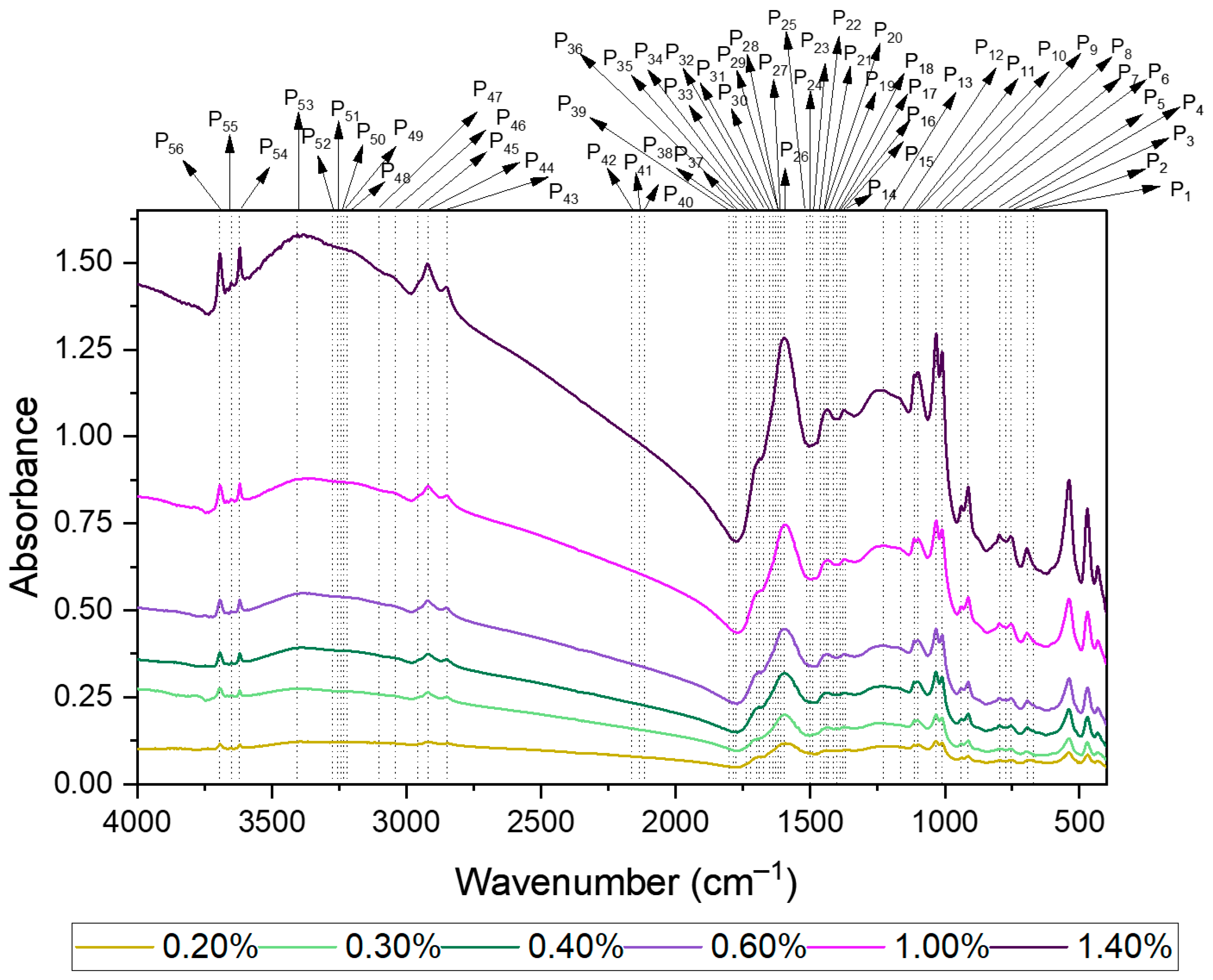
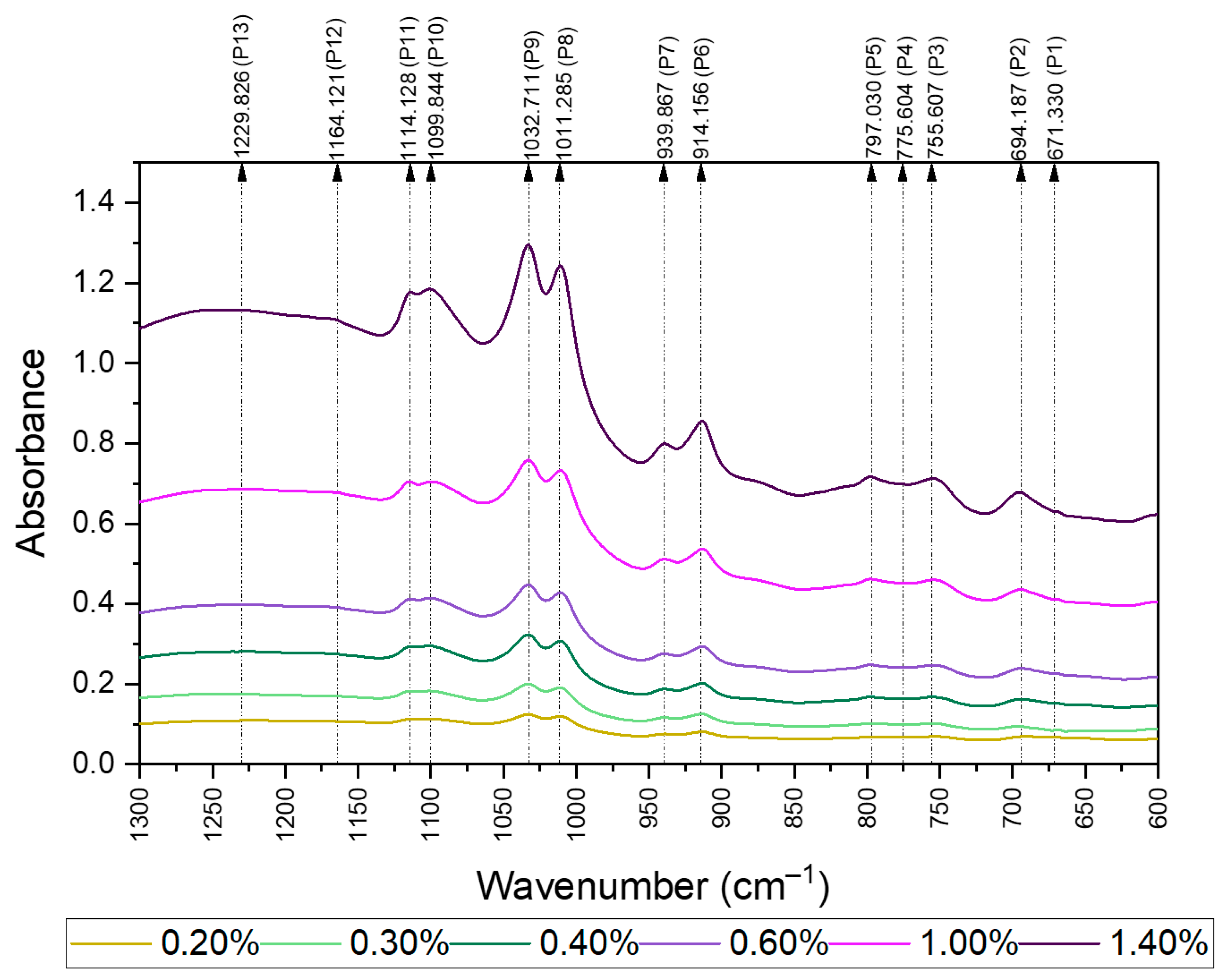
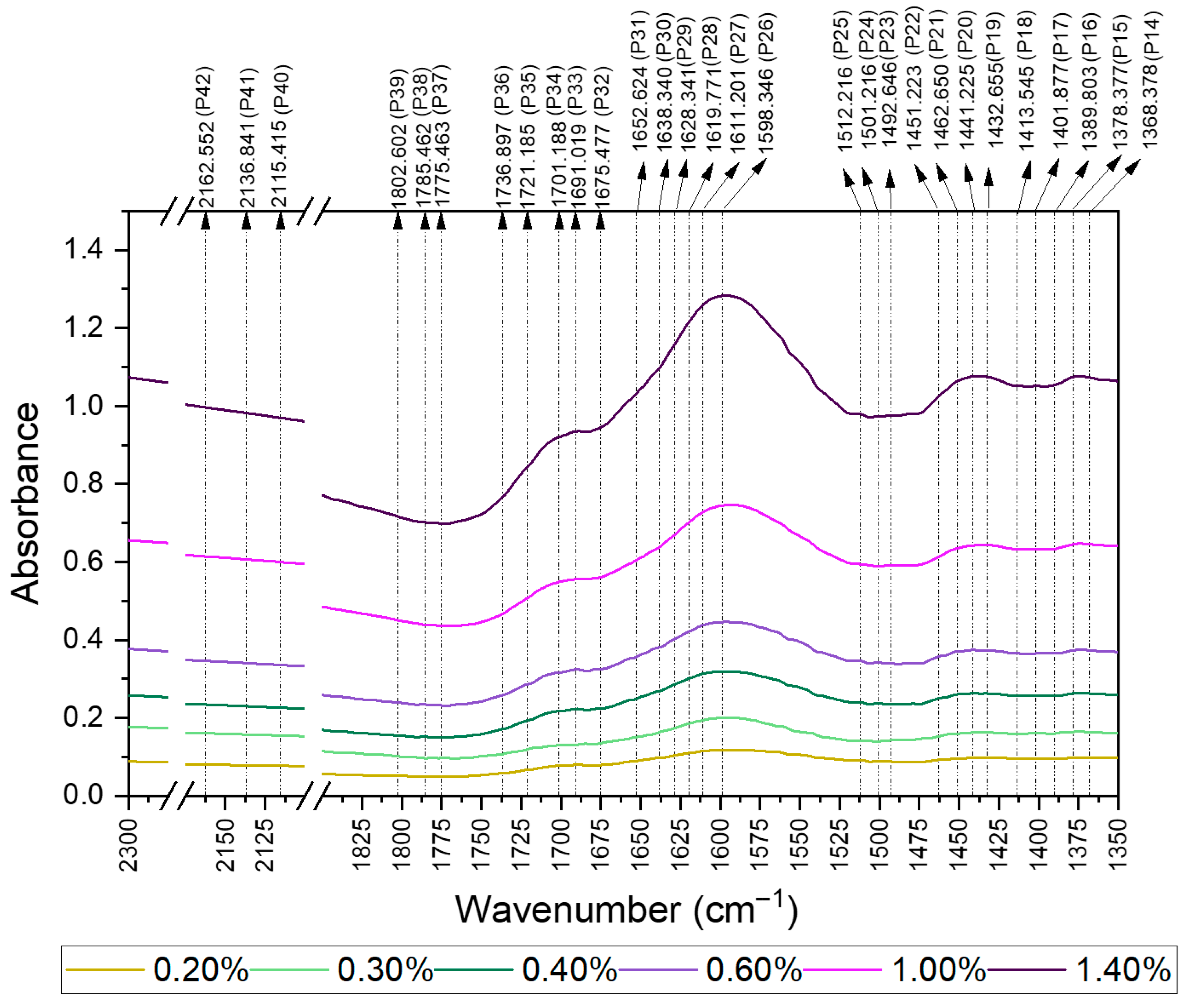
3.2. Selection of MIR Bands Suitable for GCV Determination
3.3. Model Estimation and Assessment
4. Discussion
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GCV | Gross calorific value |
| FTIR | Fourier transform infrared spectroscopy |
| BC | Bomb calorimetry |
| XRF | X-ray fluorescence spectroscopy |
| LIBS | Laser-induced breakdown spectroscopy |
| NIRS | Near-infrared spectroscopy |
| DRIFT | Diffuse reflectance infrared Fourier transform spectroscopy |
| MLR | Multiple linear regression |
| PLR | Piece-wise linear regression |
| PLS/PLSR | Partial least squares regression |
| RFR | Random forest regression |
| SVR | Support vector regression |
| XGB | Extreme gradient boosting |
| ANN | Artificial neural network |
| MME | Multi-model estimation |
| PSO-ANN | Particle swarm optimization-artificial neural network |
| ANFIS | Adaptive neuro-fuzzy inference system |
| PCA | Principal component analysis |
| K-ELM | Kernel-based extreme learning machine |
| WT-MIV-KELM | Wavelet transform with mean impact value and kernel-based extreme learning machine |
| GA | Genetic algorithm |
| V-WSP | Variance-weighted spectral preprocessing |
| MC-UVE | Monte Carlo uninformative variable elimination |
| GRNN | General regression neural network |
| RBFNN | Radial basis function neural network |
| GBRT | Gradient boosted regression trees |
| GRA-CMLM | Grey relational analysis-based committee of machine learning models |
| SAE-CMLM | Simple average ensemble-based committee of machine learning models |
| WAE-CMLM | Weighted average ensemble-based committee of machine learning models |
| R2 | Coefficient of determination |
| RMSE | Root mean square error |
| RMSE% | Root mean square error percentage |
| MBE | Mean bias error |
| MBE% | Mean bias error percentage |
| MAE | Mean absolute error |
| MSE | Mean Squared Error |
References
- IEA. Coal 2023; IEA: Paris, France, 2023. [Google Scholar]
- Mondal, C.; Pandey, A.; Pal, S.K.; Samanta, B.; Dutta, D. Prediction of Gross Calorific Value as a Function of Proximate Parameters for Jharia and Raniganj Coal Using Machine Learning Based Regression Methods. Int. J. Coal Prep. Util. 2022, 42, 3763–3776. [Google Scholar] [CrossRef]
- Liu, P.; Lv, S. Measurement and Calculation of Calorific Value of Raw Coal Based on Artificial Neural Network Analysis Method. Therm. Sci. 2020, 24, 3129–3137. [Google Scholar] [CrossRef]
- Mathews, J.P.; Krishnamoorthy, V.; Louw, E.; Tchapda, A.H.N.; Castro-Marcano, F.; Karri, V.; Alexis, D.A.; Mitchell, G.D. A Review of the Correlations of Coal Properties with Elemental Composition. Fuel Process. Technol. 2014, 121, 104–113. [Google Scholar] [CrossRef]
- Selvig, W.A.; Gibson, F.H. Calorific value of coal. In Chemistry of Coal Utilization; Lowry, H.H., Ed.; John Wiley: Hoboken, NJ, USA, 1945; Volume 1, pp. 132–144. [Google Scholar]
- Neavel, R.C.; Smith, S.E.; Hippo, E.J.; Miller, R.N. Interrelationships between Coal Compositional Parameters. Fuel 1986, 65, 312–320. [Google Scholar] [CrossRef]
- Mazumdar, B.K. Theoretical Oxygen Requirement for Coal Combustion: Relationship with Its Calorific Value. Fuel 2000, 79, 1413–1419. [Google Scholar] [CrossRef]
- Channiwala, S.A.; Parikh, P.P. A Unified Correlation for Estimating HHV of Solid, Liquid and Gaseous Fuels. Fuel 2002, 81, 1051–1063. [Google Scholar] [CrossRef]
- Küçükbayrak, S.; Dürüs, B.; Meríçboyu, A.E.; Kadioglu, E. Estimation of Calorific Values of Turkish Lignites. Fuel 1991, 70, 979–981. [Google Scholar] [CrossRef]
- Cordero, T.; Marquez, F.; Rodriguez-Mirasol, J.; Rodriguez, J.J. Predicting Heating Values of Lignocellulosics and Carbonaceous Materials from Proximate Analysis. Fuel 2001, 80, 1567–1571. [Google Scholar] [CrossRef]
- Demirbaş, A. Calculation of Higher Heating Values of Biomass Fuels. Fuel 1997, 76, 431–434. [Google Scholar] [CrossRef]
- Parikh, J.; Channiwala, S.; Ghosal, G. A Correlation for Calculating HHV from Proximate Analysis of Solid Fuels. Fuel 2005, 84, 487–494. [Google Scholar] [CrossRef]
- Raveendran, K.; Ganesh, A. Heating Value of Biomass and Biomass Pyrolysis Products. Fuel 1996, 75, 1715–1720. [Google Scholar] [CrossRef]
- Majumder, A.K.; Jain, R.; Banerjee, P.; Barnwal, J.P. Development of a new proximate analysis based correlation to predict calorific value of coal. Fuel 2008, 87, 3077–3081. [Google Scholar] [CrossRef]
- Chen, J.; He, Y.; Liang, Y.; Wang, W.; Duan, X. Estimation of Gross Calorific Value of Coal Based on the Cubist Regression Model. Sci. Rep. 2024, 14, 23176. [Google Scholar] [CrossRef] [PubMed]
- Feng, Q.; Zhang, J.; Zhang, X.; Wen, S. Proximate Analysis Based Prediction of Gross Calorific Value of Coals: A Comparison of Support Vector Machine, Alternating Conditional Expectation and Artificial Neural Network. Fuel Process. Technol. 2015, 129, 120–129. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, Y.; Lu, Z.; Dai, W.; Huang, J.; Cui, S.; Chen, B.; Wu, S.; Dong, L. Machine Learning Prediction of Calorific Value of Coal Based on the Hybrid Analysis. Int. J. Coal Prep. Util. 2023, 43, 577–598. [Google Scholar] [CrossRef]
- Yuan, T.; Wang, Z.; Lui, S.-L.; Fu, Y.; Li, Z.; Liu, J.; Ni, W. Coal Property Analysis Using Laser-Induced Breakdown Spectroscopy. J. Anal. At. Spectrom. 2013, 28, 1045. [Google Scholar] [CrossRef]
- Hou, Z.; Wang, Z.; Yuan, T.; Liu, J.; Li, Z.; Ni, W. A Hybrid Quantification Model and Its Application for Coal Analysis Using Laser Induced Breakdown Spectroscopy. J. Anal. At. Spectrom. 2016, 31, 722–736. [Google Scholar] [CrossRef]
- Zhang, L.; Gong, Y.; Li, Y.; Wang, X.; Fan, J.; Dong, L.; Ma, W.; Yin, W.; Jia, S. Development of a Coal Quality Analyzer for Application to Power Plants Based on Laser-Induced Breakdown Spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2015, 113, 167–173. [Google Scholar] [CrossRef]
- Yao, S.; Mo, J.; Zhao, J.; Li, Y.; Zhang, X.; Lu, W.; Lu, Z. Development of a Rapid Coal Analyzer Using Laser-Induced Breakdown Spectroscopy (LIBS). Appl. Spectrosc. 2018, 72, 1225–1233. [Google Scholar] [CrossRef]
- Yan, C.; Qi, J.; Liang, J.; Zhang, T.; Li, H. Determination of Coal Properties Using Laser-Induced Breakdown Spectroscopy Combined with Kernel Extreme Learning Machine and Variable Selection. J. Anal. At. Spectrom. 2018, 33, 2089–2097. [Google Scholar] [CrossRef]
- Yan, C.; Zhang, T.; Sun, Y.; Tang, H.; Li, H. A Hybrid Variable Selection Method Based on Wavelet Transform and Mean Impact Value for Calorific Value Determination of Coal Using Laser-Induced Breakdown Spectroscopy and Kernel Extreme Learning Machine. Spectrochim. Acta Part B At. Spectrosc. 2019, 154, 75–81. [Google Scholar] [CrossRef]
- Yan, C.; Liang, J.; Zhao, M.; Zhang, X.; Zhang, T.; Li, H. A Novel Hybrid Feature Selection Strategy in Quantitative Analysis of Laser-Induced Breakdown Spectroscopy. Anal. Chim. Acta 2019, 1080, 35–42. [Google Scholar] [CrossRef]
- Andrés, J.M.; Bona, M.T. ASTM Clustering for Improving Coal Analysis by Near-Infrared Spectroscopy. Talanta 2006, 70, 711–719. [Google Scholar] [CrossRef] [PubMed]
- Andrés, J.M.; Bona, M.T. Analysis of Coal by Diffuse Reflectance Near-Infrared Spectroscopy. Anal. Chim. Acta 2005, 535, 123–132. [Google Scholar] [CrossRef]
- Begum, N.; Chakravarty, D.; Das, B.S. Estimation of Gross Calorific Value of Bituminous Coal Using Various Coal Properties and Reflectance Spectra. Int. J. Coal Prep. Util. 2022, 42, 979–985. [Google Scholar] [CrossRef]
- Bona, M.; Andres, J. Coal Analysis by Diffuse Reflectance Near-Infrared Spectroscopy: Hierarchical Cluster and Linear Discriminant Analysis. Talanta 2007, 72, 1423–1431. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.-H.; Zhao, Y.; Hu, R.; Zhang, Y.-Y.; Han, X.-H. Analysis of Near-Infrared Spectra of Coal Using Deep Synergy Adaptive Moving Window Partial Least Square Method Based on Genetic Algorithm. Chin. J. Anal. Chem. 2019, 47, e19034–e19044. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Wei, G.; Hu, R.; Luo, Z.; Li, G. Improved PLS Regression Based on SVM Classification for Rapid Analysis of Coal Properties by Near-Infrared Reflectance Spectroscopy. Sens. Actuators B Chem. 2014, 193, 723–729. [Google Scholar] [CrossRef]
- Yao, S.; Qin, H.; Wang, Q.; Lu, Z.; Yao, X.; Yu, Z.; Chen, X.; Zhang, L.; Lu, J. Optimizing Analysis of Coal Property Using Laser-Induced Breakdown and near-Infrared Reflectance Spectroscopies. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 239, 118492. [Google Scholar] [CrossRef] [PubMed]
- Fysh, S.A.; Swinkels, D.A.J.; Fredericks, P.M. Near-Infrared Diffuse Reflectance Spectroscopy of Coal. Appl. Spectrosc. 1985, 39, 354–357. [Google Scholar] [CrossRef]
- Alciaturi, C.E.; Escobar, M.E.; Vallejo, R. Prediction of Coal Properties by Derivative DRIFT Spectroscopy. Fuel 1996, 75, 491–499. [Google Scholar] [CrossRef]
- Alciaturi, C.E.; Montero, T.; De La Cruz, C.; Escobar, M.E. The Prediction of Coal Properties Using Compressed Infrared Data from Osculating Polynomials. Anal. Chim. Acta 1997, 340, 233–240. [Google Scholar] [CrossRef]
- Roman Gomez, Y.; Cabanzo Hernández, R.; Guerrero, J.E.; Mejía-Ospino, E. FTIR-PAS Coupled to Partial Least Squares for Prediction of Ash Content, Volatile Matter, Fixed Carbon and Calorific Value of Coal. Fuel 2018, 226, 536–544. [Google Scholar] [CrossRef]
- Qin, H.; Lu, Z.; Yao, S.; Li, Z.; Lu, J. Combining Laser-Induced Breakdown Spectroscopy and Fourier-Transform Infrared Spectroscopy for the Analysis of Coal Properties. J. Anal. At. Spectrom. 2019, 34, 347–355. [Google Scholar] [CrossRef]
- He, X.; Liu, X.; Nie, B.; Song, D. FTIR and Raman Spectroscopy Characterization of Functional Groups in Various Rank Coals. Fuel 2017, 206, 555–563. [Google Scholar] [CrossRef]
- Jia, J.; Xing, Y.; Li, B.; Zhao, D.; Wu, Y.; Chen, Y.; Wang, D. Study on the Occurrence Difference of Functional Groups in Coals with Different Metamorphic Degrees. Molecules 2023, 28, 2264. [Google Scholar] [CrossRef]
- Shukla, A.; Prasad, A.K.; Mishra, S.; Vinod, A.; Varma, A.K. Rapid Estimation of Sulfur Content in High-Ash Indian Coal Using Mid-Infrared FTIR Data. Minerals 2023, 13, 634. [Google Scholar] [CrossRef]
- Mishra, S.; Prasad, A.K.; Shukla, A.; Vinod, A.; Preety, K.; Varma, A.K. Estimation of Carbon Content in High-Ash Coal Using Mid-Infrared Fourier-Transform Infrared Spectroscopy. Minerals 2023, 13, 938. [Google Scholar] [CrossRef]
- Vinod, A.; Prasad, A.K.; Mishra, S.; Purkait, B.; Mukherjee, S.; Shukla, A.; Desinayak, N.; Sarkar, B.C.; Varma, A.K. A Novel Multi-Model Estimation of Phosphorus in Coal and Its Ash Using FTIR Spectroscopy. Sci. Rep. 2024, 14, 13785. [Google Scholar] [CrossRef]
- Mishra, S.; Prasad, A.K.; Vinod, A.; Shukla, A.; Mukherjee, S.; Purkait, B.; Varma, A.K.; Sarkar, B.C. A Multi-Model Approach for Estimation of Ash Yield in Coal Using Fourier Transform Infrared Spectroscopy. Sci. Rep. 2025, 15, 13786. [Google Scholar] [CrossRef]
- ASTM D2234/D2234M-20; Standard Practice for Collection of a Gross Sample of Coal. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM D4749/D4749M-87(2019)E1; Standard Test Method for Performing the Sieve Analysis of Coal and Designating Coal Size. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM-D5865-12; Standard Test Method for Gross Calorific Value of Coal and Coke. ASTM International: West Conshohocken, PA, USA, 2012.
- Bottou, L.; Curtis, F.E.; Nocedal, J. Optimization Methods for Large-Scale Machine Learning. SIAM Rev. 2018, 60, 223–311. [Google Scholar] [CrossRef]
- Luenberger, D.G.; Ye, Y. Linear and Nonlinear Programming, 3rd ed.; International Series in Operations Research and Management Science; Springer: New York, NY, USA, 2008; ISBN 978-0-387-74502-2. [Google Scholar]
- Prasad, A.K.; Singh, R.P.; Tare, V.; Kafatos, M. Use of Vegetation Index and Meteorological Parameters for the Prediction of Crop Yield in India. Int. J. Remote Sens. 2007, 28, 5207–5235. [Google Scholar] [CrossRef]
- Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop Yield Estimation Model for Iowa Using Remote Sensing and Surface Parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
- Baumann, P.; Lee, J.; Frossard, E.; Schönholzer, L.P.; Diby, L.; Hgaza, V.K.; Kiba, D.I.; Sila, A.; Sheperd, K.; Six, J. Estimation of Soil Properties with Mid-Infrared Soil Spectroscopy across Yam Production Landscapes in West Africa. SOIL 2021, 7, 717–731. [Google Scholar] [CrossRef]
- Geladi, P.; Dåbakk, E. Computational Methods and Chemometrics in Near Infrared Spectroscopy. In Encyclopedia of Spectroscopy and Spectrometry; Elsevier: Amsterdam, The Netherlands, 2017; pp. 350–355. ISBN 978-0-12-803224-4. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Dhiman, G.; Bhattacharya, J.; Roy, S. Soil Textures and Nutrients Estimation Using Remote Sensing Data in North India—Punjab Region. Procedia Comput. Sci. 2023, 218, 2041–2048. [Google Scholar] [CrossRef]
- Kaur, G.; Das, K.; Hazra, J. Soil Nutrients Prediction Using Remote Sensing Data in Western India: An Evaluation of Machine Learning Models. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September 2020; IEEE: Waikoloa, HI, USA; pp. 4677–4680. [Google Scholar]
- Chiappini, F.A.; Allegrini, F.; Goicoechea, H.C.; Olivieri, A.C. Sensitivity for Multivariate Calibration Based on Multilayer Perceptron Artificial Neural Networks. Anal. Chem. 2020, 92, 12265–12272. [Google Scholar] [CrossRef] [PubMed]
- Cirovic, D.A. Feed-Forward Artificial Neural Networks: Applications to Spectroscopy. TrAC Trends Anal. Chem. 1997, 16, 148–155. [Google Scholar] [CrossRef]
- Song, J.; Zhang, H.; Wang, J.; Huang, L.; Zhang, S. High-Yield Production of Large Aspect Ratio Carbon Nanotubes via Catalytic Pyrolysis of Cheap Coal Tar Pitch. Carbon 2018, 130, 701–713. [Google Scholar] [CrossRef]
- Peng, Y.; Wang, L.; Zhao, L.; Liu, Z.; Lin, C.; Hu, Y.; Liu, L. Estimation of Soil Nutrient Content Using Hyperspectral Data. Agriculture 2021, 11, 1129. [Google Scholar] [CrossRef]
- Chelgani, S.C. Estimation of Gross Calorific Value Based on Coal Analysis Using an Explainable Artificial Intelligence. Mach. Learn. Appl. 2021, 6, 100116. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Zhu, S.; Armaghani, D.J.; Khandelwal, M.; Mohamad, E.T. Estimation of the TBM Advance Rate under Hard Rock Conditions Using XGBoost and Bayesian Optimization. Undergr. Space 2021, 6, 506–515. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Neural Networks and Deep Learning: A Textbook; Springer International Publishing: Cham, Switzerland, 2018; ISBN 978-3-319-94462-3. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Jia, J.; Xiao, L.; Wang, D.; Zhao, D.; Xing, Y.; Wu, Y. Construction and Optimization of Macromolecular Structure Model of Tiebei Lignite. PLoS ONE 2023, 18, e0289328. [Google Scholar] [CrossRef]
- Matin, S.S.; Chelgani, S.C. Estimation of Coal Gross Calorific Value Based on Various Analyses by Random Forest Method. Fuel 2016, 177, 274–278. [Google Scholar] [CrossRef]
- Solomon, P.R.; Hobbs, R.H.; Hamblen, D.G.; Chen, W.-Y.; La Cara, A.; Graff, R.S. Correlation of Coal Volatile Yield with Oxygen and Aliphatic Hydrogen. Fuel 1981, 60, 342–346. [Google Scholar] [CrossRef]
- Chen, Y.; Mastalerz, M.; Schimmelmann, A. Characterization of Chemical Functional Groups in Macerals across Different Coal Ranks via Micro-FTIR Spectroscopy. Int. J. Coal Geol. 2012, 104, 22–33. [Google Scholar] [CrossRef]
- Ibarra, J.; Munoz, E.; Moliner, R. FTIR Study of the Evolution of Coal Structure during the Coalification Process. Org. Geochem. 1996, 24, 725–735. [Google Scholar] [CrossRef]
- Clayden, J.; Greeves, N.; Warren, S. Organic Chemistry, 2nd ed.; Oxford University Press: Oxford, UK, 2012; ISBN 978-0-19-927029-3. [Google Scholar]
- Dai, F.; Zhuang, Q.; Huang, G.; Deng, H.; Zhang, X. Infrared Spectrum Characteristics and Quantification of OH Groups in Coal. ACS Omega 2023, 8, 17064–17076. [Google Scholar] [CrossRef] [PubMed]
- Pavia, D.L.; Lampman, G.M.; Kriz, G.S.; Vyvyan, J.R. Introduction to Spectroscopy, 4th ed.; Pavia, D.L., International Student, Eds.; Brooks-Cole: Belmont, CA, USA, 2009; ISBN 978-0-495-11478-9. [Google Scholar]
- Smith, B.C. Fundamentals of Fourier Transform Infrared Spectroscopy; CRC Press: Boca Raton, FL, USA, 2011; ISBN 978-0-429-14058-7. [Google Scholar]
- Streitwieser, A.; Heathcock, C.H. Introduction to Organic Chemistry; A Series of Books in Organic Chemistry; Macmillan: New York, NY, USA, 1976; ISBN 978-0-02-418010-0. [Google Scholar]
- Stuart, B.H. Infrared Spectroscopy: Fundamentals and Applications; J. Wiley & Sons: Chichester, UK, 2005; ISBN 978-0-470-01114-0. [Google Scholar]
- Wang, S.-H.; Griffiths, P.R. Resolution Enhancement of Diffuse Reflectance i.r. Spectra of Coals by Fourier Self-Deconvolution. Fuel 1985, 64, 229–236. [Google Scholar] [CrossRef]
- Boumanchar, I.; Chhiti, Y.; M’Hamdi Alaoui, F.E.; Sahibed-Dine, A.; Bentiss, F.; Jama, C.; Bensitel, M. Multiple Regression and Genetic Programming for Coal Higher Heating Value Estimation. Int. J. Green Energy 2018, 15, 958–964. [Google Scholar] [CrossRef]
- Munshi, T.A.; Jahan, L.N.; Howladar, M.F.; Hashan, M. Prediction of Gross Calorific Value from Coal Analysis Using Decision Tree-Based Bagging and Boosting Techniques. Heliyon 2024, 10, e23395. [Google Scholar] [CrossRef]
- Lawal, A.I.; Ajeboriogbon, A.F.; Onifade, M.; Bada, S.O.; Mulenga, F. A Novel Grey Relational Analysis-Based Committee of Machine Learning Methods for Enhanced Prediction of Coal Calorific Value. Fuel 2026, 406, 137070. [Google Scholar] [CrossRef]
- Zhu, W.; Xu, N.; Hower, J.C. Unveiling the Predictive Power of Machine Learning in Coal Gross Calorific Value Estimation: An Interpretability Perspective. Energy 2025, 318, 134781. [Google Scholar] [CrossRef]
- Li, J.; Gao, R.; Zhang, Y.; Wang, S.; Zhang, L.; Yin, W.; Jia, S. Coal Calorific Value Detection Technology Based on NIRS-XRF Fusion Spectroscopy. Chemosensors 2023, 11, 363. [Google Scholar] [CrossRef]
- Li, W.; Dong, M.; Lu, S.; Li, S.; Wei, L.; Huang, J.; Lu, J. Improved Measurement of the Calorific Value of Pulverized Coal Particle Flow by Laser-Induced Breakdown Spectroscopy (LIBS). Anal. Methods 2019, 11, 4471–4480. [Google Scholar] [CrossRef]
- Nguyen, H.; Bui, H.-B.; Bui, X.-N. Rapid Determination of Gross Calorific Value of Coal Using Artificial Neural Network and Particle Swarm Optimization. Nat. Resour. Res. 2021, 30, 621–638. [Google Scholar] [CrossRef]
- Onifade, M.; Lawal, A.I.; Aladejare, A.E.; Bada, S.; Idris, M.A. Prediction of Gross Calorific Value of Solid Fuels from Their Proximate Analysis Using Soft Computing and Regression Analysis. Int. J. Coal Prep. Util. 2022, 42, 1170–1184. [Google Scholar] [CrossRef]
- Lu, Z.; Mo, J.; Yao, S.; Zhao, J.; Lu, J. Rapid Determination of the Gross Calorific Value of Coal Using Laser-Induced Breakdown Spectroscopy Coupled with Artificial Neural Networks and Genetic Algorithm. Energy Fuels 2017, 31, 3849–3855. [Google Scholar] [CrossRef]
- Açikkar, M.; Sivrikaya, O. Prediction of Gross Calorific Value of Coal Based on Proximate Analysis Using Multiple Linear Regression and Artificial Neural Networks. Turk. J. Elec Eng. Comp. Sci. 2018, 26, 2541–2552. [Google Scholar] [CrossRef]
- Akhtar, J.; Sheikh, N.; Munir, S. Linear Regression-Based Correlations for Estimation of High Heating Values of Pakistani Lignite Coals. Energy Sources Part A Recovery Util. Environ. Eff. 2017, 39, 1063–1070. [Google Scholar] [CrossRef]
- Akkaya, A.V. Coal Higher Heating Value Prediction Using Constituents of Proximate Analysis: Gaussian Process Regression Model. Int. J. Coal Prep. Util. 2022, 42, 1952–1967. [Google Scholar] [CrossRef]
- Go, A.W.; Agapay, R.C.; Ju, Y.-H.; Conag, A.T. Unified Semi-Empirical Models for Predicting or Estimating the Heating Value of Coal and Related Properties—Theoretical Basis and Thermochemical Implications. Combust. Sci. Technol. 2020, 192, 1449–1474. [Google Scholar] [CrossRef]
- Chelgani, S.C.; Mesroghli, S.; Hower, J.C. Simultaneous Prediction of Coal Rank Parameters Based on Ultimate Analysis Using Regression and Artificial Neural Network. Int. J. Coal Geol. 2010, 83, 31–34. [Google Scholar] [CrossRef]
- Xu, N.; Wang, Z.; Dai, Y.; Li, Q.; Zhu, W.; Wang, R.; Finkelman, R.B. Prediction of Higher Heating Value of Coal Based on Gradient Boosting Regression Tree Model. Int. J. Coal Geol. 2023, 274, 104293. [Google Scholar] [CrossRef]
- Prasad, A.K.; Vinod, A.; Mishra, S.; Purkait, B.; Shukla, A.; Mukherjee, S.; Sarkar, B.C.; Varma, A.K. A Novel Multi-Model Method of Estimation of the Gross Calorific Value (GCV) in Coal Using Mid-Infrared Fourier Transform Infrared Spectroscopy. Indian Patent Application No. 202531012376, 28 February 2025. [Google Scholar]


| Sample No. | Moisture (wt%) | Ash (wt%) | Volatile Matter (wt%) | Fixed Carbon (wt%) | GCV (cal/g) |
|---|---|---|---|---|---|
| J_01 | 10.10 | 17.80 | 28.30 | 43.80 | 5294 |
| J_02 | 7.40 | 12.00 | 28.65 | 51.95 | 5301 |
| J_03 | 9.20 | 12.20 | 26.95 | 51.65 | 6021 |
| J_04 | 9.80 | 13.00 | 26.90 | 50.30 | 5866 |
| J_05 | 6.20 | 10.40 | 28.45 | 54.95 | 5892 |
| J_06 | 6.20 | 9.40 | 24.40 | 60.00 | 6467 |
| J_07 | 13.80 | 5.00 | 27.20 | 54.00 | 6771 |
| J_08 | 6.70 | 11.40 | 27.20 | 54.70 | 6114 |
| J_09 | 11.30 | 9.20 | 27.80 | 51.70 | 6191 |
| J_10 | 8.30 | 13.00 | 27.45 | 51.25 | 5691 |
| J_11 | 9.30 | 11.20 | 25.45 | 54.05 | 6001 |
| J_12 | 4.40 | 9.50 | 26.80 | 59.30 | 6447 |
| J_13 | 7.90 | 10.20 | 27.90 | 54.00 | 5943 |
| J_14 | 5.80 | 11.70 | 32.05 | 50.45 | 5665 |
| J_15 | 6.20 | 8.40 | 31.30 | 54.10 | 6317 |
| J_16 | 6.10 | 17.50 | 30.20 | 46.20 | 4879 |
| J_17 | 7.50 | 9.80 | 27.90 | 54.80 | 6105 |
| J_18 | 2.00 | 10.30 | 29.65 | 58.05 | 6398 |
| Mean | 7.678 | 11.222 | 28.031 | 53.069 | 5964.611 |
| Standard Error | 0.634 | 0.706 | 0.444 | 0.958 | 111.348 |
| Median | 7.450 | 10.800 | 27.850 | 54.000 | 6011.000 |
| Standard Deviation | 2.690 | 2.995 | 1.885 | 4.063 | 472.408 |
| Sample Variance | 7.234 | 8.969 | 3.554 | 16.512 | 223,169.781 |
| Range | 11.800 | 12.800 | 7.650 | 16.200 | 1892.000 |
| Minimum | 2.000 | 5.000 | 24.400 | 43.800 | 4879.000 |
| Maximum | 13.800 | 17.800 | 32.050 | 60.000 | 6771.000 |
| Peaks | Maximum | Onset | Termination | Functional Group & Bond Type | |
|---|---|---|---|---|---|
| P1 | 671.330 | 664.192 | 674.190 | Mercaptans and Thioethers | C-S |
| P2 | 694.187 | 674.190 | 718.470 | ||
| P3 | 755.607 | 725.613 | 769.893 | Phenyl trisubstituted | =C-H bending |
| P4 | 775.604 | 769.893 | 785.605 | ||
| P5 | 797.030 | 785.605 | 814.172 | ||
| P6 | 914.156 | 892.733 | 929.870 | Epoxides, Benzene ring substitution | C-O-C stretching, =C-H bending |
| P7 | 939.867 | 929.870 | 954.153 | ||
| P8 | 1011.285 | 1001.287 | 1021.284 | Alcohols, Ethers, Esters, Carboxylic acids, Anhydrides | C-O stretching |
| P9 | 1032.711 | 1021.284 | 1069.849 | ||
| P10 | 1099.844 | 1069.849 | 1108.415 | ||
| P11 | 1114.128 | 1108.415 | 1138.410 | ||
| P12 | 1164.121 | 1138.410 | 1179.833 | ||
| P13 | 1229.826 | 1179.833 | 1299.816 | ||
| P14 | 1368.378 | 1359.808 | 1374.091 | Alkanes | -CH3 |
| P15 | 1378.377 | 1374.091 | 1385.518 | ||
| P16 | 1389.803 | 1385.518 | 1395.517 | Phenol/Alcohol/Carboxylic acid | C-O-H bending |
| P17 | 1401.877 | 1395.517 | 1405.516 | ||
| P18 | 1413.545 | 1405.516 | 1416.943 | ||
| P19 | 1432.655 | 1416.943 | 1436.940 | ||
| P20 | 1441.225 | 1436.940 | 1448.367 | ||
| P21 | 1451.223 | 1448.367 | 1456.937 | Alkanes and Aromatic | Deformation vibration of CH3- and CH2-, vibration of aromatic hydrocarbon C=C skeleton |
| P22 | 1462.650 | 1456.937 | 1472.649 | ||
| P23 | 1492.646 | 1486.933 | 1495.503 | ||
| P24 | 1501.216 | 1495.503 | 1505.501 | ||
| P25 | 1512.643 | 1505.501 | 1518.357 | ||
| P26 | 1598.346 | 1585.490 | 1608.344 | Alkenes | C=C |
| P27 | 1611.201 | 1608.344 | 1615.486 | ||
| P28 | 1619.771 | 1615.486 | 1624.056 | ||
| P29 | 1628.341 | 1624.056 | 1634.055 | ||
| P30 | 1638.340 | 1634.055 | 1648.338 | ||
| P31 | 1652.624 | 1648.338 | 1671.192 | ||
| Peaks | Maximum | Onset | Termination | Functional Group & Bond Type | |
|---|---|---|---|---|---|
| P32 | 1675.477 | 1671.192 | 1682.619 | Ketones, Aldehydes, Carboxylic acids and Ester | C=O |
| P33 | 1691.190 | 1682.619 | 1696.903 | ||
| P34 | 1701.188 | 1696.903 | 1716.900 | ||
| P35 | 1721.185 | 1716.900 | 1732.612 | ||
| P36 | 1736.897 | 1732.612 | 1748.324 | ||
| P37 | 1775.463 | 1769.750 | 1779.748 | Anhydrides and Acyl halides | C=O |
| P38 | 1785.462 | 1779.748 | 1791.175 | ||
| P39 | 1802.602 | 1791.175 | 1808.316 | ||
| P40 | 2115.415 | 2108.274 | 2119.701 | Alkynes | ≡C-H |
| P41 | 2136.841 | 2128.271 | 2142.554 | ||
| P42 | 2162.552 | 2156.838 | 2165.408 | ||
| P43 | 2851.026 | 2821.303 | 2876.737 | Alkanes (Methyl and methylene symmetric and asymmetric stretching) | H-C-H |
| P44 | 2921.016 | 2876.737 | 2948.155 | ||
| P45 | 2958.154 | 2948.155 | 2982.436 | ||
| P46 | 3040.999 | 3008.147 | 3072.423 | Alkenes, Aromatic, Carboxylic acid | C=C-H, O-H |
| P47 | 3100.991 | 3072.423 | 3129.558 | ||
| P48 | 3219.545 | 3205.262 | 3223.831 | Alkynes, Carboxylic acid | ≡C-H, O-H |
| P49 | 3233.829 | 3223.831 | 3239.543 | ||
| P50 | 3245.256 | 3239.543 | 3250.970 | ||
| P51 | 3255.255 | 3250.970 | 3263.825 | ||
| P52 | 3275.252 | 3263.825 | 3282.394 | ||
| P53 | 3408.091 | 3289.536 | 3602.349 | Phenol/Alcohol/Carboxylic acid | O-H stretching |
| P54 | 3620.524 | 3602.349 | 3646.634 | ||
| P55 | 3652.342 | 3646.634 | 3660.912 | ||
| P56 | 3694.907 | 3660.912 | 3712.334 | ||
| n | PLR | PLSR | RFR | SVR | XGB | ANN | MME | |
|---|---|---|---|---|---|---|---|---|
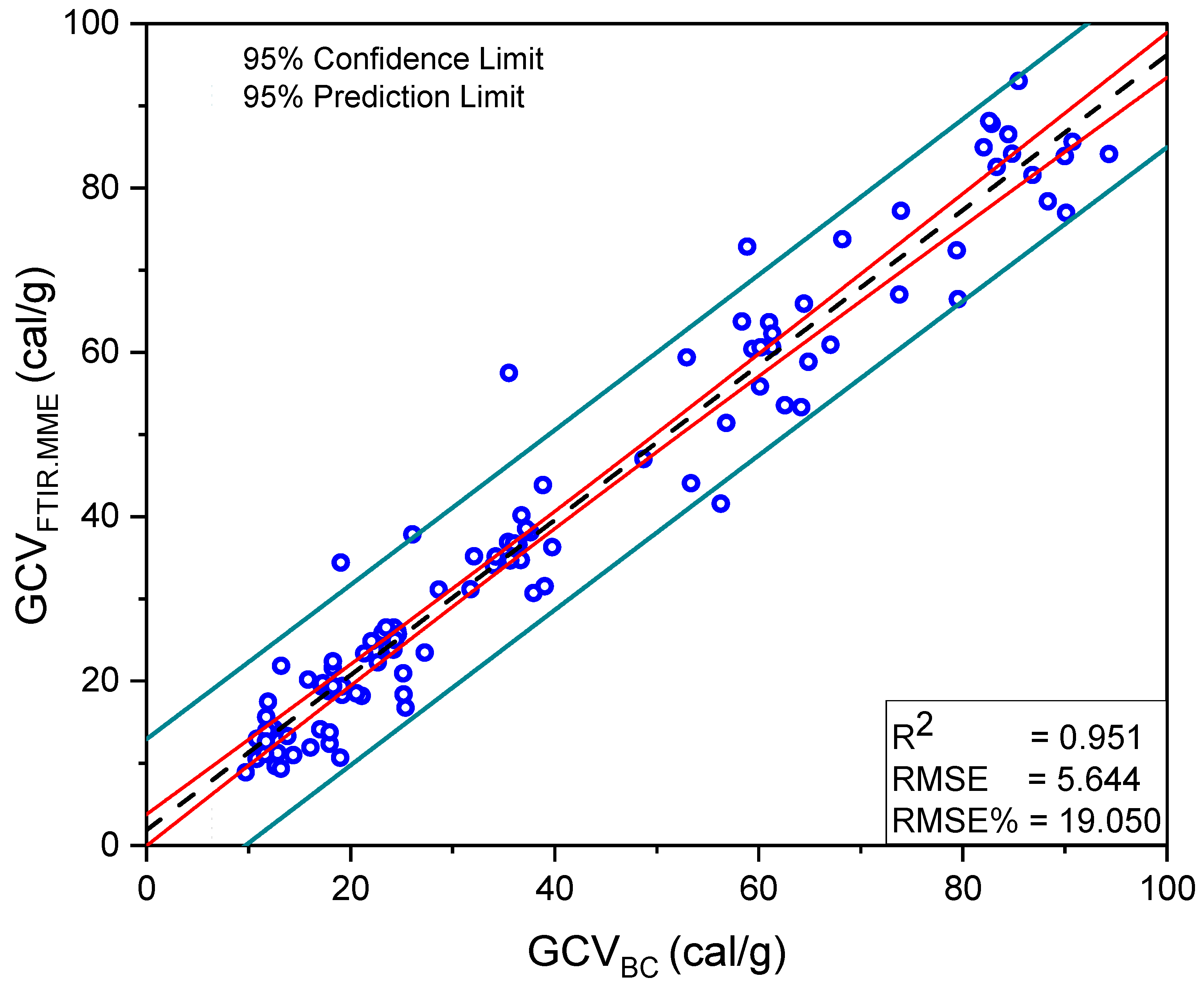
| R2 | 108 | 0.928 | 0.923 | 0.944 | 0.922 | 0.931 | 0.920 | 0.951 |
| RMSE, (cal/g) | 108 | 6.919 | 7.169 | 6.041 | 7.119 | 6.722 | 7.365 | 5.644 |
| RMSE, % | 108 | 27.595 | 27.489 | 19.837 | 22.429 | 20.159 | 20.937 | 19.050 |
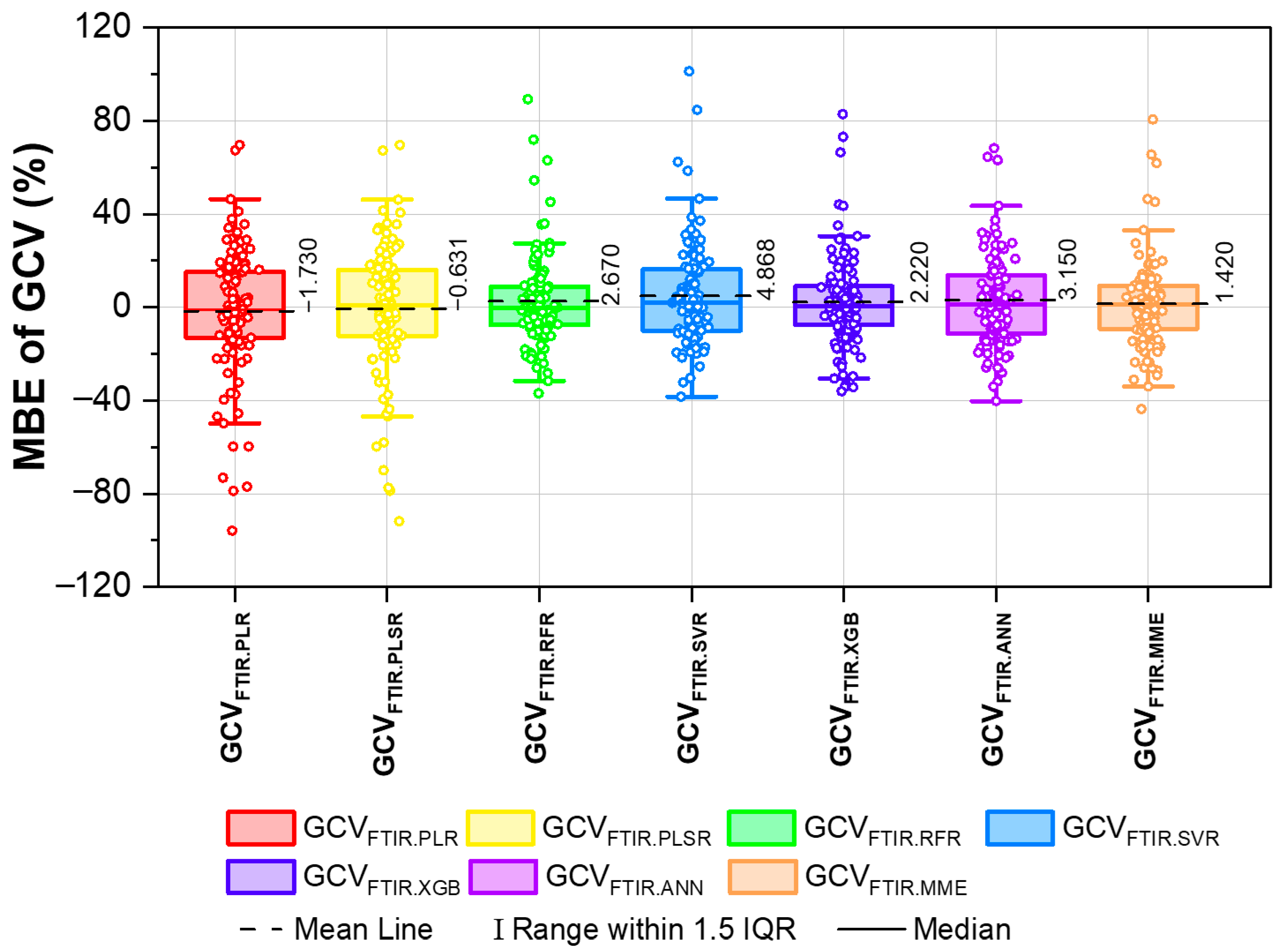
| MBE, (cal/g) | 108 | −0.646 | −0.302 | −0.132 | 0.237 | −0.575 | 0.418 | −0.336 |
| MBE, % | 108 | −1.730 | −0.631 | 2.670 | 4.868 | 2.220 | 3.150 | 1.420 |
| MAE, (cal/g) | 108 | 5.491 | 5.607 | 4.142 | 5.096 | 4.405 | 5.345 | 4.053 |
| t-Test: Paired Two Sample for Means, n = 108; df = 107, alpha = 0.01 | ||||||
|---|---|---|---|---|---|---|
| Pair | μ | σ2 | tstat | p-Value | tcritical | H0: μd = 0 |
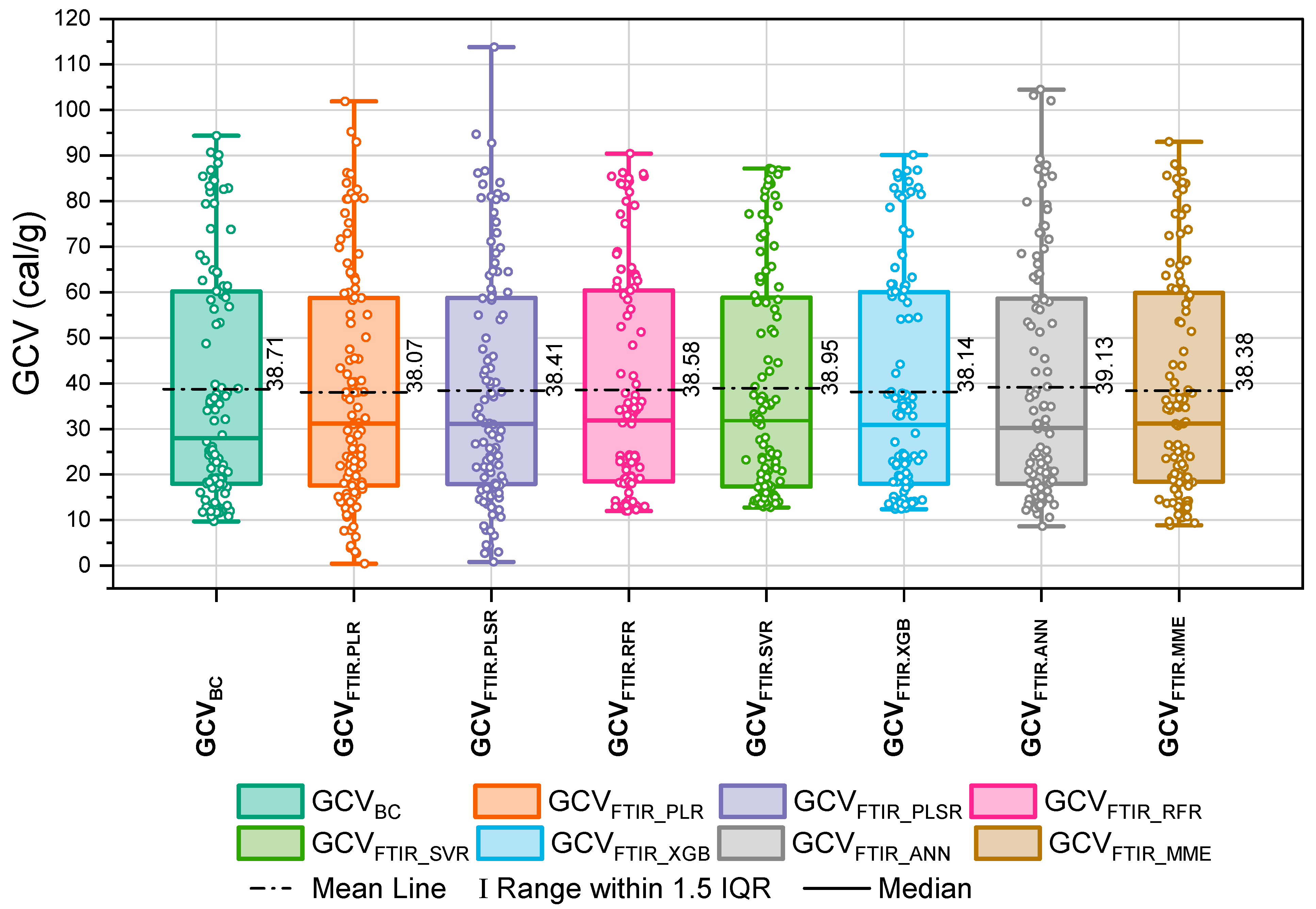
| GCVFTIR.PLR | 38.07 | 648.22 | 0.970 | 0.334 | 2.623 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.PLSR | 38.41 | 660.67 | 0.437 | 0.663 | 2.623 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.RFR | 38.58 | 615.20 | 0.226 | 0.822 | 2.623 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.SVR | 38.95 | 599.28 | −0.345 | 0.731 | 2.623 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.ANN | 39.13 | 676.00 | −0.588 | 0.558 | 2.623 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.XGB | 38.14 | 596.16 | 0.888 | 0.377 | 2.623 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.MME | 38.38 | 611.42 | 0.618 | 0.538 | 2.623 | True |
| GCVBC | 38.71 | 653.91 | ||||
| F-Test: Two Sample for Equality of Variance, n = 108, df = 107, alpha = 0.01 | ||||||
|---|---|---|---|---|---|---|
| Pair | μ | σ2 | Fstat | p-Value | CI | H0: σ2o = σ2p |
| GCVFTIR.PLR | 38.07 | 648.22 | 1.009 | 0.964 | 0.611, 1.666 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.PLSR | 38.41 | 660.67 | 0.990 | 0.958 | 0.599, 1.635 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.RFR | 38.58 | 615.20 | 1.063 | 0.753 | 0.644, 1.756 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.SVR | 38.95 | 599.28 | 1.091 | 0.653 | 0.661, 1.802 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.ANN | 39.13 | 676.00 | 0.967 | 0.864 | 0.586, 1.598 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.XGB | 38.14 | 596.16 | 1.097 | 0.633 | 0.664, 1.812 | True |
| GCVBC | 38.71 | 653.91 | ||||
| GCVFTIR.MME | 38.38 | 611.42 | 1.069 | 0.729 | 0.648, 1.766 | True |
| GCVBC | 38.71 | 653.91 | ||||
| SI. No | Method | No. of Sample | R2 | RMSE, MBE (cal/g) | RMSEP (cal/g) | MAE (cal/g) | Place (Ref.) |
|---|---|---|---|---|---|---|---|
| 1 | PLS with NIRS | 35 | 0.95 | - | 78.82 | - | China [79] |
| 2 | PLS with XRF | 35 | 0.94 | - | 93.15 | - | |
| 3 | PLS with NIRS-XRF (low-level fusion model) | 35 | 0.98 | - | 45.40 | - | |
| 4 | PLSR with NIRS-XRF (mid-level fusion model) | 35 | 0.99 | - | 38.20 | - | |
| 5 | PLS with LIBS | 16 | 0.99 | - | 109.4 | - | China [80] |
| 6 | Dominant factor-based PLS model with LIBS | 53 | 0.97 | 195.9 | 317.7 | - | China [18] |
| 7 | PLS with LIBS | 45 | 0.99 | - | 53.70 | 47.80 | China [31] |
| 8 | PLS with NIRS | 45 | 0.99 | - | 64.50 | 55.90 | |
| 9 | PLS with LIBS & NIRS | 45 | 0.99 | - | 45.90 | 40.10 | |
| 10 | MLR with Proximate parameters | 77 | 0.72 | 217.3 | - | 2.51% | India [2] |
| 11 | SVR with Proximate parameters | 77 | 0.96 | 174.4 | - | 1.58% | |
| 12 | RFR with Proximate parameters | 77 | 0.97 | 143.3 | - | 1.38% | |
| 13 | XGBoost with Proximate parameters | 77 | 0.99 | 31.0 | - | 0.32% | |
| 14 | MLR with Proximate parameters | 43 | 0.84 | 542.2 | - | 5.24% | India [27] |
| 15 | MLR with Vis-NIR spectra | 43 | 0.92 | 391.7 | - | 4.85% | |
| 16 | PSO-ANN with proximate analysis | 2583 | 0.96 | 182.5 | - | 0.016 | Vietnam [81] |
| 17 | ANFIS with proximate analysis | 32 | 0.99 | - | - | 2.04% | Vietnam [82] |
| 18 | ANN with proximate analysis | 32 | 0.99 | - | - | 683.8 | |
| 19 | MLR with proximate analysis | 32 | 0.99 | - | - | 3.55% | |
| 20 | SVR with LIBS | 550 | 0.9 | - | 293.80 | 0.91% | China [20] |
| 21 | SVR combined PCA model with LIBS | 550 | 0.91 | - | 203.00 | 0.65% | |
| 22 | K-ELM model based on PSO with LIBS | 28 | 0.99 | - | 167.20 | - | China [22] |
| 23 | WT-MIV-KELM combined with LIBS | 28 | 0.99 | - | 146.90 | - | China [23] |
| 24 | GA-optimized ANN combined with LIBS | 27 | 0.96 | 64.5 | - | 93.10 | China [83] |
| 25 | KELM combined with LIBS | 28 | 0.96 | - | 300.60 | - | China [24] |
| 26 | V-WSP-KELM with LIBS | 28 | 0.96 | - | 237.30 | - | |
| 27 | PSO-KELM with LIBS | 28 | 0.97 | - | 167.20 | - | |
| 28 | WT-KELM with LIBS | 28 | 0.96 | - | 237.30 | - | |
| 29 | WT-MIV-KELM with LIBS | 28 | 0.98 | - | 146.90 | - | |
| 30 | WT-PSO-KELM with LIBS | 28 | 0.98 | - | 116.70 | - | China [24] |
| 31 | MC-UVE-KELMwith LIBS | 28 | 0.97 | - | 432.50 | - | |
| 32 | V-WSP-PSO-KELM with LIBS | 28 | 0.99 | - | 84.40 | - | |
| 33 | MVR-Proximate | 6339 | 0.97 | - | - | - | USA [64] |
| 34 | RF−Proximate | 6339 | 0.97 | - | - | - | |
| 35 | MVR-Ultimate | 6339 | 0.99 | - | - | - | |
| 36 | RF-Ultimate | 6339 | 0.99 | - | - | - | |
| 37 | RF combined with XRF & proximate analysis | 181 | 0.99 | 0.026 | - | - | China [17] |
| 38 | MLR with proximate analysis | 6520 | 0.97 | 205.4 | - | 148.10 | Türkiye [84] |
| 39 | MLP with proximate analysis | 6520 | 0.98 | 155.2 | - | 112.30 | |
| 40 | GRNN with proximate analysis | 6520 | 0.98 | 152.9 | - | 109.90 | |
| 41 | RBFNN with proximate analysis | 6520 | 0.99 | 148.1 | - | 105.10 | |
| 42 | MLR with proximate analysis | 32 | 0.99 | - | - | 0.90% | Pakistan [85] |
| 43 | MLR with proximate analysis | 8525 | 0.98 | 206.6 | - | 142.60 | Türkiye [86] |
| 44 | GPR with proximate analysis | 8525 | 0.98 | 183.2 | - | 128.40 | |
| 45 | MLR with proximate analysis & ultimate analysis | 8500 | 0.99 | 62.1 | - | 0.88% | Philippines [87] |
| 46 | MLR with proximate analysis | 1018 | 0.69 | - | - | - | USA [88] |
| 47 | ANN with proximate analysis | 1018 | 0.84 | - | - | - | |
| 48 | GRBT with proximate analysis | 6703 | 0.99 | - | - | 110.40 | USA [89] |
| 49 | GRBT with proximate analysis | 1779 | 0.95 | - | - | 124.00 | |
| 50 | Decision tree with proximate & ultimate analysis | 6582 | 0.99 | 18,634.8 (MSE) | 74.06 | USA [76] | |
| 51 | Bagging with proximate & ultimate analysis | 6582 | 1.00 | 11,658.4 (MSE) | 56.50 | ||
| 52 | Random forest with proximate & ultimate analysis | 6582 | 1.00 | 11,320.5 (MSE) | 55.83 | ||
| 53 | Extra trees with proximate & ultimate analysis | 6582 | 1.00 | 8905.9 (MSE) | 50.72 | ||
| 54 | Adaptive boosting with proximate & ultimate analysis | 6582 | 0.98 | 63,211.7 (MSE) | 149.44 | ||
| 55 | Gradient boosting with proximate & ultimate analysis | 6582 | 1.00 | 12,491.7 (MSE) | 62.11 | ||
| 56 | XGBoost with proximate & ultimate analysis | 6582 | 1.00 | 8168.5 (MSE) | 49.56 | ||
| 57 | SVM with proximate & ultimate analysis | 3344 | 0.99 | 14.689 (MSE) | 44.40 | USA [78] | |
| 58 | RFR with proximate & ultimate analysis | 3344 | 0.99 | 16.767 (MSE) | 46.96 | ||
| 59 | GBRT with proximate & ultimate analysis | 3344 | 0.99 | 14.522 (MSE) | 44.33 | ||
| 60 | XGB with proximate & ultimate analysis | 3344 | 0.99 | 13.519 (MSE) | 42.59 | ||
| 61 | MLR with proximate analysis | 50 | 0.763 | 805.389 | - | 713.67 | South Africa [77] |
| 62 | SVR with proximate analysis | 50 | 0.734 | 2498.329 | - | 2403.96 | |
| 63 | ANN with proximate analysis | 50 | 0.564 | 2152.719 | - | 1560.62 | |
| 64 | GRA-CMLM with proximate analysis | 50 | 0.909 | 636.525 | - | 530.72 | |
| 65 | SAE-CMLM with proximate analysis | 50 | 0.919 | 679.756 | - | 574.19 | |
| 66 | WAM-CMLM with proximate analysis | 50 | 0.918 | 674.740 | - | 569.17 | |
| 67 | FTIR with PLR | 108 | 0.93 | 6.919, −0.646 | - | 5.49 | India Present study [90] |
| 68 | FTIR with PLSR | 108 | 0.92 | 7.169, −0.302 | - | 5.61 | |
| 69 | FTIR with RFR | 108 | 0.94 | 6.041, −0.132 | - | 4.14 | |
| 70 | FTIR with SVR | 108 | 0.92 | 7.119, 0.237 | - | 5.10 | |
| 71 | FTIR with XGB | 108 | 0.93 | 6.722, −0.575 | - | 4.40 | |
| 72 | FTIR with ANN | 108 | 0.92 | 7.365, 0.418 | - | 5.35 | |
| 73 | FTIR with MME | 108 | 0.95 | 5.644, −0.336 | - | 4.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinod, A.; Prasad, A.K.; Mishra, S.; Purkait, B.; Mukherjee, S.; Shukla, A.; Sarkar, B.C.; Varma, A.K. Gross Calorific Value Estimation in Coal Using Multi-Model FTIR and Machine Learning Approach. Appl. Sci. 2025, 15, 12209. https://doi.org/10.3390/app152212209
Vinod A, Prasad AK, Mishra S, Purkait B, Mukherjee S, Shukla A, Sarkar BC, Varma AK. Gross Calorific Value Estimation in Coal Using Multi-Model FTIR and Machine Learning Approach. Applied Sciences. 2025; 15(22):12209. https://doi.org/10.3390/app152212209
Chicago/Turabian StyleVinod, Arya, Anup Krishna Prasad, Sameeksha Mishra, Bitan Purkait, Shailayee Mukherjee, Anubhav Shukla, Bhabesh Chandra Sarkar, and Atul Kumar Varma. 2025. "Gross Calorific Value Estimation in Coal Using Multi-Model FTIR and Machine Learning Approach" Applied Sciences 15, no. 22: 12209. https://doi.org/10.3390/app152212209
APA StyleVinod, A., Prasad, A. K., Mishra, S., Purkait, B., Mukherjee, S., Shukla, A., Sarkar, B. C., & Varma, A. K. (2025). Gross Calorific Value Estimation in Coal Using Multi-Model FTIR and Machine Learning Approach. Applied Sciences, 15(22), 12209. https://doi.org/10.3390/app152212209








