1. Introduction
Mineral resources are an important material foundation for the economic and social development of human society [
1]. As easily accessible resources at shallow depths are gradually depleted, the mining depth is constantly increasing. The traditional open-pit mining method is facing severe challenges in terms of economic and technical feasibility, which prompts an increasing number of mines to transition in a gradual manner to underground mining production [
2,
3,
4]. This transformation not only extends the life of the mine and improves the recovery rate of resources but also to some extent reduces land occupation and ecological damage [
5,
6]. However, during the transition from open-pit to underground mining, the stress environment and structural state of the rock mass in the mine become more complex. Subsequent underground mining further disturbs the original stress balance, easily causing geological disasters such as slope instability, rock mass failure, and surface subsidence [
7,
8]. Therefore, systematically revealing the movement law of rock strata under the condition of the transition from open-pit to underground mining is of great theoretical and engineering significance for ensuring the safe and efficient mining of mines [
9,
10,
11].
Regarding the problems of slope instability, rock mass failure, and surface subsidence caused by the transition from open-pit to underground mining, scholars worldwide have conducted extensive research and achieved certain results [
12,
13]. Existing studies have shown that the stress redistribution, unloading effects, and deformation of the goaf caused by underground mining are the main factors affecting the stability of slopes and the evolution of surface subsidence [
14]. To ensure the reliability of the design for the transition from open-pit to underground mining, Wang Mingze et al. [
15] conducted an inverse analysis of the geological stress field in the mining area by combining geological and stress field measurement methods, and integrated historical mining data to provide reliable mine-scale geological stress conditions for the Jwaneng Mine. Similarly, Dintwe et al. [
10] investigated the rock mechanics problems during the transition from open-pit to underground mining at the Berezit gold–silver polymetallic deposit. They used numerical simulation methods to thoroughly explore the stress state of the rock mass at each mining stage. They evaluated the relevant parameters of the underground mining system using the Matthews graphical method and analytical relationships.
To study the rock mass movement and instability caused by underground mining under an open-pit slopes, Zhang, L. et al. [
16] proposed a double-slip surface deflection failure model for open-pit to underground mining, and based on the limit equilibrium state determined by the vector sum method, they derived the critical values of the area of the sliding body and the position of the double sliding surface. It was found that the boundary of the rock mass movement deviated under the condition of transitioning from open-pit to underground mining. The failure mode was that the towed landslide was transmitted from the goaf to the surface, which was different from the uneven settlement caused by underground mining.
Wang et al. [
17] used PFC to invert the entire process from overburden rock mass collapse to surface settlement. They explained the evolution mechanism of surface collapse from aspects such as fracture evolution, displacement variation, and force chain distribution. Meanwhile, multi-source monitoring technologies, including GPS, InSAR, microseismic monitoring, and unmanned aerial vehicle (UAV) remote sensing, have provided effective tools for dynamic monitoring of slopes and goaf areas, demonstrating promising applications in early warning, prevention, and control [
18,
19]. Although existing studies have achieved some results regarding open-pit slopes and underground mining-induced effects, the research on the response of deep rock masses, the movement patterns of rock strata during the transition from open-pit to underground mining, and the coupling effects of underground mining activities remains insufficient. Moreover, the underlying mechanisms have not been fully elucidated.
Sijiaying Iron Mine, situated in North China, is a typical large-scale metal mine transitioning from open-pit to underground mining. The deposit of this mine is located at a depth of 1000 m and has the conditions for both shallow open-pit and deep underground resource exploitation. Since the southwest side of the open-pit is adjacent to the Pingqingle Provincial Highway and the east side is close to the New Luan River, the planar expansion of open-pit mining is restricted. The mining method of the deposit is facing a transition from open-pit to underground mining. Moreover, after the transition to underground mining, controlling rock strata movement during the mining process becomes a key issue that needs to be focused on in this mine. Therefore, taking Sijiaying Iron Mine as the research object, this paper analyzes the influence law of underground mining on the deformation and evolution of slope rock mass based on numerical simulation, reveals the coupling mechanism of rock strata movement and slope stability under the transition from open-pit to underground mining conditions, and determines the parameters of rock movement angle and collapse angle through horizontal, vertical and surface inclination deformation indicators, and then proposes the reasonable monitoring and protection measures. The research results will provide a theoretical foundation for safe and efficient mining at Sijiaying Iron Mine and offer reference value for slope stability control in similar large-scale metal mines during the transition from open-pit to underground mining.
2. Rock Mass Deformation Parameters and Associated Evaluation Methods
For quantitatively characterizing the deformation responses of the surface and rock mass during the transition from open-pit to underground mining, three deformation indicators—namely, horizontal deformation, vertical deformation, and surface inclination deformation—are employed to describe the spatial deformation features and mechanical behavior of the rock mass under mining-induced disturbances.
2.1. Definition and Calculation Method of Deformation Index
2.1.1. Horizontal Deformation
Horizontal deformation is defined as the ratio of the horizontal displacement difference between the adjacent observation points to the horizontal distance between these two points. It is denoted as
εab and reflects the relative horizontal displacement per unit length. Mechanically, it indicates the tensile or compressive state of the rock mass under mining-induced disturbances. When
εab > 0, the rock mass is in a state of extension, typically observed at inflection points and boundary zones of moving basins. Conversely, when
εab < 0, the rock mass experiences compression, which is more commonly found between inflection points within basins. The calculation formula is as follows:
where
Ua and
Ub represent the horizontal displacements of surface observation points a and b, respectively, in meters;
lab denotes the horizontal distance between these two points, in meters.
2.1.2. Vertical Deformation
Vertical deformation is used to assess the surface subsidence caused by underground mining activities. It is defined as the ratio
εz of the vertical displacement difference between adjacent measurement points to their vertical spacing, reflecting the vertical displacement gradient per unit depth of the rock mass. When
εz > 0, it indicates that the rock mass has undergone collapse deformation, primarily distributed in the central region of the mobile basin. In contrast, when
εz < 0, the rock mass remains in an elastic state, where the deformation has not yet reached the critical threshold, typically located at the basin’s periphery. The calculation formula is:
where Δ
V represents the difference in vertical displacement between adjacent measurement points, in meters; Δ
H denotes the perpendicular distance between these points, in meters.
2.1.3. Surface Inclination Deformation
Surface inclination deformation is defined as the ratio of the vertical displacement difference between adjacent observation points to the horizontal distance between them, denoted as
iab. It reflects the variation in surface slope and the potential for overturning. On the inclination profile, inclining is considered positive in the upward direction along the inclination direction of the ore body and negative in the downward direction. On the strike profile, a rightward inclining is defined as positive, while a leftward inclining is negative. The calculation formula is:
where
Wa and
Wb represent the subsidence values at surface observation points a and b, respectively, in meters. The rest of the symbols are the same as before.
2.2. Calculation Methods for Rock Strata Movement Angle and Collapse Angle
In the operation process following the transition from open-pit to underground mining, as the working face advances, the surface subsidence basin gradually expands. Eventually, it evolves into a mobile basin that extends beyond the boundaries of the goaf area. This development reflects the continuous disturbance and cumulative deformation effects of underground mining on the surface rock mass. To quantify the extent of surface movement, the concept of the rock movement angle is introduced.
Under fully active mining conditions, the rock movement angle
θ1 is defined as the angle formed between two lines: the line connecting the critical deformation point on the main section of the basin and the boundary point of the goaf, and the horizontal line. This angle serves to characterize both the extent of mining influence and the boundary of slope disturbance. Moreover, it reflects the contribution of the horizontal displacement of rock strata to the expansion of the surface movement range. The formula for calculating this angle is presented as follows:
where
L1 represents the horizontal distance between the moving boundary and the ore body boundary in meters, the rest of the symbols are the same as before.
The rock collapse angle
θ2 is defined as the angle formed between the subsidence boundary of the goaf and the ore body boundary. This parameter serves to characterize the overall instability boundary of the rock mass, as well as the mechanism behind its vertical collapse. The corresponding calculation formula is expressed as follows:
where
L2 represents the horizontal distance between the moving boundary and the ore body boundary, in meters, the rest of the symbols are the same as before.
The rock movement angle and collapse angle are not only geometric parameters but also reveal the deformation transfer and vertical collapse mechanisms of the rock mass under mining disturbance. Specifically, the movement angle reflects the expansion capacity of horizontal displacement. In contrast, the collapse angle indicates the critical conditions for the overall instability of the rock mass in the open face.
3. Mechanical Modeling of Rock Strata Stability for Mining in the Transition from Open-Pit to Underground
3.1. Proposed Mining Plan of the Mine
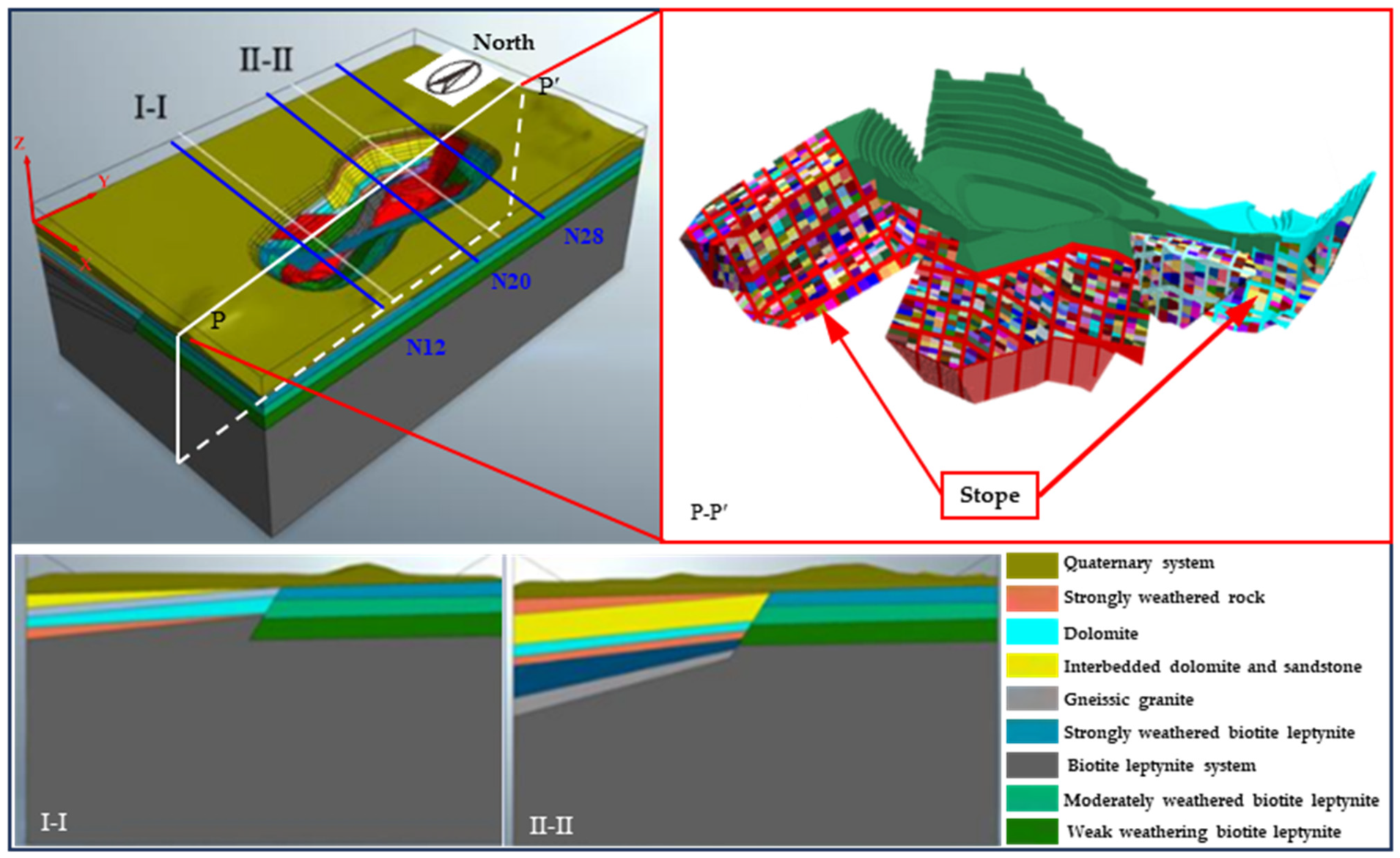
According to the feasibility study report and previous research findings, to effectively prevent surface settlement and collapse, considering the ore body’s geological characteristics, the open-stope mining with subsequent filling method will be adopted during the transition from open-pit to underground mining at Sijiaying Mine. The deposit development follows a panel layout method, which is divided into several panels along the strike of the ore body. Each panel measures 120 m in length and 60 m in height. The panel area is further subdivided into multiple ore blocks, each with a width of 20 m, a height of 60 m, and a length determined by the thickness of the ore body [
20]. Vertically, the deposit was divided into two mining areas. The lower mining area extends from −820 m to −460 m, while the upper mining area starts at −460 m and continues until the top of the ore body. The mining process is simulated level by level from bottom to top in each mining area, and each level follows a sequential process of “extraction–filling”.
To ensure overall stability, a slope boundary pillar with a thickness of 40 m and a bottom pillar of 45 m is designed and reserved during the mining process, transitioning from open-pit to underground [
21,
22]. In the process of the numerical simulation, the mining sequence follows the principle of “advancing from the center of the strike to both its wings and from the hanging wall to the foot wall of the ore body”. The first-step stopes are mined using the “mining one stope at intervals” approach, and the goaf is filled with a cement-tailings ratio of 1:6; the second-step stopes are mined in the way of “mining one stope at intervals of three stopes” followed by cemented backfill with a cement-tailings ratio of 1:10.
3.2. Numerical Model Establishment and Mechanical Parameters
3.2.1. Establishment of Numerical Models
To accurately simulate the behavior of rock strata during the transition from open-pit to underground mining, a coupled modeling approach using Midas GTS NX 2021 and FLAC3D 6.0 is employed. Midas GTS NX excels in handling the detailed geometric modeling of complex terrains, whereas FLAC3D is particularly effective in simulating the nonlinear mechanical responses induced by mining activities. The integration of both tools ensures high geometric accuracy and a realistic representation of mechanical response.
The numerical model was developed based on the distribution of the ore body and the geomechanical characteristics of the open-pit slope. The model utilizes a hybrid grid partitioning approach to strike a balance between computational efficiency and accuracy. The local mesh refinement is carried out in key deformation areas, with a gradual transition in element size. The minimum mesh size is 10 m × 10 m × 10 m, ensuring high-fidelity stress and deformation predictions in these critical areas. The in situ stress field within the study area is relatively simple, predominantly governed by gravitational loading. The model boundary conditions are set as follows: normal displacement constraints are applied on the lateral boundaries (in the x and y directions), and the bottom (in the z direction) is fixed. This simplified boundary configuration is justified by the prevailing engineering geological conditions, designed to effectively approximate the mechanical behavior of mining activities in an infinite medium. Subsequent analyses demonstrate that the primary simulation results are not significantly influenced by variations in boundary conditions located distal to the mining zone.
To ensure accurate representation of the initial geomechanical state, the numerically simulated in situ stress distribution was calibrated against limited field measurements. Through inverse analysis, key rock mass parameters were adjusted, thereby establishing a reliable basis for subsequent simulations of mining-induced disturbances. The established three-dimensional numerical model is illustrated in
Figure 1.
3.2.2. Mechanical Parameters
The mechanical parameters of the rock mass and the backfill body were derived from laboratory experiments and field investigations carried out by some of the authors of this paper. These parameters were further optimized and calibrated through numerical inversion to ensure that simulation results closely reflect actual engineering conditions. The final mechanical parameters for the ore, backfill body, and surrounding rock are summarized in
Table 1.
4. Deformation Law of Rock Strata in Mining Transition from Open-Pit to Underground
4.1. Characteristics of the Open-Pit Slope Displacement Field
Quantitative analysis of the slope displacement field provides a clear understanding of the spatial distribution characteristics of rock mass deformation and its primary controlling factors, offering fundamental data for subsequent studies on subsidence ranges affected by mining activities and the determination of rock movement and collapse angles. When the underground mining reached the final design stage, numerical simulation results revealed the displacement field distributions in the
x,
y, and
z-directions, as illustrated in
Figure 2.
As shown in
Figure 2, the displacement fields in different directions exhibit significant variation, and also allow for the observation of the following characteristics:
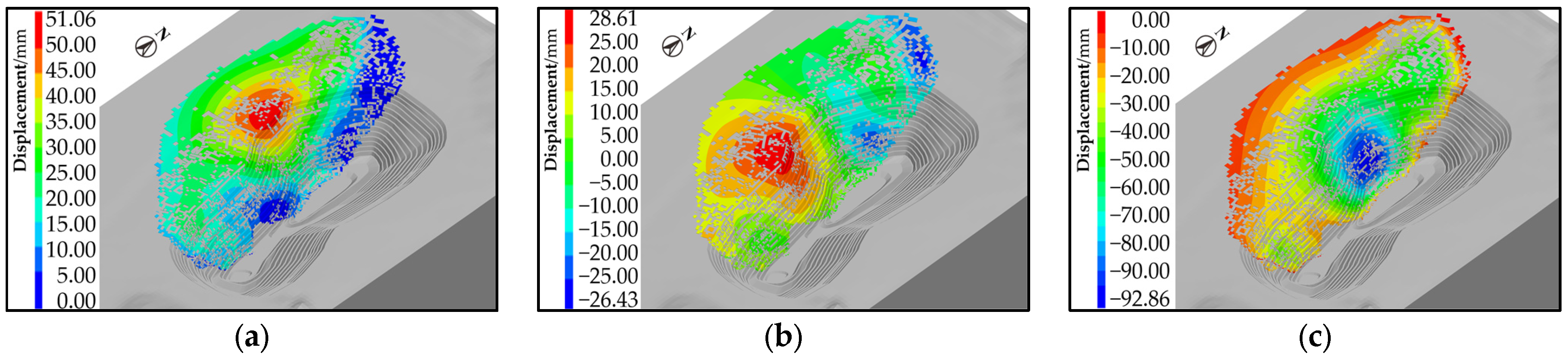
A shear slip trend along the slope surface of the open-pit characterizes the x-direction displacement field. The displacement concentration zone (>30 mm) is a spindle-shaped distributed zone between the exploration lines N20 and N28. The most intense rock mass sliding occurs between the exploration lines N22 and N26, reaching a peak of 51.06 mm. This area lies above the main underground mining goaf beside the west side of the open-pit, indicating that the combined effect of stress unloading on the abandoned face and the geometric configuration of the goaf primarily controls the formation of the shear slip zone;
In the y-direction, the rock mass shows deformation trends toward the open-pit slope surface on both sides of the underground mining goaf. The displacement concentration zone (>20 mm) is mainly distributed between exploration lines N18 and N22, as well as in the surrounding rock overlying the ore body in the northwest. The peak of displacement reaches 28.61 mm, indicating concentrated deformation of the surrounding rock toward the goaf;
In the z-direction, the overlying rock mass above the goaf experiences significant settlement. The displacement concentration zone (>50 mm) is primarily located on the west side of the open-pit and above the underground mining goaf. The most pronounced settlement occurs in the central part of the slope between exploration lines N22 and N26, with a peak of 92.86 mm, forming a spindle-shaped collapse zone that reflects the overall subsidence trend of the overlying rock mass.
These observations indicate that slope displacement is governed by both the geometric configuration of the underground mining goaf and the stress release at the open-pit surface. The spatial distribution of displacements in different directions provides a quantitative basis for determining the angle of rock stratum movement and the subsidence zone.
4.2. Deformation Distribution Characteristics in the Mining-Affected Area
4.2.1. Displacement Characteristics of the Mining Influence Zone
To accurately define the influence range of mining, a displacement feature unit extraction algorithm was developed using the FISH language. During the extraction process, anomalous deformation factors, such as floor protrusion, were excluded to ensure the accuracy of the identification results. The displacement distribution of the extracted feature units is presented in
Figure 3.
As shown in
Figure 3, the extracted feature units effectively represent the displacement characteristics in the
x,
y, and
z-directions and accurately reflect the abrupt changes in displacement gradients within the mining-affected area.
The spatial distribution of the displacement vector field influenced by underground mining, obtained through numerical simulation, is illustrated in
Figure 4.
As illustrated in
Figure 4, the displacement vector distribution of the open-pit slopes and the surface exhibits the following patterns:
In the high-displacement gradient zone (red area in
Figure 4), the slope demonstrates a clear tendency toward collapse and failure. The convergence direction of the displacement vectors is highly consistent with that of the
z-direction displacement settlement zone, indicating a failure mechanism dominated by settlement;
In the dominant slip deformation area (green area in
Figure 4), the displacement vectors point toward the geometric center of the goaf. The spatial location of the abrupt change zone in the inclination angle of the slope top vectors coincides closely with the concentrated zone of shear strain, suggesting that shear slip is the primary deformation mode in this region;
The spatial distribution of the displacement vector field aligns well with the previously extracted deformation features, effectively validating the rationality and reliability of the method used to define the mining influence zone based on displacement field characterization parameters;
The peak value of total displacement reaches 92.86 mm.
4.2.2. Deformation Characteristics of the Mining-Induced Influence Zone
To elucidate the deformation behavior of the mining-induced influence zone during the transition from open-pit to underground mining, an analysis was conducted based on the directional distribution of the deformation field. Using FISH language programming to enable automated deformation unit calculations, it was determined that the mining-induced influence zone exhibits spatially heterogeneous deformation characteristics during the transition process. In the following content, the scale of the coordinate axes is consistent with the coordinate system of the model unit (see
Figure 1).
To accurately reflect the characteristics of the displacement and deformation fields, the subsequent analysis of the displacement field uses the positive and negative signs of the data solely to indicate the direction of rock mass movement along the respective coordinate axes. In the context of deformation field analysis, positive and negative values serve only to denote whether the deformation is associated with compressive or tensile stress, respectively.
By extracting the displacement fields in the
x and
y-directions on a 10 m horizontal plane and applying the horizontal deformation gradient algorithm, the horizontal deformation distribution characteristics of the mining-induced influence zone were obtained, as shown in
Figure 5.
As shown in
Figure 5, the horizontal displacement and deformation fields in the
x and
y-directions exhibit the following patterns:
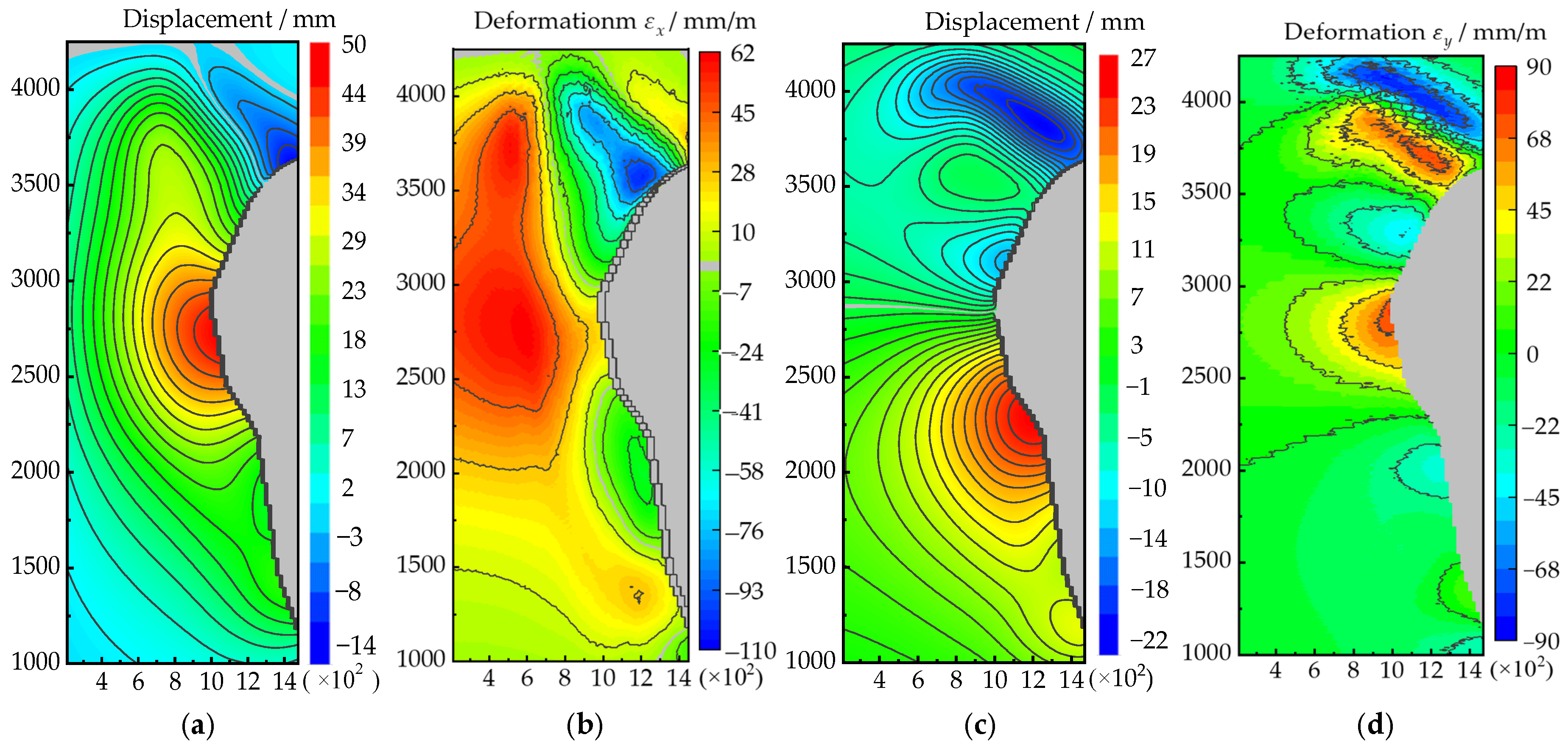
In the x-direction, the movement caused by mining shows significant non-uniformity, with regions of larger cumulative displacement displaying relatively smaller horizontal deformation gradients. Additionally, a distinct high-deformation gradient zone has formed in the northwest ore-rock contact zone, where the maximum horizontal deformation reaches 110 mm. This “large displacement–small deformation” pattern reveals the coupling mechanism between the slip plane misalignment and the overall deformation.
In the y-direction, the high-deformation gradient zone displays notable spatial agglomeration, reflecting the presence of evident spatially heterogeneous deformation characteristics within the mining-induced influence zone, specifically, in the range of exploration line N18 to N22, the high-deformation gradient zone is distributed in a band-like manner along the slope direction, with the maximum horizontal deformation reaching 90 mm, primarily concentrated within the engineering geological units of this section. The displacement of the surrounding rock overlying the ore body in the northwest varies significantly. The high-deformation gradient zone is distributed in strip-like formations, with a maximum deformation gradient of 72. These observations indicate a strong spatial coupling between the two types of high-deformation gradient zones and the overall displacement region, revealing the spatial correlation mechanism between displacement and deformation.
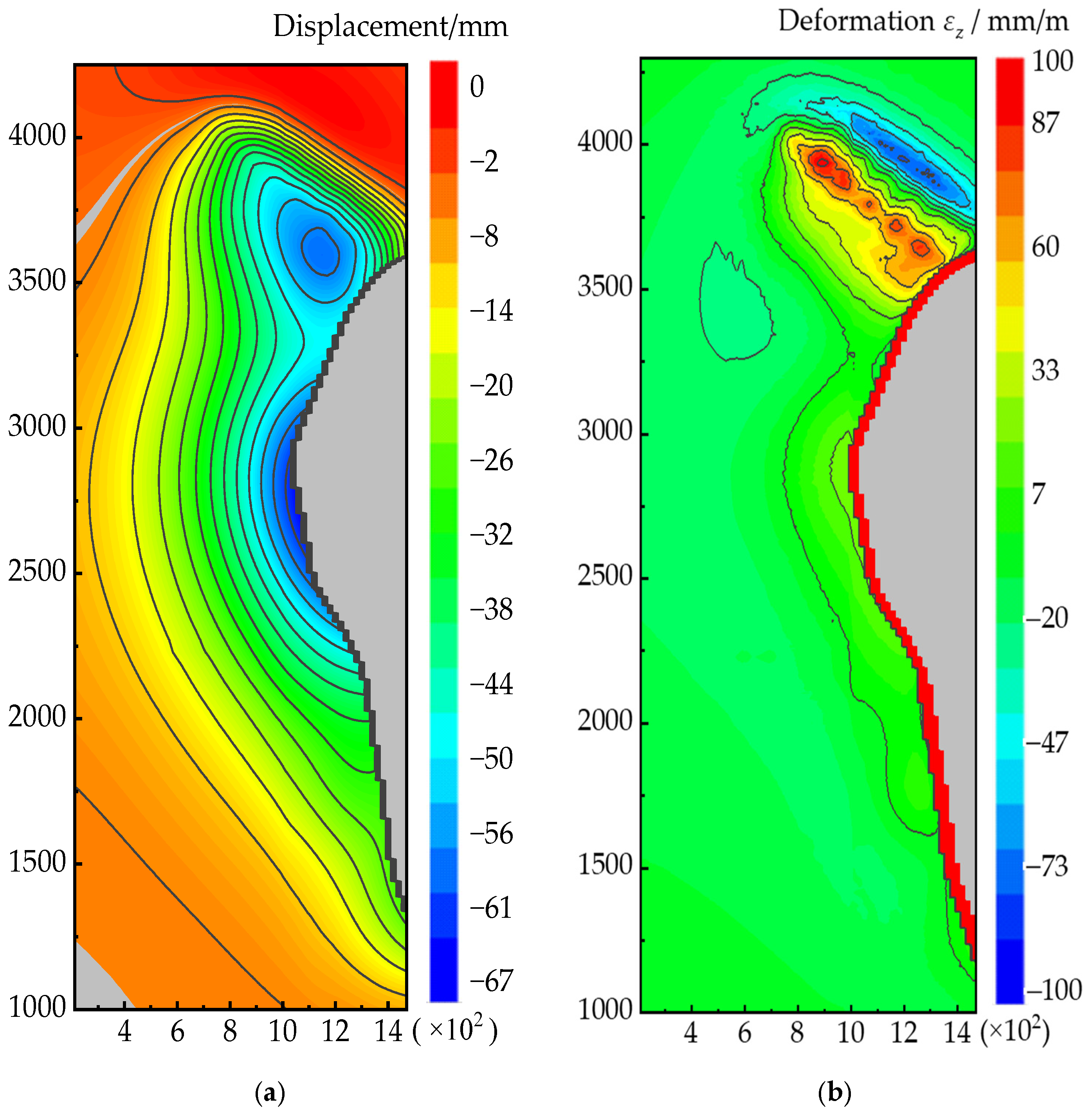
Regarding the inclination deformation, by extracting the
z-direction displacement field on the +10 m horizontal plane and applying the inclining deformation gradient algorithm, the distribution characteristics of the surface inclination deformation within the mining-affected area were obtained, as shown in
Figure 6.
As shown in
Figure 6, the mining-induced movement exhibits clear spatial non-uniformity, with a distinct correspondence between large-displacement zones and low-deformation gradient zones, reflecting the stage-slip coupling mechanism of the slope under mining disturbance. A high-deformation gradient zone forms in the northwest ore-rock contact zone, with the maximum declined deformation reaching 200 mm.
By extracting the
z-direction displacement field on the −30 m horizontal plane and applying the declined deformation gradient algorithm, the vertical deformation distribution characteristics of the sampling influence zone were obtained, as presented in
Figure 7.
As shown in
Figure 7, the mining-induced displacement exhibits significant spatial non-uniformity, with larger cumulative displacement zones showing relatively smaller deformation gradients. Notably, the northwest ore-rock contact zone forms a distinct high-deformation gradient zone, where the maximum vertical deformation reaches 100 mm.
Based on three-dimensional numerical simulation results and using FISH language programming to automate deformation unit calculations, the distribution characteristics of the total deformation field within the mining influence zone were obtained, as shown in
Figure 8.
As shown in
Figure 8, the high-deformation gradient zone is primarily distributed in the surrounding rock and open-pit slopes overlying the western mining units underground, particularly in the subsidence zone of the exploration line N22 to N26, where the maximum deformation value reaches 328 mm. This high-deformation zone exhibits a significant spatial coupling relationship with the displacement concentration zone, revealing the distinct spatial differentiation characteristics of slope deformation. The peak value of total deformation reaches 3.28 mm/m.
4.3. Analysis of Rock Movement Angle and Collapse Angle
Based on the analysis of the mining influence range and combined with the deformation patterns of the open-pit slope and the ground surface, the rock movement angle was calculated using Equation (4), and the collapse angle was simultaneously computed using Equation (5). The calculation results are shown in
Table 2.
Based on the above calculation results of the rock movement angle and collapse angle, a schematic diagram of the movement and subsidence boundaries of the rock mass during the transition from open-pit to underground mining was generated, as shown in
Figure 9.
It can be seen that the distances of 234 m and 163 m show the maximum and minimum distances between the limit boundary of surface subsidence and the hanging wall boundary of the open pit. In comparison, those of 543 m and 421 m show the distance between the limit boundary of surface movement and the hanging wall boundary of the open pit.
In summary, the movement angle and collapse angle for the deep, gently dipping ore body in the Sijiaying Iron Mine are 69° and 74°, respectively. For the northwest dipping ore body in this mine, the movement angle and collapse angle are 68.2° and 68.5°, respectively. The differences between these two regions suggest that the deep, gently dipping ore body, due to its relatively gentle dip angle, exhibits a dominant vertical component during rock strata collapse, resulting in a larger movement angle. Conversely, the steeper dip angle of the northwest ore body intensifies rock sliding along the dip direction, leading to a relatively smaller movement angle. The results provide a quantitative basis for understanding rock mass movement laws and delineating subsidence zones during the transition from open-pit to underground mining in the Sijiaying Iron Mine, offering significant engineering guidance.
5. Discussion
The displacement field and deformation characteristics indicate that the rock mass deformation is governed by the combined influence of geometric configuration and stress redistribution. The spatial variability of the failure modes primarily arises from the following coupled mechanisms:
The dominant geometric control: The orientation of the ore body directly determines the potential failure path. Gently dipping ore bodies induce predominantly vertical subsidence of overlying strata, as reflected by a significant discrepancy between the angle of movement and that of collapse. This failure mechanism is fundamentally characterized by gravitational bending and tensile fracturing of rock layers, especially on the hanging wall of the ore body. In contrast, steeply dipping ore bodies provide a favorable sliding surface along the dipping direction of the ore bodies. Geometric constraints facilitate the release of shear stresses generated through stress redistribution, resulting in shear sliding as the predominant failure mode, with the movement and collapse angles nearly coinciding, especially on the foot-wall of the ore body.
The triggering and driving factors of stress redistribution: The creation of underground goafs fundamentally disrupts the initial stress equilibrium, leading to the following consequences:
Stress in the roof strata above the mined-out area decreases, inducing bending and subsidence of the roof rock layers into the goaf. Concurrently, the stress is transferred and concentrated in adjacent regions—such as the footwall of the open-pit mine, the upper and lower boundaries of the ore body—forming a high shear stress zone.
The presence of the open pit generates a significant geological “exposed surface,” which not only provides space for rock mass movement but also alters the direction and rate of stress release. This change causes deformation resulting from stress redistribution to develop preferentially along the “exposed surface”, thereby intensifying the shear sliding tendency of the slope.
The regulatory role of engineering interventions: Backfill materials exert their influence by modifying the aforementioned geometric and stress conditions [
23,
24]. By providing lateral confinement to the mined-out zone, backfill limits uncontrolled roof caving and transforms the failure mode from abrupt collapse to controlled flexural deformation. Additionally, backfill supplies mechanical support, improves stress distribution, and mitigates stress concentration [
25,
26]. Consequently, in gently dipping deposits, engineering efforts should prioritize ensuring sufficient early strength of the backfill to enable rapid load-bearing capacity. In steeply dipping deposits, enhancing the shear resistance at the interface between backfill and surrounding rock becomes critical to counteract the shear forces dictated by the geometry.
It is of significant importance to study the behavior of strata movement during the transition from open-pit to underground mining, to verify the results of numerical simulations against on-site deformation measurements. Regrettably, as the project of mining in transition at the Sijiaying Iron Mine is currently in the pre-feasibility study phase and the underground mining system has not commenced construction, the field deformation data cannot be obtained for comparison with the simulation results presented in this study. Therefore, the findings of this research are intended to serve as a reference for supporting decision-making during the feasibility assessment stage.
6. Conclusions
During the transition from open-pit to underground mining, the overlying rock mass on the goaf exhibits three-dimensional deformation characteristics involving coupled horizontal shear slip, vertical settlement, and inclining overturning. High-deformation gradient zones predominantly correspond to weak surfaces or contact zones within the rock mass, serving as the primary controlling factors for open-pit slope failure.
When the Sijiaying Iron Mine transitions from open-pit to underground mining, the slope and surface deformation field of the open-pit show obvious spatial heterogeneity. The high-deformation gradient zone is primarily distributed between the northwest ore-rock contact zone and the N18-N26 exploration line, and has a strong coupling with the displacement concentration area. The three-dimensional deformation of the overlying rock mass is significant. The peak value of horizontal displacement is 110 mm, that of vertical displacement is 100 mm, and that of the total displacement is 328 mm. These deformations are controlled by weak structural planes, forming a pattern of “large displacement–small deformation”. In terms of quantity, the movement angle and collapse angle of the gently dipping ore body are 69° and 74°, respectively. In comparison, those of the dipping ore body are 68.2° and 68.5°, respectively, which reflect different failure mechanisms mainly characterized by vertical settlement and directional sliding. These findings have significant guiding significance for slope stability management and damage mitigation in similar mining transition projects.
Author Contributions
Investigation, formal analysis, data curation, visualization, writing—original draft, Y.L.; Investigation, resources, formal analysis, data curation, Z.L. (Zhiyi Liu); Investigation, resources, formal analysis, data curation, Y.C. and S.L.; Data curation, formal analysis, writing—review and editing Q.M.; Conceptualization, methodology, writing—review and editing D.G.; Conceptualization, methodology, writing—review and editing, supervision, project administration, funding acquisition, Z.L. (Zengxiang Lu) All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Key Science and Technology Projects of Hebei Iron and Steel Group (Grant No. HG2023215).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Conflicts of Interest
Authors Yanting Chen and Sheng Li were employed by the company Hebei Iron and Steel Group Mining Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Lu, Z.; Cai, M. Key Technology of Metal Mine in Transition from Open-Pit to Underground Mining, 1st ed.; Metallurgical Industry Press: Beijing, China, 2019. [Google Scholar]
- Bakhtavar, E.; Shahriar, K.; Oraee, K. Transition from open-pit to underground as a new optimization challenge in mining engineering. J. Min. Sci. 2009, 45, 485–494. [Google Scholar] [CrossRef]
- Flores, I.O.; Anani, A.; Li, H.; Afrooz Jalilzadeh, A. Optimizing transition: Investigating the influence of operational parameters on production scheduling optimization for mines transitioning from open pit to block caving methods. Optim. Eng. 2025, 26, 1041–1068. [Google Scholar] [CrossRef]
- Amini, E.; Alipenhani, B.; Alaei, F. Investigation of the main parameters in the determination of open-pit to underground transition depth for copper and iron deposits. Min. Met. Metall. Explor. 2025, 42, 981–1000. [Google Scholar] [CrossRef]
- Li, S.; Lu, H.; Chang, X.; Yang, T.; Mou, C. Numerical Analysis of Synergistic Ground Control Efficacy via Integrated Mining-Backfill-Roof Contact in Metallic Deposits. Appl. Sci. 2025, 15, 9760. [Google Scholar] [CrossRef]
- Badakhshan, N.; Shahriar, K.; Afraei, S.; Bakhtavar, E. Optimization of transition from open-pit to underground mining considering environmental costs. Resour. Policy 2024, 95, 105178. [Google Scholar] [CrossRef]
- Sun, S.G.; Cai, M.F.; Wang, S.J. Study of sliding mechanism for slope due to the excavation from open pit into underground mine. Chin. J. Rock. Mech. Eng. 2000, 1, 126–129. [Google Scholar]
- Yuan, K.; Ma, C.; Guo, G.; Wang, P. Slope failure of Shilu Metal Mine transition from open-pit to underground mining under excavation Disturbance. Appl. Sci. 2024, 14, 1055. [Google Scholar] [CrossRef]
- Geng, J.B.; Li, Q.H.; Li, X.S.; Zhou, T.; Liu, Z.F.; Xie, Y.L. Research on the evolution characteristics of rock mass response from open-pit to underground mining. Adv. Mater. Sci. Eng. 2021, 2021, 3200906. [Google Scholar] [CrossRef]
- Dintwe, T.K.M.; Sasaoka, T.; Shimada, H.; Hamanaka, A.; Moses, D.N.; Peng, M.; Fanfei, M.; Liu, S.; Ssebadduka, R.; Onyango, J.A. Numerical simulation of crown pillar behaviour in transition from open pit to underground mining. Geotech. Geol. Eng. 2022, 40, 2213–2229. [Google Scholar] [CrossRef]
- Phaisopha, S.; Shimada, H.; Sasaoka, T.; Hamanaka, A.; Pongpanya, P.; Shorin, S.; Senthavisouk, K. A stope mining design with consideration of hanging wall when transitioning from open pit mining to underground mining for Sepon Gold Mine Deposit, Laos. Mining 2023, 3, 463–482. [Google Scholar] [CrossRef]
- Álvarez-Fernández, M.I.; González-Nicieza, C.; Menéndez-Díaz, A.; Álvarez-Vigil, A.E. Generalization of the n–k influence function to predict mining subsidence. Eng. Geol. 2000, 80, 1–36. [Google Scholar] [CrossRef]
- Hu, Y.; Ren, F.; Ding, H.; Fu, Y.; Tan, B. Study on the process and mechanism of slope failure induced by mining under open pit slope: A case study from Yanqianshan Iron Mine, China. Adv. Civ. Eng. 2019, 2019, 6862936. [Google Scholar] [CrossRef]
- Li, X.B.; Wang, D.Y.; Li, C.J.; Liu, Z.X. Numerical simulation of surface subsidence and backfill material movement induced by underground mining. Adv. Civ. Eng. 2019, 2019, 2724370. [Google Scholar] [CrossRef]
- Wang, M.; Cai, M.; Maloney, S.; Dunn, M. Determination of mine-wide in-situ stress using numerical back analysis: A case study of Jwaneng mine. Int. J. Rock. Mech. Min. 2025, 194, 106235. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, Z.; Bao, M.; Nian, G.; Zhu, T. Stability analysis and movement process determination of rock masses under open-pit to underground mining conditions. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 148. [Google Scholar] [CrossRef]
- Wang, F.F.; Ren, Q.Y.; Wu, K.; Zheng, C.H. Formation and evolutionary mechanisms of slope instability disasters at exposed surfaces of deep-large collapse pit induced by underground mining activities. Indian. Geotech. J. 2025, in press. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Hu, B.; Yin, T.; Chen, G.; Chen, G. Three-dimensional simulation stability analysis of slopes from underground to open-pit mining. Minerals 2023, 13, 402. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, T.; Bohnhoff, M.; Zhang, P.H.; Yu, Q.L.; Zhou, J.R.; Liu, F.Y. Study of the rock mass failure process and mechanisms during the transformation from open-pit to underground mining based on microseismic monitoring. Rock. Mech. Rock. Eng. 2018, 51, 1473–1493. [Google Scholar] [CrossRef]
- Li, H.; Tian, Y.L.; Qin, J.W.; Lu, Z.X.; Wang, X.R. Design and Optimization of Open-Pit to Underground Mining Method in Sijiaying Iron Mine. Min. Res. Dev. 2025, 45, 34–41. (In Chinese) [Google Scholar]
- Li, S.; Chen, Y.T.; Zhang, C.L.; Zhang, J.; Li, W.T.; Ma, Q.Y.; Lu, Z.X.; Li, J.Q. Study on failure evolution characteristics and stability of slope boundary pillar in transition from open-pit to underground mining. Min. Res. Dev. 2025, in press. (In Chinese) [Google Scholar] [CrossRef]
- Li, S.; Rong, H.; Zhang, J.; Ma, Q.Y.; Lu, Z.X.; Li, J.Q. Instability characteristics of open-pit bottom pillar structure system based on the gravity increase method. Min. Res. Dev. 2025, 45, 43–50. (In Chinese) [Google Scholar]
- Kuzmenko, O.; Dychkovskyi, R.; Petlovanyi, M.; Buketov, V.; Howaniec, N.; Smolinski, A. Mechanism of interaction of backfill mixtures with natural rock fractures within the zone of their intense manifestation while developing steep ore deposits. Sustainability 2023, 15, 4889. [Google Scholar] [CrossRef]
- Bazaluk, O.; Petlovanyi, M.; Sai, K.; Chebanov, M.; Lozynskyi, V. Comprehensive assessment of the earth’s surface state disturbed by mining and ways to improve the situation: Case study of Kryvyi Rih Iron-ore Basin, Ukraine. Front. Environ. Sci. 2024, 12, 1480344. [Google Scholar] [CrossRef]
- Wang, J.; Huang, K.; Fu, J.; Song, W. Mechanical behavior and crack evolution of goaf surrounding rock with different roof-contacted filling rates. Materials 2023, 16, 4435. [Google Scholar] [CrossRef]
- Jirina, T.; Jan, S. Reduction of surface subsidence risk by fly ash exploitation as filling material in deep mining areas. Nat. Hazards 2010, 53, 251–258. [Google Scholar] [CrossRef]
Figure 1.
Three-dimensional numerical model of mining in transition from open-pit to underground in Sijiaying Iron Mine. N12, N20, and N28 are typical three of the exploration lines of the mine.
Figure 1.
Three-dimensional numerical model of mining in transition from open-pit to underground in Sijiaying Iron Mine. N12, N20, and N28 are typical three of the exploration lines of the mine.
Figure 2.
Distribution characteristics of the open-pit slope displacement field in different directions, the black-gray contour lines show the steps of the open-pit. (a) illustrated the displacement field characteristics in the x-direction; (b) illustrated the displacement field characteristics in the y-direction; (c) illustrated the displacement field characteristics in the z-direction.
Figure 2.
Distribution characteristics of the open-pit slope displacement field in different directions, the black-gray contour lines show the steps of the open-pit. (a) illustrated the displacement field characteristics in the x-direction; (b) illustrated the displacement field characteristics in the y-direction; (c) illustrated the displacement field characteristics in the z-direction.
Figure 3.
Displacement characteristics of feature units in different directions, the black-gray contour lines show the steps of the open-pit. (a) illustrated the displacement characteristics of feature units in the x-direction; (b) illustrated the displacement characteristics in the y-direction; (c) illustrated the displacement characteristics in the z-direction.
Figure 3.
Displacement characteristics of feature units in different directions, the black-gray contour lines show the steps of the open-pit. (a) illustrated the displacement characteristics of feature units in the x-direction; (b) illustrated the displacement characteristics in the y-direction; (c) illustrated the displacement characteristics in the z-direction.
Figure 4.
Displacement vector contour map of the mining-affected zone.
Figure 4.
Displacement vector contour map of the mining-affected zone.
Figure 5.
Horizontal displacement and deformation field. The black lines represent contour lines of value, and the gray areas indicate the boundaries of the slope. (a) illustrated the horizontal displacement field in the x-direction; (b) illustrated the horizontal deformation field in the x-direction; (c) illustrated the horizontal displacement field in the y-direction; (d) illustrated the horizontal deformation field in the y-direction.
Figure 5.
Horizontal displacement and deformation field. The black lines represent contour lines of value, and the gray areas indicate the boundaries of the slope. (a) illustrated the horizontal displacement field in the x-direction; (b) illustrated the horizontal deformation field in the x-direction; (c) illustrated the horizontal displacement field in the y-direction; (d) illustrated the horizontal deformation field in the y-direction.
Figure 6.
Ground displacement and deformation field in the z-direction at the +10 m level. The black lines represent contour lines of value, and the gray areas indicate the boundaries of the slope. (a) illustrated the surface inclination displacement field in the z-direction; (b) illustrated the surface inclination deformation field in the z-direction.
Figure 6.
Ground displacement and deformation field in the z-direction at the +10 m level. The black lines represent contour lines of value, and the gray areas indicate the boundaries of the slope. (a) illustrated the surface inclination displacement field in the z-direction; (b) illustrated the surface inclination deformation field in the z-direction.
Figure 7.
Vertical displacement and deformation field in the z-direction at the −30 m level. The black lines represent contour lines of value, and the gray areas indicate the boundaries of the slope. (a) illustrated the vertical displacement field in the z-direction; (b) illustrated the vertical deformation field in the z-direction.
Figure 7.
Vertical displacement and deformation field in the z-direction at the −30 m level. The black lines represent contour lines of value, and the gray areas indicate the boundaries of the slope. (a) illustrated the vertical displacement field in the z-direction; (b) illustrated the vertical deformation field in the z-direction.
Figure 8.
Total deformation field of the open-pit in the process of underground mining.
Figure 8.
Total deformation field of the open-pit in the process of underground mining.
Figure 9.
Surface movement and ground subsidence boundaries after the transition from open-pit to underground mining at the Sijiayang Iron Mine.
Figure 9.
Surface movement and ground subsidence boundaries after the transition from open-pit to underground mining at the Sijiayang Iron Mine.
Table 1.
The relevant mechanical parameters of rock, ore, and backfill body. All the data are derived from laboratory experiments and field investigations conducted by some of the authors of this paper.
Table 1.
The relevant mechanical parameters of rock, ore, and backfill body. All the data are derived from laboratory experiments and field investigations conducted by some of the authors of this paper.
| Rock Strata or Backfill Body | Density/kg·m−3 | Elastic Modulus/GPa | Poisson’s Ratio | Cohesion/MPa | Angle of Internal Friction/(°) |
|---|
| Quaternary system | 1500 | 0.50 | 0.30 | 0.20 | 25 |
| Strongly weathered rock | 2700 | 12.00 | 0.30 | 0.40 | 29 |
| Dolomite | 3300 | 15.00 | 0.30 | 0.60 | 35 |
| Interbedded dolomite and sandstone | 3100 | 15.00 | 0.30 | 0.60 | 37 |
| Quartz sandstone | 2700 | 16.00 | 0.28 | 0.70 | 35 |
| Gneissic granite | 3200 | 16.00 | 0.25 | 0.90 | 39 |
| Biotite leptynite | 3500 | 23.00 | 0.20 | 3.00 | 37 |
| Strongly weathered biotite leptynite | 3200 | 21.00 | 0.23 | 3.00 | 34 |
| Moderately weathered biotite leptynite | 3300 | 22.00 | 0.22 | 2.50 | 35 |
| Weak weathering biotite leptynite | 3500 | 23.00 | 0.21 | 3.00 | 37 |
| Ore body | 3163 | 33.00 | 0.20 | 4.00 | 46 |
| Rock in the fault zone | 2000 | 2.00 | 0.30 | 0.20 | 28 |
| Backfill body (cemented tailing, 1:6) | 1450 | 0.54 | 0.25 | 0.36 | 38 |
| Backfill body (cemented tailing, 1:10) | 1410 | 0.34 | 0.21 | 0.28 | 30 |
Table 2.
Calculation results of rock movement angle.
Table 2.
Calculation results of rock movement angle.
| Type of Ore Body | Movement Angle/° | Collapse Angle/° |
|---|
| Gently dipping ore body | 69.0–71.5 | 74.0–79.84 |
| Dipping ore body | 68.2–69.7 | 68.5–70.4 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).