1. Introduction
Collecting diagnostic radiographic images of large animals using systems designed for humans is difficult. The animals often do not fit into human-sized CT and MR machines, and portable X-ray devices lack the power necessary to image through the thickest sections of the animal [
1,
2,
3]. Thick anatomic regions, e.g., the equine pelvis, abdomen, or withers, pose these imaging challenges by absorbing and scattering the X-ray beam [
4,
5]. The absorbed photons never reach the image detector, resulting in lost contrast and detail. The scattered photons that reach the detector lower the signal-to-noise ratio of the image, reducing contrast. The additional absorption can be resolved with longer exposure times, higher beam current, or higher beam voltage. Increases in exposure time and beam current attempt to overcome absorption by increasing the total number of photons that interact with the object and subsequently reach the detector. However, scatter will reduce image contrast no matter the length of the exposure. Longer exposure times and higher beam currents will also increase the radiation exposure to everyone in the imaging volume, including the animal handler and device operators [
3] (pp. 30–34). The number of photons that reach the detector unattenuated can be increased by increasing the peak voltage applied to the X-ray tube. However, as the X-ray tube’s peak voltage is increased, the mechanism by which the X-rays interact with tissue changes from photoelectric interactions to Compton interactions. Since Compton interactions are not dependent upon the atomic number of the tissue, but rather only the tissue’s electron density, the greater the percentage of Compton interactions the lower the tissue contrast [
6]. Therefore, increasing X-ray tube voltage to achieve greater photon fluence provides a diminishing return for tissue contrast.
A common method to reduce scatter is an anti-scatter grid. Anti-scatter grids can be used to reject photons not traveling along the primary beam. Anti-scatter grids can improve image contrast at the cost of higher patient doses to achieve a similar number of photons reaching the detector. These grids are designed for specific source-to-image-receptor distances due to the divergence of the beam [
7,
8]. This would require the operator to change out the grid depending on the planned source-to-image-receptor distance and may be difficult to maintain with the portable systems often used on large animals. This makes anti-scatter grids non-viable in tandem with current practices.
Scanning slit projection radiographs use a narrow, fan shaped X-ray beam, linear image detector array, and beam movement to produce a radiographic image [
9]. This projection method reduces scatter by having a low aspect ratio detector that results in scattered photons being projected outside of the primary beam’s geometry, thereby not interacting with the detector. Scanning slit projection can use lower X-ray exposures to produce similar quality images to a conical beam and area detector but does require constant relative motion between the patient and machine [
9,
10,
11,
12]. Having a fixed source and detector with the patient moving would allow for the source and detector to be precisely aligned during installation but limits the versatility of the machine. In the past, additional collimators were used to produce the moving slits of radiation while otherwise keeping the source stationary [
9]. This method is impractical for arbitrarily sized animals whose anatomy may not line up with the intended imaging area. Actuating the source and detector along a single axis, such as the machine used by Melhem et al. [
10], benefits from limited complexity and being able to move along the long axis of the patient; however, this technique also requires cooperation from the patient to orient themselves appropriately for the image. Having full position and orientation control of the source and detector could enable the same machine to produce a wide variety of images with little to no repositioning of the animal—at the cost of needing to dynamically align the source and detector.
Serial robotic manipulators are well understood mechanical systems that can be used for this application. Accurate imaging requires precise alignment of the fan-beam X-ray source and the linear image detector, implying accurate knowledge of the manipulator geometry. Denavit–Hartenberg (DH) parameters have been used to model serial manipulators for decades [
13]. Measuring these parameters by hand is challenging as external features do not always align with the geometry of the DH parameters. Small errors in the model parameters can also lead to large end effector positioning errors. Therefore, it is necessary to calibrate the model parameters to be able to accurately position the source and detector [
14,
15]. Thus, the purpose of this work is to configure a DH geometric model of a 12-axis robotic slit-scan radiographic imaging system, to optimize the model using motion capture data inputs, and to assess the positioning accuracy of the resulting manipulator for imaging tasks.
2. Materials and Methods
Each half of the robot—a source side and a detector side (
Figure 1)—consists of three prismatic joints followed by three revolute joints to give each end effector the desired six degrees of freedom (DoF). A set of 12 motion capture (mocap) cameras (OptiTrack Prime13x, Motive 2.3.1) was used to track retroreflective marker arrays attached to each end effector of the robotic system [
16].
The detector used in this study is a Varex-Imaging DC Hydra photon counting detector (
Figure 2). The detector array is 6 mm × 513 mm. Time-delayed summation is used to produce a full-length image by offsetting and summing sequential frames. It uses a Cadmium Telluride converter and does not have a scintillator. Each pixel is 0.1 mm × 0.1 mm [
17]. The X-ray source is a water-cooled Varex-Imaging HPX-225-11 tube [
18] (
Figure 1).
A set of 400 uniformly distributed joint positions was defined for training the geometric model of each manipulator. These 400 points were uniformly selected from a superset of permutations of predefined joint positions. The predefined joint positions were distributed throughout the length of travel for all joints. The prismatic joints had 100 mm of spacing between each defined joint position, and the rotational joints had 5 degrees of spacing. Not all joints had the same number of predefined positions due to length of travel limitations. An additional 100 points were defined using a uniform distribution bounded by the maximum and minimum joint positions used previously. These 100 positions were used to assess model performance. One safe location was defined for each side of the system where the opposing side would not be able to reach it.
The active end effector was commanded to move to each desired location, it paused to allow any potential vibrations to damp out, mocap recorded its location, and the end effector was then moved to the next point in the sequence. The end effectors alternated every 100 points which end effector was active and which was at its safe location. The positions were recorded for 100 samples then averaged.
A two-layer Levenberg–Marquardt–Fletcher optimizer was used to refine the DH parameters [
19]. The outer layer varied the DH parameters, and the inner layer determined the transformation from the motion capture coordinate system to the base of the robot. Initial DH parameters were estimated from measurements taken by hand. The 100 test points were excluded from the optimizer. The cost functions are similar to those used by Lightcap et al. [
15], specifically the position error and model weight regularization. The orientation error was also calculated by determining the required orientation change needed for the model to match the measured orientation, then subtracting the identity quaternion. Due to the unit quaternion’s unit norm constraint causing the error to be relatively low when compared to positioning errors, the orientation error was scaled by a factor of 10. The convergence criteria were chosen to be when the sum squared error changed by less than half a percent between outer-loop iterations. Comparing subsequent iterations of the sum squared error is reasonable for this problem as the minimum nearest the initial guess should reflect the physical system the initial values were measured from. Model performance was assessed using the 100 test points’ forward error compared to the variance and residuals output by the optimizer. The initial guess fed into the optimizer was measured manually.
The end effectors were then further registered to their marker arrays using a calibrated pointer. This registration process added one additional tool point transformation to the model of each half of the robot. The pointer was used to mark the four corners of the detector to define the center and normal direction of the detector (
Figure 2). The top of the collimator slit, bottom of the collimator slit, and face of the collimator were used in conjunction with the distance from the face of the collimator to the focal point of the source provided by the manufacturer to define the center and pointing direction of the X-ray source [
18].
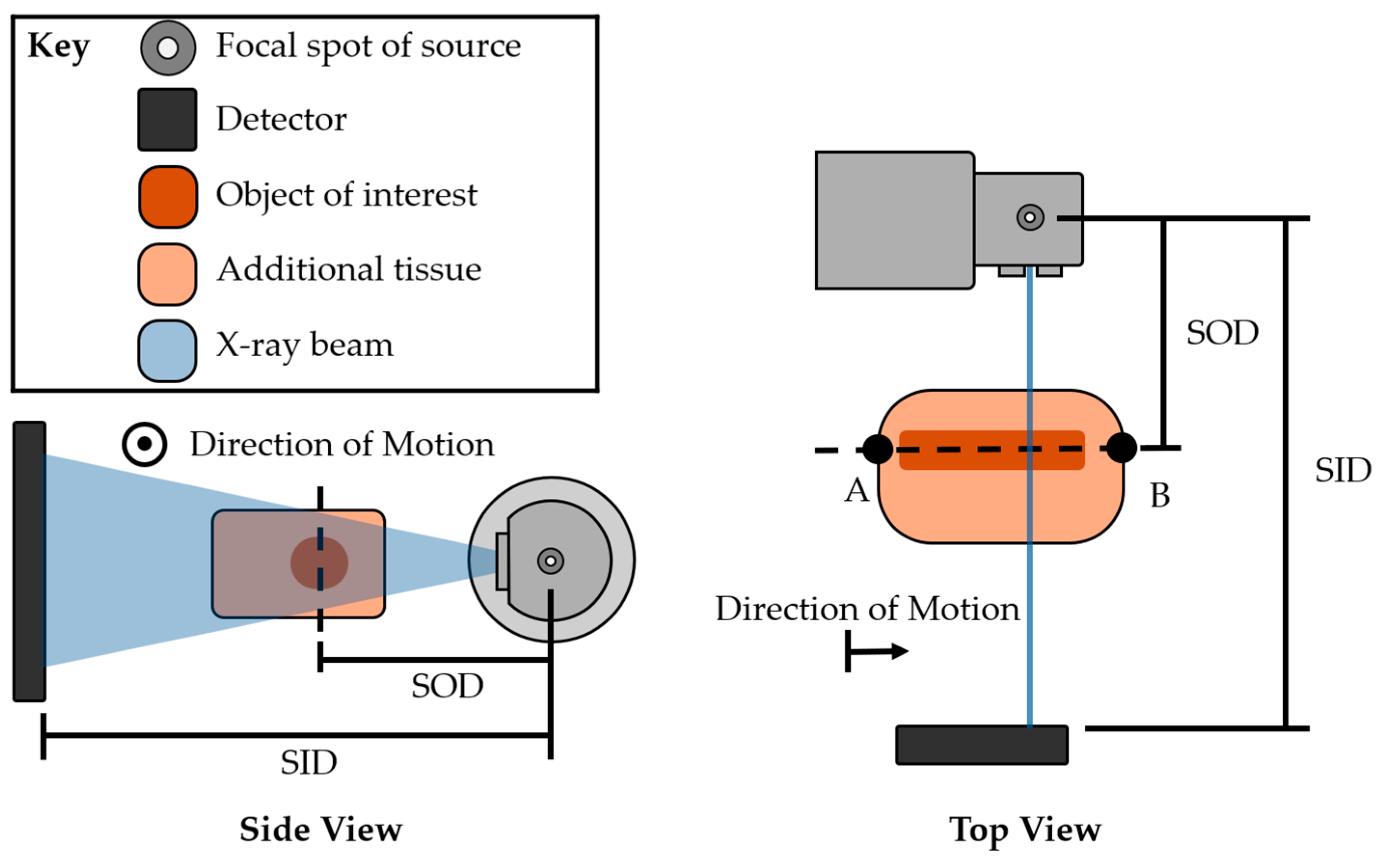
The distal forelimbs of 15 horses were imaged as a part of an IACUC-approved study (IACUC202200000393). Examples from this study are included as a demonstration of calibrated system imaging capabilities. Fan-beam slit-scan radiography stretches the intended object in the vertical direction of the image but has little to no projection increase in the horizontal direction due to the fan-beam scanning geometry and summation of thin slices at the detector. Example images have been corrected using the operator defined source-to-object distance (SOD) and source-to-image-receptor distance (SID). The horses were standing on the ground, making the imaging location at one extreme of the calibration volume used for manipulator modeling. The robotic system moved in accordance with the imaging schematic, with points A and B defined by the operator using a calibrated pointer (
Figure 3). The researchers followed an order of operation for imaging: to walk the animal in under its own power, put the animal under standing sedation to minimize its motion and maintain calm, perform scans, and allow the animal to walk out under its own power once the standing sedation had worn off. A single handler, wearing appropriate protective equipment, was required to be in the room during imaging to handle the animal.
An imaging phantom was used to demonstrate the effect of manipulator calibration on image quality. The phantom was composed of an equine lumbar bone segment embedded in ballistic gel to approximate the physical geometry and radiographic density of the equine lumbar area. Images were acquired with the uncalibrated and calibrated mechanism parameters.
3. Results
The layered optimization adjusted the joint parameters from their manually determined initial guesses, typically several millimeters and degrees (
Table 1). The translation of the origin of the base of the robot saw the largest change in the optimizer (
Table 2).
The model fitting decreased the sum squared error to 0.079% of its initial value with model optimization seen in
Figure 4, and the test points’ mean sum squared error was 80% of the final model fitting mean sum squared error.
The geometric model showed improved forward error after the optimization (
Table 3 and
Table 4). The mean error of the test points also fell within the confidence interval of the results (
Table 5).
Scans of the horses’ distal forelimb, focusing on the hock and metatarsal, were performed utilizing the calibrated DH parameters. The images are clear and permit visualization of bone trabecular-level detail (
Figure 5). For comparison, the second prismatic joint on the detector side’s θ parameter was returned to its initial value and an image of an equine lumbar segment phantom was collected (
Figure 6). There is an obvious improvement in image sharpness with the calibrated system (
Figure 6).
4. Discussion
Large animal radiography is challenging due to the large physical size of the patient, the inability for the patient to follow verbal commands, and the common need to sedate the animal with associated morbidities. Fan-beam/slit-scan radiography provides imaging access to the large girth regions of these animals by avoiding most X-ray scatter while permitting examination of the standing animal. This approach does require automatic actuation of an imaging gantry, which motivated this work. We built a pair of six-DoF (three prismatic, three revolute) robots to manipulate the X-ray source and image detector over a very large viewing volume, and present here efforts to identify a suitable geometric model that allows for accurate source/detector manipulation for high image quality. Our numerical model results, and the associated images acquired, demonstrate that this approach is adequate to realize a manipulator system capable of producing diagnostic-quality radiographic images with a large robotic gantry.
A two-level optimization scheme was adequate to converge DH mechanism parameters (outer loop) and the offset of the robotic system coordinate system from the motion capture system (inner loop). Perturbations of DH parameters from initial guesses to converged values were typically a few millimeters or degrees, except for several rotations, where the calibrated reference value is arbitrary. The offsets transforming the camera coordinate system to the base of the robot changed by upwards of 100 mm, as it was dependent upon the arbitrary positioning of the motion capture “L-frame” when the camera system was calibrated. The final errors for the optimized mechanism model showed standard deviations in the position error of approximately one millimeter, consistent with the measurement uncertainties of the motion capture system. The orientation error improved, but the initial average error was not very large. This makes sense, since the initial joint angles were the best manual measurement possible given the physical system.
Figure 6 shows that mechanism parameter optimization is necessary to produce diagnostic images with this system.
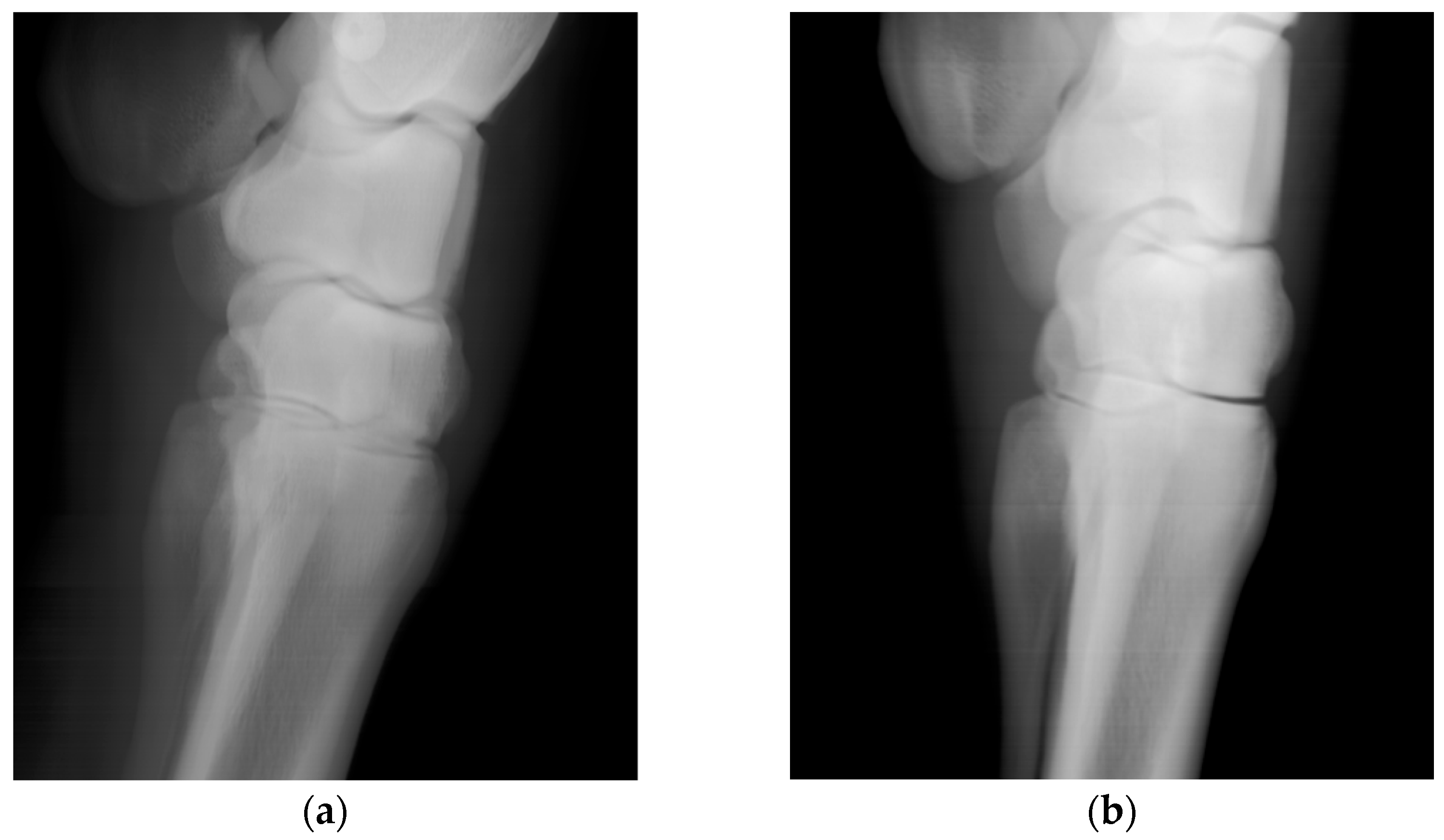
Test point positioning errors of a few tenths of a millimeter magnitude correspond to image features being offset by several pixels at the detector array. The orientation errors’ standard deviations are equivalent to a 0.2-degree cone around the intended orientation. Assuming all else is correct, this could put the center of the beam off the center of the detector by approximately 5 mm when operating at the maximum source-to-image-receptor distance of 1.5 m. This offset corresponds to 50 pixels and would be off the edge of the detector. These observations should help to inform future collimation strategies, as we aim to ensure that the primary beam, the region of the beam that is between the half values of peak intensity, fully illuminates the detector. This range of uncertainty is acceptable for imaging tasks, as demonstrated by images of the metacarpus with trabecular-level bone detail (
Figure 5). Being able to produce these images at the extreme of the calibrated range is a positive indication for performance throughout the calibrated volume. These positioning errors are comparable to the 30-parameter flexible geometric robot model of Lightcap et al. [
15], both being less than a millimeter.
The image detector and X-ray source were assumed to be perfectly registered to the end effector motion capture arrays to simplify the analysis. This assumption is useful for the data presented here, but small errors in how the source and detector are registered may lead to the primary beam of the source not hitting the detector. This could greatly affect image production, as the tightly collimated beam quickly falls off in intensity outside of the primary beam. The method used to register the end effectors to their marker arrays to produce images in this study also only used external features of the source and detector. These features, especially on the X-ray source, may not fully represent the position and direction of the end effectors. Future work will add an additional step after this parameter calibration to verify that the source and detector are correctly registered. Nevertheless, images acquired based upon the DH model with this simplifying assumption (
Figure 5) demonstrate that high-quality images can be obtained.
Slit projection radiography relies on the source and detector to be moving relative to the subject to create an image. This motion needs to be steady and perpendicular to the long axis of the detector array and the central ray of the source. The model developed in this paper does not include any dynamic effects or consider any potential flex of the links as the end effectors change position. A more complex model may improve tracking accuracy or inform design changes to reduce dynamic effects. Vibration artifacts, vertical stripes of varying intensity, are not currently seen in the images collected with the current model, but having a better understanding of the dynamics of the system could enable optimization of the acceleration ramps on the joints. The images were also produced using a point-to-point function block for the motors native to TwinCAT 3.0.0 [
20]. This function does not allow for on-the-fly changes to the setpoints, and if the subject were to move, it could lead to large motion artifacts in the image. Work is currently being carried out to write a custom setpoint generator that may be used to make on-the-fly changes and assess the feasibility of correcting for animal motion. A more complex setpoint generator would also enable the system to follow more complex paths if necessary.
In the results, the variance in position suggests an ellipsoidal region of uncertainty since the variance in each direction is different. These differences may be due to how the cameras are placed around the capture volume. Space constraints and the size of the system limited mounting locations and may skew the precision of position measurements if a subset of the cameras have a similar out of plane direction. The X-ray source also has a large cable harness that may block some cameras’ views of the markers at any given position. The combination of the harness blocking line of sight and the camera placement may have led to the observed differences in variance. Increasing the number of cameras and using more optimally distributed mounting locations may improve performance in the future.
5. Conclusions
Slit projection radiography has the potential to provide diagnostic quality imaging of the thick sections of large animals while reducing the cost, time, and morbidity associated with using human-focused imaging approaches on large animals. This approach does require advanced manipulation capabilities and precise control of moving X-ray and imaging hardware. We built a 12-DoF paired gantry manipulator to realize a slit projection X-ray system for large standing animals and describe the kinematic system using a DH parameterization. We used optical motion capture to quantify manipulator positioning over a large spatial volume and then numerically optimized the DH parameters into harmony with the motion capture data. With these optimized DH parameters, we were able to acquire diagnostic-quality images of equine subjects at the periphery of the calibration volume, validating the approach and the potential for this type of system to provide novel imaging capabilities for large animal care.
Author Contributions
Conceptualization, C.T.L. and S.A.B.; software, C.T.L., D.N.G., and X.B.; validation, D.N.G. and F.J.B.; formal analysis, C.T.L.; investigation, C.T.L., D.N.G., and X.B.; methodology, C.T.L.; resources, A.H.B.; data curation, C.T.L.; writing—original draft preparation, C.T.L.; writing—review and editing, A.H.B., F.J.B., D.N.G., X.B., and S.A.B.; visualization, C.T.L.; supervision, A.H.B., F.J.B., and S.A.B.; project administration, C.T.L.; funding acquisition, A.H.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by an internal grant from the University of Florida Department of Large Animal Clinical Sciences and College of Veterinary Medicine.
Institutional Review Board Statement
Animals were imaged for an IACUC-approved study, the approved protocol’s IACUC ID is IACUC202200000393 and was approved on 10 October 2022.
Data Availability Statement
The raw data and software supporting the conclusions of this technical note will be made available by the corresponding author on request.
Acknowledgments
The authors thank the University of Florida Large Animal Clinical Sciences Department for assisting in animal handling.
Conflicts of Interest
Author Xheni Bare was employed by the company Blue Origin. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. Authors Adam Biedrzycki, Frank Bova, and Scott Banks are inventors on a provisional patent application for the robotic imaging system presented in this paper. A fourth inventor on the patent is not an author on this paper, Shannon Ridgeway. The patent describes the overall design of the system, its use with an optical tracking system, and application to guided surgical operations for large animals. The provisional patent application was submitted 13 April 2023.
Abbreviations
The following abbreviations are used in this manuscript:
| CT | Computed tomography |
| MR | Magnetic resonance |
| DoF | Degrees of freedom |
| DH | Denavit–Hartenberg |
| mocap | Motion capture |
| SOD | Source to object distance |
| SID | Source to image receptor distance |
References
- Meomartino, L.; Greco, A.; Di Giancamillo, M.; Brunetti, A.; Gnudi, G. Imaging Techniques in Veterinary Medicine. Part I: Radiography and Ultrasonography. Eur. J. Radiol. Open 2021, 8, 100382. [Google Scholar] [CrossRef] [PubMed]
- Denoix, J.M.; Jacquet, S.; Lepeule, J.; Crevier-Denoix, N.; Valette, J.P.; Robert, C. Radiographic Findings of Juvenile Osteochondral Conditions Detected in 392 Foals Using a Field Radiographic Protocol. Vet. J. 2013, 197, 44–51. [Google Scholar] [CrossRef] [PubMed]
- International Atomic Energy Agency. Radiation Protection and Safety in Veterinary Diagnostic Radiology Using X Rays. In Radiation Protection and Safety in Veterinary Medicine; International Atomic Energy Agency: Vienna, Austria, 2021. [Google Scholar]
- Dixon, J.; Biggi, M.; Weller, R. Common Artefacts and Pitfalls in Equine Computed and Digital Radiography and How to Avoid Them. Equine Vet. Educ. 2018, 30, 326–335. [Google Scholar] [CrossRef]
- McKnight, A.L. Digital Radiography in Equine Practice. Clin. Tech. Equine Pract. 2004, 3, 352–360. [Google Scholar] [CrossRef]
- Cesareo, R.; Hanson, A.L.; Gigante, G.E.; Pedraza, L.J.; Mathaboally, S.Q.G. Interaction of keV Photons with Matter and New Applications. Phys. Rep. 1992, 213, 117–178. [Google Scholar] [CrossRef]
- Tang, C.-M.; Stier, E.; Fischer, K.; Guckel, H. Anti-Scattering X-Ray Grid. Microsyst. Technol. 1998, 4, 187–192. [Google Scholar] [CrossRef]
- Tanaka, N.; Naka, K.; Saito, A.; Morishita, J.; Toyofuku, F.; Ohki, M.; Higashida, Y. Investigation of Optimum Anti-Scatter Grid Selection for Digital Radiography: Physical Imaging Properties and Detectability of Low-Contrast Signals. Radiol. Phys. Technol. 2013, 6, 54–60. [Google Scholar] [CrossRef] [PubMed]
- Sorenson, J.A.; Nelson, J.A. Slit Radiography: Problems and Potential. In Proceedings of the Application of Optical Instrumentation in Medicine VIII, Las Vegas, NV, USA, 20–22 April 1980; SPIE: Bellingham, WA, USA, 1980; Volume 233, pp. 240–247. [Google Scholar]
- Melhem, E.; Assi, A.; El Rachkidi, R.; Ghanem, I. EOS® Biplanar X-Ray Imaging: Concept, Developments, Benefits, and Limitations. J. Child. Orthop. 2016, 10, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Després, P.; Beaudoin, G.; Gravel, P.; de Guise, J.A. Evaluation of a Full-Scale Gas Microstrip Detector for Low-Dose X-Ray Imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2005, 536, 52–60. [Google Scholar] [CrossRef]
- Samei, E.; Saunders, R.S.; Lo, J.Y.; Dobbins III, J.T.; Jesneck, J.L.; Floyd, C.E.; Ravin, C.E. Fundamental Imaging Characteristics of a Slot-Scan Digital Chest Radiographic System. Med. Phys. 2004, 31, 2687–2698. [Google Scholar] [CrossRef] [PubMed]
- Denavit, J.; Hartenberg, R.S. A Kinematic Notation for Lower-Pair Mechanisms Based on Matrices. J. Appl. Mech. 1955, 22, 215–221. [Google Scholar] [CrossRef]
- Judd, R.; Knasinski, A. A Technique to Calibrate Industrial Robots with Experimental Verification. In Proceedings of the 1987 IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 31 April 1987; IEEE: Piscataway, NJ, USA; Volume 4, pp. 351–357. [Google Scholar]
- Lightcap, C.; Hamner, S.; Schmitz, T.; Banks, S. Improved Positioning Accuracy of the PA10-6CE Robot with Geometric and Flexibility Calibration. IEEE Trans. Robot. 2008, 24, 452–456. [Google Scholar] [CrossRef]
- NaturalPoint, Inc. Motive Body, version 2.3.1; NaturalPoint, Inc.: Corvallis, OR, USA, 2021. [Google Scholar]
- DC-HYDRA Photon Counting Detectors. Available online: https://www.vareximaging.com/wp-content/uploads/2022/12/DC-HYDRA_154488-000-Rev-C.pdf (accessed on 1 October 2025).
- Varex Imaging. HPX-225-11 Datasheet. Available online: https://www.vareximaging.com/wp-content/uploads/2022/01/HPX-225-11pds_0.pdf (accessed on 14 September 2025).
- Miroslav, B. LMFsolve.m: Levenberg–Marquardt–Fletcher Algorithm for Nonlinear Least Squares Problems. Available online: https://www.mathworks.com/matlabcentral/fileexchange/16063-lmfsolve-m-levenberg-marquardt-fletcher-algorithm-for-nonlinear-least-squares-problems (accessed on 1 May 2023).
- TwinCAT, version 3.0.0; MC_MoveAbsolute, TwinCAT 3 PLC Tc2_MC2; Beckhoff New Automation Technology: Verl, Germany, 2023.
Figure 1.
The Gantry-Activated Tomographic Robotics system. The source is in the left of the image, and the detector is in the right of the image, both pointed in the general direction of the camera.
Figure 1.
The Gantry-Activated Tomographic Robotics system. The source is in the left of the image, and the detector is in the right of the image, both pointed in the general direction of the camera.
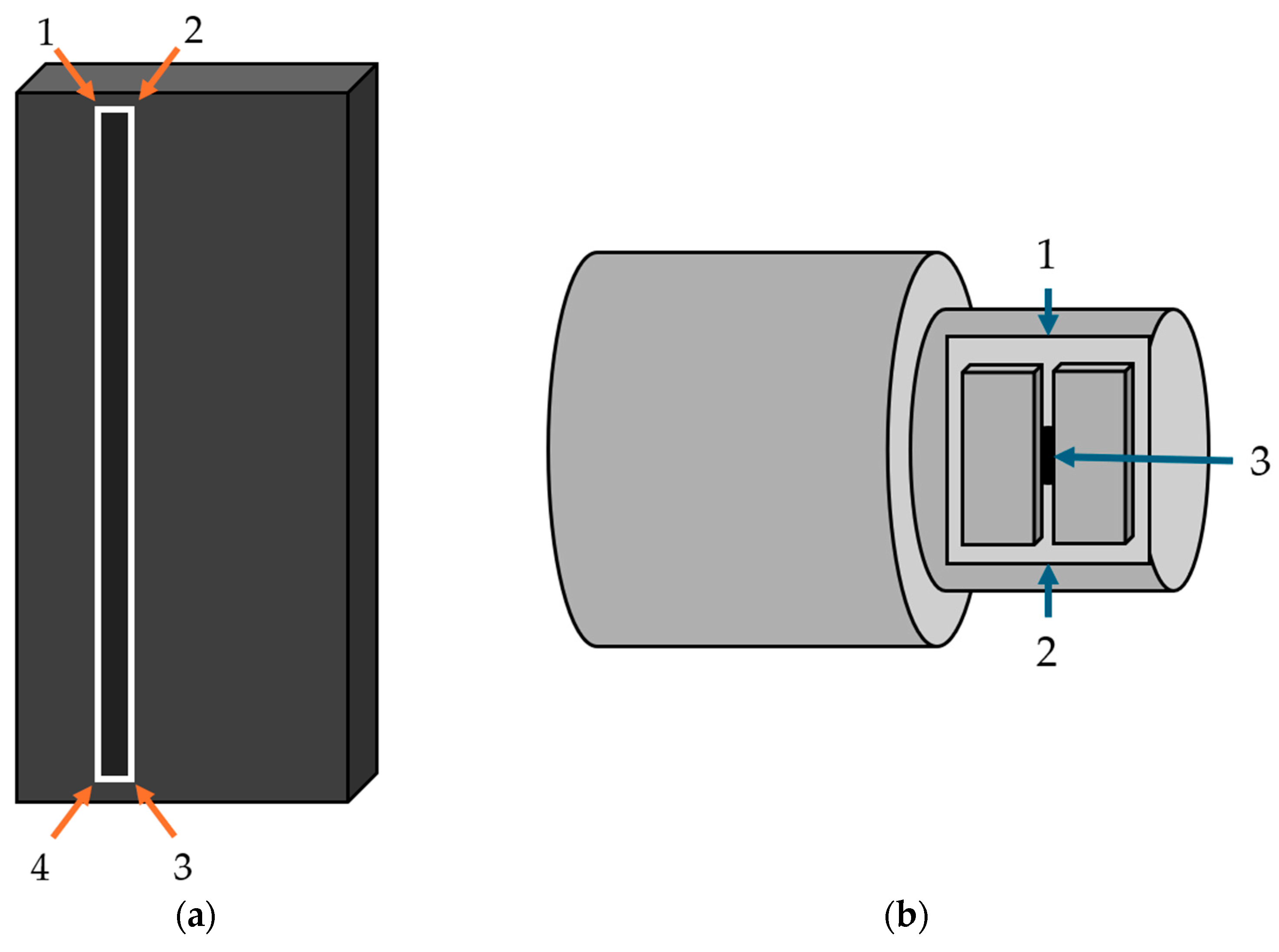
Figure 2.
Diagram of points used to register end effectors to their marker arrays. The four corners of the detector were used in the order shown to define the plane and center of the detector (a). The top and bottom of the collimator slit, points 1 and 2, and the face of the collimator leaf, point 3, were used to register the x-ray source (b).
Figure 2.
Diagram of points used to register end effectors to their marker arrays. The four corners of the detector were used in the order shown to define the plane and center of the detector (a). The top and bottom of the collimator slit, points 1 and 2, and the face of the collimator leaf, point 3, were used to register the x-ray source (b).
Figure 3.
Robotic system imaging process schematic. Point A, point B, SOD, and SID are defined by the operator. Points A and B define the position and orientation of the object of interest for the robotic system. Combined with the SOD and SID, a path can be defined to collect the image.
Figure 3.
Robotic system imaging process schematic. Point A, point B, SOD, and SID are defined by the operator. Points A and B define the position and orientation of the object of interest for the robotic system. Combined with the SOD and SID, a path can be defined to collect the image.
Figure 4.
Plot of sum squared error versus iteration of the outer loop for each half of the robot. The source took five iterations and the detector took six iterations of the outer loop to converge.
Figure 4.
Plot of sum squared error versus iteration of the outer loop for each half of the robot. The source took five iterations and the detector took six iterations of the outer loop to converge.
Figure 5.
Lateral images of an equine carpus and metacarpus acquired in vivo from a standing horse, (a) acquired with 140 kVp and 12 mA source voltage and current technique and (b) acquired with a 70 kVp and 24 mA technique. For the 15 horses imaged, the beam was on for between 15 and 20 s.
Figure 5.
Lateral images of an equine carpus and metacarpus acquired in vivo from a standing horse, (a) acquired with 140 kVp and 12 mA source voltage and current technique and (b) acquired with a 70 kVp and 24 mA technique. For the 15 horses imaged, the beam was on for between 15 and 20 s.
Figure 6.
Images showing improvements of imaging performance due to DH parameter optimization. For images (a,b) a single parameter, the θ value for the detector’s second prismatic joint, was kept at its initial value. Images (c,d) used the full set of optimized parameters. Images (b,d) are contrast-adjusted, zoomed in, and leveled to view the bony features of the lumbar segment phantom.
Figure 6.
Images showing improvements of imaging performance due to DH parameter optimization. For images (a,b) a single parameter, the θ value for the detector’s second prismatic joint, was kept at its initial value. Images (c,d) used the full set of optimized parameters. Images (b,d) are contrast-adjusted, zoomed in, and leveled to view the bony features of the lumbar segment phantom.
Table 1.
Change in DH parameters. Joints labeled with their end effector, P for prismatic or R for revolute, and then numbered sequentially.
Table 1.
Change in DH parameters. Joints labeled with their end effector, P for prismatic or R for revolute, and then numbered sequentially.
| Joint | ∆α (deg) | ∆θ (deg) | ∆a (mm) 1 | ∆S (mm) 1 |
|---|
| Source P1 | −1.19 | 0.96 | -- | -- |
| Source P2 | 0.83 | 0.17 | -- | -- |
| Source P3 | −0.64 | −0.10 | -- | -- |
| Source R4 | −1.38 | −1.50 | −5.13 | 4.45 |
| Source R5 | −0.02 | −0.02 | 0.59 | −4.24 |
| Source R6 | −4.65 | 1.15 | 6.83 | 7.12 |
| Detector P1 | −0.99 | 0.86 | -- | -- |
| Detector P2 | −0.62 | −2.11 | -- | -- |
| Detector P3 | −0.92 | 1.78 | -- | -- |
| Detector R4 | −0.44 | −4.38 | 4.02 | −0.45 |
| Detector R5 | −1.26 | 25.05 | 0.40 | 26.95 |
| Detector R6 | −4.18 | 24.89 | 0.23 | −33.88 |
Table 2.
Change in camera to robot base transformation parameters.
Table 2.
Change in camera to robot base transformation parameters.
| Side | ∆X (mm) | ∆Y (mm) | ∆Z (mm) | ∆ϕ (deg) 1 | ∆ψ (deg) 1 | ∆ω (deg) 1 |
|---|
| Source | −11.62 | 0.36 | 12.19 | 2.83 | 0.04 | −0.33 |
| Detector | 0.11 | 158.96 | 97.89 | 2.73 | 0.06 | −0.48 |
Table 3.
Manipulator positioning errors prior to optimization.
Table 3.
Manipulator positioning errors prior to optimization.
| Parameter | Source | Detector |
|---|
| X (mm) | −12.9 ± 7.6 | −37.3 ± 46.4 |
| Y (mm) | 41.1 ± 9.5 | −123.4 ± 26.0 |
| Z (mm) | −23.4 ± 17.8 | −111.3 ± 37.9 |
| Q0 | 0.0007 ± 0.0007 | 0.0012 ± 0.0004 |
| Q1 | 0.0160± 0.0165 | 0.0444 ± 0.007 |
| Q2 | −0.0203 ± 0.0141 | 0.0032 ± 0.008 |
| Q3 | −0.0128 ± 0.0097 | −0.0064 ± 0.01 |
Table 4.
Manipulator positioning errors after optimization for the training point set.
Table 4.
Manipulator positioning errors after optimization for the training point set.
| Parameter | Source | Detector |
|---|
| X (mm) | 0 ± 1.4 | 0 ± 0.5 |
| Y (mm) | 0 ± 0.5 | 0 ± 0.9 |
| Z (mm) | 0 ± 0.4 | 0 ± 0.3 |
| Q0 | 0 ± 0.00001 | 0.0001 ± 0.001 |
| Q1 | 0 ± 0.002 | −0.0002 ± 0.002 |
| Q2 | −0.001 ± 0.001 | −0.001 ± 0.002 |
| Q3 | 0 ± 0.003 | −0.0005 ± 0.001 |
Table 5.
Manipulator positioning errors for the test point set.
Table 5.
Manipulator positioning errors for the test point set.
| Parameter | Source | Detector |
|---|
| X (mm) | 0.3 ± 1.0 | −0.1 ± 0.5 |
| Y (mm) | −0.1 ± 0.3 | 0.2 ± 0.8 |
| Z (mm) | 0 ± 0.4 | 0.1 ± 0.3 |
| Q0 | 0 ± 0.00001 | 0.0004 ± 0.001 |
| Q1 | −0.001 ± 0.001 | 0.0001 ± 0.002 |
| Q2 | −0.001 ± 0.001 | −0.002 ± 0.002 |
| Q3 | −0.001 ± 0.002 | −0.001 ± 0.001 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).