Abstract
Despite the popularity of electroencephalograms (EEGs) as tools for assessing brain health, they can sometimes be abstract and prone to noise, making them difficult to interpret. The following work aims to implement a Quaternion Convolutional Neural Network (QCNN) to detect abnormal EEGs obtained from a database that includes both people with excellent mental health and individuals with different types of mental illnesses. Unlike other approaches in which the QCNN is used exclusively for image processing, in the present work, a unique architecture with mainly quaternionic layers is proposed, specifically designed for the classification of time-varying signals. Using the database “The TUH EEG Abnormal Corpus”, the signals are preprocessed using the Wavelet Transform, a mathematical tool capable of performing simultaneous time and frequency analysis, configured with a level 4 decomposition value. Subsequently, the results are subjected to a partial spectrogram-type treatment to integrate the energy parameter into the analysis. They are then conditioned in each of the elements of the quaternion and processed by the QCNN, leveraging quaternion algebra to maintain the relationships between its elements, both in the input and in the convolutional product. In this way, it is possible to obtain significant percentages in the precision, recall, and accuracy metrics with values higher than 77%. Its performance, which uses 4 times less computational memory, allows the QCNN to be considered an alternative for classifying EEG signals. Finally, a comparison of the proposed model was made with other architectures commonly used in the literature, as well as with developments in other research and with a hybrid model whose performance places it at the highest classification standard, not to mention the ability of the QCNN to preserve multi-channel dependencies in EEG signals in a more natural way, achieving parameter efficiencies by leveraging quaternion algebra, reducing the computational cost compared to real-valued CNNs.
1. Introduction
In the medical field, the development of modern, scientifically based clinical systems aims to improve the efficiency of diagnostic and treatment processes for various diseases. In this context, when assessing a patient’s neurological status, electroencephalograms (EEGs) are primarily considered due to their ease of obtaining brain signals, as well as their low cost and rapid application, allowing for optimized time and reducing errors when interpreting medical results.
For some epileptic episodes, it is common for physicians to base their analysis on the patient’s clinical history or to use an EEG to detect interictal epileptiform discharges (IEDs) and brain activity in unexpected bandwidths [1]. However, detection can be complicated if the EEG contains an excess of abrupt signals, which makes it difficult to locate abnormalities and requires more specialized international criteria [2].
Faced with these difficulties, several researchers have turned to detection methods based on advanced technologies, particularly the use of artificial intelligence. These solutions generally consist of a set of neural networks operating in the Euclidean plane, designed to identify neurological disorders by analyzing large databases through the detection of complex patterns. Although this approach has been widely explored and documented in literature, new alternatives are currently being sought to address these objectives from other perspectives, such as geometric algebra. In this context, quaternionic convolutional neural networks (QCNNs) have emerged as a promising option due to their ability to capture multidimensional relationships using a smaller number of parameters compared to other architectures commonly implemented in literature. This is thanks to the quaternion structure, which is a unit consisting of four elements whose components can be reused in convolutional products. One of the tasks where QCNNs perform excellently is the encoding and decoding of images, both black and white and color. However, they have also achieved good accuracy rates in work related to image classification, natural language processing, computer vision, and even forecasting. It is also interesting to explore their application in other fields, such as EEG signal analysis.
This work aims to implement a Quaternionic Convolutional Neural Network to detect abnormal EEGs with problems ranging from diseases such as Alzheimer’s, epilepsy, mental hemorrhages, etc., to emotional ones such as depression, this being the main contribution of this work. As preprocessing, Wavelet Transform is mainly implemented to analyze brain signals by defragmenting them into different frequency ranges, alongside the database provided by [3] which has sets to train and test classifiers. In this way, satisfactory percentages are obtained in frequent evaluation metrics, capable of competing with commonly used classification techniques, but with low computational requirements. Thus, the following contributions are made:
- Design and implement methods based on EEG processing and identification using a two-output quaternionic convolutional neural network to produce information from anomaly detection in an individual’s brain activity.
- Establish a data processing algorithm using the Wavelet transform to analyze the signal in four different frequency ranges.
- Outline and validate the quaternionic convolutional neural network by comparing its performance with neural models commonly used in classification applications, developed for related jobs and also composed of a combined structure, showing that the QCNN’s results stand out in their highest levels of reported accuracy.
The outline of the article is as follows: Section 2 mentions some works related to the problems of this research, Section 3 explains the Discrete Wavelet Transform, then Section 4 presents the proposed QCNN, while Section 5 presents the materials and methods used in the development of the project, Section 6 shows the results including comparisons with other models, Section 7 extracts the discussion and Section 8 gives the conclusions obtained from the research.
2. Related Works
The first research described that seeks to facilitate these processes is the one reported in [4], where an EEG encoder and a domain adversarial neural network (DANN) are used to detect seizures in electroencephalographic signals, obtaining 78% accuracy. Similarly, in [5] a prediction, detection and classification system for 4 types of seizures is presented using a Transformer encoder network with self-supervised learning and an Adaptive Frequency-Time Attention (AFTA) module with adaptive filtering using EEG signals, reaching scores above 80% in different metrics. While in [6] the functionality of a recurrent convolutional network is presented with a combination of a maximum pooling layer and a posterior grouper to design a seizure onset detector, obtaining accuracy percentages greater than 84%, and in [7], a comparison is presented between two neural network architectures (CNN and LeNet-5) using five different transformation methods with the aim of resizing EEG and electrocardiogram signals to classify five epilepsy states with results above 99% in different types of metrics for both models.
However, there is also research focused on the detection of brain diseases with lower risk. For example, there is a classifier based on the DenseNet201 architecture [8], designed to classify different stages of dementia using images derived from EEG processing. Using two different databases, recognition accuracy rates of approximately 94% and 77%, respectively, can be achieved. Furthermore, in [9], patients with dementia are detected using an Xgboost [10] type model combined with recursive feature selection with cross-validation to obtain a balanced accuracy of 97%. In the same form, in [11], a comparison is presented between a U-Net encoder–decoder network and Bat-based U-Net Signal Analysis (BUSA) to detect EEGs with depression rates, with accuracy percentages higher than 98% and 99%, respectively.
On the other hand, there are also investigations that seek to generalize the detection of neurological problems. For example, using the database provided by the Temple University Hospital (TUH) EEG corporation [3], in [1], it was proposed to use a supervised Random Forest (RF) classifier for two health states: abnormal and normal, with an overall classification error rate of 31.7%. The same objective with the same database was also raised in [12] using a deep CNN network and in [13] with an AlexNet type network, with accuracy percentages equal to 85.4% and 87.5%, respectively.
Finally, in [14] it was decided to implement 2 phases to classify the database of [3]: processing and categorization with deep learning. Prior to processing, a sample selection was performed, discarding measurements that covered more than 21 channels, as well as the first 5 min of each signal. The rest was sampled at 100 Hz. For the first phase, the signal was decomposed into 3 different frequency ranges (1–7 Hz, 8–30 Hz and 31–100 Hz) using the Fourier transform to subsequently be stored in matrices of size C × M, where C is the number of channels and M the number of samples. For the classification, a mathematical model combining three convolutional neural networks and a multilayer perceptron (MLP) type network was used. The authors mention that the best results were obtained with the implementation of 4096 neurons for the first two Fully Connected layers and 2048 in the third, while for the last SoftMax layer, since there are 2 classification categories, the number of neurons required was only 2. The accuracy percentage was 89.13%, this being higher than previous works due to the mixture of works of two types of neural networks; Convolutional models were used to specialize each spectrum, and MLP to structure the output. The author also mentions that different sample sizes were used, involving time periods from 60 s to 20 min, with the latter obtaining the highest score. He also mentions that this technique can be applied to patients with brain-related diseases such as Alzheimer’s, epilepsy, etc. Table 1 shows some works whose impact is significant for this research.

Table 1.
Past research directly related to the research topic. The level of relevance is displayed in ascending order.
In summary, there are currently multiple research projects focused on the classification and detection of neurological abnormalities based on EEG analysis. According to the above, most of these studies use, first, preprocessing based on mathematical tools that highlight distinguishable metrics belonging to each of the groups in question and, subsequently, classification methods based on neural networks, both deep and compound. However, due to the difficulty in reading the samples, the classifiers tend to be complex, requiring many parameters due to the construction of the network and although this work uses the same methodology to solve the same objectives, the development of the problem differs in the processing algebra by using quaternionic elements, both to preserve the existing links between them and to facilitate operational calculations.
3. Discrete Wavelet Transform
Analyzing non-stationary signals is not an easy task, and although a well-known and widely implemented tool in mathematics and engineering is the Fourier transform [18], which decomposes a signal into waves with different frequencies, this decomposition is made up of sinusoidal functions within a fixed and practically infinite range, it is difficult to locate data of interest in the measurement.
On the other hand, the Wavelet transform [19] is an instrument that uses different types of orthogonal sinusoidal shapes of short durations called wavelet functions , originating from a main function called the Mother Wavelet , by adjusting the dilation parameters and translation , with the aim of concatenating them and shifting them along the signal , obtaining information at certain instants in time, as shown in the following equation:
In this way, an indirect sweep is performed in the time and frequency domain, with the development shown in Figure 1. Some types of mother wavelets are the Haar wavelet, formed first by a positive impulse and then by a negative one; the Morlet wavelet, which maintains its shape regardless of its width or offset values; the Daubechies wavelet used by digital filters; etc. [20].
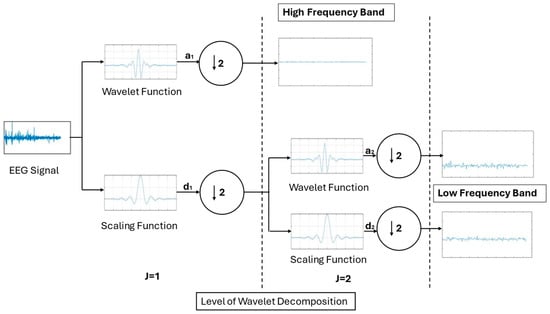
Figure 1.
Wavelet Transform Illustrative Representation. The input signal is defragmented into low- and high-frequency segments, generating the output components for each decomposition level , obtaining, in each one, an approximation signal and a detail signal from a wavelet function and a scaling function, respectively. The symbols 2↓ represent a down sampling by a factor of 2 applied to the filter outputs [21].
As a practical example of the extension of his theory in the field of control systems, we can mention what is presented in [22], where a Proportional, Integral and Derivative (PID) adaptive control is proposed to perform trajectories in a 6-degree-of-freedom haptic manipulator, using a Recurrent Quaternionic Wavelet Neural Network (QWNN) as the system identifier. For this study, the network used pure quaternion activation functions with wavelet functions derived from a RASP1-type mother wavelet, weights based on Euler angles with a direct equivalence with the rotation matrix, and the estimation error and the control signal as input. In this way, it is possible to obtain the estimated plan and the Jacobian and thus, be able to modify the gains corresponding to the control law. Subsequently, with inverse kinematics to calculate robot dynamics and a nonlinear trajectory as a reference, the convergence results can be observed, being these better compared to a classical PID. Finally, the authors emphasize the existence of a PID optimization with the QWNN, which allows it to perform precise movements even under the influence of external disturbances, such as gravitational components and the pressure exerted by the user on the haptic device. The results also highlight the relative simplicity of the network, as well as the estimation and control strategies, which provide robustness to the proposed methodology.
4. Quaternion Convolutional Neural Network
As time has passed, different types of neural networks have been created with the purpose of improving their accuracy and/or computational cost, either by reducing the number of parameters in their structures, integrating new layers, and even creating new activation functions. Another solution is to implement a new network variant known as a Quaternion Convolutional Neural Network (QCNN) [23,24], which deepens the network by integrating the quaternions, which are a type of algebra that expands the mathematical structure of complex numbers to capture orientations in 3D [25], into the normalization and convolution layers, as well as in initialization weights, to be able to work with the different dimensions of a value. For example, if we visualize a pixel in a color image as a 3-dimensional vector whose components are associated with the RGB (Red, Green, Blue) intensity values, then we can assign these 3 elements to the imaginary components of a quaternion, leaving the real part with a value equal to the modulus of the vector named pixel. In this way, a transformation from to is performed, allowing the element to be analyzed in higher dimensions, being effective for applications related to the image dehazing [26], as well as in photographic restoration processes [27]. Broadly speaking and summarizing what was developed by [25], the operation of the quaternionic convolutional layer is made up of 4 groups of fully linked filters, performing convolutional operations with the quaternionic vector of the data, allowing multiple features to be extracted in a single unit. Being a quaternionic filter, a quaternionic vector, , , and matrices with real numbers, , , and real vectors, and , and as the imaginary components of the quaternion, we have:
where
Therefore:
where , , and are the components of the quaternion convolution. Another layer that also underwent modifications for use with quaternions was the normalization layer, based on the Whitening matrix and the Cholesky decomposition to obtain a new set of values with a covariance equal to the identity formed by quaternion and matrix type parameters. Finally, for the case of the filter initialization, the variance of the quaternion weights will depend on the initialization scheme that is being implemented [25].
As a representative example of this methodology, there is the work developed in [28], where a quaternionic convolutional encoder–decoder network with Hamiltonian product (H-QCAE) can be visualized with a series of images with the objective of encoding and decoding its design in its entirety and comparing it with a network similar to H-QCAE, but using real numbers (R-CAE) instead of quaternions. With equal hyperparameter values in both networks, the results reported that during the training test with grayscale images and the evaluation with color images, those produced by H-QCAE retained their RGB values due to the quaternion’s uniqueness by respecting the link between its elements. Meanwhile, in the R-CAE network, the photographs became grayed out, since the convolutional layers became grayscale transformers, due to the acquisition of common features from the training database. Furthermore, R-CAE uses four times more parameters than H-QCAE, hence the quaternionic network stores less memory, making it more compact and robust.
This research demonstrates the efficiency of using quaternions to maintain the relationship between their parameters and highlights their potential for application in diverse domains. It also suggests that, when applied to image processing, QCNNs can be trained with RGB images by assigning each channel to a quaternionic component.
In summary, the use of QCNNs for imaging applications is not only limited to image classification or restructuring but can also be extended to encoding and decoding. This is due to its ability to preserve parameter relationships, unlike conventional CNNs. Thanks to this advantage, a broader view can be achieved when implemented on EEG recordings, defragmenting them into frequency bands equal to the number of parameters that make up the quaternion. This allows for parallelogram analysis without losing the signal’s uniqueness. Finally, it should be noted that EEGs, sometimes and in this approach, tend to have very long-time ranges, so the use of a large amount of computational memory is inevitable. With QCNNs, a reduction in computational operations is guaranteed thanks to the use of geometric algebra, specifically in the quaternionic layers of the network.
5. Materials and Methods
The focus of this research is to design an EEG classifier, detecting those that present some type of anomaly. Below there is a brief description of the different stages of development:
- -
- EEG database input: For this approach, the database provided by [3] was used, which is composed of 2 sections, a training section with 1346 abnormal (667 males and 679 females) and 1371 normal (603 males and 768 females) EEGs, and an evaluation section with 126 abnormal (63 for both genders) and 150 normal recordings (65 male and 85 female). It is important to note that the dataset intended for the training phase was partitioned at the EEG level, to form a validation group, extracting a total of 146 abnormal and 171 normal recordings, corresponding to 10% of the total training set samples. This was done with the goal of validating the performance of the proposed network with data it has not yet visualized. To perform the measurements, a total of 30 sensors were used, mostly at a frequency of 250 Hz. The files are in “edf” format, where each file contains the patient’s ID, the date and time of the exam, and the samples, mostly, totaling approximately, 300,000, equivalent to 20 min of recording. A total of 2383 subjects participated in the EEG recording acquisition, of which 1385 corresponded to the normal category and 998 to the abnormal category. The average age of the participants was approximately 51 years, with a standard deviation close to 56. Due to the sample size, some subjects appear more than once in the training data set; however, it is ensured that there is no overlap between recordings of training, test and validations sets [14].
- -
- Information Filtering: Because some of the recordings were only 16 min long, it was decided to use only samples until this time for all signals. In addition, to avoid noise obtained at the beginning of the test, the first minute was eliminated [12,13,14]. Regarding the sensors, only the first 23 were used, since in some tests, the rest were not used. However, the electrodes applied are the same for each patient.
- -
- Wavelet Transform: Since these were non-stationary signals, it was decided to implement Wavelet Transform to decompose each signal into 4 components: 3 at high frequencies and one at low frequencies. The decomposition number was 3, and the parent waveform used was the 12th-order Daubechies waveform due to its use in filters and its good performance for abrupt quadratic changes in signals. It is important to mention that tests were also carried out using different Wavelet mother waves with different orders and with different parameter values; however, the approach reported here is the one with the best observed results.
- -
- Zero Padding: Since the signals produced by the Wavelet transform are of different sizes, the Zero Padding method was chosen to equalize the dimensions to the highest value without altering their shape. This was achieved using the Fourier transform, subsequently adding zeros at high frequencies and immediately returning the result to the time domain.
- -
- Spectrogram: To facilitate the classification process, a time-frequency representation of the spectrogram of each signal was created.
- -
- QCNN: The purpose of the Wavelet transform producing four signals with different frequencies was to locate each one in the four components of the quaternion; the real part would correspond to the low-pass filter output, and the imaginary components to the high-pass filter outputs: to the last level, to the penultimate level, and to the first. In this way, the input matrix for the 4-dimensional network would be as follows:

Table 2.
QCNN for EEG anomaly detection. As input, the neural network handles quaternion-type elements to assign the EEG signal to one of two categories: abnormal or normal.
The processing algorithms were developed in MATLAB (version R2022a). The proposed neural network was implemented in Python 3.10.12, which already includes the libraries necessary for creating the QCNN-type network, using a computer running Linux (Ubuntu 22.04), equipped with 32 GB of RAM and a 24 GB GPU. Note: Due to software limitations, the already preprocessed input data set had to be subjected to subsampling, considering 1 sample of the signal for every 15.
6. Results
The objective of this approach is to develop an EEG anomaly classifier for medical purposes using a QCNN-type neural network. Therefore, it was decided to use the database of [3] and, simultaneously, compare it with other models used in the literature, as well as architectures developed in another research (k-Nearest Neighbor (kNN) and AlexNet)) and a hybrid structure, which present good classification performance whose figures allow verifying the performance of the proposed model.
Based on what was described in Section 4, the QCNN achieved an accurate rate of 76.667% on the test data, correctly labeling the corresponding class in most cases and in both classes, as shown in Figure 2. The true positive quadrant (0.73) contains the correctly classified abnormal EEG recordings. The true negative quadrant (0.80) contains the correctly identified normal EEG recordings. The false negative quadrant (0.20) groups together normal recordings that were erroneously categorized as abnormal; finally, the false positive quadrant (0.27) contains the abnormal EEG recordings that were incorrectly assigned to the normal recording category. Regarding performance, the QCNN achieved a stabilizing effect on the evolution of accuracy and a decrease in cross-entropy loss, both in the training and testing phases. This behavior can be observed in Figure 3, in the final stages of the process in both phases.
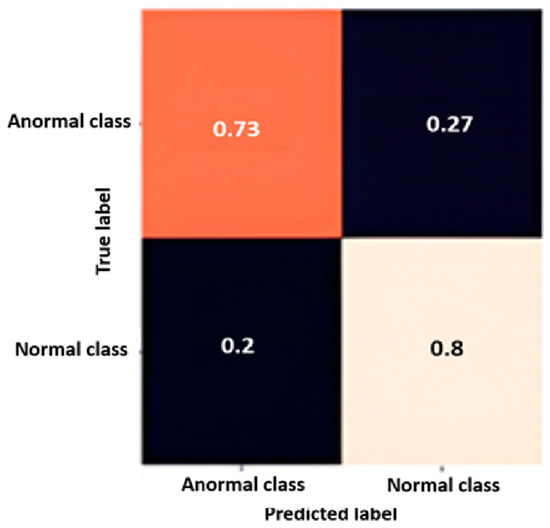
Figure 2.
Confusion Matrix of the QCNN for Anormal and Normal class. The main diagonal contains dominant values corresponding to true positive classifications.
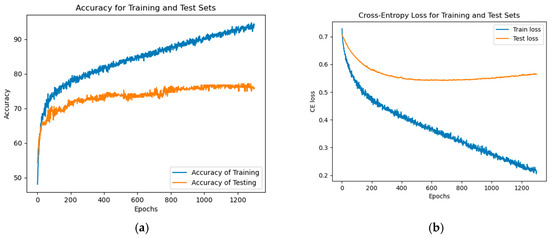
Figure 3.
Graphs of the QCNN correspond to both the training and test sets: (a) Accuracy to evaluate the model; (b) Cross-entropy loss to reflect the efficiency of the process, across the different epochs.
Thus, the first model selected to compare the performance of the QCNN is the CNN-type network, whose architecture and performance are shown in Figure 4. As we can see, its architecture is like that of the QCNN, with the difference that the CNN works with ordinary convolutional operations. As show in Figure 4a, it primarily comprises Convolutional layers, which are responsible for acquiring characteristic components of the input elements and subsequently applying them as filters. Likewise, the CNN also has Batch Normalization layers to normalize activations to accelerate training without stabilizing it, with ReLU activation functions to improve accuracy when performing nonlinear transformations, and with Linear layers to flatten the outputs and perform the desired final classification. Using the same hyperparameters as the QCNN in Figure 4b, the non-zero values in the false quadrants of the resulting confusion matrix are due, in part, to the network’s inability to maintain the relationship of each of the input components, performing independent analyses. Meanwhile, in Figure 4c, the separation between both accuracy representations of the respective sets is due to the CNN becoming specialized in the training dataset, neglecting assimilation of the test set, as shown in cross-entropy loss graphs, in Figure 4d.
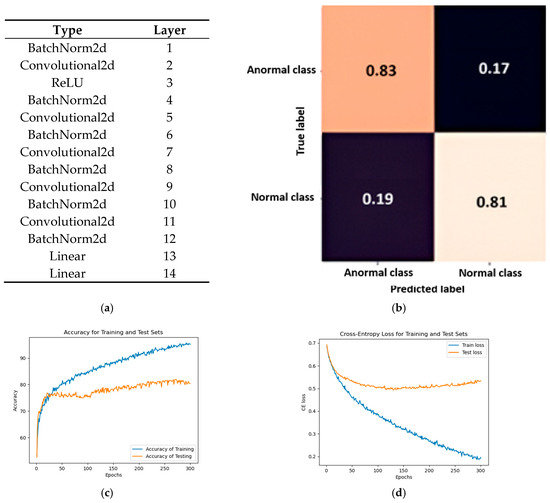
Figure 4.
CNN Features: (a) Architecture; (b) Confusion Matrix (The vertical axis represents the true labels and the horizontal axis the predicted labels); (c) Accuracy to evaluate the model; (d) Cross-entropy loss to reflect the efficiency of the process.
For the following model, the presented MLP architecture was affected by the limitations of the software used, which was described in Section 4. With an approximate number of 800,000 neurons for the first layer and 256 for the second, its Confusion Matrix demonstrates an imbalance in the categorization of the sample, unlike the previous models. Likewise, its precision and loss graphs appear to show no improvement over the epochs in both the training and testing stages. This can be verified by observing the illustrations in Figure 5.
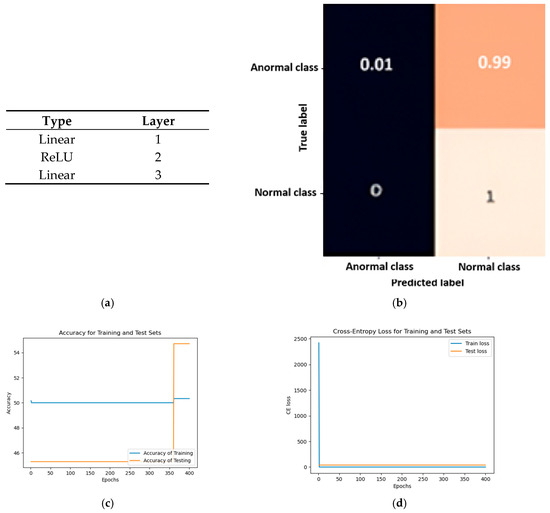
Figure 5.
MLP Features: (a) Architecture; (b) Confusion Matrix; (c) Accuracy to evaluate the model; (d) Cross-entropy loss to reflect the efficiency of the process.
The next model selected for comparison was the RF machine learning algorithm. For the latter, a total of 100 estimators were assigned, resulting in a confusion matrix like that of the QCNN and CNN, as shown in Figure 6. The accuracy and cross-entropy loss graphs could not be obtained due to the way the RF operates.
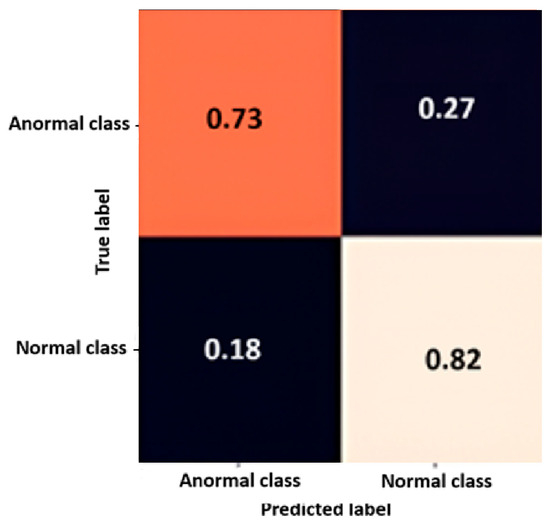
Figure 6.
Confusion Matrix of the RF. The main diagonal contains the values corresponding to the samples assigned by the network to the corresponding sector and which are higher than the rest of the matrix.
In the subsequent case, the classification obtained through the Support Vector Machine (SVM) architecture is presented, whose confusion matrix is shown in Figure 7. Due to the characteristics of the data, the model uses a Radial Basis Function, resulting in a total of 1572 support vectors. Like the RF model, the corresponding accuracy and cross-entropy loss graphs are not available.
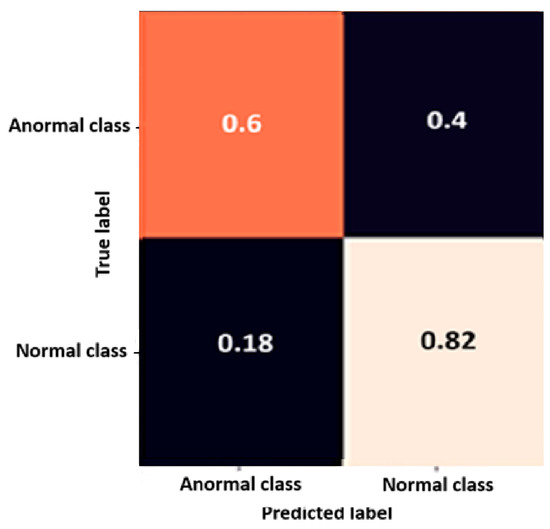
Figure 7.
Confusion Matrix of the SVM. The representation shows the evaluation of the performance of the classification model through the contrast between the true labels and the estimated labels.
Finally, the last model considered for the comparison of the QCNN’s performance is the recurrent neural network known as Long Short-Term Memory (LSTM). The selection of this model is based on the effectiveness that LSTM has demonstrated in processing sequential samples distributed over time within a signal. Detailing what is shown in Figure 8, the network comprises 64 neurons in the first layer, with each step fed back into the input vector, 32 neurons in the second layer, a 50% dropout rate in the third layer, and a sigmoid activation function in the final layer. This configuration yields a classification behavior that is both robust and clearly distinguishable. Moreover, the training curves and the cross-entropy loss indicate a consistent stabilization pattern appropriate for the employed dataset.
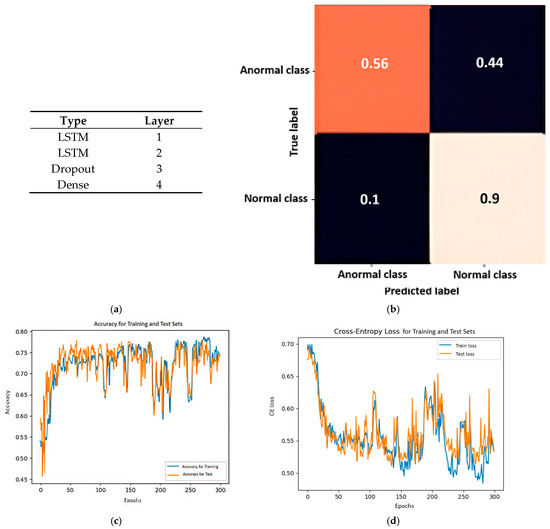
Figure 8.
LSTM Features: (a) Architecture; (b) Confusion Matrix; (c) Accuracy to evaluate the model; (d) Cross-entropy loss to reflect the efficiency of the process.
With respect to the metrics presented in Table 3, the QCNN model achieves performance percentages close to those obtained by the CNN and RF models, with accuracy values of 81% and 77%, respectively, outperforming the MLP, SVM and LSTM with approximate differences of 20%, 5% and 3% in each case, using the test sets. However, when considering the results reported in [14], where a hybrid model based on CNN and MLP networks is proposed, the performance of the QCNN remains a relatively competitive alternative to such architecture. Furthermore, the QCNN shows a smaller decrease between the accuracy percentages obtained with the training and test data sets, approximately 15%. Although these types of networks are still pioneering in this branch of science, they can generalize to levels like those of the CNN network, using a smaller number of parameters and preserving the relationship between the quaternionic components, which represent the frequency bands of the preprocessed EGG signal.

Table 3.
Metrics Comparison between models. The legend N/A indicates that the architecture analyzed does not describe or is unable to provide that value.
Similarly, Table 4 shows the QCNN as the model with the lowest number of parameters required to meet the objective proposed in this research, using up to 2 times less compared to the closest architecture, which is the LSTM. The models developed in [1,13] and [14] do not provide such data.

Table 4.
Comparison of features between models. Because the QCNN has fewer parameters than the other proposed models, this architecture can allow for longer processing times to obtain more accurate and robust results.
Finally, Figure 9 shows the Receiver Operating Characteristic (ROC) curves for each selected model, along with their respective Area Under Curve (AUC) values. Thus, the QCNN emerges as a strong classifier, achieving 77% of the covered area and ranking its trajectory higher than a model with random categorization.
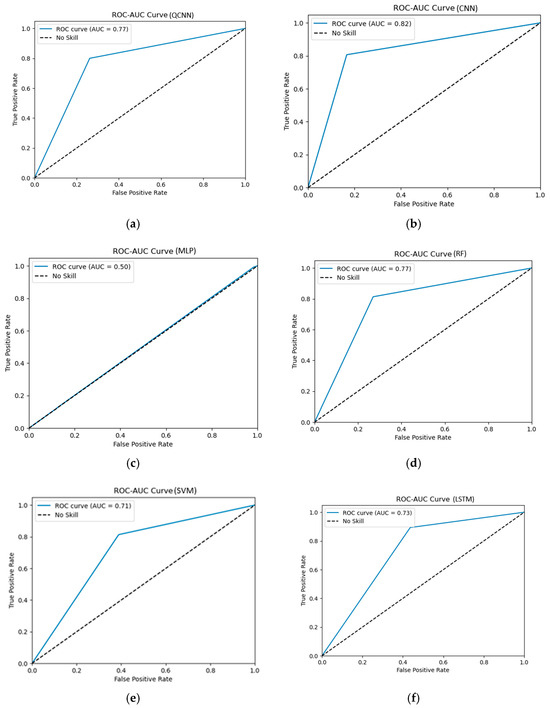
Figure 9.
ROC curve with their respective values of Area Under the Curve (AUC) to each of the models compared with randomly generated tests (No Skill): (a) QCNN; (b) CNN; (c) MLP; (d) RF; (e) SVM; (f) LSTM.
7. Discussion
Based on the implementation of the quaternionic convolutional neural network (QCNN) for anomaly detection in an EEG dataset, the results obtained indicate that the network is capable of satisfactorily fulfilling the proposed objective. Once the signal has undergone a continuous filtering process at different levels by the Wavelet transform, conditioning in a quaternionic element allows the uniqueness of the EGG to be maintained. This is reflected in an accurate percentage of approximately 77% and a confusion matrix with a clearly defined main diagonal. The non-zero values for the two false quadrants are due, in part, to the presence of EEG recordings that exhibit characteristics of both classes, both in terms of frequency and amplitude, which can make correct classification difficult. These aspects represent inherent challenges in processing EEG signals, which are highly sensitive to noise and susceptible to ambiguous behaviors derived from various causes. Likewise, each subject may present electroencephalographic characteristics whose waveform can easily be confused with a neurological abnormality. For example, if spike-and-wave activity occurs continuously, the network could classify it as an abnormal EEG, when in fact it could correspond to a normal sample with epileptiform morphological features. Knowing the patient’s neurological history would make it possible to avoid potential labeling conflicts by the QCNN, thus avoiding adding an additional level of complexity to the analysis process. When comparing this methodology with conventional models, as well as with an architecture resulting from a combination neural networks, it is observed that the QCNN offers an interesting alternative, not only because of its good percentage of accuracy in the metrics, but also because it obtains a ROC curve in the area of classifiers with good performance, which makes them an interesting option considering a smaller number of parameters used, thanks to the use of quaternions. The above can be supported by the results obtained from the experiments carried out: CNN had the best percentages in test data accuracy, precision, F1 score and specificity with 81.88%, 85.21%, 82.872% and 83.333%, respectively, while the MLP-type network led in the recall metric with 99.33%. Now, with respect to the final accuracy, CNN obtained a value of 84.94%, being the highest percentage compared to the other models, followed by the QCNN with 80.54%, LSTM with 73.67%, and finally, MLP with 53.20%. Thus, it can be mentioned that the usage situation will depend on the desired results and resource limitations. Regarding the precision and loss graphs, both in QCNN and CNN models, both show a moderate distance between the training and testing curves, which could mean a possible existence of overlearning, so the acquired learning decreases with the test dataset and the ability to identify new data sets is limited. However, although these types of samples present certain difficulties in interpretation, due to the chaotic nature of the signals and the application of technically rigorous classifiers, the implementation of the developed network yields satisfactory results, that allow it to be considered for future research in a more exhaustive way, in addition to its implementation in applications, whether related to the branch but in a more ambitious way or in other areas of science. On the other hand, although some models cannot access certain metrics due to their mathematical algorithm, there are others whose information was not included in the reported documents (N/A). However, the motivation remains intact, allowing this research to establish a comparison with various existing approaches, demonstrating the suitability of the proposed solution to compete with state-of-the-art methods.
8. Conclusions
In this work, we have demonstrated the effectiveness of a QCNN in the detection of abnormal EEGs using peculiar feature analysis tools in different engineering domains, using a database that has served as a validation method in multiple investigations. After applying continuous filtering at different levels in the frequency domain, signal conditioning using a quaternionic element makes it possible to preserve the uniqueness of the EEG, thereby ensuring the fidelity and coherence of the information obtained. In this way, an analysis of the information is performed without disturbing the connection of the input parameters, broadly generalizing the classification process. This is partly due to the ability of Wavelet Transform to analyze non-stationary functions with discontinuities and spikes in the frequency and time domains, simultaneously dividing the signals into low- and high-frequency groups. This preprocessing complements the performance of the QCNN, which, thanks to its convolutional output generation, allows a joint analysis that respects the relationship between the convolutional layers and the components of the different frequency ranges of the signal. Regarding the number of parameters, despite consuming more processing time, the QCNN proved to be superior when using a smaller quantity compared to the other models, thus allowing the simultaneous execution of other tasks without causing delays in processing. On the other hand, due to processor memory limitations, the output data from the preprocessing process was subsampled, taking one sample of the signal for every 15, reducing the total to almost 95%. Therefore, it is logical to assume that there is a considerable loss of information, which would greatly help to improve the accuracy of anomaly detection; however, this does not limit the metric balance of the network, allowing it to position itself as a reliable alternative to the level of CNNs and AlexNet, which would require more expensive computational resources compared to the network presented in this investigation.
Similarly, we intend to further investigate the development of QCNN-type networks, either with the integration of the proposed architecture or with the conversion of layers to planes of the quaternion algebra, using more evaluation metrics extending the number of samples used to attack this problem and further generalize the detection of anomalies, especially with those patients whose records were placed off-diagonal, since the results obtained expose the great potential they can have. Finally, we hope to extend their applications to determine the type of anomalies present in these data in a much shorter period and facilitate the diagnosis of some diseases that, if not detected in a timely manner, can drastically impair patients’ quality of life. We also plan to use the proposed method to classify EEG signals from body movements, either from existing databases or from real-time recordings, and use them to teleoperate a manipulator arm, both virtually and in real time.
Author Contributions
Conceptualization, G.O.-F. and E.B.-C.; methodology, G.O.-F., G.A.-E. and E.B.-C.; software, G.O.-F. and G.A.-E.; validation, G.O.-F., D.M.-R. and E.B.-C.; investigation, G.O.-F., D.M.-R. and E.B.-C.; resources, G.O.-F., G.A.-E., D.M.-R. and E.B.-C.; data curation, G.O.-F. and G.A.-E.; writing—original draft preparation, G.O.-F., D.M.-R. and E.B.-C.; writing—review and editing, G.O.-F., D.M.-R. and E.B.-C.; visualization, G.O.-F., D.M.-R. and E.B.-C.; supervision, G.O.-F., D.M.-R. and E.B.-C.; project administration, G.O.-F., D.M.-R. and E.B.-C.; funding acquisition, E.B.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Mexican Secretaría de Ciencia, Humanidades, Tecnología e Innovación (SECIHTI) through an academic grant.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We thank Ofelia Begovich for her scientific and moral support in the development of this work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| EEG | Electroencephalogram |
| QCNN | Quaternion Convolutional Neural Network |
| WT | Wavelet Transform |
| CNN | Convolutional Neural Networks |
| MLP | Multilayer Perceptron |
| RF | Random Forest |
| SVM | Support Vector Machine |
| LSTM | Long- Short Term Memory |
| IED | Interictal Epileptiform Discharge |
| DANN | Domain Adversarial Neural Network |
| AFTA | Adaptive Frequency-Time Attention |
| BUSA | Bat-based U-Net Signal Analysis |
| TUH | Temple University Hospital |
| PID | Proportional, Integral and Derivative |
| QWNN | Recurrent Quaternionic Wavelet Neural Network |
| RGB | Red, Blue and Green |
| ROC | Receiver Operating Characteristic |
| AUC | Area Under Curve |
References
- López, S.; Suarez, G.; Jungreis, D.; Obeid, I.; Picone, J. Automated Identication of Abnormal Adult EEGs. In Proceedings of the IEEE Signal Processing in Medicine and Biology Symposium, Philadelphia, PA, USA, 12 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Smith, S. EEG in the diagnosis, classification, and management of patients with epilepsy. J. Neurol. Neurosurg. Psychiatry 2005, 76, 2–7. [Google Scholar] [CrossRef] [PubMed]
- Harati, A.; Lopez, S.; Obeid, I.; Jacobson, M.; Tobochnik, S.; Picone, J. The Tuh Eeg Corpus: A Big Data Resource for Automated EEG Interpretation. In Proceedings of the IEEE Signal Processing in Medicine and Biology Symposium, Philadelphia, PA, USA, 13 December 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Choi, W.; Kim, J.; Nam, H.; Kam, T. Curriculum Learning with Sampling Scheduler for Imbalanced EEG-Based Seizure Detection. In Proceedings of the 2025 13th International Conference on Brain-Computer Interface (BCI), Gangwon, Republic of Korea, 24–26 February 2025; pp. 1–5. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, Y.; Xu, S.; Wu, D.; Wu, X. Self-Supervised Learning with Adaptive Frequency-Time Attention Transformer for Seizure Prediction and Classification. Brain Sci. 2025, 15, 382. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Matsubara, Y.; Sakurai, Y.; Sun, J. Long-Term EEG Partitioning for Seizure Onset Detection. In Proceedings of the Thirty-Ninth AAAI Conference on Artificial Intelligence, Philadelphia, PA, USA, 25 February 2025; pp. 14221–14229. [Google Scholar] [CrossRef]
- Lekkas, G.; Vrochidou, E.; Papakostas, G. Time–Frequency Transformations for Enhanced Biomedical Signal Classification with Convolutional Neural Networks. BioMedInformatics 2025, 5, 7. [Google Scholar] [CrossRef]
- Ranjan, S.; Tripathi, A.; Shende, H.; Badal, R.; Kumar, A.; Yadav, P.; Joshi, D.; Kumar, L. Deep learning-based classification of dementia using image representation of subcortical signals. BMC Med. Inform. Decis. Mak. 2025, 25, 113. [Google Scholar] [CrossRef] [PubMed]
- Jang, K.; In, Y.; Jin, H.; Joon, S.; Woon, P. Dementia classification using two-channel electroencephalography features. Sci. Rep. 2025, 15, 11513. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In KDD ’16: Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Gupta, V.; Kumar, V.; Singh, S.; Prince; Lee, Y.S.; Ra, I.H. Deep Learning Model for Analyzing EEG Signal Analysis. IEEE Access 2025, 13, 91034–91045. [Google Scholar] [CrossRef]
- Schirrmeister, R.; Gemein, L.; Eggensperger, K.; Hutter, F.; Ball, T. Deep learning with convolutional neural networks for decoding and visualization of EEG pathology. In Proceedings of the 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 2 December 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Amin, S.; Shamim, M.; Muhammad, G.; Rahmad, A. Cognitive Smart Healthcare for Pathology Detection and Monitoring. IEEE Access 2019, 7, 10745–10753. [Google Scholar] [CrossRef]
- Alhussein, M.; Muhammad, G.; Hossain, M. EEG Pathology Detection Based on Deep Learning. IEEE Access 2019, 7, 27781–27788. [Google Scholar] [CrossRef]
- Shoeb, A. Application of Machine Learning to Epileptic Seizure Onset Detection and Treatment. Ph.D. Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009; pp. 1–162. Available online: http://hdl.handle.net/1721.1/54669 (accessed on 26 February 2025).
- Prusa, J.; Khoshgoftaar, T.; Dittman, D.; Napolitano, A. Using random undersampling to alleviate class imbalance on tweet sentiment data. In Proceedings of the 2015 IEEE International Conference on Information Reuse and Integration, San Jose, CA, USA, 6–8 August 2015; pp. 197–202. [Google Scholar] [CrossRef]
- Schalk, G.; McFarland, D.; Hinterberger, T.; Birbaumer, N.; Wolpaw, J. BCI2000: A general-purpose brain-computer interface (BCI) system. IEEE Trans. Biomed. Eng. 2024, 51, 1034–1043. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, W. Computation of wavelet and multiwavelet transforms using Fast Fourier Transform. J. Port. Sci. Res. 2021, 4, 111–117. [Google Scholar] [CrossRef]
- Montoya, J. La Transformada Wavelet; Revista de la Universidad de Mendoza: Mendoza, Argentina, 2001; pp. 1–4. [Google Scholar]
- Pinto, E. Análisis y Evaluación de los Niveles de Energía Obtenidos Mediante WPT Para Defectología En Ejes; Universidad Carlos III de Madrid: Getafe, Spain, 2012; pp. 1–164. Available online: https://e-archivo.uc3m.es/bitstream/10016/16582/1/PFC_Elena_Pinto_Moreno_Anexos.pdf (accessed on 26 February 2025).
- Alzaq, H.; Ustundag, B. An optimized two-level discrete wavelet implementation using residue number system. EURASIP J. Adv. Signal Process. 2018, 2018, 41. [Google Scholar] [CrossRef]
- Bayro, E.; Ortega, G.; Martínez, G. Conformal Geometric Algebra for Medical Robotics and Quaternion Wavelet Neural Network for Adaptive PID Control of Haptic Devices. Biomed. J. Sci. Tech. Res. 2025, 61, 53444–53465. [Google Scholar]
- Altamirano, G.; Gershenson, C. Quaternion Convolutional Neural Networks: Current Advances and Future Directions. Adv. Appl. Clifford Algebras 2024, 34, 42. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, Y.; Xu, H.; Chen, C. Quaternion Convolutional Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 645–661. [Google Scholar] [CrossRef]
- Gaudet, C.; Maida, A. Deep Quaternion Networks. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Hu, E.; Wang, A.; Shiri, B.; Lin, W. VNDHR: Variational Single Nighttime Image Dehazing for Enhancing Visibility in Intelligent Transportation Systems via Hybrid Regularization. IEEE Trans. Intell. Transp. Syst. 2025, 26, 10189–10203. [Google Scholar] [CrossRef]
- Huang, C.; Li, Z.; Liu, Y.; Wu, T.; Zeng, T. Quaternion-based weighted nuclear norm minimization for color image restoration. Pattern Recognit. 2022, 128, 108665. [Google Scholar] [CrossRef]
- Parcollet, T.; Morchid, M.; Linarès, G. Quaternion convolutional neural networks for heterogeneous image processing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).