Numerical Simulation for Drill Collar Noise Signal Removal in Elemental Logging While Drilling
Abstract
1. Introduction
2. Methodology
3. Numerical Simulation
3.1. Monte Carlo Method and Simulation Model
3.2. Energy and Time Spectrum Characteristic Analysis
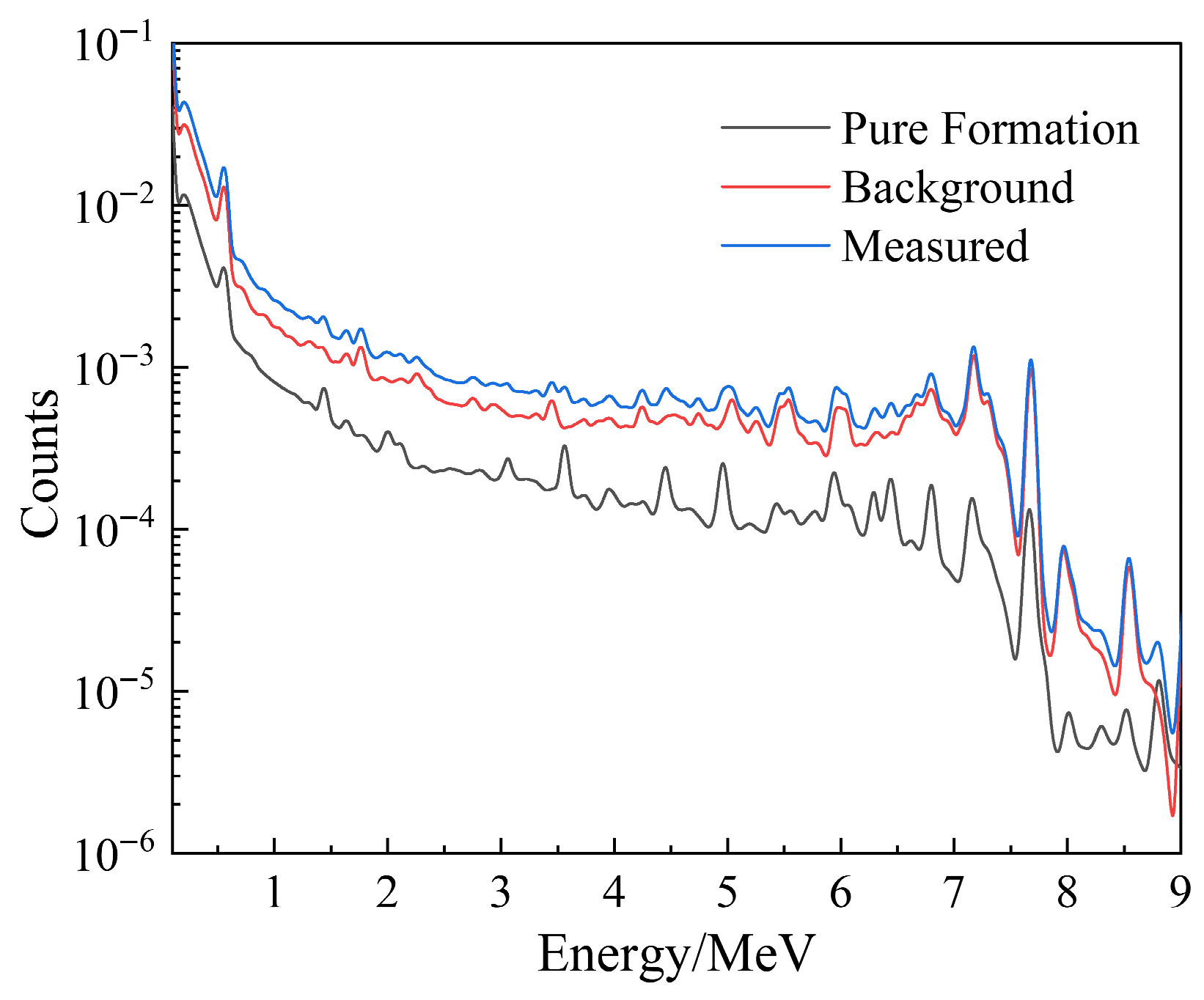
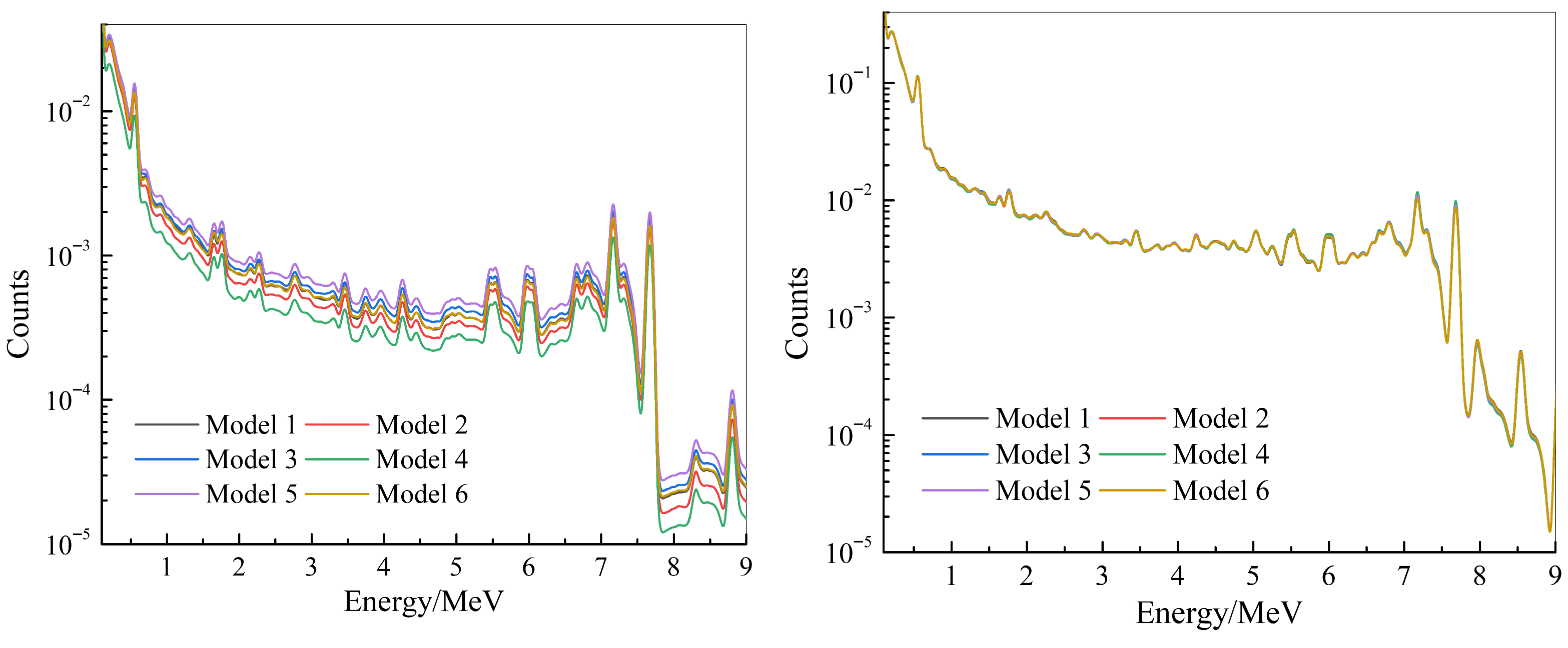
3.2.1. Capture Spectrum Recorded by Far Detector
3.2.2. Capture Spectrum Recorded by Near Detector
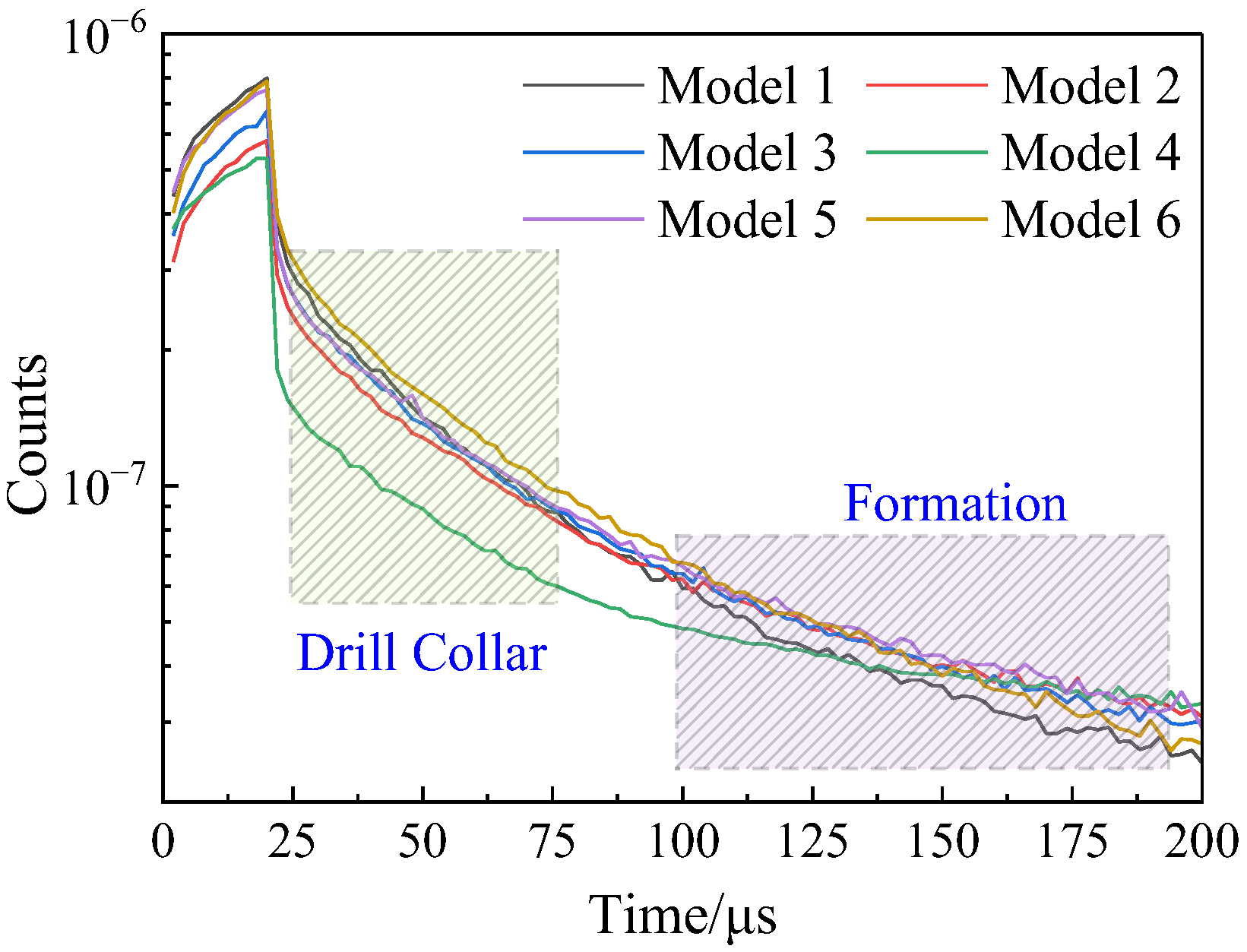
3.2.3. Gamma Time Spectrum of Dual Detector
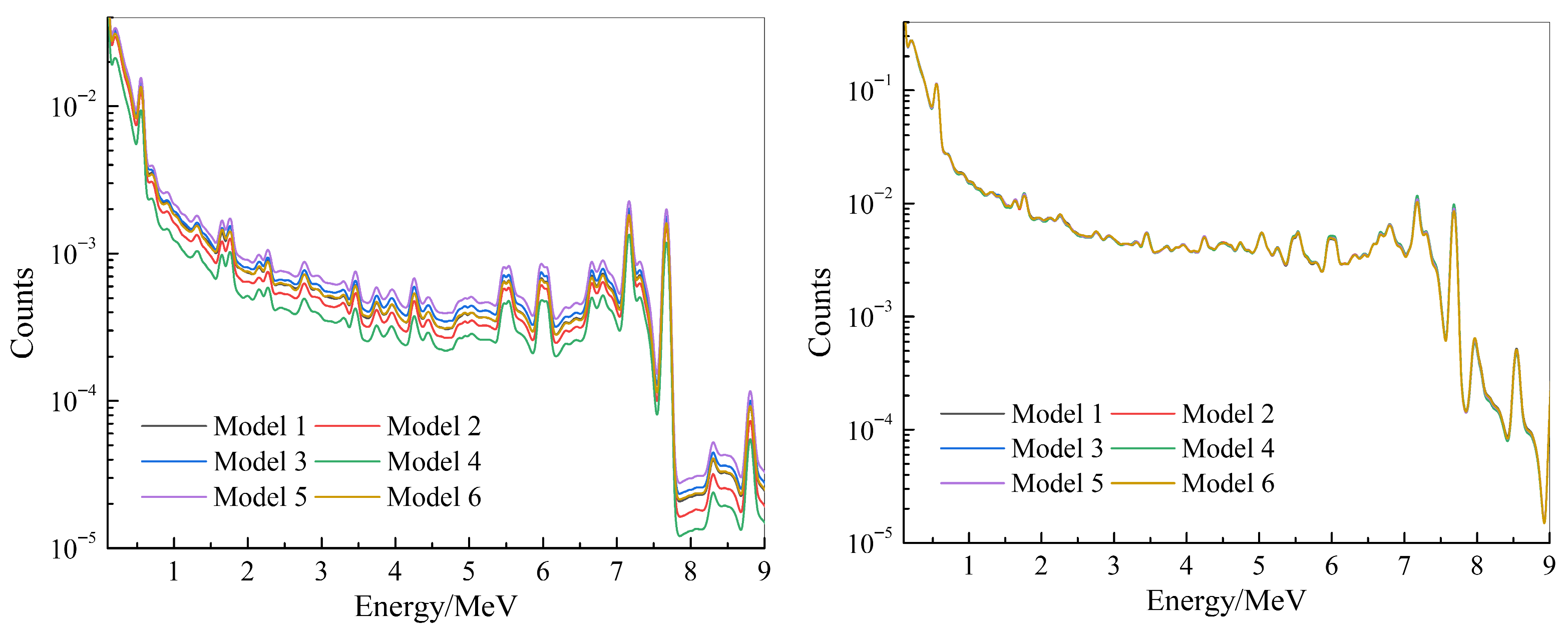
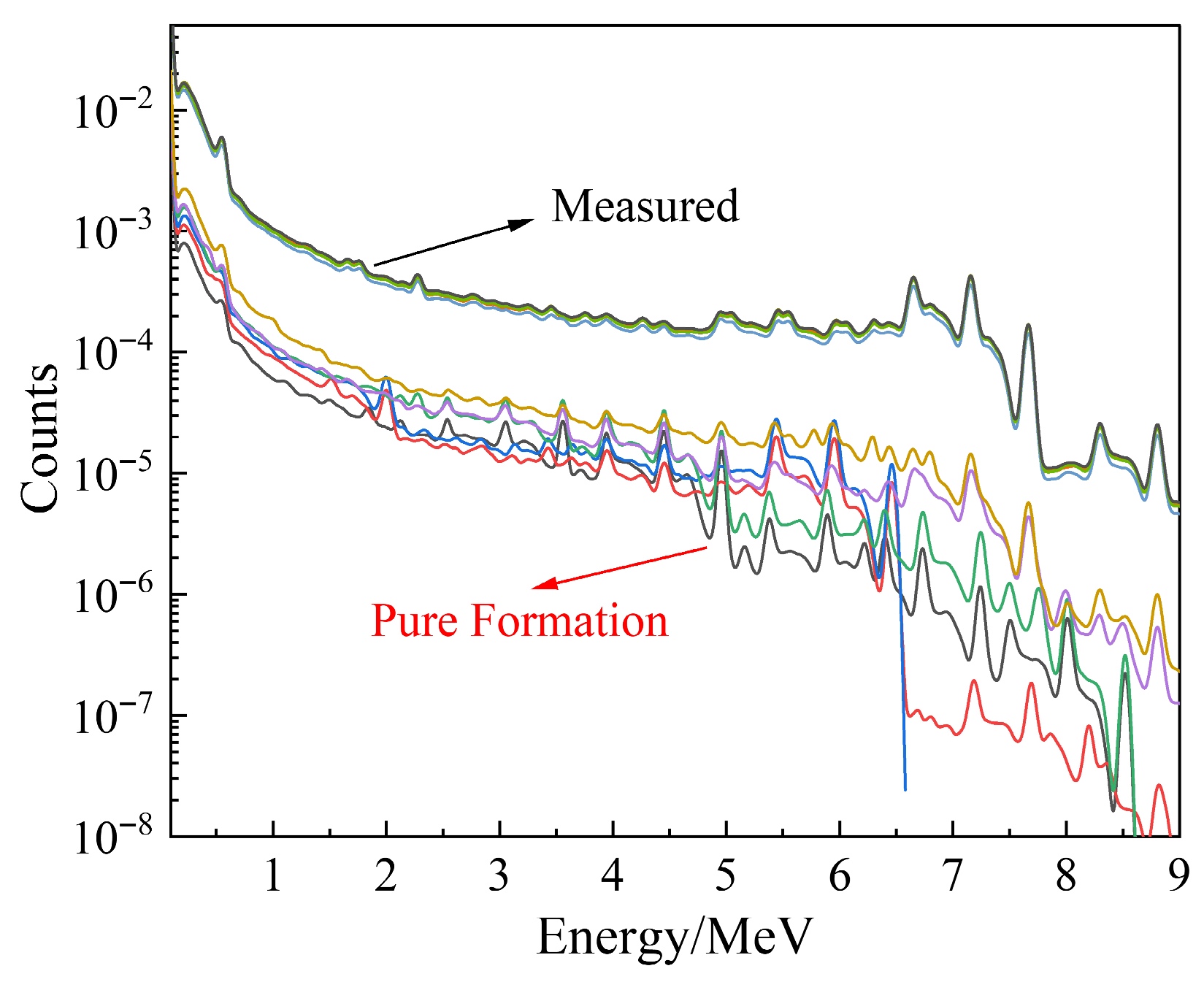
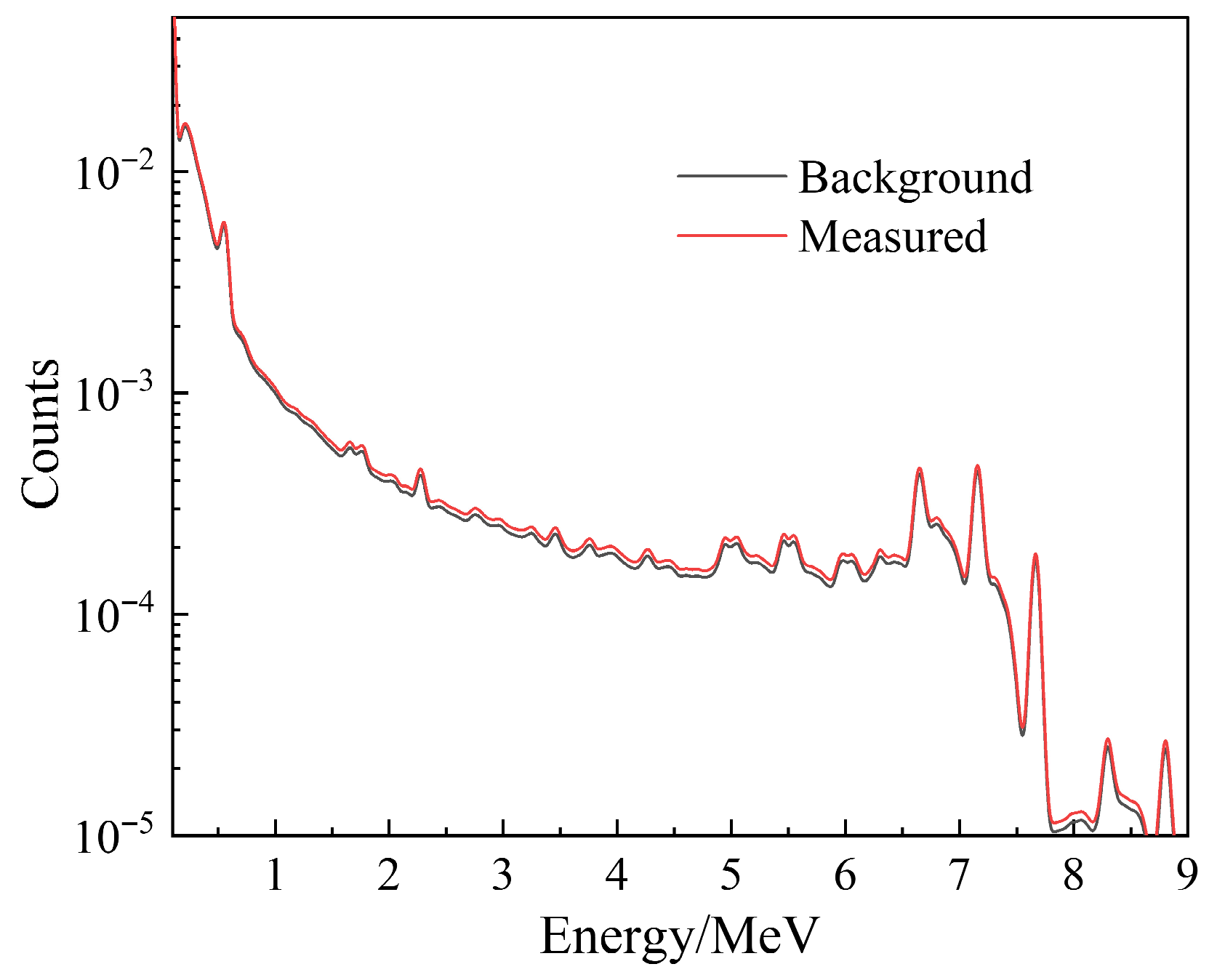
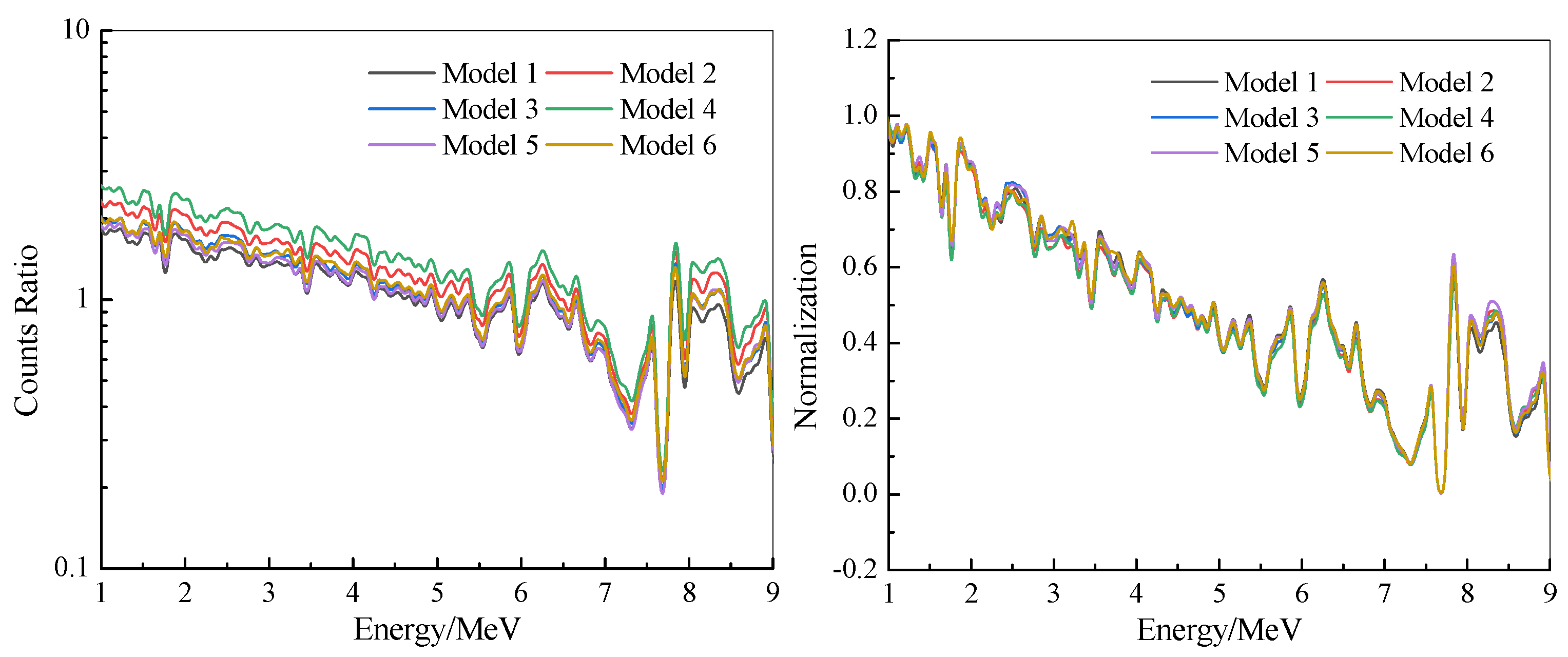
3.3. Extraction Method of Pure Formation Gamma Spectrum
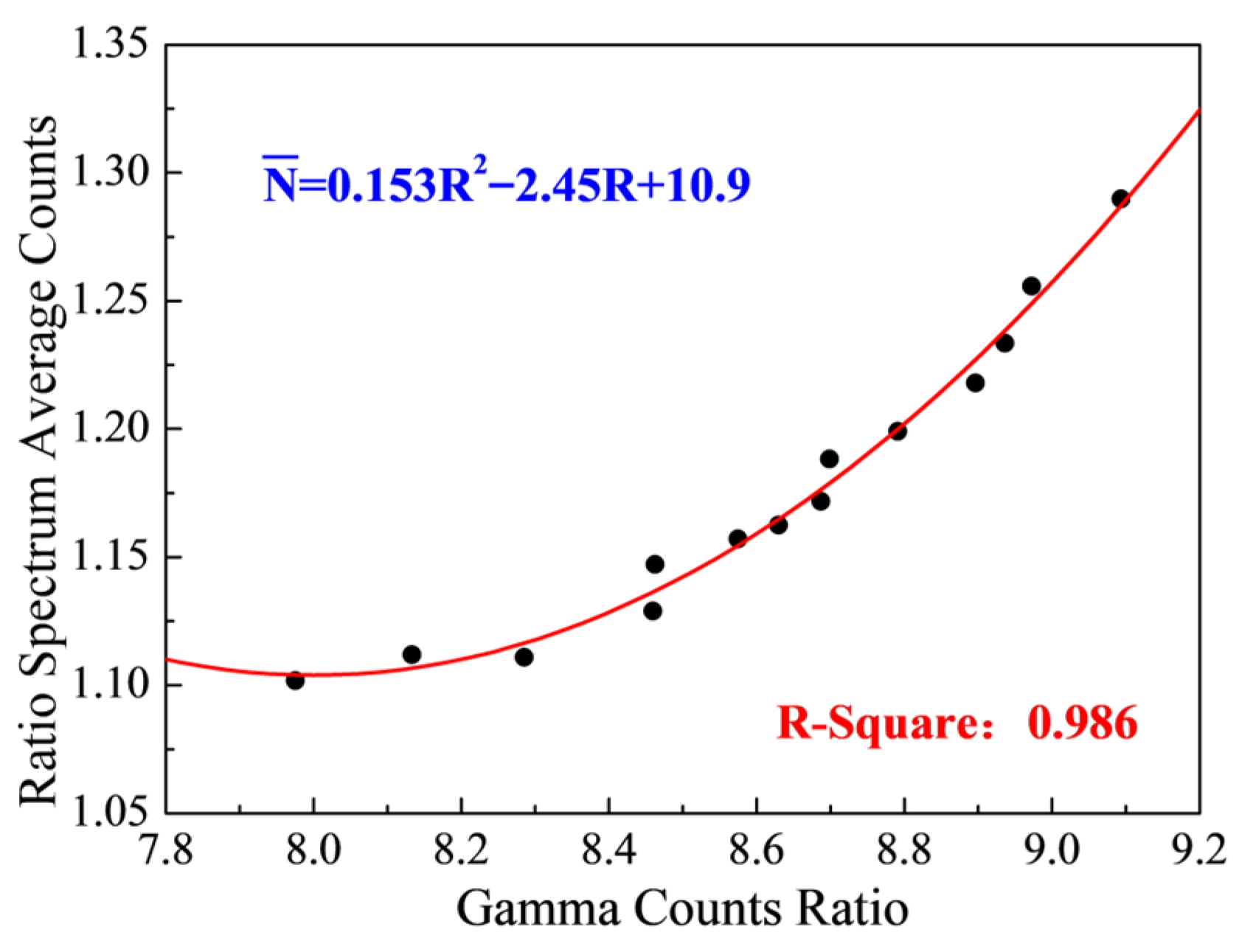
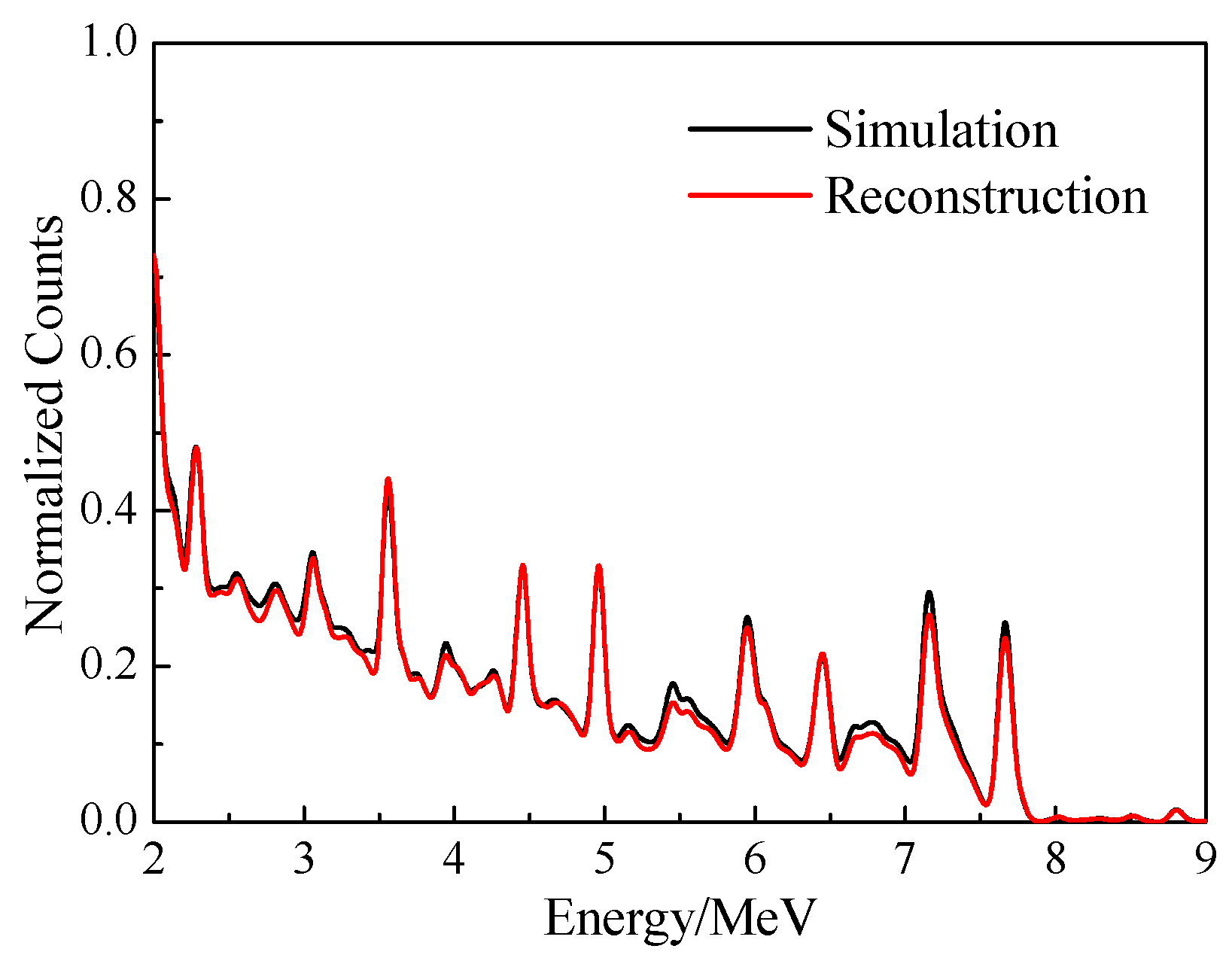
3.4. Verification of Calculation Accuracy of Element Yield
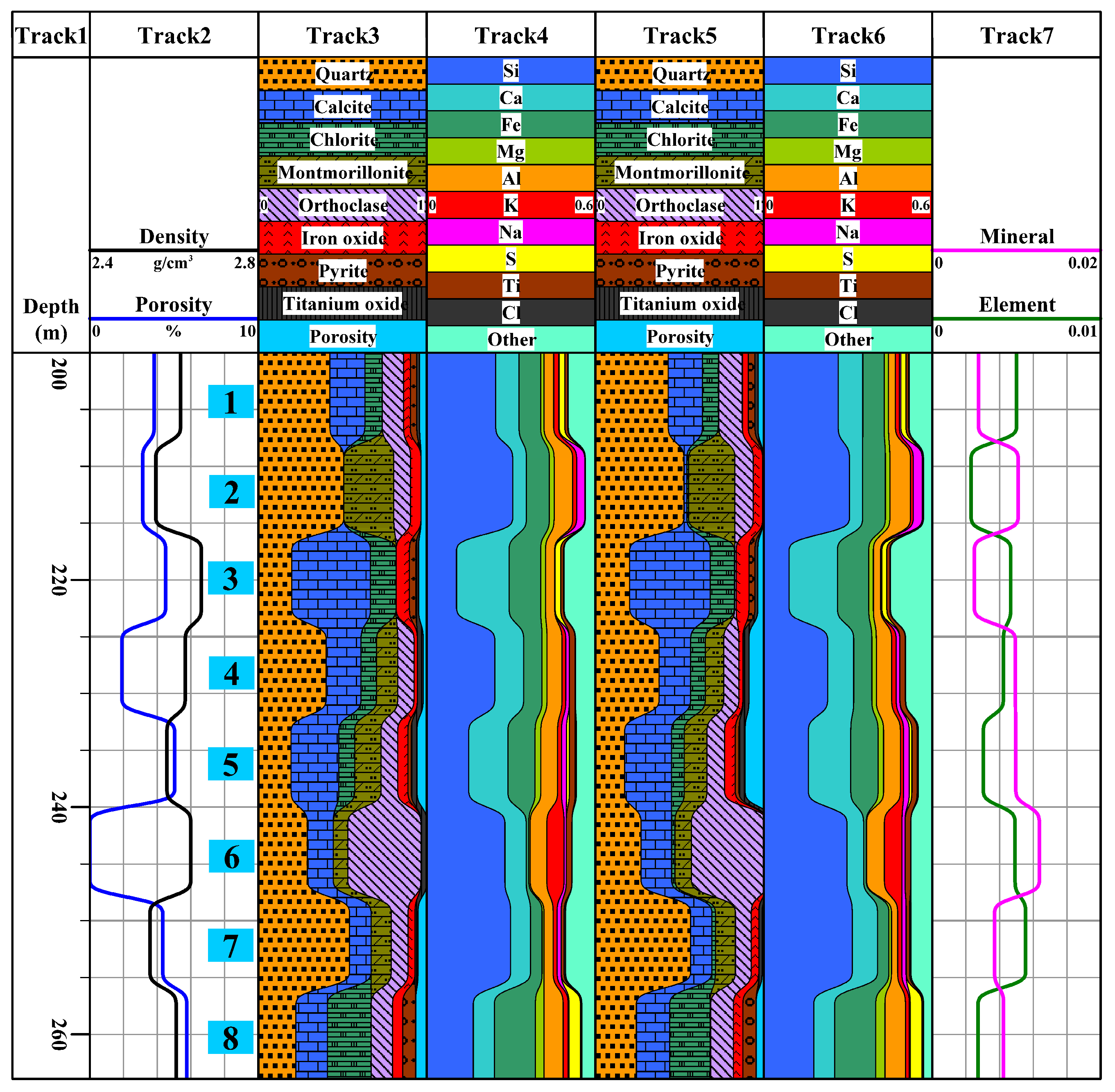
4. A Simulation Example
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pedersen, B.K.; Pedersen, E.S.; Morriss, S.L.; Constable, M.V.; Vissapragada, B.; Sibbit, A.; Stoller, C.; Almaguer, J.; Evans, M.; Shray, F.; et al. Understanding the effects of cesium/potassium formate fluid on well log response-a case study of the Kristin and Kvitebjorn fields, Offshore Norway. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Sun, J.; Chen, M.; Li, Q.; Ren, L.; Dou, M.; Zhang, J. A new method for predicting formation lithology while drilling at horizontal well bit. J. Pet. Sci. Eng. 2021, 196, 107955. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, G.; Bai, J.; Ding, W.; Yang, H.; Liu, Y. Quantitative prediction of the drilling azimuth of horizontal wells in fractured tight sandstone based on reservoir geomechanics in the Ordos Basin, central China. Mar. Pet. Geol. 2022, 136, 105439. [Google Scholar] [CrossRef]
- Herron, M.M. Mineralogy from geochemical well logging. Clays Clay Miner. 1986, 34, 204–213. [Google Scholar] [CrossRef]
- James, E.S.; Omole, O.; Diedjomahor, J.; Crowe, J. Calibration of the elemental capture spectroscopy tool using the Niger delta formation. In Proceedings of the Nigeria Annual International Conference and Exhibition, Abuja, Nigeria, 6–8 August 2007. [Google Scholar]
- Galford, J.; Quirein, J.; Shannon, S.; Truax, J.A.; Witkowsky, J. Field test results of a new neutron-induced gamma-ray spectroscopy geochemical logging tool. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Pemper, R.R.; Sommer, A.; Guo, P.; Jacobi, D.; Longo, J.; Bliven, S.; Rodriguez, E.; Mendez, F.; Han, X. A new pulsed neutron sonde for derivation of formation lithology and mineralogy. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Radtke, R.J.; Lorente, M.; Adolph, B.; Berheide, M.; Fricke, S.; Grau, J.; Herron, S.; Horkowitz, J.; Jorion, B.; Madio, D.; et al. A new capture and inelastic spectroscopy tool takes geochemical logging to the next level. In Proceedings of the SPWLA 53rd Annual Logging Symposium, Cartagena, Colombia, 16–20 June 2012. [Google Scholar]
- Grau, J.A.; Schweitzer, J.S. Prompt γ-ray spectral analysis of well data obtained with NaI (Tl) and 14 MeV neutrons. Nucl. Geophys. 1987, 1, 157–165. [Google Scholar]
- Crittin, M.; Kern, J.; Schenker, J.L. The new prompt gamma-ray activation facility at the Paul Scherrer Institute, Switzerland. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2000, 449, 221–236. [Google Scholar] [CrossRef]
- Mohamad, N.; Defrian, B.S.; Kusaka, K.; Simatupang, J. Optimization of matrix acidization by elementary capture spectroscopy log. In Proceedings of the International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 20–21 February 2002. [Google Scholar]
- AlRuwaili, S.B.; AlWaheed, H.H. Petrophysical models and techniques for shaly-sand formation evaluation. In Proceedings of the Abu Dhabi International Conference and Exhibition, Abu Dhabi, United Arab Emirates, 10–13 October 2004. [Google Scholar]
- Liu, J.; Zhang, F.; Wang, X.; Han, F.; Yuan, Z. Numerical study on determining formation porosity using a boron capture gamma-ray technique and MCNP. Appl. Radiat. Isot. 2014, 94, 266–271. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Liu, J. Monte Carlo simulation of PGNAA system for determining element content in the rock sample. J. Radioanal. Nucl. Chem. 2014, 299, 1219–1224. [Google Scholar]
- MacDonald, R.; Bradford, C.; Kersey, D.G.; Zhang, T.; Alsuhaibani, A.; Crary, S. Improved lithology determination from nuclear logs in complex carbonate environments. In Proceedings of the North Africa Technical Conference and Exhibition, Cairo, Egypt, 14–17 February 2010. [Google Scholar]
- Perez, G.; Mendez, F.E.; Alarcon, N.; Paris, M.J. Pulsed neutron through-casing technology for determination of mineralogy and total organic carbon–first case study in the Neuquén Basin, Argentina. In Proceedings of the SPWLA 56th Annual Logging Symposium, Long Beach, CA, USA, 18–22 July 2015. [Google Scholar]
- Zhou, T.; Rose, D.; Miles, J.; Gendur, J. Self-compensated cased-hole pulsed neutron spectroscopy measurements. In Proceedings of the SPWLA 61st Annual Logging Symposium, Virtual Online Webinar, 24 June–29 July 2020. [Google Scholar]
- Gjerdingen, T.; Nygaard, J.; Elshayeb, T.; Hoch, E.; Narayanan, R. Application of spectroscopy and sigma measurements to enhance petrophysical evaluations and geosteering in the mineralogical complex, thin bedded Nahr Umr sandstone reservoir. In Proceedings of the International Petroleum Technology Conference, Doha, Qatar, 7–9 December 2009. [Google Scholar]
- Weller, G.; Griffiths, R.; Stoller, C.; Allioli, F. A new integrated LWD platform brings next-generation formation evaluation services. In Proceedings of the SPWLA 46th Annual Logging Symposium, New Orleans, LA, USA, 26–29 June 2005. [Google Scholar]
- Reichel, N.; Evans, M.; Allioli, F.; Mauborgne, M.L.; Nicoletti, L.; Haranger, F.; Laporte, N.; Stoller, C.; Cretoiu, V.; El Hehiawy, E.; et al. Neutron-Gamma Density (NGD): Principles, field test results and log quality control of a radioisotope-free bulk density measurement. In Proceedings of the SPWLA 53rd Annual Logging Symposium, Cartagena, Colombia, 16–20 June 2012. [Google Scholar]
- Glasstone, S.; Edlund, M.C. The Elements of Nuclear Reactor Theory; van Nostrand: New York, NY, USA, 1952. [Google Scholar]
- Feld, B.T. The neutron. Exp. Nucl. Phys. 1953, 2, 240. [Google Scholar]
- Battistoni, G.; Cerutti, F.; Fasso, A.; Ferrari, A.; Muraro, S.; Ranft, J.; Roesler, S.; Sala, P.R. The FLUKA code: Description and benchmarking. In Proceedings of the AIP Conference Proceedings, Batavia, IL, USA, 6–8 September 2006; American Institute of Physics: College Park, MD, USA, 2007; Volume 896, pp. 31–49. [Google Scholar]

| Model Number | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Mineral and relative volume fraction (%) | Quartz | 100 | 0 | 0 | 80 | 70 | 50 |
| Dolomite | 0 | 100 | 0 | 0 | 0 | 0 | |
| Calcite | 0 | 0 | 100 | 0 | 0 | 20 | |
| Kaolinite | 0 | 0 | 0 | 20 | 0 | 0 | |
| Montmorillonite | 0 | 0 | 0 | 0 | 30 | 0 | |
| Orthoclase | 0 | 0 | 0 | 0 | 0 | 23 | |
| Iron oxide | 0 | 0 | 0 | 0 | 0 | 5 | |
| Titanium oxide | 0 | 0 | 0 | 0 | 0 | 2 | |
| Model Number | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | |
|---|---|---|---|---|---|---|---|---|---|
| Mineral and relative Volume fraction (%) | Quartz | 70 | 0 | 50 | 0 | 38 | 73 | 22 | 45 |
| Dolomite | 10 | 60 | 35 | 88 | 0 | 0 | 48 | 15 | |
| Calcite | 0 | 0 | 10 | 0 | 15 | 12 | 0 | 9 | |
| Kaolinite | 0 | 13 | 0 | 0 | 0 | 0 | 0 | 15 | |
| Montmorillonite | 0 | 0 | 0 | 10 | 0 | 0 | 0 | 12 | |
| Orthoclase | 17 | 25 | 0 | 0 | 45 | 12 | 30 | 0 | |
| Iron oxide | 3 | 0 | 4 | 2 | 0 | 2 | 0 | 3 | |
| Titanium oxide | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 1 | |
| Element Type | Simulation/% | Reconstruction/% | Absolute Error/% | Relative Error/% |
|---|---|---|---|---|
| Si | 22.70 | 23.49 | 0.79 | 3.48 |
| Ca | 16.10 | 17.19 | 1.09 | 6.76 |
| Fe | 49.61 | 47.50 | 2.11 | 4.25 |
| Al | 7.53 | 7.01 | 0.52 | 6.94 |
| Na | 4.13 | 4.61 | 0.47 | 11.45 |
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Mineral volume fraction/% | Quartz | 42 | 49 | 20 | 40 | 19 | 29 | 52 | 22 |
| Calcite | 20 | 0 | 46 | 20 | 27 | 15 | 12 | 18 | |
| Chlorite | 10 | 0 | 15 | 9 | 9 | 0 | 0 | 25 | |
| Montmorillonite | 0 | 30 | 0 | 13 | 16 | 9 | 12 | 0 | |
| Orthoclase | 13 | 10 | 0 | 10 | 10 | 45 | 10 | 13 | |
| Iron oxide | 2 | 3 | 4 | 1 | 3 | 0 | 2 | 3 | |
| Pyrite | 2 | 0 | 2 | 0 | 1 | 0 | 0 | 4 | |
| Titanium oxide | 1 | 0 | 1 | 2 | 2 | 2 | 1 | 0 | |
| Porosity/% | 10 | 8 | 12 | 5 | 13 | 0 | 11 | 15 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, J.; Zhang, Q. Numerical Simulation for Drill Collar Noise Signal Removal in Elemental Logging While Drilling. Appl. Sci. 2025, 15, 12057. https://doi.org/10.3390/app152212057
Fan J, Zhang Q. Numerical Simulation for Drill Collar Noise Signal Removal in Elemental Logging While Drilling. Applied Sciences. 2025; 15(22):12057. https://doi.org/10.3390/app152212057
Chicago/Turabian StyleFan, Jilin, and Qiong Zhang. 2025. "Numerical Simulation for Drill Collar Noise Signal Removal in Elemental Logging While Drilling" Applied Sciences 15, no. 22: 12057. https://doi.org/10.3390/app152212057
APA StyleFan, J., & Zhang, Q. (2025). Numerical Simulation for Drill Collar Noise Signal Removal in Elemental Logging While Drilling. Applied Sciences, 15(22), 12057. https://doi.org/10.3390/app152212057






