Study of Intelligent Identification of Radionuclides Using a CNN–Meta Deep Hybrid Model
Abstract
1. Introduction
2. Experimental Methods
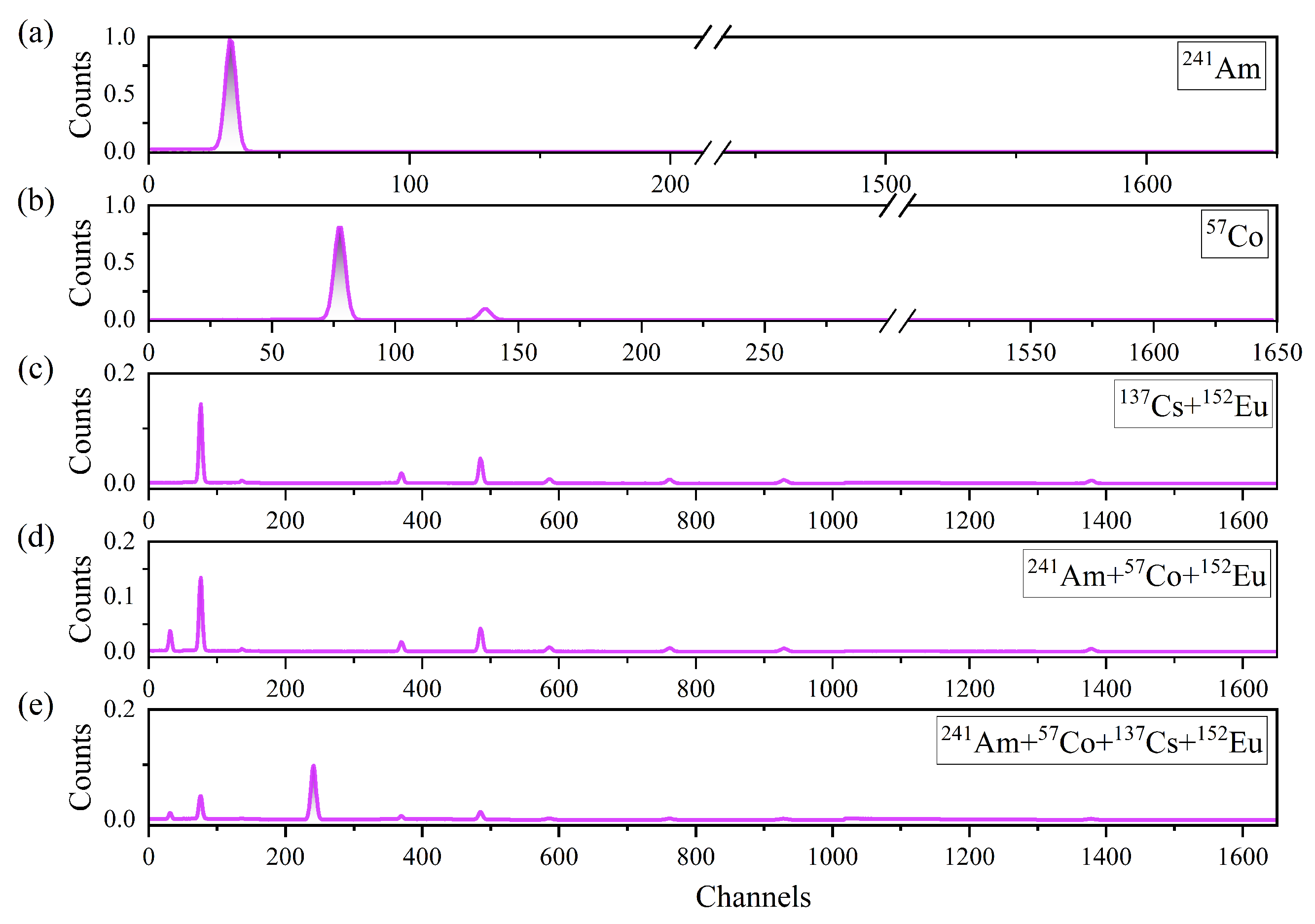
2.1. Dataset Construction
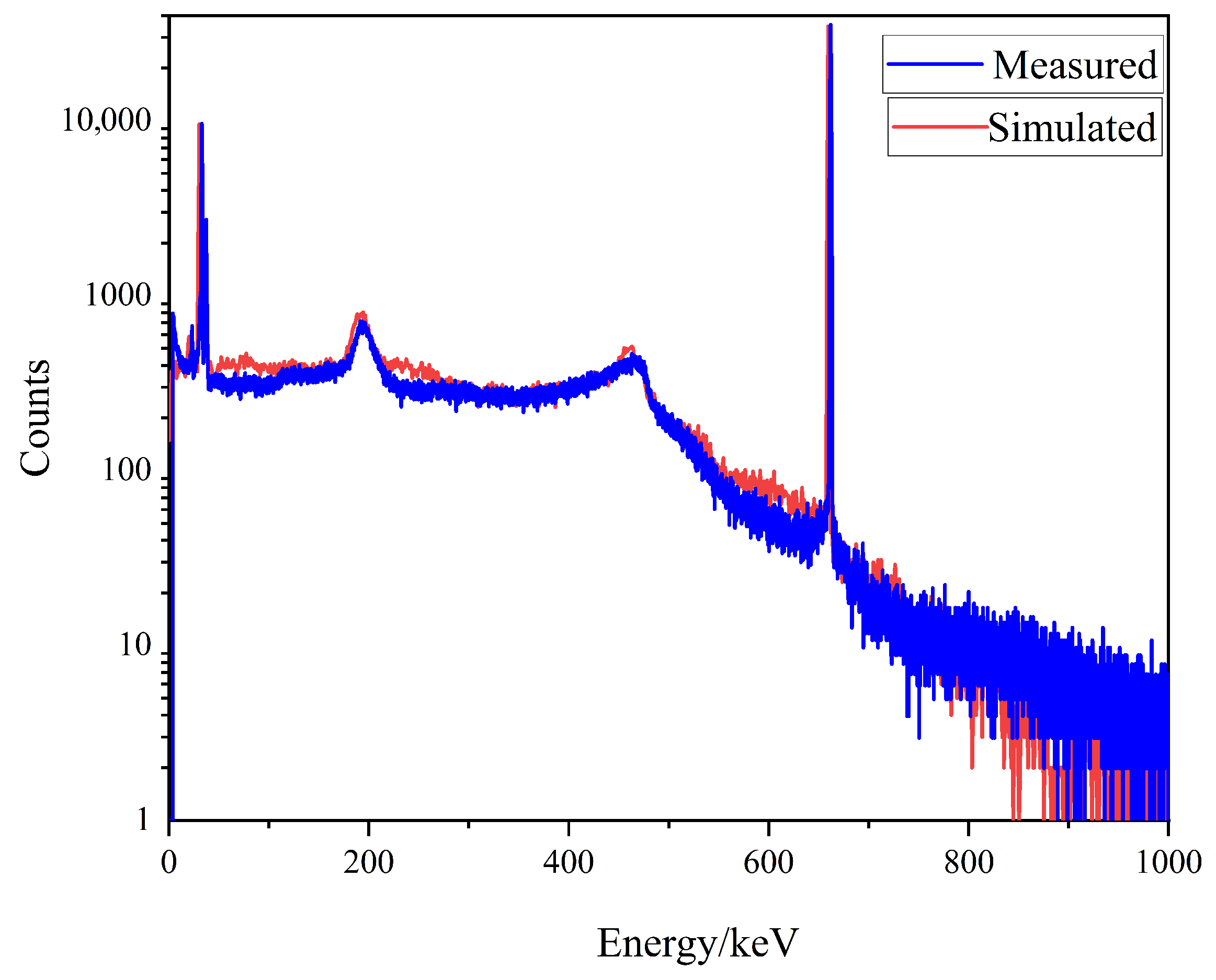
2.2. Spectral Data Preprocessing
2.3. Machine Learning Models
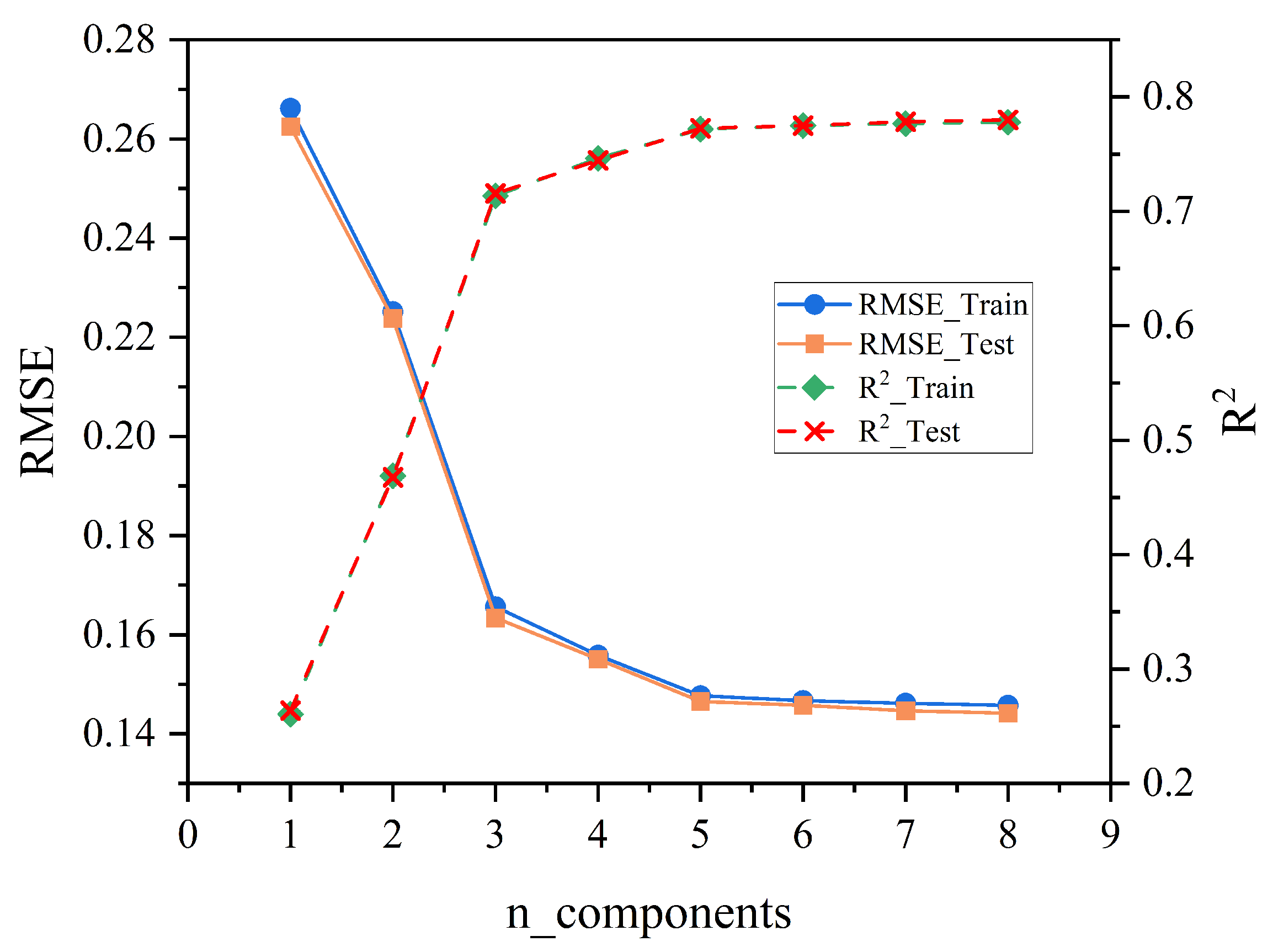
2.3.1. Partial Least Squares Regression (PLSR)
2.3.2. Random Forest (RF)
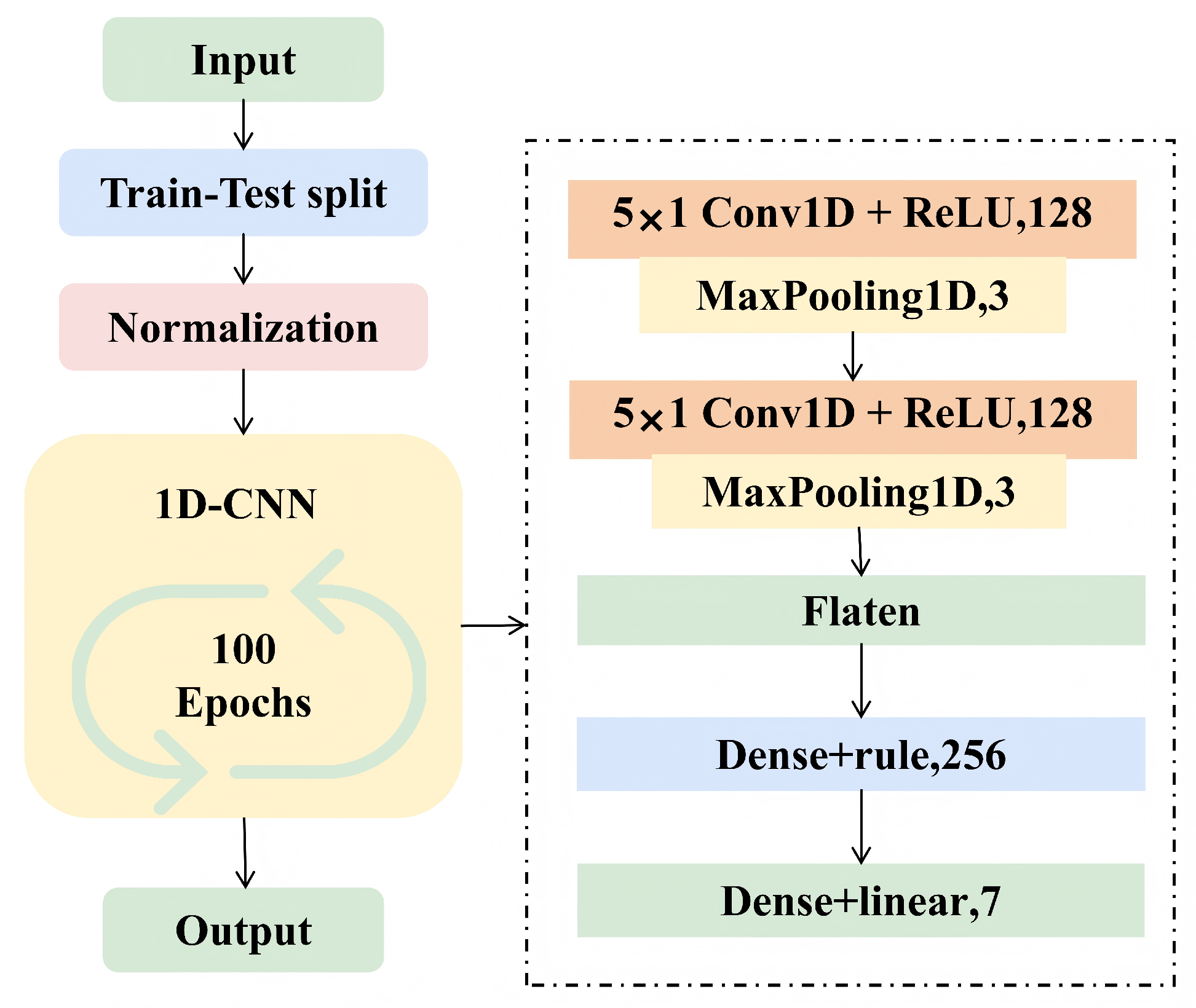
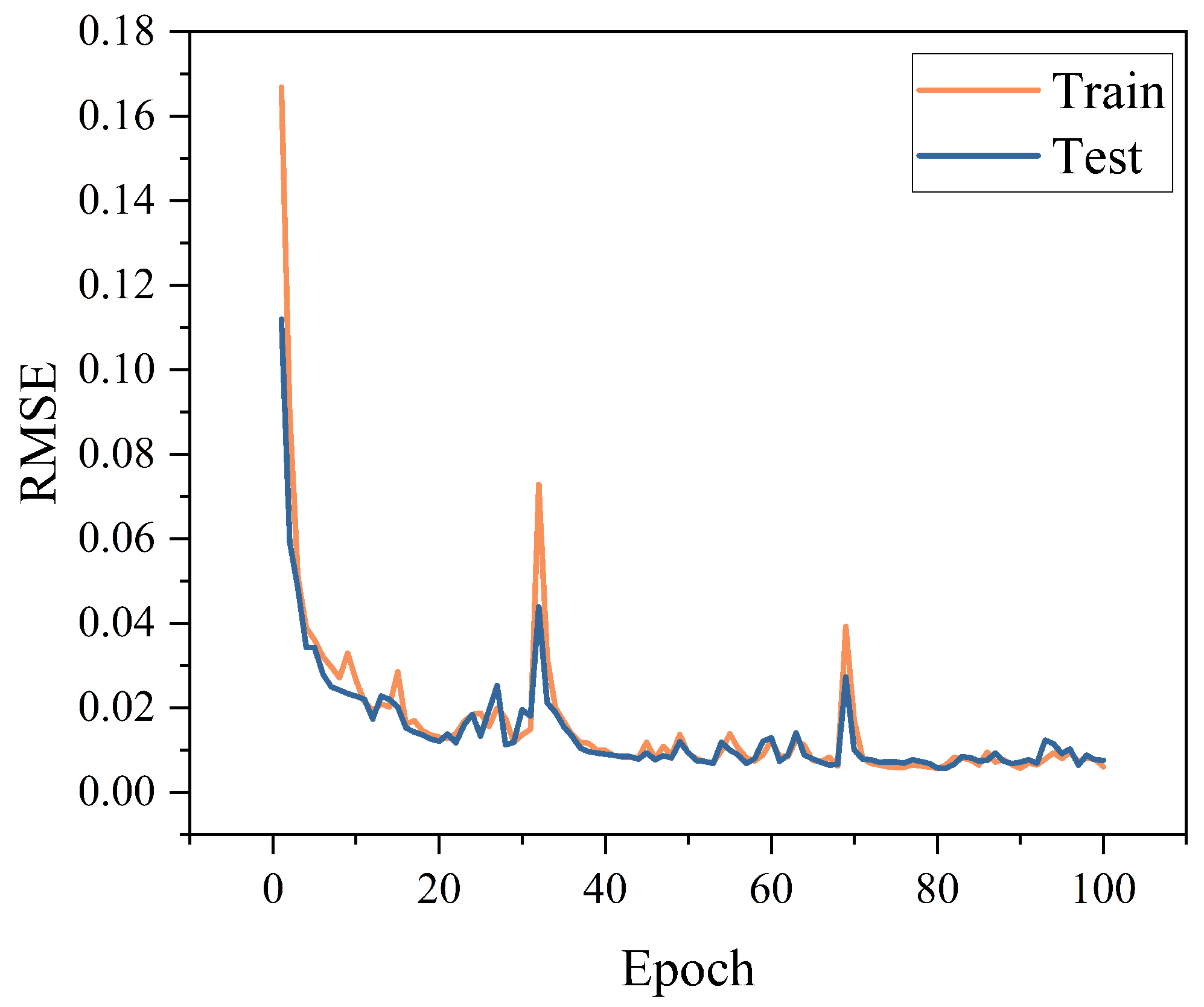
2.3.3. Convolutional Neural Network (CNN)
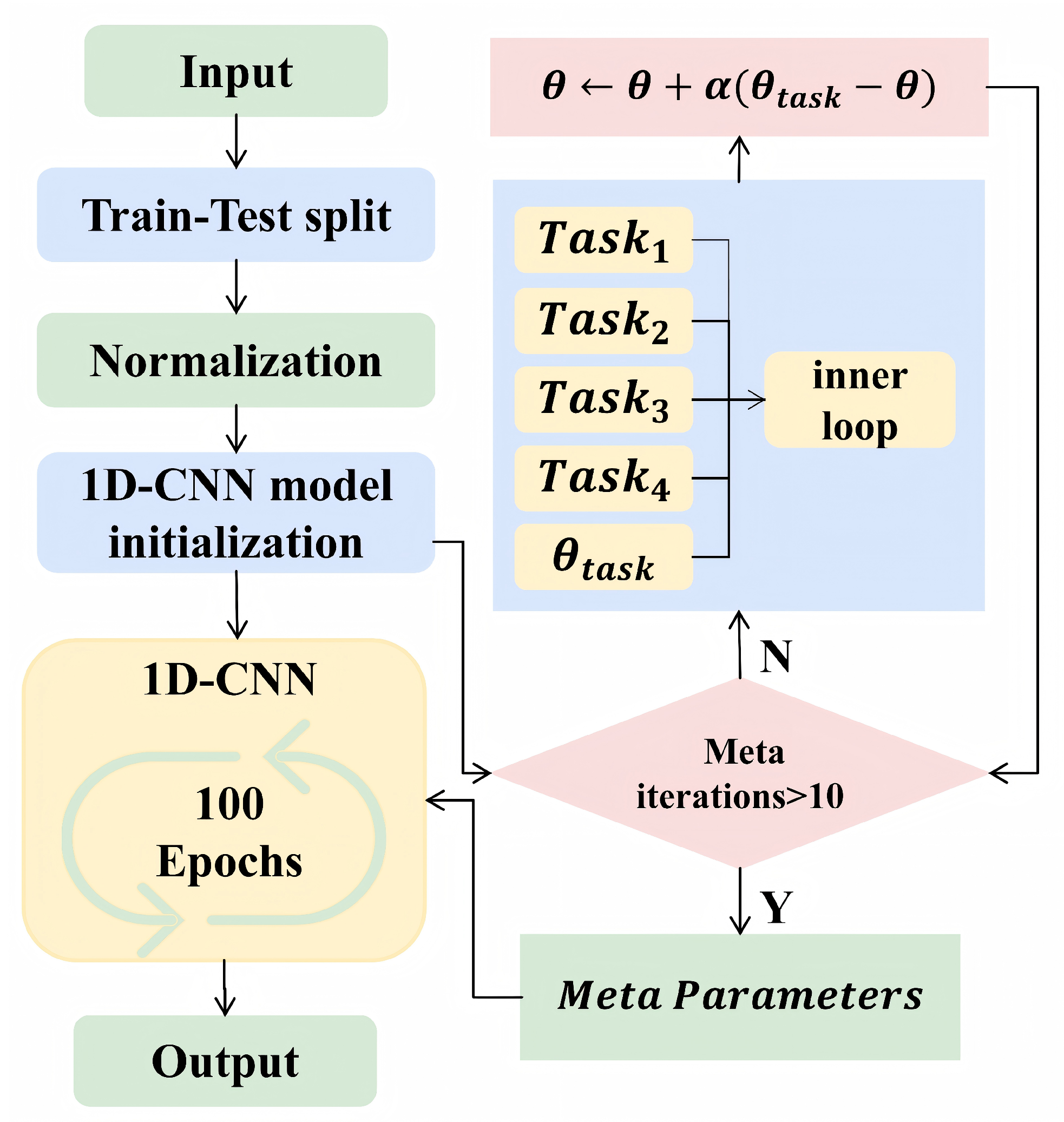
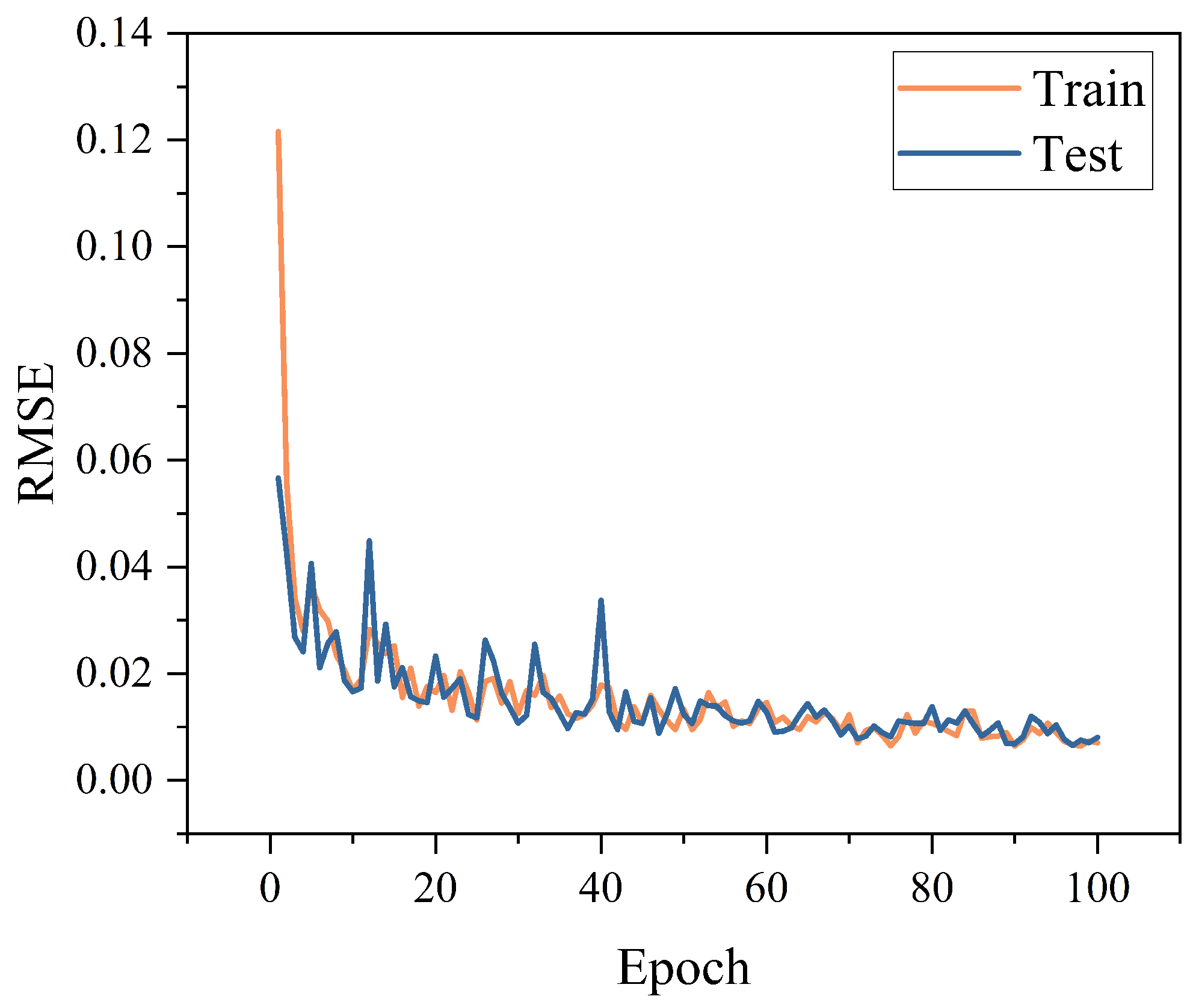
2.3.4. CNN–Meta
2.4. Evaluation Metrics
2.5. Software
3. Results and Discussion
3.1. Model Optimization Process and Results
3.1.1. Optimization of the PLSR Model
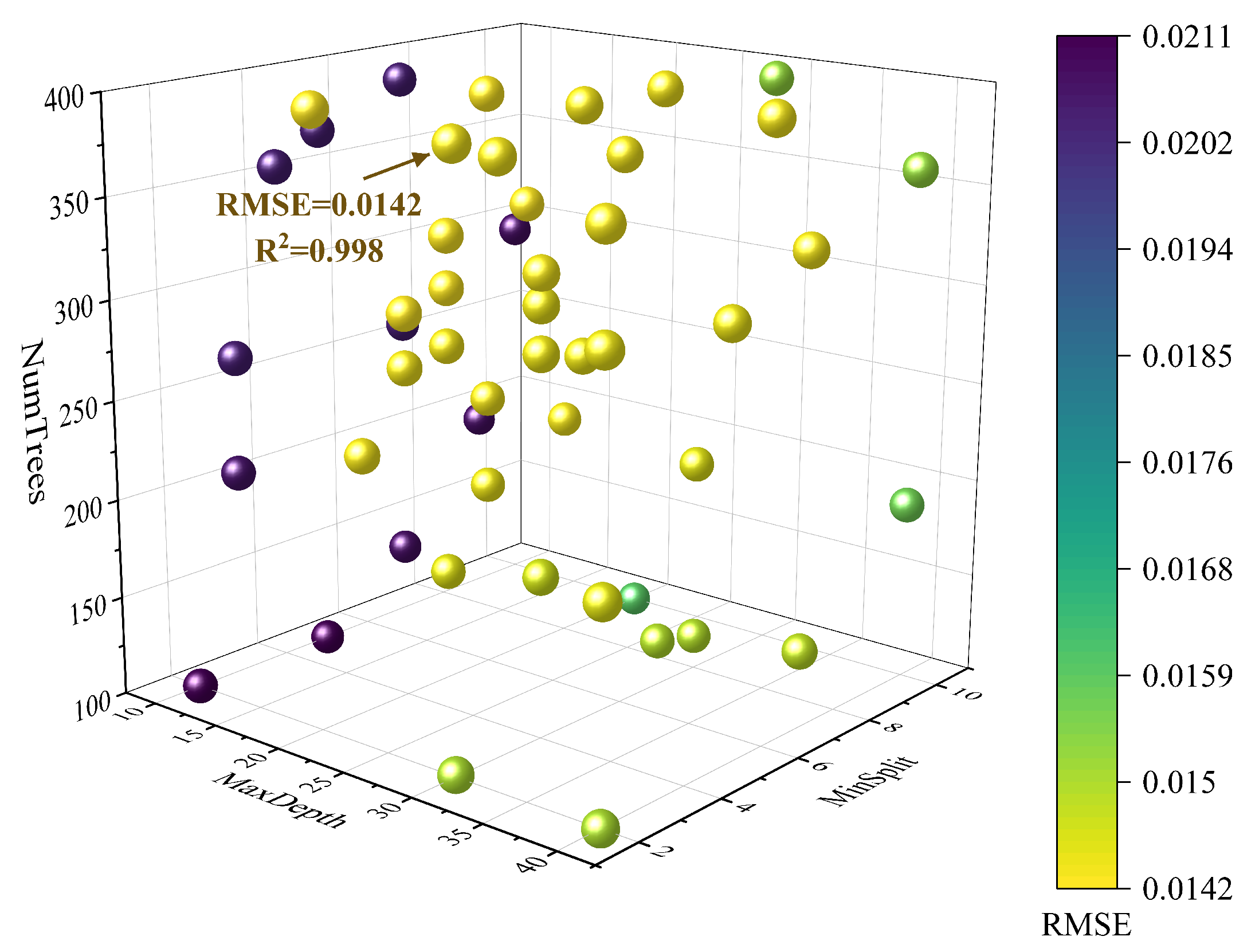
3.1.2. Optimization of the RF Model
3.1.3. Optimization of the CNN Model
3.1.4. Optimization of the CNN–Meta Model
3.2. Analysis of Training and Prediction Results for the Four Models
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sasaki, M.; Sanada, Y.; Katengeza, E.W.; Yamamoto, A. New method for visualizing the dose rate distribution around the Fukushima Daiichi Nuclear Power Plant using artificial neural networks. Sci. Rep. 2021, 11, 1857. [Google Scholar] [CrossRef]
- D’Onorio, M.; Glingler, T.; Molinari, M.; Maccari, P.; Mascari, F.; Mandelli, D.; Alfonsi, A.; Caruso, G. Nuclear safety Enhanced: A Deep dive into current and future RAVEN applications. Nucl. Eng. Des. 2024, 427, 113422. [Google Scholar] [CrossRef]
- Sanwick, A.; Chaple, I. Radiocobalt theranostic applications: Current landscape, challenges, and future directions. Front. Nucl. Med. 2025, 5, 1663748. [Google Scholar] [CrossRef] [PubMed]
- Cooper, R.J.; Amman, M.; Luke, P.N.; Vetter, K. A prototype High Purity Germanium detector for high resolution gamma-ray spectroscopy at high count rates. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2015, 795, 167–173. [Google Scholar] [CrossRef]
- Kanisch, G. Detection limit calculations for peak evaluation methods in HPGe gamma-ray spectrometry according to ISO 11929. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2017, 855, 118–132. [Google Scholar] [CrossRef]
- Russ, W.R. Library correlation nuclide identification algorithm. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2007, 579, 288–291. [Google Scholar] [CrossRef]
- Allinei, P.G.; Pérot, N.; Pérot, B.; Marchais, T.; Fondement, V.; Toubon, H.; Bruned, V.; Berland, A.; Goupillou, R. Estimation of uranium concentration in ore samples with machine learning methods on HPGe gamma-ray spectra. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2022, 1032, 166597. [Google Scholar] [CrossRef]
- Dai, W.; Zeng, Z.; Dou, D.; Ma, H.; Cheng, J.; Li, J.; Zhang, H. Marine radioisotope gamma-ray spectrum analysis method based on Geant4 simulation and MLP neural network. J. Instrum. 2021, 16, P06030. [Google Scholar] [CrossRef]
- Li, F.; Gu, Z.; Ge, L.; Li, H.; Tang, X.; Lang, X.; Hu, B. Review of recent gamma spectrum unfolding algorithms and their application. Results Phys. 2019, 13, 102211. [Google Scholar] [CrossRef]
- Hýža, M.; Dragounová, L.; Kořistková, M. Latent variable modeling of gamma-ray background in repeated measurements. Appl. Radiat. Isot. 2024, 204, 111119. [Google Scholar] [CrossRef]
- Qi, S.; Zhao, W.; Chen, Y.; Chen, W.; Li, J.; Zhao, H.; Xiao, W.; Ai, X.; Zhang, K.; Wang, S. Comparison of machine learning approaches for radioisotope identification using NaI (TI) gamma-ray spectrum. Appl. Radiat. Isot. 2022, 186, 110212. [Google Scholar] [CrossRef]
- Hata, H.; Yokoyama, K.; Ishimori, Y.; Ohara, Y.; Tanaka, Y.; Sugitsue, N. Application of support vector machine to rapid classification of uranium waste drums using low-resolution γ-ray spectra. Appl. Radiat. Isot. 2015, 104, 143–146. [Google Scholar] [CrossRef] [PubMed]
- Tomita, H.; Hara, S.; Mukai, A.; Yamagishi, K.; Ebi, H.; Shimazoe, K.; Tamura, Y.; Woo, H.; Takahashi, H.; Asama, H.; et al. Path-planning system for radioisotope identification devices using 4π gamma imaging based on random forest analysis. Sensors 2022, 22, 4325. [Google Scholar] [CrossRef] [PubMed]
- Mathew, J.; Kshirsagar, R.; Abidin, D.Z.; Griffin, J.; Kanarachos, S.; James, J.; Alamaniotis, M.; Fitzpatrick, M.E. A comparison of machine learning methods to classify radioactive elements using prompt-gamma-ray neutron activation data. Sci. Rep. 2023, 13, 9948. [Google Scholar] [CrossRef] [PubMed]
- Kamuda, M.; Zhao, J.; Huff, K. A comparison of machine learning methods for automated gamma-ray spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 954, 161385. [Google Scholar] [CrossRef]
- Turner, A.N.; Wheldon, C.; Wheldon, T.K.; Gilbert, M.R.; Packer, L.P.; Burns, J.; Freer, M. Convolutional neural networks for challenges in automated nuclide identification. Sensors 2021, 21, 5238. [Google Scholar] [CrossRef]
- Li, F.; Qi, S.; Li, Z.; Gao, H.; Yang, S.; Liu, J.; Fan, C. Comparative analysis of multi-nuclide spectrum recognition methods based on neural network. Nucl. Eng. Technol. 2025, 58, 103914. [Google Scholar] [CrossRef]
- Li, F.; Luo, C.; Wen, Y.; Lv, S.; Cheng, F.; Zeng, G.; Jiang, J.; Li, B. A nuclide identification method of γ spectrum and model building based on the transformer. Nucl. Sci. Tech. 2025, 36, 7. [Google Scholar] [CrossRef]
- Li, C.; Liu, S.; Wang, C.; Jiang, X.; Sun, X.; Li, M.; Wei, L. A new radionuclide identification method for low-count energy spectra with multiple radionuclides. Appl. Radiat. Isot. 2022, 185, 110219. [Google Scholar] [CrossRef]
- Vettoruzzo, A.; Bouguelia, M.; Vanschoren, J.; Rögnvaldsson, T.; Santosh, K. Advances and challenges in meta-learning: A technical review. IEEE Trans. Pattern Anal. Mach. Intell. 2024, 46, 4763–4779. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, H.; Huang, J.; Xiong, W.; Huang, G.; Dai, L.; Wu, Z.; Liu, G. Quantitative Alpha Spectra Isotope Identification Based on Deep Learning Method and Monte Carlo modeling. Radiat. Meas. 2025, 186, 107460. [Google Scholar] [CrossRef]
- Déjeant, A.; Bourva, L.; Sia, R.; Galoisy, L.; Calas, G.; Phrommavanh, V.; Descostes, M. Field analyses of 238U and 226Ra in two uranium mill tailings piles from Niger using portable HPGe detector. J. Environ. Radioact. 2014, 137, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Huang, X.; Yuan, Y.G.; Zhu, Y.X.; Chen, H.; Qu, J.; Tan, Z. A low-consumption multiple nuclides identification algorithm for portable gamma spectrometer. Nucl. Sci. Tech. 2025, 36, 121. [Google Scholar] [CrossRef]
- Barradas, N.P.; Vieira, A.; Felizardo, M.; Matos, M. Nuclide identification of radioactive sources from gamma spectra using artificial neural networks. Radiat. Phys. Chem. 2025, 232, 112692. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, S.; Lv, S.; Liu, G. A First-Order Meta Learning Method for Remaining Useful Life Prediction of Rotating Machinery under limited Samples. Appl. Soft Comput. 2025, 182, 113616. [Google Scholar] [CrossRef]
- Bai, H.; Jiang, W.; Du, Z.; Zhou, W.; Li, X.; Li, H. An evolution strategy of GAN for the generation of high impedance fault samples based on Reptile algorithm. Front. Energy Res. 2023, 11, 1180555. [Google Scholar] [CrossRef]
- Huisman, M.; Plaat, A.; van Rijn, J.N. Understanding transfer learning and gradient-based meta-learning techniques. Mach. Learn. 2024, 113, 4113–4132. [Google Scholar] [CrossRef]
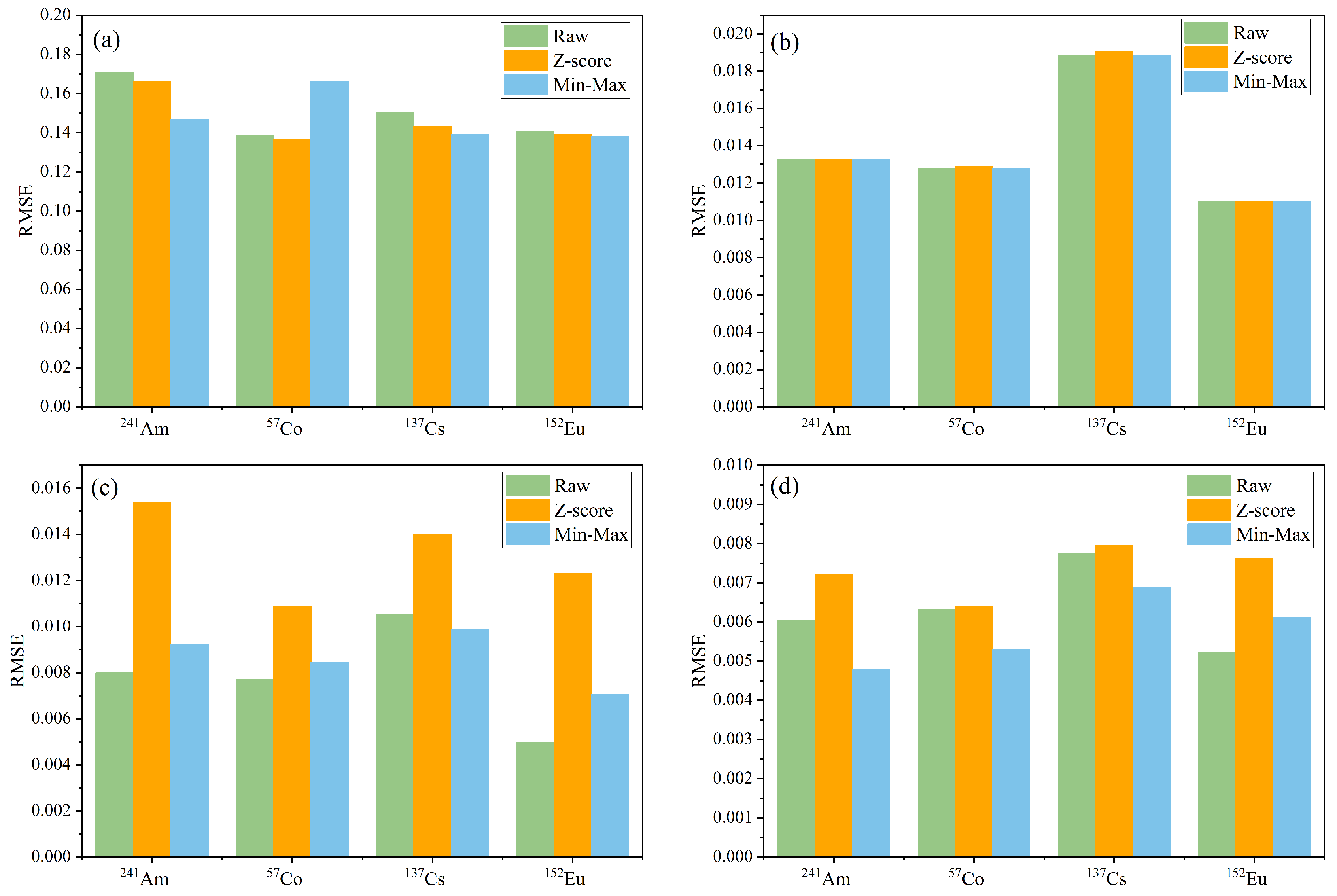
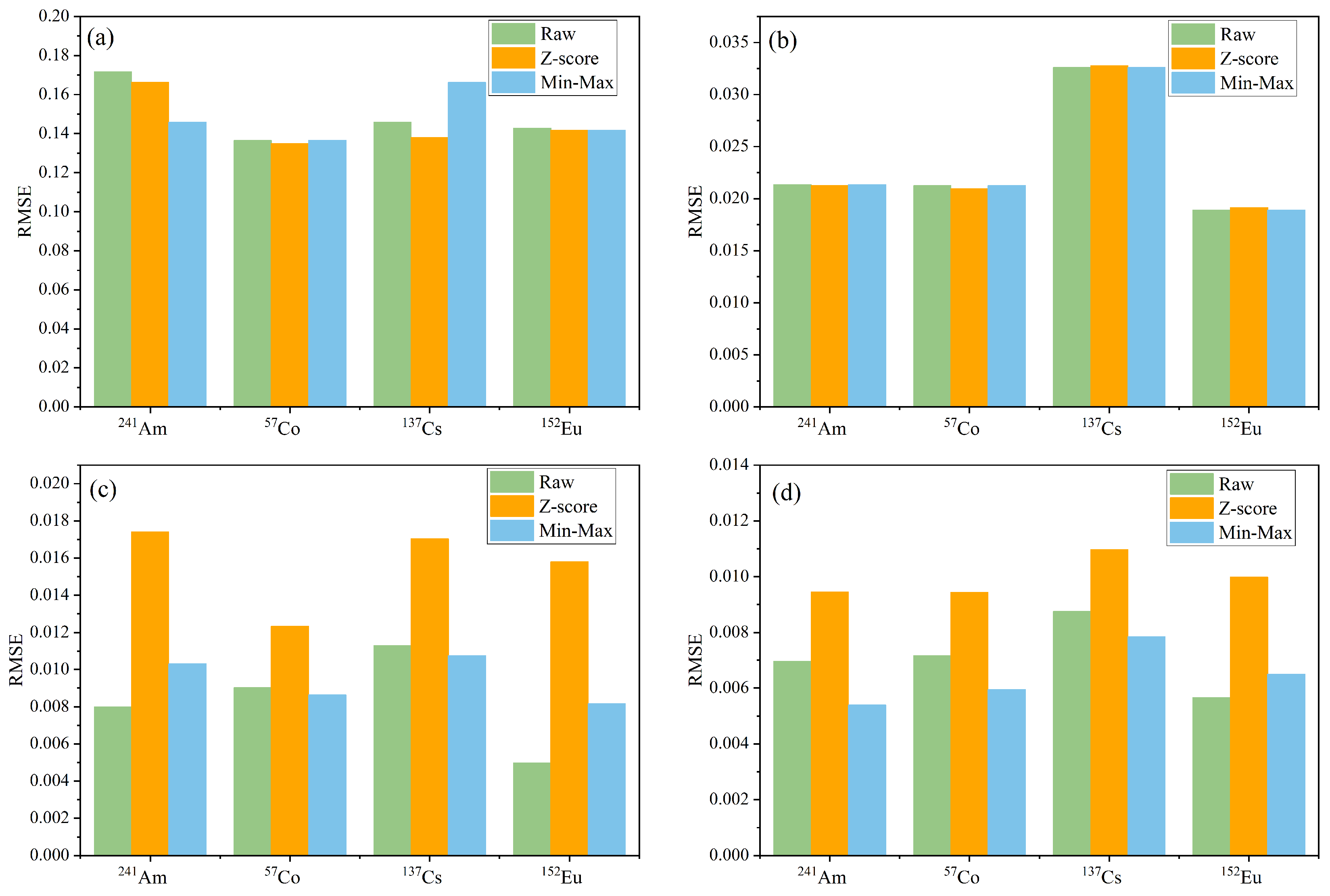
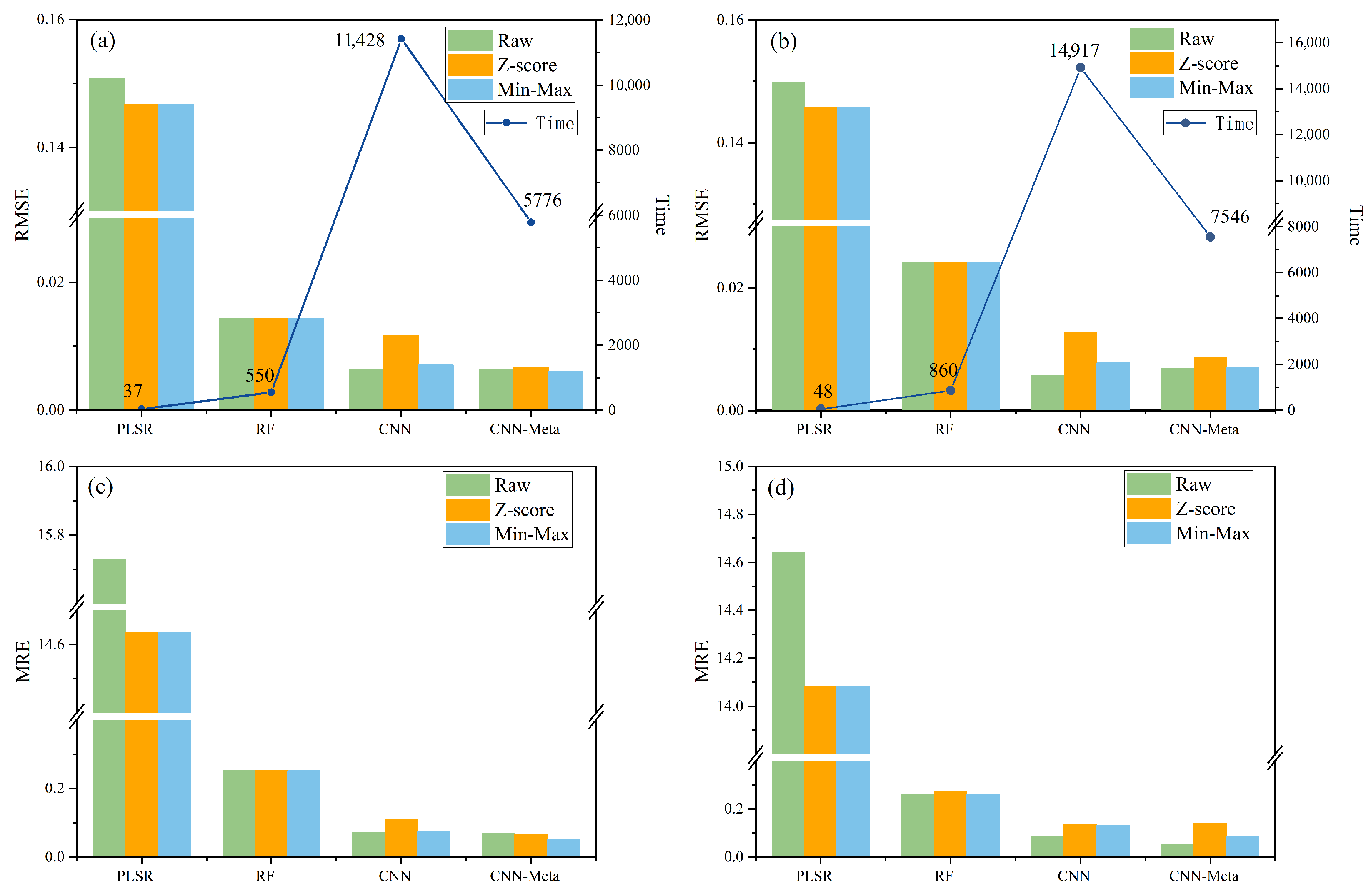
| Radionuclide | Energy/keV | Emission Rate/% | Activity/kBq |
|---|---|---|---|
| 241Am | 59.54 | 35.78 | 29.6 |
| 57Co | 122.06, 136.47 | 85.51, 10.71 | 3.75 |
| 137Cs | 661.66 | 84.99 | 20.9 |
| 152Eu | 121.78, 244.70, 344.28 | 28.14, 7.55, 26.58 | 6.5 |
| 411.12, 778.90, 964.07 | 2.24, 12.96, 14.62 | ||
| 1085.84, 1112.08 | 10.13, 13.40 | ||
| 1408.01 | 20.85 |
| Architecture | Hyperparameter | Values | Optimized Values |
|---|---|---|---|
| RF | MaxDepth | 10,20,30,40 | 20 |
| MinSamplesSplit | 2,3,4,5,6,7,8,9,10 | 6 | |
| NumTrees | 100–400 | 392 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, X.; Wang, Z.; Sun, Y.; Dong, Z.; Liu, X.; Zhang, H.; Wang, X. Study of Intelligent Identification of Radionuclides Using a CNN–Meta Deep Hybrid Model. Appl. Sci. 2025, 15, 12285. https://doi.org/10.3390/app152212285
Meng X, Wang Z, Sun Y, Dong Z, Liu X, Zhang H, Wang X. Study of Intelligent Identification of Radionuclides Using a CNN–Meta Deep Hybrid Model. Applied Sciences. 2025; 15(22):12285. https://doi.org/10.3390/app152212285
Chicago/Turabian StyleMeng, Xiangting, Ziyi Wang, Yu Sun, Zhihao Dong, Xiaoliang Liu, Huaiqiang Zhang, and Xiaodong Wang. 2025. "Study of Intelligent Identification of Radionuclides Using a CNN–Meta Deep Hybrid Model" Applied Sciences 15, no. 22: 12285. https://doi.org/10.3390/app152212285
APA StyleMeng, X., Wang, Z., Sun, Y., Dong, Z., Liu, X., Zhang, H., & Wang, X. (2025). Study of Intelligent Identification of Radionuclides Using a CNN–Meta Deep Hybrid Model. Applied Sciences, 15(22), 12285. https://doi.org/10.3390/app152212285







