Adaptive SVD Denoising in Time Domain and Frequency Domain
Abstract
1. Introduction
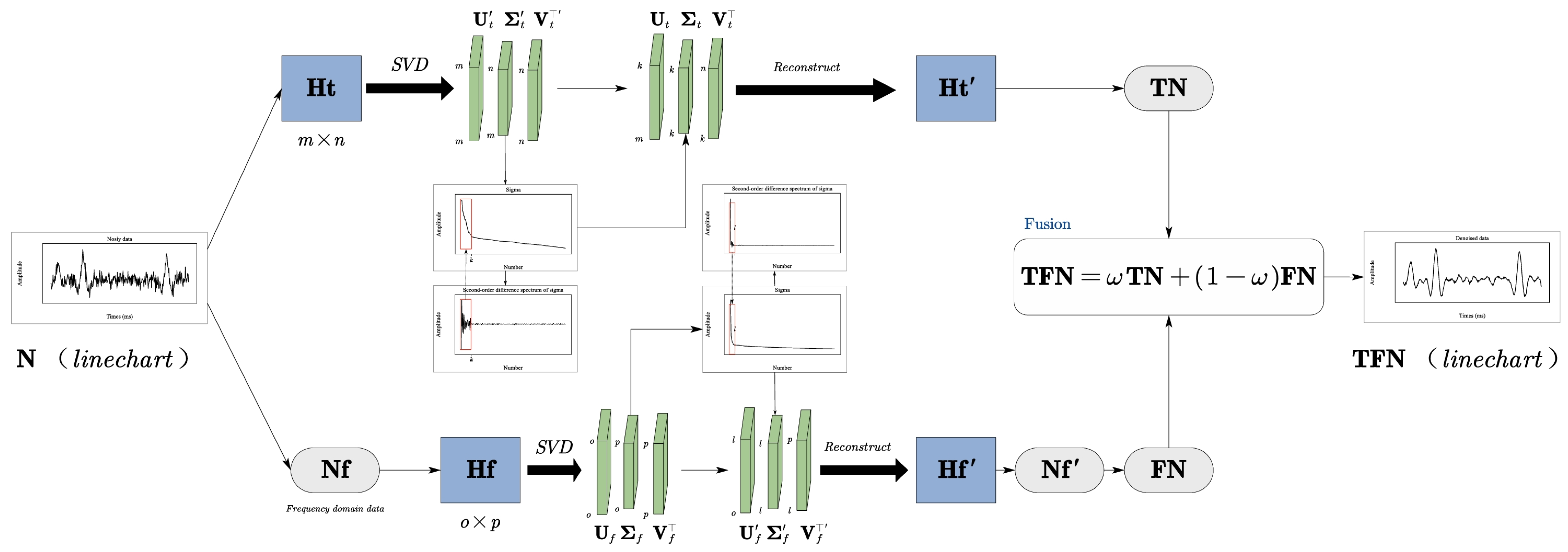
- A novel adaptive time–frequency SVD fusion framework (ASTF): This framework systematically combines denoised results from both time and frequency domains via Hankelization and adaptive weighting to harness their complementary strengths.
- A principled rank selection criterion: We introduce an adaptive singular value selection method based on the second-order difference spectrum, reducing reliance on manual parameter tuning and enhancing robustness.
- A guaranteed fusion scheme: We employ a ternary search algorithm to optimize the fusion weight, ensuring the denoising performance is maximized in terms of Peak Signal-to-Noise Ratio (PSNR), with empirical evidence supporting the convexity of the search space.
2. Theory
2.1. SVD Denoising
2.2. Frequency Domain SVD Denoising
2.3. Adaptive Selection of Singular Values
2.4. Adaptive Weight Fusion
| Algorithm 1: Adaptive SVD Denoising in Time and Frequency Domains (ASTF) |
| Input: Noisy seismic data N, Clean data X (for PSNR calculation during weight search). Output: Denoised data TFN. 1.Time Domain Processing: a. Construct Hankel matrix Ht from N. b. Perform SVD on Ht to obtain singular value matrix Σ. c. Compute the second-order difference spectrum S from Σ using Equations (5) and (6). d. Adaptively select the effective rank *r*′ using the sliding window method described in Section 2.3. e. Reconstruct matrix Ht′ using the top *r*′ singular values. f. Apply diagonal averaging to Ht′ to obtain the time domain denoised data TN. 2.Frequency Domain Processing: a. Apply FFT to N to obtain frequency domain data Nf. b. For a selected frequency slice, construct Hankel matrix Hf. c. Perform SVD on Hf, adaptively select singular values (steps 1c−1e) and reconstruct Hf′. d. Apply diagonal averaging and inverse FFT to obtain the frequency domain denoised data FN. 3.Adaptive Fusion: a. Initialize the search range for ω ∈ [0, 1]. b. While search range is sufficiently large: i. Calculate PSNR for fusion results at ω1 and ω2 (two interior points). ii. Update search range based on which point yields higher PSNR (ternary search). c. Set ω* to the value yielding the maximum PSNR. d. TFN = ω*TN + (1 − ω*)FN. |
| Note: The clean data X is used only during the weight search (Step 3) for PSNR calculation. For field data where X is unavailable, the weight can be determined on a representative synthetic dataset or using a no-reference quality metric. |
3. Experiments
3.1. Datasets Description
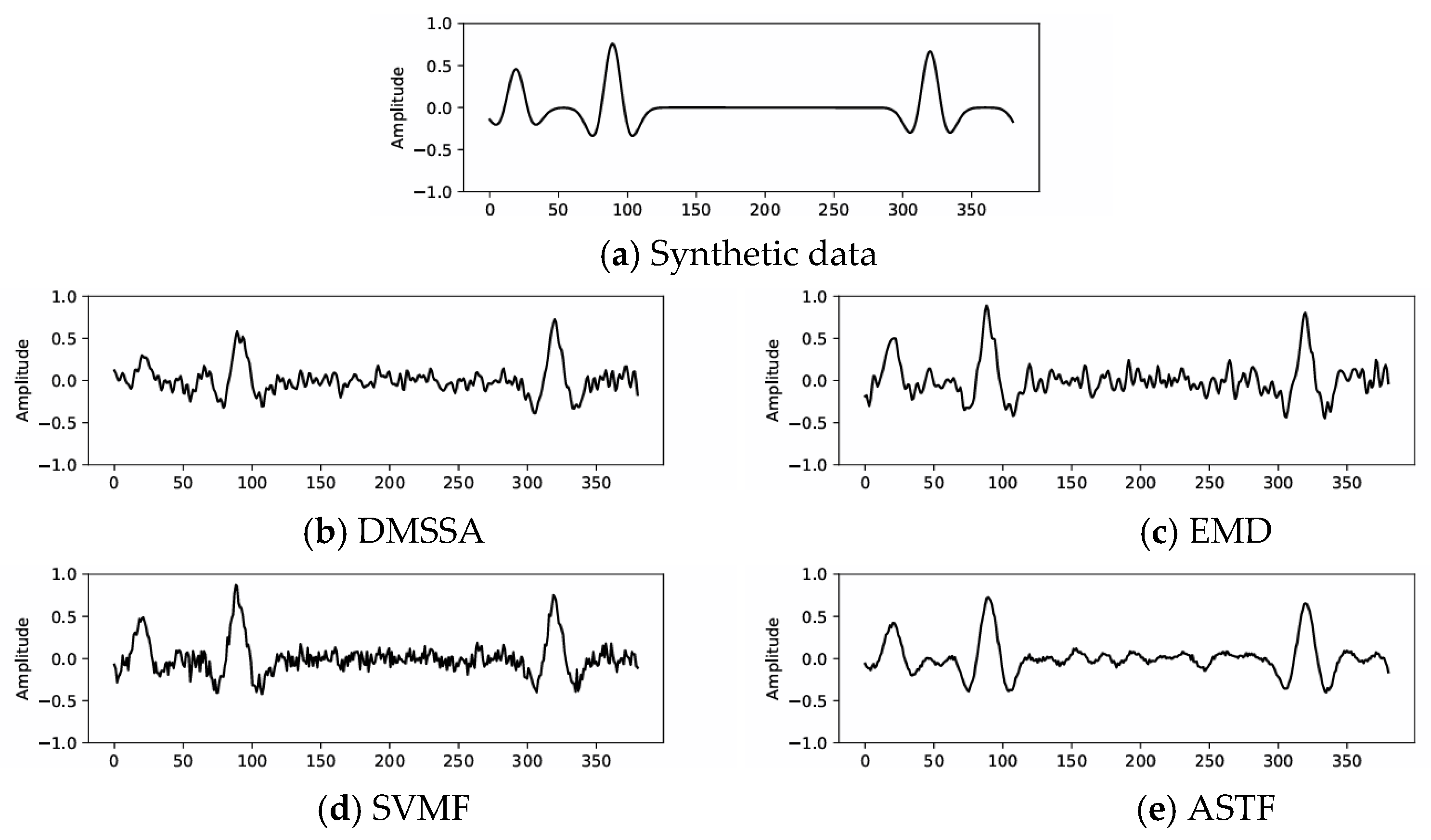
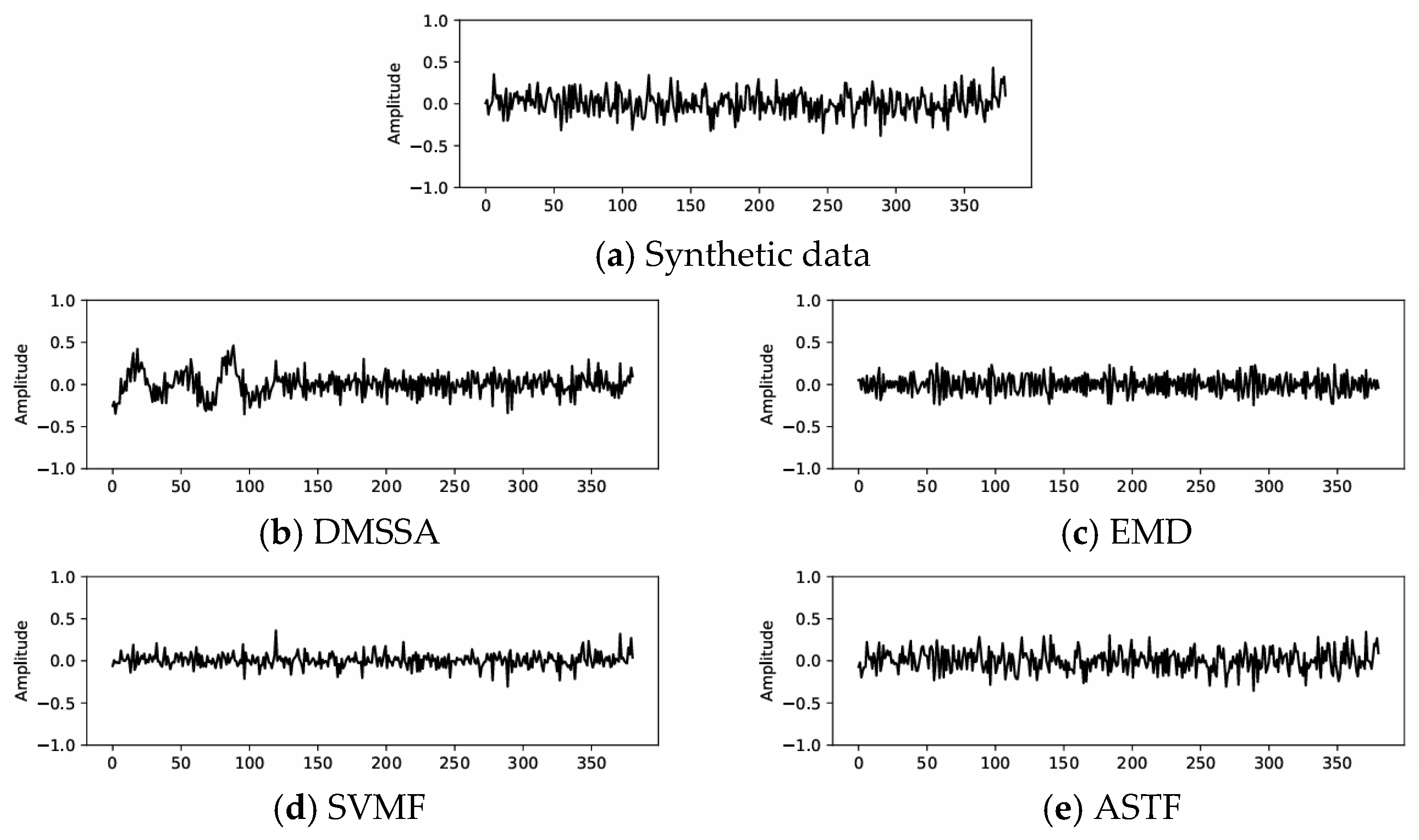
3.2. Synthetic Data
3.3. Ablation Study and Analysis
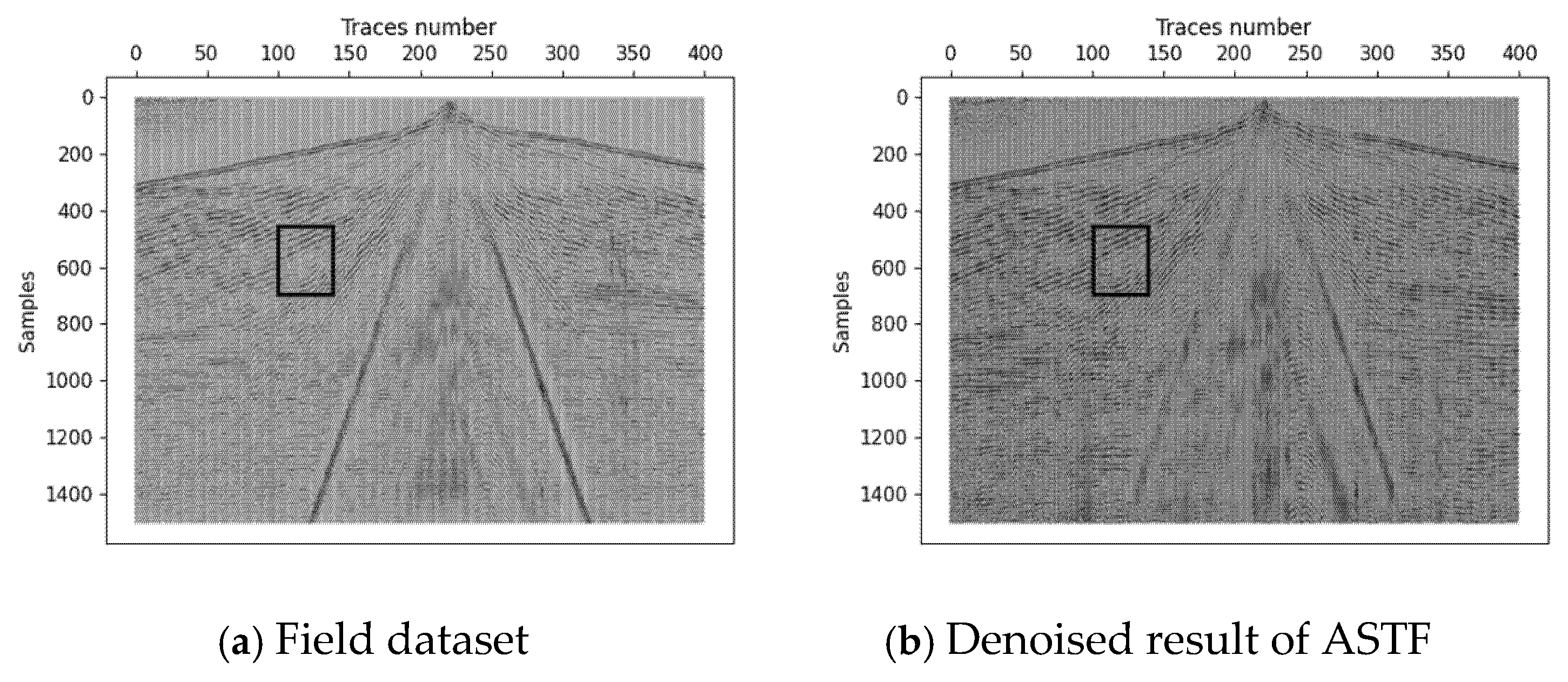
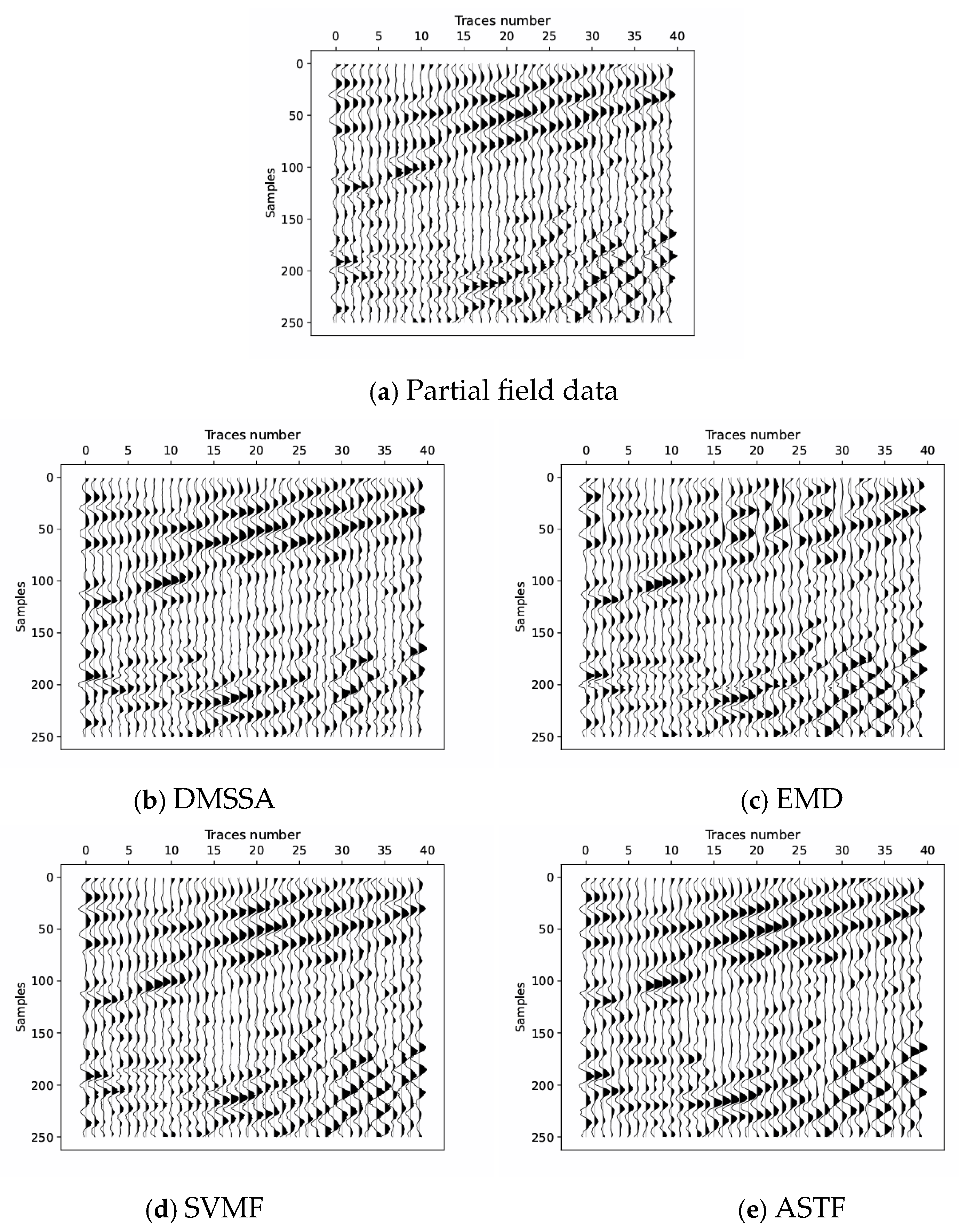
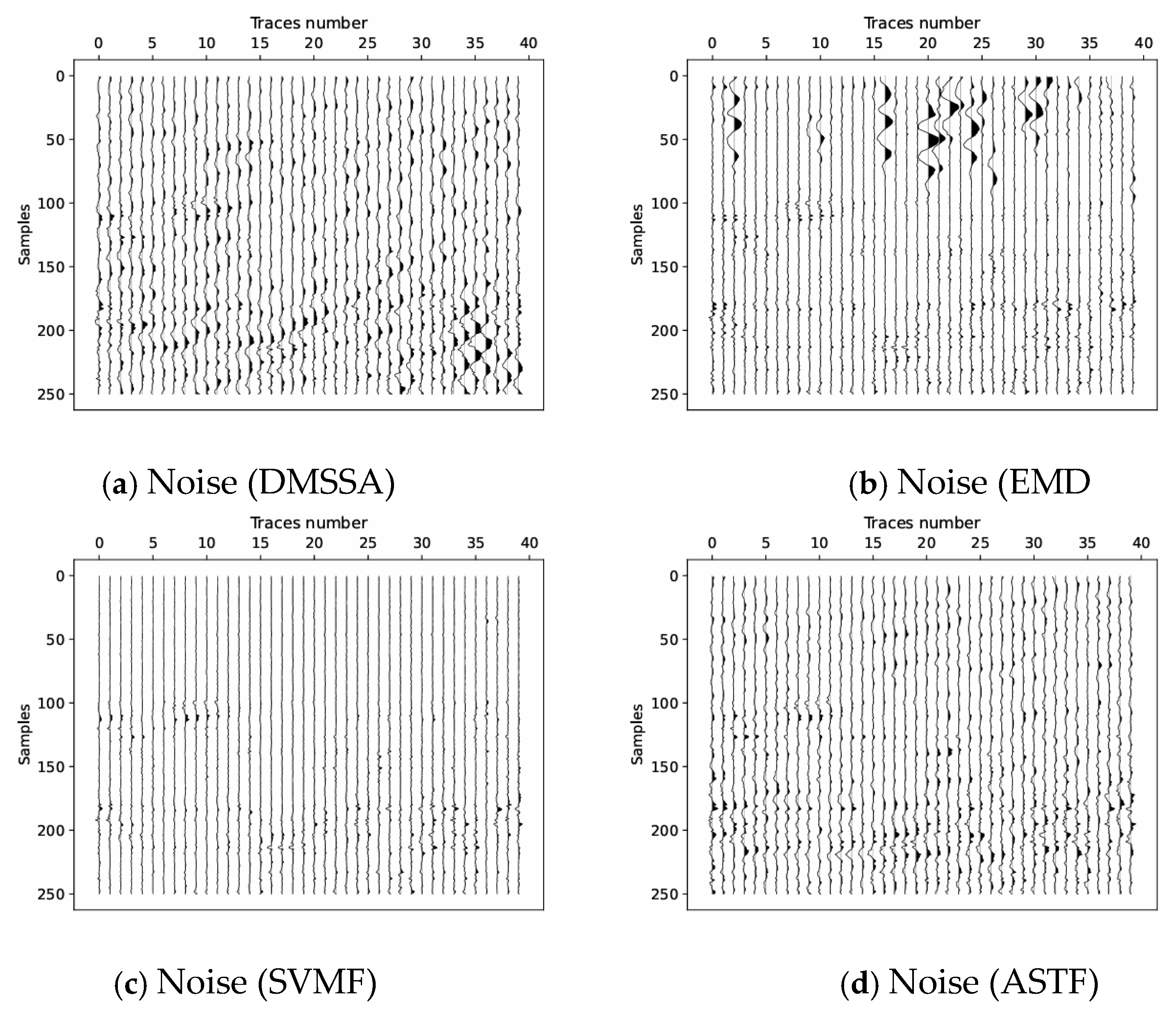
3.4. Field Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.; Cao, S.; Jiang, K.; Wang, H.; Zhang, Q. Seismic Data Denoising for Complex Structure Using BM3D and Similarity. J. Appl. Geophys. 2019, 170, 103759. Available online: https://www.sciencedirect.com/science/article/pii/S0926985119300114 (accessed on 4 November 2024). [CrossRef]
- Chen, W. Random noise reduction using a hybrid method based on ensemble empirical mode decomposition. J. Seism. Explor. 2017, 26, 227–249. [Google Scholar]
- Feng, Z. Seismic Random Noise Attenuation Using Effective and Efficient Dictionary Learning. J. Appl. Geophys. 2021, 186, 104258. Available online: https://www.sciencedirect.com/science/article/pii/S0926985121000057 (accessed on 10 November 2024). [CrossRef]
- Han, J.; van der Baan, M. Empirical mode decomposition for seismic time-frequency analysis. Geophysics 2013, 78, O9–O19. [Google Scholar] [CrossRef]
- Liu, J.; Marfurt, K. Instantaneous spectral attributes to detect channels. Geophysics 2007, 72, P23–P31. [Google Scholar] [CrossRef]
- Shan, H.; Ma, J.; Yang, H. Comparisons of Wavelets, Contourlets and Curvelets in Seismic Denoising. J. Appl. Geophys. 2009, 69, 103–115. Available online: https://www.sciencedirect.com/science/article/pii/S0926985109001050 (accessed on 12 December 2024). [CrossRef]
- Anvari, R.; Nazari Siahsar, M.A.; Gholtashee, S.; Roshandel Kahoo, A.; Mohammadi, M. Seismic Random Noise Attenuation Using Synchrosqueezed Wavelet Transform and Low-Rank Signal Matrix Approximation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6574–6581. [Google Scholar] [CrossRef]
- Morlet, J. Wave propagation and sampling theory. Geophysics 1982, 47, 203–236. [Google Scholar] [CrossRef]
- Neelamani, R.; Baumstein, A.I.; Gillard, D.G.; Hadidi, M.T.; Soroka, W.L. Coherent and random noise attenuation using the curvelet transform. Lead. Edge 2008, 27, 240–248. [Google Scholar] [CrossRef]
- Górszczyk, A.; Malinowski, M.; Bellefleur, G. Enhancing 3D post-stack seismic data acquired in hardrock environment using 2D curvelet transform. Geophys. Prospect. 2015, 63, 903–918. [Google Scholar] [CrossRef]
- Chen, Y. Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter. Geophys. J. Int. 2016, 206, 457–469. [Google Scholar] [CrossRef]
- Lv, H. Noise Suppression of Microseismic Data Based on A Fast Singular Value Decomposition Algorithm. J. Appl. Geophys. 2019, 170, 103831. Available online: https://www.sciencedirect.com/science/article/pii/S0926985119302587 (accessed on 3 March 2025). [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Gerbrands, J.J. On the Relationships between SVD, KLT and PCA. Pattern Recognit. 1981, 14, 375–381. Available online: https://www.sciencedirect.com/science/article/pii/0031320381900820 (accessed on 3 March 2025). [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001; pp. 28–29. [Google Scholar]
- Lari, H.H.; Naghizadeh, M.; Sacchi, M.D.; Gholami, A. Adaptive singular spectrum analysis for seismic denoising and interpolation. Geophysics 2019, 84, V133–V142. [Google Scholar] [CrossRef]
- Ji, G.; Wang, C. A Denoising Method for Seismic Data Based on SVD and Deep Learning. Appl. Sci. 2022, 12, 12840. [Google Scholar] [CrossRef]
- Teakle, G.; Cao, S.; Greenhalgh, S. Tube wave suppression in high frequency mine seismic data by singular value decomposition. Explor. Geophys. 1995, 26, 512–517. [Google Scholar] [CrossRef]
- Song, L.; Zhang, S. Singular value decomposition-based reconstruction algorithm for seismic traveltime tomography. IEEE Trans. Image Process 1999, 8, 1152–1154. [Google Scholar] [CrossRef]
- Maïza, B.; der Baan Mirko, V. Local singular value decomposition for signal enhancement of seismic data. Geophysics 2007, 72, V59–V65. [Google Scholar] [CrossRef]
- Bayati, F.; Trad, D. 3-D Data Interpolation and Denoising by an Adaptive Weighting Rank-Reduction Method Using Multichannel Singular Spectrum Analysis Algorithm. Sensors 2023, 23, 577. [Google Scholar] [CrossRef]
- Ma, J.; Wang, J.; Liu, G. Seismic data noise attenuation and interpolation using singular value decomposition in frequency domain. Geophys. Prospect. Pet. 2016, 55, 205–213. [Google Scholar]
- Akram, J.; Chen, Z.; Eaton, D.; Wei, X. Time-frequency denoising of microseismic data. In Proceedings of the SEG International Exposition and Annual Meeting, Houston, TX, USA, 24–29 September 2016. sEG-2016-13681108. [Google Scholar]
- Zhao, H.; Li, Y.; Zhang, C. SNR Enhancement for Downhole Microseismic Data Using CSST. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1139–1143. [Google Scholar] [CrossRef]
- Liang, X.; Li, Y.; Zhang, C. Noise suppression for microseismic data by non-subsampled shearlet transform based on singular value decomposition. Geophys. Prospect. 2018, 66, 894–903. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, J.; Tian, Z.; Pan, S. Ground microseismic data denoising based on single-channel singular value decomposetion and amplitude ratio. Geophys. Prospect. Pet. 2019, 58, 47–56+66. [Google Scholar]
- Sabbione, J.; Velis, D.; Sacchi, M. Microseismic data denoising via an apex-shifted hyperbolic Radon transform. In Proceedings of the SEG International Exposition and Annual Meeting, Houston, TX, USA, 22–27 September 2013; pp. 2155–2161. [Google Scholar]
- Chen, Y.; Zhang, D.; Jin, Z.; Chen, X.; Zu, S.; Huang, W.; Gan, S. Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method. Geophys. J. Int. 2016, 206, 1695–1717. [Google Scholar] [CrossRef]
- Chen, Y.; Fomel, S. EMD-seislet transform. Geophysics 2018, 83, A27–A32. [Google Scholar] [CrossRef]
- Chen, Y.; Zu, S.; Wang, Y.; Chen, X. Deblending of simultaneous source data using a structure-oriented space-varying median filter. Geophys. J. Int. 2020, 222, 1805–1823. [Google Scholar] [CrossRef]
- Kalman, D. A singularly valuable decomposition: The SVD of a matrix. Coll. Math. J. 1996, 27, 2–23. [Google Scholar] [CrossRef]
- Trickett, S. F-xy Cadzow noise suppression. Seg Tech. Program Expand. Abstr. 2008, 27, 2586–2590. [Google Scholar]




| Dataset | Shots | Traces | Samples | Sampling Interval | Sources |
|---|---|---|---|---|---|
| dataset1 | 1 | 200 | 1501 | 2 ms | Synthetic |
| dataset2 | 1 | 200 | 1501 | 2 ms | Synthetic |
| dataset3 | 1 | 200 | 1501 | 2 ms | Synthetic |
| dataset4 | 1 | 200 | 1501 | 2 ms | Synthetic |
| dataset5 | 1 | 200 | 1501 | 2 ms | Synthetic |
| dataset6 | 1 | 200 | 1501 | 2 ms | Synthetic |
| field dataset | 500 | 400 | 1501 | 4 ms | XinJiang |
| Dataset | Dataset1 | Dataset2 | Dataset3 | Dataset4 | |
|---|---|---|---|---|---|
| Method | SNR(dB) | PSNR(dB) | PSNR(dB) | PSNR(dB) | PSNR(dB) |
| 1 | 16.10 | 11.67 | 14.56 | 16.94 | |
| DMSSA | 3 | 18.78 | 12.76 | 16.62 | 20.80 |
| 5 | 19.87 | 13.18 | 17.35 | 22.65 | |
| 1 | 15.87 | 11.67 | 14.02 | 15.45 | |
| EMD | 3 | 19.50 | 12.77 | 16.20 | 19.41 |
| 5 | 21.29 | 13.11 | 17.27 | 21.58 | |
| 1 | 16.84 | 11.73 | 14.74 | 16.94 | |
| SVMF | 3 | 20.77 | 12.71 | 16.80 | 21.25 |
| 5 | 22.66 | 13.0 | 17.53 | 23.11 | |
| 1 | 18.96 | 12.62 | 16.43 | 20.46 | |
| ASTF | 3 | 22.57 | 13.44 | 18.08 | 25.14 |
| 5 | 23.93 | 13.86 | 18.74 | 27.06 | |
| Dataset | Dataset5 | Dataset6 | |
|---|---|---|---|
| Method | SNR(dB) | PSNR(dB) | PSNR(dB) |
| 1 | 12.01 | 11.48 | |
| T-only | 3 | 14.58 | 13.87 |
| 5 | 15.42 | 14.71 | |
| 1 | 12.40 | 11.82 | |
| F-only | 3 | 15.75 | 14.70 |
| 5 | 17.31 | 16.15 | |
| 1 | 12.85 | 12.29 | |
| NAFF | 3 | 16.47 | 15.52 |
| 5 | 17.92 | 16.96 | |
| 1 | 12.86 | 12.62 | |
| ASTF | 3 | 16.55 | 15.57 |
| 5 | 18.12 | 17.09 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, M.; Zhang, E.; Kang, Q.; Chen, L.; Zhang, M.; Gao, L. Adaptive SVD Denoising in Time Domain and Frequency Domain. Appl. Sci. 2025, 15, 12034. https://doi.org/10.3390/app152212034
Ren M, Zhang E, Kang Q, Chen L, Zhang M, Gao L. Adaptive SVD Denoising in Time Domain and Frequency Domain. Applied Sciences. 2025; 15(22):12034. https://doi.org/10.3390/app152212034
Chicago/Turabian StyleRen, Meixuan, Enli Zhang, Qiang Kang, Long Chen, Min Zhang, and Lei Gao. 2025. "Adaptive SVD Denoising in Time Domain and Frequency Domain" Applied Sciences 15, no. 22: 12034. https://doi.org/10.3390/app152212034
APA StyleRen, M., Zhang, E., Kang, Q., Chen, L., Zhang, M., & Gao, L. (2025). Adaptive SVD Denoising in Time Domain and Frequency Domain. Applied Sciences, 15(22), 12034. https://doi.org/10.3390/app152212034





