Abstract
In seismic data processing, noise not only affects velocity analysis and seismic migration, but also causes potential risks in post-stack processing because of the artifacts. The singular value decomposition (SVD) method based on the time domain and the frequency domain is effective for noise suppression, but it is very sensitive to singular value selection. This paper proposes a method of adaptive SVD denoising in both time and frequency domains (ASTF), with three steps. Firstly, two Hankel matrices are constructed in the time domain and frequency domain, respectively. Secondly, the parameters of the reconstruction matrix are adaptively selected based on the singular value second-order difference spectrum. Finally, the weights of these two matrices are learned through ternary search. Experiments were carried out on synthetic data and field data to prove the effectiveness of ASTF. The results show that this method can effectively suppress noise.
1. Introduction
Determining accurate exploration locations has always been a common demand in the oil and gas industry. People need clear underground information. However, the actual seismic data collected on site often contains a variety of noises [1]. Random noise is one of the most common interferences. Its existence may interfere with data processing steps such as static correction, velocity analysis and superposition [2,3]. Therefore, suppressing the noise is a basic and important work in seismic data processing.
Various methods have been developed to suppress random noise. According to the difference in effective signal and noise spatial distribution, noise can be located and suppressed [4,5]. Methods such as continuous wavelet transform [6,7], curvelet transform, empirical mode decomposition (EMD) and singular value decomposition (SVD) are widely used. The improved wavelet transform can find the local features of the target signal [8] in the time–frequency domain. However, a series of extended methods based on wavelet transform are not ideal for seismic data with complex events. Curvelet transform with multi-directional and multi-scale characteristics can meet this challenge well. It has achieved good results in suppressing random noise in 3D seismic data [9]. The improved two-dimensional discrete curvelet transform is more flexible for the adjustment of scale and angle threshold [10].
Empirical mode decomposition (EMD) has a good denoising ability [11]. The advantage of EMD is that the decomposition is fully automatic. It means that there is no need to set predefined parameters before decomposition [12]. However, EMD is based on experience, so it lacks a theoretical foundation based on mathematical physics. It is also prone to aliasing modal components, so that the accuracy of the calculation results is not high. To address the mode mixing problem, Ensemble EMD (EEMD) has been proposed as an improved version that adds white noise to the signal and performs the EMD over an ensemble of these noisy copies [13]. While EEMD alleviates mode mixing, it increases computational cost and still lacks a solid theoretical foundation.
Singular value decomposition (SVD) is also used for denoising due to its strong versatility and low matrix requirements [14,15]. Recent advances in SVD denoising include adaptive rank selection methods [16] and hybrid approaches combining SVD with other transforms [17]. The disadvantage of SVD denoising [18,19] is that it is difficult to meet the accuracy and generalization. Local SVD combines the advantages of f-x deconvolution, which can enhance weak events to remove background noise [20]. However, existing SVD methods typically require manual rank selection or assume horizontal events, limiting their applicability to complex seismic structures [21]. Due to the statistical characteristics of different domains, SVD can also be used in the frequency domain. Combined with the projection to convex set method, matrix decomposition is performed in the frequency domain [22]. This method can simultaneously realize the denoising and interpolation of seismic data. SVD is introduced into the non-downsampled shear wave transform coefficients [23,24], which can analyze seismic data well [25]. Single-channel SVD and amplitude ratio are introduced to improve the signal-to-noise ratio (SNR) [26], but the calculation efficiency is not ideal. In ordinary singular spectrum analysis methods, adaptive value selection can reduce the time cost of value selection [16]. The difference between effective signal and noise propagation direction can also be used to distinguish noise. Methods such as polarization filtering, random transform [27], predictive de-convolution filtering and others can also be used.
Despite the notable success of the aforementioned methods, they commonly face several critical challenges. Firstly, the performance of SVD-based methods is highly sensitive to the selection of singular values. The conventional approach of manual selection is subjective and lacks a theoretical foundation, making it difficult to guarantee the accuracy and generalization of the denoising results. Secondly, processing solely in either the time or frequency domain has inherent limitations; time domain methods struggle with dipping or curved events and require cumbersome corrections, while frequency domain methods risk attenuating valid signals when denoising broadband data. Finally, many advanced methods (e.g., curvelet transform, conventional SVD) require predefining a set of complex parameters (e.g., thresholds, rank, scales) based on data characteristics. This process often relies heavily on expert experience and extensive trial-and-error, resulting in low automation and greatly hindering their efficiency and broad application in practice.
In this paper, we propose an adaptive SVD denoising method in the time domain and frequency domain (ASTF). Figure 1 illustrates the overall structure of the method. First, the Hankel matrices are formed in the time and frequency domain for SVD, respectively. The singular values are adaptively selected according to the second-order difference spectrums of singular values to reconstruct the matrices. Then the two matrices are restored to single-channel data. They are assigned initial weights, respectively. Weights are updated iteratively through ternary search. When the peak signal-to-noise ratio (PSNR) of the fusion result reaches the maximum, the iteration is stopped. Finally, the processing results of the two domains are added according to the output weight.
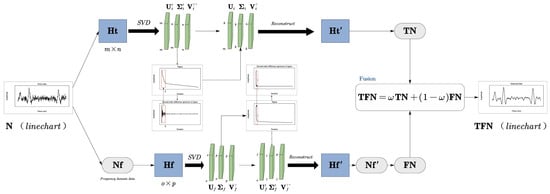
Figure 1.
The overall structure of ASTF. It is divided into upper and lower parts. The upper part is time domain adaptive SVD processing, which converts noisy data N into Hankel matrix Ht for SVD. Then, the corresponding singular values in the red box are selected to reconstruct the matrix Ht′ according to the singular value second-order difference spectrum. Finally, the time domain denoised data TN is obtained. The lower part is the frequency domain adaptive SVD, which converts N into frequency domain data Nf. Hf, Hf′ and FN are similar to Ht, Ht′ and TN in time domain processing. The final denoised result TFN is obtained by fusing TN and FN.
The ASTF method has two main advantages. On the one hand, it benefits from the different advantages of distinguishing signal and noise in the time and frequency domain. Faced with different seismic data, this method can effectively suppress random noise. On the other hand, ASTF does not require manual selection of singular values. The effectiveness of the processing results is properly guaranteed.
The principal contributions of this work are threefold:
- A novel adaptive time–frequency SVD fusion framework (ASTF): This framework systematically combines denoised results from both time and frequency domains via Hankelization and adaptive weighting to harness their complementary strengths.
- A principled rank selection criterion: We introduce an adaptive singular value selection method based on the second-order difference spectrum, reducing reliance on manual parameter tuning and enhancing robustness.
- A guaranteed fusion scheme: We employ a ternary search algorithm to optimize the fusion weight, ensuring the denoising performance is maximized in terms of Peak Signal-to-Noise Ratio (PSNR), with empirical evidence supporting the convexity of the search space.
Experiments were conducted on the synthetic datasets and field seismic dataset. We compared ASTF with three effective methods, including damped multi-channel singular spectrum analysis (DMSSA) [28], empirical mode decomposition (EMD) [29] and space-varying median filter (SVMF) [30]. The results show that our method is more effective.
2. Theory
2.1. SVD Denoising
Assuming that the matrix contains seismic signal and noise, it is expressed as follows:
where represents pure signal and represents noise. We perform SVD on as follows:
where is an orthogonal matrix composed of eigenvectors NNT, is an orthogonal matrix composed of eigenvectors NTN and Σ is a diagonal matrix composed of singular values in descending order. The first 10% or even 1% of the singular values of Σ can contain more than 90% of the energy information of N [31]. In other words, small singular values mean that their contribution to the effective signal is small.
N = X + D,
N = UΣVT,
Assuming that r is the rank of N, the effective rank of the signal matrix X is r′(r′< r). The best estimate of X can be obtained when the r′ largest singular values of N (σ1 > σ2 > …> σr′) are selected to reconstruct the matrix. The discarded singular values represent the information in the noise matrix D.
2.2. Frequency Domain SVD Denoising
The seismic data N is Fourier transformed to obtain frequency domain data Nf. A certain characteristic frequency of m seismic traces is extracted to form an array (f1, f2, …, fm) to construct a Hankel matrix Hf, which can be expressed as follows:
where l = ⌊⌋ + 1. The elements on the anti-diagonal line of the matrix are the same.
If the seismic data contains k linear events without noise, the rank of the corresponding Hankel matrix is k. When the random noise in the seismic data increases, k also increases. SVD can be used to reduce the rank of the matrix to suppress random noise. Similarly, if there are missing seismic events, the corresponding column value in the matrix is 0. The corresponding frequency domain sample value is still 0 when converted to the f-x domain. k will increase if the number of zero-valued samples in the Hankel matrix increases. A low-rank matrix similar to the original matrix without missing traces can be obtained when the Hankel matrix is reduced by SVD. The matrix is then transformed into frequency domain data. Then, the inverse Fourier transform is performed to obtain the denoising result.
2.3. Adaptive Selection of Singular Values
In actual reconstruction, the selection of the singular values depends on the correlation of the effective signal. Singular values are usually artificially selected in traditional SVD methods. If these subjective methods are applied, it is difficult to guarantee the effectiveness of the experimental results. In order to meet this challenge, we propose to adaptively select singular values.
In the time domain, we convert the single-channel seismic data into a Hankel matrix Ht. Then, the singular value matrix Σ is obtained by performing SVD on Ht. Σ is a diagonal matrix composed of singular values σx in descending order:
where r is the rank of matrix Σ and the singular value of the matrix satisfies σ1 ≥ σ2 ≥…≥ σr ≥ 0. The effective signal can be regarded as a series of coherent linear events. Random noise is messy because of its complexity. The decay speed of the singular value is from fast to slow in the Σ. The values of the fast decay part are highly correlated with the coherent information of the Hankel matrix. They represent effective signals with great energy. The values of the slow decay part mainly correspond to the weakly correlated random noise. According to the singular value second-order difference spectrum, we select the singular value corresponding to the effective signal. The first-order difference spectrum B of Σ is as follows:
The second-order difference spectrum S of Σ is as follows:
Because the decay speed of the singular value changes from fast to slow. The critical value of fast and slow decay speed is the key to selecting singular value. S does not absolutely change from large to small, and the method of finding the critical value is very important. We propose applying a sliding time window method to find it. We set a proportional range (e.g., beginTime = 0.01 to endTime = 0.25), which is equivalent to sliding a time window along the sequence of singular values. The threshold for judging the critical value is set as a fixed percentage of the average value in the initial window (controlled by the beginTime and endTime parameters). When the average value of the singular values within the sliding window falls below this threshold, the search stops, and the truncation point is determined. An advantage of this method is that it is actually a data-driven way to tune the parameter. It is worth noting that the reconstructed matrix is often not a Hankel matrix, which does not meet our expectations. This problem can be solved by a diagonal averaging method [15].
2.4. Adaptive Weight Fusion
Time domain SVD methods have a good denoising effect when they are directly applied to horizontal events. But if the events are tilted or bent, they need to add cumbersome and complicated corrections. Frequency domain SVD methods can usually overcome these limitations. They avoid assuming that the events of signals are horizontal [32]. When the frequency bandwidth of the signal is wide, however, frequency domain SVD methods will also attenuate part of the signal when suppressing random noise. We propose adaptively fusing the denoised results in the time domain and frequency domain. This combines the advantages of the time domain and the frequency domain, as described in this subsection.
The denoised results in the time domain and frequency domain are assigned initial weights for fusion. The fused matrix TFN can be expressed as follows:
where ω ∈ [0, 1] is the weight of the time domain denoised matrix, TN is the denoised matrix in the time domain and FN is the denoised matrix in the frequency domain. In the experiment, we discovered that the influence of ω on the peak signal-to-noise ratio (PSNR) of the final result is a convex function, as shown in Figure 2.
TFN = ωTN + (1 − ω)FN,
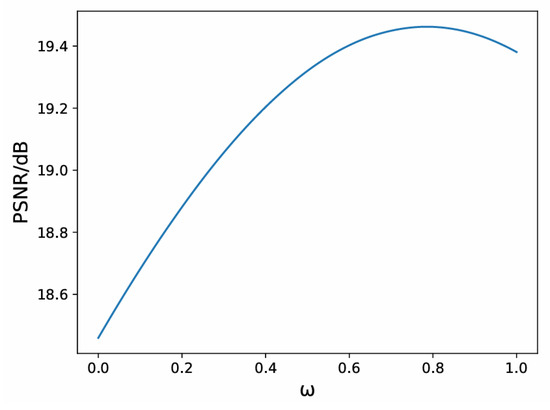
Figure 2.
The influence of ω on the PSNR.
We use ternary search to iteratively update ω and stop the iteration when PSNR reaches its maximum value:
where
where n represents the total number of samples of the seismic data, represents the cth sample of the denoised data, represents the cth sample of the clean data.
In Algorithm 1, we summarize the key steps of the ASTF method, which adaptively fuses time and frequency domain denoising results through an optimized weighting strategy.
| Algorithm 1: Adaptive SVD Denoising in Time and Frequency Domains (ASTF) |
| Input: Noisy seismic data N, Clean data X (for PSNR calculation during weight search). Output: Denoised data TFN. 1.Time Domain Processing: a. Construct Hankel matrix Ht from N. b. Perform SVD on Ht to obtain singular value matrix Σ. c. Compute the second-order difference spectrum S from Σ using Equations (5) and (6). d. Adaptively select the effective rank *r*′ using the sliding window method described in Section 2.3. e. Reconstruct matrix Ht′ using the top *r*′ singular values. f. Apply diagonal averaging to Ht′ to obtain the time domain denoised data TN. 2.Frequency Domain Processing: a. Apply FFT to N to obtain frequency domain data Nf. b. For a selected frequency slice, construct Hankel matrix Hf. c. Perform SVD on Hf, adaptively select singular values (steps 1c−1e) and reconstruct Hf′. d. Apply diagonal averaging and inverse FFT to obtain the frequency domain denoised data FN. 3.Adaptive Fusion: a. Initialize the search range for ω ∈ [0, 1]. b. While search range is sufficiently large: i. Calculate PSNR for fusion results at ω1 and ω2 (two interior points). ii. Update search range based on which point yields higher PSNR (ternary search). c. Set ω* to the value yielding the maximum PSNR. d. TFN = ω*TN + (1 − ω*)FN. |
| Note: The clean data X is used only during the weight search (Step 3) for PSNR calculation. For field data where X is unavailable, the weight can be determined on a representative synthetic dataset or using a no-reference quality metric. |
3. Experiments
In this section, synthetic datasets with simulated Gaussian-type noise are used to evaluate how effective ASTF is. We also use a field seismic dataset to illustrate the performance of the proposed method in practice. On the synthetic datasets, we utilize the widely used PSNR metric.
3.1. Datasets Description
This subsection introduces four synthetic datasets and a field seismic dataset used in the experiment. The six synthetic seismic datasets are generated by changing seismic wave speed, stratum and other conditions. This results in significant differences in their effective signals regarding event continuity, dip and curvature, thereby testing the adaptability of the ASTF method to various structural features. The field dataset (from Xinjiang) contains real-world challenges not modeled in the synthetic data, such as complex noise (e.g., coherent noise, ground roll), potential effects of irregular sampling and possible signal gaps. This constitutes the ultimate test of the algorithm’s robustness in practical applications. Table 1 lists shot points, traces, samples, sampling intervals and source information of these datasets.

Table 1.
Information of datasets.
3.2. Synthetic Data
In this subsection, we show the denoising performance of our method on synthetic datasets. In order to verify the feasibility and effectiveness of our method, we compared the other three methods on four synthetic datasets with three noise levels (SNR = 1dB, 3dB and 5dB). The results show that our method has an obvious denoising effect and can retain most of the effective signals. We first use single-channel seismic data to illustrate the method. Figure 3 shows a clean seismic trace and noisy data by adding some random noise, the SNR of which is 1dB.

Figure 3.
Synthetic example: (a) is clean synthetic data and (b) is noisy synthetic data with SNR = 1dB.
Figure 4 shows the denoising effects of DMSSA, EMD, SVMF and ASTF. Although four methods have achieved obvious results on the noisy data in Figure 3, EMD and SVMF seem to have strong residual noise. ASTF suppresses more noise, and its result is relatively smooth. Figure 5 plots the added Gaussian noise and the noise of four different noise suppression methods. EMD and SVMF are less effective in suppressing noise than the other two methods. DMSSA damages a lot of effective signals while suppressing more noise. When ASTF suppresses more noise, it can retain more effective signals.
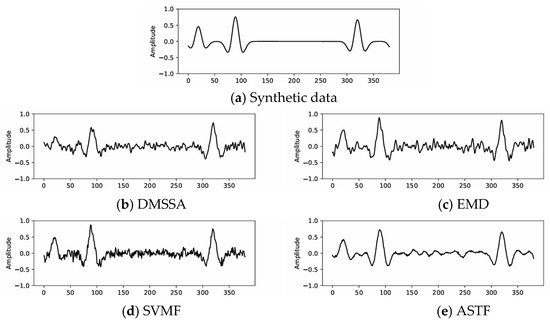
Figure 4.
Synthetic example: (a) is clean data, (b) is the denoised result of DMSSA, (c) is the denoised result of EMD, (d) is the denoised result of SVMF and (e) is the denoised result of ASTF.
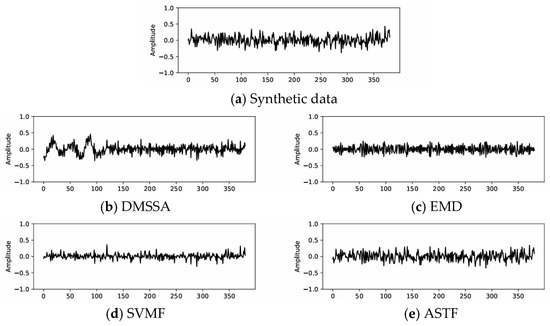
Figure 5.
Synthetic example: (a) is the added Gaussian noise, (b) is the noise suppressed by DMSSA, (c) is the noise suppressed by EMD, (d) is the noise suppressed by SVMF and (e) is the noise suppressed by ASTF.
Table 2 shows the comparison results of the four methods on four complete synthetic datasets with three noise levels. The highest PSNR is indicated in bold. The results show that ASTF performs well, especially when the signal-to-noise ratio is low; it is obviously better than other methods. Note that for synthetic data, we define the best performance by obtaining the highest PSNR, whereas for field data, the best performance is defined visually.

Table 2.
Comparison of denoising results of different methods on noisy datasets.
The ASTF algorithm’s computational complexity is dominated by the SVD operations on the Hankel matrices. For a trace of length n and Hankel matrix size l × (n − l + 1), the complexity is O(l2 (n − l + 1)). On a standard desktop PC (AMD Ryzen 9 7940HX), the average processing time for a single trace (1501 samples) was approximately 0.6 s. While more computationally intensive than EMD or SVMF, the significant performance gain justifies the cost for critical denoising tasks.
Figure 6 shows the denoised results in the time domain and frequency domain before fusion. Figure 7 shows the noise suppressed in the time domain and frequency domain, respectively. It can be seen from Figure 6 and Figure 7 that both time domain and frequency domain processing can suppress noise. The effective signal processed in the time domain is not smooth enough. Part of the effective signal is lost when processed in the frequency domain. The denoised results of the two domains are fused according to a certain weight, which can well take into account the preservation of the signal and the suppression of the noise.
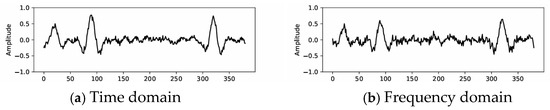
Figure 6.
Synthetic example: (a) is the denoised data in the time domain and (b) is the denoised data in the frequency domain.
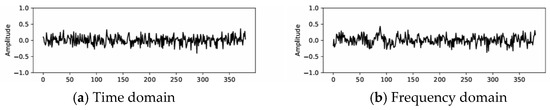
Figure 7.
Synthetic example: (a) is the noise suppressed in the time domain and (b) is the noise suppressed in the frequency domain.
3.3. Ablation Study and Analysis
This subsection investigates the individual contribution of the time domain (T) and frequency domain (F) components, as well as the necessity of adaptive fusion. We also report the computational cost.
Table 3 shows the comparison results of the four methods on two complete synthetic datasets with three noise levels and the effectiveness of the complete ASTF framework. Our proposed ASTF method consistently achieves the highest PSNR across all test conditions on both Dataset5 and Dataset6. These results demonstrate the unique contributions of both processing domains and the essential role of adaptive fusion in combining them optimally.

Table 3.
Comparison of denoising results of using time domain component alone (T-only), frequency domain component alone (F-only), non-adaptive fusion with a fixed weight (NAFF) and ASTF on noisy datasets.
3.4. Field Data
This subsection introduces the comparison between ASTF and three effective methods (including DMSSA, EMD and SVMF) on a field dataset. Table 1 and Figure 8a show the information of the dataset. The seismic events are damaged to a certain extent below the first arrival. Figure 8b shows the denoised result of ASTF. It can be seen from this that ASTF makes the seismic event clear and it effectively suppresses the noise.
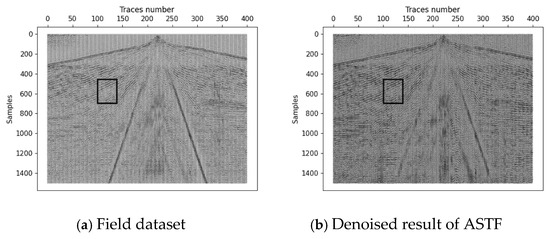
Figure 8.
Shot 1 from field dataset and our denoised result: (a) is field data and (b) is denoised result of ASTF.
In order to observe more clearly, we zoomed in on the area framed by the black rectangle in Figure 8a,b and compared the denoising effect with the other three methods. Figure 9a–e show part of the field data and the denoised results of DMSSA, EMD, SVMF and ASTF. The waveform of the signal is smooth if there is no noise. Figure 9a shows that the events are interfered with by noise. Compared with the other three results, our method has the smoothest events after denoising. The effect can be shown in particular in the lower right corner area of these Figures.
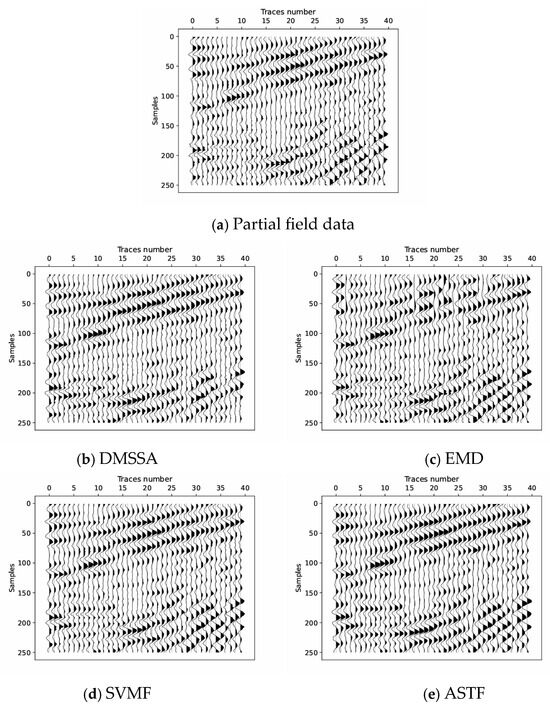
Figure 9.
Denoising effect of part of field data: (a) is part of the field data, (b) is the denoised result of DMSSA, (c) is the denoised result of EMD, (d) is the denoised result of SVMF and (e) is the denoised result of ASTF.
Figure 10 plots the noise comparison of four different noise suppression methods. It can be seen that the EMD and SVMF methods are less effective in suppressing noise than the other two methods. DMSSA and EMD lose some effective signals. ASTF achieved a good denoising effect while not obviously attenuating the effective signals.
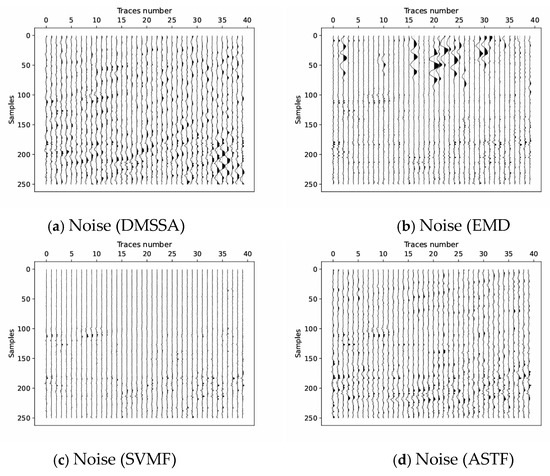
Figure 10.
(a) Noise suppressed by DMSSA, (b) noise suppressed by EMD, (c) noise suppressed by SVMF and (d) noise suppressed by ASTF.
Since the ground-truth clean signal is unavailable for the field dataset, we employed a no-reference quality metric, Local Coherence (LC), to quantitatively assess the denoising performance. A higher LC value indicates better preservation of coherent seismic events. The average LC values over the region of interest (black rectangle in Figure 8) are Original Data (0.7451), DMSSA (0.7457), EMD (0.7568), SVMF (0.7430) and ASTF (0.7601). The results show that ASTF achieves a marginally higher LC value compared to other advanced methods like SVMF and DMSSA. While the quantitative differences are subtle, it is important to note that all methods operate near the upper limit of coherence achievable for this dataset, as indicated by the high baseline value of the original data. Crucially, the quantitative ranking—where ASTF performs among the best—is fully consistent with the visual assessment in Figure 9 and Figure 10, which confirms the effectiveness of ASTF in enhancing coherence while suppressing noise.
4. Conclusions
Field seismic data often contains a lot of random noise, which sets high demands for signal enhancement. We propose a denoising method in which the time domain and frequency domain adaptive SVD denoising results are fused. It uses a data-driven model to adaptively select the singular values of the reconstruction matrix. This reduces the time cost of selection and provides an appropriate guarantee for a good denoising effect. Due to the limitations of single-domain processing, the suppressed noise may not be ideal. This fusion method can combine their advantages well to restore a smooth effective signal. This method is compared with DMSSA, EMD and SVMF. Experimental results show that it can obtain the highest peak signal-to-noise ratio. In addition, the experimental results also show that it can effectively restore smooth effective signals without obviously attenuating the signal energy. In the field of image denoising, scholars also use other matrix decomposition methods to suppress noise. Exploring how image denoising migrates to seismic data denoising will be our future work.
Author Contributions
Conceptualization, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; methodology, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; software, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; validation, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; formal analysis, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; investigation, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; resources, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; data curation, M.R., E.Z., Q.K., L.C. and L.G.; writing—original draft preparation, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; writing—review and editing, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; visualization, M.R., E.Z., Q.K., L.C., M.Z. and L.G.; supervision, M.R., E.Z. and L.G.; project administration, M.R. and L.G.; funding acquisition, M.R. and L.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Exploration and Development Research Institute, Southwest Oil and Gas Field, PetroChina, grant number 2024D109-01-03. And The APC was funded by Exploration and Development Research Institute, Southwest Oil and Gas Field, PetroChina.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study is available on request from the corresponding author. The data is not publicly available due to privacy.
Acknowledgments
The authors acknowledge the supporting from Exploration and Development Research Institute, Southwest Oil and Gas Field, PetroChina [grant number 2024D109-01-03].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, H.; Cao, S.; Jiang, K.; Wang, H.; Zhang, Q. Seismic Data Denoising for Complex Structure Using BM3D and Similarity. J. Appl. Geophys. 2019, 170, 103759. Available online: https://www.sciencedirect.com/science/article/pii/S0926985119300114 (accessed on 4 November 2024). [CrossRef]
- Chen, W. Random noise reduction using a hybrid method based on ensemble empirical mode decomposition. J. Seism. Explor. 2017, 26, 227–249. [Google Scholar]
- Feng, Z. Seismic Random Noise Attenuation Using Effective and Efficient Dictionary Learning. J. Appl. Geophys. 2021, 186, 104258. Available online: https://www.sciencedirect.com/science/article/pii/S0926985121000057 (accessed on 10 November 2024). [CrossRef]
- Han, J.; van der Baan, M. Empirical mode decomposition for seismic time-frequency analysis. Geophysics 2013, 78, O9–O19. [Google Scholar] [CrossRef]
- Liu, J.; Marfurt, K. Instantaneous spectral attributes to detect channels. Geophysics 2007, 72, P23–P31. [Google Scholar] [CrossRef]
- Shan, H.; Ma, J.; Yang, H. Comparisons of Wavelets, Contourlets and Curvelets in Seismic Denoising. J. Appl. Geophys. 2009, 69, 103–115. Available online: https://www.sciencedirect.com/science/article/pii/S0926985109001050 (accessed on 12 December 2024). [CrossRef]
- Anvari, R.; Nazari Siahsar, M.A.; Gholtashee, S.; Roshandel Kahoo, A.; Mohammadi, M. Seismic Random Noise Attenuation Using Synchrosqueezed Wavelet Transform and Low-Rank Signal Matrix Approximation. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6574–6581. [Google Scholar] [CrossRef]
- Morlet, J. Wave propagation and sampling theory. Geophysics 1982, 47, 203–236. [Google Scholar] [CrossRef]
- Neelamani, R.; Baumstein, A.I.; Gillard, D.G.; Hadidi, M.T.; Soroka, W.L. Coherent and random noise attenuation using the curvelet transform. Lead. Edge 2008, 27, 240–248. [Google Scholar] [CrossRef]
- Górszczyk, A.; Malinowski, M.; Bellefleur, G. Enhancing 3D post-stack seismic data acquired in hardrock environment using 2D curvelet transform. Geophys. Prospect. 2015, 63, 903–918. [Google Scholar] [CrossRef]
- Chen, Y. Dip-separated structural filtering using seislet transform and adaptive empirical mode decomposition based dip filter. Geophys. J. Int. 2016, 206, 457–469. [Google Scholar] [CrossRef]
- Lv, H. Noise Suppression of Microseismic Data Based on A Fast Singular Value Decomposition Algorithm. J. Appl. Geophys. 2019, 170, 103831. Available online: https://www.sciencedirect.com/science/article/pii/S0926985119302587 (accessed on 3 March 2025). [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Gerbrands, J.J. On the Relationships between SVD, KLT and PCA. Pattern Recognit. 1981, 14, 375–381. Available online: https://www.sciencedirect.com/science/article/pii/0031320381900820 (accessed on 3 March 2025). [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman & Hall/CRC: Boca Raton, FL, USA, 2001; pp. 28–29. [Google Scholar]
- Lari, H.H.; Naghizadeh, M.; Sacchi, M.D.; Gholami, A. Adaptive singular spectrum analysis for seismic denoising and interpolation. Geophysics 2019, 84, V133–V142. [Google Scholar] [CrossRef]
- Ji, G.; Wang, C. A Denoising Method for Seismic Data Based on SVD and Deep Learning. Appl. Sci. 2022, 12, 12840. [Google Scholar] [CrossRef]
- Teakle, G.; Cao, S.; Greenhalgh, S. Tube wave suppression in high frequency mine seismic data by singular value decomposition. Explor. Geophys. 1995, 26, 512–517. [Google Scholar] [CrossRef]
- Song, L.; Zhang, S. Singular value decomposition-based reconstruction algorithm for seismic traveltime tomography. IEEE Trans. Image Process 1999, 8, 1152–1154. [Google Scholar] [CrossRef]
- Maïza, B.; der Baan Mirko, V. Local singular value decomposition for signal enhancement of seismic data. Geophysics 2007, 72, V59–V65. [Google Scholar] [CrossRef]
- Bayati, F.; Trad, D. 3-D Data Interpolation and Denoising by an Adaptive Weighting Rank-Reduction Method Using Multichannel Singular Spectrum Analysis Algorithm. Sensors 2023, 23, 577. [Google Scholar] [CrossRef]
- Ma, J.; Wang, J.; Liu, G. Seismic data noise attenuation and interpolation using singular value decomposition in frequency domain. Geophys. Prospect. Pet. 2016, 55, 205–213. [Google Scholar]
- Akram, J.; Chen, Z.; Eaton, D.; Wei, X. Time-frequency denoising of microseismic data. In Proceedings of the SEG International Exposition and Annual Meeting, Houston, TX, USA, 24–29 September 2016. sEG-2016-13681108. [Google Scholar]
- Zhao, H.; Li, Y.; Zhang, C. SNR Enhancement for Downhole Microseismic Data Using CSST. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1139–1143. [Google Scholar] [CrossRef]
- Liang, X.; Li, Y.; Zhang, C. Noise suppression for microseismic data by non-subsampled shearlet transform based on singular value decomposition. Geophys. Prospect. 2018, 66, 894–903. [Google Scholar] [CrossRef]
- Hu, Y.; Huang, J.; Tian, Z.; Pan, S. Ground microseismic data denoising based on single-channel singular value decomposetion and amplitude ratio. Geophys. Prospect. Pet. 2019, 58, 47–56+66. [Google Scholar]
- Sabbione, J.; Velis, D.; Sacchi, M. Microseismic data denoising via an apex-shifted hyperbolic Radon transform. In Proceedings of the SEG International Exposition and Annual Meeting, Houston, TX, USA, 22–27 September 2013; pp. 2155–2161. [Google Scholar]
- Chen, Y.; Zhang, D.; Jin, Z.; Chen, X.; Zu, S.; Huang, W.; Gan, S. Simultaneous denoising and reconstruction of 5-D seismic data via damped rank-reduction method. Geophys. J. Int. 2016, 206, 1695–1717. [Google Scholar] [CrossRef]
- Chen, Y.; Fomel, S. EMD-seislet transform. Geophysics 2018, 83, A27–A32. [Google Scholar] [CrossRef]
- Chen, Y.; Zu, S.; Wang, Y.; Chen, X. Deblending of simultaneous source data using a structure-oriented space-varying median filter. Geophys. J. Int. 2020, 222, 1805–1823. [Google Scholar] [CrossRef]
- Kalman, D. A singularly valuable decomposition: The SVD of a matrix. Coll. Math. J. 1996, 27, 2–23. [Google Scholar] [CrossRef]
- Trickett, S. F-xy Cadzow noise suppression. Seg Tech. Program Expand. Abstr. 2008, 27, 2586–2590. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).