Hierarchical Optimization of Robotic Placement, Motion Planning, and Posture for Multi-Target Manipulation

Abstract

Efficient operation of robotic manipulators in constrained workspaces requires careful coordination of robot placement, motion planning, and posture optimization. This paper presents a hierarchical optimization framework that addresses these challenges for robot placement, motion planning, and posture determination for multi-target manipulation tasks. Initially, the workspace layout is optimized using an adaptive genetic algorithm to determine robot placement that maximizes reachability and task efficiency. Subsequently, a surrogate-assisted rapidly-exploring random tree (SA-RRT) algorithm generates collision-free paths from the start to target configurations, leveraging machine learning models to reduce computational cost while preserving path quality. Finally, the robot’s posture is optimized via a second genetic algorithm to achieve a single configuration that allows rapid access to all target positions. The effectiveness of the proposed framework was evaluated through extensive simulations in a Unity-based environment, comparing SA-RRT against the conventional target-biased nearest neighbor (TNN-RRT) algorithm. In particular, the proposed SA-RRT algorithm reduces path planning computation time by 76.17% compared to TNN-RRT and also yields lower path cost, demonstrating both efficiency and path quality improvement. Overall, the framework provides a unified methodology for integrating layout planning, motion planning, and posture optimization, facilitating more effective deployment of robotic manipulators in industrial environments.

1. Introduction

Robotic manipulators are increasingly deployed in constrained industrial environments such as assembly lines and warehouses, where efficient multi-target operation is critical. Research on layout optimization, motion planning, surrogate-assisted motion planning, and posture optimization techniques for manipulator robots in industrial settings has emerged as a critical area due to increasing demands for automation, precision, and efficiency in manufacturing processes [1,2]. Over the past decade, advancements in evolutionary computation, genetic algorithms, and multi-objective optimization have significantly enhanced the capabilities of industrial manipulators, enabling improved trajectory planning, workspace layout, and task execution [3,4]. Early research demonstrated the effective application of metaheuristics like genetic algorithms and Particle Swarm Optimization for energy-efficient robot configuration and motion planning, establishing a foundation for subsequent work in this domain [5]. The practical significance of these developments is increasing by the growing adoption of robotic systems in diverse sectors, where optimized manipulator configurations can reduce cycle times, energy consumption, and operational costs, thereby contributing to sustainable manufacturing [6,7]. For instance, energy savings of up to 20% have been reported through optimized robot placement and motion planning [7,8].

Despite these advances, the problem of simultaneously optimizing manipulator layout, motion trajectories, and posture remains complex due to the high dimensionality of configuration spaces, nonlinear constraints, and the needs to balance multiple conflicting objectives such as manipulability, stiffness, and collision avoidance [9,10,11]. Existing literature reveals a knowledge gap in integrated approaches that address layout design and motion planning concurrently while incorporating surrogate models to reduce computational costs [3,12,13]. Moreover, some studies favoring evolutionary algorithms and others using hybrid algorithms or surrogate-assisted methods have been addressed [1,14]. The limited real-world validations hinder the deployment of robust, generalizable solutions, potentially leading to suboptimal robot performance and increased downtime [15,16].

Conceptually, layout optimization involves determining the spatial arrangement of robots and workpieces to maximize accessibility and minimize operation time [17,18]. Motion planning focuses on generating collision-free, time-efficient trajectories within the robot’s workspace [10,19], while posture optimization aims to enhance robot stiffness and accuracy by selecting favorable joint configurations [20,21]. These concepts are interrelated as layout influences feasible motion paths, and posture affects both manipulability and task precision. The integration of these elements forms the foundation for developing comprehensive optimization frameworks tailored to industrial manipulators [4,22].

Co-optimizing workspace layout, motion planning, and robot posture presents several challenges. The interdependencies between robot placement, motion planning, and posture optimization result in a high-dimensional design space, complicating the optimization process. Simultaneously considering multiple objectives and constraints increases the computational complexity, necessitating efficient algorithms to achieve real-time performance. Robots often operate in dynamic settings with varying obstacles and task requirements, requiring adaptive planning strategies that can handle uncertainties and changes in the environment [23]. Integrating diverse optimization techniques, such as genetic algorithms for robot placement and posture optimization, and surrogate-assisted RRT for motion planning, poses challenges in ensuring consistency and convergence across the optimization stages.

Recent studies have attempted to address these challenges. For instance, Lu et al. [24] introduced a distributed co-design framework for motor and motion optimization in robotic manipulators, aiming to reduce computational load while enhancing scalability. Additionally, surrogate-assisted motion planning techniques have been explored to alleviate the computational burden in complex environments [25]. However, a comprehensive approach that integrates layout, motion, and posture optimization remains underexplored.

This paper introduces a holistic optimization framework that concurrently addresses the robotic cell layout, motion planning, and manipulator posture where each problem traditionally has been solved individually. The principal contribution is a novel hierarchical methodology where the output of each stage defines the constraints and objectives for the next, all governed by a unified objective function minimizing total task completion time. In contrast to conventional methods that optimize these elements separately, the proposed method can obtain global optimal solutions. The key contributions are

• Developing a genetic algorithm to optimize the placement of robot and two workpiece holders within a workspace, considering obstacle avoidance, reachability to targets, and task efficiency.
• Employing a surrogate-assisted rapidly-exploring random tree (SA-RRT) algorithm that integrates a trained surrogate model to guide the sampling and tree expansion process, enabling the generation of collision-free paths between pick-and-place targets with significantly reduced computational effort compared to conventional RRT-based planners.
• Utilizing a secondary genetic algorithm to determine an optimal robot posture that ensures quick access to multiple targets.
• The efficacy of the proposed approach is validated through direct comparison with conventional decoupled methods such as RRT, TNN-RRT, and state-of-the-art sampling-based planners like SA-RRT, demonstrating significant improvements in overall system performance.

The novelty of this research lies in the development of a unified hierarchical optimization framework that concurrently addresses workspace layout, motion planning, and posture optimization problems typically solved in isolation for robotic manipulators. By incorporating surrogate-assisted optimization into the motion planning stage, the proposed framework significantly reduces the computational burden in the optimization process. This approach reduces the total cycle time for multi-target tasks by approximately $8.44\%$ and decreases computational planning time by over $76.17\%$ compared to TNN-RRT and established sampling-based planners like SA-RRT. This work advances the field by providing a systematic methodology that enhances task efficiency, reduces cycle times, and ensures safe human–robot interactions.

The remaining part of this paper is organized as follows: Section 2 reviews related works. Section 3 provides the problem description and mathematical formulation. Section 4 details the proposed framework and algorithms, Section 5 presents the experimental results, Section 6 discusses industrial implications with future works, and Section 7 concludes this paper.

2. Literature Review

2.1. Layout Optimization Methods

Several studies employ advanced multi-objective optimization algorithms, such as NSGA-II and genetic algorithms, to effectively minimize both layout area and operation time, demonstrating practical trade-offs and Pareto optimal solutions in robotic cellular manufacturing systems [3,12]. The use of sequence-pair representations and constructive placement methods enhances the feasibility and computational efficiency of layout design [18,26]. Subsequent work introduced a sequence-triple representation to simultaneously address three-dimensional packing and motion planning, offering a more integrated approach to spatial layout and trajectory optimization [27]. Additionally, integration of kinematic constraints and joint space evaluations provides more accurate cycle time and power consumption estimations [28].

Despite these advances, many layout optimization approaches rely heavily on heuristic or evolutionary algorithms those may suffer from high computational costs and convergence to local optima [29]. The complexity of industrial environments and variability in task sequences often limit the generalizability of proposed methods. Moreover, some studies focus predominantly on static layouts without fully addressing dynamic reconfiguration or adaptability to changing workflows [30]. The integration of accessibility and collision avoidance constraints remains challenging, especially in multi-robot or dual-arm systems [15].

2.2. Motion Planning Algorithms

In the literature, robust sampling-based planners such as Rapidly-exploring Random Tree (RRT), Rapidly-exploring Random Tree Star (hereafter referred to as RRT*), and Stochastic Trajectory Optimization for Motion Planning (STOMP) have been widely applied to complex robotic motion planning tasks. RRT* extends the basic RRT by incrementally refining the search tree to guarantee asymptotic optimality, producing shorter and smoother paths through continuous rewiring of nodes. STOMP, on the other hand, is a trajectory optimization algorithm that iteratively improves an initial path by applying stochastic perturbations and minimizing a cost functional related to smoothness and collision avoidance. These motion planners are often further enhanced with manipulability measures or hybrid optimization techniques to improve path quality and ensure safe navigation in cluttered environments [10,19,31]. A novel flight cost-based (FC-RRT) sampling algorithm is developed in [32] and explicitly optimizes energy consumption during robotic pick-and-place operations, demonstrating significant energy savings compared to traditional algorithms. Surrogate-assisted and memory-based approaches, such as M-STOMP, demonstrate promising reductions in computational time by leveraging prior knowledge [33]. Multi-criteria optimization at acceleration-level and tri-criteria schemes address joint limits and smoothness, improving trajectory feasibility and stability [34,35]. Benchmarking efforts provide valuable insights into parameter tuning and planner performance across diverse scenarios [14].

Many motion planning methods still face difficulties in scaling to high-dimensional manipulators or environments with narrow passages, leading to increased planning times or suboptimal paths [14]. The stochastic nature of sampling-based planners introduces variability and non-determinism, complicating reproducibility and reliability [14]. Furthermore, surrogate models and memory-based techniques require extensive prior data and may struggle with novel or highly dynamic tasks [33]. Integration of task scheduling with motion planning remains underexplored, limiting holistic optimization of operation sequences [36].

2.3. Surrogate-Assisted Motion Planning

The use of genetic algorithms combined with simulation environments like Robot Operating System (ROS) and Open Motion Planning Library (OMPL) facilitates practical implementation and near-optimal solutions within reasonable computation times [12,14]. Surrogate models and adaptive algorithms reduce computational burdens by approximating expensive evaluations, enabling faster convergence in complex motion planning problems [33,37]. Conventional surrogate-assisted methods can be broadly divided into three categories. (i) Offline-trained global surrogates, where a model is pre-trained on extensive simulation or experimental data to approximate collision costs or dynamic feasibility [25]. These approaches achieve fast evaluations but often struggle when applied to unseen regions of the configuration space. (ii) Online-updated local surrogates, which incrementally refine the surrogate during planning [37,38]. These methods adapt better to new environments but incur additional computational overhead for model updating. (iii) Hybrid approaches, where surrogates are used selectively, for example, as a first filter before exact collision checking [33,39]. Such methods balance speed and accuracy but may introduce approximation errors that affect safety-critical tasks.

The effectiveness of these methods is based on the representativeness of training data; however, these methods are also affected by uncertainty. The trade-off between model complexity and real-time feasibility and handling uncertainty in dynamic or cluttered environments are unsolved. Despite recent advances, achieving robust, real-time surrogate-assisted motion planning in industrial contexts remains a challenge.

2.4. Posture Optimization Strategies

Posture optimization approaches incorporate comprehensive stiffness and deformation indices, considering factors such as spindle weight, cutting forces, and joint constraints to enhance machining accuracy and operational stability [11,20,21]. Multi-objective and piecewise-global optimization strategies effectively address redundancy and singularity avoidance [11,21]. Simultaneous optimization of robot posture and workpiece setup further improves stiffness thresholds and machining quality [22,40].

Despite sophisticated models, posture optimization often requires extensive computational resources and may be limited to offline or semi-online applications [11,20]. The complexity of accurately modeling robot dynamics and environmental interactions can hinder practical deployment. Moreover, many studies focus on specific machining tasks, limiting the applicability of posture optimization techniques to broader industrial manipulator operations [41]. Integration with motion planning and layout optimization is still in the development stage, reducing potential synergistic benefits.

2.5. Integrated Approaches of Layout, Motion, and Posture Optimization

Some research efforts address the interplay between layout design and motion planning, employing multi-objective algorithms to jointly minimize operation time and spatial footprint [3,12,40]. Simultaneous optimization frameworks combining placement planning and motion planning demonstrate significant reductions in operation time and computational effort [12]. An important factor of posture optimization studies is workpiece placement within the workspace to maximize stiffness and accuracy [21,42].

Comprehensive integration of layout, motion, and posture optimization remains limited, with most studies treating these aspects in isolation or sequentially [13,29]. The complexity of combined optimization problems often leads to high computational demands and challenges in formulating unified objective functions and constraints. Real-time adaptability and scalability to complex industrial environments are insufficiently addressed. Furthermore, the lack of standardized benchmarks and datasets prevents comparative evaluation of integrated approaches.

2.6. Summary of Related Works

This section maps the research landscape of the literature on layout optimization, motion planning, surrogate-assisted motion planning, and posture optimization techniques for manipulator robots in industrial settings, encompassing a broad spectrum of methodologies, including evolutionary algorithms, genetic algorithms, multi-objective optimization, and surrogate modeling. The studies in

Table 1. Literature review summary.

Reference	Problem	Approach	LO 1	MP 2	PO 3
[6,8,17,18,30]	Robotic workcell layout design, interdependencies between robot placement, energy consumption and operational efficiency	Data-driven modeling, GA, point cloud modeling	✓
[2,14,19,31,33,34,36,37]	Trajectory planning problem, reducing cycle time	Hybrid optimization algorithms, RRT*-CFS, STOMP, GA with neuro-fuzzy system, PSO		✓
[9,11,20,21,40,41,42]	Optimal posture problem with task performance, improving shiftness, avoiding singularities	Whale algorithm, redundant posture optimization based on PGOS, GA			✓
[3,12,13,15,16,22,28,29]	Robot workcell design, minimizing layout area and operation time, optimization of reconfigurable robot cells	Evolutionary and conventional algorithms, surrogate modeling, GA, NSGA-II, RRT, RRT*	✓	✓
[10,35]	Collision-free path planning for robot manipulators	Redundancy optimization, DE, RRT*		✓	✓
[4,32]	Reducing energy consumption, maximizing manipulability	Hybrid analytical and data-driven methods	✓		✓
This study	Placement planning, reducing operation and manipulation time	GA, RRT, surrogate modeling	✓	✓	✓

¹ LO: layout optimization, ² MP: motion planning, ³ PO: posture optimization.

predominantly focus on improving workspace utilization, computational efficiency, and manipulator performance through integrated approaches that combine layout design, motion trajectory planning, and posture optimization. Geographic and disciplinary diversity is evident, with contributions spanning robotics, manufacturing engineering, and computational optimization, reflecting the interdisciplinary nature of industrial robotics research. This comparative analysis is crucial for addressing the research questions related to effectiveness, computational trade-offs, and energy efficiency in industrial manipulator applications.

3. Problem Description and Mathematical Formulation

3.1. Problem Description

Industrial and service robots are increasingly required to perform pick-and-place operations in constrained environments. A key challenge in such environments is that the overall performance of the robot does not depend solely on its motion planning but also on how the robot and the surrounding workpieces are arranged within the workspace. In this study, the workspace is represented as a rectangular discretized 3D grid as shown in Figure 1. This discretization is adopted as a computational strategy as it reduces the dimensionality of the layout search space and enables rapid elimination of infeasible regions. A fully continuous formulation of layout optimization would dramatically increase search dimensionality. However, in this framework only the layout optimization stage is discretized, and both motion planning and posture optimization stages subsequently operate in continuous space. If the robot base or workpiece holders are placed in suboptimal positions, even an advanced motion planner may fail to find feasible trajectories, or the resulting paths may be unnecessarily long and inefficient. Conversely, a well-optimized layout can greatly reduce motion complexity and execution time.

   Another critical challenge lies in motion planning itself. The robot must compute collision-free and feasible paths between pick and place targets. Sampling-based approaches, such as RRT, can efficiently explore high-dimensional configuration spaces, but their performance and the quality of the solution depend heavily on the workspace layout and the initial target positions. Without integrating layout considerations, motion planning alone cannot guarantee efficient task execution.

Finally, even when feasible paths are obtained, the robot’s posture at each target significantly affects execution efficiency. Poorly chosen postures may result in excessive joint travel, poor configurations, or motions close to singularities. These issues can increase task execution time, reduce smoothness, and potentially compromise reliability. Posture optimization is therefore necessary to refine target configurations and minimize execution costs.

3.1.1. Definitions and Notation

To avoid ambiguity, the key terms used throughout this paper are defined as follows:

• Robot: In this study, the term robot refers to a 6-DOF Niryo NED robotic manipulator mounted on a fixed base. The robot model includes fixed and revolute joints and is imported into Unity using its URDF description. Kinematic and dynamic behaviors are modeled using Unity’s physics engine.
• Workspace: The workspace is defined by the set of cells denoted by $W=\{c_1,c_2,\dots ,c_n\}$, where each cell $c_i\in {\mathbb{R}}^3$ represents a discrete $\mathit{vector}\mathit{3}\sim (x,y,z)$ location in the environment. The cells within the workspace are categorized into free and obstacle cells, denoted by $W_f$ and $W_o$, respectively, such that $\{W_f,W_o\}\subset W$. Although the robot operates in a three-dimensional (3D) Cartesian space, the layout optimization is performed on a two-dimensional (2D) $(X$–$Z)$ plane that represents the discretized floor space. The selected positions are represented in 3D by assigning a fixed Y-coordinate corresponding to the ground level.
• Layout: The term layout refers to the spatial arrangement of the robot base and the surrounding task-relevant elements such as workpiece holders within the discretized workspace. The layout determines the initial positions from which subsequent motion and posture planning are performed.
• Path: A path is defined as a continuous curve in the robot’s configuration space $\mathcal{C}$ that connects an initial configuration to a target configuration. It represents a sequence of robot configurations without explicit timing information.
• Collision: A collision occurs when the geometry of the robot (links or end-effector) intersects with any workspace obstacles such as workpiece holders, conveyor belts, and other environment objects or with itself. Collision checks are performed using Unity’s built-in physics collision detection on each sampled configuration during planning.

3.1.2. Assumptions

The following assumptions are made throughout this study:

• The robot operates within its maximum reachability radius $r_{max}$. Any distance greater than $r_{max}$ is considered to be out of reach of the robot.
• All workspace obstacles, including conveyor-belt structure, are assumed to be static and known in advance. Dynamic or moving obstacles are not considered in this study.
• Both the robot base and workpiece holders are positioned exclusively on free cells within the discretized workspace. The cell size is selected such that each cell can accommodate either one robot base or one workpiece holder but not both simultaneously.
• Pick-and-place target positions are determined only after the layout optimization stage has been completed.
• A target is considered to be reached if the Euclidean distance between the end-effector and the target position is less than the tolerance.

3.1.3. Given Parameters

• Workspace parameters: Number of cells along X and Z directions and cell size.
• Robot parameters: Maximum reachability radius $r_{max}=0.44\mathrm{m}$, all six revolute joint limits and respective joint velocities, and initial robot posture.
• Layout optimization parameters: Weighting coefficients ${\alpha }_1,{\alpha }_2$ for distance cost and collision penalty, all GA parameters, and convergence threshold.
• Motion planning parameters: End-effector tolerance $0.05\mathrm{m}$ of the target, sampling resolution for configuration space, and step size for extending the RRT tree.
• Posture optimization parameters: Maximum number of generations, adaptive termination counter, population size, crossover rate, and mutation rate.

3.1.4. Decision Variables

• r: robot base position in the workspace.
• $x_1,x_2$: positions of the two workpiece holders.
• $\Pi$: the set of planned paths for the robot arm, including pick, place1, and place2 paths.
• $q_{\mathrm{target}}^j$: target postures for pick, place1, and place2 targets.
• $q^{*}$: optimized joint configurations of the robot.

3.1.5. Constraints

• Reachability: all pick-and-place targets must be within $r_{max}$ of the robot base.
• Collision avoidance: robot links and workpiece holders must not overlap.
• Workspace validity: robot and holders must not be placed in conveyor cells or outside the defined workspace.
• Kinematic feasibility: all sampled and optimized joint configurations must satisfy joint limits during sampling, motion planning, and path execution.
• Connectivity: motion planner generates collision-free paths between all task-relevant targets.

3.2. Mathematical Formulation of Objective Function

The hierarchical optimization problem addressed in this study involves three distinct but interconnected objectives. The overall goal of this study is to obtain an efficient robot configuration and motion strategy by optimizing (i) the spatial layout of the robot and workpiece holders, represented by their spatial positions $r,x_1,x_2$, within the workspace, (ii) the collision-free paths $\Pi$ between target positions, and (iii) the final robot posture $q^{*}$ that minimizes the cycle time of task execution.

3.2.1. Layout Optimization Problem Formulation

In the layout optimization, the objective is to minimize the distances between the robot and the two workpiece holders, as well as the distance to the nearest conveyor, while avoiding overlaps and violations of reach constraints. Let

• $r\in {\mathbb{R}}^3$ be the cell assigned to the robot and $x_1\in {\mathbb{R}}^3,x_2\in {\mathbb{R}}^3$ be the cells assigned to the two workpiece holders.
• $d_i\in \mathbb{R}$ be the Euclidean distance between the robot and the workpiece i.

• The layout optimization problem is formulated by Equation (1) where $\varphi (r,x_1,x_2)$ is the penalty function calculated using Equation (2).

$$\underset{(r,x_1,x_2)\in W_f}{min}{f}_{\mathrm{layout}}(r,x_1,x_2)={\alpha }_1·\sum _{i=1}^3{\displaystyle \frac{d_i}{r_{\max }}}+{\alpha }_2·\varphi (r,x_1,x_2)$$

(1)

$$\varphi (r,x_1,x_2)={\lambda }_1·{\delta }_{overlap}(r,x_1,x_2)+{\lambda }_2·{\delta }_{out}(r,x_1,x_2)+{\lambda }_3·{\delta }_{obs}(r,x_1,x_2)$$

(2)

subject to

$$\{r,x_1,x_2\}\subset W_f,r\ne x_1\ne x_2,d_i\le r_{max}$$

(3)

where

• ${\delta }_{overlap}(r,x_1,x_2)=1$ if any overlap occurs between the robot and the workpiece holders; otherwise 0.
• ${\delta }_{out}(r,x_1,x_2)=1$ if distance from the robot arm to any workpiece exceeds $r_{max}$; otherwise 0.
• ${\delta }_{obs}(r,x_1,x_2)=1$ if a robot or workpiece holder is placed in obstacle cells; otherwise 0.

The layout optimization problem is solved as a discrete optimization problem by using a genetic algorithm (GA) rather than machine learning regression models. So, the weighting coefficients $({\alpha }_1,{\alpha }_2)$ used in Equation (1) and penalty weights $({\lambda }_1,{\lambda }_2,{\lambda }_3)$ used in (2) are not normalized as coefficient normalization does not influence convergence behavior of the GA. Additionally, the formulation employs discontinuous indicator functions $\left({\delta }_z\right)$ to enforce hard feasibility constraints. Since the GA is derivative-free, the lack of differentiability does not hinder the layout optimization problem.

The solution obtained from Equation (1), which yields the robot and workpiece holder positions as a tuple $(r,x_1,x_2)$, is subsequently used to compute the pick and place target coordinates in 3D workspace. Mathematically, the task-space target positions for the inputs of motion planning stage can be expressed by Equation (4).

$$(r,x_1,x_2)⟶\left\{p_j\right\},j\in \{1,2,3\}$$

(4)

where $p_1=p_{\mathrm{pick}}$, $p_2=p_{{\mathrm{place}}_1}$, and $p_3=p_{{\mathrm{place}}_2}$. The detailed computation steps for obtaining these target positions are described in detail in Section 4.3.5.

3.2.2. Motion Planning Problem Formulation

The motion planning stage aims to generate a collision-free path for the robot from its initial configuration $q_{\mathrm{start}}$ to reach a set of predefined task-space target positions $P=\{p_1,p_2,p_3\}$, corresponding to the pickup, first placement, and second placement locations of the workpiece. Since the exact goal joint configurations are unknown beforehand, the planner incrementally explores the configuration space and records the feasible posture configurations $q_{\mathrm{target}}$ once the robot arm successfully reaches each target position. Let

• C denote the configuration space of the robot arm.
• $C_{\mathrm{free}}\subset C$ be the collision-free subset of configurations.
• $q_0\in C_{\mathrm{free}}$ be the initial configuration of the robot, where $q\in {\mathbb{R}}^6$ as the robot has six revolute joints denoted by $q=[{\theta }_1,{\theta }_2,{\theta }_3,{\theta }_4,{\theta }_5,{\theta }_6]$.
• $FK\left(q\right)$ be the forward kinematics mapping from joint configuration q to the end-effector position in task space.
• $q_{\mathrm{target}}^j\in C_{\mathrm{free}}$ be the joint configuration recorded when the robot successfully reaches target position $p_j$.

Motion planning aims to find a sequence of feasible configurations (a path) that is formulated by Equation (5) and when the robot arm end-effector reaches the target position $p_j$, target posture of the robot arm is recorded by Equation (6). A target $p_j$ is considered reached when the end-effector of the robot is within the distance tolerance $ϵ\le 0.05\mathrm{m}$ of the target.

$$\pi =\{q_0,q_1,q_2,\dots ,q_k\}$$

(5)

$$q_{\mathrm{target}}^j=q_k\in {\mathbb{R}}^6$$

(6)

subject to

$$\pi \subset C_{\mathrm{free}},\left|\right|FK\left(q_k\right)-p_j\left|\right|\le ϵ,j\in \{1,2,3\}$$

(7)

These recorded postures $\left\{q_{\mathrm{target}}^j\right\}$ are subsequently used as input to the posture optimization objective defined in Equation (9).

3.2.3. Posture Optimization Problem Formulation

Posture optimization is the final stage of the hierarchical optimization. In this stage the three target postures are treated as inputs and return a single optimal posture $\left(q^{*}\right)$ that minimizes total cycle time while remaining collision-free and within joint limits.

• The joint limits of the 6-DOF robot arm are denoted by ${\theta }_i\in [{\theta }_i^{\min },{\theta }_i^{\max }]$ for $i=1,\dots ,6$.
• Joint speeds ${\omega }^i=[{\omega }_{\max }^1,{\omega }_{\max }^2,{\omega }_{\max }^3,{\omega }_{\max }^4,{\omega }_{\max }^5,{\omega }_{\max }^6]$, where ${\omega }_{\max }^i$ is the maximum rotational speed of joint i in degrees/sec.

The cycle-time model for any two configurations $q_a,q_b\in C$ is modeled by Equation (8). The objective of the problem is to minimize the total cycle time composed of (i) a move from the cycle start $\left(q_o\right)$ to the optimal posture $\left(q^{*}\right)$ and (ii) moves from the $q^{*}$ to each target posture. This is achieved by Equation (9).

$$T(q_a\to q_b)=\sum _{i=1}^6{\displaystyle \frac{|{\theta }_i^{\left(\mathrm{b}\right)}-{\theta }_i^{\left(\mathrm{a}\right)}|}{{\omega }_{\max }^i}}$$

(8)

$$\underset{q^{*}\in C}{min}J\left(q^{*}\right)=T(q_0\to q^{*})+\sum _{j=1}^{3}T(q^{*}\to q_{\mathrm{target}}^j)$$

(9)

subject to

$$q^{*}\in C_{\mathrm{free}}$$

(10)

Thus, the hierarchical optimization framework jointly addresses workspace layout, motion feasibility, and posture refinement, ensuring safe and efficient execution of pick-and-place tasks.

4. Methodology

4.1. Hierarchical Optimization Overview

The proposed optimization framework is structured as a three-stage hierarchical pipeline, as illustrated in Figure 2. Unlike a purely sequential approach, which executes optimization stages in order without interdependence, a hierarchical structure establishes logical dependencies between higher and lower levels. In addition, Figure 2 implicitly summarizes the distribution of computational load across the three stages since each block corresponds to a distinct optimization or planning process. Each stage solves a sub-problem with distinct objectives and constraints, and its feasible solution becomes the input to the next stage. Specifically, (i) the layout optimization stage determines feasible and collision-free placements of the robot and workpiece holders, (ii) the motion planning stage computes collision-free trajectories based on that feasible layout, and (iii) the posture optimization stage refines the robot configuration to minimize cycle time while respecting joint and reachability constraints. Through this hierarchical dependency, the feasibility of lower-level stages is inherently ensured as their inputs are derived from already validated and reachable configurations obtained from the preceding stages.

A hierarchical strategy is particularly essential because solving layout, motion, and posture optimization simultaneously would create a high-dimensional, non-convex search space that is computationally intractable. A combined formulation would need to optimize robot base positions, workpiece holder placements, thousands of candidate joint trajectories, and redundant postures within a single optimization space, making convergence slow and often infeasible. By decomposing the problem hierarchically, each stage effectively reduces the dimensionality of the search, filters out infeasible solutions early, and enforces feasibility constraints for the subsequent stages. This structured decomposition improves computational efficiency and ensures that the final solution remains both kinematically feasible and operationally optimal.

At the first stage of the layout optimization, the objective is to determine the collision-free placements of the robot and two workpiece holders in the discretized workspace, and compliance with the robot’s maximum reach of $r_{max}=0.44 \mathrm{m}$. These positions serve as input for determining the target positions in the workspace and subsequent motion planning.

The second stage, motion planning, generates collision-free paths between the pick-and-place targets using a sampling-based rapidly-exploring random tree (RRT) planner. The RRT incrementally expands the search space by adding only collision-free nodes, and once a target is reached, the corresponding robot posture is recorded. If RRT fails to find a feasible path due to consecutive collisions with the obstacles present in the environment, resampling is performed by doubling the step size of the planning algorithm. This stage ensures that the robot arm can move safely and feasibly between all task-relevant positions.

Finally, in the third stage, posture optimization, the pick and place postures obtained from the RRT planner are refined using a secondary genetic algorithm (GA). The aim is to optimize a single joint configuration such that the robot minimizes its total execution time by reducing joint travel distance and ensuring smooth transitions between targets. Additionally, candidate postures are constrained to remain collision-free, within joint limits, and away from kinematic singularities, guaranteeing both safety and efficiency during task execution.

4.2. Search Space Modeling for Placement Planning

The search space for the robot and workpiece holders consists of $N_x\times N_z$ cells along the X and Z axes, with cell size s and origin $p_0$. The center position of a cell is indexed by Equation (11).

$$p_{(i,j)}=p_0+(i\times s,0,j\times s)wherei\in [-N_x/2,N_x/2-1],j\in [-N_z/2,N_z/2-1]$$

(11)

Each cell is assigned to one of three categories as follows:

$$c_{(i,j)}=\left\{\begin{array}{cc}\mathrm{Obstacle},\hfill & \mathrm{if}{p}_{(i,j)}\in {\Omega }_{\mathrm{obs}}\hfill \\ \mathrm{Conveyor},\hfill & \mathrm{if}{p}_{(i,j)}\in {\Omega }_{\mathrm{conv}}\hfill \\ \mathrm{Free},\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(12)

where ${\Omega }_{\mathrm{obs}}$ and ${\Omega }_{\mathrm{conv}}$ represent the union of all obstacle regions such as racks, walls, or other machinery equipment and conveyor regions in the environment, respectively. Thus the total set of workspace cell is defined by Equation (13), where $W_f$, $W_c$, and $W_o$ represent the set of free cells, conveyor cells, and obstacle cells, respectively.

$$W=W_f\cup W_c\cup W_o$$

(13)

However, only the set of free cells is considered as candidates for layout optimization of the robot and workpiece holders.

4.3. Layout Optimization

The genetic algorithm with adaptive termination for layout optimization is provided in Algorithm 1. Here the term adaptive refers specifically to a termination mechanism, rather than an adaptive variation of GA operators. In particular, neither mutation or crossover rates nor population size are adapted during execution. Instead, the GA terminates early when the global best cost does not improve for a predefined number of consecutive generations (stall limit $S_{\max }$). This adaptive stall-based stopping criterion prevents unnecessary evaluations once convergence behavior is detected, thereby reducing computational cost without modifying any genetic operator parameters. The population sampling, fitness evaluation, and GA operators are described in detail in the following subsections.

Algorithm 1: Genetic algorithm with adaptive termination

4.3.1. Population Sampling

In the layout optimization problem, each individual or candidate solution $L^{\left(i\right)}=\left(r^{\left(i\right)},x_1^{\left(i\right)},x_2^{\left(i\right)}\right)$ represents the positions of the robot and the two workpiece holders. The initialization step generates a set of such candidate layouts to form the first generation of the genetic algorithm. The sampling rule is defined by Equation (14), where $p_e$ denotes the placement position of entity e, and E is the set of all entities to be placed.

$$p_e\sim Uniform\left(W_f\right)\forall e\in E$$

(14)

This means that for each entity (robot or workpiece holders), a cell is randomly selected with equal probability from the set of free cells $W_f$. Formally, it can be represented by Equation (15). Thus, every free cell has the same chance of being assigned as the initial position of a robot or workpiece holder.

$$P_r(p_e=w)={\displaystyle \frac{1}{|W_f|}}\forall w\in W_f$$

(15)

To ensure physical feasibility, the sampled positions must satisfy the non-overlapping constraint provided in Equation (16). That is, no two entities can occupy the same cell. If a sampled position conflicts with an already assigned one, resampling is performed until a valid position is obtained.

$$p_{e_i}\ne p_{e_j},\forall e_i,e_j\in E,i\ne j$$

(16)

4.3.2. Cost Function

The cost of the candidate solutions is computed by Equation (17), where $d_1,d_2,d_3$ are distances, and $\Phi$ is the sum of the total penalty. Lower values of $\Gamma$ indicate better layouts, and the genetic algorithm is configured to minimize $\Gamma$ over successive generations.

$$\Gamma \left(L\right)=d_1+d_2+d_3+\Phi$$

(17)

The three euclidean distances $d_1,d_2,d_3$ are calculated using Equation (18), where $d_1$ is the distance between the robot and the first workpiece holder, $d_2$ is the distance between the robot and the second workpiece holder, and $d_3$ is the distance between the robot and the conveyor belt.

$$d_1=\left|\right|r-x_1\left|\right|,d_2=\left|\right|r-x_2\left|\right|,d_3=\underset{c\in W_c}{min}\left|\right|r-c\left|\right|$$

(18)

The total penalty $\Phi$ in (17) is the sum of the two penalties. If two objects are too close $(<\delta )$, a fixed overlap penalty is added. If a workpiece holder is beyond the robot’s reach, an additional penalty is applied. The total penalty $\Phi$ is calculated using Equation (19).

$$\Phi =\sum _{(i,j)}{\lambda }_1\times d(p_i,p_j<\delta )+\sum _{i=1}^2{\lambda }_2\times max(d_i-r_{max},0)$$

(19)

Here $\delta =0.25$ is the collision threshold distance, ${\lambda }_1,{\lambda }_2$ are the large positive constants, and $d(·)$ is the binary indicator function.

4.3.3. Selection, Elitism and Replacement

In each generation, all P individuals are evaluated and sorted according to their cost function $\Gamma \left(L\right)$ in descending order.

• Truncation selection: The top half of the population $(\mu =[\mathcal{P}/2\left]\right)$ is retained as parents for generating the next population.
• Elitism: The single best individual in the current generation is preserved and directly carried over to the next generation. This guarantees that the best solution found so far is never lost.
• Replacement: Offspring are generated from the selected parents until the population size is restored to $\mathcal{P}$.

This strategy balances exploitation (retaining the fittest solutions) with exploration (creating diversity through offspring).

4.3.4. Crossover and Mutation

The crossover operator combines two parent layouts to form a new child layout. Let $L^{\left(1\right)}=\left(r^{\left(1\right)},x_1^{\left(1\right)},x_2^{\left(1\right)}\right)$ and $L^{\left(2\right)}=\left(r^{\left(2\right)},x_1^{\left(2\right)},x_2^{\left(2\right)}\right)$ represent two parents. The child layout $L^{{(}^{\prime })}=\left(r^{{(}^{\prime })},x_1^{{(}^{\prime })},x_2^{{(}^{\prime })}\right)$ is constructed gene by gene using uniform crossover. This can be represented by Equation (20), where a is the crossover rate.

$$r^{{(}^{\prime })}=\left\{\begin{array}{cc}{r}^{\left(1\right)},\hfill & \mathrm{with}\mathrm{probabilty}=a\hfill \\ r^{\left(2\right)},\hfill & \mathrm{with}\mathrm{probabilty}=a\hfill \end{array}\right.x_1^{{(}^{\prime })}=\left\{\begin{array}{cc}{x}_1^{\left(1\right)},\hfill & \mathrm{probabilty}=a\hfill \\ x_1^{\left(2\right)},\hfill & \mathrm{probabilty}=a\hfill \end{array}\right.x_2^{{(}^{\prime })}=\left\{\begin{array}{cc}{x}_2^{\left(1\right)},\hfill & \mathrm{probabilty}=a\hfill \\ x_2^{\left(2\right)},\hfill & \mathrm{probabilty}=a\hfill \end{array}\right.$$

(20)

The mutation operator introduces diversity by perturbing the placement of the robot or containers. With probability b, the robot is reassigned to a new feasible location using Equation (21), sampled uniformly from the set of conveyor-adjacent free cells. After selecting a new robot position, the neighborhood of feasible workpiece holder positions are recomputed by Equation (22).

$$r\sim Uniform\left(W_f\right)$$

(21)

$$N\left(r\right)=\{p\in W_f|0<\left|\right|p-r\left|\right|\le r_{max}\}$$

(22)

Independently, with probability b each of the two workpiece holder positions are resampled from the neighborhood of $N\left(r\right)$ as follows:

$$x_1\sim Uniform\left(N\left(r\right)\right),x_2\sim Uniform\left(N\left(r\right)\right)$$

(23)

The final optimized solution is obtained using Equation (1). This is how layout optimization is performed using GA.

4.3.5. Computation of Targets

Once the robot and the two workpiece holder placements are determined through the layout optimization process, the next step is to compute the task-specific target positions required for motion planning. This research defines the pick position as the acquisition point where the robotic system retrieves objects from the conveyor belt, and the place positions as the target locations where these objects are deposited into specified workpiece containers. The computation of these target positions is carried out by evaluating the geometric relationships between the robot and the surrounding environment.

The nearest conveyor cell within the robot’s reachable workspace is identified using a Euclidean distance metric. If the robot base position is denoted by $p_r\in {\mathbb{R}}^3$, and the position of each conveyor cell by $p_c^i\in {\mathbb{R}}^3$, then the closest conveyor cell is determined by Equation (24).

$$p_c^{*}=\arg \underset{i}{min}\left|\right|p_r-p_c^i\left|\right|$$

(24)

To ensure feasible grasping, a small vertical offset $({\Delta }_y=0.25$ m) is added, yielding the final pick position as follows:

$$p_{pick}=p_c^{*}+{\Delta }_y$$

(25)

The two workpiece holders act as deposition targets. If the positions of the holders are $p_{x_1},p_{x_2}\in {\mathbb{R}}^3$, then the corresponding place positions are computed by Equation (26), where ${\Delta }_y^{\prime }=0.22\mathrm{m}$.

$$p_{plac{e}_1}=p_{x_1}+{\Delta }_y^{\prime }{p}_{plac{e}_2}=p_{x_2}+{\Delta }_y^{\prime }$$

(26)

This computation ensures that the robot always selects a feasible picking location on the conveyor and well-defined placing locations above the holders. These target poses, derived directly from the optimized layout, serve as input for the subsequent motion planning stage.

4.4. Motion Planning

The motion planning stage ensures that the robot transitions safely between the pick-and-place targets. In this work, motion planning is performed using a target-biased nearest-neighbor rapidly exploring random trees (TNN-RRT) algorithm, which extends the classical RRT framework. Instead of relying on uniform random sampling alone, the proposed algorithm introduces a target-biased nearest-neighbor metric that combines configuration-space distance with a bias toward the goal. While RRT* is capable of asymptotically optimal path generation, it requires significantly more computation to rewire the tree in high-dimensional joint spaces, which may become prohibitive for real-time pick-and-place tasks. In contrast, TNN-RRT prioritizes rapid exploration with goal-directed growth, achieving faster convergence while still producing feasible collision-free paths suitable for the hierarchical optimization framework. This modification improves the trade-off between exploration and exploitation, allowing the tree to expand while maintaining directed progress toward the desired end-effector posture. By directly employing TNN-RRT rather than the baseline RRT or RRT*, the planner balances computational efficiency and path quality in high-dimensional joint space subject to joint limits. The pseudocode of TNN-RRT is summarized in Algorithm 2.

Algorithm 2: Target-biased nearest neighbor (TNN-RRT) algorithm

Random samples are drawn uniformly from the feasible configuration space C. For each sampled configuration, the nearest node in the tree is selected using a blended distance provided by Equation (27).

$$q_{near}=\arg \underset{q\in \mathbb{T}}{min}[\eta D_{conf}(q,q_{rand})+(1-\eta )d\left(q\right)]$$

(27)

where

• $D_{conf}(q,q_{rand})=\left|\right|q-q_{rand}{\left|\right|}_2$ is the Euclidean distance in joint space.
• $d\left(q\right)=\left|\right|FK\left(q\right)-p_j{\left|\right|}_2$ is the task-space distance of configuration q to the target $p_j$, computed through forward kinematics $FK\left(q\right)$.
• $\eta \in [0,1]$ is the blending factor that balances exploration $(\eta \leftarrow 1)$ and goal biasing $(\eta \leftarrow 0)$.

A new candidate configuration is generated by steering from $q_{near}$ to $q_{rand}$ using Equation (28), where $sa{t}_{\infty ,s}\left(v\right)$ is the infinity-norm saturation operator provided by Equation (29). This ensures that each step respects the maximum incremental joint displacement s.

$$q_{new}=q_{near}+sa{t}_{\infty ,s}(q_{rand},q_{near})$$

(28)

$$sa{t}_{\infty ,s}\left(v\right)=\left\{\begin{array}{cc}v,\hfill & {\left|\right|v\left|\right|}_{\infty }\le s\hfill \\ {\displaystyle \frac{s}{{\left|\right|v\left|\right|}_{\infty }}}v\hfill & otherwise\hfill \end{array}\right.$$

(29)

The tree $\mathbb{T}$ is updated when $q_{new}$ is collision-free. The node $q_{new}$ is added to the tree with parent $q_{near}$. The distance to the goal is updated by Equation (30), and the best configuration so far is tracked by (31).

$$d\left(q_{new}\right)=\left|\right|FK\left(q\right)-p_j{\left|\right|}_2$$

(30)

$$q_{best}=\arg \underset{q\in \mathbb{T}}{min}\left\{d\left(q\right)\right\}$$

(31)

The path is extracted when the termination condition ($d\left(q_{new}\right)\le ϵ=0.05\mathrm{m}$) is satisfied. The extracted path is formulated using Equation (5), and the target posture is recorded using Equation (6). After the motion planner obtains all three target postures, these are transferred to the posture optimization stage to obtain a single optimal posture.

4.5. Surrogate Modeling

Despite the efficiency gains of the target-biased nearest-neighbor RRT (TNN-RRT), a fundamental bottleneck remains in the repetitive evaluation of candidate configurations through forward kinematics, collision checking, and steering operations. These computations accumulate substantial overhead, particularly when the planner is invoked repeatedly within the hierarchical optimization framework. To further reduce this computational burden, a surrogate-assisted strategy is adopted, where a data-driven model approximates the performance of candidate paths without requiring full TNN-RRT evaluations at every iteration.

As illustrated in Figure 3, the process begins with generating reference trajectories using the TNN-RRT planner. These data samples are then used to train the surrogate model, which acts as a computationally inexpensive proxy for path evaluation. This integration of surrogate modeling with TNN-RRT enables efficient exploration of the search space while maintaining accuracy and feasibility of the motion planning stage.

4.5.1. Training Data and Preprocessing

The surrogate model was constructed from trajectory datasets recorded during robot motion planning episodes. Each record contained the robot’s current base position $p_r\in {\mathbb{R}}^3$, target position $p_t\in {\mathbb{R}}^3$, robot end-effector position $p_e\in {\mathbb{R}}^3$, and joint angles $\theta =[{\theta }_1,\dots ,{\theta }_6]\in {\mathbb{R}}^6$. The associated ground-truth output variable was the task-space Euclidean distance $d\in \mathbb{R}$ between the end-effector and the target computed by Equation (32).

$$d=\left|\right|p_e-p_t{\left|\right|}_2$$

(32)

The dataset was filtered to retain only collision-free configurations (penalty, $\Phi =0$) with distances ($d_{th}<0.46$ m) within the robot’s reachable workspace. This ensures that the surrogate learns only feasible mappings. Formally, the training dataset is represented by Equation (33), where the input feature vector ${\mathbb{X}}_i$ is defined by Equation (34).

$$\mathbb{D}=\left\{({\mathbb{X}}_i,d_i)\right|i=1,\dots ,n\}$$

(33)

$$\mathbb{X}=\left[p_{r_i},p_{t_i},p_{e_i},{\theta }_i\right]\in {\mathbb{R}}^{15}$$

(34)

4.5.2. Surrogate Model Formulation and Integration

The surrogate models are formulated as a regression function $\widehat{f}:{\mathbb{R}}^{15}\to \mathbb{R}$ that approximates the mapping from configuration features $\mathbb{X}$ to the distance-to-target d as follows, where $\varphi$ denotes the learned model parameters.

$$\widehat{d}=\widehat{f}\left(\mathbb{X};\varphi \right)$$

(35)

In this study, several surrogate models were generated using the trained dataset, and the performance of these surrogate models is discussed in detail in Section 5.3. The best surrogate model was integrated into the RRT expansion step to guide sampling and steering. Specifically, when sampling new candidate configurations ${\mathbb{X}}_c$, the surrogate provides a rapid estimate $\widehat{d_c}$. Configurations with lower predicted distance obtained by Equation (36) are preferentially selected for tree expansion.

$${\mathbb{X}}^{*}=\arg \underset{x_c}{min}\widehat{f}\left({\mathbb{X}}_c\right)$$

(36)

In cases where the planner approaches but cannot directly reach the target (due to narrow passages or workspace limits), the surrogate provides near-optimal configurations retrieved from the trained dataset (minimum-distance candidates). These act as surrogate-goals that the tree biases toward, improving success rates in cluttered environments. Algorithmically, this reduces redundant sampling in infeasible regions and accelerates convergence toward valid solutions. The SA-RRT algorithm is provided in Algorithm 3.

Algorithm 3: Surrogate-Assisted RRT (SA-RRT) Algorithm

4.6. Posture Optimization

The objective of posture optimization is to determine the robot’s optimal joint configurations $\left(q^{*}\right)\in {\mathbb{R}}^6$ that minimize overall task execution cost while satisfying joint limits and ensuring collision-free motion. The algorithm used for posture optimization is provided in Algorithm 4.

Algorithm 4: Genetic algorithm for posture optimization

Each candidate posture q is evaluated using a composite cost function provided in Equation (37).

$$\xi \left(q\right)=\psi \left(q\right)+T_{cycle}(q_o,q)+T_{reach}(q,q_{pick},q_{place1},q_{place2})$$

(37)

Here $\psi \left(q\right)$ represents the collision penalty of candidate configuration q causes for self-collision or collision with the environment objects. A constant penalty is added using Equation (38). Cycle time $T_{cycle}$ between initial config $q_0$ and config q is calculated using Equation (39) and reach time $T_{reach}$ to complete the pick-and-place task sequence computed using Equation (40).

$$\psi \left(q\right)=\left\{\begin{array}{cc}\lambda =10,\hfill & \mathrm{if}\mathrm{collision}\mathrm{occurs}\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(38)

$$T_{cycle}(q_0\to q)=\sum _{i=1}^6{\displaystyle \frac{|{\theta }_i^{\left(q\right)}-{\theta }_i^{\left(q_o\right)}|}{{\omega }_{\max }^i}}$$

(39)

$$T_{reach}=\sum _{i=1}^{3}T(q\to q_i)$$

(40)

This is how the layout, motion, and posture optimization are completed using the proposed hierarchical framework.

5. Experimental Results

5.1. Experimental Setup and Conditions

The proposed framework was validated through computational experiments conducted in the Unity simulation environment (Unity 2022.3 LTS) using the built-in physics engine. All simulations were performed on a computer with an Intel Core i7-13650HX (2.60 GHz) processor, 16 GB RAM, and an NVIDIA RTX 4060 GPU. The robotic platform considered in this study is the Niryo NED, a 6-degree-of-freedom (DOF) collaborative manipulator imported into Unity via the URDF importer. The robot consists of six revolute joints with joint limits and velocity constraints summarized in

Table 2. Technical specifications of Niryo NED robot.

Joint Name	Joint Limits (Degrees)	Joint Speed (Degrees/sec)
Joint 1	−170 to +170	150
Joint 2	−120 to +35	115
Joint 3	−77 to +90	140
Joint 4	−120 to +120	180
Joint 5	−100 to +55	180
Joint 6	−145 to +145	180

.

Although Unity was used as the simulation environment, the optimization components are robot-model-based rather than simulation-dependent. All kinematic limits, forward kinematics computations, and joint feasibility checks are derived directly from the actual URDF of the Niryo NED. Therefore, the target joint configurations produced by the motion planning and posture optimization stages are physically valid and directly executable on the real Niryo NED hardware through its official control interface (e.g., Niryo Studio). In this context, Unity functions only as a visualization and physics execution platform, while the generated joint configurations remain transferable to a real robotic setup without modification to the optimization algorithms.

For layout optimization, a genetic algorithm (GA) was employed with a population size of 30 and 100 generations. Several surrogate models were trained on 8000+ samples with a training–validation split of 80%–20%. Motion planning was performed using the best surrogate-assisted rapidly exploring random trees (SA-RRT) planner. Performance was evaluated in terms of computation time, task completion time, and collision avoidance rate.

5.2. Layout Optimization Analysis

The initial and final robot placements were compared to evaluate the performance of the layout optimization stage. Figure 4 illustrates the evolution from the initial layout to three representative optimized layouts. Specifically, Figure 4a shows the initial placement, while Figure 4b–d present optimized placements obtained after 100 generations. Among these, Figure 4b corresponds to a layout solution with cost of 1.36, where one target location becomes unreachable. Figure 4c,d illustrate feasible optimized layouts with costs of 1.02 and 0.90, respectively, where all targets remain reachable. These results confirm that the GA effectively relocates the robot and workpiece holders within reachable free cells while avoiding obstacle cells, thus reducing the probability of collisions and improving the feasibility of the subsequent motion planning stage.

The convergence behavior of the GA is shown in Figure 5. It can be observed that for different crossover and mutation rates, the optimization progressively minimizes the cost function value and reaches a stable solution after approximately 20∼40 generations. The minimum theoretical value of the layout optimization cost function is $0.90$, which corresponds to the ideal arrangement where all penalty terms are zero and the distances between the robot and the two workpiece holders are minimized to their lowest possible values. Specifically, when no infeasibility penalties are applied, the total cost is determined solely by the sum of the three distances $(d_1+d_2+d_3)$. In the optimal configuration, each workpiece holder is placed in an adjacent cell relative to the robot’s base, resulting in each distance $d_i=0.30\mathrm{m}$, which exactly equals the distance between the centers of two neighboring cells in the discretized workspace. Therefore, the minimum achievable cost is $0.30\times 3=0.90$. This value is confirmed by Figure 4d, which shows the final optimized layout with a cost of $0.90$, and by Figure 5, where the convergence curve stabilizes at this theoretical minimum. Although GAs are generally stochastic in nature, the search space in this layout optimization is discrete and finite, and the theoretical minimum cost ($0.90$) is analytically known. Since the GA consistently converged to this value across multiple runs and no lower-cost configuration exists in the discretized workspace, the obtained solution can be identified as the global optimum for this problem instance. This demonstrates the ability of the GA to balance exploration and exploitation of the search space.

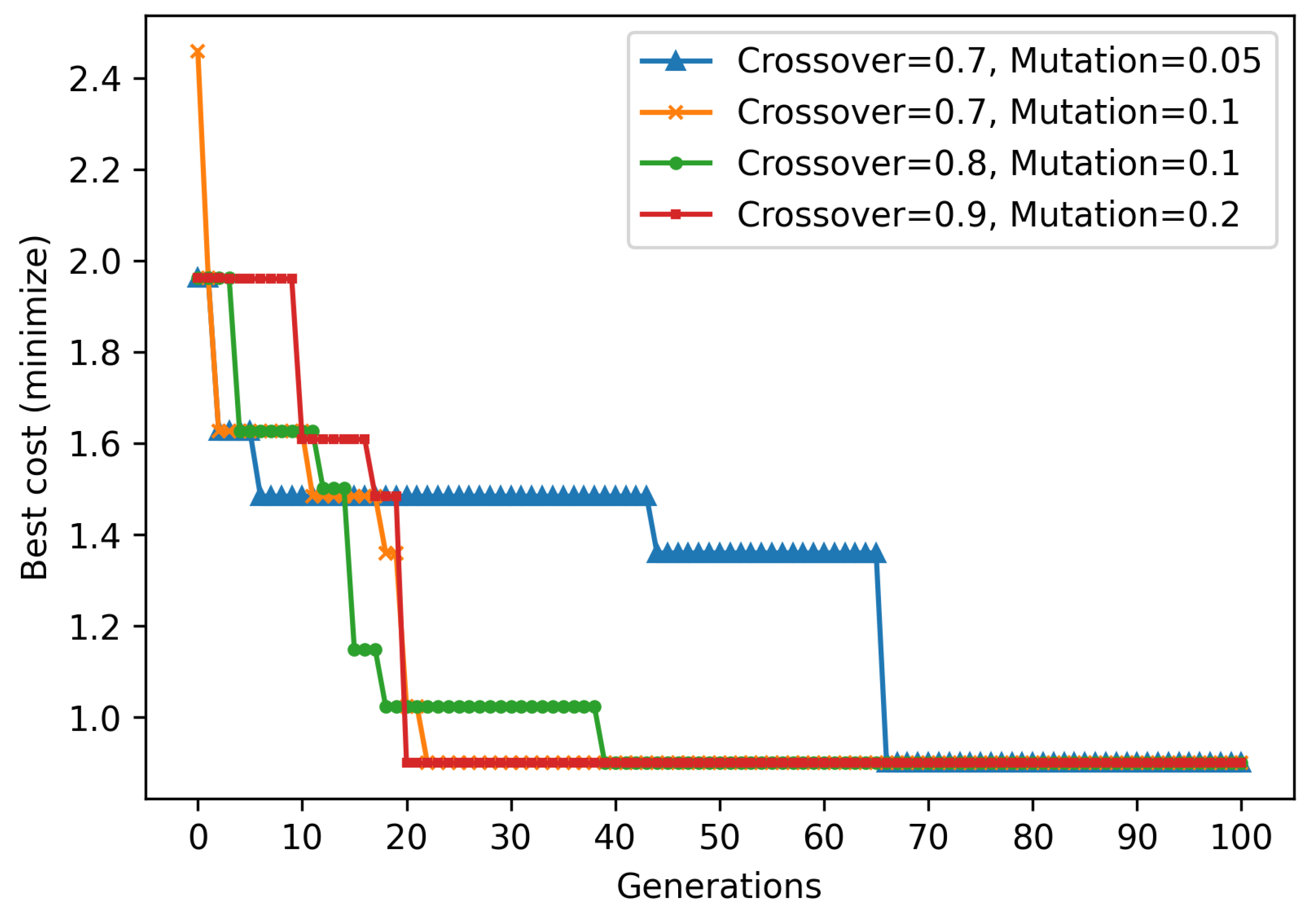
To further examine the robustness of the GA, a sensitivity analysis was performed by varying crossover and mutation probabilities. The average cost function values obtained across different generations with a fixed population size of 30 are shown in Figure 6. The results indicate that although the optimization performance is somewhat affected by parameter choices, the GA consistently converges to high-quality solutions. This confirms the reliability of the approach for layout determination.

5.3. Performance of Surrogate Modeling for Motion Planning

To evaluate the effectiveness of surrogate modeling, an experimental dataset of more than 8000 samples was generated. The dataset was split into 80% for training and 20% for testing, and multiple regression models were benchmarked using the scikit-learn library. The comparison was carried out in terms of the coefficient of determination ($R^2$), root mean squared error (RMSE), mean squared error (MSE), mean absolute error (MAE), cross-validation $R^2$ mean ($CV\_R^2$), and training time.

Table 3. Performance comparison of different regression models trained on the dataset.

Model Name	${\mathit{R}}^2$	RMSE	MSE	MAE	CV$\_{\mathit{R}}^2$	Training Time (s)
Random Forest (RFR)	0.853	0.046	0.002	0.026	0.541	19.54
Gradient Boosting (GBR)	0.774	0.057	0.003	0.041	0.547	6.11
Linear Regression (LR)	0.396	0.094	0.008	0.079	0.352	0.08
Support Vector (SVR)	0.478	0.087	0.007	0.077	0.413	1.43
K-Nearest Neighbors (KNN)	0.730	0.063	0.004	0.036	0.433	0.14
Bayesian Ridge (BR)	0.396	0.094	0.008	0.079	0.352	0.09
Extra Trees Regressor (ET)	0.925	0.033	0.001	0.018	0.584	7.58

summarizes the performance of the tested models.

The results indicate that the Extra Trees model achieved the best overall performance, with the highest $R^2$ score of 0.9250 and the lowest error metrics (RMSE = 0.033, MAE = 0.018). Despite a slightly higher training time than Gradient Boosting, it significantly outperformed all other models in terms of accuracy and generalization. Cross-validation results confirm that Extra Trees maintained reasonable generalization across different data splits, though its mean CV score (0.584) was lower than the single test set performance (0.925), indicating some sensitivity to data partitioning. These findings support the use of Extra Trees as the surrogate model for integration into the motion planning algorithm. The predictive performance of the surrogate models was evaluated using the coefficient of determination $\left(R^2\right)$ and the corresponding training time. Figure 7 presents the $\left(R^2\right)$ scores obtained for each model, while Figure 8 illustrates the associated training time.

Figure 9 shows the predictive performance of the Extra Trees surrogate model by comparing actual and predicted minimum distances for all robot–target position pairs in the test dataset. The x-axis represents the sample index, while the y-axis shows the distance in meters. Blue circles denote actual minimum distances from simulations, and green crosses indicate surrogate predictions. Their overlapping nature with few errors, mostly within ±0.06 m (red line), highlights the model’s accuracy in capturing the nonlinear mapping between robot and target configurations. When the surrogate model is integrated into the RRT framework for motion planning, the SA-RRT algorithm first checks whether the current robot–target position pair matches a surrogate position pair. If a match is found, the SA-RRT algorithm retrieves the joint angle configuration from the surrogate samples associated with the minimum distance. This enables the robot arm to move to the desired posture efficiently, avoiding redundant evaluations and demonstrating the surrogate’s effectiveness for integration into sampling-based motion planners.

5.4. Motion Planning Performance and Path Efficiency

This subsection evaluates the performance of the Surrogate-Assisted RRT (SA-RRT) in comparison to the standard target-biased nearest neighbor RRT (TNN-RRT). The assessment considers both qualitative and quantitative measures, including the efficiency of generated paths, the number of iterations required to reach the target, collision occurrences, computation time, and total task completion time.

Figure 10 provides a comparative visual analysis of the representative paths generated by the TNN-RRT in Figure 10a–c and SA-RRT in Figure 10d–f algorithms for the pick, first placement, and second placement tasks, respectively. Although neither TNN-RRT nor SA-RRT provides theoretically guaranteed global optimality for the obtained trajectories, the SA-RRT variant used in this work offers an improved trajectory quality compared to TNN-RRT. In SA-RRT, when a surrogate match exists for a robot-target position pair, it directly retrieves joint configurations that the surrogate predicts to be near-optimal (minimal end-effector distance) and expands the tree from those near-optimal states first while still preserving random exploration when no match is found. This bias systematically reduces the expected number of expansions required to reach the target and therefore converges toward shorter and smoother feasible trajectories in fewer iterations compared to the baseline TNN-RRT. The TNN-RRT trajectories exhibit longer deviations and more irregular motion patterns as shown in Figure 10a–c, whereas the SA-RRT trajectories demonstrate smoother joint transitions with reduced path deviations as shown in Figure 10d–f, respectively. This qualitative difference aligns with the quantitative performance improvements reported in

Table 4. Quantitative comparison of TNN-RRT and SA-RRT performance across the pick, first place, and second place paths.

Path Name	Algorithm	Iterations	Total Nodes in Tree	Total Nodes in Path	Number of Collided Nodes	Collision Rate (%)	Path Computation Time (s)	Task Completion Time (s)
Pick path	TNN-RRT 1	124	108	37	14	11.38	130.38	39.96
	SA-RRT 2	18	18	18	0	0.00	17.68	19.44
First place path	TNN-RRT	29	29	13	0	0.00	30.74	14.04
	SA-RRT	5	5	5	0	0.00	4.16	5.40
Second place path	TNN-RRT	70	70	36	0	0.00	74.20	38.88
	SA-RRT	18	18	18	0	0.00	17.68	19.44

¹ TNN-RRT: target-biased nearest neighbor RRT algorithm; ² SA-RRT: surrogate-assisted RRT algorithm.

and reinforces that SA-RRT consistently generates more efficient motion paths.

Table 4 quantitatively compares the two planners across multiple metrics. SA-RRT consistently requires fewer iterations to converge to the target, generates non-collided nodes, and achieves zero collision rates. Furthermore, the computation time and task completion time are significantly reduced due to the surrogate model guidance, which retrieves precomputed joint configurations for matched robot–target position pairs, avoiding excessive evaluations.

Figure 11 illustrates the evolution of the end-effector’s distance to the goal across successive nodes for both planners. For each task, both TNN-RRT and SA-RRT start from the same initial distance and converge to the same final target distance. However, the SA-RRT trajectories reach the goal in substantially fewer nodes, indicating more direct convergence and reduced exploration overhead. By contrast, TNN-RRT requires a larger number of intermediate nodes to achieve the same final distance. These results highlight that the surrogate-assisted approach enhances the efficiency of the RRT search process, enabling faster convergence toward feasible paths while preserving path quality.

5.5. Posture Optimization Analysis

In this subsection, we analyze the performance of GA-based posture optimization for the 6-DOF manipulator. The goal of the optimization is to minimize the composite cost function calculated using Equation (35), which includes collision penalties, cycle time (time to move from initial to optimized configuration), and reach time (cumulative time to reach the pick, place1, and place2 configurations from the optimized posture). The GA was executed with a population size of 30 over 100 generations, and the best solution was selected based on the lowest fitness value.

Figure 12a,b presents the initial and the optimized configuration representative snapshots of the manipulator obtained by the GA. The optimized posture reduces the required motion to reach all task configurations while remaining collision-free.

Table 5. Posture optimization analysis of different robot configurations.

Configuration	Joint 1	Joint 2	Joint 3	Joint 4	Joint 5	Joint 6	Total Joint Angle *	Cycle Time (s)	Reach Time (s)	Cost Value
Initial Config.	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.292	1.292
Pick Config.	81.72	−15.59	−21.48	−7.77	31.19	9.92	167.67	0.545	1.608	2.152
Place1 Config.	−82.41	−23.06	−19.37	−5.14	−13.71	13.36	157.05	0.549	1.675	2.224
Place2 Config.	4.71	−19.46	−16.64	−9.77	2.28	−11.18	64.04	0.169	1.094	1.263
Optimized Config.	−5.95	−9.23	−10.45	0.13	−12.73	4.46	42.95	0.080	1.183	1.263

* The values in column 2–8 are in degrees.

summarizes the posture optimization performance, including total joint motion, cycle time, and reach time. The last column of this table presents the cost value $\xi \left(q\right)$ for each evaluated posture, which is calculated using the composite cost function in Equation (35). For collision-free configurations, where the penalty term $\Psi \left(q\right)=0$, the cost value corresponds to the summation of the cycle time and the total reach time. The cycle time measures the motion duration required to move the robot from its initial home configuration $q_0$ to the candidate posture q, while the reach time represents the cumulative time to execute the subsequent pick-and-place sequence from posture q. The GA achieved a cost reduction of 2.24%, and lowered the cumulative reach time by 8.44% compared to the initial configuration. These results confirm that posture optimization can substantially improve task efficiency by providing a favorable starting posture for the subsequent task execution pipeline.

Posture optimization was performed as the final stage of the hierarchical framework to refine the manipulator’s joint configurations after feasible paths were identified. The main objective was to minimize joint displacement while ensuring collision-free execution of the planned tasks. This step is particularly important for reducing mechanical stress, improving energy efficiency, and enhancing overall task feasibility in narrow workspaces.

6. Discussion

The results presented in Section 5 provide a comprehensive evaluation of our hierarchical optimization framework for robotic pick-and-place tasks. Three key aspects—layout optimization, motion planning using SA-RRT, and posture optimization—collectively demonstrate the effectiveness of the proposed approach.

Layout Optimization: The genetic algorithm-based layout optimization successfully positions the NED robots and the workpiece holders to maximize task feasibility while minimizing interference. The optimized layouts maintain sufficient inter-robot distances and ensure that the robot can access its assigned workspace zones. These findings align with previous studies emphasizing the importance of task-specific workspace arrangement for single-robot systems [3,4,43]. Compared to arbitrary or manually chosen placements, our GA-based approach reduces potential collisions and improves accessibility, thus providing a robust foundation for subsequent motion planning.

Motion Planning with SA-RRT: The surrogate-assisted RRT reduces the number of sampled nodes required to generate collision-free trajectories to each target (pick, place1, and place2) compared to the baseline TNN-RRT. While the total end-effector path distance remains similar, the reduction in nodes results in faster computation and smoother trajectories. Importantly, SA-RRT maintains the same start and end positions as TNN-RRT, demonstrating that the surrogate model effectively guides the planner toward feasible configurations. This highlights the efficiency benefits of integrating surrogate models into RRT-based motion planning, consistent with prior work on data-driven sampling guidance [23,44].

Posture Optimization: The GA-based posture optimization identifies an initial configuration that minimizes a combined fitness metric, including collision penalties, cycle time from the initial to optimized configuration, and reach time to all three task positions. The optimized posture reduces reach time by approximately 8.44% and decreases cumulative joint angles compared to the pick and place configurations. These improvements indicate that strategic selection of the robot’s initial posture can enhance overall task efficiency, reduce mechanical strain, and lower cycle time. Previous research supports this observation, showing that optimized robot postures contribute to faster and safer task execution [20,21,45].

To contextualize our computational gains, we compare SA-RRT with three recent optimization planners. Recently, a deep reinforcement learning-based Proximal Policy Optimization (PPO) motion planning scheme for industrial manipulators [46] demonstrated 52.7–75.1% reduction in motion-planning time for UR5 configurations using sensor-based observations. The study in [47] integrated RRT with Chaotic Particle Swarm Optimization (PSO) for 6-DOF manipulators and reported 21% computation time improvement over baseline RRT, while [48] proposed a PSO-enhanced RRT* with rotation-angle constraints for mobile robots, reporting 5.6–37.2% gains for different scenarios. In contrast, the surrogate-assisted approach adopted in this work achieves a 76.17% computation time reduction in multi-target pick–place tasks. While these studies differ in platforms, environments, and metrics, the comparison indicates that surrogate-guided sampling can yield larger efficiency gains than PSO-based hybrid methods. The larger gain in our work is primarily attributable to (i) using a surrogate to avoid expensive collision checks and (ii) directly reusing previously recorded minimal-distance samples (joint postures) when a surrogate match is found. A summary is provided in

Table 6. Comparison of motion optimization planners and this work.

Authors [Ref.]	Key Method	Robot	Computation Time Reduction in (%)
Bhuiyan et al. (2023) [46]	DRL-PPO	UR5	52.7–75.1%
Wang et al. (2024) [47]	PSO + RRT	manipulator robot	21%
Zhuang et al. (2025) [48]	PSO + RRT*	Mobile robot	5.6–37.2%
This work	SA-RRT	NED	76.17%

.

The proposed hierarchical model shows strong potential for scalability and generalization. For larger workspaces with more target points, the front-end layout optimization becomes even more critical to preventing computational bottlenecks in motion planning. The SA-RRT’s efficiency would be a significant advantage in such cluttered environments. While this study utilized a specific NED robot, the framework is agnostic to the robot configuration. The posture optimization module would naturally adapt to different kinematic chains (e.g., SCARA or articulated robots with more DOFs) to find an efficient home configuration. Finally, the method’s adaptability to varying task complexities such as dynamic obstacles or different payloads could be enhanced by integrating real-time re-planning at the motion level, a promising direction for future work.

Together, these results demonstrate that a hierarchical optimization approach—starting from the layout, followed by motion planning and posture optimization—can significantly improve the efficiency and safety of single-robot pick-and-place operations. By reducing unnecessary movements and planning overhead, the framework provides practical guidance for industrial automation scenarios where time-efficient and collision-free operation is critical.

7. Conclusions

This study presented an integrated framework for optimizing workspace layout, robot motion, and posture for a single 6-DOF Niryo NED robot with two workpiece holders. Layout optimization using a genetic algorithm ensured feasible and efficient robot placement, while motion planning comparisons between TNN-RRT and SA-RRT showed that the surrogate-assisted approach significantly reduces the number of nodes and iterations without compromising collision-free paths. Posture optimization further minimized cycle and reach times by selecting joint configurations that reduce overall robot movement. The results demonstrate that the surrogate-guided strategy can substantially reduce motion-path computation time (76.17%), outperforming recent hybrid sampling–optimization planners such as PSO–RRT and PSO–RRT*. This indicates that learned surrogate guidance applied inside the sampling process provides scientific significance beyond global stochastic search approaches, with direct practical implications. Overall, the proposed methodology achieves meaningful improvements in task efficiency and safety for single-robot pick-and-place operations. However, the current approach is limited to static environments, known object locations, and a single robot platform. Future extensions may incorporate real-time implementation and tighter integration with visual perception for dynamic object updates as well as extend the hierarchical optimization strategy to multi-robot cooperative manipulation and heterogeneous workstation environments. These directions are expected to strengthen the generalization and deployment impact of the hierarchical surrogate-assisted planning framework.