Test Apparatus for Determining the Particle-to-Particle Friction Coefficient
Featured Application
Abstract
1. Introduction
2. Materials and Methods
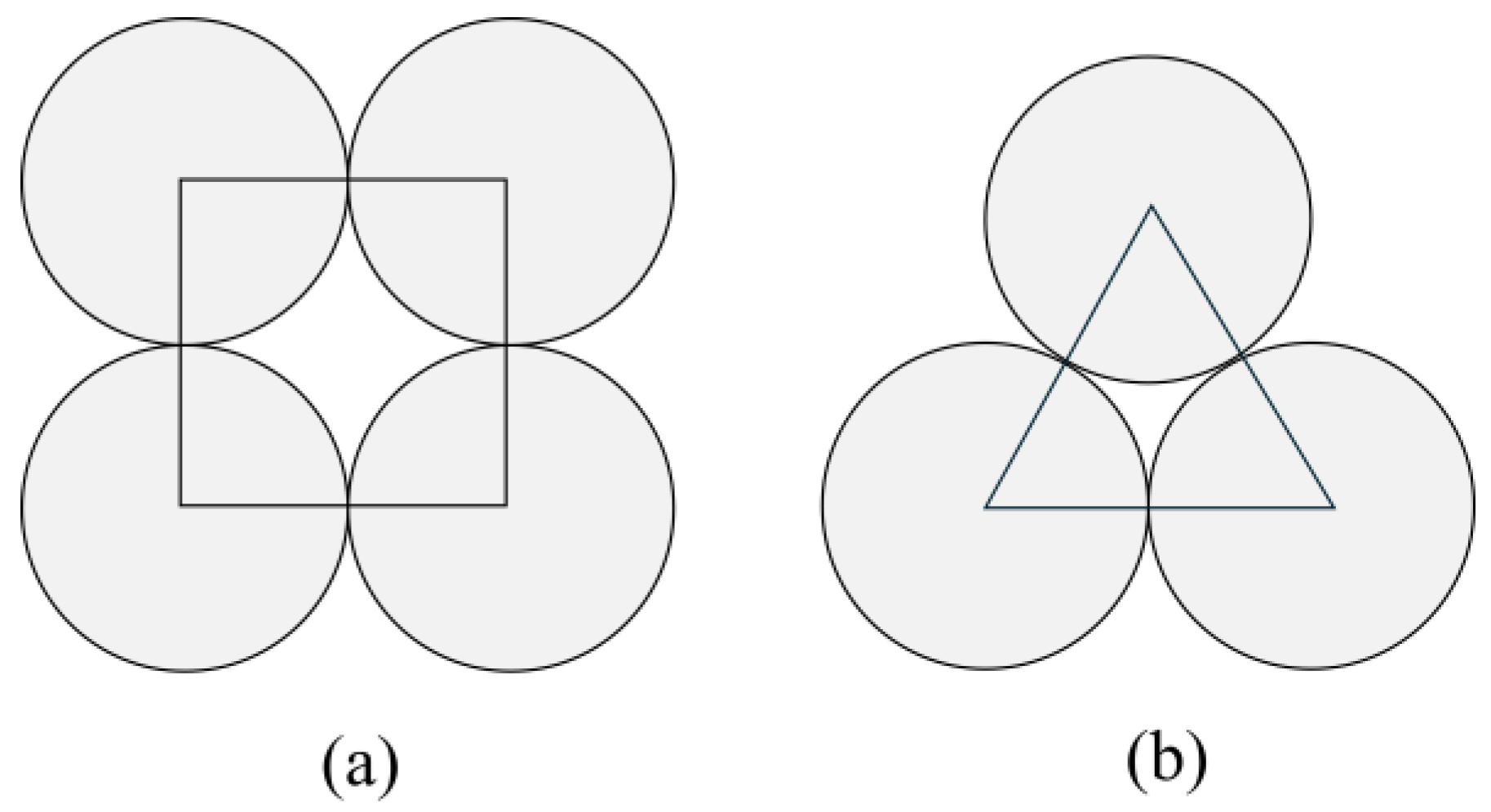
2.1. Preparation of Samples
2.2. Nomenclature
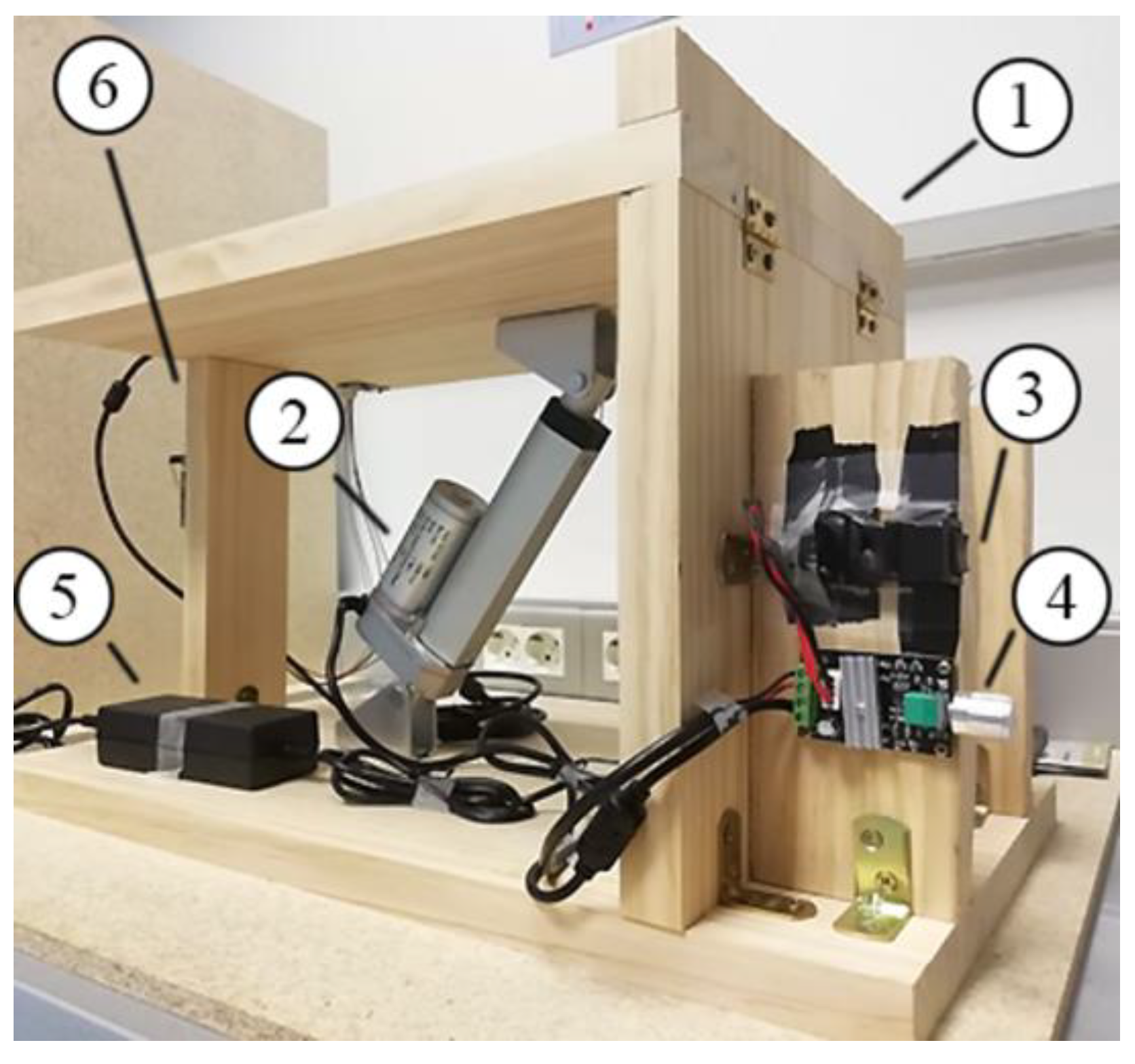
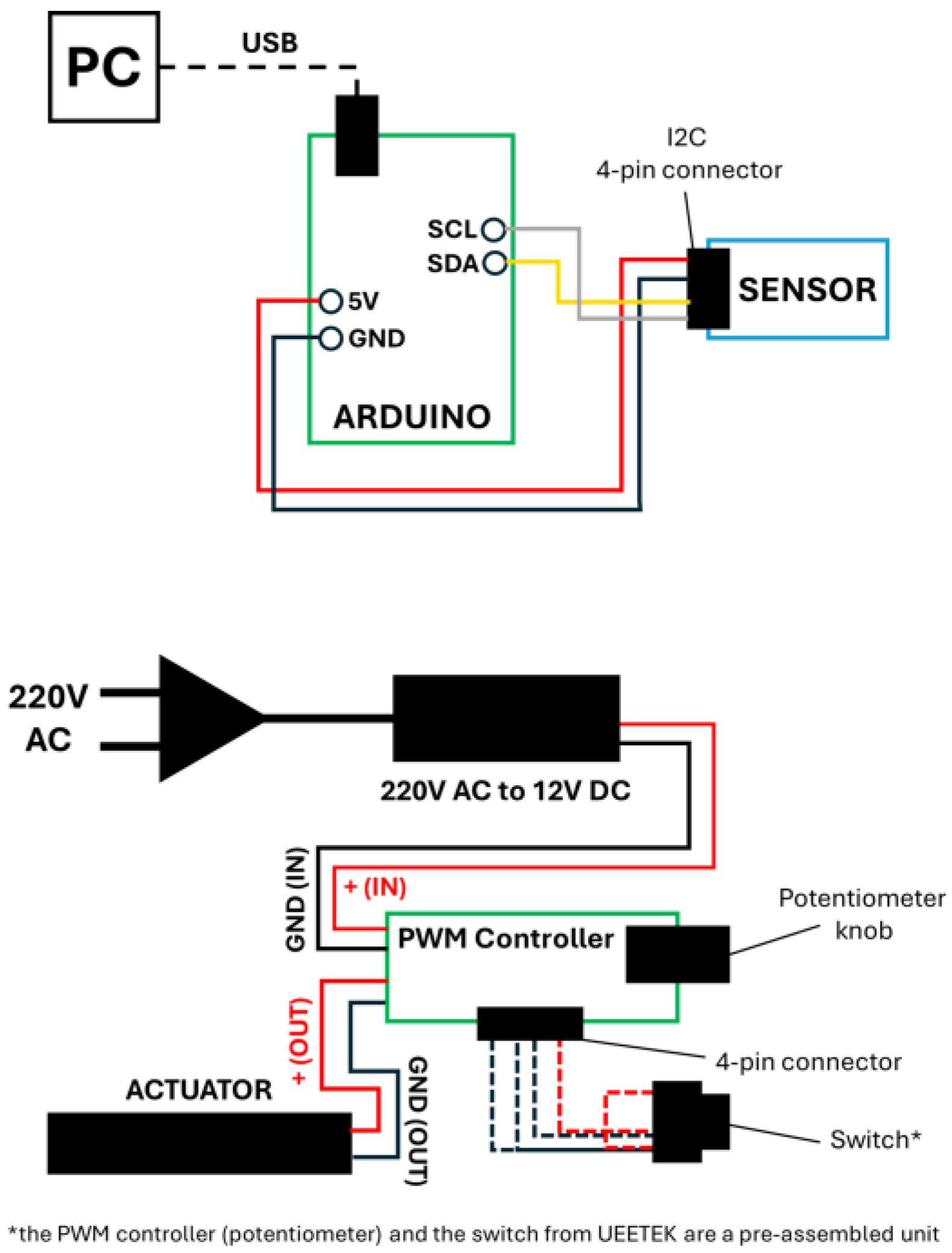
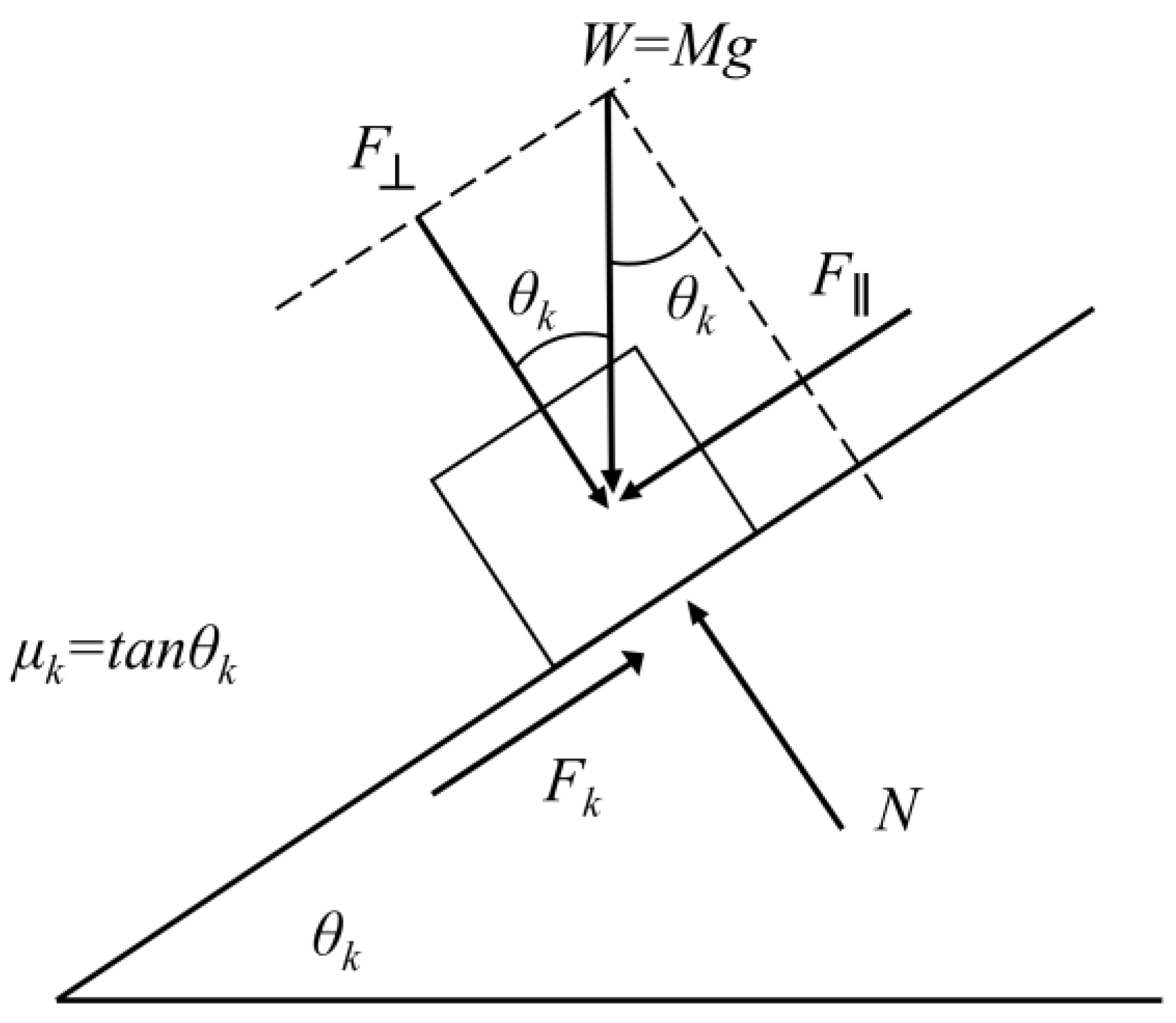
2.3. Test Apparatus
2.3.1. Design Requirements
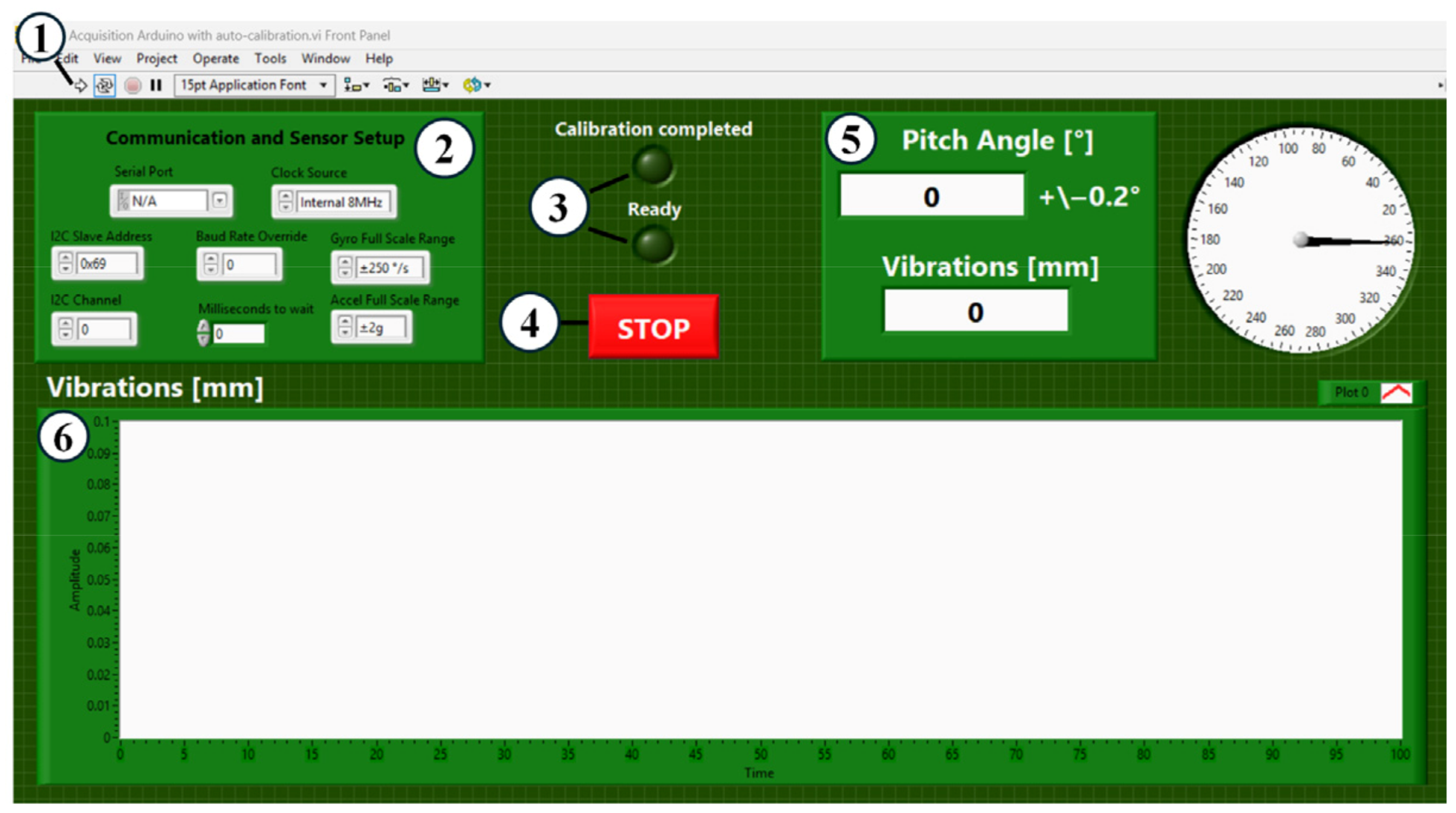
2.3.2. Software
2.4. Test Procedure
3. Results
4. Discussion
4.1. Plate–Particles vs. Particles–Particles
4.2. Orientation of the Samples
4.3. Particle Configuration
4.4. Twelve Tests
4.5. Overall Evaluation
4.6. Friction Coefficient
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brown, C.J.; Nielsen, J. Silos: Fundamentals of Theory, Behaviour and Design; CRC Press: London, UK, 1998; ISBN 9780429078637. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A Discrete Numerical Model for Granular Assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Goda, T.J.; Ebert, F. Three-Dimensional Discrete Element Simulations in Hoppers and Silos. Powder Technol. 2005, 158, 58–68. [Google Scholar] [CrossRef]
- Ramírez, A.; Nielsen, J.; Ayuga, F. On the Use of Plate-Type Normal Pressure Cells in Silos. Comput. Electron. Agric. 2010, 71, 64–70. [Google Scholar] [CrossRef]
- Kobyłka, R.; Molenda, M. DEM Simulations of Loads on Obstruction Attached to the Wall of a Model Grain Silo and of Flow Disturbance around the Obstruction. Powder Technol. 2014, 256, 210–216. [Google Scholar] [CrossRef]
- Coetzee, C.J.; Els, D.N.J. Calibration of Discrete Element Parameters and the Modelling of Silo Discharge and Bucket Filling. Comput. Electron. Agric. 2009, 65, 198–212. [Google Scholar] [CrossRef]
- Ketterhagen, W.R.; Curtis, J.S.; Wassgren, C.R.; Kong, A.; Narayan, P.J.; Hancock, B.C. Granular Segregation in Discharging Cylindrical Hoppers: A Discrete Element and Experimental Study. Chem. Eng. Sci. 2007, 62, 6423–6439. [Google Scholar] [CrossRef]
- Combarros, M.; Feise, H.J.; Zetzener, H.; Kwade, A. Segregation of Particulate Solids: Experiments and DEM Simulations. Particuology 2014, 12, 25–32. [Google Scholar] [CrossRef]
- Balevičius, R.; Kačianauskas, R.; Mróz, Z.; Sielamowicz, I. Discrete-Particle Investigation of Friction Effect in Filling and Unsteady/Steady Discharge in Three-Dimensional Wedge-Shaped Hopper. Powder Technol. 2008, 187, 159–174. [Google Scholar] [CrossRef]
- Parafiniuk, P.; Molenda, M.; Horabik, J. Discharge of Rapeseeds from a Model Silo: Physical Testing and Discrete Element Method Simulations. Comput. Electron. Agric. 2013, 97, 40–46. [Google Scholar] [CrossRef]
- Ramírez-Gómez, Á. The Discrete Element Method in Silo/Bin Research. Recent Advances and Future Trends. Part. Sci. Technol. 2018, 38, 210–227. [Google Scholar] [CrossRef]
- ASAE S368.4; Compression Test of Food Materials of Convex Shape. American Society of Agricultural and Biological Engineers (ASABE): St. Joseph, MI, USA, 2006.
- D854-10; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2010.
- Ramírez-Gómez, Á.; Gallego, E.; Fuentes, J.M.; González-Montellano, C.; Ayuga, F. Values for Particle-Scale Properties of Biomass Briquettes Made from Agroforestry Residues. Particuology 2014, 12, 100–106. [Google Scholar] [CrossRef]
- Katterfeld, A.; Coetzee, C.; Donohue, T.; Fottner, J.; Grima, A.R.; Ilic, D.; Kačianauskas, R.; Nečas, J.; Schott, D.L.; Williams, K.; et al. Calibration of DEM Parameters for Cohesionless Bulk Materials Under Rapid Flow Conditions and Low Consolidation; Delft University of Technology: Delft, The Netherlands, 2019. [Google Scholar]
- Schulze, D. Powders and Bulk Solids; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-73767-4. [Google Scholar]
- Zegzulka, J.; Gelnar, D.; Jezerska, L.; Ramirez-Gomez, A.; Necas, J.; Rozbroj, J. Internal Friction Angle of Metal Powders. Metals 2018, 8, 255. [Google Scholar] [CrossRef]
- Chung, Y.-C. Discrete Element Modelling and Experimental Validation of a Granular Solid Subject to Different Loading Conditions. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2006. [Google Scholar]
- ASTM-Method-G99-95A; Standard Test Method for Wear Testing with a Pin-on-Disk Apparatus. American Society for Testing and Materials (ASTM): West Conshohocken, PA, USA, 2000.
- Hancock, B.C.; Mojica, N.; John-Green, K.S.; Elliott, J.A.; Bharadwaj, R. An Investigation into the Kinetic (Sliding) Friction of Some Tablets and Capsules. Int. J. Pharm. 2010, 384, 39–45. [Google Scholar] [CrossRef] [PubMed]
- Grima, A.P.; Wypych, P.W. Development and Validation of Calibration Methods for Discrete Element Modelling. Granul. Matter 2011, 13, 127–132. [Google Scholar] [CrossRef]
- Cavarretta, I.; Rocchi, I.; Coop, M.R. A new interparticle friction apparatus for granular materials. Can. Geotech. J. 2011, 48, 1829–1840. [Google Scholar] [CrossRef]
- Senetakis, K.; Coop, M.R. The development of a new micro-mechanical inter-particle loading apparatus. Geotech. Test. J. 2014, 37, 1028–1039. [Google Scholar] [CrossRef]
- Li, Y.; Chan, D.; Nouri, A. Measuring Interparticle Friction of Granules for Micromechanical Modeling. Energies 2022, 15, 3967. [Google Scholar] [CrossRef]
- Jones, R. From single particle AFM studies of adhesion and friction to bulk flow: Forging the links. Granul. Matter 2003, 5, 191–204. [Google Scholar] [CrossRef]
- Schulze, D. Round robin test on ring shear testers. Adv. Powder Technol. 2011, 22, 197–202. [Google Scholar] [CrossRef]






| Sample | Type | Material | Position | Configuration | Number of Particles |
|---|---|---|---|---|---|
| PL | Plane | Clay | Bottom | -- | -- |
| S1SQT | Plate of particles | Clay | Top | Square | 48 |
| S2SQB | Plate of particles | Clay | Bottom | Square | 88 |
| S3SQT | Plate of particles | Clay | Top | Square | 49 |
| S4TT | Plate of particles | Clay | Top | Triangle | 39 |
| S5TT | Plate of particles | Clay | Top | Triangle | 52 |
| S6TB | Plate of particles | Clay | Bottom | Triangle | 105 |
| S7TT | Plate of particles | Clay | Top | Triangle | 52 |
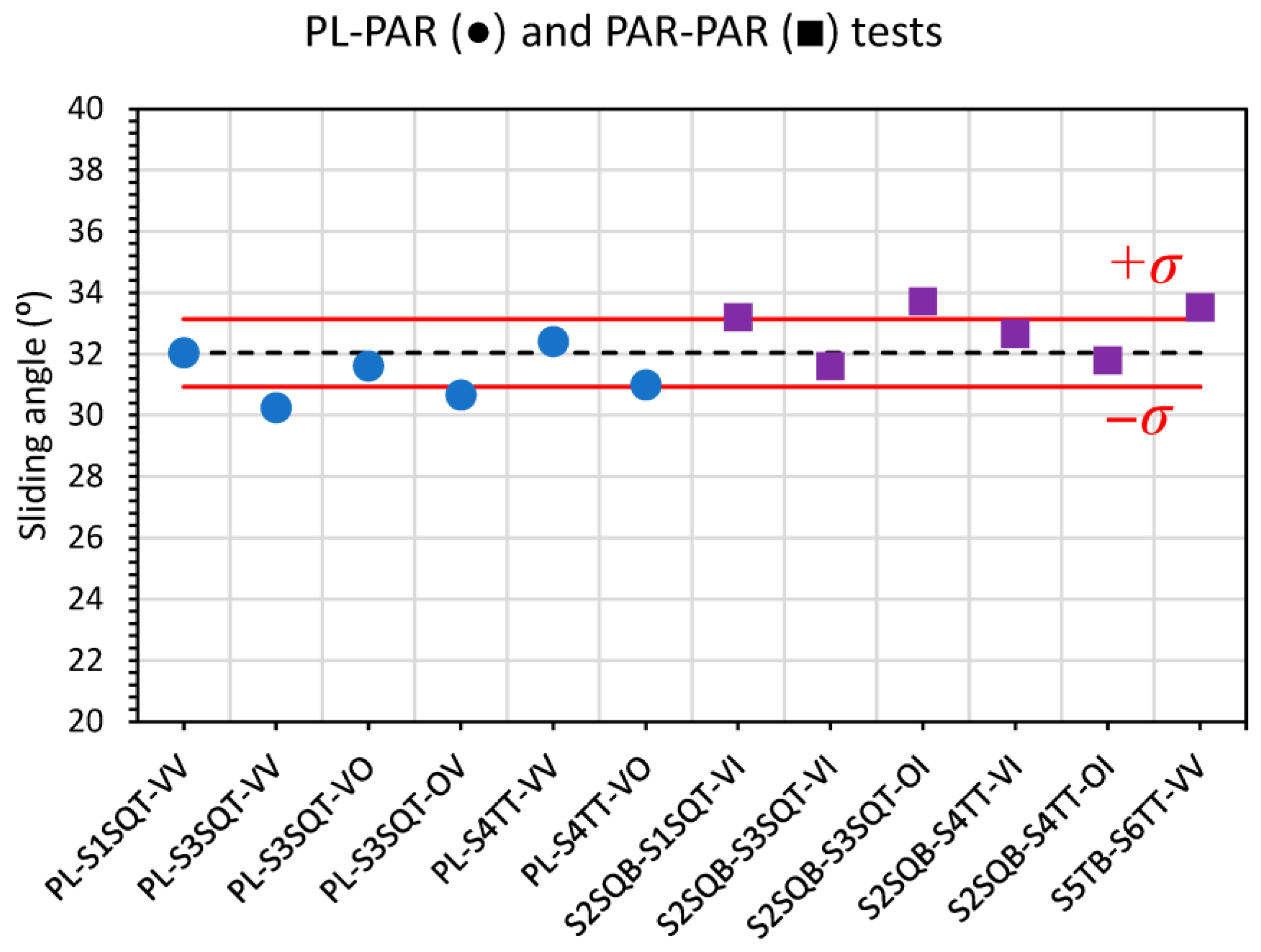
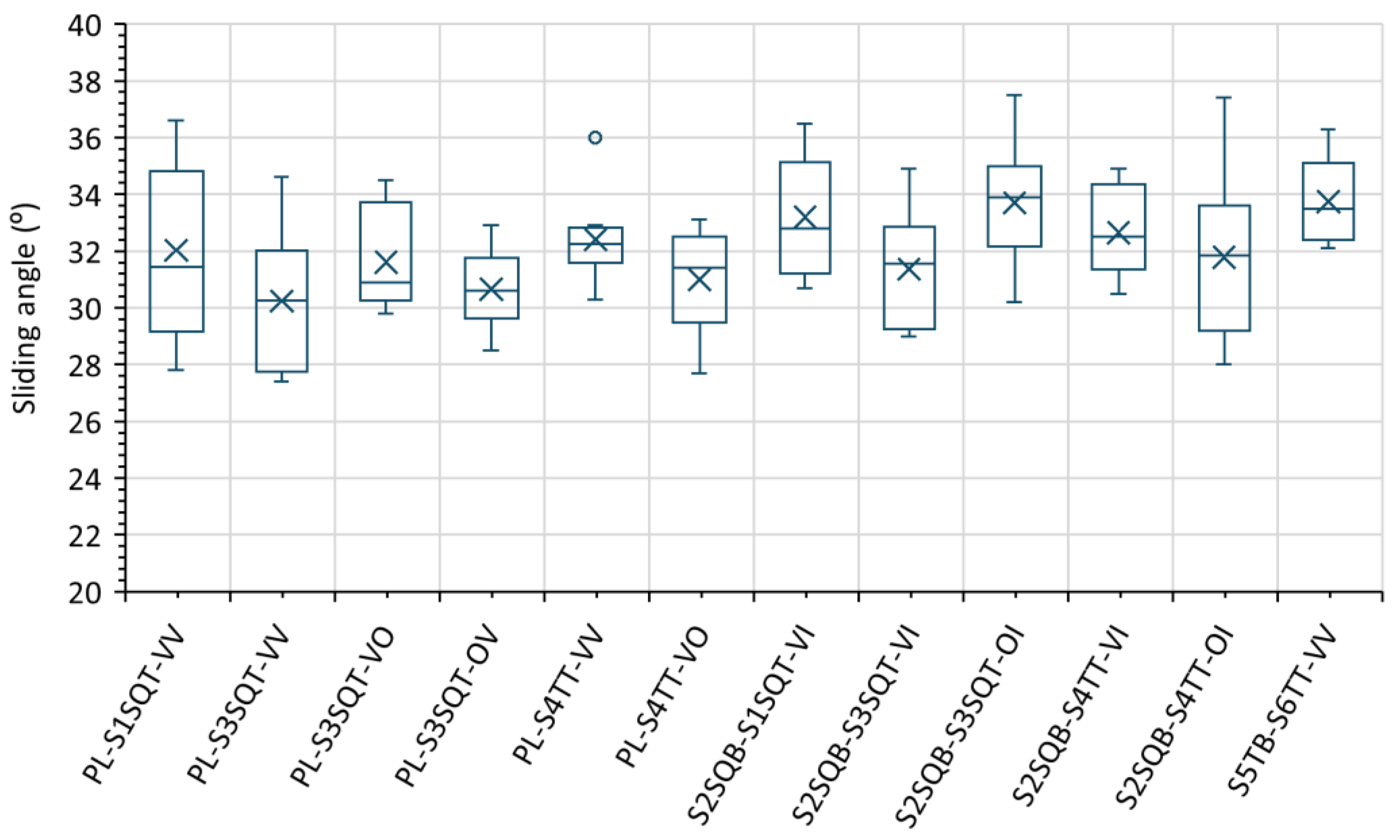
| No. | Sample | Measurements | Mean (°) | Max (°) | Min (°) | ST.DEV. (°) | μ |
|---|---|---|---|---|---|---|---|
| 1 | PL-S1SQT-VV | 10 | 32.1 | 36.6 | 27.8 | 2.9 | 0.63 |
| 2 | PL-S3SQT-VV | 10 | 30.3 | 34.6 | 27.4 | 2.3 | 0.58 |
| 3 | PL-S3SQT-VO | 10 | 31.6 | 34.5 | 29.8 | 1.7 | 0.61 |
| 4 | PL-S3SQT-OV | 10 | 30.7 | 32.9 | 28.5 | 1.4 | 0.59 |
| 5 | PL-S4TT-VV | 10 | 32.4 | 36.0 | 30.3 | 1.5 | 0.63 |
| 6 | PL-S4TT-VO | 10 | 31.0 | 33.1 | 27.7 | 1.7 | 0.60 |
| 7 | S2SQB-S1SQT-VI | 10 | 33.2 | 36.5 | 30.7 | 2.0 | 0.65 |
| 8 | S2SQB-S3SQT-VI | 10 | 31.7 | 34.9 | 29 | 2.0 | 0.62 |
| 9 | S2SQB-S3SQT-OI | 10 | 33.7 | 37.5 | 30.2 | 2.2 | 0.67 |
| 10 | S2SQB-S4TT-VI | 10 | 32.7 | 34.9 | 30.5 | 1.5 | 0.64 |
| 11 | S2SQB-S4TT-OI | 10 | 31.8 | 37.4 | 28 | 2.8 | 0.62 |
| 12 | S5TB-S6TT-VV | 10 | 33.5 | 36.3 | 31.5 | 1.6 | 0.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ramírez-Gómez, Á.; Nielsen, J.; Amodio, L.; Pagano, M. Test Apparatus for Determining the Particle-to-Particle Friction Coefficient. Appl. Sci. 2025, 15, 11939. https://doi.org/10.3390/app152211939
Ramírez-Gómez Á, Nielsen J, Amodio L, Pagano M. Test Apparatus for Determining the Particle-to-Particle Friction Coefficient. Applied Sciences. 2025; 15(22):11939. https://doi.org/10.3390/app152211939
Chicago/Turabian StyleRamírez-Gómez, Álvaro, Jørgen Nielsen, Lidia Amodio, and Maurizio Pagano. 2025. "Test Apparatus for Determining the Particle-to-Particle Friction Coefficient" Applied Sciences 15, no. 22: 11939. https://doi.org/10.3390/app152211939
APA StyleRamírez-Gómez, Á., Nielsen, J., Amodio, L., & Pagano, M. (2025). Test Apparatus for Determining the Particle-to-Particle Friction Coefficient. Applied Sciences, 15(22), 11939. https://doi.org/10.3390/app152211939







