An Interval-Valued Neutrosophic Framework: Improved VIKOR with a Preference-Aware AHP–Entropy Weight Method for Evaluating Scalp-Detection Algorithms
Abstract
1. Introduction
1.1. Background
1.2. Literature Review
1.3. Research Gap
- (1)
- From a methodological perspective, there is an absence of mature theoretical models capable of effectively addressing the inherent subjectivity, uncertainty, and group divergence in algorithm selection processes.
- (2)
- From a research perspective, algorithms are often treated merely as technical entities, neglecting their role as components of user-oriented products. This results in a disconnection between technical performance indicators and user satisfaction.
- (3)
- From an interdisciplinary application perspective, the systematic application of advanced fuzzy theoretical frameworks such as the IVNS to image detection algorithm evaluation remains largely unexplored [26]. This gap between theoretical development and practical implementation highlights the necessity and innovative value of the present study.
1.4. Research Contributions
- (1)
- From a methodological standpoint, this paper integrates the AHP with the VIKOR method and extends it to the IVNS environment. Two types of possibility functions are further defined to enhance the VIKOR mechanism, significantly improving the precision of alternative comparison and the discriminative power of ranking. This provides a more robust theoretical tool for addressing the complex cognitive uncertainty inherent in algorithm selection.
- (2)
- From the perspective of research orientation, this paper introduces NLP techniques to construct a user-preference-oriented hybrid weighting approach that combines subjective and objective information. By structurally integrating multidimensional user experience indicators, the proposed framework shifts the decision-making focus from “technically optimal” to “user-satisfactory,” effectively bridging the gap between technical performance metrics and actual user perception.
- (3)
- From an interdisciplinary application perspective, this paper applies IVNS theory to the evaluation and selection of image detection algorithms for the first time. This work not only extends the application boundary of fuzzy decision-making theory but also provides a novel theoretical reference for the development of intelligent health terminal products that integrate both technical performance and user preference.
1.5. Organization
2. Preliminaries
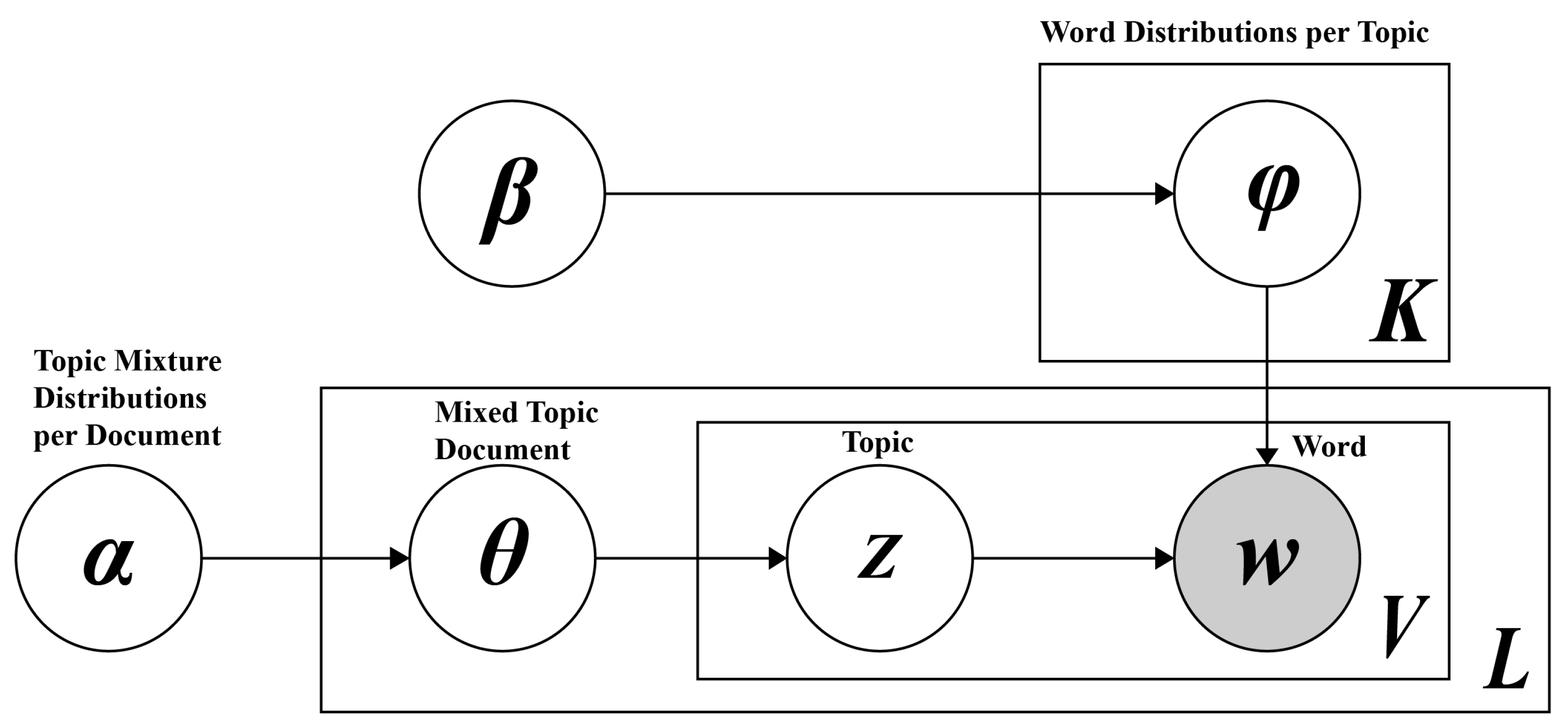
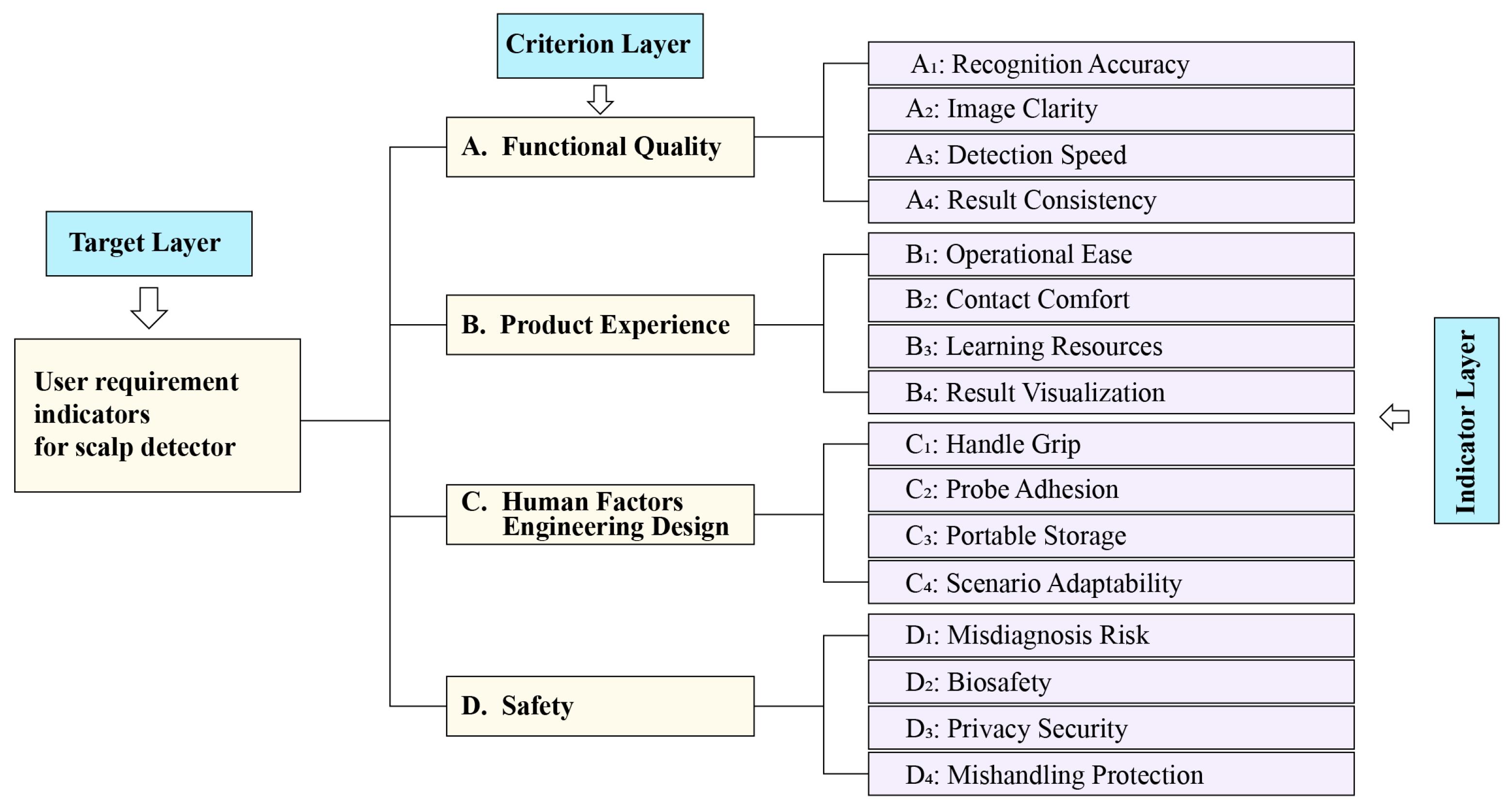
2.1. User Requirement Identification and Weighting Construction
2.1.1. TF-IDF (Term Frequency-Inverse Document Frequency) Weighting Technique
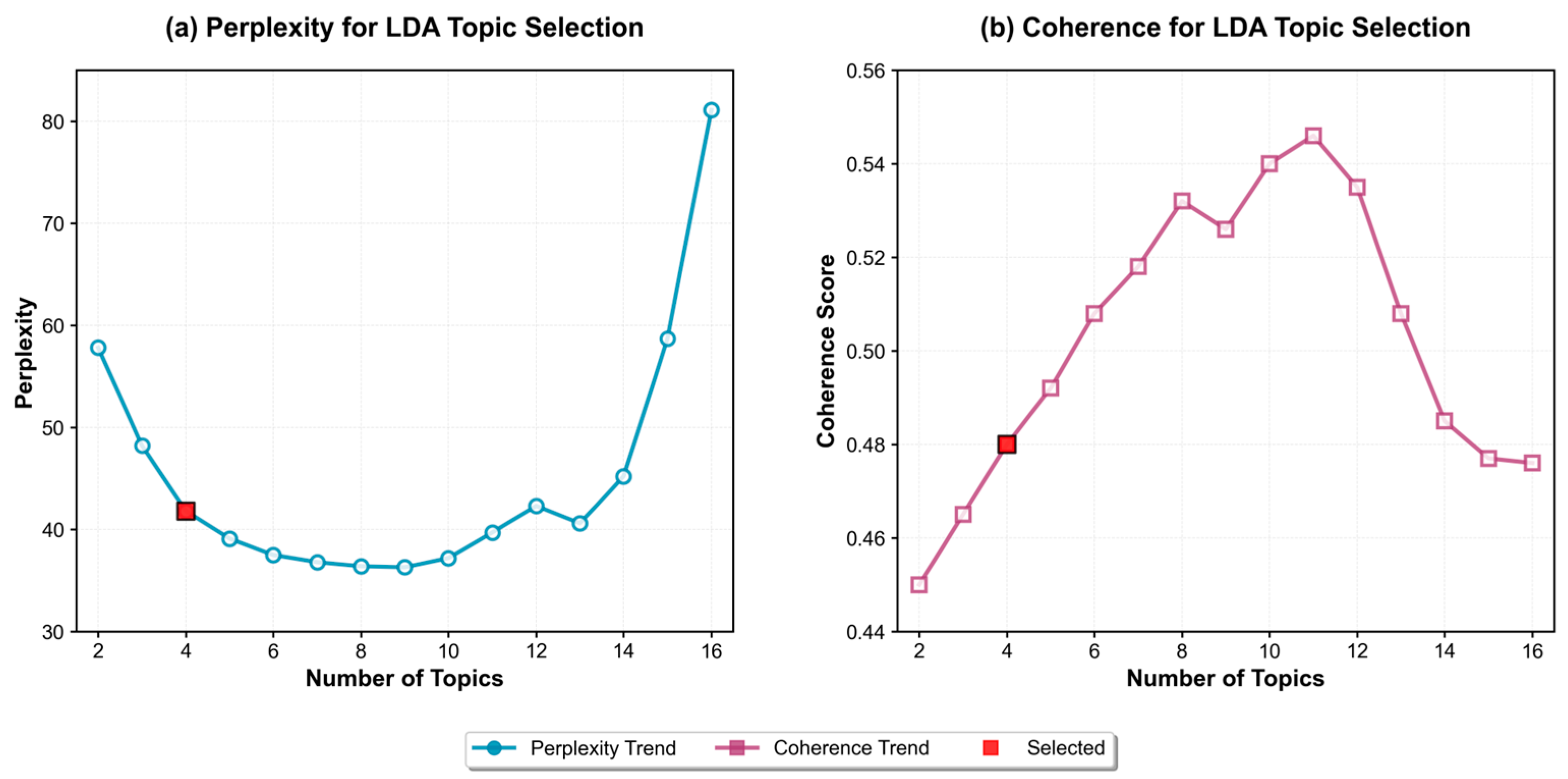
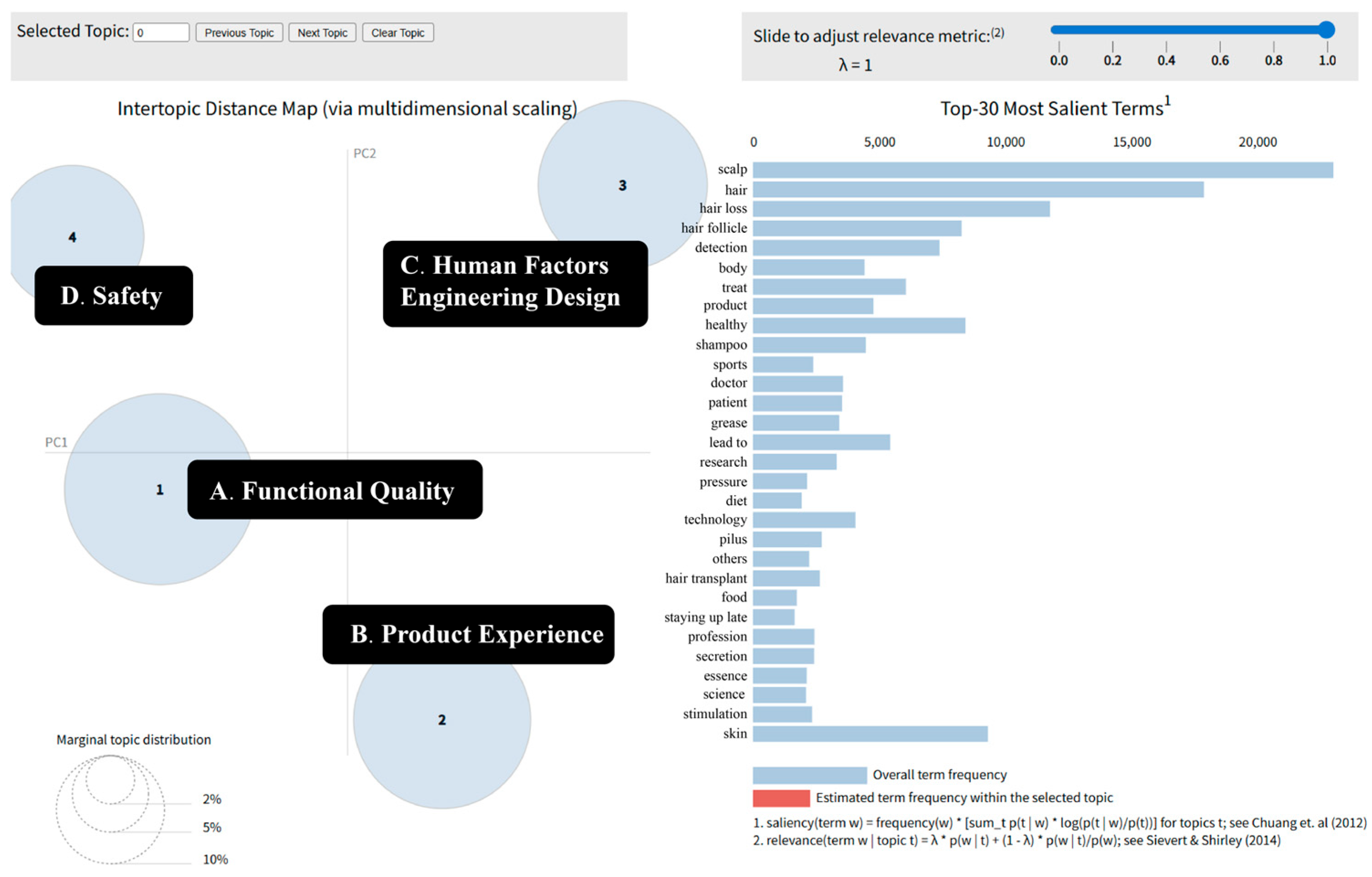
2.1.2. LDA Topic Identification and Visualization
2.1.3. User Preference Weighting
| Algorithm 1: Sentiment Analysis Using Baidu NLP API |
| Input: Text content, API Key, Secret Key |
| Output: Sentiment polarity and confidence score |
| Step 1: Authenticate with Baidu OAuth server using API Key and Secret Key |
| Step 2: Obtain access_token from the response |
| Step 3: Construct request URL with access_token |
| Step 4: Create JSON payload with the input text |
| Step 5: Send HTTP POST request to the sentiment_classify endpoint |
| Step 6: Parse JSON response |
| Step 7: Extract: |
| → sentiment ∈ {0: Negative, 1: Neutral, 2: Positive} |
| → confidence ∈ [0, 1] |
| → positive_prob, negative_prob |
| Step 8: Return sentiment result for further processing |
2.2. IVNS-Related Operations
- Indicates the true membership interval of element x belonging to set ;
- Indicates the uncertain membership interval of element x belonging to set ;
- Indicates the false membership interval of element x belonging to set ;
- and denote the lower bound and upper bound of the true membership degree interval, respectively;
- and denote the lower and upper bounds of the uncertainty membership interval, respectively;
- and denote the lower bound and upper bound of the pseudo-membership interval, respectively.
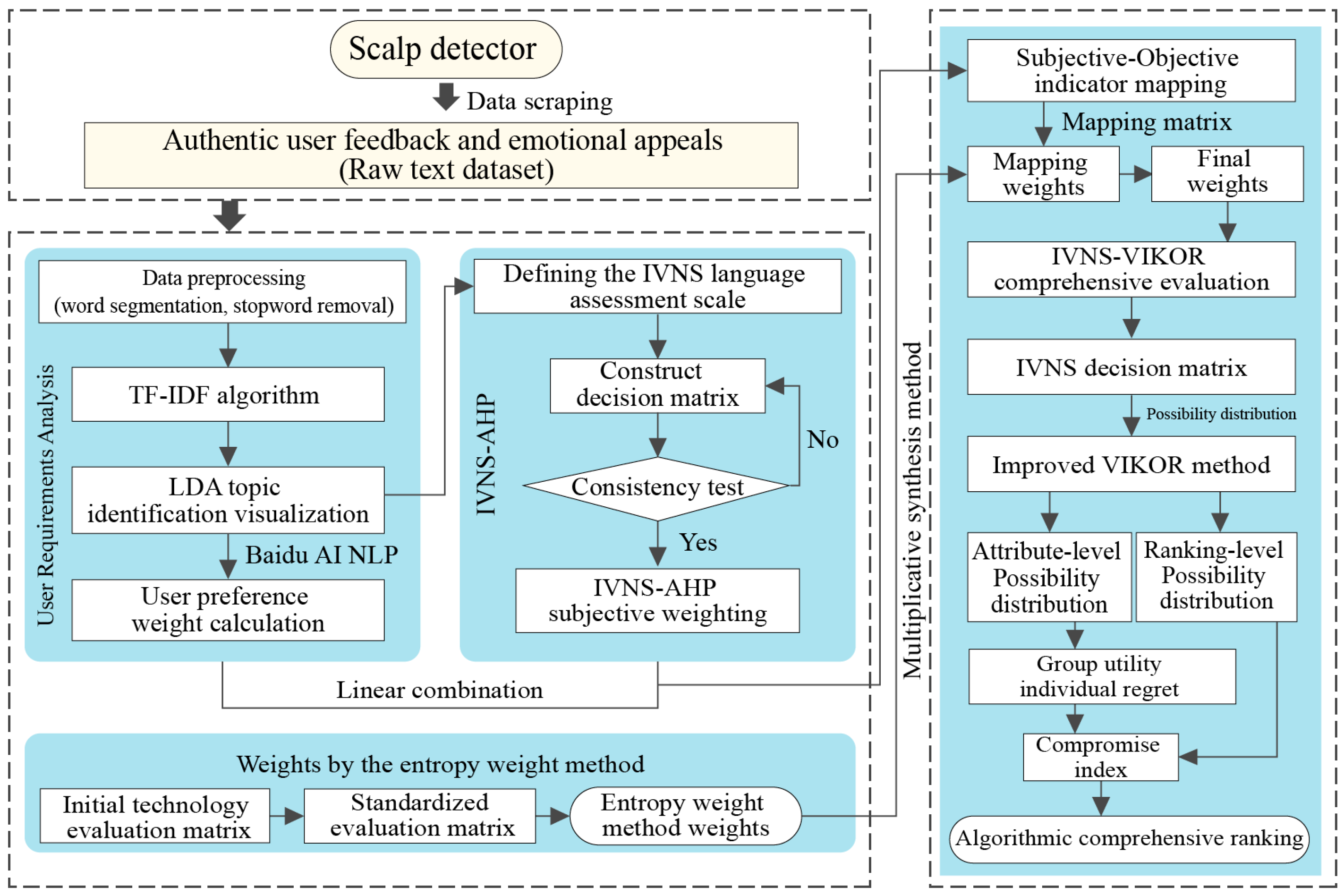
3. Methods
3.1. IVNS-AHP Subjective Empowerment
3.2. Objective Weighting Using the EWM
3.3. Subjective-Objective Indicator Mapping
3.4. Final Weighting of Indicators
3.5. Improving the IVNS-VIKOR Comprehensive Evaluation
3.5.1. Constructing the IVNS Decision Matrix
3.5.2. Determine the Positive and Negative Ideal Solutions
3.5.3. Improved VIKOR Method
4. Empirical Research
4.1. User Requirement Weight Analysis
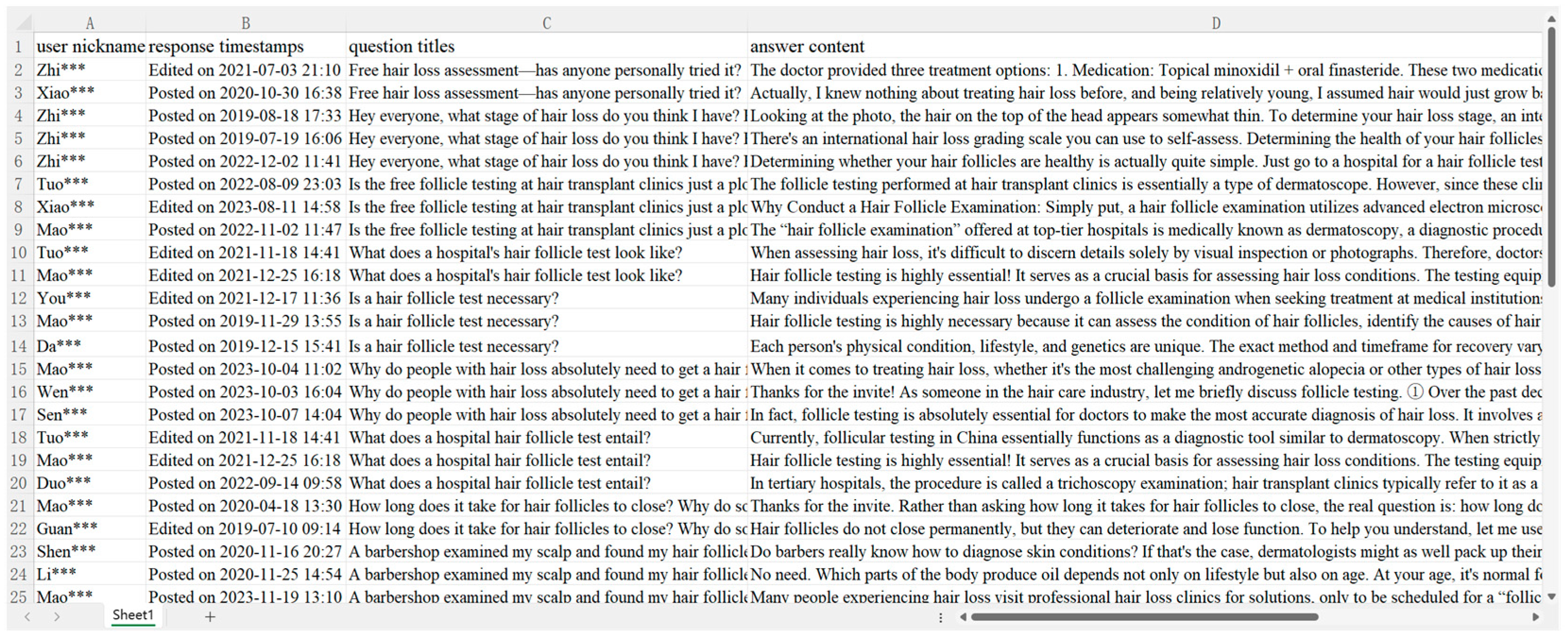
4.1.1. Data Sources and Preprocessing
- (1)
- Topic 1 “Functional Quality” focuses on product performance and reliability, covering core parameters such as resolution, accuracy, and stability to ensure that users’ expectations for detection outcomes are met.
- (2)
- Topic 2 “Product Experience” concerns the convenience of operational procedures and interface friendliness, including usability, intuitiveness, and after-sales service, which directly shape the overall user experience.
- (3)
- Topic 3 “Human Factors Engineering Design” delves into ergonomics and industrial design, involving adjustability convenience, tactile comfort, and multi-angle adaptability, balancing visual and haptic experiences.
- (4)
- Topic 4 “Safety” centers on user health and safety assurance, encompassing risk warnings and compliance measures, which constitute a critical prerequisite for product selection.
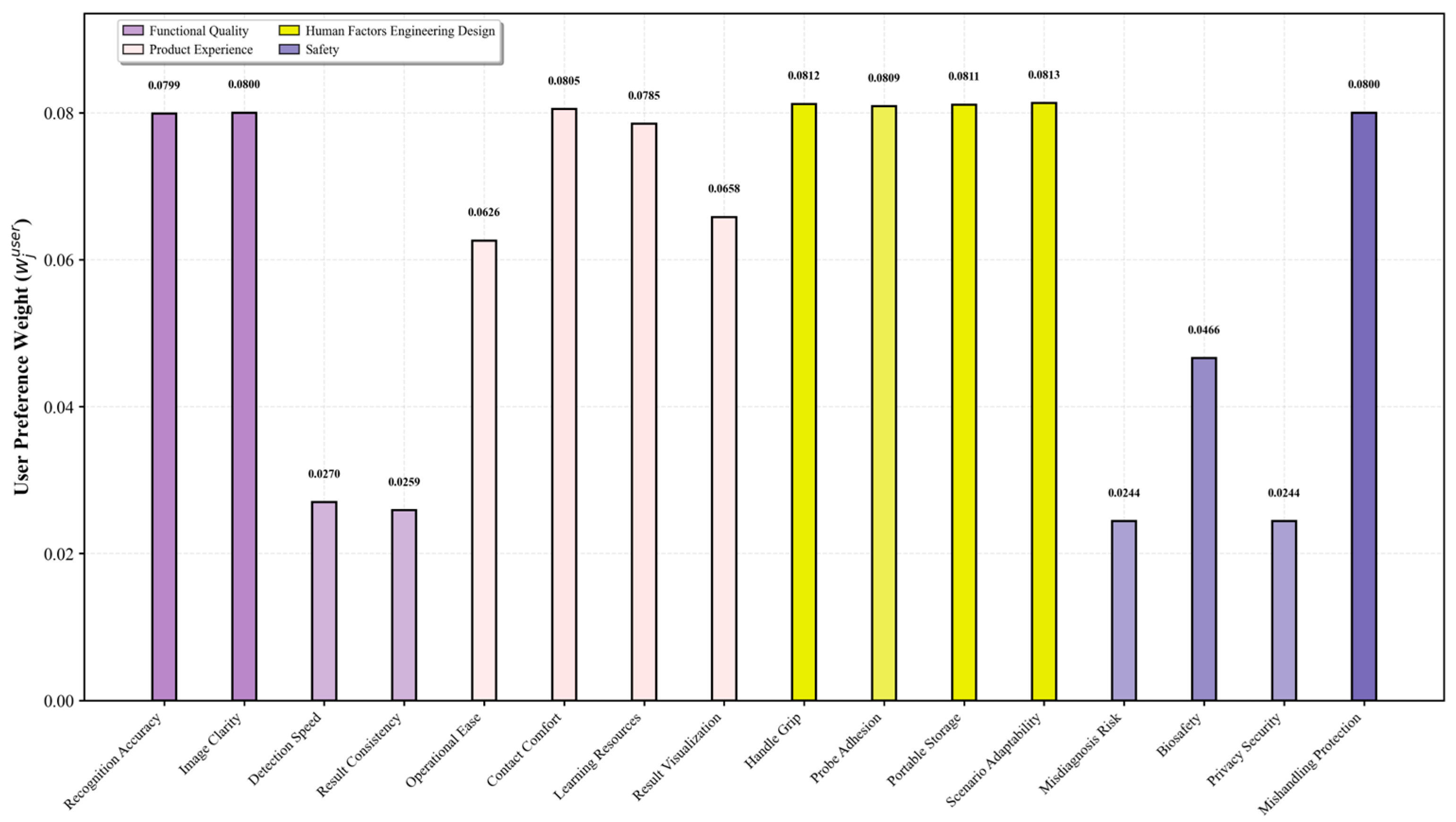
4.1.2. User Requirement Weight Calculation and Analysis
- (1)
- (2)
- IVNS-AHP Subjective Weighting
4.2. Experimental Design for Scalp
4.2.1. Experimental Environment and Parameter Configuration
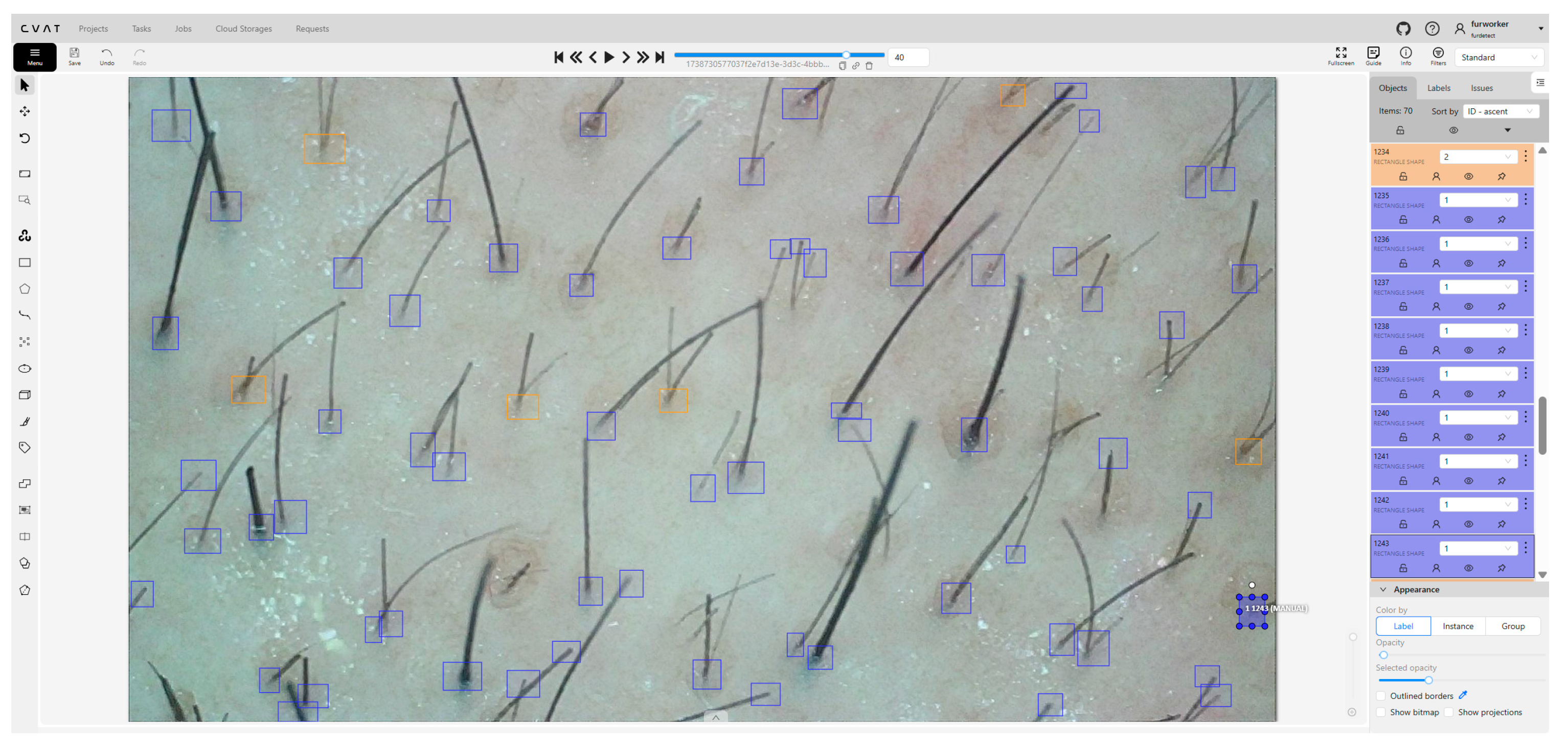
4.2.2. Dataset Construction
4.2.3. Algorithm Selection and Parameter Configuration
4.2.4. Experimental Results
4.3. Final Weighting of Technical Indicators
4.3.1. Objective Weighting of Indicators via the EWM
4.3.2. Computation of Subjective–Objective Indicator Mapping
4.3.3. Final Weight Calculation
4.4. Algorithmic Comprehensive Ranking
Improved VIKOR Method Calculation
5. Empirical Research Results Analysis
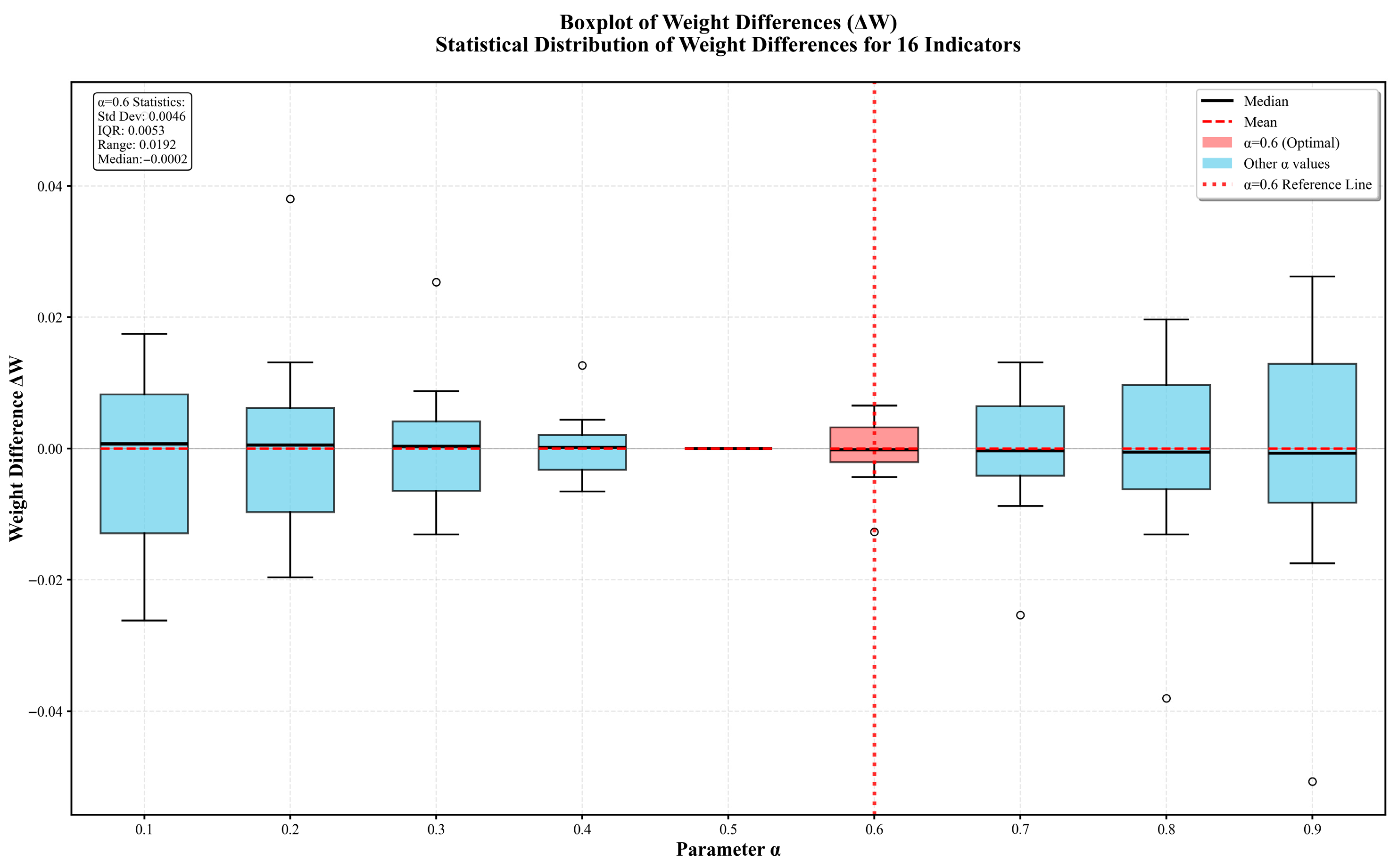
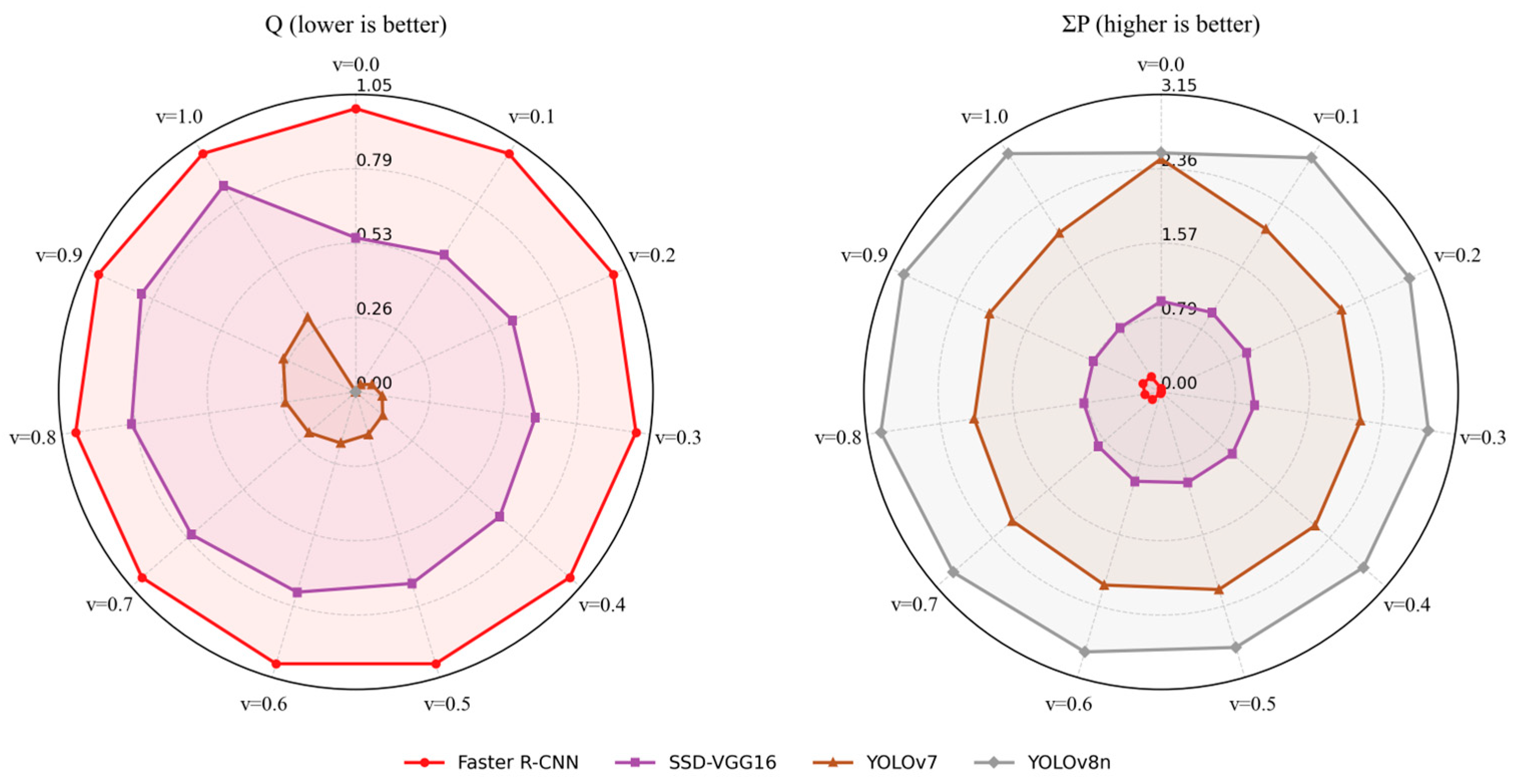
5.1. Sensitivity Analysis of the Parameter in the Composite Subjective Weight
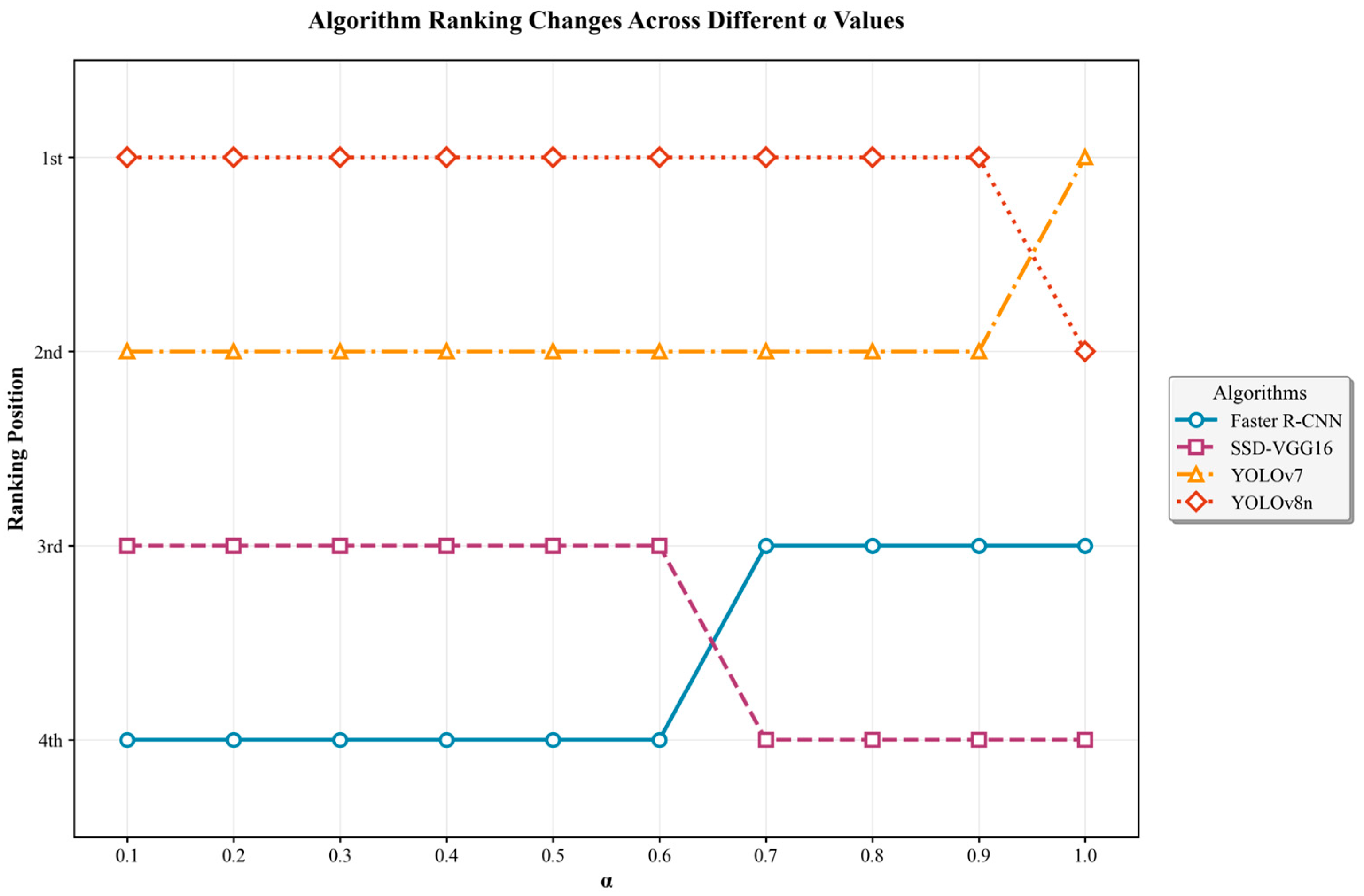
5.2. Sensitivity Analysis of Preference Parameter
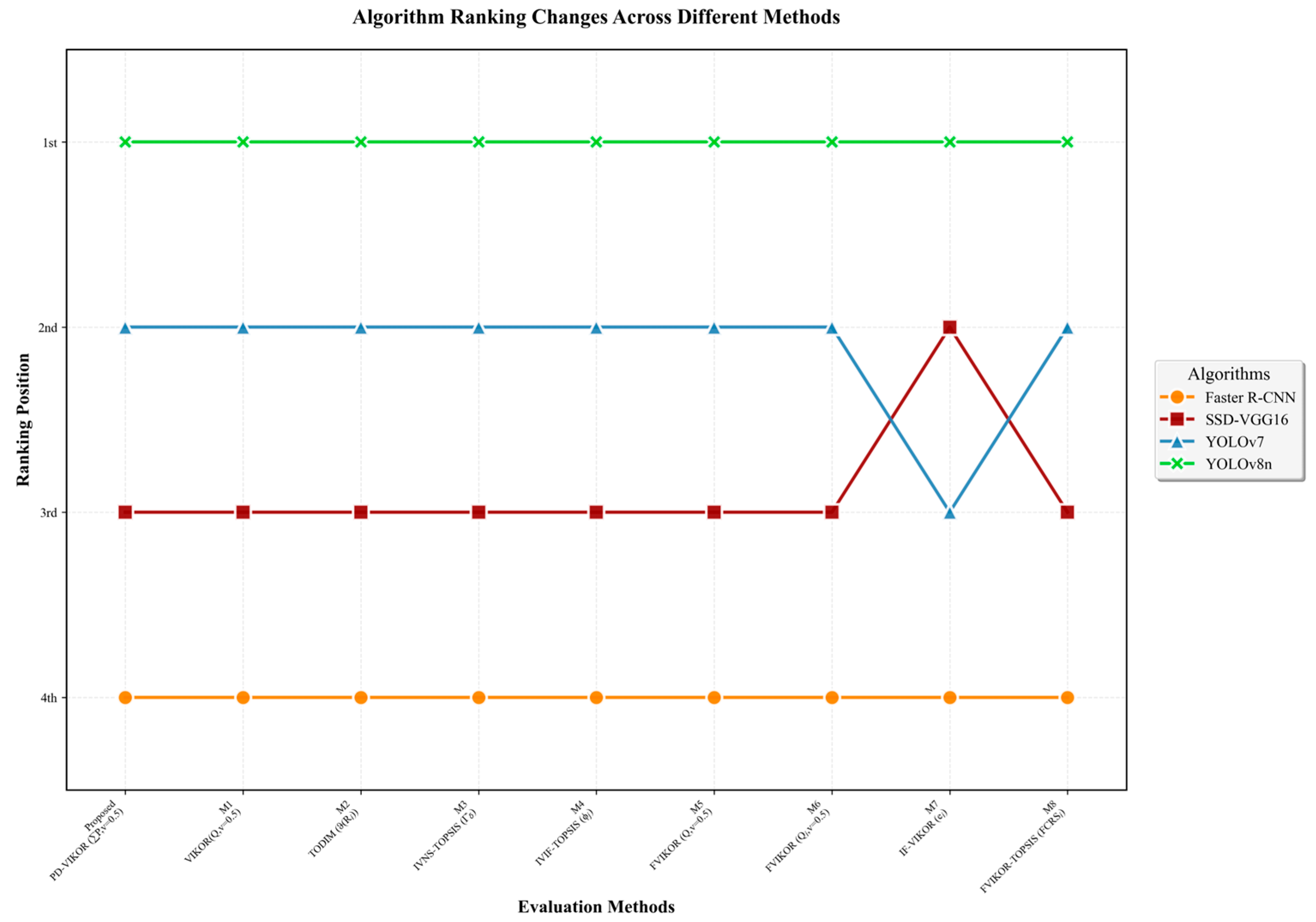
5.3. Comparison with the Reference Method
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MAGDM | multi-attribute group decision-making |
| IVNS | interval-valued neutrosophic set |
| AHP | analytic hierarchy process |
| NLP | natural language processing |
| EWM | entropy weight method |
| VIKOR | Vlse Kriterijumska Optimizacija Kompromisno Resenje |
| PD | possibility distribution |
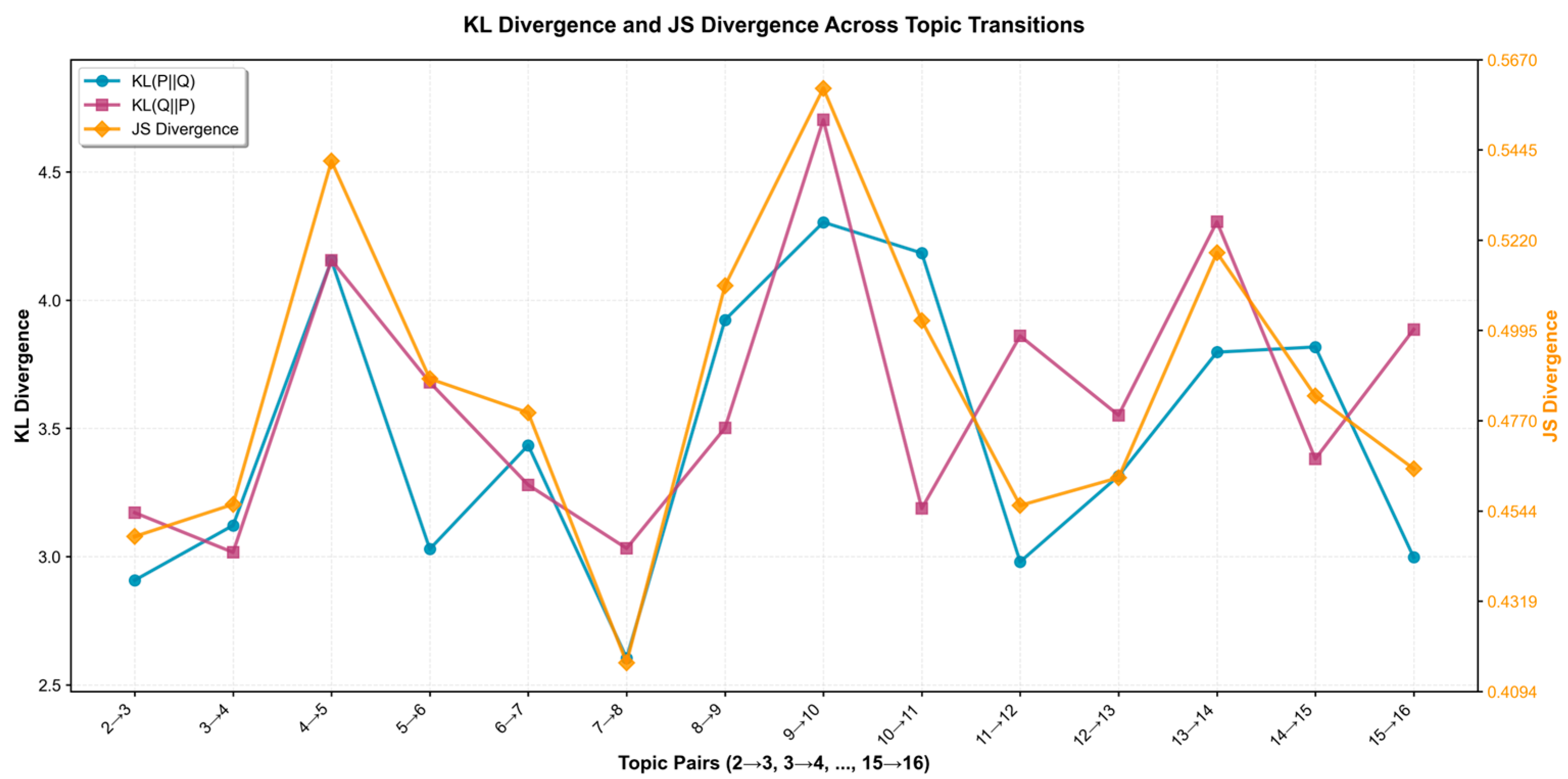
| KLD | Kullback–Leibler divergence |
| JSD | Jensen–Shannon divergence |
| mAP@50 | mean Average Precision at IoU = 0.5 |
| FPS | frames per second |
| TODIM | an acronym in Portuguese of interactive and multiple attribute decision-making |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| C-IF | circular intuitionistic fuzzy |
| IVq-ROFS | interval-valued q-rung orthopair fuzzy set |
| TF | term frequency |
| TF-IDF | term frequency-inverse document frequency |
| LDA | Latent Dirichlet Allocation |
| ALPD | attribute-level possibility distribution |
| RLPD | ranking-level possibility distribution |
References
- Wu, X.; Chen, D.; Xun, F.; Zhang, M.; Tang, X. Developingrehabilitation services to promote the achievement of the “Healthy China 2030”goals. Chin. J. Rehabil. Theory Pract. 2022, 28, 6–14. (In Chinese) [Google Scholar]
- Mathias, R.; McCulloch, P.; Chalkidou, A.; Gilbert, S. Digital Health Technologies Need Regulation and Reimbursement That Enable Flexible Interactions and Groupings. Npj Digit. Med. 2024, 7, 148. [Google Scholar] [CrossRef]
- Garg, V. Wearable Wisdom: How AI-Powered Devices Are Driving Personalized Preventive Care. World J. Adv. Eng. Technol. Sci. 2025, 15, 196–206. [Google Scholar] [CrossRef]
- Li, H.; Wang, Y.; Zhang, Q.; Yu, S.S.; Wang, F.; Chen, S.; Lim, C.P. Dynamic Personalized Health Management through the Health Assistant AI Fusion Framework. Inf. Fusion 2025, 123, 103263. [Google Scholar] [CrossRef]
- Maleki Varnosfaderani, S.; Forouzanfar, M. The Role of AI in Hospitals and Clinics: Transforming Healthcare in the 21st Century. Bioengineering 2024, 11, 337. [Google Scholar] [CrossRef]
- Pang, K.; Fu, C.; Martínez, L.; Liu, J.; Zou, L.; Lu, M. An Extended Multi-Expert Concept Lattice-Based Heterogeneous Multi-Attribute Group Decision-Making Approach. Inf. Sci. 2024, 665, 120345. [Google Scholar] [CrossRef]
- Wang, Y.; Zhan, J.; Zhang, C.; Xu, Z. A Group Consensus Model with Prospect Theory under Probabilistic Linguistic Term Sets. Inf. Sci. 2024, 653, 119800. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Goswami, S.S. A ComprehensiveReview of Multiple Criteria Decision-Making (MCDM) Methods: Advancements, Applications, and Future Directions. Decis. Mak. Adv. 2023, 1, 25–48. [Google Scholar] [CrossRef]
- Chaibate, H.; Hadek, A.; Ajana, S.; Bakkali, S. Analytical Hierarchy Process Applied to Pedagogical Method Selection Problems. Educ. Res. Int. 2021, 2021, 6664758. [Google Scholar] [CrossRef]
- Srdjevic, B.; Srdjevic, Z.; Reynolds, K.M.; Lakicevic, M.; Zdero, S. Using Analytic Hierarchy Process and Best–Worst Method in Group Evaluation of Urban Park Quality. Forests 2022, 13, 290. [Google Scholar] [CrossRef]
- Jabreel, M.; Maaroof, N.; Valls, A.; Moreno, A. Introducing Sentiment Analysis of Textual Reviews in a Multi-Criteria Decision Aid System. Appl. Sci. 2020, 11, 216. [Google Scholar] [CrossRef]
- Zheng, J.; Wang, S.; Wang, Z. Circular Pythagorean Fuzzy Deck of Cards Model for Optimal Deep Learning Architecture in Media Sentiment Interpretation. Symmetry 2025, 17, 1399. [Google Scholar] [CrossRef]
- Yadav, S.; Kaur, G.; Kapur, P.K.; Aggarwal, A.G. Intuitionistic Fuzzy and Multi-Criteria Based Ranking of Mobile Payment Apps Using Sentiment Score of Online Reviews. Int. J. Syst. Assur. Eng. Manag. 2024, 15, 1–14. [Google Scholar] [CrossRef]
- Xu, M.; Wang, X.; Xu, Z. Tour Group Prioritization Driven by Online Reviews: Using an Improved EDAS-SIR Method with Credibility. Artif. Intell. Rev. 2025, 58, 77. [Google Scholar] [CrossRef]
- Roszkowska, E.; Filipowicz-Chomko, M. Airline Ranking Using Social Feedback and Adapted Fuzzy Belief TOPSIS. Entropy 2025, 27, 879. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, Y.; Fan, L.; Li, Y. Customized Ranking for Products through Online Reviews: A Method Incorporating Prospect Theory with an Improved VIKOR. Appl. Intell. 2020, 50, 1725–1744. [Google Scholar] [CrossRef]
- Alamoodi, A.H.; Mohammed, R.T.; Albahri, O.S.; Qahtan, S.; Zaidan, A.A.; Alsattar, H.A.; Albahri, A.S.; Aickelin, U.; Zaidan, B.B.; Baqer, M.J.; et al. Based on Neutrosophic Fuzzy Environment: A New Development of FWZIC and FDOSM for Benchmarking Smart e-Tourism Applications. Complex Intell. Syst. 2022, 8, 3479–3503. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics: Neutrosophic Logic: Neutrosophy, Neutrosophic Set, Neutrosophic Probability and Statistics, 4th ed.; American Research Press: Rehoboth, DE, USA, 1998; ISBN 978-1-59973-080-6. [Google Scholar]
- Zhang, H.; Wang, L. The Service Quality Evaluation of Agricultural E-Commerce Based on Interval-Valued Intuitionistic Fuzzy GRA Method. J. Math. 2022, 2022, 3931136. [Google Scholar] [CrossRef]
- Liu, S.; Yu, W.; Chan, F.T.S.; Niu, B. A Variable Weight-based Hybrid Approach for Multi-attribute Group Decision Making under Interval-valued Intuitionistic Fuzzy Sets. Int. J. Intell. Syst. 2021, 36, 1015–1052. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, X.; Chen, Y.; Xu, X.; Li, M. A Water-Land-Energy-Carbon Nexus Evaluation of Agricultural Sustainability under Multiple Uncertainties: The Application of a Multi-Attribute Group Decision Method Determined by an Interval-Valued Intuitionistic Fuzzy Set. Expert Syst. Appl. 2024, 242, 122833. [Google Scholar] [CrossRef]
- Wang, J.-C.; Chen, T.-Y. A Compromise Decision-Support Technique with an Augmented Scoring Function within Circular Intuitionistic Fuzzy Settings. Eng. Appl. Artif. Intell. 2024, 128, 107359. [Google Scholar] [CrossRef]
- Hendiani, S.; Walther, G. Double-Layer Multi-Criteria Group Decision-Making Approach Using Neutralized Possibility Degree-Based Decision Matrix with Fuzzy Information. Eng. Appl. Artif. Intell. 2024, 133, 108276. [Google Scholar] [CrossRef]
- Chen, T.-Y. An Advanced Approach to Multiple Criteria Optimization and Compromise Solutions under Circular Intuitionistic Fuzzy Uncertainty. Adv. Eng. Inform. 2023, 57, 102112. [Google Scholar] [CrossRef]
- Mustafa, Z.; Amin, R.; Aldabbas, H.; Ahmed, N. Intrusion Detection Systems for Software-Defined Networks: A Comprehensive Study on Machine Learning-Based Techniques. Clust. Comput. 2024, 27, 9635–9661. [Google Scholar] [CrossRef]
- Zhou, Y.-J.; Zhou, M.; Yang, J.-B.; Cheng, B.-Y.; Wu, J. Decentralized Multipartite Consensus Model for Multi-Attribute Group Decision Making: A User Experience-Oriented Perspective. Expert Syst. Appl. 2025, 287, 127917. [Google Scholar] [CrossRef]
- Chen, T.; Peng, L.; Yang, J.; Cong, G. Analysis of User Needs on Downloading Behavior of English Vocabulary APPs Based on Data Mining for Online Comments. Mathematics 2021, 9, 1341. [Google Scholar] [CrossRef]
- Fang, B.; Hu, E.; Shen, J.; Zhang, J.; Chen, Y. Implicit Feedback Recommendation Method Based on User-Generated Content. Sci. Program. 2021, 2021, 3982270. [Google Scholar] [CrossRef]
- Blei, D.M.; Ng, A.Y.; Jordan, M.I. Latent Dirichlet Allocation. J. Mach. Learn. Res. 2003, 3, 993–1022. [Google Scholar]
- Wu, H.; Yi, H.; Li, C. An Integrated Approach for Detecting and Quantifying the Topic Evolutions of Patent Technology: A Case Study on Graphene Field. Scientometrics 2021, 126, 6301–6321. [Google Scholar] [CrossRef]
- Sharma, A.; Rana, N.P.; Nunkoo, R. Fifty Years of Information Management Research: A Conceptual Structure Analysis Using Structural Topic Modeling. Int. J. Inf. Manag. 2021, 58, 102316. [Google Scholar] [CrossRef]
- Broumi, S.; Talea, M.; Bakali, A.; Smarandache, F.; Nagarajan, D.; Lathamaheswari, M.; Parimala, M. Shortest Path Problem in Fuzzy, Intuitionistic Fuzzy and Neutrosophic Environment: An Overview. Complex Intell. Syst. 2019, 5, 371–378. [Google Scholar] [CrossRef]
- Alioğulları, E.; Türkan, Y.S.; Çakmak, E.; Tirkolaee, E.B. Evaluation of Risk Strategies for Supply Chain Sustainability with Interval-Valued Neutrosophic Fuzzy EDAS. Heliyon 2024, 10, e38607. [Google Scholar] [CrossRef]
- Bolturk, E.; Kahraman, C. A Novel Interval-Valued Neutrosophic AHP with Cosine Similarity Measure. Soft Comput. 2018, 22, 4941–4958. [Google Scholar] [CrossRef]
- Chen, C.-H. A Novel Multi-Criteria Decision-Making Model for Building Material Supplier Selection Based on Entropy-AHP Weighted TOPSIS. Entropy 2020, 22, 259. [Google Scholar] [CrossRef]
- Garg, H. A New Possibility Degree Measure for Interval-valued Q-rung Orthopair Fuzzy Sets in Decision-making. Int. J. Intell. Syst. 2021, 36, 526–557. [Google Scholar] [CrossRef]
- Bala, S.; Kumari, S. Comprehensive Analysis of Variants of TF-IDF Applied on LDA and LSA Topic Modelling. Int. J. Eng. Adv. Technol. 2020, 9, 531–535. [Google Scholar] [CrossRef]
- Koczkodaj, W.W.; Nowacki, M.; Pedrycz, W.; Strzalka, D. Text Mining Analysis of over 392 Million Compromised Healthcare Records. Adv. Sci. Technol. Res. J. 2024, 19, 73–81. [Google Scholar] [CrossRef]
- Rahman, M.; Frame, J.M.; Lin, J.; Nearing, G.S. Hydrology Research Articles Are Becoming More Topically Diverse. J. Hydrol. 2022, 614, 128551. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Y.; Shi, Y.; Ren, Y. From Policy to Practice: A Comparative Topic Modeling Study of Smart Forestry in China. Forests 2025, 16, 1019. [Google Scholar] [CrossRef]
- Chuang, J.; Manning, C.D.; Heer, J. Termite: Visualization Techniques for Assessing Textual Topic Models. In Proceedings of the International Working Conference on Advanced Visual Interfaces, Capri Island, Italy, 21–25 May 2012; pp. 74–77. [Google Scholar] [CrossRef]
- Sievert, C.; Shirley, K. LDAvis: A Method for Visualizing and Interpreting Topics. In Proceedings of the Workshop on Interactive Language Learning, Visualization, and Interfaces, Baltimore, MD, USA, 27 June 2014; Association for Computational Linguistics; pp. 63–70. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Kang, H.-J. Real-Time Object Detection on640x480 Image with VGG16+SSD. In Proceedings of the 2019 International Conference on Field-Programmable Technology (ICFPT), Tianjin, China, 9–13 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 419–422. [Google Scholar] [CrossRef]
- Chen, T.; Li, H.; Chen, J.; Zeng, Z.; Han, C.; Wu, W. Detection Network for Multi-Size and Multi-Target Tea Bud Leaves in the Field of View via Improved YOLOv7. Comput. Electron. Agric. 2024, 218, 108700. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, B.; Xu, H.; Zhang, L.; Zhang, X. Method for Recognizing Disordered Sugarcane Stacking Based on Improved YOLOv8n. Appl. Sci. 2024, 14, 11765. [Google Scholar] [CrossRef]
- Yu, Y.; Zutty, J. LLM-Guided Evolution: AnAutonomous Model Optimization for Object Detection. In Proceedings of the Genetic and Evolutionary Computation Conference Companion (GECCO’25 Companion), Málaga, Spain, 14–18 July 2025; ACM: New York, NY, USA, 2025; pp. 2363–2370. [Google Scholar] [CrossRef]
- Fränti, P.; Mariescu-Istodor, R. Soft Precision and Recall. Pattern Recognit. Lett. 2023, 167, 115–121. [Google Scholar] [CrossRef]
- Huynh, N.; Nguyen, K.-D. Real-Time Droplet Detection for Agricultural Spraying Systems: A Deep Learning Approach. Mach. Learn. Knowl. Extr. 2024, 6, 259–282. [Google Scholar] [CrossRef]
- Zhang, J. Evolution of YOLO: A Comparative Analysis of YOLOv5, YOLOv8, and YOLOv10. Appl. Comput. Eng. 2025, 119, 173–181. [Google Scholar] [CrossRef]
- Zhang, Y.; Song, J.; Yu, X.; Ji, X. WMC-RTDETR: A Lightweight Tea Disease Detection Model. Front. Plant Sci. 2025, 16, 1574920. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Zhou, J. Research on Lightweight Infrared Target Detection Algorithm Based on Deep Learning. Eng. Lett. 2025, 33, 2589. [Google Scholar]
- Fan, J.; Li, D.; Wu, M. An Extended TODIM Method with Unknown Weight Information Under Interval-Valued Neutrosophic Environment for FMEA. Int. J. Comput. Intell. Syst. 2020, 14, 174. [Google Scholar] [CrossRef]
- Tam, P.M.; Hang, D.T.; Thuy, P.T.; Dat, L.Q. Comprehensive Evaluation of Sustainable Consumption towards Green Growth Based on an Interval Valued Neutrosophic TOPSIS Approach. Environ. Sci. Pollut. Res. 2023, 30, 89838–89858. [Google Scholar] [CrossRef]
- Yildiz, A.; Guneri, A.F.; Ozkan, C.; Ayyildiz, E.; Taskin, A. An Integrated Interval-Valued Intuitionistic Fuzzy AHP-TOPSIS Methodology to Determine the Safest Route for Cash in Transit Operations: A Real Case in Istanbul. Neural Comput. Appl. 2022, 34, 15673–15688. [Google Scholar] [CrossRef]
- Demir, E.; Ak, M.F.; Sarı, K. Pythagorean Fuzzy Based AHP-VIKOR Integration to Assess Rail Transportation Systems in Turkey. Int. J. Fuzzy Syst. 2023, 25, 620–632. [Google Scholar] [CrossRef]
- Das, A.; Kumar, V.; Dutta, S. A Fuzzy-Based AHP-VIKOR Framework for Risk Analysis of Safety-Critical Systems: A Case Study of Nuclear Power Plant. Ann. Nucl. Energy 2024, 209, 110841. [Google Scholar] [CrossRef]
- Tripathi, D.K.; Nigam, S.K.; Cavallaro, F.; Rani, P.; Mishra, A.R.; Hezam, I.M. A Novel CRITIC-RS-VIKOR Group Method with Intuitionistic Fuzzy Information for Renewable Energy Sources Assessment. Group Decis. Negot. 2023, 32, 1437–1468. [Google Scholar] [CrossRef]
- Sarıkaya, H.A. A Hybrid MCDM Model for Personnel Evaluation: Integrating AHP, Fuzzy TOPSIS and VIKOR with Composite Scoring. J. Appl. Eng. Agric. 2025, 2, 44–71. [Google Scholar]

| Importance | Abbreviation | True Value Interval T | Uncertainty Interval I | False Value Range F |
|---|---|---|---|---|
| Equally important | EI | [0.50, 0.50] | [0.50, 0.50] | [0.50, 0.50] |
| Absolutely less important | AWI | [0.50, 0.60] | [0.35, 0.45] | [0.40, 0.50] |
| Extremely less important | EWI | [0.55, 0.65] | [0.30, 0.40] | [0.35, 0.45] |
| Less important | MWI | [0.60, 0.70] | [0.25, 0.35] | [0.30, 0.40] |
| Generally less important | GWI | [0.65, 0.75] | [0.20, 0.30] | [0.25, 0.35] |
| Generally important | GI | [0.70, 0.80] | [0.15, 0.25] | [0.20, 0.30] |
| Relatively important | MI | [0.75, 0.85] | [0.10, 0.20] | [0.15, 0.25] |
| Generally more important | GSI | [0.80, 0.90] | [0.05, 0.10] | [0.10, 0.20] |
| Relatively more important | MSI | [0.90, 0.95] | [0.00, 0.05] | [0.05, 0.15] |
| Extremely more important | ESI | [0.95, 1.0] | [0.00, 0.00] | [0.00, 0.10] |
| Absolutely more important | ASI | [1.0, 1.0] | [0.00, 0.00] | [0.00, 0.00] |
| Importance | Abbreviation | True Value Interval T | Uncertainty Interval I | False Value Range F |
|---|---|---|---|---|
| Unable to determine | UT | [0.50, 0.50] | [0.50, 0.50] | [0.50, 0.50] |
| Extremely poor | VP | [0.50, 0.60] | [0.35, 0.45] | [0.40, 0.50] |
| Very poor | VHP | [0.55, 0.65] | [0.30, 0.40] | [0.35, 0.45] |
| Poor | MP | [0.60, 0.70] | [0.25, 0.35] | [0.30, 0.40] |
| Slightly poor | SP | [0.65, 0.75] | [0.20, 0.30] | [0.25, 0.35] |
| Average | F | [0.70, 0.80] | [0.15, 0.25] | [0.20, 0.30] |
| Slightly better | SG | [0.75, 0.85] | [0.10, 0.20] | [0.15, 0.25] |
| Better | MG | [0.80, 0.90] | [0.05, 0.10] | [0.10, 0.20] |
| Very good | VHG | [0.90, 0.95] | [0.00, 0.05] | [0.05, 0.15] |
| Excellent | VG | [0.95, 1.0] | [0.00, 0.00] | [0.00, 0.10] |
| Perfect | P | [1.0, 1.0] | [0.00, 0.00] | [0.00, 0.00] |
| Keyword | TF-IDF | Frequency | |
|---|---|---|---|
| 1 | Report | 0.400 | 1034 |
| 2 | Effect | 0.399 | 3945 |
| 3 | Minutes | 0.381 | 1953 |
| 4 | Smart | 0.380 | 1132 |
| 5 | Precision | 0.371 | 945 |
| 6 | Detector | 0.351 | 1734 |
| 7 | Hair Loss | 0.350 | 10,442 |
| 8 | System | 0.344 | 1239 |
| 9 | Equipment | 0.343 | 1826 |
| 10 | Professional | 0.338 | 2497 |
| 11 | Follicle | 0.334 | 11,504 |
| 12 | Detection | 0.332 | 8446 |
| 13 | Oil | 0.305 | 2256 |
| 14 | Technology | 0.280 | 2728 |
| 15 | Scalp | 0.262 | 21,312 |
| Theme Category | Theme Keywords | |
|---|---|---|
| Topic#1 | Functional Quality | Function, capability, efficacy, resolution, process, high efficiency, precision, accuracy, detector, durability, implementation, algorithm, robustness, analyzer, sensitivity, tester, hormone levels, high quality, stability, standardization |
| Topic#2 | Product Experience | Recommendations, Operations, Feedback, Readability, Guidance, User-Friendly, Interface, Evaluation, Impression, Navigation, Aesthetics, Instructional, Exquisite, Service Attitude, Ease of Use, Consultant, Comfort Level, Service Center, Satisfaction, After-Sales Service |
| Topic#3 | Human Factors Engineering Design | Adjustment, clarity, space, distance, intuitive, height, thickness, convenience, ergonomics, hand feel, personalization, definition, indications, easy to understand, design, multi-angle, handy, adjustability, visualization, close-up distance |
| Topic#4 | Safety | Cleaning, inspection, safety, reminder, standard, caution, verification, sterilization, hidden danger, prudence, prevention, health status, warning, safety hazard, precautions, sense of security, harmlessness, standard, compliance, stability |
| Primary Indicator | Secondary Indicator | Requirement Description | Thematic Keywords | Number |
|---|---|---|---|---|
| A. Functional Quality | Recognition Accuracy | Ability to detect targets such as hair follicles and dandruff | Precision, identification, error, resolution, detector | A1 |
| Image Clarity | Clarity and detail representation of microscope/probe imaging | Clear, high-definition, imaging, detail, magnification | A2 | |
| Detection Speed | Timeliness of the detection process and efficiency of result output | Fast, real-time, response, process, minutes | A3 | |
| Result Consistency | Stability of repeated measurements on the same sample | Stable, reliable, repeatability, fluctuation, consistency | A4 | |
| B. Product Experience | Operational Ease | Simplified operation workflow and improved interface friendliness | Easy to use, simple, intuitive, friendly, tutorial | B1 |
| Contact Comfort | Comfort of probe-to-scalp contact | Gentle, imperceptible, soft, contact, pressure | B2 | |
| Learning Resources | Learning materials to help users quickly master operation | Tutorial, video, guidance, instructions, quick start | B3 | |
| Result Visualization | Intuitive presentation of detection results and progress | Prompt, visualization, report, status, progress | B4 | |
| C. Human Factors Engineering Design | Handle Grip | Ergonomically comfortable grip design | Grip, fit, anti-slip, fatigue, handle | C1 |
| Probe Adhesion | Conformity of the probe to the scalp’s curved surface | Curvature, conformity, contact, area, adaptability, angle | C2 | |
| Portable Storage | Portability of the device and ease of storage | Lightweight, compact, foldable, storage, volume | C3 | |
| Scenario Adaptability | Ability to adapt to diverse usage environments | Waterproof, dustproof, thermal drift resistance, drop resistance, shock resistance | C4 | |
| D. Safety | Misdiagnosis Risk | Reliability of identifying high-risk lesions | Misdiagnosis, risk, diagnosis, disease, fungus | D1 |
| Biosafety | Biocompatibility and hygiene assurance of contact components | Non-toxic, low-allergenicity, biocompatible, sterile, material | D2 | |
| Privacy Security | Security protection for user data storage and transmission | Encryption, privacy, storage, transmission, access control | D3 | |
| Mishandling Protection | Protective mechanisms to prevent accidental operations | Protection, locking, warning, insurance, fault tolerance | D4 |
| Text Content | Emotional Polarity | Probability of Heads | Confidence |
|---|---|---|---|
| I used it to detect the status of hair follicles, and the results seemed quite accurate, similar to what the doctor said. | Positive (2) | 0.952 | 0.894 |
| A | B | C | D | |
|---|---|---|---|---|
| A | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.75, 0.85], [0.10, 0.20], [0.15, 0.25] | [0.70, 0.80], [0.15, 0.25], [0.20, 0.30] | [0.25, 0.35], [0.70, 0.80], [0.65, 0.75] |
| B | [0.15, 0.25], [0.80, 0.90], [0.75, 0.85] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.55, 0.65], [0.30, 0.40], [0.35, 0.45] | [0.20, 0.30], [0.75, 0.85], [0.70, 0.80] |
| C | [0.20, 0.30], [0.75, 0.85], [0.70, 0.80] | [0.35, 0.45], [0.60, 0.70], [0.55, 0.65] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.10, 0.20], [0.90, 0.95], [0.80, 0.90] |
| D | [0.65, 0.75], [0.20, 0.30], [0.25, 0.35] | [0.70, 0.80], [0.15, 0.25], [0.20, 0.30] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] |
| A1 | A2 | A3 | A4 | |
|---|---|---|---|---|
| A1 | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.75, 0.85], [0.10, 0.20], [0.15, 0.25] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] |
| A2 | [0.10, 0.20], [0.90, 0.95], [0.80, 0.90] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] |
| A3 | [0.15, 0.25], [0.80, 0.90], [0.75, 0.85] | [0.05, 0.15], [0.95, 1.00], [0.90, 0.95] | [0.50, 0.50], [0.50, 0.50], [0.50,0.50] | [0.25, 0.35], [0.70, 0.80], [0.65, 0.75] |
| A4 | [0.05, 0.15], [0.95, 1.00], [0.90, 0.95] | [0.10, 0.20], [0.90, 0.95], [0.80, 0.90] | [0.65, 0.75], [0.20, 0.30], [0.25, 0.35] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] |
| B1 | B2 | B3 | B4 | |
|---|---|---|---|---|
| B1 | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] |
| B2 | [0.05, 0.15], [0.95, 1.00], [0.90, 0.95] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.75, 0.85], [0.10, 0.20], [0.15, 0.25] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] |
| B3 | [0.00, 0.10], [1.00, 1.00], [0.95, 1.00] | [0.15, 0.25], [0.80, 0.90], [0.75, 0.85] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.25, 0.35], [0.70, 0.80], [0.65, 0.75] |
| B4 | [0.10, 0.20], [0.90, 0.95], [0.80, 0.90] | [0.10, 0.20], [0.90, 0.95], [0.80, 0.90] | [0.65, 0.75], [0.20, 0.30], [0.25, 0.35] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] |
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| C1 | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.65, 0.75], [0.20, 0.30], [0.25, 0.35] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.75, 0.85], [0.10, 0.20], [0.15, 0.25] |
| C2 | [0.25, 0.35], [0.70, 0.80], [0.65, 0.75] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.70, 0.80], [0.15, 0.25], [0.20, 0.30] |
| C3 | [0.05, 0.15], [0.95, 1.00], [0.90, 0.95] | [0.00, 0.10], [1.00, 1.00], [0.95, 1.00] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.25, 0.35], [0.70, 0.80], [0.65,0.75] |
| C4 | [0.15, 0.25], [0.80, 0.90], [0.75, 0.85] | [0.20, 0.30], [0.75, 0.85], [0.70, 0.80] | [0.65, 0.75], [0.20, 0.30], [0.25, 0.35] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] |
| D1 | D2 | D3 | D4 | |
|---|---|---|---|---|
| D1 | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.70, 0.80], [0.15, 0.25], [0.20, 0.30] | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] |
| D2 | [0.20, 0.30], [0.75, 0.85], [0.70, 0.80] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.75, 0.85], [0.10, 0.20], [0.15, 0.25] | [0.30, 0.40], [0.65, 0.75], [0.60, 0.70] |
| D3 | [0.00, 0.10], [1.00, 1.00], [0.95, 1.00] | [0.15, 0.25], [0.80, 0.90], [0.75, 0.85] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] | [0.10, 0.20], [0.90, 0.95], [0.80, 0.90] |
| D4 | [0.05, 0.15], [0.95, 1.00], [0.90, 0.95] | [0.60, 0.70], [0.25, 0.35], [0.30, 0.40] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.50, 0.50], [0.50, 0.50], [0.50, 0.50] |
| Criteria Layer | Criteria Layer Weight | Indicator Layer | Indicator Layer Weight | IVNS-AHP Weight | Composite Subjective Weight | Consistency Ratio CR |
|---|---|---|---|---|---|---|
| A | 0.2907 | A1 | 0.4255 | 0.1236 | 0.0974 | 0.0673 |
| A2 | 0.2746 | 0.0798 | 0.0799 | |||
| A3 | 0.1452 | 0.0422 | 0.0331 | |||
| A4 | 0.1547 | 0.0450 | 0.0335 | |||
| B | 0.194 | B1 | 0.4524 | 0.0878 | 0.0727 | 0.0625 |
| B2 | 0.2496 | 0.0484 | 0.0677 | |||
| B3 | 0.1221 | 0.0237 | 0.0566 | |||
| B4 | 0.1759 | 0.0341 | 0.0531 | |||
| C | 0.1557 | C1 | 0.3871 | 0.0602 | 0.0728 | 0.0555 |
| C2 | 0.3096 | 0.0482 | 0.0678 | |||
| C3 | 0.1002 | 0.0156 | 0.0549 | |||
| C4 | 0.2031 | 0.0316 | 0.0614 | |||
| D | 0.3596 | D1 | 0.4205 | 0.1512 | 0.0751 | 0.0515 |
| D2 | 0.2492 | 0.0896 | 0.0638 | |||
| D3 | 0.0972 | 0.0350 | 0.0286 | |||
| D4 | 0.2332 | 0.0838 | 0.0815 |
| Parameter | Algorithm for Evaluation | |||
|---|---|---|---|---|
| Faster R-CNN | SSD-VGG16 | YOLOv7 | YOLOv8n | |
| Representative Direction | High-Precision Positioning and Classification [43] | Balancing speed and accuracy [44] | Best overall performance [45] | Lightweight and Efficient Design [46] |
| learning rate | 1 × 10−3 | 1 × 10−3 | 1 × 10−3 | 1 × 10−3 |
| batch size | 8 | 8 | 8 | 8 |
| weight decay | 5 × 10−4 | 5 × 10−4 | 5 × 10−4 | 5 × 10−4 |
| Momentum | 0.9 | 0.9 | 0.9 | 0.9 |
| Epochs | 300 | 300 | 300 | 300 |
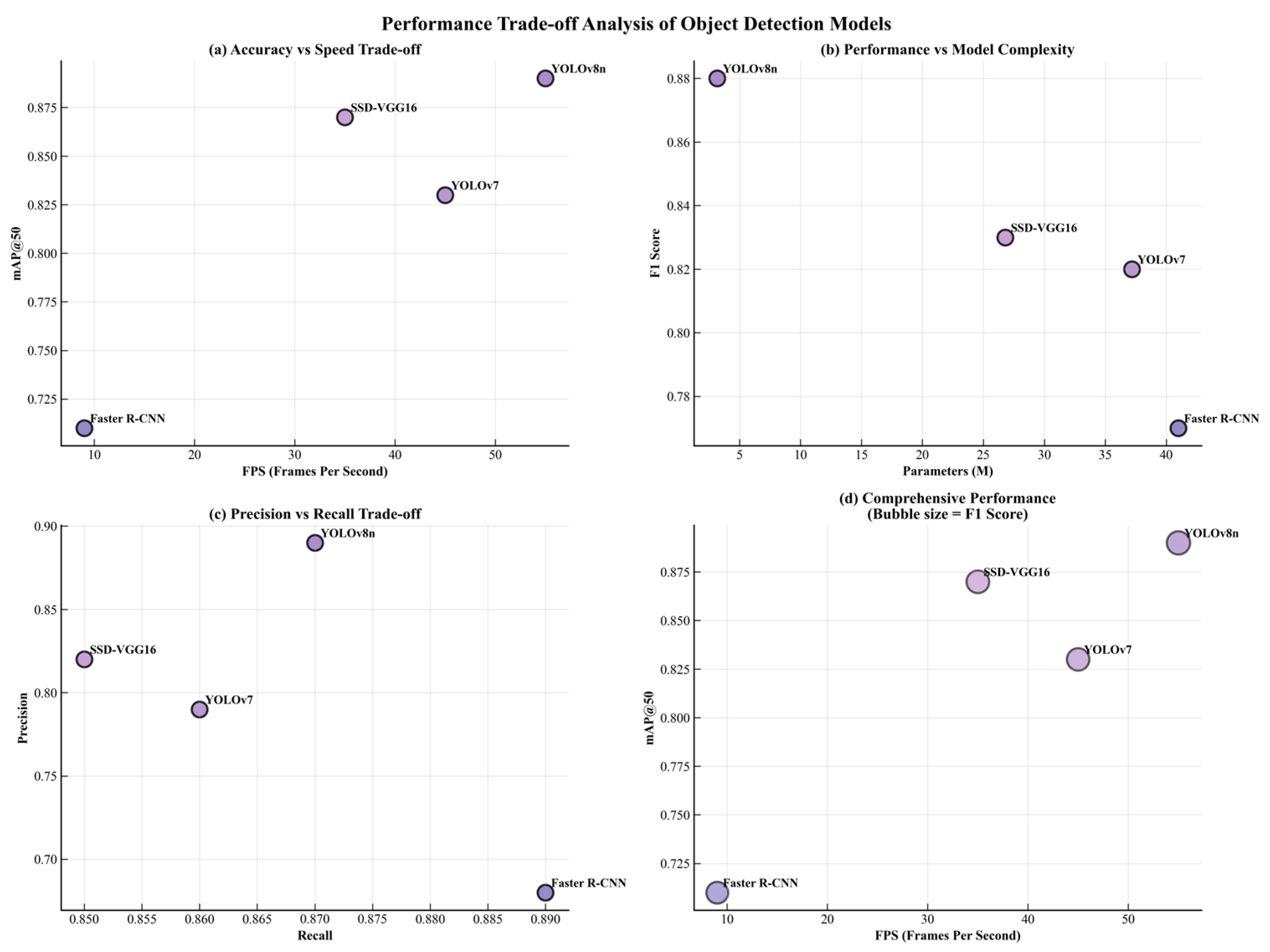
| Algorithms | mAP@50 | Precision | Recall | F1 Score | FPS | Parameters (M) |
|---|---|---|---|---|---|---|
| Faster R-CNN | 0.71 | 0.68 | 0.89 | 0.77 | 9 | 41 |
| SSD-VGG16 | 0.87 | 0.82 | 0.85 | 0.83 | 35 | 26.8 |
| YOLOv7 | 0.83 | 0.79 | 0.86 | 0.82 | 45 | 37.18 |
| YOLOv8n | 0.89 | 0.89 | 0.87 | 0.88 | 55 | 3.16 |
| Indicator | Meaning | Indicator Type | Information Entropy | Weight |
|---|---|---|---|---|
| mAP@50 | Core Metric for the Comprehensive Performance of Model Localization and Classification [47] | + 1 | 0.7827 | 0.1305 |
| Precision | Assessing the accuracy of model predictions [48] | + | 0.7662 | 0.1404 |
| Recall | The ability of a model to detect all positive class samples [49] | + | 0.6894 | 0.1865 |
| F1 score | Harmonic Mean of Precision and Recall [50] | + | 0.7485 | 0.1510 |
| FPS | Key metrics for evaluating model inference speed and real-time performance [51] | + | 0.7737 | 0.1359 |
| Parameters (M) | Core metrics for evaluating model size, complexity, and memory consumption [52] | − 2 | 0.5738 | 0.2559 |
| User Requirements | mAP@50 | Precision | Recall | F1 Score | FPS | Parameters (M) | Algorithm Weight | Attribute Classification |
|---|---|---|---|---|---|---|---|---|
| A1 | 0.35 | 0.25 | 0.20 | 0.20 | — * | — | 1.00 | Algorithm Core Performance |
| A2 | — | — | — | — | — | — | 0.00 | Hardware Dependency |
| A3 | — | — | — | — | 1.00 | — | 1.00 | Algorithm Efficiency |
| A4 | 0.20 | 0.20 | 0.30 | 0.30 | — | — | 1.00 | Algorithm Robustness |
| B1 | — | — | — | — | — | — | 0.00 | Interaction Design |
| B2 | — | — | — | — | — | — | 0.00 | Industrial Design |
| B3 | — | — | — | — | — | — | 0.00 | Product Operations |
| B4 | — | — | — | — | — | — | 0.00 | Interaction Design |
| C1 | — | — | — | — | — | — | 0.00 | Industrial Design |
| C2 | — | — | — | — | — | — | 0.00 | Industrial Design |
| C3 | — | — | — | — | — | 0.30 | 0.30 | Hybrid Metrics (Algorithm/Industrial Design) |
| C4 | 0.10 | 0.10 | 0.10 | 0.10 | — | — | 0.40 | Hybrid Metrics (Algorithm/Hardware) |
| D1 | 0.15 | 0.40 | 0.15 | 0.10 | — | — | 0.80 | Algorithm Reliability |
| D2 | — | — | — | — | — | — | 0.00 | Materials and Compliance |
| D3 | — | — | — | — | — | — | 0.00 | Information Security |
| D4 | — | — | — | — | — | — | 0.00 | System Design |
| Technical Indicators | Mapping Weight (Wmap) | Weights by the EWM (Wtech) | Wmap × Wtech | Final Weighting (Wfinal) |
|---|---|---|---|---|
| mAP@50 | 0.0582 | 0.1305 | 0.0076 | 0.1851 |
| Precision | 0.0672 | 0.1404 | 0.0094 | 0.2300 |
| Recall | 0.0469 | 0.1865 | 0.0087 | 0.2132 |
| F1 Score | 0.0432 | 0.1510 | 0.0065 | 0.1590 |
| FPS | 0.0331 | 0.1359 | 0.0045 | 0.1097 |
| Params(M) | 0.0165 | 0.2559 | 0.0042 | 0.1029 |
| Algorithms | mAP@50 | Precision | Recall | F1 Score | FPS | Parameters (M) |
|---|---|---|---|---|---|---|
| Faster R-CNN | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.50, 0.60], [0.35, 0.45], [0.40, 0.50] | [0.60, 0.70], [0.25, 0.35], [0.30, 0.40] |
| SSD-VGG16 | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] |
| YOLOv7 | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] | [0.70, 0.80], [0.15, 0.25], [0.20, 0.30] |
| YOLOv8n | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.75, 0.85], [0.10, 0.20], [0.15, 0.25] |
| Indicator | Optimal Solution | Negative Ideal Solution |
|---|---|---|
| mAP@50 | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] |
| Precision | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] |
| Recall | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] |
| F1 Score | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] | [0.80, 0.90], [0.05, 0.10], [0.10, 0.20] |
| FPS | [0.90, 0.95], [0.00, 0.05], [0.05, 0.15] | [0.50, 0.60], [0.35, 0.45], [0.40, 0.50] |
| Parameters (M) | [0.60, 0.70], [0.25, 0.35], [0.30, 0.40] | [0.95, 1.00], [0.00, 0.00], [0.00, 0.10] |
| Algorithms | Improved IVNS-VIKOR Comprehensive Evaluation Results | |||||
|---|---|---|---|---|---|---|
| Q Value (v = 0.5) | S Value | R Value | Wk 1 | ΣP 2 | Ranking | |
| Faster R-CNN | 1.0000 | 0.5487 | 0.1097 | 0 | 0.0000 | 4 |
| SSD-VGG16 | 0.7045 | 0.5000 | 0.1066 | 1 | 1.0000 | 3 |
| YOLOv7 | 0.1567 | 0.3010 | 0.1029 | 2 | 2.1809 | 2 |
| YOLOv8n | 0.0000 | 0.1878 | 0.1029 | 3 | 2.8191 | 1 |
| Method ID | Methodological Framework | Environment | Weighting Strategy | Source |
|---|---|---|---|---|
| Proposed | IVNS-AHP + EWM-VIKOR | IVNS | Subjective: User preferences + AHP (expert); Objective: EWM | This work |
| M1 | IVNS-AHP + EWM-VIKOR | IVNS | Subjective: User preferences + AHP (expert); Objective: EWM | This work (Dissolution) |
| M2 | IVNS-TODIM | IVNS | Objective: Similarity measures and information content based on cross-information | [53] |
| M3 | IVNS-MD-TOPSIS | IVNS | Objective: MD | [54] |
| M4 | IVIF-AHP-TOPSIS | IVIF | Subjective: AHP | [55] |
| M5 | IVPFN-AHP-VIKOR | IVPFN | Subjective: PFAHP | [56] |
| M6 | FIS-AHP-VIKOR | FIS | Subjective: FAHP | [57] |
| M7 | IF-CRITIC-RS-VIKOR | IF | Objective: CRITIC; Subjective: RS | [58] |
| M8 | TFN-AHP-TOPSIS-VIKOR | TFN | Subjective: AHP | [59] |
| Method ID | Sorting Methods | 1-Faster R-CNN | 2-SSD-VGG16 | 3-YOLOv7 | 4-YOLOv8n | Ranking |
|---|---|---|---|---|---|---|
| Proposed | 0.0000 | 1.0000 | 2.1809 | 2.8191 | 4 ≻ 3 ≻ 2 ≻ 1 | |
| M1 | 1.0000 | 0.9880 | 0.2945 | 0.0000 | 4 ≻ 3 ≻ 2 ≻ 1 | |
| M2 | ) | 0.0000 | 0.6183 | 0.7812 | 0.8476 | 4 ≻ 3 ≻ 2 ≻ 1 |
| M3 | 0.2174 | 0.6412 | 0.7689 | 0.9256 | 4 ≻ 3 ≻ 2 ≻ 1 | |
| M4 | 0.3065 | 0.7248 | 0.8256 | 0.8842 | 4 ≻ 3 ≻ 2 ≻ 1 | |
| M5 | 1.0000 | 0.6957 | 0.1472 | 0.0000 | 4 ≻ 3 ≻ 2 ≻ 1 | |
| M6 | 1.0000 | 0.7083 | 0.1306 | 0.0000 | 4 ≻ 3 ≻ 2 ≻ 1 | |
| M7 | 0.9512 | 0.5784 | 0.6452 | 0.1278 | 4 ≻ 2 ≻ 3 ≻ 1 | |
| M8 | 0.1216 | 0.6318 | 0.7895 | 0.9683 | 4 ≻ 3 ≻ 2 ≻ 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Sun, W.; Zhang, R. An Interval-Valued Neutrosophic Framework: Improved VIKOR with a Preference-Aware AHP–Entropy Weight Method for Evaluating Scalp-Detection Algorithms. Appl. Sci. 2025, 15, 11937. https://doi.org/10.3390/app152211937
Chen X, Sun W, Zhang R. An Interval-Valued Neutrosophic Framework: Improved VIKOR with a Preference-Aware AHP–Entropy Weight Method for Evaluating Scalp-Detection Algorithms. Applied Sciences. 2025; 15(22):11937. https://doi.org/10.3390/app152211937
Chicago/Turabian StyleChen, Xin, Wei Sun, and Ruiqiu Zhang. 2025. "An Interval-Valued Neutrosophic Framework: Improved VIKOR with a Preference-Aware AHP–Entropy Weight Method for Evaluating Scalp-Detection Algorithms" Applied Sciences 15, no. 22: 11937. https://doi.org/10.3390/app152211937
APA StyleChen, X., Sun, W., & Zhang, R. (2025). An Interval-Valued Neutrosophic Framework: Improved VIKOR with a Preference-Aware AHP–Entropy Weight Method for Evaluating Scalp-Detection Algorithms. Applied Sciences, 15(22), 11937. https://doi.org/10.3390/app152211937





