Outflow Boundary Conditions for Turbine-Integrated Rotating Detonation Combustors
Abstract
1. Introduction
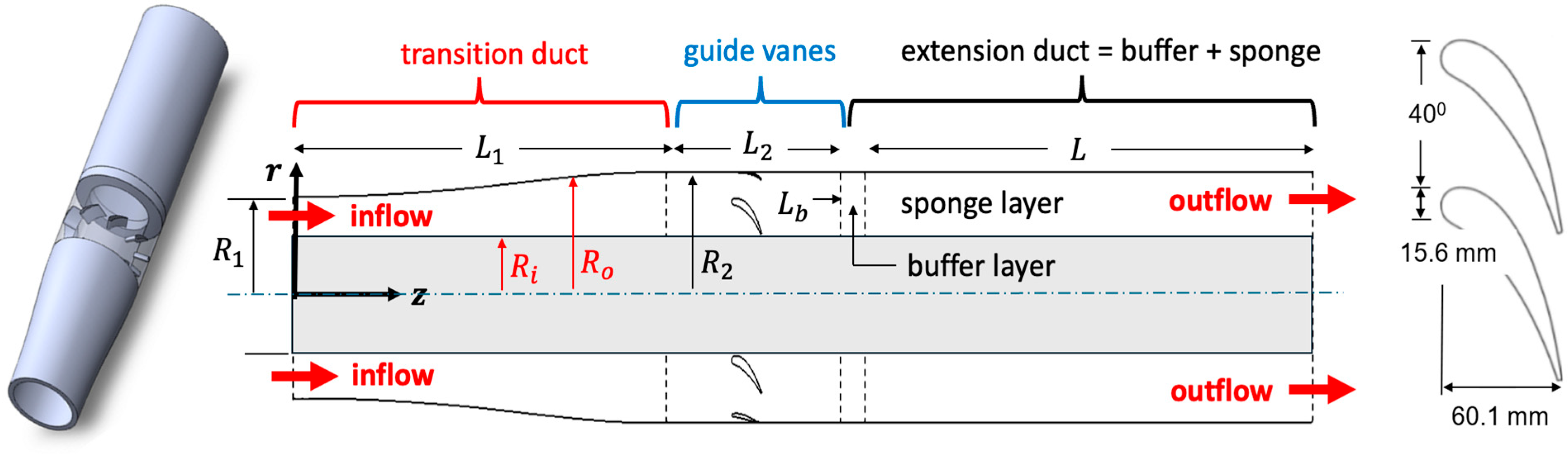
2. Problem Description
3. Problem Formulation and Numerical Method of Solution
3.1. Governing Equations
3.2. Numerical Method of Solution
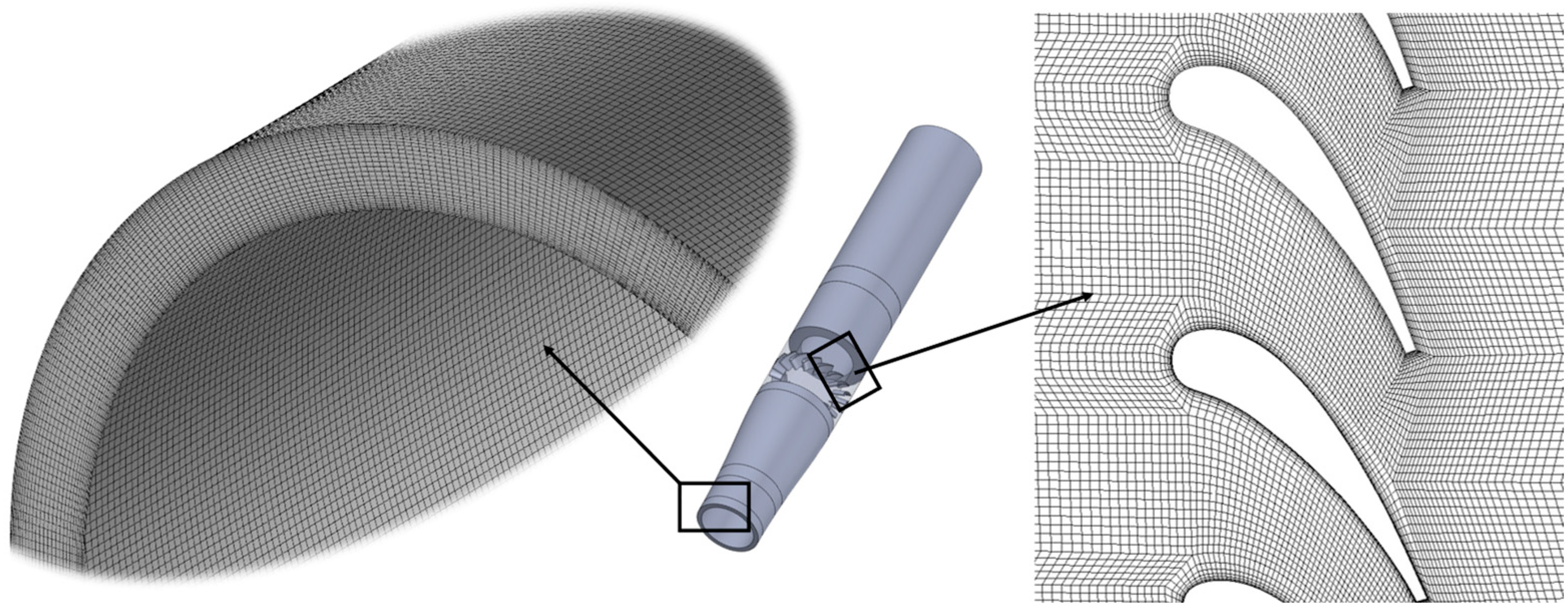
3.2.1. Grid in the Transition Duct
3.2.2. Grid in the Extension Duct
3.2.3. Discretization of the Governing Equations and Solution Algorithm
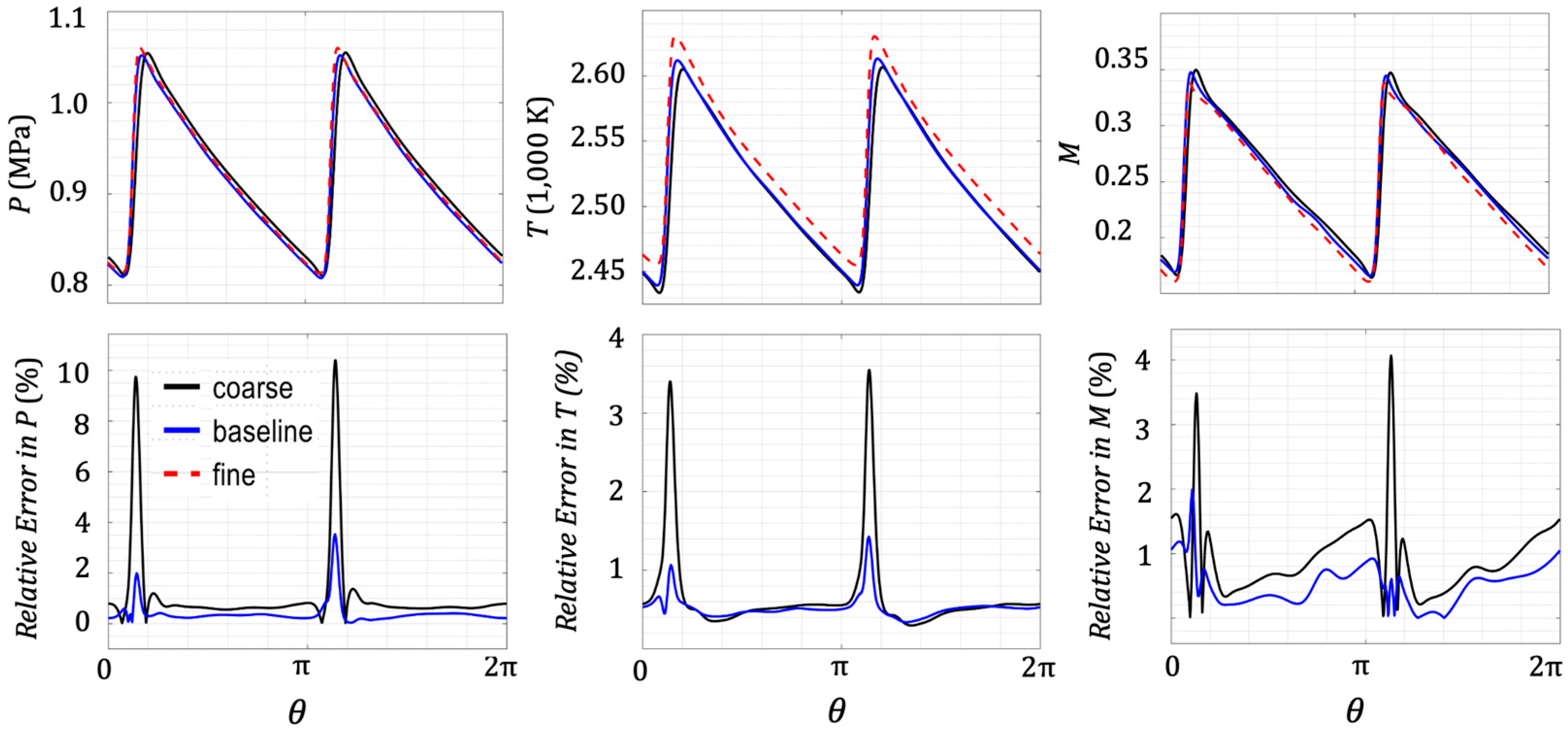
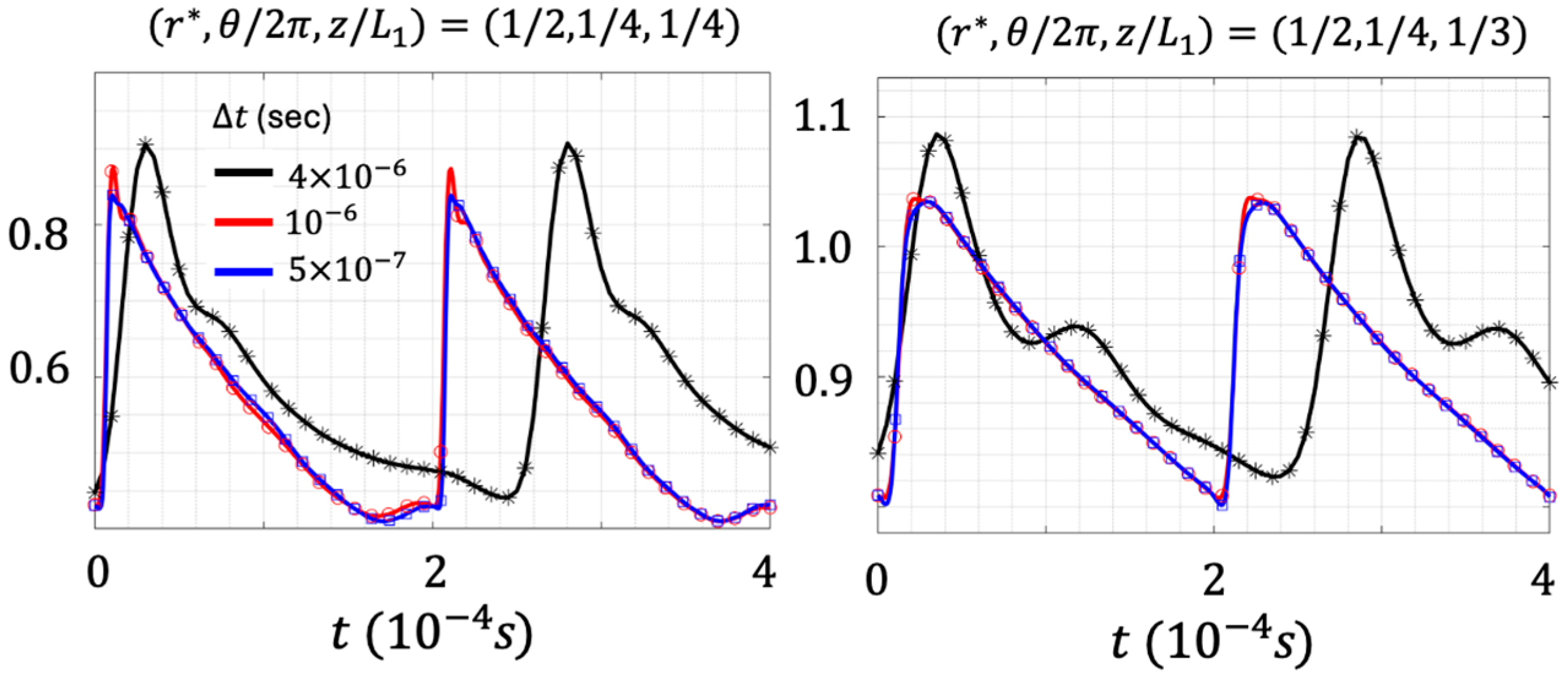
4. Grid and Time-Step Size Sensitivity Studies
5. Results
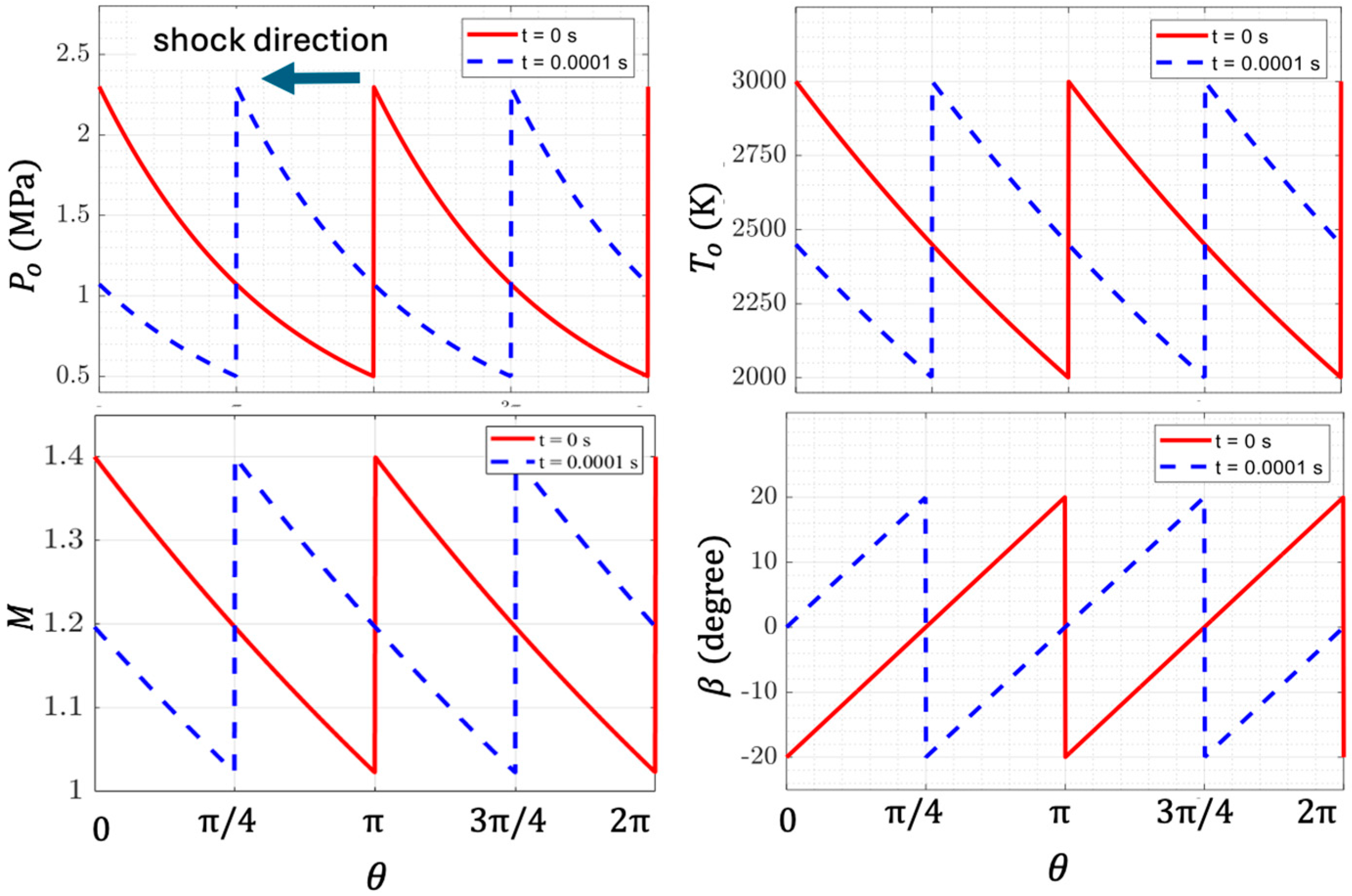
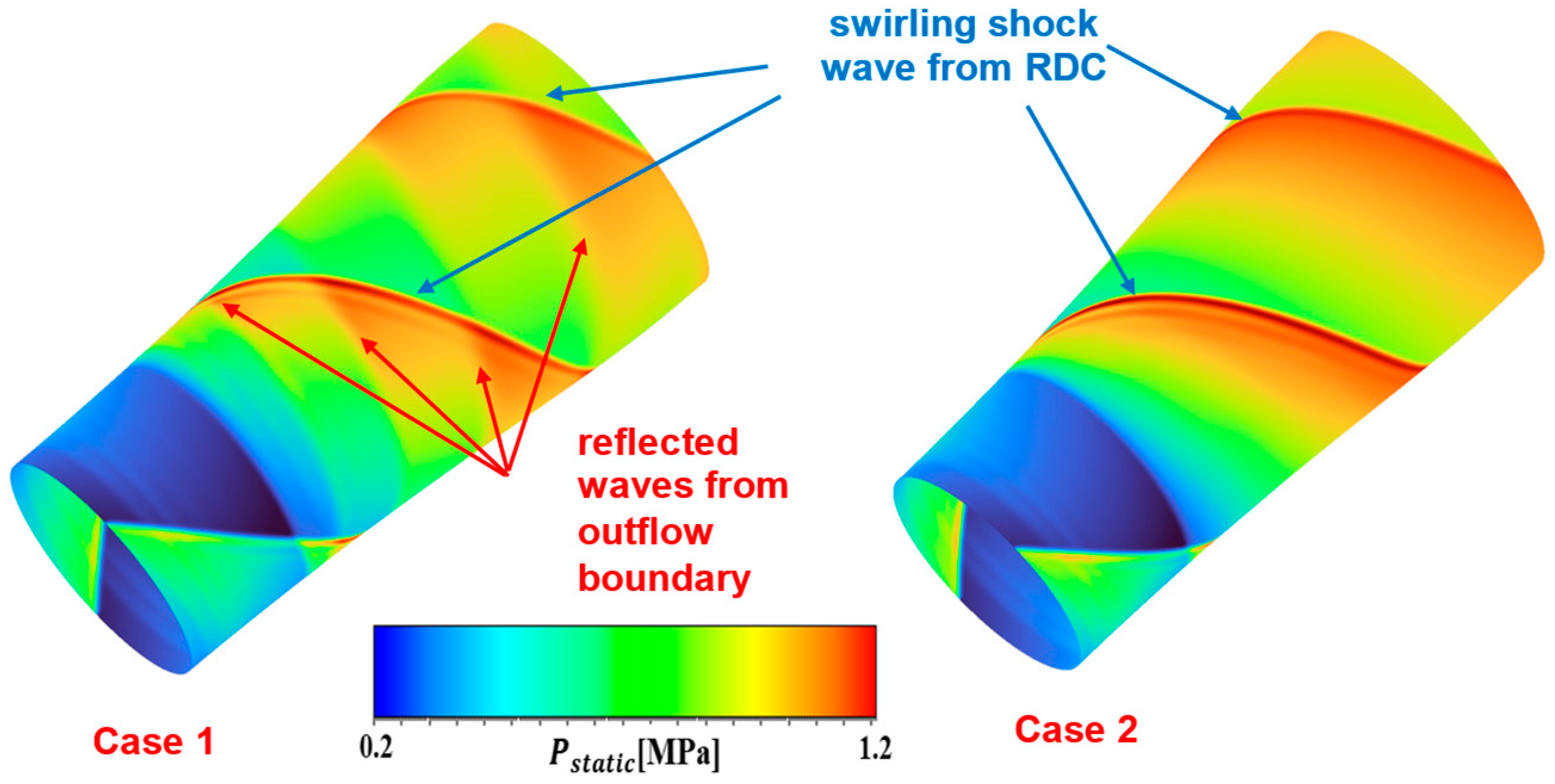
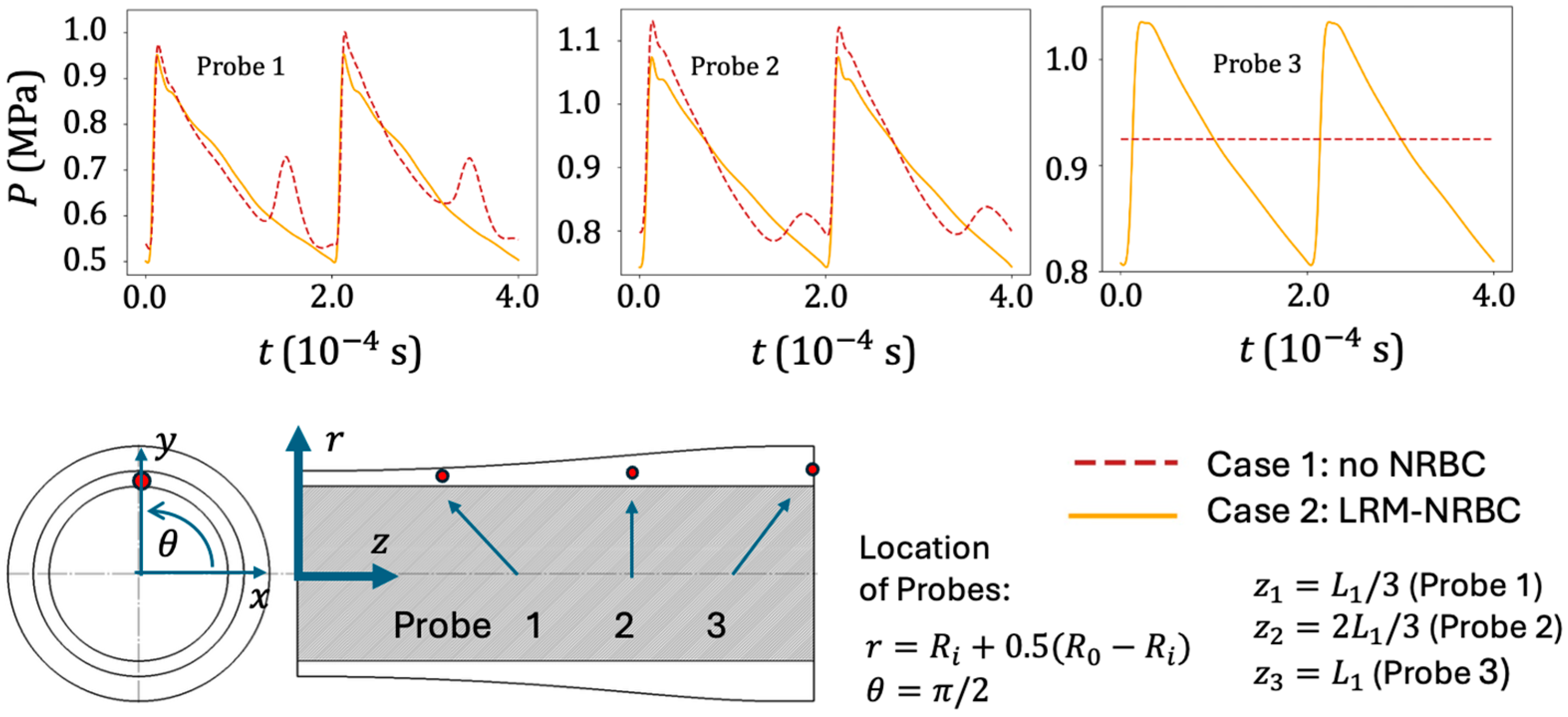
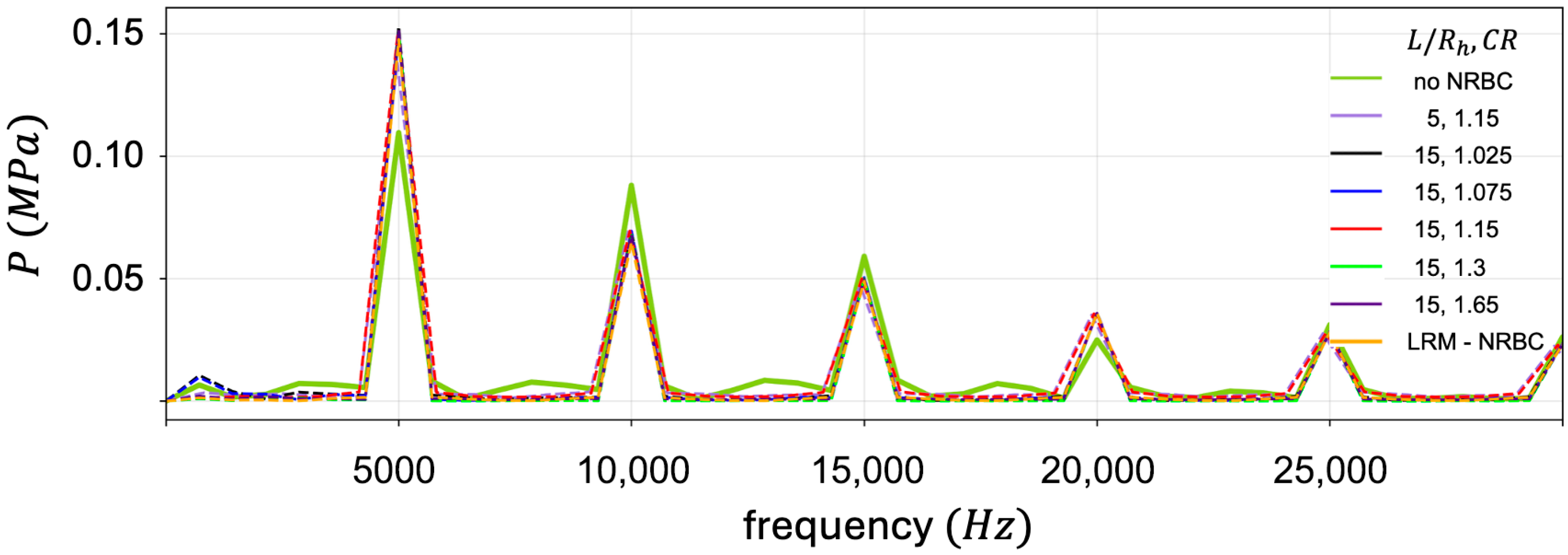
5.1. With and Without Nonreflecting BCs at the Outflow Boundary
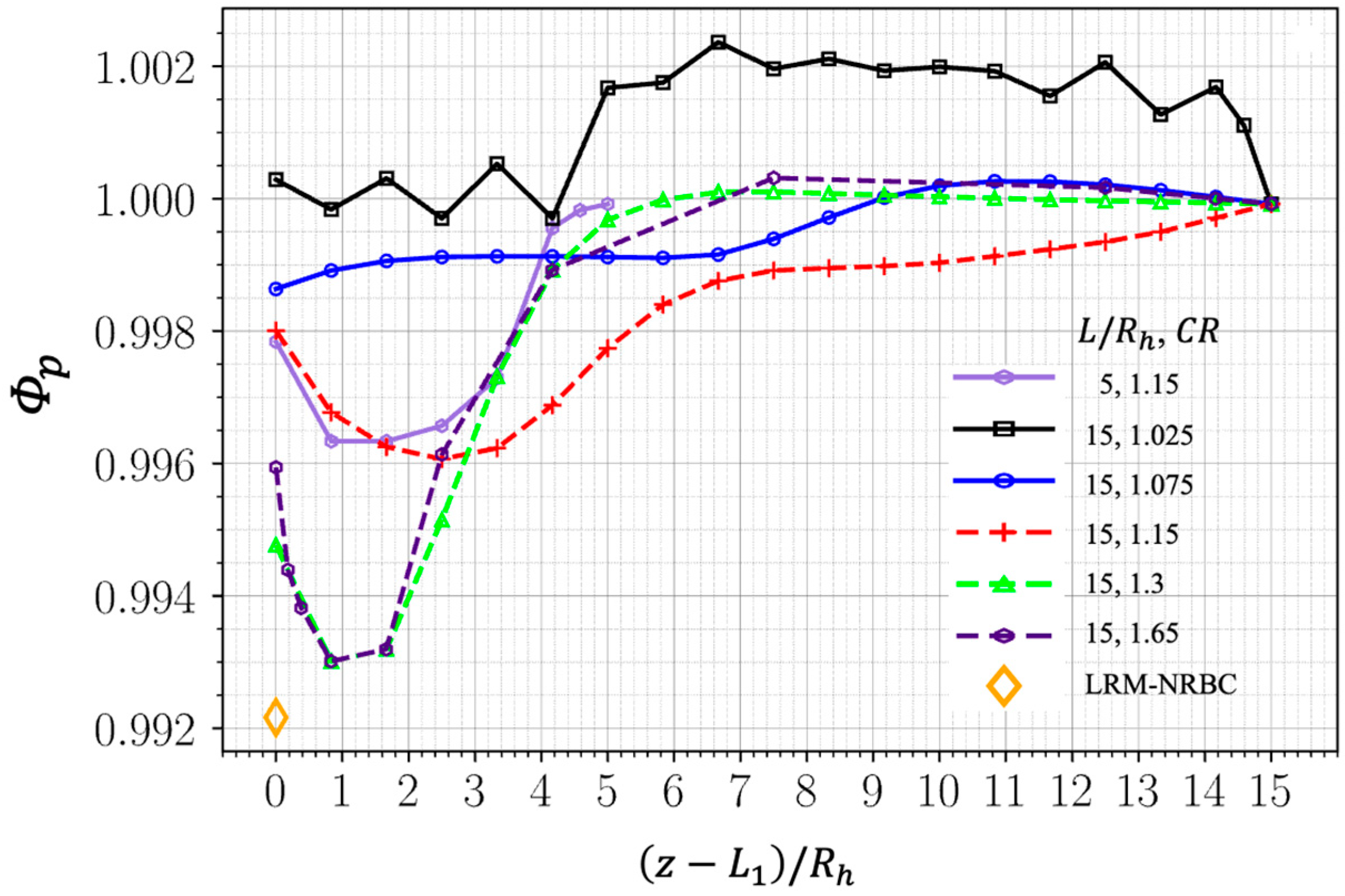
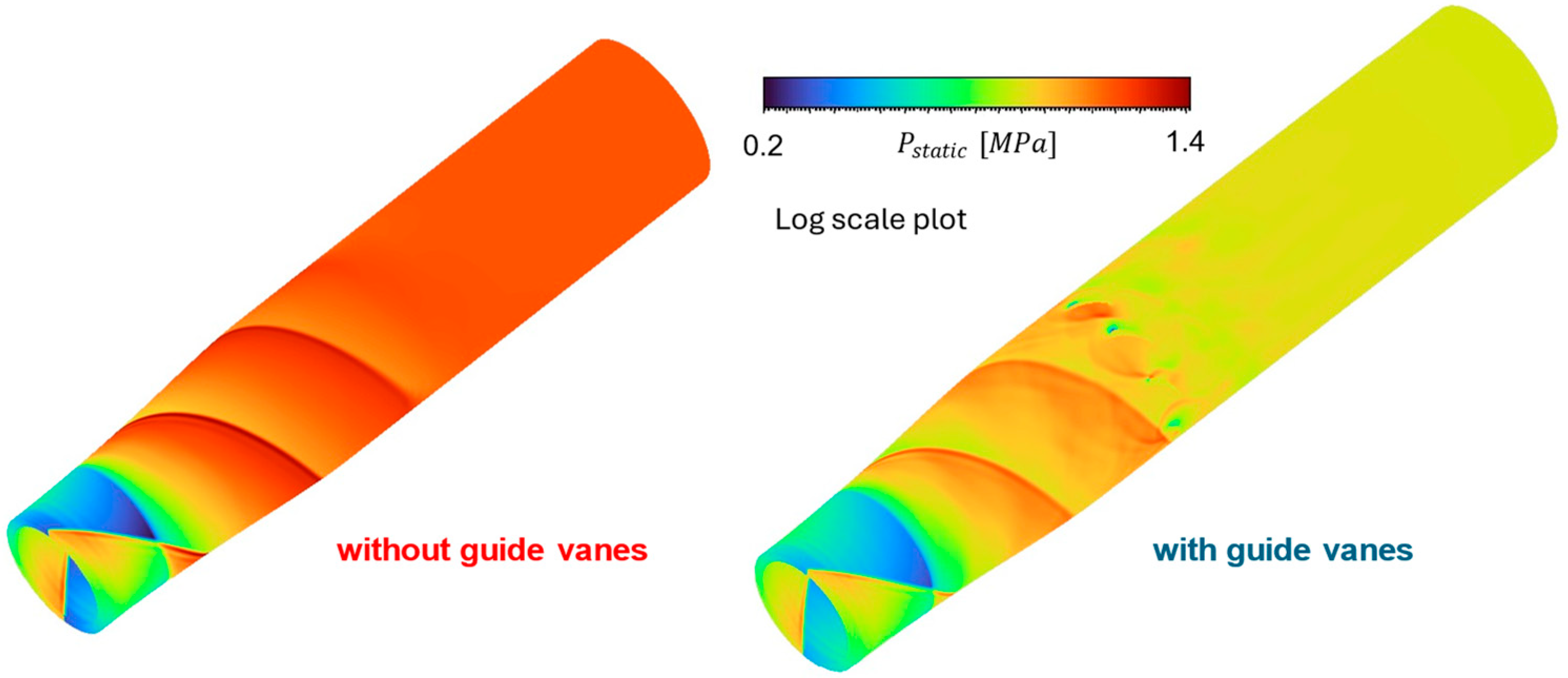
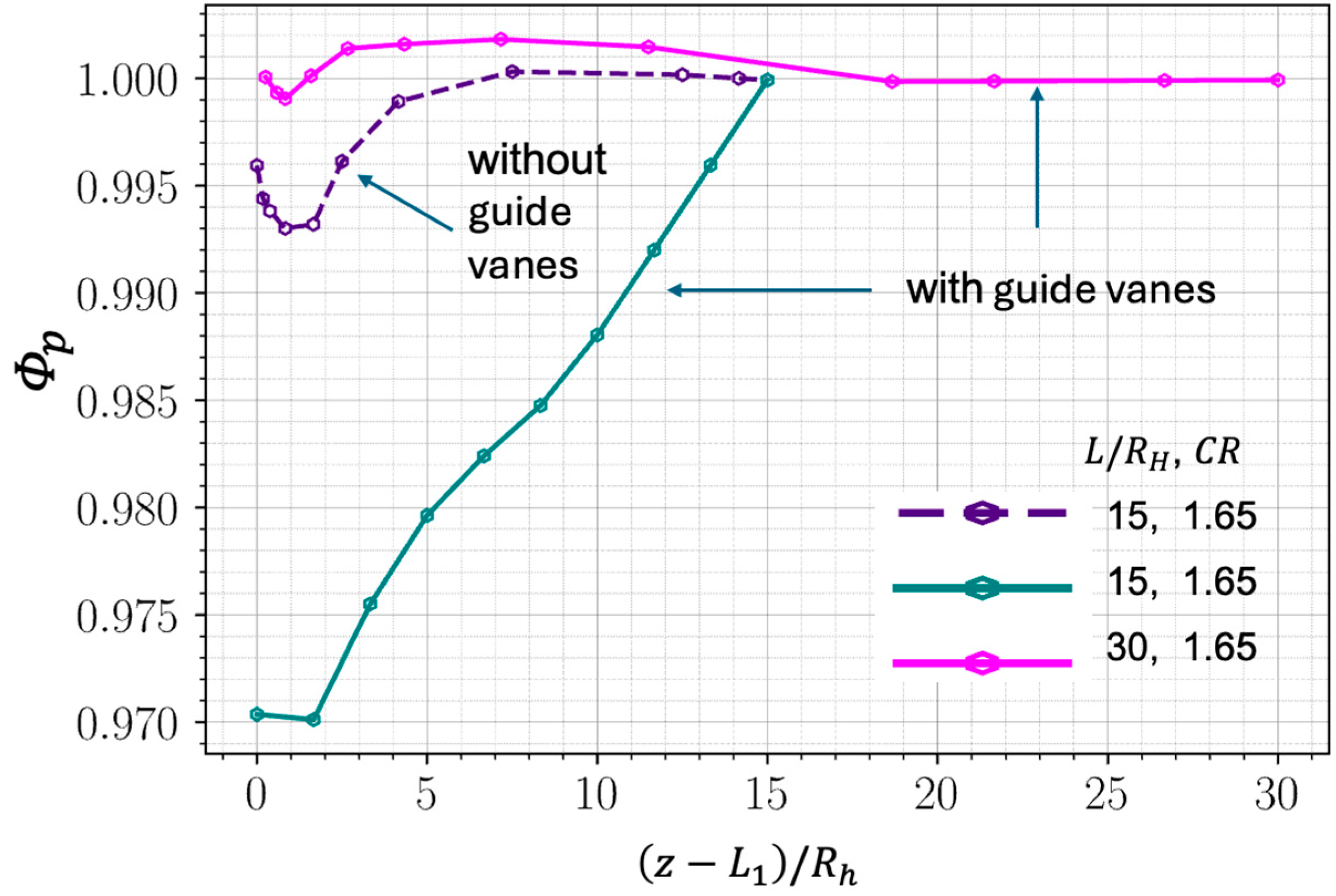
5.2. Outflow BC via an Extension Duct with a Buffer Layer and a Sponge Layer
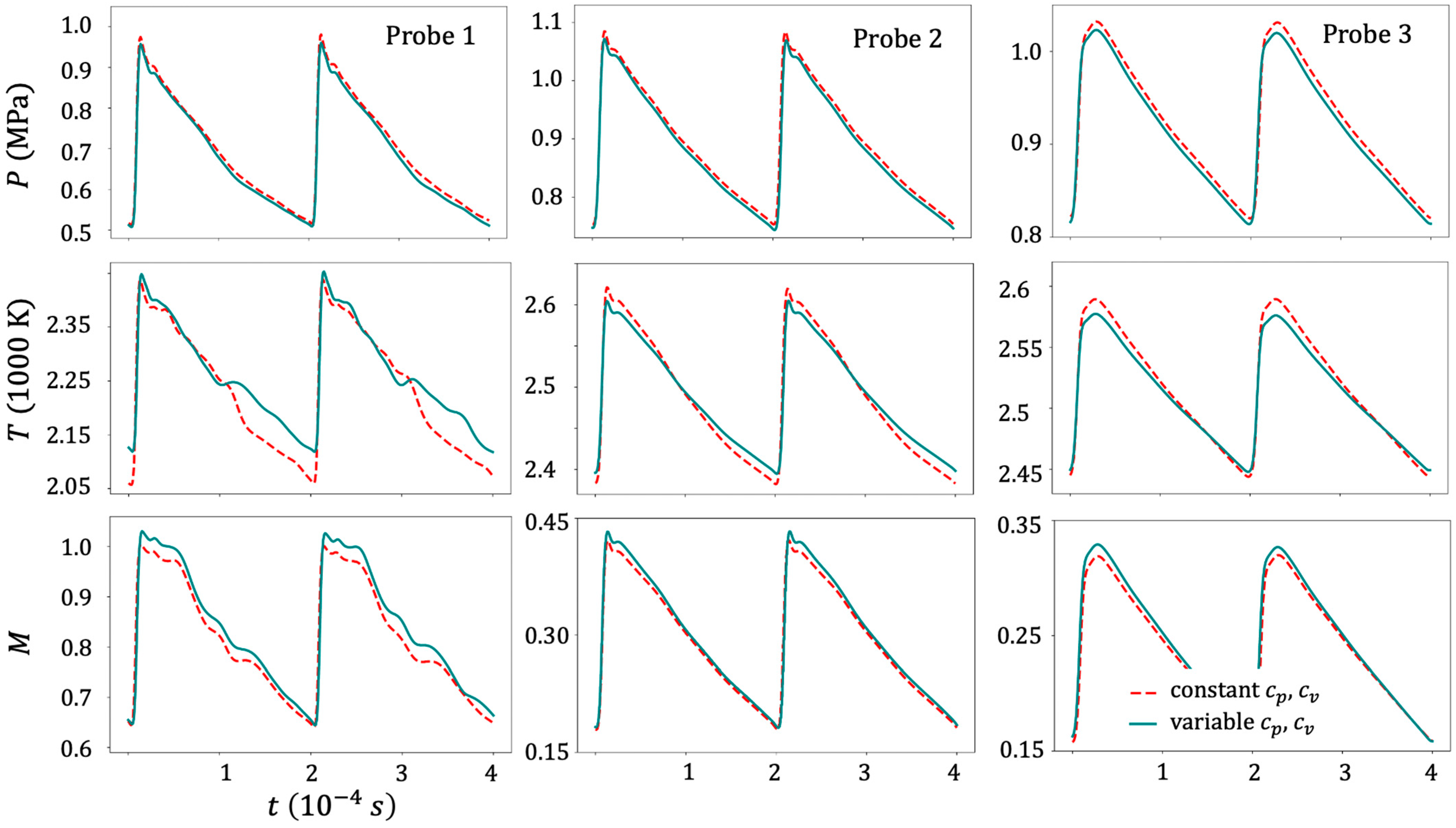
5.3. Effects of Temperature-Dependent Specific Heats
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goddard, R.H. Reaction Combustion Chamber for Unconfined Charges of Detonative Fuel Fed Intermittently to the Combustion Chamber. U.S. Patent No. 2,465,525, 29 March 1949. [Google Scholar]
- Nicholls, J.A.; Cullen, R.E.; Ragland, K.W. Feasibility Studies of a Rotating Detonation Wave Rocket Motor. J. Spacecr. Rockets 1966, 3, 893–898. [Google Scholar] [CrossRef]
- Adamson, T.C.; Olsson, G.R. Performance Analysis of a Rotating Detonation Wave Rocket Engine (Rotating Detonation Wave Rocket Engine Performance Analyzed and Compared to Conventional Rocket Engines). Acta Astronaut. 1967, 14, 405–415. [Google Scholar]
- Bykovskii, F.A.; Zhdan, S.A.; Vedernikov, E.F. Continuous Spin Detonations. J. Propul. Power 2006, 22, 1204–1216. [Google Scholar] [CrossRef]
- Lu, F.K.; Braun, E.M. Rotating Detonation Wave Propulsion: Experimental Challenges, Modeling, ad Engine Concepts. J. Propul. Power 2014, 30, 1125–1142. [Google Scholar] [CrossRef]
- Zhou, R.; Wang, J.-P. Numerical Investigation of Shock Wave Reflections near the Head Ends of Rotating Detonation Engines. Shock Waves 2013, 23, 461–472. [Google Scholar] [CrossRef]
- Escobar, S. Rotating Detonation Combustion: A Computational Study for Stationary Power Generation. Ph.D. Thesis, West Virginia University, Morgantown, WV, USA, 2014. [Google Scholar]
- Paniagua, G.; Iorio, M.C.; Vinha, N.; Sousa, J. Design and analysis of pioneering high supersonic axial turbines. Int. J. Mech. Sci. 2014, 89, 300–310. [Google Scholar] [CrossRef]
- Saracoglu, B.H.; Ozden, A. The Effects of Multiple Detonation Waves. Transp. Res. Procedia 2018, 29, 23–32. [Google Scholar] [CrossRef]
- Ji, Z.; Zhang, H.; Wang, B. Performance Analysis of Dual-Duct Rotating Detonation Aero-Turbine Engine. Aerosp. Sci. Technol. 2019, 92, 806–819. [Google Scholar] [CrossRef]
- Lietz, C.; Desai, Y.; Munipalli, R.; Schumaker, S.A.; Sankaran, V. Flowfield Analysis of a 3D Simulation of a Rotating Detonation Rocket Engine. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Zhang, S.J.; Ma, J.Z.; Wang, J. Theoretical and Numerical Investigation on Total Pressure Gain in Rotating Detonation Engine. AIAA J. 2020, 58, 4866–4875. [Google Scholar] [CrossRef]
- Liu, Z.; Braun, J.; Paniagua, G. Integration of a Transonic High-Pressure Turbine with a Rotating Detonation Combustor and a Diffuser. Int. J. Turbo Jet-Engines 2023, 40, 1–10. [Google Scholar] [CrossRef]
- Prakash, S.; Raman, V.; Lietz, C.F.; Hargus, W.A., Jr.; Schumaker, S.A. Numerical Simulation of a Methane–Oxygen Rotating Detonation Rocket Engine. Proc. Combust. Inst. 2021, 38, 3777–3786. [Google Scholar] [CrossRef]
- Sato, T.; Chacon, F.; White, L.; Raman, V.; Gamba, M. Mixing and Detonation Structure in a Rotating Detonation Engine with an Axial Air Inlet. Proc. Combust. Inst. 2021, 38, 3767–3776. [Google Scholar] [CrossRef]
- Sato, T.; Chacon, F.; Gamba, M.; Raman, V. Mass Flow Rate Effect on a Rotating Detonation Combustor with an Axial Air Injection. Shock Waves 2021, 31, 741–751. [Google Scholar] [CrossRef]
- Zhang, C.; Lin, Z.; Dong, T. Numerical Study on the Interaction Characterization of Rotating Detonation Wave and Turbine Rotor Blades. Int. J. Hydrogen Energy 2022, 47, 6898–6910. [Google Scholar] [CrossRef]
- Shen, D.; Cheng, M.; Wu, K.; Sheng, Z.; Wang, J. Effects of Supersonic Nozzle Guide Vanes on the Performance and Flow Structures of a Rotating Detonation Combustor. Acta Astronaut. 2022, 193, 90–99. [Google Scholar] [CrossRef]
- Sridhara, S.R.; Andreini, A.; Polanka, M.D.; Bohon, M.D. LES Investigation of Film Cooling in Rotating Detonation Combustors. In Proceedings of the ASME Turbo Expo 2024: Turbomachinery Technical Conference and Exposition, London, UK, 24–28 June 2024. [Google Scholar]
- Talukdar, S.; Langner, D.; Gupta, A.; Agarwal, A.K. Performance Characteristics of a Rotating Detonation Combustor Exiting into a Pressurized Plenum to Simulate Gas Turbine Inlet. J. Eng. Gas Turbines Power 2024, 146, 041015. [Google Scholar] [CrossRef]
- Shao, X.; Yang, H.; Zhao, N.; Zhai, D.; Jin, S.; Zhang, W. Numerical Study on the Interaction between Rotating Detonation Wave and Turbine Stator Blades with Multicomponent Mixtures. Int. J. Hydrogen Energy 2024, 49, 1436–1445. [Google Scholar] [CrossRef]
- Dille, K.J.; Slabaugh, C.D.; Heister, S.D. Rotating Detonation Combustor Performance Modelling Informed by Experimental Stagnation Pressure Measurements. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar]
- Pal, P.; Braun, J.; Wang, Y.; Athmanathan, V.; Paniagua, G.; Meyer, T.R. Large-Eddy Simulation Study of Flow and Combustion Dynamics in a Full-Scale Hydrogen-Air Rotating Detonation Combustor-Stator Integrated System. J. Eng. Gas Turbines Power 2025, 147, 031002. [Google Scholar] [CrossRef]
- Plaseehn, E.W.; Haynes, A.L.; Gejji, R.M.; Slabaugh, C.D. Chamber Length Limits of a Continuously Variable Geometry Rotating Detonation Combustor. J. Propul. Power 2025, 41, 135–149. [Google Scholar] [CrossRef]
- Gustafsson, B.; Sundstrom, A. Incompletely Parabolic Problems in Fluid Dynamics. SIAM J. Appl. Math. 1978, 35, 343–357. [Google Scholar] [CrossRef]
- Rudy, D.H.; Strikwerda, J.C. A Non-Reflecting Outflow Boundary Condition for Subsonic Navier–Stokes Calculations. J. Comput. Phys. 1980, 36, 55–70. [Google Scholar] [CrossRef]
- Israel, M.; Orszag, S.A. Approximation of Radiation Boundary Conditions. J. Comput. Phys. 1981, 41, 115–135. [Google Scholar] [CrossRef]
- Thompson, K.W. Time Dependent Boundary Conditions for Hyperbolic Systems. J. Comput. Phys. 1987, 68, 1–24. [Google Scholar] [CrossRef]
- Gustafsson, B. Far-Field Boundary Conditions for Time-Dependant Hyperbolic Systems. SIAM J. Sci. Stat. Comput. 1988, 9, 812–828. [Google Scholar] [CrossRef]
- Giles, M.B. Non-Reflecting Boundary Conditions for Euler Equations; TR CFDL-TR-88-1; Massachusetts Institute of Technology, Department of Aeronautics and Astronautics: Cambridge, MA, USA, 1988. [Google Scholar]
- Giles, M.B. Non-Reflecting Boundary Conditions for Euler Equation Calculations. AIAA J. 1990, 28, 2050–2058. [Google Scholar] [CrossRef]
- Thompson, K.W. Time Dependent Boundary Conditions for Hyperbolic Systems II. J. Comput. Phys. 1990, 89, 439–461. [Google Scholar] [CrossRef]
- Poinsot, T.J.; Lele, S.K. Boundary Conditions for Direct Simulations of Compressible Viscous Flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Colonius, T.; Lele, S.K.; Moin, P. Boundary Conditions for Direct Computation of Aerodynamic Sound Generation. AIAA J. 1993, 31, 1574–1582. [Google Scholar] [CrossRef]
- Selle, L.; Nicoud, F.; Poinsot, T. Actual Impedance of Nonreflecting Boundary Conditions: Implications for Computation of Resonators. AIAA J. 2004, 42, 958–964. [Google Scholar] [CrossRef]
- Hu, F.Q.; Li, X.D.; Lin, D.K. Absorbing Boundary Conditions for Nonlinear Euler and Navier-Stokes Equations Based on the Perfectly Matched Layer Technique. J. Comput. Phys. 2008, 227, 4398–4424. [Google Scholar] [CrossRef]
- Kreiss, G.; Krank, B.; Efraimsson, G. Analysis of Stretched Grids and Buffer Zones in Simulations of Wave Propagation. Appl. Numer. Math. 2016, 107, 1–15. [Google Scholar] [CrossRef]
- Li, Z.; Abdellatif, A.; Yang, R.; Jofre, L.; Capuano, F. Navier-Stokes Characteristic Boundary Conditions for Real Fluids with Kinetic-Energy- and Pressure-Equilibrium Preserving Schemes. J. Comput. Phys. 2025, 535, 114035. [Google Scholar] [CrossRef]
- Kuo, K.K. Principles of Combustion; Wiley: New York, NY, USA, 1986. [Google Scholar]
- White, F.M. Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006. [Google Scholar]
- McBride, B.J.; Zehe, M.J.; Gordon, S. NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species; NASA/TP–2002-211556; Glenn Research Center: Cleveland, OH, USA, 2002. [Google Scholar]
- Shih, T.-H.; Liou, W.; Shabbir, A.; Zhu, J. A New k-ε Eddy-Viscosity Model for High Reynolds Number Turbulent Flows—Model Development and Validation. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Kader, B. Temperature and Concentration Profiles in Fully Turbulent Boundary Layers. Int. J. Heat Mass Transfer 1981, 24, 1541–1544. [Google Scholar] [CrossRef]
- Chima, R.V.; Liou, M.S. Comparison of the AUSM+ and H-CUSP Schemes for Turbomachinery Applications. In Proceedings of the 33rd Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- ANSYS FLUENT. Computational Fluid Dynamic Code Manual, Version 2024R2. Available online: https://ansyshelp.ansys.com/public/account/secured?returnurl=/Views/Secured/prod_page.html?pn=Fluent&prodver=24.2&lang=en (accessed on 5 November 2025).



| Case No | Guide Vane | LRM-NRBC | * | |||
|---|---|---|---|---|---|---|
| 1 | no | no | 0.90 | constant | 0 | N/A |
| 2 | no | yes | 0.90 | constant | 0 | N/A |
| 3 | no | no | 0.90 | constant | 5 | 1.15 |
| 4 | no | no | 0.90 | constant | 15 | 1.15 |
| 5 | no | no | 0.90 | constant | 15 | 1.3 |
| 6 | no | no | 0.90 | constant | 15 | 1.65 |
| 7 | no | no | 0.90 | constant | 15 | 1.025 |
| 8 | no | no | 0.90 | constant | 15 | 1.075 |
| 9 | no | no | 0.90 | variable | 15 | 1.15 |
| 10 | yes | no | 0.65 | variable | 15 | 1.65 |
| 11 | yes | no | 0.65 | variable | 30 | 1.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, T.-M.; Bryden, K.M.; Dalton, R.P.; Crane, J.; Shih, T.I.-P. Outflow Boundary Conditions for Turbine-Integrated Rotating Detonation Combustors. Appl. Sci. 2025, 15, 11922. https://doi.org/10.3390/app152211922
Hsieh T-M, Bryden KM, Dalton RP, Crane J, Shih TI-P. Outflow Boundary Conditions for Turbine-Integrated Rotating Detonation Combustors. Applied Sciences. 2025; 15(22):11922. https://doi.org/10.3390/app152211922
Chicago/Turabian StyleHsieh, Tsung-Ming, K. Mark Bryden, Richard P. Dalton, John Crane, and Tom I-P. Shih. 2025. "Outflow Boundary Conditions for Turbine-Integrated Rotating Detonation Combustors" Applied Sciences 15, no. 22: 11922. https://doi.org/10.3390/app152211922
APA StyleHsieh, T.-M., Bryden, K. M., Dalton, R. P., Crane, J., & Shih, T. I.-P. (2025). Outflow Boundary Conditions for Turbine-Integrated Rotating Detonation Combustors. Applied Sciences, 15(22), 11922. https://doi.org/10.3390/app152211922






