Hybrid Deep Learning Framework for Forecasting Ground-Level Ozone in a North Texas Urban Region
Abstract
1. Introduction
- (1)
- Integrating chemical precursors and meteorological drivers,
- (2)
- Incorporating one-hour lagged input variables to enhance temporal learning,
- (3)
- Providing mechanistic interpretability using SHAP analysis, and
- (4)
- Evaluating generalization performance across heterogeneous urban airsheds.
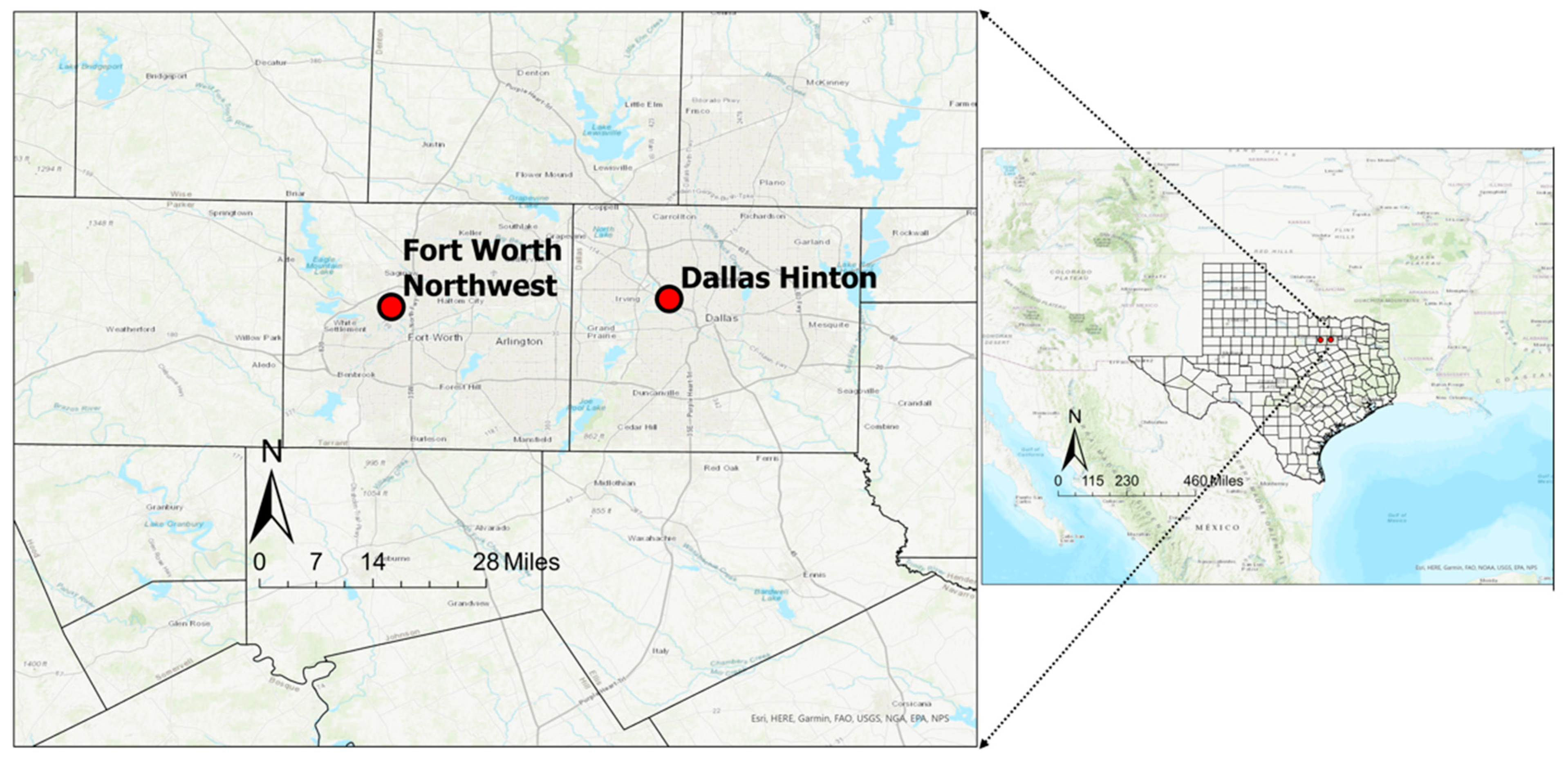
2. Data and Methods
2.1. Data
- Air pollutants: ozone (ppb), NOx (ppb), and 26 individual VOC species (ppbV) measured by Automated Gas Chromatographs (AutoGC),
- Meteorological parameters: outdoor temperature (OT, °F), peak wind gust (PWG, mph), relative humidity (RH, %), solar radiation (SR, W/m2), dew point temperature (DP, °F), resultant wind speed (WS, mph), and resultant wind direction (WD, degrees).
- Among the 26 VOCs, we selected 22 species based on data completeness (>90% coverage) and feature importance analysis with respect to ozone, identified via SHAP.
- Parameters with <10% missing data were gap-filled using temporal imputation (mean of the same date and time from neighboring years).
- Parameters with >10% missing data were excluded.
- Outlier retention was prioritized, recognizing that high ozone events and precursor spikes are critical for model learning in non-attainment areas.
2.2. Methods
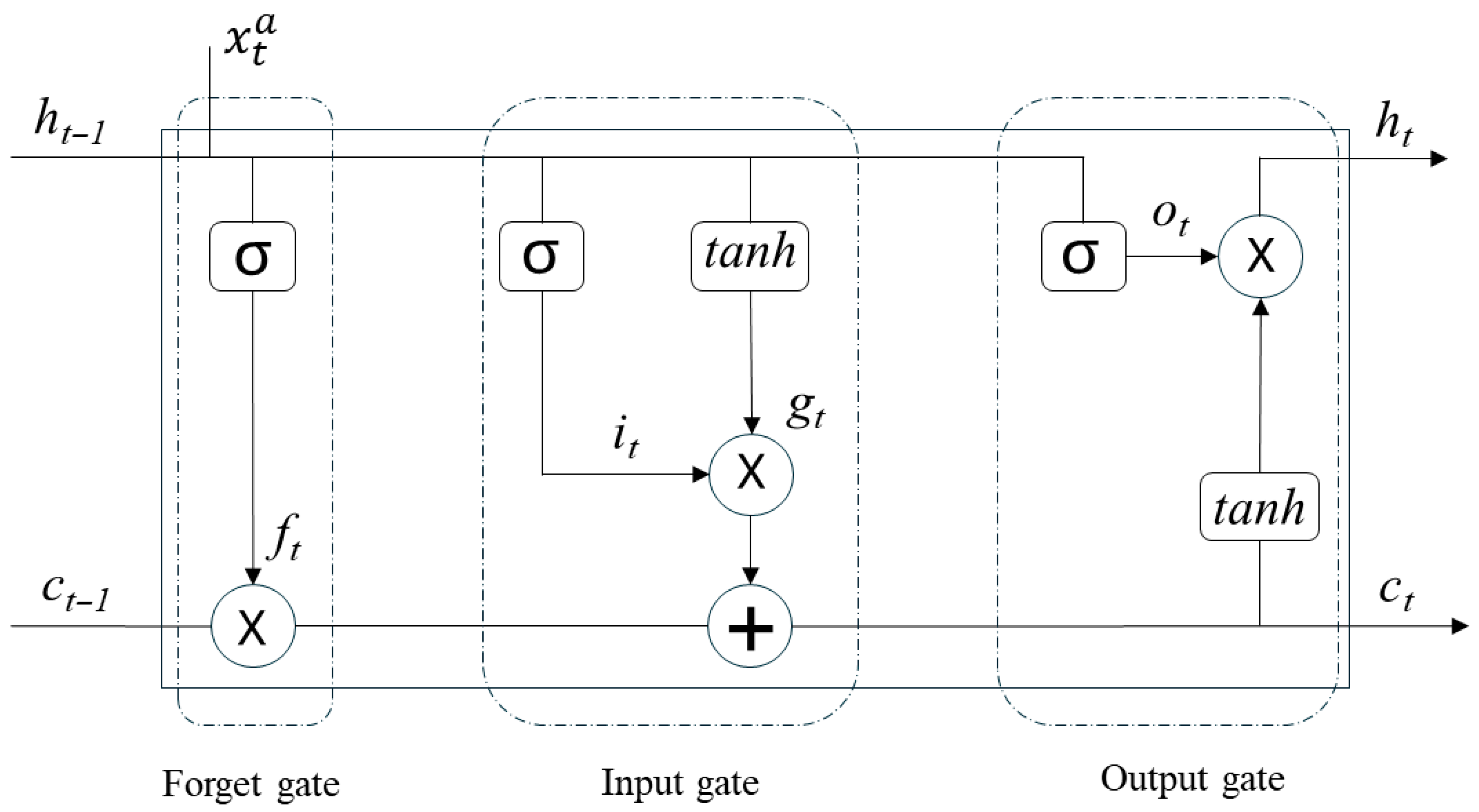
2.2.1. Long Short-Term Memory (LSTM)
- Forget gate—Determines which information from the previous cell state to discard,
- Input gate—Regulates which new information to add, combining a sigmoid filter with a tanh-generated candidate vector,
- Output gate—Controls the portion of the updated cell state exposed as output to the next layer.
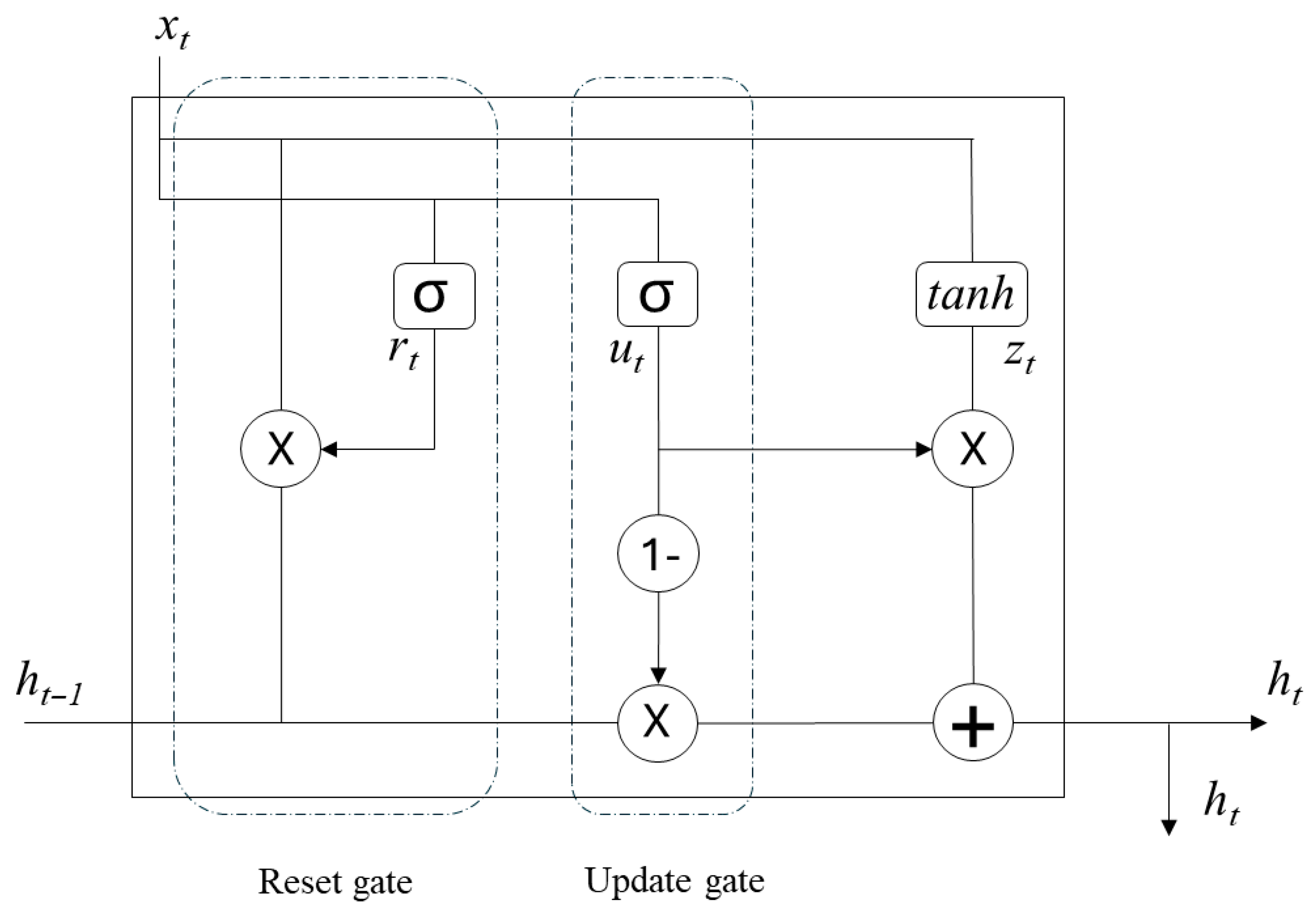
2.2.2. Gated Recurrent Unit (GRU)
- Update gate—Controls how much of the past information is retained versus updated with new input, effectively combining the roles of the input and forget gates in LSTM,
- Reset gate—Determines how much of the previous state to discard when incorporating new input, enabling flexible integration of past and present information.
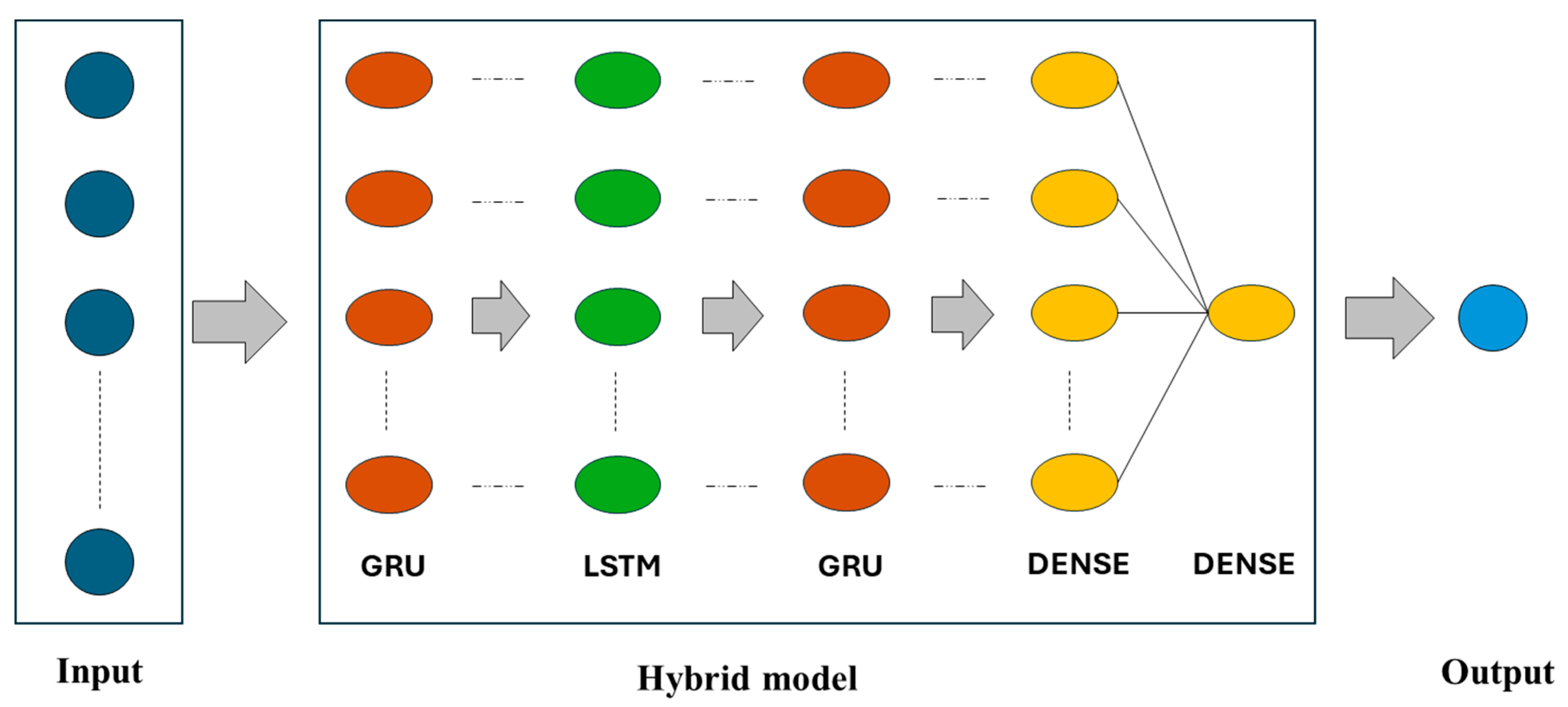
2.2.3. Hybrid Model
- First layer (GRU, 128 units): Processes the multivariate input sequence, capturing immediate temporal patterns, anomalies, and short-term dependencies, with fast convergence due to its simplified gating mechanism.
- Second layer (LSTM, 128 units): Refines the intermediate representations by modeling deeper temporal structures, leveraging its input, forget, and output gates to selectively retain long-term information relevant to ozone formation dynamics.
- Third layer (GRU, 128 units): Further abstracts the features, improving efficiency and stability by reinforcing learned temporal dependencies while minimizing computational overhead.
- Fourth layer (Dense, 64 units): Acts as a fully connected layer that consolidates high-level representations from the recurrent layers into a compact feature space suitable for output prediction.
- Final layer (Dense, 1 unit): Outputs the predicted 8 h average ozone concentration.
Experimental Details and Model Performance Evaluations
2.3. Results and Discussion
2.3.1. Overview of Parameters in the Fort Worth Northwest Region
2.3.2. Feature Importance Evaluation
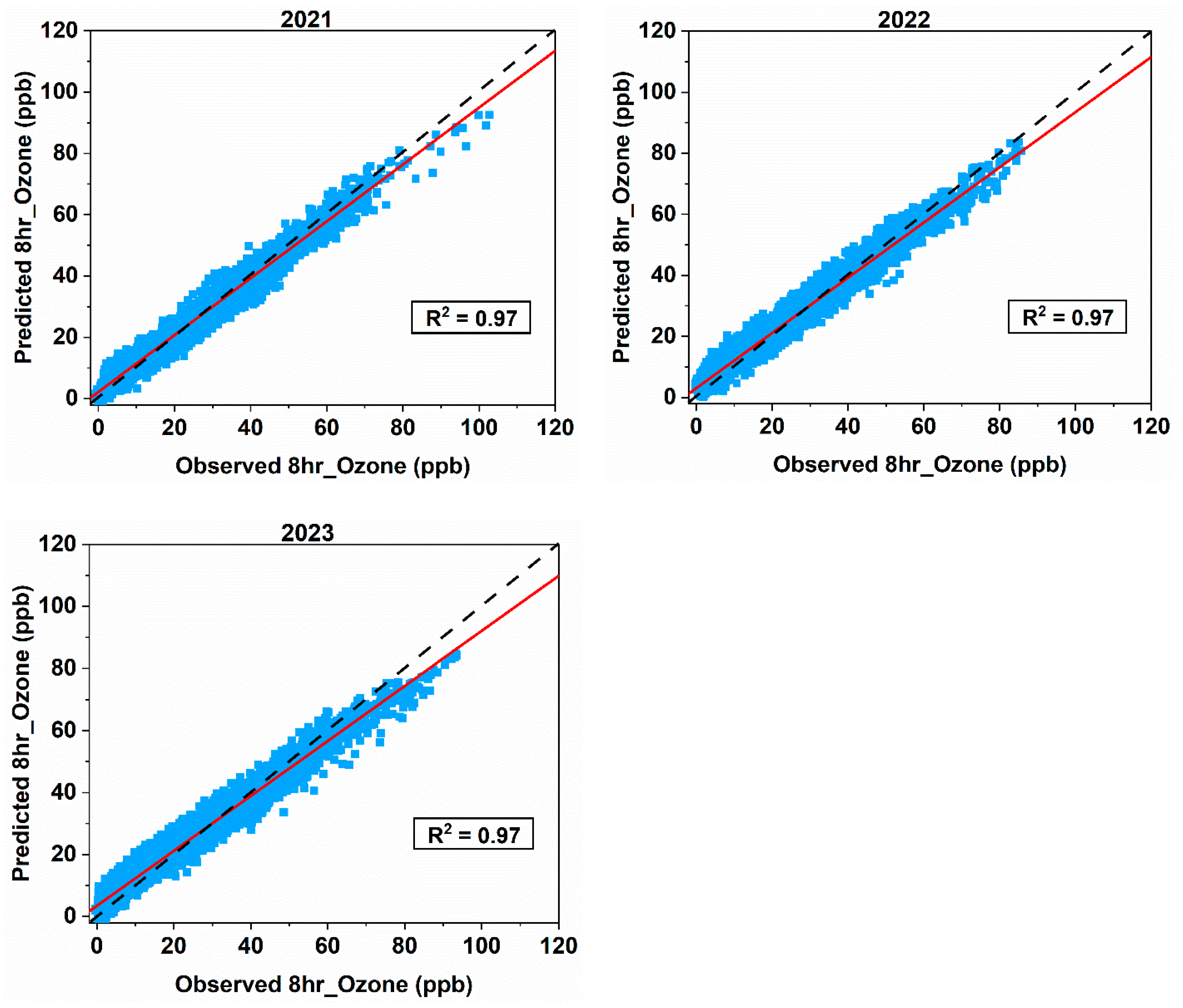
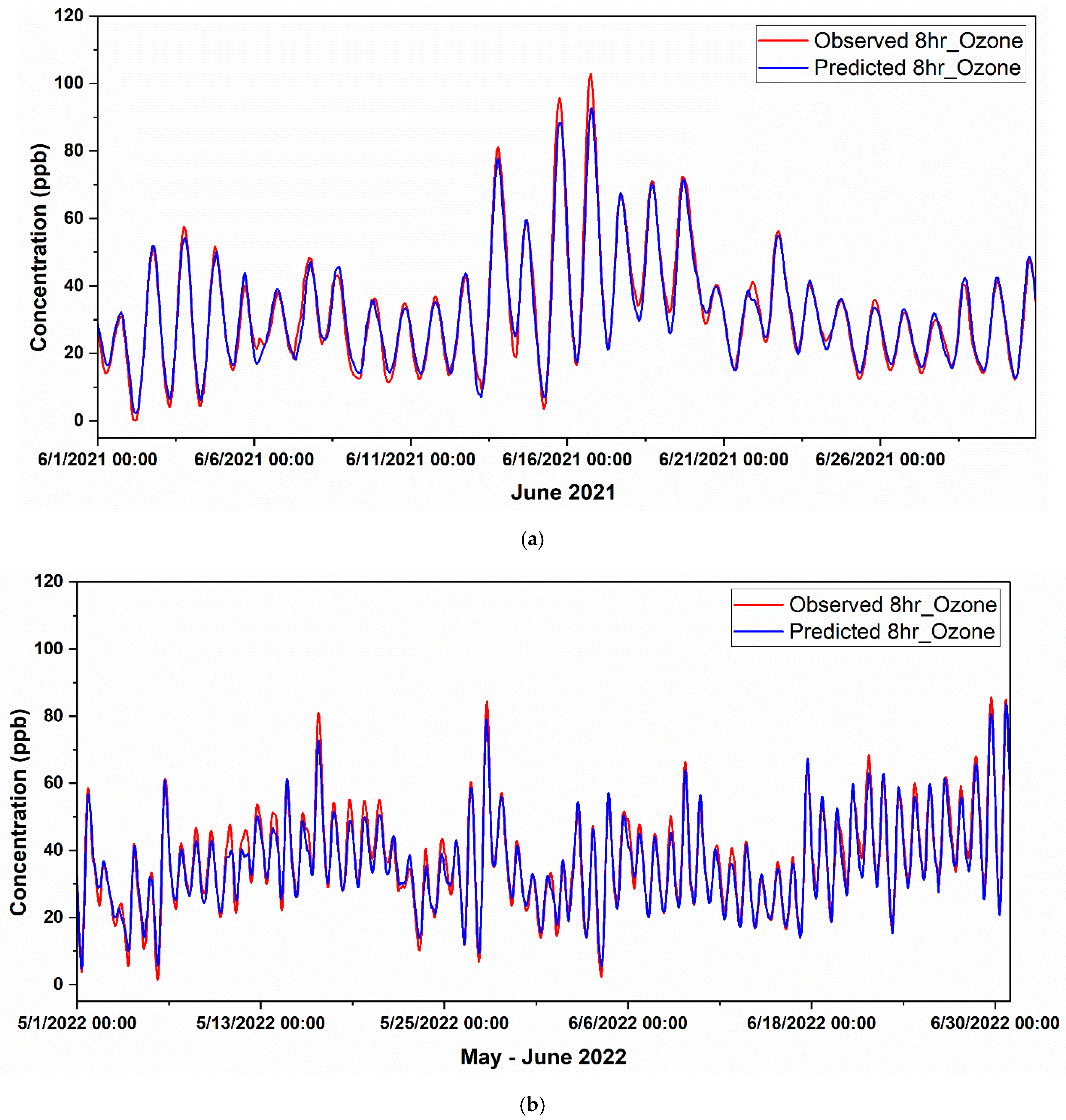
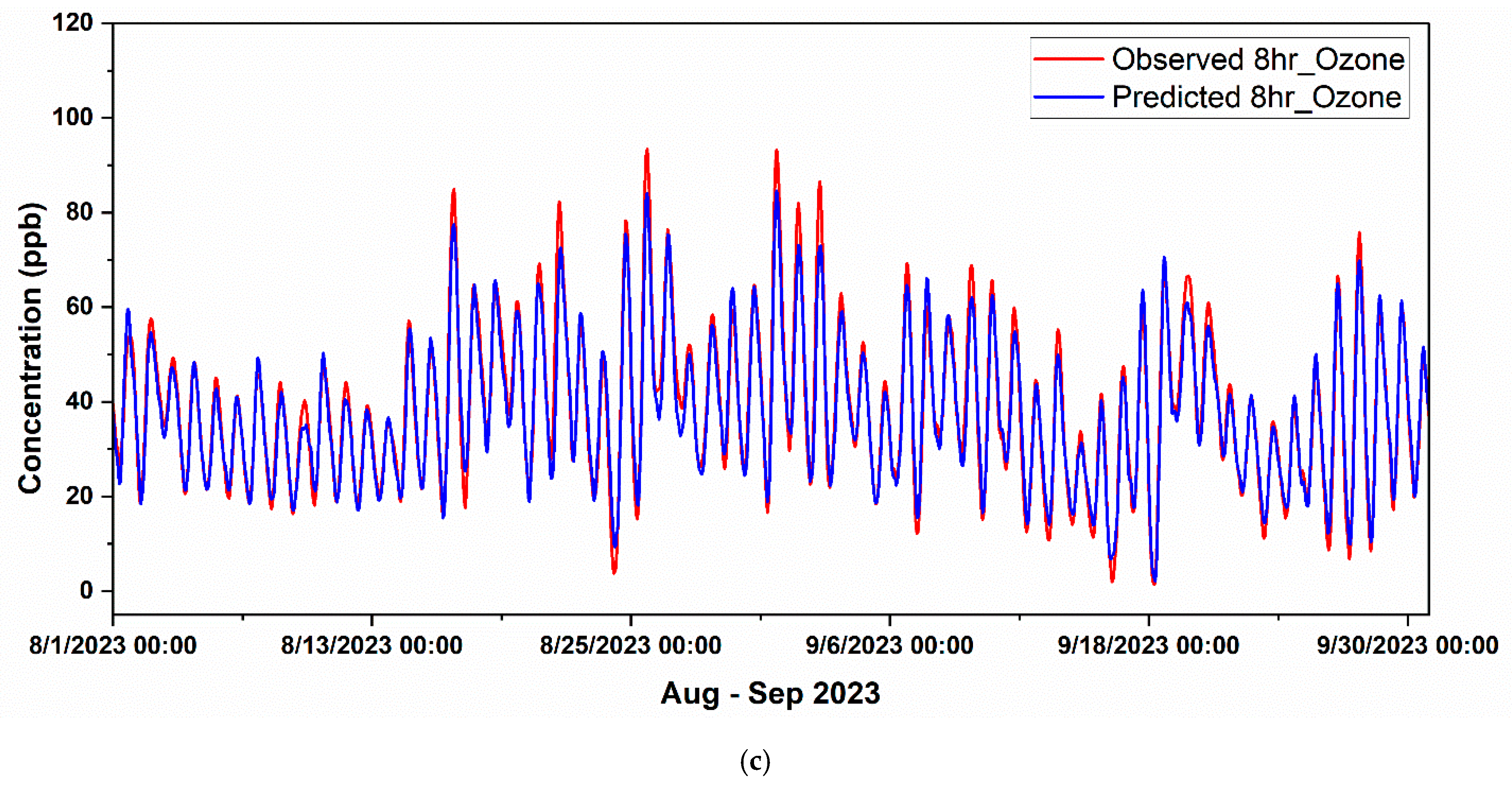
2.3.3. Prediction Using a Hybrid Model
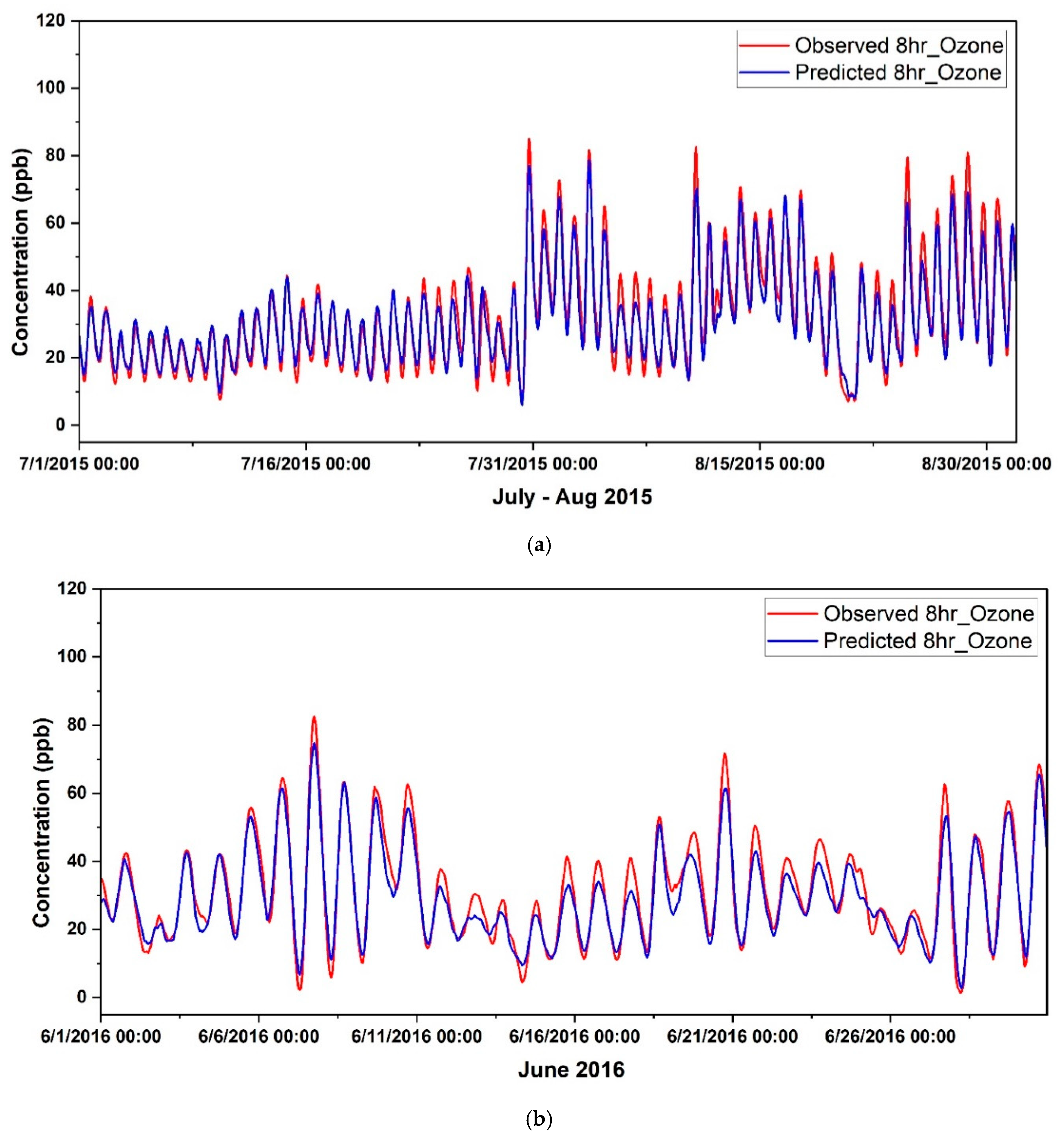
Forecasting Ozone in Fort Worth Northwest
Forecasting High-Ozone Events in Fort Worth Northwest
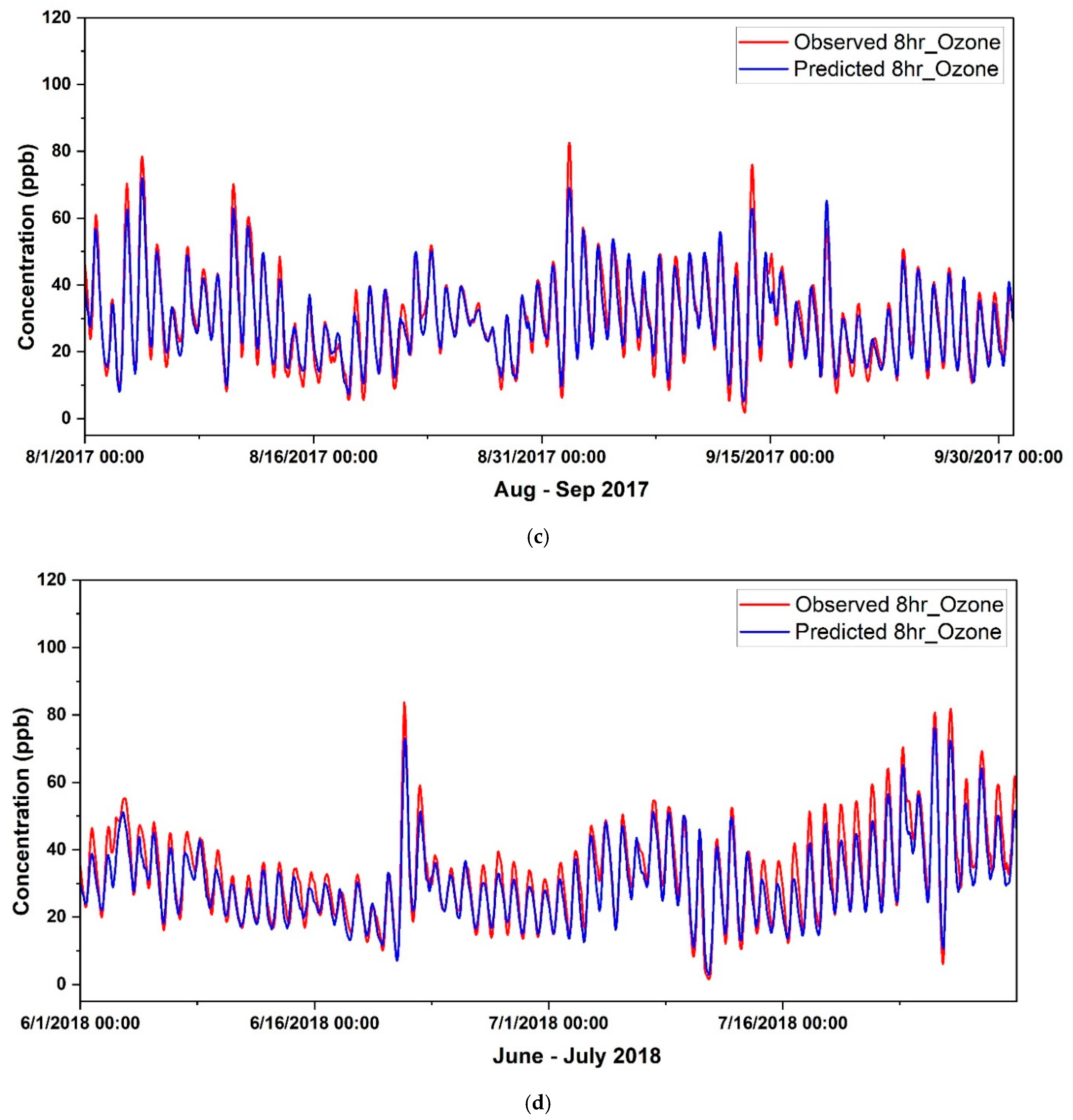
Forecasting Ozone in Dallas Hinton
Forecasting High-Ozone Events in Dallas Hinton
3. Conclusions
- Trained on CAMS 013 data (2014–2020) and tested on 2021–2023 data, the model achieved an R2 of 0.97, accurately identifying high-ozone episodes with stable performance across all years.
- When applied to CAMS 0161 (2015–2019), the model demonstrated strong generalization capability, achieving R2 values of 0.94–0.95. Although slight underprediction biases were observed (MBE: −0.13 to −1.07), the overall agreement with observations remained high (IoA > 0.95).
- The model maintained high predictive accuracy for high-ozone days, with R2 values ranging from 0.96 to 0.98 at CAMS 013 and 0.94 to 0.96 at CAMS 0161, effectively capturing interannual and seasonal ozone dynamics. However, it slightly underpredicted extreme peaks, indicating the potential for further refinement.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, T.M.; Kuschner, W.G.; Gokhale, J.; Shofer, S. Outdoor Air Pollution: Ozone Health Effects. Am. J. Med. Sci. 2007, 333, 244–248. [Google Scholar] [CrossRef]
- WHO. Review of Evidence on Health Aspects of Air Pollution–RE-VIHAAP Project: Technical Report. Tech. Doc. WHO/EURO:2013-4101-43860-61757. 2013. 309p. Available online: https://apps.who.int/iris/bitstream/handle/10665/341712/WHO-EURO-2013-4101-43860-61757-eng.pdf?sequence=1&isAllowed=y (accessed on 3 August 2025).
- Bell, M.L.; Zanobetti, A.; Dominici, F. Who is more affected by ozone pollution? A systematic review and metaanalysis. Am. J. Epidemiol. 2014, 180, 15–28. [Google Scholar] [CrossRef]
- Mills, G.; Pleijel, H.; Malley, C.S.; Sinha, B.; Cooper, O.R.; Schultz, M.G.; Neufeld HSSimpson, D.; Sharps, K.; Feng, Z.; Gerosa, G.; et al. Tropospheric Ozone Assessment Report: Present-day tropospheric ozone distribution and trends relevant to vegetation. Elem. Sci. Anthr. 2018, 6, 47. [Google Scholar] [CrossRef]
- Fleming, Z.L.; Doherty, R.M.; von Schneidemesser, E.; Malley, C.S.; Cooper, O.R.; Pinto, J.P.; Colette, A.; Xu, X.; Simpson, D.; Schultz, M.G.; et al. Tropospheric ozone assessment report: Present-day ozone distribution and trends relevant to human health. Elementa 2018, 6, 12. [Google Scholar] [CrossRef]
- U.S. EPA. Health Effects of Ozone Pollution. 2024. Available online: https://www.epa.gov/ground-level-ozone-pollution/health-effects-ozone-pollution (accessed on 16 August 2025).
- Mills, G.; Sharps, K.; Simpson, D.; Pleijel, H.; Frei, M.; Burkey, K.; Emberson, L.; Uddling, J.; Broberg, M.; Feng, Z.; et al. Closing the global ozone yield gap: Quantification and co benefits for multi stress tolerance. Glob. Change Biol. 2018, 24, 4869–4893. [Google Scholar] [CrossRef]
- Käffer, M.I.; Domingos, M.; Lieske, I.; Vargas, V.M. Predicting ozone levels from climatic parameters and leaf traits of Bel-W3 tobacco variety. Environ. Pollut. 2019, 248, 471–477. [Google Scholar] [CrossRef]
- Brulfert, G.; Galvez, O.; Yang, F.; Sloan, J. A regional modelling study of the high ozone episode of June 2001 in southern Ontario. Atmos. Environ. 2007, 41, 3777–3788. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Kumar, A.; Ying, Q.; Vandenberghe, F.; Kleeman, M.J. Separately resolving NOx and VOC contributions to ozone formation. Atmos. Environ. 2022, 285, 119224. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Lin, C.; Vu, C.T.; Cheruiyot, N.K.; Nguyen, M.K.; Le, T.H.; Lukkhasorn, W.; Vo, T.D.H.; Bui, X.T. Tropospheric ozone and NOx: A review of worldwide variation and meteorological influences. Environ. Technol. Innov. 2022, 28, 102809. [Google Scholar] [CrossRef]
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long short-term memory neural network for air pollutant concentration predictions: Method development and evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef]
- Wen, C.; Liu, S.; Yao, X.; Peng, L.; Li, X.; Hu, Y.; Chi, T. A novel spatiotemporal convolutional long short-term neural network for air pollution prediction. Sci. Total Environ. 2019, 654, 1091–1099. [Google Scholar] [CrossRef]
- Wang, M.; Sampson, P.D.; Hu, J.; Kleeman, M.; Keller, J.P.; Olives, C.; Szpiro, A.A.; Vedal, S.; Kaufman, J.D. Combining Land-Use Regression and Chemical Transport Modeling in a Spatiotemporal Geostatistical Model for Ozone and PM2.5. Environ. Sci. Technol. 2016, 50, 5111–5118. [Google Scholar] [CrossRef]
- Sharma, S.; Chatani, S.; Mahtta, R.; Goel, A.; Kumar, A. Sensitivity analysis of ground level ozone in India using WRF-CMAQ models. Atmos. Environ. 2016, 131, 29–40. [Google Scholar] [CrossRef]
- Matthias, V.; Arndt, J.A.; Aulinger, A.; Bieser, J.; Gon, H.D.V.; Kranenburg, R.; Kuenen, J.; Neumann, D.; Pouliot, G.; Quante, M. Modeling emissions for three-dimensional atmospheric chemistry transport models. J. Air Waste Manag. Assoc. 2018, 68, 763–800. [Google Scholar] [CrossRef]
- Vander Hoorn, S.; Johnson, J.S.; Murray, K.; Smit, R.; Heyworth, J.; Lam, S.; Cope, M. Emulation of a Chemical Transport Model to Assess Air Quality under Future Emission Scenarios for the Southwest of Western Australia. Atmosphere 2022, 13, 2009. [Google Scholar] [CrossRef]
- Manders, A.M.M.; van Meijgaard, E.; Mues, A.C.; Kranenburg, R.; van Ulft, L.H.; Schaap, M. The impact of differences in large-scale circulation output from climate models on the regional modeling of ozone and PM. Atmos. Chem. Phys. 2012, 12, 9441–9458. [Google Scholar] [CrossRef]
- Ahmadi, M.; Huang, Y.; John, K. Application of Spatio-Temporal Clustering For Predicting Ground-Level Ozone Pollution. In Advances in Geocomputation. Advances in Geographic Information Science; Griffith, D., Chun, Y., Dean, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Brunner, D.; Savage, N.; Jorba, O.; Eder, B.; Giordano, L.; Badia, A.; Balzarini, A.; Baró, R.; Bianconi, R.; Chemel, C.; et al. Comparative analysis of meteorological performance of coupled chemistry-meteorology models in the context of AQMEII phase 2. Atmos. Environ. 2015, 115, 470–498. [Google Scholar] [CrossRef]
- Otero, N.; Sillmann, J.; Mar, K.A.; Rust, H.W.; Solberg, S.; Andersson, C.; Engardt, M.; Bergström, R.; Bessagnet, B.; Colette, A.; et al. A multi-model comparison of meteorological drivers of surface ozone over Europe, Atmos. Chem. Phys. 2018, 18, 12269–12288. [Google Scholar] [CrossRef]
- Sillman, S. The use of NOy, H2O2, and HNO3 as indicators for ozone-NOx-hydrocarbon sensitivity in urban locations. J. Geophys. Res.-Atmos. 1995, 100, 14175–14188. [Google Scholar] [CrossRef]
- Wild, O.; Prather, M. Global tropospheric ozone modeling: Quantifying errors due to grid resolution. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Stock, Z.S.; Russo, M.R.; Pyle, J.A. Representing ozone extremes in European megacities: The importance of resolution in a global chemistry climate model. Atmos. Chem. Phys. 2014, 14, 3899–3912. [Google Scholar] [CrossRef]
- Wang, S.W.; Levy, H.; Li, G.; Rabitz, H. Fully equivalent operational models for atmospheric chemical kinetics within global chemistry-transport models. J. Geophys. Res. 1999, 104, 30417–30426. [Google Scholar] [CrossRef]
- Baklanov, A.; Schlünzen, K.; Suppan, P.; Baldasano, J.; Brunner, D.; Aksoyoglu, S.; Carmichael, G.; Douros, J.; Flemming, J.; Forkel, R.; et al. Online coupled regional meteorology chemistry models in Europe: Current status and prospects. Atmos. Chem. Phys. 2014, 14, 317–398. [Google Scholar] [CrossRef]
- Gradisar, D.; Grasic, B.; Boznar, M.Z.; Mlakar, P.; Kocijan, J. Improving of local ozone forecasting by integrated models. Environ. Sci. Pollut. Control Ser. 2016, 23, 18439–18450. [Google Scholar] [CrossRef]
- Elkamel, A.; Abdul-Wahab, S.; Bouhamra, W.; Alper, E. Measurement and prediction of ozone levels around a heavily industrialized area: A neural network approach. Adv. Environ. Res. 2001, 5, 47–59. [Google Scholar] [CrossRef]
- Aljanabi, M.; Shkoukani, M.; Hijjawi, M. Ground-level Ozone Prediction Using Machine Learning Techniques: A Case Study in Amman, Jordan. Int. J. Autom. Comput. 2020, 17, 667–677. [Google Scholar] [CrossRef]
- Jumin, E.; Zaini, N.; Ahmed, A.N.; Abdullah, S.; Ismail, M.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Machine learning versus linear regression modelling approach for accurate ozone concentrations prediction. Eng. Appl. Comput. Fluid Mech. 2020, 14, 713–725. [Google Scholar] [CrossRef]
- Aha, D.W.; Kibler, D.; Albert, M.K. Instance-based learning algorithms. Mach. Learn. 1991, 6, 37–66. [Google Scholar] [CrossRef]
- Altman, N.S. An Introduction to Kernel and Nearest-Neighbor Nonparametric Regression. Am. Stat. 1992, 46, 175–185. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Awang, N.R.; Ramli, N.A.; Yahaya, A.S.; Elbayoumi, M. Multivariate methods to predict ground level ozone during daytime, nighttime, and critical conversion time in urban areas. Atmos. Pollut. Res. 2015, 6, 726–734. [Google Scholar] [CrossRef]
- Sinharay, S. An Overview of Statistics in Education. In International Encyclopedia of Education, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 1–11. ISBN 9780080448947. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Statist. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Srinivas, A.S.; Somula, R.; Govinda, K.; Manivannan, S.S. Predicting ozone layer concentration using machine learning techniques. In Social Network Forensics. Cyber Security, and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2019; pp. 83–92. [Google Scholar] [CrossRef]
- Feng, R.; Zheng, H.J.; Zhang, A.R.; Huang, C.; Gao, H.; Ma, Y.C. Unveiling tropospheric ozone by the traditional atmospheric model and machine learning, and their comparison: A case study in Hangzhou, China. Environ. Pollut. 2019, 252, 366–378. [Google Scholar] [CrossRef]
- Ma, X.; Jia, H.; Sha, T.; An, J.; Tian, R. Spatial and seasonal characteristics of particulate matter and gaseous pollution in China: Implications for control policy. Environ. Pollut. 2019, 248, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Zhang, Q.; Li, J. An Junlin, Hybrid machine learning model for hourly ozone concentrations prediction and exposure risk assessment. Atmos. Pollut. Res. 2023, 14, 101916. [Google Scholar] [CrossRef]
- Mehdipour, V.; Stevenson, D.S.; Memarianfard, M.; Sihag, P. Comparing different methods for statistical modeling of particulate matter in Tehran. Iran. Air Qual. Atmos. Health 2018, 11, 1155–1165. [Google Scholar] [CrossRef]
- He, H.D.; Li, M.; Wang, W.L.; Wang, Z.Y.; Xue, Y. Prediction of PM2.5 concentration based on the similarity in air quality monitoring network. Build. Environ. 2018, 137, 11–17. [Google Scholar] [CrossRef]
- Sumathi, D.; Manivannan, S.S. Machine Learning-Based Algorithm for Channel Selection Utilizing Preemptive Resume Priority in Cognitive Radio Networks Validated by Ns-2. Circuits Syst. Signal Process. 2019, 39, 1038–1058. [Google Scholar] [CrossRef]
- Pan, Q.; Harroul, F.; Sun, Y. A comparison of machine learning methods for ozone pollution prediction. J. Big Data 2023, 10, 63. [Google Scholar] [CrossRef]
- Juarez, E.K.; Petersen, M.R. A Comparison of Machine Learning Methods to Forecast Tropospheric Ozone Levels in Delhi. Atmosphere 2022, 13, 46. [Google Scholar] [CrossRef]
- Lyu, Y.; Ju, Q.; Lv, F.; Feng, J.; Pang, X.; Li, X. Spatiotemporal variations of air pollutants and ozone prediction using machine learning algorithms in the Beijing-Tianjin-Hebei region from 2014 to 2021. Environ. Pollut. 2022, 306, 119420. [Google Scholar] [CrossRef] [PubMed]
- Capilla, C. Prediction of hourly ozone concentrations with multiple regression and multilayer perceptron models. Int. J. Sustain. Dev. Plan. 2016, 11, 558–565. [Google Scholar] [CrossRef]
- Vautard, R.; Moran, M.D.; Solazzo, E.; Gilliam, R.C.; Matthias, V.; Bianconi, R.; Chemel, C.; Ferreira, J.; Geyer, B.; Hansen, A.B.; et al. Evaluation of the meteorological forcing used for the Air Quality Model Evaluation International Initiative (AQMEII) air quality simulations. Atmos. Environ. 2012, 53, 15–37. [Google Scholar] [CrossRef]
- Fiore, A.M.; Naik, V.; Leibensperger, E.M. Air quality and climate connections. J. Air Waste Manag. Assoc. 2015, 65, 645–685. [Google Scholar] [CrossRef]
- Otero, N.; Sillmann, J.; Schnell, J.L.; Rust, H.W.; Butler, T. Synoptic and meteorological drivers of extreme ozone concentrations over Europe. Environ. Res. Lett. 2016, 11, 024005. [Google Scholar] [CrossRef]
- Weng, X.; Forster, G.L.; Nowack, P. A machine learning approach to quantify meteorological drivers of ozone pollution in China from 2015 to 2019. Atmos. Chem. Phys. 2022, 22, 8385–8402. [Google Scholar] [CrossRef]
- Chang, W.; Chen, X.; He, Z.; Zhou, S. A Prediction Hybrid Framework for Air Quality Integrated with W-BiLSTM(PSO)-GRU and XGBoost Methods. Sustainability 2023, 15, 16064. [Google Scholar] [CrossRef]
- Antonio, D.L.; Rosato, A.; Colaiuda, V.; Lombardi, A.; Tomassetti, B.; Panella, M. Multivariate Prediction of PM10 Concentration by LSTM Neural Networks. In Proceedings of the Photonics & Electromagnetics Research Symposium-Fall (PIERS-Fall), Xiamen, China, 17–20 December 2019; pp. 423–431. [Google Scholar] [CrossRef]
- Ko, K.; Cho, S.; Rao, R.R. Machine-Learning-Based Near-Surface Ozone Forecasting Model with Planetary Boundary Layer Information. Sensors 2022, 22, 7864. [Google Scholar] [CrossRef] [PubMed]
- Kanayankottupoyil, J.; John, K. Assessing the impact of oil and gas activities on ambient hydrocarbon concentrations in North Texas: A retrospective analysis from 2000 to 2022. Atmos. Environ. 2025, 340, 120907. [Google Scholar] [CrossRef]
- Kanayankottupoyil, J.; John, K. Characterization and Source Apportionment of Ambient VOC Concentrations: Assessing Ozone Formation Potential in the Barnett Shale Oil and Gas Region. Atmos. Pollut. Res. 2025, 16, 102327. [Google Scholar] [CrossRef]
- Wang, H.W.; Li, X.B.; Wang, D.; Zhao, J.; He, H.D.; Peng, Z.R. Regional prediction of ground-level ozone using a hybrid sequence-to-sequence deep learning approach. J. Clean. Prod. 2020, 253, 119841. [Google Scholar] [CrossRef]
- Shah, I.; Gul, N.; Ali, S.; Houmani, H. Short-Term Hourly Ozone Concentration Forecasting Using Functional Data Approach. Econometrics 2024, 12, 12. [Google Scholar] [CrossRef]
- Álvaro, G.L.; Cortés, G.A.; Álvarez, F.M.; Riquelme, J.C. A novel approach to forecast urban surface-level ozone considering heterogeneous locations and limited information. Environ. Model. Softw. 2018, 110, 52–61. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to forget: Continual prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Nowak, J.; Taspinar, A.; Scherer, R. LSTM Recurrent Neural Networks for Short Text and Sentiment Classification. In Artificial Intelligence and Soft Computing. ICAISC 2017. Lecture Notes in Computer Science; Rutkowski, L., Korytkowski, M., Scherer, R., Tadeusiewicz, R., Zadeh, L., Zurada, J., Eds.; Springer: Cham, Switzerland, 2017; Volume 10246. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Chen, S. LSTM Fully Convolutional Networks for Time Series Classification. IEEE Access 2018, 6, 1662–1669. [Google Scholar] [CrossRef]
- Liu, G.; Guo, J. Bidirectional LSTM with attention mechanism and convolutional layer for text classification. Neurocomputing 2019, 337, 325–338. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.; Woo, W. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. In Proceedings of the 2015 Advances in Neural Information Processing Systems (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; Volume 28, pp. 802–810. Available online: https://api.semanticscholar.org/CorpusID:6352419 (accessed on 2 November 2025).
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-Term Residential Load Forecasting Based on LSTM Recurrent Neural Network. IEEE Trans. Smart Grid 2019, 10, 841–851. [Google Scholar] [CrossRef]
- Yang, B.; Sun, S.; Li, J.; Lin, X.; Tian, Y. Traffic flow prediction using LSTM with feature enhancement. Neurocomputing 2019, 332, 320–327. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar] [CrossRef]
- E, J.; Ye, J.; Jin, H. A novel hybrid model on the prediction of time series and its application for the gold price analysis and forecasting. Phys. A Stat. Mech. Its Appl. 2019, 527, 121454. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean squared error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2009; Available online: https://jqichina.wordpress.com/wp-content/uploads/2012/02/the-elements-of-statistical-learning.pdf (accessed on 23 May 2025).
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: Berlin/Heidelberg, Germany, 2013; Available online: https://www.stat.berkeley.edu/~rabbee/s154/ISLR_First_Printing.pdf (accessed on 25 May 2025).
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” Measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Francis, X.D.; Robert, S.M. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 2002, 20, 134–144. [Google Scholar] [CrossRef]
- Künsch, H.R. The Jackknife and the Bootstrap for General Stationary Observations. Ann. Stat. 1989, 17, 1217–1261. [Google Scholar] [CrossRef]
- Kuerban, M.; Waili, Y.; Fan, F.; Liu, Y.; Qin, W.; Dore, A.J.; Peng, J.; Xu, W.; Zhang, F. Spatio-temporal patterns of air pollution in China from 2015 to 2018 and implications for health risks. Environ. Pollut. 2020, 258, 113659. [Google Scholar] [CrossRef]
- Wang, Y.; Ying, Q.; Hu, J.; Zhang, H. Spatial and temporal variations of six criteria air pollutants in 31 provincial capital cities in China during 2013–2014. Environ. Int. 2014, 73, 413–422. [Google Scholar] [CrossRef]
- Fenn, M.E.; Poth, M.A.; Bytnerowicz, A.; Sickman, J.O.; Takemoto, B.K. Effects of ozone, nitrogen deposition, and other stressors on montane ecosystems in the Sierra Nevada. Dev. Environ. Sci. 2003, 2, 111–155. [Google Scholar] [CrossRef]
- Bodor, Z.; Bodor, K.; Keresztesi, Á.; Szép, R. Major air pollutants seasonal variation analysis and long-range transport of PM10 in an urban environment with specific climate condition in Transylvania (Romania). Environ. Sci. Pollut. Res. 2020, 27, 38181–38199. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process Syst. 2017, 2017, 30. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Luo, X.; Zhao, H. Diagnosis of Parkinson’s disease based on SHAP value feature selection. Biocybern. Biomed. Eng. 2022, 42, 856–869. [Google Scholar] [CrossRef]
- Waspada, I.; Bahtiar, N.; Wirawan, P.W.; Awa, B.D.A. Performance analysis of isolation forest algorithm in fraud detection of credit card transactions. Khazanah Inform. J. 2022, 6. [Google Scholar] [CrossRef]
- Wang, H.; Hancock, J.T.; Khoshgoftaar, T.M. Improving medicare fraud detection through big data size reduction techniques. In Proceedings of the 2023 IEEE International Conference on Service-Oriented System Engineering (SOSE), Athens, Greece, 17–20 July 2023; pp. 208–217. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Rtayli, N.; Enneya, N. Selection features and support vector machine for credit card risk identification. Procedia Manuf. 2020, 46, 941–948. [Google Scholar] [CrossRef]
- González, S.; García, S.; Ser, J.D.; Rokach, L.; Herrera, F. A practical tutorial on bagging and boosting based ensembles for machine learning: Algorithms, software tools, performance study, practical perspectives and opportunities. Inf. Fusion 2020, 64, 205–237. [Google Scholar] [CrossRef]
- Peter, T. The stratospheric ozone layer—An overview. Environ. Pollut. 1994, 83, 69–79. [Google Scholar] [CrossRef]
- U.S. EPA. Clean Air Act. 40CFR50. 1970. Available online: https://www.ecfr.gov/current/title-40/chapter-I/subchapter-C/part-50 (accessed on 10 July 2025).
- Liang, Y.C.; Maimury, Y.; Chen, A.H.L.; Juarez, J.R.C. Machine Learning-Based Prediction of Air Quality. Appl. Sci. 2020, 10, 9151. [Google Scholar] [CrossRef]
- Maleki, H.; Sorooshian, A.; Goudarzi, G.; Baboli, Z.; Birgani, Y.T.; Rahmati, M. Air pollution prediction by using an artificial neural network model. Clean. Technol. Environ. Policy 2019, 21, 1341–1352. [Google Scholar] [CrossRef] [PubMed]
- Iskandaryan, D.; Ramos, F.; Trilles, S. Air Quality Prediction in Smart Cities Using Machine Learning Technologies Based on Sensor Data: A Review. Appl. Sci. 2020, 10, 2401. [Google Scholar] [CrossRef]
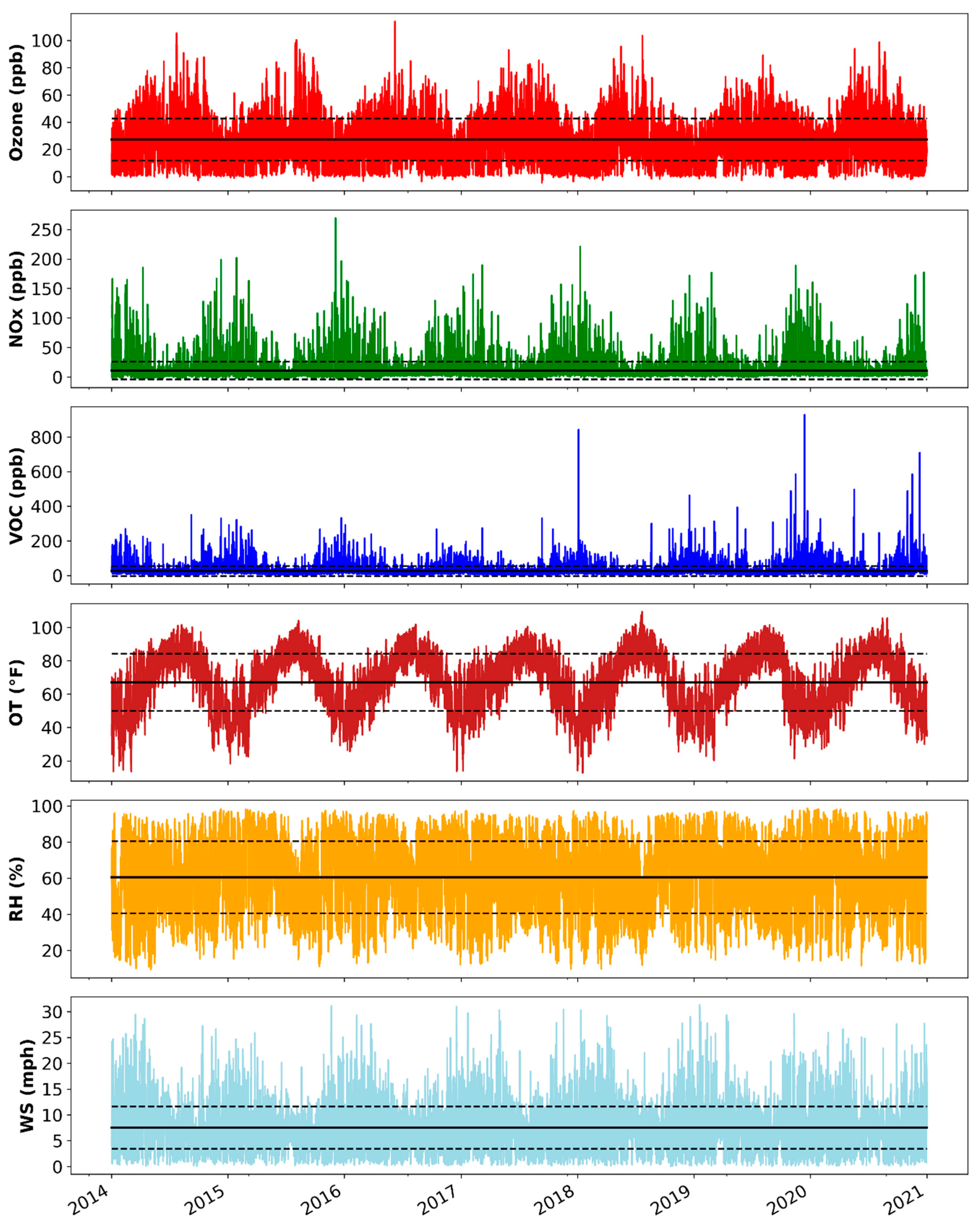
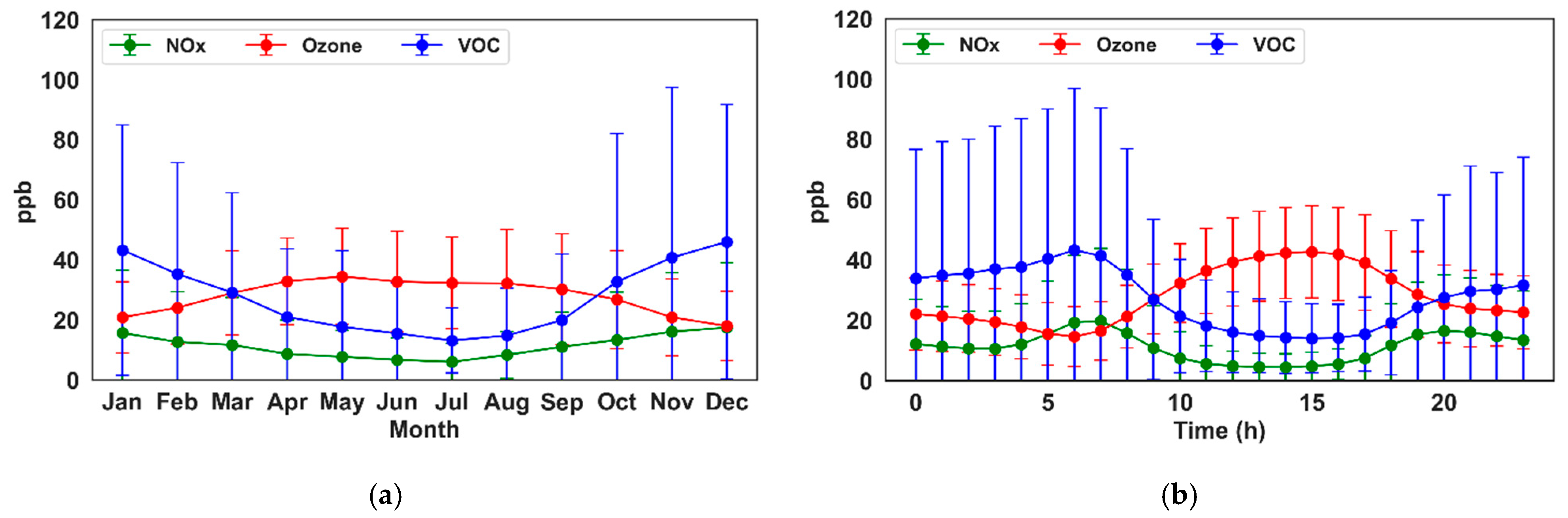
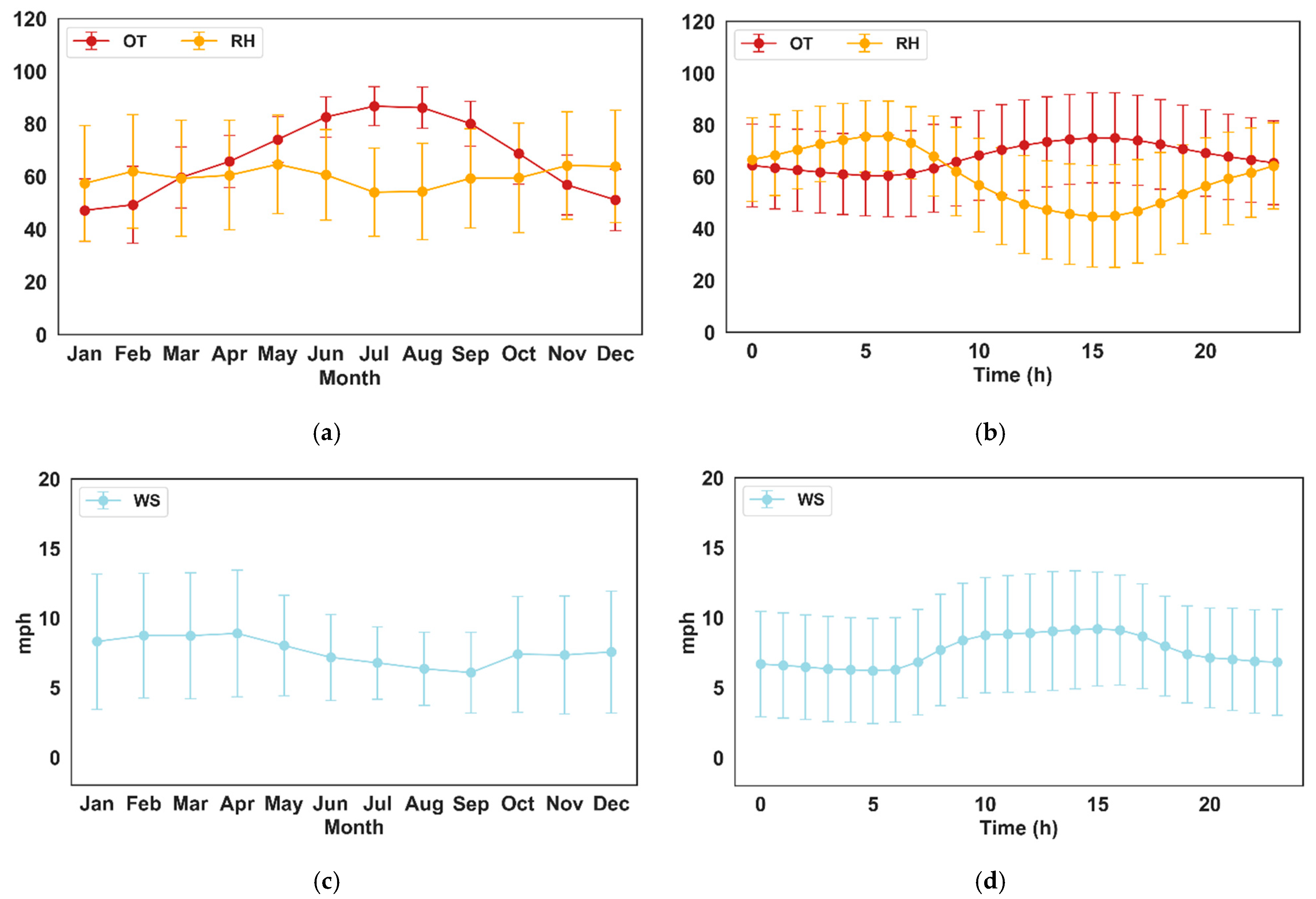
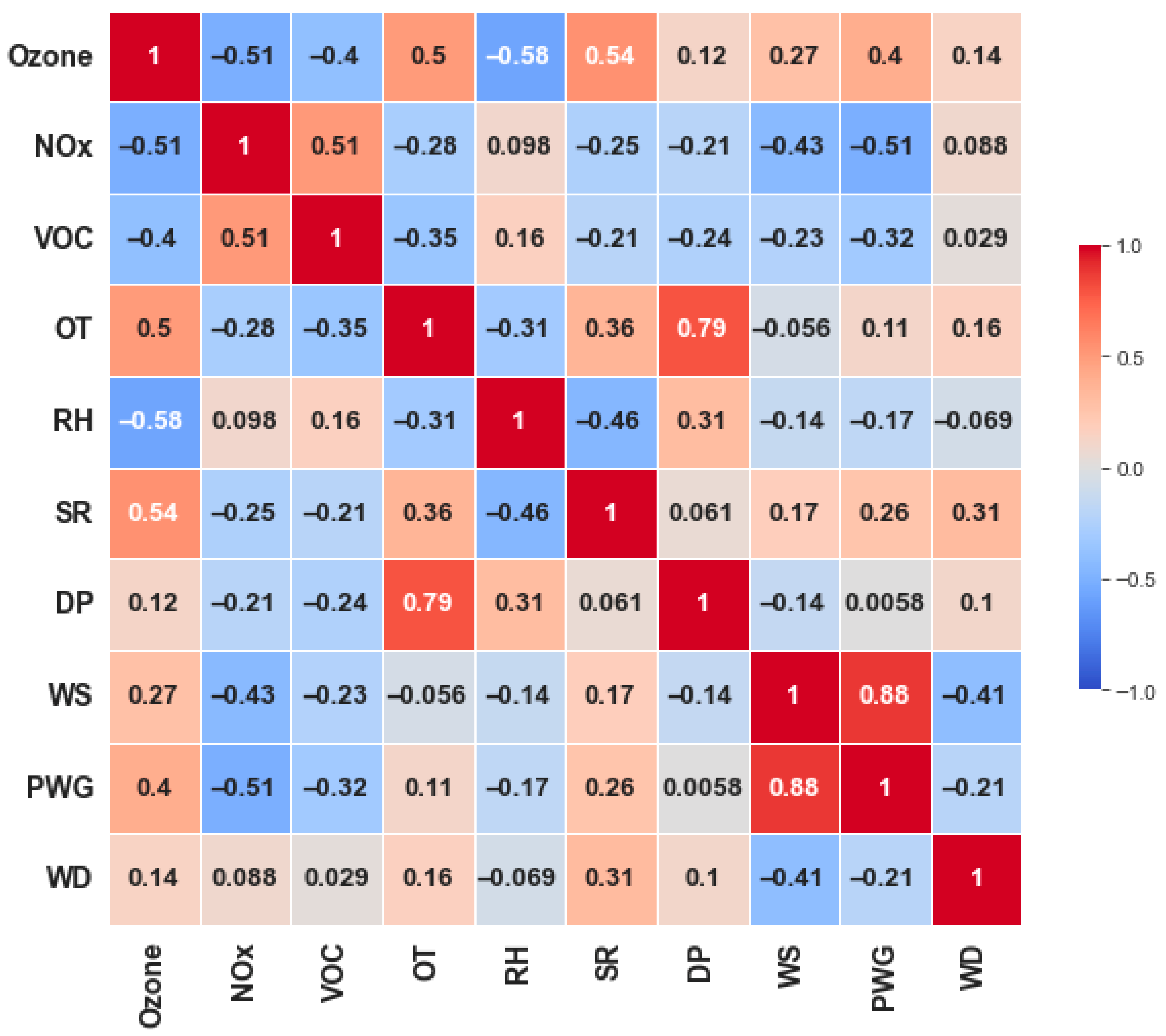
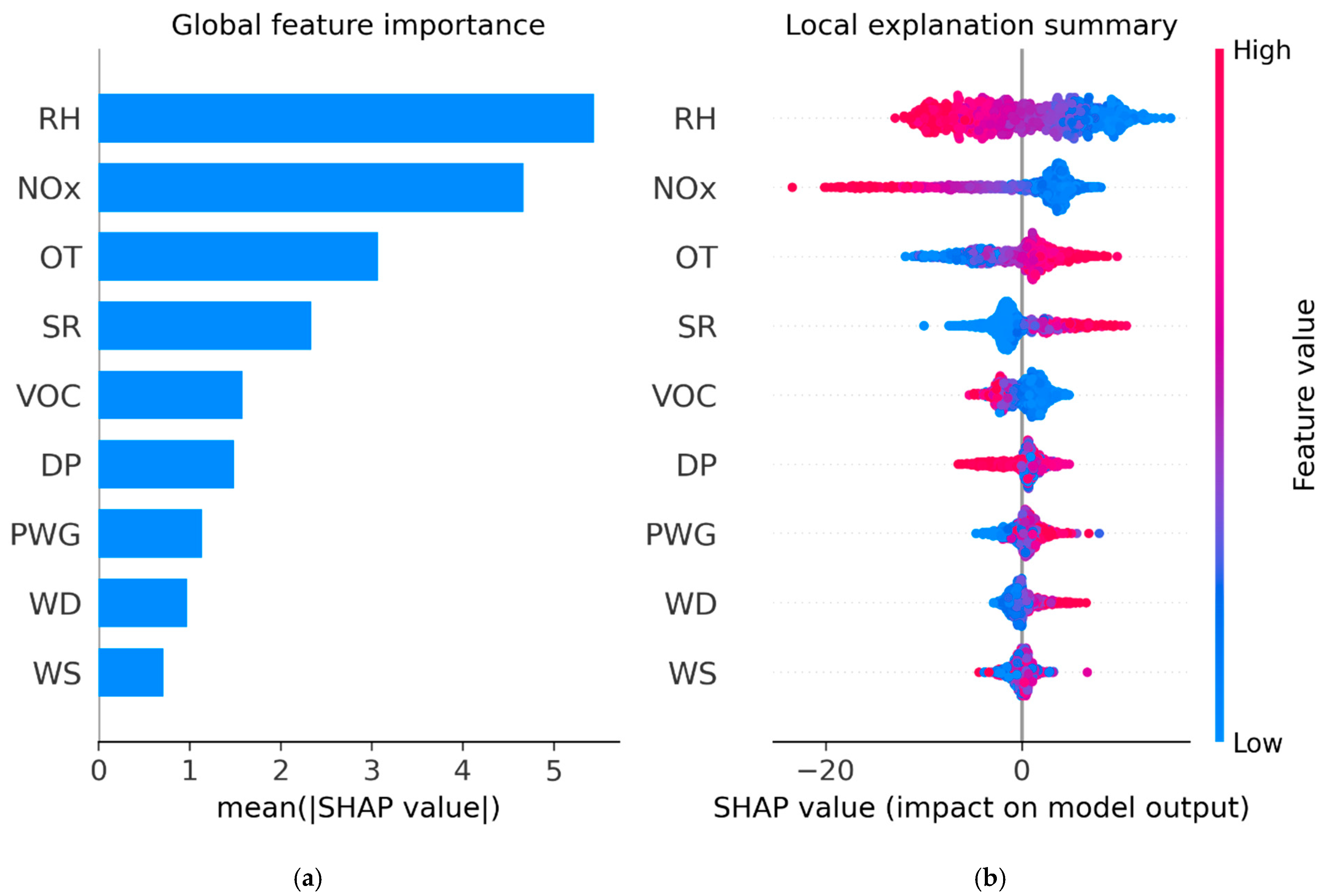

| Pollutants | Mean | Std. Dev. | Median | Min | Max | Skew |
|---|---|---|---|---|---|---|
| Ozone | 27.14 | 15.48 | 25.98 | 0.00 | 113.91 | 0.53 |
| NOx | 10.83 | 15.02 | 6.06 | 0.00 | 269.30 | 4.02 |
| VOC | 25.66 | 28.97 | 16.68 | 2.31 | 928.39 | 5.64 |
| Meteorological Parameters | ||||||
| OT | 67.09 | 17.15 | 69.04 | 12.82 | 109.43 | −0.36 |
| SR | 0.27 | 0.39 | 0.01 | 0.00 | 1.47 | 1.30 |
| DP | 51.13 | 16.25 | 55.52 | −8.11 | 76.89 | −0.66 |
| RH | 60.50 | 19.97 | 61.26 | 9.38 | 98.73 | −0.13 |
| WD | 19.31 | 10.08 | 16.36 | 0.09 | 79.84 | 2.22 |
| WS | 7.52 | 4.09 | 7.00 | 0.06 | 31.31 | 1.05 |
| PWG | 15.22 | 7.19 | 14.60 | 0.30 | 75.47 | 0.69 |
| VOC Species Concentrations | ||||||
| 1,3-Butadiene | 0.04 | 0.04 | 0.03 | 0.00 | 1.00 | 4.52 |
| 1-Butene | 0.07 | 0.06 | 0.06 | 0.00 | 2.97 | 9.43 |
| 1-Pentene | 0.02 | 0.04 | 0.02 | 0.00 | 2.05 | 16.84 |
| 2,2-Dimethylbutane | 0.03 | 0.03 | 0.02 | 0.00 | 1.28 | 8.57 |
| Acetylene | 0.42 | 0.46 | 0.31 | 0.00 | 24.40 | 10.04 |
| Benzene | 0.14 | 0.12 | 0.11 | 0.00 | 2.53 | 3.44 |
| Cyclohexane | 0.07 | 0.07 | 0.05 | 0.00 | 2.07 | 3.90 |
| Cyclopentane | 0.06 | 0.06 | 0.04 | 0.00 | 2.53 | 7.36 |
| Ethane | 12.67 | 18.77 | 7.30 | 0.74 | 803.45 | 9.66 |
| Ethylene | 0.74 | 0.85 | 0.48 | 0.00 | 15.94 | 4.11 |
| Isobutane | 0.90 | 0.93 | 0.62 | 0.00 | 27.33 | 4.33 |
| Isopentane | 1.12 | 1.36 | 0.75 | 0.00 | 63.21 | 10.31 |
| Isoprene | 0.07 | 0.11 | 0.03 | 0.00 | 2.38 | 4.05 |
| m/p Xylene | 0.11 | 0.15 | 0.07 | 0.00 | 5.37 | 6.70 |
| n-Butane | 2.41 | 3.07 | 1.53 | 0.02 | 133.36 | 9.01 |
| n-Decane | 0.02 | 0.02 | 0.01 | 0.00 | 1.01 | 6.90 |
| n-Heptane | 0.09 | 0.09 | 0.06 | 0.00 | 6.07 | 8.29 |
| n-Hexane | 0.25 | 0.25 | 0.18 | 0.00 | 6.98 | 4.45 |
| n-Nonane | 0.02 | 0.02 | 0.02 | 0.00 | 1.30 | 12.17 |
| n-Octane | 0.03 | 0.04 | 0.02 | 0.00 | 3.50 | 19.75 |
| n-Pentane | 0.76 | 0.76 | 0.53 | 0.04 | 29.82 | 5.44 |
| Propane | 4.89 | 5.25 | 3.15 | 0.13 | 84.53 | 3.36 |
| Propylene | 0.28 | 0.26 | 0.20 | 0.00 | 9.31 | 4.35 |
| Toluene | 0.35 | 0.55 | 0.22 | 0.00 | 68.36 | 39.77 |
| trans-2-Butene | 0.04 | 0.07 | 0.03 | 0.00 | 4.67 | 24.34 |
| trans-2-Pentene | 0.04 | 0.09 | 0.02 | 0.00 | 4.97 | 18.01 |
| Component | Value |
|---|---|
| Optimizer | Adam (β1 = 0.9, β2 = 0.999, ε = 10−7) |
| Learning rate | 0.002 |
| Loss | MSE |
| Reported metrics | RMSE, MAE, R2 |
| Batch size | 64 |
| Max epochs | 100 |
| Early Stopping | monitor = val_loss; patience = 10; restore_best_weights = True |
| Shuffle | True (each epoch) |
| Initialization | Glorot uniform (default) |
| Feature scaling | Min–Max [0, 1] (features and target) |
| PCA | Seven components on scaled features |
| Year | MSE | RMSE | MAE | MBE | IoA |
|---|---|---|---|---|---|
| 2021 | 24.81 | 4.98 | 3.60 | −0.48 | 0.97 |
| 2022 | 29.23 | 5.40 | 3.88 | −0.37 | 0.97 |
| 2023 | 32.93 | 5.78 | 4.18 | −0.59 | 0.96 |
| Year | MSE | RMSE | MAE | MBE | IoA |
|---|---|---|---|---|---|
| 2015 | 30.37 | 5.51 | 4.09 | −0.43 | 0.97 |
| 2016 | 32.44 | 5.69 | 4.20 | −0.65 | 0.96 |
| 2017 | 31.20 | 5.58 | 4.14 | −0.13 | 0.96 |
| 2018 | 31.56 | 5.62 | 4.20 | −0.91 | 0.96 |
| 2019 | 33.59 | 5.80 | 4.30 | −1.07 | 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanayankottupoyil, J.; Mohammed, A.A.; John, K. Hybrid Deep Learning Framework for Forecasting Ground-Level Ozone in a North Texas Urban Region. Appl. Sci. 2025, 15, 11923. https://doi.org/10.3390/app152211923
Kanayankottupoyil J, Mohammed AA, John K. Hybrid Deep Learning Framework for Forecasting Ground-Level Ozone in a North Texas Urban Region. Applied Sciences. 2025; 15(22):11923. https://doi.org/10.3390/app152211923
Chicago/Turabian StyleKanayankottupoyil, Jithin, Abdul Azeem Mohammed, and Kuruvilla John. 2025. "Hybrid Deep Learning Framework for Forecasting Ground-Level Ozone in a North Texas Urban Region" Applied Sciences 15, no. 22: 11923. https://doi.org/10.3390/app152211923
APA StyleKanayankottupoyil, J., Mohammed, A. A., & John, K. (2025). Hybrid Deep Learning Framework for Forecasting Ground-Level Ozone in a North Texas Urban Region. Applied Sciences, 15(22), 11923. https://doi.org/10.3390/app152211923






