MiS-PoW: Mirror-Selected Non-Interactive Proof of Ownership for Cloud Storage

Abstract

Cloud storage uses proofs of ownership to avoid redundant uploads while keeping file contents secret. Many existing schemes need extra round trips, or rely on predictable sampling. These choices reduce security when an adversary knows part of the file. We present MiS-PoW, a zero knowledge and non-interactive proof of ownership. The protocol derives a synchronized challenge seed from the existing HTTPS/TLS session. The seed binds a discretized time window and the file identifier. Both parties compute the same challenges locally, and the protocol adds no new messages. MiS-PoW samples blocks with a stratified policy without duplicates. The policy enforces coverage across partitions and reduces the advantage of contiguous knowledge and near duplicate files. The proof layer uses STARKs with simple AIR constraints. The constraints check that indices come from the seed, lie in range, are unique, and meet per partition counts. We analyze security and show seed unpredictability, resistance to replay, and bounds under partial knowledge with limited grinding. A prototype shows that verification time does not grow with file size, and proof and bandwidth costs remain modest. MiS-PoW is deployable, privacy preserving, and scalable for cloud storage.

1. Introduction

Background. Cloud storage is now a core service for individuals and enterprises [1]. Major providers such as Amazon S3 [2], Google Drive [3], and Dropbox [4] popularize pay as you go models that lower the barrier to large scale data management. As global data volumes grow [5], providers must optimize capacity, bandwidth, and operational efficiency. Content based deduplication is a key technique [6]. The system detects redundant chunks and reduces disk usage, network traffic, and backup time. The result is lower cost and better responsiveness.

At the client side, deduplication can prevent redundant uploads by comparing content derived tags before transmission [7]. This idea is effective but it is risky in a naive form [8]. Tags may leak through eavesdropping, breaches, or disclosure. An attacker can then pretend to own a file and try to retrieve it [9,10]. Tag leakage can also enable unauthorized distribution since a public tag can act like a download token. Privacy and data protection rules add more pressure to avoid exposing file contents [11]. A user therefore needs a cryptographic method to prove ownership without revealing the file.

Limitations of existing PoW. Proof of ownership protocols strengthen tag based deduplication by asking the client to answer content dependent challenges [8,12,13]. Many designs still scale poorly. The verifier often recomputes hash chains, Merkle paths, or block functions across large inputs. The cost then grows with file size n. Under many clients and mixed object sizes, this behavior creates head of line blocking, higher tail latency, and weak isolation.

Challenge generation is another issue. Interactive schemes use server chosen seeds or multi-round exchanges. These choices allow seed grinding and timing-based bias. Single shot uniform sampling can also be weak when the attacker knows contiguous segments. Near duplicate files are common in practice. In those cases, the true success probability is higher than models with independent unknown blocks suggest. Some schemes also require the server to access plaintext blocks when deriving or validating challenges. That behavior harms privacy and can violate policy [11].

Deployability is a third hurdle. Several schemes add extra network messages to agree on fresh randomness. Others depend on trusted setup, special hardware, or custom key distribution. These requirements do not fit common cloud front ends such as TLS termination, CDNs, and microservices. They also slow down rollout and auditing.

Motivation for a new protocol. Real deployments already establish an HTTPS/TLS session. The client and the server share an ephemeral secret as a result. A standard exporter lets both parties derive the same session bound material without any new messages. Operators also prefer challenge selection that is deterministic yet unpredictable. Both ends should be able to recompute the same challenges. The design should keep freshness and prevent replay.

These observations motivate MiS-PoW, which stands for mirror-selected non-interactive proof of ownership. Both parties derive a shared challenge seed from a TLS exporter, a discretized timestamp, and a file identifier. The seed drives a stratified and duplicate-free block sampler that enforces partition coverage. The sampler lowers the success probability for attackers who control long contiguous regions or near duplicate content. The proof layer uses zero knowledge STARKs with lightweight arithmetic constraints. The constraints check index ranges, per partition counts, and uniqueness. The verifier work does not depend on file size. The cost is on the order of $O(\lambda logc)$ for security parameter $\lambda$ and challenge count c. The protocol aligns with standard TLS stacks and common privacy requirements.

Contributions.

• Session bound and non-interactive challenges. We introduce MiS-PoW, which mirrors challenges on the client and the server. The protocol derives a common seed from the TLS exporter, a discretized time value, and a file identifier. The design removes extra round trips, prevents replay, and limits seed manipulation. The approach requires no change to the TLS trust model.
• Stratified sampling with zero knowledge enforcement. We design a stratified and duplicate-free selector that enforces coverage across partitions. The selector resists contiguous knowledge and near duplicate attacks. We provide clear bounds on success probability under partial knowledge and limited grinding. We realize the selector inside a STARK with simple constraints for range, count, and uniqueness.
• Privacy and scalability in practice. We build an implementation that fits existing TLS endpoints and standard ZK libraries. The verifier cost is independent of file size, and proof sizes remain modest. We also offer an analysis method and an evaluation plan that match large-scale cloud settings.

2. Related Work

Evolution of Proof of Ownership. Proof of ownership strengthens client side deduplication. Early schemes required content-dependent responses so that only a holder of the entire file could succeed. Halevi et al. [8] proposed a Merkle tree approach in which the prover sends sibling paths for challenged leaves. The idea is simple, yet the method needs heavy preprocessing and large path transfers. Later work reduced interaction by using single-round challenges, hash chains, or seed-derived challenges [12]. These designs still tie verifier cost to file size. Pietro et al. [14,15] and Xu et al. [16] used precomputation and new hash designs to cut on line work. You et al. [17] used Intel SGX to harden the verifier. Variants that keep Merkle proofs [18,19] remain communication heavy because path length grows with the tree height. Blasco et al. [20] introduced Bloom filter tokens, and Xiong et al. [21] extended the idea to multi server settings. False positives in those tokens weaken soundness. González-Manzano et al. [22,23] improved privacy with stronger cryptography at the cost of efficiency. In summary, many classical designs make the verifier work grow with the file, require many blocks or paths in transit, offer limited privacy, and do not fit large concurrent deployments well.

Zero Knowledge Proofs for Ownership. Zero knowledge techniques enable privacy preserving verification [24]. zk SNARKs give very small proofs and fast verification but they need trusted setup and often do not offer clear post quantum guarantees. zk STARKs [25,26] are transparent and plausibly post quantum. Their cost scales quasilogarithmically with computation, and FRI gives the core probabilistic checks [27]. Applying zero knowledge to file ownership creates special challenges. A designer must enforce sampling and coverage over very large files. A proof must stay small and the verifier must remain fast. The method must also remain secure when the adversary knows part of the file or a long contiguous segment. Practical systems also need minimal interaction and easily fit with production front ends.

2.1. Problem Statement and Motivation

Problem statement. We study client side deduplication. A user proves ownership of a file F that the provider already stores. The user does not reveal F. The verifier cost should not depend on $\left|F\right|$. The protocol should be single shot, so the client answers once after the HTTPS request. Both sides should derive deterministic and unpredictable challenges locally. The server should not access plaintext blocks. The design must work in multi-tenant and high-concurrency settings.

Limits in prior art. Many schemes rely on server chosen randomness or multi-round exchanges. These choices enable seed grinding and create replay risks across sessions and time windows. They can also break under clock skew and they add extra round trips that raise tail latency. Independent uniform block sampling ignores practice where an adversary often knows contiguous regions, as in near-duplicate versions or partial leaks. Such knowledge raises the true success probability. Zero knowledge-based proposals reduce data exposure, but some keep index legality outside the proof or force the verifier to touch many blocks. Both choices hurt scalability.

Motivation and approach. Real systems already run HTTPS and TLS. Both endpoints can call a standard exporter and derive the same per session material without new messages. If we bind this material to a discretized timestamp and to the file identifier, we obtain a mirror seed $\sigma$. Both parties can then compute the same challenge indices on their own. We therefore adopt a stratified and duplicate free sampler. The sampler enforces coverage across partitions and targets attackers who know contiguous regions. We encode index legality inside a lightweight zk STARK AIR. The constraints check that indices come from the seed, lie in range, are unique, and meet per partition counts. The resulting scheme, which we call MiS-PoW, is non-interactive and privacy preserving. The verifier cost depends on the security parameter and on the number of challenges c, not on $\left|F\right|$.

2.2. Threat Model

Parties and setting. A user $\mathcal{U}$ and a storage provider $\mathcal{S}$ run client-side deduplication. If a file F already exists, $\mathcal{S}$ keeps a canonical copy. By “canonical copy” we mean the exact byte sequence first stored by the server and bound to ${\mathsf{root}}_F$; it is the pre-deduplication, pre-transcoding version used for ownership proofs. Communication uses HTTPS over TLS 1.3 with a full handshake (0-RTT disabled). Both endpoints call the RFC-compliant exporter after the handshake. For session resumption (PSK + ECDHE), we rebind conn to the fresh handshake transcript, so each resumed session yields a fresh exporter secret (one session ⇒ one seed). The same logic applies when TLS 1.2 with RFC 5705 exporter is used; our default assumption in evaluation is TLS 1.3. We model the file as $F\in {\{0,1\}}^{\left|F\right|}$, i.e., the raw file bytes. Let B be the block size and let $n=\lceil \left|F\right|/B\rceil$ be the number of blocks; thus, n is an integer that counts blocks. On the first upload of F, $\mathcal{S}$ stores for each block i a conventional hash ${\mathsf{sha}}_i=H\left(B_i\right)$ for operations and a ZK friendly hash ${\mathsf{pos}}_i=\mathrm{Poseidon}\left(B_i\right)$ for proofs.

Seed and sampler. Let $\mathsf{fid}=H\left(F\right)$ be the file identifier. We instantiate H as SHA-256 with a 256-bit output, and set $\mathsf{fid}=H\left(F\right)$. Both parties derive a mirror seed

$$T=⌊\mathrm{unix}\_\mathrm{time}/\Delta ⌋,\mathsf{fid}=H\left(F\right).$$

(1)

Here $\mathrm{unix}\_\mathrm{time}$ denotes the UNIX time in seconds since 1970-01-01 00:00:00 UTC, measured at request receipt.

$$\sigma \leftarrow HKDF-Expand\left(Exporter(\mathtt{mispow}\_\mathtt{v}\mathtt{1}),\mathrm{info}=H\left(\mathsf{fid}\parallel \lfloor T/\Delta \rfloor \parallel \mathsf{conn}\parallel \mathsf{csalt}\right),L=32\right).$$

(2)

We follow RFC 5869 and use HKDF-Expand$(\mathsf{prk},\mathsf{info},L)$; our HKDFExpand spelling is equivalent. In our setting, $\mathsf{prk}=\mathrm{Exporter}(\mathtt{mispow}\_\mathtt{v}\mathtt{1})$, $\mathsf{info}=H(\mathsf{fid}\parallel \lfloor T/\Delta \rfloor \parallel \mathsf{conn}\parallel \mathsf{csalt})$, and $L=32$ bytes, where T is the request time, $\Delta$ is the discretization window, and $\mathsf{conn}$ binds the TLS transcript; we set $\mathsf{conn}$ to the TLS 1.3 handshake transcript hash (for TLS 1.2, the session hash over all handshake messages). The optional $\mathsf{csalt}$ is a client-chosen salt sent with the fingerprint request. It does not add a round trip. A PRF with rejection sampling expands $\sigma$ into a set $\mathcal{I}\subseteq \left[n\right]$ of c distinct indices, where $\left[n\right]\triangleq \{1,2,\dots ,n\}$. To resist contiguous knowledge, a public map $P:\left[n\right]\to \left[s\right]$ partitions the file. The system assigns quotas $(q_1,\dots ,q_s)$ with ${\sum }_k{q}_k=c$.

Adversaries. We consider three kinds of adversaries. (1) A malicious client $\mathcal{A}$ tries to forge ownership and knows at most an $\alpha$ fraction of F where $0\le \alpha <1$. The knowledge may be scattered or concentrated on contiguous segments. $\mathcal{A}$ sees public transcripts but not exporter material. $\mathcal{A}$ may perform up to Q seed attempts in one time window by restarting sessions or requests. (2) An honest but curious server follows the protocol and tries to learn more about F than allowed. (3) A network eavesdropper has no access to TLS session keys or exporter outputs.

Security goals.

• Soundness. Under PRF security and hash collision resistance, an adversary that does not know all challenged blocks succeeds with probability

  $$p_{\mathrm{forge}}\le min\left\{1-{(1-p_{\ast })}^Q,Q{p}_{\ast }\right\},$$

  (3)
  Here $p_{\ast }$ is the one shot success of the sampler. For independent knowledge we have

  $$p_{\ast }={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{\alpha n}{c}\right)}{\left(\genfrac{}{}{0pt}{}{n}{c}\right)}}\le {\alpha }^c.$$

  (4)
  For stratified sampling with partition sizes $n_k$ and quotas $q_k$,

  $$p_{\ast }\le \prod _{k=1}^s{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{min\{\alpha m_k,m_k\}}{q_k}\right)}{\left(\genfrac{}{}{0pt}{}{m_k}{q_k}\right)}}\le {\alpha }^{{\sum }_k{q}_k}={\alpha }^c.$$

  (5)
  The bound is smaller when knowledge is contiguous. Choosing c so that $Q{p}_{\ast }\le 2^{-\lambda }$ gives $\lambda$ bit soundness.
• Zero knowledge. The verifier learns nothing about F beyond $(\mathsf{fid},n)$ and the acceptance bit. The STARK proves that indices come from $\sigma$ through the specified PRF and rejection sampling, that indices are within range and pairwise distinct, that quotas hold, and that for each $i\in \mathcal{I}$ the relation $\mathrm{Poseidon}\left(B_i\right)={\mathsf{pos}}_i$ is true without revealing $B_i$.
• Unpredictability and anti replay. The seed $\sigma$ binds the TLS transcript, the discretized time value $\lfloor T/\Delta \rfloor$, and $\mathsf{fid}$ and may include $\mathsf{csalt}$. Challenges are unpredictable before the handshake and are not reusable across connections or time windows.
• Deployability. The verifier work is $\tilde{O}\left(\lambda \right)+O\left(c\right)$ for proof checks and quota and uniqueness checks. The cost does not depend on $\left|F\right|$. The protocol adds no extra messages beyond standard HTTPS.

System assumptions and mitigations.

• Handshake discipline. By default, we assume TLS 1.3. The exporter is invoked only after a full handshake; 0-RTT is disabled. For session resumption (PSK + ECDHE), we rebind $\mathsf{conn}$ to the fresh transcript so that one session yields one seed (fresh exporter secret). In TLS 1.3, KeyUpdate rotates traffic keys only and does not affect the exporter secret; combined with the binding to the discretized window T, this prevents seed grinding within a window and replay across windows.
• Grinding control. The service enforces per user and per file rate limits to bound Q. The optional $\mathsf{csalt}$ adds client entropy and prevents server bias of $\sigma$ without extra interaction.
• Storage for ZK. $\mathcal{S}$ stores $\left\{{\mathsf{pos}}_i\right\}$ or a Poseidon Merkle commitment so the proof can check openings efficiently. Operational dedup can continue to use $\left\{{\mathsf{sha}}_i\right\}$.
• Blockization. The client and the server share the same deterministic block policy such as size B and alignment. A mismatch leads to rejection and does not leak content.

3. Scheme Design

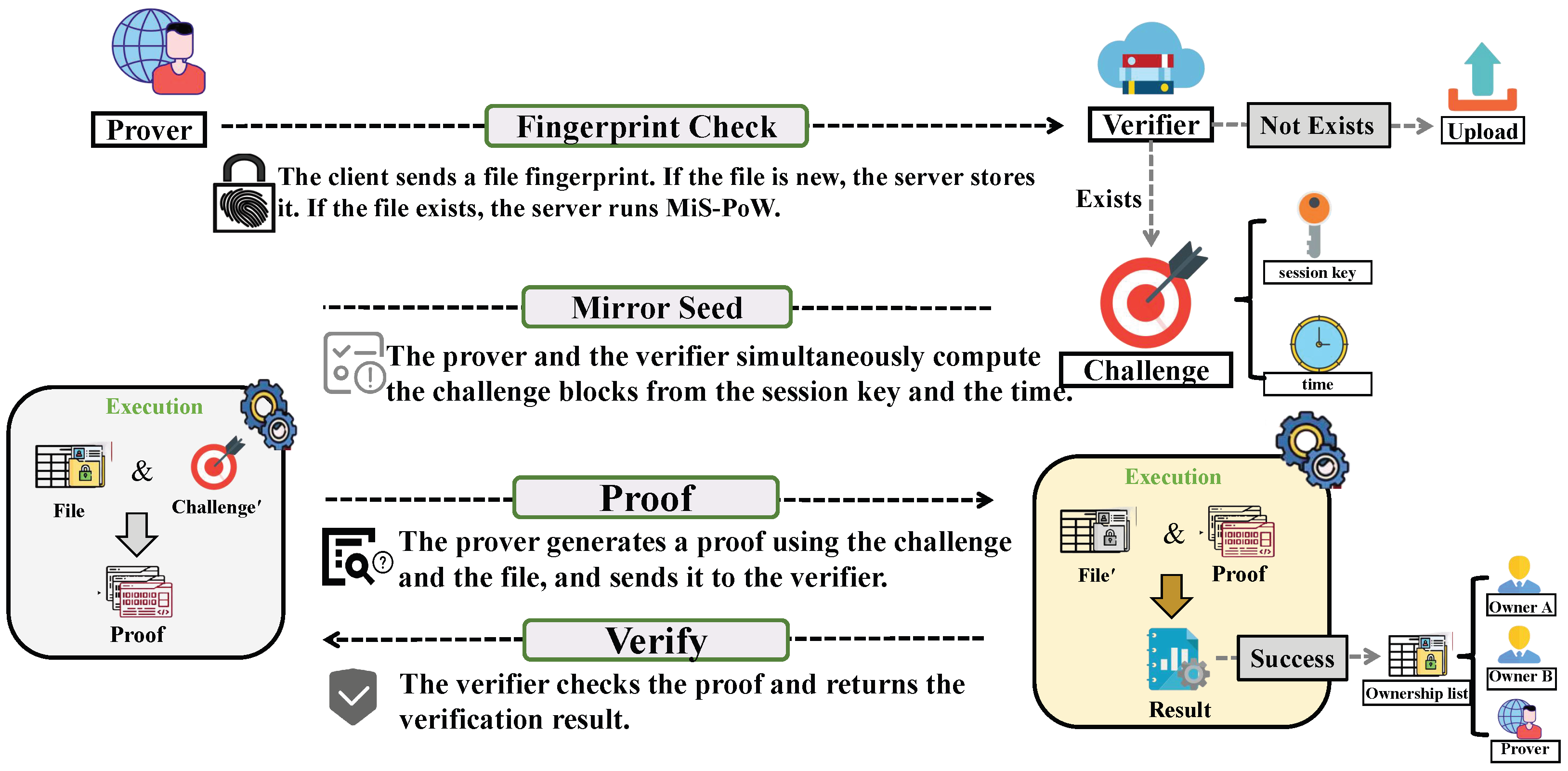
3.1. Workflow of MiS-PoW

MiS-PoW is a single-shot proof-of-ownership (PoW) protocol that (i) derives mirror challenges from an existing HTTPS/TLS session, (ii) proves ownership with a zk-STARK without exposing plaintext blocks, and (iii) keeps verifier work independent of $\left|F\right|$. The workflow has four phases. The symbols used throughout this paper are defined in

Table 1. Symbols and notation.

Symbol	Description
F	User file, $F\in {\{0,1\}}^{*}$
$\mathsf{fid}$	File identifier, $\mathsf{fid}=H\left(F\right)$
B	Block size (default $64\mathrm{KB}$)
n	Number of blocks, $n=\lceil \left|F\right|/B\rceil$
c	Number of challenge blocks
s	Number of partitions; $P:\left[n\right]\to \left[s\right]$ is the partition map
$q_k$	Quota from partition k with ${\sum }_{k=1}^s{q}_k=c$
$\lambda$	Security parameter for soundness
$\alpha$	Attacker knowledge ratio of F
Q	Maximum seed attempts per window
$H(·)$	Standard hash such as SHA256
$\mathrm{Poseidon}(·)$	ZK friendly hash used in proofs
$\mathcal{I}$	Challenge index set with $\left|\mathcal{I}\right|=c$
$\pi$	zk STARK proof
$X,W$	Public input and private witness to the STARK
$K_{\mathrm{sess}}$	Secret material from the TLS exporter
$\sigma$	Mirror seed derived from exporter and context
$T,\Delta$	Request time and discretization window
$\mathsf{conn}$	Connection binding such as transcript hash or session id
$\mathsf{csalt}$	Optional client salt included with the fingerprint request

, and the workflow of our proposed scheme is presented in Figure 1.

(1)

Session-bound seed derivation.

After a full HTTPS/TLS handshake between the user $\mathcal{U}$ and the storage provider $\mathcal{S}$, both endpoints invoke a standards-compliant exporter to obtain identical per-session keying material. We bind challenges to the file identifier and to a discretized time window of length $\Delta$ seconds. Let

$$T=⌊\mathrm{unix}\_\mathrm{time}/\Delta ⌋,\mathsf{fid}=H\left(F\right).$$

(6)

Let $\mathsf{conn}$ denote a connection-binding value (e.g., the TLS handshake transcript hash/session id). Both parties derive a 256-bit mirror seed with domain separation:

$$\sigma =\mathrm{HKDF}-\mathrm{Expand}\left(\mathrm{Exporter}(“\mathtt{mis}-\mathtt{pow}/\mathtt{v}{\mathtt{1}}^{”}),\mathsf{info}=H(\mathsf{fid}\Vert T\Vert \mathsf{conn}\Vert \mathsf{csalt}),L=32\right),$$

(7)

where $\mathsf{csalt}$ is an optional client-chosen salt that is fixed by $\mathcal{U}$ and unpredictable to $\mathcal{S}$ at handshake time, sent alongside the fingerprint within the same HTTPS request (thus adding no extra round) and kept outside the TLS handshake transcript. Because the exporter secret is fixed by the completed handshake while $\mathsf{csalt}$ is set independently by the client, $\mathcal{S}$ cannot bias $\sigma$ via handshake timing, resumption choices, or similar grinding attempts. The verifier accepts T in a small tolerance set (e.g., $\{t-1,t,t+1\}$) to accommodate benign clock skew. No messages beyond standard HTTPS are required. Intuitively, one session ⇒ one seed: challenges are fresh, replay-resistant, and unpredictable to anyone lacking exporter material. In TLS 1.3, KeyUpdate rotates only traffic keys and does not change the exporter secret; therefore, mid-connection updates cannot bias $\sigma$, and binding to the discretized window T still prevents cross-window replay.

(2)

Mirror challenge synthesis.

Let B be the block size and $n=\lceil \left|F\right|/B\rceil$ the number of blocks. Fix a security parameter $\lambda$, a challenge budget c, and a number of strata s for stratified coverage. Using $(\sigma ,n,c,s)$ and public partition metadata (Section 3.2), a deterministic selector produces a duplicate-free index set $\mathcal{I}\subseteq \left[n\right]$ with $\left|\mathcal{I}\right|=c$. Because both endpoints compute $\mathcal{I}$ from the same inputs, challenges are mirror-selected without interaction and are fresh per window $(T,\sigma )$.

(3)

Prover computation (client side).

The client extracts blocks ${\left\{B_i\right\}}_{i\in \mathcal{I}}$ and generates a zk-STARK proof $\pi$ that enforces: (i) indices are derived from $\sigma$ by the specified PRF+rejection-sampling state machine; (ii) range membership and uniqueness of indices; (iii) per-stratum quotas; and (iv) for each $i\in \mathcal{I}$,

$$\mathrm{Poseidon}\left(B_i\right)\stackrel{?}{=}{\mathsf{leaf}}_i,$$

(8)

where ${\mathsf{leaf}}_i$ denotes the i-th leaf of the Poseidon-Merkle tree that commits to F (leaves ordered by block index with ${\mathsf{leaf}}_j=\mathrm{Poseidon}\left(B_j\right)$), and ${\mathsf{root}}_F$ is the tree root stored by $\mathcal{S}$ during the first canonical upload of F. The proof carries Merkle authentication paths in the witness, so plaintext blocks never leave the circuit.

(4)

Verifier computation (server side).

The server recomputes $\sigma$ via (7), reconstructs $\mathcal{I}$ with the same selector, and verifies $\pi$ against public inputs $(\mathsf{fid},T,n,c,s,{\mathsf{root}}_F)$. Verifier time depends on the proof security parameter (FRI queries) and on c, not on n:

$$T_{\mathrm{verify}}=\tilde{O}\left(\lambda \right)+O\left(c\right).$$

(9)

If $\pi$ verifies, $\mathcal{S}$ accepts ownership; otherwise, the request is denied. Because $\sigma$ binds the TLS transcript, time window, and $\mathsf{fid}$ (plus optional $\mathsf{csalt}$), transcripts are not reusable across sessions/windows and challenges are not predictable pre-handshake.

• Public parameters and inputs.

Global: $(\lambda ,B)$ and hash choices $\{H,\mathrm{Poseidon}\}$. Public/session inputs: $(\mathsf{fid},T,n,c,s,{\mathsf{root}}_F)$ and partition descriptors. Witness: challenged blocks, PRF state traces for index generation, and Merkle authentication paths.

3.2. Mirror-Selected Stratified Challenge Design

The selector must be (i) deterministic for both endpoints, (ii) unpredictable to outsiders, (iii) duplicate-free, and (iv) coverage-aware to mitigate contiguous-knowledge adversaries. We specify it mathematically for analysis and zk integration, and then derive a closed-form rule for choosing c that justifies the deployment set $c\in \{128,256,512\}$.

3.2.1. Partitioning and Quotas

Let $\left[n\right]=\{1,\dots ,n\}$. A public partition map $P:\left[n\right]\to \left[s\right]$ splits the file into disjoint strata ${\left\{S_k\right\}}_{k=1}^s$ with sizes $m_k=\left|S_k\right|$ and ${\sum }_k{m}_k=n$ (e.g., equal-length contiguous ranges). Per-stratum quotas are proportional to size:

$${\tilde{q}}_k=c{\displaystyle \frac{m_k}{n}},q_k=\mathrm{Round}\left({\tilde{q}}_k\right),\sum _{k=1}^s{q}_k=c,$$

(10)

Arithmetic proof and rounding rule. Let $q_k^{\left(0\right)}=\lfloor {\tilde{q}}_k\rfloor$ and $r=c-{\sum }_{k=1}^s{q}_k^{\left(0\right)}$; then $0\le r<s$. Order strata by the fractional parts $\{{\tilde{q}}_k-\lfloor {\tilde{q}}_k\rfloor \}$ in descending order and set $q_k=q_k^{\left(0\right)}+1$ for the first r strata, keeping $q_k=q_k^{\left(0\right)}$ for the rest. Then ${\sum }_{k=1}^s{q}_k={\sum }_k{q}_k^{\left(0\right)}+r=c$ and each $q_k\in \{\lfloor {\tilde{q}}_k\rfloor ,\lceil {\tilde{q}}_k\rceil \}$ with $|q_k-{\tilde{q}}_k|<1$. Since we use $c\le n$, it follows that $q_k\le \lceil c{m}_k/n\rceil \le m_k$, so quotas are feasible.

3.2.2. Domain-Separated PRF Streams with De-Biasing

For each stratum k, define a domain-separated PRF stream keyed by the mirror seed $\sigma$ (cf. (7)):

$$R_{k,t}={\mathsf{\Psi }}_{64}\left({\mathrm{HMAC}}_{\mathrm{SHA}256}(\sigma ,\mathtt{“}\mathtt{blk}\mathtt{”}\Vert \mathrm{u}32\left(k\right)\Vert \mathrm{u}32\left(t\right))\right),t=0,1,2,\dots ,$$

(11)

Here $\mathrm{u}32\left(j\right)$ encodes the integer j as a 4-byte unsigned big-endian string (domain-separating the stratum id k and the local counter t), ${\mathsf{\Psi }}_{64}(·)$ returns the first 64 bits, and ${\mathrm{HMAC}}_{\mathrm{SHA}256}(\sigma ,·)$ serves as a PRF keyed by the session seed $\sigma$. Using a 64-bit sample keeps the selector efficient, makes rejection sampling effective for practical $m_k$ (e.g., $m_k\le 2^{32}$), and keeps the STARK trace narrow. To remove modulo bias for $m_k$ outcomes, let

$${\tau }_k=⌊{\displaystyle \frac{2^{64}}{m_k}}⌋·m_k,{\varphi }_k\left(r\right)=\left\{\begin{array}{cc}rmod{m}_k,\hfill & r<{\tau }_k,\hfill \\ \perp ,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(12)

Let $\mathrm{off}\left(S_k\right)$ be the starting index of $S_k$. The k-th stratum contributes a duplicate-free set $I_k\subseteq S_k$ of size $q_k$ by scanning ${\left\{R_{k,t}\right\}}_t$ and collecting the first $q_k$ distinct values

$${\mathrm{idx}}_{k,t}=\mathrm{off}\left(S_k\right)+{\varphi }_k\left(R_{k,t}\right),$$

(13)

skipping samples with ${\varphi }_k\left(R_{k,t}\right)=\perp$ or duplicates; thus ${\mathsf{idx}}_{k,t}$ lifts the within-stratum position to a global index in $\left[n\right]$. The overall challenge set is the disjoint union

$$\mathcal{I}=\underset{k=1}{\overset{s}{⨆}}{I}_k,\left|\mathcal{I}\right|=c.$$

(14)

Conditioned on ${\varphi }_k\left(R_{k,t}\right)\ne \perp$, ${\mathrm{idx}}_{k,t}$ is uniform on $S_k$; under the PRF assumption for ${\mathrm{HMAC}}_{\mathrm{SHA}256}$ keyed by $\sigma$, the sequence is computationally indistinguishable from ideal sampling. The expected number of rejected draws per stratum is $<1$ (since ${\tau }_k/2^{64}\ge 1-1/m_k$), so selector runtime is $O\left(c\right)$ PRF calls.

3.2.3. zk Integration (AIR Outline)

The AIR encodes four families of constraints: (i) Seed-derived indices: the PRF state machine and rejection-sampling logic that deterministically map $\sigma \mapsto \mathcal{I}$ (domain separation by k and t). (ii) Range and quotas: membership $\mathrm{idx}\in S_k$ and per-stratum counts ${\sum }_{i\in S_k}\mathbf{1}[i\in \mathcal{I}]=q_k$. (iii) Uniqueness: no repeated indices, enforced via sorted-difference checks or a product-accumulator argument. (iv) Ownership: for each $i\in \mathcal{I}$, $\mathrm{Poseidon}\left(B_i\right)$ opens to the Poseidon-Merkle root ${\mathsf{root}}_F$ using the provided authentication path. These constraints keep verifier work $\tilde{O}\left(\lambda \right)+O\left(c\right)$ and avoid touching any plaintext blocks.

3.2.4. Theoretical Number of Challenges

Let $X\sim \mathrm{Hypergeometric}(n,\lfloor \alpha n\rfloor ,c)$ denote the number of challenged blocks known to an adversary who possesses at most an $\alpha$ fraction of F ($0\le \alpha <1$). The attack succeeds iff $X=c$, and hence

$$P_{\mathrm{attack}}={\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{\lfloor \alpha n\rfloor }{c}\right)}{\left(\genfrac{}{}{0pt}{}{n}{c}\right)}}.$$

(15)

For sufficiently large n, Stirling’s approximation yields

$$P_{\mathrm{attack}}\approx {\left({\displaystyle \frac{\alpha n}{n}}\right)}^c={\alpha }^c.$$

(16)

To achieve $\lambda$-bit soundness, it suffices to enforce

$${\alpha }^c\le 2^{-\lambda }⟺c\ge {\displaystyle \frac{\lambda }{{log}_2(1/\alpha )}}.$$

(17)

• Parameter ranges and role of${log}_2$. We take $\alpha \in [0,1)$ as an upper bound on the adversary’s known fraction of F, $c\in \mathbb{N}$ as the challenge budget (number of sampled blocks), and $\lambda \in \mathbb{N}$ as the security parameter in bits. Here ${log}_2(·)$ is the base-2 logarithm; we use its monotonicity to solve ${\alpha }^c\le 2^{-\lambda }$ for c, which gives the sizing rule (17). If the adversary has at most $Q\in {\mathbb{N}}_{\ge 1}$ independent attempts (e.g., sessions or time windows), the total forging probability is bounded by $Q·{\alpha }^c\le 2^{-\lambda }$, yielding $c\ge (\lambda +{log}_{2}Q)/{log}_2(1/\alpha )$; setting $Q=1$ recovers (17).

Refined Bound Under Stratification

If knowledge concentrates contiguously, stratified sampling is strictly stronger. Writing ${\alpha }_k$ for the adversary’s knowledge ratio within stratum k,

$$P_{\mathrm{attack}}=\prod _{k=1}^s{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{\lfloor {\alpha }_k{m}_k\rfloor }{q_k}\right)}{\left(\genfrac{}{}{0pt}{}{m_k}{q_k}\right)}}\le \prod _{k=1}^s{\alpha }_k^{q_k}\le {\left({\alpha }_{max}\right)}^c,$$

(18)

so (17) remains conservative; in practice, stratification reduces $P_{\mathrm{attack}}$ below the i.i.d. bound ${\alpha }^c$.

Grinding Budget (Optional)

If a client can attempt up to Q seeds per window (by re-initiating sessions), the overall success is

$$P_{\mathrm{forge}}\le 1-{(1-P_{\mathrm{attack}})}^Q\le Q·P_{\mathrm{attack}},$$

(19)

so (17) holds with $\lambda$ replaced by $\lambda +{log}_{2}Q$ (equivalently, ${\alpha }_{max}\left(c\right)=2^{-(\lambda +{log}_{2}Q)/c}$).

Practical Parameterization

In practice, we pick c from a small set to balance latency and security. For a fixed c, the largest adversarial knowledge ratio $\alpha$ that still satisfies (17) is

$${\alpha }_{max}\left(c\right)=2^{-\lambda /c}.$$

(20)

For a standard target $\lambda =80$, we obtain

$${\alpha }_{max}\left(128\right)\approx 0.648,{\alpha }_{max}\left(256\right)\approx 0.805,{\alpha }_{max}\left(512\right)\approx 0.897.$$

Thus, with $c=128$ the scheme tolerates adversaries knowing up to $\sim 64.8\%$ of the file; with $c=256$, up to $\sim 80.5\%$; and with $c=512$, up to $\sim 89.7\%$. Accordingly, our deployment uses

$$c\in \{128,256,512\}:$$

• Small–medium files: $c=128$ (covers $\alpha \lesssim 0.65$).
• Large files/higher leakage risk: $c=256$ (covers $\alpha \lesssim 0.81$).
• Very large files/stricter security: $c=512$ (covers $\alpha \lesssim 0.90$).

If protection against $\alpha >0.90$ is required (e.g., $\alpha =0.95$), (17) prescribes a larger c:

$$c\ge {\displaystyle \frac{80}{{log}_2(1/0.95)}}\approx 1082.$$

• Summary. The mirror seed derived from session keys enforces a one-session/one-challenge policy with unpredictability and anti-replay, while stratified, duplicate-free sampling plus zk enforcement guarantees that verifying only a few dozen to a few hundred blocks achieves ≥80-bit soundness for typical leakage levels, justifying the compact deployment set $c\in \{128,256,512\}$.

3.3. zk-STARK Protocol Design

STARKs reduce statement checking to validating that an execution trace over a finite field satisfies low-degree constraints, committed with Merkle trees and checked by FRI under Fiat–Shamir. In MiS-PoW the verifier’s cost and the proof size are independent of the file size n; they scale only with the security parameter and the number of challenged blocks c:

$$T_{\mathrm{verify}}=\tilde{O}\left(\lambda logc\right)+O\left(c\right),\left|\pi \right|=\tilde{O}\left(\lambda logc\right),$$

(21)

where the additive $O\left(c\right)$ term accounts for c local Merkle openings. No plaintext blocks are revealed.

3.3.1. Public I/O and Witness

Public inputs. $(\mathsf{fid},T,n,c,s)$, partition descriptors (or a commitment to them), the mirror seed $\sigma$ derived as in (7), and a Poseidon-Merkle root ${\mathsf{root}}_F$ that commits to $\left(Poseidon\left(B_1\right),\dots ,Poseidon\left(B_n\right)\right)$ from the canonical copy of F.

Witness. The challenged blocks ${\left\{B_i\right\}}_{i\in \mathcal{I}}$ and their Merkle authentication paths to ${\mathsf{root}}_F$, together with the internal PRF state used by the selector that maps $\sigma$ to $\mathcal{I}$ (Section 3.2).

3.3.2. AIR: Simple, Readable Constraints

Let $\mathcal{I}=\{i_1,\dots ,i_c\}$ be the mirror-selected indices from (14). The AIR enforces four transparent families of constraints; we write them in a minimal, reviewer-friendly form.

(C1)

Indices come from the seed.

For each position $j\in \{1,\dots ,c\}$ the circuit replays the stratified selector with input $(\sigma ,n,c,s)$ and checks that the j-th output equals the provided index:

$$i_j={\mathsf{Select}}_j(\sigma ,n,c,s)\mathrm{and}1\le i_j\le n.$$

(22)

The selector is the PRF + rejection-sampling procedure of Section 3.2; its state machine is encoded directly in the trace.

(C2)

Quotas and uniqueness.

Let $P:\left[n\right]\to \left[s\right]$ be the public partition map and $q_k$ the quota for stratum k from (10). The circuit maintains s counters and checks

$$\sum _{j=1}^c\mathbf{1}\{P\left(i_j\right)=k\}=q_k(k=1,\dots ,s),i_1<i_2<\dots <i_c,$$

(23)

i.e., per-stratum counts are exact and all indices are strictly increasing (the prover presents $\mathcal{I}$ sorted), which rules out duplicates with a single inequality per step. In particular, the combination of exact per-stratum quotas and strict ordering enforces pairwise-distinct indices and realizes the same distribution as stratified uniform sampling without replacement; this is precisely the sampler analyzed in Section 3.2 and used in our soundness bounds.

(C3)

Block ownership (know the content).

For every j, the circuit hashes the challenged block and verifies its Merkle path against the public root:

$$h_j=Poseidon\left(B_{i_j}\right),MerkleVerify\left(h_j,i_j,{\mathsf{root}}_F\right)=1.$$

(24)

Thus, the proof attests that the prover knows the exact plaintext of each challenged block without revealing it.

(C4)

A compact public digest.

The circuit accumulates a short digest over the checked pairs $(i_j,h_j)$:

$$\begin{array}{cc}\hfill d_0& =Poseidon\left(\sigma \parallel \mathsf{fid}\parallel T\right),\hfill \\ \hfill d_j& =Poseidon\left(d_{j-1}\parallel i_j\parallel h_j\right)(j=1,\dots ,c),\hfill \\ \hfill \mathsf{Dig}& =d_c(\mathrm{public}\mathrm{output}).\hfill \end{array}$$

(25)

This value is later recomputed by the verifier using its own canonical digests for the same indices (no disk scan beyond c lookups).

3.3.3. Prover and Verifier Algorithms

Prover (client). The client first computes $\sigma$ from the HTTPS and TLS exporter and the pair $(\mathsf{fid},T)$. The client then derives the index set $\mathcal{I}$ with the stratified selector. For each i in $\mathcal{I}$ the client reads $B_i$, computes $h_i=Poseidon\left(B_i\right)$, and collects the Merkle path to ${\mathsf{root}}_F$. The client sorts the indices when needed and builds a trace that enforces Constraints (22) to (25). The client commits the trace with Merkle trees, derives Fiat Shamir challenges, assembles the composition polynomial, and runs FRI to produce the proof $\pi$.

Verifier (server). The server recomputes $\sigma$ with the exporter and $(\mathsf{fid},T)$. The server reconstructs $\mathcal{I}$ with the same selector and public parameters. The server obtains the canonical digests ${\left\{h_i^{\left(\mathcal{S}\right)}\right\}}_{i\in \mathcal{I}}$ with $h_i^{\left(\mathcal{S}\right)}=Poseidon\left(B_i\right)$, or it verifies the Merkle paths against ${\mathsf{root}}_F$. The server recomputes $\widehat{\mathsf{Dig}}$ with the same recurrence as in (25) after replacing $h_j$ by $h_{i_j}^{\left(\mathcal{S}\right)}$. The server then verifies the proof $\pi$ by checking Merkle openings and FRI queries and accepts only when all checks pass and $\mathsf{Dig}=\widehat{\mathsf{Dig}}$.

3.3.4. Why This Is Secure and Scalable

The scheme checks only c blocks and still gives high soundness. By (C1)–(C2), the AIR forces the realized challenge set to follow the stratified without-replacement sampler of Section 3.2; therefore, the one-shot forging bound proved for that sampler applies directly, and with rate-limited Q seed attempts yields the sizing rule below. Section 3.2 shows that an adversary who knows at most an $\alpha$ fraction of F forges with probability at most $Q·{\alpha }^c$ under the sampler, and the bound is smaller under stratification. A practical rule is

$$c\ge {\displaystyle \frac{\lambda +{log}_{2}Q}{{log}_2(1/\alpha )}},$$

(26)

which gives a target of $2^{-\lambda }$ for the total forging probability. Our deployment uses $c\in \{128,256,512\}$ with $\lambda =80$. One session gives one seed because $\sigma$ binds the exporter material, the pair $(\mathsf{fid},T)$, and an optional client salt. The design prevents replay and removes server bias. The verifier cost does not depend on n because the verifier touches only c digests or c Merkle paths and runs a standard STARK verification with complexity $\tilde{O}(\lambda logc)$.

3.3.5. Proof Object and Non-Interactive Transcript

The proof contains commitments to masked trace columns, the openings at points chosen by the verifier, the FRI transcript, and the public inputs $(\mathsf{fid},T,n,c,s,\sigma ,{\mathsf{root}}_F,\mathsf{Dig})$. All challenges come from the commitments through the Fiat Shamir transformation. The protocol needs no extra interaction beyond HTTPS and therefore remains single shot in deployment.

4. Security Analysis

We analyze MiS-PoW under the threat model of Section 1: a malicious client may know only a fraction of F (possibly contiguous), the server is honest-but-curious, and outsiders cannot access TLS exporter secrets. We focus on four properties that match the design goals: (i) unpredictable and fresh mirror challenges, (ii) computational integrity (soundness), (iii) privacy (zero knowledge), and (iv) robustness to partial knowledge and grinding. All adversaries are PPT; the TLS exporter in (7) and HKDF are modeled as PRFs; Fiat–Shamir is in the ROM; Merkle hashing is collision resistant; $\mathrm{Poseidon}$ is a ZK-friendly hash within the AIR.

4.1. Unpredictability, Freshness, and Anti-Replay

Let $\sigma$ be the session-bound seed from (7), which binds the TLS transcript, the discretized time T, the file identifier, and an optional client salt. By PRF security of the exporter/HKDF, $\sigma$ is computationally indistinguishable from uniform for anyone without the session key; therefore, the stratified selector of Section 3.2 produces an index set $\mathcal{I}$ that is indistinguishable from ideal per-stratum uniform sampling. Because $T=\lfloor \mathrm{unix}\_\mathrm{time}/\Delta \rfloor$ and the verifier only tolerates a small skew window, reusing any transcript in a different window changes the input to (7), so previously valid challenges fail except with negligible PRF advantage. The inclusion of a client salt prevents server-side bias of $\sigma$ without extra rounds. Under session resumption, $\sigma$ changes because the exporter secret derives from the new handshake; under KeyUpdate, $\sigma$ remains unchanged and cannot be biased. In both cases, binding to T ensures that cross-window replays fail except with negligible PRF advantage.

4.2. Computational Integrity (Soundness)

A cheating prover must either (a) open values inconsistent with the committed trace or Merkle structures, (b) pass a too-high-degree composition polynomial through FRI, or (c) violate the seed-to-index rule enforced in the AIR by breaking the PRF/ROM assumptions. Hence

$${\mathrm{Adv}}_{\mathrm{A}}^{\mathrm{sound}}\le {\mathrm{Adv}}_{\mathrm{Merkle}}^{\mathrm{cr}}+2^{-\lambda }+{\mathrm{Adv}}_{\mathrm{Exporter}}^{\mathrm{prf}}+{\mathrm{Adv}}_{\mathrm{HKDF}}^{\mathrm{prf}}+\mathrm{negl}\left(\lambda \right),$$

(27)

where the $2^{-\lambda }$ term is the standard FRI degree-test error. The verifier’s work and the proof size remain $\tilde{O}(\lambda logc)$ (cf. (21)), independent of $\left|F\right|$.

4.3. Partial/Contiguous Knowledge and Grinding

Let $S_1,\dots ,S_s$ be strata with sizes $m_k$, quotas $q_k$ (10), and let the adversary know an ${\alpha }_k$ fraction within $S_k$; write ${\alpha }_{max}={max}_k{\alpha }_k$. Because sampling is uniform without replacement in each stratum and quotas must all be met, the one-shot forging probability is

$$p_{\ast }=\prod _{k=1}^s{\displaystyle \frac{\left(\genfrac{}{}{0pt}{}{\lfloor {\alpha }_k{m}_k\rfloor }{q_k}\right)}{\left(\genfrac{}{}{0pt}{}{m_k}{q_k}\right)}}\le {\left({\alpha }_{max}\right)}^c,$$

(28)

which strictly improves on the i.i.d. bound ${\alpha }^c$ whenever knowledge is contiguous (only a few strata have large ${\alpha }_k$). If up to Q independent seed attempts are possible in one window (rate-limited by the service), the overall success is

$$P_{\mathrm{forge}}\le 1-{(1-p_{\ast })}^Q\le Q·p_{\ast }.$$

(29)

Selecting c to satisfy $Q·p_{\ast }\le 2^{-\lambda }$ gives $\lambda$-bit soundness. A convenient rule that upper-bounds (29) is

$$c\ge {\displaystyle \frac{\lambda +{log}_{2}Q}{{log}_2(1/{\widehat{\alpha }}_{max})}},$$

(30)

with a conservative estimate ${\widehat{\alpha }}_{max}$. For $\lambda =80$ and $Q=1$, this yields ${\alpha }_{max}\left(128\right)\approx 0.648$, ${\alpha }_{max}\left(256\right)\approx 0.805$, ${\alpha }_{max}\left(512\right)\approx 0.897$, justifying the deployment set $c\in \{128,256,512\}$ from Section 3.2.

4.4. Zero-Knowledge Privacy

MiS-PoW reveals no plaintext content. The trace columns are randomized before commitment; only masked values and Merkle openings are exposed. A standard STARK simulator that programs the ROM and replaces witness-dependent columns with masked low-degree polynomials produces transcripts indistinguishable from real ones, so for any PPT distinguisher $\mathcal{D}$ and public input X,

$$|Pr[\mathcal{D}\left(\pi \right(X\left)\right)=1]-Pr[\mathcal{D}\left(\mathcal{S}\right(X\left)\right)=1\left]\right|\le \mathrm{negl}\left(\lambda \right).$$

(31)

• Summary.

Session-bound seeds make challenges fresh and unpredictable; the AIR enforces seed-derived indices, per-stratum quotas, and uniqueness; Merkle/FRI provide succinct soundness. With stratification and the sizing rule in (30), checking only a few dozen to a few hundred blocks—our deployment uses $c\in \{128,256,512\}$—achieves at least 80-bit soundness under realistic leakage while keeping the verification cost independent of $\left|F\right|$.

5. Evaluations

5.1. Methodology

Experimental setup. We built a prototype of MiS-PoW and compared it with three representative schemes: MHT-PoW [8], SE-PoW [11], and Dynamic-PoW [28]. All tests ran on a dedicated server with an Intel Xeon Platinum 8358P CPU at $2.60\mathrm{GHz}$ with 128 cores, $377\mathrm{GB}$ RAM, and Ubuntu $22.04$ LTS. Local storage provided $22\mathrm{TB}$ of capacity. We fixed the STARK security parameter at $\lambda =80$, the block size at $B=64\mathrm{KB}$, and the challenge budget at $c\in \{128,256,512\}$ unless stated otherwise. Session-bound seed derivation that uses the TLS exporter together with HKDF was part of the initialization time. We disabled network access for data files, pinned processes to isolated cores, and warmed the binaries before recording. Each configuration was executed 1000 times, and we report the mean with the standard deviation in parentheses. Public code for the baselines was not available, so we re-implemented them from the algorithmic descriptions. We matched common parameters across schemes (block size B, hash family, security level, and challenge budget c) and used streaming buffered file I/O. Executables were built with compiler optimizations and run without GPUs. For Merkle-based baselines we used a binary tree with SHA-256 for both leaves and internal nodes and recomputed authentication paths per run (no cross-run caching). When a paper prescribes a different engineering choice (e.g., tree fan-out or indexing detail), we follow it; otherwise we keep the common defaults above. These implementation choices can shift absolute wall-clock times, so we emphasize relative behavior under equal conditions and, when present, note any intentional deviations next to the corresponding figure or table.

Dataset. We focused on how file size and the challenge budget affect cost. We therefore used synthetic data to avoid content bias and to support repeatability. We generated five file sets with sizes $64\mathrm{MB}$, $128\mathrm{MB}$, $256\mathrm{MB}$, $512\mathrm{MB}$, and $1\mathrm{GB}$. Each set contained 100 files. A cryptographically secure pseudo random generator produced all bytes. This setup isolates the effect of the number of blocks n and the challenge count c while avoiding privacy and licensing concerns.

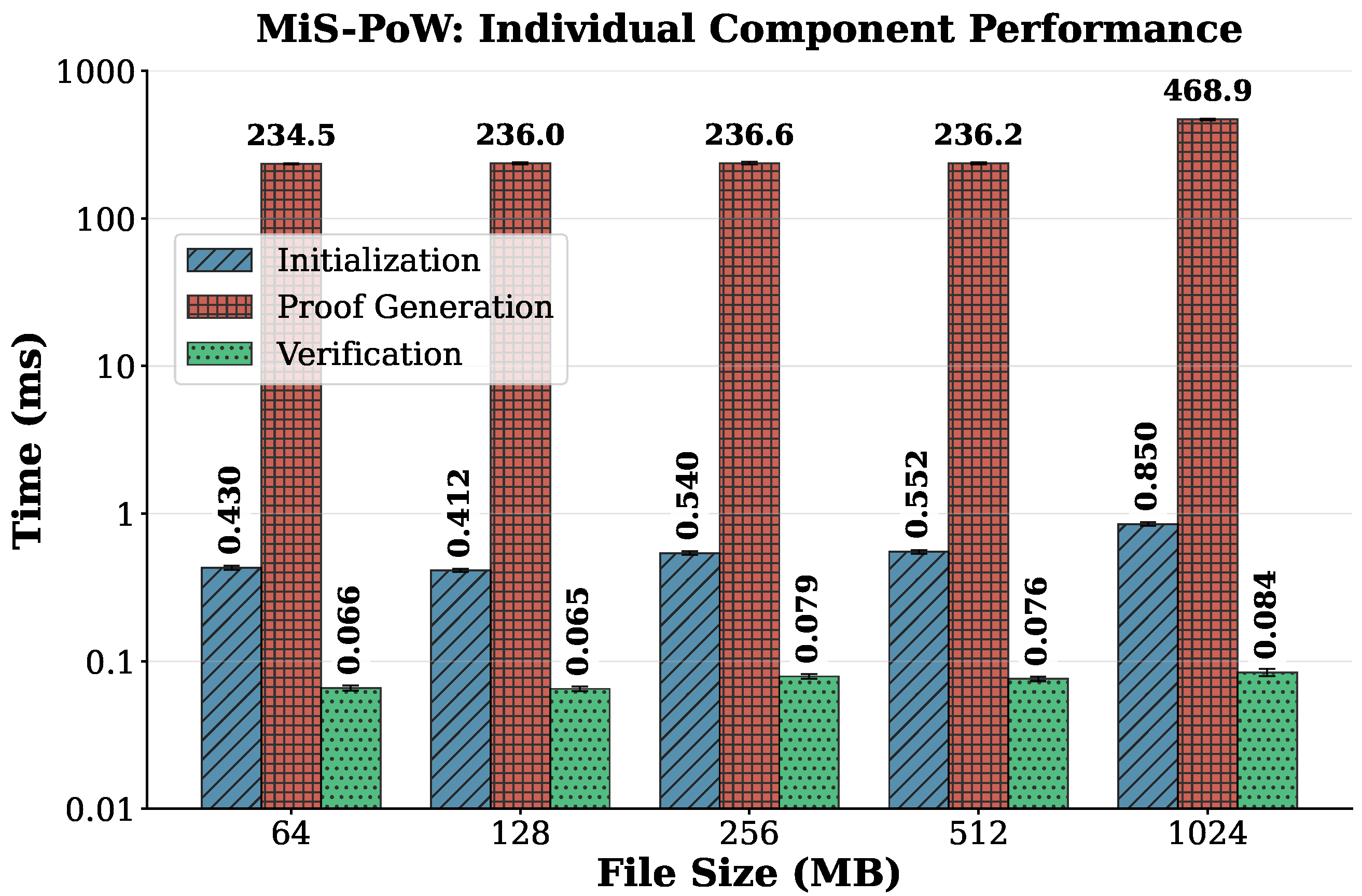
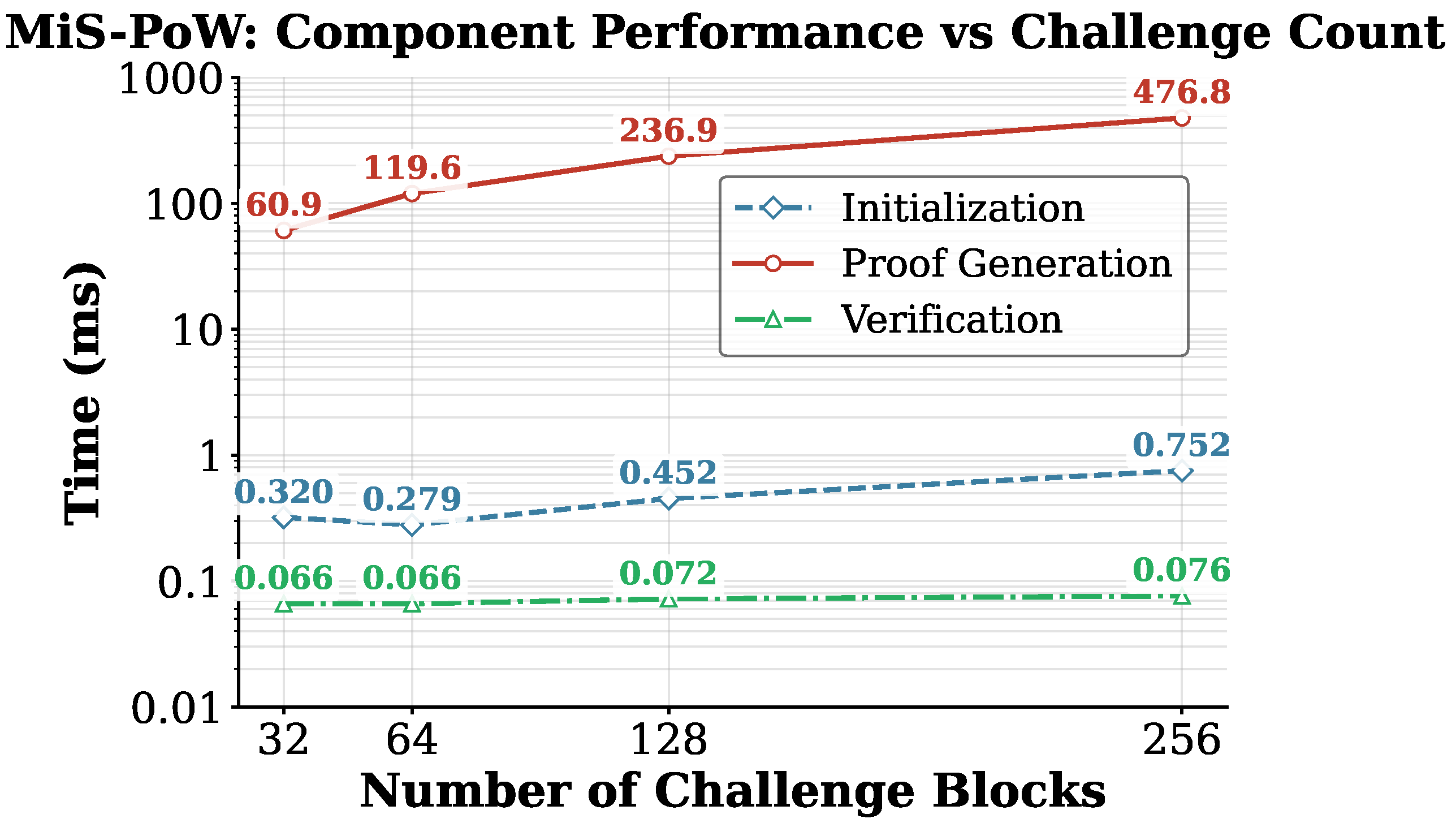
5.2. Computational Overhead Analysis

MiS-PoW processes only c challenge blocks, so both the prover and the verifier scale as $\tilde{O}(\lambda logc)$ and do not depend on the total number of blocks n. Proofs remain compact at $\lambda =80$ and $c\le 512$ because the STARK size mainly follows $\lambda$ and the number of FRI queries. Figure 2 reports initialization, proof generation, and verification times across file sizes. The curves are flat in n. Initialization includes the TLS exporter and HKDF and stays between $0.430$ and $0.850\mathrm{ms}$. Verification stays between $0.065$ and $0.084\mathrm{ms}$. Proof generation dominates and ranges from $234.5$ to $468.9\mathrm{ms}$ as we move from $64\mathrm{MB}$ to $1\mathrm{GB}$. At $128\mathrm{MB}$ the three components are $0.412\mathrm{ms}$ for initialization, $236.0\mathrm{ms}$ for proving, and $0.065\mathrm{ms}$ for verification. These results confirm that verifier cost is governed by $(\lambda ,c)$ rather than n.

5.3. Efficiency and Performance Evaluation

We next study sensitivity to the challenge budget. Figure 3 fixes the file at $1\mathrm{GB}$ and varies c from 32 to 256. Proof generation grows from $60.9$ to $476.8\mathrm{ms}$. Initialization rises mildly from $0.320$ to $0.752\mathrm{ms}$ as state grows. Verification remains essentially constant between $0.066$ and $0.076\mathrm{ms}$. The total latency therefore increases from about $61.3$ to $477.6\mathrm{ms}$ and matches the $\tilde{O}(\lambda logc)$ model.

We also perform a security stress test. The adversary holds contiguous segments and we run $10,000$ trials per configuration for $c\in \{128,256\}$. We observe no successful forgery. The result is consistent with the stratified success bound and the STARK soundness target in our analysis.

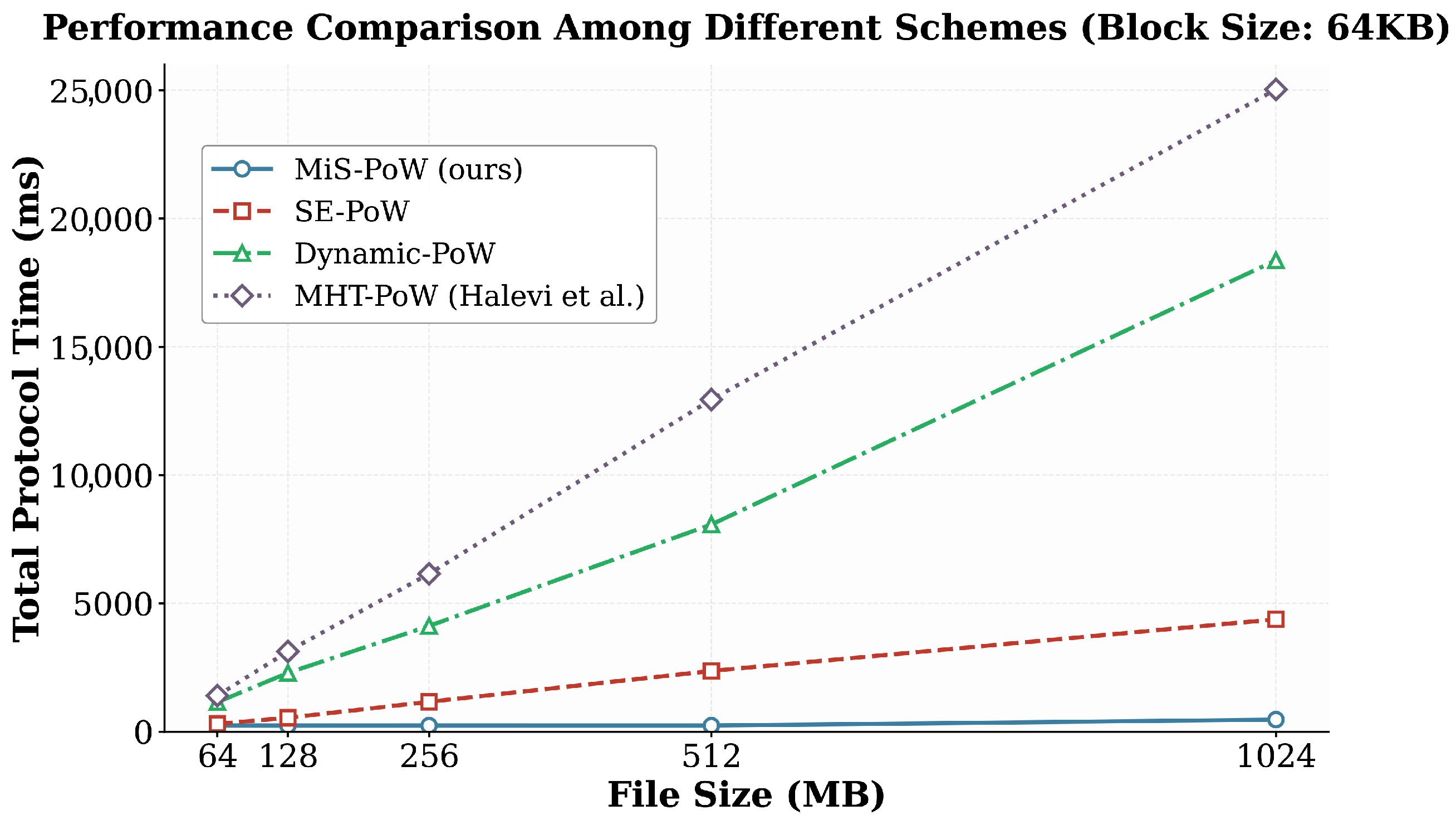
5.4. Comparison with Existing PoW Schemes

Figure 4 and

Table 2. Total time in milliseconds across file sizes.

File Size (MB)	MiS-PoW	SE-PoW	Dynamic-PoW	MHT-PoW
64	237.6	302.3	1148.2	1404.2
128	235.9	541.7	2291.6	3127.3
256	236.6	1163.3	4120.6	6152.7
512	236.2	2367.9	8075.2	12,943.6
1024	469.7	4379.2	18,372.0	25,031.5

together illustrate the end-to-end time under the same block size of $64\mathrm{KB}$. MiS-PoW remains nearly flat as n grows, while all baselines increase with file size. At $512\mathrm{MB}$ MiS-PoW completes in $236.2\mathrm{ms}$, whereas SE PoW, Dynamic PoW, and MHT PoW take $2367.9$, $8075.2$, and $12,943.6\mathrm{ms}$. The speedups are about $10.0\times$, $34.2\times$, and $54.8\times$. At $1\mathrm{GB}$ MiS-PoW takes $469.7\mathrm{ms}$, compared with $4379.2$, $18,372.0$, and $25,031.5\mathrm{ms}$, which corresponds to $9.3\times$, $39.1\times$, and $53.3\times$ improvements. Even at $64\mathrm{MB}$ MiS-PoW is about $1.27\times$ faster than SE PoW and it also provides zero knowledge privacy.

5.5. Discussion and Takeaways

MiS-PoW keeps verifier work and proof size independent of file size, which explains the flat verification series. End-to-end latency is controlled by c and follows $\tilde{O}(\lambda logc)$, so operators can plan capacity with a small parameter set. Session-derived seeds make challenge generation non-interactive and inexpensive, which keeps initialization below a millisecond and eases deployment at TLS front ends. Stratified sampling and the sizing rule show why a few dozen to a few hundred blocks are enough under realistic leakage. The advantage grows with file size because baselines perform work that scales with n, whereas MiS-PoW avoids full file traversals and replaces them with algebraic checks inside a STARK.

6. Conclusions

Client-side deduplication is ubiquitous but vulnerable to ownership forgery when fingerprints leak. We presented MiS-PoW, a non-interactive, privacy-preserving proof of ownership tailored for cloud storage. The core idea is to derive mirror challenges from a standard HTTPS/TLS session via a session-bound exporter and a discretized timestamp, so both endpoints compute the same challenge set without extra round trips. A stratified, duplicate-free sampler targets contiguous-knowledge adversaries, and a lightweight zk-STARK enforces that (i) indices come from the seed, (ii) per-stratum quotas and uniqueness hold, and (iii) the prover knows the plaintext of each challenged block via Poseidon-Merkle openings. Verifier work and proof size depend on $(\lambda ,c)$ rather than $\left|F\right|$, enabling single-shot verification that is agnostic to file length.

Our security analysis yields a simple sizing rule that links leakage level, grinding budget, and the challenge count: with $c\in \{128,256,512\}$ and $\lambda =80$, MiS-PoW achieves at least 80-bit soundness under realistic partial/contiguous-knowledge assumptions while keeping c modest. The prototype evaluation matches these claims: verification remains sub-millisecond and nearly flat in n, proof generation scales with c (hundreds of milliseconds for the tested range), and end-to-end latency is substantially lower than Merkle-based and interactive PoW baselines across file sizes, while additionally providing zero-knowledge privacy and replay resistance.