ABAC Policy Mining Using Complex Network Analysis Techniques

Abstract

Recent computing technologies and modern information systems require an access control model that provides flexibility, granularity, and dynamism. The Attribute-Based Access Control (ABAC) model was developed to address the new challenges of emerging applications. Designing and implementing an ABAC policy manually is usually a complex and costly task; therefore, many organizations prefer to keep their access control mechanisms in operation rather than incur the costs associated with the migration process. A solution to the above is to automate the process of creating access control policies. This action is known as policy mining. In this paper, we present a novel approach, based on complex network analysis, for mining an ABAC policy from an access control log. The proposed approach is based on the data and the relationships that can be generated from them. The proposed methodology is divided into five phases: (1) data preprocessing, (2) network model, (3) community detection, (4) policy rule extraction, and (5) policy refinement. The results show that it is possible to obtain an ABAC policy using the approach based on complex networks. In addition, our proposed methodology outperforms existing ABAC mining algorithms regarding quality. Finally, we present a novel access decision process that reduces the number of rules to evaluate based on a rule network.

1. Introduction

The importance of information security has increased as the world has become more interconnected [1]. The main objective of information security is to protect sensitive and confidential data from unauthorized access, use, and disclosure. According to a 2024 study by IBM and the Ponemon Institute, the average cost of a data breach was USD 4.88 million [2]. It is clear that organizations, industries, and national security depend on a robust information security program to prevent security breaches and protect critical information.

By adopting an Access Control (AC) mechanism, resources and information can be protected from unauthorized entities and malicious activity. The goal of access control is to ensure that only authorized entities are granted access to the resources and information they need to perform their job functions [3]. AC has become more important due to the development of recent technologies such as cloud computing [4], the Internet of Things [5], and Fog Computing [6].

The process by which an access request is permitted or denied depends on the AC model implemented. There are four traditional AC models: Discretionary Access Control (DAC), Mandatory Access Control (MAC), Role-based Access Control (RBAC), and Attribute-based Access Control (ABAC). The AC model, in addition to the evaluation process, has an AC policy that defines the set of rules and requirements by which the AC mechanism is regulated. When an access request is received, the AC mechanism interacts with the policy to determine whether the subject has the right to access the requested object.

In addition to traditional AC models, other AC models have been developed to improve the AC mechanism or address the limitations of the traditional approaches. For example, the RBAC and ABAC Combining Access Control (RACAC) model [7] adopts the strengths of both models. Approaches such as the Hierarchical Group and Attribute-Based Access Control (HGABAC) model [8] and Higher-order Attribute-Based Access Control (HoBAC) model [9] formally introduce the concept of hierarchy in ABAC. Ciphertext-Policy Attribute-Based Encryption (CP-ABE) [10] adds a layer of encryption to the data in the ABAC model. The Hierarchical, Extensible, Advanced, and Dynamic Access Control (HEAD) metamodel [11] is a proposal that confronts most of the challenges of recent technologies.

To address the present application problems and overcome the limitations of DAC, MAC, and RBAC models that make them less suitable for emerging large and dynamic application domains, the ABAC model was developed [12,13,14,15]. The ABAC model uses attributes to make access control decisions, making it flexible, scalable, and context-sensitive. The attributes are the characteristics of an entity (subject, object, environment) in the AC mechanism. The ABAC policy is the set of authorization rules defined over these attributes. An ABAC rule specifies whether a subject can access a resource in a particular environment. When an access request is received, the ABAC model evaluates the subject (requester)’s attributes, the object’s attributes, and the environmental conditions with a set of rules (policy) for overall attributes.

However, the main problem with implementing an ABAC model is the policy specification. Policy specification is typically performed by expert humans, which can make it costly, time-consuming, subjective, complex, and error-prone. Consequently, organizations prefer to keep traditional models (MAC, DAC, and RBAC) in operation rather than face all the challenges of the migration and implementation process. Policy mining techniques can be used to automate the policy specification process and address these challenges.

Policy mining is a technique that automates the process of AC policy specification based on an existing AC state, such as Access Control Lists (ACLs), natural language, or access logs. Specifically, the access log contains information on all access requests that are either permitted or denied by the AC mechanism. By using the access log as input, a policy mining process can generate an AC policy as an output. In the context of the ABAC model, this process involves identifying a reduced set of AC rules that properly model the request records in the access log.

Several approaches have been developed for policy mining. Xu and Stoller [16] pioneered this field by creating rules from user-permission logs, progressively refining them for broader coverage. However, their algorithm demonstrates reduced performance with larger access logs. Iyer and Masoumzadeh [17] introduced an ABAC policy mining approach using the PRISM algorithm [18]. Despite its effectiveness in generating positive and negative rules, scalability becomes a challenge with larger access logs, leading to an excess of rules. Cotrini et al. [19] proposed the Rhapsody algorithm based on APRIORI-SD [20], featuring stages for rule generation, extraction, and length reduction. While introducing a liability metric, the exponential growth of rules in the presence of numerous attributes remains a limitation. Jabal et al. [21] presented an ABAC policy mining framework integrating data mining, statistics, and machine learning techniques. Despite its effectiveness, the approach faces challenges due to the substantial number of combinations required for policy extraction. Karimi et al. [22] contributed to the first machine learning-based approach involving phases such as parameter selection, clustering, rule extraction, and clean-up. Recent investigations [23,24,25] have chosen to detect clusters of access requests before the policy mining process; then, the rule generation algorithms are applied to those clusters.

Table 1. State of the art ABAC policy mining approaches.

Authors	Data Application	Rule Extraction Approach	Negative Rule Extraction	Noisy Log	Sparse Log
Xu and Stoller, 2014 [16]	Access log.	Association rule mining algorithm.	✗	✓	✗
Iyer and Masoumzadeh, 2018 [17]	Access log.	Association rule mining algorithm.	✓	✗	✗
Cotrini et al., 2018 [19]	Access log.	Association rule mining algorithm.	✗	✗	✓
Jabal et al., 2020 [21]	Access log.	Association rule mining algorithm.	✗	✓	✗
Karimi et al., 2021 [22]	Clusters in access log.	Frequency of attribute–value tuples in a cluster.	✗	✓	✓
Davari et al., 2022 [23]	Clusters in access log.	Association rule mining algorithm.	✓	✓	✓
Quan et al., 2023 [24]	Clusters in access log.	CatBoost algorithm.	✓	✓	✓
Shang et al., 2024 [25]	Clusters in access log.	Hierarchical relation in a cluster.	✗	✓	✓

summarizes the challenges and techniques of the state-of-the-art ABAC policy mining approaches.

In summary, an AC mechanism is a complex and dynamic system in which a large number of entities (subjects, objects, environmental conditions, attributes, operations) interact with each other. A purely data-driven approach for policy mining is not sufficient to functionally capture the high complexity of the AC mechanism. To overcome these limitations, recent studies have turned to complex network theory, a powerful mathematical framework for analyzing and modeling complex systems. Specifically, an AC system network model is able to detect hidden patterns and implicit relationships between entities that may not be apparent in the original access log.

Briefly, a complex network is a network (graph) with a set of nodes (vertices) joined together in pairs by a set of links (edges). A network has the function of reducing a complex system to an abstract structure. It captures only the fundamental aspects of entities, which serve as nodes, and their connection patterns, which serve as links. This theory has been a powerful tool with which for scientists to model and analyze real-world systems across a wide range of fields such as sociology, neuroscience, biology, and technology [26,27]. Specifically, in security information research, some investigations use complex network analysis for anomaly detection in computer networks [28], vulnerability analysis [29], or modeling cyber–physical cybersecurity networks [30]. In the complex network theory, we can find several network properties such as scale-free degree distribution, community structure, density, and centrality that can help to extract hidden knowledge from the complex interaction system. With the above, we can discover a wide range of added information, e.g., how data flows on the Internet, who the most important person in a terrorist group is, the reliability of a power grid, or groups of people on social media apps.

This paper presents a new proposal for ABAC policy mining based on complex networks. Our proposal uses the access log to generate an ABAC policy that best represents the access requests in the access log. The access log reflects the behavior of the system in a real environment; therefore, it can be used to model a complex network. A bipartite network is generated based on user–resource interactions. Then, a weighted projection to the bipartite network is performed to obtain a user network. A community detection algorithm is applied to the user network to group users and attributes based on the network topology. Each detected community is analyzed to extract the patterns that best represent the community. In this way, it is possible to generate policy rules according to user and resource attributes. Finally, an algorithm is applied to refine the mined ABAC policy and increase its quality. The main contributions of this work are as follows:

• A new method based on complex network theory for mining ABAC access control policies from access records.
• A bipartite network model to represent user–resource interactions (access requests) in an access control system.
• A rule extraction algorithm to extract patterns that best represent the users and the resources of the community.
• A network model of the mined rules for evaluating access requests.

The rest of the paper is organized as follows. Section 2 defines the ABAC policy mining problem, discusses the challenges and requirements, and presents the evaluation metrics in this problem. Section 3 presents our proposed ABAC policy mining approach. In Section 4, we describe the process of access decision in our policy based on the rule network. Section 5 presents the performance of our approach on two datasets as well as detailed results for every phase of the proposed model. Finally, Section 6 provides additional discussion and conclusions.

2. Fundamental Principles

2.1. ABAC Model

In the ABAC model, the authorization of a set of requests is determined by evaluating the attributes associated with a subject, an object, an operation, and the environmental conditions against a set of rules that describe the allowed operations for a given resource.

Attributes are characteristics that define specific aspects of the subject, object, and environment. These attributes can be set by the security administrator and by the dynamics of the system. A subject is an entity that requests access to an object. A subject can be a user, application, process, or service. The object is the entity which the subjects access. The objects can be resources, files, devices, registries, processes, services, or programs. An operation is the execution of a function toward an object. Operations can read, write, execute, modify, delete, etc. A rule is the combination of attributes and operations that condition the access of a request. Rules are statements of the type "If, then" that can grant or deny resources; they can even override other rules. Each ABAC rule specifies whether a subject can access a resource in a particular environment. When an access request is received, the ABAC model evaluates the subject (requester) attributes, the object attributes, and the environmental conditions with a set of rules (policy). An example of a rule is If class = CP01 and type = task and op = read then permit. In this approach, we use an adapted ABAC policy model definition from the work [22].

Definition 1

(ABAC Policy Model). An ABAC policy model is composed of the following elements:

• U, R, S, and $OP$ refer to the set of users, resources, sessions, and operations, respectively, in the system. $E=U\cup R\cup S$ is the set of all system entities.
• $A_U$, $A_R$, and $A_S$ refer to the set of user attributes, resource attributes, and session attributes, respectively. $A=A_U\cup A_R\cup A_S$ is the set of all system attributes. Given an attribute $a\in A$, the attribute range $V_a$ is the set of all valid values for attribute a in the system.
• The $f_{ea}(e,a)$ function returns the value of attribute $a\in A$ for entity $e\in E$.
• An attribute filter is a set of tuples defined as $\mathcal{F}=\left\{\langle a,v\rangle \right|a\in A\wedge v\in V_a\}$.
• An access request is a tuple $q=\langle u,r,s,op,d\rangle$, where a user $u\in U$ initiates an operation request $op\in OP$ to the resource $r\in R$ in the session $s\in S$ and d is the access decision made by the access control system.
• An Access decision d has two possible values: permit or deny. If $d=permit$, the user u can access the resource r, performing an operation $op$ in session s. In contrast, if $d=deny$, the user u cannot access the resource r.
• The access log $\mathcal{L}$ is the union of the positive access log ${\mathcal{L}}^{+}$ and negative access log ${\mathcal{L}}^{-}$ defined as

  $$\begin{array}{c}\hfill {\mathcal{L}}^{+}=\left\{\langle q,d\rangle \right|\langle q,d\rangle \in \mathcal{L}\wedge d=permit\}\\ \hfill {\mathcal{L}}^{-}=\left\{\langle q,d\rangle \right|\langle q,d\rangle \in \mathcal{L}\wedge d=deny\}\end{array}$$

  (1)
  An access request from positive (negative) access log $q^{+}\in {\mathcal{L}}^{+}$ ($q^{-}\in {\mathcal{L}}^{-}$) is called a positive access request (negative access request).
• A rule is a tuple $\rho =\langle \mathcal{F},op,d\rangle$, where $\mathcal{F}$ is an attribute filter, $op$ is an operation, and d an access decision.
• A rule satisfies an access request $q\vDash \rho$ iff

  $$\begin{array}{c}\hfill \langle u,r,s\rangle \vDash \mathcal{F}\wedge o{p}_q=o{p}_p\end{array}$$

  (2)
• An ABAC policy is a tuple $\pi =\langle E,OP,A,f_{ea},\mathcal{P}\rangle$, where E is the set of entities, $OP$ the set of operations, A is the set of attributes, $f_{ea}$ is the attribute function, and $\mathcal{P}$ is the set of rules.
• The decision of policy $\mathcal{P}$ for an access request q denoted as $d_{\pi }\left(q\right)$ is permit if

  $$\begin{array}{c}\hfill \exists \rho \in \mathcal{P}:q\vDash \rho \end{array}$$

  (3)
  Otherwise, the decision is deny.

Policy mining algorithms help to migrate traditional AC models to the ABAC model automatically. The ABAC policy mining problem defined below is an adaptation of [22]:

Problem 1

(ABAC Policy Mining Problem). Given an access log $\mathcal{L}$, the ABAC policy mining problem is to find a set of rules $\mathcal{P}$ that achieves high quality with respect to $\mathcal{L}$, ensuring that $\mathcal{P}$ clearly defines the entities, attributes, operations, and access decisions in the AC mechanism.

We refer to the original policy as the access control policy that gave rise to the access log $\mathcal{L}$. In contrast, we refer to the mined policy as the set of rules $\mathcal{P}$ that was automatically inferred from $\mathcal{L}$. In this context, the ABAC policy mining problem aims for the mined policy to approximate or replicate the access decisions made by the original policy.

2.2. Challenges and Requirements

The following challenges associated with the ABAC policy mining problem can be highlighted:

• Accuracy: The extracted rules must be consistent with the access log of the original policy. In inconsistent situations, rules are more permissive or more restrictive than the original policy.
• Complexity: Policies are managed by humans; therefore, rules need to be easy to interpret, manage, and audit.
• Imbalanced access log: There is an imbalance between permitted and denied access requests, the former being the majority class. Denied access requests occur less frequently because they are mainly user errors.
• Sparse access log: In most cases, the access log does not represent the complete behavior of the system. Therefore, it is necessary that an access log with few records can extract a useful policy for the entire access control system.
• Noisy access log: It is possible to find access requests that are erroneous or present some inconsistency. This happens when there is a misconfiguration in the system, sometimes due to updates made by the administrators. Noisy access requests can affect the quality of the mined policy, making it more permissive or more restrictive than it originally was.
• Private access log: The data information in access control systems is sensitive; therefore, it is difficult to obtain an access log due to the security implications for the company.
• Negative rules: Both positive and negative rules can exist in access control policies. Negative rules are used to establish exceptions to what is permitted by positive rules. Therefore, generating this type of rule can help improve the quality of the mined policy.

2.3. Policy Mining Algorithms

Although there exist different approaches to policy mining, there are common processes shared between them. The general methodology comprises three phases: (1) data preprocessing, (2) rule mining, and (3) policy refinement. During the first phase, data cleaning and data preprocessing tasks are conducted, for example, the handling of missing values and the conversion of numerical values into categorical ones. In the second phase, candidate ABAC rules are generated based on the attribute–value tuple frequency. Additionally, rules are modified to generalize them, to cover a broader set of attribute–value tuples or to make them more specific. In the last phase, the complete policy generated in the previous phase is evaluated to measure its quality. An accurate and comprehensible policy is a high-quality policy. Generating new rules, merging candidate rules, or simplifying candidate rules can help to improve the policy quality.

There are some variations in the policy mining approaches. For instance, Iyer and Masoumzadeh [17], Davari et al. [23], and Quan et al.’s [24] proposals permit the generation of both positive and negative rules. Karimi et al. [22], Davari et al. [23], Quan et al. [24], and Shang et al. [25] employ an algorithm to detect clusters in their access logs for the previous rule mining process.

We can observe several limitations in state-of-the-art approaches. The algorithm’s efficiency drops as the access log expands [16,17] or if there are many attributes and values [19]. In [21,22,23,24,25], many control variables must be selected to achieve a high-quality policy.

2.4. Evaluation Metrics

To evaluate the performance of our approach, we compare the access decision made by the mined policy with the original policy. It is a classification problem where the two classes are permitted and denied. If an access request is permitted in the original policy, the same access request must be permitted by the mined policy; we call this true positive (TP). If an access request is permitted by the original policy but not in the mined policy, it is known as false negative (FN). If an access request is denied by the original policy and the mined policy, then it is a true negative (TN). If an access request is denied by the original policy and permitted by the mined policy, we call this false positive (FP).

We use the F-score to measure the accuracy of our proposal. It is the harmonic mean of precision (exactness) and recall (completeness). The precision measures how many of the permitted requests are correct, while recall measures how many of the correct requests are permitted. The F-score, precision, and recall are calculated as follows:

$$Precision={\displaystyle \frac{TP}{TP+FP}}$$

(4)

$$Recall={\displaystyle \frac{TP}{TP+FN}}$$

(5)

$$F-score=2\times {\displaystyle \frac{Precision\times Recall}{Precision+Recall}}$$

(6)

We seek mined policies that are easy to interpret, manage, and audit by human operators. The Weighted Structural Complexity (WSC) is a generalization of policy size. It was introduced for RBAC policies [31] and then adapted for ABAC policies [16]. The WSC is the sum of the attribute–value expressions used to describe the extracted rules. It is calculated using the following formulas:

$$\begin{array}{c}WSC\left(\pi \right)=WSC\left(\mathcal{P}\right)\\ WSC\left(\mathcal{P}\right)={\displaystyle \sum _{\rho \in \mathcal{P}}}WSC\left(\rho \right)\\ WSC(\rho =\langle \mathcal{F}\rangle )=\left|\mathcal{F}\right|\end{array}$$

(7)

where $\mathcal{P}$ is the ABAC rule set, $p\in \mathcal{P}$ is an ABAC rule, and $\mathcal{F}$ is the attribute filter of the ABAC rule. Our objective is to generate policies with a high F-score, which are more equivalent to the original policies, and with a low WSC, which are easier to manage.

3. Policy Mining Proposed Approach

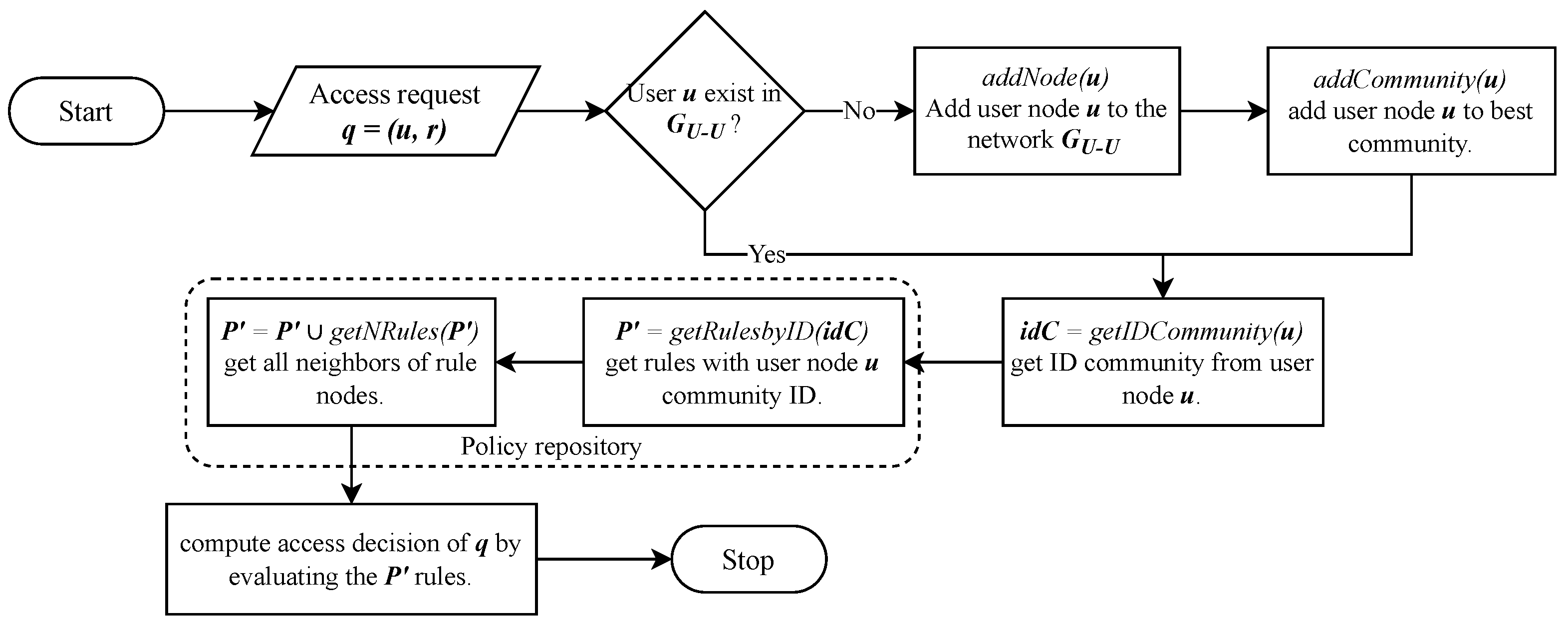
The conceptual methodology of our proposed ABAC policy mining is shown in Figure 1. Our approach is divided into five phases: (1) data preprocessing, (2) network model, (3) community detection, (4) rule extraction, and (5) rule refinement. The input of the methodology is an access log $\mathcal{L}$, and the output is a set of rules $\mathcal{P}$.

3.1. Data Preprocessing

In this phase, we convert raw data into a cleaner form so that in the next phases of the methodology, it provides more useful information. The input of the phase is the access log $\mathcal{L}$, and the output is the new clean access log $L^{\prime }$. We execute four tasks in this phase: (1) handling missing and null values, (2) converting continuous values to categorical values, (3) removing duplicated access requests, and (4) selecting the most used resources.

In the access log, we can find access requests with an error, that present some inconsistency or that are incomplete because there is a misconfiguration in the system or a modification is made by the administrators. This noisy access request and null values can affect the quality of the mined policy. For each attribute in A with a missing or null value, we introduce a unique placeholder value. For example, if there is a null value in a user attribute u.class and a missing value in a resource attribute r.type, we create two new values UNK1 and UKN2, respectively.

In the second task, we convert continuous values to categorical values. Some attributes have continuous values, for instance, the size of a resource r.size; in this case, there are an infinite number of values. To address such an issue, we map the continuous values into categories. In the example above, we can generate groups based on ranges of values.

Our bipartite network model consists of positive unique access requests; therefore, we remove all duplicated access requests, i.e., the same user accessing the same resource. In the last task, we calculate the access frequency of each resource in the access log. There are many resources with few access requests. In other words, just a small number of resources could help to extract more information to build a bipartite network model. We remove all resources under a specified threshold of number of access requests $T_R$.

3.2. Network Model

The objective of this phase is to build a network model from access log data. The input of the phase is the positive access log ${\mathcal{L}}^{+}$, and the output is a complex network that models access interactions of users and resources in the AC mechanism. In this phase, we execute three tasks: (1) bipartite network construction, (2) user network construction, and (3) user network analysis.

3.2.1. Access Request Bipartite Network

The first task is to identify both the entities that will function as the nodes of the network, and the relationship between entities that will represent the links. The basic function of the access control mechanism is to decide whether to grant or reject an access request made by a user toward a resource. Therefore, we identify two disjoint sets of nodes: users and resources. A link exists between a user node and a resource node if a user makes an access request toward a resource. A user cannot make an access request toward another user, and a resource cannot make an access request toward another resource; for this reason, the bipartite network definition condition holds. We define the access request bipartite network formally as follows:

Definition 2

(Access Request Bipartite Network (ARBN)). The access request bipartite network is triplet $G_{U-R}=(V_U,V_R,E_{U-R})$ defined as follows:

1. 

$V_U$ is the set of nodes that represent users U.

2. 

$V_R$ is the set of nodes that represent resources R.

3. 

$V_U\cap V_R=\varnothing$

4. 

$E_{U-R}$ is the set of links that exists between a user node $u\in V_U$ toward a resource node $r\in V_R$ if $q=\langle u,r\rangle \in L^{+}$.

3.2.2. User Network

Bipartite network projection is a method for obtaining two one-mode networks, in our case, a user network (a network with only user nodes) and a resource network (a network with only resource nodes). The one-mode networks are less informative than the bipartite network, but it is possible to apply a weighted projection to minimize the information loss. Our proposed approach only uses the user network. Two user nodes are joined by a link if both users have an access request for the same resource. The weight of the link is equal to the product of the importance of the common resource of each user node. The importance is determined based on the total number of resources each user accesses. We define the user network formally as follows:

Definition 3

(User Network (UN)). Let $G_{U-R}=(V_U,V_R,E_{U-R})$ be an access request bipartite network. The $V_U$ projection generates a user network $G_{U-U}=(V_{U-U},E_{U-U})$ defined as follows:

1. 

$V_{U-U}\subseteq V_U$ is the set of nodes that represent users U.

2. 

$E_{U-U}$ is the set of links that exists between two user nodes $u_i,v_j\in V_{U-U}$ if they have at least one common neighbor in $V_R$ of the network $G_{U-R}$. The weight of a link is given by

$$w\left(u_i{u}_j\right)={\displaystyle \frac{|N\left(u_i\right)\cap N\left(u_j\right){|}^2}{d\left(u_i\right)\times d\left(u_j\right)}}$$

(8)

where $N\left(u\right)$ is the neighborhood of the node u, i.e., the set of nodes that are linked to node u. $d\left(u\right)$ is the degree of the node u, i.e., the number of nodes linked to node u.

We analyze the generated user network to evaluate its properties and conclude whether we can use it as a complex network. We use the complex network definition from [32]:

Definition 4

(Complex Network). A Complex Network is a network $G=(V,E)$ consisting of a non-empty set of nodes V and a set of links E. Furthermore, it complies with the following properties:

1. 

$n=\left|V\right|$, $m=\left|E\right|$ commonly in the order of thousands or millions.

2. 

Low average degree $\langle k\rangle <<n$.

3. 

Low density $d<<1$.

4. 

Scale-free distribution $P\left(k\right)\approx k^{-\alpha }$.

5. 

Low average path length $\left(L\right)<<n$.

6. 

High average cluster coefficient $1/n<<\left(C\right)<<1$.

3.3. Community Detection

The main objective of this phase is to group the user nodes in communities or subnetworks. When we identify communities, the nodes within a community may share common properties or play similar roles in the complex network [33]. A community is a group of nodes where there are a large number of links between nodes within the same community and with the rest of the nodes in other communities. From the communities, it is feasible to extract user characteristics or properties that can help in the generation of ABAC policy rules.

The input data of this phase is the user network obtained in the previous phase. The output data will be a node partition $C_{G_{U-U}}$. In the current phase, two tasks are executed: (1) community detection and (2) community classification.

In the first task, a node partition is obtained by a community detection algorithm, and then, they are classified into three groups based on the number of resources accessed by each community.

3.3.1. Community Detection

We use the Louvain algorithm [34], which is based on optimizing the modularity quality function. The Louvain algorithm was chosen based on a prior comparative analysis of various methods, where we sought a balance between maximizing modularity and computational efficiency. The Louvain method demonstrated superior performance in this regard. Modularity is one of the most popular quality functions for measuring the quality in obtained community partition [35]. It compares the link density of each community with the density that could be obtained from the same community, but from a random network, where a community structure is not obtained [33]. By definition, $-1\le Q\left(\mathcal{P}\right)\le 1$; a value close to unity indicates a better partition. The definition of modularity is

$$Q\left(\mathcal{P}\right)={\displaystyle \frac{1}{2m}}\sum _{ij}\left[A_{ij}-{\displaystyle \frac{k_i{k}_j}{2m}}\right]\delta (C_i,C_j)$$

(9)

where m is the number of links in the network, and A is the adjacency matrix. The term ${\displaystyle \frac{k_i{k}_j}{2m}}$ represents the expected number of links given the degree of the two nodes and the total number of links in the network. The function $\delta$ returns one if the nodes i and j belong to the same community; it returns zero in the other case.

Louvain’s algorithm to detect communities iteratively executes two phases. First, each node is a new community. Next, each node joins the community of one of its neighbors which provides a higher modularity value. The above is repeated for all nodes until the modularity value does not improve with new node joins. In the second phase, all the nodes of a community are grouped, and a new network is built where the nodes are the communities of the previous phase. The time complexity of the Louvain algorithm is $O(n\times log(n\left)\right)$, where n is the number of nodes in the network. The algorithm is non-deterministic and belongs to the group of agglomerative hierarchical algorithms.

In our approach, the detected communities correspond to groups of users that exhibit similar interaction patterns within the access control system. These communities arise from the projection of the ARBN, where nodes represent users and resources, and edges indicate recorded accesses. Projecting this graph onto the set of users generates a network in which users are connected if they share access to common resources. This structured projection allows the application of community detection techniques, grouping users who access similar sets of resources. Thus, communities reflect functional groupings that can be aligned with organizational roles or access profiles, providing a structural basis for rule inference in the ABAC model. At the end of the algorithm, we will obtain the user communities defined as follows:

Definition 5

(User Communities). Let $G_{U-U}=(V_{U-U},E_{U-U})$ be a user network. A community $C=(V_{U-U}^C,E_{U-U}^C)$ is a sub-network of the user network $G_{U-U}$, where $V_{U-U}^C\subseteq V_{U-U}$ and $E_{U-U}^C\subseteq E_{U-U}$. The user communities $C_{G_{U-U}}$ of the user network $G_{U-U}$ is

$$\begin{array}{c}\hfill C_{G_{U-U}}=\{C_1,C_2,\dots ,C_l\}\mathit{where}{C}_1\cup C_2\cup \dots \cup C_l=V_{U-U}\mathit{and}\hfill \\ \hfill \mathit{for}\mathit{all}i,j=1,2,\dots ,l,C_i\cap C_j=\varnothing \mathit{as}\mathit{long}\mathit{as}i\ne j\end{array}$$

(10)

In the community partition $C_{G_{U-U}}$, we can find sparse communities, i.e., networks with a low density. Our objective is to obtain dense communities; for this reason, we apply the Louvain algorithm to those sparse communities to obtain dense sub-communities. Ultimately, we expect that all communities and sub-communities have a density value close to a unit; in other words, the groups of users detected are densely connected.

3.3.2. Community Classification

We classify communities based on the number of resources accessed by each community. There are three types of communities: F-type: focused; M-type: medium; and S-type: sparse. Regardless of the size of the community, focused communities access few resources, typically one or two. Sparse communities, on the other hand, have access to a large number of resources, greater than a threshold $T_S$. Medium communities access between three and $T_S$.

Each detected community $c\in C_{G_{U-U}}$ is evaluated based on the number of resources accessed $R^c$. To begin, we find the maximum number of resources accessed by any community, denoted as $R_{max}^C$. Two thresholds $t_{R1}$ and $t_{R2}$ are set, using a fraction of the number of resources $t_1$ and $t_2$. S-type communities have greater resources than $t_{R_1}$. M-type communities have resources between $t_{R_2}$ and $t_{R_1}$, and F-type communities have resources below $t_{R_2}$. Algorithm 1 shows the process of community classification.

Each detected community $c\in C_{G_{U-U}}$ is evaluated based on the number of resources accessed $R^c$. To begin, we find the maximum number of resources accessed by any community, denoted as $R_{max}^C$. Two thresholds $t_{R1}$ and $t_{R2}$ are set, using a fraction of the number of resources $t_1$ and $t_2$. S-type communities have greater resources than $t_{R_1}$. M-type communities have resources between $t_{R_2}$ and $t_{R_1}$, and F-type communities have resources below $t_{R_2}$. Algorithm 1 shows the process of community classification.

Algorithm 1 Community classification algorithm.

1: procedure  CommunityClassification Input:  $C_{G_{U-U}}$, $t_1$, $t_2$ Output:  $C_{G_{U-U}}^{\prime }$ 2:  $R_{max}\leftarrow max\left([R^{c}forc\in C_{G_{U-U}}]\right)$ 3: $t_{R1}=t_1\ast R_{max}$ 4: $t_{R2}=t_2\ast R_{max}$ 5: for all  $C\in C_{G_{U-U}}$  do 6:     if $R^c>t_{R1}$ then 7:         $C.type\leftarrow S$ 8:     else if $R^c>t_{R2}$ then 9:         $C.type\leftarrow M$ 10:     else 11:         $C.type\leftarrow F$ 12:     end if 13: end for

3.4. Policy Rule Extraction

In this phase, we analyze the communities and generate ABAC policy rules. Then, a rule network is generated. The input data are the classified user communities, obtained from the previous phase. The output is a network of ABAC policy rules.

According to Definition 1, a rule is a tuple $\rho =\langle \mathcal{F},op,d\rangle$. In our proposal, rules are limited to having only the attribute filter $\mathcal{F}$, and the decision value d. Additionally, we add the unique identifier of the communities from which the rules were inferred. The identifier will help the access decision in the AC. An example of a rule generated in our proposal is shown below:

$$\begin{array}{c}\hfill rule1=\langle [idCom,id1],[u.dpto=cc],[u.class=math],\\ \hfill [r.group=a],[r.classs=math],permit\rangle \end{array}$$

3.4.1. Rule Inference

There are three ways to extract rules from communities, depending on the type of community. Algorithm 2 outlines the process of inferring rules. The input to the algorithm is the community classification $C_{G_{U-U}}$, and the output is the set of rules $\mathcal{P}$.

F-type communities: The first step is to extract the resource set $R^{\prime }$ that is accessed by all users in the community. If there is more than one resource ($|R^{\prime }|>1$), all attribute–value pairs in common, among all resources in $R^{\prime }$, are taken to add to the rule. If there is only one resource that all users in the community access, then all the attribute–value tuples that identify the resource are taken to generate the rule. The next step is to obtain the attribute–value tuples of the users. The tuples with the highest frequency in the community are obtained.

M-type communities: A less frequent resource pruning process is used (Algorithm 2, line 7). In M-type communities, it is possible to identify less frequent resources that are accessed by a small number of users compared with the rest of the resources. The information that less frequent resources can offer us does not have any meaningful impact on the generation of rules; on the contrary, it could add noise to the rule. Less frequent resources do not describe or reflect user access in a community.

Algorithm 2 Rule inference algorithm.

1: procedure  RuleInference Input:  $C_{G_{U-U}},t_{R-freq}$ Output:  $\mathcal{P}$ 2: $\mathcal{P}\leftarrow \varnothing$ 3: for all  $C\in C_{G_{U-U}}$  do 4:     $R^{\prime }\leftarrow getResources\left(C\right)$ 5:                                                                             ▹ only M-type or S-type communities. 6:     if $C.type\in \{M,D\}$ then 7:         $R^{\prime }\leftarrow removeLessFrequentResources(R^{\prime },t_{R-freq})$ 8:                                                                                 ▹ only S-type communities. 9:         if $C.type\in \left\{D\right\}$ then 10:            $R_{sig}^{\prime }\leftarrow getSignificantResources\left(R^{\prime }\right)$ 11:            for all $r^{\prime }\in R_{sig}^{\prime }$ do 12:                $\rho \leftarrow \{\langle idCom=C.index\rangle \}$ 13:                $\rho \leftarrow \rho \cup attributeValue\left(r^{\prime }\right)$ 14:                $\rho \leftarrow \rho \cup attributeValueCommon\left(V_{U-U}^C\right)$ 15:                $\mathcal{P}\leftarrow \mathcal{P}\cup \left\{\rho \right\}$ 16:            end for 17:            $R^{\prime }\leftarrow R^{\prime }-R_{sig}^{\prime }$ 18:         end if 19:     end if 20:                                                                                 ▹ all communities: F-type, M-type, and S-type. 21:     $\rho \leftarrow \{\langle idCom=C.index\rangle \}$ 22:     $\rho \leftarrow \rho \cup attributeValueCommon\left(R^{\prime }\right)$ 23:     $\rho \leftarrow \rho \cup attributeValueCommon\left(V_{U-U}^C\right)$ 24:     $\mathcal{P}\leftarrow \mathcal{P}\cup \left\{\rho \right\}$ 25: end for

To prune less frequent resources, it is necessary to set a threshold based on the number of users accessing a resource $t_{R-freq}$. The threshold value can vary, but it is recommended that it be $10\%$ or up to $20\%$ for all users—for example, if there are 20 users in community C, $|V_{U-U}^C|=20$ and a threshold of $10\%$ is established; that is, $t_{R-freq}=0.10\left|V_{U-U}^C\right|$. In this example, the resources that are accessed by two users or fewer are considered less frequent resources; therefore, they are removed from the total of resources in the community. Once the resource pruning is executed, the same process is applied as for F-type communities.

S-type communities: This type of community is characterized by having a large number of users and resources. As there are more resources in the community, it is more difficult to generate rules that characterize it. It is possible to identify a small set of resources that are accessed by the most users in the community. The set of most frequent resources, called significant resources, is useful for characterizing the entire community of users.

As in the M-type communities, less frequent resources are filtered out. Subsequently, the F-type community approach is applied with a slight modification. Rules are generated with the set of significant resources, the common attribute–value tuples are taken from the set, and the rule is completed with the users of the community. Then, with the less significant resources not eliminated, rules are generated with the F-type community approach. S-type communities tend to generate more rules than the rest of the communities.

3.4.2. Rule Network Modeling

The construction of the rule network $G_{\mathcal{P}}$ takes as nodes the rules of the set $\mathcal{P}$. A link joins two nodes if the Jaccard index is above a given threshold $t_{\mathcal{P}}$ as given in Definition 6. The threshold $t_{\mathcal{P}}$ serves two key purposes: first, to ensure that the resulting network maintains a low edge density, and second, to optimize the F-score value. Through empirical evaluation, we identify the threshold value that yields the best trade-off between sparsity and classification accuracy. Having a densely connected rule network is not beneficial because it would result in all rules being connected, which is not desirable during evaluation. The goal is to preserve the distinctiveness of individual rules.

Definition 6

(Rule Network). The rule network is a tuple $G_{\mathcal{P}}=(V_{\mathcal{P}},E_{\mathcal{P}})$ defined as follows:

1. 

$V_{\mathcal{P}}$ is the set of nodes that represent rules $\mathcal{P}$.

2. 

$E_{\mathcal{P}}$ is the set of links that exists between a node ${\rho }_1\in V_{\mathcal{P}}$ toward a node ${\rho }_2\in V_{\mathcal{P}}$ if the Jaccard index $J({\rho }_1,{\rho }_2)$ is above a given threshold $t_{\mathcal{P}}$.

$$({\rho }_1,{\rho }_2)\in E⟺J({\rho }_1,{\rho }_2)>t_{\mathcal{P}}$$

(11)

where $J({\rho }_1,{\rho }_2)={\displaystyle \frac{|{\mathcal{F}}_{{\rho }_1}\cap {\mathcal{F}}_{{\rho }_2}|}{|{\mathcal{F}}_{{\rho }_1}\cup {\mathcal{F}}_{{\rho }_2}|}}$.

3.5. Policy Refinement

The objective of policy refinement is to improve the quality of the mined policy in the previous phase by tackling false negatives and false positives. We create new rules to overcome false negatives and negative rules for false positives. Negative rules restrict access to requests that match their attribute–value tuples. They have the opposite functionality of the rules generated. Because they are specific rules, they tend to contain many attribute–value tuples.

The input of policy refinement is the set of false negatives (FN), false positives (FP), and rule network $G_{\mathcal{P}}$. At the end, the output is an augmented set of rules and an updated rule network. The phase is composed of three tasks: (1) FN-refinement, (2) FP-refinement, and (3) rule network update.

FN-refinement: The set of FNs is those access requests that are allowed by the original policy but not by the mined policy. The rule inference process is applied but as the input for the access requests in the FN set. At the end of the process, a set of rules based on the FN requests will be obtained.

FP-refinement: For FPs, it is not possible to apply the complete rule inference approach because there are no relationships between users and resources in the access requests. Refinement in FP tracks the rules that produce the requests in FP and, from these rules, generates negative rules. Value attribute tuples of requests in FP are added to the positive rule generated by the FP to generate a specific negative rule.

Rule network update: Once the rules are generated in the two previous stages, the rule network $G_{\mathcal{P}}$ is updated by adding the new rules obtained in the FN-refinement. In the same way, the Jaccard similarity index is used to create new links between the existing and new nodes. For the resolution of the requests, the community identifier obtained in the rule inference phase is considered.

4. Access Decision

In the traditional ABAC, the Policy Decision Point (PDP) computes access decisions by evaluating the ABAC policy. In our approach, we add a new stage in the PDP that computes a smaller subset of rules to compare. The main advantage of our proposal is that we reduce the number of rules to evaluate. Figure 2 shows our proposal to add in the PDP the stage Rule Selection by ID (RS), which uses the topological structure of the rule network to decide the subset of rules to evaluate for a specific access request. With this, we optimize the access decision process specifically for complex and big policies.

The flow chart of the RS stage is shown in Figure 3. First, we need to know whether a user node from the access request exists in the user network. If it does not exist, we add it as a neighbor of all nodes that access the same resource. With this, we simulate the topological position of the new user node in the projection operation. The weight of the new links will be equal to 1. The Algorithm 3 shows the process. Lines 3–6 obtain all nodes that access the same resource from the access request. In line 8, we add the user node in the network and, in the last for loop, we add all links from the new user node to each node with the same resource. The next process is to assign the new user to the community with a higher modularity value. The assignCommunity function (Algorithm 4) obtains all communities from all neighbors of the user node. Then, the user node removes and moves into the community of each neighbor and calculates the modularity value. The user node is placed into the community with the greatest modularity value. At this point, the user node belongs to a community, and all rules have the ID of the communities from which they were generated. Thus, we can obtain all rules by ID user node community. The getRulesbyID function returns all rules with the ID user node community, and the getNRules function returns the rule node neighbors of each rule with the ID user node community. All the rules of both functions are used for evaluating the request and computing an access decision.

Algorithm 3 Add a new user node to the user network.

1: procedure  addNode Input:  $q=(u,r)$, $G_{U-U}=(V_{U-U},E_{U-U})$ 2: $U_{resource}\leftarrow \varnothing$ 3: for all  $n\in V_{U-U}$  do 4:     if $n.resource=q.r$ then 5:         $U_{resource}\leftarrow U_{resource}\cup \left\{n\right\}$ 6:     end if 7: end for 8: $V_{U-U}\leftarrow V_{U-U}\cup \{q.u\}$ 9: for all  $n\in U_{resource}$  do 10:     $E_{U-U}\leftarrow E_{U-U}\cup \left\{(q.u,n,1)\right\}$                    ▹ add link 11: end for

Algorithm 4 Add a new user node to the best community.

1: procedure  addCommunity Input:  $u,G_{U-U}$ 2: $Q_{max}\leftarrow 0$ 3: $C_{Qmax}\leftarrow None$ 4: for all  $v\in neighbors\left(u\right)$  do 5:     $u.community\leftarrow v.community$ 6:     $Q^{\prime }\leftarrow modularity\left(G_{U-U}\right)$ 7:     if $Q^{\prime }>Q_{max}$ then        ▹ assign to the community that increases the modularity 8:         $Q_{max}\leftarrow Q^{\prime }$ 9:         $C_{Qmax}\leftarrow v.community$ 10:     end if 11: end for 12: $u.community\leftarrow C_{Qmax}$

5. Results

5.1. Datasets

To evaluate the performance of our proposed methodology, there are two types of access logs (datasets): synthetic/manual and real-world. The synthetic access logs are manually written or randomly generated by an algorithm. It is possible to set parameters such as the number of rules, attributes, users, and resources, which is advantageous for testing purposes. The real-world access logs are extracted from access control systems implemented by an organization. The availability of real datasets is limited due to the security risk and data sensitivity. In our experiments, we use three datasets:

Healthcare (HC): This dataset has access control records of health center staff. The users are nurses, doctors, and patients. The resources are electronic health and history files. It is a synthetic dataset and is adapted from [16]. There are 1000 users and 2000 resources. The size of the access log is equal to 18,000 access requests: 9000 requests positive and negative.

Amazon Kaggle (AMZ): This dataset has access control records of Amazon’s employees. It is a real-world dataset where the users and resources are replaced by numerical values to maintain the organization’s privacy. The dataset contains more than 12,000 users, 7000 resources, and 32,000 access requests, of which 30,000 are positive access requests and 2000 are negative access requests. This dataset is from a Kaggle competition [36].

Smart Building IoT (IoT): This is a synthetic dataset for creating interactions between individuals and IoT devices in a smart building. First, we developed the policy rules. Then, we established attributes and values for users and resources. To generate the access log, we relied on the participation distribution of both users and resources in the real-world dataset from Amazon. Our dataset contains 120 users, 990 resources, and 49,925 access requests, where approximately the same number of positive and negative accesses occur.

Table 2. Details of the datasets used.

Dataset	$\left|\mathit{A}\right|$	$\left|\mathit{V}\right|$	$\left|\mathit{L}\right|$	$|{\mathit{L}}^{+}|$	$|{\mathit{L}}^{-}|$
Healthcare (HC)	12	77	18 K	9 K	9 K
Amazon Kaggle (AMZ)	7	15 K	32 K	30 K	2 K
Smart Building IoT (IoT)	9	52	$49K$ K	24 K	25 K

shows the details of the datasets. $\left|A\right|$ is the number of attributes, $\left|V\right|$ is the number of unique values that the A attributes can take in the $\mathcal{L}$ log, $\left|\mathcal{L}\right|$ shows the number of access requests in the dataset, $|{\mathcal{L}}^{+}|$ shows positive access requests, and $|{\mathcal{L}}^{-}|$ shows negative access requests by policy.

5.2. Experimental Setup

We use a computer with PopOs Linux 5.16, a 3.3 GHz Intel Core i5-2500, 8GB of RAM, and a GTX 780 graphic card. The implementation is performed in Python 3.7. We use the NetworkX library to build the network models and the igraph library for network analysis. To validate the results of our experiments, we use K-fold Cross-Validation [37] with $K=10$, $80\%$ training data, and $20\%$ testing data.

5.3. General Results

Table 3. Results at the end of each phase. Data preprocessing, network model, and community detection phase are shown as 1, 2, and 3, respectively.

Phase	HC	AMZ	IoT
1	$|{\mathcal{L}}^{+}|=2437$, $\left|U\right|=621,\left|R\right|=211$	$|{\mathcal{L}}^{+}|=9504$, $\left|U\right|=5436,\left|R\right|=150$	$|{\mathcal{L}}^{+}|=\mathrm{237,274}$, $\left|U\right|=120,\left|R\right|=990$
2	$G_{U-U}=(V_{U-U},E_{U-U})$ where $|V_{U-U}|=621$, $|E_{U-U}|=\mathrm{14,923}$	$G_{U-U}=(V_{U-U},E_{U-U})$ where $|V_{U-U}|=5436$, $|E_{U-U}|=\mathrm{743,311}$	$G_{U-U}=(V_{U-U},E_{U-U})$ where $|V_{U-U}|=120$, $|E_{U-U}|=2095$
3	Avg. $|C_{G_{U-U}}|=42$ Avg. modularity: 0.475 Avg. S-type comms.: 4% Avg. M-type comms.: 28% Avg. F-type comms.: 68%	Avg. $|C_{G_{U-U}}|=82$ Avg. modularity: 0.65 Avg. S-type comms.: 8% Avg. M-type comms.: 9% Avg. F-type comms.: 83%	Avg. $|C_{G_{U-U}}|=49$ Avg. modularity: 0.28 Avg. S-type comms.: 8% Avg. M-type comms.: 18% Avg. F-type comms.: 74%

shows the results obtained after the first three phases of both datasets. After the data preprocessing phase, we obtain 2437 access requests with 621 users and 211 resources from the HC dataset. With the AMZ dataset, we obtain 9504 access requests with 5436 users and 150 resources. In the IoT dataset, we obtain 49,925 access requests with 120 users and 990 resources. In the second phase, the network model, we generate a user network with 621 nodes and 14,923 links from the HC dataset. With the AMZ dataset, we generate a user network with 5436 nodes and 743,311 links. From the IoT dataset, we generate a user network with 120 nodes and 2095 links. In the community detection phase, we obtain a modularity value of 0.48, 0.65, and 0. for the HC, AMZ, and IoT datasets, respectively.

Table 4. Results of the quality and complexity of the policy in the phases of rule inference and policy refinement.

Dataset	Phase	FN	FP	Precision	Recall	F-Score	$\left|\mathcal{P}\right|$	$\mathbf{WSC}$
HC	4	672	17	0.9899	0.7129	0.8289	41	231
	5	63	10	0.9956	0.9730	0.9842	90	389
AMZ	4	511	30	0.9966	0.9462	0.9707	82	274
	5	134	11	0.9988	0.9858	0.9923	156	564
IoT	4	3681	2760	0.7899	0.8337	0.8112	49	203
	5	1255	1402	0.9300	0.9207	0.9254	101	461

shows the results of the quality and complexity of the policies generated after the rule inference and policy refinement phase. The results show how the F-score improves after the refinement phase in all datasets.

Table 5. Comparative analysis of policy complexity and quality of the mined policy with previous work on the mining of ABAC policies from the access log. The ‘-’ symbol represents that it was not reported by the authors.

$\mathit{\pi }$	Mining Approach	F-Score	$\left|\mathcal{P}\right|$	$\mathbf{WSC}$
${\pi }_{H{C}^{\prime }}$	Our approach	0.9842	90	389
	Karimi et al. [22]	0.62	15	67
${\pi }_{AM{Z}^{\prime }}$	Our approach	0.9923	156	564
	Quan et al. [24]	0.9951	-	-
	Karimi et al. [22]	0.97	20	44
	Cotrini et al. [19]	0.8495	1055	2431
	Jabal et al. [21]	0.8600	-	-

shows a comparative analysis of the policy quality and complexity results using Cotrini et al. [19], Jabal et al. [21], Karimi et al. [22], and Quan et al.’s [24] approaches. This is because, to the best of our knowledge, they constitute the only studies in the literature that employ the same datasets as our work. The remaining studies listed in Table 1 rely on different datasets or on modified/adapted versions for the evaluation of their approaches. The results lead us to conclude that our approach generates policies with high quality but is more complex than the state-of-the-art approaches.

While the recent approach by Quan et al. [24] achieves a marginally higher F-score on the ${\pi }_{AM{Z}^{\prime }}$ dataset, our method demonstrates distinct advantages regarding policy transparency and structural efficiency. Note that Quan et al. do not report complexity metrics ($\left|\mathcal{P}\right|$ and WSC), making a comprehensive comparison challenging. In contrast, our network-based approach generates a policy with well-defined structural properties (156 rules, WSC = 564), providing a complete and interpretable ABAC policy. This explicit modeling of policy structure offers significant practical benefits for policy analysis, maintenance, and refinement in real-world deployments, representing an important contribution beyond raw accuracy metrics.

5.4. Detailed Results

5.4.1. HC

Analyzing the HC dataset, the size of positive access requests is equal to 8735 and negative access requests equal to 8998. It contains five user attributes and six user attributes. Applying task one, we obtain ten new elements; add at least one element for each attribute. Task two does not apply to the dataset because there are no continuous values. Then, in task three, the positive access request is reduced to 6998 with 1041 users and 2113 resources. Figure 4a shows the distribution of access requests. It is observed that there is a small number of resources that have a high number of access requests. On the other hand, there is a large number of resources that have few access requests. For the experiment, all those resources that are accessed with a number of requests greater than six are used. The dotted line shows the resources with more requests, which is equal to $10\%$ of all the resources. Each request that accesses the 211 resources is accepted, i.e., 2347 positive requests with 621 users and 211 resources.

In the network model phase, the ARBN $G_{U-R}^{HC}=(V_U,V_R,E_{U-R})$, where $|V_U|=621$, $|V_R|=211$, and $|E_{U-R}|=2347$ generate the UN $G_{U-U}=(V_{U-U},E_{U-U})$, where $|V_{U-U}|=621$ and $|E_{U-U}|=$ 14,923.

Table 6. Complex network properties of HC user network.

Property	Value
1. $n=\left|V\right|$, $m=\left|E\right|$ commonly in the order of thousands or millions.	$n=621$, $m=\mathrm{14,923}$
2. Low average degree $\langle k\rangle <<n$.	$k=48.0612<<621$
3. Low density $d<<1$.	$d=0.0775<<1$
4. Scale-free distribution $P\left(k\right)\approx k^{-\alpha }$.	See Figure 5a.
5. Low average path length $\left(L\right)<<n$.	$L=2.3625<<621$
6. High average cluster coefficient $1/n<<\left(C\right)<1$.	$0.0016<<C=0.6238<1$

shows the complex network properties of the UN, and Figure 5a its degree distribution. According to the topological properties, the UN is a complex network.

In the third phase, community detection, the Louvain algorithm detects 13 communities with modularity value equal to $0.4750$. When applying sub-community detection, an average of 42 communities are generated. Then, the 42 communities are classified into three groups using $t_{R1}=0.5$ and $t_{R1}=0.2$ (see Figure 6a). The community with the largest number of resources is 94 of the 211 resources.Taking the previous community as $100\%$, the threshold for determining S-type communities is that they have access to more than 47 ($50\%$) resources, and the threshold for determining M-type communities is that they have access to more than 23 ($25\%$) resources but fewer than 48; the threshold for determining F-type communities is that they have access to fewer than 23 resources. On average, 2 S-type, 12 M-type, and 28 F-type communities are generated.

Once the communities are classified, the rule inference algorithm is applied to each community. It generates 42 rules, one per community. The $T_{R-freq}$ threshold is set to 0.2, and the $T_{R-sign}$ threshold is 0.5. With the rules, it generates a rule network $G_{\mathcal{P}}=(V_{\mathcal{P}},E_{\mathcal{P}})$ where $|V_{\mathcal{P}}|=42$ and $|E_{\mathcal{P}}|=244$ with a threshold $T_{\mathcal{P}}=3$. At this point, the generated policy has an F-score value equal to $0.8289$ and a complexity $WSC=231$.

Finally, in the policy refinement phase, the augmented rule network $G_{\mathcal{P}}^{\prime }=(V_{\mathcal{P}}^{\prime },E_{\mathcal{P}}^{\prime })$, where $|V_{\mathcal{P}}^{\prime }|=106$ and $|E_{\mathcal{P}}^{\prime }|=1247$. Figure 7 shows the rule network after the refinement phase. It is possible to identify the community where the rules were generated and in which phase of the methodology they were generated. The F-score of the generated policy is equal to $0.9842$; FN decreases, as well as FP. The former is because of applying our approach again in FN, and the latter is a result of the generation of negative rules. The complexity $WSC$ of the generated policy is equal to 389. The average total runtime is 1.16 min.

5.4.2. AMZ

This dataset has 30,872 positive access requests and 1897 negative access requests. It contains only eight user attributes. It does not have null values or continuous values. Thus, tasks one and two of the data preprocessing phase do not apply. In task three, duplicate access requests are eliminated, and positive access requests are reduced to 24,697. Figure 4b shows the distribution of access requests. At the end of the first phase, the AMZ dataset has 9501 positive access requests, 5436 users, and 150 resources.

The AMZ ARBN network $G_{U-R}^{AMZ}=(V_U,V_R,E_{U-R})$, where $|V_U|=5436$, $|V_R|=150$, and $|E_{U-R}|=9501$ generate the UN $G_{U-U}=(V_{U-U},E_{U-U})$, where $|V_{U-U}|=5436$ and $|E_{U-U}|=$ 743,311. According to the topological properties shown in

Table 7. Complex network properties of AMZ user network.

Property	Value
1. $n=\left|V\right|$, $m=\left|E\right|$ commonly in the order of thousands or millions.	$n=5436$, $m=\mathrm{743,311}$
2. Low average degree $\langle k\rangle <<n$.	$k=273.4772<<5436$
3. Low density $d<<1$.	$d=0.0503<<1$
4. Scale-free distribution $P\left(k\right)\approx k^{-\alpha }$.	See Figure 5b.
5. Low average path length $\left(L\right)<<n$.	$L=2.4426<<5435$
6. High average cluster coefficient $1/n<<\left(C\right)<1$.	$0.0002<<C=0.8424<1$

, the UN is a complex network.

In the community detection phase, the first execution of the Louvain algorithm detects 16 communities with a modularity value equal to $0.65$. Then, the second execution generates an average of 82 communities. The threshold for determining S-type communities is that they have access to more than 51 ($50\%$) resources, the threshold for determining M-type communities is that they have access to more than 25 ($25\%$) resources but fewer than 51 and the threshold for determining F-type communities is that they have access to fewer than 25 resources, as we can see in Figure 6b. On average, 7 S-type, 8 M-type, and 67 F-type communities are generated.

The fourth phase, rule inference extraction, extracts 82 rules, one per community. Like the CS dataset, the same values are used for the thresholds: $T_{R-freq}=0.2$ and $T_{R-sign}=0.5$. The generated rule network $G_{\mathcal{P}}=(V_{\mathcal{P}},E_{\mathcal{P}})$, where $|V_{\mathcal{P}}|=82$ and $|E_{\mathcal{P}}|=946$, with a threshold $T_{\mathcal{P}}=2$. At this point, the generated policy has an F-score value equal to $0.9707$ and a complexity $WSC=274$.

In the last phase, the augmented rule network $G_{\mathcal{P}}^{\prime }=(V_{\mathcal{P}}^{\prime },E_{\mathcal{P}}^{\prime })$, where $|V_{\mathcal{P}}^{\prime }|=189$ and $|E_{\mathcal{P}}^{\prime }|=1366$. Figure 8 shows the rule network after the refinement phase. We can see a large number of isolated nodes, about $50\%$ of all the nodes. This type of node describes a small set of access requests that have particular attribute–value tuples; for this reason, it is not possible to reach the threshold of similarity to add a link with other rules. The F-score of the generated policy is equal to $0.9923$ and its complexity $WSC=564$. The average total runtime is 2.35 min.

5.4.3. IoT

In the preprocessing phase, the first three tasks—handling missing/null values, converting continuous values, and removing duplicate requests—are skipped due to the absence of such cases in the dataset. However, a selection of the most frequently accessed resources are still selected. Figure 4c shows the distribution of the frequency of accesses to each resource. From a total of 990 resources, 400 more frequent resources are obtained. In the end, we obtain 120 users and 400 resources with about 17 K of requests.

In the network model phase, we generate an IoT ARBN $G_{U-R}^{IoT}=(V_U,V_R,E_{U-R})$, where $|V_U|=120$, $|V_R|=400$ and $|E_{U-R}|=$ 17,525. Then, we generate the UN $G_{U-U}=(V_{U-U},E_{U-U})$, where $|V_{U-U}|=120$ and $|E_{U-U}|=1380$. According to the topological properties shown in

Table 8. Complex network properties of IoT user network.

Property	Value
1. $n=\left|V\right|$, $m=\left|E\right|$ commonly in the order of thousands or millions.	$n=120$, $m=1380$
2. Low average degree $\langle k\rangle <<n$.	$k=23<<120$
3. Low density $d<<1$.	$d=0.1933<<1$
4. Scale-free distribution $P\left(k\right)\approx k^{-\alpha }$.	See Figure 5c.
5. Low average path length $\left(L\right)<<n$.	$L=1.5<<120$
6. High average cluster coefficient $1/n<<\left(C\right)<1$.	$0.0083<<C=0.8357<1$

, the UN is a complex network.

In the third phase, community detection, the first execution of the Louvain algorithm detects 11 communities with a modularity value equal to 0.75. Then, the second execution generates an average of 49 communities. The threshold to determine S-type communities is that 200 ($50\%$) resources, M-type communities access to lower than 200 resources and greater than 100 ($18\%$). F-type communities have access to less than 40 resources. Figure 6c shows the number of resource distribution. On average, eleven S-type, five M-type, and five type F communities are generated.

The fourth phase, rule inference, extracts 49 rules. The thresholds values used are $T_{R-freq}=0.2$ and $T_{R-sign}=0.5$. The generated rule network $G_{\mathcal{P}}=(V_{\mathcal{P}},E_{\mathcal{P}})$ where $|V_{\mathcal{P}}|=49$ and $|E_{\mathcal{P}}|=515$ with a threshold $T_{\mathcal{P}}=3$. At this point, the mined policy has a F-score value equal to $0.8112$ and a complexity $WSC=203$.

Finally, in the policy refinement phase, the augmented rule network $G_{\mathcal{P}}^{\prime }=(V_{\mathcal{P}}^{\prime },E_{\mathcal{P}}^{\prime })$ where ${\left|V_{\mathcal{P}}\right|}^{\prime }=101$ and $|E_{\mathcal{P}}^{\prime }|=1722$. Figure 9 shows the rule network after the refinement phase. The F-score of the mined policy is equal to $0.9254$. The complexity $WSC$ of the generated policy es equal to 461. The average total runtime is 3.20 min.

5.5. Evaluation Under Data and Structural Variations

This subsection presents an evaluation of the proposed algorithm under different data and structural conditions. We examined its performance with noisy and sparse datasets, tested its sensitivity to community classification thresholds, and compared its effectiveness against randomized network structures. Each experimental configuration was executed 10 times, and the reported results represent the average values obtained across all runs.

We assessed the efficiency of the proposed algorithm on datasets corrupted with synthetic noise, as well as on sparse datasets (hereafter referred to as partial datasets). The former was achieved by randomly reversing the access decisions (grant/deny) of a random subset of access requests; a 10% noisy dataset was produced by altering 10% of the complete access log. To evaluate performance on sparse data, we generated partial datasets by randomly selecting subsets of access requests from the complete access log.

Table 9. Results of policy complexity and quality with noisy and partial versions of the datasets.

Dataset	F-Score	$\left|\mathcal{P}\right|$	$\mathbf{WSC}$
HC	0.9837	91	391
Noisy HC (10%)	0.8019	89	379
Partial HC (90%)	0.8408	88	383
AMZ	0.9918	155	567
Noisy AMZ (10%)	0.8115	146	538
Partial AMZ (90%)	0.8462	152	592
IoT	0.9249	48	205
Noisy IoT (10%)	0.7827	46	190
Partial IoT (90%)	0.8113	45	206

summarizes the results of policy quality and complexity under noisy and partial conditions for the three evaluated datasets. The results show that the proposed approach maintains a stable policy structure even when the access logs are affected by noise or incompleteness. For all datasets, the F-score decreases moderately, indicating that the method is robust against perturbations in the input data. The number of mined rules ($\left|\mathcal{P}\right|$) and the weighted structural complexity (WSC) remain nearly constant, suggesting that the underlying structure of the mined policy is preserved despite degraded data quality.

The results of the policy complexity and quality analysis across different threshold values are presented in

Table 10. Analysis of policy complexity and quality employing diverse threshold values for community classification. The values in bold represent the best results for each dataset.

Dataset	${\mathit{t}}_1$	${\mathit{t}}_2$	F-Score	$\left|\mathcal{P}\right|$	$\mathbf{WSC}$
HC	0.4	0.15	0.9822	95	407
	0.5	0.25	0.9842	90	389
	0.6	0.35	0.9854	93	396
AMZ	0.4	0.15	0.9839	143	569
	0.5	0.25	0.9923	156	564
	0.6	0.35	0.9862	139	550
IoT	0.4	0.15	0.9133	45	199
	0.5	0.25	0.9254	49	203
	0.6	0.35	0.9254	46	207

. The data indicates a clear trade-off between policy quality, measured by F-score, and complexity, measured by the number of policies ($\left|\mathcal{P}\right|$) and the WSC. For the HC and AMZ datasets, the configuration with thresholds $t_1=0.5$ and $t_2=0.25$ achieved the highest F-score (0.9842 and 0.9923, respectively), while also maintaining or reducing the WSC compared with other threshold pairs. The IoT dataset showed a different trend, where the F-score improved from 0.9133 to a peak of 0.9254 at $t_1=0.5$, with no further improvement at $t_6=0.6$, although at the cost of a slight increase in WSC. Overall, these findings suggest that an intermediate threshold value of $t_1=0.5$ and $t_2=0.25$ provides a balance, consistently yielding high-quality access control policies with manageable complexity across diverse datasets. It is important to note, however, that, while these specific threshold values ($t_1=0.5$, $t_2=0.25$) yielded the best results in this study, they are inherently data-dependent; the optimal parameters may vary for other datasets with different characteristics and distributions.

For comparative analysis, random networks were generated using the configuration model, preserving the original network’s degree sequence while randomizing connections. Edge weights were assigned randomly, and node attributes were copied from the original networks. The comparative evaluation of our proposed model against a random network structure is summarized in

Table 11. Evaluation of policy complexity and quality within a random network structure. The values in bold represent the best results for each dataset.

Dataset	Network	F-Score	$\left|\mathcal{P}\right|$	$\mathbf{WSC}$
HC	Our model	0.9838	89	387
	Random	0.8059	96	411
AMZ	Our model	0.9919	157	562
	Random	0.7115	148	594
IoT	Our model	0.9247	48	205
	Random	0.8208	44	186

. The results demonstrate a consistent and significant superiority of our model in terms of policy quality, as reflected by the F-score. Specifically, our model achieved markedly higher F-scores across all datasets compared to the random network. In terms of complexity, the random network occasionally produced a marginally lower number of policies or WSC. These findings conclusively indicate that our model’s structured approach yields a far more favorable balance between quality and complexity, effectively prioritizing high-fidelity policy generation without a significant increase in structural overhead.

5.6. Computational Efficiency

Table 12. Time complexity of all phases and tasks in our approach. Notation: L is the access log, $O\left(\right|L^{+}\left|\right)$ is the positive access log, A is the set of attributes, $V_U$ is the set of user nodes in the ARBN, $V_{U-U}$ is the set of user nodes in the UN, R is the set of resources, $\mathcal{P}$ is the initial set of rules, ${\mathcal{P}}^{\prime }$ is the refined set of rules, FN is the set of false negatives, and FP is the set of false positives.

Phase	Task	Time Complexity
Data Preprocessing	Null values	$O\left(\right|L|\times |A\left|\right)$
	Continuous to categorical	$O\left(\right|L|\times |A\left|\right)$
	Remove duplicates	$O\left(\right|L\left|\right)$
	Frequent resources	$O\left(\right|L\left|\right)$
Network Model	ARBN	$O\left(\right|L^{+}\left|\right)$
	UN	$O\left(\right|V_U\left|\right)$
Community Detection	Community detection	$O\left(\right|V_{U-U}|\times log|V_{U-U}\left|\right)$
	Community classification	$O\left(\right|U|\times |L\left)\right|$
Rule Mining	Rule inference	$O\left(\right|V_{U-U}|\times |R\left|\right)$
	Rule network	$O\left(\right|\mathcal{P}{|}^2)$
Policy Refinement	FN refinement	$O\left(\right|\mathcal{P}|\times |FN\left|\right)$
	FP refinement	$O\left(\right|\mathcal{P}|\times |FP\left|\right)$
	Rule network	$O\left(\right|{\mathcal{P}}^{\prime }{|}^2)$

summarizes the time complexity of each phase and task in our approach. The first phase of our proposal includes four tasks: handling missing/null values, converting continuous values, removing duplicates, and selecting frequently accessed resources. The first two tasks have a time complexity of $O\left(\right|L\left|\right|A\left|\right)$, while the last two run in $O\left(\right|L^{+}\left|\right)$. The time complexity of the first phase is dominated by $O\left(\right|L\left|\right|A\left|\right)$. In the second phase, the bipartite network task has a time complexity of $O\left(\right|L^{+}\left|\right)$, and the user network task, $O\left(\right|V_U\left|\right)$.

Note that $|V_U|<<O(|L^{+}\left|\right)$ in all datasets; thus, the network model phase is determined by $O\left(\right|L^{+}\left|\right)$. The community detection phase has a time complexity obtained by the Louvain algorithm $O\left(\right|V_{U-U}\left|log\right|V_{U-U}\left|\right)$. In the fourth phase, the rule inference task has a time complexity where the $R^C$ is the resources in the community c. The time complexity of the rule network is equal to $O\left({\mathcal{P}}^2\right)$; thus, the time complexity of the rule mining phase is dominated by the rule inference task, i.e., $O\left(\right|V_{U-U}|\times |R^c\left|\right)$. Finally, the policy refinement phase is determined by the number of false negatives or false positives. The policy rule extraction phase dominates the total complexity of our proposal.

6. Conclusions and Discussions

In this work, a novel approach for ABAC policy mining based on the analysis of complex networks is proposed. Each phase of the proposal is described, and experimental results are presented. Our work receives as input an access control log which contains the records of access requests, both permitted and denied. The output is the ABAC access control policy, modeled as a network, which contains the rules and their relationships that will be evaluated to determine whether an access request is permitted or denied.

Our approach transforms access logs into a bipartite network of users and resources, which is converted into a user network through weighted projection based on shared resources. The Louvain algorithm detects communities in this network, classified into three types by resource access patterns. For each community, rules are inferred from attribute frequencies and adapted to community characteristics, forming a structured rule network.

The initial rule network is refined by addressing uncovered positive requests and incorporating negative rules, resulting in an augmented policy with improved accuracy. This network-based methodology leverages topological properties to identify functional roles and access patterns, proving to be an effective alternative to traditional clustering techniques while maintaining interpretability and scalability in access control management.

Our network-analysis-based approach generates ABAC policies with high accuracy; that is, they replicate with high similarity the access control policy that originated the access log. The set of extracted rules is modeled as a network; the policy obtained is not a list of rules but a structure of rules which helps in the process of rule evaluation. This constitutes a novel approach to modeling access control rules not previously reported in the literature.

The comprehensive evaluation demonstrates the robustness and adaptability of our approach under various challenging conditions. When tested on noisy datasets, generated by randomly reversing access decisions, and sparse datasets, created by randomly selecting subsets of access requests, our method maintained stable policy structures with only moderate decreases in F-score. This resilience to data perturbations confirms that the underlying network structure effectively captures essential access patterns rather than overfitting to specific data points. Furthermore, our investigation of threshold parameters revealed that intermediate values ($t_1=0.5$, $t_2=0.25)$ generally provide an optimal balance between policy quality and complexity across diverse datasets, though we acknowledge that these parameters may require adjustment for datasets with substantially different characteristics.

Crucially, comparative analysis against randomly structured networks—generated using the configuration model with random edge weights—validates the significance of our structured approach. The substantially higher F-scores achieved by our model across all datasets, with only minimal increases in complexity metrics, demonstrate that the discovered network topology contains meaningful access control information beyond mere connectivity patterns. This superior performance persists even when the random networks occasionally achieve slightly lower complexity, indicating that our method’s quality improvements justify the modest complexity overhead.

While our approach demonstrates strong performance in replicating access control policies and introduces a novel network-based modeling framework, it also presents certain limitations. One notable challenge is the high number of rules generated, which can increase the complexity of the mined policy and potentially affect its manageability. Although we propose viewing complexity through the lens of rule network structure, further work is needed to develop formal metrics that capture structural interpretability and operational efficiency.

Moreover, the current methodology relies on a fixed network modeling strategy, which may not be optimal across all datasets or organizational contexts. To address this, future work will explore more flexible and context-aware modeling approaches, including alternative community detection strategies that better adapt to the structure of user–resource interactions. Additionally, we plan to investigate automated threshold selection methods and expand our evaluation to include more diverse organizational settings and security policies to further validate the generalizability of our approach.