Self-Supervised Depth and Ego-Motion Learning from Multi-Frame Thermal Images with Motion Enhancement

Abstract

Thermal cameras are known for their ability to overcome lighting constraints and provide reliable thermal radiation images. This capability facilitates methods for depth and ego-motion estimation, enabling efficient learning of poses and scene structures under all-day conditions. However, the existing studies on depth prediction for thermal images are limited. In practical applications, thermal cameras capture sequential frames. Unfortunately, the potential of this multi-frame aspect is underutilized by the previous methods, resulting in limitations on the depth prediction accuracy of thermal videos. To leverage the multi-frame advantages of thermal videos and to improve the accuracy of monocular depth estimation from thermal images, we propose a framework for self-supervised depth and ego-motion learning from multi-frame thermal images. We construct a multi-view stereo (MVS) cost volume from temporally adjacent thermal frames. The construction process is adjusted based on the estimated pose, which serves as a motion hint. To stabilize the motion hint and improve pose estimation accuracy, we design a motion enhancement module that utilizes self-generated poses for additional supervisory signals. Additionally, we introduce RGB images in the training phase to form a multi-spectral loss, thereby augmenting the performance of the thermal model. The experimental results, conducted on a public dataset, demonstrate the proposed method’s accurate estimation of depth and ego-motion across varying light conditions, surpassing the performance of the self-supervised baseline.

1. Introduction

Understanding depth within images and the ego-motion of cameras is crucial for 3D vision perception. Its significance extends to practical applications like autonomous driving [1], object detection [2], and mixed reality [3]. Although sensors like LiDAR can directly measure object distances, their high expense and sparse depth motivate the investigation of visual self-supervised methods for their versatility and applicability. Self-supervised learning of depth and pose, extensively researched [4,5,6], demands neither expensive hardware nor intricate labels. It adeptly generates dense depth solely from visual data. Nevertheless, most studies concentrate on estimating depth in RGB images. The sensitivity of RGB image quality to illumination conditions results in information loss and heightened noise [7], especially in dim environments like nighttime or tunnels. These challenges, inherent in the real world, compromise the performance and generalization capabilities of RGB-based methods in low-light conditions.

Self-supervised learning from thermal images emerges as a potential remedy to close the performance gap. In contrast to RGB cameras, thermal cameras function independently of extra light sources and can seamlessly operate in complete darkness. Thermal cameras detect the Long-Wave Infrared (LWIR) radiation emitted from objects directly and then convert the raw radiation data into a temperature distribution represented in a visible image for human perception [8]. LWIR radiation’s ability to penetrate certain transparent mediums empowers thermal cameras to operate effectively in adverse weather, like rain and fog. In real-world scenarios, the thermal camera can provide more than one frame during testing, such as vehicles carrying thermal cameras for inspection tasks. However, the existing methods for self-supervised depth and ego-motion learning [9,10,11] fall short in fully utilizing the potential of multiple frames provided by thermal cameras.

To utilize the benefits of the multi-frame property and optimize the network predictions from thermal videos, we propose a self-supervised depth and ego-motion estimation framework based on multi-view stereo (MVS) for thermal videos. A cost volume is constructed by considering temporally adjacent frames from thermal videos with various hypothesized depth values. Then, the cost volume is decoded to generate an MVS depth. However, in large-scale outdoor scenes with slow camera movement, MVS methods face challenges. Owing to minimal disparities and insufficient triangulation [12] in such situations, the network acquires limited new information, potentially resulting in geometry ambiguity in the predicted depth results.

In response to this problem, we adopt a strategy that adaptively adjusts the range of depth candidate sampling guided by motion hints. Depending on the poses generated by the network, the MVS depth will be shrunk to the single-frame depth when the camera is static. To bolster motion hint stability and refine pose estimation accuracy, we design a motion enhancement module based on epipolar geometry constraints. This module utilizes self-generated supervisory signals to aid in network training. Moreover, to address the lower resolution and unclear structures and edges in thermal images, we integrate a depth warping operation into the proposed framework. It combines the thermal camera with a visible camera. This integration facilitates the combination of thermal loss and photometric loss into a multi-spectral loss, providing rich self-supervisory signals. The experimental results on the public dataset demonstrate that our method is capable of predicting depth and ego-motion under low-light conditions, exhibiting performance superior to state-of-the-art baselines, as shown in Figure 1.

In summary, we make the following contributions:

• We propose a self-supervised multi-frame depth and ego-motion learning framework for monocular thermal videos. It successfully leverages the temporal advantages of multiple thermal frames by constructing the multi-view stereo. The accuracy of prediction results is further improved through the integration of motion hints and multi-spectral properties.
• We design a motion enhancement module that utilizes self-generated motion constraints to complement self-supervised signals. It enhances the stability of motion hints within the framework, consequently improving the accuracy of pose estimation.
• We employ an efficient objective function that combines photometric loss, thermal loss, and motion loss to address the challenges in real-world scenarios, including unavoidable low-light conditions.

2. Related Work

2.1. Self-Supervised Depth and Ego-Motion Learning

The goal of depth and ego-motion learning [13,14,15] is to simultaneously estimate the depth of each pixel in an image and the camera poses between image sequences. Self-supervised methods avoid the use of challenging-to-obtain ground-truth by using the view synthesis mechanism. SfM-Learner, proposed by Zhou et al. [4], stands as a pioneering work in this field. It utilizes the generated single-frame depth and poses to project source frame images onto the target frame, synthesizing an image. Subsequently, it calculates the photometric loss between the original and synthesized images for training. Some self-supervised methods [5,16,17,18] build upon this approach to improve depth prediction performance. Extending the work of SfM-Learner, Bian et al. [17] introduce a scale-consistency loss to address scale-ambiguity in each frame. Bian et al. [18] integrate estimation networks with the conventional visual odometry ORB-SLAM2 [19], achieving heightened accuracy. EDS-Depth [20] enhances self-supervised depth estimation in dynamic scenes using frame interpolation and pseudo-labels derived from optical flow. To improve depth estimation with dynamic objects or a static camera, Feng et al. [21] separate static from temporal features via a dual-path encoder and synthesize full-resolution depth using a learnable offset field.

Recent works [22,23,24,25] introduce multi-view stereo (MVS) into depth learning. These methods can generate dense geometry structures of scenes using multiple frames. Assuming static scenes, Watson et al. [24] introduce MVS into self-supervised depth learning. The method requires neither ground-truth nor any pretrained networks. IAFMVS [26] enhances iterative MVS by leveraging deformable convolutions for adaptive feature extraction and attention for feature matching, specifically targeting texture-less regions. Cheng et al. [22] improve the robustness of depth estimation systems under inaccurate camera poses by adaptively fusing high-confidence single-view and multi-view depth information. Emphasizing its MVS foundation, Wang et al. [27] use a cross-attention mechanism to fuse geometric constraints from multi-frame optical flow, enabling recurrent refinement of scene detail. Compared to single-frame depth estimation methods, MVS-based methods can effectively utilize information from various perspectives, exhibiting more robust geometry structures and reduced sensitivity to occlusion. MVS methods hold significant research potential in self-supervised depth prediction, offering broad applicability across diverse scenarios. The potential value of MVS methods in self-supervised depth prediction suggests promising applications in various scenarios.

2.2. Depth and Ego-Motion Learning with Thermal Images

In contrast to the abundant methods for depth and pose estimation from RGB images, the research on estimation from thermal images is limited. RGB cameras are susceptible to illumination conditions, whereas thermal cameras offer image capture under broader conditions, including nighttime and adverse weather environments. This provides a distinct advantage to thermal images in 3D vision perception. Some works [28,29] employ additional motion and ranging sensors, such as IMU and radar, to assist thermal cameras in ego-motion estimation. However, these methods primarily concentrate on localization rather than environmental perception.

Recently, only a limited number of works have focused on depth learning from thermal images. Kim et al. [10] design a system composed of two RGB cameras and one thermal camera. The system utilizes the spatial relationship between the stereo cameras to predict the depth of the current frame. However, this method requires a complex geometry configuration between the cameras and does not estimate the camera poses. Lu et al. [9] propose a similar method to Kim et al. [10], incorporating two RGB cameras and two thermal cameras. They initialize the disparity map with RGB images and design a specialized network module to translate a thermal image from RGB images. In their final step, triangulation using the translated thermal images and original thermal images provides depth ground-truth. Nevertheless, their system still does not estimate ego-motion. Shin et al. [11] propose the first self-supervised method for simultaneously estimating ego-motion and depth from thermal images based on the SfM-Learner framework. They train pose and depth networks by reconstructing thermal images. However, networks from these methods utilize the single-frame image to predict depth, insufficiently exploiting the temporal and multi-frame advantages of thermal videos, thereby limiting improvements in estimation accuracy.

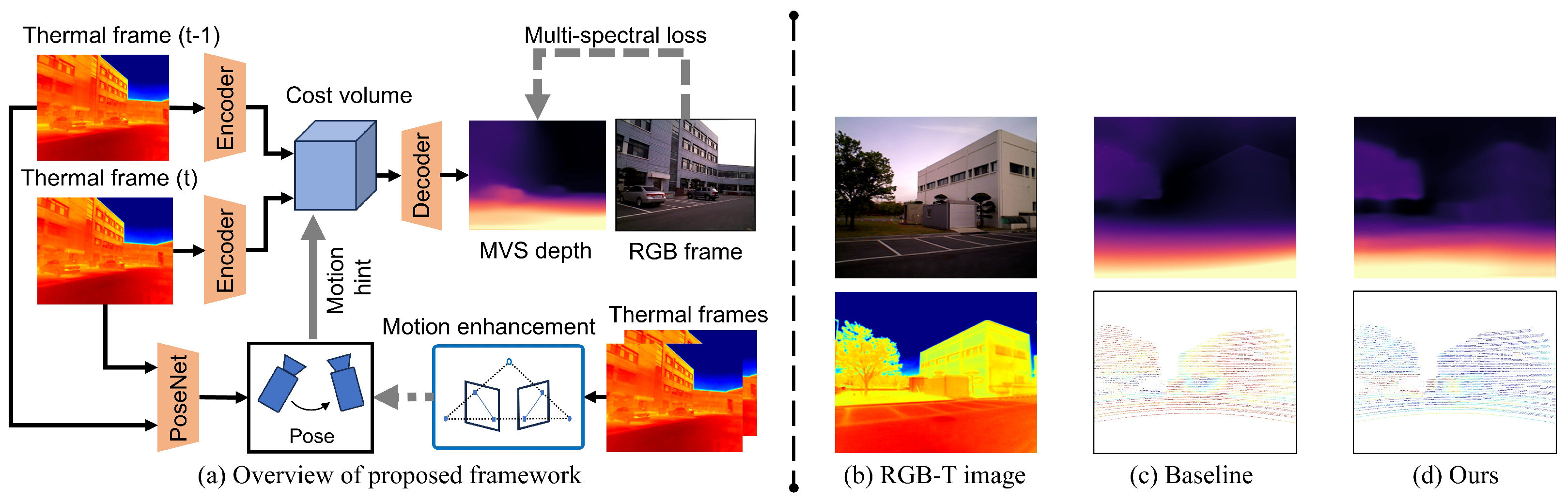
3. Method

3.1. Method Overview

Our framework is designed to jointly train neural networks for estimating depth and camera pose from monocular thermal videos. For this goal, we utilize a self-generated multi-spectral supervision signal and a motion supervision signal from a motion enhancement module to optimize the network.

To refine estimation accuracy, we construct a cost volume between temporally adjacent thermal frames, enabling the direct utilization of geometry constraints from MVS. This approach exploits the strengths of multi-frame thermal images. Additionally, the motion enhancement module, as designed, aims to improve pose estimation accuracy and maintain the stability of cost volume construction. Since the proposed framework employs self-supervised learning, no ground-truth is required at training time.

The main architecture of the proposed framework is illustrated in Figure 2. For a given thermal video input, (a) the PoseNet is employed initially to estimate the camera poses between thermal frames. This combines the poses from the motion enhancement module to compute the motion loss. (b) Subsequently, we utilize the DepthNet to predict the single-frame depth of the current thermal image. (c) We construct a cost volume from the multiple thermal frames. During this process, the predicted single-frame depth serves as a geometry prior, and the predicted poses act as a motion hint to assist the construction of the cost volume. Upon decoding the cost volume, the MVS depth and confidence map are generated. A more accurate depth is achieved through fusing the single-frame depth with the MVS depth.

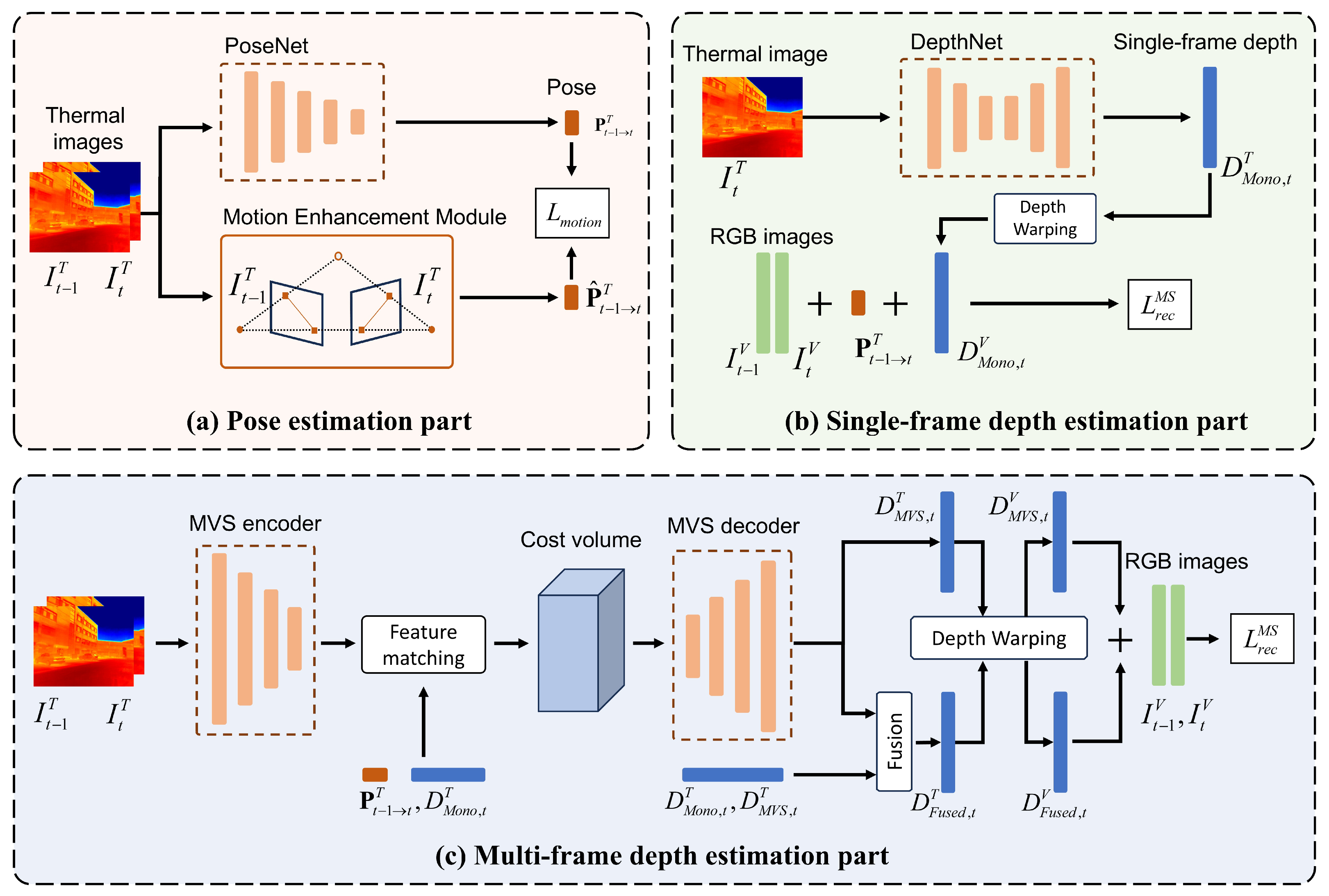
3.2. Single-Frame Self-Supervised Depth Learning

As illustrated in Figure 2a,b, single-frame self-supervised depth learning relies on the view synthesis mechanism [4] and reconstruction loss. The current thermal frame $I_t^T$ can be reconstructed from the previous frame $I_{t-1}^T$. This mechanism is based on the warping operation:

$$p_{t-1}={\mathbf{K}}^T{\mathbf{P}}_{t-1\to t}^T{D}_{Mono,t}^T\left(p_t\right){\left({\mathbf{K}}^T\right)}^{-1}{p}_t,$$

(1)

in which $D_{Mono,t}^T\left(p_t\right)$ is the generated depth of $I_t^T$ from DepthNet. ${\mathbf{P}}_{t-1\to t}^T$ is the estimated pose between $I_t^T$ and $I_{t-1}^T$. ${\mathbf{K}}^T$ is the intrinsic matrix of the thermal camera. The reconstructed frame ${\widehat{I}}_t^T$ is then synthesized by a bi-linear sampling operation. Utilizing ${\widehat{I}}_t^T$ and $I_t^T$, we can compute the multi-spectral reconstruction loss, which is described in detail in the subsequent section.

3.3. Multi-Frame Depth Learning from Thermal Images with Motion Hint

Our multi-frame pipeline, detailed in Figure 3, employs a shared MVS encoder to process adjacent thermal frames $\left\{I_t^T,I_{t-1}^T\right\}$. The encoder begins with a convolutional stem, followed by downsampling blocks using $5\times 5$ and $3\times 3$ convolutions to create a feature pyramid [30]. These features are then warped into a cost volume, with the depth sampling range adaptively guided by a motion hint derived from prior depth and pose estimates. A U-Net-like MVS decoder [31], built upon $3\times 3\times 3$ 3D convolutional layers, processes this volume. The decoder leverages skip connections to fuse multi-scale information and uses a final softmax layer to compute a depth probability map. Finally, a lightweight confidence network processes this probability map to generate a weighting map, which fuses the geometrically robust MVS depth with the single-frame depth to produce the refined output.

Following the previous works [23,24,25], our MVS depth estimation part constructs a cost volume by warping the encoded source frame to the target frame. The cost volume is derived from the measurement of geometric similarity between two thermal frames. It signifies the likelihood of the correct depth for each pixel among a set of different depth values. The decoded cost volume then generates the highest-activated depth value for each pixel. The MVS-based method mitigates geometry ambiguity in single-frame depth and enhances prediction accuracy.

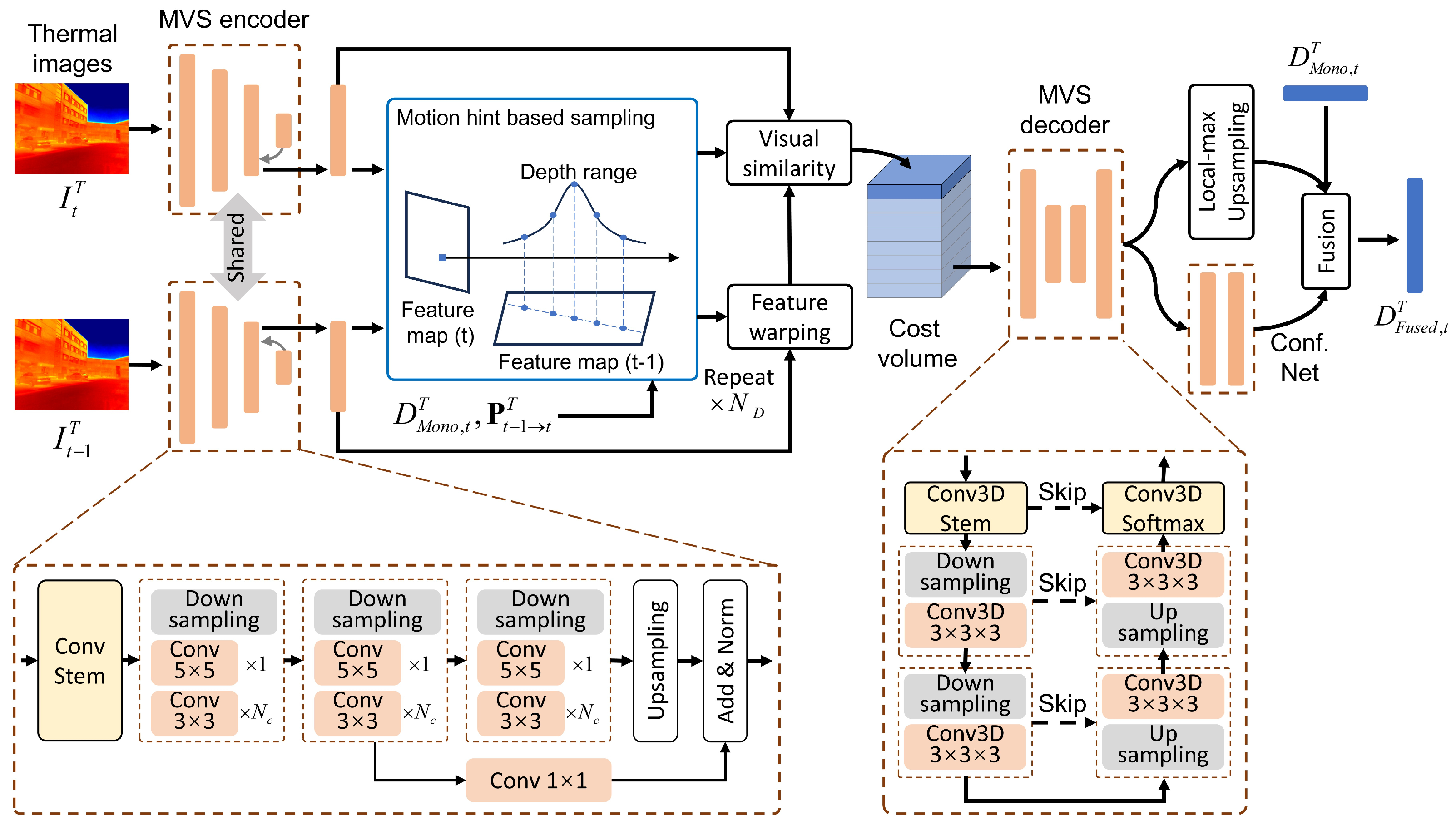
3.3.1. Cost Volume Construction

The MVS encoder (Figure 2c) extracts the feature of the current thermal frame $I_t^T$ and the previous frame $I_{t-1}^T$ to produce feature maps denoted as $F_{t+i}\in {\mathbb{R}}^{H/4\times W/4\times C}$, $i\in \{-1,0\}$. Then, the previous feature map is warped to the current feature map:

$$p_{t-1,j}={\mathbf{K}}^T{\mathbf{P}}_{t-1\to t}^T{D}_j\left(p_t\right){\left({\mathbf{K}}^T\right)}^{-1}{p}_t,$$

(2)

with $p_t$ being the pixels on the current feature map, $D_j\left(p_t\right)$ stands for the depth value of the j-th hypothesized depth value, and $p_{t-1,j}$ corresponds to the pixel on the previous frame’s feature map. Through the warping, we construct the feature volume $Z_{t-1}\in {\mathbb{R}}^{H/4\times W/4\times C\times N_D}$, in which $N_D$ represents the number of depth values.

The cost volume between the two feature maps is constructed by computing visual similarity:

$$q_i=〈z_i,{\mathrm{f}}_i〉,$$

(3)

here, $〈·,·〉$ is the inner product operation. $z_i\in {\mathbb{R}}^{C\times N_D}$ is the feature of the i-th pixel in feature volume $Z_{t-1}$, and ${\mathrm{f}}_i\in {\mathbb{R}}^{C\times 1}$ denotes the feature of the i-th pixel in the feature map $F_t$. Then, all pixel features form the cost volume $Q_t\in {\mathbb{R}}^{H/4\times W/4\times G\times N_D}$.

3.3.2. Depth Sampling with Motion Hint

Within the construction of the cost volume, the candidate depth set is formed by various depth values. However, the observed outdoor scenes are not static, and specifying a fixed range of depth values with predetermined maximum and minimum values would result in redundant depth candidates. To mitigate this, we leverage single-frame depth as prior information. Subsequently, we employ motion hints to adjust the adaptive range of the depth set, guiding the depth sampling process.

As the thermal camera moves, the velocity of the camera significantly influences the thermal frame disparity [12]. Higher velocities lead to more abundant triangulation for multi-view geometry, resulting in larger disparities. Conversely, lower velocities reduce triangulation, yielding smaller disparities and hindering the MVS network to acquire new information. Leveraging this knowledge, we utilize the estimated ego-motion as the motion hint to adaptively adjust the depth range:

$$\begin{array}{c}{d}_{min}=\left(1-\gamma {∥trans\left({\mathbf{P}}_{t-1\to t}^T\right)∥}_2\right)D_{Mono,t}^T\\ d_{max}=\left(1+\gamma {∥trans\left({\mathbf{P}}_{t-1\to t}^T\right)∥}_2\right)D_{Mono,t}^T\end{array},$$

(4)

where ${∥trans\left({\mathbf{P}}_{t-1\to t}^T\right)∥}_2$ denotes the camera’s velocity, and $trans\left(·\right)$ indicates the translational part of the camera’s pose. $\gamma$ is a hyperparameter determined by the camera’s frame rate. To maintain training stability, $\gamma {∥trans\left({\mathbf{P}}_{t-1\to t}^T\right)∥}_2$ is clamped to the range $(0,1)$. We set $\gamma =0.15$. For depth sampling, an inverse sampling strategy [23] is employed to ensure that sampling results are closer to $D_{Mono,t}^T$ when the camera is static or moving at a low velocity:

$$d_j={\left(d_{max}^{-1}+{\displaystyle \frac{j}{N_D-1}}\left(d_{min}^{-1}-d_{max}^{-1}\right)\right)}^{-1}.$$

(5)

Following the sampling process, the cost volume is fed into the MVS decoder to produce the depth probability map $M_{prob}\in {\mathbb{R}}^{H/4\times W/4\times N_D}$. The MVS depth $D_{MVS,t}^T$ for the current thermal image is then computed from $M_{prob}\in {\mathbb{R}}^{H/4\times W/4\times N_D}$ by the local-max function [32]:

$$D_{MVS}\left(p_t\right)=\sum _{j=\mathcal{J}-ϵ}^{\mathcal{J}+ϵ}{D}_j\left(p_t\right){\displaystyle \frac{M_{prob}(j,p_t)}{{\Sigma }_{i=\mathcal{J}-ϵ}^{\mathcal{J}+ϵ}{M}_{prob}(i,p_t)}}.$$

(6)

Here, $\mathcal{J}$ represents the index of the maximum value within the per-pixel probability vector $M_{prob}(·,p_t)$. The parameter $ϵ$ is the index radius along the depth dimension, which we set to 1. The resulting low-resolution depth map $D_{MVS}\left(p_t\right)$ is then upsampled to its original resolution.

3.3.3. Depth Fusing

To further enhance the accuracy of MVS depth and leverage the strengths of single-frame depth, we rectify regions with lower confidence [33] in the MVS depth using the results from the single-view depth. The confidence map $M_{conf}$ is generated by computing the information entropy of the decoded depth probability map $M_{prob}$:

$$M_{conf}={\theta }_{conf}\left(-{\sum }_{j=0}^{D-1}{M}_{prob,j}\ast log{M}_{prob,j}\right),$$

(7)

here, * denotes element-wise multiplication, and ${\theta }_{conf}$ represents the confidence network. The final fused depth is calculated using the following formula:

$$D_{Fused,t}^T=\left(1-M_{conf}\right)\ast D_{Mono,t}^T+M_{conf}\ast D_{MVS,t}^T.$$

(8)

3.4. Motion Enhancement Using Epipolar Geometry Constraint

Visual localization systems [19,34,35] often rely on matching sparse stable features like keypoints and lines to achieve robust localization. These systems then employ well-established geometry tools to compute relative camera poses. Namely, the relative ego-motion between two frames can be calculated using the epipolar geometry constraint, and iterative optimization diminishes the estimation error, providing effective guidance for training networks. Therefore, to guarantee stability for the motion hint-driven method and enhance pose estimation accuracy, we design a motion enhancement module, as illustrated in Figure 4. Through offline processing, these geometry elements serve as prior information and self-supervised signals integrated into the neural network training.

3.4.1. Epipolar Geometry Constraint

As the scenes observed by the thermal frames $\left\{I_{t-1}^T,I_t^T\right\}$ are similar, we extract keypoints from the thermal frames and obtain a set of feature matches for keypoint pairs by associating their SIFT feature descriptors [36]. According to the epipolar geometry constraint, the relationship between keypoint pairs and the relative camera pose is as follows:

$$p_t^{\top }{\left({\mathbf{K}}^T\right)}^{-\top }\mathbf{E}{\left({\mathbf{K}}^T\right)}^{-1}{p}_{t-1}=0,p_t=\mathbf{H}{p}_{t-1},$$

(9)

with $p_{t-1}$ and $p_t$ denoting the homogeneous coordinates of a pair of keypoints between two frames. $\mathbf{H}$ is the homography matrix, and $\mathbf{E}$ is the essential matrix. The pose $\left[{\mathbf{R}}_{t-1\to t}|{\mathbf{t}}_{t-1\to t}\right]$ between the two frames can be determined using the formula $\mathbf{E}={\left[{\mathbf{t}}_{t-1\to t}\right]}_{\times }{\mathbf{R}}_{t-1\to t}$, where ${\left[·\right]}_{\times }$ represents the skew-symmetric matrix of a three-dimensional vector.

3.4.2. Matrix Scoring and Selection

We calculate the homography matrix and the essential matrix separately and select the one that best fits the current frame situation. With an RANSAC scheme, $\mathbf{E}$ and $\mathbf{H}$ are computed using the eight-point algorithm [37] and the DLT algorithm [38], respectively. At each iteration, the score for the solution is calculated using the following formula:

$$s=\sum _i\left(e_{t-1\to t}^2\left(p_{t,i},p_{t-1,i}\right)+e_{t\to t-1}^2\left(p_{t,i},p_{t-1,i}\right)\right),$$

(10)

where $e^2$ represents the symmetric transfer error [38], calculated through mutual projection between the two frames. $p_{t,i}$ and $p_{t-1,i}$ are the i-th keypoint pairs. Finally, we preserve $\mathbf{E}$ and $\mathbf{H}$ associated with the highest score.

In situations where the scene is planar or exhibits low parallax, explaining it using the essential matrix may lead to wrong results in ego-motion recovery. We should choose the homography matrix for pose retrieval. Conversely, in scenes with sufficient parallax, the homography matrix can only solve for pose using keypoint pairs on the planes, whereas the essential matrix yields more accurate results. Thus, matrix selection is determined by the following:

$$s_{ratio}={\displaystyle \frac{s_H}{s_H+s_E}},$$

(11)

with $s_{ratio}$ being the ratio of scores from the homography matrix. If $s_{ratio}>0.45$, it indicates situations involving either a low parallax or the camera detecting the extensive planar. In such cases, the scene is processed using the homography matrix. Conversely, the essential matrix is selected.

3.4.3. Montion Recovery

After the matrix selection, to guarantee the validity of the pose solving, we examine the motion hypothesis. In the case of the homography matrices, we perform the hypothesis verification [39] on the eight solutions. Solutions where keypoints go behind the camera are discarded. From the remaining solutions, those with significant parallax and minimal reprojection errors are selected. For essential matrices, the four solutions are examined using the Singular Value Decomposition (SVD), and erroneous solutions are removed using the similar approach as with homography matrices. Then, the pose between the two frames is determined.

3.4.4. Motion Loss

The poses generated by the motion enhancement module are converted from the transformation matrix to the 6DoF representation. We incorporate the pose, computed based on the epipolar geometry constraint, into the motion loss function for optimization:

$$\begin{array}{cc}\hfill L_{motion}& =w^r{∥{\widehat{\mathbf{r}}}_{t-1\to t}-{\mathbf{r}}_{t-1\to t}∥}_2\hfill \\ \hfill & +w^t{∥{\widehat{\mathbf{t}}}_{t-1\to t}-{\mathbf{t}}_{t-1\to t}∥}_2,\hfill \end{array}$$

(12)

where $\left\{{\widehat{\mathbf{r}}}_{t-1\to t},{\widehat{\mathbf{t}}}_{t-1\to t}\right\}$ and $\left\{{\mathbf{r}}_{t-1\to t},{\mathbf{t}}_{t-1\to t}\right\}$ are the 6-DoF relative poses from the motion enhancement module and PoseNet, respectively. $w^r$ and $w^t$ denote the weights corresponding to rotation and translation. Notably, normalization of the translation is applied for scale consistency. We empirically set $w^r=10$ and $w^t=1$.

3.5. Multi-Spectral Loss

In the training phase, conducting view synthesis on thermal and RGB images allows us to calculate thermal loss and photometric loss, respectively. This provides the network with sufficient multi-spectral self-supervision signals. In the testing phase, our framework solely requires thermal frames to estimate depth. To calculate loss terms from visible images, a depth warping operation is employed to establish the relationship between the two cameras, allowing the depth warping from the thermal camera coordinate system to the RGB camera coordinate system.

3.5.1. Thermal Reconstruction Loss

After the networks generate depths at three levels (single-frame depth $D_{Mono,t}^T$, MVS depth $D_{MVS,t}^T$, and fused depth $D_{Fused,t}^T$), the thermal image ${\widehat{I}}_t^T$ is synthesized using the estimated pose ${\mathbf{P}}_{t-1\to t}^T$ and the previous thermal frame $I_{t-1}^T$, as described in Section 3.2. Utilizing both the original thermal image $I_t^T$ and the synthesized image ${\widehat{I}}_t^T$, we compute the thermal reconstruction loss:

$$L_{rec}^T=minte\left(I_t^T,{\widehat{I}}_t^T\right),$$

(13)

in which $te$ is a thermal error and is defined as a combination of an SSIM loss and an L1 loss:

$$\begin{array}{cc}\hfill te\left(I_t^T,{\widehat{I}}_t^T\right)& ={\displaystyle \frac{w^T}{2}}\left(1-SSIM\left(I_t^T,{\widehat{I}}_t^T\right)\right)\hfill \\ \hfill & +\left(1-w^T\right){∥I_t^T-{\widehat{I}}_t^T∥}_1,\hfill \end{array}$$

(14)

here, $SSIM\left(·,·\right)$ represents the Structural Similarity Index (SSIM) loss [40], and $w^T$ is the weight of the SSIM loss. The SSIM loss remains effective for training due to the diverse structures and shapes of thermal sources in the scenes. Empirically, we set $w^T=0.15$.

3.5.2. Depth Warping

The photometric loss derived from RGB images effectively supplements self-supervision signals, mitigating inherent deficiencies in thermal images, such as weak textures and blurred boundaries. However, the photometric loss typically demands an additional RGB network to process visible images. To address this challenge, a depth warping operation is employed to enable the depth warping from the thermal camera to the RGB camera, eliminating the requirement for an extra neural network to infer visible images. Initially, exploiting the rigid geometry association of the two cameras and the generated depth maps, we calculate the thermal–visible rigid flow between the thermal and visible frames:

$$S^{T\to V}\left(p_t\right)={\mathbf{K}}^V{\mathbf{P}}^{T\to V}{D}_t^T\left(p_t\right){\left({\mathbf{K}}^V\right)}^{-1}{p}_t-p_t,$$

(15)

where $D_t^T$ is the depth of the current thermal frame, and $p_t$ represents the pixels in the current thermal frame. ${\mathbf{K}}^V$ is the intrinsic matrix of the visible camera, and ${\mathbf{P}}^{T\to V}$ is the extrinsic matrix between the two cameras.

Subsequently, with the flow reversal operation and the differentiable sampling, the depth of the current visible frame is obtained as follows:

$$D_t^V=f_{sample}\left(D_t^T,f_{reverse}\left(S^{T\to V}\right)\right),$$

(16)

where $f_{reverse}\left(·\right)$ is the flow reversal layer [41], which is designed to reverse the computed optical flow of pixels. $f_{sample}\left(·,·\right)$ denotes the spatially sampling function [42], utilized for calculating the visible frame depth, which is transferred with the pixel offset of the optical flow. As the two operations are differentiable, they are allowed for backward propagation during training.

3.5.3. Photometric Reconstruction Loss

The depth $D_t^V$, computed through the depth warping module, can be utilized for synthesizing visible images ${\widehat{I}}_t^V$. Following [5], the photometric reconstruction loss for visible images is expressed as

$$L_{rec}^V=minpe\left(I_t^V,{\widehat{I}}_t^V\right),$$

(17)

$$\begin{array}{cc}\hfill pe\left(I_t^V,{\widehat{I}}_t^V\right)& ={\displaystyle \frac{w^V}{2}}\left(1-SSIM\left(I_t^V,{\widehat{I}}_t^V\right)\right)\hfill \\ \hfill & +\left(1-w^V\right){∥I_t^V-{\widehat{I}}_t^V∥}_1,\hfill \end{array}$$

(18)

where $pe$ is the photometric error. $w^V$ is the SSIM loss weight for visible images and is set as $w^V=0.85$.

Then, the multi-spectral loss $L_{rec}^{MS}$ is formed by the thermal loss and the photometric loss:

$$L_{rec}^{MS}={\lambda }_T{L}_{rec}^T+{\lambda }_V{L}_{rec}^V,$$

(19)

3.5.4. Total Loss Function

Our framework is trained in a self-supervised manner, and we have the total loss, which is formulated as

$$L_{total}=L_{rec}^{MS}+{\lambda }_M{L}_{motion}+{\lambda }_S\left(L_S^T+L_S^V\right),$$

(20)

where $L_S$ represents the edge-aware smoothness loss [43], which is commonly incorporated in existing works to deal with the discontinuity in depth map:

$$L_S={\sum }_i^N\left|\nabla D_t\left(p_i\right)\right|·e^{-|\nabla I_t\left(p_i\right)|},$$

(21)

where N is the number of pixels in an image. ∇ represents the 2D differential operator. $L_S$ is applicable to both RGB part (V) and thermal part (T). $L_{rec}^{MS}$ signifies the multi-spectral reconstruction loss, composed of the thermal loss and the photometric loss. $L_{motion}$ denotes the motion loss term from the motion enhancement module. ${\lambda }_S$ and ${\lambda }_M$ are weights assigned to the smoothness loss and the motion loss.

4. Experiments

4.1. Datasets

To validate the effectiveness of our framework, we conduct training and testing using the public and available VIVID dataset [44]. This dataset is highly suitable for our task as it comprises multimodal data streams with temporal properties, containing raw thermal images, RGB images, sensor extrinsic calibration results, camera poses (serving as ego-motion ground-truth), and LiDAR point clouds (serving as depth ground-truth). It encompasses challenging scenes from both daytime and nighttime, various lighting conditions, and scenarios with different motion conditions. For our experiments, we utilize 6958 samples for training and 1058 samples for testing, and all images are processed at a 320 × 256 resolution. As our method is self-supervised, the ground-truth data (e.g., LiDAR depth and camera poses) is not required during training. The training phase solely utilizes the thermal images, the corresponding RGB images, and the sensor calibration parameters to compute the loss functions. During inference, our model is fully independent and requires only the monocular thermal frames as input. The ground-truth data is used exclusively for the quantitative evaluation of our method’s performance during the testing phase. Hence, the VIVID dataset provides satisfactory and comprehensive resources for training and evaluating the proposed framework.

4.2. Thermal Image Preprocessing

To meet the training requirements, we perform a multi-step preprocessing pipeline. Typically, the 8-bit thermal images produced by the thermal camera undergo an automatic frame-wise min–max rescaling. The 8-bit thermal images lack temporal consistency, which is unsuitable for the self-supervised training of consecutive image sequences. On the other hand, the 14-bit raw thermal images, due to the expansive temperature measurement range, are impractical for depth and ego-motion estimation, leading to the compression of a substantial amount of valuable information.

Therefore, to ensure temporal consistency while enhancing structural details, we employ a comprehensive pipeline. The resized 14-bit raw data ($I^{T,raw}$) is first clamped to the predefined temperature hyperparameters $\{{\tau }_{min},{\tau }_{max}\}$ and normalized to the [0, 1] range. This normalized image, which often suffers from low contrast, then undergoes a mild contrast adjustment. We apply Contrast Limited Adaptive Histogram Equalization (CLAHE), which boosts local features while avoiding the introduction of excessive noise. Finally, this single-channel image is remapped using a jet colormap to 3-channels and standardized. This full pipeline can be formulated as a single operation:

$$I^T=f_{std}\left(f_{map}\left(f_{adj}\left({\displaystyle \frac{f_{clamp}(I^{T,raw},{\tau }_{max},{\tau }_{min})-{\tau }_{min}}{{\tau }_{max}-{\tau }_{min}}}\right)\right)\right)$$

(22)

where $f_{clamp}(·)$ is the clamping function, $f_{adj}(·)$ is the contrast adjustment function, $f_{map}(·)$ is the colormap function, and $f_{std}(·)$ is the standardization. Figure 5 illustrates the visualization of the results of this preprocessing. The subsequent ablation study demonstrates the effectiveness of this processing in improving the performance of the networks.

4.3. Implementation Details

Training Configuration

For the depth prediction network of single-frame part (DepthNet) and PoseNet, we utilize the architectures from Monodepth2 [16] and SfMLearner [4] with the ResNet-18 [45] encoder, respectively. The confidence network is constructed with a three-layer 2D CNN and a Sigmoid layer. The ResNet blocks are pretrained with ImageNet, and other network layers are trained from scratch. Our method was implemented using the PyTorch (version 2.2.2) deep learning library [46]. All networks are trained on a single NVIDIA RTX 3080Ti GPU using the ADAM optimizer [47].

For data augmentation, we employed an offline strategy. Multiple augmented sequences were generated to expand the original dataset by applying varied parameters for horizontal flipping, scaling, and cropping. We shuffle and randomly sample from this entire original and augmented pool. During training, the single-frame depth prediction network and pose estimation network receive three consecutive thermal frames $\left\{I_{t-1}^T,I_t^T,I_{t+1}^T\right\}$, and the MVS depth network takes two frames $\left\{I_t^T,I_{t-1}^T\right\}$. To balance the loss, we assign weights $\left\{{\lambda }_T,{\lambda }_V,{\lambda }_S,{\lambda }_M\right\}$ as $\left\{1.0,0.1,0.001,1.0\right\}$, respectively. The temperature parameters $\left\{{\tau }_{min},{\tau }_{max}\right\}$ in the thermal image preprocessing are set as $\left\{0.0,30.0\right\}$ (in degrees Celsius). The batch size is set to 4, and the learning rate is 0.0001. A total of 300 epochs are conducted for training.

4.4. Depth Prediction Results

In evaluating the performance of the proposed method, we compare it with state-of-the-art self-supervised depth estimation methods. The work of Shin et al. [11] is set as the baseline. Additionally, the methods employing monocular RGB supervision are included for comparison. The evaluation uses the metrics proposed by Eigen et al. [14], which are widely employed in modern depth estimation methods for RGB images, to measure the performance. The metrics include the error metrics (smaller is better) and the accuracy rate metrics (larger is better):

$$\mathrm{Abs}\mathrm{Rel}:{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{\left|D\left(p_i\right)-D_{\mathrm{gt}}\left(p_i\right)\right|}{D_{\mathrm{gt}}\left(p_i\right)}}$$

(23)

$$\mathrm{Sq}\mathrm{Rel}:{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\displaystyle \frac{{∥D\left(p_i\right)-D_{\mathrm{gt}}\left(p_i\right)∥}^2}{D_{\mathrm{gt}}\left(p_i\right)}}$$

(24)

$$\mathrm{RMSE}:\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{∥D\left(p_i\right)-D_{\mathrm{gt}}\left(p_i\right)∥}^2}$$

(25)

$$\mathrm{RMSE}\log :\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{∥logD\left(p_i\right)-log{D}_{\mathrm{gt}}\left(p_i\right)∥}^2}$$

(26)

$$\mathrm{Accuracy}:\%\mathrm{of}D\left(p_i\right)\mathrm{s}.\mathrm{t}.max\left({\displaystyle \frac{D\left(p_i\right)}{D_{\mathrm{gt}}\left(p_i\right)}},{\displaystyle \frac{D_{\mathrm{gt}}\left(p_i\right)}{D\left(p_i\right)}}\right)=\delta <\mathrm{thr}$$

(27)

where $D\left(p_i\right)$ and $D_{\mathrm{gt}}\left(p_i\right)$ are the estimated and ground-truth depth values, respectively. thr is a threshold, which is set to $1.25$, ${1.25}^2$, and ${1.25}^3$.

Our framework’s performance in monocular depth estimation was rigorously evaluated on the VIVID dataset. The experiments, summarized in

Table 1. Quantitative comparison between our method and other self-supervised methods for depth prediction on the VIVID dataset. The evaluation encompasses scenes from daytime and nighttime, testing each method’s performance under varying light conditions. The “Input” column specifies the types of images fed into the network. “V” and “T” represent visible RGB images and thermal images, respectively. The table highlights results with the minimum errors and the highest accuracy in bold.

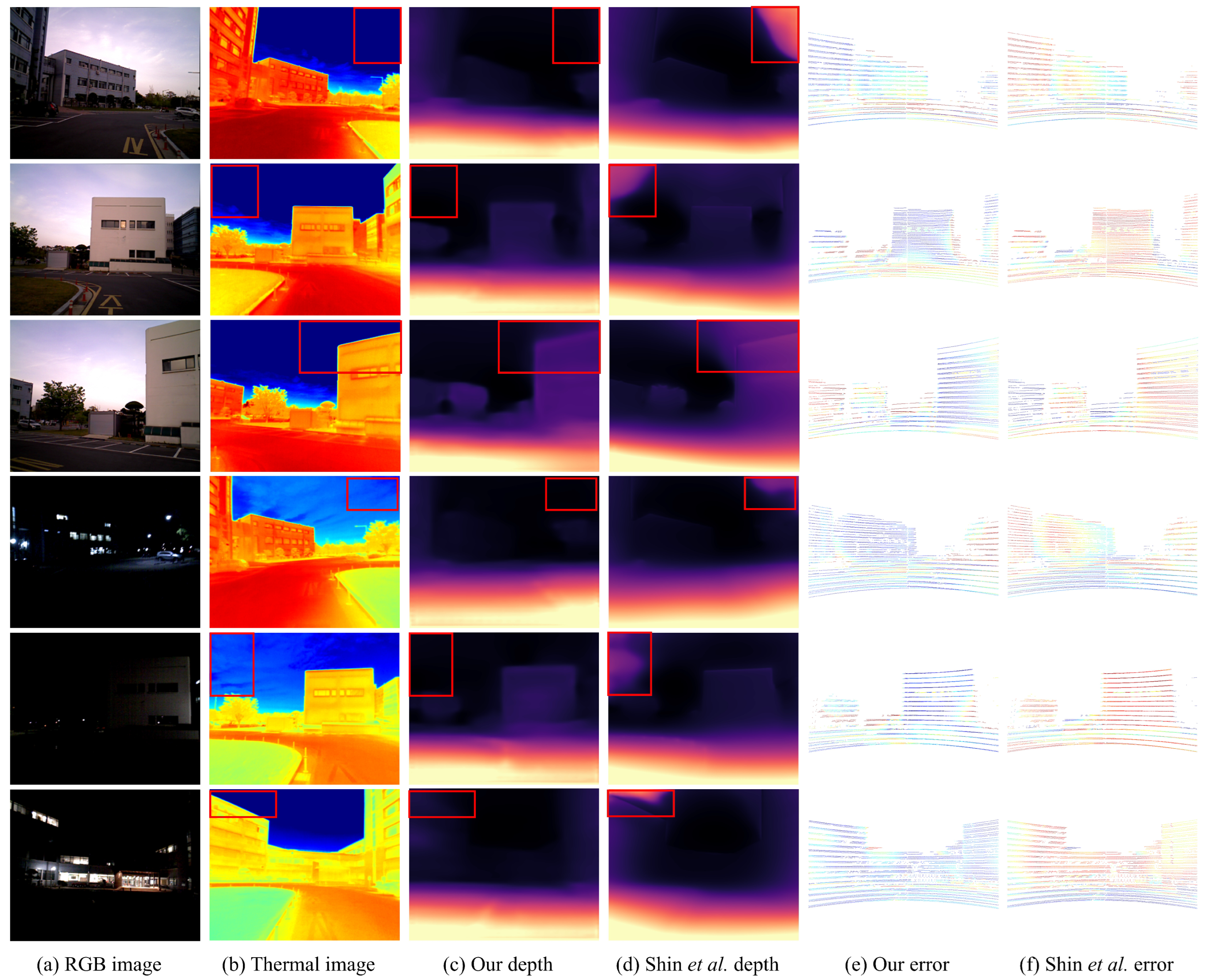
Scene	Methods	Input	Error (Lower Is Better)				Accuracy (Higher Is Better)
			Abs. Rel.	Sq. Rel.	RMSE	RMSElog	$\mathit{\delta }<\mathbf{1.25}$	$\mathit{\delta }<{\mathbf{1.25}}^{\mathbf{2}}$	$\mathit{\delta }<{\mathbf{1.25}}^{\mathbf{3}}$
Outdoor day1	SfMLearner [4]	V	0.200	1.549	6.394	0.248	0.684	0.922	0.975
	Monodepth2 [5]	V	0.436	6.318	9.967	0.454	0.491	0.719	0.840
	Bian et al. [17]	V	0.136	1.464	5.638	0.179	0.844	0.977	0.991
	Watson et al. [24]	V	0.166	1.472	6.358	0.220	0.754	0.945	0.986
	Shin et al. [11] (T)	T	0.143	0.766	4.547	0.180	0.790	0.979	0.996
	Shin et al. [11] (MS)	T	0.142	0.792	4.730	0.181	0.788	0.980	0.996
	Ours	T	0.115	0.683	4.310	0.159	0.869	0.980	0.996
Outdoor day2	SfMLearner [4]	V	0.192	1.652	6.511	0.235	0.702	0.941	0.978
	Monodepth2 [5]	V	0.435	6.915	9.576	0.438	0.591	0.752	0.843
	Bian et al. [17]	V	0.131	1.376	5.899	0.185	0.822	0.976	0.991
	Watson et al. [24]	V	0.197	2.281	7.707	0.241	0.695	0.922	0.982
	Shin et al. [11] (T)	T	0.148	0.933	4.736	0.188	0.802	0.970	0.991
	Shin et al. [11] (MS)	T	0.145	0.917	4.784	0.187	0.804	0.971	0.991
	Ours	T	0.122	0.957	4.787	0.170	0.855	0.968	0.991
Outdoor night1	SfMLearner [4]	V	0.429	4.584	8.624	0.445	0.468	0.698	0.834
	Monodepth2 [5]	V	0.704	11.75	12.53	0.636	0.362	0.559	0.701
	Bian et al. [17]	V	0.520	6.413	10.40	0.516	0.381	0.596	0.755
	Watson et al. [24]	V	0.469	5.690	10.96	0.466	0.332	0.612	0.839
	Shin et al. [11] (T)	T	0.158	0.844	4.634	0.192	0.754	0.977	0.996
	Shin et al. [11] (MS)	T	0.156	0.856	4.813	0.192	0.752	0.976	0.996
	Ours	T	0.119	0.747	4.189	0.162	0.850	0.979	0.996
Outdoor night2	SfMLearner [4]	V	0.373	4.215	8.294	0.396	0.548	0.773	0.879
	Monodepth2 [5]	V	0.602	10.84	11.72	0.562	0.477	0.650	0.759
	Bian et al. [17]	V	0.464	6.376	9.887	0.472	0.511	0.685	0.807
	Watson et al. [24]	V	0.416	4.860	10.16	0.428	0.383	0.692	0.873
	Shin et al. [11] (T)	T	0.159	1.084	5.115	0.204	0.772	0.957	0.989
	Shin et al. [11] (MS)	T	0.156	1.049	5.166	0.202	0.775	0.957	0.989
	Ours	T	0.124	0.899	4.694	0.179	0.829	0.963	0.990

and Figure 6 and Figure 7, conclusively demonstrate the superiority of our approach, which arises from the synergistic integration of multi-frame geometric constraints and multi-spectral supervision.

As shown in Table 1, our method consistently outperforms baseline self-supervised techniques across all scenarios and metrics. The key to this performance lies in our departure from traditional single-frame estimation. Unlike the baseline [11], which predicts depth from a single image and thus fails to exploit temporal data, our framework is built upon an MVS cost volume. By constructing this volume from temporally adjacent thermal frames, our model effectively leverages multi-view geometry to resolve ambiguities inherent in a single perspective, leading to more robust and accurate geometric structures. This architectural advantage is the primary driver behind the significant 19.8% reduction in absolute relative error (Abs. Rel.) compared to the baseline.

The results particularly highlight our method’s ability to maintain performance across extreme variations in illumination, especially when compared to RGB-based approaches. As predicted, RGB-based methods suffer a catastrophic performance degradation at night, underscoring their unreliability for continuous operation. While thermal imaging is inherently advantageous in these conditions, our method proves more stable than even the thermal-based baseline. From day to night, our model’s Abs. Rel. error increases by a mere 2.55%, whereas the baseline degrades by 8.72%. This enhanced stability can be attributed to the multi-spectral loss employed during training. By using a depth warping operation to incorporate a photometric reconstruction loss from registered RGB images, our thermal network learns richer, more generalized features that better capture object boundaries and fine-grained textures—details often blurred or subtle in thermal data alone. This robust feature representation, learned via multi-spectral supervision, translates directly to more consistent and accurate predictions when presented with only thermal images during inference.

To visually corroborate the quantitative results from Table 1, Figure 6 provides a qualitative comparison. The visualization highlights a key limitation of relying on standard cameras: in the challenging nighttime scene (bottom row), the RGB-based method (e) fails completely, producing incoherent geometry. In stark contrast, both our method (c) and the thermal baseline (d) robustly generate plausible depth maps that align with the ground-truth structure (f), underscoring the advantage of using thermal imagery for all-day operation.

A more granular analysis in Figure 7 reveals the improvements our method offers over the thermal baseline. This figure provides a detailed side-by-side comparison with the baseline, including error maps. The baseline frequently produces noticeable geometric distortions and artifacts. These are common failure modes for single-frame methods. In contrast, our results are geometrically coherent and artifact-free, a direct benefit of the MVS cost volume that aggregates spatial information over time to form a more complete and consistent 3D understanding of the scene.

Furthermore, the error maps (e, f) provide a granular view of our method’s precision. Our error map (e) is predominantly blue (low error), whereas the baseline’s (f) shows significant concentrations of red and orange (high error), especially around object edges. This visual evidence confirms that our framework, which combines the strengths of MVS with a final depth fusing step, achieves a superior level of per-pixel accuracy and produces more reliable depth maps for the downstream tasks.

4.5. Pose Estimation Results

In addition to depth, accurate ego-motion estimation is critical for autonomous navigation. The results presented in

Table 2. Quantitative comparison of our method to other self-supervised methods for pose estimation. The comparison methods include the trained RGB-based self-supervised methods, and the scenes encompass both daytime and nighttime situations. Smaller errors in the table indicate better performance. Results with the minimum errors are highlighted in bold.

Methods	Input	Outdoor Day1		Outdoor Day2		Outdoor Night1		Outdoor Night2
		Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
SfMLearner [17]	V	0.0774	0.0407	0.0867	0.0414	0.0657	0.0342	0.0579	0.0279
Monodepth2 [5]	V	0.0525	0.0305	0.0544	0.0266	0.0552	0.0302	0.0545	0.0277
Bian et al. [17]	V	0.0503	0.0255	0.0514	0.0285	0.0886	0.0439	0.0888	0.0390
Shin et al. [11] (T)	T	0.0751	0.0371	0.0784	0.0391	0.0744	0.0417	0.0793	0.0402
Shin et al. [11] (MS)	T	0.0541	0.0307	0.0643	0.0365	0.0590	0.0315	0.0604	0.0315
Ours	T	0.0429	0.0251	0.0450	0.0248	0.0464	0.0288	0.0442	0.0252

demonstrate that our framework surpasses the baseline method in self-supervised pose estimation from thermal video.

As detailed in Table 2, our method achieves the lowest Absolute Trajectory Error (ATE) [48] across all the daytime and nighttime sequences. The most significant contributor to this success is the proposed motion enhancement module. This module provides a geometrically grounded supervisory signal by leveraging epipolar geometry constraints to compute a highly accurate pose offline. This extra poses supervision signal is then used to formulate a motion loss that guides the training of our PoseNet. This additional supervision stabilizes the learning process and forces the network to adhere to geometric principles, resulting in a 24.94% improvement in ATE over the baseline. This module also ensures the stability of the motion hint used for MVS depth sampling, creating a virtuous cycle where better poses lead to better depth and vice versa.

Moreover, similar to our depth results, our pose estimation network maintains exceptional performance from day to night, with its ATE degrading by only 1.51%. Compared to RGB-supervised methods, our method exhibits robustness to changes in illumination. In well-lit daytime scenes, RGB-based self-supervised methods perform well, but, as the scenes transition to poorly lit nighttime conditions, the errors in these methods increase. For instance, the method proposed by Bian et al. [18] shows that performance decreases by 74.43%.

4.6. Ablation Study

In the evaluation experiments, our method reveals superior performance on ego-motion and depth estimation compared to the other approaches. However, the individual contributions and improvements made by each component of the proposed framework remain unclear. Therefore, we conduct ablation experiments on the VIVID dataset to analyze and evaluate the contributions of each component and loss term within the framework. The results, presented in

Table 3. Ablation study on various components. The best results are marked in bold.

Methods	Abs. Rel.	RMSE	$\mathit{\delta }<1.25$
Ours (full)	0.127	4.305	0.831
Ours (w/o depth warping)	0.144	4.729	0.815
Ours (w/o motion enhancement)	0.138	4.763	0.824
Ours (w/o motion hint)	0.140	4.798	0.816
Ours (w/o remapping)	0.140	4.832	0.813
Ours (w/o depth fusing)	0.136	4.478	0.816

and

Table 4. Ablation study on various loss terms. The experiment labeled “w/o RGB loss” indicates setting the reconstruction loss based on photometric consistency to zero. The best results are marked in bold.

Methods	Abs. Rel.	RMSE	$\mathit{\delta }<1.25$
Ours (full)	0.127	4.305	0.831
Ours (w/o thermal loss)	-	-	-
Ours (w/o motion loss)	0.138	4.763	0.824
Ours (w/o smoothness loss)	0.140	4.742	0.799
Ours (w/o RGB loss)	0.144	4.729	0.815

, systematically deconstruct our framework and quantify the importance of each element.

4.6.1. Effect of Each Component

This study, summarized in Table 3, assesses the impact of each core architectural module by selectively toggling them on or off within the proposed framework. By toggling various components on or off within the proposed framework, we show their respective importance. Table 3 presents the performance test results for depth prediction.

“Ours(full)” represents the results using all the components, and the other rows correspond to the results with the removal of each respective component. The results indicate that “Ours(full)” achieves the best performance. Removing different components leads to varying degrees of performance decline, with increased prediction errors and decreased accuracy. For “Ours (w/o depth warping),” we deactivate the depth transfer module, thus not receiving any supervisory signals from visible images. In the case of “Ours (w/o motion enhancement),” the motion enhancement module is turned off, omitting the utilization of the epipolar geometry constraint for pose generation. In the “w/o motion hint” experiment, the depth candidate range is half of the single-frame depth value. As for “Ours (w/o remapping),” training is conducted using the original 14-bit thermal images. For “Ours (w/o depth fusing),” the model solely outputs MVS depth without performing depth map fusion.

The underlying rationale for the motion enhancement module is to provide a supervisory signal with a different failure mode than the primary reconstruction-based supervision. The dense reconstruction signal can be ambiguous in photometrically poor regions, where an incorrect pose might still yield a low error. Our module provides an additional signal that relies on sparse structural features rather than dense texture content. To validate the quality of this mechanism, Figure 8 visually demonstrates its core feature-matching process. The module successfully extracts a dense and geometrically consistent set of feature correspondences, confirming that it provides a reliable geometric constraint. The benefit of adding this geometrically rigid constraint is then shown in Table 3. The “Ours (w/o motion enhancement)” experiment, which relies solely on the potentially ambiguous dense signal, shows a corresponding drop in pose estimation accuracy.

4.6.2. Effect of Each Loss Term

The ablation study is conducted on different loss terms by setting them to zero. The depth prediction evaluation results for the experiments are presented in Table 4. “Ours(full)” employs all the loss terms and achieves the best results. The thermal reconstruction loss is found to be crucial and foundational to our framework as removing it results in non-convergent training. Although removing the smoothness loss enhances the visibility of the structural details in the depth map, it results in an overall increase in errors. Similarly, removing the photometric reconstruction loss or the motion loss leads to increased errors and decreased accuracy in depth prediction.

5. Discussion

While our framework demonstrates robust performance, we acknowledge several avenues for future work. Our method does not explicitly model dynamic objects, a common challenge for self-supervised methods relying on view synthesis. Thus, incorporating dynamic-aware modules remains a valuable direction. We also acknowledge that the multi-spectral loss requires RGB data during the training phase. Although this is a training-only optimization (our model is fully independent at inference and our ablation study shows that it remains effective without this signal), this reliance does reduce data collection flexibility. A promising future direction is to enhance this flexibility by applying domain adaptation techniques to reduce this RGB dependence. In terms of deployment, while the MVS cost volume adds computational load, our full model achieves 43 FPS (23 ms per frame), comfortably meeting real-time requirements. We also note that the motion enhancement module is a training-only component and does not impact runtime. For more resource-constrained hardware, model compression and knowledge distillation remain promising avenues for optimization. Finally, while validated on a comprehensive benchmark, extending the framework’s applicability presents a clear direction for future work, such as evaluating its generalization to broader domains, including diverse scenarios and fusion with sensors like LiDAR and IMU.

6. Conclusions

In this paper, we introduce a self-supervised learning framework for depth and pose estimation from multi-frame thermal images. Firstly, the proposed framework constructs an MVS cost volume from multiple thermal frames. The poses generated by the network adaptively guide and adjust the construction process, directing MVS depth towards single-frame depth in scenarios with slow or static camera movement. Secondly, to bolster the stability of this mechanism, a motion enhancement module based on epipolar geometry constraints provides self-generated supervision signals to optimize the training process. Finally, a depth warping operation links visible and thermal cameras, establishing a loss term based on the multi-spectral property to aid in training the thermal network.

The experimental evaluations on the public dataset showcase that the proposed method demonstrates improved accuracy in depth and pose estimation compared to state-of-the-art methods. It exhibits effectiveness and accuracy even under challenging light conditions. We expect further improvements in the results by incorporating additional geometry features and employing multi-sensor fusion methods to boost the accuracy and robustness of depth and pose predictions.