SP-Transformer: A Medium- and Long-Term Photovoltaic Power Forecasting Model Integrating Multi-Source Spatiotemporal Features
Abstract
1. Introduction
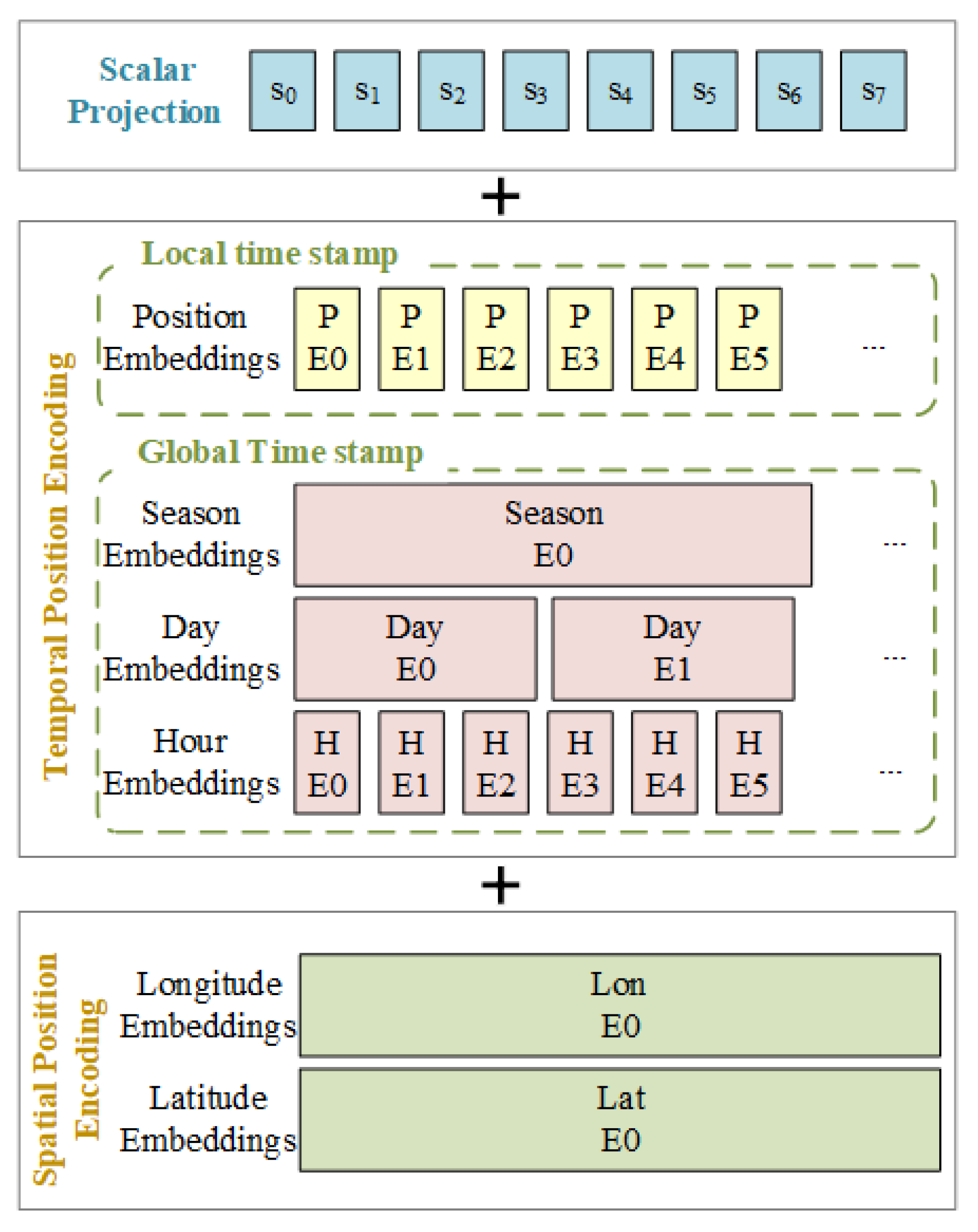
- In this paper, a spatiotemporal position encoding method is proposed. By embedding encoded vectors containing spatial information of sites into the input meteorological time series, the model is able to more accurately capture the spatiotemporal dependencies between different locations. This enhancement improves prediction accuracy and effectively mitigates the impact of abrupt PV power fluctuations caused by spatial differences on the power system.
- This study proposes a spatiotemporal probsparse self-attention mechanism, which enhances the accuracy and efficiency of PV power forecasting by incorporating the Haversine distance metric and a probabilistic sparsity strategy.
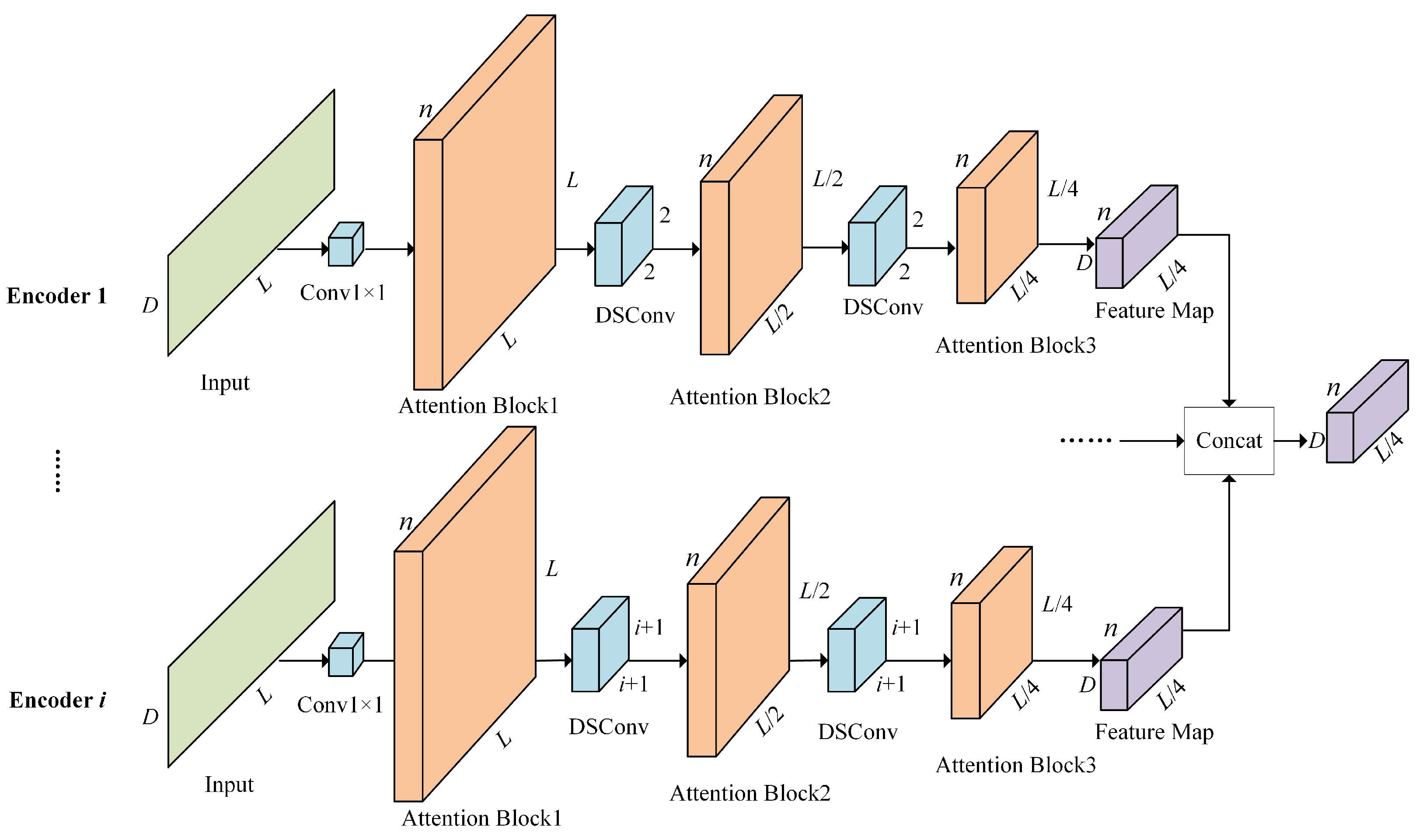
- To address the issue of low efficiency in medium- to long-term photovoltaic power forecasting, this paper proposes a feature pyramid self-attention distillation module (FPSA). The FPSA employs multi-scale depthwise separable convolutions to construct a hierarchical feature pyramid structure, which ensures efficient feature extraction and comprehensive information transmission, thereby significantly reducing information loss and enhancing model stability. The proposed module effectively captures latent spatiotemporal patterns in photovoltaic power data, achieving high prediction accuracy and strong generalization capability under complex environmental conditions. This provides a solid foundation for tackling the key challenges associated with long-term forecasting.
2. Materials and Methods
2.1. Materials
2.1.1. Dataset
2.1.2. Experimental Setup and Scheme
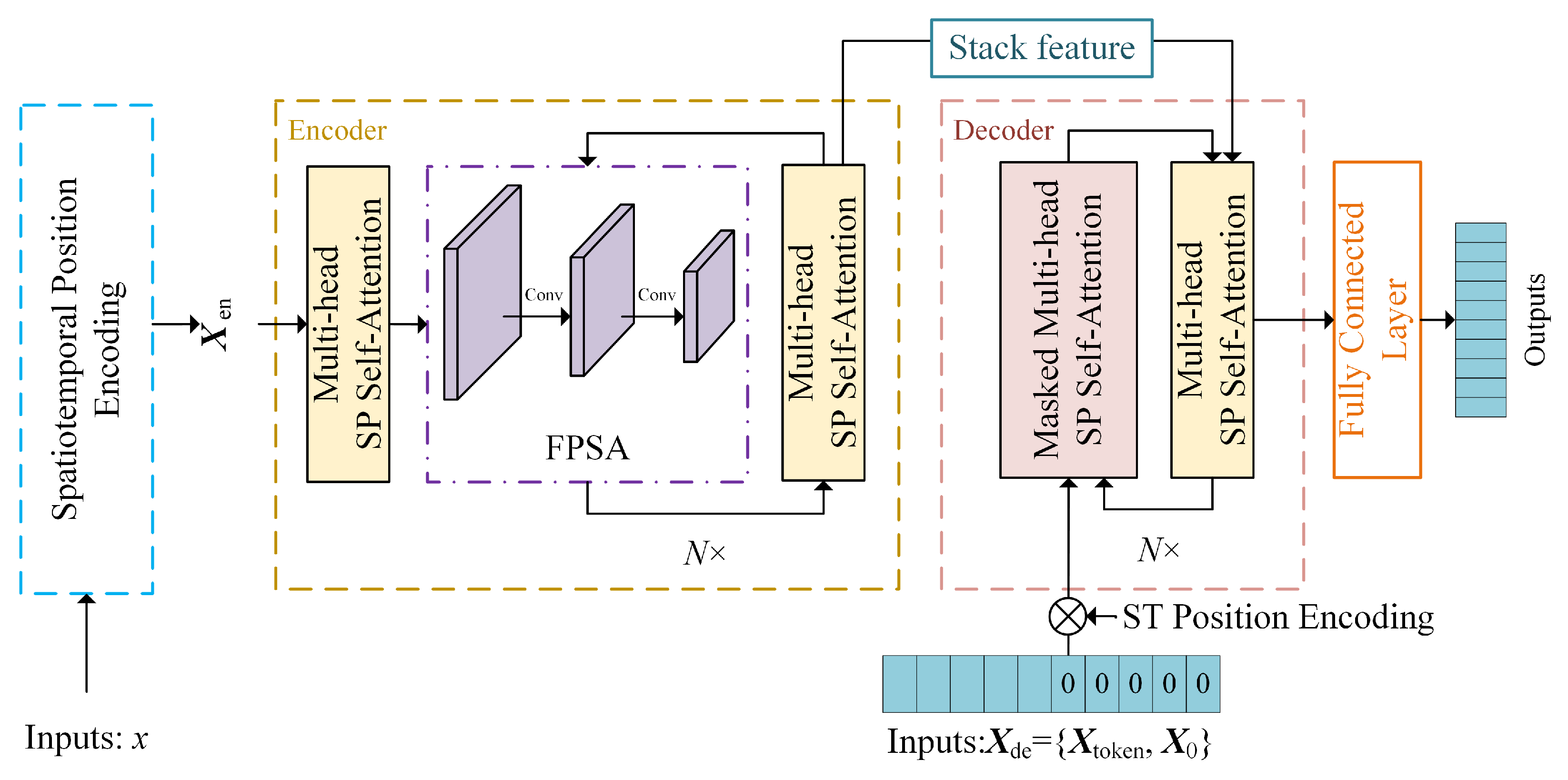
2.2. Model Method
2.2.1. Spatiotemporal Position Encoding
2.2.2. Spatiotemporal Probsparse Self-Attention Mechanism
2.2.3. Feature Pyramid Self-Attention Distillation Module
2.3. Experimental Method
2.3.1. Comparative Experimental Setup
2.3.2. Ablation Experimental Setup
2.4. Evaluation Method
3. Results and Discussion
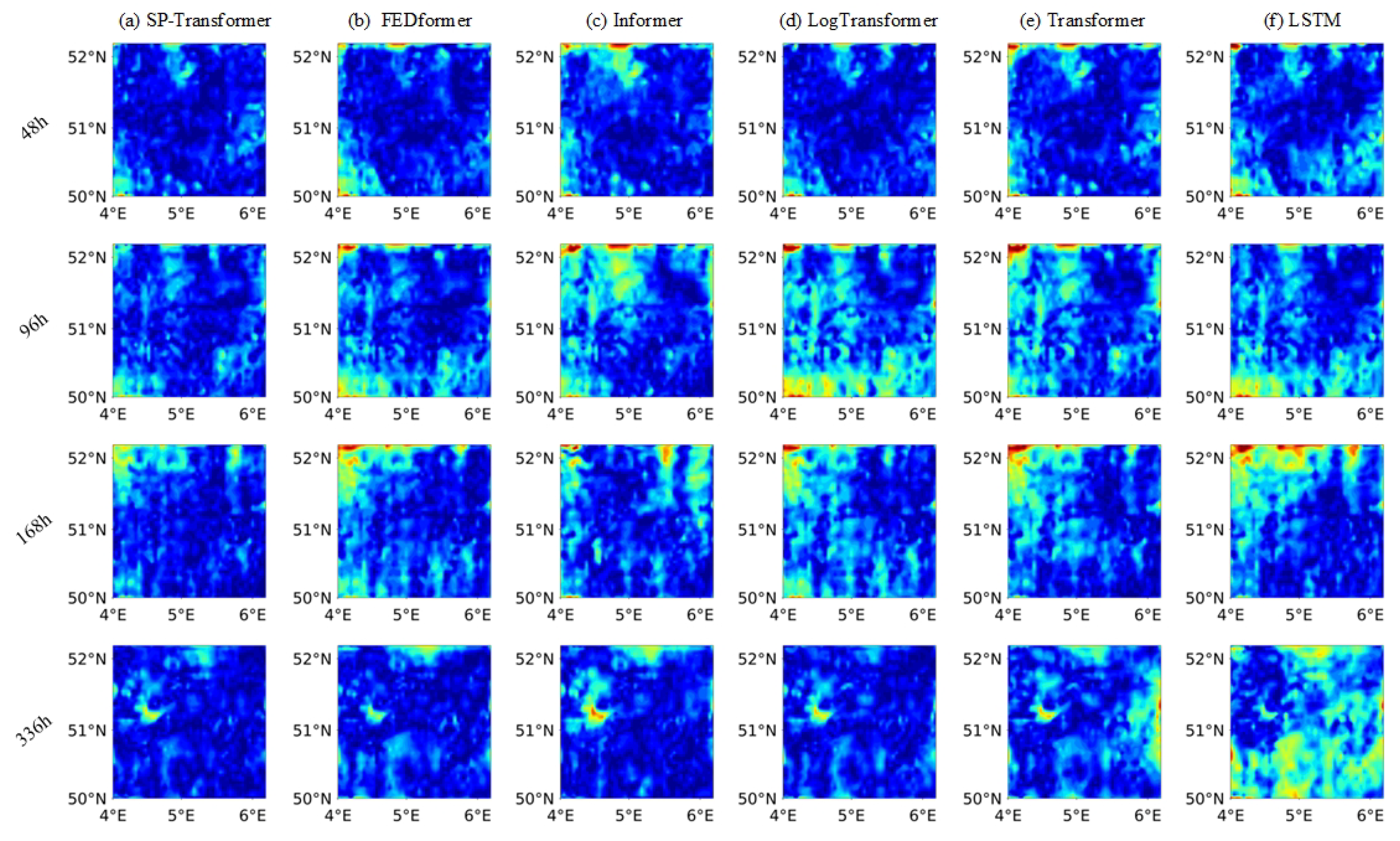
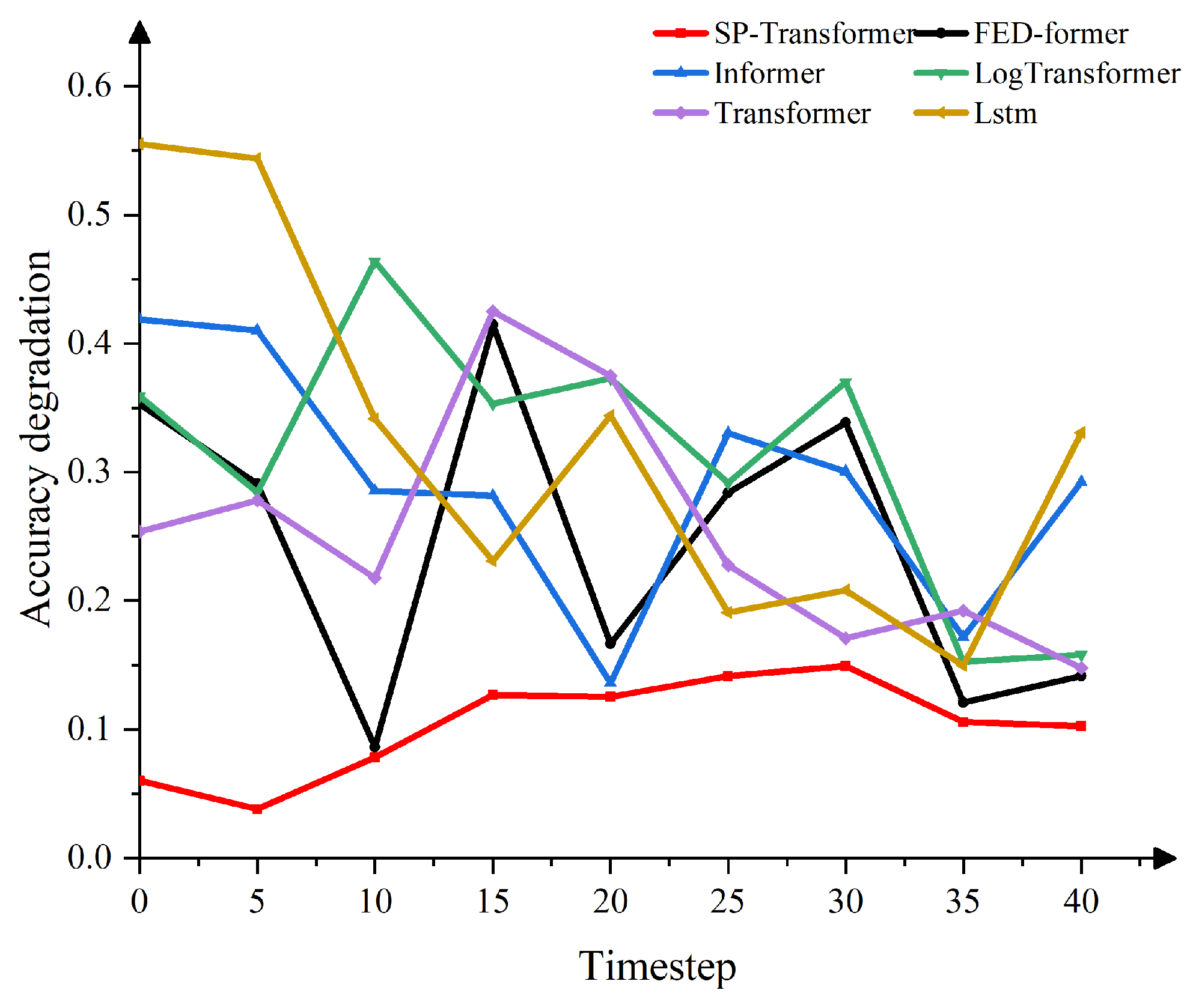
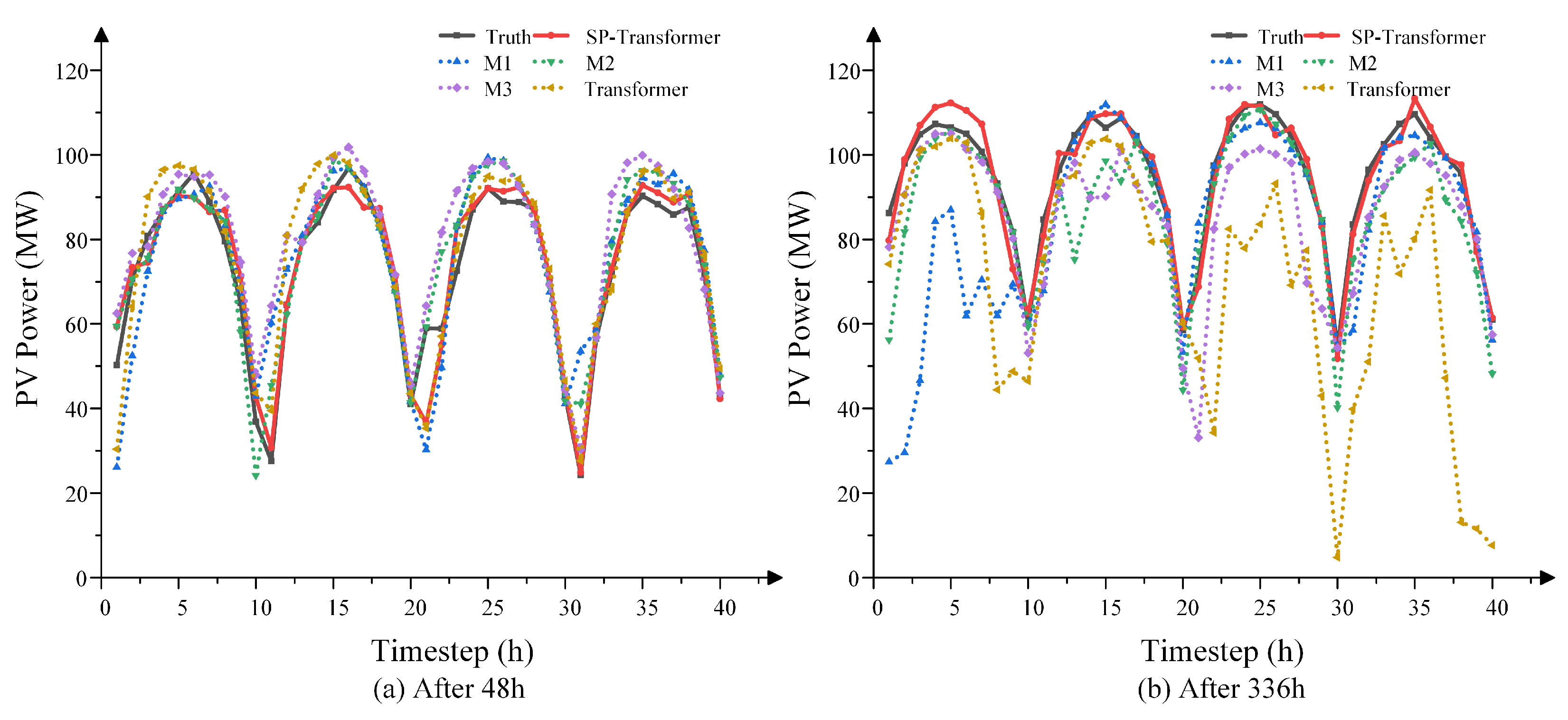
3.1. Comparative Experimental Results
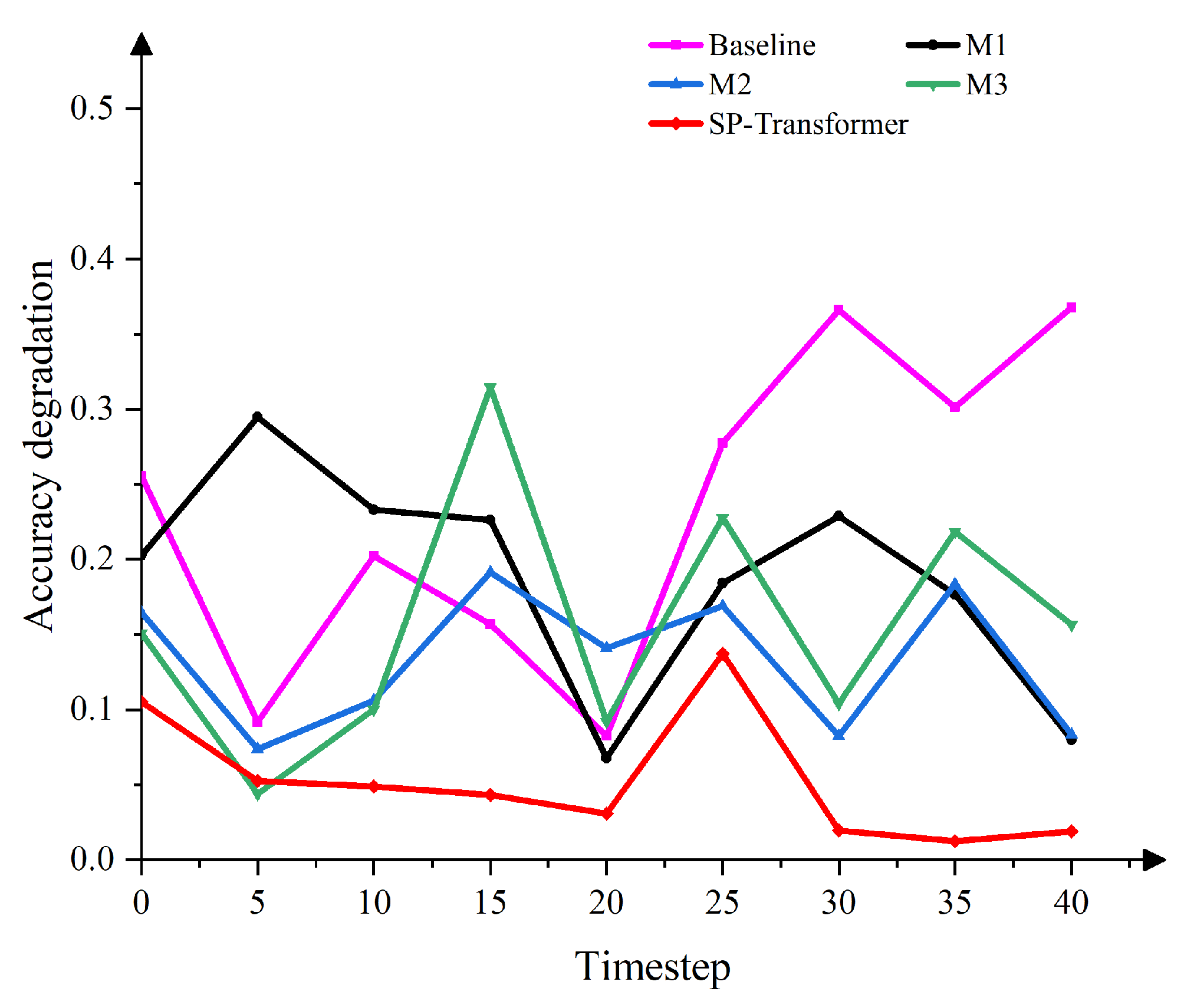
3.2. Ablation Experimental Results
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qiu, T.; Wang, L.; Lu, Y.; Zhang, M.; Qin, W.; Wang, S.; Wang, L. Potential assessment of photovoltaic power generation in China. Renew. Sustain. Energy Rev. 2022, 154, 111900. [Google Scholar] [CrossRef]
- Yang, Y.; Che, J.; Deng, C.; Li, L. Sequential grid approach based support vector regression for short-term electric load forecasting. Appl. Energy 2019, 238, 1010–1021. [Google Scholar] [CrossRef]
- VanDeventer, W.; Jamei, E.; Thirunavukkarasu, G.S.; Seyedmahmoudian, M.; Soon, T.K.; Horan, B.; Mekhilef, S.; Stojcevski, A. Short-term PV power forecasting using hybrid GASVM technique. Renew. Energy 2019, 140, 367–379. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, M.; Guo, M.; Deng, J.; Du, Q.; Wei, W.; Zhang, Y. Innovative approaches to solar energy forecasting: Unveiling the power of hybrid models and machine learning algorithms for photovoltaic power optimization. J. Supercomput. 2025, 81, 20. [Google Scholar] [CrossRef]
- Nguyen, R.; Yang, Y.; Tohmeh, A.; Yeh, H.G. Predicting PV power generation using SVM regression. In Proceedings of the 2021 IEEE Green Energy and Smart Systems Conference (IGESSC), Long Beach, CA, USA, 1–2 November 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, L.; Dai, N.Y. Day-ahead power forecasting model for a photovoltaic plant in Macao based on weather classification using SVM/PCC/LM-ANN. In Proceedings of the 2021 IEEE Sustainable Power and Energy Conference (iSPEC), Nanjing, China, 23–25 December 2021; pp. 775–780. [Google Scholar] [CrossRef]
- Niu, D.; Wang, K.; Sun, L.; Wu, J.; Xu, X. Short-term photovoltaic power generation forecasting based on random forest feature selection and CEEMD: A case study. Appl. Soft Comput. 2020, 93, 106389. [Google Scholar] [CrossRef]
- Ali, M.; Prasad, R.; Xiang, Y.; Khan, M.; Farooque, A.A.; Zong, T.; Yaseen, Z.M. Variational mode decomposition based random forest model for solar radiation forecasting: New emerging machine learning technology. Energy Rep. 2021, 7, 6700–6717. [Google Scholar] [CrossRef]
- Gao, Y.; Wang, J.; Guo, L.; Peng, H. Short-Term Photovoltaic Power Prediction Using Nonlinear Spiking Neural P Systems. Sustainability 2024, 16, 1709. [Google Scholar] [CrossRef]
- Huang, X.; Li, Q.; Tai, Y.; Chen, Z.; Liu, J.; Shi, J.; Liu, W. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Wang, L.; Mao, M.; Xie, J.; Liao, Z.; Zhang, H.; Li, H. Accurate solar PV power prediction interval method based on frequency-domain decomposition and LSTM model. Energy 2023, 262, 125592. [Google Scholar] [CrossRef]
- Hochreiter, S. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Qu, J.; Qian, Z.; Pei, Y. Day-ahead hourly photovoltaic power forecasting using attention-based CNN-LSTM neural network embedded with multiple relevant and target variables prediction pattern. Energy 2021, 232, 120996. [Google Scholar] [CrossRef]
- Limouni, T.; Yaagoubi, R.; Bouziane, K.; Guissi, K.; Baali, E.H. Accurate one step and multistep forecasting of very short-term PV power using LSTM-TCN model. Renew. Energy 2023, 205, 1010–1024. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Y.; Zhang, F.; Li, Y.; Li, J.; Zhang, C. CrossWaveNet: A dual-channel network with deep cross-decomposition for Long-term Time Series Forecasting. Expert Syst. Appl. 2024, 238, 121642. [Google Scholar] [CrossRef]
- Wang, S.; Ma, J. A novel GBDT-BiLSTM hybrid model on improving day-ahead photovoltaic prediction. Sci. Rep. 2023, 13, 15113. [Google Scholar] [CrossRef]
- Kushwaha, V.; Pindoriya, N.M. A SARIMA-RVFL hybrid model assisted by wavelet decomposition for very short-term solar PV power generation forecast. Renew. Energy 2019, 140, 124–139. [Google Scholar] [CrossRef]
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-term load forecasting based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, G.; Luo, D.; Bavirisetti, D.P.; Xiao, G. Multi-timescale photovoltaic power forecasting using an improved Stacking ensemble algorithm based LSTM-Informer model. Energy 2023, 283, 128669. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.; Xiao, G.; He, S.; Deng, K. TransformGraph: A novel short-term electricity net load forecasting model. Energy Rep. 2023, 9, 2705–2717. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, R.; Ma, H.; Ekanayake, C.; Cui, Y. On vision transformer for ultra-short-term forecasting of photovoltaic generation using sky images. Sol. Energy 2024, 267, 112203. [Google Scholar] [CrossRef]
- Zhang, L.; Wilson, R.; Sumner, M.; Wu, Y. Advanced multimodal fusion method for very short-term solar irradiance forecasting using sky images and meteorological data: A gate and transformer mechanism approach. Renew. Energy 2023, 216, 118952. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Li, S.; Jin, X.; Xuan, Y.; Zhou, X.; Chen, W.; Wang, Y.X.; Yan, X. Enhancing the locality and breaking the memory bottleneck of transformer on time series forecasting. arXiv 2019, arXiv:1907.00235. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Online, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar] [CrossRef]
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. Fedformer: Frequency enhanced decomposed transformer for long-term series forecasting. In Proceedings of the International Conference on Machine Learning PMLR, Baltimore, MD, USA, 17–23 July 2022; pp. 27268–27286. [Google Scholar] [CrossRef]


| References | Contribution Points | Shortcomings |
|---|---|---|
| [18] | A hybrid model combining adaptive noise and fully integrated empirical mode decomposition, sample entropy, and Transformer is proposed. | Position encoding can only obtain temporal information, without considering the impact of the relative position of photovoltaic sites on the prediction results. |
| [19] | A LSTM Informer model based on an improved Stacking ensemble algorithm is proposed. | |
| [20] | Propose a combined Transformer and graph convolutional network model for power grid load forecasting. | The full connectivity of self-attention mechanism leads to an increase in quadratic complexity as the sequence length increases, greatly increasing the computational burden of the model when processing long sequence data. |
| [21] | Developed a prediction framework that integrates Vision Transformer model and gated loop unit. | |
| [22] | Propose a Transformer based prediction framework model that combines images with quantitative measurement of solar irradiance. |
| Method | 48 h | 96 h | 168 h | 336 h | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| Ours | 0.761 | 0.558 | 0.784 | 0.562 | 0.905 | 0.655 | 1.061 | 0.768 |
| [26] | 0.795 | 0.659 | 0.885 | 0.725 | 0.987 | 0.799 | 1.123 | 0.924 |
| [25] | 0.854 | 0.663 | 0.913 | 0.706 | 1.053 | 0.811 | 1.096 | 0.844 |
| [24] | 0.956 | 0.714 | 1.002 | 0.739 | 1.084 | 0.847 | 1.209 | 0.952 |
| [23] | 1.151 | 0.932 | 1.162 | 0.914 | 1.394 | 0.952 | 1.232 | 0.976 |
| [12] | 2.360 | 1.934 | 2.363 | 1.946 | 2.418 | 1.934 | 4.384 | 3.494 |
| Method | 48 h | 96 h | 168 h | 336 h | ||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | |
| Ours | 0.761 | 0.558 | 0.784 | 0.562 | 0.905 | 0.655 | 1.061 | 0.768 |
| Model 1 | 0.854 | 0.663 | 0.913 | 0.706 | 1.053 | 0.811 | 1.209 | 0.952 |
| Model 2 | 0.956 | 0.714 | 1.002 | 0.737 | 1.139 | 0.874 | 1.096 | 0.835 |
| Model 3 | 0.800 | 0.659 | 0.885 | 0.706 | 0.987 | 0.800 | 1.061 | 0.835 |
| Transformer | 1.151 | 0.932 | 1.162 | 0.959 | 1.190 | 0.952 | 1.232 | 0.995 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Chen, J.; Zhu, Y.; Fan, J.; Hu, J.; Tan, L. SP-Transformer: A Medium- and Long-Term Photovoltaic Power Forecasting Model Integrating Multi-Source Spatiotemporal Features. Appl. Sci. 2025, 15, 11846. https://doi.org/10.3390/app152111846
Wang B, Chen J, Zhu Y, Fan J, Hu J, Tan L. SP-Transformer: A Medium- and Long-Term Photovoltaic Power Forecasting Model Integrating Multi-Source Spatiotemporal Features. Applied Sciences. 2025; 15(21):11846. https://doi.org/10.3390/app152111846
Chicago/Turabian StyleWang, Bin, Julong Chen, Yongqing Zhu, Junqiu Fan, Jiang Hu, and Ling Tan. 2025. "SP-Transformer: A Medium- and Long-Term Photovoltaic Power Forecasting Model Integrating Multi-Source Spatiotemporal Features" Applied Sciences 15, no. 21: 11846. https://doi.org/10.3390/app152111846
APA StyleWang, B., Chen, J., Zhu, Y., Fan, J., Hu, J., & Tan, L. (2025). SP-Transformer: A Medium- and Long-Term Photovoltaic Power Forecasting Model Integrating Multi-Source Spatiotemporal Features. Applied Sciences, 15(21), 11846. https://doi.org/10.3390/app152111846






