Multi-Granularity Content-Aware Network with Semantic Integration for Unsupervised Anomaly Detection
Abstract
1. Introduction
- 1.
- The proposed MGCA-Net, consisting of CAABs, MGSIB, and SGFBs to model the content consistency in images. In our model, images are divided into superpixels to generate tokens.
- 2.
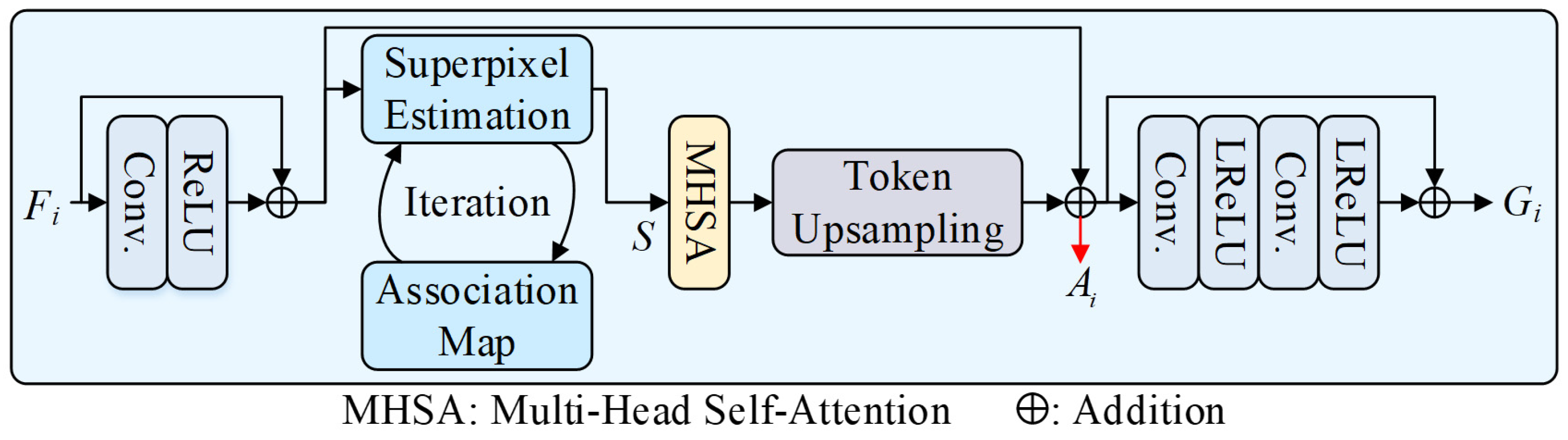
- We design CAABs to capture the content consistency in anomaly and abnormal regions. By iterative optimization and segmentation in CAABs, the spatial structures of objects, such as defects and artifacts, are preserved.
- 3.
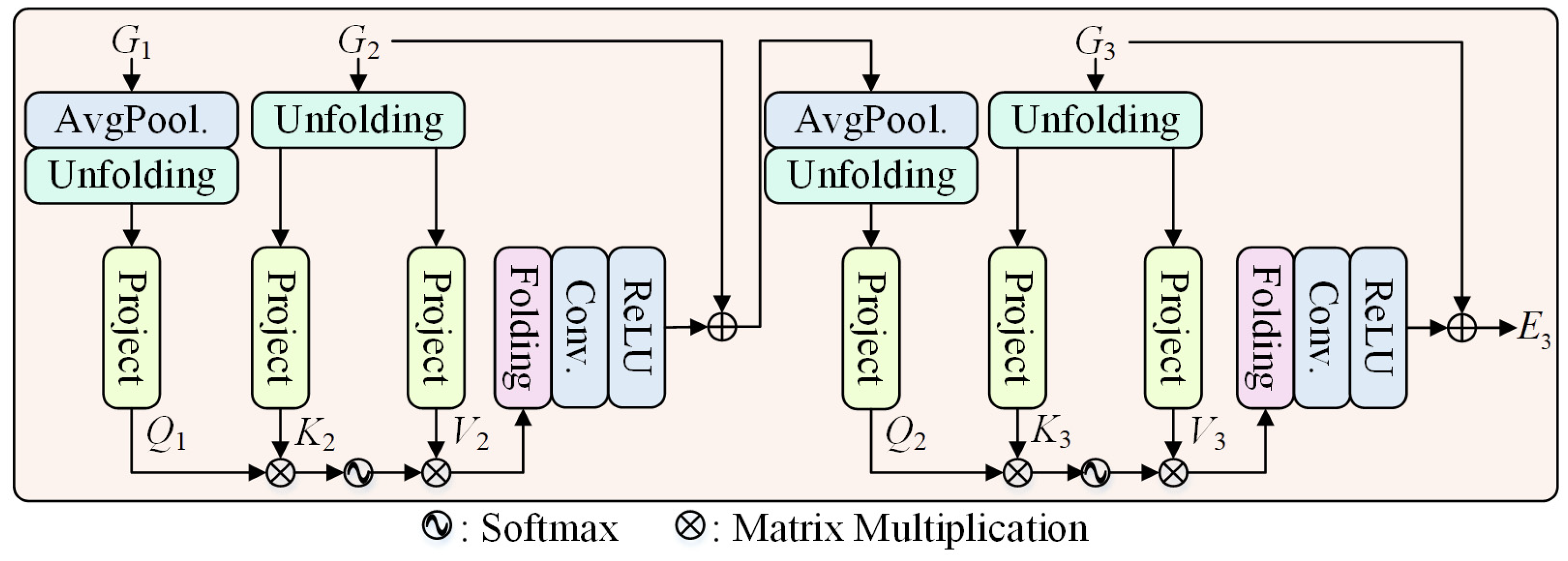
- We construct the MGSIB to integrate the features from fine, medium, and coarse granularities. By progressive cross-granularity attention, the global semantic information at all granularities is efficiently merged.
2. Related Work
2.1. Supervised Anomaly Detection
2.2. Unsupervised Anomaly Detection
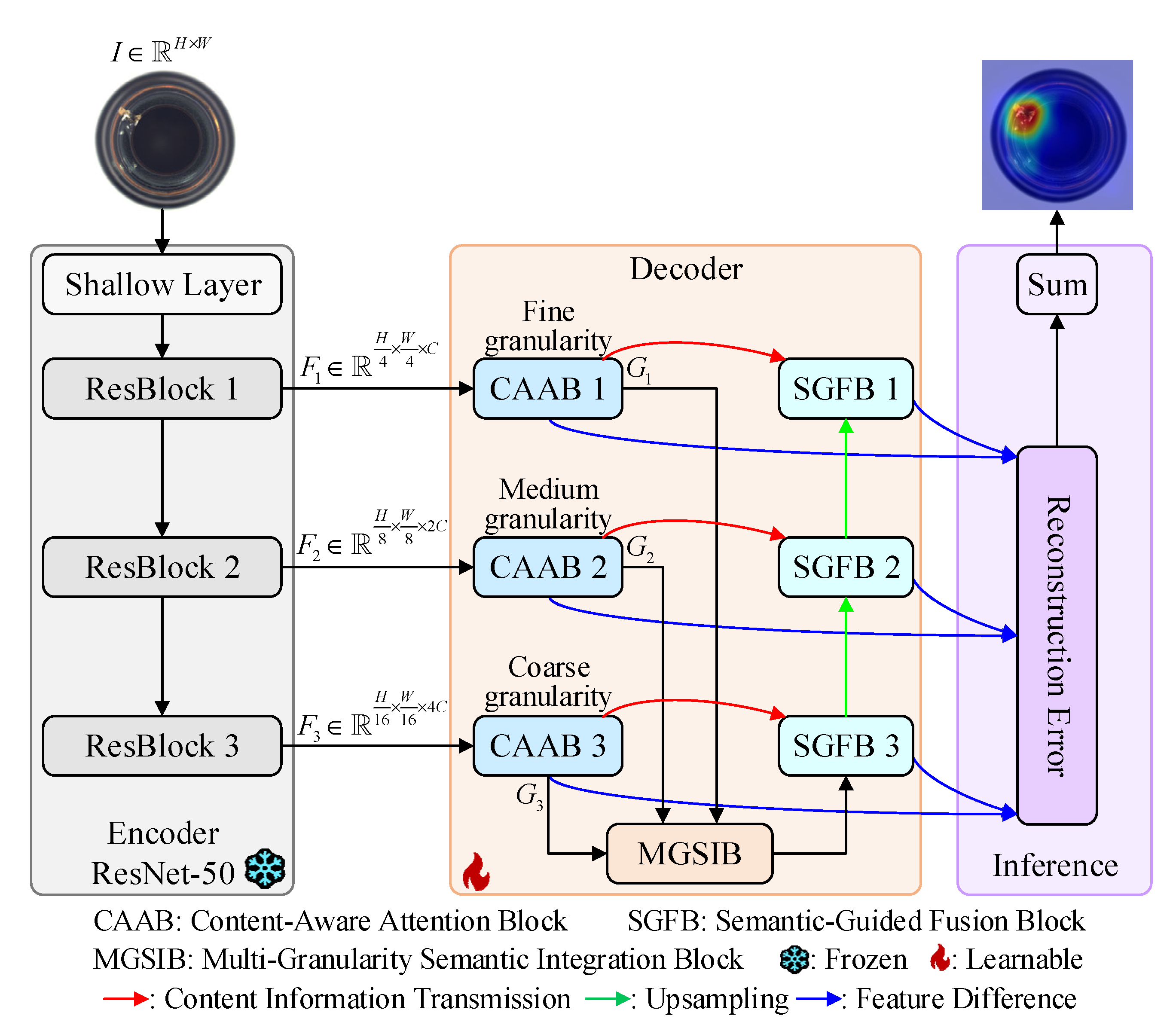
3. Proposed MGCA-Net
3.1. Content-Aware Attention Block
3.2. Multi-Granularity Semantic Integration Block
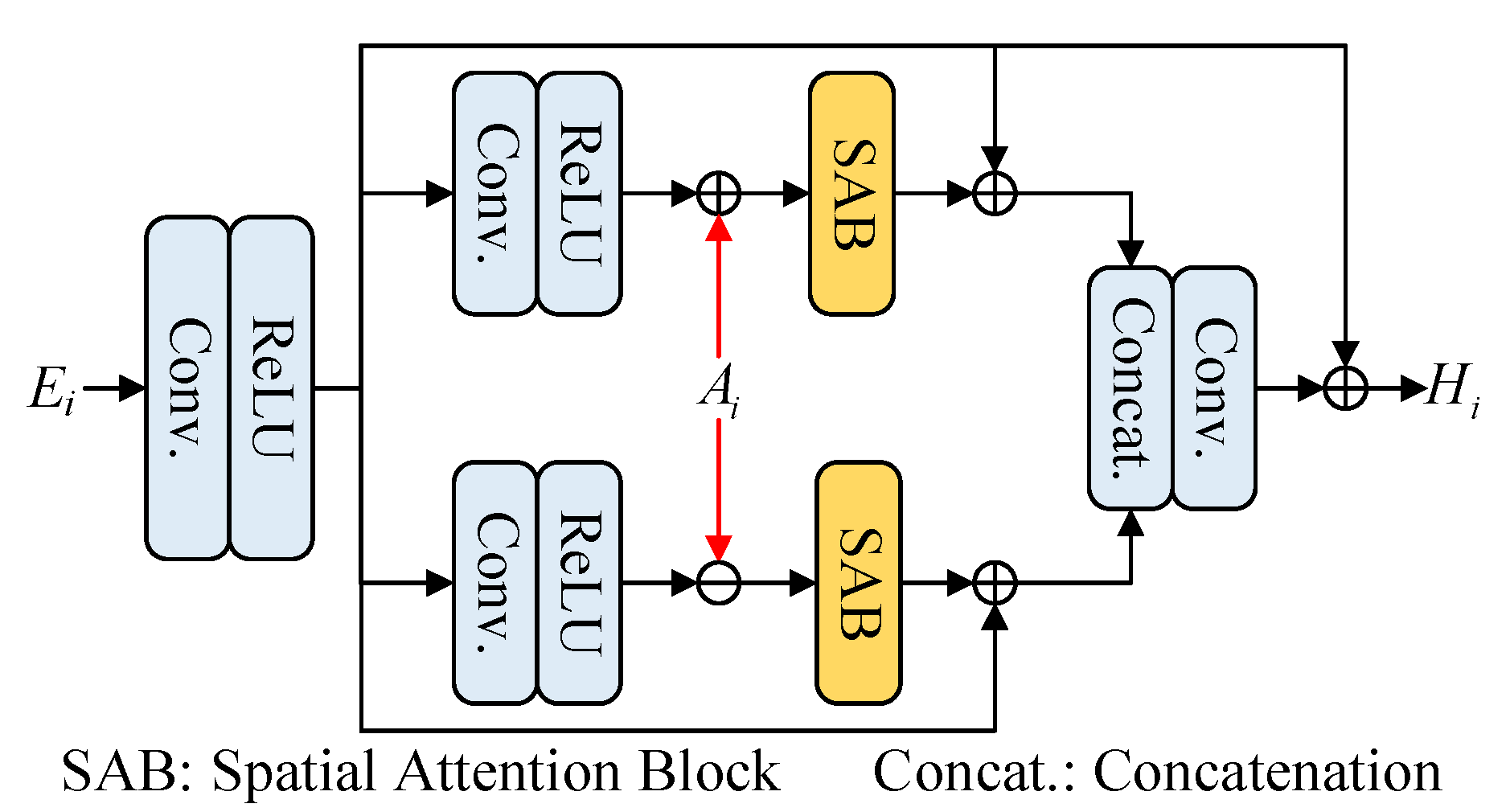
3.3. Semantic-Guided Fusion Block
3.4. Model Optimization and Inference
3.4.1. Model Optimization
3.4.2. Inference
4. Experimental Results and Analysis
4.1. Experimental Setup
4.1.1. Experiment Settings
4.1.2. Compared Methods
4.1.3. Evaluation Metrics
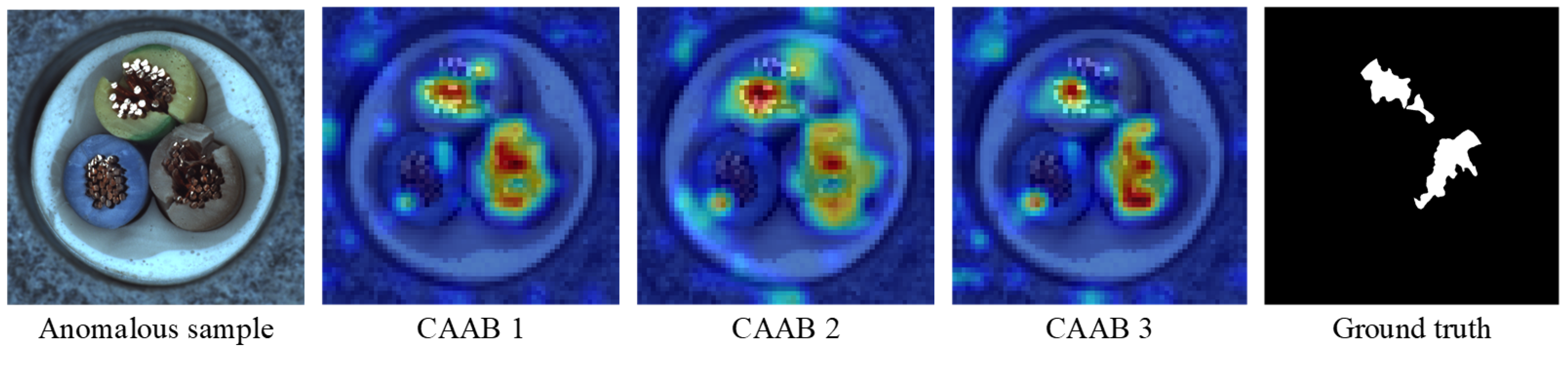
4.2. Content Consistencies at Different Granularities
4.3. Experiments on the MVTec-AD Dataset
4.4. Experiments on the VisA Dataset
4.5. Ablation Study
4.6. Feature Visualization
4.7. Computational Complexity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yousif, I.; Burns, L.; El Kalach, F.; Harik, R. Leveraging computer vision towards high-efficiency autonomous industrial facilities. J. Intell. Manuf. 2025, 54, 2983–3008. [Google Scholar] [CrossRef]
- Tao, X.; Gong, X.; Zhang, X.; Yan, S.; Adak, C. Deep learning for unsupervised anomaly localization in industrial images: A survey. IEEE Trans. Instrum. Meas. 2022, 71, 5018021. [Google Scholar] [CrossRef]
- Xie, G.; Wang, J.; Liu, J.; Lyu, J.; Liu, Y.; Wang, C.; Zhang, F.; Jin, Y. IM-IAD: Industrial image anomaly detection benchmark in manufacturing. IEEE Trans. Cybern. 2025, 54, 2720–2733. [Google Scholar] [CrossRef]
- Gong, D.; Liu, L.; Le, V.; Saha, B.; Mansour, M.R.; Venkatesh, S.; Hengel, A.V.D. Memorizing normality to detect anomaly: Memory-augmented deep autoencoder for unsupervised anomaly detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1705–1714. [Google Scholar]
- Schlegl, T.; Seebock, P.; Waldstein, S.M.; Langs, G.; Schmidt-Erfurthb, U. f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Med. Image Anal. 2019, 54, 30–44. [Google Scholar] [CrossRef]
- Yao, H.; Yu, W. Generalizable industrial visual anomaly detection with self-induction vision transformer. arXiv 2022, arXiv:2211.12311. [Google Scholar] [CrossRef]
- Lee, Y.; Kang, P. AnoViT: Unsupervised anomaly detection and localization with vision transformer-based encoder-decoder. IEEE Trans. Access 2022, 10, 46717–46724. [Google Scholar] [CrossRef]
- Yang, Q.; Guo, R. An unsupervised method for industrial image anomaly detection with vision transformer-based autoencoder. Sensors 2024, 24, 2440. [Google Scholar] [CrossRef]
- Yao, H.; Luo, W.; Yu, W.; Zhang, X.; Qiang, Z.; Luo, D.; Shi, H. Dual-attention transformer and discriminative flow for industrial visual anomaly detection. IEEE Trans. Autom. Sci. Eng. 2024, 21, 6126–6140. [Google Scholar] [CrossRef]
- Huang, H.; Zhou, X.; Cao, J.; He, R.; Tan, T. Vision transformer with super token sampling. arXiv 2022, arXiv:2211.11167. [Google Scholar]
- Meng, Z.; Zhang, T.; Zhao, F.; Chen, G.; Liang, M. Multiscale super token transformer for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2024, 21, 5508105. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Huang, H.; Wang, P.; Pei, J.; Wang, J.; Alexanian, S.; Niyato, D. Deep learning advancements in anomaly detection: A comprehensive survey. IEEE Internet Things J. 2025, 12, 44318–44342. [Google Scholar] [CrossRef]
- Liu, J.; Xie, G.; Wang, J.; Li, S.; Wang, C.; Zheng, F.; Jin, Y. Deep industrial image anomaly detection: A survey. Mach. Intell. Res. 2024, 21, 104–135. [Google Scholar] [CrossRef]
- Baitieva, A.; Hurych, D.; Besnier, V.; Bernard, O. Supervised anomaly detection for complex industrial images. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 17754–17762. [Google Scholar]
- Kawachi, Y.; Koizumi, Y.; Harada, N. Complementary set variational autoencoder for supervised anomaly detection. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2366–2370. [Google Scholar]
- Yao, X.; Li, R.; Zhang, J.; Sun, J.; Zhang, C. Explicit boundary guided semi-push-pull contrastive learning for supervised anomaly detection. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 24490–24499. [Google Scholar]
- Yeh, M.-F.; Luo, C.-C.; Liu, Y.-C. Optimization of Gabor convolutional networks using the Taguchi method and their application in wood defect detection. Appl. Sci. 2025, 15, 9557. [Google Scholar] [CrossRef]
- Zhou, F.; Wang, G.; Zhang, K.; Liu, S.; Zhong, T. Semi-supervised anomaly detection via neural process. IEEE Trans. Knowl. Data Eng. 2023, 35, 10423–10435. [Google Scholar] [CrossRef]
- Liu, J.; Song, K.; Feng, M.; Yan, Y.; Tu, Z.; Zhu, L. Semi-supervised anomaly detection with dual prototypes autoencoder for industrial surface inspection. Opt. Lasers Eng. 2021, 136, 106324. [Google Scholar] [CrossRef]
- Wu, P.; Zhou, X.; Pang, G.; Yang, Z.; Yan, Q.; Wang, P.; Zhang, Y. Weakly supervised video anomaly detection and localization with spatio-temporal prompts. In Proceedings of the 32nd ACM International Conference on Multimedia, New York, NY, USA, 20–27 February 2024; pp. 9301–9310. [Google Scholar]
- Yang, Z.; Liu, J.; Wu, P. Text prompt with normality guidance for weakly supervised video anomaly detection. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–22 June 2024; pp. 17754–17762. [Google Scholar]
- Zhou, Y.; Song, X.; Zhang, Y.; Liu, F.; Zhu, C.; Liu, L. Feature encoding with autoencoders for weakly supervised anomaly detection. IEEE Trans. Neural Netw. Learn. Syst. 2023, 33, 2454–2465. [Google Scholar] [CrossRef]
- Bilal, M.; Hanif, M.S. Fast anomaly detection for vision-based industrial inspection using cascades of Null subspace PCA detectors. Sensors 2025, 15, 4853. [Google Scholar] [CrossRef]
- Tang, S.; Xu, X.; Li, H.; Zhou, T. Unsupervised detection of surface defects in varistors with reconstructed normal distribution under mask constraints. Appl. Sci. 2025, 15, 10479. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Wang, S.; Dai, P.; Li, Q. LRGAN: Visual anomaly detection using GAN with locality-preferred recoding. J. Vis. Commun. Image Represent. 2021, 79, 103201. [Google Scholar] [CrossRef]
- Lin, S.C.; Lee, H.W.; Hsieh, Y.S.; Ho, C.Y.; Lai, S.H. Masked attention ConvNeXt Unet with multi-synthesis dynamic weighting for anomaly detection and localization. In Proceedings of the 34th British Machine Vision Conference (BMVC), Aberdeen, UK, 20–24 November 2023; p. 911. [Google Scholar]
- Zhou, W.; Zhou, S.; Cao, Y.; Yang, J.; Liu, H. Unsupervised anomaly detection method for electrical equipment based on audio latent representation and parallel attention mechanism. Appl. Sci. 2025, 15, 8474. [Google Scholar] [CrossRef]
- He, H.; Zhang, J.; Chen, H.; Chen, X.; Li, Z.; Chen, X.; Xie, L. A diffusion-based framework for multi-class anomaly detection. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Vancouver, BC, Canada, 20–27 February 2024; pp. 8472–8480. [Google Scholar]
- Akshay, S.; Narasimhan, N.L.; George, J.; Balasubramanian, V.N. A unified latent schrodinger bridge diffusion model for unsupervised anomaly detection and localization. In Proceedings of the 2025 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 11–15 June 2025; pp. 25528–25538. [Google Scholar]
- Zhang, X.; Li, N.; Li, J.; Dai, T.; Jiang, Y.; Xia, S.T. Unsupervised surface anomaly detection with diffusion probabilistic model. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 6782–6791. [Google Scholar]
- Park, S.; Choi, D. Exploring the potential of anomaly detection through reasoning with large language models. Appl. Sci. 2025, 15, 10384. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Zhang, J.; He, Q.; Chen, H.; Gan, Z.; Xie, L. MambaAD: Exploring state space models for multi-class unsupervised anomaly detection. In Proceedings of the 38th Advances in Neural Information Processing Systems (NeuriPS), Vancouver, BC, Canada, 16–20 December 2024; pp. 71162–71187. [Google Scholar]
- Guo, J.; Lu, S.; Zhang, W.; Chen, F.; Li, H.; Liao, H. Dinomaly: The less is more philosophy in multi-class unsupervised anomaly detection. In Proceedings of the 2025 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 11–15 June 2025; pp. 20405–20415. [Google Scholar]
- Yao, H.; Luo, W.; Lou, J.; Yu, W.; Zhang, X.; Qiang, Z.; Shi, H. Scalable industrial visual anomaly detection with partial semantics aggregation vision transformer. IEEE Trans. Instrum. Meas. 2023, 73, 5004217. [Google Scholar] [CrossRef]
- Park, S.; Kim, J.; Kim, J.; Wang, S. Fault Diagnosis of air handling units in an auditorium using real operational labeled data across different operation modes. J. Comput. Civ. Eng. 2025, 39, 04025065. [Google Scholar] [CrossRef]
- Wang, S. A hybrid SMOTE and Trans-CWGAN for data imbalance in real operational AHU AFDD: A case study of an auditorium building. Energy Build. 2025, 348, 116447. [Google Scholar] [CrossRef]
- Jampani, V.; Sun, D.; Liu, M.Y.; Yang, M.H.; Kautz, J. Superpixel sampling networks. In Proceedings of the 2018 European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 1–17. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.; Kweon, I. CBAM: Convolutional Block Attention Module. In Proceedings of the 2018 European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 1–17. [Google Scholar]
- Bergmann, P.; Fauser, M.; Sattlegger, D.; Steger, C. MVTec AD—A comprehensive real-world dataset for unsupervised anomaly detection. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 9584–9592. [Google Scholar]
- Zou, Y.; Jeong, J.; Pemula, L.; Zhang, D.; Dabeer, O. Spot-the-difference self-supervised pre-training for anomaly detection and segmentation. In Proceedings of the 2022 European Conference on Computer Vision (ECCV), Tel Aviv, Israel, 23–27 October 2022; pp. 1–17. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Li, F. ImageNet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Zavrtanik, V.; Kristan, M.; Skocaj, D. DRAEM-A discriminatively trained reconstruction embedding for surface anomaly detection. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Virtual, 11–17 October 2021; pp. 8330–8339. [Google Scholar]
- You, Z.; Cui, L.; Shen, Y.; Yang, K.; Lu, X.; Zheng, Y.; Le, X. A unified model for multi-class anomaly detection. In Proceedings of the 36th Advances in Neural Information Processing Systems (NeuriPS), New Orleans, LA, USA, 28 November–9 December 2022; pp. 4571–4584. [Google Scholar]
- Deng, H.; Li, X. Anomaly detection via reverse distillation from one-class embedding. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 19–24 June 2022; pp. 9737–9746. [Google Scholar]
- Liu, Z.; Zhou, Y.; Xu, Y.; Wang, Z. SimpleNet: A Simple Network for Image Anomaly Detection and Localization. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 20402–20411. [Google Scholar]
- Zhang, J.; Chen, X.; Wang, Y.; Wang, C.; Liu, Y.; Li, X.; Yang, M.H.; Tao, D. Exploring plain ViT features for multi-class unsupervised visual anomaly detection. Comput. Vis. Image Underst. 2025, 253, 104308. [Google Scholar] [CrossRef]
- Li, Z.; Yan, Y.; Wang, X.; Ge, Y.; Meng, L. A survey of deep learning for industrial visual anomaly detection. IEEE Trans. Instrum. Meas. 2025, 58, 279. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the 2017 IEEE/CVF International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Liu, Y.; Zhang, K.; Guan, C.; Zhang, S.; Li, H.; Wan, W.; Sun, J. Building change detection in earthquake: A multi-scale interaction network with offset calibration and a dataset. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5635217. [Google Scholar] [CrossRef]





| Metrics | DRAEM [43] | UniAD [44] | RD4AD [45] | SimpleNet [46] | ViTAD [47] | MGCA-Net | |
|---|---|---|---|---|---|---|---|
| Image- level | AUROC | 88.1 | 96.5 | 94.6 | 95.3 | 98.3 | 98.7 |
| AP | 94.7 | 98.8 | 96.5 | 98.4 | 99.4 | 99.4 | |
| F1 | 92.0 | 96.2 | 95.2 | 95.8 | 97.3 | 97.7 | |
| Pixel- level | AUROC | 88.6 | 96.8 | 96.1 | 96.9 | 97.7 | 98.1 |
| AP | 52.6 | 43.4 | 48.6 | 45.9 | 55.3 | 56.1 | |
| F1 | 48.6 | 49.5 | 53.8 | 49.7 | 58.7 | 59.3 |
| Metrics | DRAEM [43] | UniAD [44] | RD4AD [45] | SimpleNet [46] | ViTAD [47] | MGCA-Net | |
|---|---|---|---|---|---|---|---|
| Image- level | AUROC | 79.5 | 88.8 | 92.4 | 87.2 | 90.5 | 91.4 |
| AP | 82.8 | 90.8 | 92.4 | 87.0 | 91.7 | 92.3 | |
| F1 | 79.4 | 85.8 | 89.6 | 81.8 | 86.3 | 88.9 | |
| Pixel- level | AUROC | 91.4 | 98.3 | 98.1 | 96.8 | 98.2 | 98.9 |
| AP | 24.8 | 33.7 | 38.0 | 34.7 | 36.6 | 38.6 | |
| F1 | 30.4 | 39.0 | 42.6 | 37.8 | 41.1 | 43.1 |
| Metrics | Case 1 | Case 2 | Case 3 | Case 4 | MGCA-Net | |
|---|---|---|---|---|---|---|
| Image- level | AUROC | 97.7 | 98.5 | 98.2 | 98.2 | 98.7 |
| AP | 98.6 | 98.9 | 99.0 | 99.3 | 99.4 | |
| F1 | 96.8 | 97.3 | 96.9 | 97.1 | 97.7 | |
| Pixel- level | AUROC | 97.2 | 97.8 | 97.7 | 98.0 | 98.1 |
| AP | 55.4 | 55.6 | 56.1 | 55.8 | 56.1 | |
| F1 | 58.4 | 58.3 | 58.1 | 59.2 | 59.3 |
| Metrics | Case 1 | Case 2 | Case 3 | Case 4 | MGCA-Net | |
|---|---|---|---|---|---|---|
| Image- level | AUROC | 89.8 | 90.2 | 90.7 | 91.1 | 91.4 |
| AP | 90.6 | 90.7 | 91.2 | 91.7 | 92.3 | |
| F1 | 86.4 | 88.0 | 87.3 | 87.9 | 88.9 | |
| Pixel- level | AUROC | 96.3 | 96.7 | 96.8 | 97.3 | 98.9 |
| AP | 37.6 | 37.9 | 37.5 | 38.1 | 38.6 | |
| F1 | 41.8 | 42.3 | 41.6 | 42.1 | 43.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, X.; Zhao, S.; Xue, J.; Liu, D.; Han, X.; Zhang, S.; Zhang, Y. Multi-Granularity Content-Aware Network with Semantic Integration for Unsupervised Anomaly Detection. Appl. Sci. 2025, 15, 11842. https://doi.org/10.3390/app152111842
Guo X, Zhao S, Xue J, Liu D, Han X, Zhang S, Zhang Y. Multi-Granularity Content-Aware Network with Semantic Integration for Unsupervised Anomaly Detection. Applied Sciences. 2025; 15(21):11842. https://doi.org/10.3390/app152111842
Chicago/Turabian StyleGuo, Xinyu, Shihui Zhao, Jianbin Xue, Dongdong Liu, Xinyang Han, Shuai Zhang, and Yufeng Zhang. 2025. "Multi-Granularity Content-Aware Network with Semantic Integration for Unsupervised Anomaly Detection" Applied Sciences 15, no. 21: 11842. https://doi.org/10.3390/app152111842
APA StyleGuo, X., Zhao, S., Xue, J., Liu, D., Han, X., Zhang, S., & Zhang, Y. (2025). Multi-Granularity Content-Aware Network with Semantic Integration for Unsupervised Anomaly Detection. Applied Sciences, 15(21), 11842. https://doi.org/10.3390/app152111842






