Abstract
Permeability evolution is one of the key parameters influencing the efficient exploitation of deep unconventional energy resources, as it reflects the dynamic development of pore-fracture structures under complex engineering effects. Using fractal geometry to describe the pore-fracture system, rock permeability enhancement can be quantitatively evaluated. In this study, fractured coal specimens were analyzed under simulated mining-induced stress relief and CH4 release conditions based on fractal geometry theory. The permeability-enhancement rate was derived and verified through CT (Computed Tomography) characterization of the pore-fracture network. The fractal dimension of the fracture aperture distribution and the tortuosity of fracture paths were determined to establish a fractal permeability-enhancement model, and its sensitivity was analyzed. The results indicate that permeability evolution undergoes four distinct stages: a stable stage, a slow-growth stage, a rapid-growth stage, and a stable or declining stage. The mining-induced stress relief and gas desorption effects significantly accelerate permeability enhancement, providing new insights into the mechanisms governing gas flow and pressure relief in deep coal seams. The proposed model, highly sensitive to the fracture aperture ratio (λmin/λmax), reveals that a smaller aperture span leads to greater permeability enhancement during the damage and fracture stage. These findings offer practical guidance for predicting permeability evolution, optimizing gas drainage design, and enhancing the safety and efficiency of coal mining and methane extraction operations.
1. Introduction
As for the deep tight reservoirs with low porosity and low flow capacity (like coal), the permeability is one of the key parameters closely related to the exploitation of deep energy resources [1,2,3]. When it comes to coal mining, the impact of the mining effect is one of the most important factors for the coal permeability enhancement [4]. Xie et al. [5,6] took the evolution of fracture network into consideration and discussed the permeability enhancement effect during the loading and unloading conditions of mining effect in the laboratory, in which the fracture porosity was evaluated through the strain results. Huo and Meguid [7] employed an integrated approach combining steady-state flow testing, high-resolution laser scanning, and 3D numerical simulations to analyze the permeability evolution and fracture closure characteristics of Lac du Bonnet granite. Similar modeling strategies have been successfully adopted to elucidate the impact of lithological heterogeneities on physical responses in carbonate systems [8]. Xue et al. [9] examined how mining-induced damage affects the evolution of coal permeability and proposed a damage-based permeability model to quantify the enhancement of permeability due to engineering disturbance. The model incorporates damage evaluation based on the elastic, plastic softening, and residual stages of coal behavior. However, the permeability of coal is primarily governed by its pore-fracture structures [10,11], while the seepage characteristics directly influence the safety and efficiency of coal mining operations [12,13]. The fundamental mechanism underlying permeability variation lies in the propagation and evolution of these structures. The complexity and connectivity of the pore-fracture network are the dominant influencing factors, and a permeability model can therefore be developed on the basis of these structural characteristics.
Pore and fracture dimensions in porous-fractured media exhibit fractal characteristics and follow statistically self-similar patterns, as documented in previous studies [14,15,16]. These geometric irregularities can be quantitatively described by fractal theory, which provides a powerful framework for characterizing the complexity of pore-fracture systems. Consequently, developing the permeability model through the fractal description may be an applicable method worthy of being tried.
Building on this concept, numerous studies have explored fractal permeability models and the associated fractal flow behavior in various porous materials. The fractal tortuous capillary model has been widely adopted to describe fluid flow through complex media. Yu and Cheng [17] integrated Hagen-Poiseuille flow into this approach to formulate a permeability model for bi-dispersed porous structures. Hao and Cheng [18] applied the same fractal capillary framework to analyze anisotropic permeability in fuel cell materials. Miao et al. [19] derived an analytical expression for dimensionless permeability to model fluid transfer from the porous matrix to fractures. Their model incorporates the fractal dimensions of both pore area and flow path tortuosity, and accounts for permeability contributions from both the matrix and the fracture-wall porous surface. Similarly, Wu and Wang [20] developed a fractal-based apparent permeability model for shale gas reservoirs using Fick’s law, showing that permeability increases with the pore-area fractal dimension but decreases with the tortuosity fractal dimension. Further, Dong et al. [21] combined Darcy’s law, the Poiseuille equation, and SEM image analysis to construct a predictive permeability model for tight sandstones that considers microstructural parameters and tortuosity effects. Xie et al. [22] introduced a dual-fractal index encompassing both pore size and fracture spatial distribution to quantify the structural complexity of coal fracture networks. Their results revealed a non-monotonic relationship between permeability and the pore-fracture fractal dimension—initially decreasing and then increasing with rising fractal dimension. Despite these advances, a key limitation of existing fractal permeability models is the assumption of constant fractal dimensions, which does not reflect the continuous evolution of pore-fracture geometry under mining-induced stress and gas desorption effects. Since permeability enhancement in fractured coal is inherently linked to the dynamic propagation and reconnection of fractures, a model that incorporates the evolving fractal characteristics of the pore-fracture network is needed to better capture permeability behavior under engineering disturbance.
This work focuses on coal with a complex fracture network, and the laboratory simulation of mining-induced stress relief and gas release effects is taken into consideration. Firstly, in order to describe the permeability enhancement during the complex loading conditions, a fractal permeability-enhanced rate model is proposed, in which the fractal dimension of the size distribution of fracture aperture and the tortuous curved trace of fracture length are considered. Secondly, a laboratory test of gas flow is conducted, and the permeability-enhanced rate is quantitatively evaluated. Finally, the impact of the fracture aperture ratio on the fractal permeability-enhanced rate model is discussed. This investigation provides new insights into the quantitative relationship between evolving fracture geometry and permeability enhancement, offering a theoretical foundation for improved prediction and control of gas flow behavior in deep coal mining and methane extraction operations.
2. Fractal Description of Permeability-Enhanced Rate Model
Owing to the mining-induced effect, the initial fracture network will continuously develop, and the mining-induced fracture network will continuously grow; a more complex fracture network will be generated, which will increase the space of the gas flow paths and can result in an obvious permeability-enhanced effect. Conventional permeability models are predominantly founded on poroelastic theory, wherein variations in effective stress solely induce volumetric strain within the pre-existing pore-fracture structure under elastic conditions. In contrast, the formation of mining-induced fracture networks constitutes a fundamentally irreversible process of damage evolution, typically accompanied by significant material dilation [6]. Therefore, macroscopic volumetric strain must be incorporated as a key parameter in permeability models aimed at characterizing the evolution of coal permeability under mining-induced conditions. Xie et al. [23] defined the permeability-enhanced rate as the change in the permeability per unit of the volumetric strain to describe the effect of coal permeability enhancement with mining-induced effects. Based on this definition, Xie et al. [5] proposed the definition of the permeability-enhanced rate as the increment of the permeability increment ratio per unit of volume or per damage variable. The equation of the permeability-enhanced rate can be described as follows:
where ω is the permeability-enhanced rate, k is the permeability, k0 is the initial permeability, εv is the volumetric strain, and Ω is the damage variable.
As for the structure of the coal, it usually contains a coal matrix, porous structure, and fracture structure; the fracture system will have a great impact on the deformation process and permeability evolution [24,25]. The pore-fracture system usually presents an obvious fractal characteristic [22]. Developing the coal permeability model from the perspective of fractal theory is a worthy way to try. There are at least two kinds of fractal dimension for the coal pore-fracture system. One is the fractal dimension of the distribution of pore-fracture aperture (the diameter of capillary flow), which is noted as δ. Another is the fractal dimension of tortuous curved trace of fluid flow in pore structure, which is noted as D. Specifically, δ reflects the variability and scaling behavior of fracture apertures observed in three-dimensional CT (Computed Tomography) reconstructions, while D quantifies the curvature and connectivity of the fracture network derived from the tortuous flow traces. When it comes to the coal fracture media, even for the same fracture aperture λ, the length of fracture depth perpendicular to the macro seepage direction of the fracture is also different. In order to solve this problem, two patterns are usually used to be equivalent to the fracture medium (as shown in Figure 1): (1) the fracture medium is equivalent to the parallel plate with the fracture aperture of λ, and all the fracture depths of unit section A0 are converted into unit depth; (2) the fracture medium is equivalent to the capillary with a diameter of λ.
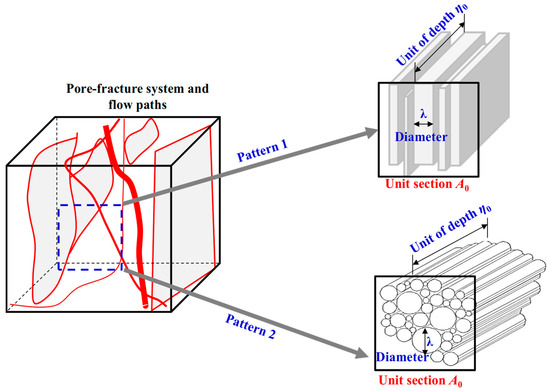
Figure 1.
Schematic view of two methods equivalent to the fracture medium.
2.1. The Fracture Media Is Assumed to Be Composed of a Number of Parallel Plates
As for the first equivalent method, in the unit section A0, the relationship between the fractal dimension of the distribution of the fracture aperture δ and the equivalent number Nc of fractures per unit depth with the fracture aperture greater than λ (λi ≥ λ) can be noted as follows:
where λi is the aperture of any fracture in unit section, and λmax is the maximum aperture in the unit section. Deriving the crack aperture at both sides of the above formula, the relationship can be described as:
where −dNc > 0, representing the equivalent number of unit depth of fractures with fracture aperture in the interval of λ and λ + dλ.
When it comes to the fractal dimension D of the tortuous curved trace of fluid flow in pore-pore-fracture system, the relationship between the macroscopic fluid flow length Lt and the straight line length L can be noted as [17,26]:
The derivative of the apparent length L at both ends of the above formula can be obtained as follows:
Based on the traditional fluid flow law of cubic, the flow rate per unit depth η0 of a tortuous single fracture can be expressed as:
Therefore, the total flow rate through the unit section A0 can be calculated as:
where , considering the unit section A0 = η0 × η0, the fluid flow velocity can be obtained as:
Taking Darcy’s law into consideration, the permeability can be expressed as [27]:
where the porosity of the research area can be calculated as:
Therefore, Equation (9) can be rewritten as follows:
Considering the initial tortuous fractal dimension D0 and the original fracture aperture λ0, the initial permeability can be noted as:
To simplify the analytical process, the rock mass is assumed to be under a hydrostatic pressure state. Under this condition, the volumetric strain of the fracture system (εf) is typically three times the strain in the fracture aperture direction (εbx). Considering the loading-unloading impact or the mining-induced effect, the strain along the direction of fracture aperture can be suggested as εbx = εf/3 = εv/(3η0). Furthermore, by incorporating the link between porosity and volumetric strain , the permeability after deformation of the pore-fracture system can be expressed as:
As a result, the permeability ratio is:
The permeability-enhanced rate can be derived by differentiating both sides of the above equation with respect to volumetric strain:
2.2. The Fracture Media Is Assumed to Be Composed of a Number of Capillaries
As for the second equivalent method, the fracture media is assumed to be composed of a number of capillaries, the fractal dimension of the distribution of the diameter of capillary flow, and the fractal dimension of the tortuous curved trace of fluid flow in pore structure are also accorded with Equations (2) to (5). The flow rate of a single capillary can be expressed as follows [28]:
Therefore, the total fracture flow rate through section A can be noted as:
Based on Darcy’s law, the permeability can be calculated as:
with the condition of this equivalent method, the porosity of the research area can be written as:
therefore, Equation (18) can be rewritten as:
taking the initial tortuous fractal dimension D0 and the original fracture aperture λ0 into consideration, the initial permeability can be obtained as:
assumed that the strain along the fracture aperture εbx = εf/3 = εv/(3η0), and taking the relationship between the porosity and volumetric strain into consideration, the permeability ratio after deformation of the pore-fracture system can be expressed as:
based on the definition of permeability-enhanced rate, it can be obtained by the derivative of the volume strain at both ends of the above formula:
All in all, with the conditions of the two equivalent methods, Equations (15) and (23) are the permeability-enhanced models using double media fractal theory. The two formulations of the permeability enhancement rate model are nearly identical, differing only in certain coefficients. Parameters, including the fractal dimensions of capillary diameter distribution and flow path tortuosity, initial maximum fracture aperture, initial porosity, and volumetric strain, can be determined experimentally at the laboratory scale.
However, current laboratory techniques face challenges in capturing the real-time evolution of fracture networks under dynamic loading and unloading conditions. Therefore, alternative approaches are required to estimate the fractal dimensions associated with capillary diameter distribution and fluid flow path tortuosity. Yu and Li [29] postulated a self-similar nature in both the size and spatial distribution of pores within porous media, with the minimum and maximum pore sizes denoted as χmin and χmax. As a result, the relationship between the fractal dimension, porosity, and χmin/χmax can be expressed as:
where dE is the Euclid fractal dimension. The dE = 2 and dE = 3 correspond to the two- and three-dimensional conditions. Meanwhile, the porosity in the above formula also corresponds to the two- and three-dimensional conditions. Yu and Li [30] also pointed out that the above formula is not only applicable to specific self-similar structures, such as the Sierpinski blanket model and the Sierpinski gasket model, but also to other fractal porous media that satisfy self-similarity. Therefore, assuming that the macroscopic fractal fracture network is equivalent to porous fractal media on the laboratory scale, the fracture structure also satisfies Equation (24), and the size ratio of χmin/χmax can correspond to the fracture aperture ratio (diameter ratio of capillaries) λmin/λmax. Generally, the minimum size of pores χmin is two orders of magnitude smaller than the maximum size of pores χmax [29,31].
To simplify the model, area and volume porosity are considered equivalent, and the fracture aperture ratio is assumed equal in both two and three dimensions. Considering the volume deformation of the rock matrix, the fractal dimension of the capillary diameter during deformation can be expressed as:
When it comes to the fractal dimension of the tortuous curved trace of fluid flow during the deformation process, the tortuosity τ should be considered when deducing the theoretical equation. The tortuosity is defined as the ratio of the length of the irregular curved channel to the apparent length:
Combining with Equation (4), the relationship between the tortuosity and D can be expressed as [30]:
where τaverage and λaverage are the average tortuosity and average diameter. Based on the previous research results [32], the relationship between the average tortuosity τaverage and porosity can be noted as:
where C is the experimental fitting constant. Comiti and Renaud [32] suggested that C can be equal to 0.41 and 0.63 when the media is equivalent to spherical particles and a cube. In this research, the C is considered to be 0.63.
In addition, the theoretical expression of L0/λaverage can be noted as [31]:
By introducing Equations (28) and (29) into Equation (27), it can be obtained that:
Finally, using Equations (15), (23), (25), and (30), the permeability-enhanced rate can be calculated on a laboratory scale. In the permeability-enhanced rate model proposed in this study, the fractal dimension is introduced as a dynamic variable rather than a fixed constant. By establishing a linkage between the stress-strain response, fracture evolution, and permeability, the model provides a more realistic representation of the permeability behavior of fractured coal under mining-induced stress conditions. To evaluate the permeability-enhanced rate model, the permeability tests of fractured coal samples were conducted. In addition, to obtain the permeability-enhanced effect under the mining effect, the simulation of mining-induced stress relief and gas release effect has also been conducted in the laboratory.
3. Preparation of Fractured Coal Samples
All the samples used in this manuscript are from the coal seam of group Ji in the Pingdingshan mining area, Henan Province, China. The coal belongs to coking coal with a soft texture, and the coal seam has obvious gas control problems. In accordance with standard rock mechanics testing procedures, coal blocks collected from the mining face were machined into cylindrical samples measuring 50 mm in diameter and 100 mm in height. The experimental set comprised one intact coal sample (noted as 10-4-3) and three pre-fractured coal specimens (noted as 3-8-5, 3-19-2, and 6-5-1). The average diameter and height are 49.28 mm and 100.06 mm. The density of all coal specimens ranged from 1.297 to 1.328 g/cm3. To guarantee the use of genuinely fractured coal, samples were deliberately drilled from blocks exhibiting macroscopic fracture structures. It should be noted that the coring of intact standard specimens from such blocks is technically challenging, as excessive fragmentation often occurs. Nevertheless, this approach ensures that the selected specimens preserve authentic fracture morphology and connectivity, which are critical for examining permeability evolution mechanisms. Finally, three representative specimens with distinct fracture complexities were chosen to capture the variability of fracture networks and to assess how structural heterogeneity influences permeability enhancement. Although the number of samples is limited, each represents a different level of fracture density and connectivity, thereby enabling a comparative analysis that directly supports the development and validation of the proposed fractal permeability-enhancement model.
In order to obtain the fracture morphology characteristics of fractured coal specimens, the industrial CT scanning test system V/tome/X L 300 of Sichuan University was used to measure the fracture structure of fractured coal specimens (Figure 2). The slice thickness range of the device is 0.004 mm ~ 0.4 mm, and the overall resolution of the device is less than or equal to 2 μm. During the scanning process, the scanning current is 140 μA, the scanning voltage is 180 kV, and the exposure time is 500 ms. The measured resolution of all coal samples is controlled within 60 ~ 70 μm. It should be illustrated that the original CT data for three pre-fractured coal specimens in this study were sourced from reference [5]. After the completion of CT scanning, the quantitative analysis module of VGStudio 2.5.5 post-processing software is used to set the threshold range and select the pore fracture structure. The geometric parameters of the pore-fracture structure can be quantified. The equivalent pore-fracture diameter, in particular, serves as the basis for calculating the fractal dimension of capillary flow diameter distribution within fractured coal samples. In addition, based on the function of the post-processing system, the fracture distribution information of the top section, front section, and right section of the fractured coal specimen can be obtained (Figure 3), which can provide a data source for tortuous fractal dimension calculation of the fractured coal specimen.

Figure 2.
Schematic view of fractured coal samples and the reconstruction results of fracture network by CT scanning test (revised from reference [5]).

Figure 3.
Schematic view of the fracture distribution within different view sections.
The fractal dimension of pore-fracture scale serves as an indicator of fracture abundance and size distribution within a rock sample. The tortuosity fractal dimension characterizes the length and flow resistance of the seepage path along a given macroscopic trajectory. Meanwhile, the spatial fractal dimension of fractures reflects the structural complexity of the fracture networks organization. Considering the diameter distribution of the circumscribed sphere, the fractal dimension Dscale satisfies the following relationship [33]:
where Nc is the number of pore-fracture structures with a diameter larger than d, dmax is the maximum diameter of pore-fracture structures.
The cube covering method enables the calculation of the tortuosity fractal dimension D from digitized cross-sections and spatial data of the pore-fracture network. A series of squares (r × r) of different sizes is used to cover the pore-fracture structure of each section; the number of squares or cubes covering the whole pore-fracture structure N(r) can be obtained. The relationship between the D and N(r) can be noted as follows:
where D is the tortuous fractal dimension, which can be calculated by the slope of the fitting line of lnN(r) − ln(r); the opposite of the slope is the tortuous fractal dimension. As a result, based on the Dscale, D, and mechanical information, the permeability evolution can be quantitatively evaluated by the proposed fractal permeability model.
4. Gas Flow Test and Results
4.1. Gas Flow Testing System
As shown in Figure 4, the multi-field coupling seepage system was employed to perform coal gas flow experiments. This system can apply controlled stress, gas pressure, and temperature conditions, while continuously monitoring gas flow dynamics throughout the deformation process. The setup is capable of applying axial stress and confining pressure up to 100 MPa and 10 MPa, respectively, while measuring axial displacement and confining deformation up to 60 mm and 6 mm. The maximum axial displacement and confining deformation can be 60 mm and 6 mm. The control accuracy is ±0.5% of the reading, with a test accuracy of ±1% of the reading. The temperature control range is from room temperature to 100 °C, and the temperature was maintained at room temperature during this study. The data acquisition frequency was set to 1 sample per second. The gas type belongs to CH4, and the maximum gas pressure can reach 6 MPa. Experiments were conducted under axial loading controlled by either force or displacement, with all relevant parameters such as stress, strain, gas pressure, and flow rate being automatically acquired. Owing to the flow capacity of the fractured coal specimen being much larger than that of the intact one, a large flowmeter with a range of 0~10 L/min was used to avoid the condition that the flow rate exceeds the maximum testing range.

Figure 4.
Schematic view of the testing system for gas flow test (revised from reference [5]).
4.2. Testing Scheme
In laboratory investigations related to the simultaneous extraction of coal and gas, the evolution of mining-induced stress is typically simplified by gradually increasing the axial pressure while decreasing the confining pressure [34], thereby approximating the stress evolution process that occurs as the mining face advances. In actual mining operations, gas drainage techniques are commonly implemented to take advantage of the permeability enhancement resulting from stress relief. Consequently, modeling conditions that incorporate both stress relief and gas release can more accurately reproduce the complex in situ environment of combined coal and gas mining. In this manuscript, in order to further simulate the combination effect of mining pressure relief and gas release in the laboratory, the role of coal gas diffusion is ignored, and the gas release effect is simplified as the gas pressure reduction in the process of pressure relief. The experiment scheme is shown in Figure 5. The confining pressure of all coal specimens is set as 8 MPa, and the initial gas pressure is set at 3 MPa.
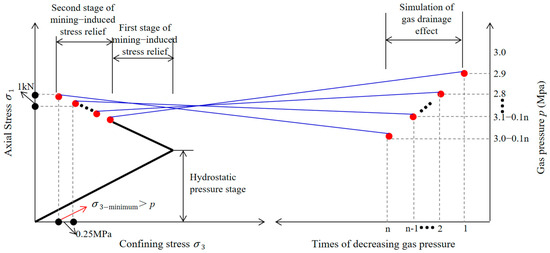
Figure 5.
Testing scheme of the simulation of mining-induced stress relief and gas release effect in the laboratory.
The whole experiment includes the following steps: (1) Following sample preparation, initial axial stress and confining pressure were applied, and the gas pressure was maintained at 1 MPa until adsorption equilibrium was achieved. (2) During hydrostatic loading, the confining pressure was increased to 8 MPa at 0.05 MPa/s, while the axial stress was raised to 8 MPa at 0.1 kN/s. (3) In the first unloading phase, the gas pressure remained constant; the axial pressure was increased to 12 MPa at 0.02 kN/s, and the confining pressure was reduced to 4.8 MPa at 0.005 MPa/s. (4) Throughout the second unloading stage, the confining pressure continued to decrease at 0.005 MPa/s, and the axial pressure was further increased at 0.02 kN/s. During this phase, axial pressure, confining pressure, and gas pressure were varied in a coordinated manner: for every 1 kN increase in axial stress, the confining pressure was reduced by 0.25 MPa and the gas pressure by 0.1 MPa. The axial deformation and confining deformation should be recorded until the gas flow becomes stable, then it can go through the next stage of axial stress increase, confining pressure decrease, and gas pressure decrease. (5) Repeat the above experimental design steps until the axial deformation, confining deformation, or gas flow present continuous growth and cannot be stabilized at a specific value; the loading and unloading test by steps should stop immediately. Subsequently, the gas pressure was held constant, while the axial loading mode was switched to displacement control. The confining pressure continued to decrease at the predetermined rate until the coal specimen reached complete failure. It is crucial to note that during the final stage, confining pressure unloading was halted immediately upon reaching 2.05 MPa to maintain confining pressure above gas pressure. Mechanical, deformation, and gas flow parameters were continuously monitored and recorded throughout the entire experiment.
The permeability of the coal sample during seepage was evaluated based on Darcy’s law, expressed by the following formula [5]:
where q is the gas flow rate, m3/s; k is permeability, m2; μ is the viscosity coefficient of gas, where μ is 1.087 × 10−11 MPa∙s at 20 degrees centigrade; L is the length of the coal specimen after deformation, m; A is the cross-sectional area of the specimen after deformation occurred, m2; p0, p1 and p2 are the atmospheric pressure, gas pressure at the inlet and the outlet, MPa.
4.3. Testing Results
As shown in Figure 6, the mechanical response and deformation of the fractured coal specimen under mining-induced stress relief and gas release are presented (excluding residual strain from pre-fracturing). The results indicate a distinct difference in mechanical behavior between the combined effect of mining pressure relief with gas release and mining-induced stress relief alone. Generally, most of the coal specimens showed some obvious post-peak characteristics after axial deformation control was achieved, which resulted in an obvious volume expansion phenomenon. However, the volume expansion under the superposition condition is smaller than that under the mining-induced stress relief condition, and there was no obvious peak deformation platform. This phenomenon can be attributed to two primary factors: (1) from the perspective of the experimental conditions, the stress peak value changes from force control to axial displacement control in the laboratory simulation of the superposition condition, and the deformation rate of the whole coal specimen is relatively low, which cannot form the effect of rapid circumferential expansion deformation under loading condition of axial force control, and would result in a low probability of significant volume expansion deformation in a short time; (2) regarding the internal deformation mechanism, the expansion effect of gas adsorption can increase the deformation ability of coal samples to a certain extent. However, the gas in the coal will gradually desorb, escape, and migrate under the action of release, and the effective confining pressure will gradually increase under the same stress state. Then, the deformation capacity will become weak and the coal specimen is more likely to suddenly lose stability during the stage of peak stress, and finally, the probability of forming the peak deformation platform is smaller.

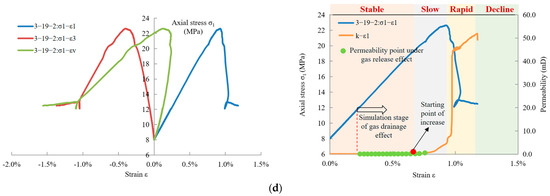
Figure 6.
The mechanical behavior and gas flow characteristics under the simulation of mining-induced stress relief and gas release effect: (a) Unfractured coal specimen (10-4-3); (b) Fractured coal specimen 1 (3-8-5); (c) Fractured coal specimen 2 (6-5-1); (d) Fractured coal specimen 3 (3-19-2).
The mechanical behavior and volumetric deformation of coal under superimposed mining-induced stress relief and gas release significantly influence its seepage evolution. Experimental results indicate that the permeability increase in all fractured coal samples initiated during the gas release simulation phase. The permeability evolution can be categorized into four distinct stages: stable, slow growth, rapid growth, and stable or decline. During the initial stable stage, unlike conventional triaxial loading conditions, the permeability of fractured coal did not decrease at the onset of loading. This is attributed to the presence of macroscopic fractures parallel to the axial direction, which span the entire sample height. The compressional effect under axial loading was counteracted by pressure relief-induced expansion, resulting in stable permeability. Upon entering the gas release phase, the reduction in gas pressure disrupted the initial adsorption equilibrium, leading to an increase in effective stress. Concurrently, gas desorption caused coal matrix shrinkage, which enlarged the effective seepage aperture of fractures. Notably, matrix shrinkage was the dominant factor in this experiment, leading to a gradual increase in permeability. When the stress is close to the peak value, obvious damage and fracture will be produced by mining pressure relief, the mining fracture network and the original fracture body structure connect each other in a short period of time, which will provide enough seepage space for gas migration, and the permeability shows a rapid growth trend. In the post-peak stage, the mining-induced fracture network has been fully formed, the fractured coal specimen enters the broken state, and the small matrix stripping block will block the main seepage channel, and the seepage presents a stable or downward trend. It can be seen that the complexity and spatial distribution of the fractured body are important factors affecting the seepage of fractured coal. The influence of the spatial distribution of the fractured body on the seepage of the fractured rock mass still needs further quantitative description and analysis. In general, the more complex the initial fractured body is, the greater the maximum permeability of fractured coal is. The peak permeability of fractured coal specimen 3 is 4.13, 10.19, and 69.98 times higher than that of fractured coal specimen 1, fractured coal specimen 2, and unfractured coal specimen.
As for the actual engineering problems, the gas drainage measures will reduce the gas pressure, and the gas in the fractured structure of the coal mass after mining-induced stress relief will also result in escape. The superimposed influence of mining-induced stress relief and gas release leads to a reduction in the deformability of fractured coal. The peak stress stage is more likely to lose stability, the instability failure point has no obvious warning, and the strain energy will suddenly release, which can easily cause accidents. The mechanisms of mining-induced stress relief, along with gas diffusion and migration, are key factors that significantly influence disaster occurrences during the simultaneous extraction of coal and gas.
The experimental findings demonstrate a marked permeability enhancement in fractured coal specimens under superimposed mining-induced stress relief and gas release. Compared with the only condition of mining-induced stress relief, the permeability enhancement process under this superposition condition has certain differences. In the following analysis, the new proposed permeability-enhanced rate model developed will be used to quantitatively evaluate the permeability evolution of fractured coal under the superposition conditions of mining-induced stress relief and gas release. The relationship between the measured gas flow behavior and the predicted permeability evolution is discussed to verify the model’s applicability under mining-induced stress relief and gas release conditions.
5. Permeability-Enhanced Rate Evolution of Fractured Coal Samples
Based on the definition of the permeability-enhanced rate, using Equations (15), (23), (25), and (30), the permeability-enhanced rate considering the evolution of fractal dimension was calculated. Figure 7 presents the evolution of permeability and its mining-enhanced rate throughout the process. The evolution of permeability and mining-enhanced rate during the whole process was presented. Different from the experimental results of only mining pressure relief condition [5], the superposition of gas release effect can affect the deformation mechanism of fractured coal to a certain extent. At the initial stage of mining pressure relief, the macroscopic volume of fractured coal is in a state of compression. With the superposition of gas release, the shrinkage effect of the coal matrix after gas desorption is greater than that of effective stress increase after gas pressure reduction, the effective seepage aperture of the initial macroscopic seepage channel gradually increases, and the seepage capacity begins to increase. When the damage of fractured coal occurs, the original fracture structure begins to develop, the damage effect and gas release effect overlap with each other, and the rate of permeability enhancement begins to increase. At the end of gas release (at the end of gas pressure reduction), the compression effect of effective stress and damage effect show a game state after losing the release effect, and the permeability presents a short-term decrease stage or a stable stage, and then the fracture structure is fully developed under the damage effect, and the space provided for gas seepage gradually increases, and the permeability increases rapidly. As for the permeability-enhanced rate, the onset of damage coincides with the initiation of permeability increase, exhibiting a three-stage evolution pattern characterized by slow growth, rapid growth, and subsequent stabilization. The evolution of the permeability enhancement rate, as described by the tablet fluid model and the capillary model, effectively captures both the progression and failure processes of the damage variable. This approach provides a comprehensive reflection of the overall permeability variation and the corresponding evolution of failure within the coal during the permeability enhancement process.

Figure 7.
Permeability-enhanced rate evolution of fractured coal specimens: (a) Fractured coal specimen 1 (3-8-5); (b) Fractured coal specimen 2 (6-5-1); (c) Fractured coal specimen 3 (3-19-2).
The experimental results demonstrate that the proposed model for the permeability-enhanced rate effectively characterizes the behavior of fractured coal under the combined influence of mining-induced pressure relief and gas release. The model quantitatively captures changes in volumetric expansion, damage evolution, and permeability improvement during the enhancement process. Mining pressure relief serves as a key driver of permeability increase in coal seams, while gas release further accelerates the onset of this enhancement. Therefore, integrating gas release strategies with mining pressure relief is recommended to improve gas control outcomes.
It should be noted that during the simultaneous extraction of coal and gas, field monitoring should be employed to accurately identify the critical points of volumetric change, the onset of permeability, and the initiation of permeability enhancement. Capturing this key information is essential for scientifically guiding mining operations and optimizing the timing of extraction activities. The laboratory scale of the above characteristic points can be accurately obtained by precise technical methods. However, due to the limitations and unknowns of the field mining space and the inaccuracy of the permeability test technology, it is difficult to obtain the above key information by engineering-scale monitoring. Additionally, it is relatively easy to obtain the above key information only through mining stress, fracture pressure precursor information, and regional microseismic monitoring. These indirect quantities can determine the temporal and spatial distribution characteristics of in situ permeability-enhanced rate effect to guide mining.
6. Discussion
6.1. Klinkenberg Effect of Coal Under the Effect of CH4 Pressure Release
When it comes to the porous medium, the slippage of gas molecules around the free surface wall usually happens, especially under the situation of gas pressure change [5,35,36]. The decrease in gas pressure usually induces the shrinkage of the mean path for the gas flow, while gas molecules will accelerate due to the slippage effect and the reduced drag between the gas molecules [37]. This phenomenon is widely called the Klinkenberg effect, in which the relationship between the gas pressure and permeability ratio is as follows [5]:
where k is the real-time permeability for gas flow, k0 is the absolute permeability for liquid, pavg is the average gas pressure of two different states of gas pressure, and bk is the Klinkenberg coefficient.
Referring to the fractured coal sample, the complex pores and fractures are the main gas flow path, and the Klinkenberg effect cannot be ignored. Considering the simultaneous simulation of mining stress relief and gas pressure release of this study, both the Klinkenberg effect and the newly generated pore-fractures induced by the mining effect will happen during the simulation process. Figure 8 depicts the permeability ratio versus average gas pressure under simulated mining stress relief and gas release, with the permeability at 3.0 MPa taken as the absolute reference value for each coal specimen. It is obviously suggested that the Klinkenberg coefficient is not equal to zero, and the permeability ratio is clearly increasing with the increase in 1/pavg. As shown in Figure 8a, the evolution of the permeability ratio presents two obvious linear stages. While the increasing speed of the Klinkenberg coefficient of other coal specimens is gradually improved. At the initial stage of gas pressure release, the evolution of newly generated fractures is relatively limited, and the contraction of pre-existing pores and fractures predominates. During this phase, the Klinkenberg effect serves as the primary contributor to the observed permeability enhancement. As the stress continues to unload, the formation and evolution of new fracture networks become increasingly pronounced, leading to a rapid rise in permeability. When coupled with the Klinkenberg effect, this process results in an accelerated increase in the permeability ratio with the increase of 1/pavg.

Figure 8.
The relationship between the k/k0 and 1/pavg: (a) Fractured coal specimen 1 (3-8-5); (b) Fractured coal specimen 2 (6-5-1); (c) Fractured coal specimen 3 (3-19-2).
6.2. Impact Mechanism of the λmin/λmax for the New Fractal Permeability-Enhanced Rate Model
As for the equation of the permeability-enhanced rate model, the ratio of fracture aperture λmin/λmax is an important factor for the evolution of the permeability-enhanced rate. Considering three conditions that the λmin/λmax is equal to 0.010, 0.005, and 0.001. The maximum fracture aperture λmax is relatively easy to obtain through the CT scanning results in the VGStudio post-processing software. The initial maximum fracture apertures of the coal specimens 3-8-5, 6-5-1, and 3-19-2 are 0.9119 mm, 0.9500 mm, and 0.6116 mm. Owing to that, the experiment system cannot achieve the condition of CT scanning during the loading-unloading test, so the scale fractal dimension Dscale and tortuous D cannot be directly obtained. As a result, the two fractal dimensions can only be deduced from the evolution characteristics of porosity using Equations (25) to (30). As shown in Figure 9, the evolution of the fractal dimension with an increase in porosity under different conditions of the λmin/λmax.

Figure 9.
The fractal dimension increases with an increase in porosity under different conditions of the λmin/λmax. (a) Fractured coal specimen 1 (3-8-5); (b) Fractured coal specimen 2 (6-5-1); (c) Fractured coal specimen 3 (3-19-2).
Generally speaking, with the increase in porosity during the loading process, the fracture structure is developing continuously, the number of fractures is increasing, and the fractal dimension of the scale diameter is increasing. At the same time, the development of fracture structure leads to the gradual formation of a macroscopic seepage channel, the complexity of the seepage path is reduced, and the tortuous fractal dimension shows a downward trend. Once the fractured coal specimen reaches the failure stage, porosity continues to increase due to the expansion effect of fracturing; however, the growth rate of the aperture fractal dimension slows, and the tortuosity fractal dimension gradually stabilizes. When the fracture aperture ratio λmin/λmax changes from two orders of magnitude to three, the fracture aperture ratio has a significant influence on the diameter fractal dimension and the tortuous fractal dimension. The larger the fracture aperture ratio is, the smaller the fracture aperture span is, the smaller the scale fractal dimension is, and the larger the tortuous fractal dimension is. It can be suggested that under the condition of porosity evolution or the change in fracture aperture ratio, the scale fractal dimension and the tortuous fractal dimension present an opposite evolution characteristic. Compared with the fracture structure with different complexity, the evolution trend of tortuous fractal dimension and scale fractal dimension is basically consistent, but the variation range of them is still different. As the complexity of the fracture network increases, the range of variation in both the tortuous fractal dimension and the scale fractal dimension tends to decrease. The relative growth percentage of the scale fractal dimension of the initial fracture structure of the three fractured specimens (1 to 3) is 14.93%, 13.77%, and 11.15%. The relative decrease percentage of tortuous fractal dimension is 4.34%, 4.33% and 3.47%.
6.3. Evolution Mechanism of Permeability Enhancement of Fractured Coal Under Different Fracture Aperture Ratio λmin/λmax
To further investigate the role of fracture aperture ratio, the evolution of fractured coal under different aperture ratios was compared (Figure 10). The results show consistent trends in permeability enhancement rate across all ratios; however, the magnitude of enhancement varied significantly. Specifically, during the damage and fracture stage, a higher aperture ratio-indicating a narrower fracture size distribution-resulted in greater permeability. Therefore, the assessment of the fracture aperture ratio plays a crucial role in characterizing the permeability enhancement behavior of fractured coal within laboratory-scale analyses of mining-induced fracture networks. However, since the fracture aperture ratio is typically assumed to remain constant during the deformation process of fractured coal, its actual evolution law under deformation requires further investigation.

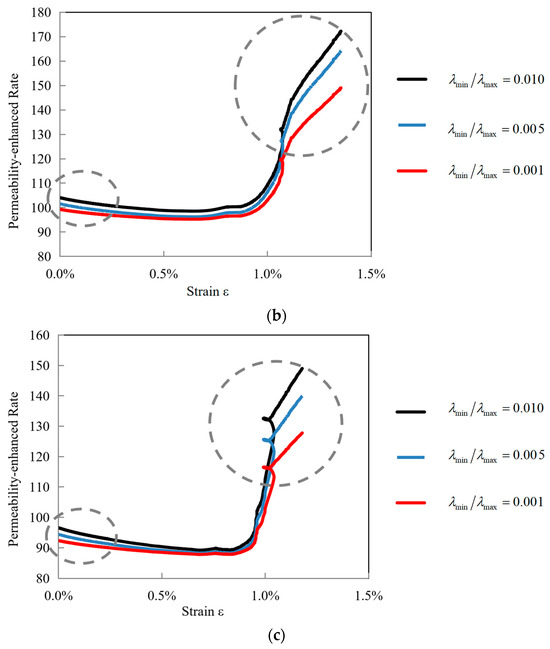
Figure 10.
The evolution of permeability-enhanced rate with different values of the λmin/λmax. (a) Fractured coal specimen 1 (3-8-5); (b) Fractured coal specimen 2 (6-5-1); (c) Fractured coal specimen 3 (3-19-2).
7. Conclusions and Remarks
From the perspective of fractal geometry, a fractal model of permeability-enhanced rate evolution of fractured coal is developed to describe the permeability-enhanced rate of coal under the simulation of mining-induced stress relief and gas release effect in the laboratory. The results can be concluded as follows:
- A fractal model for the permeability-enhanced rate is developed, incorporating the fractal dimensions of both fracture aperture size distribution and flow path tortuosity. These dimensions are determined from volumetric strain and the ratio between minimum and maximum fracture apertures, providing an indirect characterization of the evolving complexity of the fracture network under mechanical loading.
- Experimental results indicate that the onset of permeability enhancement in fractured coal occurs primarily during the stage of gas release simulation. The combined influence of mining-induced stress relief and gas desorption significantly accelerates the permeability growth rate, confirming the strong coupling between mechanical disturbance and gas flow behavior.
- Based on the Tablet fluid model and capillary flow model, the new proposed fractal permeability-enhanced rate model of fractured coal can well reflect the permeability enhancement behavior of fractured coal under the superimposed conditions of mining pressure relief and gas release effect.
It is worth noting that the ratio λmin/λmax strongly governs both the diameter and tortuosity fractal dimensions. The proposed fractal permeability enhancement model exhibits high sensitivity to this fracture aperture ratio, particularly during the damage and fracture stages of coal. Therefore, reasonable control of the ratio λmin/λmax may contribute to safer and more efficient coal mining operations.
The proposed model in this investigation offers a theoretical basis for predicting permeability evolution in fractured coal seams and optimizing gas drainage and pressure-relief design in deep mining operations. Quantitatively linking fracture geometry with permeability changes provides new insights for enhancing safety and extraction efficiency in underground coal mines. However, the present study is limited to laboratory-scale simulations and does not fully account for field-scale heterogeneity, multiphase flow effects, or time-dependent fracture propagation. Future research will aim to integrate field monitoring data, apply the model under in situ stress conditions, and extend it to multi-physical coupling frameworks to further improve its predictive capability and engineering applicability.
Author Contributions
Conceptualization, Y.D. and M.L.; methodology, Z.Z., J.X., and L.R.; software, S.Q.; validation, S.Q., S.N. and Z.Z.; formal analysis, S.N.; investigation, Y.D.; resources, L.R.; data curation, Z.Z.; writing—original draft preparation, Y.D. and J.X.; writing—review and editing, Y.D.; visualization, Z.Z.; supervision, Y.D.; project administration, M.L.; funding acquisition, J.X. and M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This investigation was financially supported by the National Natural Science Foundation of China (42377143, 52004167, 52225403) and the Xizang Science and Technology Program of China (XZ202501ZY0073).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Huang, J.; Xu, G.; Liang, Y.; Hu, G.; Chang, P. Improving coal permeability using microwave heating technology—A review. Fuel 2020, 266, 117022. [Google Scholar] [CrossRef]
- Fan, D.; Ettehadtavakkol, A.; Wang, W. Apparent liquid permeability in mixed-wet shale permeable media. Transp. Porous Media 2020, 134, 651–677. [Google Scholar] [CrossRef]
- Li, M.H.; Zhang, B.H.; Wu, Z.Q.; Luo, S.C.; Lu, J.; Zhang, D.M.; Xie, H.P. A novel permeability calculation model to simultaneously quantify the impacts of pore and fracture with full feature size. Int. J. Min. Sci. Technol. 2025, 35, 609–618. [Google Scholar] [CrossRef]
- Gao, M.; Xie, J.; Gao, Y.; Wang, W.; Li, C.; Yang, B.; Liu, J.; Xie, H. Mechanical behavior of coal under different mining rates: A case study from laboratory experiments to field testing. Int. J. Min. Sci. Technol. 2021, 31, 825–841. [Google Scholar] [CrossRef]
- Xie, J.; Gao, M.; Zhang, R.; Liu, J.; Lu, T.; Wang, M. Gas flow characteristics of coal samples with different levels of fracture network complexity under triaxial loading and unloading conditions. J. Pet. Sci. Eng. 2020, 195, 107606. [Google Scholar] [CrossRef]
- Xie, J.; Gao, M.; Liu, J.; Li, C.; Peng, G. Permeability-enhanced rate model for coal permeability evolution and its application under various triaxial stress conditions. Arab. J. Geosci 2020, 13, 106–116. [Google Scholar] [CrossRef]
- Huo, J.; Meguid, M.A. Systematic investigation of stress-induced fracture closure and permeability evolution in Lac du Bonnet granite. Int. J. Rock Mech. Min. Sci. 2025, 191, 106113. [Google Scholar] [CrossRef]
- Tomassi, A.; de Franco, R.; Trippetta, F. High-resolution synthetic seismic modelling: Elucidating facies heterogeneity in carbonate ramp systems. Pet. Geosci. 2025, 31, petgeo2024-047. [Google Scholar] [CrossRef]
- Xue, Y.; Gao, F.; Liu, X.; Li, J.; Liang, M.; Li, X. Theoretical and numerical simulation of the mining-enhanced permeability model of damaged coal seam. Geotech. Geol. Eng. 2016, 34, 1425–1433. [Google Scholar] [CrossRef]
- Bandyopadhyay, K.; Mallik, J.; Suman, S.; Dhar, R.; Shaik, N.A.; Vedanti, N. Field scale coal permeability modeling and sweet-spotting using seismic attributes. Int. J. Coal Sci. Technol. 2025, 12, 89. [Google Scholar] [CrossRef]
- Jiao, H.Z.; Chen, X.; Zhang, T.G.; Michael, Q.; Yang, Y.X.; Yang, X.L.; Yang, T.Y. In situ loading of a pore network model for quantitative characterization and visualization of gas seepage in coal rocks. Deep Undergr. Sci. Eng. 2025, 4, 437–451. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.; Ren, Z.; Wang, F. Compaction and seepage characteristics of broken coal and rock masses in coal mining: A review in laboratory tests. Rock Mech. Bull. 2024, 3, 100102. [Google Scholar] [CrossRef]
- Zhao, Y.; Yan, Y.; Liu, K.; Zhao, X.; Li, H.; Cao, J.; Zhang, S.; Ma, K. Analysis of coal mine safety accident features in China, 2017–2022. Geohazard Mech. 2024, 2, 108–120. [Google Scholar] [CrossRef]
- Barenblatt, G.I.; Zheltov, I.P.; Kochina, I.N. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, D.; Yang, J.Y.; Wang, B.; Liu, T. Fractal analysis of CT images of tight sandstone with anisotropy and permeability prediction. J. Pet. Sci. Eng. 2021, 205, 108919. [Google Scholar] [CrossRef]
- Yang, B.B.; Liu, Y. Application of Fractals to Evaluate Fractures of Rock Due to Mining. Fractal Fract. 2022, 6, 96. [Google Scholar] [CrossRef]
- Yu, B.M.; Cheng, P. A fractal permeability model for bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Lattice Boltzmann simulations of anisotropic permeabilities in carbon paper gas diffusion layers. J. Power Sources 2009, 186, 104–114. [Google Scholar] [CrossRef]
- Miao, T.; Chen, A.; Xu, Y.; Cheng, S.; Yu, B. A fractal permeability model for porous-fracture media with the transfer of fluids from porous matrix to fracture. Fractals 2019, 27, 1950121. [Google Scholar] [CrossRef]
- Wu, T.; Wang, S. A fractal permeability model for real gas in shale reservoirs coupled with knudsen diffusion and surface diffusion effects. Fractals 2020, 28, 2050017. [Google Scholar] [CrossRef]
- Dong, S.; Xu, L.; Dai, Z.; Xu, B.; Yu, Q.; Yin, S.; Zhang, X.; Zhang, C.; Zang, X.; Zhou, X.; et al. A novel fractal model for estimating permeability in low-permeable sandstone reservoirs. Fractals 2020, 28, 204005. [Google Scholar] [CrossRef]
- Xie, J.; Gao, M.; Zhang, R.; Ren, L.; Peng, G.; Ai, T.; Yang, B. Experimental investigation on the gas flow characteristics of coal samples with different fracture network complexities. J. Nat. Gas Sci. Eng. 2020, 82, 103487. [Google Scholar] [CrossRef]
- Xie, H.; Xie, J.; Gao, M.; Zhang, R.; Zhou, H.; Gao, F.; Zhang, Z. Theoretical and experimental validation of mining-enhanced permeability for simultaneous exploitation of coal and gas. Environ. Earth Sci. 2015, 73, 5951–5962. [Google Scholar] [CrossRef]
- Hgab, C.; Htab, C.; Ywab, C.; Kai, W.; Chao, X. Gas seepage in underground coal seams: Application of the equivalent scale of coal matrix-fracture structures in coal permeability measurements. Fuel 2020, 288, 119641. [Google Scholar]
- Wei, M.; Liu, J.; Elsworth, D.; Liu, Y.; He, Z. Impact of equilibration time lag between matrix and fractures on the evolution of coal permeability. Fuel 2021, 290, 120029. [Google Scholar] [CrossRef]
- Yu, B.M.; Lee, L.J. A fractal in-plane permeability model for fabrics. Polym. Compos. 2002, 23, 201–221. [Google Scholar] [CrossRef]
- Kong, X. Advanced Seepage Mechanics; Press of University of Science and Technology of China: Hefei, China, 2010. [Google Scholar]
- Xie, H.; Gao, F.; Zhou, H.; Cheng, H.; Zhou, F. On theoretical and modeling approach to mining-enhanced permeability for simultaneous exploitation of coal and gas. J. China Coal Soc. 2013, 38, 1101–1108. [Google Scholar]
- Yu, B.M.; Li, J.H. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Yu, B. Analysis of flow in fractal porous media. Appl. Mech. Rev. 2008, 61, 1239–1249. [Google Scholar] [CrossRef]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Comiti, J.; Renaud, M. A new model for determining mean structure parameters of fixed beds from pressure drop measurements: Application to beds packed with parallelepipedal particles. Chem. Eng. Sci. 1989, 44, 1539–1545. [Google Scholar] [CrossRef]
- Xie, H. Fractals in Rock Mechanics; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Zhang, Z.; Zhang, R.; Xie, H.; Gao, M.; Xie, J. Mining-Induced Coal Permeability Change Under Different Mining Layouts. Rock Mech. Rock Eng. 2016, 49, 3753–3768. [Google Scholar] [CrossRef]
- Wojnarowski, P.; Czarnota, R.; Janiga, D.; Stopa, J. Novel liquid-gas corrected permeability correlation for dolomite formation. Int. J. Rock Mech. Min. Sci. 2018, 112, 11–15. [Google Scholar] [CrossRef]
- Li, Z.; Ripepi, N.; Chen, C. Using pressure pulse decay experiments and a novel multi-physics shale transport model to study the role of Klinkenberg effect and effective stress on the apparent permeability of shales. J. Pet. Sci. Eng. 2020, 189, 107010. [Google Scholar] [CrossRef]
- Zheng, J.; Chen, L.F.; Huang, G.; Wang, J.; Geng, W.L. On Gas Seepage Regularity in Different Structural Bituminous Coal and Its Influence on Outburst-Coal Breaking. Appl. Sci. 2025, 15, 7167. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).