Ship Traffic Flow Analysis and Prediction in High-Traffic Areas Under Complex Environments
Abstract
1. Introduction
- (1)
- To address the forecasting challenges arising from intensified nonlinearities in vessel traffic flow within traffic-intensive and complex inland canal environments, this study proposes a WOA-enhanced VMD framework. Specifically, the Whale Optimization Algorithm (WOA) is leveraged for parameter optimization in Variational Mode Decomposition (VMD), enabling the adaptive derivation of multi-frequency intrinsic mode functions (IMFs). This process improves the stationarity of vessel traffic flow series and constructs a more informative input space for subsequent prediction.
- (2)
- We develop a hybrid VMD-MHA-LSTM triple-integration model: by employing a multi-head attention (MHA) mechanism to adaptively attend to the decomposed multi-frequency features and strengthening the LSTM’s sensitivity to localized feature variations through spatio-temporal weighting, the model is able to maintain reduced forecasting errors and enhanced robustness even under complex inland waterway environments characterized by the interaction of meteorological fluctuations and hydrological dynamics.
2. Related Work
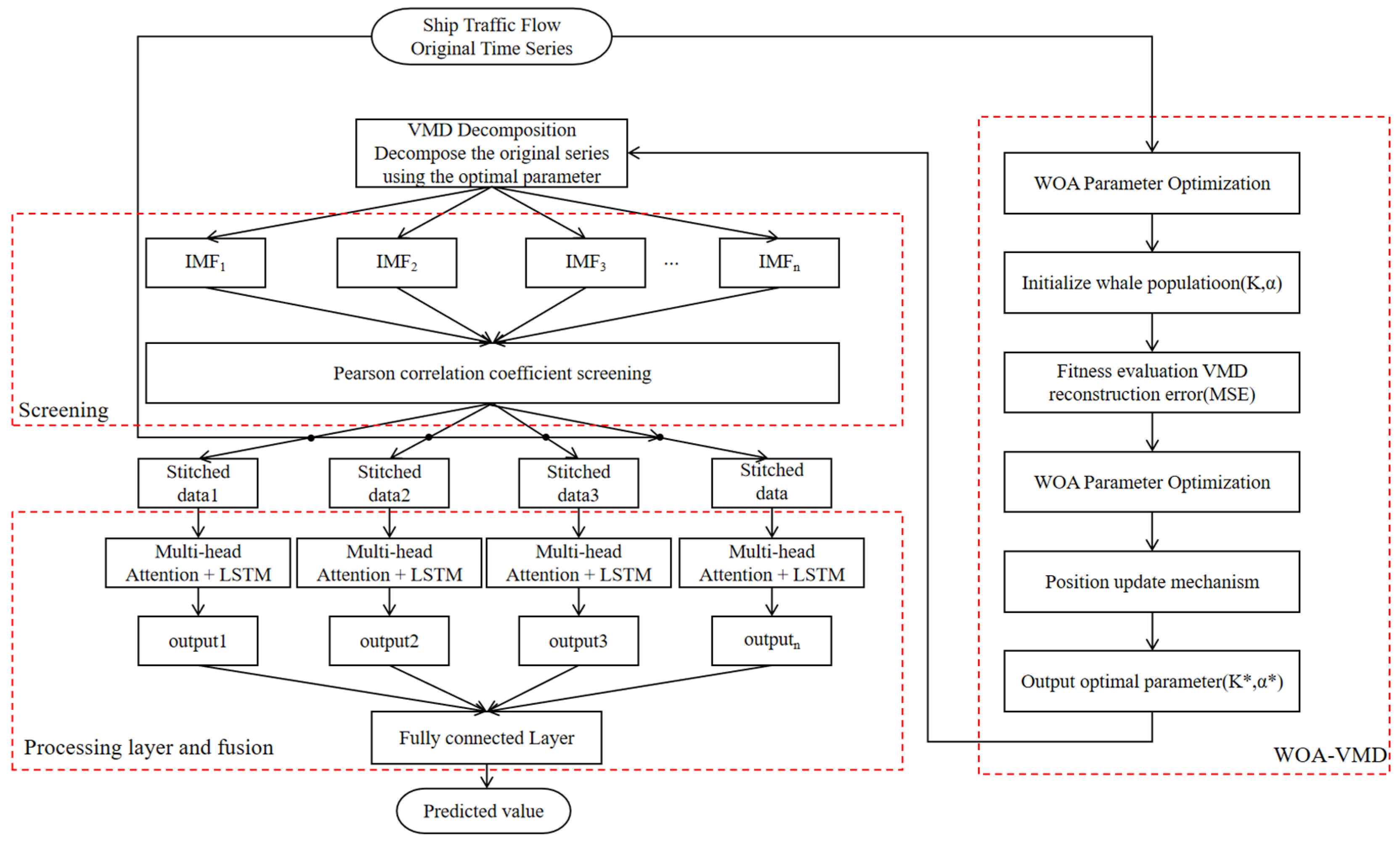
3. System Architecture and Key Algorithms
3.1. WVMA-LSTM Model
| Algorithm 1 WVMA-LSTM Prediction Procedure |
| Input: Original Time Series x0(t) |
| 1: Determine the optimal parameter configuration of VMD by employing the Whale Optimization Algorithm (WOA). |
| 2: Decompose x0(t)x_0(t)x0(t) into KKK intrinsic mode functions (IMFs): |
| 3: for i = 1 to K do |
| 4: |
| 5: Xi, Yi = (, n_in, n_out) |
| 6: MaxAbsScaler(Xi, Yi) |
| 7: = Attention-LSTM(vp2_train, vt2_train) |
| 8: Pi(t) ← inverse_transform() |
| 9: end for |
| 10: |
| 11: MSE, RMSE, R2 |
| Output: Predicted Results |
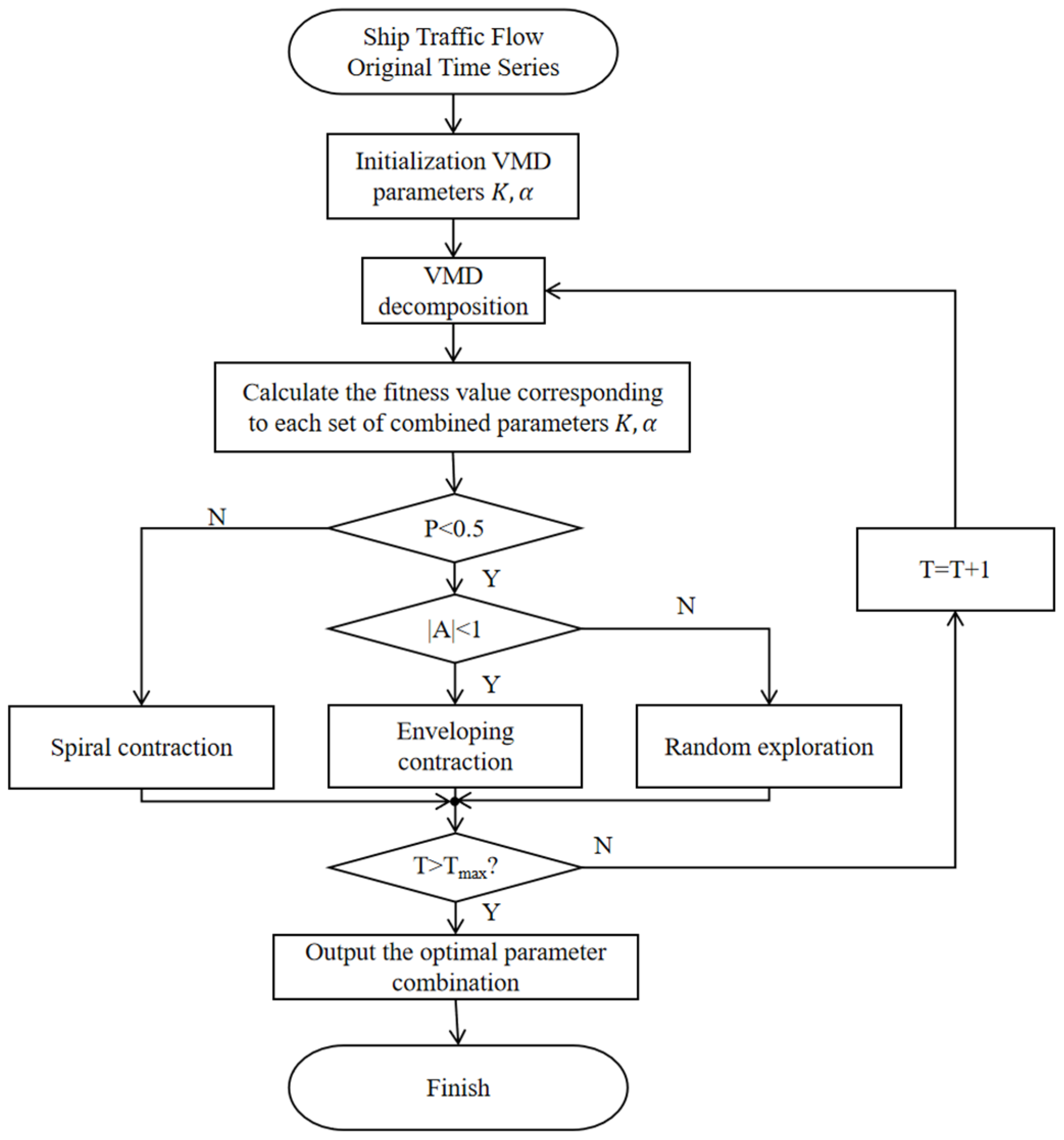
3.2. WOA-Based Optimization of VMD Parameters
3.2.1. Variational Mode Decomposition (VMD)
3.2.2. Whale Optimization Algorithm for VMD Parameter Optimization
- (1)
- Initialization and fitness evaluation: The parameter ranges of and are initialized, and N individuals are randomly generated within the defined ranges. The maximum number of iterations is specified. For each individual, VMD is performed, and the mean squared reconstruction error (MSE) is adopted as the fitness function.
- (2)
- Position update mechanism:
- (3)
- Stopping criterion: the optimal solution is returned when the maximum number of iterations is reached or a convergence criterion is met.
3.3. Pearson Correlation Coefficient (PCC)
3.4. Multi-Head Attention Mechanism Integrated with LSTM
- (1)
- Input layer: The IMFs are combined with auxiliary features such as geospatial coordinates (latitude, longitude and vessel speed), and others to form the input tensor , where B denotes the batch size, T the time steps, and F the input feature dimension.
- (2)
- Multi-Head Attention Mechanism: To capture the global temporal dependencies across different time steps in ship traffic flow sequences, the multi-head attention mechanism is introduced to derive informative representations from the input sequence. Specifically, the sequence X is linearly projected into query (Q), key (K), and value (V) vectors. Attention weights are then computed to assign varying levels of importance to different features, thereby enhancing the model’s capacity to characterize nonlinear dynamics and multi-scale variations.
- (3)
- LSTM-based temporal modeling: The sequence features encoded by the attention mechanism are fed into the LSTM network to capture the temporal dependency and dynamic evolution patterns of ship traffic flow. The LSTM achieves dynamic memory and information updating through its gating structure, thereby effectively extracting the temporal evolution characteristics of the traffic sequence. Finally, the output layer of the LSTM predicts the ship traffic flow values at future time steps. The model employs a multi-head attention mechanism to enhance the global representation capability of the input features and an LSTM network to capture temporal dependencies, thereby achieving high-accuracy prediction of vessel traffic flow in high-traffic maritime areas under complex weather conditions.
4. Experimental Results and Analysis
4.1. Experimental Evaluation Index
- (1)
- Mean Squared Error (MSE) is defined as the mean of the squared residuals between predicted and actual values, quantifying the overall deviation of predictions from observations, as formally expressed in Equation (8).
- (2)
- Root Mean Squared Error (RMSE) measures the standard deviation of the residuals, with smaller values indicating higher predictive accuracy, as defined in Equation (9).
- (3)
- The coefficient of determination (R2) is a statistical metric that evaluates the goodness-of-fit of the model by indicating the proportion of variance in the observed data explained by the predictions.
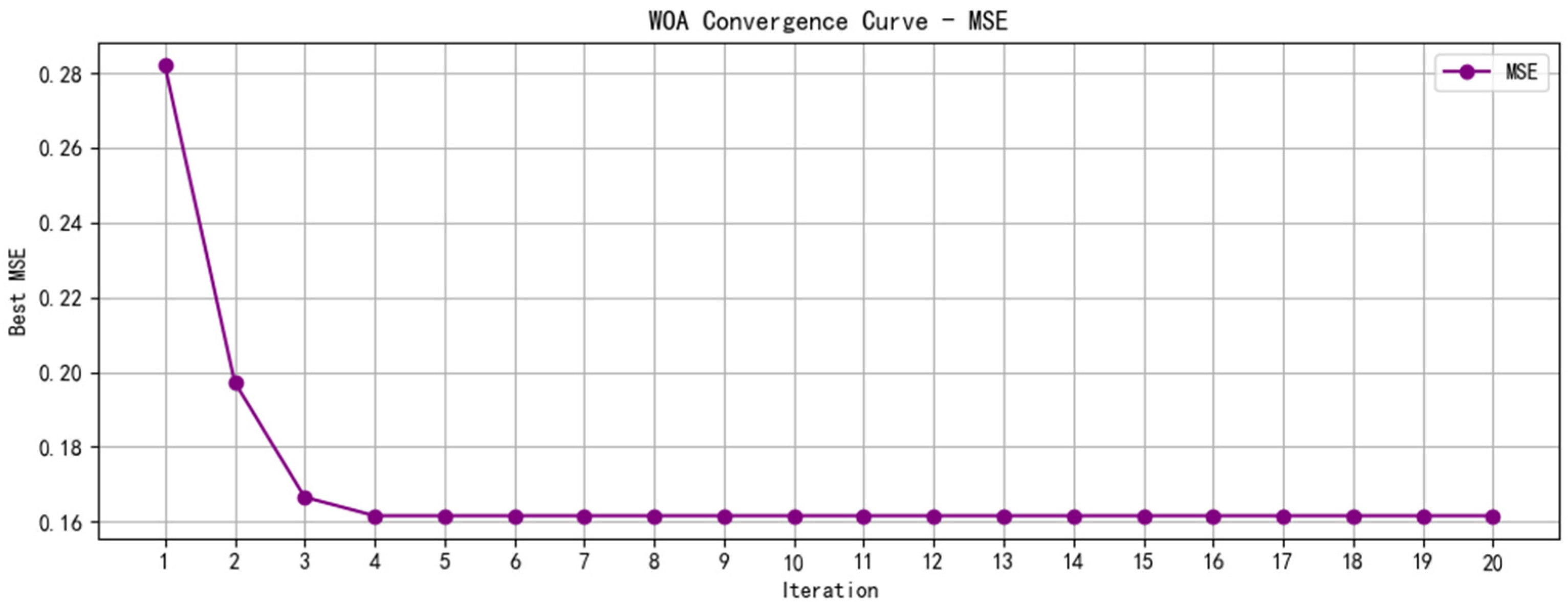
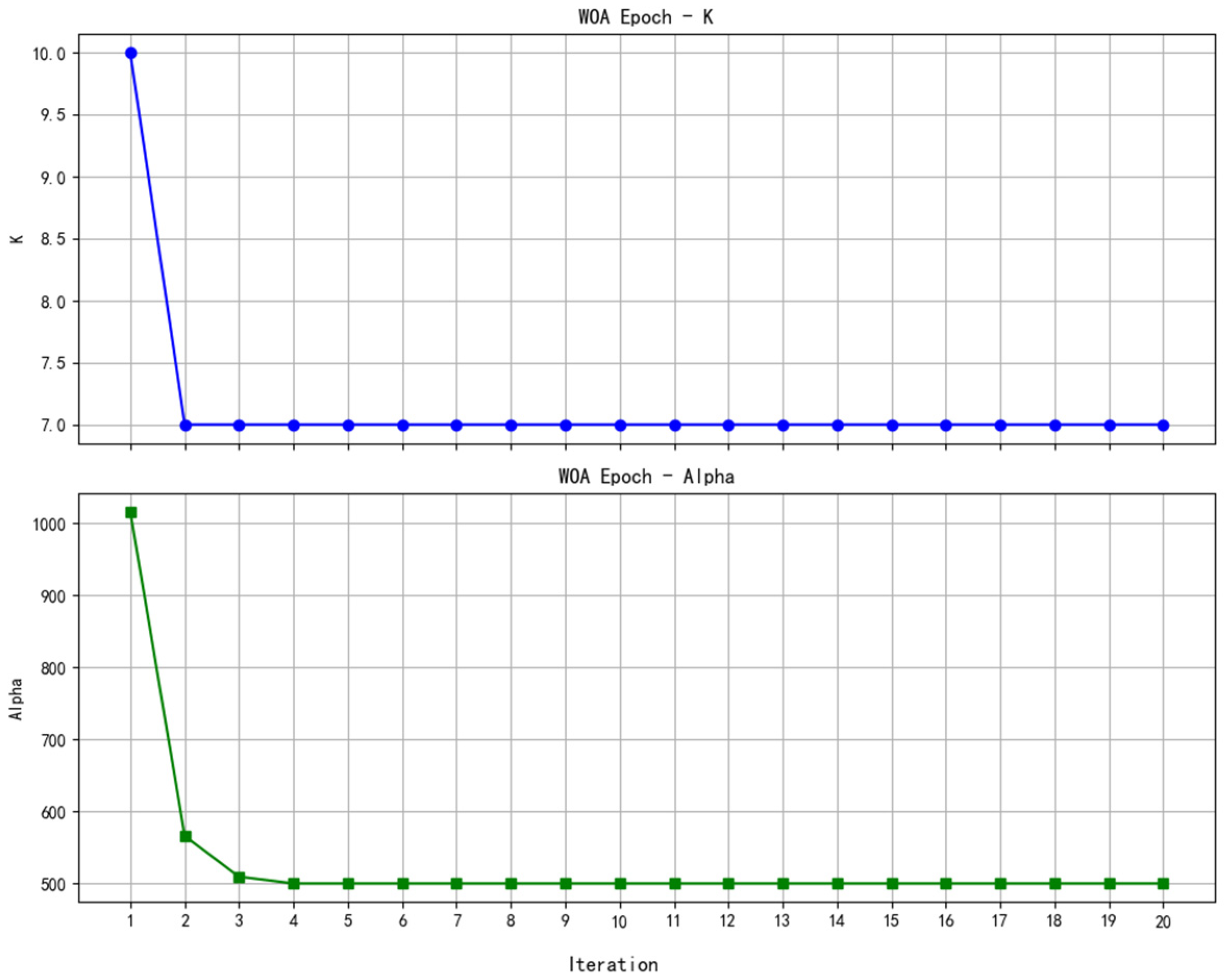
4.2. WOA-VMD Parameter Selection
4.3. WVMA-LSTM Model Prediction Results
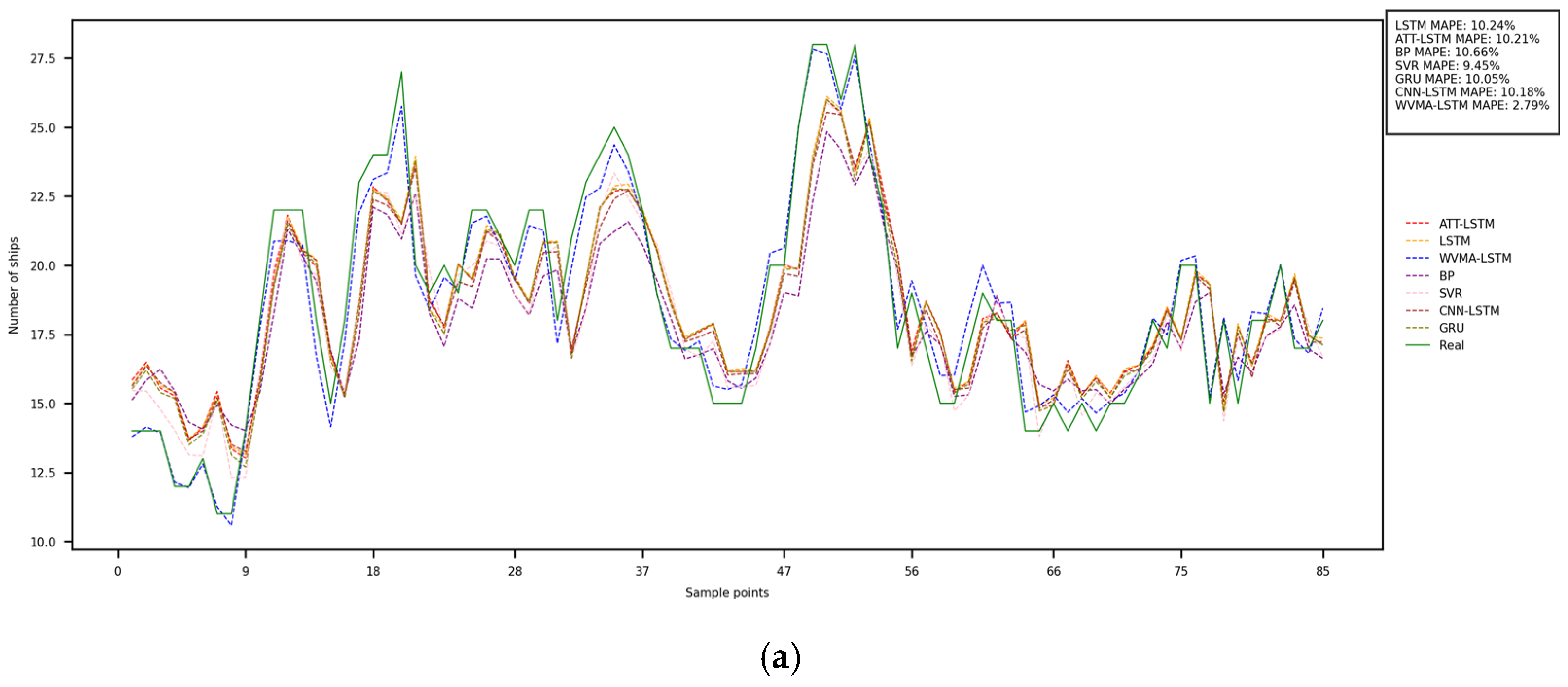
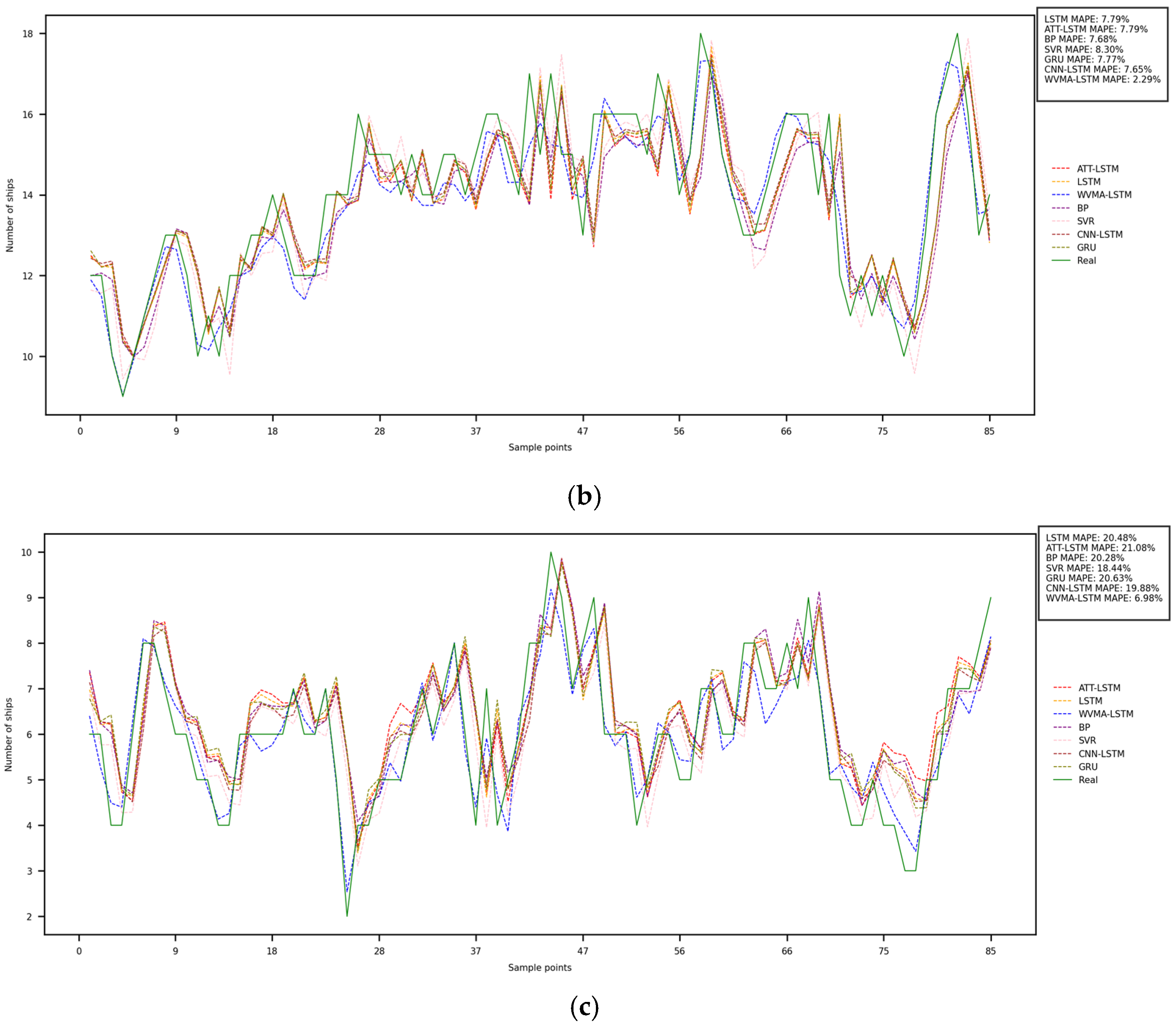
4.3.1. Optimization Contrast Experiment
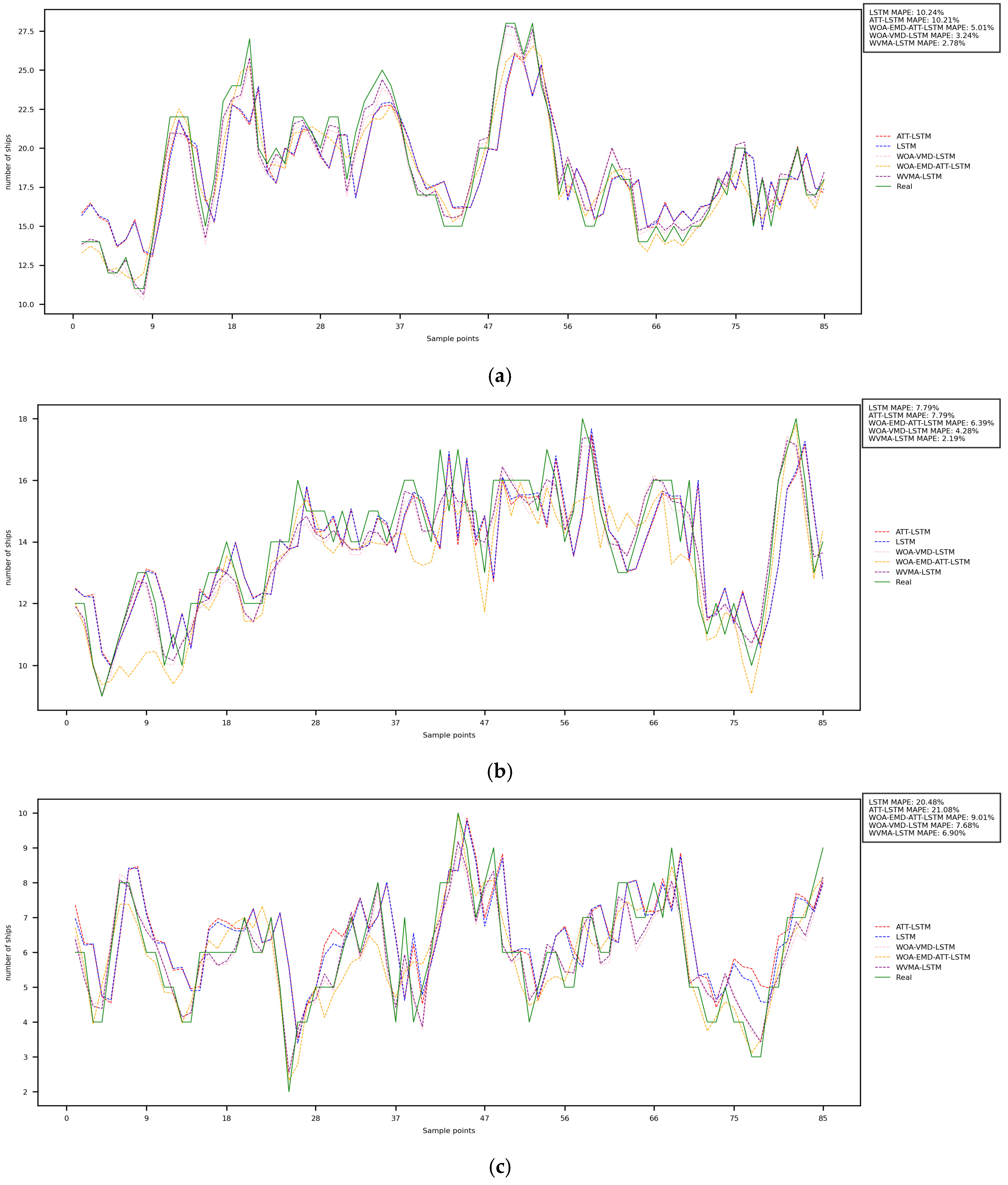
4.3.2. Ablation Experiment
5. Conclusions and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baldauf, M.; Fischer, S.; Kitada, M.; Mehdi, R.; Al-Quhali, M.; Fiorini, M. Merging conventionally navigating ships and MASS—Merging VTS, FOC and SCC. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 495–501. [Google Scholar] [CrossRef]
- Praetorius, G. Vessel Traffic Service (VTS): A Maritime Information Service or Traffic Control System: Understanding Everyday Performance and Resilience in a Socio-Technical System under Change. Ph.D. Thesis, Chalmers Tekniska Högskola, Gothenburg, Sweden, 2014. [Google Scholar]
- Relling, T.; Praetorius, G.; Hareide, O.S. A socio-technical perspective on the future Vessel Traffic Services. Necesse 2019, 4, 112–129. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder–decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Xu, X.; Bai, X.; Xiao, Y.; Sun, X.; Xu, Z. A port ship flow prediction model based on the automatic identification system and gated recurrent units. J. Mar. Sci. Appl. 2021, 20, 572–580. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.H.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Wang, Y.B.; Papageorgiou, M. Real-time freeway traffic state estimation based on extended Kalman filter: A general approach. Transp. Res. Part B Methodol. 2005, 39, 141–167. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control. J. Oper. Res. Soc. 1976, 22, 199–201. [Google Scholar]
- He, W.; Zhong, C.; Sotelo, M.A.; Chen, H.; Zhao, D. Short-term vessel traffic flow forecasting by using an improved Kalman model. Clust. Comput. 2019, 22, 7907–7916. [Google Scholar] [CrossRef]
- Zhao, W.; Gao, Y.; Ji, T.; Chen, L.; Zhang, Y. Deep temporal convolutional networks for short-term traffic flow forecasting. IEEE Access 2019, 7, 114496–114507. [Google Scholar] [CrossRef]
- Man, J.; Chen, D.; Wu, B.; Wan, C.P.; Yan, X.P. An effective approach for Yangtze River vessel traffic flow forecasting: A case study of Wuhan area. Ocean Eng. 2024, 296, 116899. [Google Scholar] [CrossRef]
- Lee, T.-L. Back-propagation neural network for the prediction of the short-term storm surge in Taichung Harbor, Taiwan. Eng. Appl. Artif. Intell. 2008, 21, 63–72. [Google Scholar] [CrossRef]
- Wang, X.; Li, J.; Zhang, T. A machine-learning model for zonal ship flow prediction using AIS data: A case study in the South Atlantic States region. J. Mar. Sci. Eng. 2019, 7, 463. [Google Scholar] [CrossRef]
- Ma, X.; Tao, Z.; Wang, Y.; Yu, H.; Wang, Y. Long short-term memory neural network for traffic speed prediction using remote microwave sensor data. Transp. Res. Part C Emerg. Technol. 2015, 54, 187–197. [Google Scholar] [CrossRef]
- Chen, S.; Lin, C.; Gu, Y.; Sheng, J.; Hariri-Ardebili, M.A. Dam deformation data preprocessing with optimized variational mode decomposition and kernel density estimation. Remote Sens. 2025, 17, 718. [Google Scholar] [CrossRef]
- Zhang, Z.G.; Yin, J.C.; Wang, N.N.; Liu, H.; Li, X. Vessel traffic flow analysis and prediction by an improved PSO-BP mechanism based on AIS data. Evol. Syst. 2019, 10, 397–407. [Google Scholar] [CrossRef]
- Lu, W.; Dong, B.; Wang, Z. Short-term traffic flow prediction based on CNN–SVR hybrid deep learning model. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 68–74. (In Chinese) [Google Scholar]
- Cai, L.; Lei, M.; Zhang, S.; Yu, Y.; Zhou, T.; Qin, J. A noise-immune LSTM network for short-term traffic flow forecasting. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 023135. [Google Scholar] [CrossRef] [PubMed]
- Muthukumaran, V.; Natarajan, R.; Kaladevi, A.C.; Devi, M.; Sharma, R. Traffic flow prediction in inland waterways of Assam region using uncertain spatiotemporal correlative features. Acta Geophys. 2022, 70, 2979–2990. [Google Scholar] [CrossRef]
- Zhuang, W.; Cao, Y. Short-term traffic flow prediction based on a K-nearest neighbor and bidirectional long short-term memory model. Appl. Sci. 2023, 13, 2681. [Google Scholar] [CrossRef]
- Dong, Z.; Zhou, Y.; Bao, X. A short-term vessel traffic flow prediction based on a DBO-LSTM model. Sustainability 2024, 16, 5499. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall–runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a long short-term memory-based encoder–decoder framework for multi-step-ahead flood forecasting. J. Hydrol. 2020, 583, 124596. [Google Scholar] [CrossRef]
- Akopov, A.S.; Beklaryan, L.A. Evolutionary synthesis of high-capacity reconfigurable multilayer road networks using a multiagent hybrid clustering-assisted genetic algorithm. IEEE Access 2025, 13, 53448–53474. [Google Scholar] [CrossRef]
- Tseng, Y.-T.; Ferng, H.-W. An improved traffic rerouting strategy using real-time traffic information and decisive weights. IEEE Trans. Veh. Technol. 2021, 70, 9741–9751. [Google Scholar] [CrossRef]
- Xiao, H.; Zhao, Y.; Zhang, H. Predict vessel traffic with weather conditions based on multimodal deep learning. J. Mar. Sci. Eng. 2023, 11, 39. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Wang, H. Integrated optimization of lock scheduling and vessel traffic flow under adverse weather. Transp. Res. Part C Emerg. Technol. 2023, 147, 105789. [Google Scholar]
- Pavlyuk, D. Spatiotemporal cross-validation of urban traffic forecasting models. Transp. Res. Procedia 2021, 52, 179–186. [Google Scholar] [CrossRef]
- Gao, R.; Du, L.; Suganthan, P.N.; Zhou, Q.; Yuen, K.F. Random vector functional link neural network-based ensemble deep learning for short-term load forecasting. Expert Syst. Appl. 2022, 206, 117784. [Google Scholar] [CrossRef]
- Zhang, J.; Xin, X.; Shang, Y.; Wang, Y.; Zhang, L. Nonstationary significant wave height forecasting with a hybrid VMD–CNN model. Ocean Eng. 2023, 285, 115338. [Google Scholar] [CrossRef]
- Ouyang, M.; Shen, P. Prediction of remaining useful life of lithium batteries based on WOA–VMD and LSTM. Energies 2022, 15, 8918. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Yin, G. Research on Useful Life Prediction of Rolling Bearing Based on Pearson-KPCA Multi-Feature Fusion. Master’s Thesis, Harbin University of Science and Technology, Harbin, China, 2021. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Engle, R.F. Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica 1982, 50, 987–1007. [Google Scholar] [CrossRef]


| Interrelation | Coefficient Values |
|---|---|
| Very weakly correlated or uncorrelated | 0.0–0.2 |
| Weakly correlated | 0.2–0.4 |
| Moderate correlated | 0.4–0.6 |
| Strongly related | 0.6–0.8 |
| Extremely strong correlation | 0.8–1.0 |
| Dataset | Time | Channel Characteristics | Weather Conditions |
|---|---|---|---|
| Dataset A | 4 April–21 May 2021 | Inland river freight corridor. | 5/16–19 Thunderstorm + gale 5/17 Extreme rainfall days 15–17 Overall weather is changeable. |
| Dataset B | 19 April–4 June 2021 | Affected by port dispatching and tidal changes, traffic fluctuates greatly. | 5/21–21 Mid to heavy rain 6/4 High wind |
| Dataset C | 11 May–26 June 2021 | It includes the Desen Island Lock and the Marces Lock, where traffic flow exhibits pronounced fluctuations and the navigational conditions are highly complex. | 6/20–21 Severe storm 6/21–26 Heavy rain and tornadoes |
| Parameter Name | Parameter Setting | Parameter Name | Parameter Setting |
|---|---|---|---|
| Number of trainings | 100 | Optimizer | Adam |
| Learning rate | 1 × 10−3 | Dropout rate | 0.2 |
| Input step size | 5 | Batch size | 32 |
| Output step length | 1 | Loss function | MSE |
| Parameter Name | Parameter Value |
|---|---|
| Number of whales | 10 |
| Number of iterations | 20 |
| Number of variables | 2 |
| IMF scope | [3, 15] |
| Scope | [500, 5000] |
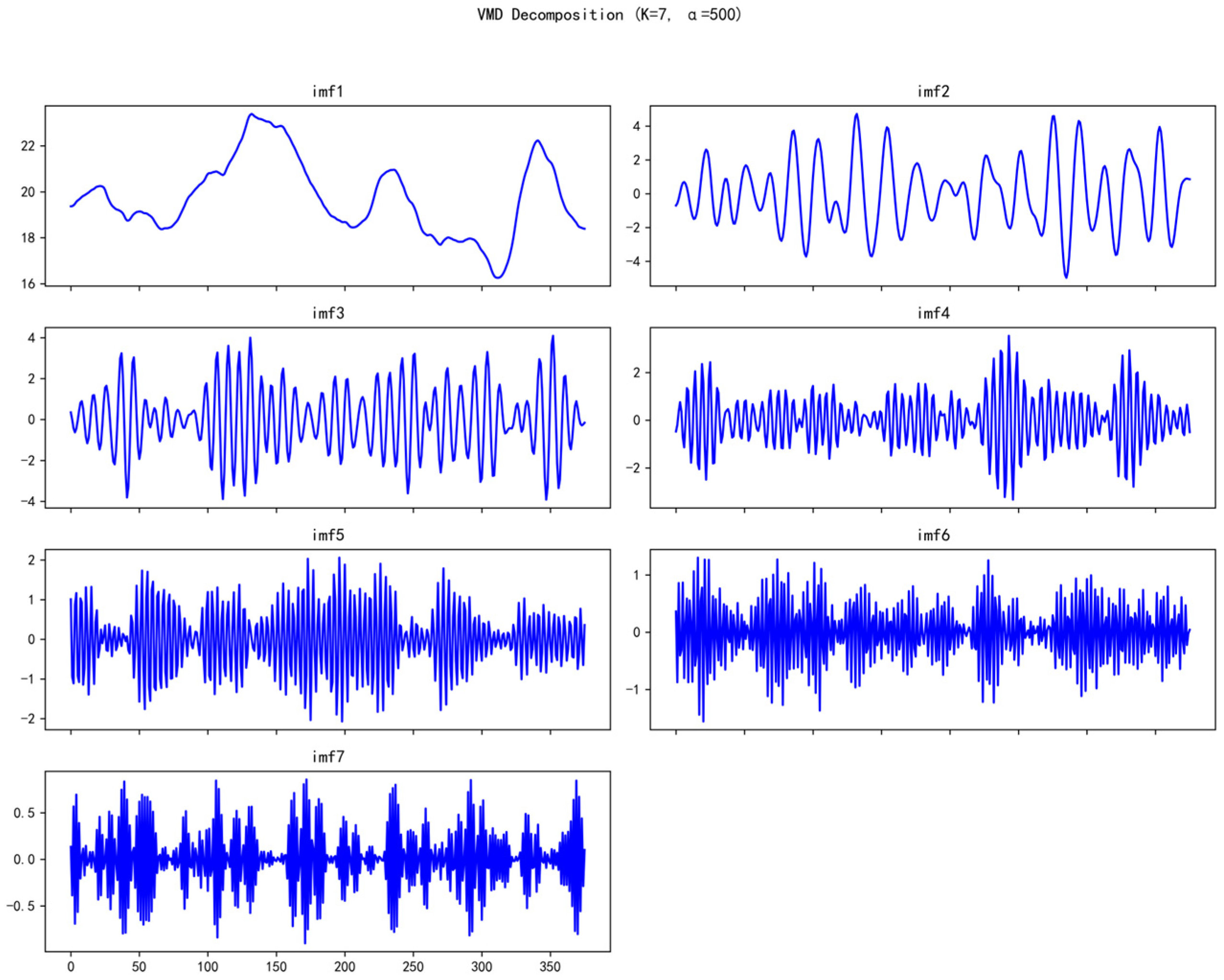
| Modal Component | Correlation Coefficient | Modal Component | Correlation Coefficient |
|---|---|---|---|
| IMF1 | 0.5126 | IMF5 | 0.2812 |
| IMF2 | 0.6235 | IMF6 | 0.2042 |
| IMF3 | 0.5338 | IMF7 | 0.1495 |
| IMF4 | 0.3679 |
| Dataset | Dataset A | Dataset B | Dataset C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Evaluating Indicator | MSE | RMSE | R2 (%) | MSE | RMSE | R2 (%) | MSE | RMSE | R2 (%) |
| ATT-LSTM | 3.106 | 1.260 | 68.637 | 1.882 | 1.372 | 56.537 | 1.681 | 1.297 | 31.620 |
| LSTM | 3.105 | 1.256 | 68.644 | 1.855 | 1.353 | 57.158 | 1.601 | 1.265 | 34.899 |
| BP | 4.102 | 1.470 | 62.525 | 1.829 | 1.353 | 57.753 | 1.582 | 1.258 | 35.899 |
| SVR | 2.832 | 1.198 | 70.321 | 2.035 | 1.426 | 53.009 | 1.433 | 1.197 | 41.731 |
| CNN-LSTM | 1.184 | 1.277 | 68.162 | 1.753 | 1.324 | 59.515 | 1.552 | 1.246 | 36.881 |
| GRU | 3.082 | 1.254 | 68.787 | 1.827 | 1.352 | 57.801 | 1.636 | 1.279 | 33.464 |
| WVMA-LSTM | 0.377 | 0.614 | 93.682 | 0.438 | 0.662 | 89.876 | 0.226 | 1.475 | 90.822 |
| Dataset | Dataset A | Dataset B | Dataset C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Evaluating Indicator | MSE | RMSE | R2 (%) | MSE | RMSE | R2 (%) | MSE | RMSE | R2 (%) |
| ATT-LSTM | 3.106 | 1.260 | 68.637 | 1.882 | 1.372 | 56.537 | 1.681 | 1.297 | 31.620 |
| LSTM | 3.105 | 1.256 | 68.644 | 1.855 | 1.353 | 57.158 | 1.601 | 1.265 | 34.899 |
| WEA-LSTM | 1.109 | 1.187 | 91.347 | 1.354 | 1.164 | 68.723 | 0.413 | 0.643 | 83.620 |
| WV-LSTM | 0.589 | 0.754 | 92.507 | 0.533 | 0.731 | 83.687 | 0.291 | 0.539 | 88.181 |
| WVMA-LSTM | 0.367 | 0.606 | 93.743 | 0.438 | 0.662 | 89.876 | 0.221 | 0.470 | 91.019 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, L.; Wang, M.; Qiu, C.; Kan, R.; Shen, X.; Feng, L. Ship Traffic Flow Analysis and Prediction in High-Traffic Areas Under Complex Environments. Appl. Sci. 2025, 15, 11776. https://doi.org/10.3390/app152111776
Luo L, Wang M, Qiu C, Kan R, Shen X, Feng L. Ship Traffic Flow Analysis and Prediction in High-Traffic Areas Under Complex Environments. Applied Sciences. 2025; 15(21):11776. https://doi.org/10.3390/app152111776
Chicago/Turabian StyleLuo, Liulu, Mei Wang, Chen Qiu, Ruixiang Kan, Xianhao Shen, and Lanjin Feng. 2025. "Ship Traffic Flow Analysis and Prediction in High-Traffic Areas Under Complex Environments" Applied Sciences 15, no. 21: 11776. https://doi.org/10.3390/app152111776
APA StyleLuo, L., Wang, M., Qiu, C., Kan, R., Shen, X., & Feng, L. (2025). Ship Traffic Flow Analysis and Prediction in High-Traffic Areas Under Complex Environments. Applied Sciences, 15(21), 11776. https://doi.org/10.3390/app152111776






