Quantitative Detection of Carbamate Pesticide Residues in Vegetables Using a Microwave Ring Resonator Sensor
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Vegetable Extract Samples
2.2. Theoretical Background of Dielectric Property Measurement
3. Sensor Design and Theoretical Modeling
3.1. Sensor Configuration
3.2. S-Parameter Response and Electromagnetic Coupling
3.3. Sensor Performance
3.3.1. Resonance Frequency Shift
3.3.2. Sensitivity and Linear Regression Model
4. Results and Discussion
4.1. Simulation and Resonance Characteristics
4.2. Experimental Dielectric Characterization
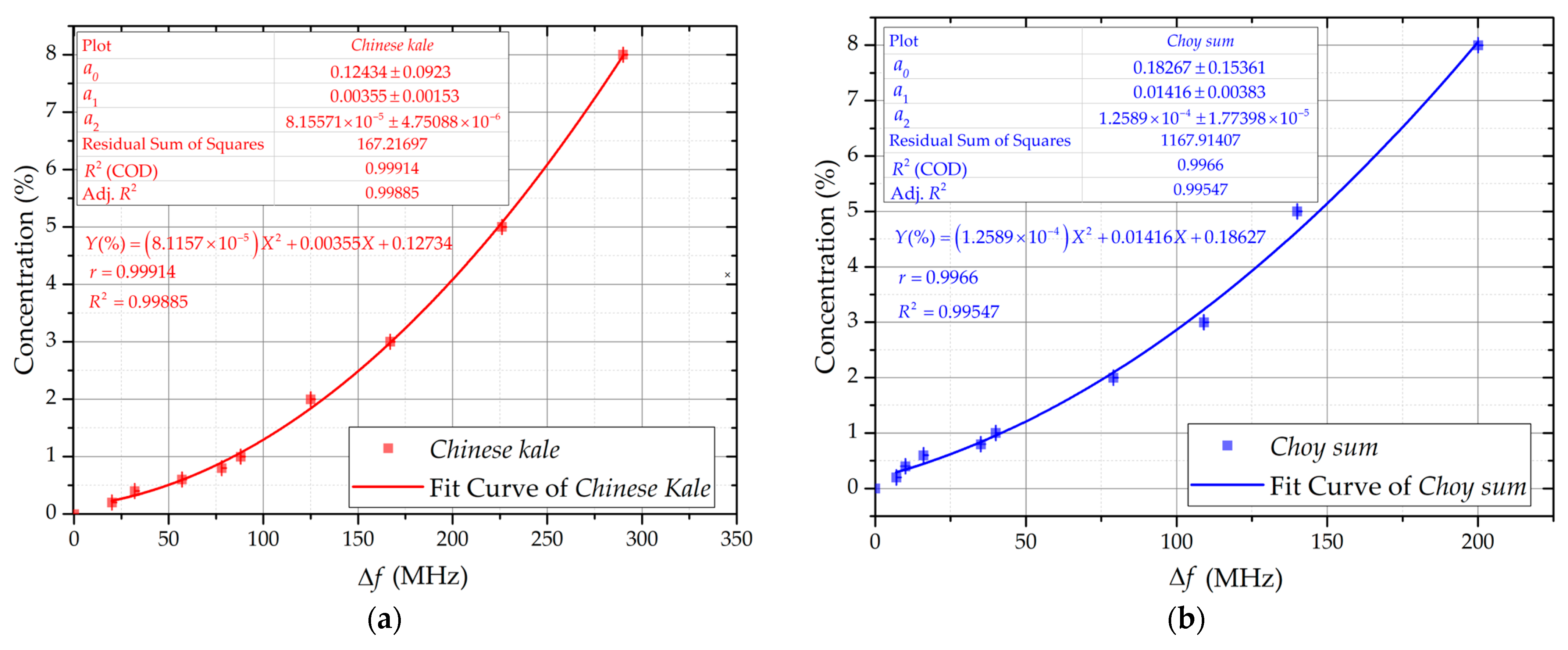
4.3. Resonance Frequency Shift with Pesticide Concentration
4.4. Quantitative Regression and Sensitivity Analysis
4.5. Discussion
| Reference | Sensor Type/ Structure | Operating Frequency (GHz) | Analyte/ Application | Normalized Sensitivity, S (%) | Key Features/ Remarks |
|---|---|---|---|---|---|
| [17] | OCSRR differential sensor | 0.9 | NaCl solution (liquid) | 1.86 | Differential mode, cross-coupled response, high accuracy |
| [18] | SIW dual-band negative-order resonator | 1.6 (1.405–1.795)/ 2.417 (2.095–2.470) | Dielectric permittivity (solid/liquid) | 3.4/3.1 | Dual transmission zeros, compact size |
| [19] | Flexible complementary spiral resonator (CSR) | 1.85 | PET flexible substrate | 5.03 | Bendable, exponential fit (R2 = 0.99976) |
| [21] | Parallel interdigital capacitor resonator | 2.45 | Solid permittivity (dielectric slabs) | 3.98 | Dual-gap IDC, high accuracy (>99%) |
| [22] | Triple CSRR | 1.2/2.335 | Liquid permittivity | 0.879/0.623 | Polynomial fitting, low fabrication cost |
| [23] | CSRR metamaterial sensor | 2.45 | Solids and liquids | Solid/liquid 4.12/0.78 | Microfluidic channel, multi-sample detection |
| This work | Four-port CLRR sensor | 1.05 (m = 1)/ 2.10 (m = 2)/ 3.12 (m = 3)/ 4.11 (m = 4)/ | Leafy vegetables (Chinese kale, Choy sum) | 6.39–6.54 at m = 3 | High sensitivity, High linearity, simple PCB design, FR-4 substrate |
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CLRR | Closed-loop ring resonator |
| OCSRR | Open complementary split ring resonator |
| SIW | Substrate integrated waveguide |
| CSRs | Complementary spiral resonator |
| IDC | Inter-digital capacitor |
| CSRR | Complementary split-ring resonator |
| GC | Gas chromatography |
| LC-MS | Liquid chromatography–tandem mass spectrometry |
| VNA | Vector Network Analyzer |
| SUT | Sample under test |
| MUT | Material under test |
Appendix A
- Input Port (Port 1):
References
- Gama, J.; Neves, B.C.; Pereira, A. Developmental inequity and the impact of pesticide exposure on gut and brain health in developing nations—A Brazilian perspective. Humanit. Soc. Sci. Commun. 2025, 12, 122. [Google Scholar] [CrossRef]
- Tesi, G.O.; Okpara, K.E.; Tesi, J.N.; Agbozu, I.E.; Techato, K. Assessment of organophosphate pesticides in soils and vegetables from agricultural areas of Delta Central District, Nigeria. Sci. Rep. 2025, 15, 8267. [Google Scholar] [CrossRef] [PubMed]
- Mdeni, N.L.; Adeniji, A.O.; Okoh, A.I.; Okoh, O.O. Analytical Evaluation of Carbamate and Organophosphate Pesticides in Human and Environmental Matrices: A Review. Molecules 2022, 27, 618. [Google Scholar] [CrossRef] [PubMed]
- Ogwu, M.C.; Izah, S.C.; Aigberua, A.O.; Ngun, C.T. Editorial: Detection, risk analysis and monitoring of chemical contaminants from agro-aqua food production and processing: Implications on the One Health triad. Front. Sustain. Food Syst. 2024, 8, 1501930. [Google Scholar] [CrossRef]
- Jones, A.; Ali, M.U.; Mayhew, A.; Aryal, K.; Correia, R.H.; Dash, D.; Manis, D.R.; Rehman, A.; O’COnnell, M.E.; Taler, V.; et al. Environmental risk factors for all-cause dementia, Alzheimer’s disease dementia, vascular dementia, and mild cognitive impairment: An umbrella review and meta-analysis. Environ. Res. 2025, 270, 121007. [Google Scholar] [CrossRef]
- Derewiaka, D.; Pydyn, M. Quantitative Analysis of Sterols and Oxysterols in Foods by Gas Chromatography Coupled with Mass Spectrometry. Appl. Sci. 2024, 14, 7934. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H.; Sun, B. Recent progress in food flavor analysis using gas chromatography–ion mobility spectrometry (GC–IMS). Food Chem. 2020, 315, 126158. [Google Scholar] [CrossRef]
- Pang, M.; Lee, J.; Choi, M.K.; Song, I.S. Pharmacokinetics and Tissue Distribution of Enavogliflozin in Mice Using a Validated Liquid Chromatography–Tandem Mass Spectrometry Method. Appl. Sci. 2025, 15, 1445. [Google Scholar] [CrossRef]
- Fan, Z.; Li, Y.; Fan, X.; Wang, P.; Yang, R.; Xie, C. Simultaneous Determination of Three Active Forms of Vitamin B12 In Situ Produced During Fermentation by LC-MS/MS. Foods 2025, 14, 309. [Google Scholar] [CrossRef]
- Albu, C.; Chira, A.; Radu, G.L.; Eremia, S.A.V. Advances in Cost-Effective Chemosensors for Sustainable Monitoring in Food Safety and Processing. Chemosensors 2025, 13, 113. [Google Scholar] [CrossRef]
- Rivera-Rivera, D.M.; Quintanilla-Villanueva, G.E.; Luna-Moreno, D.; Sánchez-Álvarez, A.; Rodríguez-Delgado, J.M.; Cedillo-González, E.I.; Kaushik, G.; Villarreal-Chiu, J.F.; Rodríguez-Delgado, M.M. Exploring Innovative Approaches for the Analysis of Micro- and Nanoplastics: Breakthroughs in (Bio)Sensing Techniques. Biosensors 2025, 15, 44. [Google Scholar] [CrossRef]
- Zhu, X.; Zhao, Y.; Wu, L.; Gao, X.; Huang, H.; Han, Y.; Zhu, T. Advances in Biosensors for the Rapid Detection of Marine Biotoxins: Current Status and Future Perspectives. Biosensors 2024, 14, 203. [Google Scholar] [CrossRef]
- Alahnomi, R.A.; Zakaria, Z.; Yussof, Z.M.; Althuwayb, A.A.; Alhegazi, A.; Alsariera, H.; Rahman, N.A. Review of Recent Microwave Planar Resonator-Based Sensors: Techniques of Complex Permittivity Extraction, Applications, Open Challenges and Future Research Directions. Sensors 2021, 21, 2267. [Google Scholar] [CrossRef]
- Omer, A.E.; Gigoyan, S.; Shaker, G.; Safavi-Naeini, S. Whispering-Gallery-Mode Microwave Sensing Platform for Oil Quality Control Applications. IEEE Internet Things J. 2022, 9, 4065–4075. [Google Scholar] [CrossRef]
- Raju, R.; Bridges, G.E. A Compact Wireless Passive Harmonic Sensor for Packaged Food Quality Monitoring. IEEE Trans. Microw. Theory Tech. 2022, 70, 2389–2397. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Shen, Z.; Liu, B.; Sun, C.; Xue, Q. Microwave biosensors utilizing metamaterial enhancement: Design and application. Nanotechnol. Precis. Eng. 2025, 8, 015001. [Google Scholar] [CrossRef]
- Velez, P.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Highly-sensitive microwave sensors based on Open Complementary Split Ring Resonators (OCSRRs) for dielectric characterization and solute concentration measurement in liquids. IEEE Access 2018, 6, 48324–48338. [Google Scholar] [CrossRef]
- Mohammadi, P.; Teimouri, H.; Mohammadi, A.; Demir, S.; Kara, A. Dual Band, Miniaturized Permittivity Measurement Sensor with Negative-Order SIW Resonator. IEEE Sens. J. 2021, 21, 22695–22702. [Google Scholar] [CrossRef]
- Su, L.; Huang, X.; Guo, W.; Wu, H. A Flexible Microwave Sensor Based on Complementary Spiral Resonator for Material Dielectric Characterization. IEEE Sens. J. 2020, 20, 1893–1903. [Google Scholar] [CrossRef]
- Nikkhah, N.; Keshavarz, R.; Abolhasan, M.; Lipman, J.; Shariati, N. Highly Sensitive Differential Microwave Sensor Using Enhanced Spiral Resonators for Precision Permittivity Measurement. IEEE Sens. J. 2024, 24, 14177–14188. [Google Scholar] [CrossRef]
- Wang, C.; Ali, L.; Meng, F.-Y.; Adhikari, K.K.; Zhou, Z.L.; Wei, Y.C.; Zou, D.Q.; Yu, H. High-Accuracy Complex Permittivity Characterization of Solid Materials Using Parallel Interdigital Capacitor-Based Planar Microwave Sensor. IEEE Sens. J. 2021, 21, 6083–6093. [Google Scholar] [CrossRef]
- Buragohain, A.; Mostako, A.T.T.; Das, G.S. Low-Cost CSRR Based Sensor for Determination of Dielectric Constant of Liquid Samples. IEEE Sens. J. 2021, 21, 27450–27457. [Google Scholar] [CrossRef]
- Han, X.; Liu, K.; Zhang, S.; Peng, P.; Fu, C.; Qiao, L.; Ma, Z. CSRR Metamaterial Microwave Sensor for Measuring Dielectric Constants of Solids and Liquids. IEEE Sens. J. 2024, 24, 14167–14176. [Google Scholar] [CrossRef]
- Kiani, S.; Rezaei, P.; Navaei, M. Dual-sensing and dual-frequency microwave SRR sensor for liquid samples permittivity detection. Measurement 2020, 160, 107805. [Google Scholar] [CrossRef]
- Ali, L.; Mohammed, M.U.; Khan, M.; Yousuf, A.H.B.; Chowdhury, M.H. High-Quality Optical Ring Resonator-Based Biosensor for Cancer Detection. IEEE Sens. J. 2020, 20, 1867–1875. [Google Scholar] [CrossRef]
- Shekhar, A.; Mandal, S. Z-Domain Modeling and Performance Evaluation of Triple Optical Ring Resonator With Embedded Bragg Gratings as Optical Filter and Biosensor. IEEE Sens. J. 2025, 25, 30727–30734. [Google Scholar] [CrossRef]
- Wongsa, F.; Sritan, N.; Phunklang, S.; Krachodnok, P. A Study of the Frequency Response of a Microwave Ring Resonator Circuit for Use as a Sensor. In Proceedings of the ITC-CSCC 2022—37th International Technical Conference on Circuits/Systems, Computers and Communications, Phuket, Thailand, 5–8 July 2022; pp. 926–929. [Google Scholar] [CrossRef]
- Ritthirong, A.; Sinloyma, P. Determination of Organophosphate and Carbamate Pesticide Residues in Vegetables Used in Nutrition Division of Police Cadet Academy. Suan Dusit Grad. Sch. Acad. J. 2022, 18, 87–103. Available online: https://so19.tci-thaijo.org/index.php/SDUGSAJ/article/view/228 (accessed on 1 October 2025).
- Wongta, A.; Hongsibsong, S.; Anand, P.; Jaitum, U.; Sawarng, N.; Wongwilai, W.; Dhumtanom, P. Developing an in-house colorimetric method for detecting organophosphate and carbamate residue using cricket cholinesterase. Chem. Biol. Technol. Agric. 2023, 10, 65. [Google Scholar] [CrossRef]
- Jaitham, U.; Kawichai, S.; Yadoung, S.; Tongchai, P.; Jeeno, P.; Yana, P.; Chuttong, B.; Danmek, K.; Hongsibsong, S. Development of an organophosphate and carbamate pesticide test kit by using a magnetic particle coated with esterase enzyme from honey bee heads. Chem. Biol. Technol. Agric. 2024, 11, 77. [Google Scholar] [CrossRef]
- Kornsing, S.; Phunklang, S.; Thongsopa, C.; Krachodnok, P.; Santalunai, N.; Santalunai, S. Development of a Dielectric Heating System for Selective Thermal Targeting of Liver Fluke Regions in Cirrhinus microlepis. Appl. Sci. 2025, 15, 5466. [Google Scholar] [CrossRef]
- Liu, C.; Liao, C.; Peng, Y.; Zhang, W.; Wu, B.; Yang, P. Microwave Sensors and Their Applications in Permittivity Measurement. Sensors 2024, 24, 7696. [Google Scholar] [CrossRef]
- El Khaled, D.; Novas, N.; Gazquez, J.A.; Garcia, R.M.; Manzano-Agugliaro, F. Fruit and Vegetable Quality Assessment via Dielectric Sensing. Sensors 2015, 15, 15363–15397. [Google Scholar] [CrossRef]
- Bogaerts, W.; De Heyn, P.P.; Van Vaerenbergh, T.T.; De Vos, K.K.; Selvaraja, S.K.; Claes, T.T.; Dumon, P.; Bienstman, P.; Van Thourhout, D.D.; Baets, R.R. Silicon microring resonators. Laser Photon Rev. 2012, 6, 47–73. [Google Scholar] [CrossRef]
- Rashidian, A.; Aligodarz, M.T.; Klymyshyn, D.M. Dielectric characterization of materials using a modified microstrip ring resonator technique. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1392–1399. [Google Scholar] [CrossRef]
- Sabory-García, R.; Arteche-Alday, B.; Ortega-Blanco, C.; Gomez-Fuentes, R.; Noriega, J.R.; García-Juárez, A.; Delgado, L.A.G.; Pérez-Alcocer, R.; Acosta-Enríquez, M.C. Relative permittivity estimation of patch antennas on FR4 substrates for S and C frequency bands. Int. J. Model. Simul. 2024, 45, 1573–1583. [Google Scholar] [CrossRef]
- Sritan, N.; Phunklang, S.; Krachodnok, P. The Study of Bandwidth Expansion of Metamaterial Antenna Designed by Using Spiral Resonator. In Proceedings of the 2021 9th International Electrical Engineering Congress, iEECON 2021, Pattaya, Thailand, 10–12 March 2021; pp. 237–240. [Google Scholar] [CrossRef]
- Sonasang, S.; Prabpal, P.; Sirikan, P.; Hakaew, P.; Pham, N.T.; Yupapin, P.; Ray, K.; Boonkirdram, S. Rabi antenna using microstrip add-drop multiplexer for electron warp speed investigation. Chin. Opt. Lett. 2022, 20, 073901. [Google Scholar] [CrossRef]
- Santalunai, N.; Santalunai, S.; Meesawad, P.; Tongsopa, C.; Santalunai, S. Plus-Shape of Mushroom-Like EBG with Square Microstrip Emitter to Expand the Working Space in Dielectric Heating Applications. Int. J. Intell. Eng. Syst. 2021, 14, 189–200. [Google Scholar] [CrossRef]
- Islam, M.R.; Islam, M.T.; M Salaheldeen, M.; Bais, B.; Almalki, S.H.A.; Alsaif, H.; Islam, S. Metamaterial sensor based on rectangular enclosed adjacent triple circle split ring resonator with good quality factor for microwave sensing application. Sci. Rep. 2022, 12, 6792. [Google Scholar] [CrossRef] [PubMed]
- Chuma, E.L.; Rasmussen, T. Metamaterial-Based Sensor Integrating Microwave Dielectric and Near-Infrared Spectroscopy Techniques for Substance Evaluation. IEEE Sens. J. 2022, 22, 19308–19314. [Google Scholar] [CrossRef]
- Anwar, S.; Khan, S.; Ali, G.; Khan, M. Sensing of Microorganisms and Pesticides Based on Metamaterial Refractive Index Sensor. Sens. Imaging 2024, 25, 48. [Google Scholar] [CrossRef]
- Bagci, F.; Alp, K.; Akaoglu, B. Multi-band microwave dielectric sensing using a defected ground structure with dual interdigital capacitor units. Measurement 2026, 257, 118705. [Google Scholar] [CrossRef]
- Phunklang, S.; Mesawad, P.; Krachodnok, P. Utilizing Moisture Sensors for Accurate Measurement of Starch Content in Cassava. In Proceedings of the ICPEI 2024—6th International Conference on Power, Energy and Innovations, Nakhon Ratchasima, Thailand, 16–18 October 2024; pp. 114–117. [Google Scholar] [CrossRef]
- Heebner, J.E.; Wong, V.; Schweinsberg, A.; Boyd, R.W.; Jackson, D.J. Optical transmission characteristics of fiber ring resonators. IEEE J. Quantum Electron. 2004, 40, 726–730. [Google Scholar] [CrossRef]
- Azhigulov, D.; Nakarmi, B.; Ukaegbu, I.A. High-speed thermally tuned electro-optical logic gates based on micro-ring resonators. Opt. Quantum Electron. 2020, 52, 412. [Google Scholar] [CrossRef]
- Kundu, S.; Hossain, M.; Mandal, S. Modeling of silicon microring resonator-based programmable logic device for various arithmetic and logic operation in Z-domain. Opt. Quantum Electron. 2023, 55, 175. [Google Scholar] [CrossRef]
- Hill, T.P.; Miller, J. How to combine independent data sets for the same quantity. Chaos An Interdiscip. J. Nonlinear Sci. 2011, 21, 033102. [Google Scholar] [CrossRef] [PubMed]
- Yueanket, A.; Phunklang, S.; Kornsing, S.; Kupimai, M.; Innok, A.; Pumpoung, T.; Todnatee, S. AIoT-Based Water Management Solutions for Sustainable Sugarcane Farming. In Proceedings of the ICPEI 2024—6th International Conference on Power, Energy and Innovations, Nakhon Ratchasima, Thailand, 16–18 October 2024; pp. 19–23. [Google Scholar] [CrossRef]
- Tran, V.L.; Doan, T.N.C.; Ferrero, F.; Le Huy, T.; Le-Thanh, N. The Novel Combination of Nano Vector Network Analyzer and Machine Learning for Fruit Identification and Ripeness Grading. Sensors 2023, 23, 952. [Google Scholar] [CrossRef]
- Bahadoran, M.; Amiri, I.S. Double critical coupled ring resonator-based add–drop filters. J. Theor. Appl. Phys. 2019, 13, 213–220. [Google Scholar] [CrossRef]


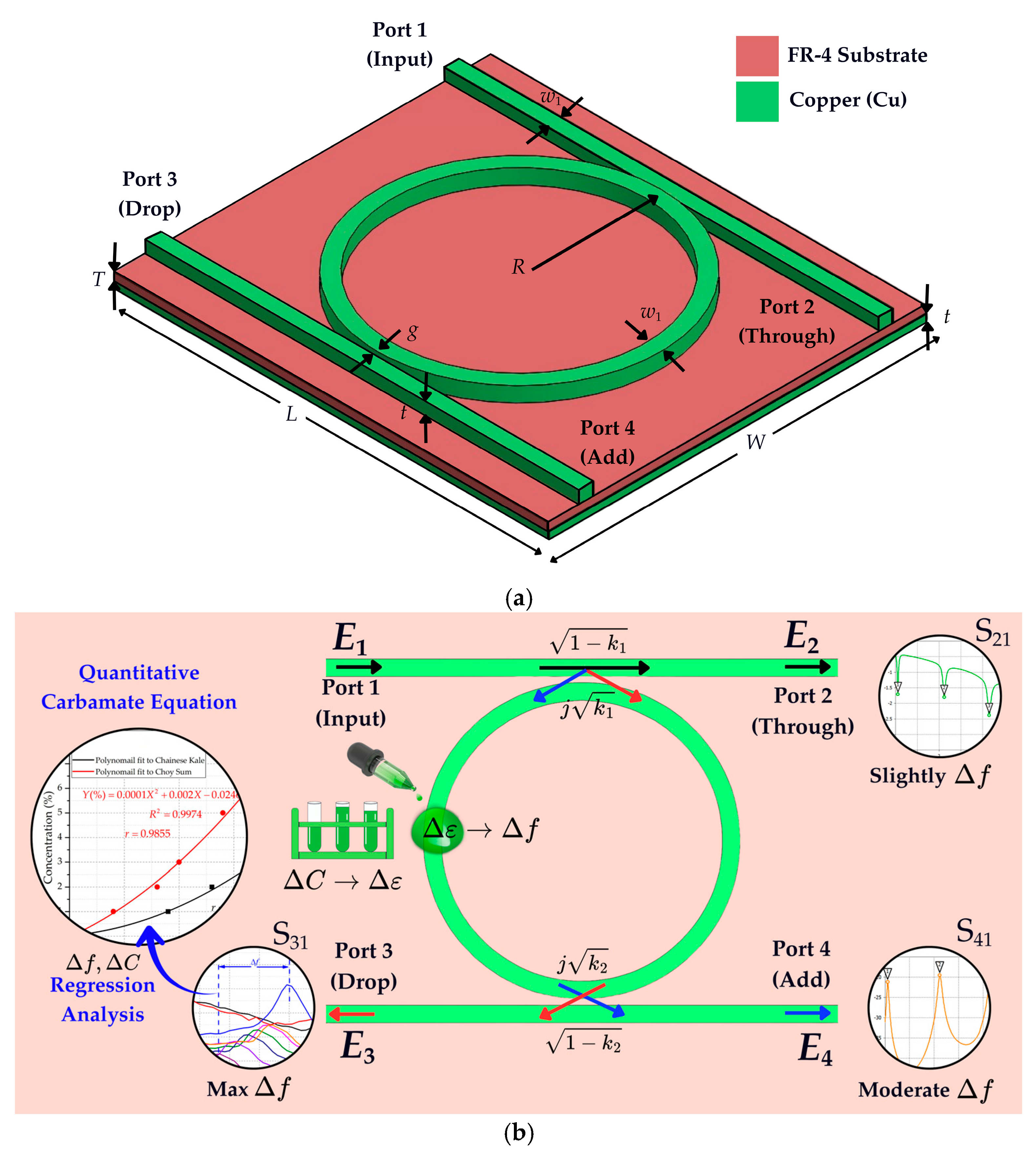




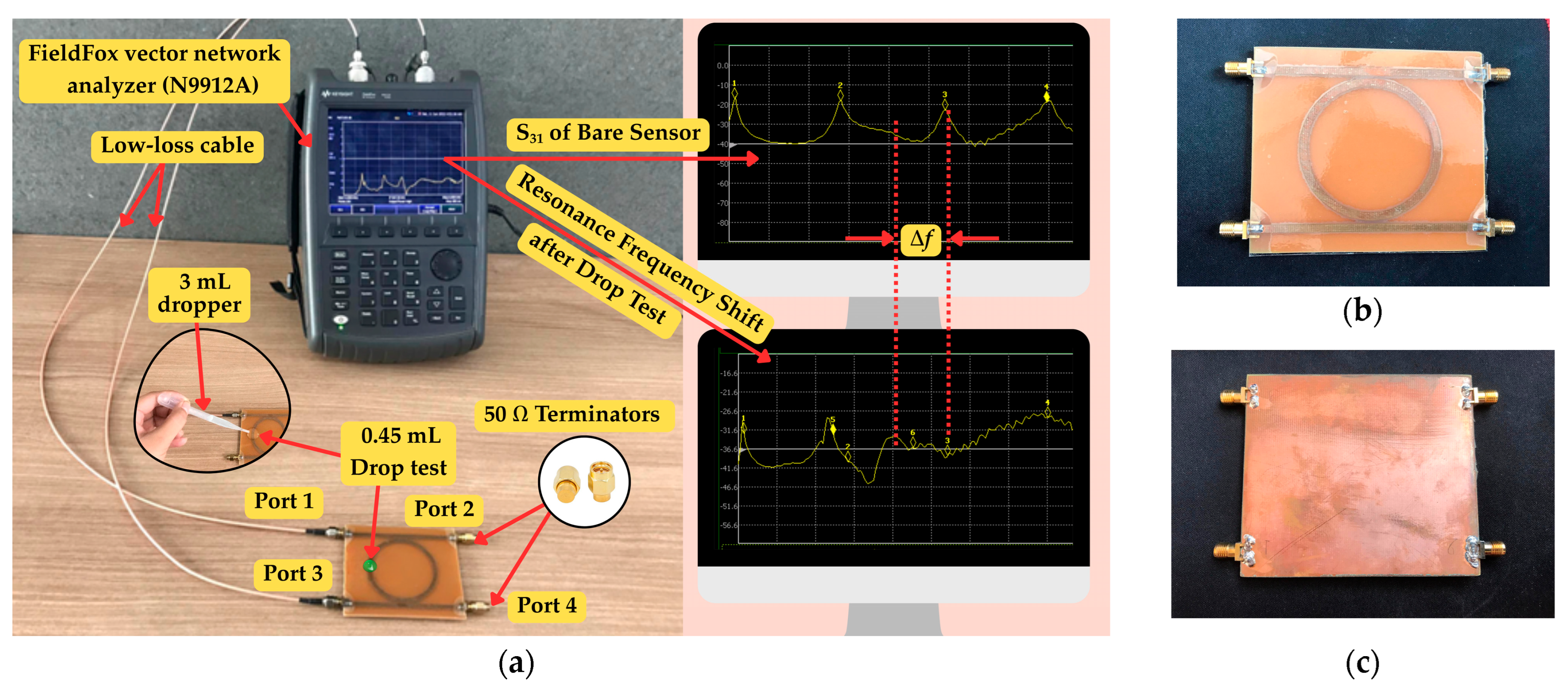

| Parameter | Description | Dimension (mm) |
|---|---|---|
| R | Radius of the ring resonator | 25 |
| g | Coupling gap | 0.2 |
| w1 | Width of ring and microstrip line | 3 |
| L | Overall length of the layout | 86 |
| W | Overall width of the layout | 75 |
| T | Substrate thickness | 1.6 |
| t | Copper thickness | 0.035 |
| Mode (m) | Calculated Operating Frequency (GHz) | Simulated Operating Frequency (GHz) | Measured Operating Frequency (GHz) |
|---|---|---|---|
| 1 | 1.058 | 1.057 | 1.051 |
| 2 | 2.117 | 2.110 | 2.101 |
| 3 | 3.174 | 3.148 | 3.121 |
| 4 | 4.232 | 4.155 | 4.111 |
| Concentrate (% w/v) | Chinese kale | |||||||
|---|---|---|---|---|---|---|---|---|
(GHz) ± SD | (GHz) ± SD | (MHz) ± SD | (ε) ± SD | (ε) ± SD | (Δε) ± SD | S (MHz/Δε’) ± SD | S (%) | |
| 0% (Organic) | 2.750 ± 0.015 | - | - | 76.81 ± 0.020 | - | - | - | - |
| 0.2% | - | 2.730 ± 0.013 | 20 ± 0.020 | - | 76.70 ± 0.050 | 0.11 ± 0.054 | 181.82 ± 0.089 | 6.61% |
| 0.4% | - | 2.718 ± 0.010 | 32 ± 0.018 | - | 76.62 ± 0.030 | 0.19 ± 0.036 | 168.42 ± 0.032 | 6.12% |
| 0.6% | - | 2.693 ± 0.012 | 57 ± 0.019 | - | 76.48 ± 0.050 | 0.33 ± 0.054 | 172.73 ± 0.028 | 6.28% |
| 0.8% | - | 2.672 ± 0.010 | 78 ± 0.018 | - | 76.37 ± 0.020 | 0.44 ± 0.028 | 177.27 ± 0.011 | 6.45% |
| 1% | - | 2.662 ± 0.005 | 88 ± 0.016 | - | 76.33 ± 0.030 | 0.48 ± 0.036 | 183.33 ± 0.014 | 6.67% |
| 2% | - | 2.625 ± 0.010 | 125 ± 0.018 | - | 76.12 ± 0.050 | 0.69 ± 0.054 | 181.16 ± 0.014 | 6.59% |
| 3% | - | 2.583 ± 0.012 | 167 ± 0.019 | - | 75.89 ± 0.040 | 0.92 ± 0.045 | 181.52 ± 0.009 | 6.60% |
| 5% | - | 2.524 ± 0.010 | 226 ± 0.018 | - | 75.59 ± 0.050 | 1.22 ± 0.054 | 185.25 ± 0.008 | 6.74% |
| 8% | - | 2.460 ± 0.005 | 290 ± 0.016 | - | 75.25 ± 0.020 | 1.56 ± 0.028 | 185.90 ± 0.003 | 6.76% |
| Test sample (market) | - | 2.68 ± 0.012 | 70 ± 0.019 | |||||
| Concentrate (% w/v) | Choy sum | |||||||
(GHz) ± SD | (GHz) ± SD | (MHz) ± SD | (ε) ± SD | (ε) ± SD | (Δε) ± SD | S (MHz/Δε’) ± SD | S (%) | |
| 0% (Organic) | 2.600 ± 0.010 | - | - | 76.88 ± 0.030 | - | - | - | - |
| 0.2% | - | 2.593 ± 0.012 | 7 ± 0.016 | - | 76.84 ± 0.020 | 0.04 ± 0.036 | 175.00 ± 0.158 | 6.73% |
| 0.4% | - | 2.590 ± 0.015 | 10 ± 0.018 | - | 76.82 ± 0.020 | 0.06 ± 0.036 | 166.67 ± 0.100 | 6.41% |
| 0.6% | - | 2.584 ± 0.018 | 16 ± 0.021 | - | 76.78 ± 0.030 | 0.10 ± 0.042 | 160.00 ± 0.067 | 6.15% |
| 0.8% | - | 2.565 ± 0.016 | 35 ± 0.019 | - | 76.66 ± 0.020 | 0.22 ± 0.036 | 159.09 ± 0.026 | 6.12% |
| 1% | - | 2.560 ± 0.005 | 40 ± 0.011 | - | 76.64 ± 0.050 | 0.24 ± 0.058 | 166.67 ± 0.040 | 6.41% |
| 2% | - | 2.521 ± 0.008 | 79 ± 0.013 | - | 76.41 ± 0.040 | 0.47 ± 0.050 | 168.09 ± 0.018 | 6.46% |
| 3% | - | 2.491 ± 0.010 | 109 ± 0.013 | - | 76.18 ± 0.050 | 0.70 ± 0.058 | 155.71 ± 0.013 | 5.99% |
| 5% | - | 2.460 ± 0.008 | 140 ± 0.014 | - | 76.06 ± 0.030 | 0.82 ± 0.042 | 170.73 ± 0.009 | 6.57% |
| 8% | - | 2.400 ± 0.005 | 200 ± 0.011 | - | 75.73 ± 0.020 | 1.15 ± 0.036 | 173.91 ± 0.005 | 6.69% |
| Test sample (market) | - | 2.580 ± 0.010 | 20 ± 0.014 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wongsa, F.; Phunklang, S.; Yueanket, A.; Kornsing, S.; Santalunai, N.; Mesawad, P.; Santalunai, S.; Narakaew, S.; Krachodnok, P. Quantitative Detection of Carbamate Pesticide Residues in Vegetables Using a Microwave Ring Resonator Sensor. Appl. Sci. 2025, 15, 11775. https://doi.org/10.3390/app152111775
Wongsa F, Phunklang S, Yueanket A, Kornsing S, Santalunai N, Mesawad P, Santalunai S, Narakaew S, Krachodnok P. Quantitative Detection of Carbamate Pesticide Residues in Vegetables Using a Microwave Ring Resonator Sensor. Applied Sciences. 2025; 15(21):11775. https://doi.org/10.3390/app152111775
Chicago/Turabian StyleWongsa, Fongnapha, Sirigiet Phunklang, Apisit Yueanket, Supatinee Kornsing, Nuchanart Santalunai, Patawee Mesawad, Samran Santalunai, Samroeng Narakaew, and Piyaporn Krachodnok. 2025. "Quantitative Detection of Carbamate Pesticide Residues in Vegetables Using a Microwave Ring Resonator Sensor" Applied Sciences 15, no. 21: 11775. https://doi.org/10.3390/app152111775
APA StyleWongsa, F., Phunklang, S., Yueanket, A., Kornsing, S., Santalunai, N., Mesawad, P., Santalunai, S., Narakaew, S., & Krachodnok, P. (2025). Quantitative Detection of Carbamate Pesticide Residues in Vegetables Using a Microwave Ring Resonator Sensor. Applied Sciences, 15(21), 11775. https://doi.org/10.3390/app152111775












