Software System for Thrust Prediction and Preliminary Engineering Design of Aircraft Using Visual Recognition and Flight Parameters

Abstract

Accurate estimation of engine thrust and overload is crucial for ensuring structural integrity and optimizing the aircraft’s life-cycle design. To address this issue, this study develops an integrated thrust and load prediction framework that combines vision-based flight maneuver recognition with an improved transformer-based deep learning model (YOLO), leveraging measured flight parameters. After maneuver recognition, the model achieves a mean absolute error of 1.86 and R² of 0.97 in prediction. The framework is implemented via a Python-based software system with a MySQL database, supporting functionalities including thrust/load prediction, trajectory visualization, and performance evaluation. Comparative experiments demonstrate that the framework achieves an average maneuver recognition accuracy of 81.06%, outperforming the existing PLR-PIP and DTW methods. This approach provides high-precision and reliable thrust data as well as tool support for real-time thrust estimation, fatigue life assessment, and flight safety risk prevention.

1. Introduction

Aircraft often operate in extreme environments, where the actual operational thrust and overload frequently deviate from the predefined design spectrum. Accurate estimation of the in-service thrust and overload spectrum is therefore essential for ensuring structural integrity, extending component life, and supporting reliable design. Conventional approaches rely on multiple flight tests to collect flight parameter data, which are then used to construct deep learning models for thrust and load prediction [1]. While promising, such models often suffer from limited accuracy, primarily because they require prior recognition of flight maneuvers and separate training for each maneuver type—an approach analogous to clustering in machine learning. Existing methods [2] typically achieve flight maneuver recognition by adding numerous rules or by comparing time-series consistency. In practice, however, many aircraft generate wake records during flight testing, and visual images can also be synthetically produced by onboard computers or simulators. Incorporating vision-based recognition of flight maneuvers from wake patterns and trajectories provides a more accurate and efficient means of identifying maneuver types automatically, thereby enhancing load prediction accuracy and improving the applicability of deep learning models to engineering design.

Internationally, the estimation methods for aircraft thrust and overload have been extensively studied [3,4,5,6,7,8]. Wang et al. [9] designed an aircraft thrust estimator using a Deep Convolutional Neural Network (DCNN), which was trained and tested with simulation-generated data samples, demonstrating excellent thrust estimation performance. In recent years, research on this issue has also been carried out [10,11,12,13,14,15]. For instance, research has addressed problems such as the difficulty in extracting degraded parameters monitored by aircraft sensors, vulnerability to noise interference, and insufficient accuracy in predicting the Remaining Useful Life (RUL) of engines. Zhang et al. [16] proposed an integrated deep learning-based aero-engine surge diagnostic method. The ASDA algorithm is used to generate datasets, and models such as 1D-CNN are optimized. The network achieves a test set classification accuracy of over 99%, verifying the effectiveness of deep learning. Chen et al. [17] integrated the monitored degradation information of multiple performance parameters through an information fusion model to conduct reliability prediction for aircraft, thereby achieving accurate assessment of the health status of aircraft fleets. Zhang Wei et al. [14] proposed a combined model based on ARIMA and BP neural network to enhance the short-term prediction accuracy of aircraft thrust attenuation. Although these studies have made progress in specific fields, they still have certain limitations in data processing and analysis methods, lacking the capability for comprehensive processing and analysis of large-scale flight parameter data.

Building upon the existing maneuver recognition method developed by our research group [18], this paper proposes an aircraft thrust and overload estimation method based on flight parameter load data, combined with the finite element concept and vector analysis. Through comprehensive analysis of aircraft flight performance parameters, a complete estimation process for aircraft thrust and overload has been established. Additionally, this paper has developed corresponding thrust design spectrum prediction software v1.0 for certain aircraft, which realizes functions such as flight parameter data import, classification management, preprocessing, segmentation and identification, maneuver reproduction, and prediction of flight parameters including engine required thrust. This software system further improves the accuracy and efficiency of thrust and overload estimation, providing a new technical means for aircraft design and performance analysis.

2. Flight Parameter Data Processing

2.1. Preprocessing of Flight Parameter Data

Aircraft data preprocessing is crucial for ensuring the accuracy of flight parameters and load information. Based on a set of measured flight data of a certain aircraft type, this paper selects 30 key flight parameters, including attitude angles, three-axis overload, airspeed, and altitude. To address distortion issues in the measured data, such as over-limit values, abnormal parameter change rates, and outliers [19], this paper adopts methods including removing over-limit values, replacing abnormal change rates, and eliminating outliers. To reduce high-frequency noise in aircraft flight data, this paper employs Fourier transform [20], low-pass filtering technology, and moving average filtering to eliminate random errors.

2.2. Flight Maneuver Recognition

2.2.1. Review of the Previous Work

Previously, the PLR-PIP algorithm and Fast-DTW algorithm [18] were used to classify the flight maneuver states of the aircraft. The simplified workflow of these two algorithms is shown in Figure 1. The PLR-PIP algorithm extracts Perceptually Important Points from the time series, which effectively reduces data dimensionality while preserving key trends. This not only improves the efficiency of data processing but also enhances the capability to capture flight maneuver features. The Fast-DTW algorithm significantly accelerates the computation speed of the Dynamic Time Warping (DTW) algorithm by optimizing the search space. Meanwhile, combined with the improved hierarchical clustering algorithm, it enables the comprehensive analysis of multiple parameters.

Figure 1. Algorithm flowchart: (a) PLR-PIP algorithm; (b) Fast-DTW algorithm.

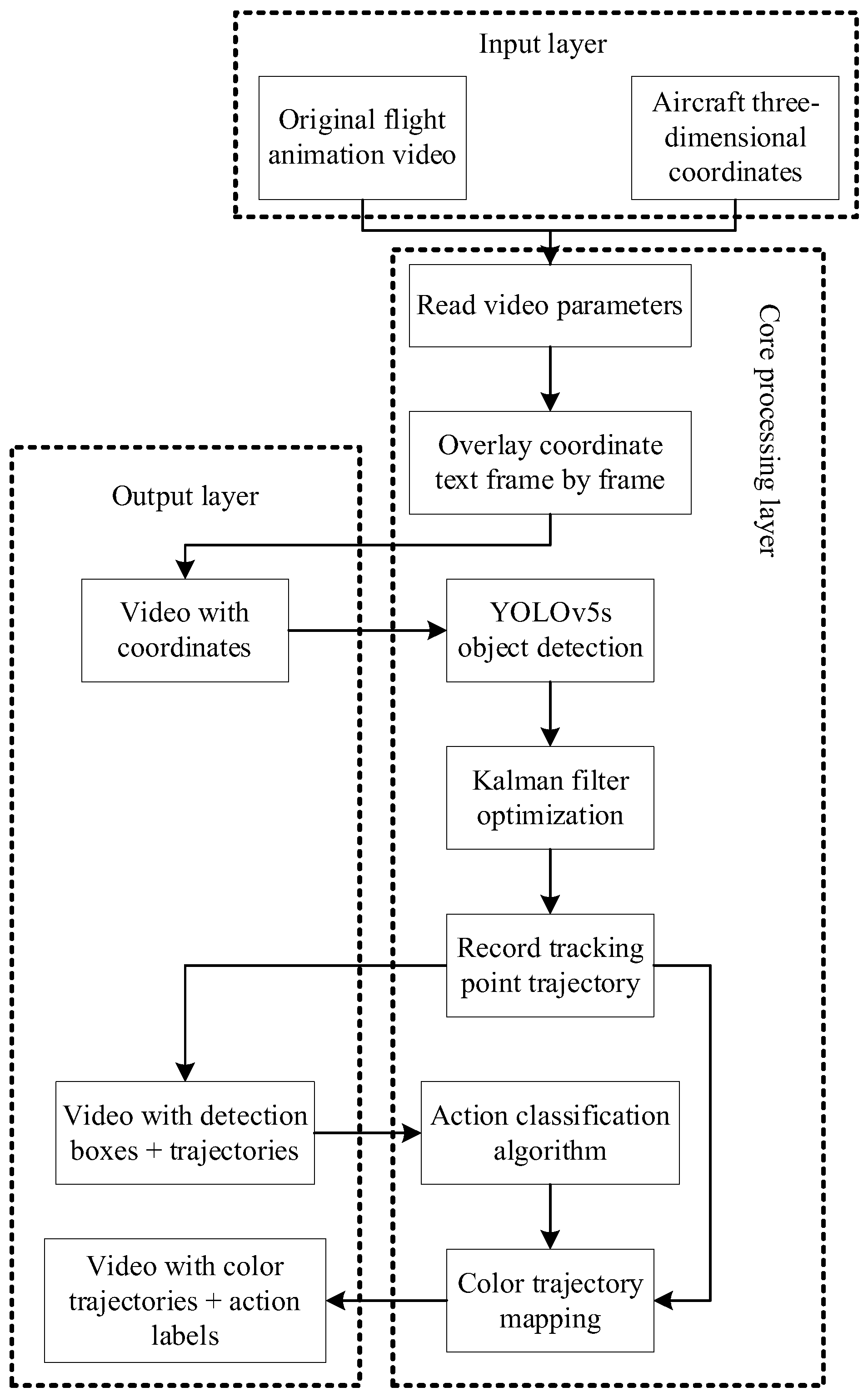
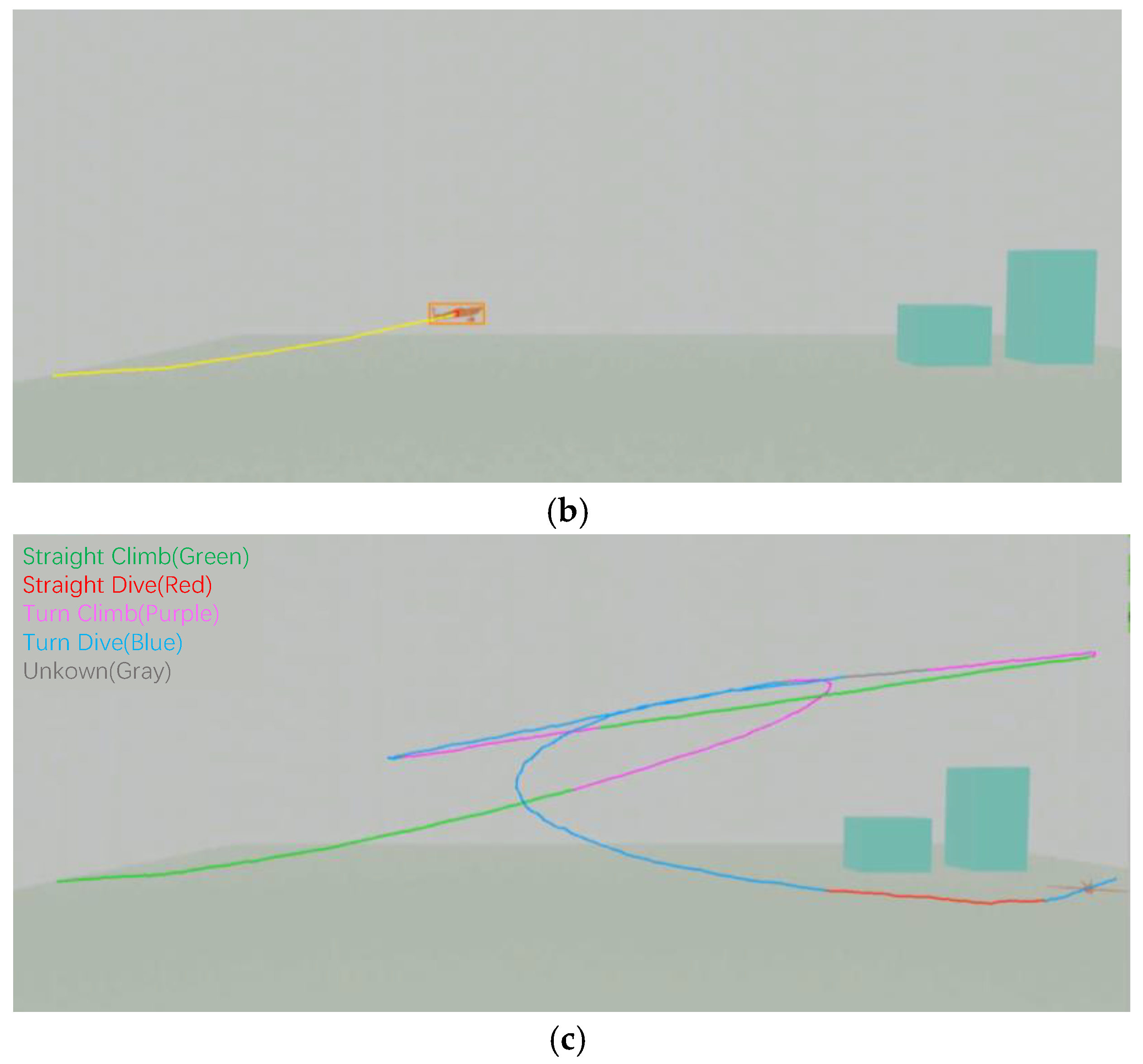
2.2.2. Vision-Based Recognition of Flight Maneuver

This paper designs an aircraft tracking and maneuver recognition system based on computer vision technology. Through a three-stage processing workflow, the system realizes complete functions from raw video data to aircraft 3D coordinate annotation, stable target tracking, and maneuver classification. The system adopts the YOLOv5 model for target detection, combines the Kalman filter algorithm to optimize tracking stability, realizes automatic aircraft maneuver classification based on 3D coordinate data, and intuitively displays tracking results and maneuver types through visualization technology. The overall system architecture is shown in Figure 2. The pseudo-code of main framework is described in Algorithm 1.

Figure 2. Flowchart of a computer vision-based aircraft tracking and maneuver recognition system.

In the aircraft capture module, the system performs object detection based on the YOLOv5s model (yolov5s.pt). YOLOv5 model is used for frame-by-frame detection and localization of aircraft targets in video sequences, thereby extracting the visual coordinate information of targets on the image plane. The Kalman filter, on the other hand, realizes temporal smoothing and trajectory prediction based on this information to eliminate jitter and noise during the detection process, ensuring the continuity and stability of visual tracking trajectories. By setting a confidence threshold (0.1), candidate targets are filtered, and the bounding box with the highest confidence is selected as the detection result. To enhance tracking stability, a Kalman filter algorithm is introduced, constructing a 4-dimensional state space encompassing position (x, y) and velocity (v_x, v_y). The Kalman filter, on the other hand, realizes temporal smoothing and trajectory prediction based on this information to eliminate jitter and noise during the detection process, ensuring the continuity and stability of visual tracking trajectories. The “prediction-correction” mechanism smooths the trajectory, with the state transition matrix built upon a constant velocity linear motion model. The measurement matrix maps the 4-dimensional state to 2-dimensional positional observations, while the process noise covariance is set to 0.03 to control the degree of filtering smoothness. Meanwhile, the coordinates of tracking points are recorded in real-time, forming a yellow trajectory through line connections and visualized.

Algorithm 1: Vision—based flight maneuver recognition program

1.   Function AircraftTracking() 2.       input: video, csv 3.       output: output video 4.       Load YOLO model 5.       Initialize Kalman filter 6.       trajectory = [] 7.       for each frame in video: 8.           if YOLO.detect(frame): 9.               Update Kalman filter 10.             point = Kalman state 11.         else 12.             point = Kalman prediction 13.         trajectory.append(point) 14.         if frame index > 0: 15.             dz = current z—previous z 16.             angle = calculate angle() 17.             maneuver = classify(dz, angle) 18.         DrawTrajectory(trajectory, maneuver) 19.         DisplayInfo(maneuver) 20.         Write output frame 21.     return output video 22.     function classify(dz, angle) 23.         if dz > 0: 24.             return “turn climb” if angle > 45 else “straight climb” 25.         else: 26.             return “turn dive” if angle > 45 else “straight dive”

We compared the recognition accuracy of the visual recognition method with that of previous methods, such as DTW, PCA, CTW, and PCR-PIP, using the same dataset, and plotted the 1-NN graph in Table 1 and Figure 3. Compared with the comparison methods, the visual recognition method proposed in this paper has significant advantages in the recognition accuracy of flight maneuvers.

Table 1. Accuracy of maneuver recognition (Unit: %).

Maneuver	DTW	PCA	CTW	PLR-PIP	Visual Recognition
Climb	75.12	80.36	64.86	86.46	88.41
Dive	70.34	77.69	39.54	87.35	91.42
Turn climb	66.79	65.35	46.82	69.11	72.36
Turn Dive	72.52	77.67	68.51	70.62	71.58
Level Flight and Level Turn	76.36	79.34	60.33	80.97	81.56
Average accuracy	72.97	76.63	56.73	79.25	81.06

Figure 3. Comparison chart of accuracy between visual recognition and other methods.

In terms of visualization, a color mapping scheme is employed to represent different flight maneuvers, where green, purple, red, orange, and gray correspond to straight climb, turning climb, straight dive, turning dive, and unrecognized maneuvers, respectively. The current maneuver type, along with a legend, is displayed in real-time within the video frames. Some trajectories (grey segments) in Figure 4c remain unrecognizable due to the limitation of visual recognition for maneuver segments—which only allows analysis from the main perspective. When the aircraft flies at the same horizontal level, the specific maneuver type cannot be determined, so these trajectories are classified as level flight or level turn.

Figure 4. Screenshot of the animation generated by the visual-driven maneuver recognition model: (a) the original flight animation; (b) video with detection boxes + trajectories; (c) video with color trajectories + action labels.

As illustrated in Figure 4a shows a screenshot of the original aircraft flight animation, Figure 4b displays the trajectory video restored with flight coordinates. The yellow lines represent the identified flight trajectory, the orange box indicates the recognized aircraft attitude, and the blue short pillars denote the flight scene settings. Figure 4c presents the video annotated with labels and color-coded trajectories following visual recognition. The visual recognition is achieved by learning fundamental maneuver segments. Specifically, a dataset of 2000 images covering diverse maneuvers—including climb, cruise, landing, ascending turn, and descending turn—was generated. Maneuvers are identified by evaluating the overlap and compatibility between the current frame and the learned maneuver images. This approach enables real-time reflection of the aircraft’s actions and records time-series data, which is then used to segment flight parameter data for subsequent training of multiple high-precision deep learning models tailored to specific maneuver types.

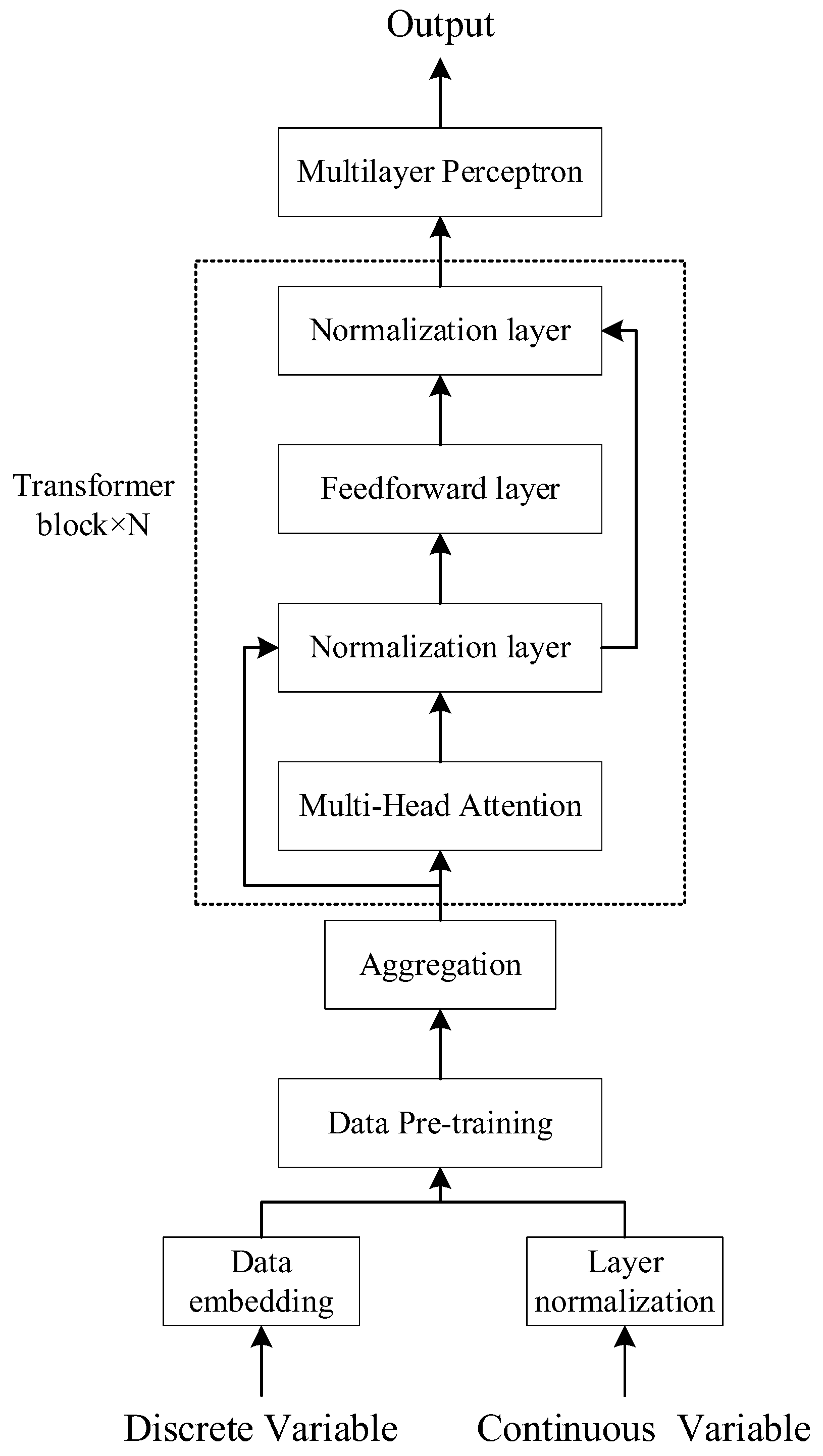
2.3. Aircraft Maneuver Data Prediction

After completing the maneuver segmentation, a series of maneuver segments can be obtained. Conducting segmented fitting and prediction for different segments can effectively improve the prediction accuracy, thereby enhancing the accuracy of subsequent engine thrust estimation based on the predicted parameters.

To address issues such as insufficient temporal feature capture and poor data adaptability of the traditional Transformer model in aircraft load prediction, improvements are made from three aspects: in terms of the attention mechanism, a convolutional self-attention mechanism is introduced, where Query and Key are preprocessed through 1D convolution operations to fuse local temporal features, thus enhancing the prediction accuracy of load extreme points; in terms of data input, a linear transformation layer is used to map continuous flight parameters to a vector space with a unified dimension, and at the same time, a dual-dimensional positional encoding including feature dimension encoding and relative importance is designed to adapt to the characteristics of flight parameters; in terms of model architecture, the decoder is removed and a linear regression layer is connected to reduce computational complexity, and a masked feature learning pre-training module is also added to improve the model’s generalization ability under the condition of limited flight data. The architecture diagram of the improved model is shown in Figure 5.

Figure 5. Diagram of the improved model architecture.

In the performance comparison experiment, BP, LSTM + Attention, and the improved Transformer were selected as prediction models. Mean Absolute Error (MAE), Mean Squared Error (MSE), and coefficient of determination (R²) were used as evaluation metrics to measure prediction accuracy.

$$MAE={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|}$$

(1)

$$MSE={\displaystyle \frac{1}{n}}{{\displaystyle \sum _{i=1}^n\left(y_i-{\widehat{y}}_i\right)}}^2$$

(2)

$$R^2=1-{\displaystyle \frac{{\displaystyle {\sum }_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}}{{\displaystyle {\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}$$

(3)

Among them, $y_i$ is the true value of the ith sample, ${\widehat{y}}_i$ is the predicted value of the ith sample, n is the total number of samples, and $\overline{y}$ is the mean value of the true values. A smaller MAE value indicates a smaller prediction error of the model. The advantage of MAE lies in its insensitivity to outliers, enabling it to well reflect the average level of the model’s prediction errors. Unlike MAE, MSE assigns higher weights to larger errors. Therefore, MSE is generally more suitable for evaluating the model’s performance in handling larger errors. R² is a statistical indicator used to assess the goodness of fit of regression models. It represents the proportion of the total variance of the dependent variable that can be explained by the model, with a range between 0 and 1. A higher R² value means the model has a better fitting effect on the data. The final results are presented in Table 2, and the detailed load history results before and after maneuver identification are plotted in Figure 6 and Figure 7.

Table 2. Comparison of prediction results of different models before and after maneuver recognition.

Model	Whether to Perform Maneuver Recognition	MAE	MSE	${\mathit{R}}^2$
BP	NO	15.79	361.4	0.41
	YES	9.17	90.36	0.68
LSTM + Attention	NO	7.71	61.23	0.71
	YES	4.10	19.59	0.87
Improved Transformer	NO	4.92	29.43	0.85
	YES	1.86	6.27	0.97

Figure 6. Prediction results of different models before maneuver recognition.

Figure 7. Prediction results of different models after maneuver recognition.

The results show that the improved Transformer model significantly improves the prediction accuracy. By introducing the convolutional self-attention mechanism, the improved model can better capture local temporal features and overcome the limitations of the original Transformer in processing temporal data. At the extreme points of load, the improved model exhibits smaller prediction errors compared with other models. Meanwhile, the model’s ability to handle long-term dependencies is also enhanced, enabling it to better adapt to the characteristics of temporal data in the aircraft load prediction task.

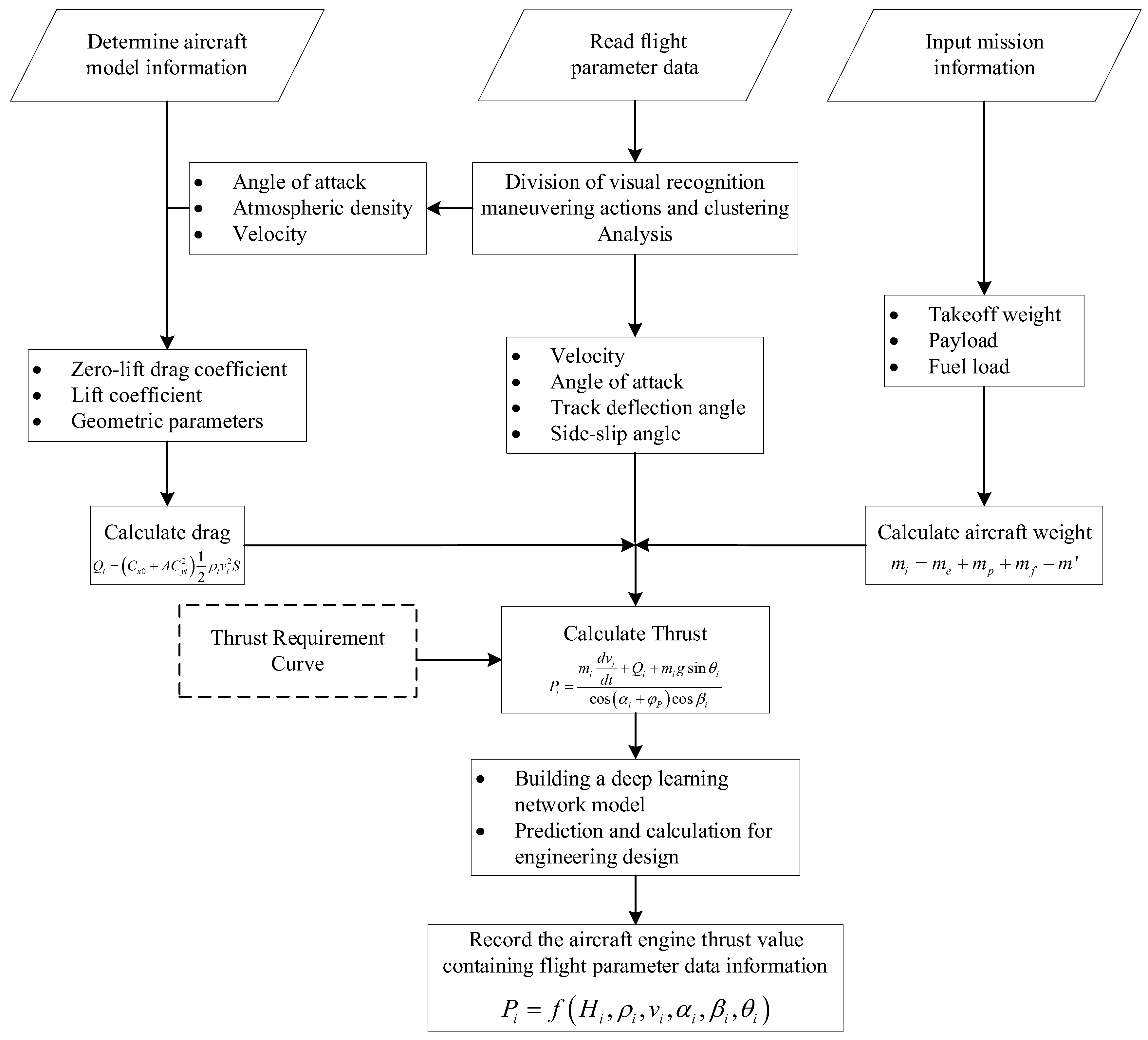
3. Aircraft Thrust Estimation Method

The main idea of the aircraft thrust estimation method adopted in this paper [21] is as follows: using existing flight parameter data to derive the design data (such as aircraft lift coefficient and drag coefficient) under the real-time operational conditions of the aircraft; formulating the aircraft’s centroid dynamic equations in the time domain based on the vector analysis method; and calculating the thrust estimation value of a new aircraft type based on the predicted flight parameter data, thereby generating the aircraft’s design thrust spectrum in the time domain.

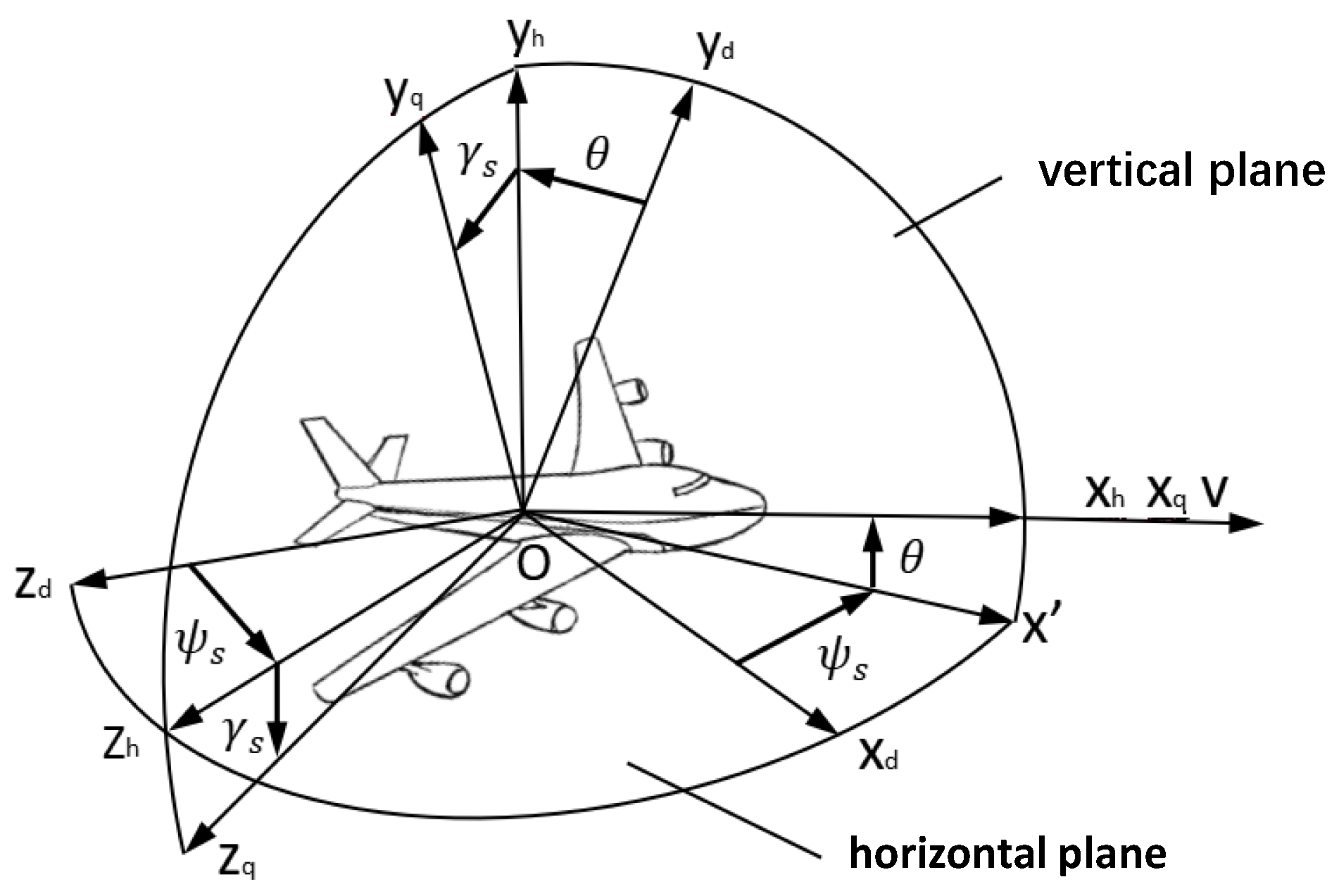
3.1. Aircraft Centroid Dynamic Differential Equations

The flight parameter data required for solving the aircraft’s centroid motion equations mainly include: the altitude $H_i$ of the aircraft type at its current flight path, atmospheric density ${\rho }_i$, velocity $v_i$ in the flight path coordinate system, angle of attack ${\alpha }_i$, sideslip angle ${\beta }_i$, and flight path angle ${\theta }_i$. The aircraft mass $m_i$ is determined by the payload $m_p$, fuel load $m_f$, and flight tasks (including whether the tasks involve unloading operations or other activities that cause changes in aircraft mass). The aircraft mass $m_i$ within the current flight path segment is calculated based on the aircraft’s empty weight $m_e$, payload $m_p$, fuel load $m_f$, and whether the completed tasks include unloading mass $m\prime$.

$$m_i=m_e+m_p+m_f-m\prime$$

(4)

The aircraft drag $Q_i$ within the current flight path segment is calculated in accordance with the aircraft drag calculation formula.

$$Q_i={\left(C_x\right)}_i{\displaystyle \frac{1}{2}}{\rho }_i{v}_i^{2}S=\left(C_{x0}+A{C}_{yi}^2\right){\displaystyle \frac{1}{2}}{\rho }_i{v}_i^{2}S$$

(5)

Among them, $S$ denotes the wing area, $A$ represents the lift-induced drag factor (polar curve camber coefficient), $C_{x0}$ stands for the zero-lift drag coefficient, $C_y$ stands for the lift coefficient.

Based on the relationship between wind coordinate (system with subscript q), flight path coordinate system (system with subscript h), and ground coordinate system (system with subscript d) in Figure 8, the dynamic differential equations of the aircraft’s centroid can be derived using the transformation matrix between the body coordinate system and the flight path coordinate system:

$$\left\{\begin{array}{c}m{\displaystyle \frac{d\nu }{dt}}=P\cos (\alpha +{\phi }_P)\cos \beta -Q-mg\sin \theta \\ m\nu {\displaystyle \frac{d\theta }{dt}}=P[\cos (\alpha +{\phi }_P)\sin \beta \sin {\gamma }_s+\sin (\alpha +{\phi }_P)\sin {\gamma }_s]+Y\cos {\gamma }_s-Z\sin {\gamma }_s-mg\cos \theta \\ -m\nu \cos \theta {\displaystyle \frac{d{\psi }_s}{dt}}=P[-\cos (\alpha +{\phi }_P)\sin \beta \cos {\gamma }_s+\sin (\alpha +{\phi }_P)\sin {\gamma }_s]+Y\sin {\gamma }_s+Z\cos {\gamma }_s\end{array}\right.$$

(6)

Figure 8. The relationship between wind coordinate system, flight path coordinate system, and ground coordinate system.

Among them, $P$ represents the engine thrust, which forms an angle ${\phi }_P$ (The engine installation angle) with the body axis, ${\gamma }_s$ is the velocity roll angle, ${\psi }_s$ is the flight path deflection angle, $Y$ is the lift force, and $Z$ is the side force.

3.2. Aircraft Requirement Inference and Calculation

By analyzing the dynamic differential equations in the flight path coordinate system, this paper focuses on the dynamic differential equation along the x-axis of the flight path coordinate system. In this direction, if the drag of the aircraft within the studied flight path segment can be solved, the current thrust estimation value $P_i$ of the aircraft can be calculated:

$$P_i={\displaystyle \frac{m_i\frac{d{v}_i}{dt}+Q_i+m_{i}g\sin {\theta }_i}{\cos \left({\alpha }_i+{\phi }_P\right)\cos {\beta }_i}}$$

(7)

Record the aircraft thrust estimation value of the current flight path segment and the current aircraft state (relevant flight parameters included in the aircraft thrust estimation function):

$$P_i=f\left(H_i,{\rho }_i,v_i,{\alpha }_i,{\beta }_i,{\theta }_i\right)$$

(8)

Based on the flight parameters in the aforementioned function, the engine thrust estimation value can be derived, thereby establishing an aircraft thrust estimation model indexed by flight parameter data.

For a specified aircraft type, multiple calculations are performed using large-scale flight parameter data. The engine thrust estimation values under various flight states are recorded and plotted as the aircraft thrust demand curve for a single takeoff and landing. After each thrust estimation is completed, data indexing and classification are conducted sequentially according to parameters such as altitude $H_i$, atmospheric density ${\rho }_i$, velocity $v_i$, angle of attack ${\alpha }_i$, sideslip angle ${\beta }_i$, and flight path deflection angle ${\theta }_i$. Data correction analysis is performed on the thrust estimation values with existing indices to improve the accuracy of thrust estimation. New indices are established for the engine thrust estimation values under new states to supplement and improve the aircraft thrust model. The thrust estimation values within a single takeoff and landing are plotted into a thrust demand curve, providing theoretical and data support for the overall aircraft design. The flow chart of aircraft thrust estimation is shown in the following Figure 9.

Figure 9. Aircraft thrust estimation process.

Up to this point, the proposed method first achieves accurate classification of flight states through maneuver recognition, laying a foundation for subsequent high-precision flight parameter prediction. In the flight parameter data processing stage, relying on limited measured flight parameter data and leveraging the high-precision prediction model we constructed, it specifically predicts the key flight parameter data that “have not been actually measured but are essential for engine thrust estimation”—solving the core problem in traditional methods where “thrust calculation is interrupted due to missing data”. Subsequently, the complete predicted flight parameter results are substituted into the physical equation for engine thrust estimation, ultimately generating an accurate engine thrust load spectrum. This scheme not only provides a comprehensive solution for aircraft covering the entire process of “state recognition—data prediction—load generation” but also can offer key performance constraint basis and technical guidance for the design and development of aero-engines.

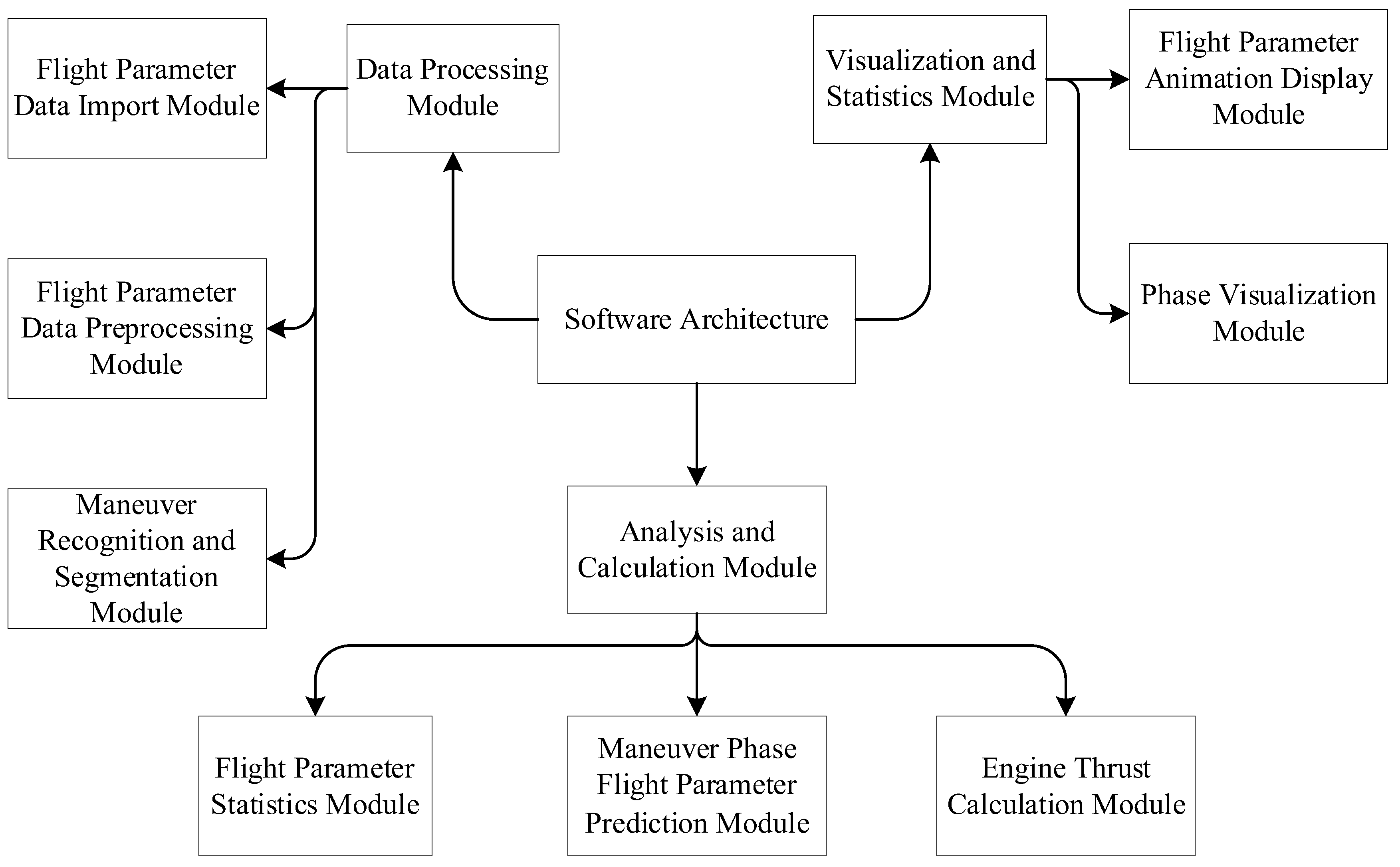
4. Aircraft Required Thrust Design Spectrum Prediction Software

In this paper, corresponding software system is developed in accordance with the basic principles of engineering software development [22]. Its overall design covers hardware configuration, software development platform, software architecture, and detailed design of independent functional modules. The interface language of this software is Chinese. In this paper, key modules and functions of the software will be labeled and explained in the interface screenshots.

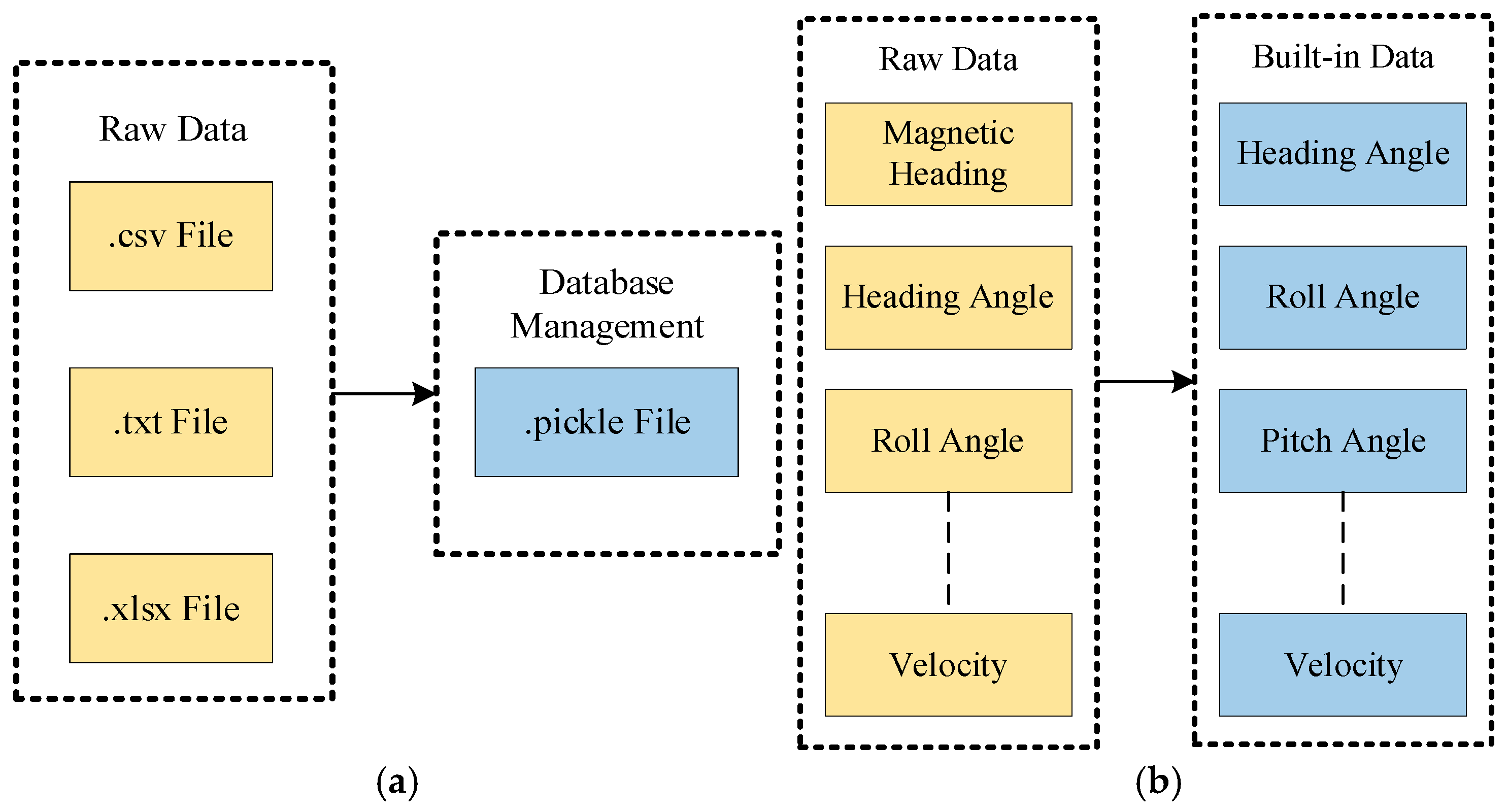
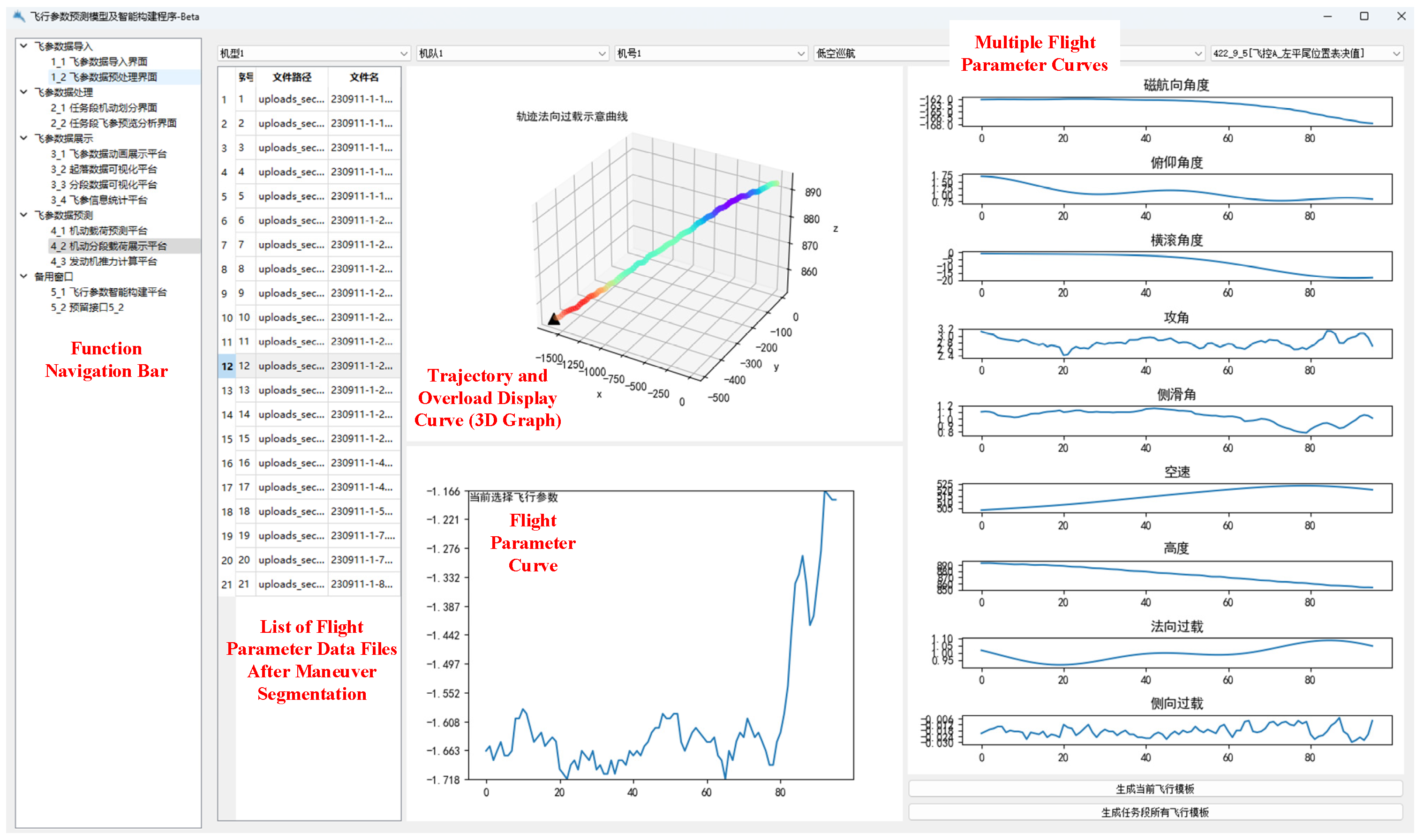
4.1. Flight Parameter Management

The aircraft thrust design spectrum prediction system constructed in this paper consists of two major components: (1) Database Management Server; (2) Software Development Tools.

MySQL 8.0 [23] is selected as the database management server. It features stability, reliability, multi-threading, and an efficient query engine, excelling in handling large datasets, high-concurrency requests, and complex queries. For software development, Python is adopted as the programming language, with PyQt5 as the GUI development tool. Python offers cross-platform compatibility and a rich standard library, while PyQt5 enables full Qt functionality access via Python, providing abundant widgets and supporting MVC architecture to enhance code organization and maintainability. Considering the popularity and efficiency of software usage, Windows 10 x64 is selected as the development and operating environment for this program. The database and software are integrated through the Python language. Details regarding the specific development environment and operating conditions of the software are presented in Table 3.

Table 3. Software development environment and operating requirements.

Name	Requirements
Operating System	Windows 10
Integrated Development Environment (IDE)	Visual Studio Code 1.97
Programming Language Environment	Python 3.9
Database Management System	MySQL 8.0
Desktop Application Development Tool	PyQt
Mainly Used Toolkits	PySide5, NumPy 1.25.2, Pandas 2.0.3
Acceptable File Types	csv/.xlsx/.txt
Memory Requirements	Minimum 1 GB of RAM and 500 MB of hard disk space

4.2. Software Database Management

In the face of diverse and complex flight parameter data, it is necessary to conduct comprehensive classification management of the original flight parameter data. By establishing a clear classification system, flight parameter data can be organized and retrieved more effectively, thereby accelerating the speed and accuracy of data processing.

Currently, supporting diverse imported file formats and ensuring good compatibility has become a mainstream trend. As shown in Figure 10a, formats such as .csv, .xlsx, and .txt are all converted into pickle files. Converting data to pickle files has notable advantages: as an efficient binary serialization format in Python, it effectively stores various data types, supports cross-platform compatibility, offers good compression, takes up minimal storage space, and is especially critical for large-scale flight parameter data. Additionally, since different aircraft types record different data, the same type of data may have different names (for example, the heading angle may be called magnetic heading in different datasets, and the roll angle may be referred to as bank angle). To enable quick identification and comparison of data from different aircraft types, the software has built-in some universal flight parameter names, as illustrated in Figure 10b. When inputting flight parameter data, the data to be saved is correlated with the software’s built-in universal flight parameters, thereby improving the overall consistency of the data.

Figure 10. Database management: (a) data format unification; (b) raw data and built-in data.

Through intelligent correspondence and mapping, the software ensures that the entered flight parameter data can follow consistent parameter naming standards when saved, providing a foundation for subsequent aircraft data management and analysis.

4.3. Software Functional Structure

To achieve efficient processing, analysis, and visualization of flight parameters, this system adopts a modular architecture design, and the specific data flow and functional relationship between modules can be intuitively illustrated in Figure 11.

Figure 11. The structure module diagram of the software system.

Users can select the folder containing the data to be analyzed, and the program will automatically perform maneuver segmentation calculations on all flight parameter data within that folder. The information obtained after maneuver segmentation is saved as a new CSV file. It contains partial maneuver segmentation information including key flight states, maneuver names, altitude variation, and start nodes. In trajectory visualization, representing a specific parameter’s magnitude via trajectory curve color intensity is an intuitive, effective method. It allows users to directly perceive the parameter’s variation trend on a single graph, facilitating a comprehensive understanding of the aircraft’s flight status. After the flight parameter data segmentation is completed, the segmented data can be visualized within the software. The 2D curve in Figure 12 displays the variation of the selected parameter over time, intuitively presenting the temporal trend. The 3D trajectory diagram uses RGB color changes to represent the parameter magnitude, vividly depicting the dynamic changes of the parameter during the flight process. Short-wavelength colors are used to represent low load factors, while long-wavelength colors are used to represent high load factors. This visualization method helps to accurately evaluate parameter changes under specific maneuvers.

Figure 12. Aircraft flight data visualization interface.

In the maneuver flight parameter prediction module, users can select different flight parameter files to build or update high-precision models. Meanwhile, they can check the loss changes during training through the loss curve and evaluate the model performance with model evaluation metrics including R², MAE, MSE, etc. Models with favorable evaluation metrics can be applied to subsequent prediction for datasets with incomplete flight parameters, thereby enabling engine thrust estimation.

Based on the calculation logic of engine required thrust, the Engine Thrust Calculation Platform establishes dynamic equations according to the aircraft’s current state, combined with the design parameters and initial state of different aircraft models. The interface of the thrust estimation platform is shown in Figure 13. Finally, it calculates the target value of engine thrust required to maintain the current flight state and visualizes the results.

Figure 13. Engine thrust calculation interface.

5. Conclusions

In this study, we first used flight parameters to reconstruct trajectories and employed vision to recognize aircraft maneuvering actions. The recognition results were then fed into an improved Transformer model to predict the parameters required for engine thrust estimation, which were subsequently substituted into the differential equation for aircraft thrust estimation. Ultimately, the prediction of the engine thrust spectrum was achieved. This framework can quantitatively determine the actual thrust output state of the engine in real time, providing early warnings for overload thrust damage risks caused by thrust abnormalities or serving as a basis for fault diagnosis and formulating maintenance plans. Through the proposed method and comparative verification, the following conclusions are drawn:

• In terms of flight trajectory and maneuver analysis, trajectory reconstruction was conducted using flight parameters, and aircraft maneuver recognition was accomplished via visual technology, enabling the identification and segmentation of typical flight maneuvers. Compared with traditional algorithms such as PLR-PIP (with an average recognition accuracy of 79.25%), DTW (72.97%), PCA (76.63%), and CTW (56.73%), the vision-based maneuver recognition method proposed in this study achieved an average accuracy of 81.06%.
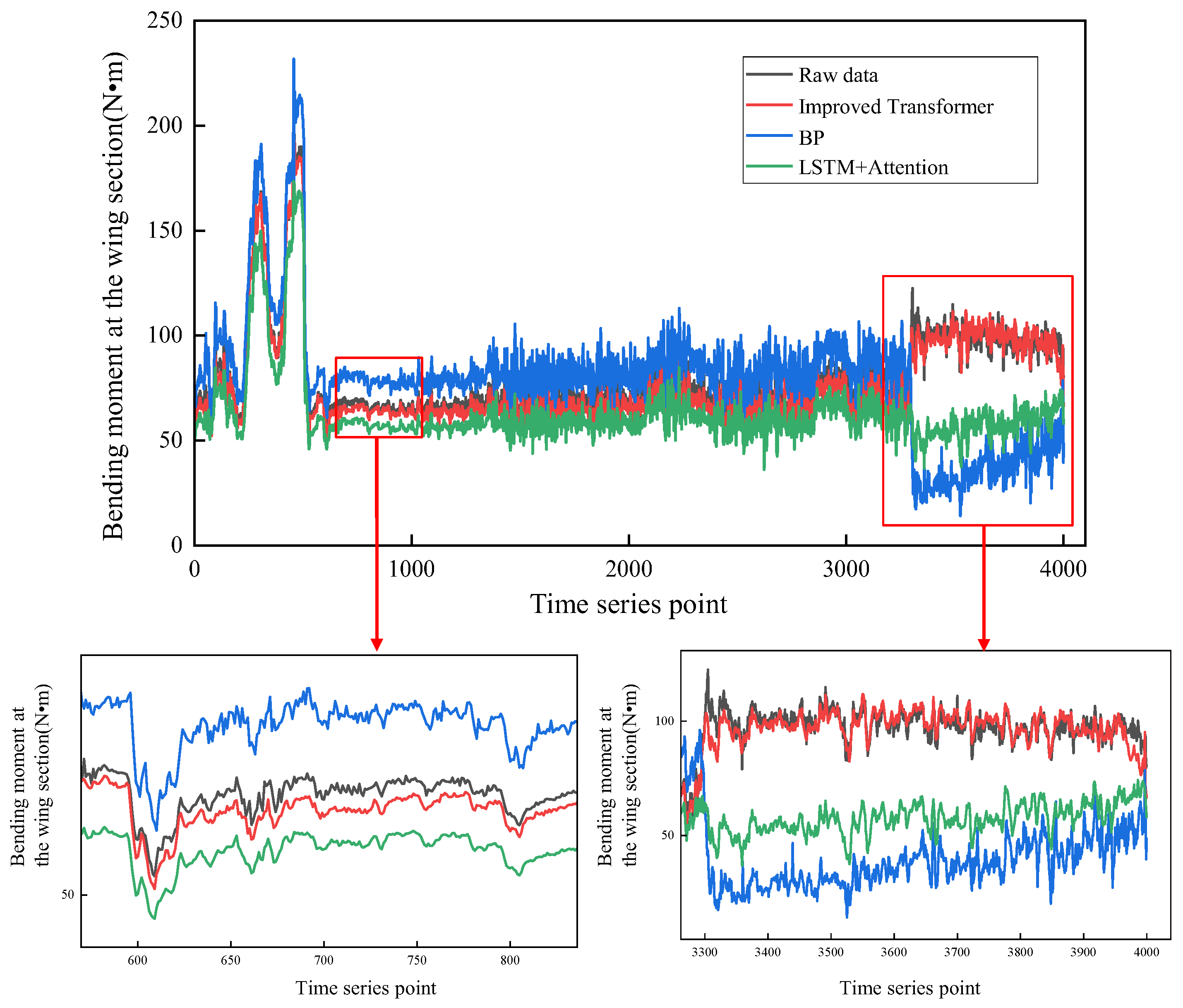
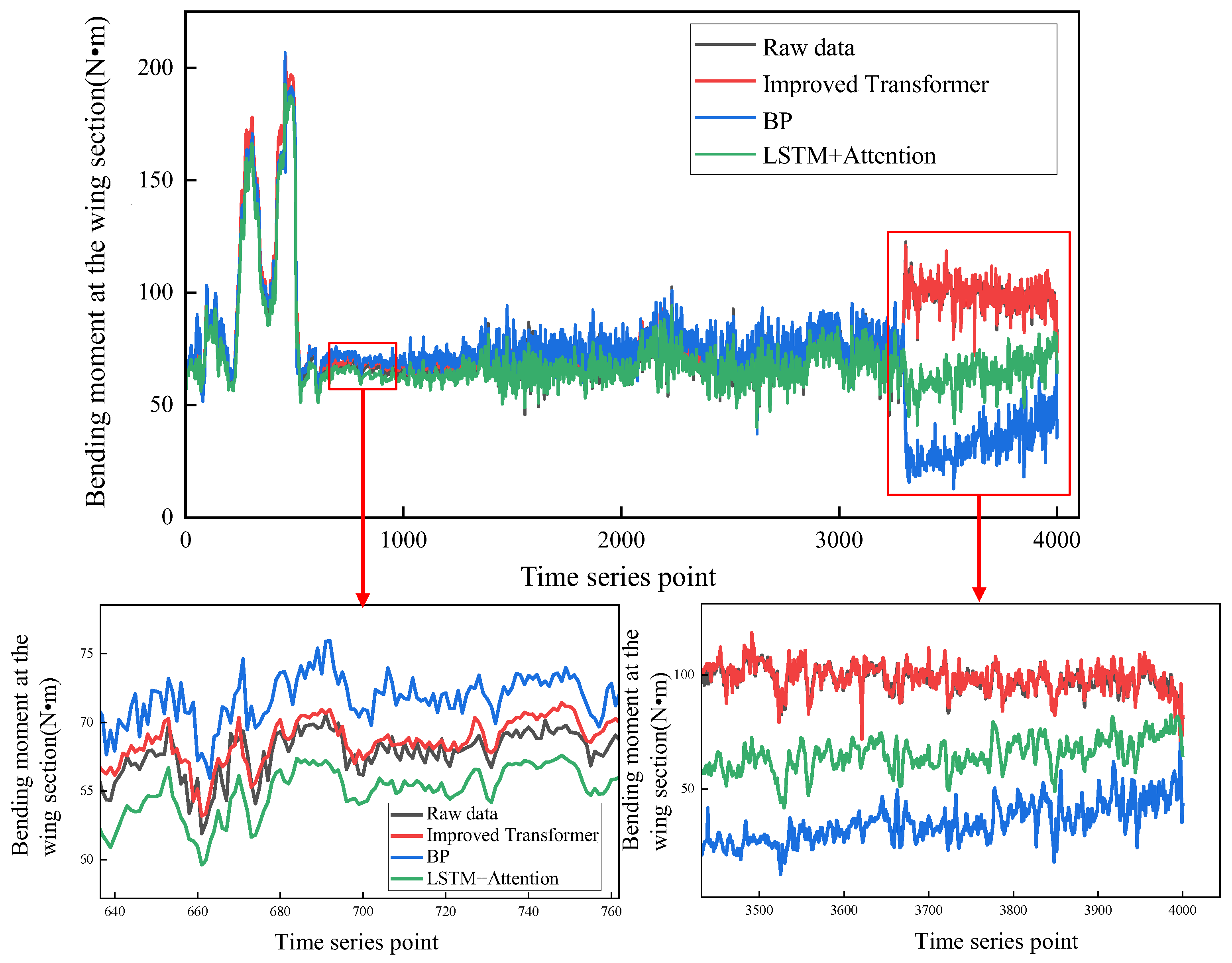
• By improving the attention mechanism, data input, and model architecture of the traditional Transformer model, the prediction accuracy of the model for flight parameter data has been enhanced. Flight parameter prediction results with low errors can effectively improve the accuracy of engine thrust estimation outcomes.
• A MySQL database and Python-based software system were developed for this framework, with functionalities for thrust/load prediction, trajectory analysis, and performance evaluation.

Currently, due to the limitation of the visual recognition system relying on a single front view, there are still a small number of unrecognized “gray segments” where specific maneuvers (level flight and horizontal turn) cannot be distinguished. In the future, by integrating a top-down view or adopting other methods, it is expected to realize the differentiation between level flight and horizontal turn maneuvers. Furthermore, the software system is limited by its Chinese-only interface. Future work will focus on multilingual adaptation. Once stabilized, the complete software code will be released on open-source platforms, providing a reference for related research, enabling technical exchange, and supporting further development.