Hybrid Frequency–Temporal Modeling with Transformer for Long-Term Satellite Telemetry Prediction
Abstract
1. Introduction
- We propose a new Transformer architecture with a frequency-aware hybrid encoder, eliminating attention from the encoder and enabling efficient modeling of both global periodicity and local transitions.
- We introduce a Dual-Path Mixer with a channel-wise fusion gate, allowing adaptive time–frequency fusion at the feature-channel granularity.
- We conduct extensive experiments on real satellite telemetry data, demonstrating significant improvements over baseline models in terms of forecasting accuracy, stability, and scalability, especially on long-term horizons.
2. Methods
2.1. Method Overview
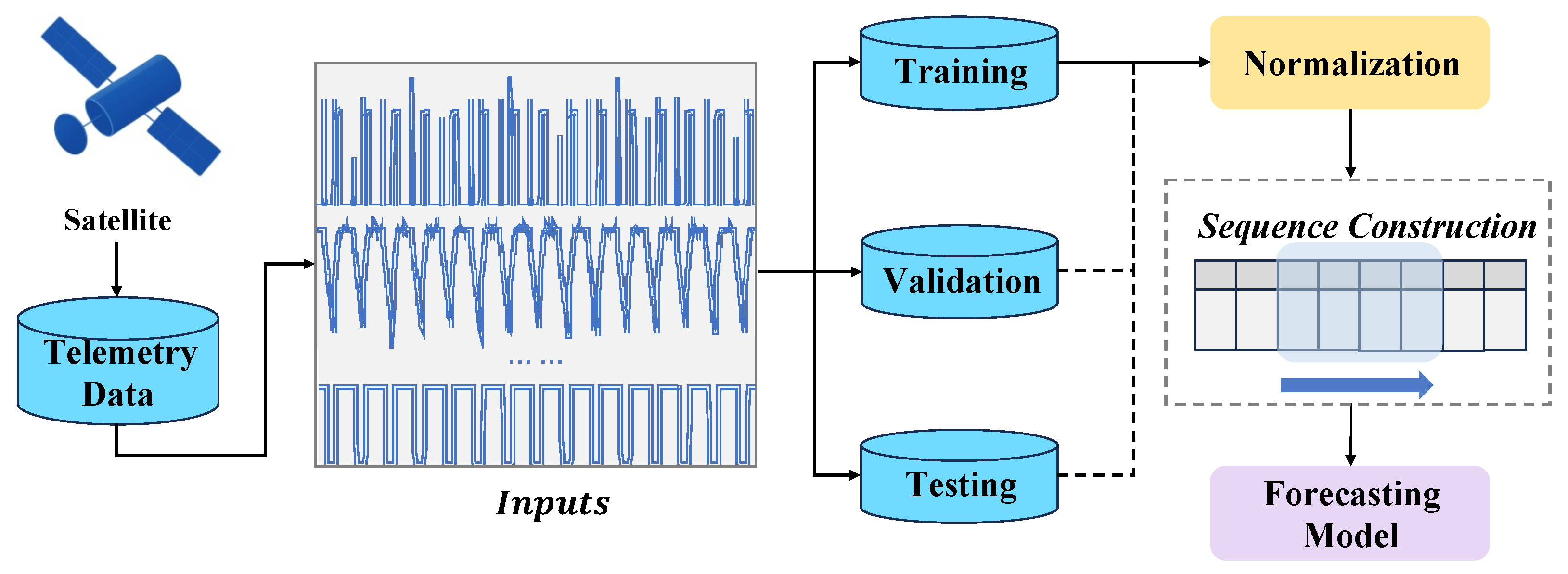
2.1.1. Data Processing
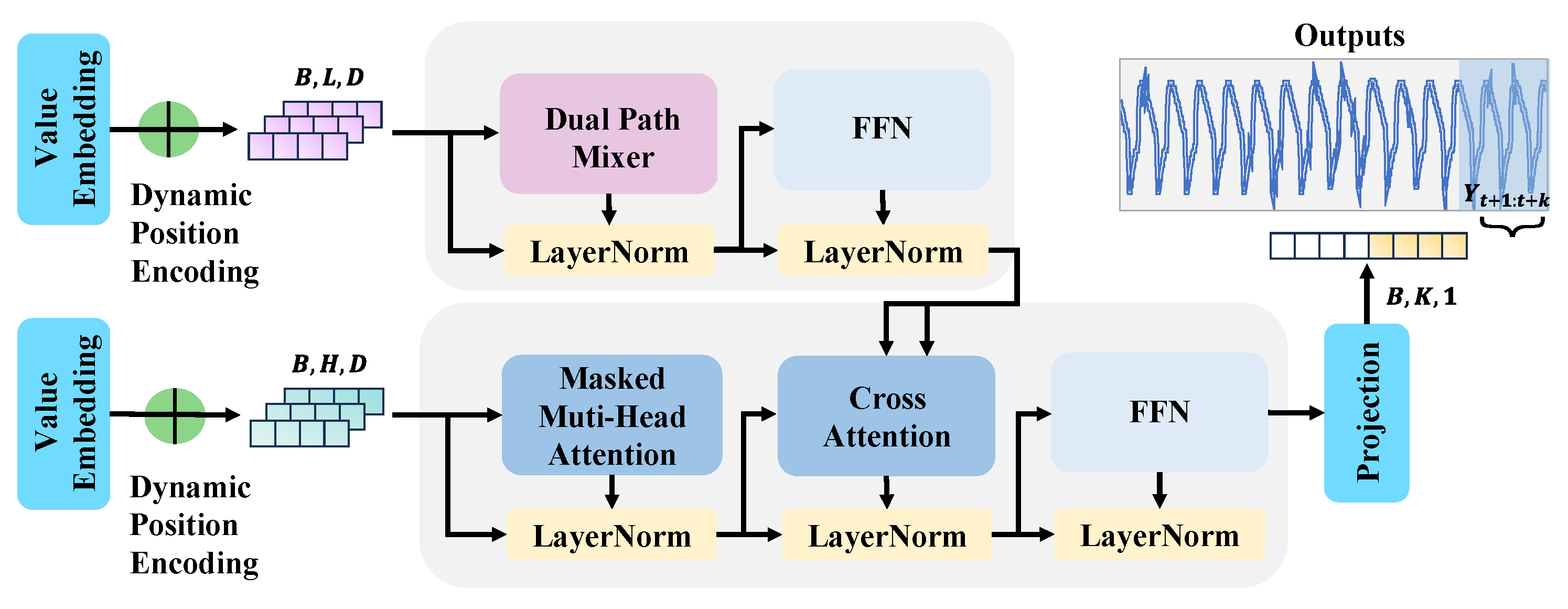
2.1.2. Model Architecture
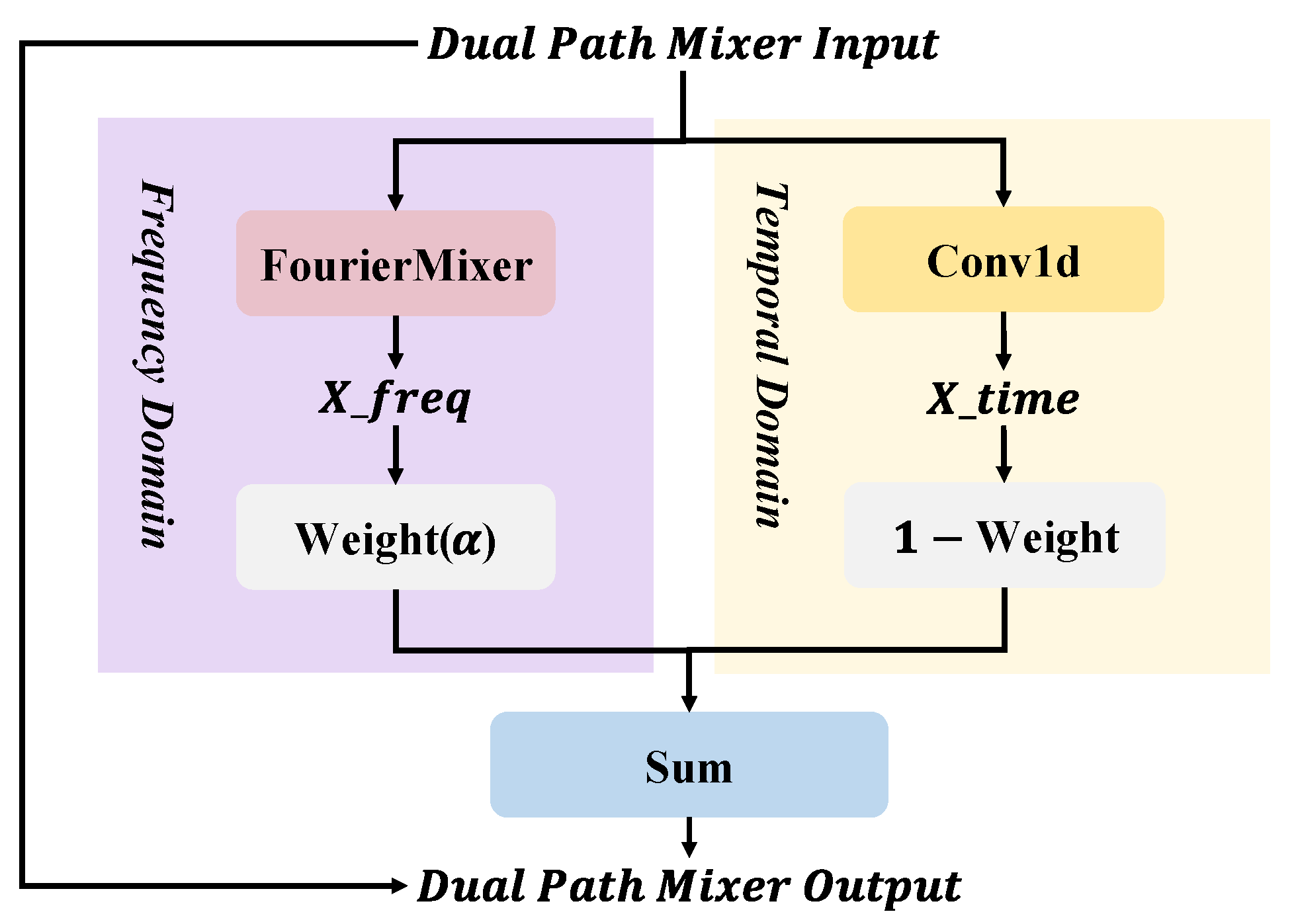
2.2. DPM-Based Encoder
2.2.1. Parallel Frequency and Temporal Paths
2.2.2. Channel-Wise Gating Fusion
2.2.3. Residual Enhancement
2.2.4. Advantages
2.3. Fourier Mixer Module
2.3.1. Fourier Transform Path
2.3.2. Temporal Convolution Path and Fusion
2.3.3. Complexity Analysis and Advantages
2.4. Decoder and Attention Mechanisms
2.5. Dynamic Positional Encoding
3. Results
3.1. Dataset Description
- Power system diagnostics: multiple bus voltages, battery voltages, and current readings;
- Component-specific telemetry: sensor voltages (e.g., star sensor, gyroscope);
- Thermal control indicators: internal temperatures from distributed sensors.
3.2. Experimental Settings
3.2.1. Model Configuration
3.2.2. Sequence Setup
3.2.3. Evaluation Metrics
3.2.4. Hardware and Implementation
3.3. Comparison with Baselines
3.3.1. Quantitative Evaluation of Forecasting Performance
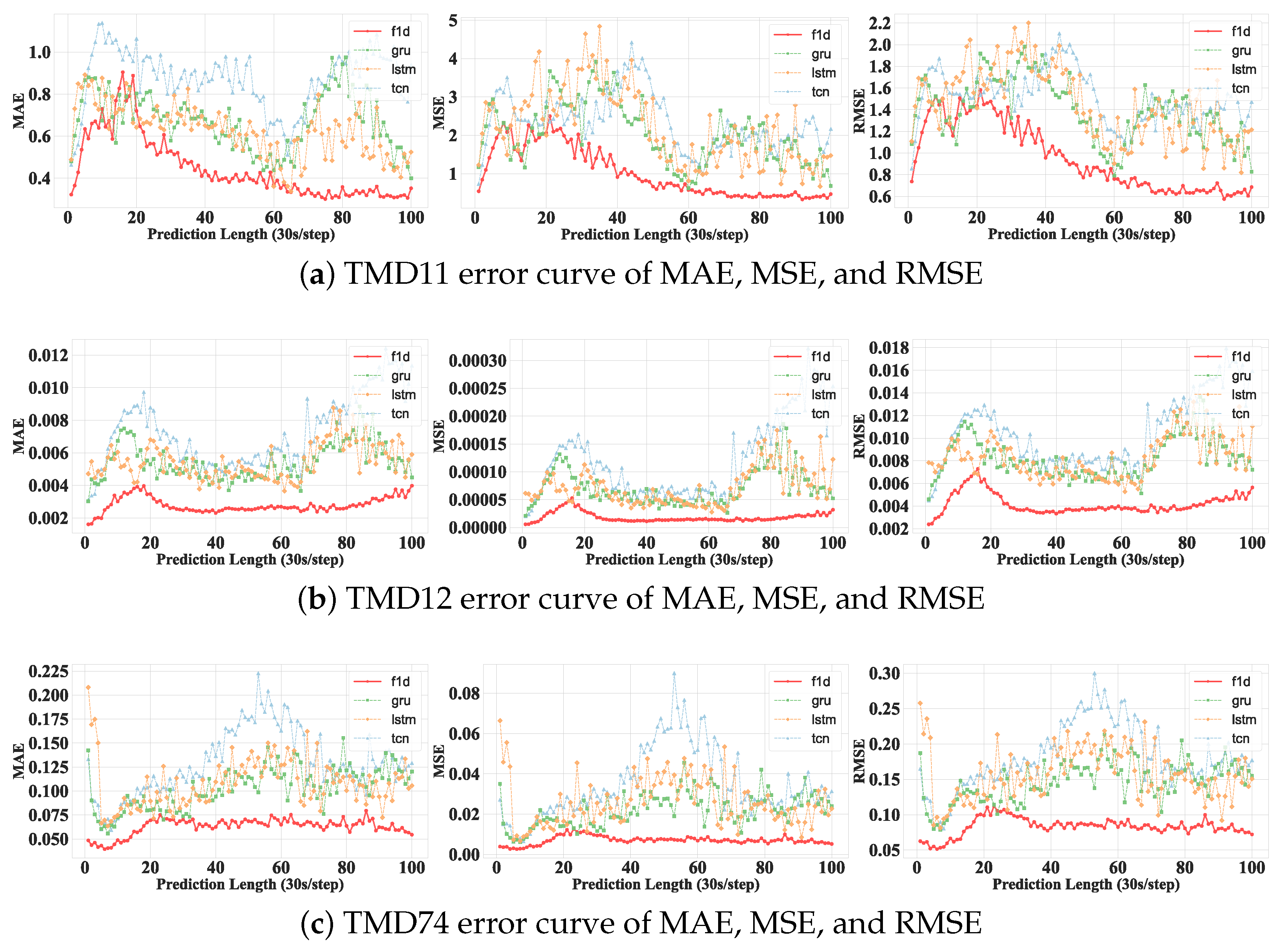
3.3.2. Error Curve Analysis
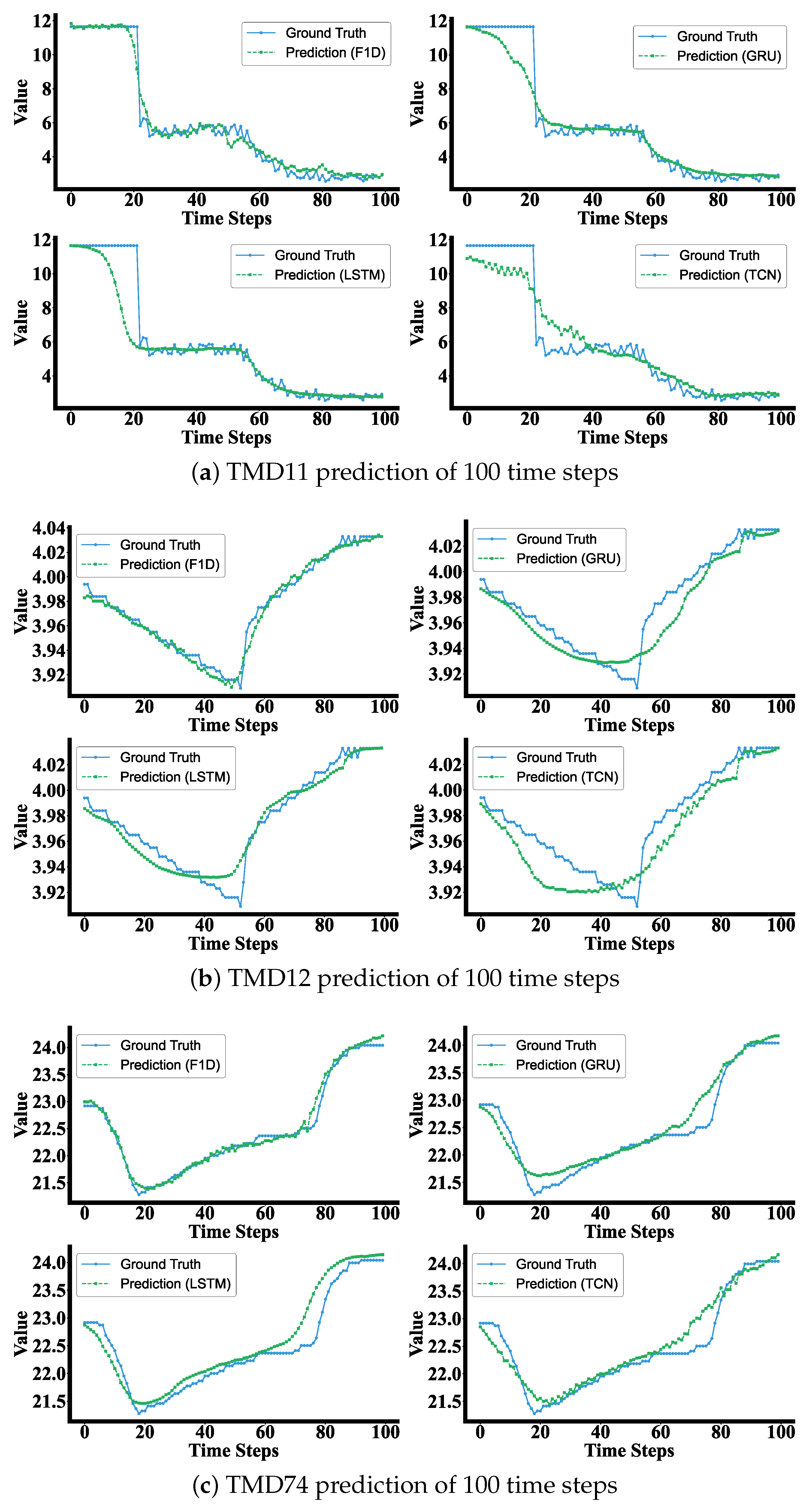
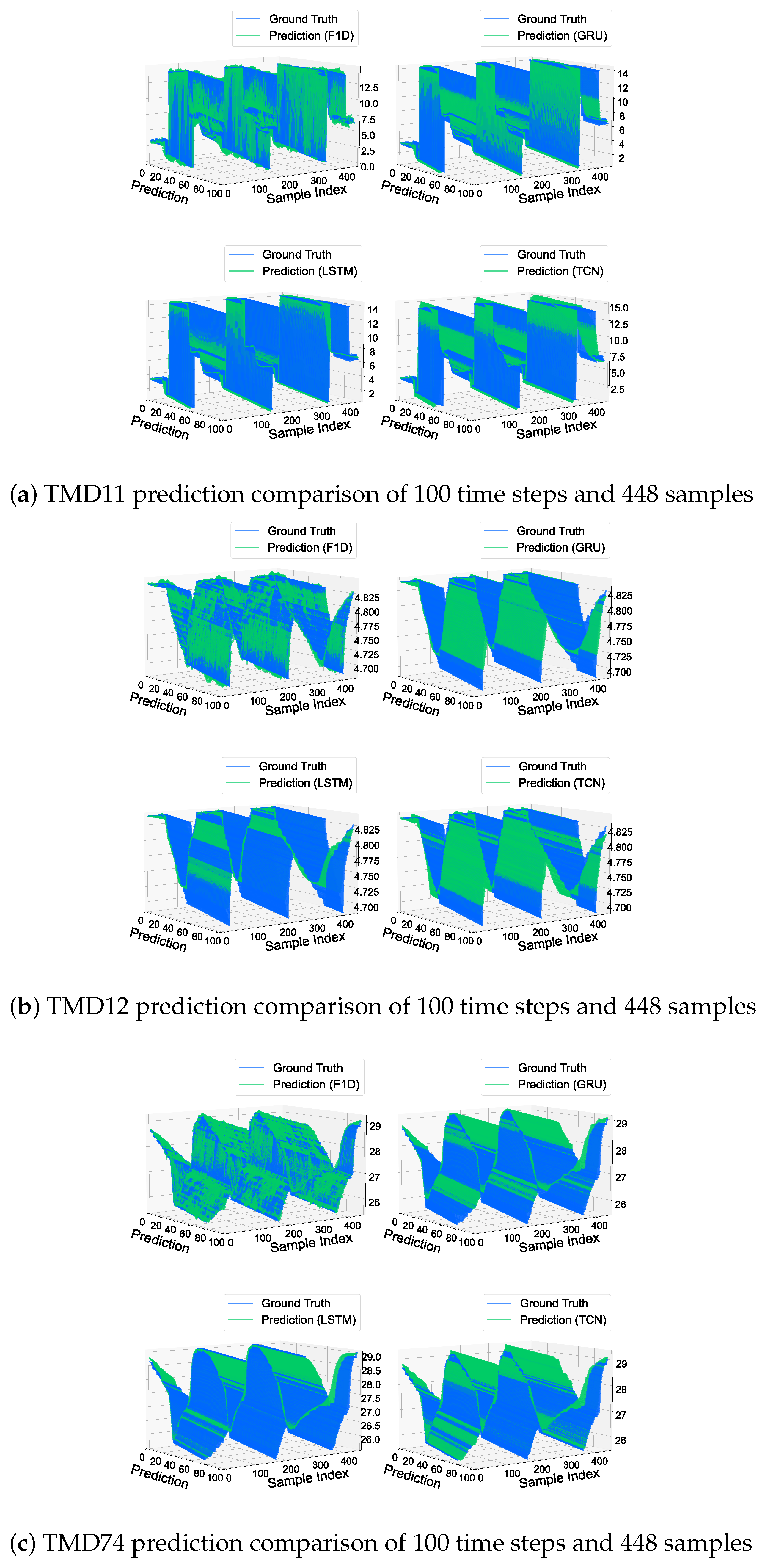
3.3.3. Samples Comparative Visualization
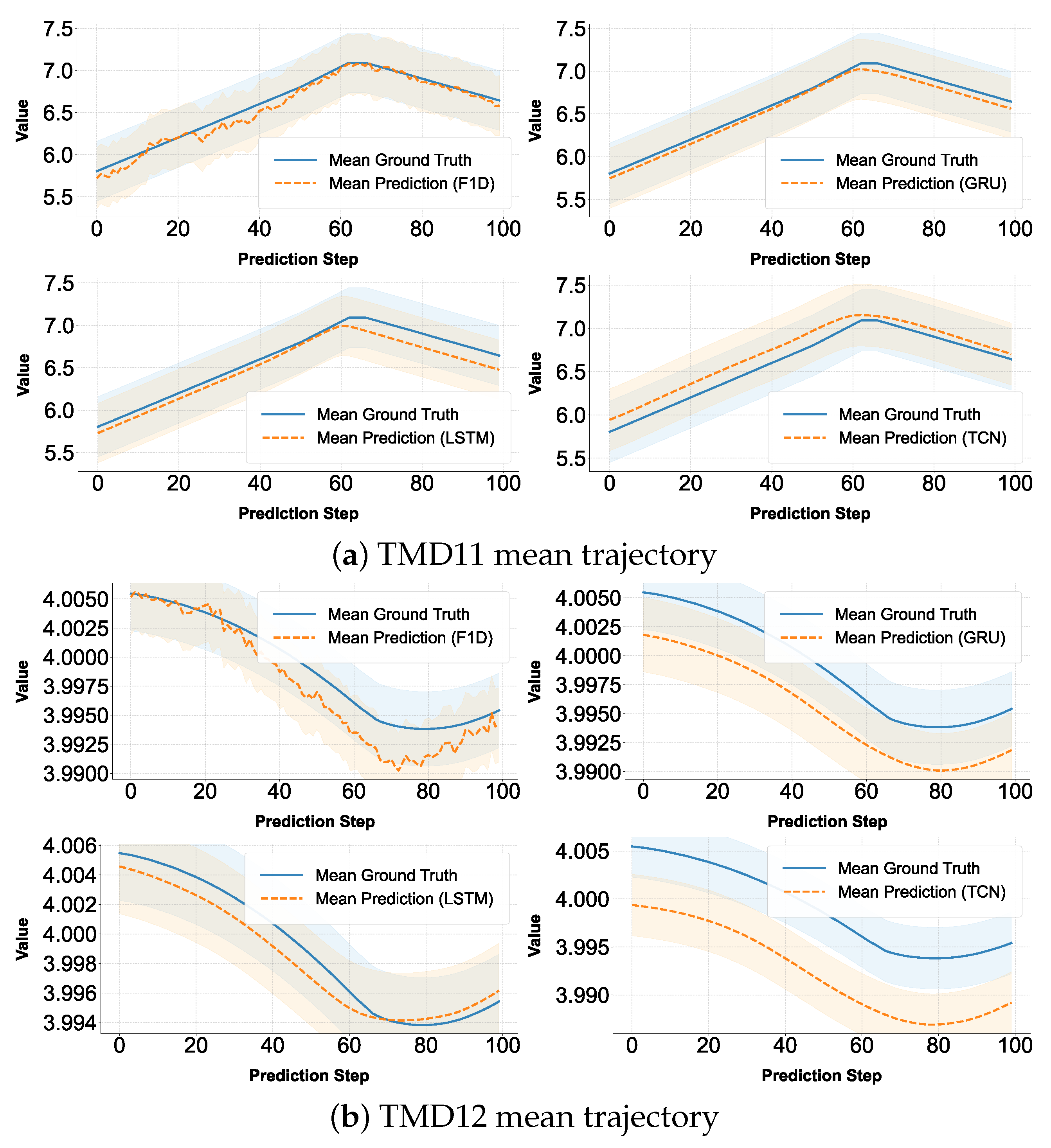
3.3.4. Mean Trajectory Analysis
3.3.5. Error Heatmap Analysis
3.4. Ablation Study
3.4.1. Quantitative Evaluation of Forecasting Performance
- F1D (Full Model): The complete architecture, which incorporates a 1D Fast Fourier Transform (FFT) for temporal frequency decomposition, followed by a Dual-Path Mixer that integrates both time-domain and frequency-domain processing streams. It also includes dynamic positional encoding for adaptive representation of temporal positions.
- F1: A variant that retains only the 1D FFT-based frequency encoder while removing the dual-path design. This isolates the effect of 1D frequency transformation alone.
- F2D: A version that replaces the 1D FFT with a 2D FFT encoder, capturing joint time–frequency correlations across both temporal and feature dimensions. The dual-path mixer is retained.
- F2: A variant that applies only the 2D FFT module without dual-path modeling or positional encoding, aiming to evaluate the standalone effectiveness of global spectral representations.
- Transformer: The standard Transformer encoder with self-attention and fixed sinusoidal positional encoding, but without any frequency-domain modeling. This serves as the baseline.
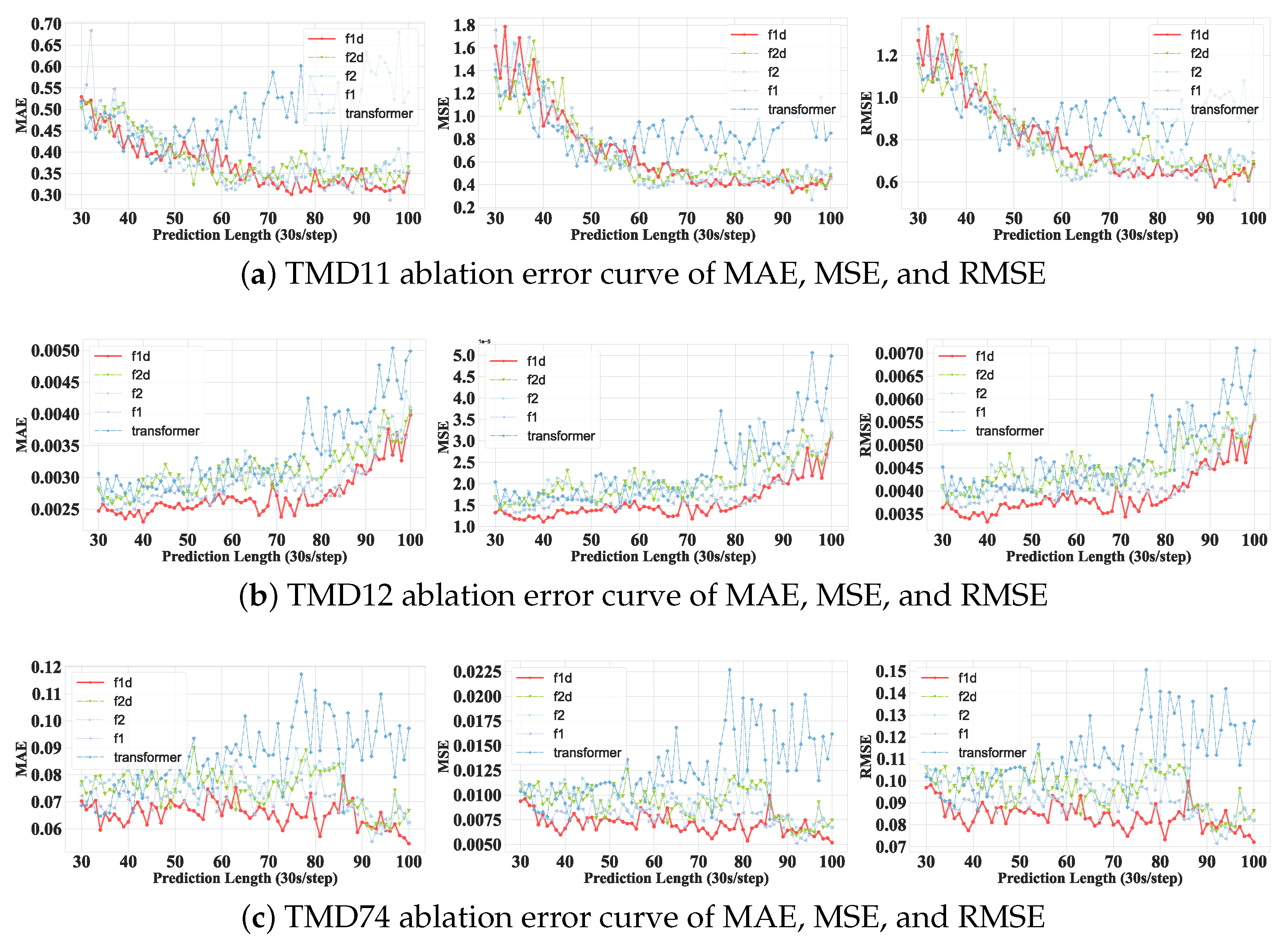
3.4.2. Error Curve Analysis
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wan, P.; Zhan, Y.; Jiang, W. Study on the Satellite Telemetry Data Classification Based on Self-Learning. IEEE Access 2019, 8, 2656–2669. [Google Scholar] [CrossRef]
- Lai, Y.; Zhu, Y.; Li, L.; Lan, Q.; Zuo, Y. STGLR: A Spacecraft Anomaly Detection Method Based on Spatio-Temporal Graph Learning. Sensors 2025, 25, 310. [Google Scholar] [CrossRef]
- Napoli, C.; De Magistris, G.; Ciancarelli, C.; Corallo, F.; Russo, F.; Nardi, D. Exploiting Wavelet Recurrent Neural Networks for Satellite Telemetry Data Modeling, Prediction and Control. Expert Syst. Appl. 2022, 206, 117831. [Google Scholar] [CrossRef]
- Fejjari, A.; Delavault, A.; Camilleri, R.; Valentino, G. A Review of Anomaly Detection in Spacecraft Telemetry Data. Appl. Sci. 2025, 15, 5653. [Google Scholar] [CrossRef]
- Neto, J.C.A.; Farias, C.M.; Araujo, L.S.; Filho, L.A.D.L. Time Series Forecasting for Multidimensional Telemetry Data Using GAN and BiLSTM in a Digital Twin. arXiv 2025, arXiv:2501.08464. [Google Scholar] [CrossRef]
- Lin, C.; Junyu, C. Using Long Short-Term Memory Neural Network for Satellite Orbit Prediction Based on Two-Line Element Data. IEEE Trans. Aerosp. Electron. Syst. 2025, 2025, 1–10. [Google Scholar] [CrossRef]
- Guo, Y.; Li, B.; Shi, X.; Zhao, Z.; Sun, J.; Wang, J. Enhancing Medium-Orbit Satellite Orbit Prediction: Application and Experimental Validation of the BiLSTM-TS Model. Electronics 2025, 14, 1734. [Google Scholar] [CrossRef]
- Kricheff, S.; Maxwell, E.; Plaks, C.; Simon, M. An Explainable Machine Learning Approach for Anomaly Detection in Satellite Telemetry Data. In Proceedings of the 2024 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2024; pp. 1–14. [Google Scholar] [CrossRef]
- Xu, Y.; Yao, W.; Zheng, X.; Chen, J. A Hybrid Monte Carlo Quantile EMD-LSTM Method for Satellite In-Orbit Temperature Prediction and Data Uncertainty Quantification. Expert Syst. Appl. 2024, 255, 124875. [Google Scholar] [CrossRef]
- Knap, V.; Bonvang, G.A.P.; Fagerlund, F.R.; Krøyer, S.; Nguyen, K.; Thorsager, M.; Tan, Z.-H. Extending Battery Life in CubeSats by Charging Current Control Utilizing a Long Short-Term Memory Network for Solar Power Predictions. J. Power Sources 2024, 618, 235164. [Google Scholar] [CrossRef]
- Peng, Y.; Jia, S.; Xie, L.; Shang, J. Accurate Satellite Operation Predictions Using Attention-BiLSTM Model with Telemetry Correlation. Aerospace 2024, 11, 398. [Google Scholar] [CrossRef]
- Xu, Z.; Cheng, Z.; Guo, B. A Multivariate Anomaly Detector for Satellite Telemetry Data Using Temporal Attention-Based LSTM Autoencoder. IEEE Trans. Instrum. Meas. 2023, 72, 3296125. [Google Scholar] [CrossRef]
- Wang, Y.; Gong, J.; Zhang, J.; Han, X. A Deep Learning Anomaly Detection Framework for Satellite Telemetry with Fake Anomalies. Int. J. Aerosp. Eng. 2022, 2022, 1–9. [Google Scholar] [CrossRef]
- Zeng, Z.; Jin, G.; Xu, C.; Chen, S.; Zhelong, Z.; Zhang, L. Satellite Telemetry Data Anomaly Detection Using Causal Network and Feature-Attention-Based LSTM. IEEE Trans. Instrum. Meas. 2022, 71, 1–21. [Google Scholar] [CrossRef]
- Yang, L.; Ma, Y.; Zeng, F.; Peng, X.; Liu, D. Improved Deep Learning Based Telemetry Data Anomaly Detection to Enhance Spacecraft Operation Reliability. Microelectron. Reliab. 2021, 126, 114311. [Google Scholar] [CrossRef]
- Tao, L.; Zhang, T.; Peng, D.; Hao, J.; Jia, Y.; Lu, C.; Ding, Y.; Ma, L. Long-Term Degradation Prediction and Assessment with Heteroscedasticity Telemetry Data Based on GRU-GARCH and MD Hybrid Method: An Application for Satellite. Aerosp. Sci. Technol. 2021, 115, 106826. [Google Scholar] [CrossRef]
- Gallon, R.; Schiemenz, F.; Menicucci, A.; Gill, E. Convolutional Neural Network Design and Evaluation for Real-Time Multivariate Time Series Fault Detection in Spacecraft Attitude Sensors. Adv. Space Res. 2025, 76, 2960–2976. [Google Scholar] [CrossRef]
- Tang, H.; Cheng, Y.; Lu, N.; Han, X. Anomaly Detection in Satellite Attitude Control System Based on GAT-TCN. In Proceedings of the 2024 Global Reliability and Prognostics and Health Management Conference (PHM-Beijing), Beijing, China, 17–20 June 2024; pp. 1–8. [Google Scholar] [CrossRef]
- Zeng, Z.; Lei, J.; Jin, G.; Xu, C.; Zhang, L. Detecting Anomalies in Satellite Telemetry Data Based on Causal Multivariate Temporal Convolutional Network. In Proceedings of the 2022 IEEE 5th International Conference on Big Data and Artificial Intelligence (BDAI), Fuzhou, China, 17–19 December 2022; pp. 63–74. [Google Scholar] [CrossRef]
- Noh, S.-H. Analysis of Gradient Vanishing of RNNs and Performance Comparison. Information 2021, 12, 442. [Google Scholar] [CrossRef]
- Tu, T. Bridging Short- and Long-Term Dependencies: A CNN-Transformer Hybrid for Financial Time Series Forecasting. arXiv 2025, arXiv:2504.19309. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence (AAAI 2021), Virtual, 2–9 February 2021; pp. 11106–11115. [Google Scholar] [CrossRef]
- Zhou, H.; Li, J.; Zhang, S.; Zhang, S.; Yan, M.; Xiong, H. Expanding the Prediction Capacity in Long Sequence Time-Series Forecasting. Artif. Intell. 2023, 318, 103886. [Google Scholar] [CrossRef]
- Su, L.; Zuo, X.; Li, R.; Wang, X.; Zhao, H.; Huang, B. A Systematic Review for Transformer-Based Long-Term Series Forecasting. Artif. Intell. Rev. 2025, 58, 80. [Google Scholar] [CrossRef]
- Qiao, Y.; Wang, T.; Lü, J.; Liu, K. TEMPO: Time-Evolving Multi-Period Observational Anomaly Detection Method for Space Probes. Chin. J. Aeronaut. 2025, 38, 103426. [Google Scholar] [CrossRef]
- Song, B.; Guo, B.; Hu, W.; Zhang, Z.; Zhang, N.; Bao, J.; Wang, J.; Xin, J. Transformer-Based Time-Series Forecasting for Telemetry Data in an Environmental Control and Life Support System of Spacecraft. Electronics 2025, 14, 459. [Google Scholar] [CrossRef]
- Park, K.-S.; Yun, S.-T. A Data-Driven Battery Degradation Estimation Method for Low-Earth-Orbit (LEO) Satellites. Appl. Sci. 2025, 15, 2182. [Google Scholar] [CrossRef]
- Gao, Y.; Qiu, S.; Liu, M.; Zhang, L.; Cao, X. Fault Warning of Satellite Momentum Wheels with a Lightweight Transformer Improved by FastDTW. IEEE/CAA J. Autom. Sin. 2025, 12, 539–549. [Google Scholar] [CrossRef]
- Zhao, H.; Qiu, S.; Yang, J.; Guo, J.; Liu, M.; Cao, X. Satellite Early Anomaly Detection Using an Advanced Transformer Architecture for Non-Stationary Telemetry Data. IEEE Trans. Consum. Electron. 2024, 70, 4213–4225. [Google Scholar] [CrossRef]
- Lan, Q.; Zhu, Y.; Lin, B.; Zuo, Y.; Lai, Y. Fault Prediction for Rotating Mechanism of Satellite Based on SSA and Improved Informer. Appl. Sci. 2024, 14, 9412. [Google Scholar] [CrossRef]
- Lee-Thorp, J.; Ainslie, J.; Eckstein, I.; Ontanon, S. FNet: Mixing Tokens with Fourier Transforms. arXiv 2022, arXiv:2105.03824. [Google Scholar] [CrossRef]




| Parameter | Type | Unit | Description |
|---|---|---|---|
| TMD01 | Integer | Counts | Total count of telemetry request commands (CAN bus) |
| TMD07 | Float | V | Voltage of the 42 V main power bus |
| TMD08 | Float | V | Voltage of the 30 V power bus |
| TMD09 | Float | V | Total voltage of the battery pack |
| TMD11 | Float | V | Voltage of BEA (specific module/component) |
| TMD12 | Float | V | Voltage of the 1st lithium-ion cell in the pack |
| TMD21 | Float | V | Voltage measured across the 1st shunt |
| TMD37 | Float | V | Output of charge voltage setpoint (charging module) |
| TMD52 | Float | A | Total load current of the 42 V bus |
| TMD54 | Float | A | Battery charging current |
| TMD55 | Float | A | Battery discharging current |
| TMD56 | Float | A | Output current of the S4R1 solar array |
| TMD59 | Float | A | Output current of BDR (module 1) |
| TMD69 | Float | °C | Internal temperature of the power controller |
| TMD74 | Float | °C | Temperature from the 5th battery-pack sensor |
| Category | Configuration |
|---|---|
| Model Architecture | |
| Encoder input dimension | 69 |
| Decoder input dimension | 69 |
| Output dimension | 1 |
| Model dimension () | 512 |
| Feedforward dimension () | 2048 |
| Encoder layers | 2 |
| Decoder layers | 1 |
| Attention heads | 4 |
| Attention type | Full (scaled dot-product) |
| Dropout rate | 0.03 |
| Activation function | GELU |
| Distillation | Disabled |
| Dynamic positional encoding | Enabled |
| Training Hyperparameters | |
| Batch size | 32 |
| Learning rate | |
| Loss function | MAE |
| Learning rate adjustment | Type-1 scheduler |
| Training epochs | 50 |
| Patience (early stopping) | 3 |
| Precision | FP32 (AMP disabled) |
| Optimizer workers | 0 (single-threaded dataloader) |
| Prediction Settings | |
| Prediction length () | 1–100 |
| Label length () | |
| Input length () | |
| Category | Configuration |
|---|---|
| Framework | PyTorch 2.1.0 |
| Language | Python 3.8.20 |
| GPU | NVIDIA GeForce RTX 4060 Laptop GPU, 8 GB VRAM |
| CUDA/Driver | CUDA 12.6/NVIDIA Driver 560.94 |
| CPU | Intel Core i7-13650HX, 14 Cores/20 Threads, 2.6 GHz |
| Memory | 24 GB DDR5 4800 MHz |
| Storage | 512 GB SSD |
| OS | Microsoft Windows 11 |
| Horizon | F1D (Proposed) | GRU | LSTM | TCN | ||||
|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 1 | 0.5589 | 0.3570 | 1.1089 | 0.4568 | 1.2602 | 0.4614 | 0.7010 | 0.4686 |
| 10 | 2.2619 | 0.7298 | 1.3630 | 0.6737 | 2.2500 | 0.8761 | 3.0238 | 1.1381 |
| 20 | 2.0615 | 0.7201 | 2.7341 | 0.8023 | 2.0022 | 0.6416 | 2.8871 | 1.0630 |
| 30 | 1.6141 | 0.5290 | 1.7556 | 0.5798 | 3.7219 | 0.6692 | 2.9599 | 0.9361 |
| 40 | 0.9151 | 0.4358 | 3.3284 | 0.6810 | 2.7973 | 0.6502 | 3.6741 | 0.9034 |
| 50 | 0.6674 | 0.3873 | 1.6462 | 0.6783 | 2.9623 | 0.6083 | 3.0700 | 0.8588 |
| 60 | 0.5788 | 0.3686 | 0.6247 | 0.4371 | 0.8159 | 0.3611 | 1.4289 | 0.6582 |
| 70 | 0.5105 | 0.3476 | 1.9781 | 0.6461 | 1.7336 | 0.6218 | 1.9826 | 0.7837 |
| 80 | 0.4882 | 0.3583 | 2.2666 | 0.9422 | 1.0332 | 0.5741 | 1.8660 | 0.9531 |
| 90 | 0.5228 | 0.3605 | 1.8598 | 0.7721 | 2.7893 | 0.7358 | 2.1879 | 1.0832 |
| 100 | 0.4706 | 0.3520 | 0.6860 | 0.3994 | 1.4760 | 0.5245 | 2.1660 | 0.9379 |
| Horizon | F1D (Proposed) | GRU | LSTM | TCN | ||||
|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 1 | 4.3 | 0.0014 | 1.6 | 0.0024 | 1.3 | 0.0023 | 1.7 | 0.0029 |
| 10 | 2.6 | 0.0030 | 0.0001 | 0.0067 | 9.7 | 0.0060 | 0.0001 | 0.0076 |
| 20 | 2.9 | 0.0034 | 6.8 | 0.0053 | 0.0001 | 0.0068 | 0.0001 | 0.0087 |
| 30 | 1.3 | 0.0025 | 6.2 | 0.0048 | 6.1 | 0.0054 | 7.1 | 0.0056 |
| 40 | 1.1 | 0.0023 | 6.9 | 0.0053 | 5.5 | 0.0049 | 5.6 | 0.0050 |
| 50 | 1.4 | 0.0025 | 4.8 | 0.0047 | 5.1 | 0.0050 | 6.3 | 0.0054 |
| 60 | 1.4 | 0.0027 | 4.1 | 0.0047 | 4.4 | 0.0047 | 6.4 | 0.0062 |
| 70 | 1.5 | 0.0027 | 7.0 | 0.0057 | 5.7 | 0.0048 | 8.0 | 0.0067 |
| 80 | 1.5 | 0.0026 | 0.0001 | 0.0069 | 0.0001 | 0.0071 | 0.0002 | 0.0084 |
| 90 | 2.0 | 0.0031 | 0.0001 | 0.0072 | 0.0001 | 0.0066 | 0.0003 | 0.0113 |
| 100 | 3.2 | 0.0040 | 5.2 | 0.0045 | 0.0001 | 0.0059 | 0.0003 | 0.0114 |
| Horizon | F1D (Proposed) | GRU | LSTM | TCN | ||||
|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 1 | 0.0035 | 0.0473 | 0.0075 | 0.0666 | 0.0058 | 0.0580 | 0.0070 | 0.0638 |
| 10 | 0.0044 | 0.0488 | 0.0128 | 0.0725 | 0.0114 | 0.0748 | 0.0101 | 0.0711 |
| 20 | 0.0097 | 0.0695 | 0.0141 | 0.0802 | 0.0165 | 0.0897 | 0.0233 | 0.1055 |
| 30 | 0.0094 | 0.0703 | 0.0116 | 0.0737 | 0.0255 | 0.0919 | 0.0289 | 0.1151 |
| 40 | 0.0067 | 0.0626 | 0.0203 | 0.0944 | 0.0273 | 0.1096 | 0.0379 | 0.1364 |
| 50 | 0.0075 | 0.0686 | 0.0276 | 0.1147 | 0.0411 | 0.1331 | 0.0610 | 0.1744 |
| 60 | 0.0068 | 0.0649 | 0.0247 | 0.1137 | 0.0344 | 0.1270 | 0.0518 | 0.1629 |
| 70 | 0.0064 | 0.0638 | 0.0208 | 0.1055 | 0.0201 | 0.1001 | 0.0319 | 0.1270 |
| 80 | 0.0065 | 0.0638 | 0.0266 | 0.1216 | 0.0223 | 0.1004 | 0.0260 | 0.1156 |
| 90 | 0.0064 | 0.0624 | 0.0296 | 0.1222 | 0.0161 | 0.0941 | 0.0247 | 0.1222 |
| 100 | 0.0052 | 0.0545 | 0.0240 | 0.1204 | 0.0227 | 0.1056 | 0.0312 | 0.1290 |
| Horizon | F1D (Proposed) | F1 | F2D | F2 | Transformer | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 1 | 0.5589 | 0.3570 | 0.5415 | 0.3281 | 0.5497 | 0.3346 | 0.5346 | 0.3122 | 0.5574 | 0.3398 |
| 10 | 2.2619 | 0.7298 | 2.1974 | 0.6348 | 1.7490 | 0.7386 | 1.8149 | 0.6788 | 2.0300 | 0.6027 |
| 20 | 2.0615 | 0.7201 | 2.1138 | 0.6116 | 2.0954 | 0.6403 | 1.9407 | 0.6642 | 2.0033 | 0.7147 |
| 30 | 1.6141 | 0.5290 | 1.7554 | 0.5172 | 1.3371 | 0.5027 | 1.4567 | 0.5125 | 1.4070 | 0.5198 |
| 40 | 0.9151 | 0.4358 | 1.2588 | 0.4503 | 1.2251 | 0.4795 | 1.1874 | 0.4662 | 1.3014 | 0.4345 |
| 50 | 0.6674 | 0.3873 | 0.8931 | 0.3982 | 0.7897 | 0.3918 | 0.6690 | 0.4207 | 0.7678 | 0.4587 |
| 60 | 0.5788 | 0.3686 | 0.4862 | 0.3295 | 0.4712 | 0.3495 | 0.3980 | 0.3471 | 0.9499 | 0.4716 |
| 70 | 0.5105 | 0.3476 | 0.4136 | 0.3236 | 0.5245 | 0.3410 | 0.5079 | 0.3498 | 0.9739 | 0.5393 |
| 80 | 0.4882 | 0.3583 | 0.4829 | 0.3611 | 0.4901 | 0.3302 | 0.6304 | 0.3984 | 0.8272 | 0.5436 |
| 90 | 0.5228 | 0.3605 | 0.4215 | 0.3197 | 0.4302 | 0.3340 | 0.4624 | 0.3452 | 0.9519 | 0.5456 |
| 100 | 0.4706 | 0.3520 | 0.4536 | 0.3551 | 0.4848 | 0.3648 | 0.5451 | 0.3968 | 0.8516 | 0.5395 |
| Horizon | F1D (Proposed) | F1 | F2D | F2 | Transformer | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 1 | 4.3 | 0.0014 | 6.1 | 0.0017 | 5.5 | 0.0016 | 5.3 | 0.0015 | 5.3 | 0.0015 |
| 10 | 2.6 | 0.0030 | 2.9 | 0.0033 | 2.7 | 0.0034 | 3.1 | 0.0037 | 2.7 | 0.0031 |
| 20 | 2.9 | 0.0034 | 2.9 | 0.0034 | 3.4 | 0.0038 | 2.4 | 0.0034 | 2.3 | 0.0032 |
| 30 | 1.3 | 0.0025 | 1.6 | 0.0028 | 1.6 | 0.0028 | 1.7 | 0.0029 | 2.0 | 0.0031 |
| 40 | 1.1 | 0.0023 | 1.4 | 0.0025 | 1.8 | 0.0029 | 1.6 | 0.0027 | 1.8 | 0.0029 |
| 50 | 1.4 | 0.0025 | 1.6 | 0.0028 | 1.6 | 0.0027 | 1.7 | 0.0028 | 1.6 | 0.0026 |
| 60 | 1.4 | 0.0027 | 1.7 | 0.0029 | 1.9 | 0.0030 | 2.0 | 0.0030 | 1.8 | 0.0030 |
| 70 | 1.5 | 0.0027 | 1.5 | 0.0027 | 1.9 | 0.0032 | 2.0 | 0.0033 | 1.7 | 0.0029 |
| 80 | 1.5 | 0.0026 | 1.6 | 0.0027 | 1.9 | 0.0030 | 1.9 | 0.0029 | 2.4 | 0.0034 |
| 90 | 2.0 | 0.0031 | 2.0 | 0.0030 | 2.3 | 0.0033 | 2.4 | 0.0034 | 2.7 | 0.0037 |
| 100 | 3.2 | 0.0040 | 3.1 | 0.0040 | 3.1 | 0.0040 | 3.2 | 0.0041 | 4.9 | 0.0050 |
| Horizon | F1D (Proposed) | F1 | F2D | F2 | Transformer | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | MSE | MAE | |
| 1 | 0.0035 | 0.0473 | 0.0027 | 0.0410 | 0.0032 | 0.0450 | 0.0027 | 0.0425 | 0.0025 | 0.0398 |
| 10 | 0.0044 | 0.0488 | 0.0040 | 0.0465 | 0.0041 | 0.0471 | 0.0050 | 0.0529 | 0.0053 | 0.0527 |
| 20 | 0.0097 | 0.0695 | 0.0093 | 0.0654 | 0.0095 | 0.0674 | 0.0089 | 0.0715 | 0.0169 | 0.0802 |
| 30 | 0.0094 | 0.0703 | 0.0107 | 0.0723 | 0.0113 | 0.0774 | 0.0113 | 0.0762 | 0.0104 | 0.0687 |
| 40 | 0.0067 | 0.0626 | 0.0082 | 0.0708 | 0.0111 | 0.0833 | 0.0116 | 0.0818 | 0.0092 | 0.0436 |
| 50 | 0.0075 | 0.0686 | 0.0081 | 0.0736 | 0.0088 | 0.0744 | 0.0094 | 0.0780 | 0.0113 | 0.0850 |
| 60 | 0.0068 | 0.0649 | 0.0073 | 0.0690 | 0.0103 | 0.0809 | 0.0090 | 0.0770 | 0.0107 | 0.0807 |
| 70 | 0.0064 | 0.0638 | 0.0088 | 0.0733 | 0.0091 | 0.0721 | 0.0101 | 0.0778 | 0.0116 | 0.0872 |
| 80 | 0.0065 | 0.0638 | 0.0082 | 0.0731 | 0.0108 | 0.0824 | 0.0116 | 0.0833 | 0.0198 | 0.1113 |
| 90 | 0.0064 | 0.0624 | 0.0080 | 0.0710 | 0.0078 | 0.0704 | 0.0078 | 0.0696 | 0.0124 | 0.0855 |
| 100 | 0.0052 | 0.0545 | 0.0067 | 0.0623 | 0.0075 | 0.0668 | 0.0067 | 0.0623 | 0.0162 | 0.0973 |
| Model | Count |
|---|---|
| F1D (Proposed) | 37 |
| F1 | 20 |
| F2D | 5 |
| F2 | 4 |
| Transformer | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Yang, J.; Yin, Z.; Wu, Y.; Zhong, L.; Jia, Q.; Chen, Z. Hybrid Frequency–Temporal Modeling with Transformer for Long-Term Satellite Telemetry Prediction. Appl. Sci. 2025, 15, 11585. https://doi.org/10.3390/app152111585
Chen Z, Yang J, Yin Z, Wu Y, Zhong L, Jia Q, Chen Z. Hybrid Frequency–Temporal Modeling with Transformer for Long-Term Satellite Telemetry Prediction. Applied Sciences. 2025; 15(21):11585. https://doi.org/10.3390/app152111585
Chicago/Turabian StyleChen, Zhuqing, Jiasen Yang, Zhongkang Yin, Yijia Wu, Lei Zhong, Qingyu Jia, and Zhimin Chen. 2025. "Hybrid Frequency–Temporal Modeling with Transformer for Long-Term Satellite Telemetry Prediction" Applied Sciences 15, no. 21: 11585. https://doi.org/10.3390/app152111585
APA StyleChen, Z., Yang, J., Yin, Z., Wu, Y., Zhong, L., Jia, Q., & Chen, Z. (2025). Hybrid Frequency–Temporal Modeling with Transformer for Long-Term Satellite Telemetry Prediction. Applied Sciences, 15(21), 11585. https://doi.org/10.3390/app152111585






