Iterative Forecasting of Short Time Series
Abstract
1. Introduction
2. Materials and Methods
2.1. Generalized Moments Method (GMM)
2.2. Stochastic Differential Equation
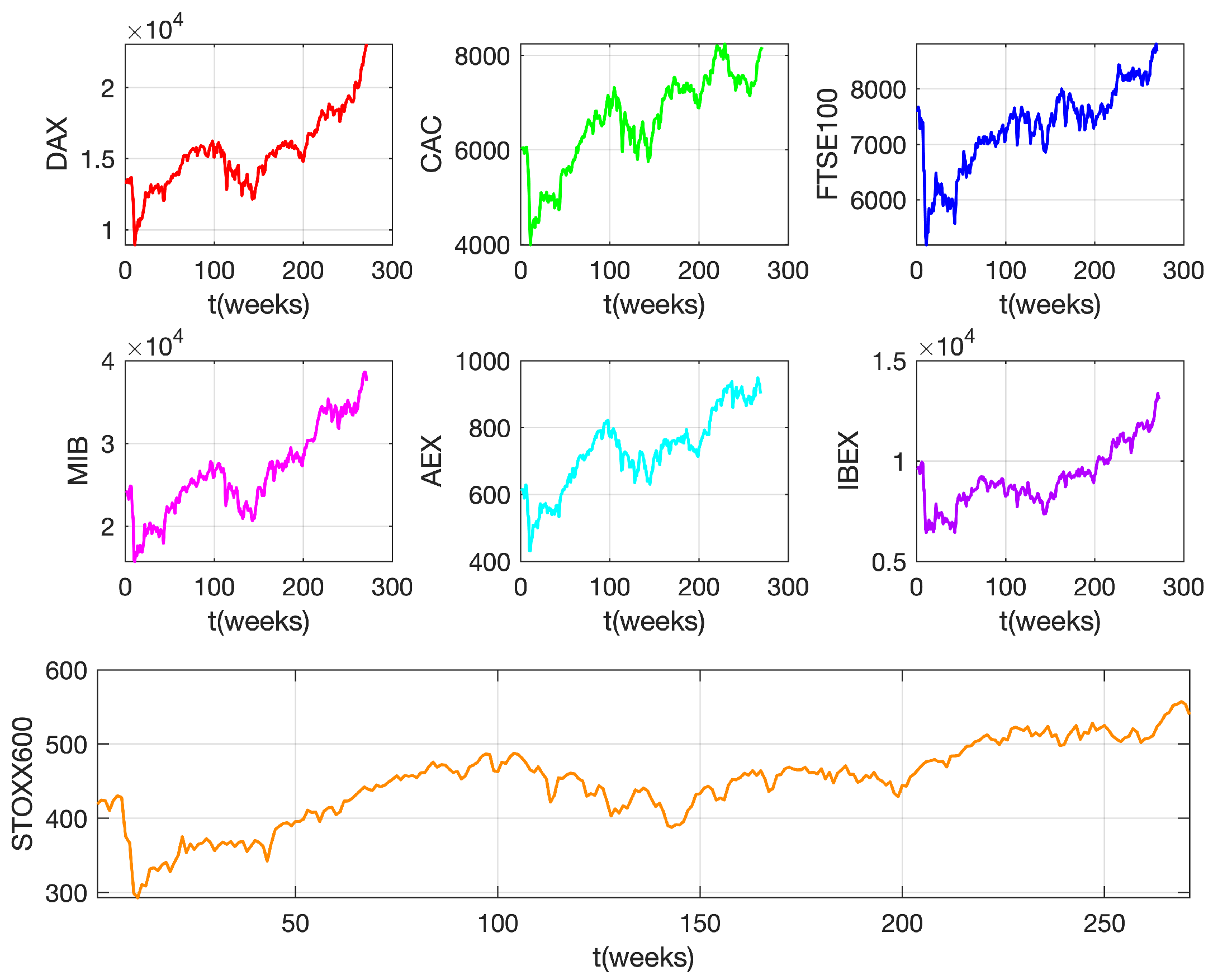
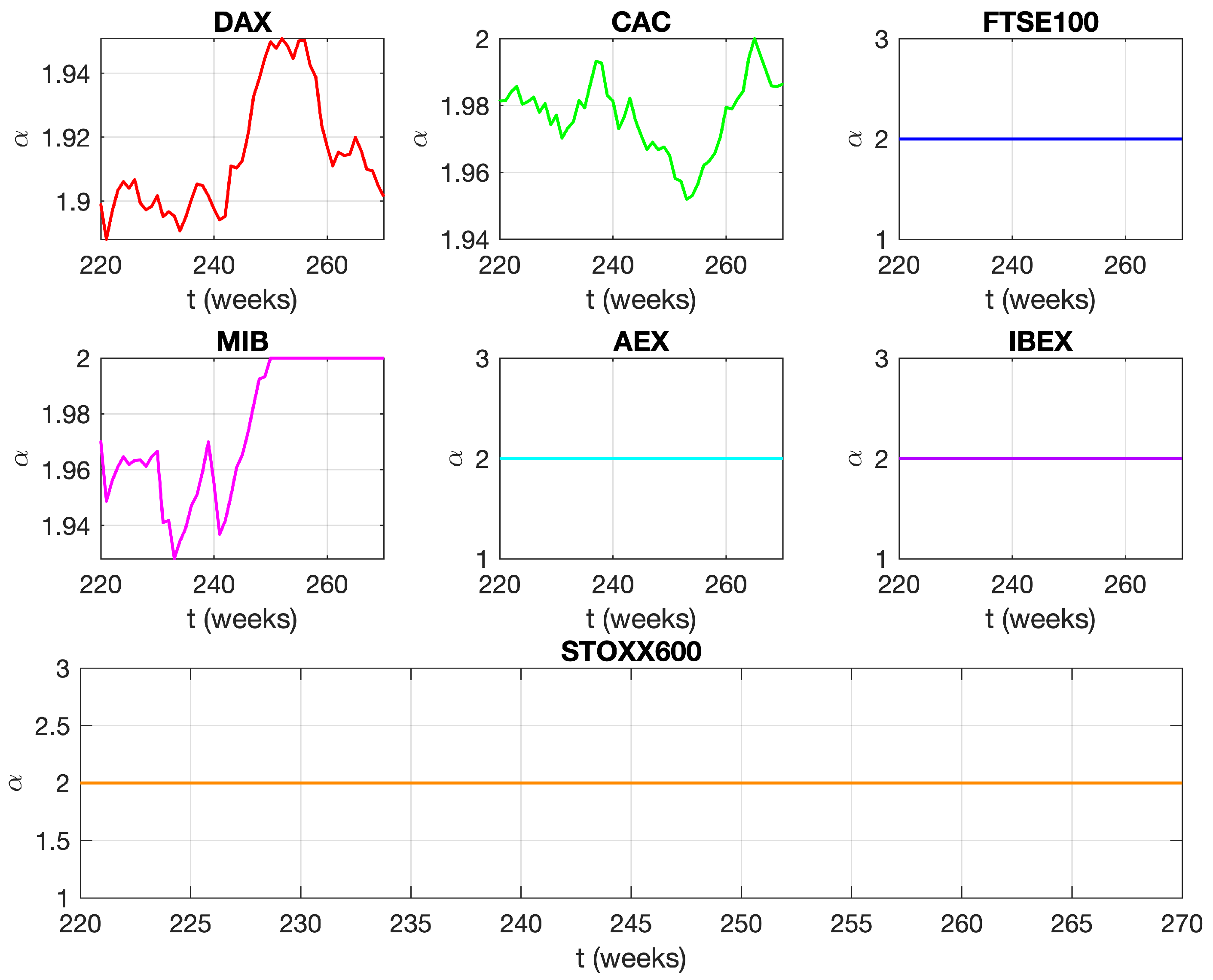
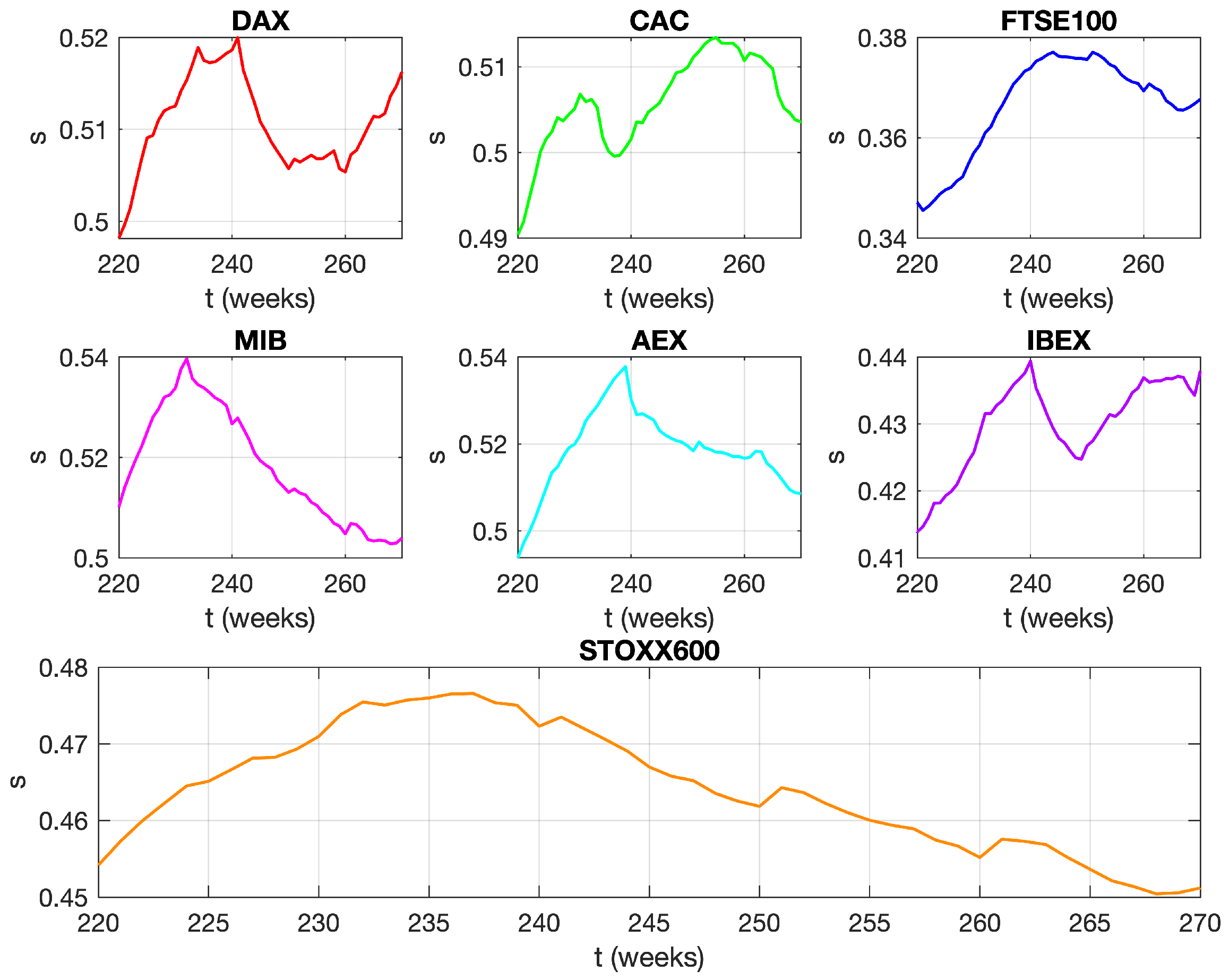
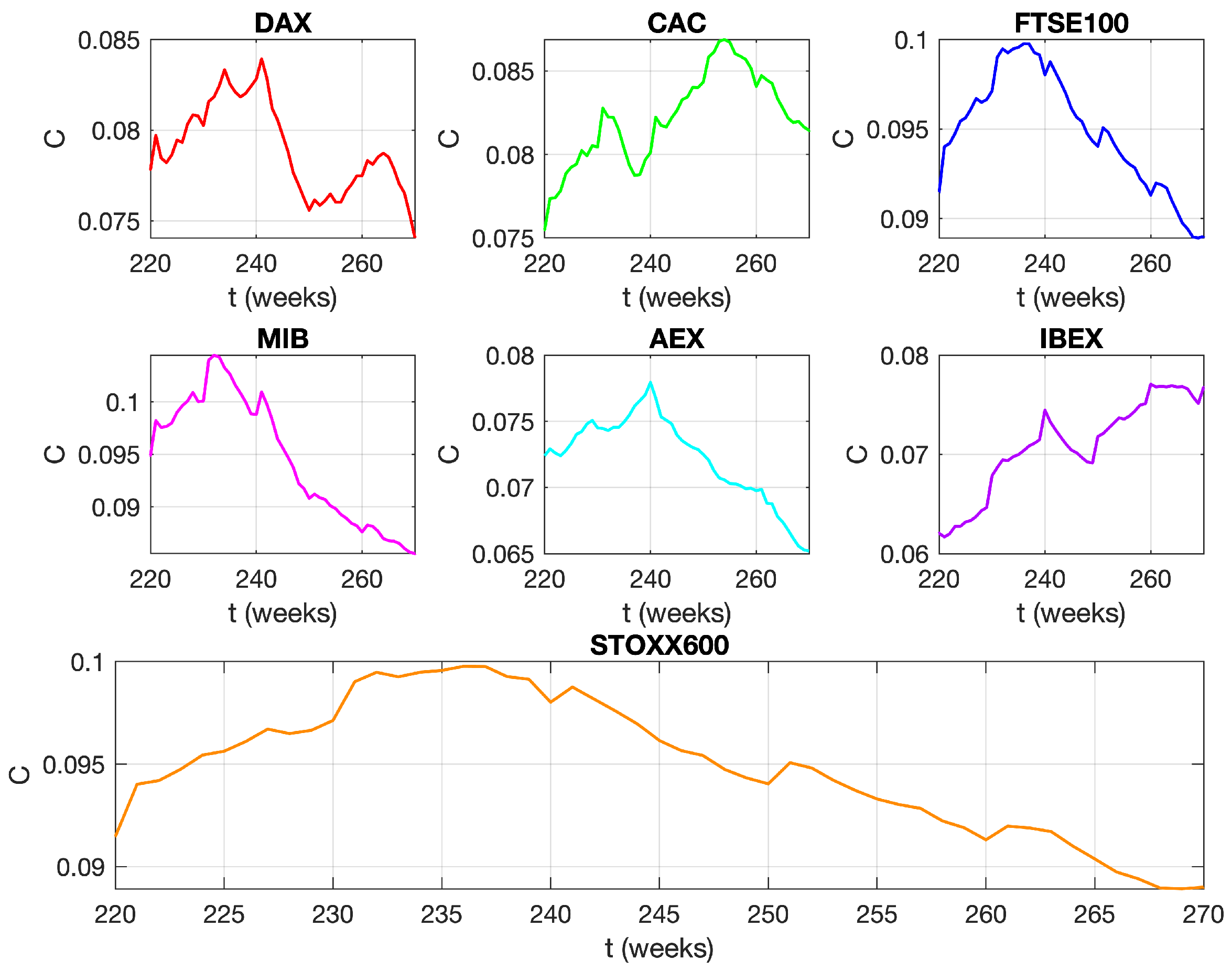
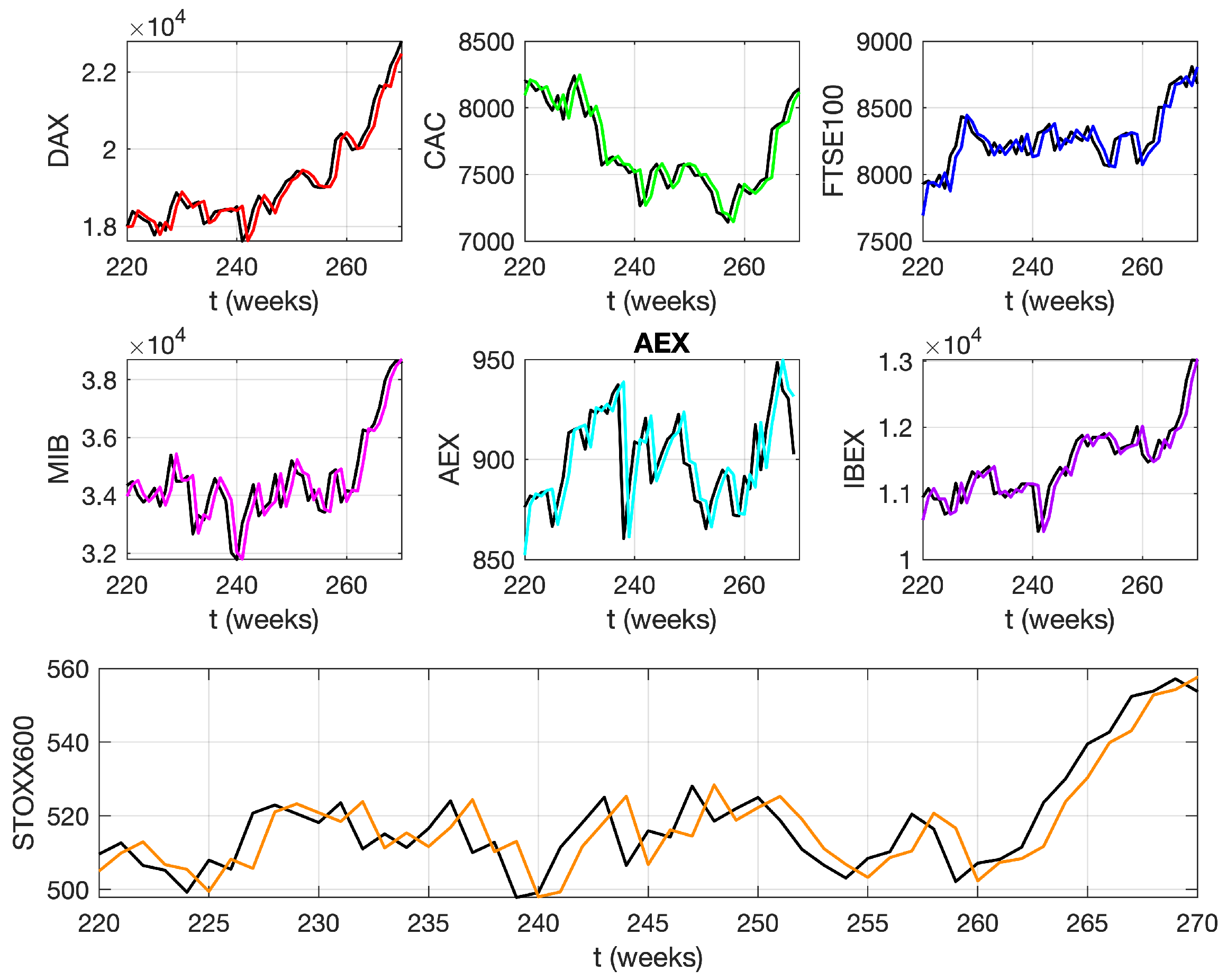
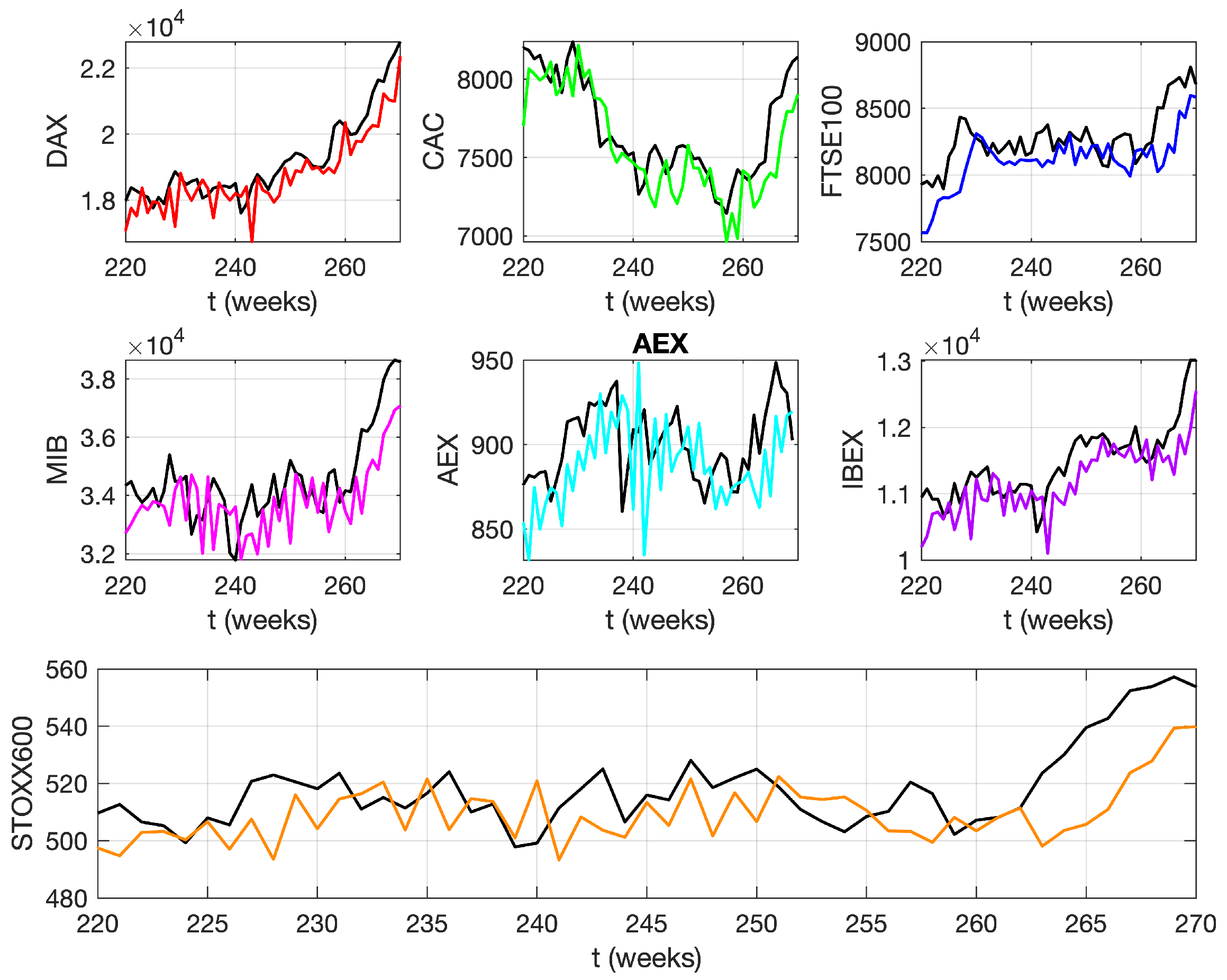
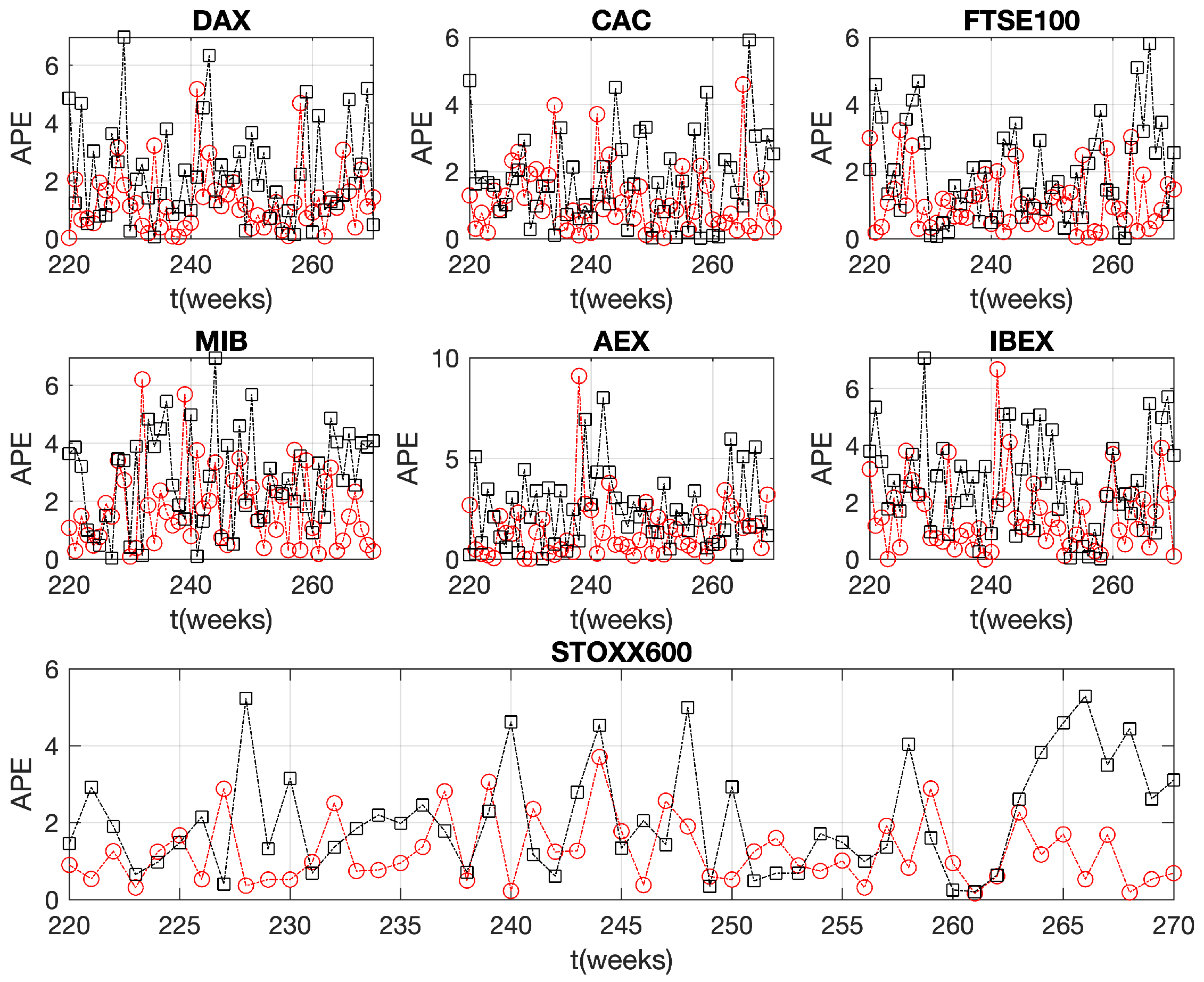
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| fBm | fractional Brownian motion |
| fGn | fractional Gaussian noise |
| mfBm | multifractional fractional Brownian motion |
| fLsm | fractional Lévy stable motion |
| fLsn | fractional Lévy stable noise |
| ARIMA | Autoregressive Integrated Moving Average |
| MC | Monte Carlo |
| DM | Diebold–Mariano test |
References
- Börner, K.; Rouse, W.B.; Trunfio, P.; Stanley, H.E. Forecasting innovations in science, technology, and education. Proc. Natl. Acad. Sci. USA 2018, 115, 12573–12581. [Google Scholar] [CrossRef]
- Baker, G.L.; Gollub, J.P. Chaotic Dynamics an Introduction, 2nd ed.; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Prado, T.L.; Boaretto, B.R.; Corso, G.; dos Santos, L.G.Z.; Kurths, J.; Lopes, S.R. A direct method to detect deterministic and stochastic properties of data. New J. Pjys. 2022, 24, 033027. [Google Scholar] [CrossRef]
- Hänggi, P.; Thomas, H. Stochastic processes: Time evolution, symmetries and linear response. Phys. Rep. 1982, 88, 207–319. [Google Scholar] [CrossRef]
- Bakalis, E.; Lugli, F.; Zerbetto, F. Daughter Coloured Noises: The Legacy of Their Mother White Noises Drawn from Different Probability Distributions. Fractal Fract. 2023, 7, 600. [Google Scholar] [CrossRef]
- Eke, A.; Herman, P.; Bassingthwaighte, J.; Raymond, G.; Percival, D.; Cannon, M.; Balla, I.; Ikrényi, C. Physiological time series: Distinguishing fractal noises from motions. Pflugers Arch. 2000, 439, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Bakalis, E.; Gavriil, V.; Cefalas, A.-C.; Kollia, Z.; Zerbetto, F.; Sarantopoulou, E. Viscoelasticity and Noise Properties Reveal the Formation of Biomemory in Cells. J. Phys. Chem. B 2021, 125, 10883–10892. [Google Scholar] [CrossRef]
- Hurst, H.E. Long term storage capacity of reservoirs. Trans. Am. Soc. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wallis, J.R. Robustness of the rescaled range R/S in the measurement of noncyclic long run Statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar] [CrossRef]
- Di Matteo, T. Multi-scaling in finance. Quant. Financ. 2007, 7, 21–36. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Viscek, T. Multifractality of self-affine fractals. Phys. Rev. A 1991, 44, 2730. [Google Scholar] [CrossRef]
- Bakalis, E.; Höfinger, S.; Venturini, A.; Zerbetto, F. Crossover of two power laws in the anomalous diffusion of a two lipid membrane. J. Chem. Phys. 2015, 142, 215102. [Google Scholar] [CrossRef] [PubMed]
- Sändig, N.; Bakalis, E.; Zerbetto, F. Stochastic analysis of movements on surfaces: The case of C60 on Au(1 1 1). Chem. Phys. Lett. 2015, 633, 163–168. [Google Scholar] [CrossRef]
- Bakalis, E.; Mertzimekis, T.J.; Nomikou, P.; Zerbetto, F. Breathing modes of Kolumbo submarine volcano (Santorini, Greece). Sci. Rep. 2017, 7, 46515. [Google Scholar] [CrossRef]
- Caccia, D.C.; Percival, D.; Cannon, M.J.; Raymond, G.; Bassingthwaighte, J.B. Analyzing exact fractal time series: Evaluating dispersional analysis and rescaled range methods. Physica A 1997, 246, 609–632. [Google Scholar] [CrossRef] [PubMed]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L.R. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef]
- Peng, C.-K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 685–1689. [Google Scholar] [CrossRef]
- Kantelhardt, J.W.; Zschiegner, S.A.; Koscielny-Bunde, E.; Havlin, S.; Bunde, A.; Stanley, H.E. Multifractal detrended fluctuation analysis of nonstationary time series. Physica A 2002, 316, 87–114. [Google Scholar] [CrossRef]
- Bakalis, E.; Ferraro, A.; Gavriil, V.; Pepe, F.; Kollia, Z.; Cefalas, A.-C.; Malapelle, U.; Sarantopoulou, E.; Troncone, G.; Zerbetto, F. Universal Markers Unveil Metastatic Cancerous Cross-Sections at Nanoscale. Cancers 2022, 14, 3728. [Google Scholar] [CrossRef]
- Gómez-Águila, A.; Trinidad-Segovia, J.E.; Sánchez-Granero, M.A. Improvement in Hurst exponent estimation and its application to financial markets. Financ. Innov. 2022, 8, 86. [Google Scholar] [CrossRef]
- Taqqu, M.S.; Teverovsky, V.; Willinger, W. Estimators for long-range dependence: An empirical study. Fractals 1995, 3, 785–798. [Google Scholar] [CrossRef]
- Barunik, J.; Kristoufek, L. On Hurst exponent estimation under heavy-tailed distributions. Physica A 2010, 389, 3844–3855. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Rosenow, B.; Amaral, L.A.N.; Stanley, H.E. Econophysics: Financial time series from a statistical physics point of view. Physica A 2000, 279, 443–456. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Variation of Certain Speculative Prices. J. Bus. 1963, 36, 394–419. [Google Scholar] [CrossRef]
- Mantegna, R.; Stanley, H.E. Scaling behaviour in the dynamics of an economic index. Nature 1995, 376, 46–49. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Potters, M.; Meyer, M. Apparent multifractality in financial time series. Eur. Phys. J. B 2000, 13, 595–599. [Google Scholar] [CrossRef]
- Scalas, E. Scaling in the market of futures. Physica A 1998, 253, 394–402. [Google Scholar] [CrossRef]
- Calvet, L.; Fisher, A. Multifractality in Asset Returns: Theory and Evidence. Rev. Econ. Stat. 2002, 84, 381–406. [Google Scholar] [CrossRef]
- Ruipeng, L.; Di Matteo, T.; Lux, T. Multifractality and long-range dependence of asset returns: The scaling behaviour of the Markov-switching multifractal model with lognormal volatility components. Adv. Complex Syst. 2008, 11, 669–684. [Google Scholar] [CrossRef]
- Mantegna, R.N. Lévy walks and enhanced diffusion in Milan stock exchange. Physica A 1991, 179, 232–242. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M. Stable Non-Gaussian Random Processes: Stochastic Models with Infinte Variance, 1st ed.; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar]
- Fama, E.F.; Roll, R. Some properties of symmetric stable distributions. Am. Stat. Assoc. J. 1968, 63, 817–836. [Google Scholar] [CrossRef]
- Kogon, S.M.; Manolakis, G. Signal modeling with self-similar α/-stable processes: The fractional Levy stable motion model. IEEE Trans. Signal Process. 1996, 44, 1006–1010. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M. Linear models with long-range dependence and with finite and infinite variance. In New Directions in Time Series Analysis. The IMA Volumes in Mathematics and Its Applications, 1st ed.; Brillinger, D., Caines, P., Geweke, J., Parzen, E., Rosenblatt, M., Taqqu, M.S., Eds.; Springer: New York, NY, USA, 1993; pp. 325–340. [Google Scholar]
- Song, W.; Cattani, C.; Chi, C.-H. Multifractional Brownian motion and quantum-behaved particle swarm optimization for short term power load forecasting: An integrated approach. Energy 2020, 194, 116847. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.; Li, M.; Kudreyko, A.; Zio, E. Fractional Lévy stable motion: Finite difference iterative forecasting model. Chaos 2020, 133, 109632. [Google Scholar] [CrossRef]
- Bakalis, E.; Zerbetto, F. Iterative Forecasting of Financial Time Series: The Greek Stock Market from 2019 to 2024. Entropy 2025, 27, 497. [Google Scholar] [CrossRef]
- Bakalis, E.; Parent, L.R.; Vratsanos, M.; Chiwoo, P.; Gianneschi, N.C.; Zerbetto, F. Complex Nanoparticle Diffusional Motion in Liquid-Cell Transmission Electron Microscopy. J. Phys. Chem. C 2020, 124, 14881. [Google Scholar] [CrossRef]
- Schertzer, D.; Lovejoy, S. Physical modeling and Analysis of Rain and Clouds by Anisotropic Scaling of Multiplicative Processes. J. Geophys. Res. 1987, 92, 9693–9714. [Google Scholar] [CrossRef]
- Laskin, N.; Lambadaris, I.; Harmantzis, F.C.; Devetsikiotis, M. Fractional Lévy motion and its application to network traffic modeling. Comput. Netw. 2002, 40, 363–375. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. The Fractal Geometry of Nature, 1st ed.; W. H. Freeman & Company: New York, NY, USA, 2008; p. 480. [Google Scholar]
- Lyra, M.L.; Tsallis, C. Nonextensivity and multifractality in low-dimensional dissipative systems. Phys. Rev. Lett. 1998, 80, 53–56. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef]
- Bakalis, E.; Fujie, H.; Zerbetto, F.; Tanaka, Y. Multifractal structure of microscopic eye–head coordination. Physica A 2018, 512, 945–953. [Google Scholar] [CrossRef]
- Janicki, A.; Weron, A. Can One See α-Stable Variables and Processes? Stat. Sci. 1994, 9, 109–126. [Google Scholar] [CrossRef]
- Available online: https://www.statista.com/search/?q=weekly+indexes+2020+-+2025+europe&Search=&p=1 (accessed on 21 July 2025).
- The MathWorks Inc. MATLAB, Version: 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022.
- Kasdin, N. Discrete simulation of colored noise and stochastic processes and 1/fα power law noise generation. Proc. IEEE 1995, 83, 802–827. [Google Scholar] [CrossRef]
- Zhivomirov, H. Pink, Red, Blue and Violet Noise Generation with Matlab Implementation, Version 1.6. Available online: https://www.mathworks.com/matlabcentral/fileexchange/42919-pink-red-blue-and-violet-noise-generation-with-matlab-implementation (accessed on 15 November 2017).
- Chen, Z. Asset Allocation Strategy with Monte-Carlo Simulation for Forecasting Stock Price by ARIMA Model. In Proceedings of the IC4E ’22: Proceedings of the 2022 13th International Conference on E-Education, E-Business, E-Management, and E-Learning, Tokyo, Japan, 14–17 January 2022; pp. 481–485. [Google Scholar] [CrossRef]
- Diebold, F.X.; Mariano, R.S. Comparing Predictive Accuracy. J. Bus. Econ. Stat. 1995, 13, 253–263. [Google Scholar] [CrossRef]
- Harvey, D.; Leybourne, S.; Newbold, P. Testing the equality of prediction mean squared errors. Int. J. Forecast. 1997, 13, 281–291. [Google Scholar] [CrossRef]
- Ibisevic, S. Diebold-Mariano Test Statistic. MATLAB Central File Exchange. Available online: https://ch.mathworks.com/matlabcentral/fileexchange/33979-diebold-mariano-test-statistic (accessed on 15 October 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bakalis, E. Iterative Forecasting of Short Time Series. Appl. Sci. 2025, 15, 11580. https://doi.org/10.3390/app152111580
Bakalis E. Iterative Forecasting of Short Time Series. Applied Sciences. 2025; 15(21):11580. https://doi.org/10.3390/app152111580
Chicago/Turabian StyleBakalis, Evangelos. 2025. "Iterative Forecasting of Short Time Series" Applied Sciences 15, no. 21: 11580. https://doi.org/10.3390/app152111580
APA StyleBakalis, E. (2025). Iterative Forecasting of Short Time Series. Applied Sciences, 15(21), 11580. https://doi.org/10.3390/app152111580






