Research on Fault Diagnosis Method for Autonomous Underwater Vehicles Based on Improved LSTM Under Data Missing Conditions
Abstract
1. Introduction
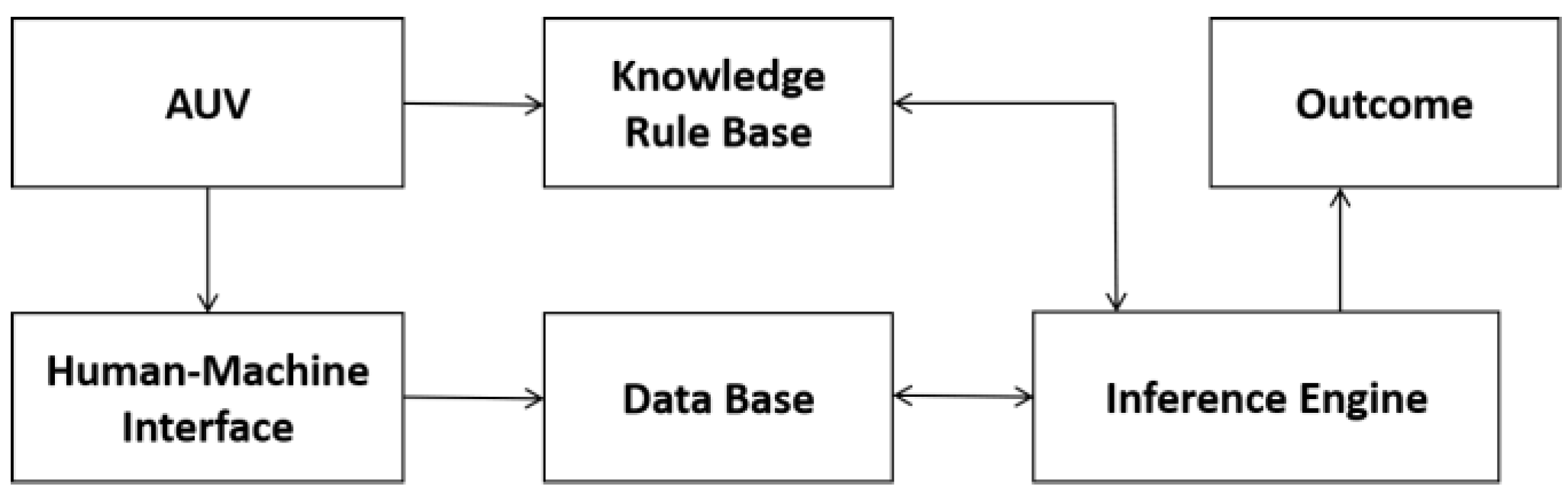
1.1. Rule-Based Diagnosis
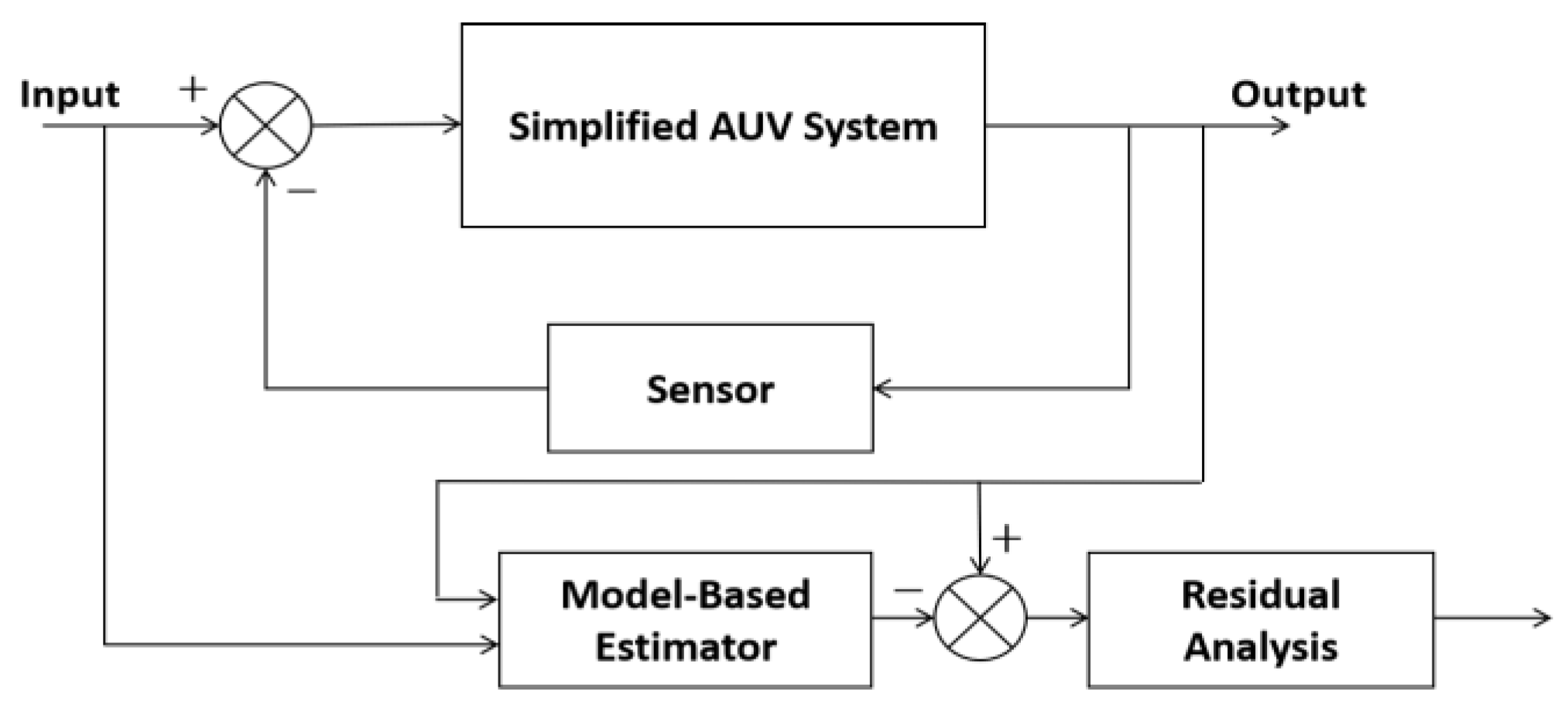
1.2. Model-Based Diagnosis
1.3. Data-Driven Diagnosis
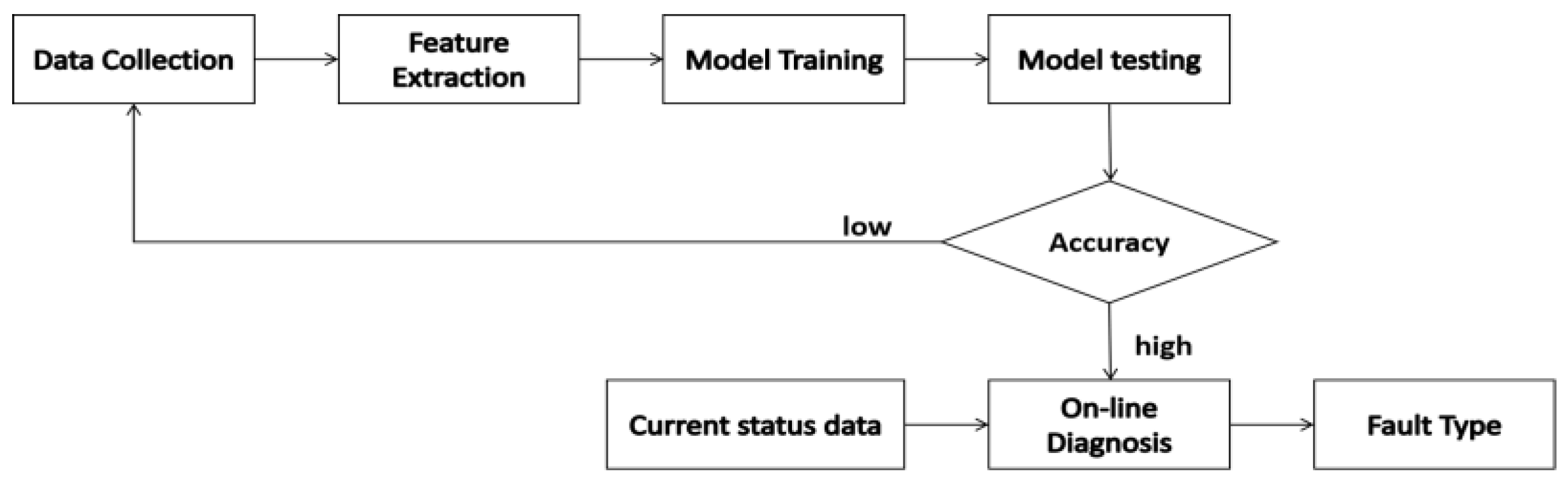
2. Diagnostic Process
3. Data and Features
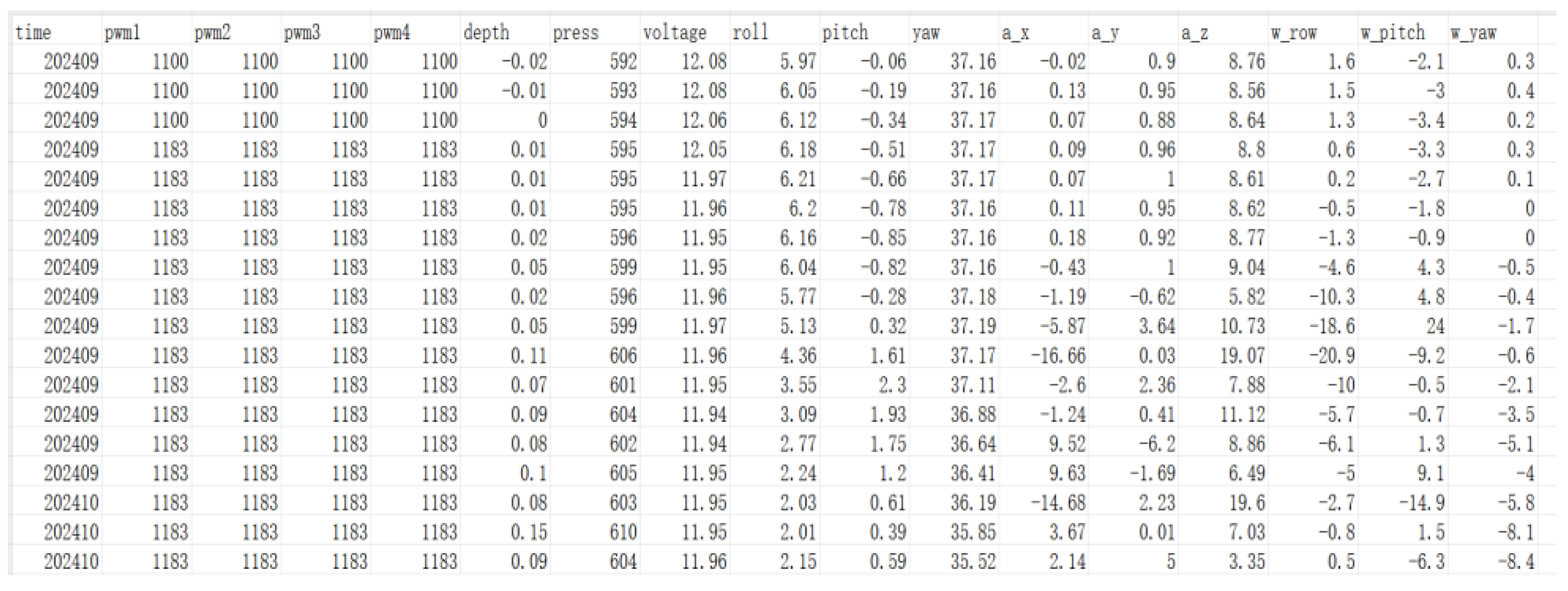
3.1. Data Collection
3.2. Feature Extraction
3.2.1. Data Normalization
- (1)
- Calculating the Median
- (2)
- Clculating the Interquartile Range (IQR)
- (3)
- Performing Robust Normalization
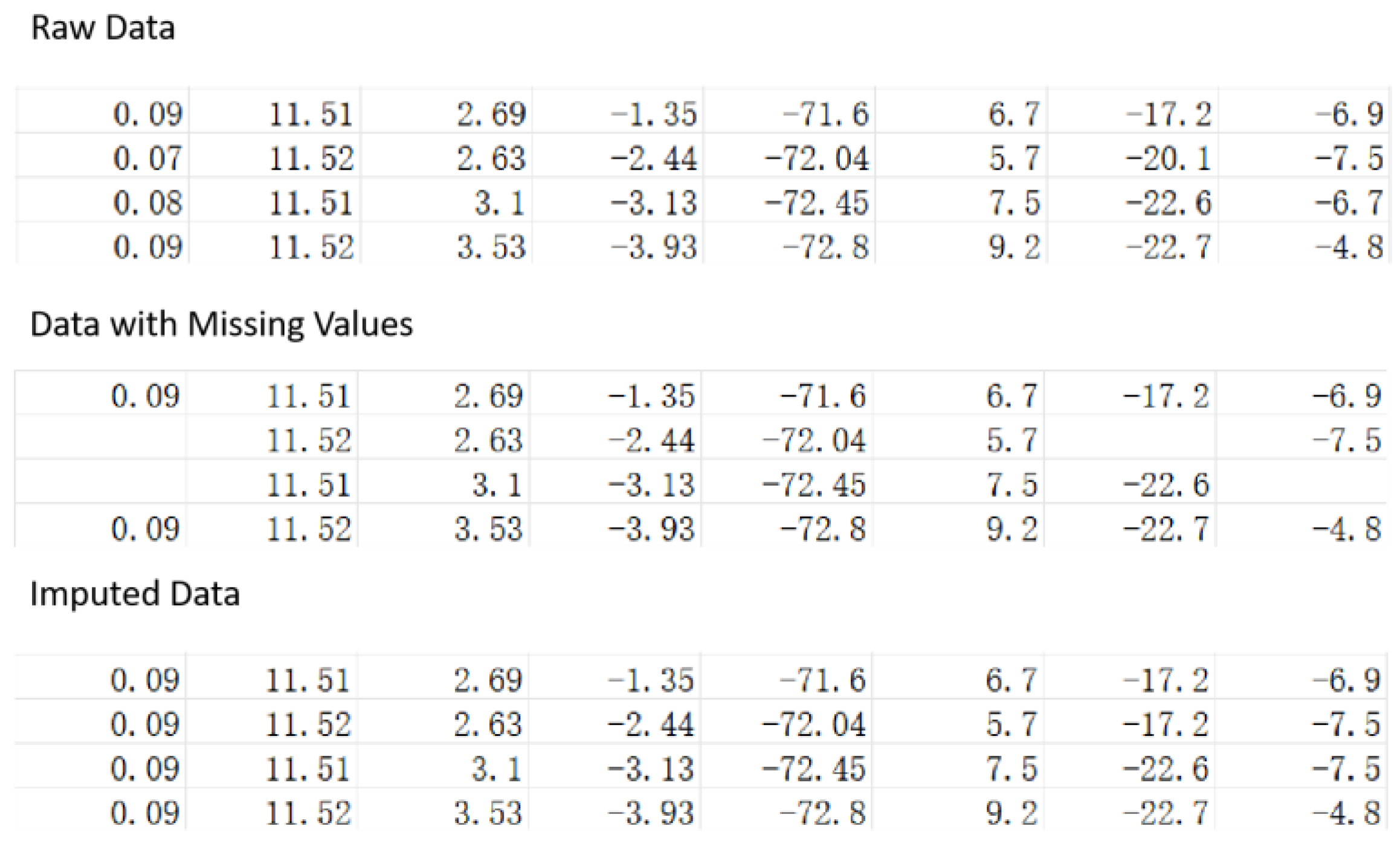
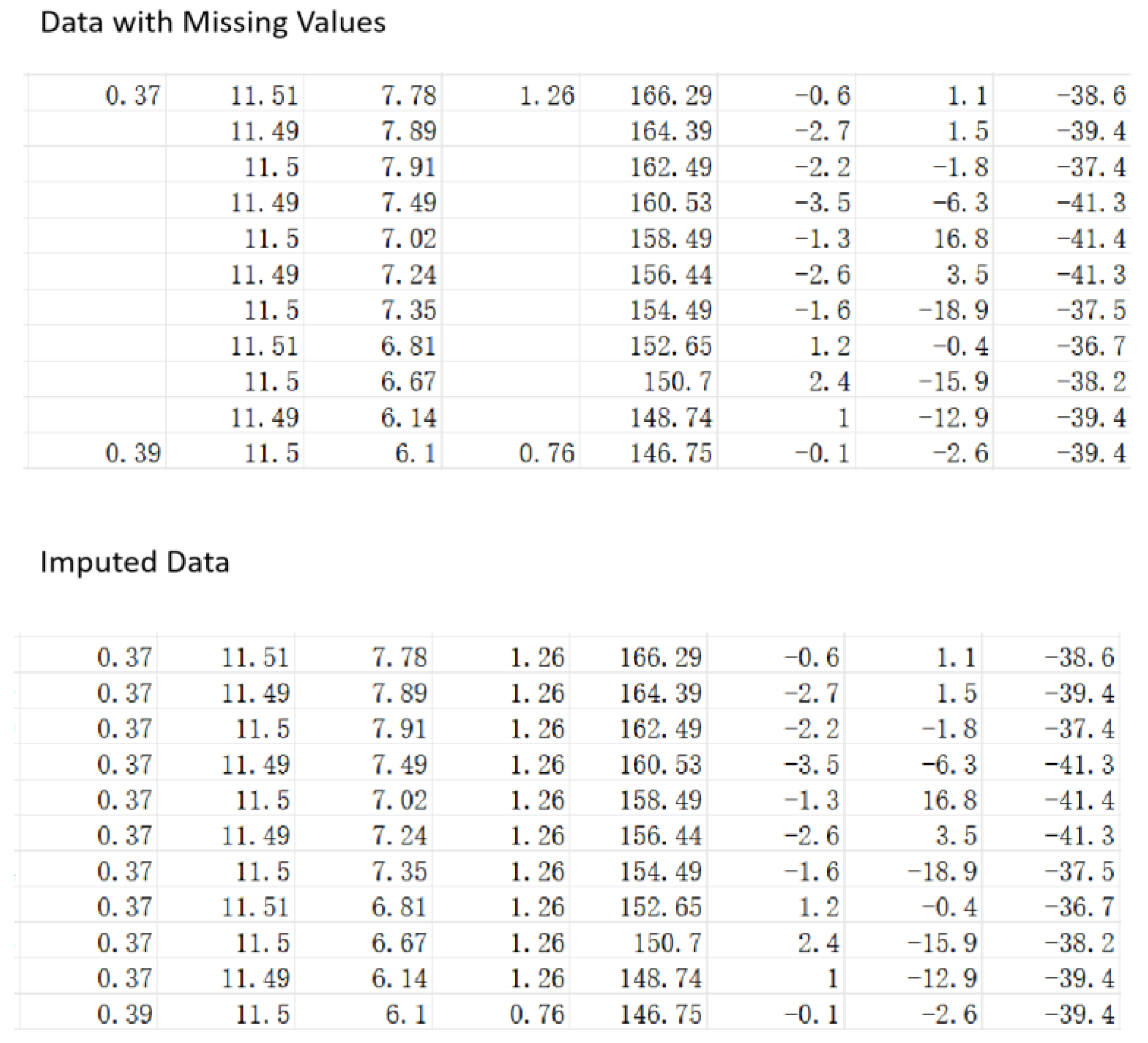
3.2.2. Missing Value Processing
- (1)
- Forward fill imputation
- (2)
- Local mean imputation
4. Model
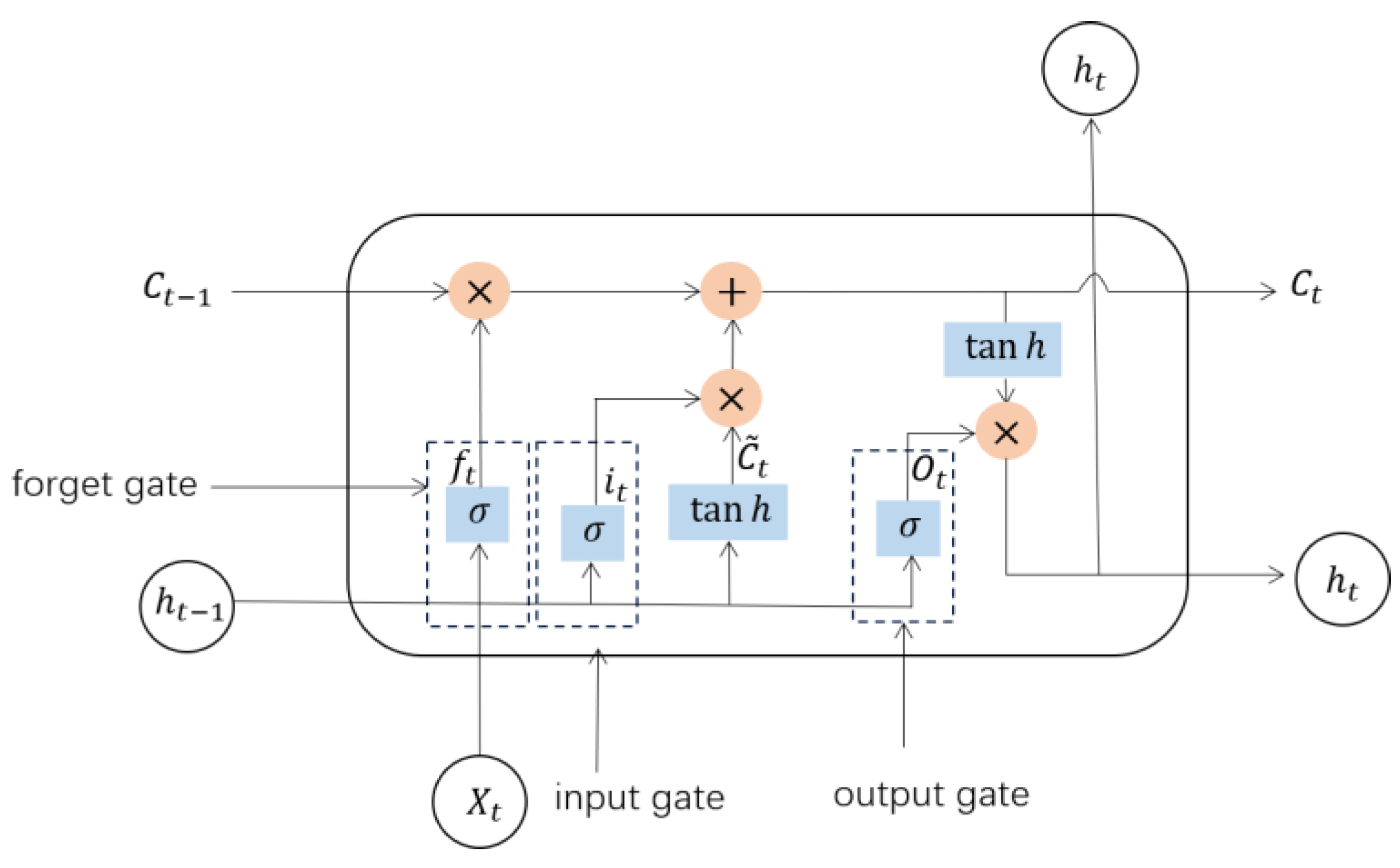
4.1. LSTM
- (1)
- Forget gate
- (2)
- Input gate
- (3)
- Output gate
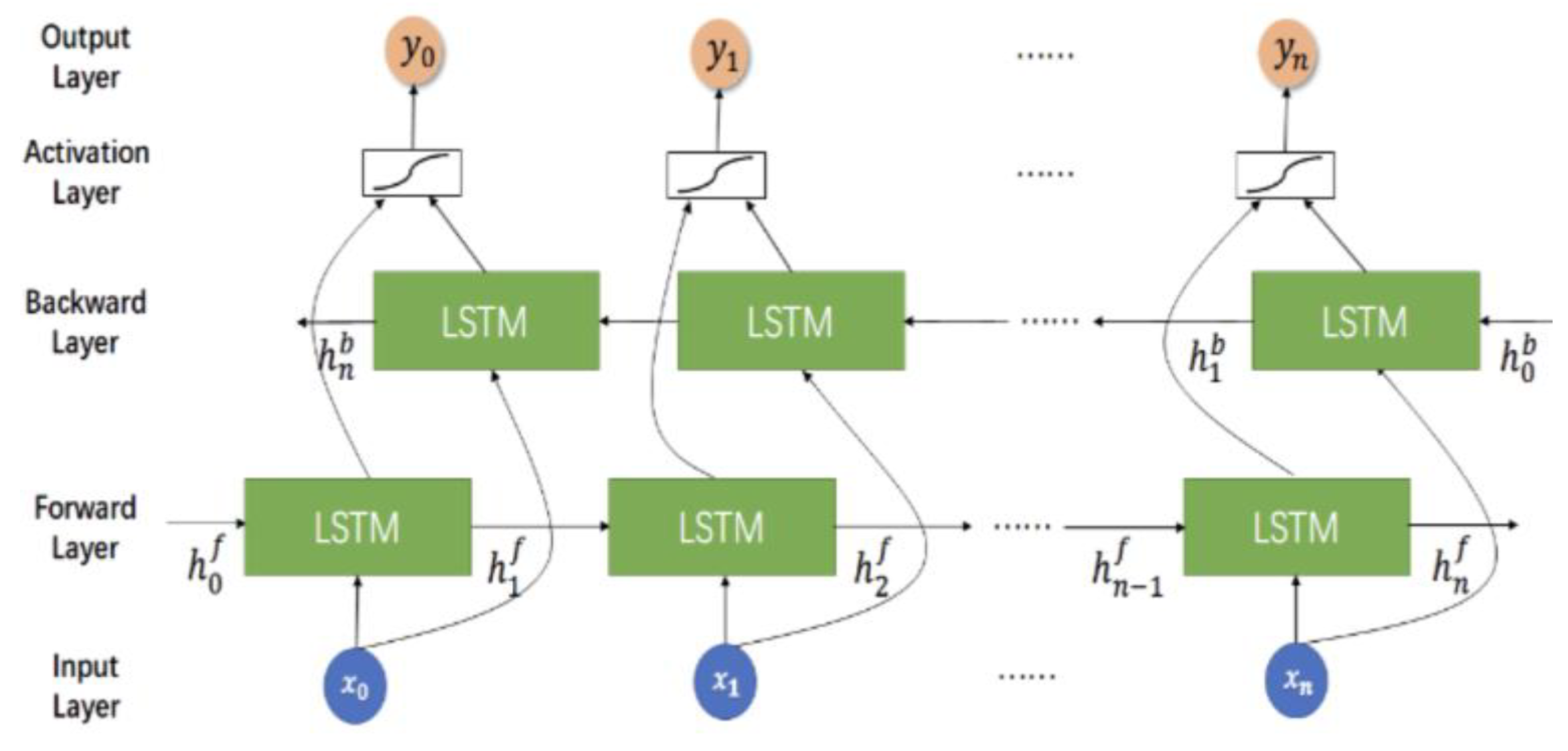
4.2. BiLSTM
4.3. Training
4.4. Modification
4.4.1. Improve the Loss Function
4.4.2. Incorporate the Attention Mechanism
- (1)
- Temporal Analysis
- (2)
- Global Analysis
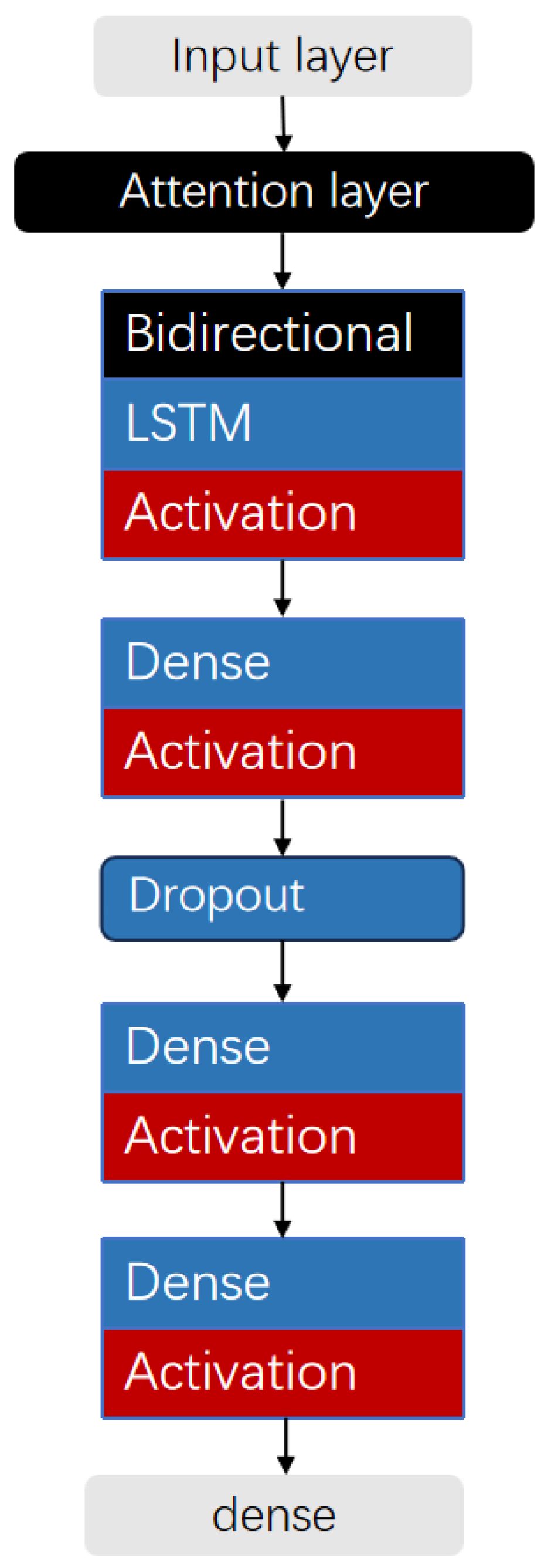
4.5. BiLSTM-Attention-MiniLoss
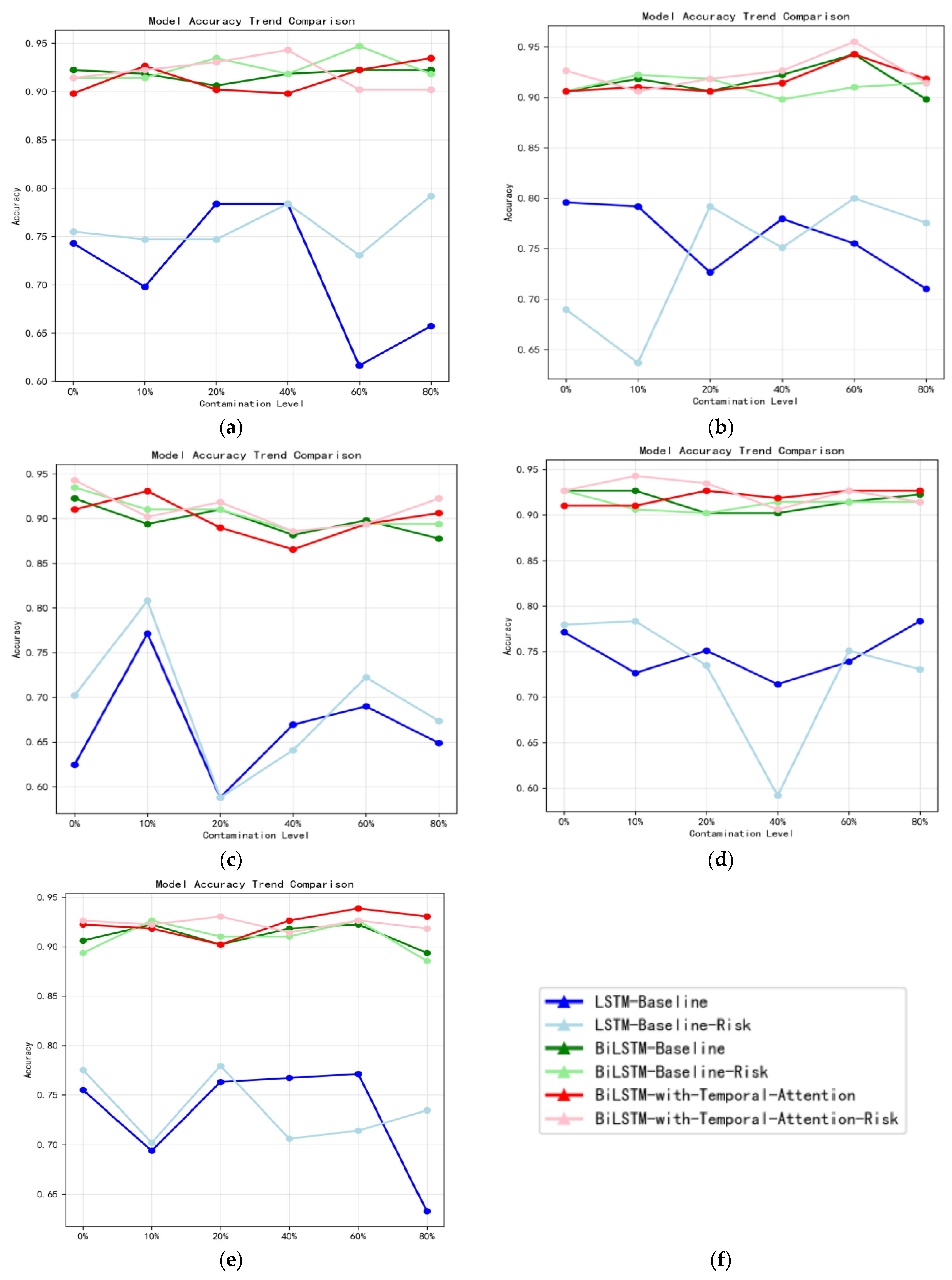
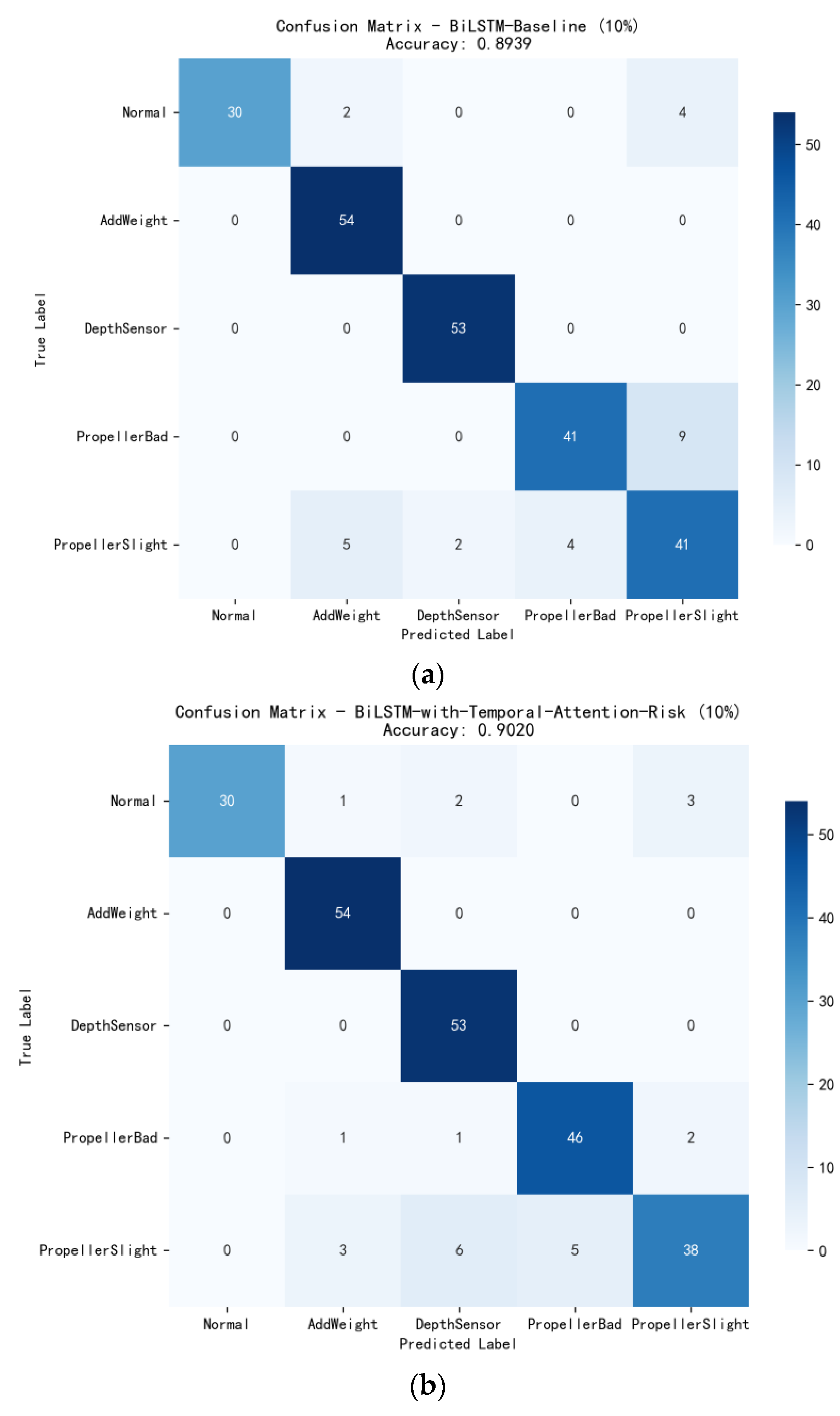
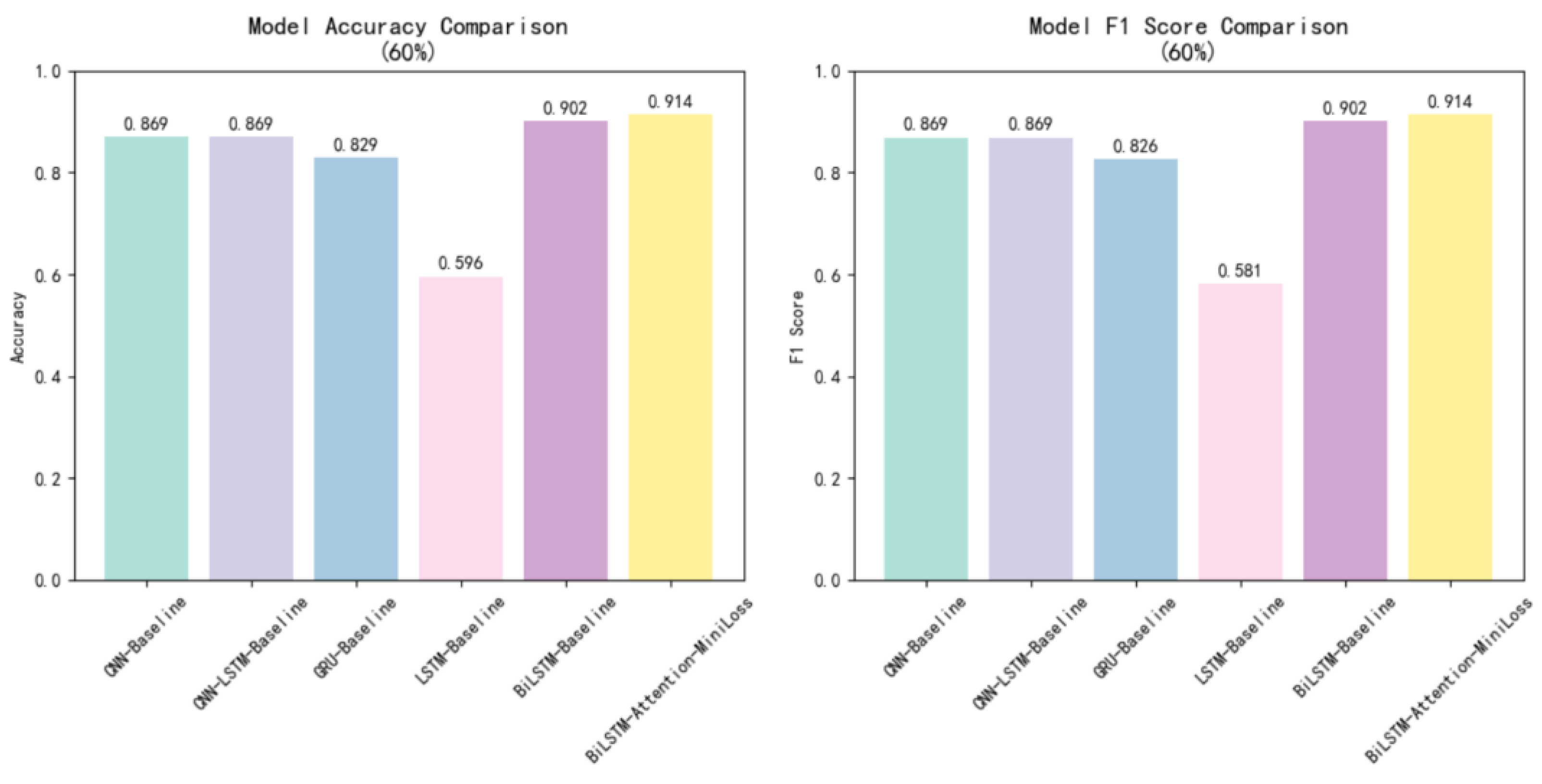
5. Experiment
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, T.; Hou, S.; Li, D. Overview and research progress of fault identification method. Prog. Geophys. 2018, 33, 1507–1514. [Google Scholar]
- Zhang, M.; Liu, C.; Wang, Y.; Chen, T. Fault Diagnosis for Autonomous Underwater Vehicles Using a Combined Model-Based and Data-Driven Approach. IEEE J. Ocean. Eng. 2021, 46, 987–1001. [Google Scholar]
- Li, Y.; Zhao, W.; Zhang, J. Actuator Fault Diagnosis and Fault-Tolerant Control for Autonomous Underwater Vehicles. Ocean Eng. 2019, 172, 37–46. [Google Scholar]
- Huang, J.; Zhang, M.; Wang, S. A Review of Fault Diagnosis and Fault-Tolerant Control for Autonomous Underwater Vehicles. Annu. Rev. Control. 2018, 45, 42–54. [Google Scholar]
- Wang, Y.; Zhang, Q.; He, B. Sensor Fault Diagnosis and Reconstruction for Autonomous Underwater Vehicles Based on Deep Learning. IEEE Sens. J. 2022, 22, 15231–15242. [Google Scholar]
- Zhang, T.; Li, X.; Zhang, Y. Fault Detection and Isolation for Autonomous Underwater Vehicles Using Sliding Mode Observers. Int. J. Adapt. Control Signal Process. 2017, 31, 735–751. [Google Scholar]
- Ranganathan, N.; Patel, M.I.; Sathyamurthy, R. An intelligent system for failure detection and control in an autonomous underwater vehicle. IEEE Trans. Syst. Man Cybern.-Part A Syst. Hum. 2001, 31, 762–767. [Google Scholar] [CrossRef]
- Hamilton, K.; Lane, D.M.; Brown, K.E.; Evans, J.; Taylor, N.K. An integrated diagnostic architecture for autonomous underwater vehicles. J. Field Robot. 2007, 24, 497–526. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, G.; Chen, Z.; Liu, Y.; Shen, X. A finite state machine based diagnostic expert system of large-scale autonomous unmanned submarine. In Proceedings of the 2018 IEEE 8th International Conference on Underwater System Technology: Theory and Applications (USYS), Wuhan, China, 1–8 December 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6. [Google Scholar]
- Miguelanez, E.; Patron, P.; Brown, K.E.; Petillot, Y.R.; Lane, D.M. Semantic knowledge-based framework to improve the situation awareness of autonomous underwater vehicles. IEEE Trans. Knowl. Data Eng. 2010, 23, 759–773. [Google Scholar] [CrossRef]
- Alireza, M.; Zhang, Y.; Zhang, J. A hybrid fault diagnosis framework for autonomous underwater vehicles: Enhancing rule-based systems with neural networks. Ocean Eng. 2021, 235, 109357. [Google Scholar]
- Xu, D.; Jiang, B.; Shi, P. A hybrid fault diagnosis methodology for autonomous underwater vehicles based on fuzzy logic and partial least squares. Int. J. Adapt. Control Signal Process. 2017, 31, 394–409. [Google Scholar]
- Wang, Y.; Gao, Z.; Zhang, Q. Data-driven fault diagnosis for AUVs: Addressing the challenges of expert knowledge dependency and multiple faults. In Proceedings of the 2019 IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 6123–6129. [Google Scholar]
- Ji, D.; Yao, X.; Li, S.; Tang, Y.; Tian, Y. Model-free fault diagnosis for autonomous underwater vehicles using sequence Convolutional Neural Network. Ocean Eng. 2021, 232, 108874. [Google Scholar] [CrossRef]
- Shumsky, A.; Zhirabok, A.; Hajiyev, C. Observer based fault diagnosis in thrusters of autonomous underwater vehicle. In Proceedings of the 2010 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 6–8 October 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 11–16. [Google Scholar]
- Chu, Z.; Chen, Y.; Zhu, D.; Zhang, M. Observer-based fault detection for magnetic coupling underwater thrusters with applications in jiaolong HOV. Ocean Eng. 2020, 210, 107570. [Google Scholar] [CrossRef]
- Jiang, C.; Lv, J.; Liu, Y.; Wang, G.; Xu, X.; Deng, Y. STF-based diagnosis of AUV thruster faults. In E3S Web of Conferences; EDP Sciences: Shenyang, China, 2022; Volume 360, p. 01048. [Google Scholar]
- Li, Z.; Sun, J.; Zhang, W.; Du, J.; Hu, X. Modeling and controller design for underactuated AUVs in the presence of unknown ocean currents. Ocean Eng. 2023, 285, 115367. [Google Scholar]
- Wang, Y.; Liu, J.; Zhang, M.; Du, J.; Li, Z. A robust fault diagnosis scheme for autonomous underwater vehicles with sensor faults under ocean current disturbances. Ocean Eng. 2022, 266, 113107. [Google Scholar]
- Lei, Y.; Yang, B.; Jiang, X.; Jia, F.; Li, N.; Nandi, A.K. Applications of machine learning to machine fault diagnosis: A review and roadmap. Mech. Syst. Signal Process. 2020, 138, 106587. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, D.; Yang, S.X. Unmanned underwater vehicles fault identification and fault-tolerant control method based on FCA-CMAC neural networks, applied on an actuated vehicle. J. Intell. Robot. Syst. 2012, 66, 463–475. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, J.; Chu, Z. Multi-fault diagnosis for autonomous underwater vehicle based on fuzzy weighted support vector domain description. China Ocean Eng. 2014, 28, 599–616. [Google Scholar] [CrossRef]
- Nascimento, S.; Valdenegro-Toro, M. Modeling and soft-fault diagnosis of underwater thrusters with recurrent neural networks. Int. Fed. Autom. Control-Pap. 2018, 51, 80–85. [Google Scholar] [CrossRef]
- Jiang, Y.; He, B.; Lv, P.; Guo, J.; Wan, J.; Feng, C.; Yu, F. Actuator fault diagnosis in autonomous underwater vehicle based on principal component analysis. In Proceedings of the 2019 IEEE Underwater Technology (UT), Kaohsiung, Taiwan, 16–19 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5. [Google Scholar]
- Xia, S.; Zhou, X.; Shi, H.; Li, S.; Xu, C. A fault diagnosis method with multi-source data fusion based on hierarchical attention for AUV. Ocean Eng. 2022, 266, 112595. [Google Scholar] [CrossRef]
- Li, Y.; Ye, Y.; Zhang, Z.; Wen, L. A New Incremental Learning Method Based on Rainbow Memory for Fault Diagnosis of AUV. Sensors 2025, 25, 4539. [Google Scholar] [CrossRef]
- Zhang, S.; Ye, F.; Wang, B.; Zhang, J.; Han, Y.; Chang, H. A deep transfer learning based data-driven method for ship energy system fault diagnosis. Ocean Eng. 2023, 285, 115353. [Google Scholar]
- Wang, J.; Liang, Y.; Zheng, Y.; Zhang, A.; Liu, Z. A deep learning-based method for bearing fault diagnosis with anti-strong noise and variable load capability. Measurement 2020, 165, 108100. [Google Scholar]
- Mai, J.; Huang, H.; Wei, F.; Yang, C.; He, W. Autonomous underwater vehicle fault diagnosis model based on a deep belief rule with attribute reliability. Ocean Eng. 2025, 321, 120472. [Google Scholar] [CrossRef]
- Mai, J.; Luo, Z.; Ge, G.; Zhang, G.; He, W. A Fault Diagnosis Method for Autonomous Underwater Vehicles Based on Online Extended Belief Rule Base with Dynamic Rule Reduction. IEEE Access 2024, 12, 165407–165424. [Google Scholar] [CrossRef]
- Ji, D.; Yao, X.; Li, S.; Tang, Y.; Tian, Y. Autonomous underwater vehicle fault diagnosis dataset. Data Brief 2021, 39, 107477. [Google Scholar] [CrossRef] [PubMed]
- Huo, Y.; Gang, S.; Guan, C. FCIHMRT: Feature Cross-Layer Interaction Hybrid Method Based on Res2Net and Transformer for Remote Sensing Scene Classification. Electronics 2023, 12, 4362. [Google Scholar] [CrossRef]





| Fault State | Label | Dataset Size | Training | Test |
|---|---|---|---|---|
| Normal | 0 | 182 | 146 | 36 |
| AddWeight | 1 | 268 | 214 | 54 |
| PressureGain_constant | 2 | 266 | 213 | 53 |
| PropellerDamage_bad | 3 | 249 | 199 | 50 |
| PropellerDamage_slight | 4 | 260 | 208 | 52 |
| True Label Predicted Label | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0.2 | 0 | 0 | 0 | 0 |
| 2 | 0.2 | 0 | 0 | 0 | 0 |
| 3 | 1.0 | 0 | 0 | 0 | 0 |
| 4 | 0.6 | 0 | 0 | 0 | 0 |
| Layer Model | LSTM |
|---|---|
| LSTM layer (128 units) | 4 × (8 × 128 + 128 × 128 + 128) = 70,144 |
| Dense layer (64 units) | 128 × 64 + 64 = 8256 |
| Dense layer (32 units) | 64 × 32 + 32 = 2080 |
| Dense layer (5 units) | 32 × 5 + 5 = 165 |
| Layer Model | BiLSTM |
|---|---|
| BiLSTM layer (128 units) | 2 × [4 × (8 × 128 + 128 × 128 + 128)] = 140,288 |
| Dense layer (64 units) | 128 × 64 + 64 = 8256 |
| Dense layer (32 units) | 64 × 32 + 32 = 2080 |
| Dense layer (5 units) | 32 × 5 + 5 = 165 |
| Layer Model | Attention |
|---|---|
| Conv1D (32 filters) | (5 × 8 + 1) × 32 = 1312 |
| Temporal weight | 32 × 8 = 256 |
| Global weight | 24 × 2 + 2 = 50 |
| Global weight | 2 × 8 + 8 = 24 |
| Working Conditions | LSTM-CE | LSTM-MiniLoss | BiLSTM-CE | BiLSTM-MiniLoss | BiLSTM-Attention_CE | BiLSTM-Attention-MiniLoss |
|---|---|---|---|---|---|---|
| a | 0.7136 | 0.7592 | 0.9184 | 0.9245 | 0.9136 | 0.9190 |
| b | 0.7632 | 0.7407 | 0.9157 | 0.9116 | 0.9163 | 0.9245 |
| c | 0.6653 | 0.6891 | 0.8973 | 0.8998 | 0.8993 | 0.9109 |
| d | 0.7476 | 0.7286 | 0.9156 | 0.9129 | 0.9197 | 0.9252 |
| e | 0.7306 | 0.7354 | 0.9109 | 0.9088 | 0.9231 | 0.9231 |
| Missing Rate | LSTM-CE | LSTM-MiniLoss | BiLSTM-CE | BiLSTM-MiniLoss | BiLSTM-Attention_CE | BiLSTM-Attention-MiniLoss |
|---|---|---|---|---|---|---|
| 0% | 0.9970 | 0.7929 | 0.2393 | 0.2053 | 0.2355 | 0.2250 |
| 10% | 0.6147 | 0.5437 | 0.2966 | 0.2553 | 0.2158 | 0.2906 |
| 20% | 1.0649 | 1.0766 | 0.2485 | 0.2720 | 0.2689 | 0.2249 |
| 40% | 0.9564 | 0.9793 | 0.3818 | 0.3066 | 0.3762 | 0.2899 |
| 60% | 0.7268 | 0.7219 | 0.2671 | 0.3058 | 0.2418 | 0.3020 |
| 80% | 0.8831 | 0.8011 | 0.3068 | 0.3201 | 0.2504 | 0.2465 |
| Mean loss | 0.8738 | 0.8193 | 0.2900 | 0.2775 | 0.2648 | 0.2632 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Huo, Y. Research on Fault Diagnosis Method for Autonomous Underwater Vehicles Based on Improved LSTM Under Data Missing Conditions. Appl. Sci. 2025, 15, 11570. https://doi.org/10.3390/app152111570
Dong L, Huo Y. Research on Fault Diagnosis Method for Autonomous Underwater Vehicles Based on Improved LSTM Under Data Missing Conditions. Applied Sciences. 2025; 15(21):11570. https://doi.org/10.3390/app152111570
Chicago/Turabian StyleDong, Lingyan, and Yan Huo. 2025. "Research on Fault Diagnosis Method for Autonomous Underwater Vehicles Based on Improved LSTM Under Data Missing Conditions" Applied Sciences 15, no. 21: 11570. https://doi.org/10.3390/app152111570
APA StyleDong, L., & Huo, Y. (2025). Research on Fault Diagnosis Method for Autonomous Underwater Vehicles Based on Improved LSTM Under Data Missing Conditions. Applied Sciences, 15(21), 11570. https://doi.org/10.3390/app152111570






