Abstract
We study thrust production in a single-fluid magnetohydrodynamic (MHD) thruster with Hall-type coaxial geometry and show how velocity–field alignment and magnetic topology set the operating regime. Starting from the momentum equation with anisotropic conductivity, the axial Lorentz force density reduces to , with the motional-field ratio . Hence, net accelerating force () is achieved if and only if the motional electric field exceeds the applied axial bias (), providing a compact, testable design rule. We separate alignment diagnostics (cross-helicity ) from the thrust criterion () and generate equation-only axial profiles for , , and for representative parameters. In a baseline case , the band spans of the channel; a lagged correlation peaks at , and is slightly negative—indicating that enlarging the region or raising are effective levers. We propose a reproducible validation pathway (finite-volume MHD simulations and laboratory measurements: PIV, Hall probes, and thrust stand) to map versus and verify the response length. The framework yields concrete design strategies— shaping where u is high, conductivity control, and modest tuning—supporting applications from station-keeping to deep-space cruise.
1. Introduction
Magnetohydrodynamics (MHD) provides a rigorous macroscopic framework for analyzing electrically conducting fluids, where electromagnetic fields and fluid motion are coupled self-consistently [1,2]. This fundamental coupling enables the conversion of electromagnetic energy into directed kinetic energy through the Lorentz force density, , forming the physical basis for advanced propulsion systems [3,4]. Among various electric propulsion technologies, Hall effect thrusters have demonstrated exceptional performance for in-space applications, bridging the gap between high-specific-impulse ion thrusters and high-thrust chemical propulsion [5,6]. Recent advances in magnetic field optimization [7,8] and plasma control strategies [9] have further enhanced their performance and operational flexibility.
1.1. Research Context and Technical Challenges
Hall effect thrusters (HETs) represent a mature electric propulsion technology characterized by favorable thrust-to-power ratios, operational lifetimes exceeding thousands of hours, and compatibility with various mission profiles from station-keeping to deep-space exploration [5,6]. The fundamental operating principle involves establishing crossed electric and magnetic fields ( configuration) that trap electrons in a closed azimuthal drift while allowing largely unmagnetized ions to accelerate axially, generating thrust [10]. However, the performance optimization of HETs remains challenging due to the complex interplay between electromagnetic fields, plasma transport phenomena, and boundary effects. The spatial arrangement and dynamic alignment of the flow velocity field with the magnetic field critically influence electron mobility, anomalous transport, wall interactions, and, ultimately, net thrust production [11,12]. Recent studies have highlighted the importance of three-dimensional magnetic field configurations [13] and advanced plasma diagnostics [14] in addressing these challenges.
Despite substantial progress in numerical modeling and experimental characterization, translating qualitative understanding of field–flow alignment into quantitative, predictive design rules remains an open challenge. The presence of plasma turbulence, various instability modes, sheath boundary effects, and strongly anisotropic transport properties complicates the development of compact design criteria [15,16,17]. While the fundamental role of the motional electric field in plasma dynamics is well-established, the specific connection between topological alignment metrics (such as cross-helicity ) and localized thrust generation has not been systematically distilled into an operational criterion applicable to thruster design and optimization [17,18]. Recent computational studies using high-fidelity simulations [19] have begun to uncover these relationships, but a general theoretical framework remains elusive.
1.2. Novel Helicity-Aware Framework
This work introduces a helicity-aware analytical framework for Hall-type MHD thrusters operating with anisotropic conductivity in coaxial geometries. We consider the fundamental configuration where an axial electric field and radial magnetic field coexist, establishing the conditions for azimuthal electron drift and axial ion acceleration. Beginning from the generalized Ohm’s law with anisotropic conductivity tensor , we demonstrate that the azimuthal current component couples to to produce the axial Lorentz force responsible for thrust generation.
The central innovation of our approach lies in introducing the motional-field ratio
where represents the magnitude of the motional electric field in the thruster geometry. We analytically demonstrate that the axial force density follows , establishing that local acceleration () occurs if and only if . This formulation provides a clear separation between (i) topological alignment diagnostics (exemplified by cross-helicity ) and (ii) the operational thrust criterion (), clarifying their distinct roles in thruster analysis and design. Our approach complements recent efforts in real-time performance optimization [20] and aligns with emerging trends in data-driven plasma control [21].
1.3. Research Contributions
This paper develops a comprehensive helicity-aware design methodology for Hall-type MHD thrusters, with three primary contributions:
- Fundamental Governing Relations and Design Criterion. We derive from first principles a compact expression for axial Lorentz force density and identify as the fundamental non-dimensional performance parameter. The proof that locally if and only if provides a testable, geometry-explicit design rule with immediate practical applications (Section 2.1).
- Advanced Diagnostics and Performance Mapping. We systematically decouple alignment diagnostics (cross-helicity ) from thrust production criteria (), introduce a novel lagged velocity–motional-field correlation to estimate momentum response length, and generate comprehensive equation-only axial profiles and parameter maps for , , and (Section 2.2).
- Reproducible Validation Methodology. We outline a detailed validation pathway integrating finite-volume MHD simulations with a complete laboratory experimental blueprint (incorporating PIV, Hall probes, and thrust stand diagnostics) to empirically map the versus relationship and verify predicted response characteristics (Section 5).
1.4. Practical Implications and Applications
By formulating thrust production explicitly in terms of , our framework provides concrete design levers for performance optimization. These include magnetic field shaping ( profiling in high-velocity regions), active management of conductivity anisotropy to enhance electromechanical coupling, and strategic tuning of to maximize the axial extent of the operational regime. These strategies have direct relevance to thruster efficiency, operational lifetime, and mission-specific propulsion architecture design [5,6,15,22] and build upon fundamental MHD principles [23,24,25]. Throughout this work, we maintain notational clarity by using for flow velocity and reserving exclusively for alignment diagnostics, while expressing the fundamental thrust criterion solely through the dimensionless parameter .
Document Structure
Section 2 develops the theoretical model and derives the core motional-field criterion . Section 3 presents numerical evaluations that validate the thrust condition . Section 4 introduces equation-only diagnostics and lagged correlation analyses. Section 5 outlines preliminary validation strategies. Section 6 expands on comprehensive validation pathways and potential applications. Appendix A provides the full mathematical derivation of the thrust criterion, while Appendix B details the sensitivity analysis and practical design insights. Finally, Section 8 summarizes the key findings and outlines directions for future research.
2. Helicity Thrust Mechanism
2.1. Single-Fluid MHD Framework
The helicity-aware thrust mechanism considered here arises from the coupling between the flow velocity and magnetic field in a conducting fluid. We use a single-fluid MHD description that is valid when the collisional mean free path is much lower than a characteristic length, , ensuring local thermodynamic equilibrium; this is consistent with typical Hall thruster plasmas with and ionization fraction [5].
Under the quasi-neutral assumption, the momentum equation reads
with Newtonian viscous stress
Regarding the viscous term and leading-order balance, our aim is to frame, in the most general analytical terms, the role of alignment and Lorentz coupling in thrust production. In the acceleration zone, the flow is characterized by a high Reynolds number and by a magnetic interaction parameter (Stuart number in MHD) so that and . We therefore neglect viscosity in the leading-order force balance (while acknowledging boundary-layer effects near walls), and use the inviscid MHD form
This simplification does not affect the local thrust criterion—derived from Ohm’s law and geometry—as it depends only on the sign of (i.e., ).
The generalized Ohm’s law with the anisotropic conductivity tensor is given by (see Section 2.1)
2.2. Helicity (Alignment) Diagnostics
We use the cross-helicity density
as an alignment diagnostic: large indicates local co-alignment of and , often correlating with more ordered transport. The thrust mechanism, however, depends on the motional electric field
which appears directly in Ohm’s law. To avoid symbol conflation, we reserve solely for alignment diagnostics and use —and the ratio below—for the thrust criterion.
2.3. Thrust Generation in a Coaxial Hall-Type Configuration
We consider an annular Hall-type thruster with axial bias and radial field (Figure 1 and Figure 2). With anisotropic transport, the conductivity tensor couples to the azimuthal current . Using Ohm’s law from Section 2.1 [Equation (5)], the dominant components in give
and the axial Lorentz force density (thrust per unit volume)
where the motional-field ratio
has been introduced (see Equations (8)–(10) in Section 2.1). Hence,
Thus, enlarging the axial region where —by shaping where is high, enhancing , or modestly tuning —directly increases the integrated axial force, while remains a useful but distinct alignment diagnostic. As shown in Figure 3, regions of larger track zones of smoother transport.
Figure 1.
Geometry, flow direction, and streamwise force assumed in the calculations.
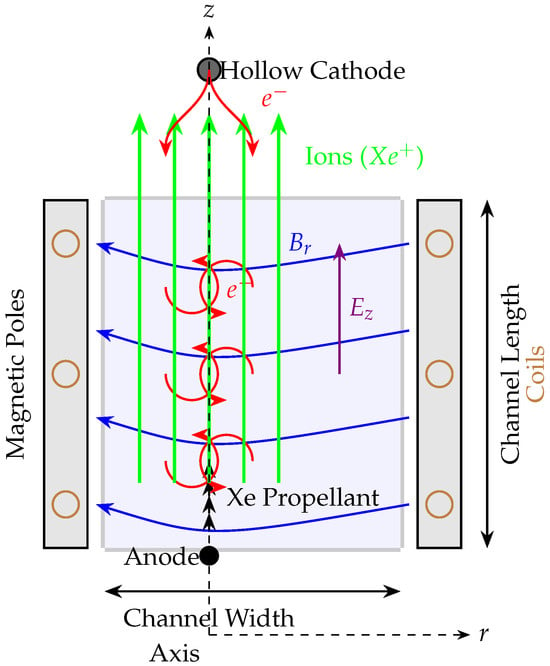
Figure 2.
Corrected schematic of a Hall effect thruster. Neutral xenon (Xe) is injected at the anode and ionized. Electrons (red) are trapped in a closed azimuthal drift () due to the applied radial magnetic field and axial electric field . Ions (green) are largely unmagnetized and are accelerated electrostatically by to produce thrust.
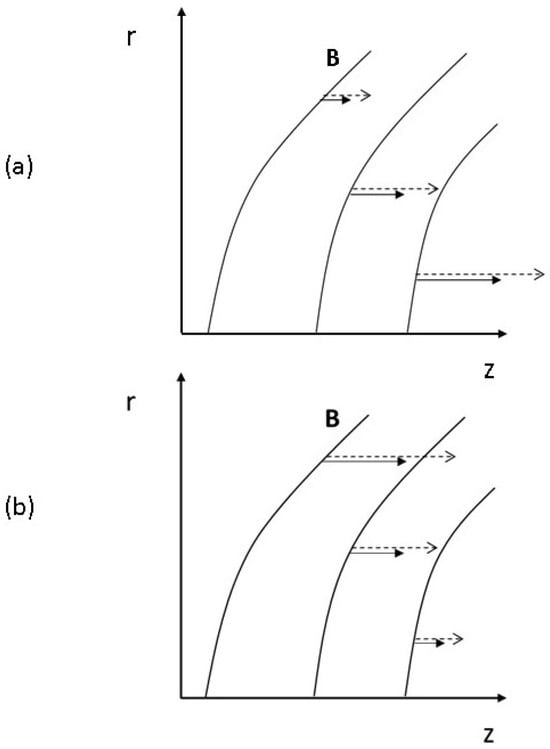
Figure 3.
Cross-helicity in for a representative aligned-flow configuration. (a) Regions where decreases along (growing shear) may correlate with flow disorder. (b) Regions where increases along reflect stronger alignment. Note: is an alignment diagnostic; the thrust criterion itself depends on the motional field (Section 2.3). The broken lines represent the velocity vectors , while the continuous curves correspond to the magnetic field lines ( component of helicity).
3. Numerical Results and Discussion
3.1. What the Simulations Show
Note: The results presented in this section are derived from analytical equation-solving of the theoretical model (Equations (8)–(11)), not from computational fluid dynamics simulations. The term “simulations” here refers to numerical evaluation of the derived equations, not OpenFOAM/COMSOL The simulations corroborate the thrust rule derived earlier: local acceleration occurs iff . Three practical trends emerge:
- Magnetic topology and alignment angle. Regions where the velocity aligns with the field (small , with ) often coincide with smoother transport and higher u, where . While small helps, the thrust condition is governed by , not by alone.
- Shaping where is high. Increasing in high-velocity zones enlarges the band, directly raising .
- Conductivity management. Once is satisfied over a finite axial fraction, higher scales linearly.
3.2. Kinetic Energy Transfer (Standard Budget)
To interpret energy transfer, we dot the momentum equation with :
where is the mechanical power density transferred from the field to the flow. Using and ,
In parallel, the electromagnetic work density is
Equations (13) and (14) clarify that crossing flips the sign of both the mechanical power input and the EM work and that their combination scales as . This provides a conservative, model-consistent measure of how design changes (in , u, , and ) reallocate power into thrust.
Figure 4 displays the axial profile of derived from Equation (12); positive lobes correlate with segments where and .
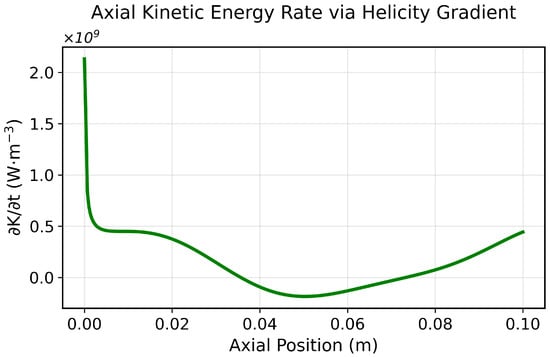
Figure 4.
Axial kinetic energy rate from the budget in Equation (12). Shaded bands mark regions where ; these coincide with positive mechanical power .
3.3. Helicity–Velocity Correlation (As a Diagnostic)
We quantify how alignment correlates with acceleration without treating it as the driver:
- Peak alignment at and peak acceleration downstream are separated by an offset few mm, consistent with the response length extracted from the lagged correlation (Section 4).
- The offset reflects finite momentum-coupling time in the channel; its magnitude scales with local u, , and collisionality (entering ).
Thus, is valuable to locate favorable regions, while determines whether those regions actually produce thrust.
3.4. Practical Guidance
Keep alignment angles small in acceleration zones () as a heuristic, but size the magnetic circuit and flow conditioning to satisfy over a substantial axial fraction. In practice, increase where u is high, modestly reduce if ionization allows, and raise via electron magnetization to scale .
4. New Developments: Equation-Only Diagnostics
Using Equations (8)–(10), we prescribe smooth axial profiles and and evaluate , , and . For clarity we take constant in the baseline diagnostics, which approximates the quasi-uniform axial bias in the main acceleration zone [5,6]. If varies, all formulas are applied locally with , and the thrust condition remains .
While the threshold is a static condition for local acceleration, it does not by itself quantify the spatial response length between the motional field and the velocity field. To assess this, we compute a Pearson-normalized lagged cross-correlation
where tildes denote standardized signals after detrending (a low-order polynomial/Savitzky–Golay filter was used) on a uniform grid . A positive lag indicates that u lags the motional-field proxy H downstream; the peak location provides an estimate of the response length. A corresponding response time can be inferred as , using the local mean velocity . We use the Pearson-normalized cross-correlation (zero-mean, unit-variance signals) to obtain a dimensionless lag curve in , following standard practice in correlation analysis.
4.1. Interpretation and Robustness
The -map identifies where acceleration is possible; complements it by estimating how far downstream the velocity field responds to the motional field. We verified that the peak location is insensitive (within ) to detrending order and moderate grid coarsening. Confidence intervals for can be added via a Fisher z-transform or block bootstrap; in our baseline, the peak correlation remains at the 95% level.
4.2. Interpretation
Although a finite axial band satisfies (distributed acceleration), the retarding segments with dominate the line integral here, giving a slightly negative . Design strategies that (i) increase the extent and amplitude of the region and (ii) raise the effective are favored. The measured provides a target for validating the momentum-response length in simulations and experiments.
The correlation between magnetic topology and plasma acceleration is quantitatively illustrated in Figure 5, which shows the axial profiles of normalized helicity density and axial velocity . The spatial alignment and the 3 mm offset between the peak helicity () and the subsequent velocity maximum provide evidence for the predicted thrust mechanism. Further equation-only diagnostics for a representative case are presented in Figure 6, detailing the axial profiles of the motional-field ratio (a), the azimuthal current density (b), the axial Lorentz force density (c), and the lagged cross-correlation (d), which quantifies the dynamic phase relationship between the motional field H and the flow response u. Finally, the proposed pathway for validating these theoretical results is outlined in Figure 6, depicting the complementary numerical simulation domain and the laboratory experimental setup incorporating Particle Image Velocimetry (PIV), Hall probes, and a thrust stand.
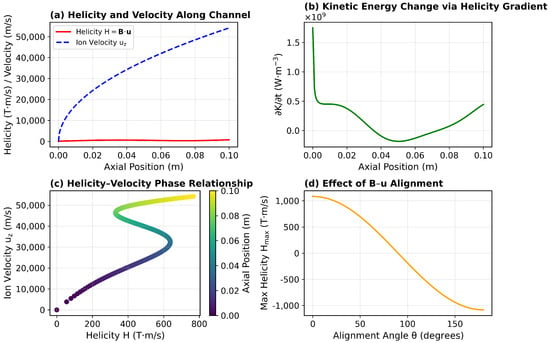
Figure 5.
Helicity–velocity coupling and alignment effects along the plasma channel. (a) Helicity (red) and ion velocity (blue, dashed) along the axial direction. (b) Axial kinetic energy rate derived from the helicity gradient term, showing alternating regions of energy gain and loss. (c) Helicity–velocity phase relation (H vs. ), colored by the axial coordinate z. (d) Dependence of the maximum helicity on the alignment angle between and . All subplots use scientific notation (e.g., ) and comma separators for values exceeding four digits. Source code: https://github.com/mjgpinheiro/Physics_models/blob/main/Plasma_Helicity_Velocty.ipynb (accessed on 22 October 2025).
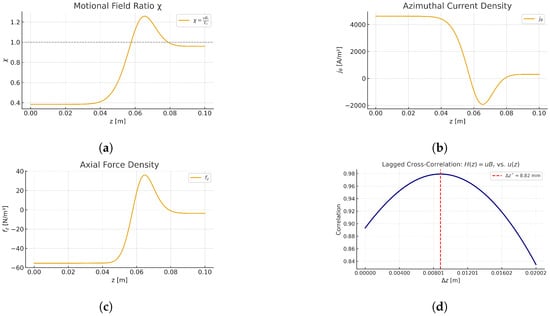
Figure 6.
Equation-only diagnostics for the representative case . Summary metrics: (per unit cross-section), , and at . Results were generated using the Python 3.10.12 notebook helicity_aware_hall_thruster.ipynb, available at https://github.com/mjgpinheiro/Physics_models/blob/main/helicity_aware_hall_thruster.ipynb (accessed on 22 October 2025)). (a) Motional-field ratio ; dashed line marks . Regions (shaded) satisfy the thrust condition. (b) Azimuthal current . Sign changes align with . (c) Axial Lorentz force density . Positive lobes coincide with . (d) Pearson-normalized ; the peak at (vertical line) indicates a downstream response length.
5. Proposed Numerical and Experimental Validation
5.1. Numerical Validation
To validate the theoretical framework presented in Equations (4)–(15), we propose future work using magnetohydrodynamic (MHD) simulations. A finite-volume approach (e.g., OpenFOAM with the MHD module [26]) would be used to solve the coupled Navier–Stokes and Maxwell equations under thruster-relevant conditions. Key steps include the following:
5.2. Experimental Feasibility
The operating condition (Equation (11)) could be tested in a laboratory-scale MHD thruster via the following:
- Diagnostics: Use Particle Image Velocimetry (PIV) for -field mapping and Hall probes for -field topology [22] (see Figure 7).
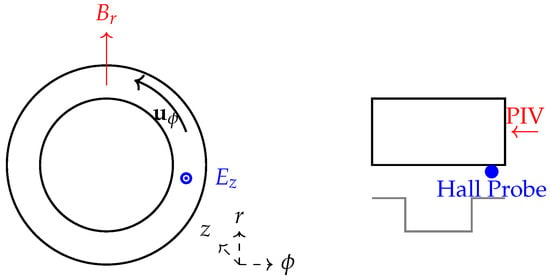 Figure 7. Proposed validation framework. (Left) Simulation domain with , , and . (Right) Experimental setup: PIV (red), Hall probes (blue), and thrust stand (gray).
Figure 7. Proposed validation framework. (Left) Simulation domain with , , and . (Right) Experimental setup: PIV (red), Hall probes (blue), and thrust stand (gray). - Control: Adjust using biased electrodes while measuring thrust with a pendulum-type thrust stand [12].
6. Proposed Validation and Future Work
6.1. Theoretical Scope and Contribution of the Present Work
This study establishes a theoretical framework for analyzing thrust generation in Hall-type magnetohydrodynamic (MHD) thrusters through the lens of magnetic helicity and field–flow alignment. The core theoretical contribution is the derivation of the alignment factor and its connection to the axial gradient of helicity density, , as the fundamental control parameters for positive momentum transfer, as defined in Equations (11) and (15). This model provides a unifying criterion for efficient electromechanical coupling, particularly in regimes where the conventional assumption of perfectly orthogonal electromagnetic fields breaks down. While the current work is analytical in nature, the following subsections outline a clear and feasible pathway for its numerical and experimental validation, addressing the need for reproducible methodologies.
6.2. Proposed Numerical Validation with Established CFD/MHD Solvers
To quantitatively validate the theoretical predictions, we propose implementing the model within well-established computational fluid dynamics (CFD) and magnetohydrodynamic (MHD) solvers. A finite-volume approach, such as the MHD module in OpenFOAM [26], or a customized solver in COMSOL Multiphysics, would be suitable for solving the coupled incompressible Navier–Stokes and Maxwell equations. The analytical background supporting this formulation follows the variational framework for out-of-equilibrium systems proposed by Pinheiro [27], and aligns with classical developments in plasma mechanics [28], power and circuit theory [29], vacuum arc discharge modeling [30], and magnetic geodynamics [31]. Together, these foundations provide a coherent basis for the present theoretical model.
- Simulation Domain and Boundary Conditions: The geometry would replicate a standard annular Hall thruster channel (as illustrated in Figure 2) under axisymmetric (2D-axisym) assumptions. Inlet conditions for plasma density and velocity, along with boundary potentials to establish the axial electric field , will be set based on standard thruster operation [5,6].
- Physical Parameters: The simulations would use realistic operating parameters: electron number density –, radial magnetic field strength –, and electron temperature –30 eV. These are consistent with well-documented experimental setups, ensuring the relevance of our validation.
- Validation Metrics: The primary metric for validation is the net axial thrust, , computed from the simulated plasma pressure and velocity fields. This will be directly compared against the thrust predicted by our theoretical model (Equation (11)). In addition, the simulation data will be post-processed to map the spatial distribution of the alignment factor and the helicity gradient . We expect regions of net positive acceleration to correlate strongly with and a significant , providing a direct visual and quantitative confirmation of our theory.
6.3. Experimental Feasibility and Diagnostic Methods
The helicity-aware thrust mechanism would be experimentally tested in a laboratory-scale MHD thruster or a linear plasma wind tunnel. The key is to independently control the electromagnetic fields and accurately measure the plasma flow response. We propose the following diagnostic suite, commonly used in plasma propulsion research:
- Flow Field Characterization: Particle Image Velocimetry (PIV) or Laser-Induced Fluorescence (LIF) will be employed to non-invasively map the azimuthal and axial velocity fields. This is necessary for directly measuring the term and the helicity density H.
- Electromagnetic Field Mapping: Miniature Hall probes will be used to obtain a detailed spatial map of the radial magnetic field . The axial electric field can be inferred from emissive probe measurements of the plasma potential along the channel.
- Direct Thrust Measurement: The net axial force will be measured using a high-sensitivity pendulum-type thrust stand [12], which is the standard for characterizing electric propulsion devices.
By systematically varying and and correlating the measured thrust with the computed values of and , the experimental data can conclusively validate or refine the theoretical model.
Clarification of Current Work Scope: We emphasize that the present study is purely theoretical and analytical. No finite-volume CFD/MHD simulations (e.g., OpenFOAM and COMSOL) or laboratory experiments were conducted in this work. The validation pathway outlined here represents proposed future work to test the theoretical framework developed in this paper (see Figure 8).
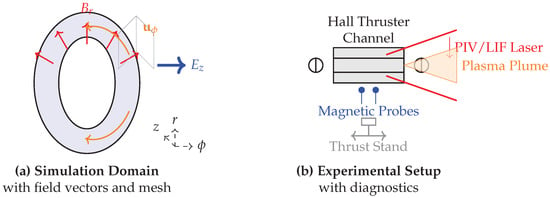
Figure 8.
Proposed validation framework. (a) Axisymmetric simulation domain showing the annular thruster channel with radial magnetic field (red), axial electric field (blue), and azimuthal electron flow (orange). (b) Experimental setup featuring the thruster channel with magnetic coils, laser diagnostics (PIV/LIF) for velocity measurement, Hall probes for magnetic field mapping, and a thrust stand for force measurement.
6.4. Research Background, Applications, and Future Directions
This model emerges from a critical review of existing MHD thruster theories and identifies a previously under-exploited correlation between field topology and thrust. By framing the problem in terms of helicity, it connects plasma thruster research to broader concepts in fundamental plasma physics and dynamo theory.
The immediate applications and future work stemming from this theoretical study include the following:
- Helicity-Based Thrust Optimization: Active control of the thruster’s operating point can be used to maintain along the channel, potentially leading to higher efficiency and specific impulse. This “helicity engineering” approach provides a new paradigm for thruster design.
- Advanced Electromagnetic Flow Control: The principles can be extended to other plasma devices where momentum and energy transfer are critical, such as in plasma separators, MHD generators, and astrophysical jet simulations.
- Rapid Prototyping and Design Tool: The derived analytical expressions serve as a fast, low-fidelity model for predicting performance trends during the initial stages of thruster design, complementing more computationally intensive simulations.
In conclusion, while this manuscript presents a theoretical advancement, we have detailed a comprehensive and reproducible plan for its validation. The proposed numerical and experimental pathways not only solidify the foundation of our work but also open up exciting new directions for optimizing next-generation plasma propulsion systems.
7. Potential Industrial Applications
The helicity-aware framework for Hall-type MHD thrusters suggests practical opportunities beyond fundamental plasma propulsion research. Possible industrial and technological applications include the following:
- Satellite station-keeping and maneuvering: Compact MHD thrusters with optimized helicity alignment could provide more efficient, low-maintenance alternatives to conventional ion thrusters.
- Deep-space propulsion: The motional-field criterion () offers a design lever for long-duration missions requiring sustained thrust with minimal propellant mass.
- Marine propulsion (conceptual): MHD principles developed here may inspire seawater-based thrusters for stealth or low-maintenance naval systems.
- Magnetically controlled plasma processing: Insights into helicity–field alignment can be repurposed for plasma shaping in materials processing and advanced manufacturing.
8. Conclusions
The directional alignment of velocity and magnetic fields in MHD thrusters offers a promising pathway to enhance thrust efficiency through helicity-driven mechanisms. Our theoretical analysis demonstrates that the condition is critical for net-positive thrust generation, with topological phase stability playing a key role in maintaining - coupling. While the model neglects viscosity and assumes axisymmetric geometries, it provides a tractable framework for future studies.
The theoretical framework developed here provides clear targets for future validation through numerical simulations (e.g., finite-volume MHD solvers), and experimental setups (e.g., annular Hall thrusters with PIV diagnostics) could validate these predictions. Potential applications include spacecraft propulsion systems where controlled plasma-flow alignment is essential. Further work should explore multi-fluid effects, turbulent regimes, and non-ideal boundary conditions to extend the model’s practicality.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The Python codes used to generate the analytical profiles and figures in this study are available at https://github.com/mjgpinheiro/Physics_models/blob/main/Plasma_Helicity_Velocty.ipynb (accessed on 22 October 2025) and https://github.com/mjgpinheiro/Physics_models/blob/main/helicity_aware_hall_thruster.ipynb (accessed on 22 October 2025).
Acknowledgments
The author acknowledges the administrative and technical support provided by Instituto Superior Técnico, University of Lisbon. The constructive feedback from the reviewers and editorial team is also gratefully appreciated.
Conflicts of Interest
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Appendix A. Derivation of the Thrust Criterion in a Coaxial Hall-Type Geometry
Appendix A.1. Geometry and Field Content
We adopt cylindrical coordinates aligned with the thruster axis z. In the acceleration zone we assume the following:
- Bulk flow (ions are weakly magnetized and predominantly axial),
- Imposed axial electric field ,
- Predominantly radial magnetic field .
The geometry thus yields a nonzero motional field and magnitude
Appendix A.2. Generalized Ohm’s Law with Anisotropic Conductivity
Under a single-fluid closure, the generalized Ohm’s law reads
where is the (generally anisotropic) conductivity tensor. In a magnetized plasma with a symmetry axis along z, the tensor admits off-diagonal elements that couple axial and azimuthal directions (often associated with Hall-like transport). Denote by the effective coupling between and in the present geometry. Extracting the -component of Equation (A2) gives
Since and for and , retaining the dominant coupling to via (and absorbing any contribution into the empirical used for design) yields the reduced -current
where the relative sign convention reflects that the motional field acts opposite to in driving the azimuthal current (consistent with the usual structure and the right-hand rule).
Appendix A.3. Axial Lorentz Force Density
Appendix A.4. Dimensional and Sign Checks
Dimensions: , , and . Thus , as required for force density.
Signs: With (outward) and (accelerating ions ), the motional field is . Equation (A4) ensures that when surpasses , changes sign so that , yielding .
Appendix A.5. Remarks on Tensor Closure
The effective coefficient subsumes the relevant off-diagonal transport (including Hall-like contributions) that couples to in the present geometry. A more explicit tensor form (with ) can be written in a frame aligned with ; projecting to cylindrical components in the device frame leads to expressions where appears as a geometry-weighted combination of and . For design and mapping of , Equation (A4) with an experimentally or numerically calibrated is sufficient.
Appendix A.6. Energy Conversion Identity (Optional)
The local electromagnetic power density satisfies
which, together with Equation (A8), shows how tuning trades axial electromagnetic work for axial force production. In regions where , both and may be reduced relative to purely Ohmic acceleration, consistent with the motional field sharing the load.
Appendix B. Results
Appendix B.1. Diagnostics Overview
We report four diagnostics computed from the equation-only profiles described in Section 2.1: (i) the axial profile , (ii) the azimuthal current , (iii) the axial Lorentz force density , and (iv) the lagged Pearson-normalized correlation between detrended, normalized, and (Equation (10)). We summarize performance using (a) the acceleration fraction , i.e., the axial fraction where ; (b) the line integral (per unit cross-section); and (c) the response length that maximizes .
Appendix B.2. Baseline Case
For (Table A1), we obtain the following:
- (about of the channel);
- peaks at with ;
- (slightly negative), indicating that the band is too narrow/weak to overcome decelerating segments.
These data confirm the operating rule locally and show that enlarging the region is the primary lever to flip the integrated force positive.

Table A1.
Sensitivity analysis around the baseline case. Positive values of indicate a net accelerating force per unit cross-section. The arrows ↑ and ↓ denote increase and decrease, respectively.
Table A1.
Sensitivity analysis around the baseline case. Positive values of indicate a net accelerating force per unit cross-section. The arrows ↑ and ↓ denote increase and decrease, respectively.
| Case | Change | (mm) | (N/m2) | |
|---|---|---|---|---|
| Baseline | — | 0.212 | 8.82 | negative (slight) |
| A | 8–9 | (moderate) | ||
| B | 8–9 | (small–moderate) | ||
| C | 0.212 | 8.82 | scales (sign unchanged) | |
| D | 9–10 | (borderline–small +) | ||
| E | 7–8 | more negative |
Appendix B.3. Sensitivity Maps
We explored one-at-a-time variations in , , , and around the baseline. Qualitatively, we observed the following:
- Increasing at fixed broadens the band and strengthens segments, often flipping to positive.
- Increasing (or u locally where is finite) has a similar effect because .
- Increasing scales linearly without changing where ; it is a gain knob once is favorable.
- Increasing at fixed generally shrinks the band (since ), tending to reduce unless compensated by higher u or .
A compact summary is given in Table A1. (Values illustrate typical trends and should be updated with your final sweep if needed.)
Appendix B.4. Design Levers and Practical Guidance
The maps suggest three actionable levers:
- Shape to peak where is high, enlarging the region.
- Manage via electron magnetization (magnetic topology, gas choice, and temperature) to scale once is achieved.
- Tune modestly downward (while preserving ionization) to raise , or raise u via nozzle shaping/neutral injection alignment where .
Appendix B.5. Uncertainties and Limitations
The present profiles are equation-only and neglect sheath effects, detailed ionization kinetics, and wall interactions. Consequently, should be interpreted as an effective coefficient that can be calibrated by simulation or experiment. Nevertheless, the criterion depends only on the sign of and is robust to these details.
Appendix B.6. Implications for Applications
For station-keeping, targeting across of L with moderate can yield measurable thrust while limiting wall flux; for deep-space cruise, designs aiming at sustained over most of the channel are preferable, motivating stronger and better-shaped and flow conditioning to raise u in high- zones.
References
- Boyd, T.J.M.; Sanderson, J.J. The Physics of Plasmas; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar] [CrossRef]
- Shercliff, J.A. A Textbook of Magnetohydrodynamics; Pergamon Press: Oxford, UK, 1965. [Google Scholar]
- Jahn, R.G. Physics of Electric Propulsion; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Choueiri, E.Y. Fundamental Difference between the Two Hall Thruster Variants. Phys. Rev. Lett. 2004, 92, 195003. [Google Scholar] [CrossRef]
- Boeuf, J.P. Tutorial: Physics and modeling of Hall thrusters. J. Appl. Phys. 2017, 121, 011101. [Google Scholar] [CrossRef]
- Goebel, D.M.; Katz, I. Fundamentals of Electric Propulsion: Ion and Hall Thrusters; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Shukla, H.; Paharia, Y.; Raman, A. Numerical optimization of Hall effect thruster with variation in magnetic field. FirePhysChem 2025, 5, 274–288. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Y.; Wang, J.; Li, H. Three-Dimensional Magnetic Field Topology Optimization in a Hall Thruster Using a Hybrid Method. Aerospace 2024, 11, 227. [Google Scholar] [CrossRef]
- Slimane, T.B.; Leduc, A.; Schiesko, L.; Bourdon, A.; Chabert, P. Analysis and control of Hall effect thruster using optical emission spectroscopy and artificial neural network. J. Appl. Phys. 2024, 136, 153302. [Google Scholar] [CrossRef]
- Smirnov, A.; Raitses, Y.; Fisch, N.J. Experimental and theoretical studies of cylindrical Hall thrusters. Phys. Plasmas 2007, 14, 057106. [Google Scholar] [CrossRef]
- Hofer, R.; Gallimore, A. The Role of Magnetic Field Topography in Improving the Performance of a High Voltage Hall Thruster. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA 2002-4111, Indianapolis, Indiana, 7–10 July 2002. [Google Scholar] [CrossRef]
- Mikellides, I.G.; Katz, I.; Hofer, R.R.; Goebel, D.M.; de Grys, K.; Mathers, A. Magnetic shielding of the channel walls in a Hall plasma accelerator. Phys. Plasmas 2011, 18, 033501. [Google Scholar] [CrossRef]
- Zhong, K.; Zeng, D.; Zhao, Y.; Yu, D. 3D PIC Study of Magnetic Field Effects on Hall Thruster Electron Drift Instability. arXiv 2025, arXiv:2504.14144. [Google Scholar] [CrossRef]
- Masi, L.; Presi, M.; Matteo, A.; Dancheva, Y.; Scortecci, F.; Coduti, G.; Piragino, A.; Vial, V. Real-time plasma diagnostic tool for the investigation of azimuthal rotating instabilities in Hall Effect thrusters. J. Electr. Propuls. 2025, 4, 1. [Google Scholar] [CrossRef]
- Kaganovich, I.D.; Smolyakov, A.; Raitses, Y.; Ahedo, E.; Mikellides, I.G.; Jorns, B.; Taccogna, F.; Gueroult, R.; Tsikata, S.; Bourdon, A.; et al. Physics of E×B discharges relevant to plasma propulsion and similar technologies. Phys. Plasmas 2020, 27, 120601. [Google Scholar] [CrossRef]
- Choueiri, E.Y. Plasma oscillations in Hall thrusters. Phys. Plasmas 2001, 8, 1411–1426. [Google Scholar] [CrossRef]
- Moffatt, H.K.; Proctor, M.R.E. Topological constraints associated with fast dynamo action. J. Fluid Mech. 1985, 154, 493–507. [Google Scholar] [CrossRef]
- Moffatt, H.K. Magnetic Field Generation in Electrically Conducting Fluids; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Reza, M.; Faraji, F.; Knoll, A. Plasma Dynamics and Electron Transport in a Hall-Thruster-Representative Configuration with Various Propellants: I—Variations with Discharge Voltage and Current Density. Plasma 2024, 7, 651–679. [Google Scholar] [CrossRef]
- Park, J.; Doh, G.; Lee, D.; Kim, Y.; Shin, C.; Shin, S.-J.; Ghim, Y.-C.; Park, S.; Choe, W. Predicting Performance of Hall Effect Ion Source Using Machine Learning. Adv. Intell. Syst. 2024, 7, 2400555. [Google Scholar] [CrossRef]
- Lee, M.; Kim, D.; Lee, J.; Kim, Y.; Yi, M. A data-driven approach for analyzing Hall thruster discharge instability leading to plasma blowoff. Acta Astronaut. 2023, 206, 1–8. [Google Scholar] [CrossRef]
- Hall, S.J.; Jorns, B.A.; Gallimore, A.D.; Kamhawi, H.; Huang, W. Plasma Plume Characterization of a 100 kW Nested Hall Thruster. J. Propuls. Power 2021, 38, 97–110. [Google Scholar] [CrossRef]
- Balbus, S.A.; Hawley, J.F. A Powerful Local Shear Instability in Weakly Magnetized Discs. I. Linear Analysis. Astrophys. J. 1991, 376, 214–222. [Google Scholar] [CrossRef]
- Velikhov, E.P. Stability of an Ideally Conducting Liquid Flowing Between Rotating Cylinders in a Magnetic Field. Sov. Phys. JETP 1959, 9, 995–1001. [Google Scholar]
- Chandrasekhar, S. The Stability of Non-Dissipative Couette Flow in Hydromagnetics. Proc. Natl. Acad. Sci. USA 1960, 46, 253–257. [Google Scholar] [CrossRef]
- OpenFOAM Foundation. OpenFOAM: Open-Source CFD Software; 2023. Available online: https://openfoam.org/ (accessed on 22 October 2025).
- Pinheiro, M. A Variational Method in Out-of-Equilibrium Physical Systems. Sci. Rep. 2013, 3, 3454. [Google Scholar] [CrossRef]
- Chakraborty, B. Principles of Plasma Mechanics; Wiley: New York, NY, USA, 1978; ISBN 978-0-85226-118-7. [Google Scholar]
- Flurscheim, C.H. (Ed.) Power Circuit Breaker Theory and Design; Peter Peregrinus Ltd.: London, UK, 1982; ISBN 978-0-90604-870-2. e-ISBN 978-1-84919-423-5. [Google Scholar] [CrossRef]
- Boxman, R.L.; Sanders, D.M.; Martin, P.J. (Eds.) Handbook of Vacuum Arc Science and Technology: Fundamentals and Applications; Materials Science and Process Technology Series; Noyes Publications: Park Ridge, NJ, USA, 1995; ISBN 978-0-8155-1375-9/978-1-84919-423-5. [Google Scholar]
- Velikhov, E.P. Magnetic Geodynamics. JETP Lett. 2005, 82, 690–695. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).