State-of-Charge-Dependent Anisotropic Lithium Diffusion and Stress Development in Ni-Rich NMC Cathodes: A Multiscale Simulation Study
Abstract
1. Introduction
2. Methods
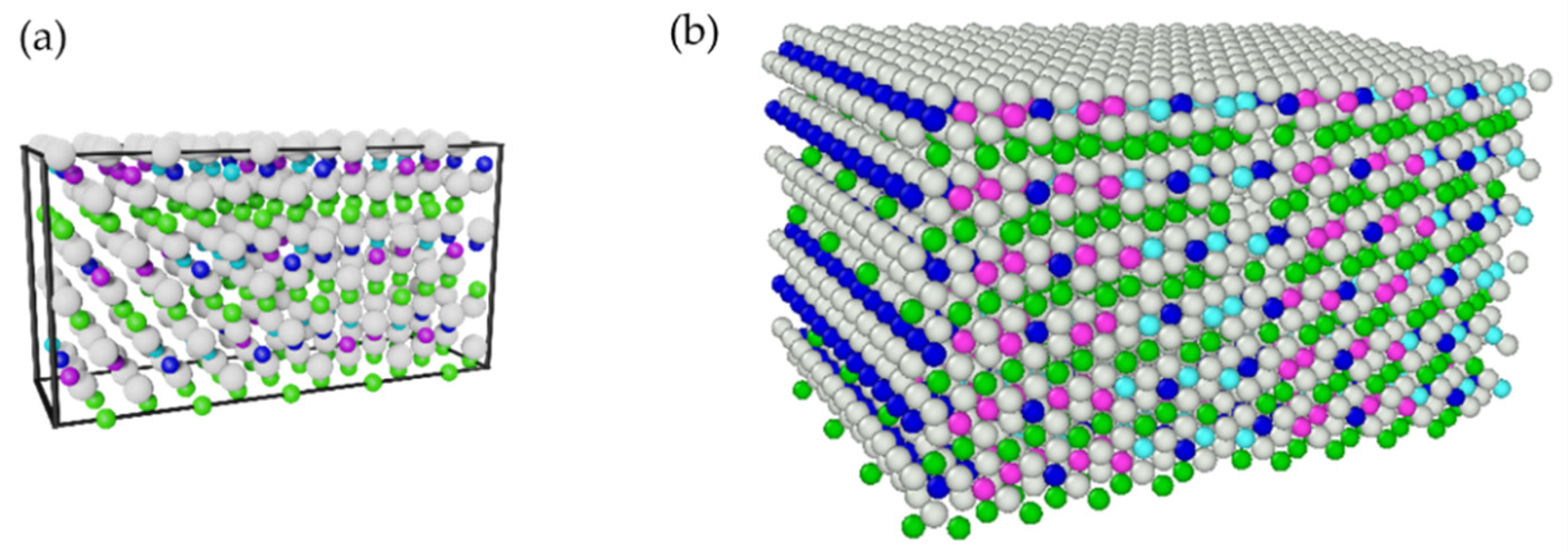
2.1. Molecular Dynamics Simulations
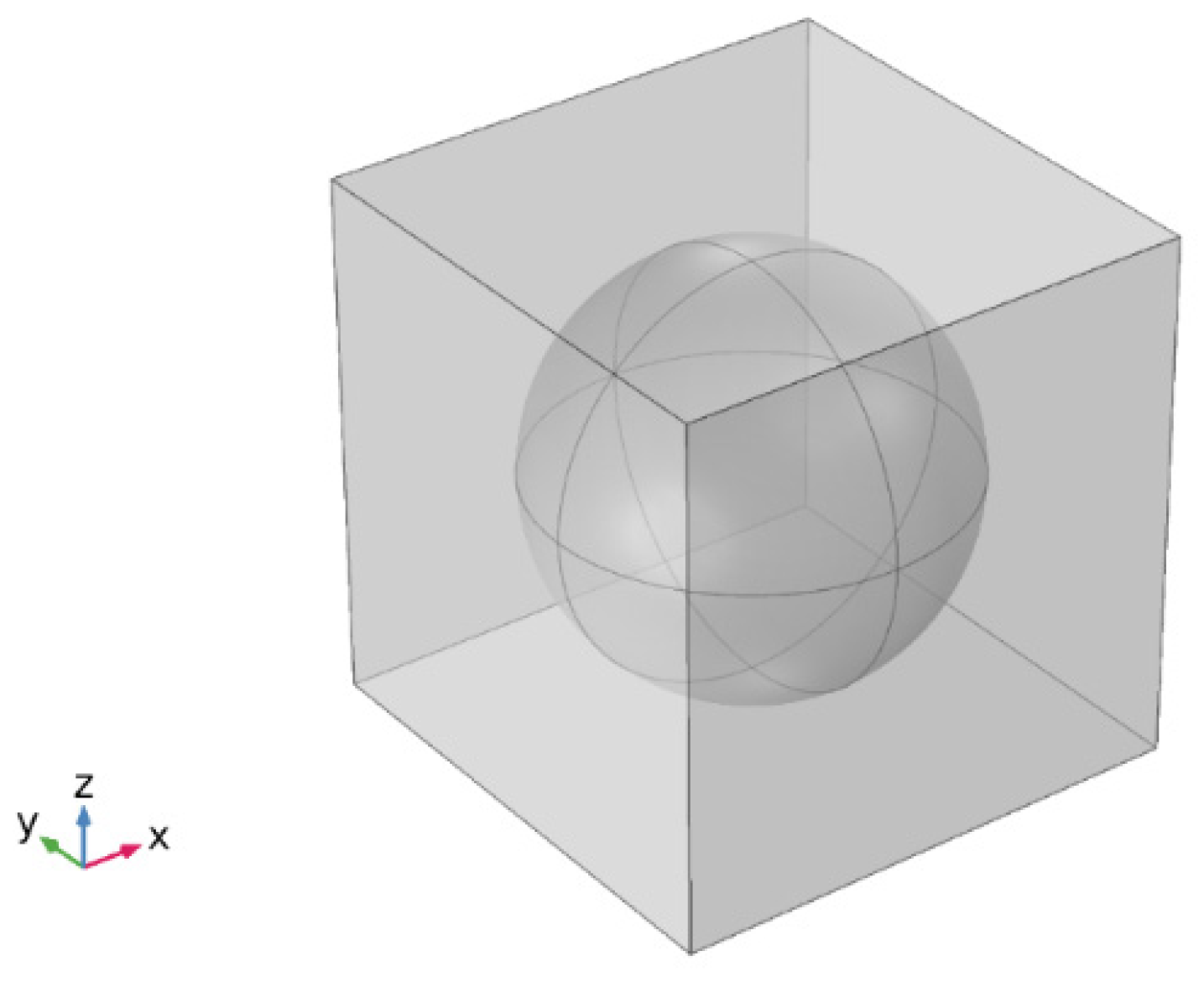
2.2. Continuum Simulations
3. Results
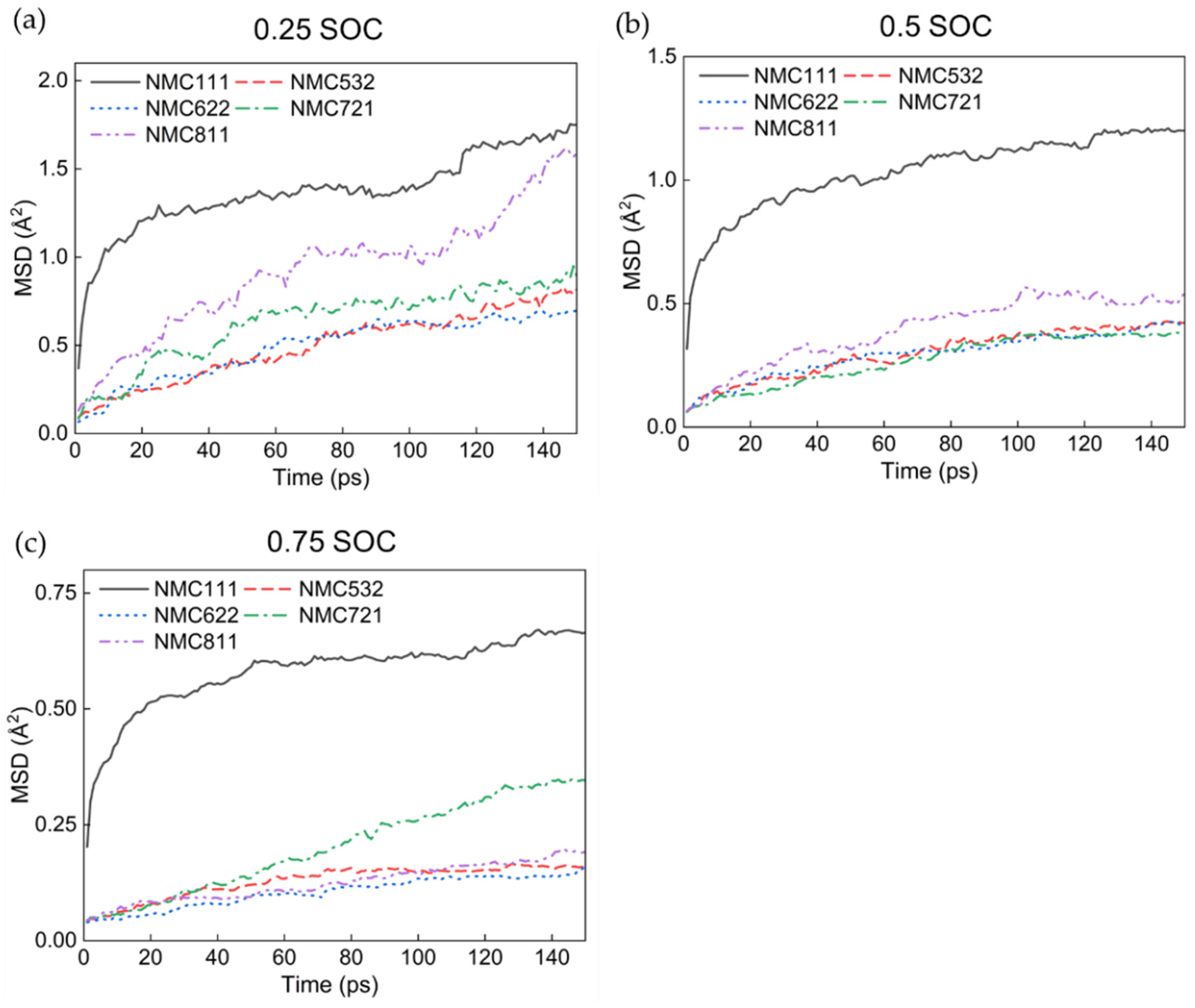
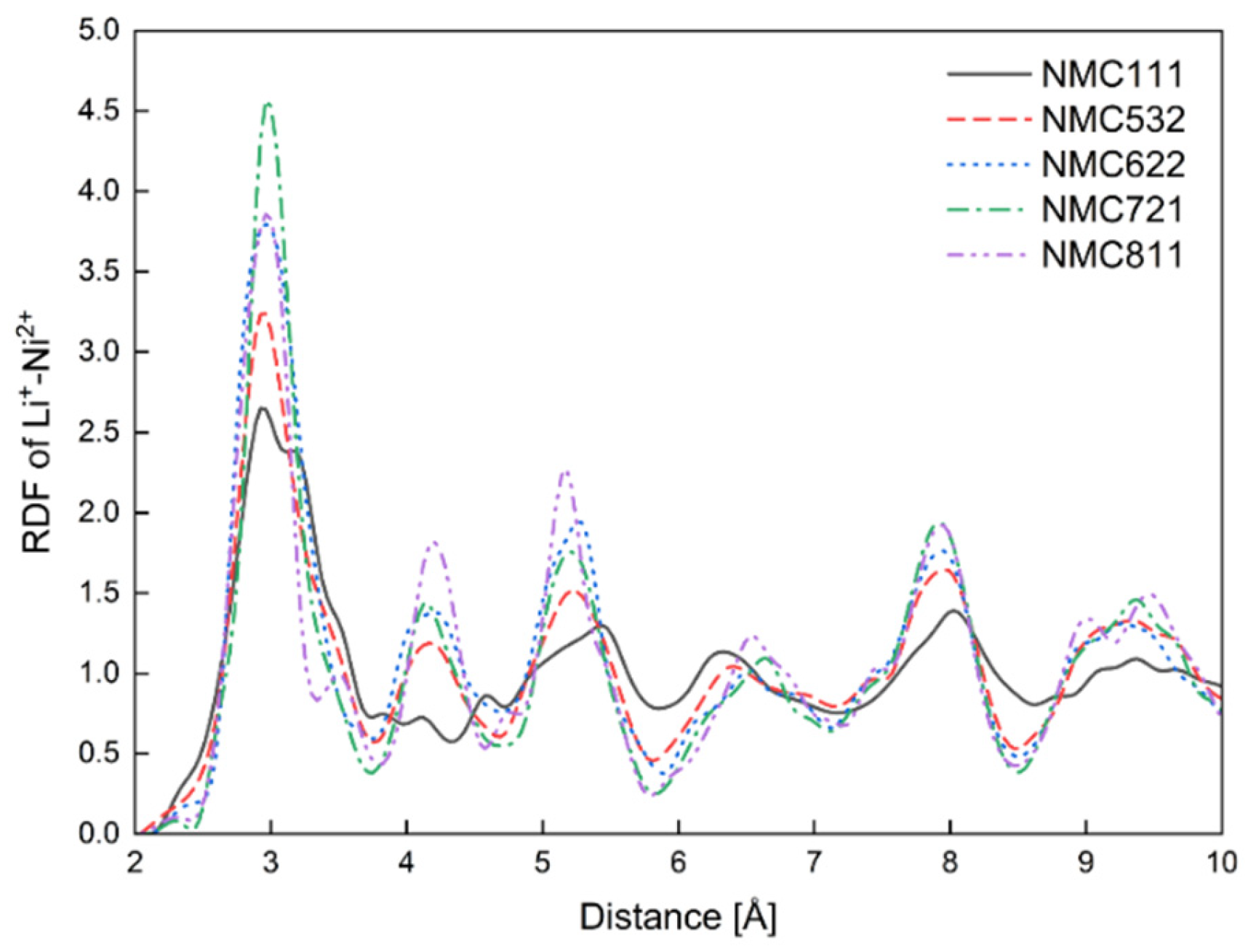
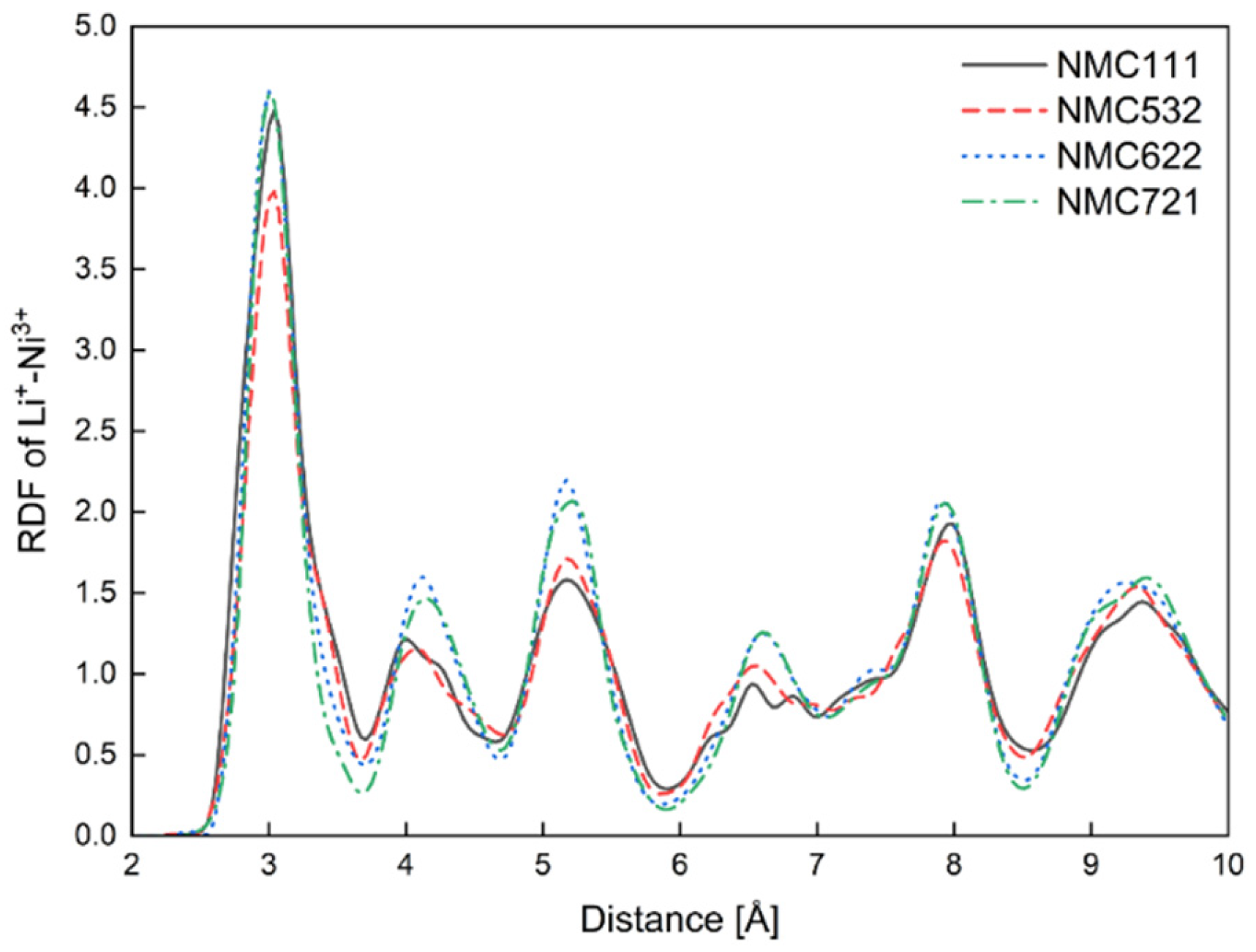
3.1. MD Calculations
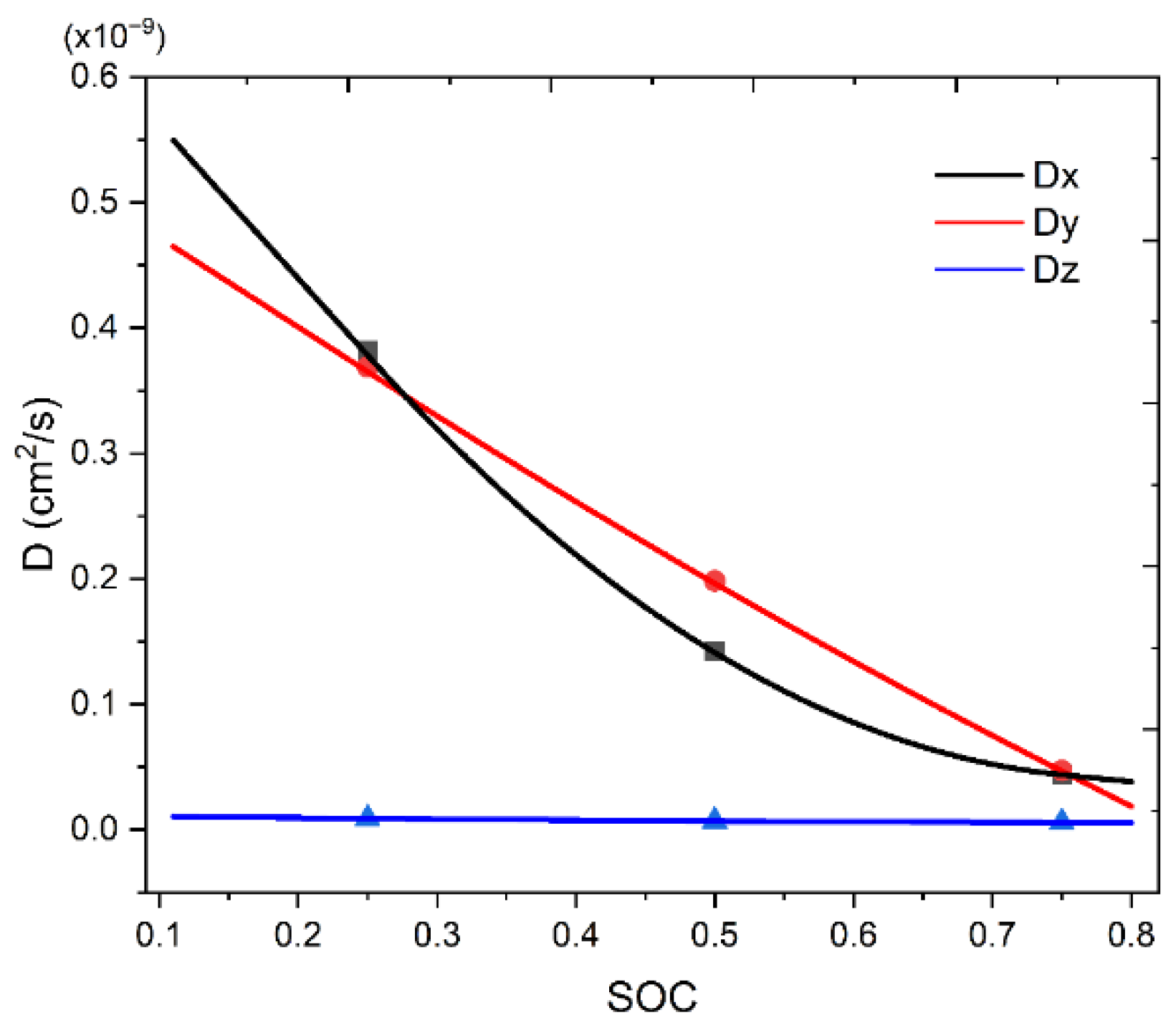
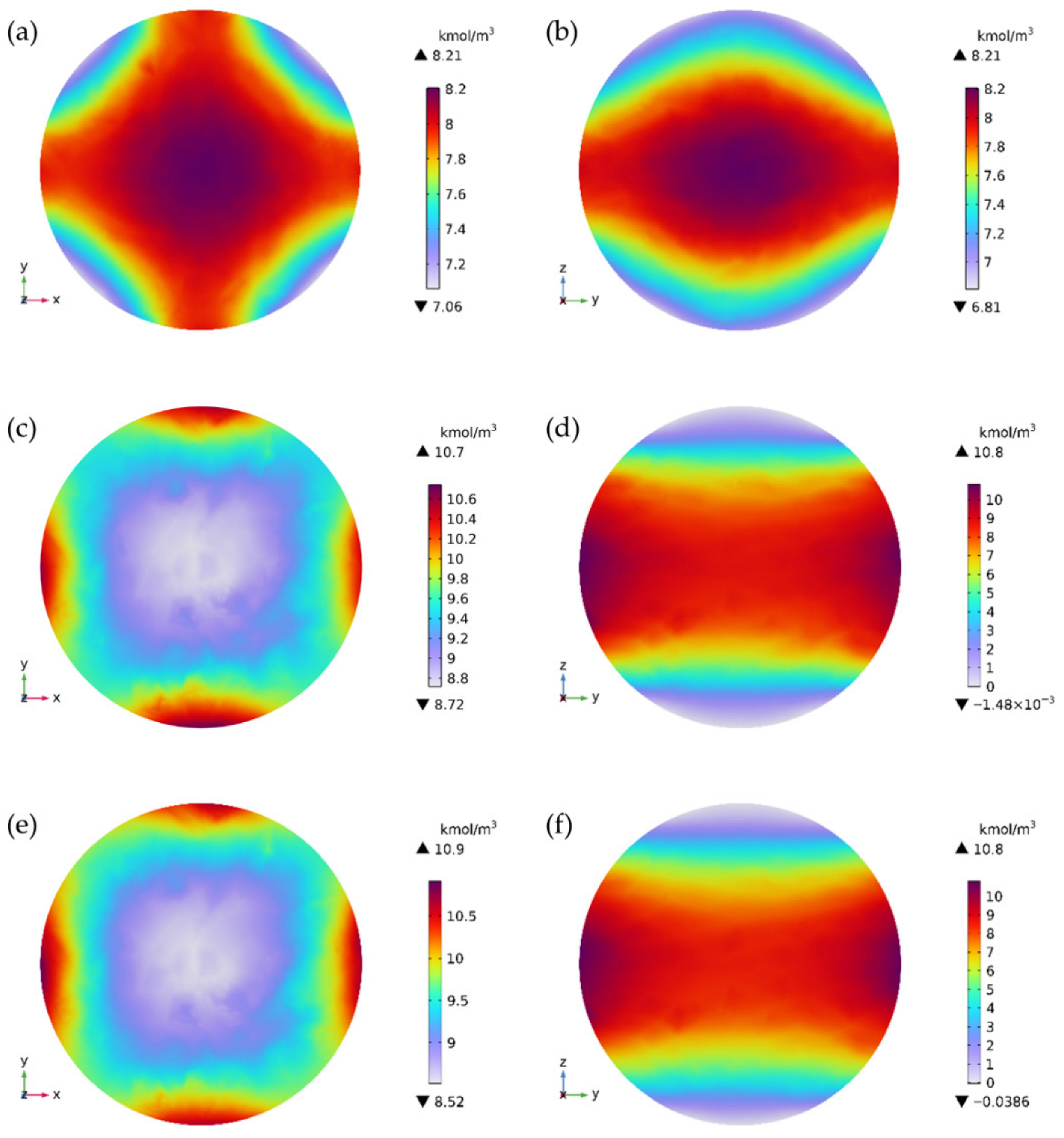
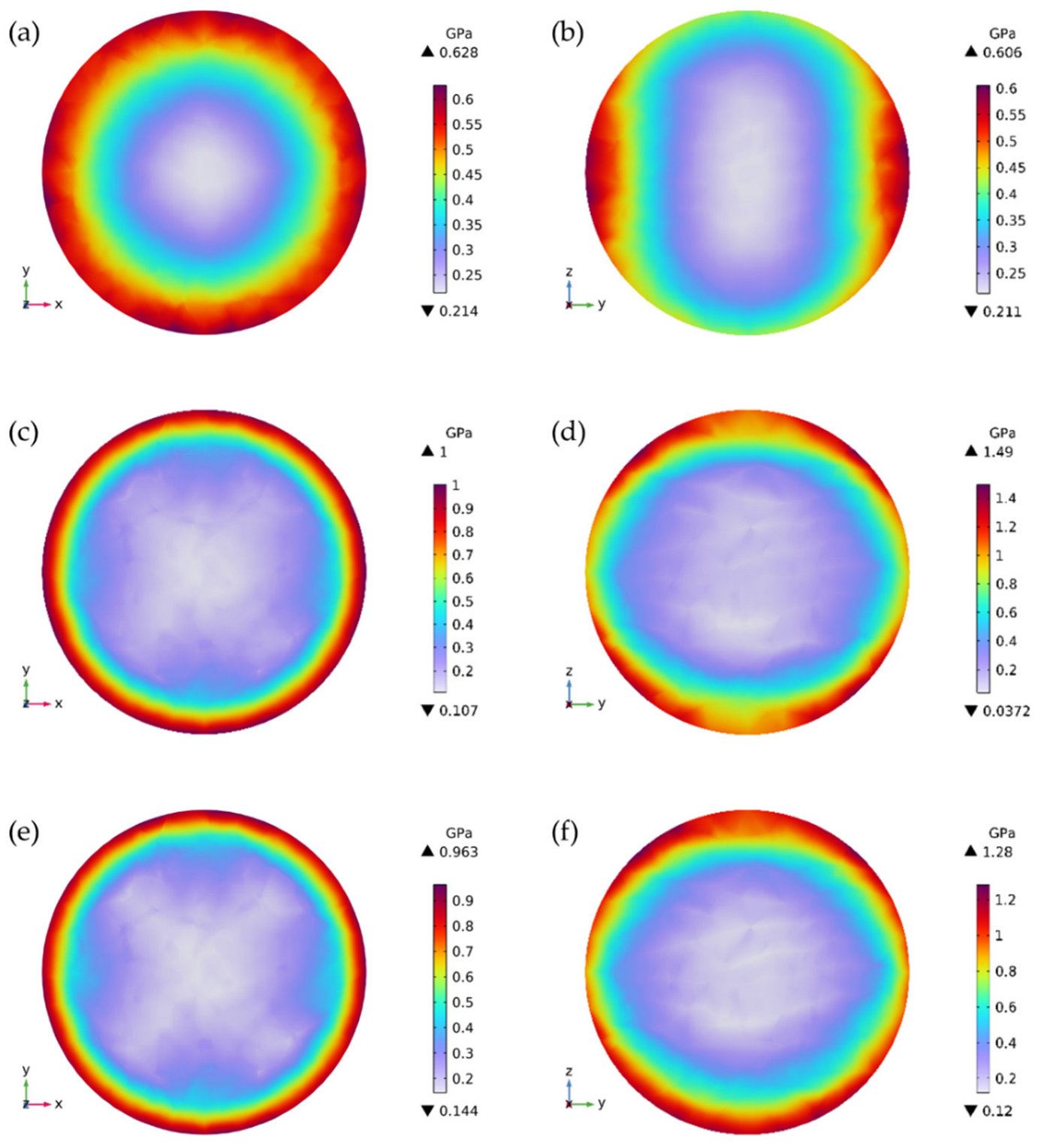
3.2. Stress Development from SOC-Dependent Anisotropic Diffusion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farhan, M.; Naeem, R.; Shoaib, H.M.; Irshad, A.; Ismail, M.; Rabia, R.; Ramzan, R.; Hamza, M.; Munir, F. Comprehensive Review of Emerging Lithium and Sodium-Ion Electrochemical Systems for Advanced Energy Storage Applications. Sch. J. Phys. Math. Stat. 2025, 12, 188–198. [Google Scholar] [CrossRef]
- Wang, Z.; Luo, H.; Liu, H.; Wu, F.; Zhang, C.; Wang, Z.; Yu, P. Electrochemical Performance and Structural Stability of Layered Li–Ni–Co–Mn Oxide Cathode Materials in Different Voltage Ranges. Ceram. Int. 2021, 47, 8490–8497. [Google Scholar] [CrossRef]
- Guo, D.; Shi, Z.; El-Demellawi, J.K.; Wahyudi, W.; Arsalan, M.; Zhang, H.; Alshareef, H.N. Lithium Metal Batteries for High Temperature Environments. Adv. Energy Mater. 2025, e02943. [Google Scholar] [CrossRef]
- Morgan, L.M.; Islam, M.M.; Yang, H.; O’Regan, K.; Patel, A.N.; Ghosh, A.; Kendrick, E.; Marinescu, M.; Offer, G.J.; Morgan, B.J.; et al. From Atoms to Cells: Multiscale Modeling of LiNixMnyCozO2 Cathodes for Li-Ion Batteries. ACS Energy Lett. 2022, 7, 108–122. [Google Scholar] [CrossRef]
- Chakraborty, A.; Kunnikuruvan, S.; Kumar, S.; Markovsky, B.; Aurbach, D.; Dixit, M.; Major, D.T. Layered Cathode Materials for Lithium-Ion Batteries: Review of Computational Studies on LiNi1−x−yCoxMnyO2 and LiNi1−x−yCoxAlyO2. Chem. Mater. 2020, 32, 915–952. [Google Scholar] [CrossRef]
- Ryu, H.-H.; Namkoong, B.; Kim, J.-H.; Belharouak, I.; Yoon, C.S.; Sun, Y.-K. Capacity Fading Mechanisms in Ni-Rich Single-Crystal NCM Cathodes. ACS Energy Lett. 2021, 6, 2726–2734. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, Y.; Chen, H.; Luan, W. The Diffusion Induced Stress and Cracking Behaviour of Primary Particle for Li-Ion Battery Electrode. Int. J. Mech. Sci. 2020, 178, 105608. [Google Scholar] [CrossRef]
- Phillip, N.D.; Westover, A.S.; Daniel, C.; Veith, G.M. Structural Degradation of High Voltage Lithium Nickel Manganese Cobalt Oxide (NMC) Cathodes in Solid-State Batteries and Implications for Next Generation Energy Storage. ACS Appl. Energy Mater. 2020, 3, 1768–1774. [Google Scholar] [CrossRef]
- Daubner, S.; Weichel, M.; Hoffrogge, P.W.; Schneider, D.; Nestler, B. Modeling Anisotropic Transport in Polycrystalline Battery Materials. Batteries 2023, 9, 310. [Google Scholar] [CrossRef]
- Mao, K.; Yao, Y.; Chen, Y.; Li, W.; Shen, X.; Song, J.; Chen, H.; Luan, W.; Wu, K. Fracture Mechanisms of NCM Polycrystalline Particles in Lithium-Ion Batteries: A Review. J. Energy Storage 2024, 84, 110807. [Google Scholar] [CrossRef]
- Morzy, J.K.; Dose, W.M.; Vullum, P.E.; Lai, M.C.; Mahadevegowda, A.; De Volder, M.F.L.; Ducati, C. Origins and Importance of Intragranular Cracking in Layered Lithium Transition Metal Oxide Cathodes. ACS Appl. Energy Mater. 2024, 7, 3945–3956. [Google Scholar] [CrossRef]
- Roque, E.; Segurado, J.; Montero-Chacón, F. Phase-Field Modeling and Computational Design of Structurally Stable NMC Materials. Mater. Des. 2024, 248, 113464. [Google Scholar] [CrossRef]
- Chen, W.-X.; Allen, J.M.; Rezaei, S.; Furat, O.; Schmidt, V.; Singh, A.; Weddle, P.J.; Smith, K.; Xu, B.-X. Cohesive Phase-Field Chemo-Mechanical Simulations of Inter- and Trans- Granular Fractures in Polycrystalline NMC Cathodes via Image-Based 3D Reconstruction. J. Power Sources 2024, 596, 234054. [Google Scholar] [CrossRef]
- Iqbal, N.; Lee, S. Anisotropic Model to Describe Chemo-Mechanical Response of Ni-Rich Cathode Materials. Int. J. Mech. Sci. 2024, 269, 109034. [Google Scholar] [CrossRef]
- de Klerk, N.J.J.; van der Maas, E.; Wagemaker, M. Analysis of Diffusion in Solid-State Electrolytes through MD Simulations, Improvement of the Li-Ion Conductivity in β-Li3PS4 as an Example. ACS Appl. Energy Mater. 2018, 1, 3230–3242. [Google Scholar] [CrossRef] [PubMed]
- Haq, I.U.; Lee, S. Unveiling State-of-Charge Effects on Elastic Properties of LiCoO2 via Deep Learning and Empirical Models. Appl. Sci. 2025, 15, 7809. [Google Scholar] [CrossRef]
- Chandel, S.; Garapati, V.K.; Dingari, N.N.; Mynam, M.; Rai, B. Multiscale Molecular Dynamics and Electrochemical Modelling of Sodium-Ion Batteries: Impact of Electrolyte Composition. J. Energy Storage 2025, 123, 116749. [Google Scholar] [CrossRef]
- Mabrouk, Y.; Safaei, N.; Hanke, F.; Carlsson, J.M.; Diddens, D.; Heuer, A. Reactive Molecular Dynamics Simulations of Lithium-Ion Battery Electrolyte Degradation. Sci. Rep. 2024, 14, 10281. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, L.; Gao, M. Molecular Dynamics Study on the Li Diffusion Mechanism and Delithiation Process of Li2MnO3. Solid State Ion. 2020, 346, 115195. [Google Scholar] [CrossRef]
- Fallahzadeh, R.; Farhadian, N. Molecular Dynamics Simulation of Lithium Ion Diffusion in LiCoO2 Cathode Material. Solid State Ion. 2015, 280, 10–17. [Google Scholar] [CrossRef]
- Zhou, Z.; Cazorla, C.; Gao, B.; Luong, H.D.; Momma, T.; Tateyama, Y. First-Principles Study on the Interplay of Strain and State-of-Charge with Li-Ion Diffusion in the Battery Cathode Material LiCoO2. ACS Appl. Mater. Interfaces 2023, 15, 53614–53622. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Tao, G. Molecular Dynamics Simulations on Lithium Diffusion in LiFePO4: The Effect of Anti-Site Defects. J. Mater. Chem. A 2015, 3, 20399–20407. [Google Scholar] [CrossRef]
- Lee, E.; Lee, K.-R.; Lee, B.-J. Interatomic Potential of Li–Mn–O and Molecular Dynamics Simulations on Li Diffusion in Spinel Li1–xMn2O4. J. Phys. Chem. C 2017, 121, 13008–13017. [Google Scholar] [CrossRef]
- Ji, J.; Lee, B.-J. Analyzing the Effect of Li/Ni Intermixing on Ni-Rich Layered Cathode Structures Using Atomistic Simulation of the Li–Ni–Mn–Co–O Quinary System. J. Power Sources 2023, 556, 232535. [Google Scholar] [CrossRef]
- Lee, S.; Park, S.S. Atomistic Simulation Study of Mixed-Metal Oxide (LiNi1/3Co1/3Mn1/3O2) Cathode Material for Lithium Ion Battery. J. Phys. Chem. C 2012, 116, 6484–6489. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, Y.; Du, R.; Tang, M.; Wang, B.; Zhang, J. Effect of Ni2+ on Lithium-Ion Diffusion in Layered LiNi1−x−yMnxCoyO2 Materials. Crystals 2021, 11, 465. [Google Scholar] [CrossRef]
- Mirzanejad, A.; Varganov, S. Derivation of Morse Potential Function. ChemRxiv 2023. [Google Scholar] [CrossRef]
- Haq, I.U.; Lee, S. Molecular Dynamics Study of the Ni Content-Dependent Mechanical Properties of NMC Cathode Materials. Crystals 2025, 15, 272. [Google Scholar] [CrossRef]
- Saaid, F.I.; Kasim, M.F.; Winie, T.; Elong, K.A.; Azahidi, A.; Basri, N.D.; Yaakob, M.K.; Mastuli, M.S.; Amira Shaffee, S.N.; Zolkiffly, M.Z.; et al. Ni-Rich Lithium Nickel Manganese Cobalt Oxide Cathode Materials: A Review on the Synthesis Methods and Their Electrochemical Performances. Heliyon 2023, 10, e23968. [Google Scholar] [CrossRef]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A Flexible Simulation Tool for Particle-Based Materials Modeling at the Atomic, Meso, and Continuum Scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Baktash, A.; Reid, J.C.; Roman, T.; Searles, D.J. Diffusion of Lithium Ions in Lithium-Argyrodite Solid-State Electrolytes. npj Comput. Mater. 2020, 6, 162. [Google Scholar] [CrossRef]
- Ul Hassan, H.; Choi, J.; Shah, S.F.; Lee, S. Unraveling Stress Mechanisms in Ni-Rich NMC Particles: The Dominance of Anisotropic Deformation over Diffusion. J. Power Sources 2025, 656, 238136. [Google Scholar] [CrossRef]
- Belharouak, I.; Sun, Y.-K.; Liu, J.; Amine, K. Li(Ni1/3Co1/3Mn1/3)O2 as a Suitable Cathode for High Power Applications. J. Power Sources 2003, 123, 247–252. [Google Scholar] [CrossRef]
- Bie, X.; Du, F.; Wang, Y.; Zhu, K.; Ehrenberg, H.; Nikolowski, K.; Wang, C.; Chen, G.; Wei, Y. Relationships between the Crystal/Interfacial Properties and Electrochemical Performance of LiNi0.33Co0.33Mn0.33O2 in the Voltage Window of 2.5–4.6V. Electrochim. Acta 2013, 97, 357–363. [Google Scholar] [CrossRef]
- Ishidzu, K.; Oka, Y.; Nakamura, T. Lattice Volume Change during Charge/Discharge Reaction and Cycle Performance of Li[NixCoyMnz]O2. Solid State Ion. 2016, 288, 176–179. [Google Scholar] [CrossRef]
- Sun, H.; Zhao, K. Electronic Structure and Comparative Properties of LiNixMnyCozO2 Cathode Materials. J. Phys. Chem. C 2017, 121, 6002–6010. [Google Scholar] [CrossRef]
- Dahbi, M.; Saadoune, I.; Amarilla, J.M. LixNi0.7Co0.3O2 Electrode Material: Structural, Physical and Electrochemical Investigations. Electrochim. Acta 2008, 53, 5266–5271. [Google Scholar] [CrossRef]
- Kondrakov, A.O.; Schmidt, A.; Xu, J.; Geßwein, H.; Mönig, R.; Hartmann, P.; Sommer, H.; Brezesinski, T.; Janek, J. Anisotropic Lattice Strain and Mechanical Degradation of High- and Low-Nickel NCM Cathode Materials for Li-Ion Batteries. J. Phys. Chem. C 2017, 121, 3286–3294. [Google Scholar] [CrossRef]
- Wei, Y.; Zheng, J.; Cui, S.; Song, X.; Su, Y.; Deng, W.; Wu, Z.; Wang, X.; Wang, W.; Rao, M.; et al. Kinetics Tuning of Li-Ion Diffusion in Layered Li(NixMnyCoz)O2. J. Am. Chem. Soc. 2015, 137, 8364–8367. [Google Scholar] [CrossRef]
- Lee, E.; Lee, K.-R.; Lee, B.-J. An Interatomic Potential for the Li-Co-O Ternary System. Comput. Mater. Sci. 2018, 142, 47–58. [Google Scholar] [CrossRef]
- Li, J.; Liang, G.; Zheng, W.; Zhang, S.; Davey, K.; Pang, W.K.; Guo, Z. Addressing Cation Mixing in Layered Structured Cathodes for Lithium-Ion Batteries: A Critical Review. Nano Mater. Sci. 2023, 5, 404–420. [Google Scholar] [CrossRef]

| Interaction Pair | D0 (eV) | r0 (Å) | α (Å−1) |
|---|---|---|---|
| Li+–O2− | 0.001114 | 2.681360 | 3.429506 |
| Ni2+–O2− | 0.029356 | 2.500754 | 2.679137 |
| Ni3+–O2− | 0.029356 | 2.500754 | 2.679137 |
| Mn4+–O2− | 0.029658 | 2.440000 | 3.012000 |
| Co3+–O2− | 0.010958 | 2.400628 | 3.461272 |
| O2−–O2− | 0.042395 | 3.358701 | 1.659316 |
| Composition (NMCxyz) | Ni2+ | Ni3+ | Mn4+ | Co3+ |
|---|---|---|---|---|
| NMC111 | 0.33 | 0.00 | 0.33 | 0.33 |
| NMC532 | 0.30 | 0.20 | 0.30 | 0.20 |
| NMC622 | 0.20 | 0.40 | 0.20 | 0.20 |
| NMC721 | 0.20 | 0.50 | 0.20 | 0.10 |
| NMC811 | 0.10 | 0.70 | 0.10 | 0.10 |
| Parameters | Symbol | Units | Values |
|---|---|---|---|
| Universal gas constant | R | Jmol−1K−1 | 8.3145 |
| Absolute temperature | T | K | 300 |
| Partial molar strain in x direction | η1 | - | 0.019029 |
| Partial molar strain in y direction | η2 | - | 0.019029 |
| Partial molar strain in z direction | η3 | - | 0.045407 |
| Young’s modulus | E | GPa | 194.4 |
| Maximum lithium concentration | cmax | molm−3 | 37,825 |
| Poisson’s ratio | - | 0.25 | |
| Density | kgm−3 | 4750 |
| Composition (NMCxyz) | Simulation Result (Å) | Reference Result (Å) | |||
|---|---|---|---|---|---|
| x-Axis | z-Axis | x-Axis | z-Axis | [Ref] | |
| NMC111 | 2.955 | 14.703 | 2.862 | 14.238 | [33] |
| 2.865 | 14.249 | [34] | |||
| 2.865 | 14.250 | [35] | |||
| 2.868 | 14.213 | [25] | |||
| 2.813 | 14.420 | [36] | |||
| NMC532 | 2.951 | 14.685 | 2.925 | 14.420 | [36] |
| NMC622 | 2.936 | 14.610 | 2.910 | 14.390 | [36] |
| NMC721 | 2.942 | 14.638 | 2.857 | 14.158 | [37] |
| NMC811 | 2.932 | 14.590 | 2.830 | 14.300 | [38] |
| Axis | Composition (NMCxyz) | SOC | ||
|---|---|---|---|---|
| 0.25 | 0.5 | 0.75 | ||
| x | NMC111 | 0.23193 | 0.16178 | 0.07625 |
| NMC532 | 0.22500 | 0.11000 | 0.03500 | |
| NMC622 | 0.18750 | 0.09638 | 0.03664 | |
| NMC721 | 0.22154 | 0.11052 | 0.11126 | |
| NMC811 | 0.38202 | 0.14268 | 0.04433 | |
| y | NMC111 | 0.27028 | 0.15097 | 0.08978 |
| NMC532 | 0.28785 | 0.08932 | 0.06946 | |
| NMC622 | 0.27841 | 0.08889 | 0.04816 | |
| NMC721 | 0.31358 | 0.09236 | 0.10592 | |
| NMC811 | 0.36881 | 0.19839 | 0.04718 | |
| z | NMC111 | 0.10928 | 0.06187 | 0.01524 |
| NMC532 | 0.07844 | 0.01121 | 0.00782 | |
| NMC622 | 0.05887 | 0.00497 | 0.00665 | |
| NMC721 | 0.00295 | 0.01306 | 0.01054 | |
| NMC811 | 0.00914 | 0.00706 | 0.00585 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haq, I.U.; Hassan, H.U.; Lee, S. State-of-Charge-Dependent Anisotropic Lithium Diffusion and Stress Development in Ni-Rich NMC Cathodes: A Multiscale Simulation Study. Appl. Sci. 2025, 15, 11566. https://doi.org/10.3390/app152111566
Haq IU, Hassan HU, Lee S. State-of-Charge-Dependent Anisotropic Lithium Diffusion and Stress Development in Ni-Rich NMC Cathodes: A Multiscale Simulation Study. Applied Sciences. 2025; 15(21):11566. https://doi.org/10.3390/app152111566
Chicago/Turabian StyleHaq, Ijaz Ul, Haseeb Ul Hassan, and Seungjun Lee. 2025. "State-of-Charge-Dependent Anisotropic Lithium Diffusion and Stress Development in Ni-Rich NMC Cathodes: A Multiscale Simulation Study" Applied Sciences 15, no. 21: 11566. https://doi.org/10.3390/app152111566
APA StyleHaq, I. U., Hassan, H. U., & Lee, S. (2025). State-of-Charge-Dependent Anisotropic Lithium Diffusion and Stress Development in Ni-Rich NMC Cathodes: A Multiscale Simulation Study. Applied Sciences, 15(21), 11566. https://doi.org/10.3390/app152111566






